Architectural Knitted Windbreaks for Improved Wind Comfort in the City: A Wind Tunnel Study of Custom-Designed Porous Textile Screens
Abstract
:1. Introduction
1.1. Textiles in Architecture
1.2. Existing Design Guidelines for Windbreaks
1.3. Windbreak Performance Evaluation Methods
1.4. Objectives
2. Materials and Methods
2.1. Knitted Textiles
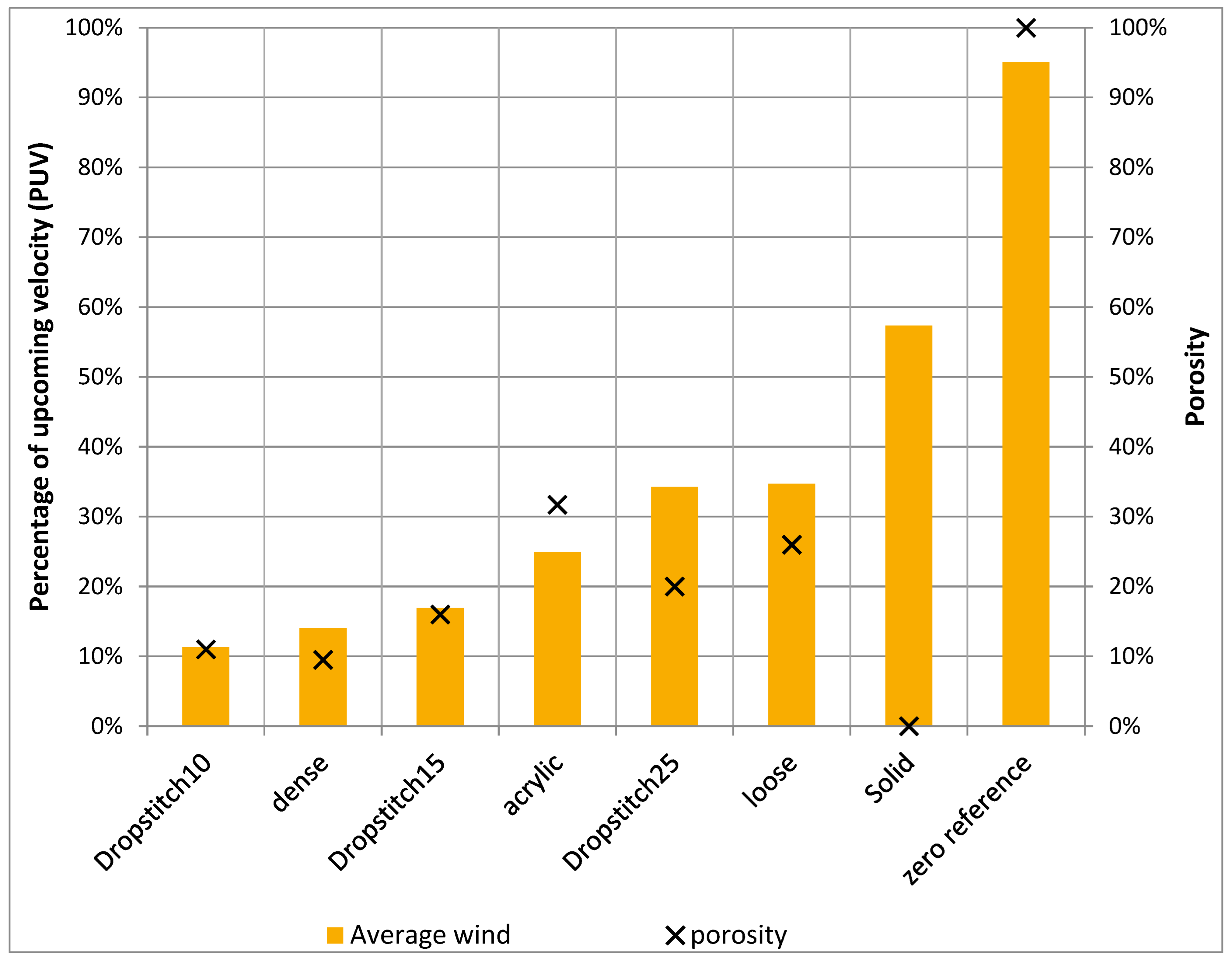
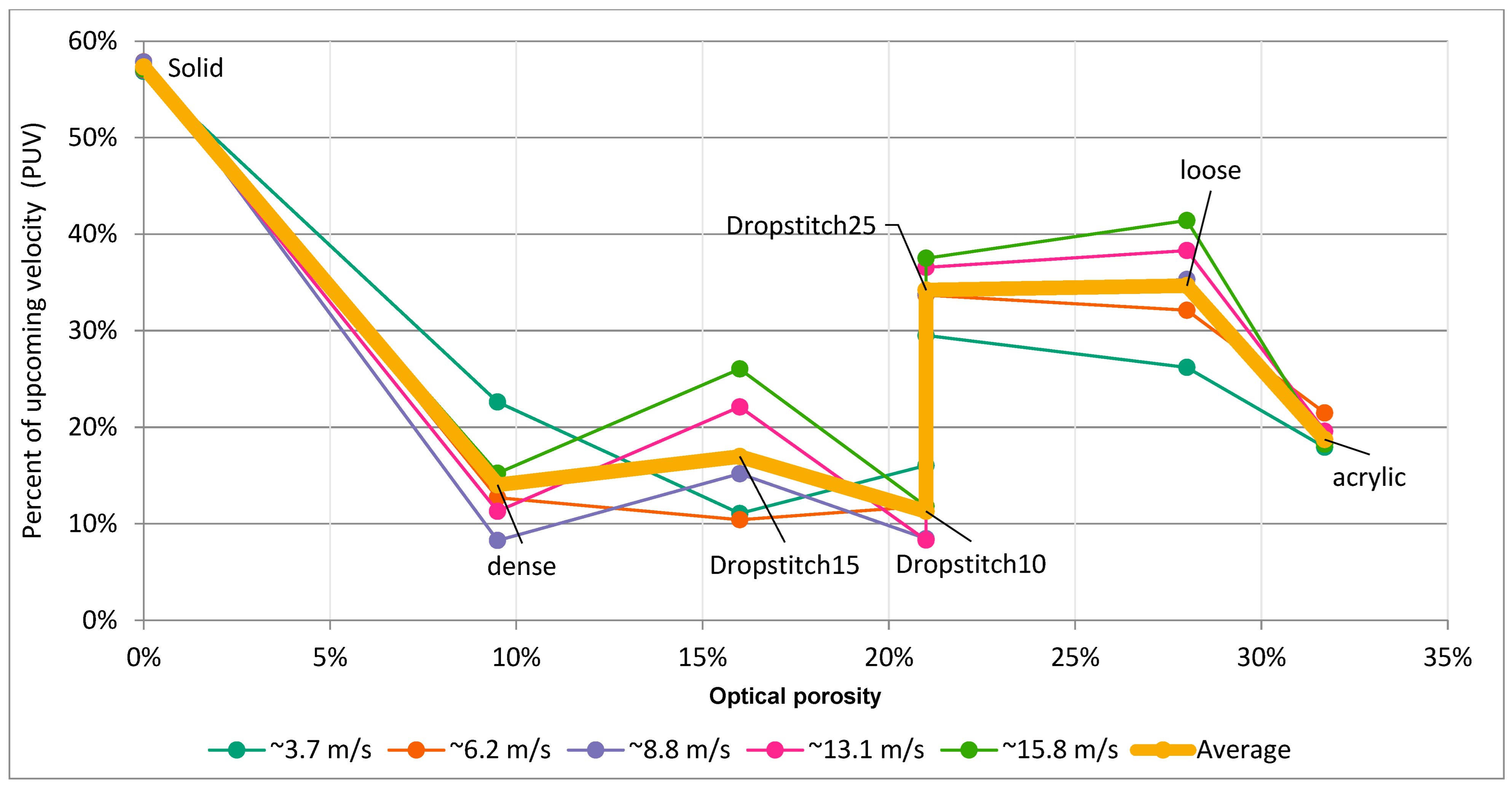
2.2. Calculating the Porosity
2.3. Wind Tunnel Setup
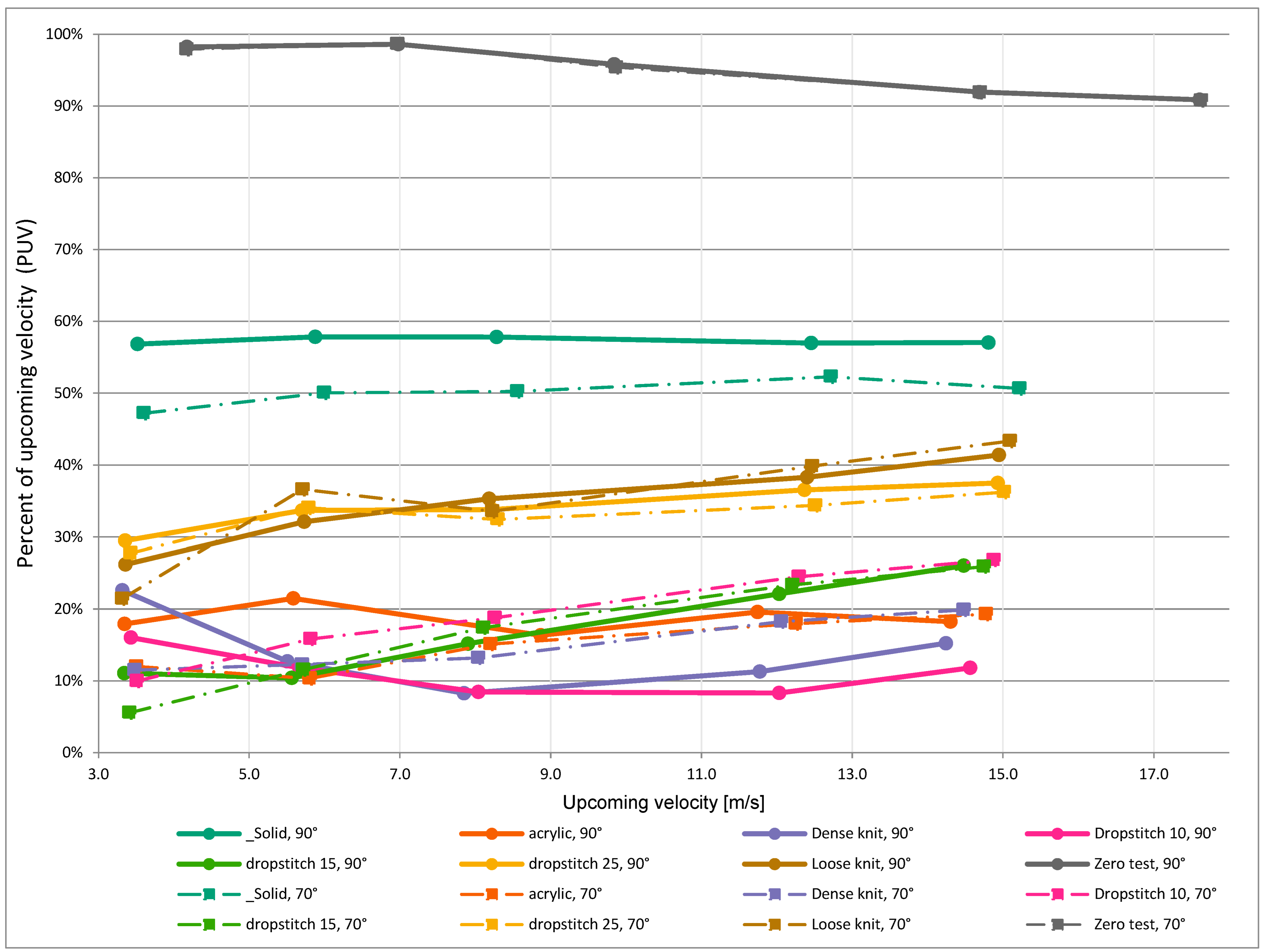
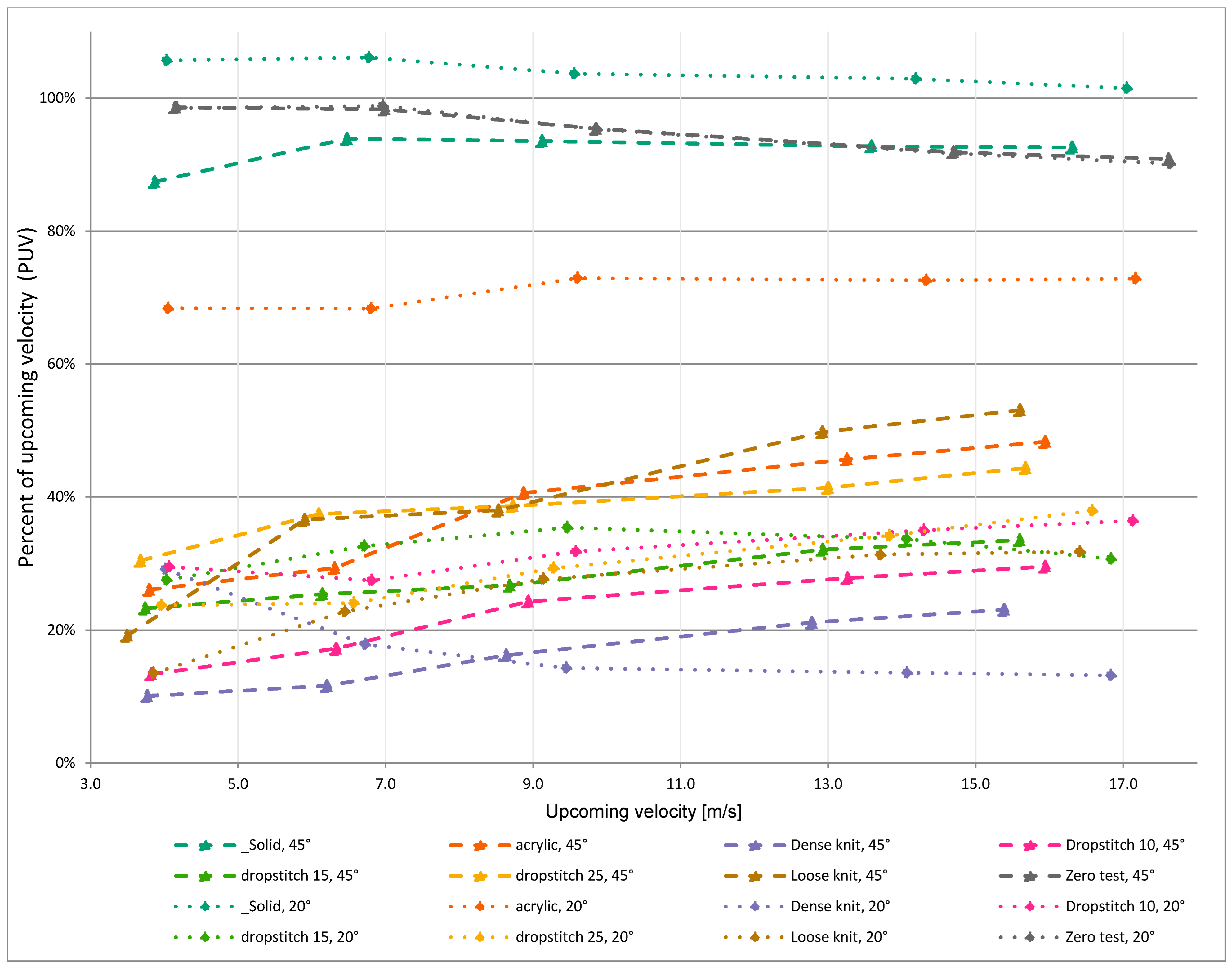
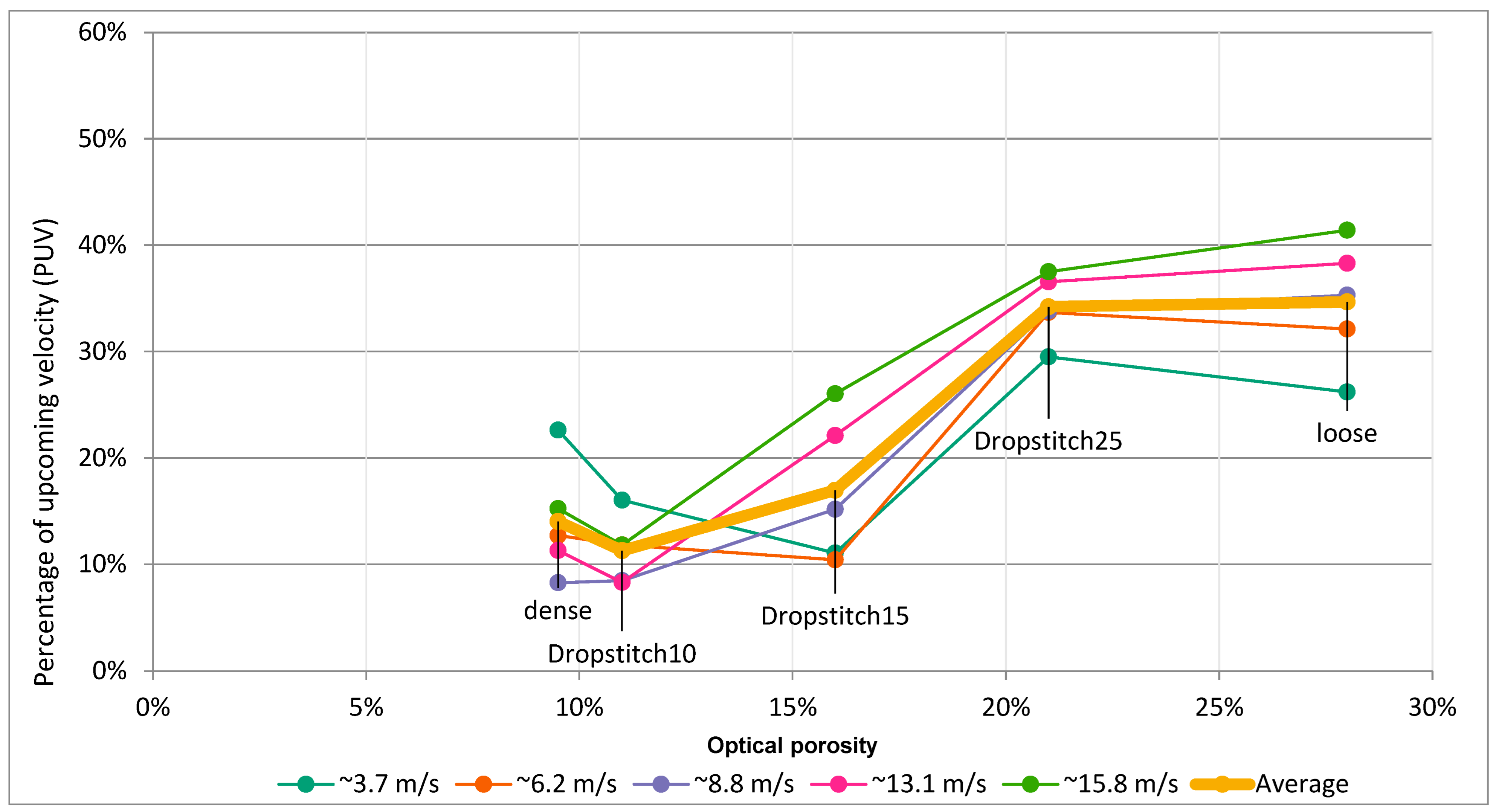
3. Results
3.1. Reduction and Altering of the Wind
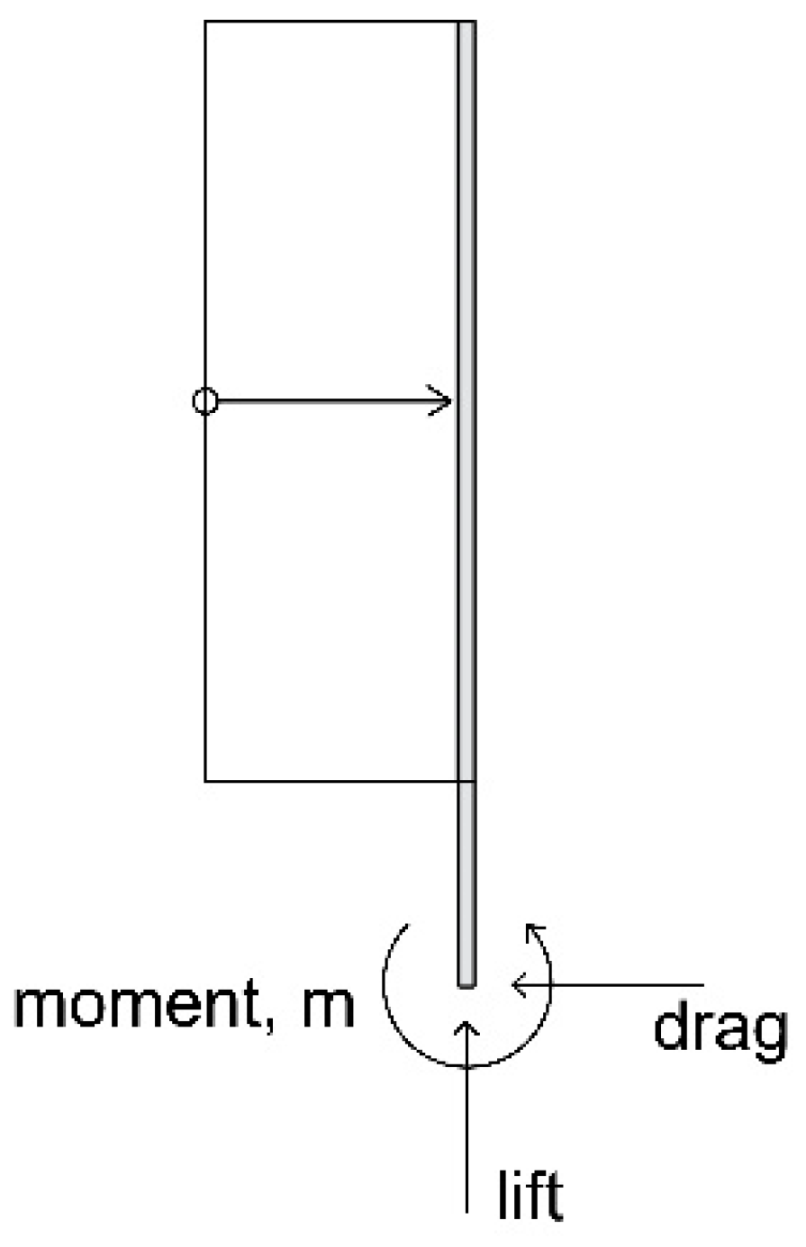
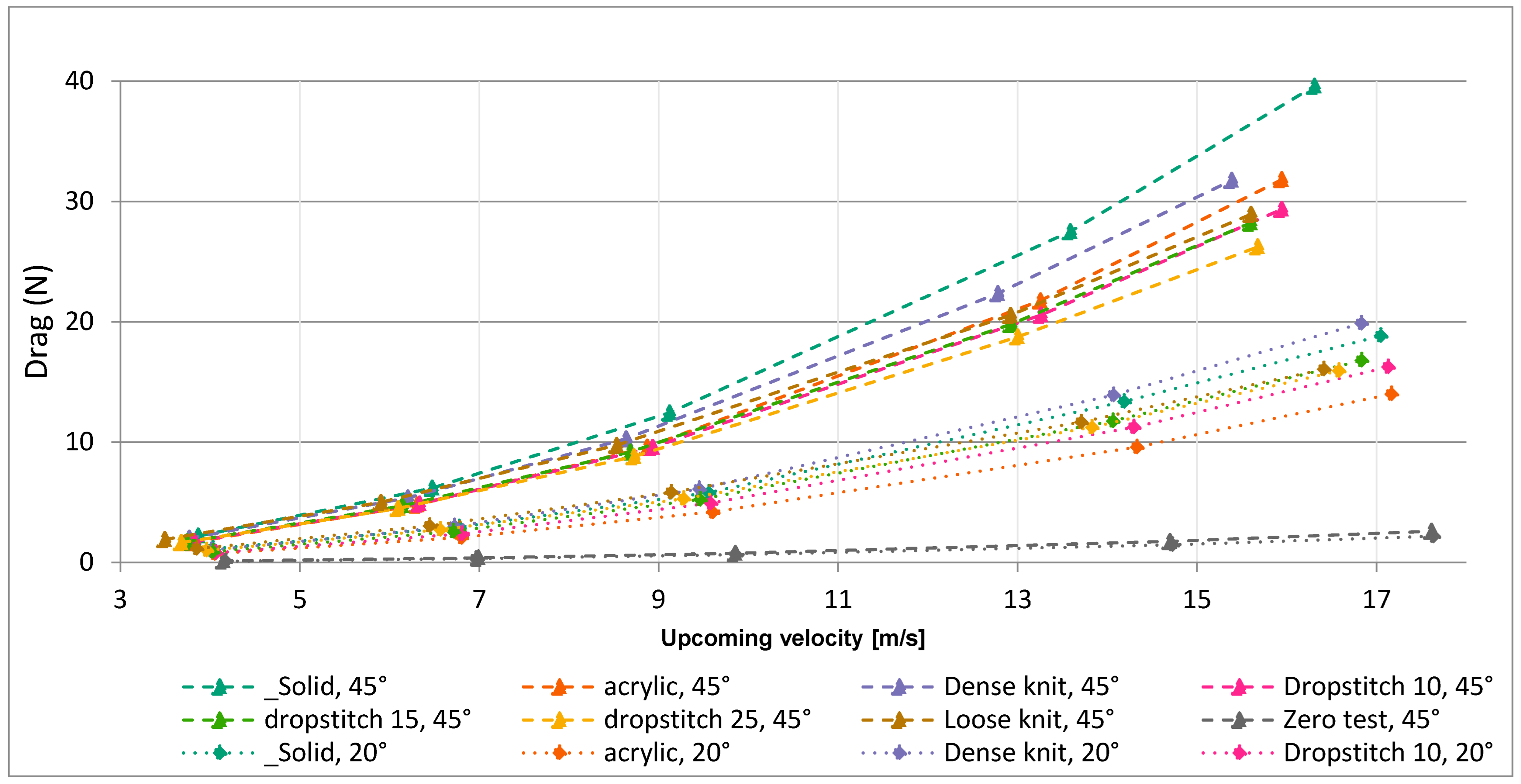
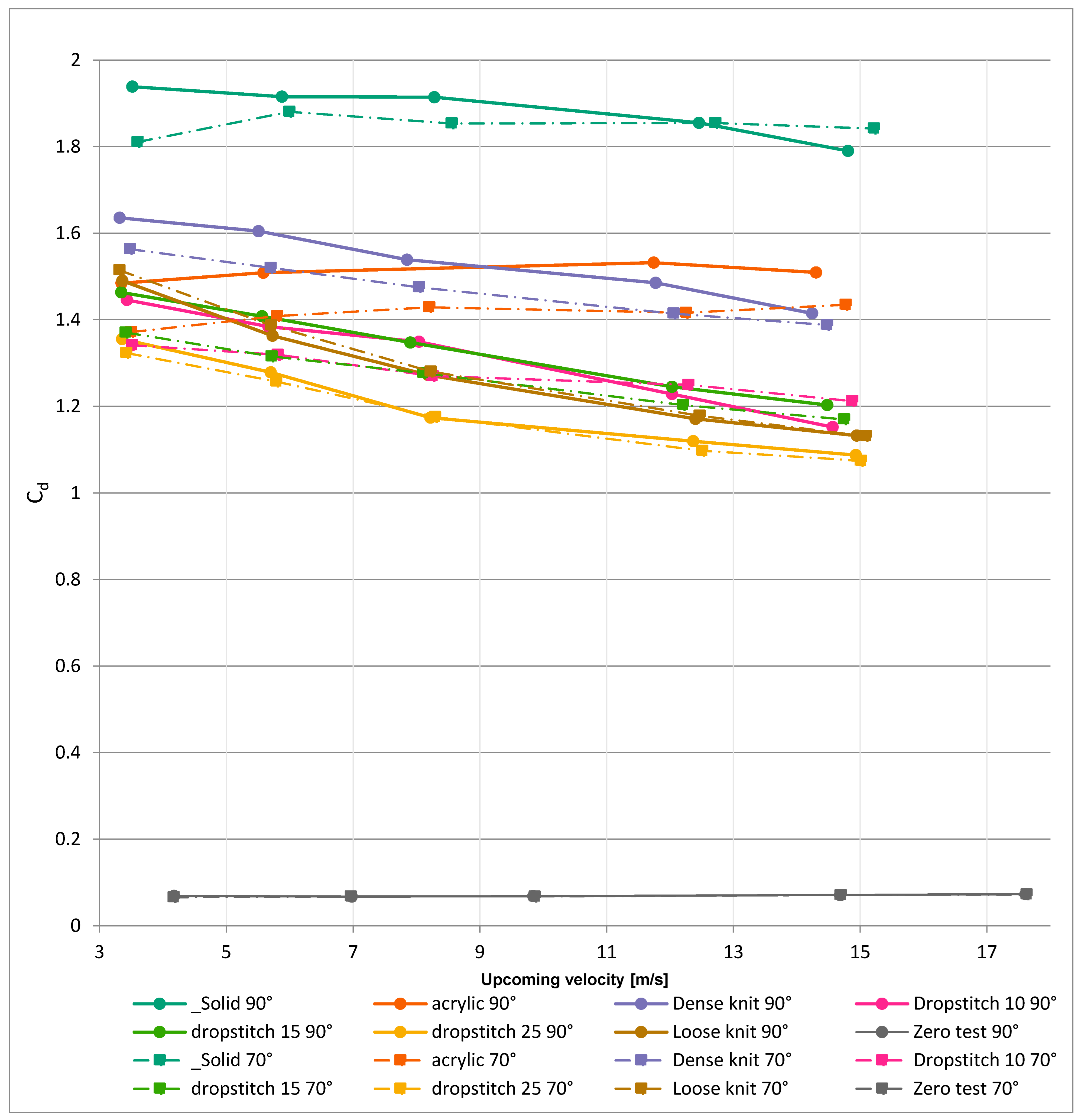
3.2. Forces Acting on the Models
3.3. Geometric Deformation and Wind Pattern
4. Discussion
4.1. Limitations
4.2. Future Research and Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Appendix A. Wind Tunnel Tests: Turbulence and Wind Direction
| Turbulence | Wind Direction | ||
|---|---|---|---|
| 0 | Steady laminar flow | 0 | Same as in flow |
| 1 | Tufts shiver | 1 | Some tufts have changed direction slightly |
| 2 | Several tufts move noticeably sideways | 2 | Some tufts have clearly changed direction |
| 3 | A few tufts shake in the magnitude of 90° to the wind direction | 3 | Most of the tufts have clearly changed direction or a few have changed 90° |
| 4 | Several tufts shake considerably, or a few rotate | 4 | Several tufts have changed direction, at least, 90° |
| 5 | Several tufts rotate around the sticks | 5 | Several tufts have turned 180° |
| Sample | Angle | Windspeed in (U) | Hotwire Output | PUV | Turbulence | Changed Direction | Notes |
|---|---|---|---|---|---|---|---|
| _Solid | 90 | 3.5 | 2 | 57% | 3 | 5 | A vortex has taken shape behind the screen. |
| _Solid | 90 | 5.9 | 3.4 | 58% | 5 | 4 | A vortex has taken shape behind the screen. |
| _Solid | 90 | 8.3 | 4.79 | 58% | 5 | 5 | A vortex has taken shape behind the screen. |
| _Solid | 90 | 12.5 | 7.1 | 57% | 5 | 5 | A vortex has taken shape behind the screen. |
| _Solid | 90 | 14.8 | 8.45 | 57% | 5 | 5 | A vortex has taken shape behind the screen. Value on hot-wire anemometer varies a bit. |
| _Solid | 70 | 3.6 | 1.7 | 47% | 4 | 4 | A vortex has taken shape behind the screen. |
| _Solid | 70 | 6.0 | 3 | 50% | 4 | 4 | A vortex has taken shape behind the screen. |
| _Solid | 70 | 8.6 | 4.3 | 50% | 4 | 4 | A vortex has taken shape behind the screen. Value on hot-wire anemometer varies a lot. |
| _Solid | 70 | 12.7 | 6.65 | 52% | 4 | 4 | A vortex has taken shape behind the screen. Value on hot-wire anemometer varies a lot. |
| _Solid | 70 | 15.2 | 7.71 | 51% | 5 | 4 | A vortex has taken shape behind the screen. |
| _Solid | 45 | 3.9 | 3.38 | 87% | 4 | 4 | Difficult to tell where to draw the line between turbulence and changed direction. Resonance in forces sideways and lift. |
| _Solid | 45 | 6.5 | 6.08 | 94% | 3 | 4 | Difficult to tell where to draw the line between turbulence and changed direction. |
| _Solid | 45 | 9.1 | 8.53 | 94% | 3 | 4 | Difficult to tell where to draw the line between turbulence and changed direction. |
| _Solid | 45 | 13.6 | 12.6 | 93% | 4 | 3 | Difficult to tell where to draw the line between turbulence and changed direction. |
| _Solid | 45 | 16.3 | 15.1 | 93% | 4 | 3 | Difficult to tell where to draw the line between turbulence and changed direction. |
| _Solid | 20 | 4.0 | 4.26 | 106% | 1 | 3 | . |
| _Solid | 20 | 6.8 | 7.19 | 106% | 1 | 3 | . |
| _Solid | 20 | 9.6 | 9.91 | 104% | 1 | 3 | . |
| _Solid | 20 | 14.2 | 14.6 | 103% | 1 | 3 | . |
| _Solid | 20 | 17.0 | 17.3 | 101% | 1 | 3 | . |
| Acrylic | 90 | 3.3 | 0.6 | 18% | 2 | 0 | Value on hot-wire anemometer varies a lot. |
| Acrylic | 90 | 5.6 | 1.2 | 21% | 3 | 0 | Value on hot-wire anemometer varies a lot. |
| Acrylic | 90 | 8.9 | 1.45 | 16% | 4 | 0 | Some measuring data lost. |
| Acrylic | 90 | 11.7 | 2.3 | 20% | 5 | 0 | There is a tendency for a vortex to shape, but the wind fluctuates too much. Value on hot-wire anemometer varies a lot. |
| Acrylic | 90 | 14.3 | 2.61 | 18% | 5 | 0 | There is a tendency for a vortex to shape, but the wind fluctuates too much. Value on hot-wire anemometer varies a lot. |
| Acrylic | 70 | 3.5 | 0.42 | 12% | 2 | 1 | Value on hot-wire anemometer still fluctuates. |
| Acrylic | 70 | 5.8 | 0.6 | 10% | 3 | 1 | Value on hot-wire anemometer still fluctuates. |
| Acrylic | 70 | 8.2 | 1.24 | 15% | 2 | 4 | A vortex has taken shape behind the screen. Value on hot-wire anemometer still fluctuates. |
| Acrylic | 70 | 12.3 | 2.2 | 18% | 3 | 5 | A vortex has taken shape behind the screen. Value on hot-wire anemometer varies a lot. |
| Acrylic | 70 | 14.8 | 2.85 | 19% | 3 | 5 | A vortex has taken shape behind the screen. Value on hot-wire anemometer varies a lot. |
| Acrylic | 45 | 3.8 | 0.99 | 26% | 2 | 2 | Value on hot-wire anemometer varies a lot. |
| Acrylic | 45 | 6.3 | 1.85 | 29% | 2 | 2 | Value on hot-wire anemometer varies a lot. |
| Acrylic | 45 | 8.9 | 3.6 | 41% | 3 | 3 | Value on hot-wire anemometer varies a lot. |
| Acrylic | 45 | 13.3 | 6.05 | 46% | 2 | 3 | Tufts close to model moves vertically. |
| Acrylic | 45 | 15.9 | 7.7 | 48% | 2 | 3 | Value on hot-wire anemometer somewhat more stable. |
| Acrylic | 20 | 4.1 | 2.77 | 68% | 1 | 1 | . |
| Acrylic | 20 | 6.8 | 4.65 | 68% | 1 | 1 | . |
| Acrylic | 20 | 9.6 | 7 | 73% | 1 | 1 | . |
| Acrylic | 20 | 14.3 | 10.4 | 73% | 1 | 1 | . |
| Acrylic | 20 | 17.2 | 12.5 | 73% | 1 | 1 | . |
| Dense knit | 90 | 3.3 | 0.75 | 23% | 2 | 0 | Value on hot-wire anemometer varies a lot. |
| Dense knit | 90 | 5.5 | 0.7 | 13% | 2 | 0 | . |
| Dense knit | 90 | 7.9 | 0.65 | 8% | 1 | 0 | Value on hot-wire anemometer still unstable. |
| Dense knit | 90 | 11.8 | 1.33 | 11% | 1 | 0 | . |
| Dense knit | 90 | 14.2 | 2.17 | 15% | 1 | 0 | . |
| Dense knit | 70 | 3.5 | 0.4 | 12% | 2 | 1 | Value on hot-wire anemometer varies a lot. |
| Dense knit | 70 | 5.7 | 0.7 | 12% | 2 | 1 | Value on hot-wire anemometer varies a lot. |
| Dense knit | 70 | 8.0 | 1.06 | 13% | 2 | 1 | . |
| Dense knit | 70 | 12.1 | 2.2 | 18% | 1 | 1 | . |
| Dense knit | 70 | 14.5 | 2.88 | 20% | 1 | 1 | . |
| Dense knit | 45 | 3.8 | 0.38 | 10% | 3 | 2 | Value on hot-wire anemometer varies a lot. |
| Dense knit | 45 | 6.2 | 0.72 | 12% | 2 | 1 | . |
| Dense knit | 45 | 8.6 | 1.4 | 16% | 1 | 1 | . |
| Dense knit | 45 | 12.8 | 2.7 | 21% | 1 | 1 | . |
| Dense knit | 45 | 15.4 | 3.55 | 23% | 1 | 1 | . |
| Dense knit | 20 | 4.0 | 1.17 | 29% | 2 | 2 | . |
| Dense knit | 20 | 6.7 | 1.2 | 18% | 2 | 2 | . |
| Dense knit | 20 | 9.5 | 1.35 | 14% | 2 | 2 | . |
| Dense knit | 20 | 14.1 | 1.91 | 14% | 2 | 2 | . |
| Dense knit | 20 | 16.8 | 2.22 | 13% | 2 | 1 | . |
| Drop-stitch 10 | 90 | 3.4 | 0.55 | 16% | 2 | 0 | . |
| Drop-stitch 10 | 90 | 5.7 | 0.67 | 12% | 2 | 0 | . |
| Drop-stitch 10 | 90 | 8.0 | 0.68 | 8% | 2 | 0 | . |
| Drop-stitch 10 | 90 | 12.0 | 1 | 8% | 3 | 0 | . |
| Drop-stitch 10 | 90 | 14.6 | 1.72 | 12% | 2 | 0 | . |
| Drop-stitch 10 | 70 | 3.5 | 0.35 | 10% | 1 | 1 | . |
| Drop-stitch 10 | 70 | 5.8 | 0.92 | 16% | 1 | 1 | . |
| Drop-stitch 10 | 70 | 8.3 | 1.55 | 19% | 1 | 1 | . |
| Drop-stitch 10 | 70 | 12.3 | 3.01 | 24% | 1 | 1 | . |
| Drop-stitch 10 | 70 | 14.9 | 3.99 | 27% | 1 | 1 | . |
| Drop-stitch 10 | 45 | 3.8 | 0.51 | 13% | 1 | 2 | . |
| Drop-stitch 10 | 45 | 6.3 | 1.09 | 17% | 1 | 2 | . |
| Drop-stitch 10 | 45 | 8.9 | 2.17 | 24% | 1 | 2 | . |
| Drop-stitch 10 | 45 | 13.3 | 3.69 | 28% | 1 | 2 | . |
| Drop-stitch 10 | 45 | 15.9 | 4.71 | 30% | 1 | 2 | . |
| Drop-stitch 10 | 20 | 4.1 | 1.2 | 30% | 1 | 2 | . |
| Drop-stitch 10 | 20 | 6.8 | 1.87 | 27% | 1 | 2 | . |
| Drop-stitch 10 | 20 | 9.6 | 3.05 | 32% | 1 | 2 | . |
| Drop-stitch 10 | 20 | 14.3 | 5 | 35% | 2 | 2 | . |
| Drop-stitch 10 | 20 | 17.1 | 6.24 | 36% | 2 | 2 | . |
| Drop-stitch 15 | 90 | 3.3 | 0.37 | 11% | 1 | 0 | . |
| Drop-stitch 15 | 90 | 5.6 | 0.58 | 10% | 1 | 0 | . |
| Drop-stitch 15 | 90 | 7.9 | 1.2 | 15% | 1 | 0 | . |
| Drop-stitch 15 | 90 | 12.0 | 2.66 | 22% | 1 | 0 | . |
| Drop-stitch 15 | 90 | 14.5 | 3.77 | 26% | 1 | 0 | . |
| Drop-stitch 15 | 70 | 3.4 | 0.19 | 6% | 1 | 0 | . |
| Drop-stitch 15 | 70 | 5.7 | 0.66 | 12% | 1 | 0 | . |
| Drop-stitch 15 | 70 | 8.1 | 1.41 | 17% | 1 | 0 | . |
| Drop-stitch 15 | 70 | 12.2 | 2.85 | 23% | 1 | 0 | . |
| Drop-stitch 15 | 70 | 14.7 | 3.82 | 26% | 1 | 0 | . |
| Drop-stitch 15 | 45 | 3.7 | 0.87 | 23% | 1 | 1 | . |
| Drop-stitch 15 | 45 | 6.1 | 1.56 | 25% | 1 | 1 | . |
| Drop-stitch 15 | 45 | 8.7 | 2.32 | 27% | 1 | 1 | . |
| Drop-stitch 15 | 45 | 12.9 | 4.15 | 32% | 1 | 0 | . |
| Drop-stitch 15 | 45 | 15.6 | 5.23 | 34% | 1 | 0 | . |
| Drop-stitch 15 | 20 | 4.0 | 1.11 | 28% | 1 | 1 | . |
| Drop-stitch 15 | 20 | 6.7 | 2.19 | 33% | 1 | 1 | . |
| Drop-stitch 15 | 20 | 9.5 | 3.35 | 35% | 1 | 0 | . |
| Drop-stitch 15 | 20 | 14.1 | 4.74 | 34% | 1 | 0 | . |
| Drop-stitch 15 | 20 | 16.8 | 5.17 | 31% | 1 | 0 | . |
| Drop-stitch 25 | 90 | 3.4 | 0.99 | 30% | 1 | 0 | . |
| Drop-stitch 25 | 90 | 5.7 | 1.92 | 34% | 1 | 0 | . |
| Drop-stitch 25 | 90 | 8.2 | 2.78 | 34% | 1 | 0 | . |
| Drop-stitch 25 | 90 | 12.4 | 4.52 | 37% | 1 | 0 | . |
| Drop-stitch 25 | 90 | 14.9 | 5.6 | 38% | 1 | 0 | . |
| Drop-stitch 25 | 70 | 3.4 | 0.95 | 28% | 1 | 0 | . |
| Drop-stitch 25 | 70 | 5.8 | 1.97 | 34% | 1 | 0 | . |
| Drop-stitch 25 | 70 | 8.3 | 2.69 | 32% | 1 | 0 | . |
| Drop-stitch 25 | 70 | 12.5 | 4.3 | 34% | 1 | 0 | . |
| Drop-stitch 25 | 70 | 15.0 | 5.44 | 36% | 1 | 0 | . |
| Drop-stitch 25 | 45 | 3.7 | 1.12 | 30% | 1 | 0 | . |
| Drop-stitch 25 | 45 | 6.1 | 2.28 | 37% | 1 | 0 | . |
| Drop-stitch 25 | 45 | 8.7 | 3.37 | 39% | 1 | 0 | . |
| Drop-stitch 25 | 45 | 13.0 | 5.38 | 41% | 1 | 0 | . |
| Drop-stitch 25 | 45 | 15.7 | 6.95 | 44% | 1 | 0 | . |
| Drop-stitch 25 | 20 | 4.0 | 0.94 | 24% | 1 | 0 | . |
| Drop-stitch 25 | 20 | 6.6 | 1.58 | 24% | 1 | 0 | . |
| Drop-stitch 25 | 20 | 9.3 | 2.72 | 29% | 1 | 0 | . |
| Drop-stitch 25 | 20 | 13.8 | 4.73 | 34% | 1 | 0 | . |
| Drop-stitch 25 | 20 | 16.6 | 6.29 | 38% | 1 | 0 | . |
| Loose knit | 90 | 3.4 | 0.88 | 26% | 1 | 0 | . |
| Loose knit | 90 | 5.7 | 1.84 | 32% | 1 | 0 | . |
| Loose knit | 90 | 8.2 | 2.89 | 35% | 1 | 0 | . |
| Loose knit | 90 | 12.4 | 4.75 | 38% | 1 | 0 | . |
| Loose knit | 90 | 14.9 | 6.19 | 41% | 1 | 0 | . |
| Loose knit | 70 | 3.3 | 0.71 | 21% | 1 | 0 | . |
| Loose knit | 70 | 5.7 | 2.09 | 37% | 1 | 0 | . |
| Loose knit | 70 | 8.2 | 2.76 | 34% | 1 | 0 | . |
| Loose knit | 70 | 12.5 | 4.97 | 40% | 1 | 0 | . |
| Loose knit | 70 | 15.1 | 6.54 | 43% | 1 | 0 | . |
| Loose knit | 45 | 3.5 | 0.67 | 19% | 1 | 0 | . |
| Loose knit | 45 | 5.9 | 2.16 | 37% | 1 | 0 | . |
| Loose knit | 45 | 8.5 | 3.24 | 38% | 1 | 0 | . |
| Loose knit | 45 | 12.9 | 6.43 | 50% | 1 | 0 | . |
| Loose knit | 45 | 15.6 | 8.28 | 53% | 1 | 0 | . |
| Loose knit | 20 | 3.9 | 0.52 | 14% | 1 | 0 | . |
| Loose knit | 20 | 6.4 | 1.47 | 23% | 1 | 0 | . |
| Loose knit | 20 | 9.1 | 2.53 | 28% | 1 | 0 | Knit moves on rod. |
| Loose knit | 20 | 13.7 | 4.3 | 31% | 1 | 0 | Start to touch the pins. |
| Loose knit | 20 | 16.4 | 5.22 | 32% | 1 | 0 | . |
| Zero test | 90 | 4.2 | 4.1 | 98% | 1 | 0 | . |
| Zero test | 90 | 7.0 | 6.88 | 99% | 1 | 0 | . |
| Zero test | 90 | 9.8 | 9.43 | 96% | 1 | 0 | . |
| Zero test | 90 | 14.7 | 13.5 | 92% | 1 | 0 | . |
| Zero test | 90 | 17.6 | 16 | 91% | 1 | 0 | . |
| Zero test | 70 | 4.2 | 4.08 | 98% | 1 | 0 | . |
| Zero test | 70 | 7.0 | 6.87 | 99% | 1 | 0 | . |
| Zero test | 70 | 9.9 | 9.41 | 95% | 1 | 0 | . |
| Zero test | 70 | 14.7 | 13.5 | 92% | 1 | 0 | . |
| Zero test | 70 | 17.6 | 16 | 91% | 1 | 0 | . |
| Zero test | 45 | 4.1 | 4.09 | 99% | 1 | 0 | . |
| Zero test | 45 | 7.0 | 6.87 | 98% | 1 | 0 | . |
| Zero test | 45 | 9.9 | 9.4 | 95% | 1 | 0 | . |
| Zero test | 45 | 14.7 | 13.5 | 92% | 1 | 0 | . |
| Zero test | 45 | 17.6 | 16 | 91% | 1 | 0 | . |
| Zero test | 20 | 4.2 | 4.11 | 98% | 1 | 0 | . |
| Zero test | 20 | 7.0 | 6.88 | 99% | 1 | 0 | . |
| Zero test | 20 | 9.9 | 9.4 | 95% | 1 | 0 | . |
| Zero test | 20 | 14.7 | 13.5 | 92% | 1 | 0 | . |
| Zero test | 20 | 17.6 | 15.9 | 90% | 1 | 0 | . |
References
- Blocken, B.; Stathopoulos, T.; van Beeck, J.P.A.J. Pedestrian-Level Wind Conditions around Buildings: Review of Wind-Tunnel and CFD Techniques and Their Accuracy for Wind Comfort Assessment. Build. Environ. 2016, 100, 50–81. [Google Scholar] [CrossRef]
- Zhen, M.; Chen, Z.; Zheng, R. Outdoor Wind Comfort and Adaptation in a Cold Region. Buildings 2022, 12, 476. [Google Scholar] [CrossRef]
- Penwarden, A.D. Acceptable Wind Speeds in Towns. Build. Sci. 1973, 8, 259–267. [Google Scholar] [CrossRef]
- Lai, D.; Liu, W.; Gan, T.; Liu, K.; Chen, Q. A Review of Mitigating Strategies to Improve the Thermal Environment and Thermal Comfort in Urban Outdoor Spaces. Sci. Total Environ. 2019, 661, 337–353. [Google Scholar] [CrossRef] [PubMed]
- Cochran, L. Design Features to Change and/or Ameliorate Pedestrian Wind Conditions. In Proceedings of the Structures Congress 2004, Nashville, TN, USA, 22–26 May 2004; pp. 1–8. [Google Scholar] [CrossRef]
- Fernando, S.; Fernando, S.; Mendis, P. Pedestrian Wind Comfort Study Using Computational Fluid Dynamic (CFD) Simulation. In Proceedings of the International Conference on Sustainable Built Environment (ICSBE 2018), Banjarmasin, Indonesia, 11–13 October 2018; Dissanayake, R., Mendis, P., Eds.; Springer: Singapore, 2020; pp. 323–339. [Google Scholar]
- Stathopoulos, T. Wind and Comfort. In Proceedings of the 5th European and African Conference on Wind Engineering, EACWE 5, Florence, Italy, 19–23 July 2009. [Google Scholar]
- Heisler, G.M.; Dewalle, D.R. 2. Effects of Windbreak Structure on Wind Flow. Agric. Ecosyst. Environ. 1988, 22–23, 41–69. [Google Scholar] [CrossRef]
- Bitog, J.P.; Lee, I.-B.; Hwang, H.-S.; Shin, M.-H.; Hong, S.-W.; Seo, I.-H.; Mostafa, E.; Pang, Z. A Wind Tunnel Study on Aerodynamic Porosity and Windbreak Drag. For. Sci. Technol. 2011, 7, 8–16. [Google Scholar] [CrossRef]
- Zhou, X.H.; Brandle, J.R.; Mize, C.W.; Takle, E.S. Three-Dimensional Aerodynamic Structure of a Tree Shelterbelt: Definition, Characterization and Working Models. Agrofor. Syst. 2005, 63, 133–147. [Google Scholar] [CrossRef]
- Dong, Z.; Luo, W.; Qian, G.; Wang, H. A Wind Tunnel Simulation of the Mean Velocity Fields behind Upright Porous Fences. Agric. For. Meteorol. 2007, 146, 82–93. [Google Scholar] [CrossRef]
- Lee, S.-J.; Kim, H.-B. Laboratory Measurements of Velocity and Turbulence Field behind Porous Fences. J. Wind. Eng. Ind. Aerodyn. 1999, 80, 311–326. [Google Scholar] [CrossRef]
- Lee, S.-J.; Lim, H.-C. A Numerical Study on Flow around a Triangular Prism Located behind a Porous Fence. Fluid Dyn. Res. 2001, 28, 209. [Google Scholar] [CrossRef]
- Sari, D.P.; Cho, K.-P. Performance Comparison of Different Building Shapes Using a Wind Tunnel and a Computational Model. Buildings 2022, 12, 144. [Google Scholar] [CrossRef]
- Hershcovich, C.; van Hout, R.; Rinsky, V.; Laufer, M.; Grobman, Y.J. Thermal Performance of Sculptured Tiles for Building Envelopes. Build. Environ. 2021, 197, 107809. [Google Scholar] [CrossRef]
- Kormaníková, L.; Achten, H.; Kopřiva, M.; Kmeť, S. Parametric Wind Design. Front. Archit. Res. 2018, 7, 383–394. [Google Scholar] [CrossRef]
- Hörteborn, E.; Zboinska, M.A. Exploring Expressive and Functional Capacities of Knitted Textiles Exposed to Wind Influence. Front. Archit. Res. 2021, 10, 669–691. [Google Scholar] [CrossRef]
- Koch, K.-M.; Habermann, K.J.; Forster, B. Membrane Structures: Innovative Building with Film and Fabric; Prestel Publishing: Munich, Germany, 2004. [Google Scholar]
- Popescu, M.; Rippmann, M.; Liew, A.; Reiter, L.; Flatt, R.J.; Van Mele, T.; Block, P. Structural Design, Digital Fabrication and Construction of the Cable-Net and Knitted Formwork of the KnitCandela Concrete Shell. Structures 2020, 31, 1287–1299. [Google Scholar] [CrossRef]
- Hörteborn, E. Textile Architecture Informed by Wind; Chalmers University of Technology: Gothenburg, Sweden, 2020. [Google Scholar]
- Hagen, L.J.; Skidmore, E.L. Turbulent Velocity Fluctuations and Vertical Flow as Affected Bv Windbreak Porositv. Trans. ASAE 1971, 14, 634–637. [Google Scholar]
- Raine, J.K.; Stevenson, D.C. Wind Protection by Model Fences in a Simulated Atmospheric Boundary Layer. J. Wind. Eng. Ind. Aerodyn. 1977, 2, 159–180. [Google Scholar] [CrossRef]
- Richardson, G.M.; Richards, P.J. Full-Scale Measurements of the Effect of a Porous Windbreak on Wind Spectra. J. Wind. Eng. Ind. Aerodyn. 1995, 54–55, 611–619. [Google Scholar] [CrossRef]
- Wilson, J.D. Numerical Studies of Flow through a Windbreak. J. Wind. Eng. Ind. Aerodyn. 1985, 21, 119–154. [Google Scholar] [CrossRef]
- Cornelis, W.M.; Gabriels, D. Optimal Windbreak Design for Wind-Erosion Control. J. Arid. Environ. 2005, 61, 315–332. [Google Scholar] [CrossRef]
- Caborn, J.M. Shelterbelts and Microclimate; The Forestry Department of Edinburgh University: Edinburgh, UK, 1957; pp. 1–164. [Google Scholar]
- Hong, S.-W.; Lee, I.-B.; Seo, I.-H. Modelling and Predicting Wind Velocity Patterns for Windbreak Fence Design. J. Wind. Eng. Ind. Aerodyn. 2015, 142, 53–64. [Google Scholar] [CrossRef]
- Park, C.-W.; Lee, S.-J. Verification of the Shelter Effect of a Windbreak on Coal Piles in the POSCO Open Storage Yards at the Kwang-Yang Works. Atmos. Environ. 2002, 36, 2171–2185. [Google Scholar] [CrossRef]
- Mahgoub, A.O.; Ghani, S. Numerical and Experimental Investigation of Utilizing the Porous Media Model for Windbreaks CFD Simulation. Sustain. Cities Soc. 2021, 65, 102648. [Google Scholar] [CrossRef]
- Hörteborn, E.; Zboinska, M.; Dumitrescu, D.; Williams, C.; Felbrich, B. Architecture from Textiles in Motion. In Proceedings of the Form and Force, CIMNE, Barcelona, Spain, 7–10 October 2019; pp. 2316–2323. [Google Scholar]
- Liu, M.B.; Liu, G.R. Smoothed Particle Hydrodynamics (SPH): An Overview and Recent Developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef]
- Hosain, M.L.; Domínguez, J.M.; Bel Fdhila, R.; Kyprianidis, K. Smoothed Particle Hydrodynamics Modeling of Industrial Processes Involving Heat Transfer. Appl. Energy 2019, 252, 113441. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Oger, G.; Le Touzé, D. Smoothed Particle Hydrodynamics Method for Fluid Flows, towards Industrial Applications: Motivations, Current State, and Challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Aynsley, R.M. Shape and Flow: The Essence of Architectural Aerodynamics. Archit. Sci. Rev. 1999, 42, 69–74. [Google Scholar] [CrossRef]
- Liu, B.; Qu, J.; Zhang, W.; Tan, L.; Gao, Y. Numerical Evaluation of the Scale Problem on the Wind Flow of a Windbreak. Sci. Rep. 2014, 4, 6619. [Google Scholar] [CrossRef]
- Li, W.; Wang, F.; Bell, S. Simulating the Sheltering Effects of Windbreaks in Urban Outdoor Open Space. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 533–549. [Google Scholar] [CrossRef]
- Obasaju, E.D.; Robins, A.G. Simulation of Pollution Dispersion Using Small Scale Physical Models—An Assessment of Scaling Options. In Urban Air Quality: Monitoring and Modelling: Proceedings of the First International Conference on Urban Air Quality: Monitoring and Modelling University of Hertfordshire, Hatfield, UK, 11–12 July 1996; Sokhi, R.S., Ed.; Springer: Dordrecht, The Netherlands, 1998; pp. 239–254. ISBN 978-94-011-5127-6. [Google Scholar]
- Yeh, C.-P.; Tsai, C.-H.; Yang, R.-J. An Investigation into the Sheltering Performance of Porous Windbreaks under Various Wind Directions. J. Wind. Eng. Ind. Aerodyn. 2010, 98, 520–532. [Google Scholar] [CrossRef]
- Guan, D.; Zhang, Y.; Zhu, T. A Wind-Tunnel Study of Windbreak Drag. Agric. For. Meteorol. 2003, 118, 75–84. [Google Scholar] [CrossRef]
- Liu, D.; Christe, D.; Shakibajahromi, B.; Knittel, C.; Castaneda, N.; Breen, D.; Dion, G.; Kontsos, A. On the Role of Material Architecture in the Mechanical Behavior of Knitted Textiles. Int. J. Solids Struct. 2017, 109, 101–111. [Google Scholar] [CrossRef]
- Francis, N.; Sparkes, B. 3-Knitted Textile Design. In Textile Design; Briggs-Goode, A., Townsend, K., Eds.; Woodhead Publishing Series in Textiles; Woodhead Publishing: Sawston, UK, 2011; pp. 55–87e. ISBN 978-1-84569-646-7. [Google Scholar]















| Knit | Pattern | Zoomed in Pattern | Porosity | |
|---|---|---|---|---|
| Drop-Stitch 10% |  |  |  | 21% (11% unstretched) |
| Drop-Stitch 15% |  |  |  | 16% |
| Drop-Stitch 25% |  |  |  | 21% |
| Loose |  |  |  | 28% |
| Dense |  |  |  | 9.5% |
| Acrylic Board |  |  |  | 32% |
| Model Name | Weight (g) |
|---|---|
| Drop-stitch 10% | 45 |
| Drop-stitch 15% | 49 |
| Drop-stitch 25% | 57 |
| Loosely knitted | 61 |
| Densely knitted | 49 |
| Solid board | 193 |
| Perforated board (acrylic) | 609 |
| Steel frame | 966 |
| Photo | Sample Name | Wind Velocity (m/s) | Angle (°) |
|---|---|---|---|
 | Drop-stitch 10% | 12.0 | 90 |
 | Drop-stitch 15% | 12.0 | 90 |
 | Drop-stitch 25% | 12.4 | 90 |
 | Dense | 11.8 | 90 |
 | Loose | 12.5 | 90 |
 | Perforated board (acrylic) | 11.7 | 90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hörteborn, E.; Zboinska, M.A.; Chernoray, V.; Ander, M. Architectural Knitted Windbreaks for Improved Wind Comfort in the City: A Wind Tunnel Study of Custom-Designed Porous Textile Screens. Buildings 2023, 13, 34. https://doi.org/10.3390/buildings13010034
Hörteborn E, Zboinska MA, Chernoray V, Ander M. Architectural Knitted Windbreaks for Improved Wind Comfort in the City: A Wind Tunnel Study of Custom-Designed Porous Textile Screens. Buildings. 2023; 13(1):34. https://doi.org/10.3390/buildings13010034
Chicago/Turabian StyleHörteborn, Erica, Malgorzata A. Zboinska, Valery Chernoray, and Mats Ander. 2023. "Architectural Knitted Windbreaks for Improved Wind Comfort in the City: A Wind Tunnel Study of Custom-Designed Porous Textile Screens" Buildings 13, no. 1: 34. https://doi.org/10.3390/buildings13010034
APA StyleHörteborn, E., Zboinska, M. A., Chernoray, V., & Ander, M. (2023). Architectural Knitted Windbreaks for Improved Wind Comfort in the City: A Wind Tunnel Study of Custom-Designed Porous Textile Screens. Buildings, 13(1), 34. https://doi.org/10.3390/buildings13010034







