An Effective Metaheuristic Approach for Building Energy Optimization Problems
Abstract
1. Introduction
- The development of POSCO, a powerful hybrid metaheuristic method based on single candidate and pelican optimization, has been made.
- Thirteen popular benchmarking functions are used to evaluate POSCO’s performance for numerical function optimization, and the findings are contrasted with those of other widely used optimization techniques.
- To show how well the suggested method works when used on real-life issues, the new method is used to build the energy optimization problem.
- The efficiency of the proposed POSCO for BEO is investigated and the results acquired are contrasted with those previously assessed by the other procedures.
2. Pelican Optimization Algorithm
- a.
- Moving Approaching the Prey or Exploration Phase:
- b.
- Exploitation Phase or Water Surface Winging:
| Algorithm 1: Pseudo-code of the pelican optimization algorithm |
| Determine the POA population size (N) and the number of iterations (T) Initialization of the position of pelicans randomly based on Equation (1) Calculate the objective function of the population For t = 1:T Generate the position of the prey at random For I = 1:N Phase 1: Moving towards prey (exploration phase) For j = 1:m Calculate new status of the jth dimension using Equation (4) End Update the ith population member using Equation (5) Phase 2: Winging on the water surface (exploitation phase) For j = 1:m. Calculate new status of the jth dimension using Equation (6) End Update the ith population member using Equation (7) End Update best candidate solution End Output best solution obtained by POA |
3. Single Candidate Optimizer
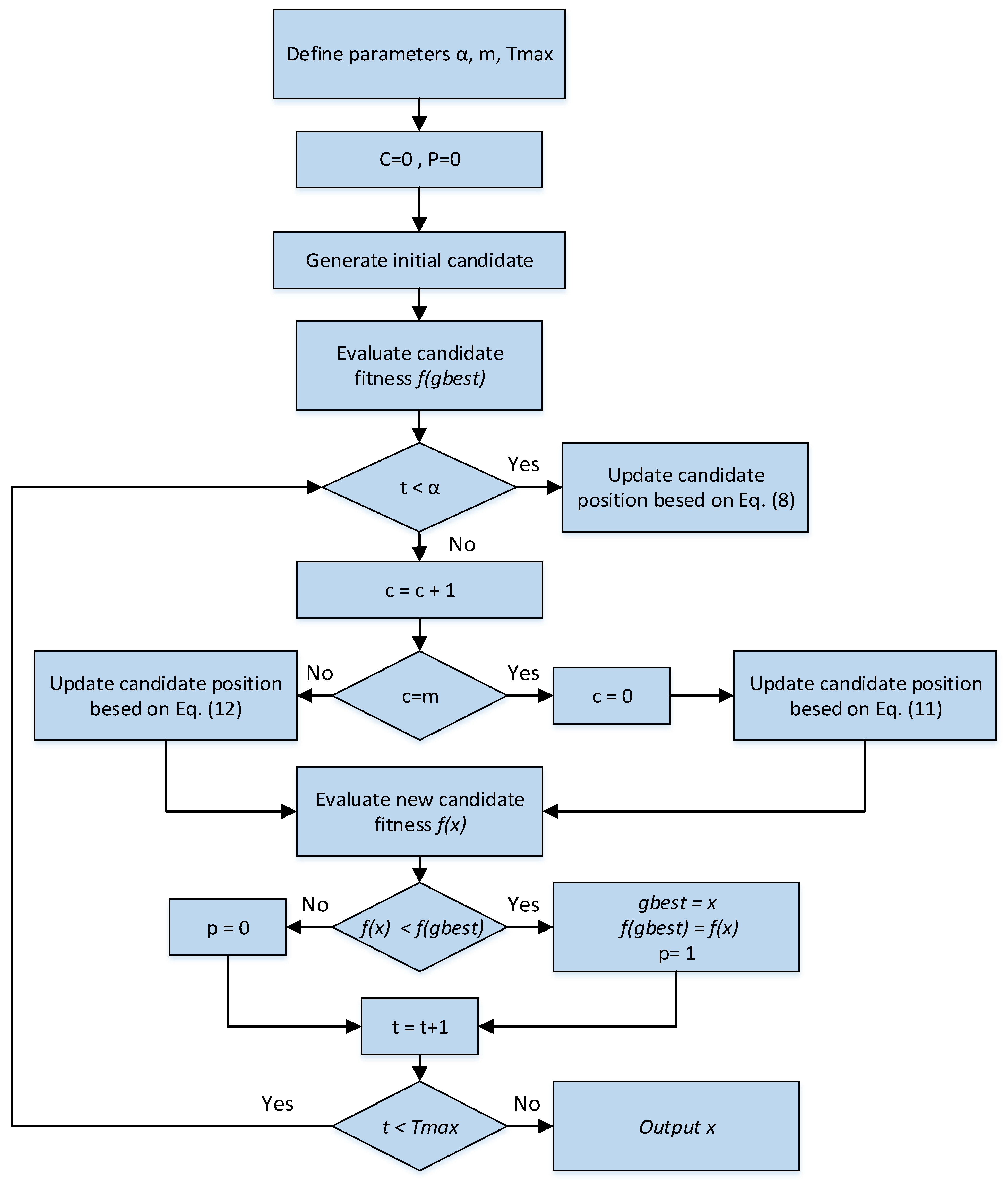
4. Hybrid Pelican and Single Candidate Optimizer
5. Building Energy Optimization Problems
5.1. Simple Office Building
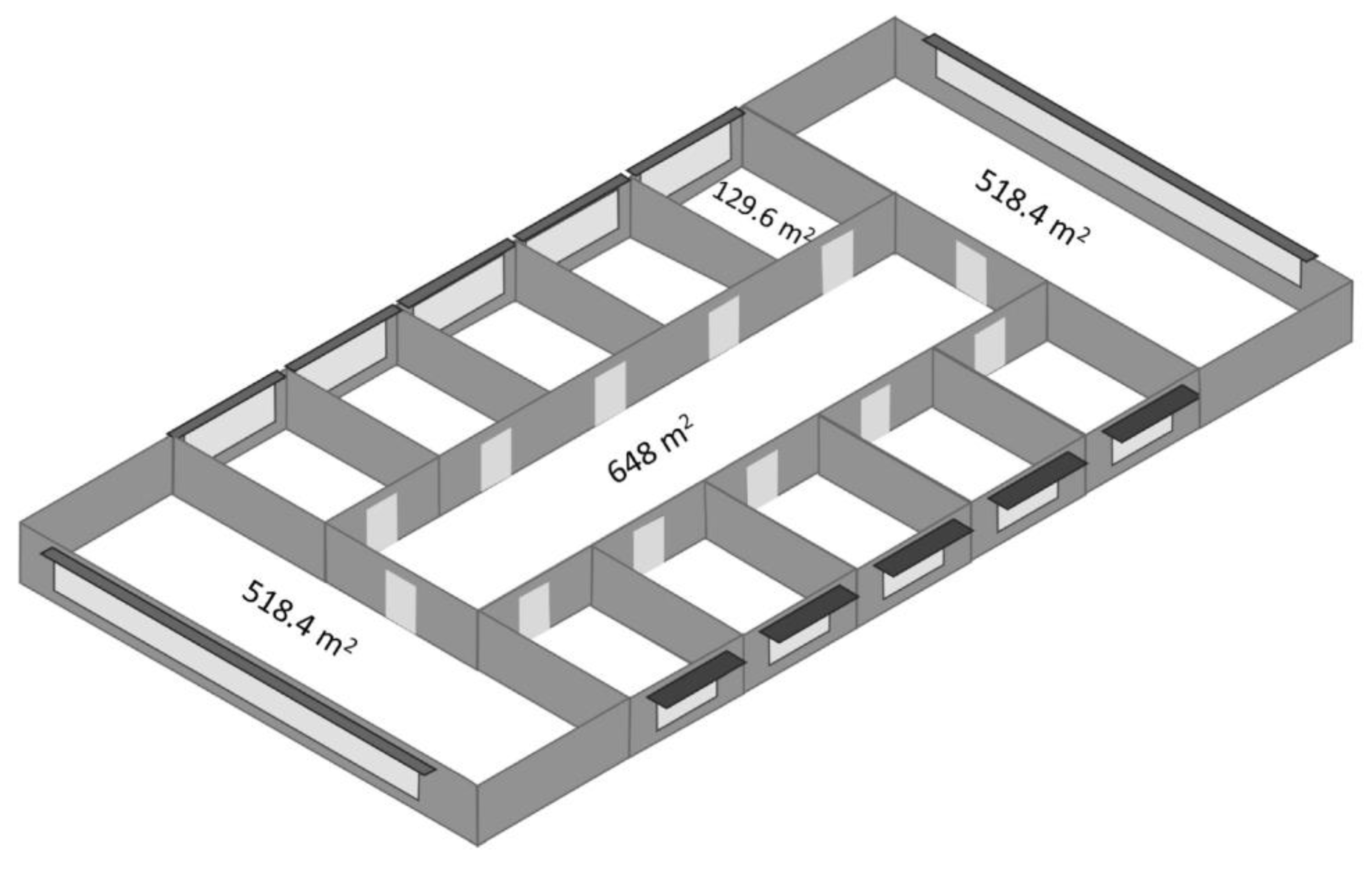
5.2. Detailed Office Building
5.3. Simulation Software for Building Energy Consumption
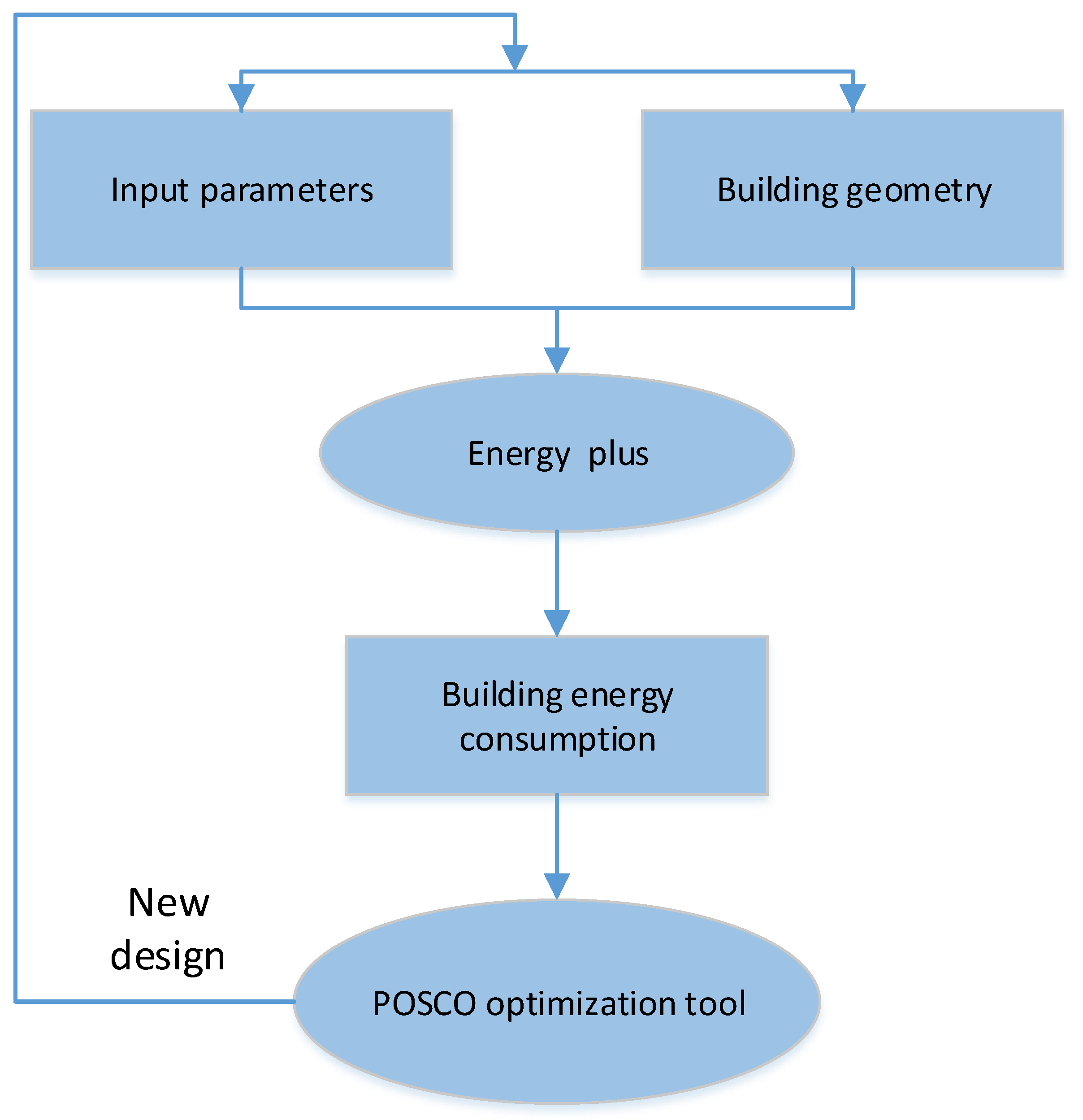
5.4. Combining the POSCO Algorithm with EP
6. Verification of the POSCO
7. Results and Comparison
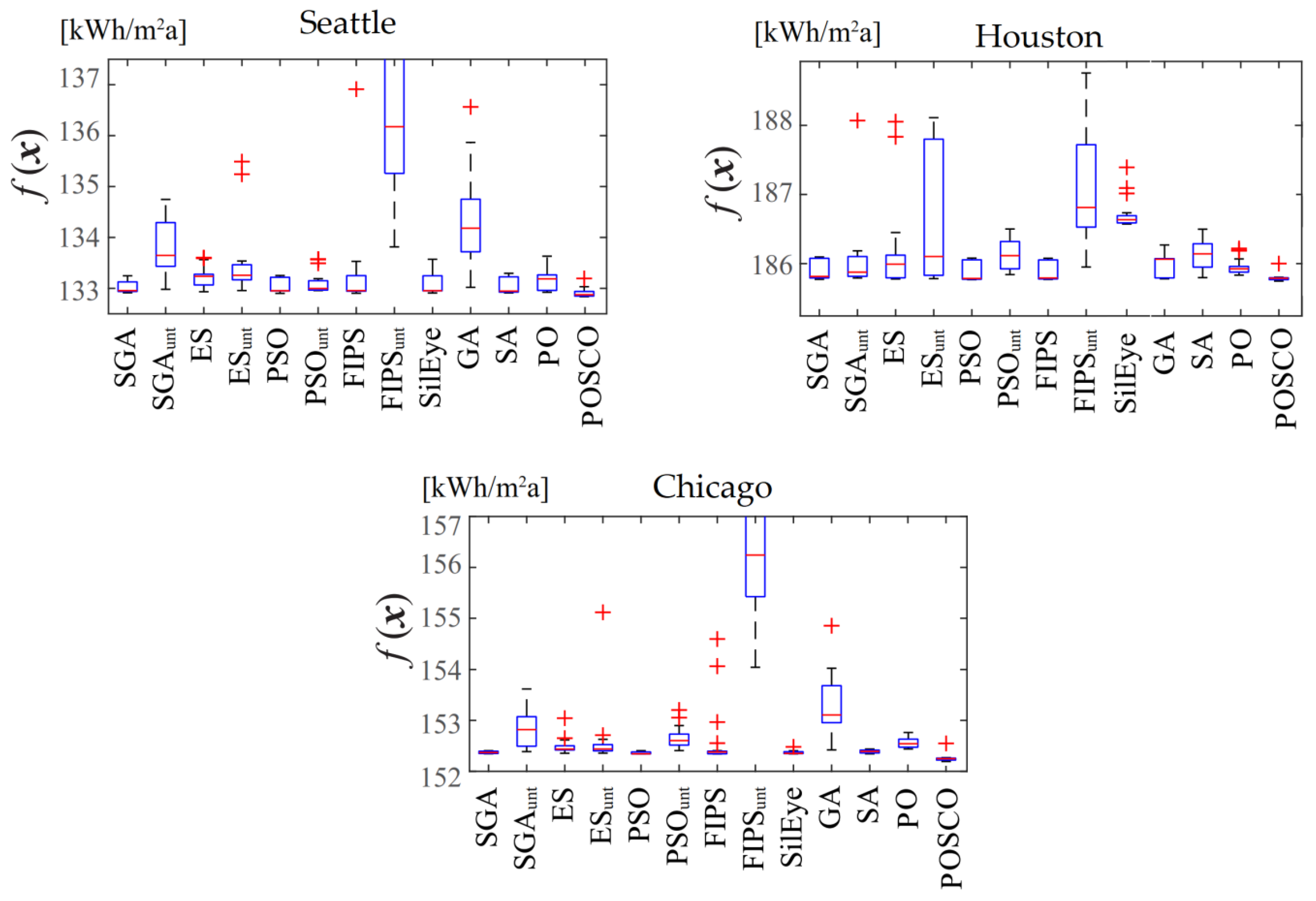
7.1. Simple Office Building Results
7.2. Detailed Office Building Results
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tian, Z.; Chen, W.; Tang, P.; Wang, J.; Shi, X. Building energy optimization tools and their applicability in architectural conceptual design stage. Energy Procedia 2015, 78, 2572–2577. [Google Scholar] [CrossRef]
- Si, B.; Tian, Z.; Jin, X.; Zhou, X.; Shi, X. Ineffectiveness of optimization algorithms in building energy optimization and possible causes. Renew. Energy 2019, 134, 1295–1306. [Google Scholar] [CrossRef]
- Wetter, M.; Wright, J. Comparison of a generalized pattern search and a genetic algorithm optimization method. In Proceedings of the 8th IBPSA Conference, Eindhoven, The Netherlands, 11–14 August 2003; pp. 1401–1408. [Google Scholar]
- Si, B.; Tian, Z.; Jin, X.; Zhou, X.; Tang, P.; Shi, X. Performance indices and evaluation of algorithms in building energy efficient design optimization. Energy 2016, 114, 100–112. [Google Scholar] [CrossRef]
- Gu, M.; Cai, X.; Fu, Q.; Li, H.; Wang, X.; Mao, B. Numerical Analysis of Passive Piles under Surcharge Load in Extensively Deep Soft Soil. Buildings 2022, 12, 1988. [Google Scholar] [CrossRef]
- Zhang, C.; Ali, A.; Sun, L. Investigation on low-cost friction-based isolation systems for masonry building structures: Experimental and numerical studies. Eng. Struct. 2021, 243, 112645. [Google Scholar] [CrossRef]
- Fu, Q.; Gu, M.; Yuan, J.; Lin, Y. Experimental Study on Vibration Velocity of Piled Raft Supported Embankment and Foundation for Ballastless High Speed Railway. Buildings 2022, 12, 1982. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Yang, C. Driving mechanism of digital economy based on regulation algorithm for development of low-carbon industries. Sustain. Energy Technol. Assess. 2022, 102909. [Google Scholar] [CrossRef]
- Zheng, W.; Zhou, Y.; Liu, S.; Tian, J.; Yang, B.; Yin, L. A deep fusion matching network semantic reasoning model. Appl. Sci. 2022, 12, 3416. [Google Scholar] [CrossRef]
- Noori, A.; Shahbazadeh, M.J.; Eslami, M. Designing of wide-area damping controller for stability improvement in a large-scale power system in presence of wind farms and SMES compensator. Int. J. Electr. Power Energy Syst. 2020, 119, 105936. [Google Scholar] [CrossRef]
- Eslami, M.; Neshat, M.; Khalid, S.A. A novel hybrid sine cosine algorithm and pattern search for optimal coordination of power system damping controllers. Sustainability 2022, 14, 541. [Google Scholar] [CrossRef]
- Noroozi, M.; Mohammadi, H.; Efatinasab, E.; Lashgari, A.; Eslami, M.; Khan, B. Golden Search Optimization Algorithm. IEEE Access 2022, 10, 37515–37532. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Optimal location of PSS using improved PSO with chaotic sequence. In Proceedings of the International Conference on Electrical, Control and Computer Engineering 2011 (InECCE), Kuantan, Malaysia, 21–22 June 2011; pp. 253–258. [Google Scholar]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Coordinated design of PSS and SVC damping controller using CPSO. In Proceedings of the 2011 5th International Power Engineering and Optimization Conference, Shah Alam, Malaysia, 6–7 June 2011; pp. 11–16. [Google Scholar]
- Khajehzadeh, M.; Keawsawasvong, S.; Nehdi, M.L. Effective hybrid soft computing approach for optimum design of shallow foundations. Sustainability 2022, 14, 1847. [Google Scholar] [CrossRef]
- Rad, M.M.; Ibrahim, S.K. Optimal plastic analysis and design of pile foundations under reliable conditions. Period. Polytech. Civ. Eng. 2021, 65, 761–767. [Google Scholar]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Shi, X.; Tian, Z.; Chen, W.; Si, B.; Jin, X. A review on building energy efficient design optimization rom the perspective of architects. Renew. Sustain. Energy Rev. 2016, 65, 872–884. [Google Scholar] [CrossRef]
- Lorestani, A.; Ardehali, M. Optimization of autonomous combined heat and power system including PVT, WT, storages, and electric heat utilizing novel evolutionary particle swarm optimization algorithm. Renew. Energy 2018, 119, 490–503. [Google Scholar] [CrossRef]
- Pereira, R.; Aelenei, L. Optimization assessment of the energy performance of a BIPV/T-PCM system using Genetic Algorithms. Renew. Energy 2019, 137, 157–166. [Google Scholar] [CrossRef]
- Zheng, W.; Yin, L.; Chen, X.; Ma, Z.; Liu, S.; Yang, B. Knowledge base graph embedding module design for Visual question answering model. Pattern Recognit. 2021, 120, 108153. [Google Scholar] [CrossRef]
- Huang, M.-S.; Gül, M.; Zhu, H.-P. Vibration-based structural damage identification under varying temperature effects. J. Aerosp. Eng. 2018, 31, 04018014. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Damping Controller Design for Power System Oscillations Using Hybrid GA-SQP. Int. Rev. Electr. Eng.-IREE 2011, 6, 888–896. [Google Scholar]
- Huang, M.; Lei, Y.; Li, X.; Gu, J. Damage identification of bridge structures considering temperature variations-based SVM and MFO. J. Aerosp. Eng. 2021, 34, 04020113. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. Artificial bee colony algorithm for large-scale problems and engineering design optimization. J. Intell. Manuf. 2012, 23, 1001–1014. [Google Scholar] [CrossRef]
- Arabali, A.; Khajehzadeh, M.; Keawsawasvong, S.; Mohammed, A.H.; Khan, B. An Adaptive Tunicate Swarm Algorithm for Optimization of Shallow Foundation. IEEE Access 2022, 10, 39204–39219. [Google Scholar] [CrossRef]
- Luo, J.; Huang, M.; Xiang, C.; Lei, Y. Bayesian damage identification based on autoregressive model and MH-PSO hybrid MCMC sampling method. J. Civ. Struct. Health Monit. 2022, 12, 361–390. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Opposition-based firefly algorithm for earth slope stability evaluation. China Ocean. Eng. 2014, 28, 713–724. [Google Scholar] [CrossRef]
- Huang, M.; Cheng, X.; Lei, Y. Structural damage identification based on substructure method and improved whale optimization algorithm. J. Civ. Struct. Health Monit. 2021, 11, 351–380. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2022, 1–25. [Google Scholar] [CrossRef]
- Shami, T.M.; Grace, D.; Burr, A.; Mitchell, P.D. Single candidate optimizer: A novel optimization algorithm. Evol. Intell. 2022, 1–25. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Pelican optimization algorithm: A novel nature-inspired algorithm for engineering applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef]
- Cherki, I.; Chaker, A.; Djidar, Z.; Khalfallah, N.; Benzergua, F. A Sequential Hybridization of Genetic Algorithm and Particle Swarm Optimization for the Optimal Reactive Power Flow. Sustainability 2019, 11, 3862. [Google Scholar] [CrossRef]
- Wetter, M.; Wright, J. A comparison of deterministic and probabilistic optimization algorithms for nonsmooth simulation-based optimization. Build. Environ. 2004, 39, 989–999. [Google Scholar] [CrossRef]
- Waibel, C.; Wortmann, T.; Evins, R.; Carmeliet, J. Building energy optimization: An extensive benchmark of global search algorithms. Energy Build. 2019, 187, 218–240. [Google Scholar] [CrossRef]
- Crawley, D.B.; Lawrie, L.K.; Pedersen, C.O.; Winkelmann, F.C. Energy plus: Energy simulation program. ASHRAE J. 2000, 42, 49–56. [Google Scholar]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.; Dhiman, G. Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November—1 December 1995; pp. 1942–1948. [Google Scholar]
- Yang, X.S. Firefly algorithms for multimodal optimization. Lect. Notes Comput. Sci. 2009, 5792, 169–178. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]



| Variables | X1 | X2 | X3 | X4 |
|---|---|---|---|---|
| Description | Building orientation | Window width West | Window width East | Shading transmit-tance |
| Bounds | [−180, 180] | [0.1, 5.9] | [0.1, 5.9] | [0.2, 0.8] |
| Units | ◦ | m | m | - |
| Variables | Description | Bounds | Units |
|---|---|---|---|
| X1 | Window width North | [1.224, 5.8321] | m |
| X2 | Window width West | [7.344, 25.668] | m |
| X3 | Window width East | [7.344, 25.668] | m |
| X4 | Window width South | [1.224, 5.8321] | m |
| X5 | Overhang depth West | [0.05, 1.05] | m |
| X6 | Overhang depth East | [0.05, 1.05] | m |
| X7 | Overhang depth South | [0.05, 1.05] | m |
| X8 | Shading set point West | [100, 600] | W/m2 |
| X9 | Shading set point East | [100, 600] | W/m2 |
| X10 | Shading set point South | [100, 600] | W/m2 |
| X11 | Night cooling summer, set point | [20, 25] | °C |
| X12 | Night cooling winter, set point | [20, 25] | °C |
| X13 | Supply air temperature cooling | [12, 18] | °C |
| Function | Range | n (Dim) | |
|---|---|---|---|
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 |
| Function | Range | n (Dim) | |
|---|---|---|---|
| 428.9829 × n | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 | ||
| 0 | 30 |
| F | Index | POSCO | POA | PSO | FA | MVO | SSA | TSA |
|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 0.00 | 2.42 × 10−97 | 4.98 × 10−9 | 7.11 × 10−3 | 2.81 × 10−1 | 3.29 × 10−7 | 8.31 × 10−56 |
| Std. | 0.00 | 7.22 × 10−97 | 1.40 × 10−8 | 3.21 × 10−3 | 1.11 × 10−1 | 5.92 × 10−7 | 1.02 × 10−58 | |
| F2 | Mean | 0.00 | 1.16 × 10−52 | 7.29 × 10−4 | 4.34 × 10−1 | 3.96 × 10−1 | 1.9111 | 8.36 × 10−35 |
| Std. | 0.00 | 2.55 × 10−52 | 1.84 × 10−3 | 1.84 × 10−1 | 1.41 × 10−1 | 1.6142 | 9.86 × 10−35 | |
| F3 | Mean | 4.37 × 10−178 | 7.84 × 10−81 | 1.40 × 10 | 1.66 × 103 | 4.31 × 10 | 1.50 × 103 | 1.51 × 10−14 |
| Std. | 5.76 × 10−181 | 3.49 × 10−80 | 7.13 | 6.72 × 102 | 8.97 | 707.05 | 6.55 × 10−14 | |
| F4 | Mean | 2.58 × 10−106 | 4.57 × 10−46 | 6.00 × 10−1 | 1.11 × 10−1 | 8.80 × 10−1 | 2.44 × 10−5 | 1.95 × 10−5 |
| Std. | 4.49 × 10−108 | 9.98 × 10−46 | 1.72 × 10−1 | 4.75 × 10−2 | 2.50 × 10−1 | 1.89 × 10−5 | 4.49 × 10−4 | |
| F5 | Mean | 2.71 × 10−1 | 2.80 × 10 | 4.93 × 10 | 7.97 × 10 | 1.18 × 102 | 136.56 | 28.4 |
| Std. | 5.68 × 10−1 | 8.73 × 10−1 | 3.89 × 10 | 7.39 × 10 | 1.43 × 102 | 154.00 | 0.842 | |
| F6 | Mean | 4.77 × 10−17 | 2.15 | 6.92 × 10−2 | 6.94 × 10−3 | 2.02 × 10−2 | 5.72 × 10−7 | 3.67 |
| Std. | 2.25 × 10−7 | 4.47 × 10−1 | 2.87 × 10−2 | 3.61 × 10−3 | 7.43 × 10−3 | 2.44 × 10−7 | 0.3353 | |
| F7 | Mean | 3.73 × 10−6 | 1.51 × 10−4 | 8.94 × 10−2 | 6.62 × 10−2 | 5.24 × 10−2 | 8.82 × 10−5 | 0.0018 |
| Std. | 3.36 × 10−6 | 1.33 × 10−4 | 0.0206 | 4.23 × 10−2 | 1.37 × 10−2 | 6.94 × 10−5 | 4.62 × 10−4 |
| F | Index | POSCO | POA | PSO | FA | MVO | SSA | TSA |
|---|---|---|---|---|---|---|---|---|
| F8 | Mean | –1.22 × 104 | −1.01 × 104 | −6.01 × 103 | −5.85 × 103 | −6.92 × 103 | −7.46 × 103 | −7.89 × 103 |
| Std. | 5.21 × 102 | 1.70 × 103 | 1.30 × 103 | 1.61 × 103 | 9.19 × 102 | 634.67 | 599.26 | |
| F9 | Mean | 0.00 | 0.00 | 4.72 × 10 | 1.51 × 10 | 1.01 × 102 | 55.45 | 151.45 |
| Std. | 0.00 | 0.00 | 1.03 × 10 | 1.25 × 10 | 1.89 × 10 | 18.27 | 35.87 | |
| F10 | Mean | 8.88 × 10−16 | 8.77 × 10−16 | 3.86 × 10−2 | 4.58 × 10−2 | 1.15 | 2.84 | 2.409 |
| Std. | 0.00 | 0.00 | 2.11 × 10−1 | 1.20 × 10−2 | 7.87 × 10−1 | 6.58 × 10−1 | 1.392 | |
| F11 | Mean | 0.00 | 0.00 | 5.50 × 10−3 | 4.23 × 10−3 | 5.74 × 10−1 | 2.29 × 10−1 | 0.0077 |
| Std. | 0.00 | 0.00 | 7.39 × 10−3 | 1.29 × 10−3 | 1.12 × 10−1 | 1.29 × 10−1 | 0.0057 | |
| F12 | Mean | 1.35 × 10−5 | 1.25 × 10−1 | 1.05 × 10−2 | 3.13 × 10−4 | 1.27 | 6.82 | 6.373 |
| Std. | 1.48 × 10−5 | 5.41 × 10−2 | 2.06 × 10−2 | 1.76 × 10−4 | 1.02 | 2.72 | 3.458 | |
| F13 | Mean | 2.46 × 10−4 | 1.99 | 4.03 × 10−1 | 2.08 × 10−3 | 6.60 × 10−2 | 21.31 | 2.897 |
| Std. | 2.92 × 10−4 | 2.51 × 10−1 | 5.39 × 10−1 | 9.62 × 10−4 | 4.33 × 10−2 | 16.99 | 0.643 |
| Variables | X1 | X2 | X3 | X4 | F(x) |
|---|---|---|---|---|---|
| Description | Building orientation | Window width West | Window width East | Shading transmittance | Objective function |
| Units | ◦ | m | m | - | |
| Optimum value (Seattle) | 71.924 | 5.9 | 5.9 | 0.2876 | 132.6 |
| Optimum value (Chicago) | 70.342 | 4.1 | 5.9 | 0.3126 | 152.2 |
| Optimum value (Houston) | 75.564 | 5.1 | 3.5 | 0.4873 | 185.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, X.; Karbasforoushha, M.A.; Syah, R.B.Y.; Khajehzadeh, M.; Keawsawasvong, S.; Nehdi, M.L. An Effective Metaheuristic Approach for Building Energy Optimization Problems. Buildings 2023, 13, 80. https://doi.org/10.3390/buildings13010080
Yuan X, Karbasforoushha MA, Syah RBY, Khajehzadeh M, Keawsawasvong S, Nehdi ML. An Effective Metaheuristic Approach for Building Energy Optimization Problems. Buildings. 2023; 13(1):80. https://doi.org/10.3390/buildings13010080
Chicago/Turabian StyleYuan, Xinzhe, Mohammad Ali Karbasforoushha, Rahmad B. Y. Syah, Mohammad Khajehzadeh, Suraparb Keawsawasvong, and Moncef L. Nehdi. 2023. "An Effective Metaheuristic Approach for Building Energy Optimization Problems" Buildings 13, no. 1: 80. https://doi.org/10.3390/buildings13010080
APA StyleYuan, X., Karbasforoushha, M. A., Syah, R. B. Y., Khajehzadeh, M., Keawsawasvong, S., & Nehdi, M. L. (2023). An Effective Metaheuristic Approach for Building Energy Optimization Problems. Buildings, 13(1), 80. https://doi.org/10.3390/buildings13010080









