Optimal Design of Nonlinear Negative-Stiffness Damper with Flexible Support for Mitigating Cable Vibration
Abstract
:1. Introduction
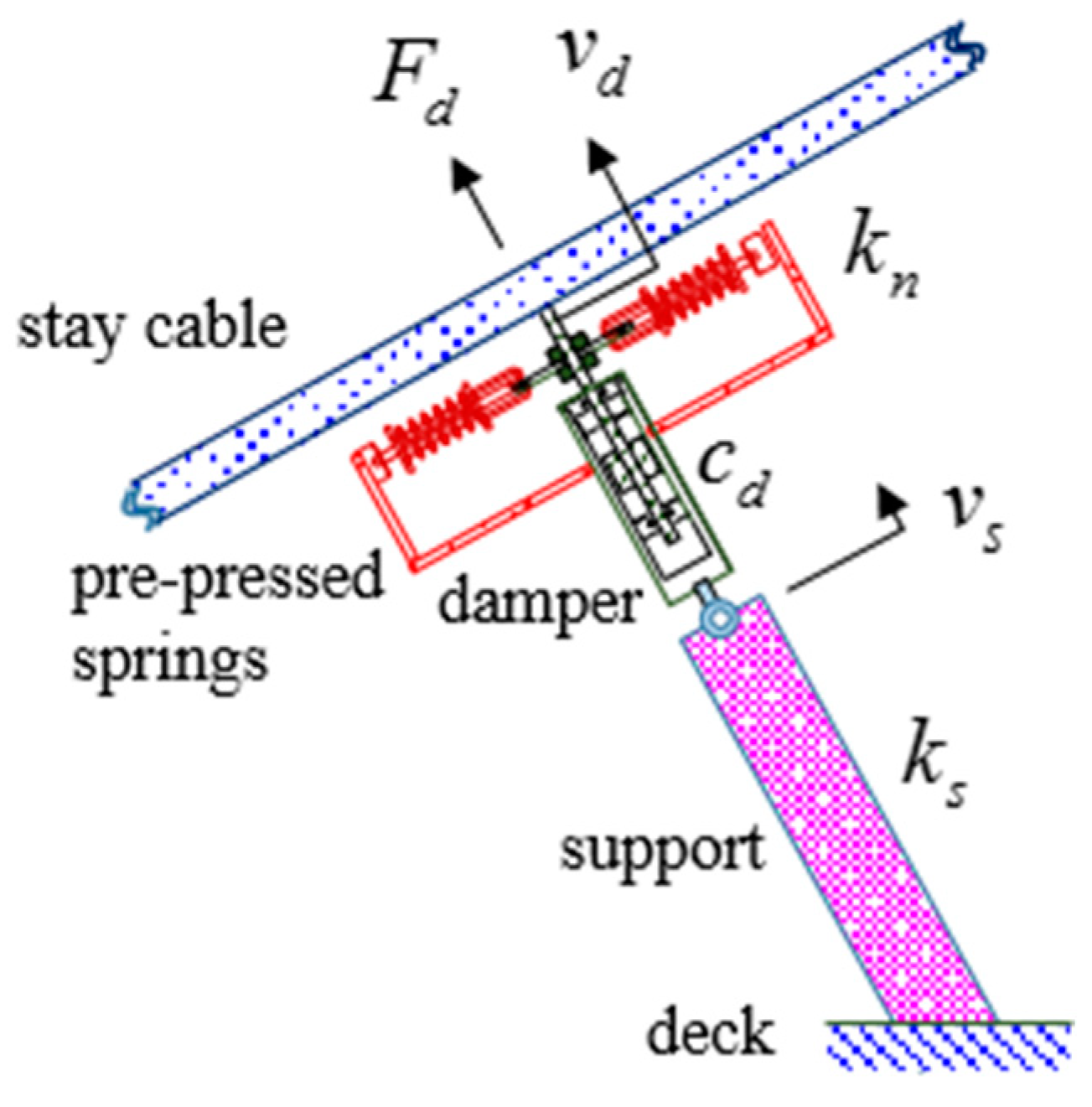
2. Negative-Stiffness Damper with a Flexible Support on Cables
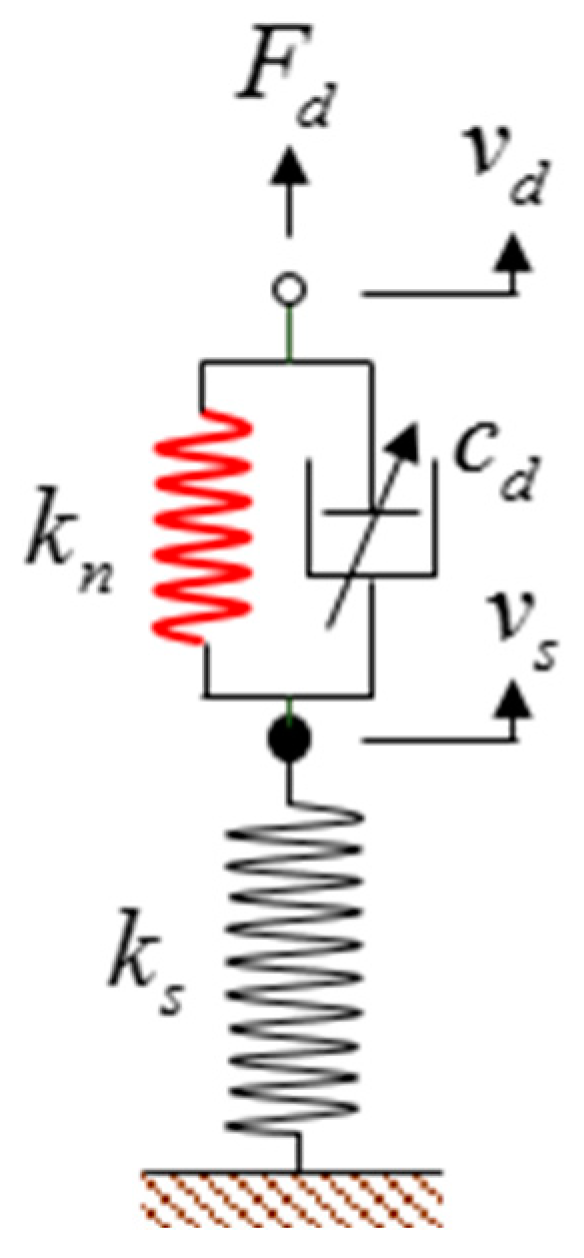
2.1. Simplified Model of the Damper Support System
2.2. Equivalent Model for the Case of Linear Viscous Damping
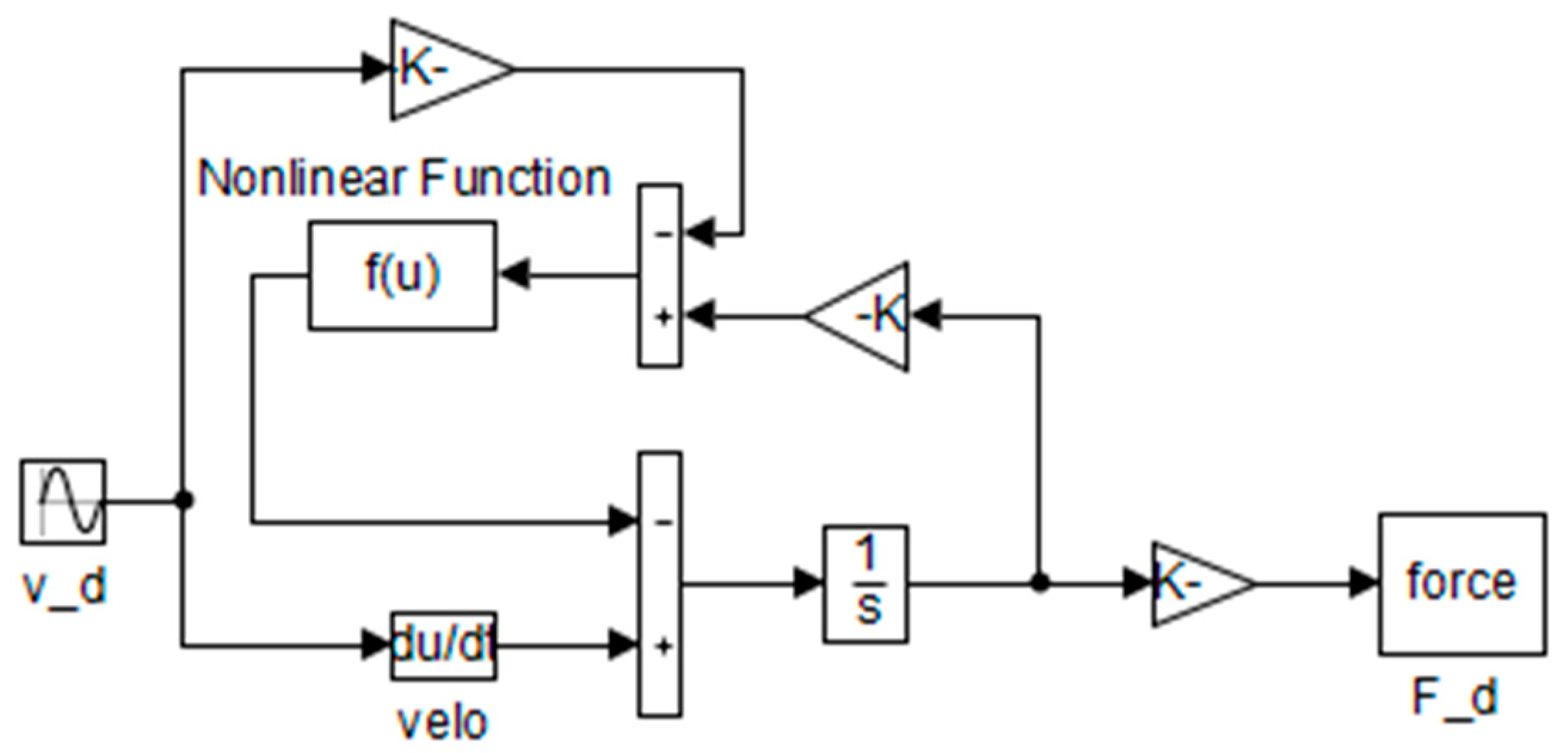
2.3. Equivalent Model for the Case of Friction
3. Optimization of Negative-Stiffness Damper with a Flexible Support for Cable Vibration Control
3.1. Problem Formulation
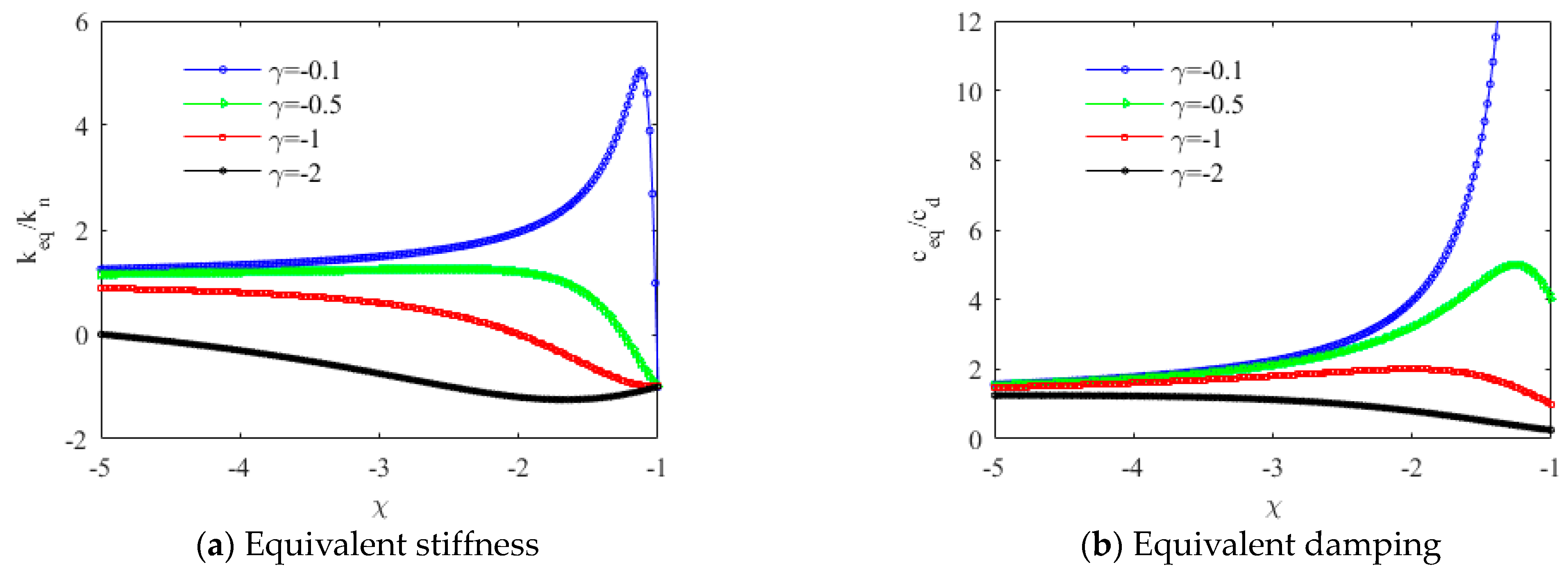
3.2. Optimized Parameters of Linear Negative-Stiffness Damper with a Flexible Support
3.3. Numerical Studies for Designing Negative-Stiffness Dampers with Supports
3.4. Simplified Design of Nonlinear Negative-Stiffness Damper for Mitigating Cable Vibration
4. Conclusions
- A properly flexible support is able to enlarge the equivalent negative stiffness and damping under both linear and nonlinear conditions.
- An optimization process is developed for multimodal cable vibration. It is sufficient to only consider the highest mode to obtain the optimized size of a negative-stiffness damper and its corresponding support.
- Nonlinear negative-stiffness dampers have the ability of transferring vibration energy into high-order modes, thereby realizing superior performance in reducing cable vibration.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.; Tao, T.; Gao, Y.; Xu, F. Measurement of wind effects on a kilometer-level cable-stayed bridge during typhoon Haikui. J. Struct. Eng. 2018, 144, 04018142. [Google Scholar] [CrossRef]
- Ge, C.; Chen, A. Vibration characteristics identification of ultra-long cables of a cable-stayed bridge in normal operation based on half-year monitoring data. Struct. Infrastruct. Eng. 2019, 15, 1567–1582. [Google Scholar] [CrossRef]
- Daniotti, N.; Jakobsen, J.B.; Snæbjörnsson, J.; Cheynet, E.; Wang, J. Observations of bridge stay cable vibrations in dry and wet conditions: A case study. J. Sound Vib. 2021, 503, 116106. [Google Scholar] [CrossRef]
- Kim, S.; Kim, S.; Kim, H.K. High-mode vortex-induced vibration of stay cables: Monitoring, cause investigation, and mitigation. J. Sound Vib. 2022, 524, 116758. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Vo, D.H. Further Explanation on the Excitation Mechanism of Stay Cable Vibration in Dry Conditions. Buildings 2023, 13, 1543. [Google Scholar] [CrossRef]
- Zhang, M.J.; Xu, F.Y. Tuned mass damper for self-excited vibration control: Optimization involving nonlinear aeroelastic effect. J. Wind. Eng. Ind. Aerodyn. 2022, 220, 104836. [Google Scholar] [CrossRef]
- Chen, L.; Sun, L.; Xu, Y.; Di, F.; Xu, Y.; Wang, L. A comparative study of multi-mode cable vibration control using viscous and viscoelastic dampers through field tests on the Sutong Bridge. Eng. Struct. 2020, 224, 111226. [Google Scholar] [CrossRef]
- Lu, L.; Duan, Y.-F.; Spencer, B.F.; Lu, X.; Zhou, Y. Inertial mass damper for mitigating cable vibration. Struct. Control Health Monit. 2017, 24, e1986. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, S.Y. Dynamic characteristics of stay cables with inerter dampers. J. Sound Vib. 2018, 423, 287–305. [Google Scholar] [CrossRef]
- Wang, Z.H.; Xu, Y.W.; Gao, H.; Chen, Z.Q.; Xu, K.; Zhao, S.B. Vibration control of a stay cable with a rotary electromagnetic inertial mass damper. Smart Struct. Syst. 2019, 23, 627–639. [Google Scholar]
- Shi, X.; Shi, W.; Lin, K.; Xing, L.; Zhu, S. Optimal design of tuned inerter dampers with series or parallel stiffness connection for cable vibration control. Struct. Control Health Monit. 2021, 28, e2673. [Google Scholar] [CrossRef]
- Gao, H.; Wang, H.; Li, J.; Wang, Z.; Liang, R.; Xu, Z.; Ni, Y. Optimum design of viscous inerter damper targeting multi-mode vibration mitigation of stay cables. Eng. Struct. 2021, 226, 111375. [Google Scholar] [CrossRef]
- Li, H.; Liu, M.; Ou, J.P. Negative stiffness characteristics of active and semiactive control systems for stay cables. Struct. Control Health Monit. 2008, 15, 120–142. [Google Scholar] [CrossRef]
- Weber, F.; Distl, H. Semi-active damping with negative stiffness for multi-mode cable vibration mitigation: Approximate collocated control solution. Smart Mater. Struct. 2015, 24, 115015. [Google Scholar] [CrossRef]
- Xu, Y.-W.; Xu, Z.-D.; Guo, Y.-Q.; Zhou, M.; Zhao, Y.-L.; Yang, Y.; Dai, J.; Zhang, J.; Zhu, C.; Ji, B.-H.; et al. A programmable pseudo negative stiffness control device and its role in stay cable vibration control. Mech. Syst. Signal Process. 2022, 173, 109054. [Google Scholar] [CrossRef]
- Pasala, D.T.R.; Sarlis, A.A.; Nagarajaiah, S.; Reinhorn, A.M.; Constantinou, M.C.; Taylor, D. Adaptive negative stiffness: New structural modification approach for seismic protection. J. Struct. Eng. 2013, 139, 1112–1123. [Google Scholar] [CrossRef]
- Attary, N.; Symans, M.; Nagarajaiah, S.; Reinhorn, A.M.; Constantinou, M.C.; Sarlis, A.A.; Pasala, D.T.R.; Taylor, D. Performance evaluation of negative stiffness devices for seismic response control of bridge structures via experimental shake table tests. J. Earthq. Eng. 2015, 19, 249–276. [Google Scholar] [CrossRef]
- Attary, N.; Symans, M.; Nagarajaiah, S.; Reinhorn, A.M.; Constantinou, M.C.; Sarlis, A.A.; Pasala, D.T.R.; Taylor, D. Numerical simulations of a highway bridge structure employing passive negative stiffness device for seismic protection. Earthq. Eng. Struct. Dyn. 2015, 44, 973–995. [Google Scholar] [CrossRef]
- Chen, L.; Sun, L.M.; Nagarajaiah, S. Cable with discrete negative stiffness device and viscous damper: Passive realization and general characteristics. Smart Struct. Syst. 2015, 15, 627–643. [Google Scholar] [CrossRef]
- Zhou, P.; Li, H. Modeling and control performance of a negative stiffness damper for suppressing stay cable vibrations. Struct. Control Health Monit. 2016, 23, 764–782. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, M.; Xiao, H.G.; Li, H. Feasibility of using a negative stiffness damper to two interconnected stay cables for damping enhancement. Int. J. Struct. Stab. Dyn. 2019, 19, 1950058. [Google Scholar] [CrossRef]
- Liu, M.; Zhou, P.; Li, H. Novel self-centering negative stiffness damper based on combination of shape memory alloy and pre-pressed springs. J. Aerosp. Eng. 2018, 31, 04018100. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, S.Y. Magnetic negative stiffness dampers. Smart Mater. Struct. 2015, 24, 072002. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, S.Y.; Spencer, B.F. Experimental study on passive negative stiffness damper for cable vibration mitigation. J. Eng. Mech. 2017, 143, 04017070. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, S.Y.; Nagarajaiah, S. Performance comparison between passive negative stiffness damper and active control in cable vibration mitigation. J. Bridge Eng. 2017, 22, 04017054. [Google Scholar] [CrossRef]
- Xu, Y.L.; Zhou, H.J. Damping cable vibration for a cable-stayed bridge using adjustable fluid dampers. J. Sound Vib. 2007, 306, 349–360. [Google Scholar] [CrossRef]
- Fournier, J.A.; Cheng, S.H. Impact of damper stiffness and damper support stiffness on the efficiency of a linear viscous damper in controlling stay cable vibrations. J. Bridge Eng. 2014, 19, 04013022. [Google Scholar] [CrossRef]
- Huang, Z.; Jones, N.P. Damping of taut-cable systems: Effects of linear elastic spring support. J. Eng. Mech. 2011, 137, 512–518. [Google Scholar] [CrossRef]
- Javanbakht, M.; Cheng, S.H.; Ghrib, F. Multimode vibration control of stay cables using optimized negative stiffness damper. Struct. Control Health Monit. 2020, 27, e2503. [Google Scholar] [CrossRef]
- Javanbakht, M.; Cheng, S.; Ghrib, F. Impact of support stiffness on the performance of negative stiffness dampers for vibration control of stay cables. Struct. Control Health Monit. 2020, 27, e2610. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, M.; Li, H. A passive negative stiffness damper in series with a flexible support: Theoretical and experimental study. Struct. Control Health Monit. 2020, 27, e2594. [Google Scholar] [CrossRef]
- Dong, Q.M.; Cheng, S.H. Impact of Damper Stiffness and Damper Support Stiffness on the Performance of a Negative Stiffness Damper in Mitigating Cable Vibrations. J. Bridge Eng. 2021, 26, 04020131. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Z.; Zou, Y.; Wang, M.; Nagarajaiah, S.; Sun, F.; Sun, L. Practical negative stiffness device with viscoelastic damper in parallel or series configuration for cable damping improvement. J. Sound Vib. 2023, 560, 117757. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, M.; Li, H. Optimized negative stiffness damper with flexible support for stay cables. Struct. Control Health Monit. 2021, 28, e2717. [Google Scholar] [CrossRef]
- Chen, W.L.; Li, H.; Ou, J.P.; Li, F.C. Field Monitoring of vortex induced vibration of stay cables of cable-stayed bridge. In Proceedings of the 9th International Symposium on Cable Dynamics, Shanghai, China, 18–20 October 2011; pp. 257–264. [Google Scholar]


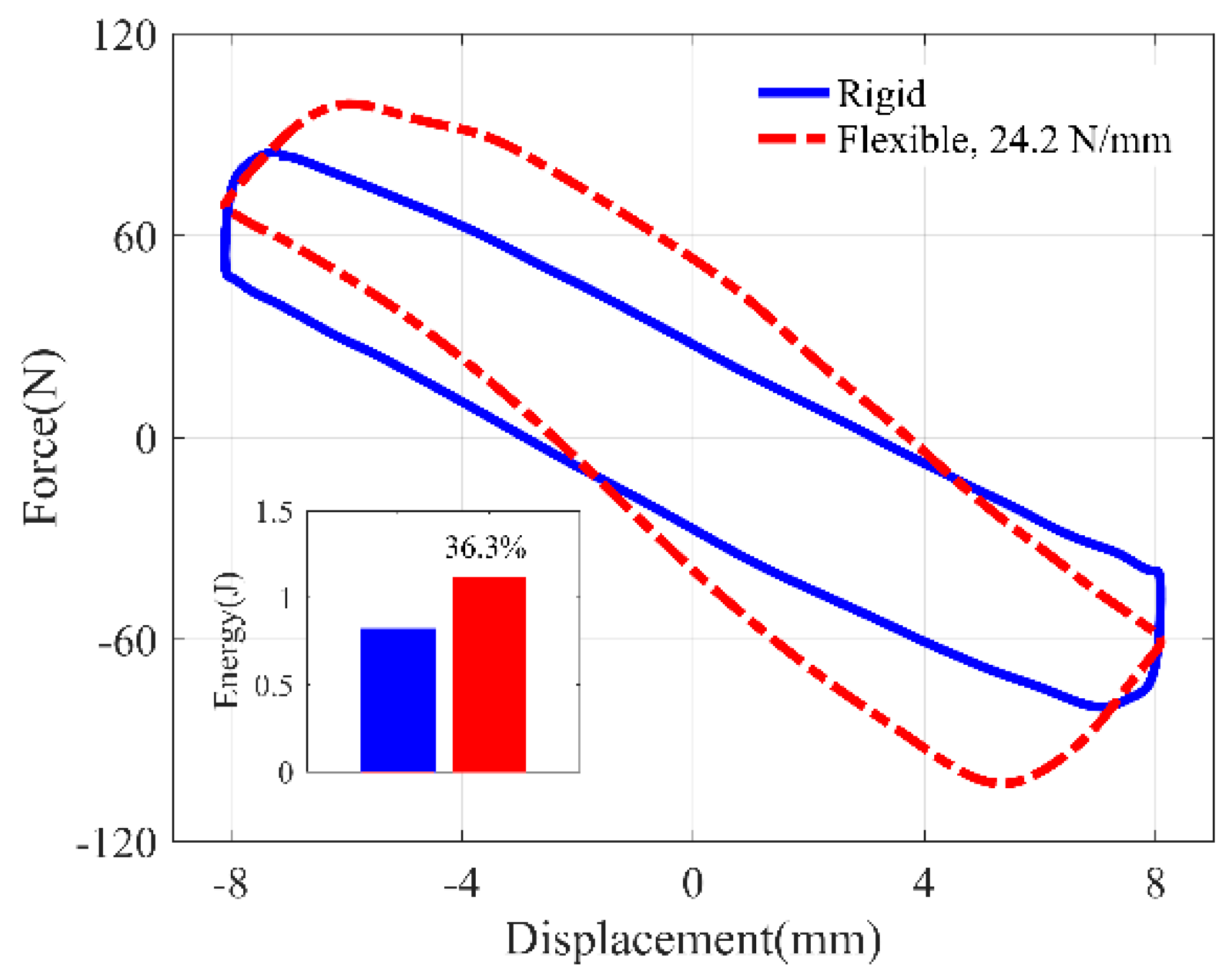
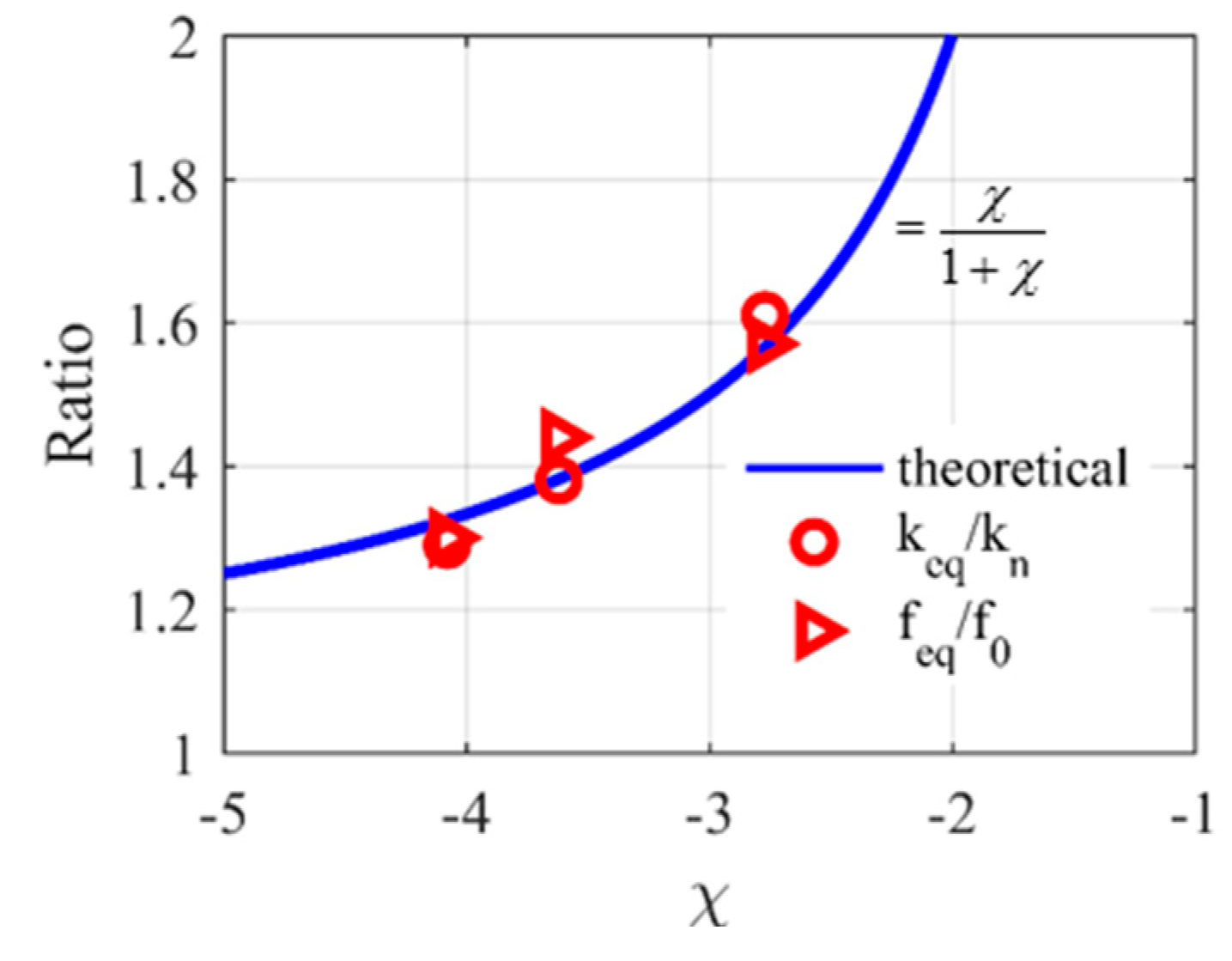

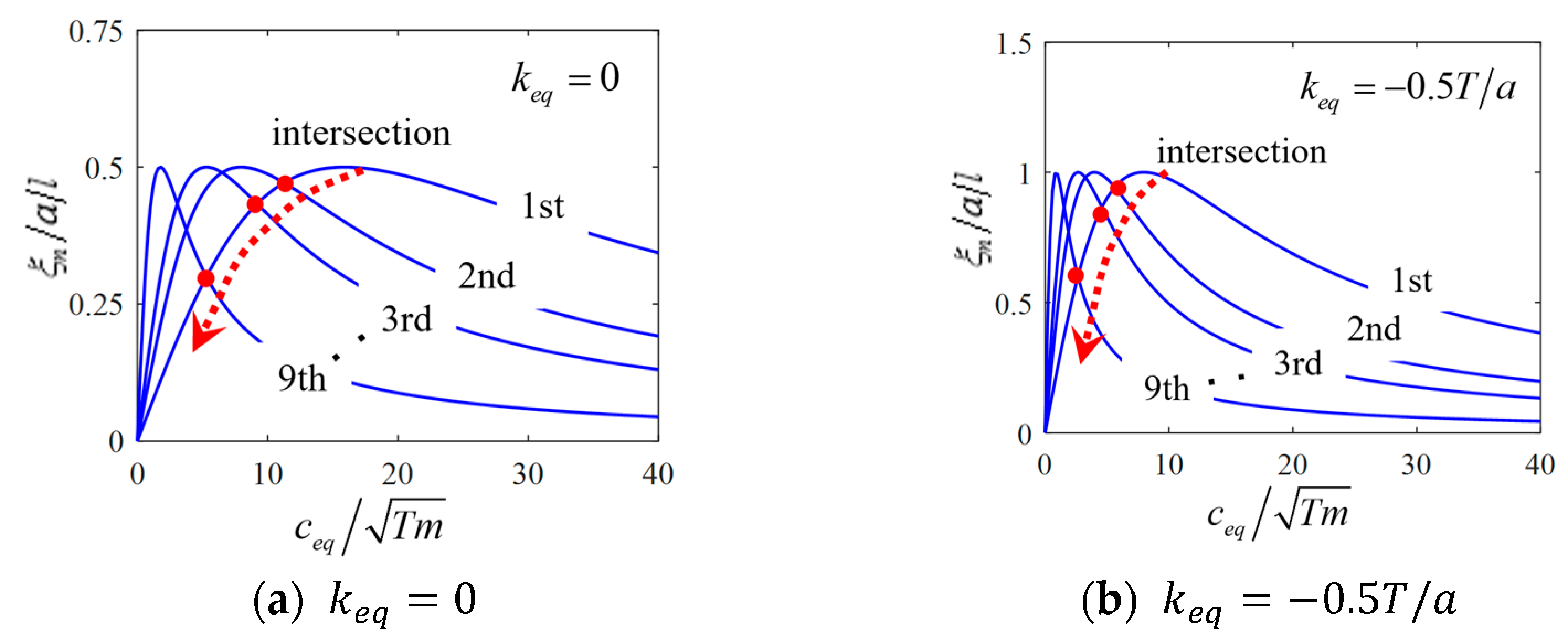


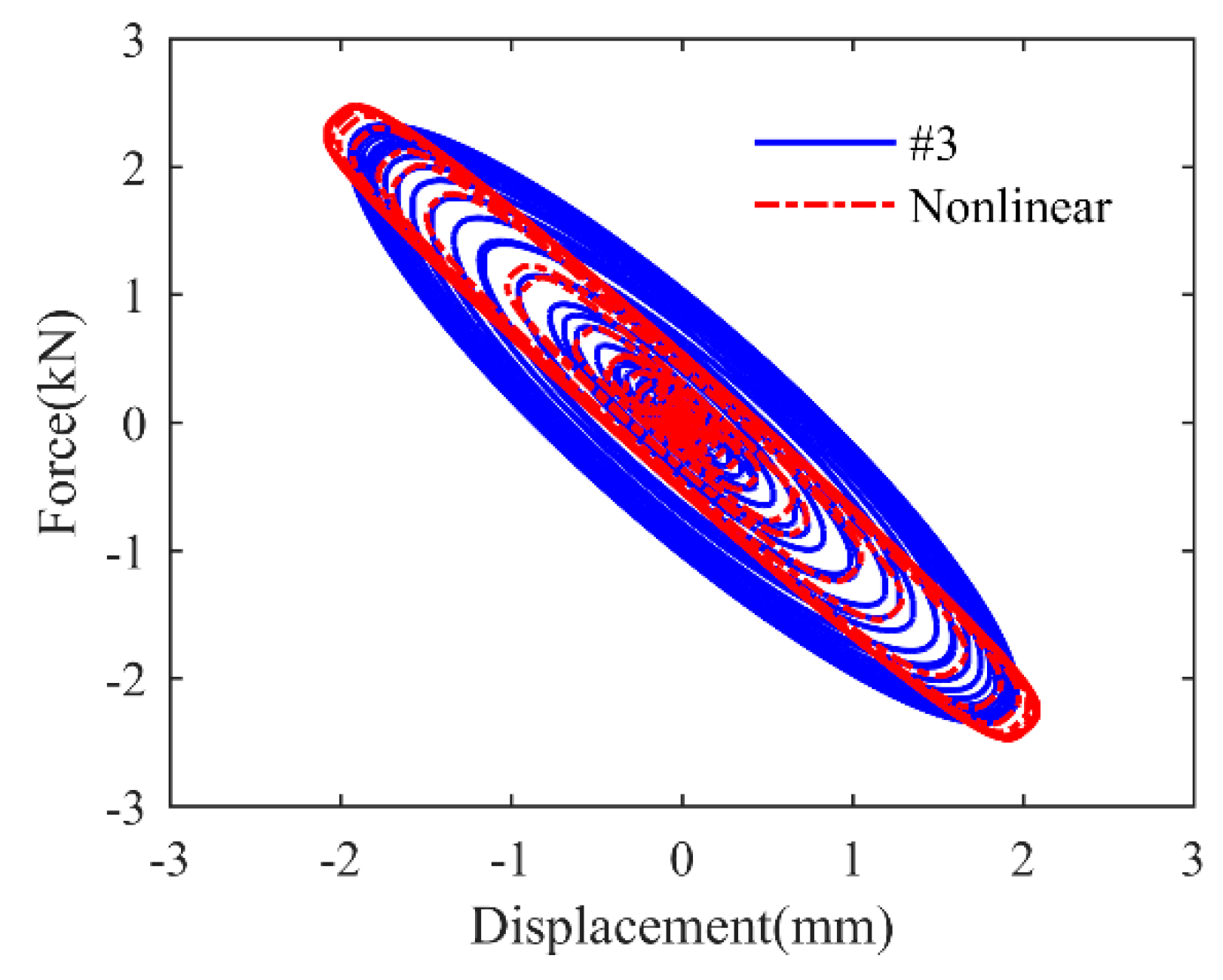

| Original Damper | Support Stiffness | Identified Equivalent Parameters | ||
|---|---|---|---|---|
| kn (N/mm) | (N) | (N/mm) | (N/mm) | (N) |
| −8.75 | 31.0 | Rigid | −8.75 | 31.0 |
| 35.7 | −11.3 | 40.3 | ||
| 31.7 | −12.1 | 44.6 | ||
| 24.2 | −14.0 | 48.7 | ||
| Damper | Support | Related Studies | Analysis Parameters | Results | |
|---|---|---|---|---|---|
| Type | Characteristics | ||||
| Adjustable fluid | Nonlinear | Flexible | Xu and Zhou [26] | , , | Decreasing support stiffness would reduce the efficiency of a damper positive or zero stiffness. |
| Viscous | Linear | Flexible | Fournier and Cheng [27] | , | |
| Viscous or friction | Linear and nonlinear | Flexible | Huang and Jones [28] | or , | |
| Negative stiffness | Linear and nonlinear | Rigid | Xu et al. [15], Zhou and Li [20], Zhou et al. [21], Liu et al. [22], Shi and Zhu [23], Shi et al. [24,25] | , , | Support flexibility is not considered. |
| Negative stiffness | Linear | Flexible | Javanbakht et al. [29,30], Dong and Cheng [32] | , , | A more flexible support would enhance performance of negative-stiffness damper with proper parameters. |
| Negative device with viscoelastic damper | Linear | Flexible | Chen et al. [33] | , , | Combining negative device with viscoelastic damper would be efficient but sensitive to parameters. |
| Negative stiffness | Linear and nonlinear | Flexible | Present work | , , , | A properly flexible support could enlarge equivalent parameters for both linear and nonlinear conditions. |
| Design Schemes | Damping Ratios (j = 1,2,3,4) | Location a/l | Negative-Stiffness Damper | Support Stiffness (kN/m) | |
|---|---|---|---|---|---|
| (kN s/m) | (kN/m) | ||||
| #1 | 1.5% | 135.5 | −298.6 | Rigid | |
| #2 | 169.3 | −1194.4 | |||
| #3 | 42.3 | −597.2 | 1194.4 | ||
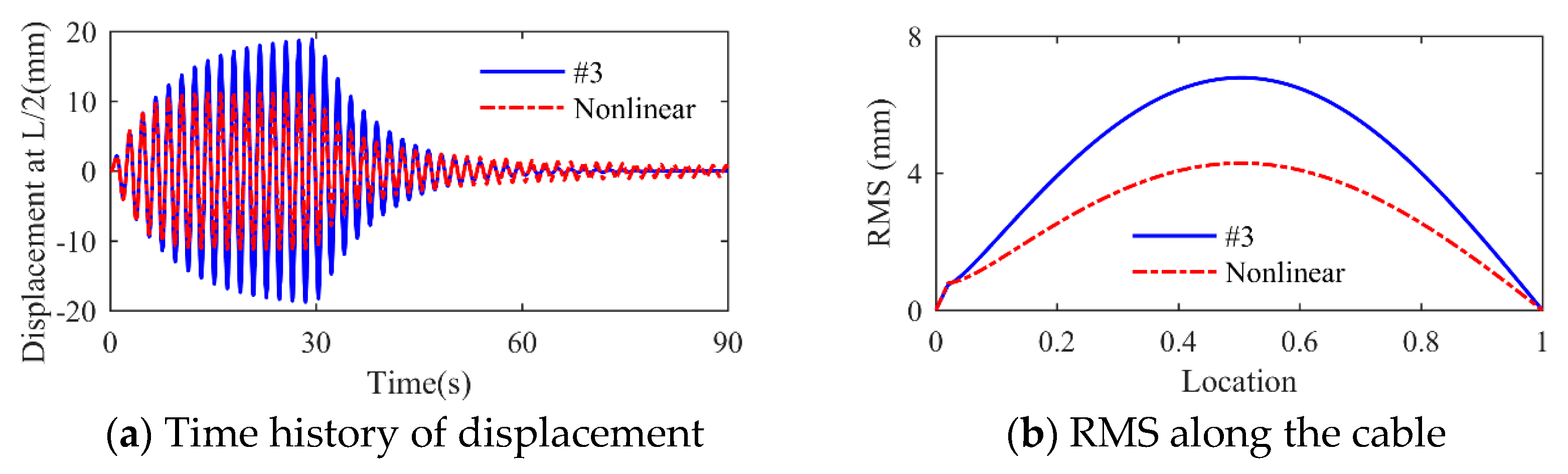
| Mode | Damper Parameters | Maximum Control Force (kN) | RMS at Nodes (mm) | |||
|---|---|---|---|---|---|---|
| Linear | Nonlinear | Linear | Nonlinear | Linear | Nonlinear | |
| 1 | Design scheme #3 | Other parameters unchanged | 2.35 | 2.48 | 6.79 | 4.29 |
| 2 | 1.21 | 1.25 | 3.27 | 2.10 | ||
| 3 | 0.83 | 0.85 | 1.69 | 1.12 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Zhou, P.; Yu, T.; Li, Z. Optimal Design of Nonlinear Negative-Stiffness Damper with Flexible Support for Mitigating Cable Vibration. Buildings 2023, 13, 2620. https://doi.org/10.3390/buildings13102620
Liu G, Zhou P, Yu T, Li Z. Optimal Design of Nonlinear Negative-Stiffness Damper with Flexible Support for Mitigating Cable Vibration. Buildings. 2023; 13(10):2620. https://doi.org/10.3390/buildings13102620
Chicago/Turabian StyleLiu, Guanliang, Peng Zhou, Tong Yu, and Zeping Li. 2023. "Optimal Design of Nonlinear Negative-Stiffness Damper with Flexible Support for Mitigating Cable Vibration" Buildings 13, no. 10: 2620. https://doi.org/10.3390/buildings13102620






