Urban Construction Waste Recycling Path: Robust Optimization
Abstract
:1. Introduction
2. Literature Review
2.1. Design of the Construction Waste Recycling Path in a Deterministic Environment
2.2. Optimizing Construction Waste Recycling Path in an Uncertain Environment
2.3. Optimization Methods
3. Materials and Methods
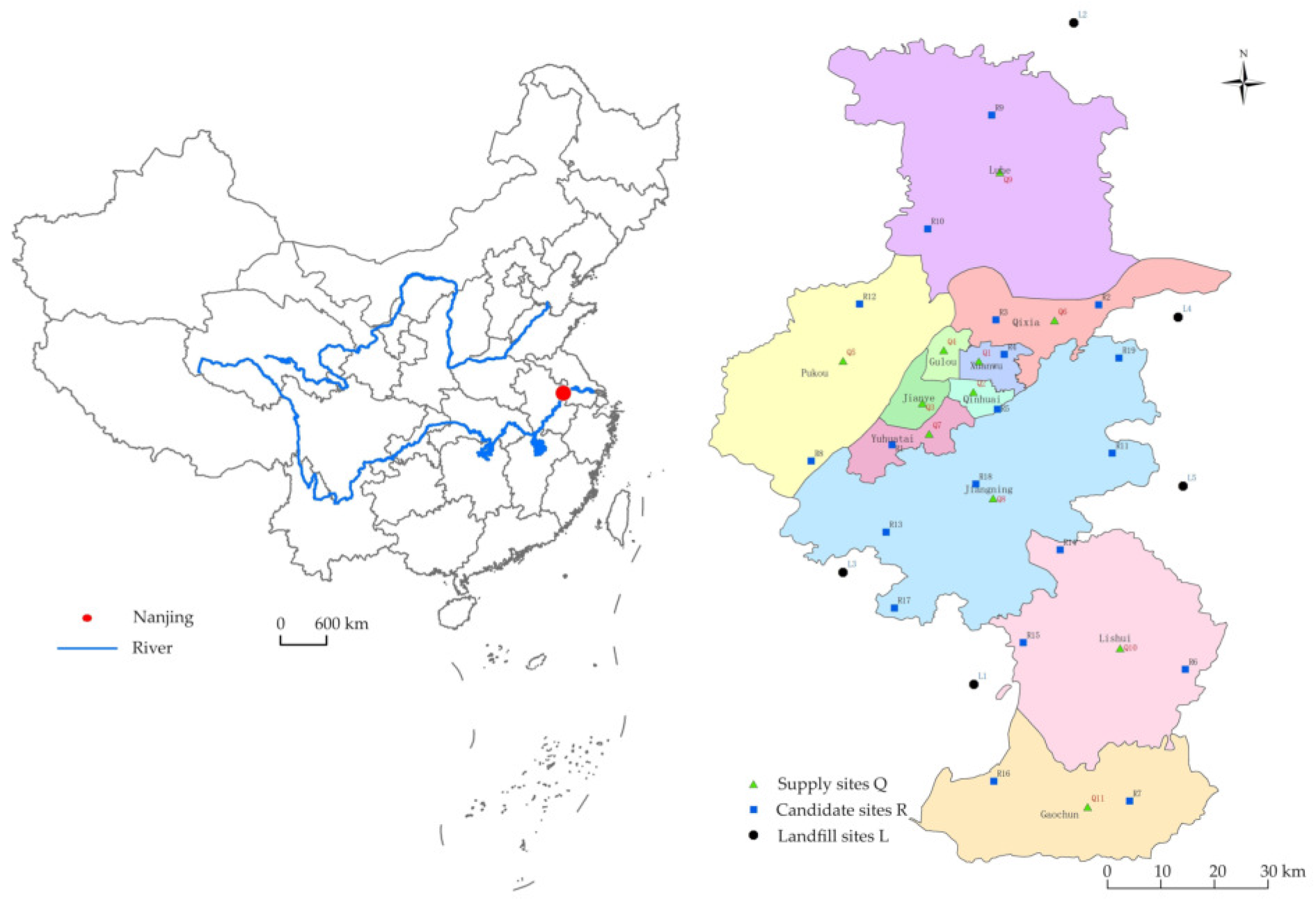
3.1. Case City Overview
3.2. Model Parameters and Data Sources
3.3. Single-Objective Planning Model in a Deterministic Environment
3.3.1. Underlying Hypotheses of the Model
3.3.2. Objective Function of the Model
- (a)
- Facility construction costs
- (b)
- Transportation costs
- (c)
- Treatment costs
- (d)
- Total cost
3.3.3. Constraints of the Model
- (a)
- Flow balance constraint
- (b)
- Capacity and capability constraints
- (c)
- Environmental and social impact constraints
3.4. Robust Optimization Model in Uncertain Environments
4. Results and Discussion
4.1. Performance Comparison
4.1.1. Total Cost Comparison
4.1.2. Comparison of Treatment Capacity
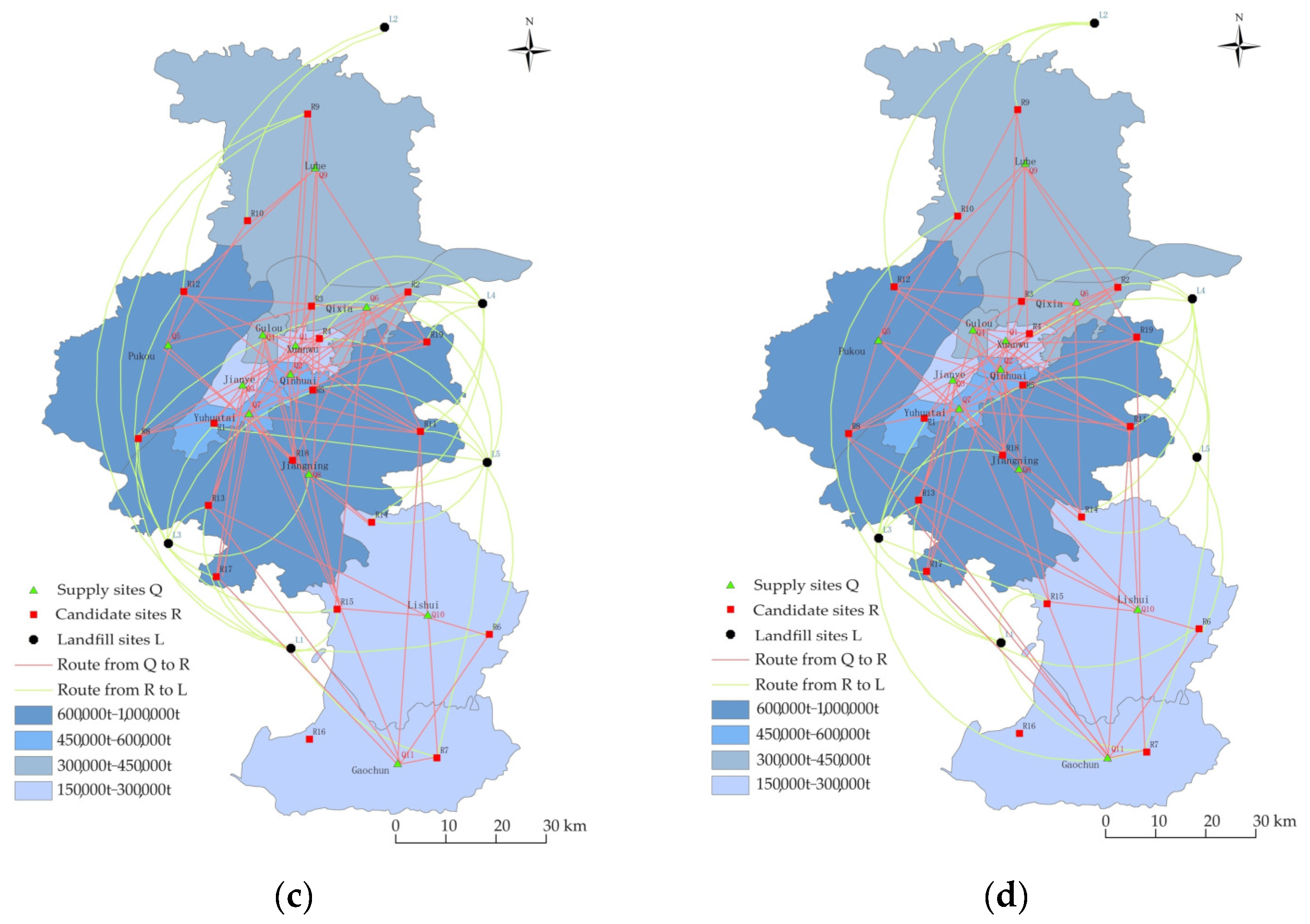
4.2. Analysis of the Evolution of the Recycling Path
4.2.1. MATLAB Calculation Results
4.2.2. Analysis of Results
- (1)
- Comparison of treatment plant sites under different levels of uncertainty
- (2)
- Comparison of transport paths under different levels of uncertainty
5. Conclusions
- This paper built a deterministic model and robust model considering the reality of Nanjing. The reality is generally consistent with our hypotheses. Hypotheses 1–3 hold. The robust model has a better total cost. From the deterministic model to the robust model, the total cost increases rapidly. And the total cost increases at a slower rate when uncertainty increases. Costs are linearly related to distance and quantities, so the robust model has a greater total cost than the deterministic model. Hypotheses 4–6 hold. The robust model is cost-effective in the face of uncertainty in supply.
- The robust model has better treatment capacity. From the deterministic model to the robust model, the total treatment capacity increases rapidly due to opening more treatment plants. There is no difference in technology among the treatment plants, but treatment capacity and capability are limited. The robust model has more treatment plants, so it has greater total treatment capacity. Hypotheses 7–9 hold. The robust model is immune to supply uncertainty at the cost of building additional treatment plants. Thus, even in the worst-case scenario, it can guarantee a higher treatment capacity.
- Both models follow the proximity principle, transporting and landfilling near the supply and treatment site, while a few other models consider long-distance transportation. This is consistent with the hypothesis that there is no direct landfill. Construction waste should be transported to treatment plants before landfilling. Hypothesis 10 holds. Compared with the deterministic model, the robust model has longer total transportation distances. However, the total cost increases very slowly, because the proximity principle significantly reduces the transportation costs and to some extent offsets the construction and treatment costs of the treatment plants, and ultimately achieves the optimization objective of the model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qiao, X.; Lee, H.; Shen, Q.; Li, Y.C. Research on the Tripartite Evolutionary Game of Zero-Waste City Construction in China. Sustainability 2023, 15, 10507. [Google Scholar] [CrossRef]
- Hu, R.; Chen, K.; Fang, W.; Zheng, L.; Xu, J. The technology-environment relationship revisited: Evidence from the impact of prefabrication on reducing construction waste. J. Clean. Prod. 2022, 341, 130883. [Google Scholar] [CrossRef]
- Tam, V.W.Y.; Hao, J.J.L. Prefabrication as a mean of minimizing construction waste on site. Int. J. Constr. Manag. 2014, 14, 113–121. [Google Scholar] [CrossRef]
- Jin, R.; Li, B.; Zhou, T.; Wanatowski, D.; Piroozfar, P. An empirical study of perceptions towards construction and demolition waste recycling and reuse in China. Resour. Conserv. Recycl. 2017, 126, 86–98. [Google Scholar] [CrossRef]
- Aslam, M.S.; Huang, B.; Cui, L. Review of construction and demolition waste management in China and USA. J. Environ. Manag. 2020, 264, 110445. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Lv, Y.; Huang, S.; Liu, Y.; Li, X. The Evolution of Research on C&D Waste and Sustainable Development of Resources: A Bibliometric Study. Sustainability 2023, 15, 9141. [Google Scholar] [CrossRef]
- Han, S.; Zhao, S.; Lu, D.; Wang, D. Performance Improvement of Recycled Concrete Aggregates and Their Potential Applications in Infrastructure: A Review. Buildings 2023, 13, 1411. [Google Scholar] [CrossRef]
- Zeng, M.; Huang, H.; Zhang, X. Experiment on the Performance of Recycled Powder of Construction Waste on Adobe Materials. Buildings 2023, 13, 1358. [Google Scholar] [CrossRef]
- Abarca-Guerrero, L.; Lobo-Ugalde, S.; Méndez-Carpio, N.; Rodríguez-Leandro, R.; Rudin-Vega, V. Zero Waste Systems: Barriers and Measures to Recycling of Construction and Demolition Waste. Sustainability 2022, 14, 15265. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.; Xue, L.; Gou, W. The Evolution of the Construction Waste Recycling System and the Willingness to Use Recycled Products in China. Sustainability 2022, 14, 12541. [Google Scholar] [CrossRef]
- Qun, Z.; Rong, W.L. Progress of Research on Reverse Logistics Network Design. Chin. J. Manag. Sci. 2016, 24, 165–176. [Google Scholar] [CrossRef]
- Bao, Z.; Lee, W.M.W.; Lu, W. Implementing on-site construction waste recycling in Hong Kong: Barriers and facilitators. Sci. Total Environ. 2020, 747, 141091. [Google Scholar] [CrossRef] [PubMed]
- Aydin, N. Designing reverse logistics network of end-of-life-buildings as preparedness to disasters under uncertainty. J. Clean. Prod. 2020, 256, 120341. [Google Scholar] [CrossRef]
- Ma, M.; Tam, V.W.Y.; Le, K.N.; Li, W. Challenges in current construction and demolition waste recycling: A China study. Waste Manag. 2020, 118, 610–625. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Xie, Q.; Feng, Y.; Zhang, P.; Yao, P. Towards a robust facility location model for construction and demolition waste transfer stations under uncertain environment: The case of Chongqing. Waste Manag. 2020, 105, 73–83. [Google Scholar] [CrossRef] [PubMed]
- Bouzon, M.; Govindan, K.; Rodriguez, C.M.T. Evaluating barriers for reverse logistics implementation under a multiple stakeholders’ perspective analysis using grey decision making approach. Resour. Conserv. Recycl. 2018, 128, 315–335. [Google Scholar] [CrossRef]
- Hammes, G.; De Souza, E.D.; Taboada Rodriguez, C.M.; Rojas Millan, R.H.; Mojica Herazo, J.C. Evaluation of the reverse logistics performance in civil construction. J. Clean. Prod. 2020, 248, 119212. [Google Scholar] [CrossRef]
- Chileshe, N.; Rameezdeen, R.; Hosseini, M.R.; Martek, I.; Li, H.X.; Panjehbashi-Aghdam, P. Factors driving the implementation of reverse logistics: A quantified model for the construction industry. Waste Manag. 2018, 79, 48–57. [Google Scholar] [CrossRef] [PubMed]
- Pan, X.; Xie, Q.; Feng, Y. Designing recycling networks for construction and demolition waste based on reserve logistics research field. J. Clean. Prod. 2020, 260, 120841. [Google Scholar] [CrossRef]
- Galan, B.; Dosal, E.; Andrés, A.; Viguri, J. Optimisation of the construction and demolition waste management facilities location in Cantabria (Spain) under economical and environmental criteria. Waste Biomass Valori. 2013, 4, 797–808. [Google Scholar] [CrossRef]
- Li, X.; Dong, C.; Chunxiang, G.; Xinyi, S. Logistics Network Design for Construction Waste Reduction System under Multidimensional Perspective. Syst. Eng. Theory Pract. 2019, 39, 2842–2854. [Google Scholar] [CrossRef]
- Balancing the Pillars for Sustainable Development. Available online: https://www.un.org/en/development/desa/news/sustainable/sustainable-development-pillars.html (accessed on 31 March 2023).
- Barros, A.I.; Dekker, R.; Scholten, V. A two-level network for recycling sand: A case study. Eur. J. Oper. Res. 1998, 110, 199–214. [Google Scholar] [CrossRef]
- Shi, Q.; Ren, H.; Ma, X.; Xiao, Y. Site selection of construction waste recycling plant. J. Clean. Prod. 2019, 227, 532–542. [Google Scholar] [CrossRef]
- Michael, H.; Julian, S.; Jens, L. Matching construction and demolition waste supply to recycling demand: A regional management chain model. Build. Res. Inf. 2011, 39, 333–351. [Google Scholar] [CrossRef]
- Rahimi, M.; Ghezavati, V. Sustainable multi-period reverse logistics network design and planning under uncertainty utilizing conditional value at risk (CVaR) for recycling construction and demolition waste. J. Clean. Prod. 2018, 172, 1567–1581. [Google Scholar] [CrossRef]
- Trochu, J.; Chaabane, A.; Ouhimmou, M. A carbon-constrained stochastic model for eco-efficient reverse logistics network design under environmental regulations in the CRD industry. J. Clean. Prod. 2020, 245, 118818. [Google Scholar] [CrossRef]
- Listeş, O.; Dekker, R. A stochastic approach to a case study for product recovery network design. Eur. J. Oper. Res. 2005, 160, 268–287. [Google Scholar] [CrossRef]
- Gabrel, V.; Murat, C.; Thiele, A. Recent advances in robust optimization: An overview. Eur. J. Oper. Res. 2014, 235, 471–483. [Google Scholar] [CrossRef]
- Alumur, S.A.; Nickel, S.; Saldanha-da-Gama, F. Hub location under uncertainty. Transp. Res. Part B Methodol. 2012, 46, 529–543. [Google Scholar] [CrossRef]
- Hu, C.; Liu, X.; Lu, J. A bi-objective two-stage robust location model for waste-to-energy facilities under uncertainty. Decis. Support Syst. 2017, 99, 37–50. [Google Scholar] [CrossRef]
- Nanjing City Map. Available online: http://zrzy.jiangsu.gov.cn/jsbzdt/index.html#mao4 (accessed on 31 March 2023).
- Notice of the General Office of the Municipal Government on the Issuance of the ‘Thirteenth Five-Year Plan’ for the Harmless Treatment of Domestic Waste in Nanjing. Available online: https://www.nanjing.gov.cn/index.html (accessed on 31 March 2023).
- Nanjing Statistical Yearbook 2021. Available online: http://tjj.nanjing.gov.cn/material/njnj_2021/index.htm (accessed on 31 March 2023).
- Disposal Site Public Notice. Available online: http://cgj.nanjing.gov.cn/ (accessed on 31 March 2023).
- Construction Waste Reutilization Project Environmental Impact Report. Available online: http://ghj.nanjing.gov.cn/ (accessed on 31 March 2023).
- Google Maps. Available online: https://www.google.com.hk/maps/?hl=zh-CN (accessed on 31 March 2023).
- Soyster, A.L. Technical Note—A Duality Theory for Convex Programming with Set-Inclusive Constraints. Oper. Res. 1974, 22, 892–898. [Google Scholar] [CrossRef]
- Ahmed, R.R.; Zhang, X. Multi-stage network-based two-type cost minimization for the reverse logistics management of inert construction waste. Waste Manag. 2021, 120, 805–819. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Zhu, L.; Wang, Y.; Xie, L.; Su, H. Integrated forward and reverse logistics network design for a hybrid assembly-recycling system under uncertain return and waste flows: A fuzzy multi-objective programming. J. Clean. Prod. 2020, 243, 118591. [Google Scholar] [CrossRef]
- Yang, C.; Chen, J. Robust design for a multi-echelon regional construction and demolition waste reverse logistics network based on decision Maker’s conservative attitude. J. Clean. Prod. 2020, 273, 122909. [Google Scholar] [CrossRef]
- Tsai, F.M.; Bui, T.; Tseng, M.; Wu, K. A causal municipal solid waste management model for sustainable cities in Vietnam under uncertainty: A comparison. Resour. Conserv. Recycl. 2020, 154, 104599. [Google Scholar] [CrossRef]
- Bavaghar Zaeimi, M.; Abbas Rassafi, A. Designing an integrated municipal solid waste management system using a fuzzy chance-constrained programming model considering economic and environmental aspects under uncertainty. Waste Manag. 2021, 125, 268–279. [Google Scholar] [CrossRef] [PubMed]

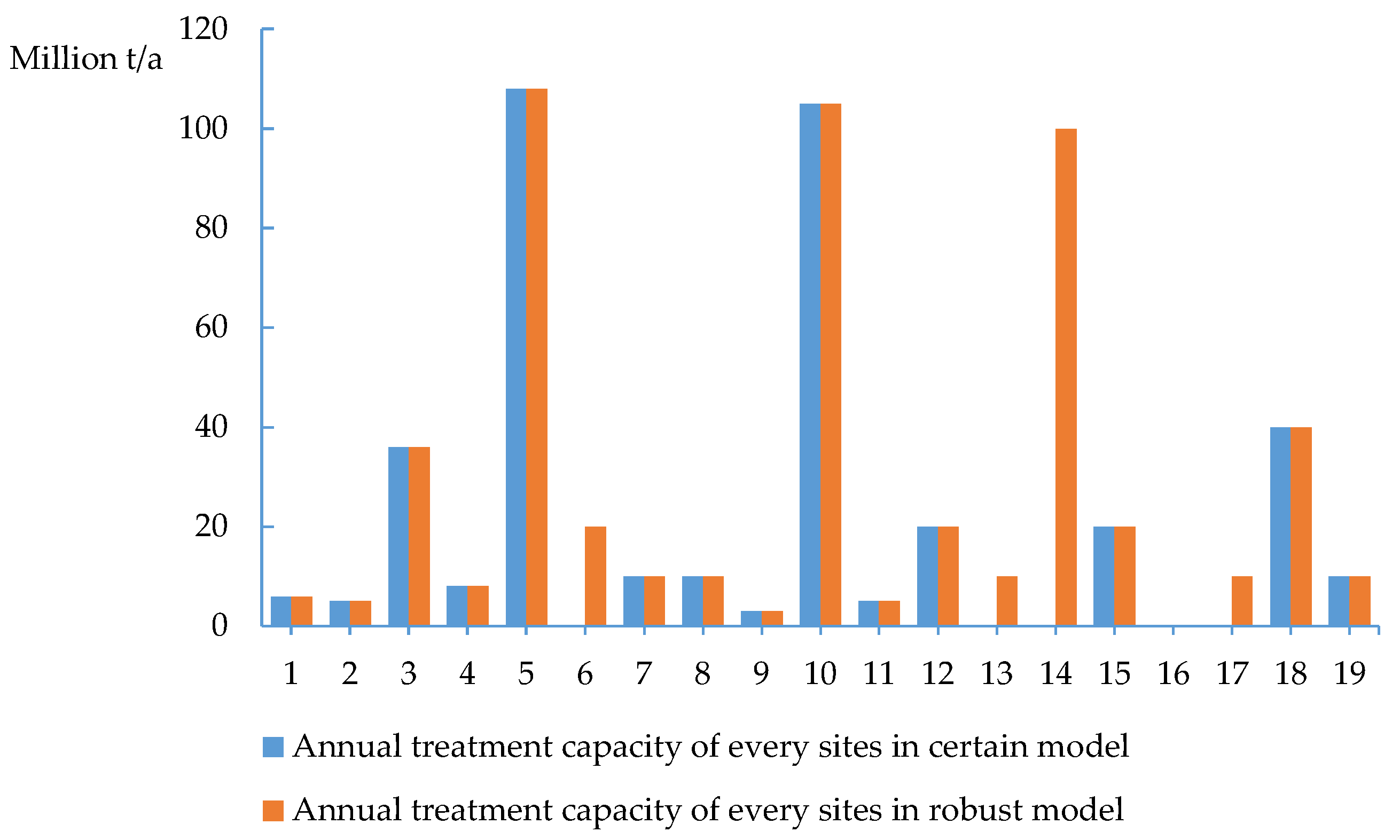

| Symbols | Meaning | Data Sources |
|---|---|---|
| i | Supply sites | The data are from the map of Nanjing, selected from the center of each administrative district [32]. |
| j | Candidate sites for treatment plants | The data are from the “14th Five-Year Plan for Harmless Treatment of Domestic Waste in Nanjing” [33]. |
| qi | Supply of construction waste at point i | Urban construction waste supply (tons/year) = number of inhabitants or households in the city or region × number of people or households per unit construction waste generation base (0.5–1.0 t/year). The data are from Nanjing Statistical Yearbook 2021 [34], with a value of 0.5 t per capita construction waste generation. |
| r | Rate of residue | The rate of residue is 10%, the unit transportation cost is CNY 1/t, the unit treatment cost at the treatment plant is CNY 15/t and the unit landfill cost at the landfill site is CNY 150/t. The data are from the January 2022 investigation. |
| c2 | Unit transportation costs | |
| c3 | Unit treatment cost | |
| c4 | Unit landfill costs | |
| m | Landfill sites | The data are from the public information on disposal sites published by the Nanjing Municipal Bureau of Urban Management [35]. |
| Vm | Maximum capacity of the landfill at point m | |
| c1 | Construction costs of the treatment plant at point j | The data are from the environmental impact reports of various construction waste reutilization projects [36]. |
| Gj | Design capacity of treatment plant at point j | |
| dij | Distance from point i to point j | The data are from Google Maps [37]. |
| djm | Distance from point j to point m |
| Symbols | Meanings | |
|---|---|---|
| Collection | I | Set of potential construction waste supply sites; each element of the set is denoted by i |
| J | Set of potential construction waste treatment plants; each element of the set is denoted by j | |
| M | Set of potential landfill sites; each element of the set is denoted by m | |
| Parameter | qi | Amount of construction waste supplied at site i |
| c1 | Construction cost of treatment plant j | |
| Gj | Design treatment capacity at treatment plant j | |
| r | Rate of construction waste treatment residue | |
| c2 | Unit transportation cost; the transportation cost per unit mass of waste is proportional to the distance traveled | |
| c3 | Unit treatment cost of treatment plant j | |
| c4 | Unit landfill cost of landfill m | |
| Vm | Maximum capacity of landfill m | |
| dij | Distance from i to j | |
| djm | Distance from j to m | |
| uij’ | Transport capacity of construction waste from i to treatment plant j | |
| uij | Actual amount of construction waste transported from i to treatment plant j | |
| ujm’ | Transport capacity of construction waste from j to landfill m | |
| ujm | Actual quantity of construction waste transported from j to landfill m | |
| Decision variable | Xj | 1 if the treatment plant is established at j; 0 otherwise |
| Tij | 1 if supply site i is assigned to j; 0 otherwise | |
| Yjm | 1 if the treatment plant is assigned to m; 0 otherwise |
| Uncertainty ρ | Qi(Rj) |
|---|---|
| 0 | Q1(R1R4R11)Q2(R17)Q3(R1)Q4(R8R13)Q5(R8R12)Q6(R2R4R19)Q7(R1R13R17)Q8(R17R18)Q9(R9R12)Q10(R7)Q11(R7) |
| 0.3 | Q1(R1R2R4R8R9R11R17R19)Q2(R1R2R4R6R11R12R15R18R19)Q3(R1R8R11R13R17)Q4(R3R4R6R11R15R18) Q5(R5R8R10R12R18)Q6(R2R3R4R6R18R19)Q7(R1R4R8R11R13R17R18R19)Q8(R5R14R18)Q9(R1R2R3R4R8R9R12R18R19) Q10(R1R2R4R6R7R8R9R11R12R13R15R19)Q11(R1R2R4R6R7R8R9R11R13R15R17R19) |
| 0.6 | Q1(R1R2R4R7R8R9R11R12R19)Q2(R2R3R4R6R7R9R11R12R15R18R19)Q3(R1R2R4R8R11R13R15R17)Q4(R3R4R6R11R13R15R17R18) Q5(R5R8R10R12R14R18)Q6(R2R3R4R6R11R12R15R18R19)Q7(R1R2R4R8R11R13R15R17R18R19)Q8(R5R14R18) Q9(R1R2R3R4R8R9R10R12R18R19)Q10(R1R2R4R6R7R8R9R11R12R13R15R19)Q11(R1R2R4R6R7R8R9R11R13R15R17R19) |
| 0.9 | Q1(R1R2R4R8R9R11R12R17R18R19)Q2(R2R3R4R6R11R12R15R18R19)Q3(R1R2R4R8R11R13R15R17)Q4(R3R4R11R12R13R14R18) Q5(R5R8R10R12R14R18)Q6(R2R3R4R12R14R18R19)Q7(R1R2R4R8R11R13R17R18R19)Q8(R5R14R18) Q9(R1R2R3R4R8R9R10R12R18R19)Q10(R1R2R4R6R7R8R9R11R12R13R15R18R19)Q11(R1R2R4R6R7R8R9R11R13R15R17R19) |
| Uncertainty ρ | Rj(Lm) |
|---|---|
| 0 | R1(L3)R2(L4)R3(L4)R4(L4)R5(L5)R7(L1)R8(L3)R9(L2)R10(L1)R11(L4)R12(L2)R15(L1)R18(L3)R19(L4) |
| 0.3 | R1(L3)R2(L4L5)R3(L4)R4(L4L5)R5(L3L5)R6(L1L5)R7(L1L3L4)R8(L1L3)R9(L2)R10(L1L2)R11(L4L5)R12(L2)R13(L1L3) R14(L4L5)R15(L1L3)R17(L1L3)R18(L3L5)R19(L4L5) |
| 0.6 | R1(L3L5)R2(L4L5)R3(L4L5)R4(L4L5)R5(L3L5)R6(L1L5)R7(L1L5)R8(L1L3L4)R9(L1L3)R10(L1L2)R11(L4L5)R12(L2L3) R13(L1L3)R14(L4L5)R15(L1L3)R17(L1L3)R18(L3L5)R19(L4L5) |
| 0.9 | R1(L3)R2(L4)R3(L4)R4(L4)R5(L3L5)R6(L1L5)R7(L1L3L4)R8(L3)R9(L2)R10(L1L2)R11(L4)R12(L2)R13(L1L3)R14(L4L5) R15(L1L3)R17(L1L3)R18(L3)R19(L4L5) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Mei, S.; Xu, H.; Hsu, W.-L. Urban Construction Waste Recycling Path: Robust Optimization. Buildings 2023, 13, 2802. https://doi.org/10.3390/buildings13112802
Wu F, Mei S, Xu H, Hsu W-L. Urban Construction Waste Recycling Path: Robust Optimization. Buildings. 2023; 13(11):2802. https://doi.org/10.3390/buildings13112802
Chicago/Turabian StyleWu, Fan, Shue Mei, Haiying Xu, and Wei-Ling Hsu. 2023. "Urban Construction Waste Recycling Path: Robust Optimization" Buildings 13, no. 11: 2802. https://doi.org/10.3390/buildings13112802
APA StyleWu, F., Mei, S., Xu, H., & Hsu, W.-L. (2023). Urban Construction Waste Recycling Path: Robust Optimization. Buildings, 13(11), 2802. https://doi.org/10.3390/buildings13112802









