Post-Cracking Shear Stiffness Model of Reinforced Concrete Beams
Abstract
:1. Introduction
2. Post-Cracking Shear Stiffness Model of Reinforced Concrete Beams
2.1. Intial Elastic Shear Stiffness Ke
2.2. Stirrup Yielding Shear Stiffness Ky Based on Truss Model
2.3. Shear Stiffness Degradation Rules for Partially Shear-Cracked RC Beams
- Before shear cracking, the elastic shear stiffness Ke can be calculated using Equation (1) and used for the calculation of elastic shear deformation;
- The cracking shear force Vcr and stirrup yielding force Vy of the critical section are calculated using Equations (8) and (9);
- After shear cracking, the yielding shear stiffness Ky can be obtained from Formula (2), and which the shear stiffness degradation coefficient ξy can be calculated using Equation (3);
- The shear increment V-Vcr under the shear load V at different loading levels is calculated and substituted into the selected formula from Equations (4)–(7) to calculate the effective shear stiffness Keff of the RC beam with shear cracks;
- The average shear strain or shear deformation of the corresponding beam segment is calculated according to the effective shear stiffness Keff under a specific shear load.
3. Determination of Strut Angle, θy
3.1. Strut Angle Based on Minimum Energy Principle
3.2. Simplification Formula for Strut Angle
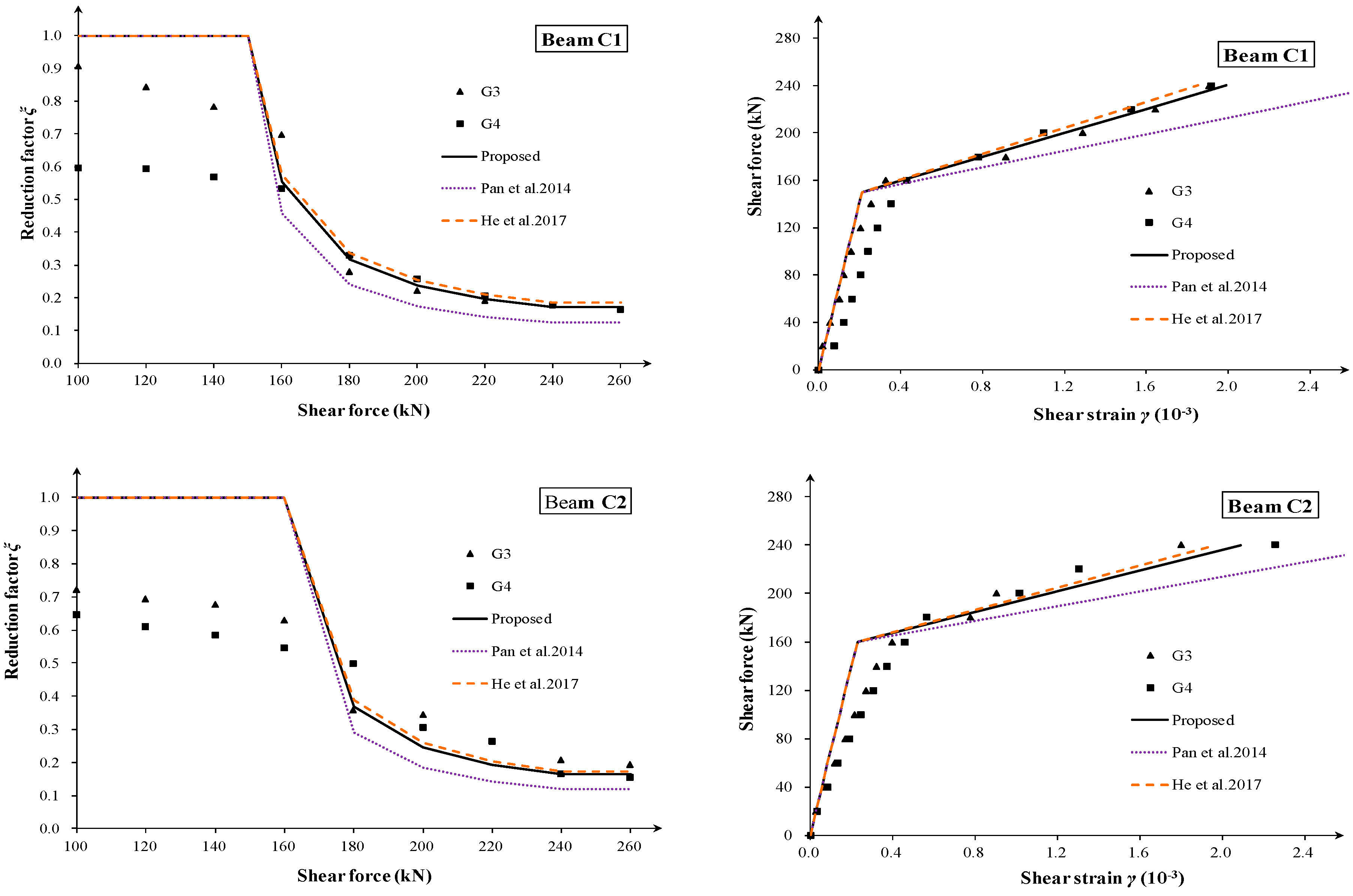
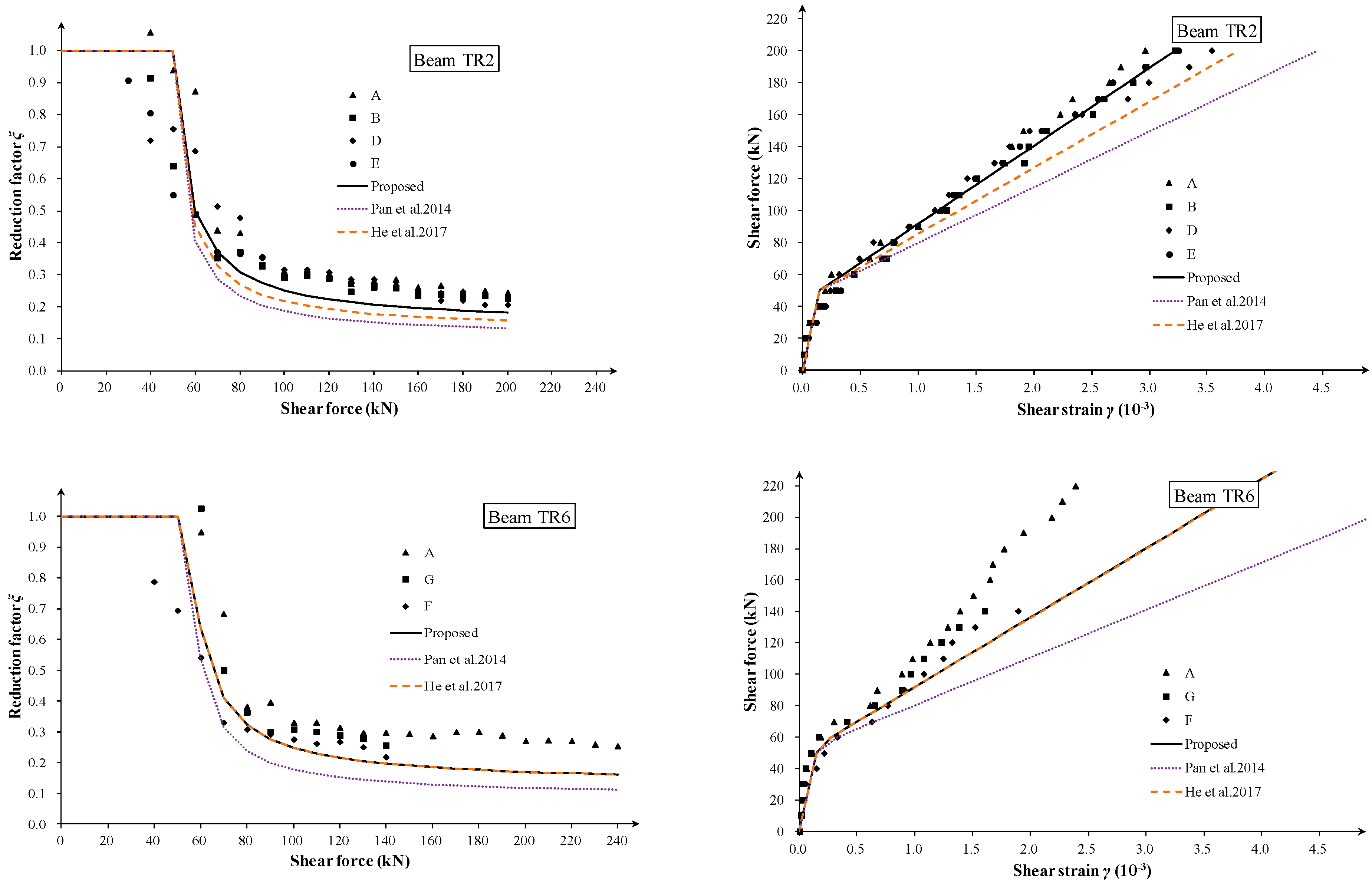
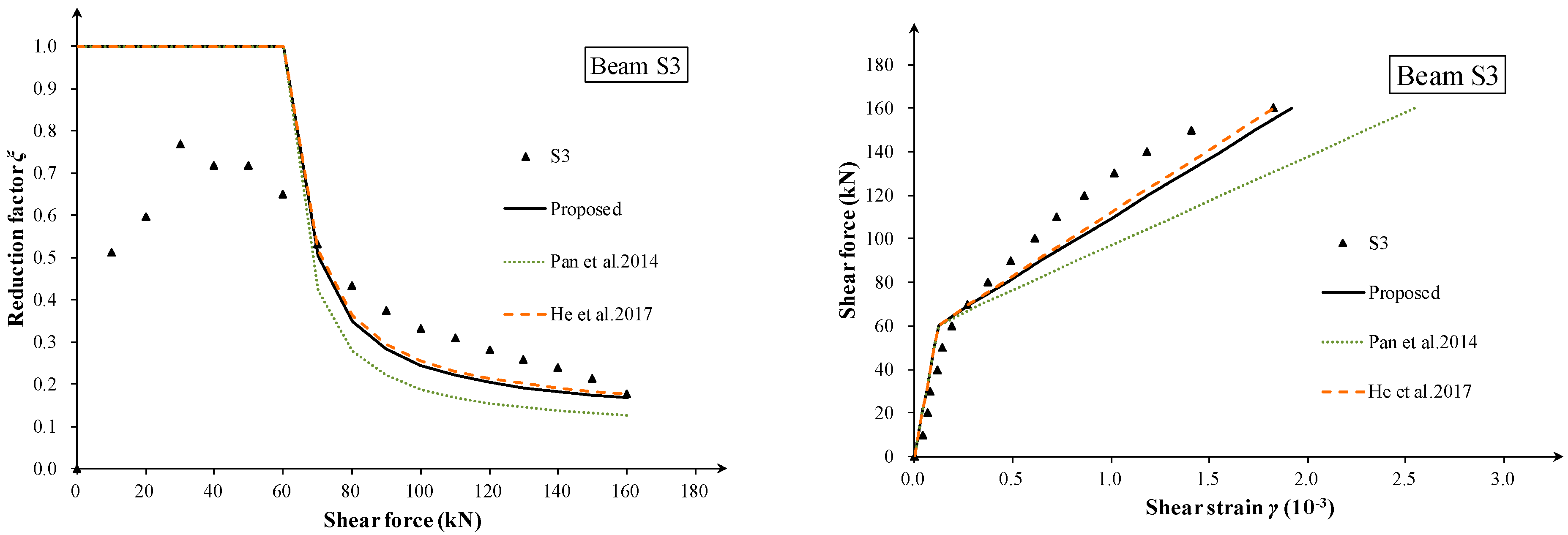
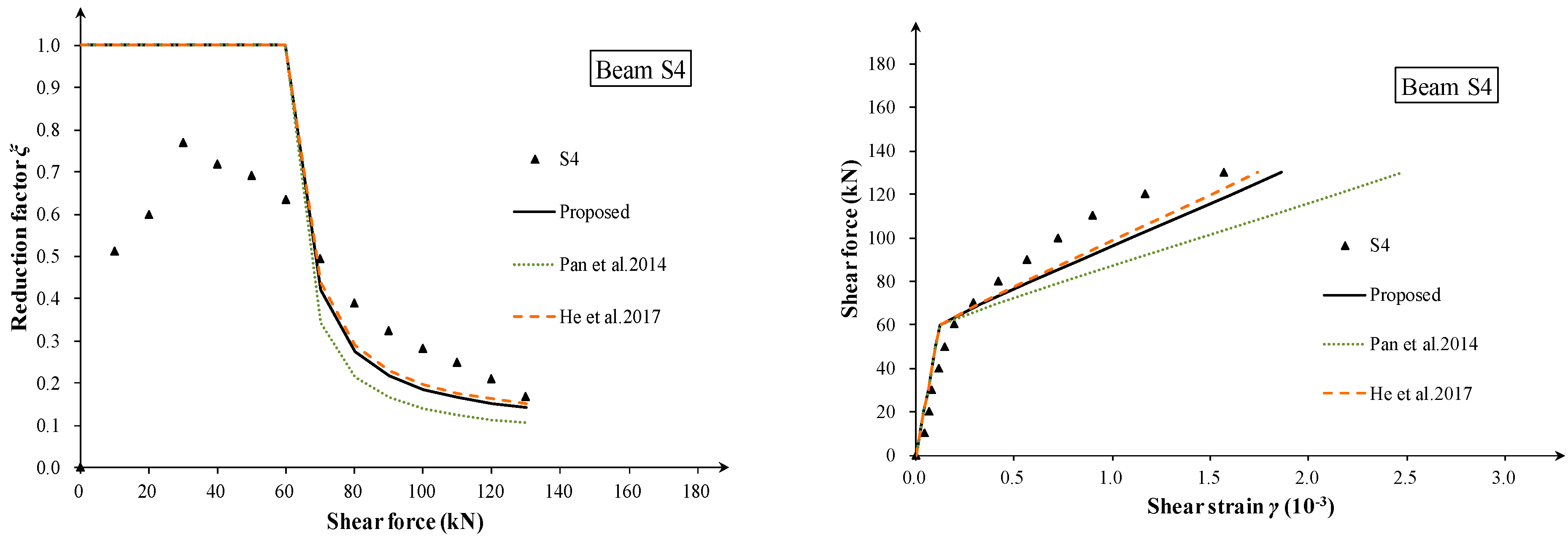
4. Experimental Validation
4.1. Shear Deformation Test in the Literature
4.2. Comparison of Strut Angle and Degradation Coefficient
4.3. Comparison of Effective Shear Stiffness and Shear Strain
5. Conclusions
- Based on the variable-angle truss model, the relationship between the stirrup yielding shear stiffness and elastic shear stiffness was established. Then, a practical linear tangent shear stiffness degradation model, which depicts the main features of shear strain curves of slender RC beams at the post-cracking stage, was adopted to evaluate the effective shear stiffness.
- The strut angle θy, which was found as a function of the stirrup ratio, longitudinal reinforcement ratio, and elasticity modulus ratio, was determined using the minimum energy principle. Compared with other two methods in the literature, the proposed angle equation tended to give a moderate prediction of strut angles and degradation coefficients for varying beam parameters.
- A turning point occurs in the shear strain curves corresponding to the first diagonal crack. Behind the turn point, the tangent slope of the curve remains nearly constant before the stirrup yielding, especially for thin-webbed beams. Additionally, the shear span-to-depth ratio λMV has little effect on the shear deformation of slender RC beams at the post-cracking stage.
- The analytical prediction was compared with the shear strain data of 23 zones. The results showed that the proposed method gives a good and consistent prediction of the effective shear stiffness and shear strain. The proposed degradation model can be used for the post-cracking shear stiffness evaluation of shear-cracked RC beams.
- In practice, the procedure introduced in Section 2.3 can be used for a quick shear stiffness evaluation of concrete box girder bridges in service, on which performing experimental tests may be impractical and costly.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ACI318-19; Building Code Requirements for Structural Concrete and Commentary. ACI: Farmington Hills, MI, USA, 2019.
- AASHTO. LRFD Bridge Design Specifications, 9th ed.; AASHTO: Washington, DC, USA, 2020. [Google Scholar]
- Zheng, K.; Zhou, S.; Zhang, Y.; Wei, Y.; Wang, J.; Wang, Y.; Qin, X. Simplified evaluation of shear stiffness degradation of diagonally cracked reinforced concrete beams. Materials 2023, 16, 4752. [Google Scholar] [CrossRef] [PubMed]
- Hansapinyo, C.; Pimanmas, A.; Maekawa, K.; Chaisomphob, T. Proposed model of shear deformation of reinforced concrete beam after diagonal cracking. J. Div. Mater. Concr. Struct. Pavements 2003, 725, 305–319. [Google Scholar] [CrossRef] [PubMed]
- Debernardi, P.G.; Taliano, M. Shear deformation in reinforced concrete beams with thin web. Mag. Concr. Res. 2006, 58, 157–171. [Google Scholar] [CrossRef]
- Zheng, K.; Kuwornu, M.; Liu, Z. Shear test of variable depth rc beams with inflection point. MATEC Web Conf. 2019, 275, 02003. [Google Scholar] [CrossRef]
- Pan, Z.; Bing, L.; Lu, Z. Effective shear stiffness of diagonally cracked reinforced concrete beams. Eng. Struct. 2014, 59, 95–103. [Google Scholar] [CrossRef]
- Wang, T.; Dai, J.G.; Zheng, J.J. Multi-angle truss model for predicting the shear deformation of rc beams with low span-effective depth ratios. Eng. Struct. 2015, 91, 85–95. [Google Scholar] [CrossRef]
- He, Z.; Liu, Z.; Ma, Z.J. Shear deformations of RC beams under service loads. J. Struct. Eng. 2017, 143, 04016153. [Google Scholar] [CrossRef]
- Huang, Z.; Tu, Y.; Meng, S.; Ohlsson, U.; Taljsten, B.; Elfgren, L. A practical method for predicting shear deformation of reinforced concrete beams. Eng. Struct. 2020, 206, 110116. [Google Scholar] [CrossRef]
- Liu, J.; Jia, Y.; Zhang, G.; Wang, J. Effect of diagonal cracks on shear stiffness of pre-stressed concrete beam. Int. J. Struct. Integr. 2018, 9, 414–428. [Google Scholar] [CrossRef]
- Park, R.; Paulay, P. Reinforcement Concrete Structures; John Wiley & Sons: Christchurch, New Zealand, 1975; pp. 315–319. [Google Scholar]
- Branson, D.E. Deformation of Concrete Structures; McGraw-Hill Companies: Toronto, ON, Canada, 1977; pp. 545–546. [Google Scholar]
- ACI 445-R99; Committee Recent Approaches to Shear Design of Structural Concrete. American Concrete Institute: Farmington Hills, MI, USA, 2009.
- Leonhardt, F.; Walther, R. The Stuttgart Shear Tests; Cement and Concrete Association: London, UK, 1964; Volume 111, pp. 1–134. [Google Scholar]
- Kupfer, H. Generalization of Morsch’s truss analogy using the principle of minimum strain energy. CEB Bull. 1964, 40, 44–57. [Google Scholar]
- Vecchio, F.J.; Collins, M.P. The modified compression field theory for reinforced concrete elements subjected to shear. ACI Struct. J. 1986, 83, 219–231. [Google Scholar]
- Bentz, E.C. Sectional Analysis of Reinforced Concrete Members; University of Toronto: Toronto, ON, Canada, 2000. [Google Scholar]
- Desalegne, A.S.; Lubell, A.S. Consideration of shear deformations for slender concrete beams. ACI Spec. Publ. 2012, SP284-15, 1–18. [Google Scholar]
- Pang, X.B.; Hsu, T.T.C. Fixed-angle softened-truss model for reinforced concrete. ACI Struct. J. 1996, 93, 197–207. [Google Scholar]
- Zhu, R.; Hsu, T.T.; Lee, J.Y. Rational shear modulus for smeared-crack analysis of reinforced concrete. ACI Struct. J. 2001, 98, 443–450. [Google Scholar]
- Barzegar, F. Analysis of RC membrane elements with anisotropic reinforcement. J. Struct. Eng. 1989, 115, 647–665. [Google Scholar] [CrossRef]
- Rahal, K.N. Post-cracking shear modulus of reinforced concrete membrane elements. Eng. Struct. 2010, 32, 218–225. [Google Scholar] [CrossRef]
- Kim, J.H.; Mander, J.B. Influence of transverse reinforcement on elastic shear stiffness of cracked concrete elements. Eng. Struct. 2007, 29, 1798–1807. [Google Scholar] [CrossRef]
- Li, B.; Tran CT, N. Reinforced concrete beam analysis supplementing concrete contribution in truss models. Eng. Struct. 2008, 30, 3285–3294. [Google Scholar] [CrossRef]
- Zheng, K.; Liu, Z.; Zhang, Y.; Qin, S. Practical evaluation method for shear stiffness of concrete beam bridges with web diagonal cracks. Bridge Constr. 2015, 45, 46–51. (In Chinese) [Google Scholar]
- Kuo, W.W.; Hsu, T.T.; Hwang, S.J. Shear Strength of Reinforced Concrete Beams. ACI Struct. J. 2014, 111, 809–818. [Google Scholar] [CrossRef]
- Słowik, M. Shear failure mechanism in concrete beams. Procedia Mater. Sci. 2014, 3, 1977–1982. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Hatzigeorgiou, G.D.; Karamani, C.; Skentou, A.; Zoumpoulaki, I.; Asteris, P.G. Soft computing-based techniques for concrete beams shear strength. Procedia Struct. Integr. 2019, 17, 924–933. [Google Scholar] [CrossRef]
- Wang, Y.D.; Yang, S.; Han, M. Experimental study of section enlargement with reinforced concrete to increase shear capacity for damaged reinforced concrete beams. Appl. Mech. Mater. 2013, 256, 1148–1153. [Google Scholar] [CrossRef]
- Muttoni, A.; Fernández Ruiz, M. Shear strength of members without transverse reinforcement as function of critical shear crack width. ACI Struct. J. 2008, 105, 163–172. [Google Scholar]
- Duan, M.; Zou, X.; Bao, Y.; Li, G.; Chen, Y.; Li, Z. Experimental investigation of headed studs in steel-ultra-high performance concrete (UHPC) composite sections. Eng. Struct. 2022, 270, 114875. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, C.; Liu, J.; Zou, X.; Sneed, L.H.; Bao, Y.; Wang, L. Prediction of FRP-concrete interfacial bond strength based on machine learning. Eng. Struct. 2023, 74, 115156. [Google Scholar] [CrossRef]
- Huang, Z.; Tu, Y.; Meng, S.; Sabau, C.; Popescu, C.; Sas, G. Experimental study on shear deformation of reinforced concrete beams using digital image correlation. Eng. Struct. 2019, 181, 670–698. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Y.; Ding, M.; Zhao, K.; Zheng, K. Combinatorial design and flexural behavior of laminated bamboo-timber composite beams. Thin-Walled Struct. 2022, 181, 109993. [Google Scholar] [CrossRef]




| Inducement | Member | Force | Unit Load | Length | Rigidity | Deformation |
|---|---|---|---|---|---|---|
| Shear force V | Stirrups | 1 | ||||
| Inclined Strut | ||||||
| Upper chord | ||||||
| Lower chord | ||||||
| Moment M | Upper chord | |||||
| Lower chord |
| Resources | Specimen ID | f’c (MPa) | Ec (GPa) | dv (mm) | bw (mm) | fyv (MPa) | ρv (%) | ρs (%) | Vcr (kN) | Vy (kN) |
|---|---|---|---|---|---|---|---|---|---|---|
| Zheng [6] | C1 | 39.0 | 29.4 | 684 | 100 | 327 | 0.5 | 4.8 | 150 | 240 |
| C2 | 36.0 | 28.2 | 684 | 100 | 327 | 0.4 | 4.8 | 160 | 240 | |
| Debernardi [5] | TR1 | 22.0 | 22.0 | 300 | 100 | 570 | 0.5 | 0.74 | 40 | 160 * |
| TR2 | 22.0 | 22.0 | 300 | 100 | 570 | 0.5 | 1.34 | 50 | 200 | |
| TR3 | 20.0 | 21.0 | 300 | 100 | 570 | 0.5 | 0.74 | 40 | 160 * | |
| TR6 | 33.5 | 27.2 | 300 | 100 | 570 | 0.5 | 1.34 | 55 | 240 | |
| Hansapinyo [4] | S1 | 33.0 | 27.0 | 350 | 150 | 370 | 0.47 | 4.26 | 73.6 | 180 |
| S2 | 33.0 | 27.0 | 320 | 150 | 370 | 0.47 | 4.26 | 64.1 | 170 | |
| S3 | 33.0 | 27.0 | 320 | 150 | 370 | 0.47 | 2.13 | 61.3 | 160 | |
| S4 | 33.0 | 27.0 | 320 | 150 | 370 | 0.31 | 2.13 | 61.6 | 130 |
| Resources | Specimen ID | Zone | a/h or M/(Vh) |
|---|---|---|---|
| Zheng [6] | C1, C2 | G3 | 0.5 |
| G4 | 0 | ||
| Debernardi [5] | TR1, TR2 | A, E | 1.67 |
| B, D | 2.5 | ||
| TR3 | A, E | 2.08 | |
| B, D | 2.92 | ||
| TR6 | A | 2 | |
| G | 4 | ||
| F | 4.83 | ||
| Hansapinyo [4] | S1, S2, S4 | - | 2.6 |
| S3 | - | 3.5 |
| Resource | Specimen ID | θy (Degree) | θP (Degree) | θH (Degree) | ξy | ξP | ξH | ξexp | ξy/ξexp | ξP/ξexp | ξH/ξexp |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Zheng [6] | C1 | 26.3 | 31.3 | 25.1 | 0.182 | 0.156 | 0.186 | 0.190 | 0.96 | 0.69 | 0.97 |
| C2 | 25.2 | 30.0 | 24.1 | 0.169 | 0.145 | 0.173 | 0.178 | 0.95 | 0.71 | 0.98 | |
| Debernardi [5] | TR1 * | 33.9 | 42.3 | 35.0 | 0.164 | 0.107 | 0.156 | - | - | - | - |
| TR2 | 31.1 | 38.5 | 35.0 | 0.183 | 0.132 | 0.156 | 0.225 | 0.81 | 0.59 | 0.69 | |
| TR3 * | 34.0 | 42.4 | 36.1 | 0.169 | 0.112 | 0.154 | - | - | - | - | |
| TR6 | 30.8 | 38.4 | 30.8 | 0.162 | 0.113 | 0.162 | 0.253 | 0.64 | 0.45 | 0.64 | |
| Hansapinyo [4] | S1 | 26.4 | 31.5 | 26.8 | 0.179 | 0.152 | 0.178 | 0.155 | 1.15 | 0.98 | 1.15 |
| S2 | 26.4 | 31.5 | 26.8 | 0.179 | 0.152 | 0.178 | 0.143 | 1.25 | 1.06 | 1.24 | |
| S3 | 28.5 | 35.2 | 26.8 | 0.170 | 0.128 | 0.178 | 0.178 | 0.96 | 0.72 | 1.00 | |
| S4 | 26.1 | 32.5 | 23.8 | 0.142 | 0.106 | 0.152 | 0.168 | 0.85 | 0.63 | 0.90 | |
| Average | 0.95 | 0.76 | 0.95 | ||||||||
| CV | 0.19 | 0.25 | 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, K.; Ni, S.; Zhang, Y.; Gu, J.; Gao, M.; Wei, Y. Post-Cracking Shear Stiffness Model of Reinforced Concrete Beams. Buildings 2023, 13, 2814. https://doi.org/10.3390/buildings13112814
Zheng K, Ni S, Zhang Y, Gu J, Gao M, Wei Y. Post-Cracking Shear Stiffness Model of Reinforced Concrete Beams. Buildings. 2023; 13(11):2814. https://doi.org/10.3390/buildings13112814
Chicago/Turabian StyleZheng, Kaiqi, Siwen Ni, Yaohui Zhang, Junxuan Gu, Mingming Gao, and Yang Wei. 2023. "Post-Cracking Shear Stiffness Model of Reinforced Concrete Beams" Buildings 13, no. 11: 2814. https://doi.org/10.3390/buildings13112814
APA StyleZheng, K., Ni, S., Zhang, Y., Gu, J., Gao, M., & Wei, Y. (2023). Post-Cracking Shear Stiffness Model of Reinforced Concrete Beams. Buildings, 13(11), 2814. https://doi.org/10.3390/buildings13112814








