The Effect of Bottom Reinforcement Spacers on Reinforced Concrete Structures Loaded by Explosion
Abstract
:1. Introduction
2. Experiment Setup
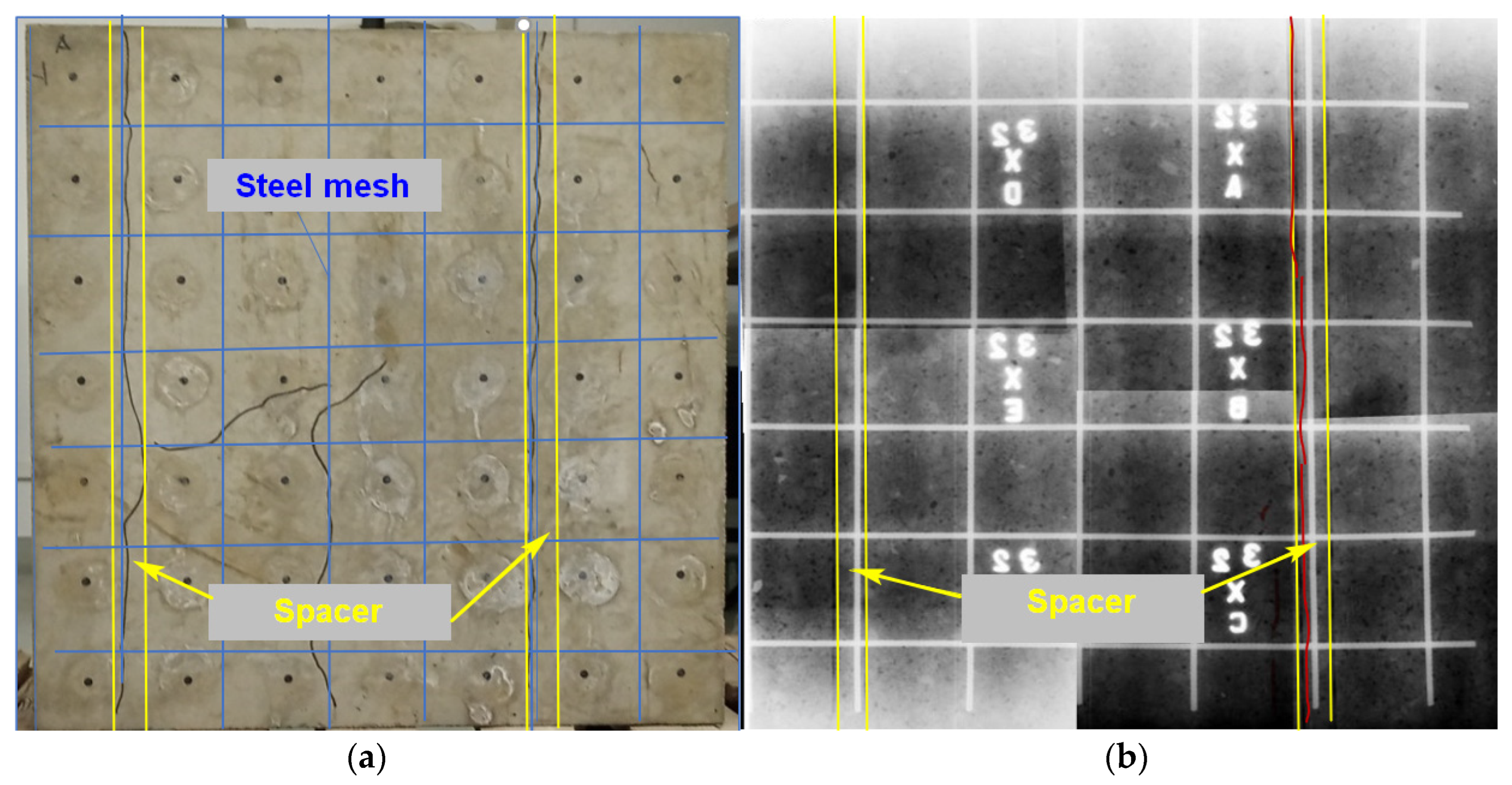
3. Verification of Changes in Material Properties of Loaded Specimens by Radiography
4. Destructive Determination of Residual Strength of the Slabs in Extrusion Laboratory
5. Computational Model
6. Discussion
- There are only a limited number of published articles on the Web of Science; the oldest article is from 2016.
- The influence of spacers (material, shape) is not included in any standard for the design calculation of concrete structures.
- Unlike other concrete components, spacers do not fall into specific families of construction products covered by the harmonized standard regulation (EU) No 305/2011 [12].
7. Conclusions
- The use of linear spacers creates a local discontinuity in the resistance of the material because the mechanical resistance of the concrete is significantly different from the plastic bar, which weakens the cross-section of the concrete element.
- Mechanical weakening of the cross-section is not an issue in conventionally designed structures because the concrete cover serves to protect the concrete reinforcement and is not considered in the structural calculation. However, extraordinary loads, such as blasts, will stress the structure beyond its ultimate capacity and, therefore, accentuate any weakening of the structure, which then determines its load capacity.
- A porous interface formed between the spacer, the steel mesh, and the concrete forms a continuous connection that extends over the entire depth of the reinforcement cover.
- A weak bond between the plastic and the concrete was created. There was also a greater difference in material properties in terms of shrinkage on drying and thermal expansion between the two different materials.
- There are different mechanical properties, such as plastic, metal, and concrete.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dubec, B.; Maňas, P.; Štoller, J.; Zezulová, E.; Dvořák, P.; Hejmal, Z. Numerical Identification of Material Model Parameters of UHPFRC Slab under Blast Loading. Appl. Sci. 2023, 13, 70. [Google Scholar] [CrossRef]
- Figuli, L.; Kavický, V.; Picot, S. Analysis of the Different Approaches to Protection of Critical Infrastructures in France and Slovakia. In Durability of Critical Infrastructure, Monitoring and Testing; Kravcov, A., Cherepetskaya, E.B., Pospichal, V., Eds.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2017; pp. 120–128. ISBN 978-981-10-3246-2. [Google Scholar] [CrossRef]
- Figuli, L.; Jangl, Š.; Picot, S. Different Approaches to Setting the Blast Load of Structure. In Durability of Critical Infrastructure, Monitoring and Testing; Kravcov, A., Cherepetskaya, E.B., Pospichal, V., Eds.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2017; pp. 148–155. ISBN 978-981-10-3246-2. [Google Scholar] [CrossRef]
- Dubec, B.; Maňas, P.; Štoller, J. Analytical approach in assessment of deflection of thick concrete plates. In Proceedings of the 2021 8th International Conference on Military Technologies, ICMT 2021, Brno, Czech Republic, 8–11 June 2021; Kolar, P., Ed.; Institute of Electrical and Electronics Engineers Inc.: Brno, Czech Republic, 2021. ISBN 978-1-6654-3724-0. [Google Scholar] [CrossRef]
- Collepardi, M. The New Concrete; Grafiche Tintoretto: Treviso, Italy, 2006; p. 436. [Google Scholar]
- Štefan, R.; Foglar, M.; Fládr, J.; Horníková, K.; Holan, J. Thermal, spalling, and mechanical behaviour of various types of cementitious composites exposed to fire: Experimental and numerical analysis. Constr. Build. Mater. 2020, 262, 119676. [Google Scholar] [CrossRef]
- Ivančo, M.; Trajkovski, J.; Figuli, L.; Erdélyiová, R. Determination of blast resistance of selected structural elements. In Proceedings of the MATEC Web of Conferences, Vyhne, Slovak Republic, 24–28 May 2020; Volume 313. ISSN 2261-236X. [Google Scholar] [CrossRef]
- Alzyoud, S.; Wong, H.S.; Buenfeld, N.R. Influence of reinforcement spacers on mass transport properties and durability of concrete structures. Cem. Concr. Res. 2016, 87, 31–44. [Google Scholar] [CrossRef]
- Muslim, F.; Wong, H.S.; Choo, T.H.; Buenfeld, N.R. Influence of supplementary cementitious materials on microstructure and transport properties of spacer-concrete interface. Cem. Concr. Res. 2021, 149, 106561. [Google Scholar] [CrossRef]
- Muslim, F.; Wong, H.S.; Cheng, G.; Alexandrou, C.; Liu, B.; Buenfeld, N.R. Combined effects of vertical spacers and segregation on mass transport properties of reinforced concrete. Mater. Struct. 2020, 53, 151. [Google Scholar] [CrossRef]
- Geiker, M.; Danner, T.; Michel, A.; Revert, A.B.; Linderoth, O.; Hornbostel, K. 25 years of field exposure of pre-cracked concrete beams; combined impact of spacers and cracks on reinforcement corrosion. Constr. Build. Mater. 2021, 286, 122801. [Google Scholar] [CrossRef]
- Regulation (EU) No 305/2011 of the European Parliament and of the Council of 9 March 2011 Laying down Harmonised Conditions for the Marketing of Construction Products and Repealing Council Directive 89/106/EEC Text with EEA Relevance, L 88/5. Online. Official Journal of the European Union. The European Parliament and the Council of the European Union. 2011. Available online: http://data.europa.eu/eli/reg/2011/305/oj (accessed on 12 November 2023).
- Zezulová, E.; Hasilová, K.; Dvořák, P.; Dubec, B.; Komárková, T.; Štoller, J. Experimental Campaign to Verify the Suitability of Ultrasound Testing Method for Steel Fiber Reinforced Concrete Fortification Structures. Appl. Sci. 2021, 11, 8759. [Google Scholar] [CrossRef]
- Zezulová, E.; Hasilová, K.; Komárková, T.; Stoniš, P.; Štoller, J.; Anton, O. NDT Methods Suitable for Evaluation the Condition of Military Fortification Construction in the Field. Appl. Sci. 2020, 10, 8161. [Google Scholar] [CrossRef]
- Komárková, T.; Láník, J.; Anton, O. Evaluation of Selected Physicomechanical Properties of SFRC according to Different Standards. Adv. Mater. Sci. Eng. 2018, 2018, 7098065. [Google Scholar] [CrossRef]
- EN 12390-1; Testing of Hardened Concrete—Part 1: Shape, Dimensions and Other Requirements for Test Bodies and Moulds. CSA: Prague, Czech Republic, 2013.
- EN 12390-2; Testing of Hardened Concrete—Part 2: Manufacture and Treatment of Test Bodies for Strength Tests. CSA: Prague, Czech Republic, 2009.
- EN 12390-3; Testing of Hardened Concrete—Part 3: Compressive Strength of the Test Body. CSA: Prague, Czech Republic, 2020.
- EN 12390-5; Testing of Hardened Concrete—Part 5: Flexural Tensile Strength of Test Bodies. 5.5 Tests for Concrete Structures—Tests for Structural Analysis of Concrete Structures—Part 5.5.5. BSI: London, UK, 2019.
- Livermore Software Technology Corporation. LS-Dyna, Theory Manual; Livemore Software Technology Corporation: Livemore, CA, USA, 2015. [Google Scholar]
- Riedel, W.; Thoma, K.; Hiermaier, S.; Schmolinske, E. Penetration of reinforced concrete by BETA-B-500, numerical analysis using a new macroscopic concrete model for hydrocodes. In Proceedings of the 9th International Symposiumon Interaction of the Effects of Munitions with Structures, Berlin, Germany, 3–7 May 1999; pp. 315–322. [Google Scholar]
- Borrvall, T.; Riedel, W. The RHT Concrete model in Ls-Dyna. In Proceedings of the 8th European LS-DYNA Users Conference, Strasbourg, France, 23–24 May 2011. [Google Scholar]
- Tian, H.F.; Bao, T.; Li, Z.; Peng, H.; You, S.; Xiao, S.L. Determination of Constitutive Parameters of Crystalline Limestone Based on Improved RHT Model. Adv. Mater. Sci. Eng. 2022, 2022, 3794898. [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation. LS-Dyna, Keyword User’s Manual, Volume I, 10/18/16 (r:7991); Livermore Software Technology Corporation: Livemore, CA, USA, 2014. [Google Scholar]
- Atoui, O.; Kechagiadakis, G.; Moumen, A.; Maazoun, A.; Belkassem, B.; Pyl, L.; Lecompte, D. An Explosive Driven Shock Tube-Based Laboratory Scale Test for Combined Blast and Fragment Impact Loading. Appl. Sci. 2022, 12, 6854. [Google Scholar] [CrossRef]
- Trevino, T. Applications of Arbitrary Lagrangian Eulerian (ALE) Analysis Approach to Underwater and Air Explosion Problems; Naval Postgraduate School: Monterey, CA, USA, 2000. [Google Scholar]
- Zukas, J.A.; Walter, W. Explosive Effects and Applications (Shock Wave and High Pressure Phenomena); Springer: London, UK, 2002; ISBN 978-0387955582. [Google Scholar]
- Trajkovski, J.; Kunc, R.; Perenda, J.; Prebil, I. Minimum mesh design criteria for blast wave development and structural response—MMALE method. Lat. Am. J. Solids Struct. 2014, 11, 1999–2017. [Google Scholar] [CrossRef]
- Koli, S.; Chellapandi, P.; Rao, L.B.; Sawant, A. Study on JWL equation of state for the numerical simulation of near-field and far-field effects in underwater explosion scenario. Eng. Sci. Technol. Int. J. 2020, 23, 758–768. [Google Scholar] [CrossRef]
- Niaki, M. Fracture mechanics of polymer concretes: A review. Theor. Appl. Fract. Mech. 2023, 125, 103922. [Google Scholar] [CrossRef]
- Lhonneur, J.; Jamin, F.; Monerie, Y.; Pélissou, C. Experimental Study of Concrete Normal Mode Cohesive behavior at the Centimeter Scale. Procedia Struct. Integr. 2022, 42, 513–521. [Google Scholar] [CrossRef]
- Li, Y.; Hao, Z.B.; Shen, Z.H.; Fu, P.; Zhang, J. Mesoscopic modeling and simulation of tensile properties of cracked concrete using cohesive model. Case Stud. Constr. Mater. 2023, 18, e02186. [Google Scholar] [CrossRef]
- Schwer, L. Modeling Rebar: The forgotten sister in reinforced concrete modeling. In Proceedings of the 13th-International-LSDyna-Conference, Wien, Austria, 8–10 June 2014. [Google Scholar]
- Shoaib Karam, M.; Nakamura, H.; Yamamoto, Y.; Miura, T. Numerical evaluation of the perfobond (PBL) shear connector with transverse rebar using coupled rigid Body spring model (RBSM) and solid finite element method (FEM). Structures 2022, 45, 1544–1560, ISSN 2352-0124. [Google Scholar] [CrossRef]
- Gu, X.; Dong, Q. Laboratory Test and Numerical Simulation of Bond Performance between Basalt Fiber Reinforced Polymer Rebar and Concrete. J. Test. Eval. 2012, 40, 1–8. [Google Scholar] [CrossRef]
- Castedo, R.; Segarra, P.; Alañon, A.; Lopez, L.; Santos, A.; Sanchidrian, J. Air blast resistance of full-scale slabs with different compositions: Numerical modeling and field validation. Int. J. Impact Eng. 2015, 86, 145–156. [Google Scholar] [CrossRef]
- Li, J.; Hao, H. Numerical study of concrete spall damage to blast loads. Int. J. Impact Eng. 2014, 68, 41–55. [Google Scholar] [CrossRef]
- Maazoun, A.; Matthys, S.; Belkassem, B.; Lecompte, D.; Vantomme, J. Blast response of retrofitted reinforced concrete hollow core slabs under a close distance explosion. Eng. Struct. 2019, 191, 447–459. [Google Scholar] [CrossRef]
- Thai, D.-K.; Nguyen, D.-L.; Pham, T.-H.; Doan, Q.H. Prediction of residual strength of FRC columns under blast loading using the FEM method and regression approach. Constr. Build. Mater. 2021, 276, 122253. [Google Scholar] [CrossRef]
- Su, Q.; Wu, H.; Fang, Q. Calibration of KCC model for UHPC under impact and blast loadings. Cem. Concr. Compos. 2022, 127, 104401. [Google Scholar] [CrossRef]
- Mao, L.; Barnett, S.; Tyas, A.; Warren, J.; Schleyer, G.; Zaini, S. Response of small scale ultra high-performance fibre reinforced concrete slabs to blast loading. Constr. Build. Mater. 2015, 93, 822–830. [Google Scholar] [CrossRef]










| Marking of Samples | A3 (RC) | |
|---|---|---|
| Cement 42.5 R—Wet | 455 | |
| Water | 165 | |
| Water/cement ratio | 0.36 | |
| Type of aggregate | Quartz | |
| Aggregate fractions | 0–4 | 880 |
| 4–8 | 220 | |
| 8–16 | 660 | |
| Superplasticizer | 4.55 (Stachement 787) | |
| Reinforcement | B500A steel mesh Ø6/100 × 100 | |
| Specimen No. | Specimen ID | Length | Height | Width | Weight | Density | Force | Compressive Strength |
|---|---|---|---|---|---|---|---|---|
| (–) | (–) | (mm) | (mm) | (mm) | (g) | (kg/m3) | (kN) | (MPa) |
| 1 | A3-1K | 150.4 | 150.2 | 150.2 | 7965 | 2347 | 1372.32 | 60.7 |
| 2 | A3-2K | 149.5 | 148.0 | 149.3 | 7900 | 2392 | 1679.06 | 75.9 |
| 3 | A3-3K | 149.6 | 150.9 | 149.5 | 8010 | 2375 | 1569.77 | 69.6 |
| 4 | A3-4K | 149.1 | 146.4 | 149.2 | 7635 | 2345 | 1499.76 | 68.7 |
| 5 | A3-5K | 149.2 | 151.1 | 149.0 | 7940 | 2365 | 1603.85 | 71.2 |
| Average | 2365 ± 55 | 69.2 ± 3.0 |
| Specimen No. | Specimen ID | Width | Height | Length | Weight | Density | Force | Flexural Strength |
|---|---|---|---|---|---|---|---|---|
| (–) | (–) | (mm) | (mm) | (mm) | (g) | (kg/m3) | (kN) | (MPa) |
| 6 | A3-6 | 100.7 | 100.6 | 400.0 | 9325.9 | 2333 | 7.56 | 5.9 |
| 7 | A3-7 | 97.1 | 100.1 | 399.9 | 9214.4 | 2337 | 8.13 | 6.5 |
| 8 | A3-8 | 98.2 | 99.7 | 400.0 | 9327.9 | 2339 | 6.75 | 5.4 |
| Average | 2335 ± 54 | 5.9 ± 0.17 |
| Slab Batch | Mark | TNT Blast Load |
|---|---|---|
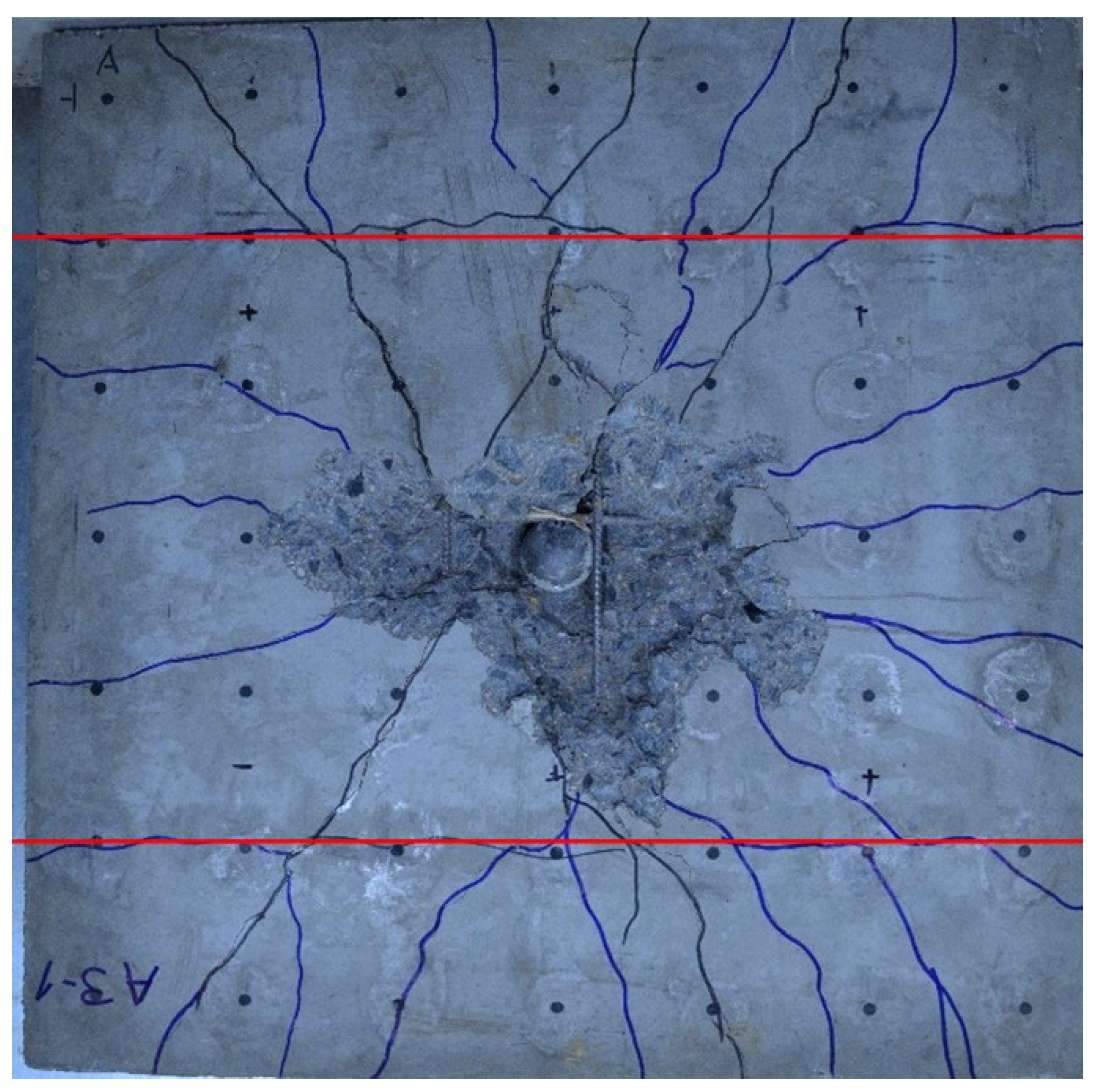
| A3 (RC) | A3_1 | 350 g |
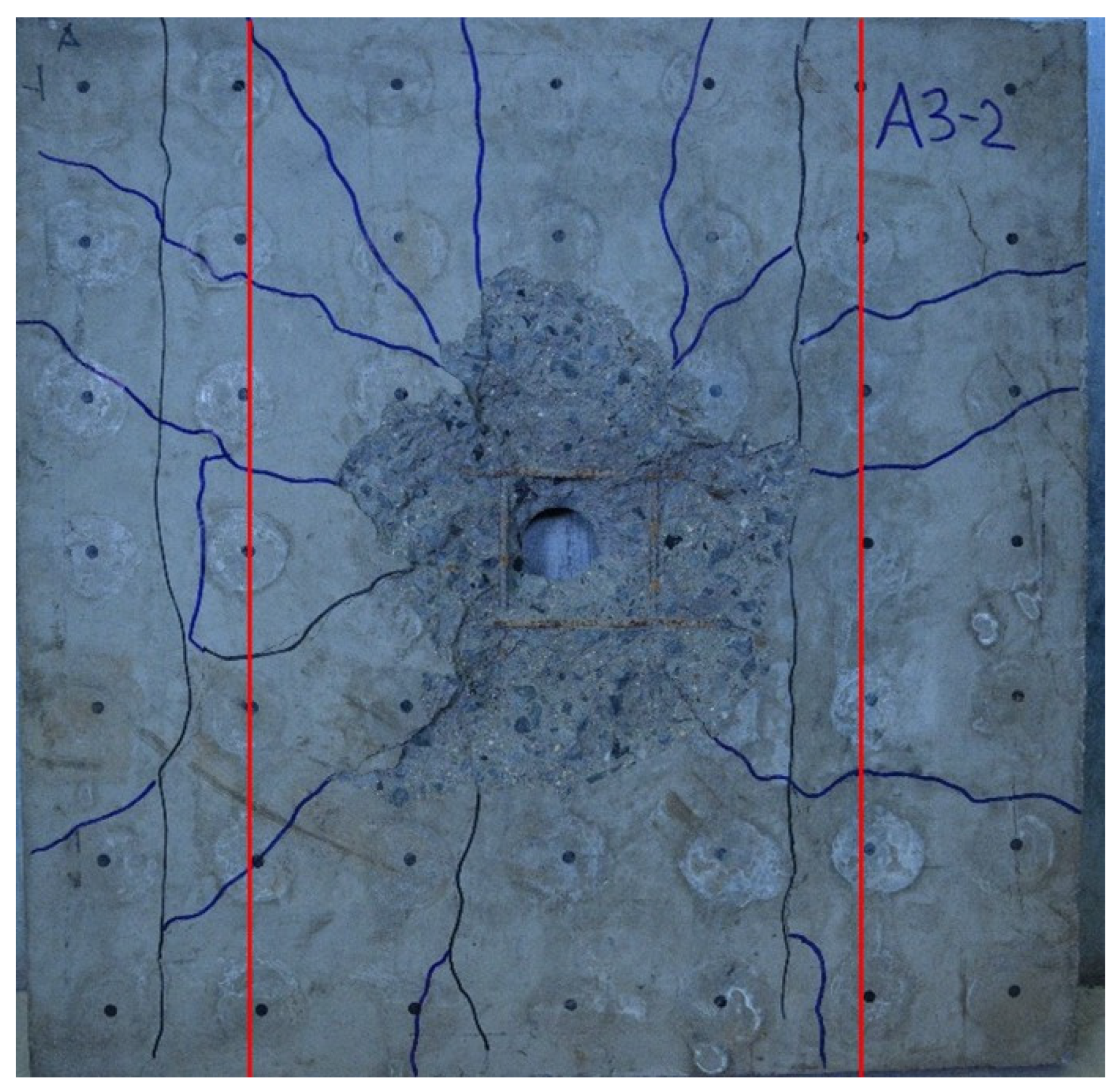
| A3_2 | 275 g | |
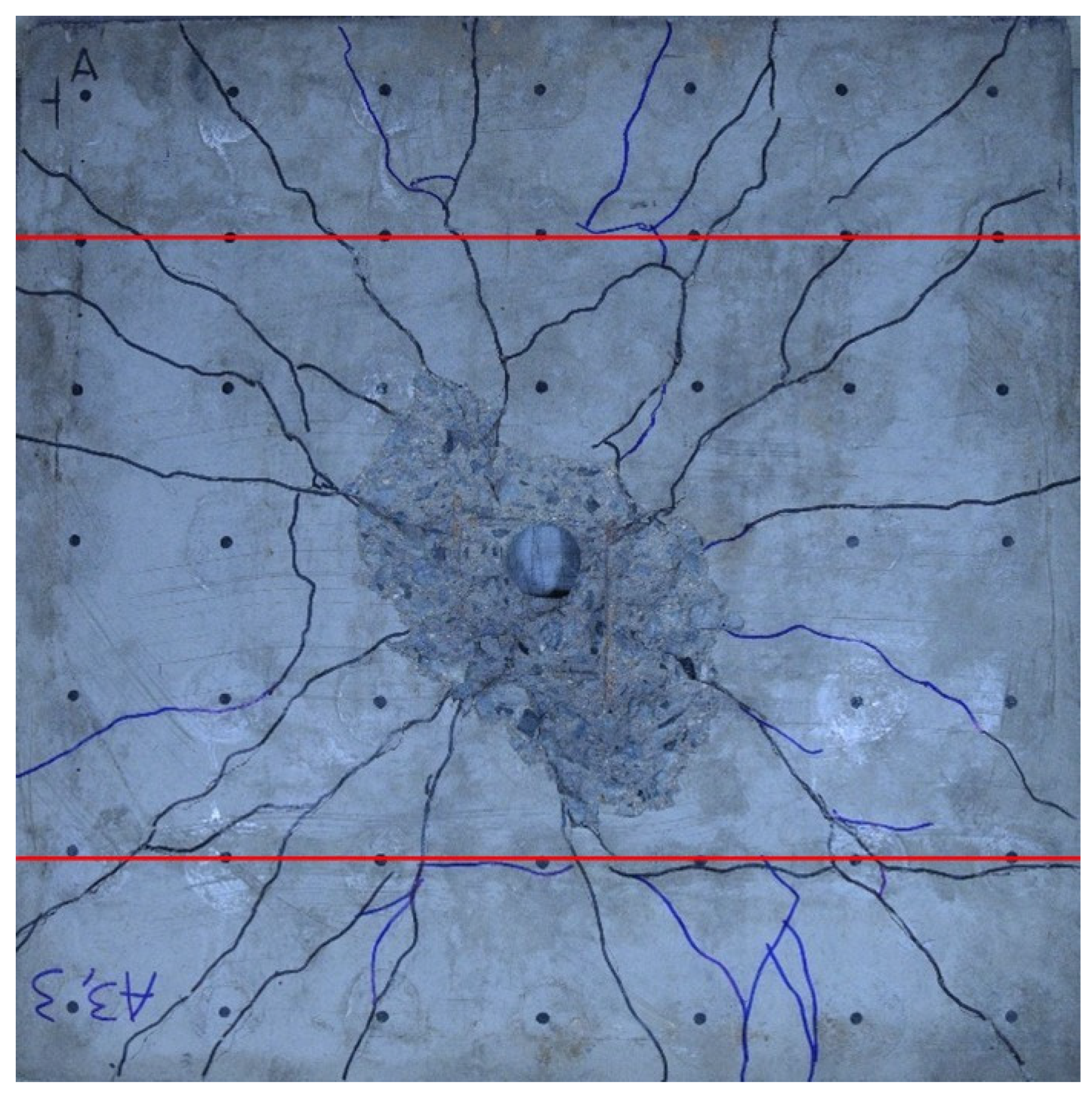
| A3_3 | 600 g |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Mass density (kg/mm3) | 2.365 × 10−6 | Yield surface parameter gty | 7.0 × 10−1 |
| Shear modulus (GPa) | 1.8436 × 101 | Shear reduction factor xi | 5.0 × 10−1 |
| Eroding plastic strain e | 0.00 | Damage parameter D1 | 4.0 × 102 |
| Failure surface parameter A | 1.60 | Damage parameter D2 | 1.00 |
| Failure surface exponent n | 6.1 × 10−1 | Residual damaged strain epm | 1.00 × 10−2 |
| Compressive strength fc (GPa) | 6.9 × 10−2 | Residual surface parameter Af | 1.60 |
| Relative shear strength fs | 1.8 × 10−1 | Residual surface parameter nf | 6.1 × 10−1 |
| Relative tensile strength ft | 1.0 × 10−1 | EOS parameter B0 | 1.22 |
| Lode angle dependence parameter Qo | 6.8 × 10−1 | EOS parameter B1 | 1.22 |
| Lode angle dependence parameter B | 1.05 × 10−2 | EOS parameter T1 | 3.527 × 101 |
| Compressive reference strain rate e0c | 3.0 × 10−8 | EOS parameter T2 | 0.00 |
| Tensile reference strain rate e0t | 3.0 × 10−9 | Gruneisen gamma | 0.00 |
| Compressive break strain rate ec | 1.0 × 1027 | Hugoniot parameter A1 (GPa) | 3.527 × 101 |
| Tensile break strain rate et | 1.0 × 1027 | Hugoniot parameter A2 (GPa) | 3.958 × 101 |
| Compressive strain rate exponent bc | 1.7621 × 10−2 | Hugoniot parameter A3 (GPa) | 9.04 |
| Tensile strain rate exponent bt | 2.2472 × 10−2 | Crush pressure pel (GPa) | 4.5967 × 10−2 |
| Compressive continuity parameter gc | 4.0582 × 10−9 | Compaction pressure pco (GPa) | 6.00 |
| Tensile continuity parameter gt | 6.2844 × 109 | Compaction exponent N | 3.00 |
| Yield surface parameter gcy | 5.3 × 10−1 | Initial porosity α0 | 1.1570 |
| Parameter’s Name | Mass Density | Young’s Modulus | Poisson Ratio | Yield Tress | Tangent Modulus | Failure Strain |
|---|---|---|---|---|---|---|
| (unit) | (kg/m3) | (GPa) | (–) | (GPa) | (GPa) | (–) |
| Parameter’s value | 7860 | 203 | 0.30 | 0.95 | 3.00 | 0.45 |
| Parameter’s Name | Mass Density | Young’s Modulus | Poisson Ratio | Yield Tress | Tangent Modulus | Failure Strain |
|---|---|---|---|---|---|---|
| (unit) | (kg/m3) | (GPa) | (–) | (GPa) | (GPa) | (–) |
| Parameter’s value | 1530 | 9.80 | 0.35 | 0.055 | 0.11 | 0.45 |
| Linear Polynomial EOS | Null Material | |||
|---|---|---|---|---|
| C4 | C5 | E0 | V0 | ρ |
| (–) | (–) | (J/m3) | (–) | (kg/m3) |
| 0.4 | 0.4 | 253.4 × 103 | 1 | 1.225 |
| Jones–Wilkins–Lee Equation of State | High-Explosive Burn Material | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| A | B | R1 | R2 | ω | E0 | V0 | ρ | D | Pcj |
| (GPa) | (GPa) | (–) | (–) | (–) | (J/m3) | (–) | (kg/m3) | (m/s) | (GPa) |
| 3.712 | 3.231 | 4.15 | 0.95 | 0.3 | 7 × 109 | 1 | 1590 | 6930 | 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zezulová, E.; Dubec, B.; Dvořák, P.; Fládr, J.; Cibulová, K. The Effect of Bottom Reinforcement Spacers on Reinforced Concrete Structures Loaded by Explosion. Buildings 2023, 13, 2963. https://doi.org/10.3390/buildings13122963
Zezulová E, Dubec B, Dvořák P, Fládr J, Cibulová K. The Effect of Bottom Reinforcement Spacers on Reinforced Concrete Structures Loaded by Explosion. Buildings. 2023; 13(12):2963. https://doi.org/10.3390/buildings13122963
Chicago/Turabian StyleZezulová, Eva, Branislav Dubec, Petr Dvořák, Josef Fládr, and Klára Cibulová. 2023. "The Effect of Bottom Reinforcement Spacers on Reinforced Concrete Structures Loaded by Explosion" Buildings 13, no. 12: 2963. https://doi.org/10.3390/buildings13122963
APA StyleZezulová, E., Dubec, B., Dvořák, P., Fládr, J., & Cibulová, K. (2023). The Effect of Bottom Reinforcement Spacers on Reinforced Concrete Structures Loaded by Explosion. Buildings, 13(12), 2963. https://doi.org/10.3390/buildings13122963







