Abstract
Sky radiative cooling is a kind of passive cooling technology that uses the “atmospheric window” to emit the object’s own heat to the low temperature of outer space; this technology has low energy consumption, no pollution, and other useful characteristics, so in recent years it has attracted widespread attention. The cooling effect of the sky radiative cooler is mainly affected by the constantly changing outdoor ambient temperature. In addition, the structure of the radiative cooler itself also means that its radiative cooling power undergoes obvious changes. Here, we utilized COMSOL simulation software to establish a numerical heat transfer model for radiative cooling, aimed at investigating the influencing factors on the sky radiative cooler and methods to enhance the structure of the radiative cooling. This study discusses outdoor ambient wind speed, the inlet flow rate of the cooler, installation angle of the cooler, and different cooler structures. Based on simulation results, it is observed that, for varying wind speeds, when the ambient radiation temperature is higher than the surface temperature of the cooler, a larger ambient wind speed leads to a poorer refrigeration effect. The maximum temperature difference in surface temperature at wind speeds of 0 m/s and 4 m/s is 0.59 °C. When the ambient temperature is lower than the surface temperature of the cooler, a smaller wind speed results in a greater net refrigeration power. The maximum temperature difference in this scenario is 0.32 °C. The net refrigeration power of the radiative cooler increases with an increase in water flow rate. As the water flow rate increases from 0 L/min to 5 L/min, the net refrigeration power increases from 25 W/m2 to 200 W/m2 and gradually stabilizes. Considering the radiative impact of the cooler on the surrounding environment, as the installation angle increases from 0° to 90°, the surface temperature of the cooler first increases and then decreases, reaching its highest temperature of 29.26 °C at 45°. The surface temperature of the cooler varies with the thickness of the air sandwich, increasing from 1 cm to 12 cm, and then decreasing. The lowest temperature of 23.4 °C is achieved at a thickness of 8 cm. The increase in the fin structure on the surface of the radiative cooler leads to a decrease in its refrigeration performance, and the difference between the inlet and outlet temperatures of the radiative cooler with a flat plate structure is always greater than that of the finned plate, and the difference in the average radiance is 23.52 W/m2. Finally, the energy-saving effect of the sky radiative cooling composite system is analyzed. Taking a typical small office building as an example, an energy consumption analysis model is set up, and the energy consumption of the composite system is simulated in four cities with different climates, using EnergyPlus software (version 8.6); the system’s power consumption is the largest in hot and humid climates. Compared with the traditional vapor-compression refrigeration system, the composite system reduces air conditioning power consumption by 25.7%, 32.5%, 37.1%, and 44.8% in Guangzhou, Shanghai, Jinan, and Shenyang, respectively. The main innovations of this paper include analyzing and studying the influence of the tilt angle change of the radiative plate on the refrigeration performance of the cooler and the relationship between the surrounding buildings, adding air sandwiches and ribs to the radiative cooler to analyze the influence of convective heat transfer on the refrigeration effect, which plays a guiding role in the design and research of the sky radiative cooler.
1. Introduction
With global warming, the rapid development of industry, and the improvement of people’s living standards, the energy consumption of building refrigeration has increased dramatically, and it is more and more imperative to find new cooling methods and cooling systems. Radiative cooling is a passive cooling technology which emits heat in the form of infrared thermal radiation through the “atmospheric window”, with a wavelength of 8–13 μm, to external spaces and does not require any energy input from the outside. Compared to other refrigeration technologies, this technology is characterized by no consumption of electricity and no pollution to the environment, and has received extensive attention from the engineering field in recent years [1,2,3,4].
At present, the main research on radiative cooling technology focuses on the research and development of new radiative materials, the optimization of the internal and external structure of the cooler, and other aspects [5,6,7,8]. The intensity of solar radiation during the day is relatively large, resulting in higher heat absorption by the radiator, so the earliest radiative cooling technology is mainly applied at night, but the cold load required by the building is still mainly concentrated in the daytime, especially in summer [9]. With the development of materials science, some scholars have now made use of the effect of radiative cooling under direct sunlight during the day. Raman et al. [5], with silver as a substrate, alternately lay seven layers of SiO2 and HfO2 while constructing the cooler, which can reflect up to 97% of the sun’s rays and, in the atmospheric window, achieve an average emissivity of 0.65, realizing a breakthrough in the reduction in daytime temperature by 5 °C in direct sunlight. Kou et al. [6] used fused silica as an interlayer and coated the top and bottom of their cooler with silver and polydimethylsiloxane, which increased the cooling power to 127 W/m2 during the daytime and achieved a temperature drop of 8.21 °C. Huichun Liu [7] added a kind of semi-contact ribs to the inside of the cooler tubes, thus eliminating the localized heat transfer in the area and improving the convective heat transfer. Wang Wenzhuo et al. [8] added bumps to the surface of a nighttime radiative cooler, which improved its cooling efficiency with respect to a conventional cooler.
In addition to the materials themselves, environmental conditions are an equally important factor in the effectiveness of radiative cooling, as coolers are located outdoors. In outdoor environments, convective heat transfer due to wind is the biggest contributor to the cooling effect. Golakal A. et al. [10] investigated the effect of wind baffles on the convective heat flux of the ambient airflow blowing over a horizontal surface used for radiative cooling at night by means of hydrodynamic calculations and wind tunnel experiments under conditions suitable for the Thai climate. It was found that wind baffles with a height of 25 mm slightly increased convective heat transfer due to increased surface turbulence, but wind baffles with heights of 50 and 100 mm reduced convection due to the separation of the main airflow from the surface.
Due to the time-consuming construction of the experimental bench and the cumbersome structural changes to the cooler, many scholars have used mathematical modeling to improve the effect of radiative cooling. Zhang et al. [11] proposed a pipe network, with low-pump-power demand, for a power plant to collect the cold energy generated from radiative cooler surfaces using water as the heat transfer fluid, and the storage of the cold water in an intermediate storage unit, using a structural T-shaped pipe network design and developing analytical models for head loss and heat loss, which can achieve 4096 kWh/day of cooling. Liu C.Y. et al. [12] described how to estimate the performance of a radiative cooler with different water vapor concentrations and simulated the atmospheric transmittance and emitted radiation, as well as the cooling performance, of an ideal selective emitter and found that the cooling power decreases by 86.64 W/m2 with an increase in the total water vapor column. The cooling performances of the integrated photonic solar reflectors and thermal emitters for the atmospheric profiles of California and Hong Kong were also calculated and compared with the experimental results. The theoretical and experimental analyses reveal how the ambient humidity affects the radiative cooling performance, which is of great significance for the further development of applications for radiative coolers.
From this point of view, the enhanced heat transfer in radiative coolers is a focus of the current research, and in order to further study the effects of various factors, such as outdoor wind speed and cooler structure, on the effectiveness of radiative cooling. This paper establishes a numerical model of the sky radiative cooler and simulates the refrigeration performance of the sky radiative cooler using COMSOL software (version 6.1), which provides a reference for the application and optimization of sky radiative cooling.
2. Materials and Methods
2.1. Geometry and Heat Balance of the Sky Radiative Cooler
2.1.1. Simulation of the Operating Environment and Boundary Conditions
In this paper, COMSOL Multiphysics 6.1 simulation software is used to simulate and apply the surface-to-surface radiative module, the solid heat transfer module, and the fluid flow module, to analyze the influencing factors on sky radiative cooling as well as to provide accurate calculations for the optimal design of the cooler. For the operation principle of the sky radiative cooler, the discrete coordinate method is used in this paper for the simulation calculation. The default parameters of the software are used for the operating environment: the pressure is 101,325 Pa, the reference position is far-point, and gravity is not taken into account.
The experimental heat dissipation process is mainly the radiation heat transfer between the surface of the radiative cooler and the outside space, the perimeter and bottom of said radiative cooler are set as insulated, and the initial conditions of the computer simulation model are the ambient temperature at the initial moment.
The boundary condition settings include the cooling water inlet and the parameter settings on the upper surface of the sky radiative cooler. The types of boundary conditions used in this article are:
(1). The inlet boundary—the velocity-inlet boundary condition (Velocity-inlet): The inlet and outlet velocities and all parameters needed for the calculation are known. The flow in the internal fluid of the sky radiative cooler is in the form of a steady state incompressible flow and the turbulence parameters are determined by the turbulence intensity as well as the hydraulic diameter. Turbulence intensity is defined as I = 0.16Re(−1/8), where I is the turbulence intensity and Re is the Reynolds number.
(2). The outlet boundary—free outflow (Outflow): Applicable to the outlet pressure or velocity are unknown parameters, which need to be obtained through simulation. In this paper, we choose the exit boundary conditions of free flow.
(3). The upper surface boundary—solid wall boundary (Wall): in this paper, due to the existence of convective and radiative heat transfer, the upper surface is set as a hybrid interface, so as to realize the convection and radiation coupling of the sky radiative cooler side, and the bottom of the adiabatic wall set; the density of the heat flow is entered as zero.
2.1.2. Geometric Modeling of the Sky Radiative Cooler
The geometric model of the sky radiative cooler and the external heat transfer process is shown in Figure 1; the established model is 3 m long, 1 m wide, 1 cm thick, and consists of twelve stainless steel rectangular tubes with a thickness of 1 mm, each connected to the structure at both ends, with a high emissivity external coating RLHY-2-C1 (emissivity 0.89). Both sides of the cooler are accessed by the refrigeration system via the circular stainless steel water tubes, and the diameter of each water tube is 20 mm.
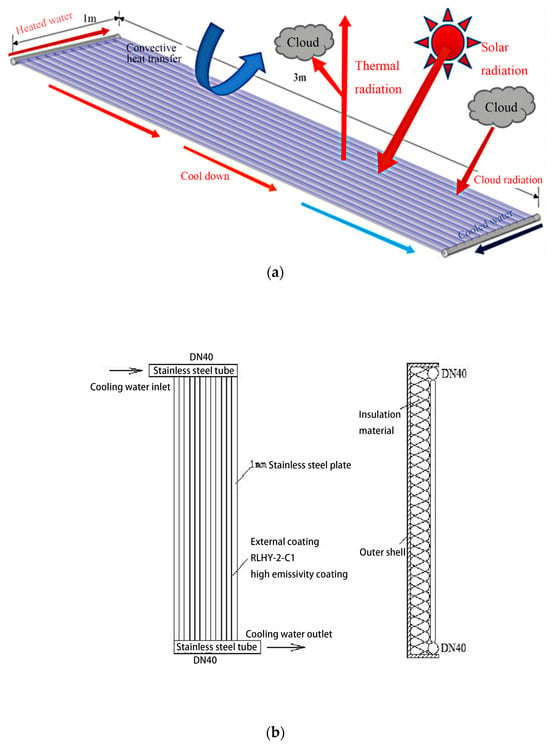
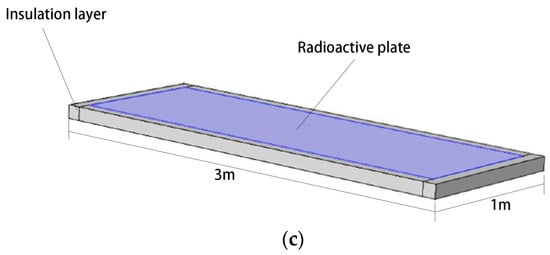
Figure 1.
(a) Geometrical model of the sky radiative cooler and the external heat transfer process; (b) structural diagram of the sky radiative cooler; (c) simplified diagram of the sky radiative cooler’s geometry.
The structure of the sky radiative cooler is shown in Figure 1b; in this paper, when we only study the temperature change on the surface of the sky radiative cooler and the radiative power on the surface of the sky radiative cooler, we can simplify the sky radiative cooler of Figure 1b, as shown in Figure 1c. While considering the twelve stainless steel rectangular tubes as a whole large flat plate and disregarding the circular water tubes at both ends of the radiative cold plate, we assume that the radiative cooler is wrapped with an adiabatic material 10 cm thick, the radiative heat flow passes through the upper surface of the radiative plate only, and the temperature of the outer surface of the adiabatic material is kept at the same temperature as the ambient temperature.
The emissivity of the radiative material in each band is expressed as a segmented function under Switch in COMSOL, and the atmospheric emissivity in each band is expressed as a segmented function in the COMSOL global definition. The solar radiation is represented by an external radiation source under surface-to-surface radiation, in which the azimuth of the sun and the intensity of the radiation can be set.
In the simulation process, the initial temperature of the surface of the radiative cooler and the water flow inside the cooler is set to 30 °C, the inlet temperature is 30 °C, and the inlet flow rate is 2 L/min. The meteorological station data of the Jinan area on September 1, which comes with COMSOL, are used as the environmental conditions.
The sun is the largest source of energy for the Earth, and for the atmosphere; when solar radiation hits the Earth, the atmosphere still absorbs and reflects some of that energy. In addition, the atmosphere itself emits a certain amount of atmospheric radiation into outer space, while the atmosphere also absorbs a certain amount of heat from the ground and produces atmospheric inverse radiation. The ground is also part of the process of absorbing and reflecting solar radiation, and at the same time, in the night, it dissipates radiation heat, but most of the dissipated heat is still absorbed by the atmosphere [13,14]. In terms of the external heat transfer of the cooler, this is mainly through thermal radiation from the external surface via the “atmospheric window” to discharge heat to the low temperature outside, while the cooler transfers heat mainly through water and the internal wall of the cooler via convection heat transfer, as shown in Figure 2.
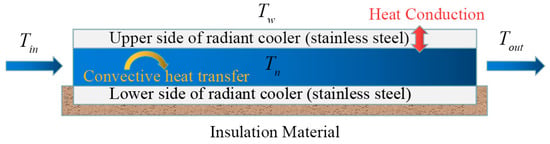
Figure 2.
Internal heat transfer process of the sky radiative cooler.
According to the heat balance principle of the sky radiative cooler, the net radiant power of the cooler can be expressed as [15]
Pnet—Net radiant power of the surface material of the cooler, (W/m2);
Prad—Thermal radiant power of the radiating surface itself, (W/m2);
Patm—Atmospheric radiation absorbed by the radiating surfaces, (W/m2);
Pnonrad—Non-radiation heat transfer between radiant surfaces and the surrounding environment, (W/m2);
Psun—Solar radiation absorbed by the radiating surfaces, (W/m2).
2.2. Numerical Modeling and Control Equations for the Sky Radiative Cooler
2.2.1. Fluid Numerical Model
The flow of a fluid can be described by a variety of mathematical models; the use of partial differential equations provides a more accurate and complete description of the flow of a fluid, and the flow field can be characterized by the balance of mass, momentum, and energy. The three basic governing equations of fluid dynamics are the continuity equation (mass conservation equation), the momentum equation (Navier–Stokes equation), and the energy conservation equation, all of which are described in Cartesian coordinates to solve for the physical quantities in the flow’s field.
The fluid flow and heat transfer process inside and outside the cooler follow the three basic equations of fluid mechanics. For the continuity equation this is [16]
where ρ is the fluid density and u, v, and w are the velocity fields in the x, y, and z directions, respectively. For the momentum equation (Navier–Stokes equation) these are
where f is the volume force per unit fluid micro cluster, τ is the tangential stress, and P is the positive stress. The momentum equation applies to Newtonian incompressible fluids. The energy conservation equation can be expressed in the following form:
Thus for the energy conservation equation its mathematical expression is as follows:
where e is the internal energy and q is the heat flow density.
2.2.2. Control Equations and Boundary Conditions for Radiant Heat Transfer
For an arbitrarily shaped rigid body without implicated motion, the heat conduction equation can be expressed as
—The density of the material;
—The specific heat capacity of the material;
—Temperature distribution as a function of time and space;
—Thermal conductivity;
—Heat generated by the endothermic source in unit volume per unit time.
The temperature field distribution of the material can be obtained by predefining the initial and boundary conditions of the differential Equation (20).
For boundary conditions there are usually three types:
The first type of boundary condition is the temperature on a given boundary:
The second type of boundary condition is the heat flow density distribution on a given boundary:
The third type of boundary condition is the surface heat transfer coefficient of a given material and the ambient temperature:
where Tamb—surface ambient temperature, K.
For this simulation, radiative boundary conditions are used and the equations are as follows:
Material thermal radiant power, atmospheric radiant power, and solar radiant power are all dependent on temperature, wavelength, and angle [17]. Figure 3 shows the zenith angle and azimuth angle in the spherical coordinate system. In conventional radiation boundary conditions, assuming that the emissivity of the material is independent of wavelength and angle, the total blackbody radiated power can be calculated via the following equation:
where σ is the Boltzmann constant, σ = 5.68 × 108 W/m2 K4, and IλB (λ, TB) is the intensity of the spectral radiation of the blackbody at temperature TB.
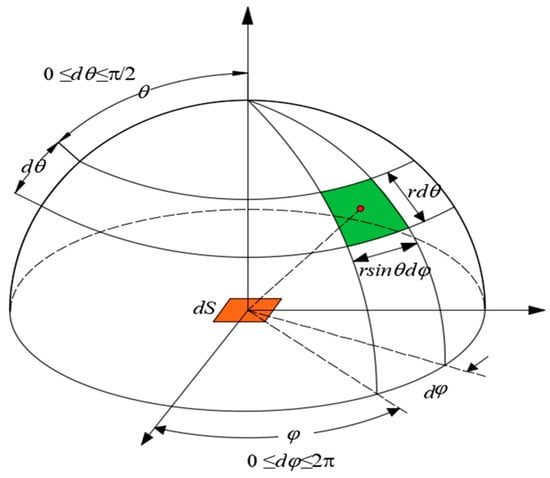
Figure 3.
Zenith angle and azimuth angle in the spherical coordinate system.
The atmospheric emissivity is regarded as the gray body emissivity at the same temperature, in order to simplify the solar radiant power, just as the temperature, wavelength, and angle on the material thermal radiant power, are to simplify the atmospheric radiant power. Considering the effect of cloud cover and an effective emissivity given as , the thermal radiant power of the material and its atmospheric radiant power are simplified into the following equation [18]:
where A is the surface area of the object, m2; Tsky is the effective sky temperature, K; and is the atmospheric emissivity, which is empirically taken to be 0.5–0.6 for clear skies, 0.8–0.9 for sea level, and 1.0 for cloudy skies.
The expression for effective sky temperature versus ambient temperature is given below [19]:
The correlation equation between the effective sky emissivity (εsky) and the dew point temperature (Td) is as follows [20]:
where the cloudiness factor is calculated as
where n is the total volume of opaque clouds; n = 0 under clear sky and n = 1 under cloudy conditions.
The absorbed solar radiation can be calculated by the following equation:
where γ is the absorption coefficient and is the incident solar radiation.
Thus the radiation boundary condition can be expressed as:
2.2.3. Surface-to-Surface Radiative Model
In this model, thermal radiation is considered as an energy transfer between the boundary and the heat source, and the medium is not involved in the radiation (a transparent medium) [21,22]. The effective radiation force at the surface of the object is
where is the effective radiative force on the surface of the object, ; G is the radiative power of the inputs, is the blackbody radiative force. For this model, . Treat the sky radiative cold plate as horizontal, thus .
The heat transfer between two diffuse gray surfaces Q1,2 can be calculated by the following equation:
where denotes the radiant energy emitted from surface 1 onto surface 2 and denotes the radiant energy emitted from surface 2 onto surface 1. As the angular coefficients are interchangeable, it is known that = , so is
To obtain the effective radiation and the angular coefficients need to be determined, and for the angular coefficients the Hemicube method [23], which comes with COMSOL, is used.
2.2.4. Performance Analysis of Sky Radiative Cooling
The cooling efficiency of the radiative cooler can be written as the following equation [24]:
where η𝑐𝑜𝑜𝑙 is the cooling power, 𝜀𝑠𝑘𝑦 is the effective sky emissivity at ambient temperature, 𝜎 is the Boltzmann constant, and 𝑇𝑎 is the ambient temperature.
2.2.5. Turbulence Numerical Simulation Methods and Model Selection
The form of fluid flow, as laminar or turbulent, can be judged via the Reynolds number; the flat plate convection Reynolds number is calculated as follows:
where ρ is the fluid density, v is the fluid flow velocity, L is the characteristic length (e.g., pipe diameter), and μ is the dynamic viscosity of the fluid.
The critical Reynolds number of the fluid flowing through the flat plate in parallel is about 5 × 105. In this paper, the flow state of the airflow at the plate wall in the simulation is laminar flow when the wind speed is less than 0.7 m/s, and turbulent flow when the wind speed is more than 0.7 m/s.
In this paper, a turbulence numerical simulation method based on the RANS equation is used. The Reynolds Averaged Numerical Simulation (RANS) is mainly used to solve the computational analysis of all numerical problems in the range of Reynolds number. In terms of the RANS, its numerical simulation method is less computationally intensive, but its computational results are greatly affected by the turbulence model, and, at the same time, the model gives less consideration to the vortex dynamics and kinematics, which cannot accurately describe the mechanism of the flow.
In order to ensure the accuracy of the simulation, the standard k-ε turbulence model is used for the fluid flow of the sky radiative cooler. The k-ε two-equation model is the most widely used, and its expression is as follows:
where ε is the turbulent kinetic energy dissipation rate of the fluid per unit mass flow rate, which is expressed as follows:
Two important dimensionless parameters in the simulation of the natural convection problem are the Rayleigh number, Ra, and the Prandtl number, Pr, which can be calculated via Equation (24), respectively.
where is the force of gravity, is the coefficient of thermal expansion, is the high temperature, is the low temperature, is the height of the computational domain, is the kinematic viscosity, and is the thermal diffusivity. The magnitude of can determine whether natural convection can be generated in the fluid, and the intensity of natural convection; reflects the interactions between the process of energy and momentum migration in the fluid.
The critical Rayleigh number, Ra, for natural convection is between 1600 and 1800.
Meteorological data at 12:00 noon on September 1 in the Jinan area were used: the air sandwich, taken as 12 cm as an example for the calculation; and the sky radiative cooler heat transfer process, Ra, taken to be 5.7 × 104 in the day and 1.1 × 104 at night. Thus, most of the time, the cooler’s heat transfer process is accompanied by convection heat transfer.
3. Model Validation
3.1. Mesh Irrelevance Verification
Since the surface temperature of the radiative cooler, which is the main object of study, is only related to the surface of the cooler, the cooler model is simplified to a two-dimensional model. The point in the middle of the surface of the sky radiative cooler is selected for mesh irrelevance verification. Figure 4 shows the mesh division of the sky radiative cooler.
Figure 4.
Schematic diagram of the sky radiative cooler meshing.
Three sets of meshes were selected for the grid-independent verification of this model, and the simulation results are shown in Table 1.

Table 1.
Grid independence test.
From the principle of finite element analysis, the finer the meshing, the higher the accuracy of the solution results. However, in the design and application, when the number of the meshes reaches a certain number, the improvement of the calculation’s accuracy is not obvious, so it is necessary to choose the appropriate meshing method and the number of meshes to obtain the best possible results with a lower calculation cost.
Table 1 shows that the grid accuracy of the three cells from Grid 1 to Grid 3 gradually decreases, and that the relative error between Grid 1 and Grid 3 is 2.2‱ and the relative error between Grid 2 and Grid 3 is 0.9‱, which shows that although the number of grids is decreasing, the error rate of the calculation results is small, and the data simulated using Grid 3 can respond to the laws required for the experiment without affecting the research and analysis, and can simplify the calculation process and reduce the burden on the simulation system. So, Grid 3 is used for the simulation and calculations.
3.2. Simulation Verification
The accuracy of the model is verified by simulating the experiments in previous work [25]. Set up the same conditions as the experiment: the material is porous anodized aluminum oxide (AAO), which has an emissivity of 0.98 in the atmospheric window and an absorption of 0.054 for solar radiation; the atmospheric emissivity of the AI substrate in the bands of 0~2 μm, 2~8 μm, 8~13 μm, 13~25 μm is approximated to be 0.1, 0.2, 0.9, and 1, respectively; and the convective heat transfer coefficient between the radiator and its surroundings is determined according to the external natural convection conditions in the COMSOL software. Figure 5 shows a sketch of the AAO-based radiative cooler.
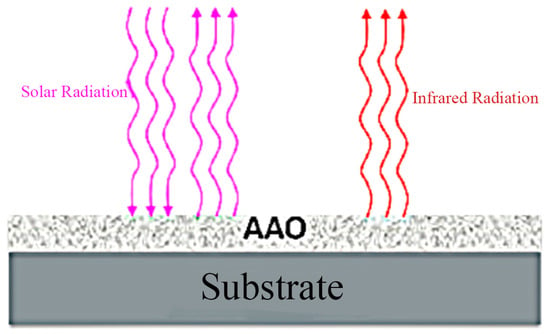
Figure 5.
Sketch of the AAO-based radiative cooler.
Since the external temperature is variable, the cosine wave function is utilized as a function of ambient temperature variation based on the temperature variation data provided in the literature:
In order to obtain a more accurate wavefunction of the ambient temperature change, the accuracy of the ambient temperature is improved by adjusting the amplitude, A. The amplitude coefficients of 0.5, 0.45, 0.43, and 0.4 are selected, and the results are obtained as shown in Figure 6, and the ambient errors are 3.8%, 0.04%, 0.00015%, and 1.44%, respectively. Therefore, the ambient temperature wave function with an amplitude coefficient of 0.43 is selected as the simulated ambient temperature.
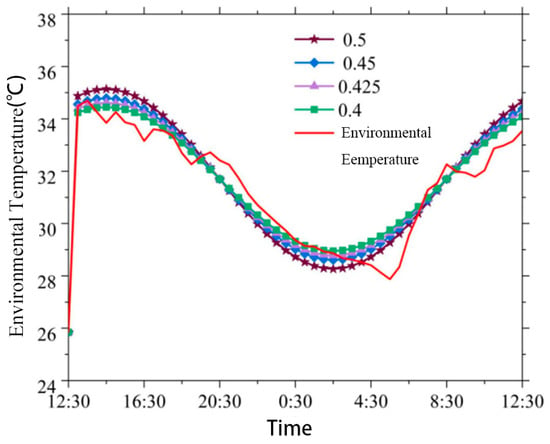
Figure 6.
Comparison of the waveform function of ambient temperature variations at different amplitudes with the actual ambient temperature.
The simulation was verified based on the parameters and ambient temperatures that had been determined for the simulation, and a line graph comparing the simulated cooler surface temperatures with the experimental results from study [26] is shown in Figure 7.
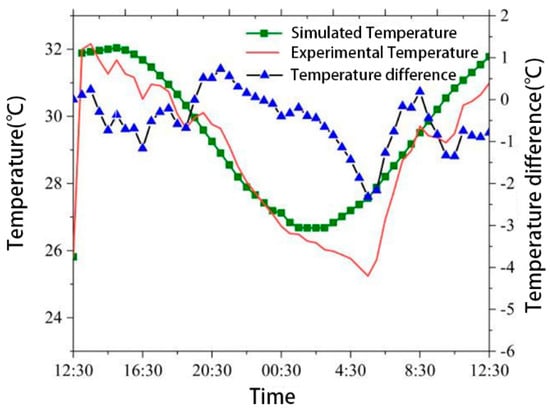
Figure 7.
Comparison of simulation results with experimental results for the surface temperature of the radiator.
The green-square line graph in the figure shows the simulated results of the radiator surface temperature, the red solid line shows the experimental measurements, and the blue triangular line graph shows the temperature difference between the simulation and the experiment. It can be seen that maximum temperature difference between the experimental and simulation results is 2.32 °C, the minimum temperature difference is 0.0047 °C, and the average temperature difference is 0.12 °C, which is due to the uncertainty of the ambient temperature change. The average error rate between the experimental results and the simulation results is 0.34%, which is much less than 5%, proving that the boundary conditions, parameters, and simulation methods of this simulation are feasible, and more accurate results can be obtained under the condition of obtaining accurate environmental data.
4. Simulation Results
The heat exchange of the sky radiative cooler is mainly divided into two parts; one is the heat exchange between the fluid in the tube and the surface of the cooler, and the other is the heat exchange between the surface of the cooler and the surrounding environment and space. There are two main physical quantities for evaluating the performance of the sky radiative cooler: the surface temperature of the cooler, T, and the net radiant power, Pnet, and we focus on the trends of these two quantities. The simulated material emissivity results are shown in Figure 8.
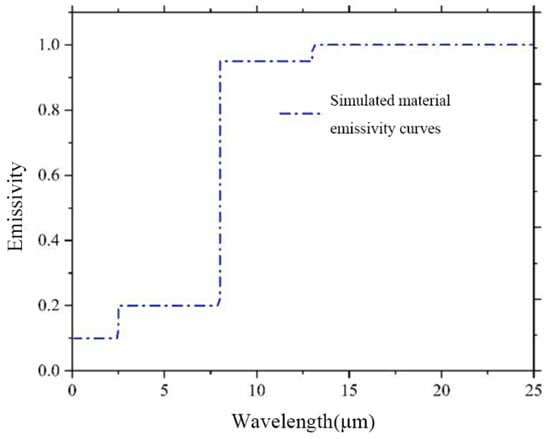
Figure 8.
Emissivity curves of simulated materials.
4.1. Analysis of the Radiative Cooler’s Performance for Different Cloud Thicknesses
The state of the cloud cover is an important factor affecting the performance of sky radiative coolers. In real life, cloud cover is a common weather condition, and in the atmosphere, greenhouse gases such as water vapor, CO2, and ozone have a strong absorption effect on long-wave radiation, so cloud cover has an important influence on the effect of sky radiative cooling.
Cloud cover is divided into a variety of situations, such as different types of clouds (cirrus clouds, stratocumulus clouds), different cloud heights, different cloud thicknesses, different cloud movement states, etc., and all the different states will affect the effect of radiative cooling. For clouds, their main components are condensed water droplets and ice crystals and their average emissivity is 0.92~0.98, although relatively thick clouds can reach 1 emissivity. Even in completely cloudy weather, when the rate of passage of the “atmospheric window” can reach 0, if the cloud temperature is lower than the temperature of the radiative cooler, the system is can still realize a cooling effect. In humid air, if the height of the clouds is known, the atmospheric temperature can be obtained through the rate of decrease of the cloud temperature, but if the height of the clouds is relatively low, it can be assumed that the cloud temperature is the same as the temperature of the cooler, and the cooling power is 0.
Jinan City, Shandong Province, for example, is accessed through the simulation software with its meteorological parameters set as either clear, cloudy, or overcast. Three kinds of weather were simulated to discuss the performance of the radiative cooler; the inlet temperature of the cooler was set to 30 °C; the convection heat transfer coefficient was set to 10 W/(m2∙K); the initial temperature of the cooler was the ambient temperature; and the flow rate was 2 L/min. The experimental results are shown in Figure 9.
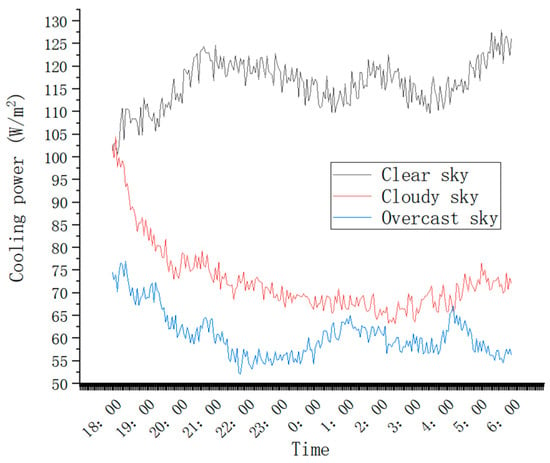
Figure 9.
Cooling efficiency in different weather.
At the same ambient temperature, the average radiative cooling power of sunny, cloudy, and overcast days are 115.26 W/m2, 72.73 W/m2, and 60.72 W/m2, respectively, which is a decrease of 42.53 W/m2 and 54.54 W/m2 relative to the average radiative cooling power of sunny days, which shows that the effect of cloud cover on radiative cooling is great. The average radiative cooling power in cloudy conditions is 12.01 W/m2 higher than that in overcast conditions, and the difference is not as big as that in sunny conditions, so it can be inferred that with the increase in cloud thickness, the degree of decrease in radiative cooling power gradually decreases.
The cloud cover factor is calculated as shown in Equation (14). When it is clear weather, opaque cloud n = 0, so the cloud coefficient , while when cloudy or overcast, n = 1, > 1, and the increase in will lead to a rise in ; will be reduced. Therefore, theoretically, the increase in cloud thickness will lead to a decrease in radiative cooling. From the experimental results it can be seen that there is a significant difference between cooling power of the radiative cooler across the different thicknesses of the cloud states, and that the cooling power of the radiative cooler in clear weather is much greater than that on cloudy and overcast days, which proves the correctness of the theoretical results.
Therefore, under realistic weather conditions, the thicker the cloud cover, the worse the cooling performance of the sky radiative cooler, and in cloudy and foggy weather or areas, the application of the sky radiative cooling system is not effective. But, with the gradual increase in cloud thickness, the difference in the performance of the cooler will gradually decrease. In order to facilitate the simulation of the following experiments, all the simulation calculations in this paper were carried out as if in clear weather.
4.2. Influence of the Ambient Wind Speed on the Radiative Cooling Effect
In 0~8 m/s ambient wind speed, the heat transfer coefficient equation [27] is as follows:
The ambient wind speed is set as 0 m/s, 1 m/s, 2 m/s, 3 m/s, and 4 m/s for the simulation, respectively. The total heat transfer coefficients at different wind speeds were found to be 2.5 W/(m2∙K), 4.5 W/(m2∙K), 6.5 W/(m2∙K), 8.5 W/(m2∙K), and 10.5 W/(m2∙K), respectively, using Equation (26). The ambient temperature was set to 26 °C, the initial temperature of the cooler was 30 °C, and the temperature of its outer surface insulation layer was consistent with the ambient temperature. In setting the solar radiation as an external radiation source of 1000 W/m2, the source position is an infinite distance away and the direction of the incident radiation is (0, 0, −1); the simulation results are shown in Figure 10.
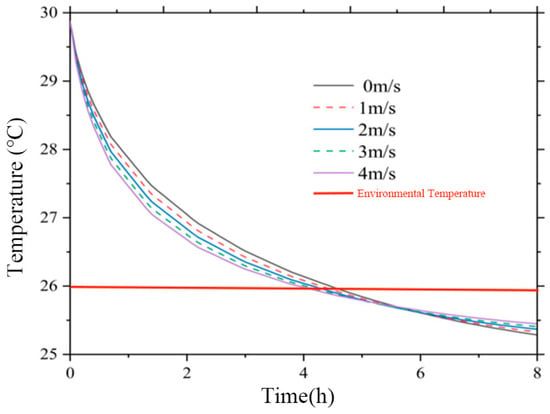
Figure 10.
Variation of surface temperature of the radiative cooler at different wind speeds.
It can be seen from the curve in Figure 10 that the surface temperature of the cooler decreases with time. When the surface temperature of the radiative cooler is higher than the ambient temperature, the higher the air velocity, the faster the rate of temperature drop. This phase reaches a maximum temperature difference of 0.59 °C at 2 h of operation. When the surface temperature of the radiative cooler is lower than the ambient temperature, the smaller the wind speed, the more conducive the conditions are to a further reduction in the surface temperature; this phase reaches a maximum temperature difference of 0.32 °C at 8 h of operation. This is because different ambient temperatures are both favorable and unfavorable to the cooler’s convection heat transfer. When the ambient temperature is higher than the surface temperature of the cooler, the outdoor wind speed brings heat to the cooler; when the ambient temperature is lower than the surface temperature of the cooler, the outdoor wind speed will take heat away from the cooler. Therefore, the best rate of the wind speed in different situations is different, depending on the size of the cooler surface and the outdoor temperature.
4.3. Influence of the Inlet Flow to the Sky Radiative Cooler on the Cooling Performance
The water flow rate affects the water temperature at the outlet of the radiative cooler, so the water flow rate is also an important parameter in the continuous cooling of the sky radiative cooling system. The environmental conditions are unified with the meteorological data in COMSOL; the inlet temperature of the cooler is set to 30 °C, the convective heat transfer coefficient is set to 10 W/(m2∙K), and the initial temperature of the cooler is the ambient temperature without considering the influence of solar radiation. The experimental results are shown in Figure 11.
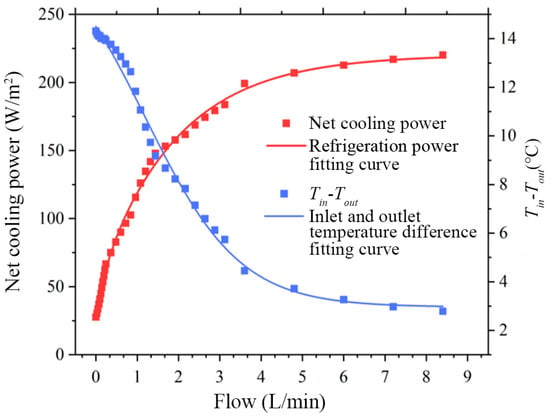
Figure 11.
Variation of surface temperature of the radiative cooler at different flow rates.
It can be seen that as the flow rate increases, the net cooling power gradually increases, the temperature difference between the inlet and outlet gradually decreases, and the rate of change of the two slows down. When the flow rate grows from 0 L/min to 5 L/min, the net refrigeration power grows rapidly, reaching about 200 W/m2 at 5 L/min, and the temperature difference between the inlet and outlet is 4.2 °C. When the flow rate is greater than 5 L/min, the net refrigeration power tends to stabilize; in these conditions the flow rate is too large, resulting in the system’s inability to fully exchange heat with the radiative plate, thus the refrigeration effect of the cooler is smaller.
4.4. Influence of the Installation Angle of the Sky Radiative Cooler on the Radiation Performance
As mentioned before, the radiant power of the material, its atmospheric radiant power and solar radiant power, is affected by the radiation angle, so q is set as 0°, 15°, 30°, 45°, 60°, and 75° for the simulation, respectively. Figure 12 shows a schematic diagram of the radiation angle of the cooler, and q is the angle between the cooler and the ground.
Figure 12.
Schematic installation of the sky radiative cooler.
By assuming that the initial temperature of the sky radiative cooler is the same as the ambient temperature of 30 °C, the convective heat transfer coefficient on the surface of the cooler is 10 W/(m2∙K), and the intensity of the solar radiation is 850 W/m2, the simulation results are as shown in Figure 13.
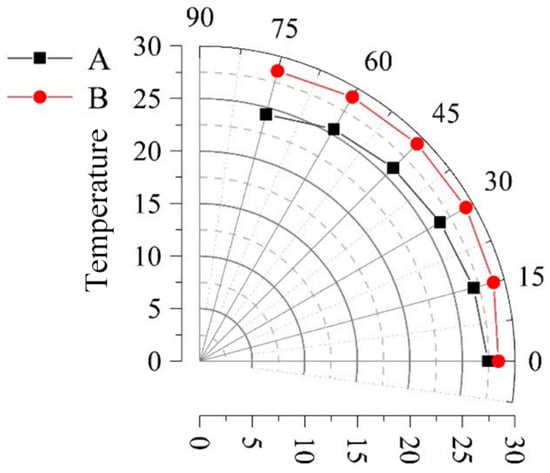
Figure 13.
Sector diagram of the variation of the surface temperature of the radiative cooler with q for different conditions (q, r), with the direction of the radius representing the temperature change.
To compare with ideal conditions, we established two working conditions: line A indicates that there is no radiation heat transfer between the cooler and the surrounding objects, and line B indicates that there is radiation heat transfer. For line A, the larger the angle θ is, the lower the surface temperature of the radiating cooler is, and the temperature decreases from 27.43 °C to 24.32 °C as θ changes from 0° to 75°. For line B, the temperature first shows an upward trend from 28.43 °C (0°) to 29.26 °C (45°), because the increased amount of radiation heat transfer from the surrounding objects to the surface of the cooler is greater than the reduced absorption of solar radiation by the surface of the cooler due to the change in angle, and then later as the angle continues to increase (greater than 45°), the increased radiation heat transfer is no longer dominant, so the temperature gradually decreases to 28.6 °C (75°).
It seems appropriate that increasing the installation angle of the radiative cooler is conducive to improving the cooling performance, but if the angle is too small it may increase radiation heat transfer from the surrounding objects and buildings to the radiative cooler surface, while too large an angle may increase the cost, so the appropriate angle should be chosen according to the actual conditions at the site.
4.5. Influence of the Structural Form of the Sky Radiative Cooler on the Cooling Effect
The sky radiative cooler is a device that radiates energy to the outside world to lower its own temperature. The cooling performance of the cooler can exhibit large differences due to different structures and materials. Therefore, in this section, different structures of the radiative cooler are simulated to explore the effect of structure on the cooling performance.
4.5.1. Effect of PE Film on the Sky Radiative Cooler’s Performance
In this section, a low-density polyethylene (PE) film with a thickness of 0.2 mm was used to suppress the intensity of non-radiation heat transfer. The PE film has good infrared transmittance, which has a small effect on the radiation heat transfer between the radiating material and the external environment. The PE film was placed on 2.5 cm of the radiative cooler’s surface, and the environmental conditions were fluctuated between 20–25 °C, using the weather station data that comes with COMSOL, to verify the effect of its transparency on the performance parameters of radiative cooling in space by simulating the cooler with and without the PE film.
This controlled experiment only records the temperature changes on the surface of the sky radiative cooler. The data acquisition system collected data every minute. Figure 14 gives the temperature variations of the radiative cooler with and without PE film from 11:00 to 10:00 the next day as the solar radiation changes. The sky radiative-cooled flat plate with the PE film applied is referred to as plate number one, and the radiative-cooled flat plate without PE film is plate number two. Figure 14 demonstrates that the radiative material has a high solar radiation absorption rate and has no cooling effect during the day. The maximum surface temperature reached 51 °C for plate one and 50 °C for plate two. During the daytime, the average surface temperature of the second plate was 32.65 °C, and the average surface temperature of the first plate during the daytime was 32 °C. The average temperature difference between the two during the daytime was only 0.65 °C. At about 8:30, when the intensity of the solar radiation was lower, the surface temperature of plate one was 7.46 °C lower than that of plate two, and the maximum temperature difference was reached. The curves of the two control experiments basically match each other, which could indicate that the influence of the PE film’s transparency on sky radiative cooling can be neglected.
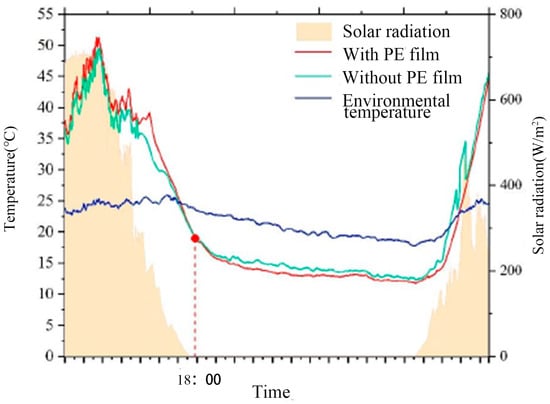
Figure 14.
Plot of experimental results of the surface temperature change and ambient temperature change of sky radiative cooler.
4.5.2. Analysis of the Sky Radiative Cooler’s Performance at Different Air Sandwich Heights
In order to minimize the non-radiation heat transfer that normally exists between a radiative cooler and the atmosphere, a convection cover is usually placed on the cooler’s surface. An air sandwich exists between the cooler surface and the convection cover, as shown in Figure 15. The heat transfer between the cooler surface and the environment is different for different heights of the air sandwich. Therefore, the relationship that exists between the two was simulated using COMSOL software. In the simulation, the environmental conditions used the weather station data that come with COMSOL. Specifically set for the Jinan area at 12 noon on September 1, with an external solar radiation intensity of 850 W/m2, the convection cover plate and the environment for the external natural convection heat transfer of the horizontal plate were determined. The convection cover plate thickness was 0.05 mm and the material was LDPE (Low-Density Polyethylene Film).
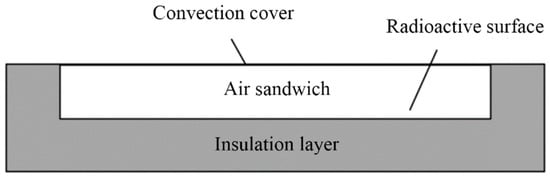
Figure 15.
Schematic diagram of the structure of the radiative cooler.
Air sandwich thicknesses of 1 cm, 2 cm, 4 cm, 6 cm, 8 cm, 10 cm, and 12 cm were taken separately for the simulation. The variation of surface temperature of the radiative cooler with the air sandwich thickness is shown in Figure 16.
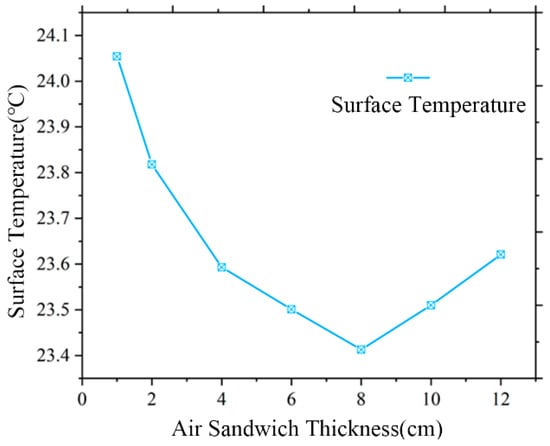
Figure 16.
Changing surface temperature of the radiative cooler with air sandwich thickness.
It can be observed that the surface temperature of the cooler decreases and then increases as the thickness of the air sandwich increases. The inflection point occurs when the thickness is 8 cm. When the sandwich is very thin, the air flow resistance is large, and the air inside the sandwich is almost static, effectively blocking the heat exchange between the surface of the radiative cooler and the convection cover. As the thickness of the sandwich increases from 1 cm to 8 cm, the natural convection of the air inside is strengthened, but the heat exchange increased by natural convection is smaller than the heat exchange hindered by the increased thermal resistance of the air sandwich. The temperature drop brought about by the increase in the thickness of the sandwich is gradually reduced. However, when the thickness of the sandwich increased from 8 cm to 12 cm, the temperature difference between the upper and lower layers increased and the natural convection strength of the internal air also increased, so the radiative cooler indicated that the temperature began to rise. The greater the thickness of the sandwich, the greater the intensity of the natural convection of the internal air, resulting in the production of heat exchange at the surface of the radiative cooler via natural convection between the air in the sandwich and the convection cover’s plate. Figure 17 shows the air flow inside the sandwich at 2 cm, 8 cm, and 12 cm.
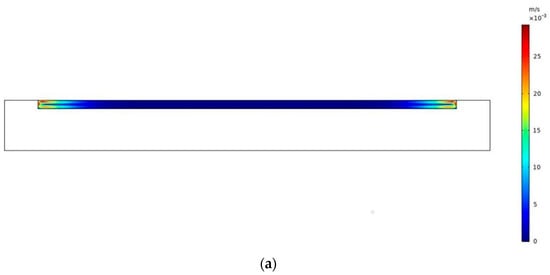
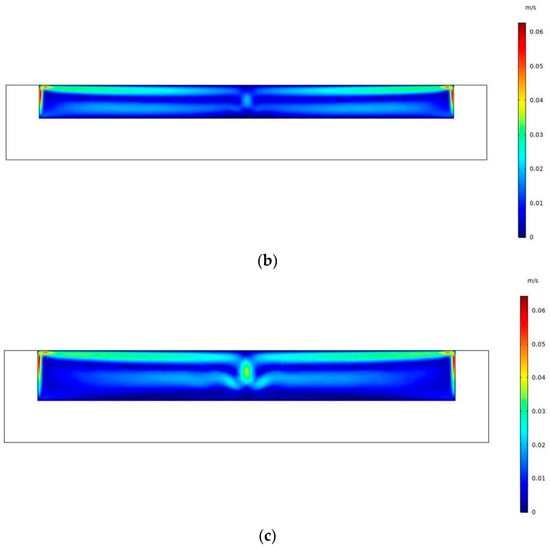
Figure 17.
Velocity field distribution for the natural convection of air inside the sandwich for an (a) air sandwich of 2 cm; (b) air sandwich of 8 cm; and (c) air sandwich of 12 cm.
According to the above results, appropriately increasing the thickness of the air sandwich can realize the effect of reducing the surface temperature of the radiative cold plate to a certain extent, but if the increase is too large it will instead have the opposite effect.
4.5.3. Influence of the Surface Structure of the Sky Radiative Cooler on Its Cooling Performance
In general, the cooling medium inside a sky radiative cooler is water. The temperature at the outlet is low only when the water flow velocity is very low, so the flow state is laminar. The heat transfer between the core region of the fluid and the surface can be hindered by the flow boundary layer, so it is understood that the laminar flow boundary layer can be disrupted by changing the geometry of the cooler and thus enhancing its heat transfer. In this section, the performance of the radiative cooler with the addition of fins is simulated.
The local schematic of the meshing of the radiative cooler after changing the surface structure is shown in Figure 18a. We divided the mesh at the wall more tightly, and the calculation improved the accuracy; the rectangular fins are uniformly distributed on the surface of the radiative cooler. The initial temperature of the water flow on the surface of the radiative cooler and inside the cooler is 30 °C, the inlet temperature is 30 °C, and the inlet flow rate is 2 L/min. We use the data from the weather station in the Jinan area for one day in September, which come with COMSOL, as the environmental conditions, while the initial time is 12:30, and the convective heat transfer coefficient of the surface is 10 W/(m2∙K). Twenty 1 cm × 1 cm square fins were uniformly arranged on the surface of the 3 m long radiative cooling plate; each fin was spaced 12.5 cm apart and a distance of 31 cm from both the inlet and outlet was left, as shown in Figure 18b.
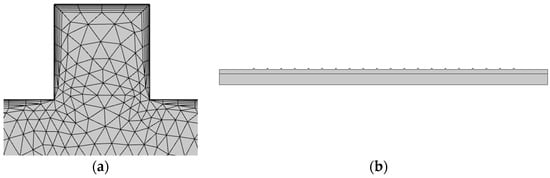
Figure 18.
(a) Mesh delineation; (b) schematic representation of the results for the radiative cooler.
According to Figure 19a, the temperature difference between the inlet and outlet of the radiative cooler with the flat plate structure is always greater than that with the finned plate, with a maximum difference of 0.23 °C between the two. The surface temperature of the flat plate structure is always lower than that of the finned plate structure, and the maximum difference is 0.3 °C. Figure 19b shows the distribution of the finned surface’s radiance; the surface radiance of the horizontal surface is greater than the vertical surface radiance, and the presence of the vertical surface leads to a decrease in the average surface radiance, as shown in Figure 19d. The average surface radiance of the flat plate cooler is larger than that of the finned cooler, with an average difference of 23.52 W/m2. According to Figure 19c, surfaces 1 and 3 have higher radiative cooling powers (including convective heat transfer), which result in the outlet temperature of the radiative cooler with fins being higher than that of the flat plate radiative cooler. The flow rate distribution inside the radiative cooler is shown in Figure 20. The flow rate inside the fins is almost zero, and the heat transfer is only through thermal conduction, which is smaller than the laminar heat transfer rate. Therefore, adding fins to the surface of the radiative cooler has little effect on destroying the internal laminar boundary layer, but rather reduces the heat transfer rate.
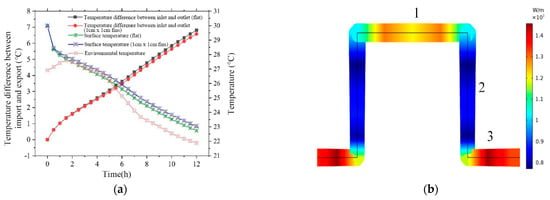
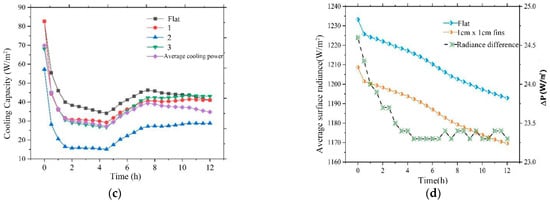
Figure 19.
(a) Changes in inlet and outlet temperature differences and surface temperatures of radiative coolers with two different surface structures; (b) surface radiance of different surfaces of the finned plate; (c) changes in net cooling power between the flat plate surface and the different surfaces of the finned plate; and (d) changes in the average surface radiance and the radiance difference of the radiative coolers with two different surface structures with respect to time. The flat plate in the figure refers to the radiative cooler without fins.
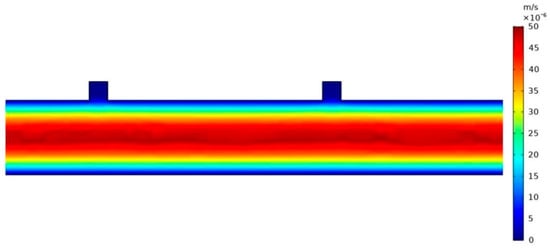
Figure 20.
Localized view of the fluid velocity distribution in the pipe.
5. Energy Efficiency Analysis of the Sky Radiative Cooling Composite System
5.1. The Sky Radiative Cooling Composite Cooling System
Figure 21 shows a schematic diagram of the sky radiative cooling composite system. The system consists of a sky radiative cooling system (1-4-3-2-1), a cold storage system (4-7-8-6-5-4), and a vapor-compression refrigeration unit, with air supplied via a variable air volume system at the end of the building.
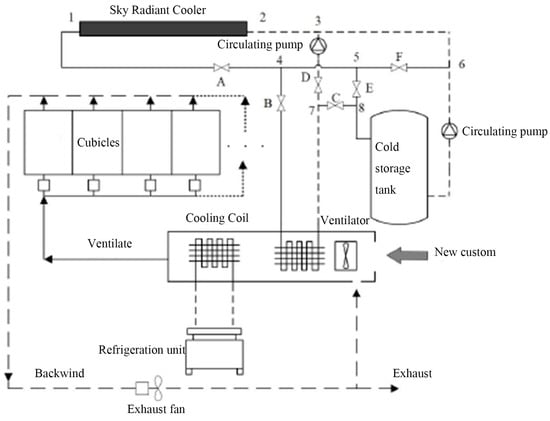
Figure 21.
Schematic diagram of the sky radiative cooling composite system.
The composite cold source system is categorized into three modes of operation under different conditions:
(1) The cooling capacity of the sky radiative cooling system is less than the load in the room, there is no cold capacity in the cold water storage tank, the radiative cooling system supplies cold directly, and the sky radiative cooling and the refrigeration unit operate together to meet the load requirements in the room. At this time, valves A, B, and D are open, and the rest of the valves are closed.
(2) The cooling capacity of the sky radiative cooling system is larger than the load in the room, the refrigeration unit stops working, the sky radiative cooling system operates separately to meet the load in the room, and the excess cooling capacity is stored in the cold water storage tank. At this time, valves A, B, and C open, the rest of the valves are closed.
(3) The volume of cold water stored in the cold water storage tank meets the load in the room, and the sky radiative cooling system and the refrigeration unit stop operating. At this time, valves B, C, and F are open, and the other valves are closed.
5.2. Building Modeling and Simulation Software
In order to facilitate the analysis and calculation, a typical small office building is selected as the building energy consumption analysis model, which is derived from the DOE (Department of Energy) commercial building reference model [28].
As shown in Figure 22, the small office building occupies an area of 510.967 m2 (5500 ft2), the number of floors is 1, the aspect ratio is 1.5, the window-to-wall ratio is 15%, the height of the walls is 3 m, and there are a total of five thermal zones; more detailed information on the internal loads of the building can be found in Ref. [29].
Figure 22.
Axonometric drawing of a small office building.
The building envelope performance meets the minimum standards of the ASHRAE (American Society of Heating Refrigerating and Airconditioning Engineer) 90.1-2019 [30].
In this section, the energy consumption of the sky radiative cooling system + variable air volume (VAV) system will be evaluated and analyzed using EnergyPlus, a large-scale energy analysis and calculation software based on DOE-2, which has been integrated since 1998 to incorporate the strong features of DOE-2 and to develop a new functionality at the same time. The modules include the heat load calculation module, the air conditioning system module, the computer room module, and the economic analysis module. The software simulates the energy consumption of buildings and their related heating, ventilation, and air conditioning (HVAC) equipment, according to dynamic load theory, the coefficient of the reactivity method and the component modules in the VAV system can be utilized to calculate the energy consumption of buildings and their related heating, ventilation, and air conditioning (HVAC) equipment.
Example file objects were assembled in EnergyPlus V9.3.0. Since there is no off-the-shelf radiative cooler module in EnergyPlus, a custom radiative cooler model was created using the Energy Management System (EMS, Energy Management System) module in EnergyPlus, which simulates a higher-order, generalized, managerial-level control methodology, which can be used during a simulation run to update some of the model parameters by obtaining the results of calculations at multiple places in the model and using those results to perform control operations. The custom-created models of the radiative cooler are directly linked to specific systems in EnergyPlus. In Section 3, the radiative cooling was an integral of wavelength and angle, but the EMS does not support integral calculations, so an approximation was used and a regression equation, calculated using MATLAB [31], was derived.
The regression equation is as follows.
where 𝑞𝑛𝑒𝑡 is the net radiant power and ∆𝑇𝑟𝑎𝑑 is the difference between the ambient temperature and the surface temperature of the radiative cooler. The regression coefficients in Equation (27) are, a = 50.93, b = −24,506, c = 0.01359, d = 0.9139, e = 0.005619, f = −0.8513, g = −0.01768, h = −0.0271, i = 0.0000578, and j = −0.02216.
5.3. Determination of Specifications for the Components of Sky Radiative Cooling Composite Systems
In order to simplify the number of calculations for the exit temperature of the radiative cooler as well as the average temperature of the radiative cooler, it is necessary to discretize the radiative cooler; the temperature in each discretized region is derived based on the energy change in the previous segment, so that the exit temperature can be calculated according to Equation (28), as follows:
where 𝑇𝑋,𝑡 is the outlet temperature of segment X at time step t, 𝑇𝑋−1,𝑡 is the inlet temperature of segment X at time step t, 𝑞𝑛𝑒𝑡 is the net heat exchange rate of the segment, 𝑚̇ is the mass flow rate of the segment, and cp is the specific heat capacity of water.
If the circulating water pump of the sky radiative cooling subsystem is stopped, the cooling rate of the radiative cooler is related to the time of the simulation and the amount of water in the radiative cooler, thus the outlet water temperature can be calculated by the following equation:
The discretized radiative cooler is divided into a number of segments, and the indicated temperature of each segment is approximated by the average of the inlet and outlet temperatures of the segment, and the outlet temperature 𝑇𝑋,𝑡 of the current time step is approximated by the outlet temperature 𝑇𝑋,𝑡−1 of the previous time step, and thus the surface temperature of the radiative cooler within the current time period of a particular discretized segment, Trad,t, may be expressed using the following equation [32]:
The average radiated power of the metamaterial is 110 W/m2 [33]. 𝑞𝑐𝑜𝑜𝑙𝑖𝑛𝑔_𝑙𝑜𝑎𝑑·𝑗 is the hour-by-hour cooling load of the building, and the hour-by-hour cooling load of the small office building in different regions is calculated using the cooling load of the design day. Df is the design factor (1.15 for cooling according to ASHRAE [30]).
The length of the circulating water pump and piping can be determined based on the cooling capacity of the radiative cooling subsystem. The volume of the cold storage tank can be adjusted according to the maximum demanded cold storage capacity. The volume of the water storage tank is determined based on the area of the sky radiative cooler, and the volume of the water storage tank corresponding to each square meter of the radiative cooler is 3.15 L. The flow rate of the radiative cooling loop is determined based on the surface area of the radiative cooler, and the flow rate corresponding to each square meter is 20 kg/h [34].
The component parameters of the radiative cooling system are shown in Table 2. The coefficients of the performance of the coolers and the sizing of the water loop of the VAV subsystem were automatically controlled via EnergyPlus.

Table 2.
Parameters of radiative cooling system components in different cities.
5.4. Simulation Location Selection and Annual Energy Consumption Analysis
Four cities are selected as the simulation sites in this section: Jinan (temperate monsoon climate), Shanghai (northern subtropical monsoon climate), Shenyang (temperate continental climate), and Guangzhou (oceanic subtropical monsoon climate). The climate files for each city were selected from the EnergyPlus weather files.
Figure 23 shows the annual refrigeration power consumption in four different cities, and the refrigeration power consumption of the sky radiative cooling composite cold-source system is lower than that of the single electric compression refrigeration system. In the Guangzhou region, a single electric compression refrigeration system has an annual refrigeration power consumption of 18,502.78 KWh, the sky radiative cooling composite cold-source system has an annual cooling power consumption of 13,747.56 KWh; the annual savings in refrigeration power are 4755.21 KWh, a reduction in refrigeration power consumption by 25.7%. The annual refrigeration power consumption of the single electric compression refrigeration system in the Jinan area is 14,672.22 KWh, the annual refrigeration power consumption of the sky radiative cooling composite cold source system is 9228.83 KWh, and the annual saving of refrigeration power is 5443.39 KWh, which reduces the refrigeration power consumption by 37.1%. The annual refrigeration power consumption of the single compression-type refrigeration VAV system in Shanghai is 15,469.44 KWh, the annual refrigeration power consumption of the sky radiative cooling composite cold-source system is 10,441.88 KWh, and the annual saving of refrigeration power is 5027.57 KWh, which is a reduction in refrigeration power consumption by 32.5%. The annual refrigeration power consumption of the single electric compression refrigeration system in the Shenyang area is 12,883.33 KWh, the annual refrigeration power consumption of the sky radiative cooling composite cold-source system is 7111.6 KWh, and the annual saving of refrigeration power is 5771.73 KWh, meaning that the refrigeration power consumption is reduced by 44.8%.
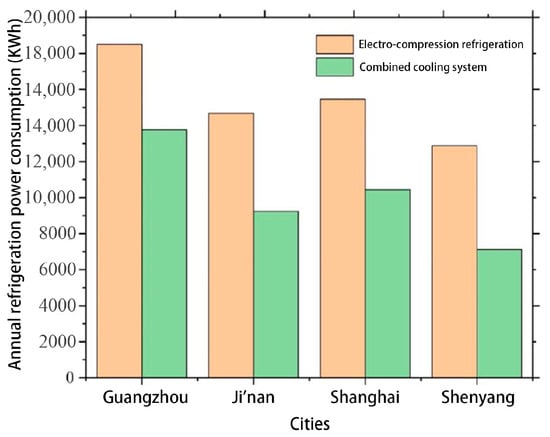
Figure 23.
Comparison chart of electricity consumption for annual cooling requirements.
6. Conclusions
In this paper, the effects of the wind speed, inlet flow rate of the radiative cooler, installation angle of the radiative cooler, and the structural form of different radiators, on the effect of radiative cooling were simulated and the following conclusions are drawn:
- 1.
- Different cloud thicknesses have different effects on the sky radiative cooler; the thicker the cloud thickness, the worse the cooling performance of the radiative cooler, but in a completely cloudy environment, the sky radiative cooler can still realize a cooling effect. The cooling power of the radiative cooler decreased by 42.53 W/m2 and 54.54 W/m2 under cloudy and overcast conditions, respectively, compared with that of the radiative cooler under sunny conditions.
- 2.
- When the ambient temperature is the same, the larger the wind speed, the faster the rate of change of the surface temperature of the radiative cooler. When the ambient temperature is higher than the surface temperature of the cooler, the outdoor environment is exothermic to the cooler; the greater the wind speed, the greater the net cooling power, and the temperature difference can reach a maximum of 0.59 °C. In these conditions, insulating the surface of the radiative cooler from the environment can reduce non-radiation heat transfer. When the ambient temperature is lower than the surface temperature of the cooler, the cooler is exothermic to the outdoor environment; the lower the wind speed the larger the net cooling power, and the temperature difference can reach a maximum of 0.32 °C. In these conditions, non-radiation heat transfer is strengthened.
- 3.
- When the ambient temperature is held constant, the lower the water flow rate of the sky radiative cooling system, the lower the exit temperature of the radiative cooler, however, the net radiative cooling power is also smaller. The difference between the inlet and outlet temperatures and the net radiative cooling power with the increase in the flow rate of change slows down when the flow rate is greater than 5 L/min. Here, the flow rate is too large to lead to uneven heat transfer; the flow rate of the difference between the inlet and outlet temperatures and the net refrigeration power of the cooling system is negligible.
- 4.
- Consideration of the installation angle of the radiative cooler on the cooling effect should be considered when the impact of the buildings around the cooler and the ambient temperature are certain; the cooler and the surrounding objects do not generate radiant heat transfer. The larger the angle of inclination of the cooler, the more the absorption of solar radiation is reduced, and the lower the temperature of the cooler’s surface; when the radiative cooler is near a building, trees, or other objects, due to the surrounding objects, the radiant heat transfer from the surface of the cooler increases due to the reduction in solar radiation caused by changes in the angle of the surface of the cooler. The temperature first shows a rising trend as the angle continues to increase; the surrounding objects on the surface of the cooler increase until the amount of radiation heat transfer is no longer dominant, so the temperature will gradually decrease.
- 5.
- By simulating and analyzing the radiative cooler with and without fins, it was found that, when the ambient temperature was constant, the addition of fins to the surface leads to a decrease in the cooling effect of the radiative cooler and thus to an increase in the outlet temperature. Therefore, when using a sky radiative cooler, the surface of the radiative cooler should have a flat structure.
- 6.
- Sky radiative cooling composite systems in Guangzhou, Shanghai, Jinan, and the Shenyang region reduce the amount of cooling power consumption compared to traditional vapor compression cooling units by 25.7%, 32.5%, 37.1%, and 44.8%, respectively. It can be seen that, in hot and humid areas, the sky radiative cooling composite system’s energy-saving effect is worse than in dry areas, where its energy-saving effect is good.
The simulation results show that when the radiative cooler is applied in conditions lower than the ambient temperature, the cooling effect is weakened when the wind speed is higher. There is an interdependent relationship between the temperature differences between the inlet and outlet and the net cooling power, where a lower flow rate results in a lower outlet temperature, and a higher net cooling power is achieved when the flow rate is higher. When the flow rate is greater than 5 L/min, the effect of the flow rate on the performance of the sky radiative cooler is negligible. Increasing the mounting angle of the radiative cooler is beneficial to the cooling performance, but too large an angle will increase the installation cost and may increase the radiation heat transfer between the radiative cooler’s surface and the surrounding objects and buildings. The cooling effect is best when the thickness of the air sandwich between the radiative cooling surface and the convection cover is 8 cm, and it was found through simulation that the cooling effect is best when there are no fins on the radiation surface; the surface of the radiative cooler should give priority to the use of flat structures.
Author Contributions
Z.Z., formal analysis, survey, software, methodology, writing—original draft, and writing—review and editing; X.Y., formal analysis, investigation, methodology, software, validation, data management, and writing—original draft; M.T. and K.X., resources and data curation; Y.X. and X.B., data curation and visualization. All authors have read and agreed to the published version of the manuscript.
Funding
In this paper, the research was sponsored by the Natural Science Foundation of Shandong Province (Grant No. ZR2022ME102), the Plan of Introduction and Cultivation for Young Innovative Talents in Colleges and Universities of Shandong Province (2021), the Scientific and Technological Innovation Project for Youth of Shandong Provincial Colleges and Universities (Grant No. 2019KJH012), the Research on the Development of Intelligent Management System and Energy Saving Technology for Public Hospital Building Energy Use (Grant No. GYZ2022HQ44), the Shandong Province Science and Technology Small and Medium Enterprises Innovation Ability Enhancement, Project Grant Nos. 2023TSGC0052. 2023TSGC0074), and the Research Fund for the Taishan Scholar Project of Shandong Province (tsan202306064).
Data Availability Statement
The data presented in this study are available in article.
Acknowledgments
The authors of this study wish to acknowledge the contributions of all partners.
Conflicts of Interest
Author Kun Xie was employed by the company China Construction Shanghai Design & Research Institute Co., Ltd. And author Mengyan Tang was employed by the company Shandong Superego Ground Source Heat Pump Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zeyghami, M.; Goswami, D.Y.; Stefanakos, E. A review of clear sky radiative cooling developments and applications in renewable power systems and passive building cooling. Sol. Energy Mater. Sol. Cells 2018, 178, 115–128. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Li, S.; Valenzuela, C.; Shi, S.; Jiang, C.; Wu, S.; Ye, L.; Wang, L.; Zhou, Z. Emerging materials and engineering strategies for performance advance of radiative sky cooling technology. Chem. Eng. J. 2023, 453, 139739. [Google Scholar] [CrossRef]
- Sun, X.; Sun, Y.; Zhou, Z.; Alam, M.A.; Bermel, P. Radiative sky cooling: Fundamental physics, materials, structures, and applications. Nanophotonics 2017, 6, 997–1015. [Google Scholar] [CrossRef]
- Vall, S.; Castell, A. Radiative cooling as low-grade energy source: A literature review. Renew. Sustain. Energy Rev. 2017, 77, 803–820. [Google Scholar] [CrossRef]
- Rephaeli, E.; Raman, A.; Fan, S. Ultrabroadband photonic structures to achieve high-performance daytime radiative cooling. Nano Lett. 2013, 13, 540–544. [Google Scholar] [CrossRef]
- Kou, J.L.; Jurado, Z.; Chen, Z.; Fan, S.; Minnich, A.J. Daytime Radiative Cooling Using Near-Black Infrared Emitters. ACS Photonics 2017, 4, 626–630. [Google Scholar] [CrossRef]
- Liu, H. Numerical Simulation of Flow Field and Heat Transfer in a Rectangular Pipe with Ribs. Master’s Thesis, University of Science and Technology of China, Hefei, China, 2010. [Google Scholar]
- Wang, W. Research on structure optimization and cooling performance of night sky radiators. J. Sol. Energy 2019, 40, 1842–1847. [Google Scholar]
- Chen, J.; Lu, L.; Gong, Q. Techno-economic and environmental evaluation on radiative sky cooling-based novel passive envelope strategies to achieve building sustainability and carbon neutrality. Appl. Energy 2023, 349, 121679. [Google Scholar] [CrossRef]
- Zhang, K.; Zhao, D.; Zhai, Y.; Yin, X.; Yang, R.; Tan, G. Modelling study of the low-pump-power demand constructal T-shaped pipe network for a large scale radiative cooled-cold storage system. Appl. Therm. Eng. 2017, 127, 1564–1573. [Google Scholar] [CrossRef]
- Golaka, A.; Exell, R.H.B. An investigation into the use of a wind shield to reduce theconvective heat flux to a nocturnal radiative cooling surface. Renew. Energy 2007, 32, 593–608. [Google Scholar] [CrossRef]
- Liu, C.; Wu, Y. Effect of atmospheric water vapor on radiative cooling performance of different surfaces. Sol. Energy 2019, 183, 218–225. [Google Scholar] [CrossRef]
- Liu, J.; Tang, H.; Jiang, C.; Wu, S.; Ye, L.; Zhao, D.; Zhou, Z. Micro-Nano Porous Structure for Efficient Daytime Radiative Sky Cooling. Adv. Funct. Mater. 2022, 32, 2206962. [Google Scholar] [CrossRef]
- Aili, A.; Zhao, D.; Tan, G.; Yin, X.; Yang, R. Reduction of water consumption in thermal power plants with radiative sky cooling. Appl. Energy 2021, 302, 117515. [Google Scholar] [CrossRef]
- Zhao, B. Research on Sky Radiation Cooling and Its Comprehensive Utilization with Solar Photovoltaic Conversion. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2020. [Google Scholar]
- Zaite, A.; Belouaggadia, N.; Abid, C.; Kaiss, A.; Kanso, H. Integrate of night radiative cooling technology using a photovoltaic thermal collector under three different climates. Int. J. Thermofluids 2022, 16, 100252. [Google Scholar] [CrossRef]
- Hu, M.; Zhao, B.; Ao, X.; Cao, J.; Wang, Q.; Riffat, S.; Su, Y.; Pei, G. Applications of radiative sky cooling in solar energy systems: Progress, challenges, and prospects. Renew. Sustain. Energy Rev. 2022, 160, 112304. [Google Scholar] [CrossRef]
- Meir, M.G.; Rekstad, J.B.; LØvvik, O.M. A study of a polymer-based radiative cooling system. Sol. Energy 2002, 73, 403–417. [Google Scholar] [CrossRef]
- Collins, T.; Parker, S. Technology Installation Review: White Cap Roof Spray Cooling System; Pacific Northwest National Laboratory: Richland, WA, USA, 1998; Volume 23, p. 2015. [Google Scholar]
- Berdahl, P.; Martin, M. Emissivity of clear skies. Sol. Energy 1984, 32, 663–664. [Google Scholar] [CrossRef]
- Chen, J.; Lu, L.; Gong, Q.; Lau, W.Y.; Cheung, K.H. Techno-economic and environmental performance assessment of radiative sky cooling-based super-cool roof applications in China. Energy Convers. Manag. 2021, 245, 114621. [Google Scholar] [CrossRef]
- Wu, Y.; Zhao, H.; Sun, H.; Duan, M.; Lin, B.; Wu, S. A review of the application of radiative sky cooling in buildings: Challenges and optimization. Energy Convers. Manag. 2022, 265, 115768. [Google Scholar] [CrossRef]
- Cohen, M.E.; Greenberg, D.P. The Hemi-Cube: A Radiosity Solution for Complex Environments. Comput. Graph. 1985, 19, 31–40. [Google Scholar] [CrossRef]
- Matsuta, M.; Terada, S.; Ito, H. Solar heating and radiative cooling using a solar collector-sky radiator with a spectrally selective surface. Pergamon 1987, 39, 183–186. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, J.; Su, Y.S.; Du, W.; Ma, Y.G. Daytime passive radiative cooler using porous alumina. Sol. Energy Mater. Sol. Cells 2019, 191, 50–54. [Google Scholar] [CrossRef]
- Glass, M.W. Chaparral—A Library Package for Solving Large Enclosure Radiation Heat Transfer Problems; Sandia National Laboratories: Albuquerque, NM, USA, 1995; pp. 1–38. [Google Scholar]
- Zhao, D.; Aili, A.; Zhai, Y.; Lu, J.; Kidd, D.; Tan, G.; Yin, X.; Yang, R. Subambient cooling of water: Toward real-world applications of daytime radiative cooling. Joule 2019, 3, 111–123. [Google Scholar] [CrossRef]
- DOE, Commercial Prototype Building Models, Building Energy Codes Program, Department of Energy [EB/OL]. 2019. Available online: https://www.energycodes.gov/commercialprototype-building-models (accessed on 5 June 2023).
- Thornton, B.A.; Rosenberg, M.I.; Richman, E.E.; Wang, W.; Xie, Y.; Zhang, J.; Cho, H.; Mendon, V.V.; Athalye, R.A.; Liu, B. Achieving the 30% Goal: Energy and Cost Savings Analysis of ASHRAE Standard 90.1-2010; Technical Report PNNL-20405; Pacific Northwest National Laboratory: Richland, WA, USA, 2011. [Google Scholar]
- ASHRAE, ANSI/ASHRAE Standard 90.1-2019; Energy Standard for Buildings except Low-Rise Residential Buildings. American Society of Heating, Refrigerating and Air Conditioning Engineers, Inc.: Atlanta, GA, USA, 2019.
- Fernandez, N.; Wang, W.; Alvine, K.; Katipamula, S. Energy Savings Potential of Radiative Cooling Technologies; Pacific Northwest National Laboratory: Richland, WA, USA, 2015. [Google Scholar]
- Zhao, D.; Yin, X.; Xu, J.; Tan, G.; Yang, R. Radiative sky cooling-assisted thermoelectric cooling system for building applications. J. Technol. Sci. 2020, 190, 116322. [Google Scholar] [CrossRef]
- Zhai, Y.; Ma, Y.; David, S.N.; Zhao, D.; Lou, R.; Tan, G.; Yang, R.; Yin, X. Scalable-manufactured randomized glass-polymer hybrid metamaterial for daytime radiative cooling. Science 2017, 355, 1062–1066. [Google Scholar] [CrossRef]
- Eicker, U.; Dalibard, A. Photovoltaic-thermal collectors for night radiative cooling of buildings. Sol. Energy 2011, 85, 1322–1335. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).