Lateral Load-Carrying Capacity of Low-Rise Reinforced Concrete Walls in Nuclear Safety-Related Structures

Abstract

Nuclear safety-related structures are crucial for ensuring the safety of nuclear facilities and preventing the leakage of radioactive materials, with the primary structural component being low-rise reinforced concrete (LRC) walls. These walls are required to carry combined in-plane axial and horizontal loads, making the accurate prediction of their lateral load-carrying capacity particularly important. In this study, six LRC walls with aspect ratios between 0.33 and 1 were tested and a model for the prediction of the lateral load-carrying capacity of LRC walls was established based on the observed failure mode and plastic limit theory. The parameter in the model was calibrated using the obtained results in this test along with a database containing 131 walls in the literature. Compared to the equations in the American standard ACI 349 and the French standard RCC-CW, the proposed equation is most suitable for assessing the lateral load-carrying capacity of LRC walls in nuclear safety-related structures. The calculated values of the proposed equation exhibit a ratio closest to 1 when compared to experimental values and possess the minimum degree of variation. The computational results reveal that the proposed equations in this study exhibit superior precision and stability.

1. Introduction

Nuclear safety-related structures refer to constructions employed in nuclear facilities. In addition to fulfilling general building functions, they are designed to ensure the security of nuclear energy systems. Considering the need to prevent radiation and the leakage of radioactive materials in structures related to nuclear safety [1], walls are often constructed using reinforced concrete. Furthermore, due to the intricate layout of nuclear power equipment, walls in nuclear safety-related structures are primarily low-rise, with an aspect ratio generally not exceeding one. Low-rise reinforced concrete (LRC) walls also need to ensure the capacity to carry the combined in-plane axial and horizontal loads resulting from earthquake actions. Due to their critical role in safety related structures, a precise assessment of their lateral load-carrying capacity is the main concern in the design of nuclear safety-related structures.

In conventional civil structures, reinforced concrete walls with a high aspect ratio are typically employed to primarily carry in-plane bending moments, whereas in nuclear safety-related structures, LRC walls are predominantly used to carry in-plane shear forces. The difference in the load transfer mechanism for these two types of RC walls results in significant diversity for the calculation of their lateral load-carrying capacity. Aiming at the difference, Barda [2] firstly proposed a shear strength calculation equation applicable to reinforced concrete walls with an aspect ratio of less than 2. In current nuclear safety-related structural design codes, the equation adopted in the American ASCE/SEI 43-05 [3], French RCC-CW-15 [4], and Chinese NB/T 20256-13 [5] standards evolved from the equation proposed by Barda [2]. However, research indicates that this equation overestimates the lateral load-carrying capacity of LRC walls [6]. The updated standard ASCE/SEI 43-19 [7] no longer employs this equation. Another commonly used design code ACI 349-13 [8] adopts the same equation as ACI 318-08 [9]. This equation is developed from the modified truss analogy approach [6], which is unsuitable for predicting the shear behavior of low-rise walls. The significant scatter of prediction results via these equations may attribute to the complex shear failure mechanism of LRC walls [6,10].

Recognizing the shortcomings of the equations in current design code, researchers conducted extensive studies to explore the lateral load-carrying capacity of LRC walls [11,12,13,14,15]. The softened truss model [11] provides reasonably accurate predictions for LRC walls. In the softened truss model, the stress state is always assumed to be uniform, which is inappropriate for disturbed stress fields at the top and bottom of the walls. In addition, solving the model requires iteration; hence, its application in engineering poses certain difficulties. Another widely used model is the strut-and-tie model [12,13], which aims to model the balance at concrete nodes within the web and ties, with the failure mechanism believed to be related to concrete crushing. Unlike the previous two models, Gulec and Whittaker [14] proposed a fitted empirical equation by performing parameter studies based on an extensive database and assumed crack pattern, which was later modified by Luna [16]. In summary, some equations rely solely on empirical data without the support of a corresponding physical model. On the other hand, while certain equations are substantiated by physical models, their practical application presents certain inconveniences. Additionally, shear sliding phenomena may occur at the bottom of LRC walls [17,18]. Therefore, it is necessary to incorporate shear friction mechanism into the load-carrying capacity model.

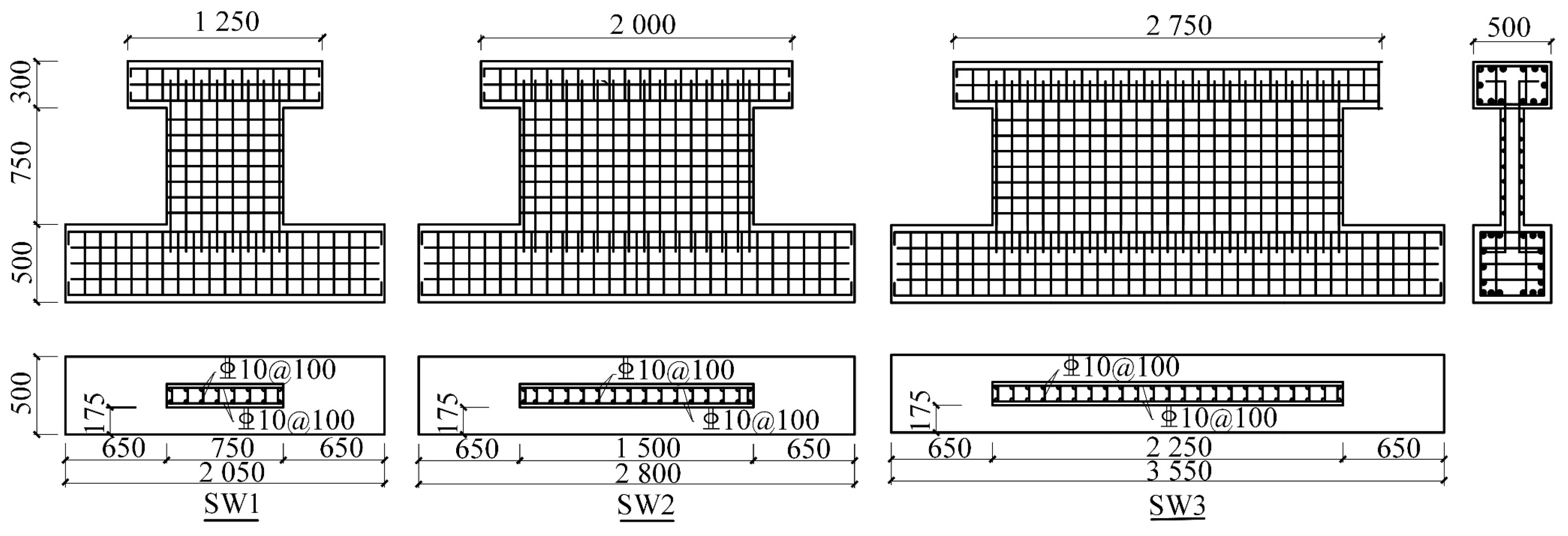
In the above context, this study conducted research on the calculation equation for the lateral load-carrying capacity of LRC walls. Initial experimental assessments of the lateral load-carrying capacity were performed on six low-rise reinforced concrete walls with aspect ratios ranging from 0.33 to 1. Subsequently, a mechanical model was established based on experimental observations, and equations for evaluating the lateral load-carrying capacity were proposed using the established mechanical model and plastic limit theory. Finally, the efficiencies of the proposed equations were verified with 106 LRC walls containing 6 walls in this study under axial compressive force and 25 LRC walls under axial tensile force collected in the literature. Additionally, the performance of the proposed equations was compared with those in the American code ACI 349 [8] and the French code RCC-CW [4]. These results can inform the development and improvement of current design practices for LRC walls in nuclear safety-related structures.

2. Experimental Program

The failure mode of LRC walls is affected by many factors, such as the aspect ratio, horizontal and vertical reinforcement ratios, and axial compressive ratio. According to the specifications of ACI 349 [8], boundary elements can be omitted when the aspect ratio is of less than 2. Additionally, Luna’s experimental results [16] have shown that the peak shear strength of LRC walls is independent of the total vertical reinforcement distribution. Therefore, the failure mode of LRC walls without boundary elements is fundamentally different from the failure mode of conventional reinforced concrete walls. An experimental program including six LRC walls was conducted to support the derivation of the load-carrying capacity equation.

2.1. Test Specimens

Six LRC walls (denoted by SW1 to SW6) with the same thickness (b = 150 mm) and height (h = 750 mm) were designed, constructed, and tested. The designed specimens encompass three aspect ratios, specifically 0.33, 0.5, and 1. Accordingly, the length (l) of the specimens is 750 mm, 1500 mm, and 2250 mm, respectively. The aspect ratio within this range is considered representative of typical dimensions for nuclear safety-related structures and aligns with industry standards and practices in this field. The specimen dimensions and steel bars of SW1~SW3 are depicted in Figure 1. It should be noted that all specimens were not equipped with boundary elements. The same reinforcement meshes were arranged at two sides of the wall. Both spacings of the horizontal and vertical reinforcement were 100 mm. The axial compression ratio for all specimens was 0.1, except for SW4, which had an axial compression ratio of 0.3. The length direction of the specimen is defined as the x-direction, and the height direction is defined as the z-direction. The detailed properties of the specimens are summarized in

Table 1. Properties of wall specimens.

Specimen	b/mm	h/mm	l/mm	Steel Bars	${\mathit{\rho }}_{\mathit{x}}$/%	${\mathit{\rho }}_{\mathit{z}}$/%	n
SW1	150	750	750	D10@100	1.12	0.98	0.1
SW2	150	750	1500	D10@100	1.12	0.98	0.1
SW3	150	750	2250	D10@100	1.07	0.98	0.1
SW4	150	750	750	D10@100	1.12	0.98	0.3
SW5	150	750	1500	D8@100	0.71	0.63	0.1
SW6	150	750	2250	D8@100	0.69	0.63	0.1

Note: n = N/(A_cf_c), where N is the applied axial compressive force, A_c is the sectional area of the wall; f_c is the actual compressive strength of concrete; b is the wall thickness; ${\rho }_{\mathrm{x}}$ and ${\rho }_{\mathrm{z}}$ denote the reinforcement ratios in x and z direction.

.

All wall specimens were prepared using the same batch of concrete, and the compressive strength of 150 mm cubic concrete specimens, which were cured under the same conditions as the wall specimens, was tested. The measured average concrete cube compressive strength was 45.1 MPa. In accordance with the Chinese Code for Design of Concrete Structures GB 50010-2010 [19], the actual compressive strength (f_c) of concrete was taken as 0.75f_cu, equal to 33.7 MPa, and the actual tensile strength (f_t) of concrete was considered to be 0.395f_cu^0.55, which is 3.2 MPa. Additionally, D8 and D10 steel bars (diameter = 8 mm and 10 mm) were placed for reinforcement meshes. The measured average yield strength of D8 and D10 steel bars was 450.4 MPa and 454.6 MPa, respectively; and the measured average tensile strength of D8 and D10 steel bars was 659.7 MPa and 650.1 MPa, respectively.

For the convenience of loading, RC beams were constructed both at the top and bottom of the wall specimens. The vertical and horizontal loadings were ensured to be in the same plane, with the bottom beam firmly clamped to the floor. The horizontal hydraulic actuator was placed at the same height as the center of the top beam, while a rigid steel beam was placed between the top beam and the vertical hydraulic actuator to uniformly distribute the axial compressive force to the top beam. The test loading configuration is depicted in Figure 2. The vertical load was initially applied to the top beam and held constant throughout the entire testing process. Subsequently, a monotonic horizontal load was applied through a displacement-controlled horizontal hydraulic actuator until the load decreased to 75% of the peak load to ensure the capture of sufficient information during the experiment based on the Chinese code JGJ 101-2015 [20], at which point the loading was halted.

2.2. Test Results

Figure 3 illustrates the crack patterns upon the failure of six specimens. It is evident that specimens SW1 and SW4, with an aspect ratio of 1, predominantly exhibited flexural-shear failure, whereas specimens SW2, SW3, SW5, and SW6, with an aspect ratio of less than 1, leaned towards shear failure. Given the central focus of this paper on the calculation of the lateral load-carrying capacity of LRC walls,

Table 2. Measured lateral load-carrying capacity (V_e).

Specimens	SW1	SW2	SW3	SW4	SW5	SW6
Ve/kN	347.8	1221.1	2300.9	477.1	1042.0	2051.2

provides the measured lateral load capacities (V_e) of the specimens. Additionally, key conclusions pertaining to the derived equations are presented below:

(1)

The response of LRC walls significantly differs from high-rise reinforced concrete walls designed for flexural failure control. For low-rise walls with an aspect ratio of less than 1 and subjected to constant axial pressure, inclined cracks initially appear under increased lateral loads. As the load continues to increase, these inclined cracks extend to the interface between the web wall and basement beams, forming an inclined crack–shear friction failure mechanism.

(2)

The lateral load-carrying capacity of LRC walls is influenced by the aspect ratio, axial compression ratio, and reinforcement ratio. Among these factors, the aspect ratio exerts the most significant influence on the lateral load-carrying capacity of LRC walls. For LRC walls of equal height, a smaller aspect ratio corresponds to a higher lateral load-carrying capacity, with the length of shear friction along the base interface of the wall increasing accordingly.

3. Mechanical Model and Basic Equation of the Lateral Load-Carrying Capacity

3.1. Mechanical Model

Under the action of horizontal load, LRC walls carry primary shear forces and minor bending moments. Figure 4a shows the shear failure model established based on the experimental results in this study. As the specimen approaches its ultimate load-carrying capacity, the presence of multiple inclined cracks can be observed. At the same time, a shear friction crack develops at the intersection surface between the wall and the bottom beam. However, during the development of the calculated model, a deliberate decision was made to select the most prominent crack (i.e., the primary crack) to represent the mechanical behavior of the specimen more effectively. This is primarily because attempting to accurately model multiple cracks could potentially increase the complexity of the model. Therefore, to simplify the structure of the model and ensure its reliability, a decision was made to use the primary crack as a representative, reflecting the overall behavior of the specimen when reaching its load-carrying limit. The line AB in Figure 4a represents a primary shear crack, with a projection length in the x-direction of h/k, where k = tan$\theta$ and $\theta$ is the angle between crack AB and the x direction. The line BC represents a shear friction crack along the beam, with a length of l − h/k. The stress state of the concrete and two-directional steel bars in a microelement along the inclined crack AB is shown in Figure 4b, while Figure 4c illustrates the stress state of concrete at the shear friction interface. Equations for determining the lateral load-carrying capacity of LRC walls are derived from the model depicted in Figure 4 based on plastic limit theory.

The plastic limit theory is a commonly used method for analyzing the limit load-carrying capacity of members or structures. In plastic limit analysis, the ideal rigid–plastic constitutive relationship is adopted, which means the material is either rigid without elastic deformation or in a plastic flow state caused by plastic deformation. For most RC structures or members, the elastic range is small, and elastic deformation can be neglected in comparison to plastic deformation, which forms the foundation of the rigid–plastic material assumption. It is reasonable to regard steel and concrete with reduced strength as rigid–plastic materials [21]. Based on the rigid–plastic material assumption, structures transfer from a rigid state to a completely plastic state directly, and the stress of the material remains unchanged. Therefore, the limit analysis of reinforced concrete members or structures can be accomplished in a single step, differing from the typical inelastic analysis, which requires encompassing the entire process from the elastic phase to the plastic phase while considering the inelastic stress–strain relationship of both concrete and steel.

When employing the plastic limit theory to analyze reinforced concrete structures, it is common to utilize an idealized rigid–plastic constitutive relationship. As depicted in Figure 5, the stress–strain curves for both steel and concrete are typically idealized as equivalent horizontal lines. The rigid–plastic theory assumes that the material is ideally rigid before yielding and undergoes plastic flow after yielding. For steel bars, the yield strength is considered to be the true yield strength of the material, as shown in Figure 5a. For concrete, an equivalent strength f_ce is used as its yield strength, where f_ce = ν_c f_c, and ν_c is a reduction factor for compressive strength. It is noteworthy that there is a significant deviation between the actual stress–strain relationship of concrete and the assumptions of this model. This is primarily due to the fact that when concrete is subjected to tension and cracks appear, the compressive strength of concrete parallel to the direction of the crack significantly decreases due to the action of tensile forces. Nielsen and Hoang [21] suggested ν_c = 0.7 − f_c/200. In this study, a reduction factor of 0.6 was adopted to obtain a stress–strain curve that approximates the area under the actual curve, as shown in Figure 5b. Furthermore, it is assumed that there is a perfect bond between the steel bars and the concrete.

3.2. Shear Force Carried by Inclined Crack Plane

As depicted in Figure 4a, the lateral load-carrying capacity of LRC walls is composed of the shear force carried by the inclined crack plane AB and the shear force carried by the shear friction crack plane BC.

Regarding crack AB, as shown in Figure 4b, our previous work [15] derived the limit shear strength (v₁) of a micro-element based on the Mohr–Coulomb criterion and limit plastic analysis. The detailed derivation can be found in Appendix A:

$$v_1\left(\theta \right)=\frac{c\cos \phi }{\sin (2\theta )}+\left({\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}-{\sigma }_{\mathrm{x}}\right)\frac{\sin \phi -\cos (2\theta )}{2\sin (2\theta )}+\left[{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}-{\sigma }_{\mathrm{z}}(x)\right]\frac{\sin \phi +\cos (2\theta )}{2\sin (2\theta )}$$

(1)

where ${\sigma }_{\mathrm{x}}$ and ${\mathsf{\sigma }}_{\mathrm{z}}$ represent the normal stress in the x and z directions of the micro-element; ${\rho }_{\mathrm{x}}$, ${\rho }_{\mathrm{z}}$, f_yx and f_yz denote the reinforcement ratio and yielding strength of steel bars in the x and z direction; and c and $\phi$ are the cohesion force and friction angle in the Mohr–Coulomb criterion, respectively. Both c and $\phi$ can be expressed as functions of the equivalent tensile strength (f_et) and compressive strength (f_ec), as follows:

$$c=\frac{f_{\mathrm{ec}}(1-\sin \phi )}{2\cos \phi }=\frac{1}{2}\sqrt{f_{\mathrm{ec}}{f}_{\mathrm{et}}}$$

(2)

$$\sin \phi =\frac{f_{\mathrm{ec}}-f_{\mathrm{et}}}{f_{\mathrm{ec}}+f_{\mathrm{et}}}$$

(3)

The tensile strength of concrete is small and can be ignored, causing the equivalent tensile strength (f_et) of concrete to become 0. This results in the values of c and φ being 0 and 90°, respectively, as indicated in Equations (2) and (3). Consequently, this simplifies Equation (1) into the following form:

$$v_1\left(\theta \right)=\left({\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}-{\sigma }_{\mathrm{x}}\right)\frac{1-\cos (2\theta )}{2\sin (2\theta )}+\left({\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}-{\sigma }_{\mathrm{z}}(x)\right)\frac{1+\cos (2\theta )}{2\sin (2\theta )}$$

(4)

Due to k = $\tan \theta$, Equations (5) and (6) can be derived.

$$\frac{1-\cos (2\theta )}{2\sin (2\theta )}=\frac{{\sin }^2\theta +{\cos }^2\theta -{\cos }^2\theta +{\sin }^2\theta }{4\sin \theta \cos \theta }=\frac{2\sin \theta }{4\cos \theta }=\frac{1}{2}\tan \theta =\frac{1}{2}k$$

(5)

$$\frac{1+\cos (2\theta )}{2\sin (2\theta )}=\frac{{\sin }^2\theta +{\cos }^2\theta +{\cos }^2\theta -{\sin }^2\theta }{4\sin \theta \cos \theta }=\frac{2\cos \theta }{4\sin \theta }=\frac{1}{2}\cot \theta =\frac{1}{2k}$$

(6)

Hence, Equation (1) can be reformulated as follows:

$$v_1\left(k,x\right)=\frac{1}{2}k\left({\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}-{\sigma }_{\mathrm{x}}\right)+\frac{1}{2k}\left[{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}-{\sigma }_{\mathrm{z}}(x)\right]$$

(7)

The stress in the z direction is not constant for walls carrying in-plane horizontal and vertical loadings and varies with distance from the origin in the x direction. On the assumption that the wall is rigid, the stress in the z direction is expected to follow a specific distribution pattern, described as follows:

$${\sigma }_{\mathrm{z}}(x)=q_1+\frac{x}{l}(q_2-q_1)$$

(8)

With

$$q_1=-\frac{N}{A_{\mathrm{c}}}+\frac{hV}{2W}$$

(9)

$$q_2=-\frac{N}{A_{\mathrm{c}}}-\frac{hV}{2W}$$

(10)

where h, l, and b are the height, length, and thickness of the wall, respectively; A_c is the horizontal section area of the wall; V is the lateral load-carrying capacity of the wall; and W is the section modulus in bending, calculated as W = bl²/6; q₁ and q₂ are stress at the ends of the wall. Figure 6 illustrates the vertical stress at the top of the wall resulting from both vertical and horizontal loadings.

It is essential to clarify that the vertical stress presented in Figure 6 does not perfectly align with reality. Accurately determining the distribution of vertical stress in the wall poses challenges. This arises due to the necessity of calculating the vertical stress distribution based on the distribution of vertical strain along the horizontal axis and the stress–strain relationship of the concrete within the wall. For LRC walls, the strain distribution in the section deviates from the conventional assumption of a slender section analysis, rendering the strain distribution in the wall section unknown. Although the equation for calculating the lateral carrying capacity obtained through the analysis of the wall cross-section stress distribution using Equation (8) is approximate, it is simple and practical. In this study, a primary equation is first put forward and then calibrated using experimental data.

By integrating v₁(x) along with the projection of crack AB on the x-axis, the shear force carried by the inclined crack plane AB is expressed as follows:

$$V_{\mathrm{AB}}={\displaystyle {\int }_0^{h/k}{v}_1\left(k,x\right)}\mathrm{d}x=b{\displaystyle {\int }_0^{h/k}\left[\frac{k}{2}\left({\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}-{\sigma }_{\mathrm{x}}\right)+\left({\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}-{\sigma }_{\mathrm{z}}(x)\right)\frac{1}{2k}\right]}\mathrm{d}x$$

(11)

The external horizontal stress acting on the wall is equal to zero, namely ${\sigma }_{\mathrm{x}}$ = 0. By substituting Equation (8) into Equation (11), the shear force carried by the inclined crack plane AB is as follows:

$$V_{\mathrm{AB}}=\frac{b}{2}\left[\frac{3h^{3}V}{l^{3}b{k}^3}+{\rho }_{\mathrm{x}}{f}_{\mathrm{xy}}{h}_2+\frac{h}{k^2}\left({\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}+\frac{N}{A_{\mathrm{c}}}-3\frac{hV}{b{l}^2}\right)\right]$$

(12)

3.3. Shear Force Carried by Shear Friction Crack Plane

Regarding crack BC as depicted in Figure 4c, shear friction failure plane is formed via the combined effects of concrete cohesion, friction, and dowel action force provided by steel bars perpendicular to the failure plane under axial compressive force. In accordance with the requirements in Eurocode 2 (EN 1992-1-1:2004) [22], the shear stress carried by concrete and steel bars at the shear friction plane can be determined via the following equation:

$$v_2=c_1{f}_{\mathrm{t}}+\mu {\sigma }_{\mathrm{n}}+{\rho }_z{f}_{\mathrm{yz}}(\mu \sin \alpha +\cos \alpha )\le 0.5\nu f_{\mathrm{c}}$$

(13)

where c₁ and $\mu$ are factors related to roughness degree of shear friction plane; f_t is the concrete tensile strength; f_c is the concrete compressive strength; f_yz is the yield strength of steel bars across the friction plane; ${\rho }_{\mathrm{z}}$ is the steel bar ratio across the friction plane; ${\sigma }_{\mathrm{n}}$ is the normal stress crossing the friction plane (positive in compression, negative in tension), ${\sigma }_{\mathrm{n}}$ < 0.6f_c; cf_t equals zero when ${\sigma }_{\mathrm{n}}$ is tensile stress; $\alpha$ is the angle between steel bars and shear friction plane, usually 90° for RC walls in nuclear safety-related engineering; and $\nu$ is an efficient factor.

Considering ${\sigma }_{\mathrm{n}}$ is positive for compression, ${\sigma }_{\mathrm{n}}$ = −${\sigma }_{\mathrm{z}}$(x) is applied here. By substituting $\alpha =$ 90° and ${\sigma }_{\mathrm{n}}$ = −${\sigma }_{\mathrm{z}}$(x) into Equation (13), the following equation can be obtained:

$$v_2(x)=c_1{f}_{\mathrm{t}}+\mu \left[-{\sigma }_{\mathrm{z}}(x)+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\right]$$

(14)

According to Equation (14), shear force V_BC carried by shear friction plane BC is as follows:

$$V_{\mathrm{BC}}=b{\displaystyle {\int }_{h/k}^l{v}_2(x)}\mathrm{d}x=b{\displaystyle {\int }_{h/k}^l\left[c_1{f}_{\mathrm{t}}+\mu \left(-{\sigma }_{\mathrm{z}}(x)+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\right)\right]}\mathrm{d}x$$

(15)

Substituting Equation (14) into Equation (15) gives the following:

$$V_{\mathrm{BC}}=3\frac{\mu h^{2}V}{k{l}^2}\left(1-\frac{h}{kl}\right)+b\left(c_1{f}_{\mathrm{t}}+\mu {\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}+\mu \frac{N}{A_{\mathrm{c}}}\right)\left(l-\frac{h}{k}\right)$$

(16)

3.4. Total Lateral Load-Carrying Capacity of Walls

The total load-carrying capacity of the LRC wall, represented as V = V_AB + V_BC, can be obtained by substituting Equations (12) and (16) and solving for V:

$$V=\frac{\frac{bh}{2k^2}\left[{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}+\frac{N}{A_{\mathrm{c}}}+\left({\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}-{\sigma }_{\mathrm{x}}\right)k^2\right]+b\left(l-\frac{h}{k}\right)\left(c_1{f}_{\mathrm{t}}+\mu \frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\mu \right)}{\frac{3\left(2k\mu -1\right)}{2k^3}{\left(\frac{h}{l}\right)}^2\left(\frac{h}{l}-k\right)+1}$$

(17)

In accordance with the requirements specified in Eurocode 2 [22], the friction coefficient c₁ = 0.25, and $\mu$ = 0.5 are used in this study. Equation (17) presents the upper-bound solution for determining the lateral load-carrying capacity of LRC walls using the limit plastic theory. This is because Equation (1), upon which Equation (17) relies, is essentially an upper-bound solution. The actual lateral load-carrying capacity of LRC walls can be calculated by computing the values of V for different k factors and identifying its minimum value. Figure 7 illustrates the variation of the load-carrying capacity for SW1 to SW6 with respect to factor k. The minimum lateral load-carrying capacity and the corresponding k values are listed in

Table 3. Calculated lateral load-carrying capacity (V).

Specimen	SW1	SW2	SW3	SW4	SW5	SW6
k	1.67	1.67	1.69	1.83	1.65	1.65
V/kN	634.7	1162.9	1691.4	901.3	896.0	1324.7
Ve/kN	347.8	1221.1	2300.9	477.1	1042.0	2051.2

.

Table 3 indicates that the lateral load-carrying capacity of SW1 and SW4, as calculated using the limit plastic theory, exceeds the experimental values, while the load-carrying capacity of SW2 and SW5 aligns closely with the experimental values. It is observed that the lateral load-carrying capacity of SW3 and SW6 is lower than the experimental values. The deviation between the calculated results and experimental values can be attributed to the difference in assumptions and the real conditions. The value range of coefficient k is 1.65 to 1.83, which is consistent with the experimental observations.

4. Simplification and Calibration of Equation

In practical engineering design, obtaining the lateral load-carrying capacity of the LRC walls by minimizing Equation (17) is a very inconvenient task. Therefore, it is necessary to simplify Equation (17). Additionally, adopting the vertical stress distribution shown in Figure 6 leads to a relatively straightforward calculation equation as previously mentioned, but it also introduces inaccuracies in the results. There is room for improvement in terms of the accuracy and performance of the equation. The upcoming sections will focus on simplifying Equation (17) and calibrating the involved parameter using experimental data to facilitate engineering applications and enhance computational precision.

4.1. Simplification of Equation Denominator

The denominator of Equation (17) is as follows:

$$K=\frac{3}{2k^3}{\left(\frac{h}{l}\right)}^2\left(\frac{h}{l}-k\right)\left(k-1\right)+1$$

(18)

For the LRC walls studied in this article, the range of aspect ratio is 0.25 to 2.0. Figure 8 represents the values of K for different h/l values as k varies from h/l to 2. When k = h/l, K = 1.0, and when k approaches positive infinity, K = 1.0. Within the range of k from h/l to 2.0, the change in K is relatively small.

Therefore, it can be approximated that K remains unchanged with variations in k. Further analysis of the experimental data reveals that Equation (18) can be simplified into a function independent of k, as follows:

$$K=x{\left(\frac{h}{l}\right)}^2+1$$

(19)

where x is a factor determined through experimental data. Based on the experimental data from one hundred LRC walls collected in the literature [10] and from this study, x can be taken as 0.5 through a non-linear fitting of the coefficients.

4.2. Simplification of Equation Numerator

As aforementioned, the denominator term in Equation (17) can be regarded as independent of k. Thus, to find the value of k that minimizes Equation (17), it is sufficient to determine the value of k that minimizes the numerator term of Equation (17).

By taking the derivative of Equation (17) and setting it equal to zero, Equation (20) can be obtained.

$$k=\frac{{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}+\frac{N}{A_{\mathrm{c}}}}{c_1{f}_{\mathrm{t}}+\mu \frac{N}{A_{\mathrm{c}}}+\mu {\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}}$$

(20)

The value of k’ corresponding to the dashed vertical line in Figure 7 is determined via Equation (20) for the specimens in this study. It can be observed that although the calculated k value based on Equation (20) does not perfectly match the minimum value shown in the curve in Figure 7, the difference between the two is not substantial (both falling within the range of 1.4 to 1.8). Furthermore, the lateral load-carrying capacity of the LRC wall, calculated using k’ as a substitute for k in Equation (17), is very close to its minimum value. Thus, approximating the minimum load-carrying capacity of the wall using Equation (20) is feasible.

By substituting Equation (20) into the numerator (V_n) of Equation (17) and simplifying, the following equation can be obtained.

$$\begin{array}{ll}{V}_n& =\frac{bh}{2k^2}\left({\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}+\frac{N}{A_{\mathrm{c}}}\right)+\frac{1}{2}bh{\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}+bl\left(c_1{f}_{\mathrm{t}}+\mu \frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\mu \right)-\frac{bh}{k}\left(c_1{f}_{\mathrm{t}}+\mu \frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\mu \right)\\ & =\frac{bh}{2}\frac{{\left(c_1{f}_{\mathrm{t}}+\mu \frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\mu \right)}^2}{{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}+\frac{N}{A_{\mathrm{c}}}}+\frac{1}{2}bh{\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}+bl\left(c_1{f}_{\mathrm{t}}+\mu \frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\mu \right)-\frac{bh{\left(c_1{f}_{\mathrm{t}}+\mu \frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\mu \right)}^2}{{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}+\frac{N}{A_{\mathrm{c}}}}\\ & =\frac{1}{2}bh{\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}+bl\left(c_1{f}_{\mathrm{t}}+\mu \frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\mu \right)-\frac{bh}{2}\cdot \frac{{\left(c_1{f}_{\mathrm{t}}+\mu \frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\mu \right)}^2}{{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}+\frac{N}{A_{\mathrm{c}}}}\\ & =\frac{1}{2}bh{\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}+bl\left(c_1{f}_{\mathrm{t}}+\mu \frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\mu \right)-\frac{bh}{2}\cdot \frac{{(c_1{f}_{\mathrm{t}})}^2+2(c_1{f}_{\mathrm{t}})\mu \left(\frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\right)+{\left(\mu \frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\mu \right)}^2}{{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}+\frac{N}{A_{\mathrm{c}}}}\end{array}$$

(21)

Note that the term ${\left(c_1{f}_{\mathrm{t}}\right)}^2/\left({\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}+N/A_{\mathrm{c}}\right)$ in Equation (21) equals zero approximately with the assumption that f_t can be ignored. Then, Equation (21) can be simplified as follows:

$$V_{\mathrm{n}}=\frac{1}{2}bh{\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}+bl\left(c_1{f}_{\mathrm{t}}+\mu \frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\mu \right)-\frac{bh}{2}\left[2\mu c_1{f}_{\mathrm{t}}+{\mu }^2\left(\frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\right)\right]$$

(22)

As before, the shear friction parameters, c₁ = 0.25, $\mu$ = 0.5, referring to Eurocode 2 are substituted into Equation (22), and V_n is then rewritten as follows:

$$V_{\mathrm{n}}=0.5b\left[h{\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}+\left(l-0.25h\right)\left(0.5f_{\mathrm{t}}+\frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\right)\right]$$

(23)

The final form is as in Equation (24).

$$V=\frac{V_{\mathrm{n}}}{K}=\frac{0.5b\left[h{\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}+\left(l-0.25h\right)\left(0.5f_{\mathrm{t}}+\frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\right)\right]}{0.5{\left(\frac{h}{l}\right)}^2+1}$$

(24)

Equation (24) is developed based on limit analysis and calibrated with experimental data. As a result, it is a theoretical and experimentally based equation.

5. Comparison with Test Results and Equations in Current Codes

After obtaining the lateral load-carrying capacity equation of LRC walls, it is necessary to prove its validity by comparing it with equations in existing codes. Equations proposed in this study are compared with equations provided in ACI 349-13 and RCC-CW without consideration of safety factors. The equations in chapter 11 of ACI 349-13 are listed below:

$$V_{\mathrm{n}2}=V_{\mathrm{c}}+V_{\mathrm{s}}\le 0.83\sqrt{f_{\mathrm{c}}^{\prime }}{t}_{\mathrm{w}}{d}_1$$

(25)

$$V_{\mathrm{c}}=\min \left\{0.27\sqrt{f_{\mathrm{c}}^{\prime }}{t}_{\mathrm{w}}{d}_1+\frac{N{d}_1}{4l_{\mathrm{w}}},\left[0.05\sqrt{f_{\mathrm{c}}^{\prime }}+\frac{l_{\mathrm{w}}\left(0.1\sqrt{f_{\mathrm{c}}^{\prime }}+\frac{0.2N}{l_{\mathrm{w}}{t}_{\mathrm{w}}}\right)}{\frac{M_{\mathrm{u}}}{V_{\mathrm{u}}}-\frac{l_{\mathrm{w}}}{2}}\right]t_{\mathrm{w}}{d}_1\right\}$$

(26)

$$V_{\mathrm{s}}=\frac{A_{\mathrm{v}}{f}_{\mathrm{yt}}{d}_1}{s}$$

(27)

where V_c is the shear strength provided by concrete; V_s is the shear strength provided by steel bars; l_w is wall length; t_w is the wall thickness; d₁ is the distance from extreme compression fiber to the center of force of all steel bars in tension, assuming it to equal 0.8l_w; N is the axial force, positive in tension; M_u is the bending moment; V_u is the shear force; A_v is the area of horizontal steel bar within spacing s; f_yt is the yield strength of the horizontal steel bar; f_c′ is the compressive strength of concrete.

The equations in appendix DJ of RCC-CW-15 are as follows:

$$V_{\mathrm{n}3}=\left[0.7\sqrt{f_{\mathrm{c}}^{\prime }}-0.28\sqrt{f_{\mathrm{c}}^{\prime }}\left(\frac{h_{\mathrm{w}}}{l_{\mathrm{w}}}-0.5\right)+0.25\frac{N}{l_{\mathrm{w}}{t}_{\mathrm{w}}}+{\rho }_{\mathrm{se}}{f}_{\mathrm{y}}\right]t_{\mathrm{w}}{d}_2$$

(28)

$${\rho }_{\mathrm{se}}=A\cdot {\rho }_{\mathrm{v}}+B\cdot {\rho }_{\mathrm{h}}$$

(29)

where d₂ is the distance from the extreme compression fiber to the center of force of all steel bars in tension, assuming these are equal to 0.6l_w; h_w is the wall height; f_y is the yield strength of steel bars; ${\rho }_{\mathrm{v}}$ and ${\rho }_{\mathrm{h}}$ are the reinforcement ratios of vertical and horizontal steel bars, respectively. Coefficients A and B are calculated according to

Table 4. Values of coefficients A and B.

	A	B
$h_{\mathrm{w}}/l_{\mathrm{w}}\le 0.5$	1	0
$0.5\le h_{\mathrm{w}}/l_{\mathrm{w}}\le 1.5$	$-h_{\mathrm{w}}/l_{\mathrm{w}}+1.5$	$h_{\mathrm{w}}/l_{\mathrm{w}}-0.5$
$1.5\ge h_{\mathrm{w}}/l_{\mathrm{w}}$	0	1

.

One hundred LRC walls selected from the literature [10] as mentioned in Section 4.1 and six walls in this study were used to validate the calculation equations for lateral load-carrying capacity under axial vertical compressive and horizontal loadings. The statistical results of the ratio of the calculated values using Equation (24) to the measured load-carrying capacity are presented in

Table 5. Statistical parameters of ratio of calculated values to experimental values.

	Mean	Standard Deviation	COV	Minimum	Median	Maximum
Equation (24)/Vexp	0.996	0.203	0.204	0.566	1.029	1.468
Vn2/Vexp	1.077	0.367	0.341	0.459	1.048	2.124
Vn3/Vexp	1.529	0.382	0.250	0.597	1.600	2.360

. It can be observed from Table 5 that Equation (24) demonstrated excellent predictive performance, yielding a mean value of 0.996, which is closest to 1, and the lowest coefficient of variation (COV) among the three methods assessed. On average, the ACI 349 equation tends to overestimate the lateral load-carrying capacity when compared to the experimental results. The equation proposed by RCC-CW overvalues the experimental results by nearly 50%. In general, Equation (24) proposed in this study shows excellent predictive performance, and it can reliably predict the load-carrying capacity with an adequate safety margin and less scatter.

To further evaluate the performance of the proposed equations, Figure 9 illustrates the scatter diagram of the calculated values with the test results (V_exp). The load-carrying capacity calculated via Equation (24) exhibits the smallest deviation and shows a proportional trend to the measured values. Figure 10 presents the variation of V_cal/V_exp with the aspect ratio h/l. It can be observed that the ratio of the values calculated via Equation (24) to the experimental values exhbits the narrowest band with a range of 0.566 to 1.468. These comparative results further demonstrate the superior stability of Equation (24) compared to the other two equations.

6. Lateral Load-Carrying Capacity under Axial Tensile Force

Equation (24) has been derived and calibrated for LRC walls subjected to compressive forces. For nuclear safety-related internal structures under seismic actions, LRC walls may also carry axial tensile force and horizontal loading. A total of 25 specimens from references [23,24,25,26] were employed to calibrate Equation (24) for LRC walls subjected to axial tensile forces. The aspect ratio of these 25 specimens ranged from 0.9 to 1.3. The calibration process indicates that a minor revision to Equation (24) results in a more accurate prediction of the lateral load-carrying capacity of LRC walls under axial tensile forces. The revised expression for the prediction of lateral load-carrying capacity under axial tensile force is as follows:

$$V=\frac{0.5bl\left[{\rho }_{\mathrm{x}}{f}_{\mathrm{yx}}\frac{h}{l}+\left(1-0.25\frac{h}{l}\right)\left(0.5f_{\mathrm{t}}+\frac{N}{A_{\mathrm{c}}}+{\rho }_{\mathrm{z}}{f}_{\mathrm{yz}}\right)\right]}{0.4{\left(\frac{h}{l}\right)}^2+1}$$

(30)

Equation (30) was also compared with the test results and the equations provided by ACI 349 and RCC-CW. The statistical parameters of the ratio of the calculated values to the experimental values are presented in

Table 6. Statistical parameters of ratio of calculated values to experimental values.

	Mean	Standard Deviation	COV	Minimum	Median	Maximum
Equation (30)/Vexp	1.000	0.206	0.206	0.722	0.966	1.573
Vn2/Vexp	0.750	0.344	0.459	0.307	0.695	1.614
Vn3/Vexp	1.777	0.717	0.404	0.958	1.572	4.065

. The results obtained from Equation (30) exhibit the mean value closest to 1.0 and the lowest coefficient of variation (COV) of 0.206. For specimens subjected to significant tensile forces, the contribution of concrete is zero according to the equation in ACI 349. Only the contribution of horizontal reinforcement to the load-carrying capacity is considered, resulting in underestimated calculation results. The prediction results of RCC-CW significantly overestimate the load-carrying capacity. Figure 11 illustrates the comparison between the prediction results obtained from Equation (30) and those from ACI 349 and RCC-CW. The relationship between the calculated values of Equation (30) and the experimental values shows a close linear correlation.

7. Conclusions

The experiment was conducted on six LRC walls to identify their failure modes and lateral load-carrying capacities. The equations for evaluating the LRC walls were derived based on the plastic limit theory and calibrated using the test data from this study, along with data collected from the literature. Comparisons were drawn between the results predicted via the proposed equations and the test results, as well as between the results predicted via the equations in ACI 349 and RCC-CW codes. The main conclusions are as follows:

(1)

The experimental results indicate that the inclined crack appears and extends to the wall base and bottom beam interfaces under constant axial compressive force and horizontal loading for LRC walls with an aspect ratio between 0.33 and 1. The failure mode of LRC walls can be recognized as a combination of inclined crack and shear friction crack. The aspect ratio has a dominant effect on the lateral load-carrying capacity of LRC walls. The smaller the aspect ratio, the longer the length of the shear friction interface along the wall base.

(2)

The equation proposed in this study accurately predicts the lateral load-carrying capacity of 106 LRC walls under axial compressive force. The proposed equation provides an average calculated-to-experimental ratio of 0.996 and a minimum coefficient of variation (COV) of 0.203. It was found that both equations in ACI 349 and RCC-CW overestimate the lateral load-carrying capacity by 8% and 53%, with coefficients of variation (COV) of 0.341 and 0.250, respectively.

(3)

The proposed equation is also applicable to LRC walls subjected to axial tensile force and horizontal loads, with minor modifications. For 25 LRC walls under axial tensile force collected from the literature, it provides an average calculated-to-experimental ratio of 1.000, with a coefficient of variation (COV) of 0.206. In comparison to the prediction results from the equations in ACI 349 and RCC-CW, the proposed equation demonstrates greater accuracy. The equation in ACI 349 underestimates the lateral load-carrying capacity by nearly 25%, while the equation in RCC-CW overestimates it by approximately 77%.