Wind Effects on Re-Entrant Wing Faces of Plus Plan-Shaped Building
Abstract
:1. Introduction
2. Verification and Validation
3. Numerical Simulation with Methodology
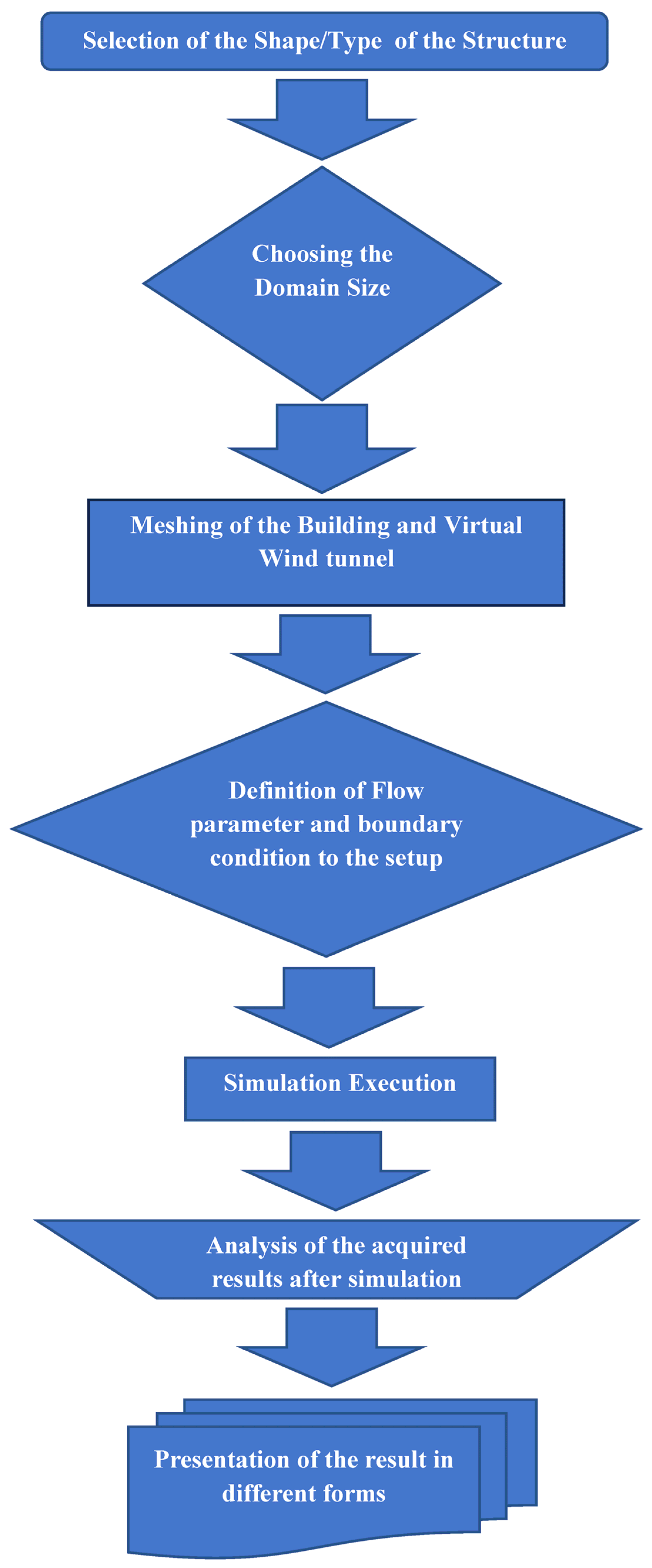
3.1. Flow Chart
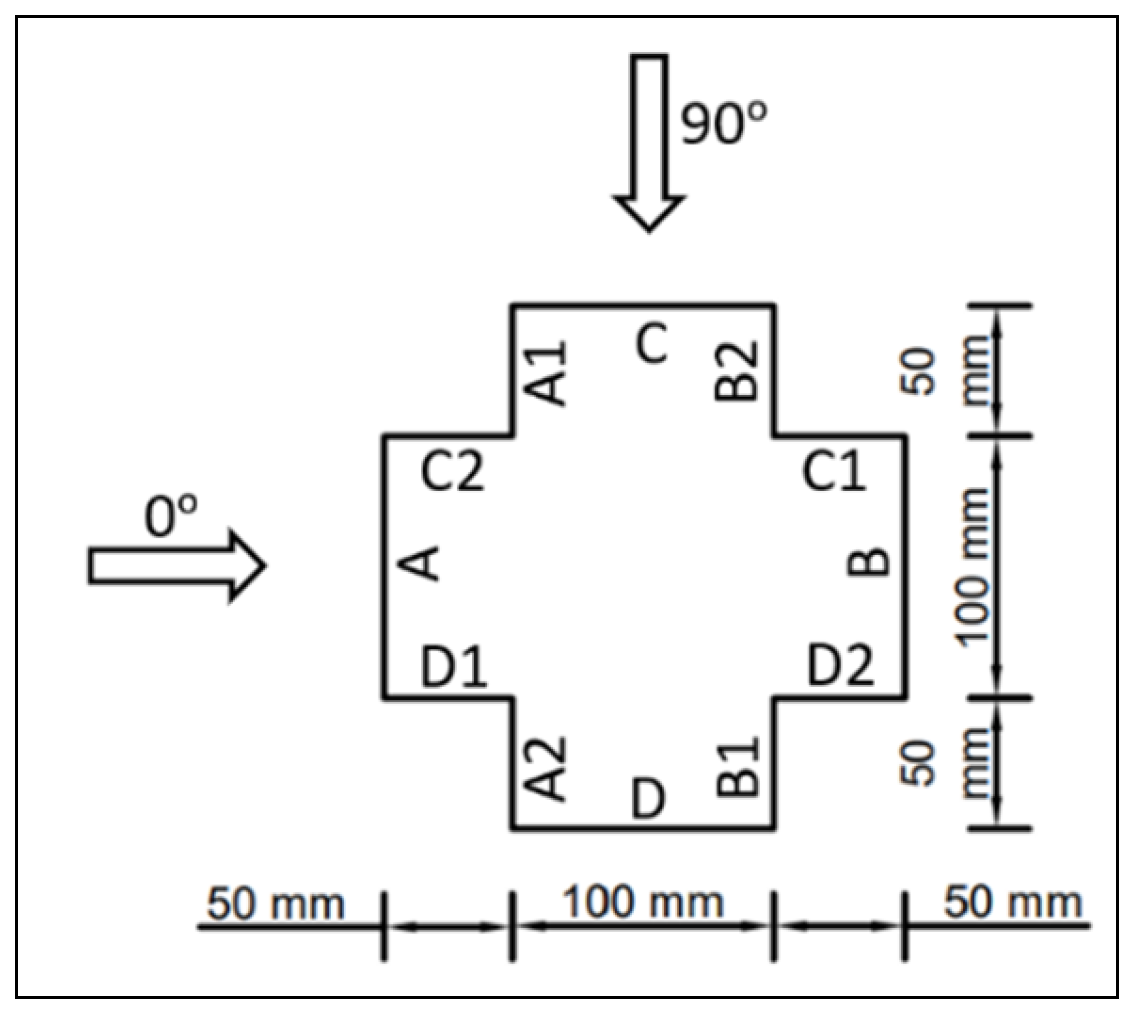
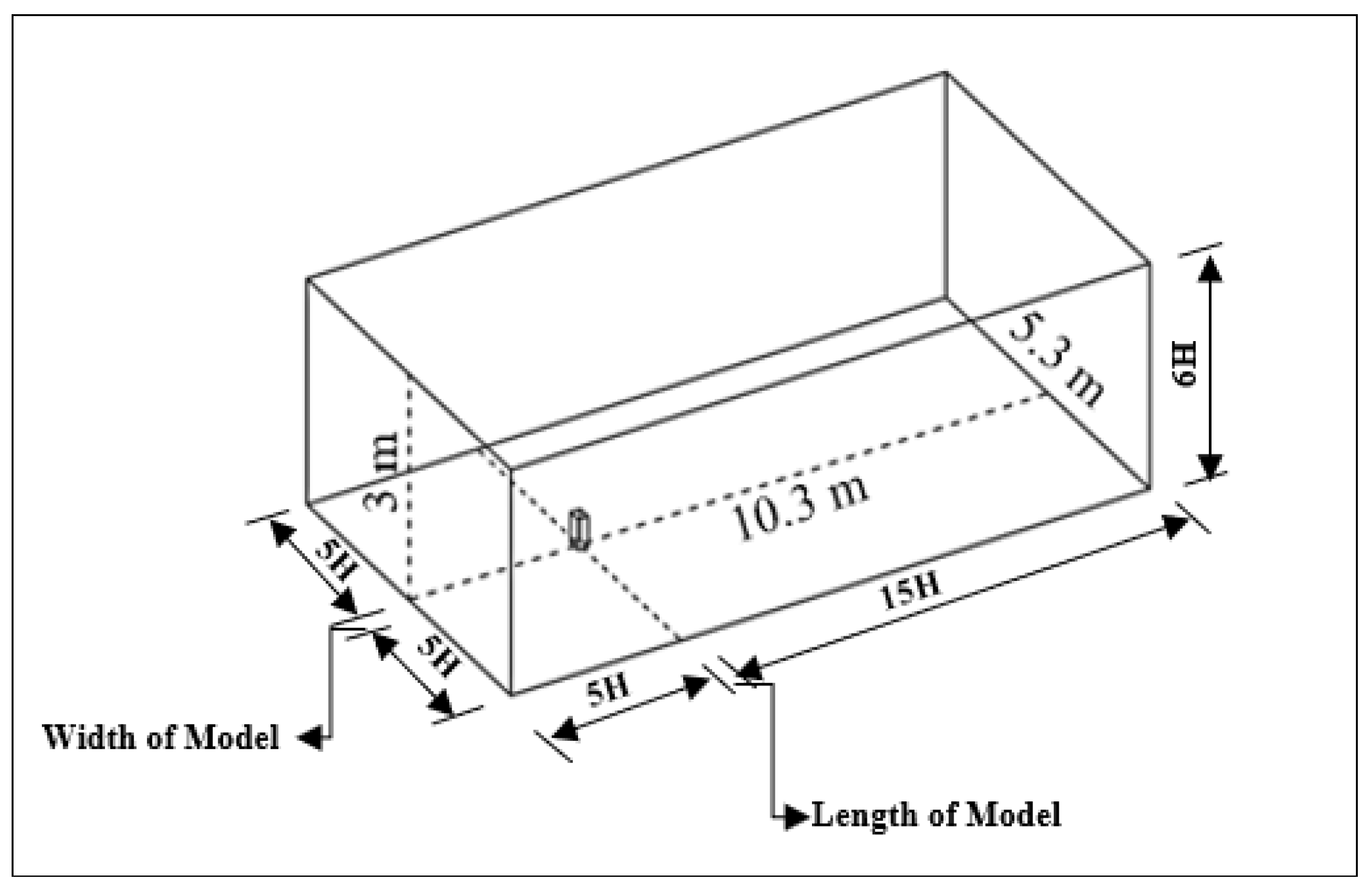
3.2. Model and Computational Domain
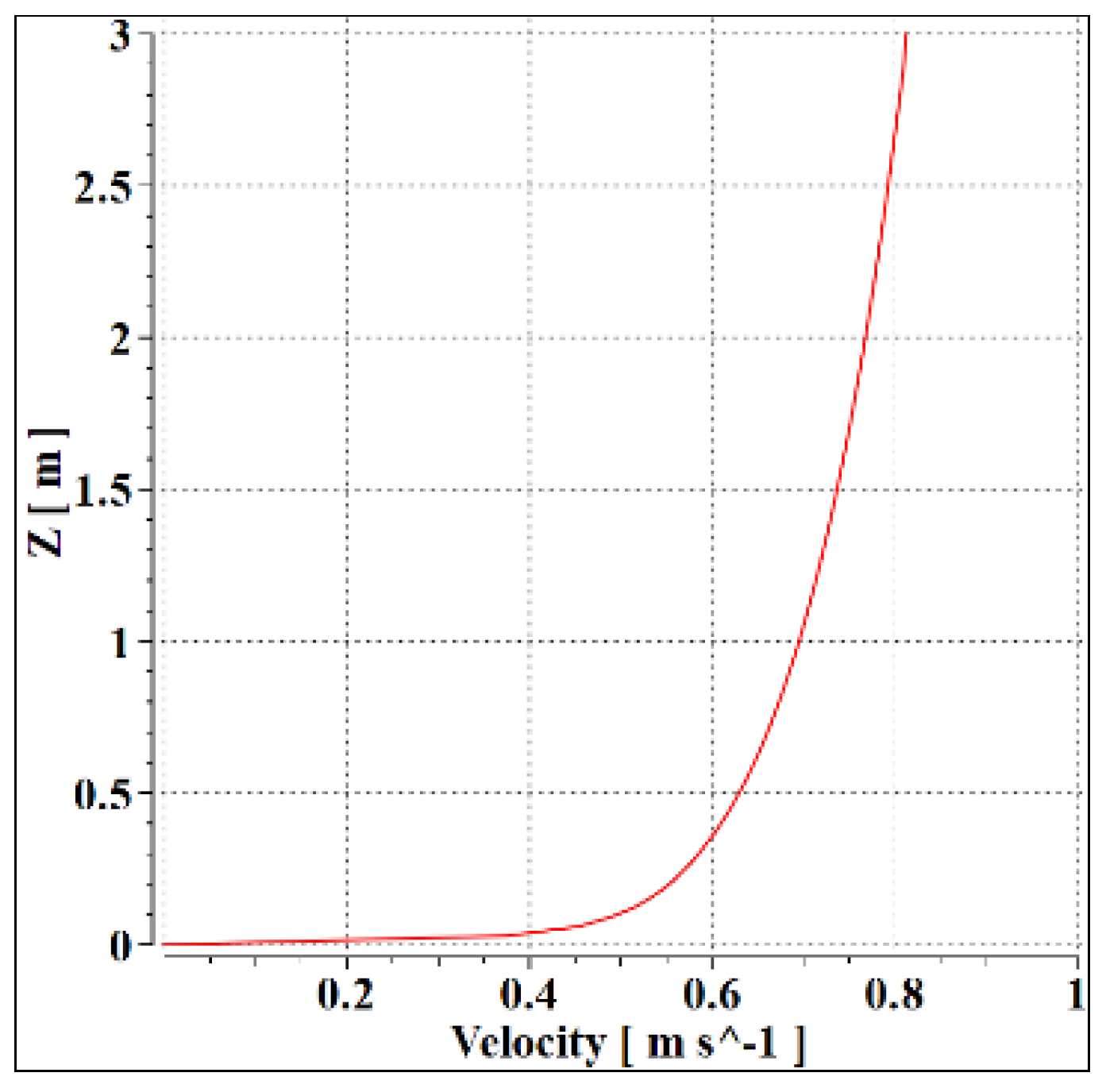
4. Mean Velocity Characteristics
5. Grid Independence and Convergence
5.1. Grid Independence
5.2. Convergence
6. Boundary Conditions and Limitations
6.1. Boundary Conditions as Defined during Numerical Simulation
6.2. Limitations of Numerical Simulation
7. Result and Discussion
7.1. Flow Characteristics
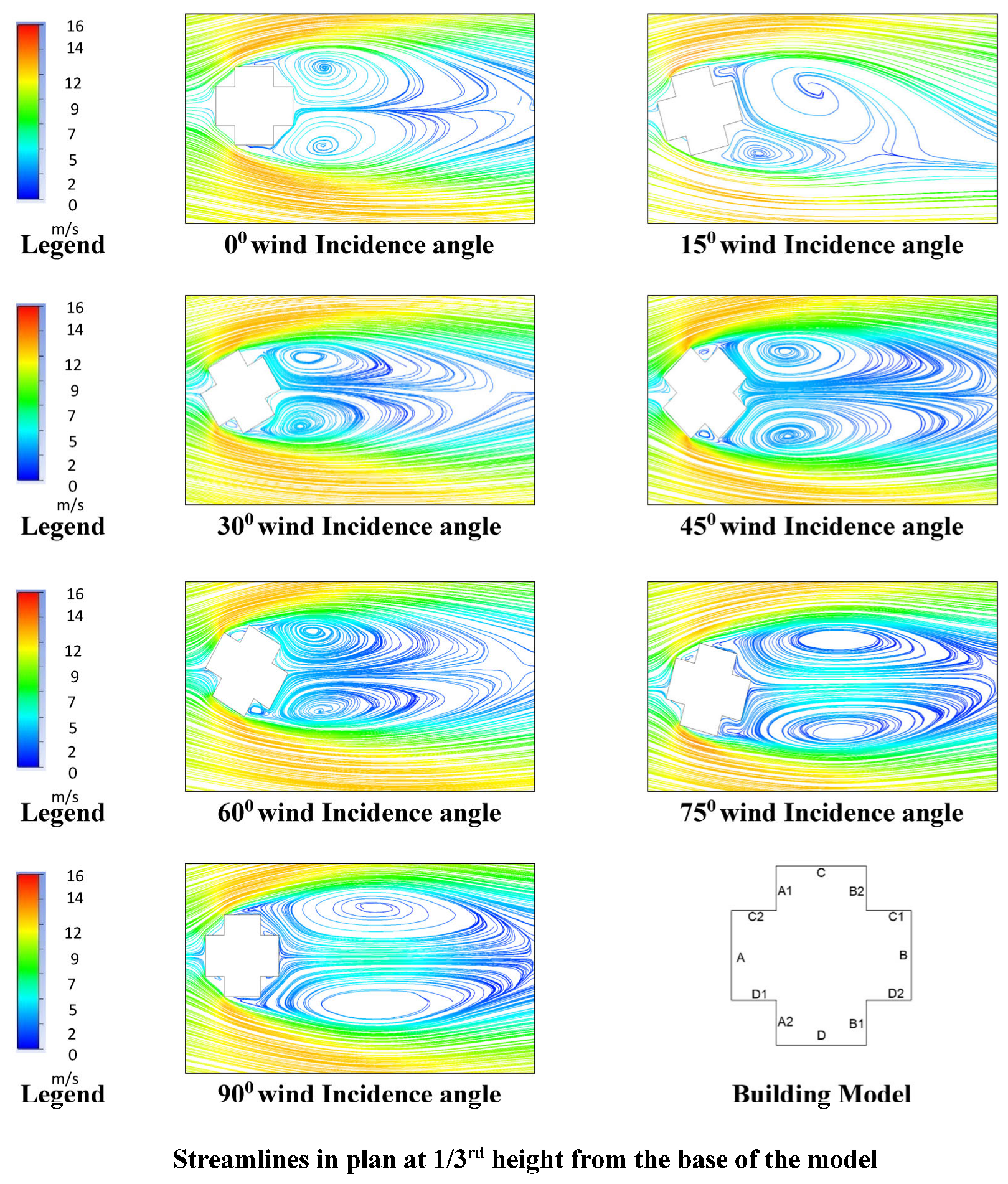
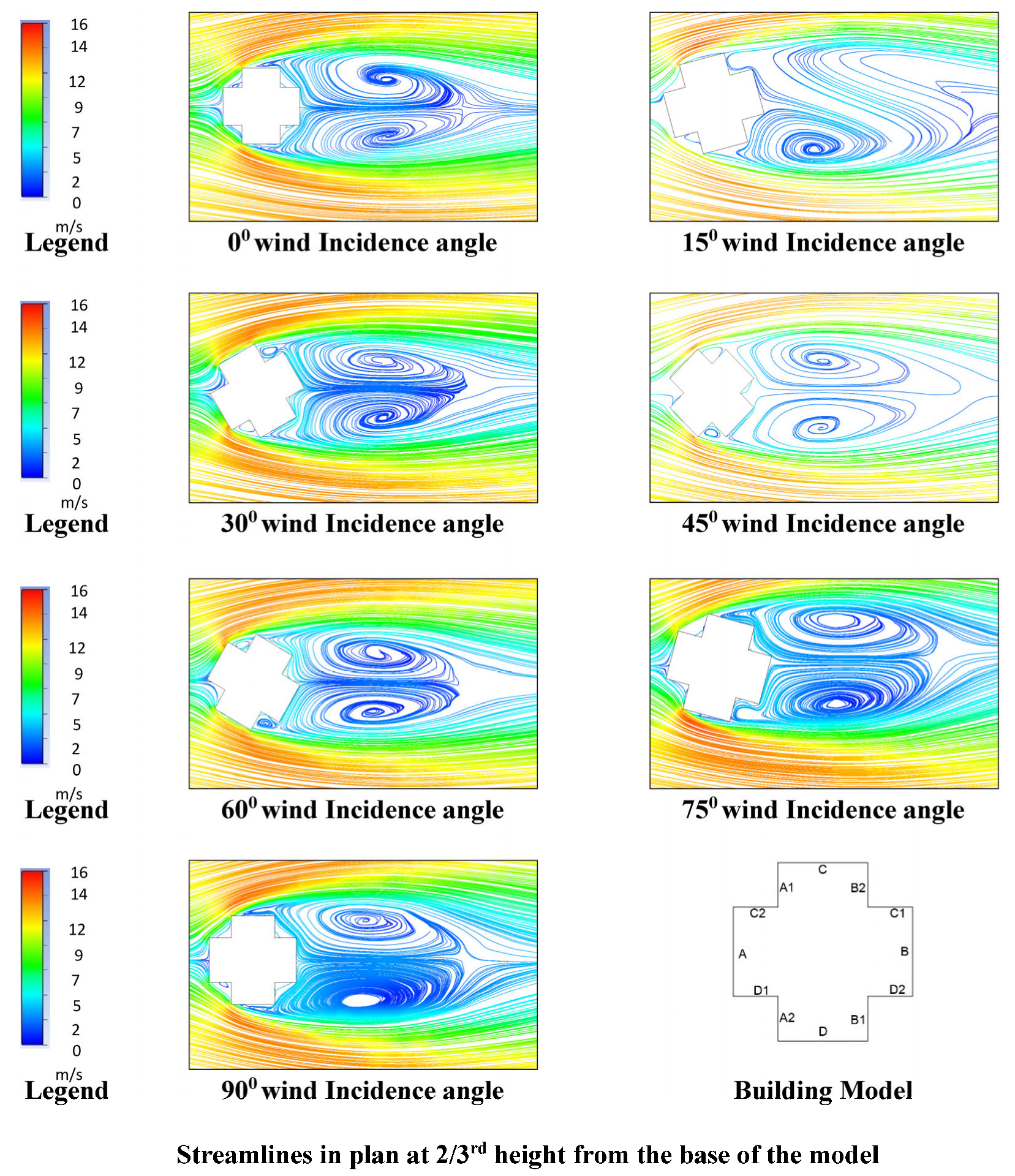
7.1.1. Streamlines on Horizontal Planes
7.1.2. Streamlines on Central Vertical Plane
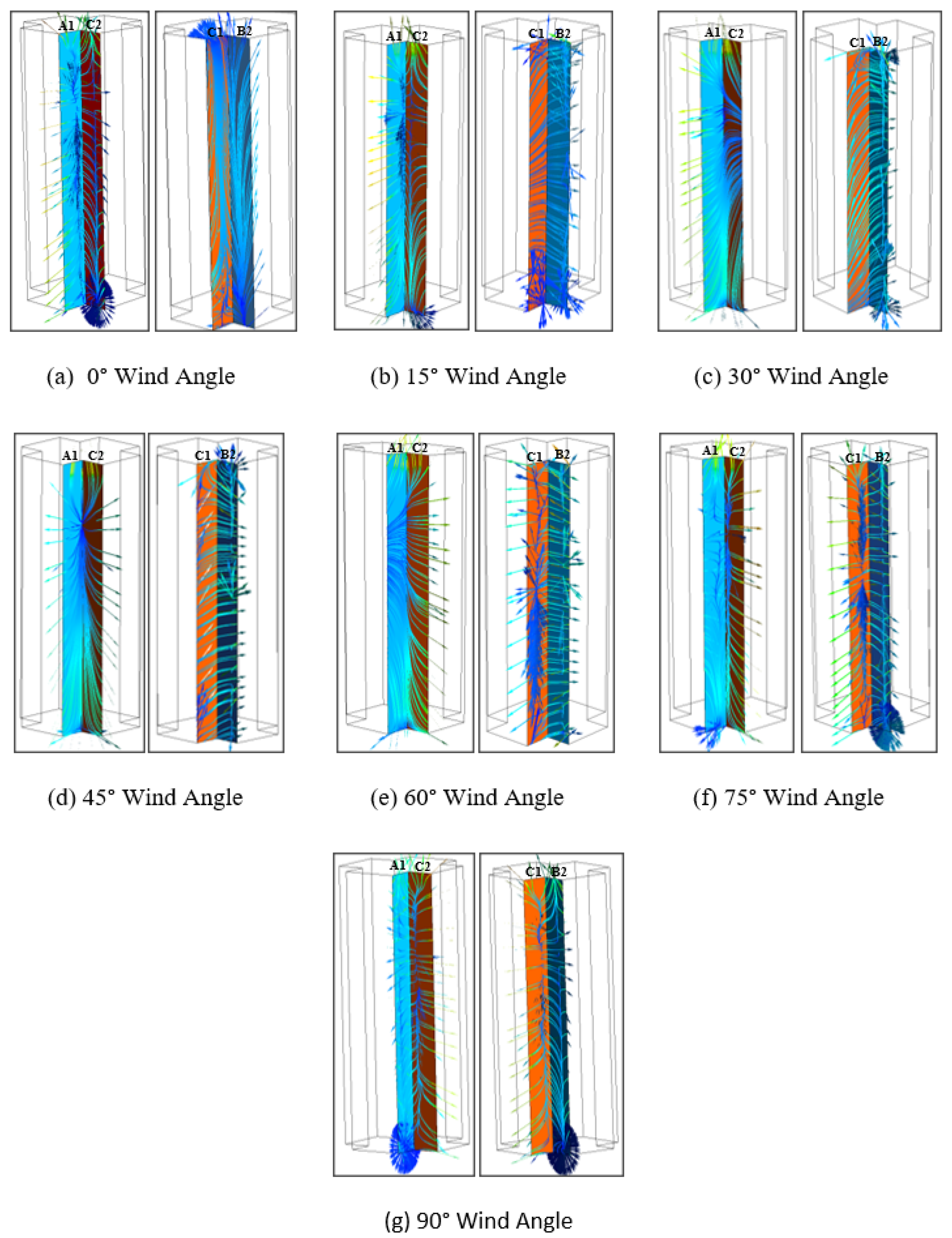
7.1.3. Streamlines on Re-Entrant Corner Faces
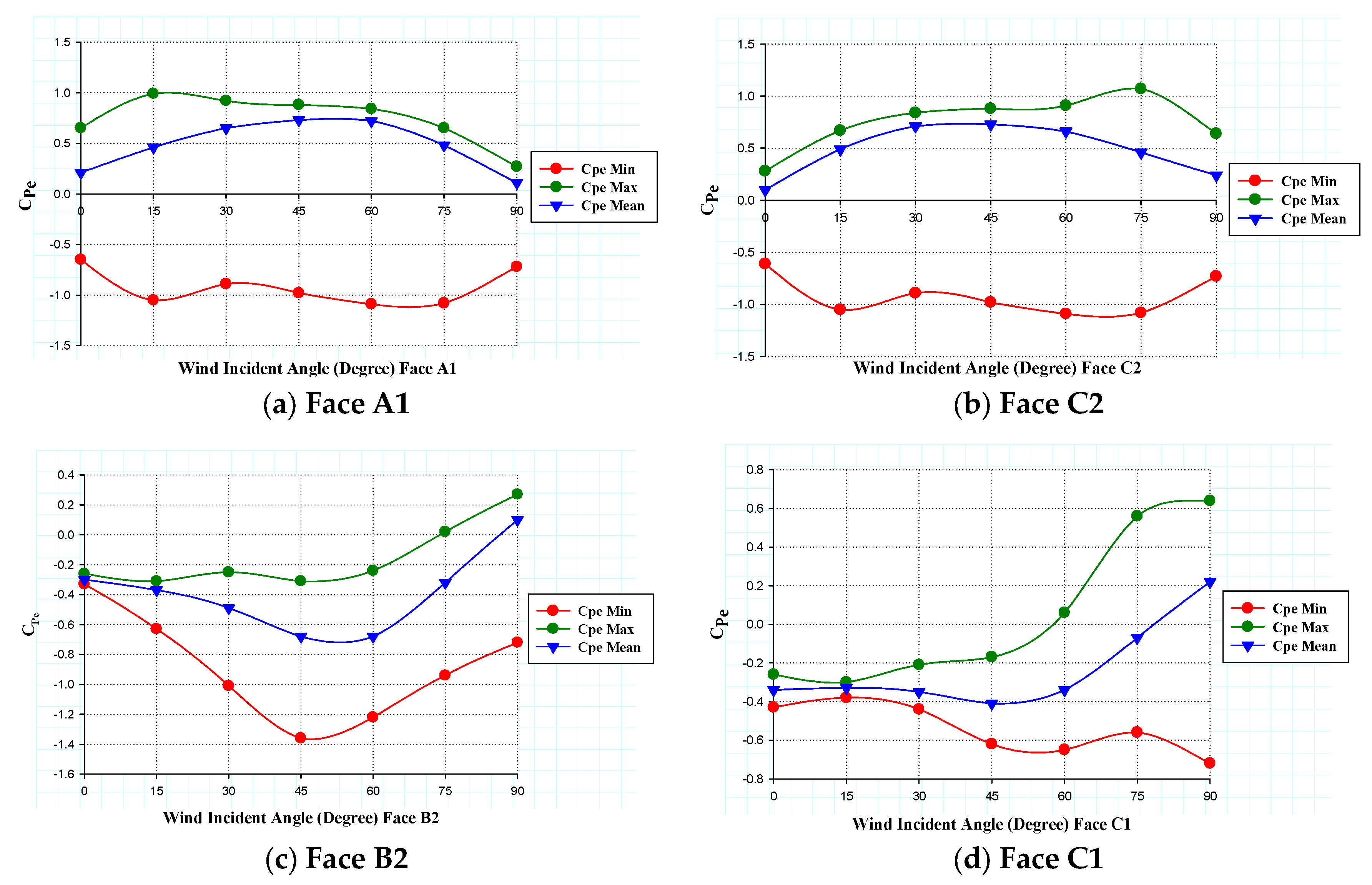
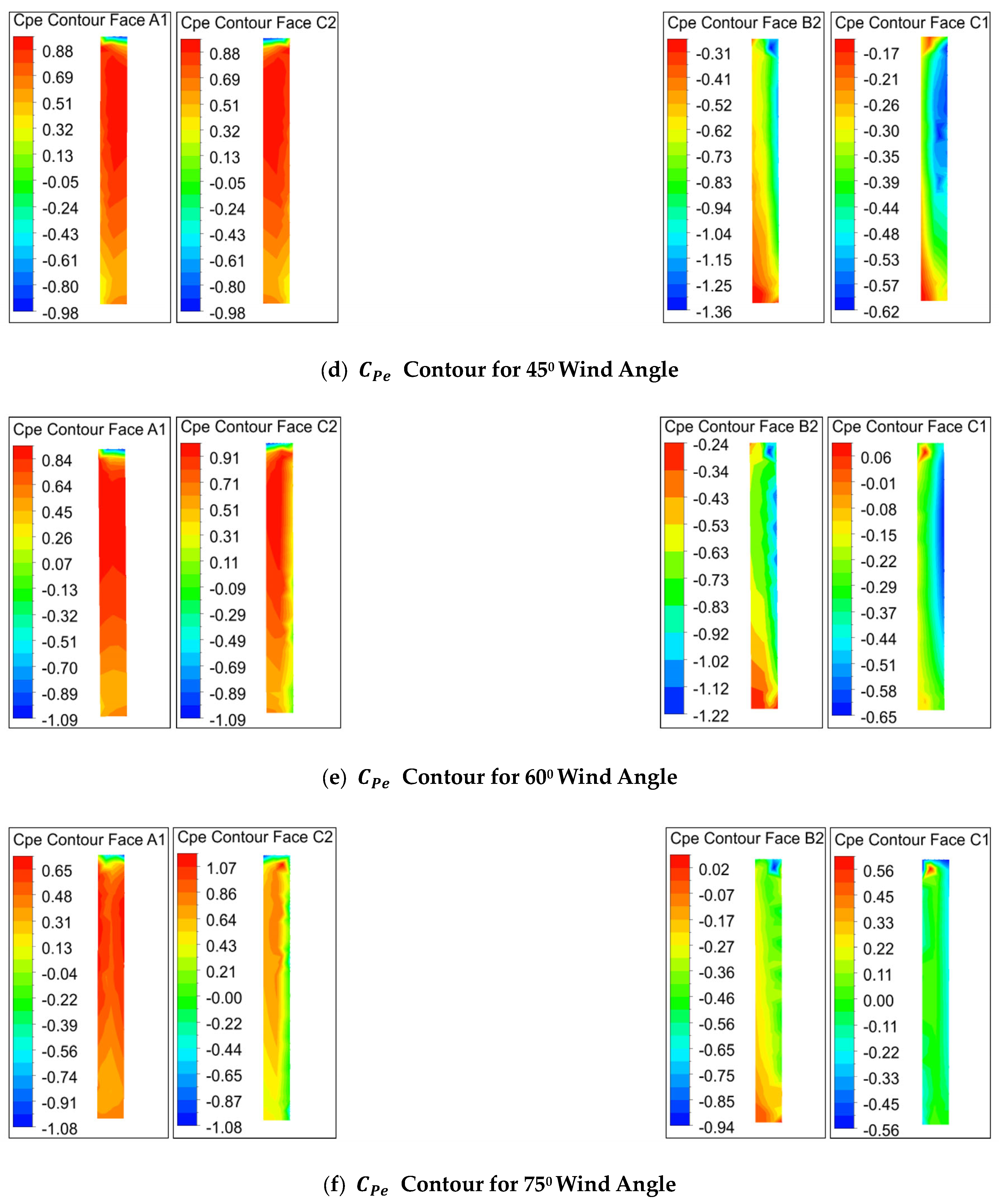
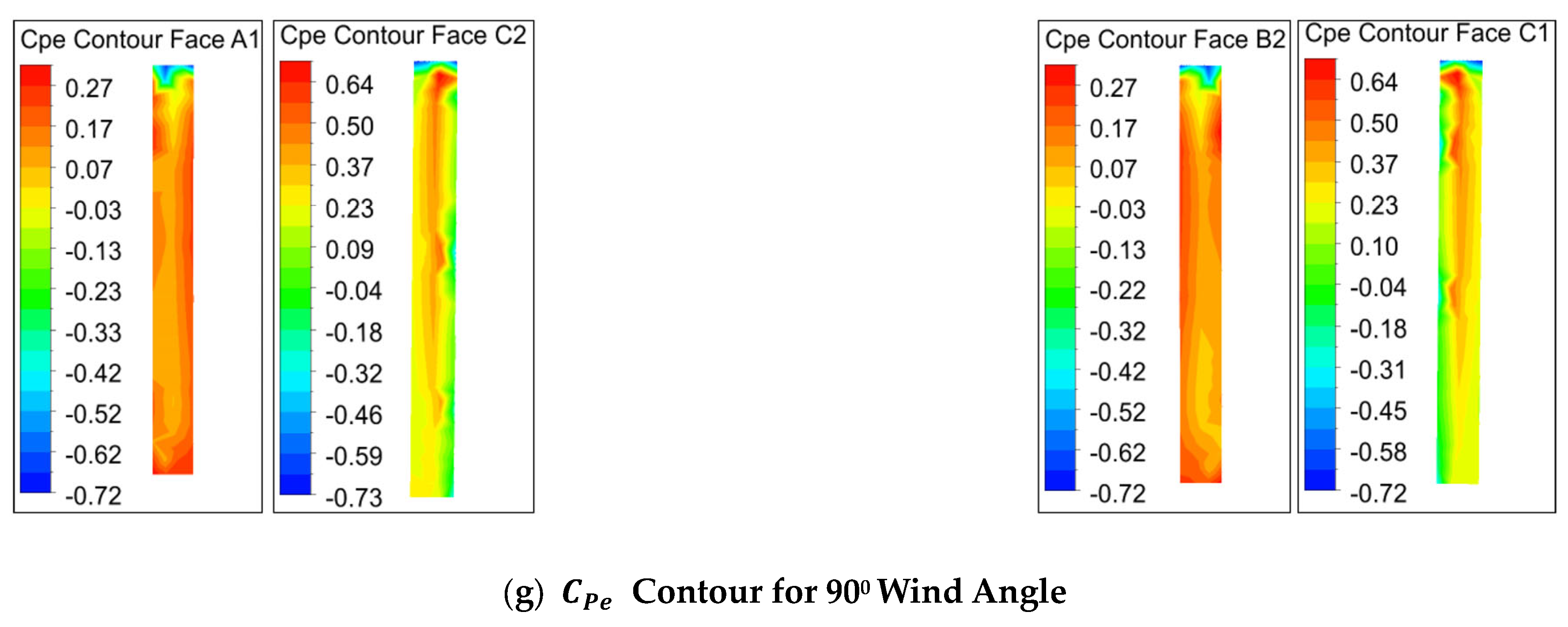
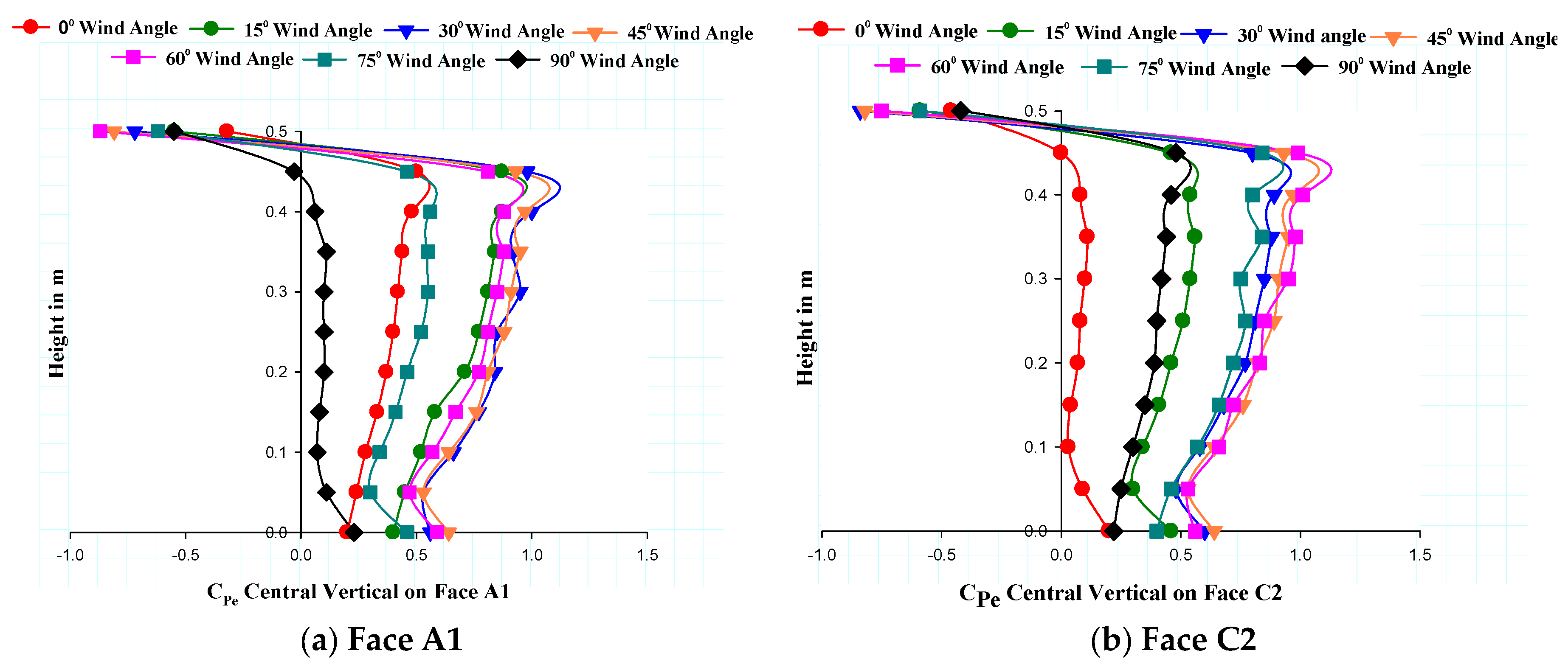
7.2. Pressure/Pressure Coefficient on Re-Entrant Faces
7.2.1. Minimum, Maximum, and Mean
7.2.2. Contours
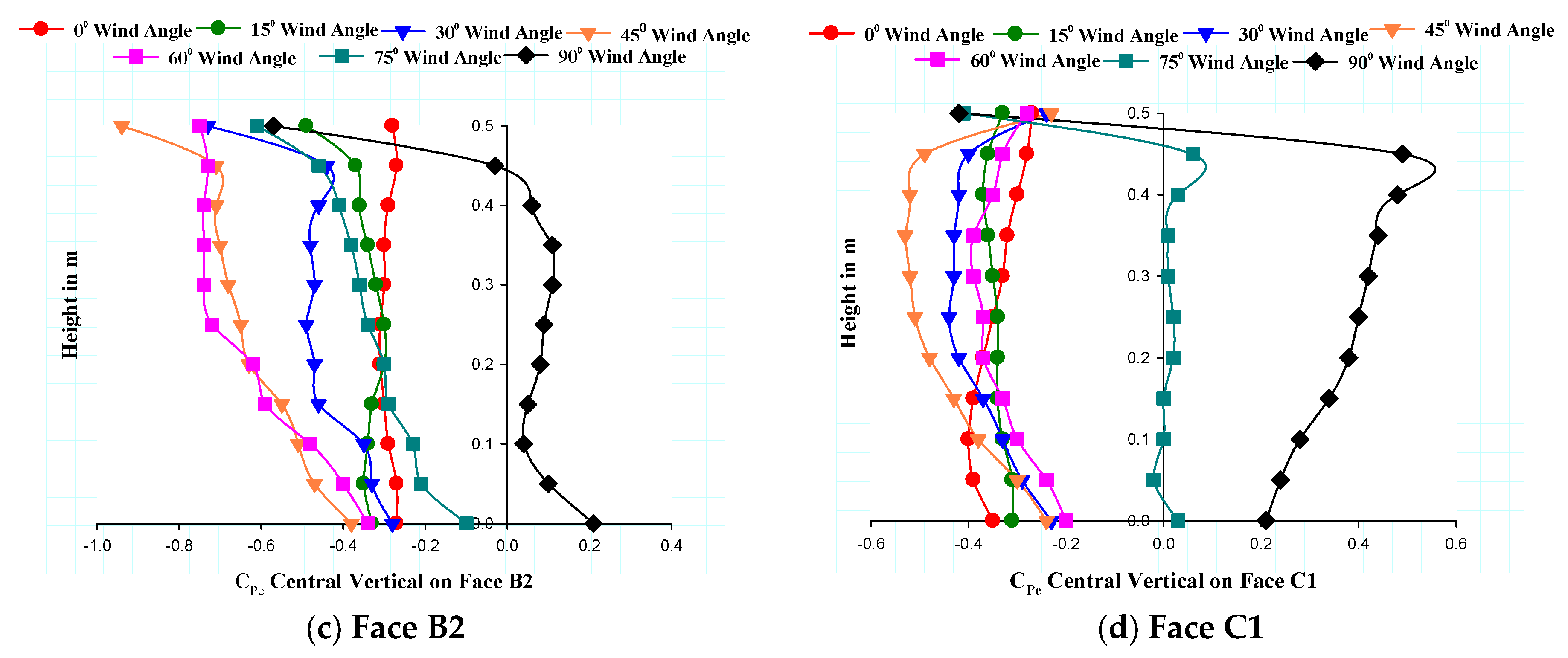
7.2.3. Central Vertical on Faces
8. Conclusions
- The study observed a substantial influence of wind incidence angles on the corner faces of plus plan-shaped buildings in terms of the variations in pressure on these faces for different wind incidence angles.
- The height of the building and the relative length of dimensions of the wing faces are crucial factors affecting the pressure distribution on these faces. These factors are significant for designing cladding units and necessitate consideration by design engineers.
- The simulation results demonstrate good agreement, especially for wind directions orthogonal to the building’s faces; some differences are noted for other wind angles due to the wind’s complex, anisotropic, unsteady, three-dimensional flow behavior.
- The influence of streamlines in the bottom portion of the structure is relatively minimal in contrast to the upper portion, which also exhibits robust vortices, particularly noticeable within wind angles varying from 0° to 30°.
- The vortices remain relatively consistent in size and intensity for both the top and bottom portions of the building model in the 45° wind incidence angle.
- In the case of tall buildings featuring re-entrant corners, the investigation uncovered a significant stagnation zone at a wind incidence angle of 30°, located at the mid-height of the building model. Under these conditions, there was observable flow separation emanating from the leading edge.
- At a wind incidence angle of 75°, a re-circulation cavity was noticeable at the re-entrant corner of the building. The vortices’ size on the re-entrant corner was found to be constant for wind angles of 0° and 90°.
- Architects can leverage the observed data for ventilation planning, and structural designers can use them for precise wind load analysis, enhancing the accuracy of engineering calculations and decision making.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rizzo, F.; Sepe, V.; Sabbà, M.F. Investigation of the Pressure Coefficients Correlation Field for Low-Rise Building Roofs. Appl. Sci. 2022, 12, 10790. [Google Scholar] [CrossRef]
- Sari, D.P.; Cho, K.P. Performance Comparison of Different Building Shapes Using a Wind Tunnel and a Computational Model. Buildings 2022, 12, 144. [Google Scholar] [CrossRef]
- Yan, B.; Li, Y.; Li, X.; Zhou, X.; Wei, M.; Yang, Q.; Zhou, X. Wind Tunnel Investigation of Twisted Wind Effect on a Typical super-tall building. Buildings 2022, 12, 2260. [Google Scholar] [CrossRef]
- Ivánková, O.; Hubová, O.; Macák, M.; Vojteková, E.; Konečná, L.B. Wind Pressure Distribution on the Façade of Stand-Alone Atypically Shaped High-Rise Building Determined by CFD Simulation and Wind Tunnel Tests. Designs 2022, 6, 77. [Google Scholar] [CrossRef]
- IS: 875 (2015); Indian Standard Design Loads (other than Earthquake) for Buildings and Structures-Code of Practice, Part 3 (Wind Loads). Bureau of Indian Standards: New Delphi, India, 2015.
- Code of Practice on Wind Effects in Hong King 2019; Building Authority: Hong Kong, China, 2019.
- ASCE: 7-16 (2017); Minimum Design Loads and Associated Criteria for Buildings and Other Structures. Structural Engineering Institute of the American Society of Civil Engineering: Reston, VA, USA, 2017. [CrossRef]
- ASCE: 49-12 (2012); Wind Tunnel Testing for Buildings and Other Structures. Structural Engineering Institute of the American Society of Civil Engineering: Reston, VA, USA, 2012. Available online: www.asce.org/pubs (accessed on 11 December 2023).
- AS/NZS-1170.2 (2002); Structural Design Actions, Part-2: Wind Actions. Standards Australia: Sydney, NSW, Australia; Standards New Zealand: Wellington, New Zealand, 2002.
- ES ISO 4354 (2012); Wind Actions on Structures, vol. 2012. ISO: Geneva, Switzerland, 2012; (English). Available online: http://scholar.google.com/scholar?start=10&q=asi+interface&hl=es&as_sdt=0,5#6 (accessed on 11 December 2023).
- EN: 1991-1-4; Eurocode-1: Actions on Structures-Part 1–4: General Actions-Wind Actions. Management Centre: Brussels, Belgium, 2010.
- Kim, B.; Yuvraj, N.; Preethaa, K.R.S.; Hu, G.; Lee, D.-E. Wind-Induced Pressure Prediction on Tall Buildings Using Generative Adversarial Imputation Network. Sensors 2021, 21, 2515. [Google Scholar] [CrossRef] [PubMed]
- Gomes, M.G.; Rodrigues, A.M.; Mendes, P. Experimental and numerical study of wind pressures on irregular-plan shapes. J. Wind. Eng. Ind. Aerodyn. 2005, 93, 741–756. [Google Scholar] [CrossRef]
- Mendis, P.; Ngo, T.; Haritos, N.; Hira, A.; Samali, B.; Cheung, J. Wind Loading on Tall Buildings. EJSE Load. Struct. 2007, 7, 51–54. [Google Scholar] [CrossRef]
- Fu, J.Y.; Li, Q.S.; Wu, J.R.; Xiao, Y.Q.; Song, L.L. Field measurements of boundary layer wind characteristics and wind-induced responses of super-tall buildings. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1332–1358. [Google Scholar] [CrossRef]
- Tanaka, H.; Tamura, Y.; Ohtake, K.; Nakai, M.; Kim, Y.C.; Bandi, E.K. Experimental Investigation of Aerodynamic Forces and Wind Pressure Acting on Tall Buildings with Various Unconventional Configuration. J. Wind. Eng. Aerodyn. 2013, 107, 179–191. [Google Scholar] [CrossRef]
- Amin, J.A.; Ahuja, A.K. Effects of Side Ratio on Wind-Induced Pressure Distribution on Rectangular Buildings. J. Struct. 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Dalui, S.K.; Ahuja, A.K. Wind Induced Pressure on ‘E’ Plan Shaped Tall Buildings. Jordan J. Civ. Eng. 2014, 8, 120–134. Available online: https://www.researchgate.net/publication/264548132 (accessed on 11 December 2023).
- Yi, J.; Li, Q.S. Wind tunnel and full-scale study of wind effects on a super-tall building. J. Fluids Struct. 2015, 58, 236–253. [Google Scholar] [CrossRef]
- Mukherjee, A.; Bairagi, A.K. Wind Pressure and Velocity Pattern Around ‘N’ Plan Shape Tall Building—A Case Study. Asian J. Civil Eng. 2017, 18, 1241–1258. [Google Scholar]
- Mallick, M.; Mohanta, A.; Kumar, A.; Raj, V. Modelling of Wind Pressure Coefficients on C-Shaped Building Models. Model. Simul. Eng. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Sanyal, P.; Dalui, S.K. Effects of side ratio for ‘Y’ plan shaped tall building under wind load. Build. Simul. 2021, 14, 1221–1236. [Google Scholar] [CrossRef]
- Mallick, M.; Mohanta, A.; Kumar, A. Multivariate adaptive regression spline approach to the assessment of surface mean pressure coefficient on surfaces of C-shaped building. Sci. Iran. 2020, 27, 2967–2984. [Google Scholar] [CrossRef]
- Chakraborty, S.; Dalui, S.K.; Ahuja, A.K. Experimental Invstigation of Surface Pressure on ‘+’ Plan Shape Tall Building. Jordan J. Civ. Eng. 2014, 8, 251–261. [Google Scholar]
- Jendzelovsky, N.; Antal, R. CFD and experimental study of wind pressure distribution on the high-rise building in the shape of an equilateral acute triangle. Fluids 2021, 6, 81. [Google Scholar] [CrossRef]
- You, J.; Lee, C. Experimental study on the effects of aspect ratio on the wind pressure coefficient of piloti buildings. Sustainability 2021, 13, 5206. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS CFX-Solver Theory Guide. 2009. Available online: http://www.ansys.com (accessed on 11 December 2023).
- ASCE. Manuals and Reports on Engineering Practice No. 67. In Wind Tunnel Studies of Buildings and Structures; ASCE: Reston, VA, USA, 1999. [Google Scholar] [CrossRef]
- Franke, J. Impact of Wind and Storm on City Life and Built Environment. Recommendation on the Use of CFD in Wind. Eng. COST Action C14 on the Use of CFD in Predicting Pedestrian Wind Environment. 2004, pp. 1–12. Available online: https://www.jstage.jst.go.jp/article/jawe1982/2006/108/2006_108_529/_pdf (accessed on 11 December 2023).
- Revuz, J.; Hargeaves, D.M.; Owen, J.S. On the Domain Size for the Steady State CFD Modeling of a Tall Building. Wind. Struct. 2012, 15, 313–329. [Google Scholar] [CrossRef]
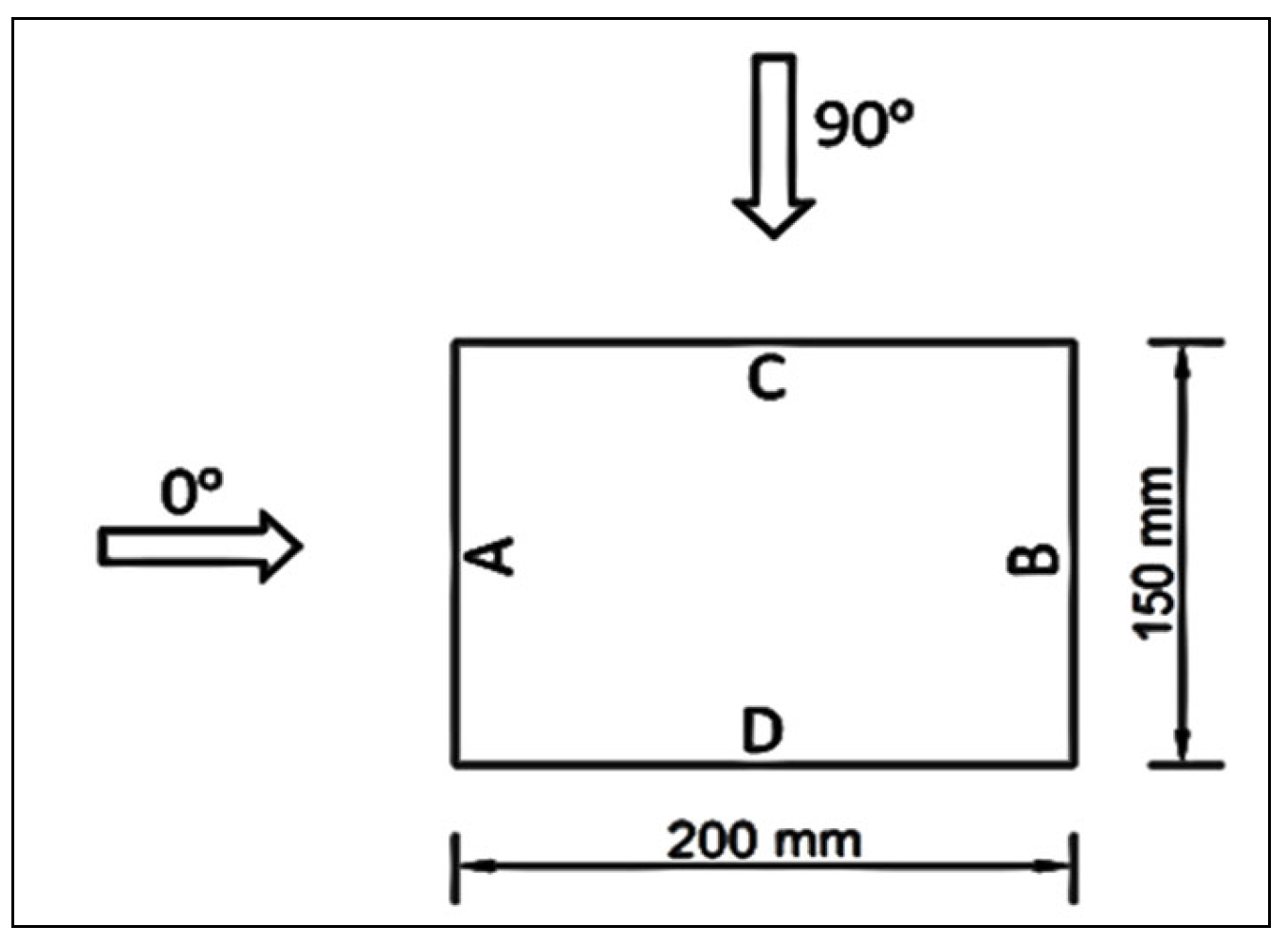



| Wind Angle | Face A | Face B | Face C | Face D | |
|---|---|---|---|---|---|
| ANSYS (CFX) [27] | 0° | +0.68 | −0.27 | −0.60 | −0.60 |
| 90° | −0.60 | −0.60 | 0.70 | −0.28 | |
| IS: 875 (Part 3): 2015 [5] | 0° | +0.8 | −0.25 | −0.8 | −0.8 |
| 90° | −0.8 | −0.8 | 0.8 | −0.25 | |
| ASCE/SEI 7-16 [7] | 0° | +0.8 | −0.5 | −0.7 | −0.7 |
| 90° | −0.7 | −0.7 | 0.8 | −0.5 | |
| AS/NZS-1170.2 (2002) [9] | 0° | +0.8 | −0.5 | −0.65 | −0.65 |
| 90° | −0.65 | −0.65 | 0.8 | −0.5 | |
| EN: 1991-1-4 [11] | 0° | 0.8 | −0.55 | −0.8 | −0.8 |
| 90° | −0.8 | −0.8 | 0.8 | −0.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Meena, R.K.; Raj, R.; Khan, M.I.; Khatib, J.M. Wind Effects on Re-Entrant Wing Faces of Plus Plan-Shaped Building. Buildings 2023, 13, 3108. https://doi.org/10.3390/buildings13123108
Kumar A, Meena RK, Raj R, Khan MI, Khatib JM. Wind Effects on Re-Entrant Wing Faces of Plus Plan-Shaped Building. Buildings. 2023; 13(12):3108. https://doi.org/10.3390/buildings13123108
Chicago/Turabian StyleKumar, Arun, Rahul Kumar Meena, Ritu Raj, Mohammad Iqbal Khan, and Jamal M. Khatib. 2023. "Wind Effects on Re-Entrant Wing Faces of Plus Plan-Shaped Building" Buildings 13, no. 12: 3108. https://doi.org/10.3390/buildings13123108
APA StyleKumar, A., Meena, R. K., Raj, R., Khan, M. I., & Khatib, J. M. (2023). Wind Effects on Re-Entrant Wing Faces of Plus Plan-Shaped Building. Buildings, 13(12), 3108. https://doi.org/10.3390/buildings13123108










