The Price Premium in Green Buildings: A Spatial Autoregressive Model and a Multi-Criteria Optimization Approach

Abstract

The energy issue has given rise to a prolific research field, which branches into several strands. One of these strands focuses on the role played by building energy features in shaping property prices. Indeed, market players are expected to show a higher willingness to pay for building units characterized by higher energy performance. The study of the so-called price premium for building energy efficiency has flourished in the last decade or so; plenty of evidence is now available concerning its occurrence, although its magnitude is still debated. The literature relies on the methodological frameworks of statistical modeling and multiple regression, primarily employing hedonic price models. Lately, spatial autoregressive models have also been adopted. Here, we propose to deal with estimation of the price premium by adopting an innovative perspective. In particular, we use a methodological framework in which regression models are complemented with a multi-criteria optimization approach. Using a spatial autoregressive model first, and with D as the reference energy rating band, we find the following price premiums: 55% for A4, 42% for A3 to A, 20% for B or C, −14% for F, and −29% for G. The multi-criteria optimization approach proves efficient in estimating the price premium. The estimates above are essentially confirmed: the results converge for all the energy rating bands except for G.

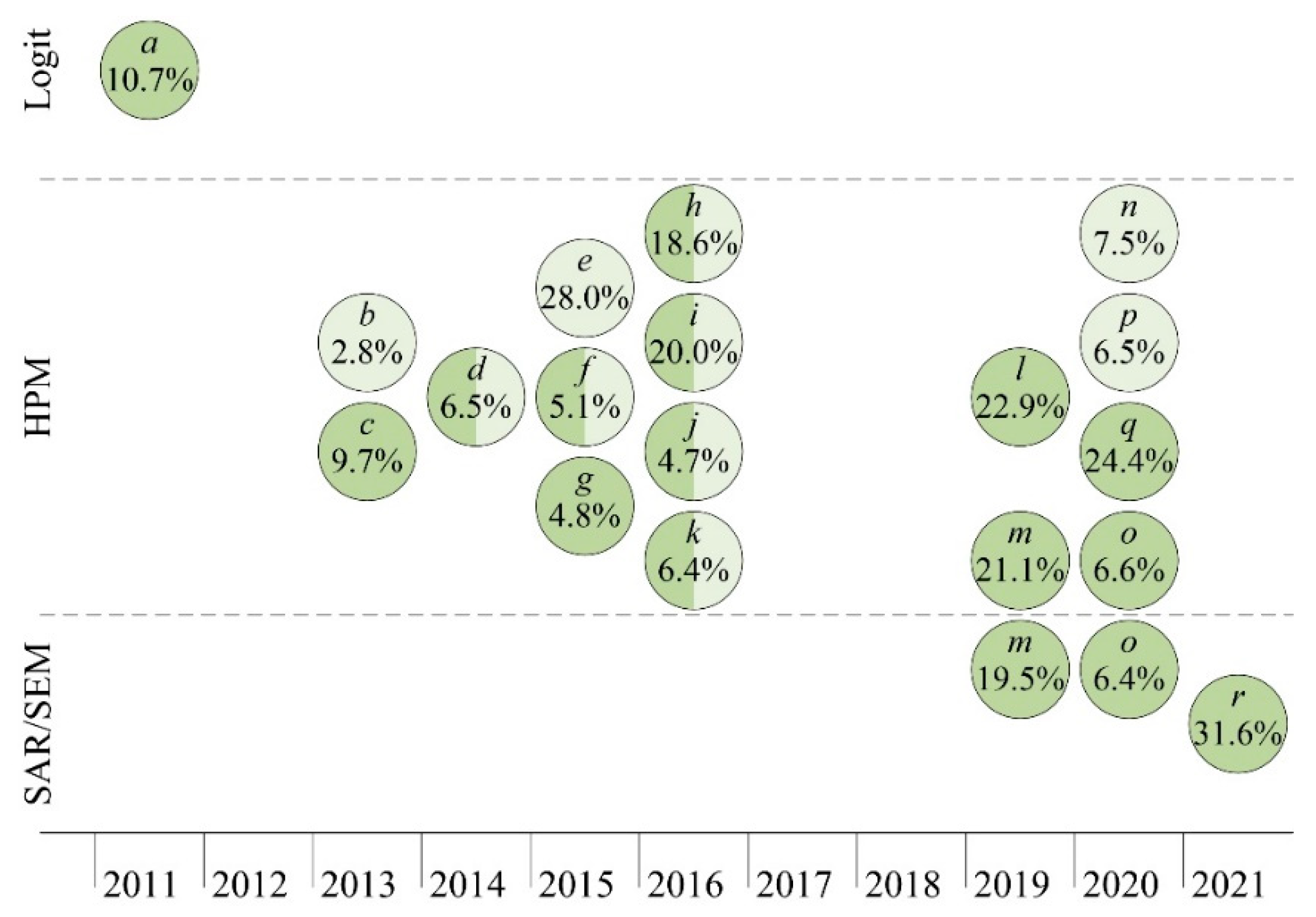
1. Introduction and Background Literature

Two of the main questions raised by the energy issue in the building industry are as follows [1]: does a cost premium exist when a green construction is built? And does a price premium occur when a green building is sold? Both questions have a solid background rooted in economic theory. Concerning the first, pursuing energy efficiency in buildings requires using additional building materials and state-of-the-art systems; hence, higher upfront costs should be expected [2,3]. Regarding the second issue, energy-efficient building units provide occupants lower management costs and higher comfort levels; thus, a higher willingness to pay when buying them should also be expected [4]. Although an affirmative answer should follow the two previous questions—as both an additional cost and a higher-than-normal price are anticipated for green buildings compared to traditional ones—the literature shows that the situation is somewhat more complicated, especially when it comes to the magnitude of those premiums.

Despite the lack of a large corpus of studies on the topic of cost premiums for green buildings, and even though extensive and conclusive empirical findings are still missing, reviews of the available works have been published recently [5,6]. Aside from the studies advocating that the gap in costs is basically nil, or not statistically significant [7,8], the consensus leans towards the occurrence of a small cost premium, on the order of a few percentage points [9,10,11,12,13] or slightly more [14,15,16]. However, from different perspectives, several works show that the cost premium depends on the expected performance outcome and increases exponentially with it. Cost-optimal solutions for refurbishing outdated residential buildings are found in the range of 58–41 kWh/m² y as far as the primary energy need is concerned [17]. Furthermore, pushing the performance far below the threshold of 50 kWh/m² y implies incurring ever-higher costs [18,19]. Similar findings are reported for commercial buildings depending on different certification levels [20].

Early investigations into the price premium for energy-efficient buildings date back to the late eighties [21,22]. Still, the research strand has flourished in the last decade, primarily due to the availability of large datasets once energy certification systems have been implemented and have become established in real estate markets. The Green Mark (GM) label in Singapore [23,24,25,26,27,28] and the Energy Performance Certificates (EPCs) in Europe [29,30,31] are cases in point. Comprehensive literature reviews of previous studies have been published looking at both the residential and commercial markets [4,32]. An up-to-date review—focusing on the green price premium for dwellings only—can be found in a recent study [19]. The analyses performed so far consider both residential [33,34,35,36,37] and commercial [38,39,40,41] buildings in a variety of geographic and climatic areas, especially in the US [42,43,44,45,46,47,48,49] and European countries [50,51,52].

From a perusal of the literature, some intriguing remarks arise regarding methods and models. While most of the studies employ linear or semi-logarithmic functional forms, a few others make use of a double-logarithmic function to estimate the price premium in terms of elasticity, and thus the percentage change in housing price for a percent change in energy consumption [53,54,55,56,57,58]. Also, there has been a radical shift in the models used to estimate the price premium over the years. While early studies were building upon the hedonic price model [59,60,61] as derived from the seminal work of Rosen [62], spatial statistics has made its way into this research strand recently [63,64,65,66]. However, even though there is a large consensus regarding the occurrence of a premium for building energy efficiency, uncertainty still characterizes the estimated size of that price differential, as can be seen from the results of the studies focusing on the market effect of EPCs (Figure 1). Empirical evidence suggests that the price premium is within 10% when comparing the A and B energy rating bands with the D one. Nonetheless, some works indicate a premium of up to around 20%, and a couple of studies even find a premium of about 30%.

As can be understood from the above literature review, the analyses on the occurrence of a price premium—and, notably, the estimation of its magnitude—rely essentially on the methodological frameworks of statistical modeling and multiple regression. Most studies employ hedonic price models, sometimes controlling for fixed space and time effects. Other recent works show the opportunity to exploit spatial data analysis, especially the excellent properties of the spatial autoregressive model (SAR) and spatial error model (SEM). Even the few studies using different approaches—such as the hierarchical Bayes model [26], quantile regression [67], evolutionary polynomial regression [68], and geographically weighted regression [50]—still fall into the same methodological framework.

The purpose of this study—and its original contribution as well—lies in addressing the currently-debated topic of price premiums in green buildings from an innovative perspective. We aim to delve into the following research questions. Is it possible to address the estimation of the price premium by adopting other methods, especially a multi-criteria optimization approach? Does it provide equally reliable estimates as those offered by the spatial regression models? What are the pros and cons of the method we propose here, and is there room for its wide-scale adoption? The choice of a multi-criteria optimization approach has its roots in the relationship that can be established between the hedonic approach and the multi-attribute utility model. This implies that the multi-criteria optimization approach can be adapted to estimate how the building features—and the energy performance among them—affect the property price and, hence, the size of the price premium. The motivation underlying this exploratory study is twofold. On the one hand, the novel approach may help improve the estimation of the price premium. On the other hand, we expect that the multi-criteria optimization technique will lend itself to be further developed and applied, especially as far as the inclusion of energy aspects in property valuation is concerned.

To answer the above research questions, the remainder of this paper is structured as follows. Section 2 focuses on the method and models we propose to adopt to complement the statistical analysis of the price premium for building energy efficiency. Section 3 presents the case study—namely, the housing market in a medium-sized city in Northeastern Italy—and the data-gathering process. Section 4 is devoted to discussing the results, especially as far as the magnitude of the price premium is concerned, and the limitations of this work. Finally, Section 5 draws the conclusion and outlines further developments in this research strand.

Figure 1. Timeline of studies on the market effect of Energy Performance Certificates (Logit: logistic regression; HPM: Hedonic price model; SAR/SEM: Spatial autoregressive and spatial error models; the reference energy rating band is D unless otherwise stated; percentages are the price premium for the energy rating bands A (dark green) or B (light green); percentages are corrected according to [69] when appropriate; a: [70]; b: [71]; c: [72]; d: [73]; e: [74]; f: [75]; g: [76]; h: [77]; i: [78]; j: [79]; k: [80]; l: [81]; m: [82]; n: [67]; o: [83] with G as the reference energy rating band; p: [84]; q: [85]; r: [19]).

Figure 1. Timeline of studies on the market effect of Energy Performance Certificates (Logit: logistic regression; HPM: Hedonic price model; SAR/SEM: Spatial autoregressive and spatial error models; the reference energy rating band is D unless otherwise stated; percentages are the price premium for the energy rating bands A (dark green) or B (light green); percentages are corrected according to [69] when appropriate; a: [70]; b: [71]; c: [72]; d: [73]; e: [74]; f: [75]; g: [76]; h: [77]; i: [78]; j: [79]; k: [80]; l: [81]; m: [82]; n: [67]; o: [83] with G as the reference energy rating band; p: [84]; q: [85]; r: [19]).

2. Method and Models

2.1. Hedonic Price Model and Spatial Regression Approach

What is the monetary effect of a building characteristic on property price, net of the impact of other significant land and building attributes and potential confounders? The issue has long since been at the top of real estate research, and thanks to the seminal work by S. Rosen in 1974 [62] it has been subsequently addressed using the method known as hedonic pricing and specifically the following model:

$$y=\mathsf{\alpha }+{\mathsf{\beta }}_k{X}_k+\mathsf{\epsilon },\hspace{1em}\mathsf{\epsilon }~\mathrm{IN}(0,{\mathsf{\sigma }}^2),$$

(1)

where y is the price of a property, X_k is a set of land and building characteristics while β_k stands for their coefficients (with k = 1, …, l), α is the constant, and ε is the error term.

The underlying assumption of Rosen’s model is that product differentiation does matter in shaping property prices. Hence, narrow price differentials are expected to reflect minor dissimilarities, just as major differences are supposed to cause significant price gaps. As argued in the introductory section, the literature finds that energy-related features are usually among the significant X_k commanding noticeable shifts in prices, be they expressed as the energy rating bands [19,81], the energy performance index [55,57], or score [50,52]. Probably due to difficulties in data collection, the energy attributes are seldom defined based on the actual energy consumption [58].

The linear model of Equation (1) is often turned into semi-linear or nonlinear variants. A well known and widely used model is the log-linear one. Taking the natural logarithm of the dependent variable (see Equation (2) below) has the virtue of returning the coefficients β_k as the percentage changes in property price y due to unit changes in the independent variables X_k, net of a small transformation suggested in Halvorsen and Palmquist [69] for dummy variables (see Equation (3) below).

$$\ln y=\mathsf{\alpha }+{\mathsf{\beta }}_k{X}_k+\mathsf{\epsilon },\hspace{1em}\mathsf{\epsilon }~\mathrm{IN}(0,{\mathsf{\sigma }}^2),$$

(2)

$$\mathsf{\Delta }y=e^{{\beta }_k}-1,$$

(3)

where Δy is the percentage effect of the attribute on the dependent variable.

The introduction of spatial autoregressive terms represents a fascinating improvement to the traditional hedonic price model, based on the premise that property prices are shaped by spatial dependence, too. Several ecological, social, and economic phenomena are thought to be driven—at least partly—by the diffusion of habits among communities, sharing of information across networks, and emulation between peers. Under this framework, energy use is no exception [86,87]. Likewise, the price of a property may be affected by the prices and attributes of neighboring properties [88,89,90], though the relationship is likely to fade as distance increases, according to Tobler’s first law of geography [91]. Hence, the model of Equation (2) can be extended to accommodate for neighborhood effects and spatial spillover effects, such as in the Spatial Durbin Model (SDM), which is a general Spatial Autoregressive model (SAR) [92]:

$$\ln y=\mathsf{\alpha }+\mathsf{\rho }{W}_y+{\mathsf{\beta }}_k{X}_k+{\mathsf{\gamma }}_{k}W{X}_k+\mathsf{\epsilon },\hspace{1em}\mathsf{\epsilon }~ \mathrm{IN}(0,{\mathsf{\sigma }}^2),$$

(4)

where ρ and γ_k are the coefficients of the spatially lagged dependent variable and the spatially lagged independent variables, respectively, while W stands for the spatial weights matrix. W is usually a positive symmetric matrix, each element of which (w_i,j with i, j = 1, …, n) represents the kind of spatial relationship that is supposed to tie the n units of analysis. Typical measures of proximity used to build W are shared boundaries and inverse distances. By standard convention, and assuming self-influence does not matter in the property market, W has a zero diagonal (w_i,i = 0 for all i = 1, …, n).

In the analysis we perform here, we introduce two changes as far as the previous Equation 4 is concerned. In the first place, we adopt the notion of nearest northwestern neighbor (NNWN) to build the W matrix, as detailed in the study by Copiello and Grillenzoni [93], which proves helpful in avoiding correlation between the spatially lagged dependent variable and the error term, as well as biased estimates of the coefficients. Also, as in similar studies, we use a reduced SAR model. We include the term ρWy on the right-hand side of the model, which is meant to account for the neighborhood effect—namely, spatial dependence between neighboring properties. But we omit the term γ_jWX_j, assuming that the attributes of neighboring properties exert no influence on a property’s price—that is, that there is no spatial spillover effect.

Where the model assumptions are concerned, independent variables are supposed to be mostly uncorrelated to each other or only mildly correlated, if you will. Furthermore, the residuals are expected to be independent, homoscedastic, and normally distributed. Finally, a share of spatial autocorrelation should not remain hidden within the residuals. The lack of significant correlation among the predictors is checked using the Variance Inflation Factor (VIF), a high value of which means that multicollinearity is likely to occur:

VIF_k = 1/(1 − R²_k),

(5)

where R²_k is the coefficient of determination resulting from the regression of each independent variable on the others. Homoscedasticity and normal distribution assumptions are checked using Chi-square tests, where the null hypothesis (H₀) is that the residuals are homoscedastic and normally distributed, respectively. Finally, the lack of a share of unexplained spatial autocorrelation is checked by regressing the residuals on the spatial lag of the residuals themselves:

ε = α + λWε + u.

(6)

2.2. Multi-Criteria Optimization Approach

The first research question we aim to address here—namely, whether or not the price premium can be estimated using a multi-criteria method—requires laying the ground for coupling the hedonic approach of the previous section with the structure of multi-criteria analysis. The model in Equation (1) can be easily read in terms of a linear additive multi-attribute utility (MAU) model, which is indeed extensively estimated using multiple regression approaches [94]. It means that the X_k land and building characteristics—the so-called “utility-bearing attributes” in the words of Rosen [62]—can be interpreted as the items—or criteria, if you will—of a property that are valued by market players. The perceived utility for the significant items or criteria is thus summarized in the same property’s market value. Under this premise, it appears straightforward and promising to reframe the hedonic approaches discussed in the previous section according to a multi-criteria evaluation technique [95,96,97], specifically, the Analytic Hierarchy Process (AHP) developed by T.L. Saaty in the late seventies and early eighties [98,99,100]. Thus, in a bottom-up reading of the hierarchical value tree, we can establish the following equivalences. The properties whose price y is known—that is to say, the n units of analysis—are the alternatives. The X_k land and building characteristics—including the spatially lagged dependent variable Wy—are the criteria. The β_k coefficients—including the ρ coefficient of the spatial lag—are proxies of the weights of the criteria. The goals can be defined as follows:

• to rank the n alternatives (namely, properties) according to their price y;
• to rank separately the same n alternatives (namely, properties) according to the criteria (namely, attributes) X_k and Wy;
• to compare the two rankings and match them so to elicit the weights of the criteria (namely, attributes).

Below is a description of the methodological steps we take to that end. An early draft of this multi-criteria optimization approach has been tested on very few properties and discussed at a recent conference [101]. To the best of the authors’ knowledge, no other use of the approach to estimating the price premium of energy efficiency can be found in the literature.

As far as the first step is concerned, a pairwise comparison matrix of size n $\times$ n is used to compare the ith and jth properties according to the ratio of their prices y_i and y_j, so that the entries m_i,j in the upper triangle of the matrix are given as follows:

m_i,j = y_i/y_j.

(7)

As customary in the AHP model, all the entries on the main diagonal are equal to one, while the entries in the lower triangle are given by the reciprocal of the elements in the upper triangle:

m_i,i = y_i/y_i = 1,

(8)

m_j,i = 1/(y_i/y_j) = y_j/y_i.

(9)

Taking the nth root of the product of the values in each row of the above pairwise comparison matrix and then normalizing it leads to identifying the priority p_i associated with each property and, thus, the ranking of the properties according to their price:

$$p_i=\sqrt[n]{{\prod }_{j=1}^n{m}_{i,j}}/{\sum }_{i=1}^n\sqrt[n]{{\prod }_{j=1}^n{m}_{i,j}}.$$

(10)

Let us now turn to the second methodological step we take. A set of l + 1 (as stated in the previous subsection, k = 1, …, l) pairwise comparison matrices—each of size n $\times$ n—are built to compare the ith and jth properties according to the kth characteristic—namely, the utility-bearing attribute—as well as the price Wy of neighboring properties. Just as in Equations (7)–(9), for each kth attribute, the comparison is made using the ratios between the values x_{k i} and x_{k j}:

r_{k i,j} = x_{k i}/x_{k j}.

(11)

r_{k i,i} = x_{k i}/x_{k i} = 1,

(12)

r_{k i,j} = 1/(x_{k i}/x_{k j}) = x_{k j}/x_{k i}.

(13)

The local priority z_{k i} for each property i on each attribute k is derived following the calculation in previous Equation (10); thus, by taking the nth root of the product of the values in each row of the kth pairwise comparison matrix and then normalizing it:

$$z=\sqrt[n]{{\prod }_{j=1}^n{r}_{k i,j}}/{\sum }_{i=1}^n\sqrt[n]{{\prod }_{j=1}^n{r}_{k i,j}},$$

(14)

the calculation is repeated for all the l + 1 pairwise comparison matrices and, eventually, the global priorities ${\widehat{p}}_i$ can be elicited as follows:

$${\widehat{p}}_i={\sum }_{k=1}^{l+1}\left(z_{ki}·{\widehat{\beta }}_k\right),$$

(15)

where ${\widehat{\beta }}_k$ is the weight of the kth attribute.

Let us take a closer look at Equation (15). Each weight ${\widehat{\beta }}_k$ can be interpreted as the strength by which the local preference z_{k i} for the kth attribute shapes the global preference ${\widehat{p}}_i$ for the ith property: the higher the weight, the stronger the influence exerted by that land or building characteristic. According to Equations (1)–(4), the price of a property is assumed to be a function of the same property’s characteristics; in short, y = ƒ(X_k). Therefore, the priorities p_i identified according to the prices y_i in Equation (10) and the priorities ${\widehat{p}}_i$ identified according to the attributes X_k and the weights ${\widehat{\beta }}_k$ in Equation (15) should converge. Also, while m_i,j in Equation (10) and z_{k i} in Equation (15) are given since they are derived from prices and characteristics of the properties, ${\widehat{\beta }}_k$ is the unknown quantity, which can be varied to get ${\widehat{p}}_i$ as close as possible to p_i. To that end, we define a loss function based on the notion of squared distances, which resembles the ordinary least squares (OLS) estimator used in regression analysis, and solve the following minimization problem under the constraint that ${\widehat{\beta }}_k$ values are all higher than or equal to zero:

$${\widehat{\beta }}_k=\underset{{\widehat{\beta }}_k}{\min }\frac{1}{n}{\sum }_{i=1}^n{\left({\widehat{p}}_i-p_i\right)}^2,$$

(16)

$${\widehat{\beta }}_k=\underset{{\widehat{\beta }}_k}{\min }\frac{1}{n}{\sum }_{i=1}^n{\left[{\sum }_{k=1}^{l+1}\left(z_{ki}·{\widehat{\beta }}_k\right)-\left(\sqrt[n]{{\prod }_{j=1}^n{m}_{i,j}}/{\sum }_{i=1}^n\sqrt[n]{{\prod }_{j=1}^n{m}_{i,j}}\right)\right]}^2.$$

(17)

The multi-criteria optimization process detailed in this section is meant to be applied to subsets, each including properties belonging to two energy rating bands: the D rating band as the reference band and another rating band for comparison purposes.

Concerning the second research question that we aim to address here—whether or not the multi-criteria method can provide reliable estimates—the weight ${\widehat{\beta }}_k$ resulting from Equation (17) for any energy rating band compared to the D one is expected to converge to the coefficient β_k for the same rating band resulting from Equation (4).

3. Case Study and Data

The method and models discussed in the previous section are applied to data from the real estate market of Padua, a medium-sized city in northeastern Italy. The role played by the energy rating bands in shaping property prices has already been studied there using hedonic price models [76,102] and spatial autoregressive models [19]. The city is representative of many middle-sized settlements in Northern Italy, especially the Po Valley, the country’s most inhabited part. Also, it is characterized by a moderately continental climate, enabling us to compare the results with other European studies.

During the time frame from March to July 2022, 733 advertisements of properties offered for sale were checked. While preprocessing the data, 286 of them were dropped due to missing information, especially as far as the construction year and other building features are concerned. An additional 112 cases were omitted due to unreliable values of the energy performance index compared to the energy rating bands (when the index is unavailable, the advertisements usually display conventional average or minimum values, such as 175.00 or 3.51 kWh/m² y). Furthermore, 16 cases were omitted since they are located on the upper left edge of the area of analysis, so they have no nearest northwestern neighbor. Hence, the analyzed dataset consists of 321 real estate units.

The dependent variable is the asking price in Euros per square meter. A digression is in order here. We use the asking price rather than the sale price—as other authors do [56,103,104,105]—due to the poor transparency of the real estate market in Italy, because of which the actual prices agreed upon in transactions involving properties are hardly known. Though asking prices are mostly representative of supply-side players’ behavior, there are hints that they can be usefully employed in hedonic studies. In the first place, significant gaps between asking and selling prices only characterize rapidly rising or falling markets; otherwise, those gaps narrow down and fall to as low as 1% [106]. Furthermore, asking prices have been shown to play a significant role in shaping sale prices and, ultimately, market values [107,108].

Along with the dependent variable, the predictors are listed in

Table 1. List of the variables used for the spatial autoregressive model.

Variable	Description	Scale of Measurement	Unit of Measure or Coding System
y	Property price	Ratio	Euros/m2
Sa	Saleable area	Ratio	m2
ERB	Energy rating band	Ordinal	A4; A3 to A; B or C; D (reference); E; F; G
EPI	Energy performance index	Ratio	kWh/m2 y
Bt	Building typology	Nominal	1 = Flat; 2 = Studio; 3 = Detached house; 4 = Terraced house; 5 = Semi-detached house
Cy	Construction year	Interval
Mc	Maintenance conditions	Nominal	1 = New or refurbished; 2 = Fit for residential use; 3 = To be renovated
Rm	Rooms	Interval
Br	Bathrooms	Interval
Gr	Garage	Dichotomous	1 = yes
Pl	Privately owned parking lots	Interval
Gd	Private garden	Dichotomous	1 = yes
Lf	Lift	Dichotomous	1 = yes
Fl	Floor level	Interval
Ns	Number of stories	Interval
Ph	Penthouse	Dichotomous	1 = yes
Etics	External thermal insulation cladding system	Dichotomous	1 = yes
Fw	Windows and frames	Nominal	1 = Single glazed, wood frame; 2 = Single glazed, other frame; 3 = Double glazed, wood frame; 4 = Double glazed, solid metal frame
Hs	Heating system	Nominal	1 = Floor heating; 2 = Fan coils; 3 = Radiators
Mev	Mechanical extract ventilation	Dichotomous	1 = yes
Hp	Heat pump	Dichotomous	1 = yes
Ps	Photovoltaic system	Dichotomous	1 = yes
Oe	‘Out of the ordinary’ equipment *	Dichotomous	1 = yes
Cc	Distance to the city center	Ratio	km
Ml	Distance to the nearest mall	Ratio	km
Bw	Distance to the closest beltway ramp	Ratio	km

* e.g., Home alarm security system, livable basement, oversize balcony, whirlpool bath, swimming pool.

. Aside from the energy rating bands and the energy performance index, they can be roughly clustered into two groups, as is usual in real estate hedonic modeling [109,110]: building features, on the one hand, and land characteristics, on the other. For the selection of building and land attributes, we referred to the broad literature on hedonic price modeling [111,112,113,114]. However, data availability is limited because not all the relevant information is included in real estate advertisements. Building features—which are meant to describe the structure, finishes, and systems of the building units—include the following: typology; age; maintenance conditions; the number of rooms, bathrooms, and parking lots; the presence of a garage, garden, and lift; floor level and the number of stories; whether the unit is a penthouse or not. Specific attention is paid to the building features related to energy performance, with variables focusing on: windows and frames; heating system; the presence of an external thermal insulation cladding system, mechanical extraction ventilation, heat pump, or photovoltaic system. Since all the analyzed properties are geolocated (Figure 2), land characteristics—which are meant to describe the location and accessibility of the building units—can be included in the analysis. They are as follows: distance to the city center, to the nearest mall, and the closest beltway ramp.

The gathering of data on the energy performance index and energy rating band for each property for sale is made possible by a recent shift in energy policies, namely, the mandatory disclosure of building energy performance [115]. Although it is unclear whether or not the outcomes of compulsory disclosure outweigh those to be obtained by voluntary disclosure [116,117], the former is expected to permit landlords, prospective buyers, and prospective tenants to include energy aspects in their decisions concerning building units. As far as Italy is concerned, starting from the implementation of Directive 2010/31/EU (on the energy performance of buildings, from which the acronym EPBD is derived) by Decree Law 63/2013, it is mandatory to include the energy label and the energy performance index in real estate advertisements. The subsequent Ministerial Decree 26 June 2015 defines a ten-level scale—from G, the worst energy rating band, to A4, the best—and clarifies the calculation of the energy performance index—in kWh/m² y—as the sum of indexes expressing the amount of non-renewable, primary energy required for heating and cooling purposes, hot water production, mechanical ventilation if present, and lighting. Details on the EPCs and energy rating bands system concerning the building industry and the real estate market in Italy can be found in recent studies [118,119]. In the analysis below, energy rating bands are aggregated as follows (Figure 3); otherwise, some of them would be underrepresented: A4 alone (13% of cases); all the labels between A3 and A (included) in a single group (10%); B and C are merged (11%); D (10%); E (15%); F (17%); G (23%).

4. Results and Discussion

4.1. Results for the Spatial Autoregressive Model

4.1.1. Overview of the Significant Attributes

We run two distinct variants of the model in Equation (4), one featuring the energy rating bands (ERBs) among the predictors but not the energy performance index (EPI), the other including EPI and omitting ERBs. The underlying reason is relatively straightforward: they use different scales of measurement, units of measure, and coding systems, but they essentially describe the same phenomenon, namely, the energy efficiency level of a building unit. Both models meet the standard assumptions of regression. The VIFs are steadily below the threshold of 2.5—while higher values would be a source of concern, as suggested in the literature [120]—and mostly fall in a range between 1.2 and 1.6. Heteroscedasticity is absent (H₀), with a Chi²(15) statistic of 13.0713 (p-value 0.5968) for the model with ERBs and a Chi²(14) statistic of 9.3502 (p-value 0.8080) for the model with EPI. Residuals are normally distributed (H₀) with a Chi²(2) statistic of 1.9936 (p-value 0.3691) for the model with ERBs and a Chi²(2) statistic of 1.7959 (p-value 0.4074) for the model with EPI (Figure 4).

As far as the overall results are concerned (

Table 2. Results for the spatial autoregressive model.

	Model for ERBs				Model for EPI
	Coeff.	Std. Err.	t-Stat +	p-Value	Coeff.	Std. Err.	t-Stat +	p-VALUE
const	8.8170	0.9004	9.792 ***	0.0000	7.0920	0.3452	20.540 ***	0.0000
ys−1 ++	0.0909	0.0418	2.172 **	0.0306	0.1038	0.0469	2.214 **	0.0276
Sa	−0.0013	0.0002	−6.069 ***	0.0000	−0.0015	0.0003	−5.139 ***	0.0000
A4 +++	0.5638	0.0561	10.050 ***	0.0000
A3-A +++	0.4535	0.0543	8.345 ***	0.0000
B-C +++	0.1611	0.0495	3.256 ***	0.0013
F +++	−0.1030	0.0413	−2.496 **	0.0131
G +++	−0.2446	0.0404	−6.054 ***	0.0000
EPI					−0.0015	0.0002	−7.871 ***	0.0000
Cy	−0.0009	0.0004	−2.201 **	0.0285
Mc(2)	0.2042	0.0339	6.020 ***	0.0000	0.1105	0.0386	2.864 ***	0.0045
Br					0.0591	0.0283	2.085 **	0.0379
Fl	−0.0442	0.0107	−4.123 ***	0.0000	−0.0504	0.0120	−4.186 ***	0.0000
Ph	0.2751	0.0591	4.657 ***	0.0000	0.3188	0.0617	5.169 ***	0.0000
Fw(1)					−0.1397	0.0622	−2.245 **	0.0255
Fw(2)					−0.1373	0.0573	−2.395 **	0.0172
Fw(4)	−0.1160	0.0325	−3.570 ***	0.0004	−0.1138	0.0351	−3.244 ***	0.0013
Mev					0.2140	0.0539	3.970 ***	0.0001
Cc	−0.1160	0.0107	−10.85 ***	0.0000	−0.1112	0.0113	−9.870 ***	0.0000
Ml	0.0661	0.0159	4.159 ***	0.0000	0.0742	0.0160	4.635 ***	0.0000
Bw	0.0689	0.0208	3.314 ***	0.0010	0.0813	0.0223	3.638 ***	0.0003
Adj. R2	0.6034				0.5281
AIC ++++	12.3985				67.2394

⁺ Significance levels: ** 0.05; *** 0.01; ⁺⁺ Spatial lag of the dependent variable; ⁺⁺⁺ Energy rating bands; ⁺⁺⁺⁺ Akaike information criterion.

), it is worth mentioning that spatial dependence once again plays a significant role in shaping property prices. The spatial lag of the dependent variable has a positive sign with similar values in the two variants: 0.0909 in the model for ERBs and 0.1038 in the model for EPI. Both coefficients are statistically significant at the 0.05 significance level. Furthermore, there is no clue that a share of spatial dependence remains unexplained and somewhat hidden in the residuals, as shown by the results of the model in Equation (6) for ERBs and EPI, respectively (t-statistic below the coefficient and p-value in brackets):

ε = 0.0001 + 0.0226 Wε + u,
      0.4140 (0.6792)

(18)

ε = 0.0013 + 0.0531 Wε + u.
      0.9636 (0.3360)

(19)

The minus sign before the coefficient of two significant predictors—saleable area (Sa) and distance to the city center (Cc)—confirms the reliability of the results. As far as the former is concerned, the overall price of a property grows as its size increases, but the unit price—which is the dependent variable here—is known to decline as the size increases. That is consistent with the law of diminishing marginal utility. Namely, the marginal utility derived from the availability of each additional square meter declines. Hence, a negative relationship between the unit price and the saleable area has to be expected [121,122].

Concerning the other predictor with a negative sign, property prices in monocentric cities such as Padua are expected to diminish when moving from the core area toward the outskirts. The real estate market monitor of the Italian Revenue Agency confirms this (Figure 5). Consistently, the coefficient of the predictor distance to the city center (Cc) takes a negative sign and implies that property prices decrease by 11–12% per each additional kilometer.

The positive sign for the coefficients of two other predictors—distance to the nearest mall (Ml) and the closest beltway ramp (Bw)—likely grasps the same phenomenon, though from a different angle, since malls and beltway ramps are located in suburban areas far from the central districts. Hence, the farther a property is from a mall or a beltway ramp, the closer it is to the city center, and the higher its value is.

The negative influence of floor level (Fl) on property price is somewhat unexpected, although it may depend on the fact that many buildings, especially older ones, are not provided with a lift. Instead, penthouses (Ph) command a premium of about 32–38% compared to traditional flats.

A final remark is in order about the variables meant to represent building features related to energy performance. External thermal insulation cladding systems, heat pumps, photovoltaic systems, and the type of heating system turn out to be not significant. At the same time, mechanical extraction ventilation (Mev) is statistically significant and positively affects the property price, as expected. Concerning windows and frames, you can expect a price lower by 13% with single-glazed windows in comparison to double-glazed windows, provided they are set in wood frames.

4.1.2. Energy Rating Bands and Energy Performance Index

The reliability of the results is further confirmed by the values of the coefficients for the energy rating bands, which are in a monotonic descending order, as well as by the minus sign before the coefficient of the energy performance index. It is worth mentioning that the omission of the spatial lag of the dependent variable would have biased the estimation of the price premium, especially for the A4 and A3-to-A labels (Figure 6), even though the gap is hardly noticeable.

Nevertheless, there is a reliability issue to address. The price premiums we find here are substantial, and they are as follows according to the model with ERBs: 76% for the energy rating band A4 (in comparison to the D one); 57% for the energy rating bands A3, A2, A1, and A; 17% for the B and C-labeled properties. Instead, F and G-rated building units are sold at a discount: −10% and −22%, respectively. Similarly huge price premiums are found in a few other works [19,71,81] and seem to indicate that energy-efficient properties are highly valued in the market.

However, we cannot rule out a plausible alternative explanation for this finding. The price premiums turn out to be much smaller when looking at the model with EPI. Multiplying the coefficient of the energy performance index by the average EPI of each energy rating band, the price premiums are as follows (Figure 7): 17% for the energy rating band A4 (again in comparison to the D one); 14% for the energy rating bands A3, A2, A1, and A; 7% for the B and C-labeled properties; −7% and −18% for the F and G-rated building units, respectively. The model with EPI accommodates more predictors referring to building features, such as the number of bathrooms (Br), single-glazed windows both on wood and other kinds of frames (Fw), and the presence of a mechanical ventilation system (Mev), which are instead not statistically significant in the model with ERBs. That said, it seems conceivable that the market appreciation for several building characteristics—as can be the case of top-quality construction materials and finishes—is, in a way, subsumed into the market appreciation for energy labels. It follows that ERBs’ coefficients may be inflated—in part, at least—in the sense that they account for more than the value that market players put on the energy performance per se. It would mean that the 76% gap we find between a D-rated property and an A4-rated one is partly attributable to the fact that the latter is likely more livable than the former and perhaps brings other kinds of benefits as far as health and safety are concerned [19,123,124].

Another possible reason behind the previous finding should be considered. The narrow price premiums we find according to the model with EPI may be evidence of nonlinearity in the relationship between the energy performance index and property prices. As a matter of fact, by running an auxiliary regression where quadratic terms are added, both the energy performance index and its square (sqEPI) turn out to be statistically significant. Aside from the multicollinearity issue (the VIFs of EPI and sqEPI are still within the threshold suggested by Marquardt [125]), the LM test (H₀: the relationship is linear, Chi²(2) statistic 34.1872, p-value 0.0000) suggests that nonlinearity should be taken into consideration. This new model meets the standard assumptions of regression: heteroscedasticity is absent (Chi²(14) statistic 12.6919, p-value 0. 5509); the residuals are normally distributed (Chi²(2) statistic 2.0396, p-value 0.3607). The inclusion of EPI and sqEpi in the model (

Table 3. Results for the spatial autoregressive model with the quadratic term of EPI.

	Model for EPI and sqEPI
	Coeff.	Std. Err.	t-Stat +	p-Value
const	7.2164500	0.3340	21.600 ***	0.0000
ys−1 ++	0.1054310	0.0445	2.367 **	0.0186
Sa	−0.0015717	0.0003	−5.520 ***	0.0000
EPI	−0.0037067	0.0004	−9.144 ***	0.0000
sqEPI	0.0000054	0.0000	6.426 ***	0.0000
Mc(2)	0.1832250	0.0364	5.030 ***	0.0000
Br	0.0592567	0.0274	2.161 **	0.0315
Fl	−0.0451867	0.0120	−3.771 ***	0.0002
Ph	0.3210940	0.0619	5.188 ***	0.0000
Fw(2)	−0.1011550	0.0532	−1.900 *	0.0584
Fw(4)	−0.1184110	0.0327	−3.618 ***	0.0003
Mev	0.1469560	0.0534	2.753 ***	0.0063
Cc	−0.1126880	0.0110	−10.250 ***	0.0000
Ml	0.0724747	0.0153	4.726 ***	0.0000
Bw	0.0635119	0.0219	2.901 ***	0.0040
Adj. R2	0.5540
AIC +++	49.1543

⁺ Significance levels: * 0.10; ** 0.05; *** 0.01; ⁺⁺ Spatial lag of the dependent variable; ⁺⁺⁺ Akaike information criterion.

) leads to different estimates of the price premiums, which are as follows (Figure 7):

• 55% for the energy rating band A4 (again in comparison to the D one);
• 42% for the energy rating bands A3, A2, A1, and A;
• 20% for the B and C-labeled properties;
• −14% and −29% for the F and G-rated building units, respectively.

Though they are closer to the estimates from the model with ERBs, the difference is still noticeable, which may imply that there are still grounds for looking into the reasoning put forward above. In other words, there are still hints that the price premiums derived from the model with ERBs go beyond the value that market players put into building energy performance.

4.2. Results for the Multi-Criteria Optimization Model

4.2.1. Role Played by Land and Building Attributes in Shaping Property Prices

The multi-criteria optimization model adopted here is first helpful in identifying the contribution brought by the most significant attributes in shaping property prices. The AHP model also turns out to be more selective—and, perhaps, less sensitive—than the SAR model. Accordingly, a few previously significant building characteristics are found to play a minor role. They are the construction year (Cy), maintenance conditions (Mc), and windows and frames (Fw).

On the whole, location attributes are particularly significant in shaping property prices, as their weight is up to 28.4% in the model with EPI and 40.9% in the model with ERBs. The distance to the city center (Cc) alone represents between 26.0% and 32.1% of the price. Incidentally, this result is corroborated by the data published in the technical journal Consulente Immobiliare, a biweekly publication of the 24 ORE Group [126,127]. This source states that—as of 2016—land leverage [128] for the city of Padua ranges from 23% in suburban and fringe areas to 41% in the core districts.

Other land characteristics, such as the distance to the nearest mall (Ml) and the closest ramp of the beltway (Bw), are less critical, with weights varying in the range between 2.4% and 5.6%. An additional share of the property prices—between 10.0% and 13.3%—is affected by the values of neighboring properties, which is a piece of empirical evidence supporting the role played by spatial dependence in the real estate market.

Building attributes—on the whole—shape between 45.8% and 61.6% of property prices. More than half of this contribution is brought by building energy performance: 26.6% considering the rating bands; 46.8% as far as the energy performance index is concerned. Such a significant influence may again suggest that the weights of ERBs and EPI represent not only the market appreciation for energy performance and high efficiency. Possibly, they also act as proxies of the market players’ willingness to pay more for state-of-the-art building materials, innovative building systems, and high-performance finishes.

Other building attributes explain a share of the property prices that range between 14.8% and 19.2%, the most important being the saleable area. Minor contributions are brought by attributes such as maintenance conditions (Mc), floor level (Fl), and whether the unit is a penthouse or not (Ph).

4.2.2. Role Played by Energy Rating Bands in Shaping Property Prices

By segmenting the data and separately comparing the properties belonging to each energy rating band with the D-rated ones, the multi-criteria optimization model allows us to identify the weight of each energy rating band in shaping the property price. According to the model of Equations (7)–(17), that weight is the price premium of each energy rating band in comparison to the reference one. The results from the multi-criteria optimization model are expected to converge with those of the spatial autoregressive model. Namely, the weights of the ERBs identified using the AHP model should align with the price premiums extrapolated from the SAR model.

That is largely true for several energy rating bands, with just one notable exception (Figure 8). In fact, the price premiums in the AHP model are found to be as follows:

• 53.4% for the A4 band in comparison to D (54.7% in the SAR model with EPI and sqEPI, with a gap as low as 1.3%);
• 45.3% for the A to A3 bands compared to D (42.0% in the SAR model with EPI and sqEPI and a margin of error of 3.3%);
• 19.4% for the B or C band in comparison to D (19.5% in the SAR model with EPI and sqEPI, which marks the narrowest gap of 0.1%);
• −10.4% for the F band (−14.1% in the SAR model with EPI and sqEPI and a margin of error of 3.7%);
• −10.8% for the G band (−29.3% in the SAR model with EPI and sqEPI, which marks the most significant gap of 18.5%).

Due to low significance, several variables are often dropped: construction year (Cy) and maintenance conditions (Mc) concerning the building characteristics, distance to the nearest mall (Ml) and the closest beltway ramp (Bw) regarding land attributes. Nonetheless, the weights of the energy rating bands—and thus, their price premiums—are not inflated. They also are in strictly decreasing order, as expected, and tend to converge to the values identified as best estimates in the statistical analysis. The only exception is the result of the comparison between the G-rated and the D-rated properties.

4.3. Limitations

The multi-criteria model adopted here has at least two limitations worth discussing. First, that model implies the construction of several pairwise comparison matrices, each of remarkable size. Pairwise comparison matrices in AHP are known to be subject to consistency issues [129], and inconsistency is more likely to occur as the size of the matrices increases [130,131]. However, inconsistency also depends on the judgment scale used to approximate priorities [132], while a ratio scale leads—by definition—to perfectly consistent matrices [133]. Since ratios are used here to fill all the pairwise comparison matrices, inconsistency is not an issue, as perfect consistency is always guaranteed. Aside from that, dealing with several large-size matrices poses considerable computational burdens. Not to mention that the sample size of this study is small compared to other works in this field, as thousands of properties are sometimes investigated, meaning much larger pairwise comparison matrices that are difficult to handle.

The second limitation is even more severe. Contrary to the SAR model—and regression models in general—the multi-criteria model does not include recognized tests and statistics to identify the significance of the weight for each attribute, as well as of the same weights on the whole. A weight that turns out close or equal to zero is the only sign that an attribute is irrelevant in shaping the property price. Furthermore, the minimum value of the sum of squared distances in Equations (16) and (17) provides an indication that can be interpreted in terms of goodness of fit (Figure 9). Other than that, there is no measure of statistical significance.

5. Conclusions and Further Developments

The novelty of this study lies in the way we address the issue of the price premium for building energy efficiency. The first research question we try to answer is whether or not the price premium can be estimated using an optimization process applied to a multi-criteria technique known as the analytical hierarchy process. Here, we show that the multi-criteria optimization approach proves effective in dealing with the estimation problem at hand. The second research question we try to answer concerns the reliability of the result. Here, we show that the alternative approach provides results that align with those derived from the spatial autoregressive model.

The research strand focused on the price premium for building energy efficiency has advanced consistently during the last decade or so, mainly due to studies carried out since the adoption of certification systems, such as GM in Singapore and EPC in the European Union. There is increasing evidence of an often substantial price premium.

This study is no exception. The results we have obtained confirm the occurrence of large price gaps for green buildings compared to traditional ones. Energy-efficient building units are sold at a premium compared to those characterized by mediocre performance. Using the D rating band as a reference, significant price premiums are to be expected for all the A-rated properties (from A to A4) and, to a lesser extent, for the B or C-rated ones. On the contrary, the properties of the F and G energy rating bands are sold at a two-digit discount. The estimates with the multi-criteria optimization approach are as follows: between 45.3% and 53.4% for the A-rated properties, 19.4% for the B or C-rated building units, and −10.4% for the F-rated properties. The large premiums we find for the best energy rating bands suggest that mandatory disclosure of building energy performance plays a major role in energy policies. It is thus essential for the market players as it conveys information that is otherwise asymmetrically distributed.

The multi-criteria optimization approach we employ here lends itself to further applications. That especially holds for real estate research into the role played by land and building features in shaping property prices, including the energy rating bands among the most significant building attributes. Property valuation methods are usually clustered into three groups: the market approach, the cost approach, and the income approach. In turn, the approaches and the methods branch themselves into several models and techniques. As far as the first is concerned, the sales comparison approach is among the most widely used. It refers to models and techniques—such as the adjustment grid and the matched pair adjustment—that compare the appraised property to similar properties—the so-called comparables. The main feature of the sales comparison approach lies in the fact that the appraiser is expected to account for each land and building attribute’s effect on property price. Also, the appraiser is meant to assess each attribute—to weigh it, if you will—relying on past experience and current knowledge of the market. That leaves enough room for semi-random and perhaps unreliable valuations. By contrast, the multi-criteria optimization approach we propose here has the merit of letting attribute weights emerge from the data and making them fit the property prices. Accordingly, we deem it promising to conduct further studies on the suitability of multi-criteria optimization to complement the sales comparison approach. To that end, it is essential to investigate whether the reliability of the results holds when the sample size decreases, given the limited number of comparables usually employed. This implies the need to address the trade-off between the computational costs we mentioned in the previous section and the results’ accuracy.