Response Characteristics of Pre-Stressed Strand Cables Subjected to Low-Velocity Impact: Experiment Test
Abstract
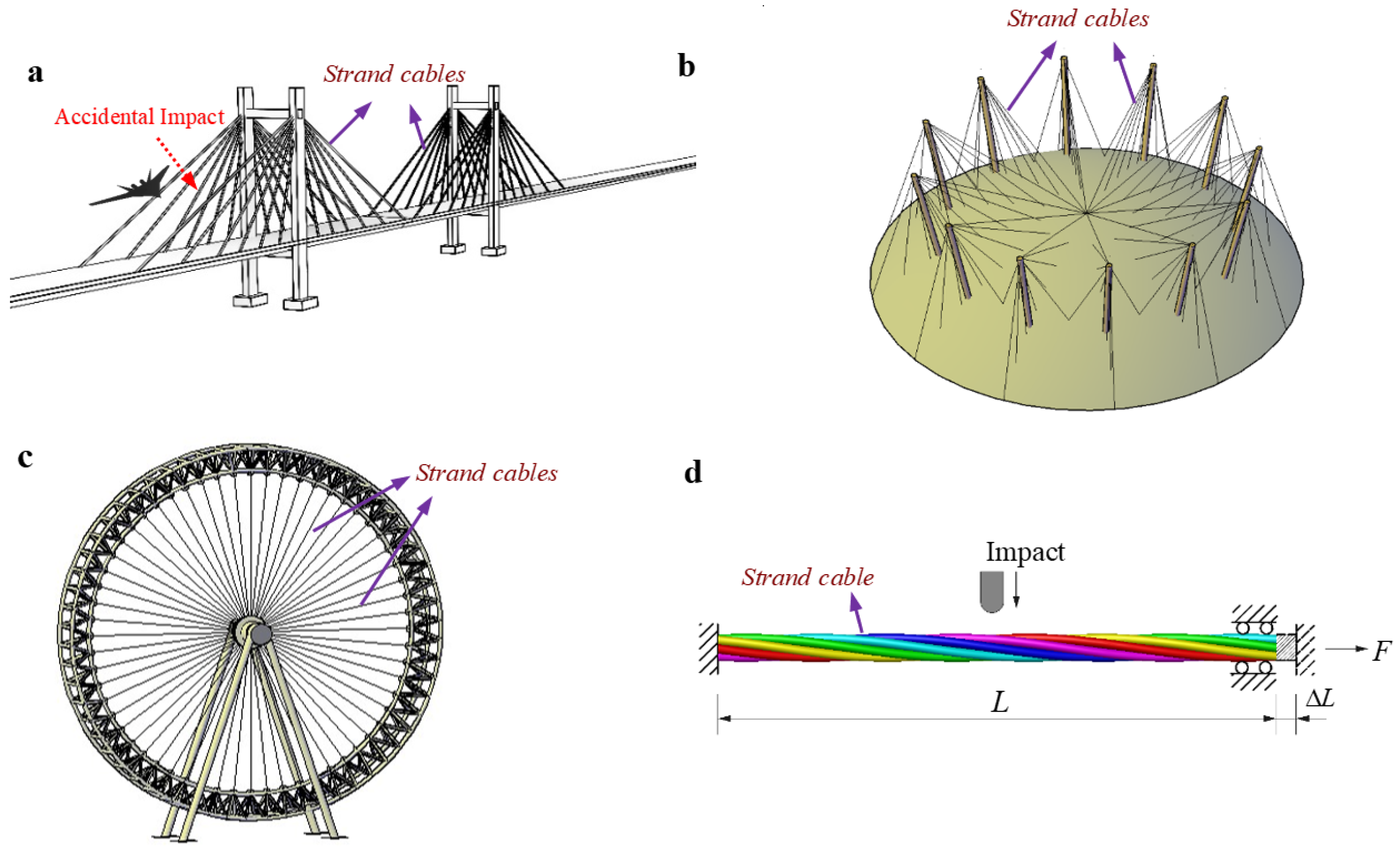
:1. Introduction
2. Methods—Description of Experiment
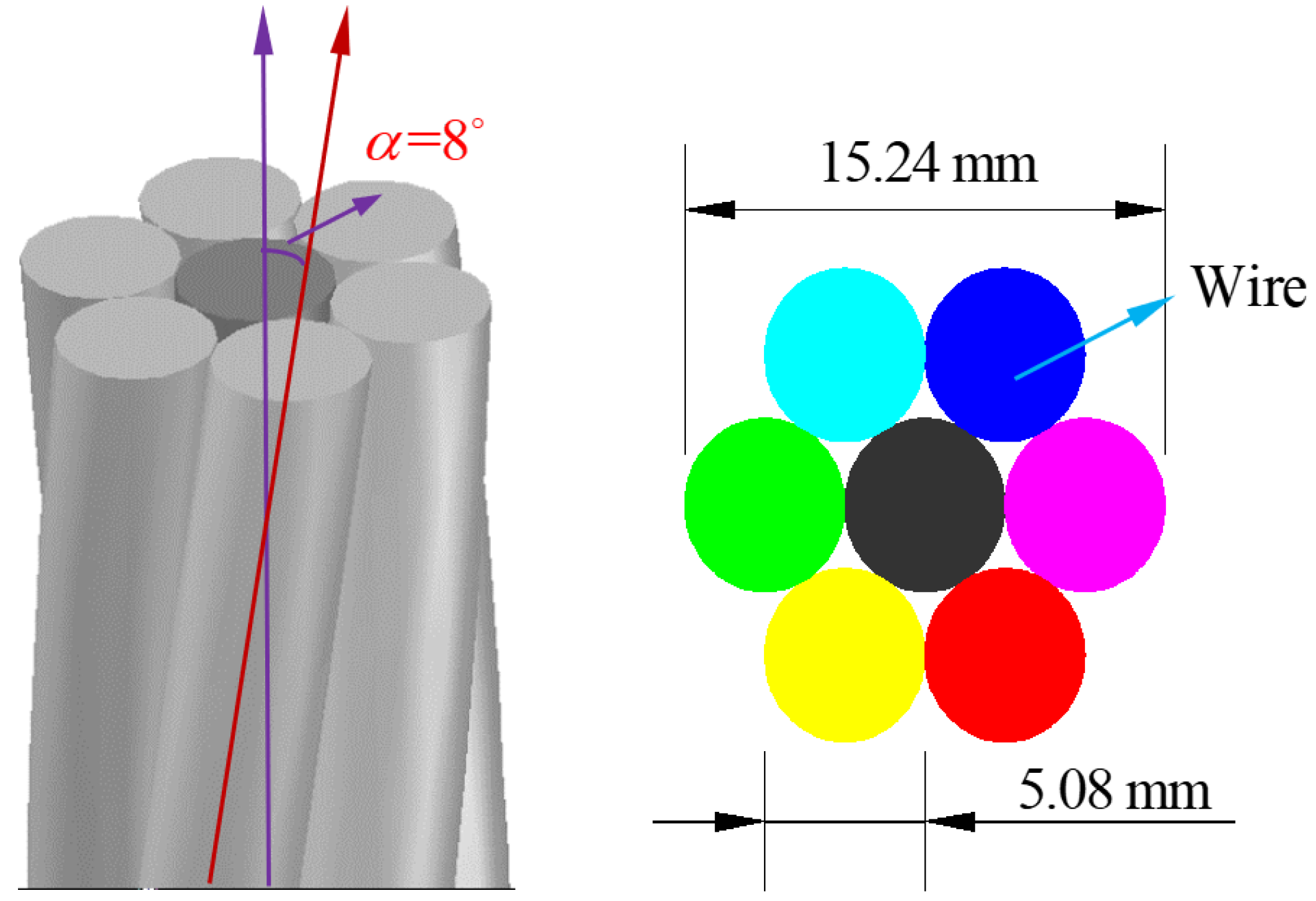
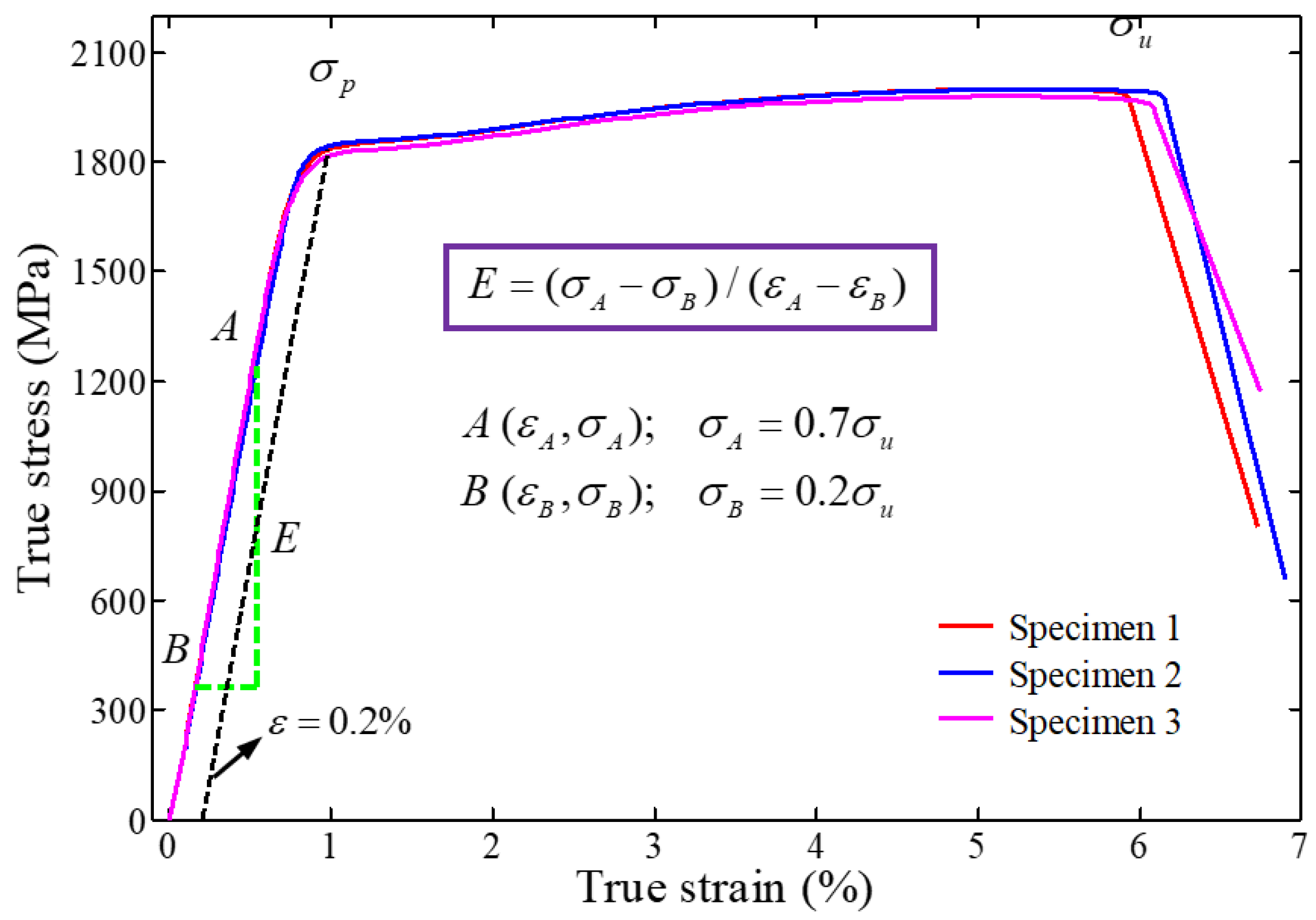
2.1. Test Specimen and Material Properties
2.2. Test Setup
2.3. Test Process and Working Cases
3. Results
3.1. Response Process
- Stage 1:
- Local disturbance and flexural wave. The sudden impact of the indenter causes a shear loading at the mid−span of the cable which generates a flexural wave. The position of this wave moves along the cable as time progresses and is clearly observed in early times presented in Figure 6. For instance, at t = 1.5 ms, bending deformation was found concentrated around the impact point while no deformation was observed elsewhere. At t = 5.0 ms, however, the flexural fluctuation reaches the root of the cable and then reflects and interacts with the subsequent waves. This behavior is similar to the initial response modes observed by Reid [36], Yu [37] and Xi [38] when investigating the elastic−plastic behavior of beams.
- Stage 2:
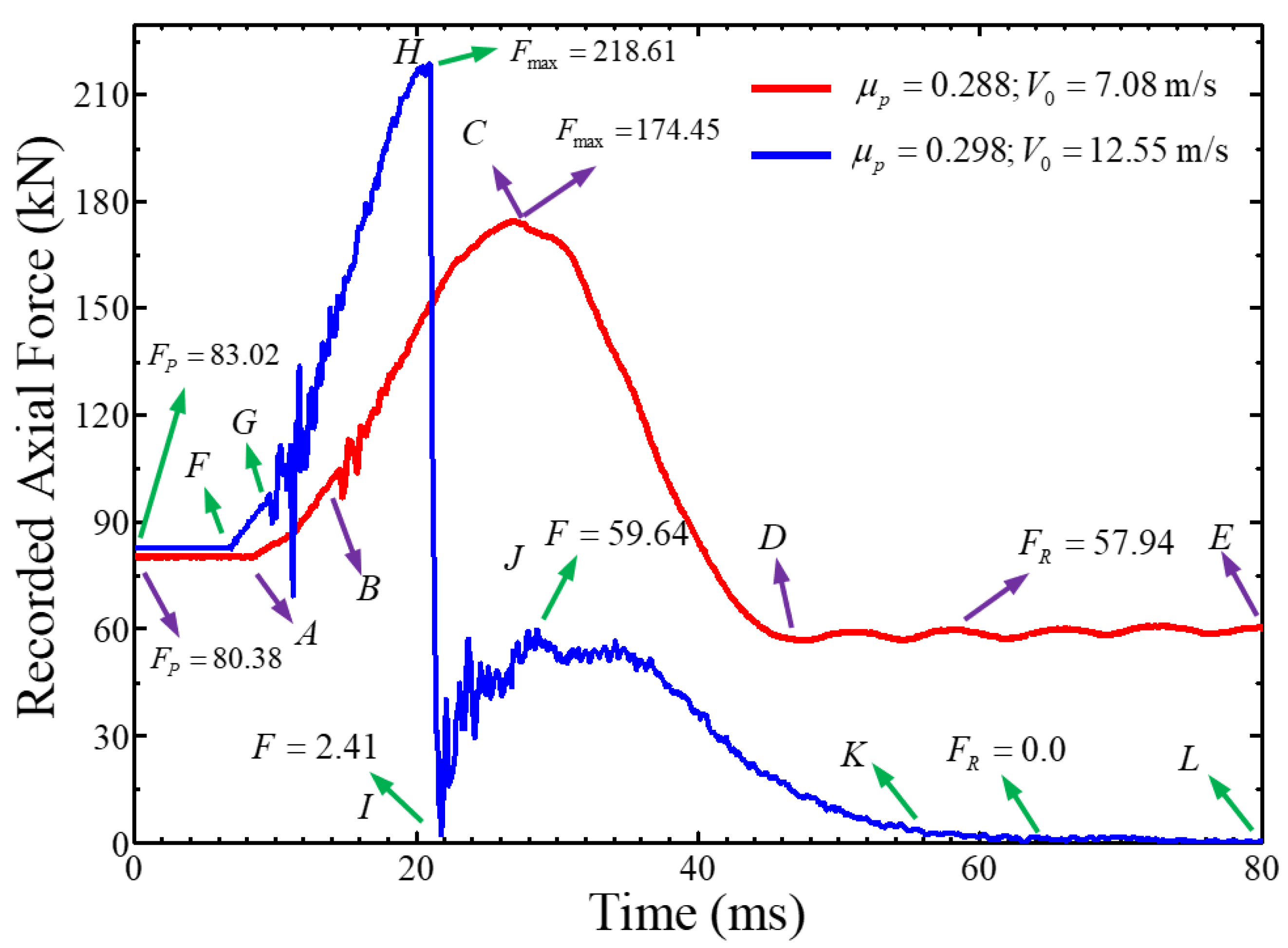
- Axial stretching. The triangle−shaped configuration is continually expanding until at instant t = 20.0 ms when the velocity of the indenter drops to zero and the strand cable reaches the maximum lateral displacement (). As shown in Figure 7, the axial force of the test piece increases (segment BC) with rapid rate but significant oscillation and finally reached a maximum value of F = 174.5 kN (). The oscillation may be caused by a slight slip between the test piece and the anchor or by interactions between the indenter and the test piece which produce denting or splay of wires limited to the impact zone. Detailed failure patterns are presented in the following sections.
- Stage 3:
- Rebound and elastic vibration. Starting from t = 20.0 ms, the specimen and the drop hammer generate a reverse motion from the maximum lateral displacement until the instant t = 45.5 ms, from which they are completely separated from each other. As shown in Figure 7, the elastic rebound causes the axial force of the test piece to slowly unload to 57.97 kN (). Compared to the initial pre−tensioned force, it can be found that about 27.90% of the axial force is lost during the impact process. On the other hand, after separation from the test specimen, the indenter moves opposite to the impact direction at a speed v = 5 m/s, whose kinetic energy is about 49.87% of the input kinetic energy, which indicates that only a small portion of the energy is dissipated by the inelastic deformation of the strand during the collision of the drop hammer, contrarily, most of it is accumulated as the elastic strain energy of the specimen during the deformation process, and then is retransmitted to the specimen during the rebound process. The key reason for this phenomenon should be attributed to the high strength of the steel strand wires, which makes it difficult for the impact loading to exceed its elastic regime.
- Stage 1:
- After the end of the local disturbance and flexural wave propagation (t = 0–2.5 ms), the specimen gradually evolve into an expanding triangle−shaped configuration with the impact area as the apex. At t = 14.5 ms, three wires on the upper surface of the cable and right underneath the indenter in the impact zone fractured brittlely without warning. This sudden break accelerates the wires contracting toward the clamp end along the longitudinal axis of the test piece. Meanwhile, the broken wires interact with the others and form a “birdcage” knot beside the support (t = 18.5 ms) due to the winding structure of the wires and the rigid restraint of the clamped end. Furthermore, on the instant that the wire breaks, there is a clearly visible “spark” generated together with a crisp and harsh sound.
- Stage 2:
- From t = 14.5 ms, the vertical displacement of the strand continues to increase until t = 24.5 ms, reaching the maximum lateral displacement (). Subsequently, both the test specimen and the indenter bounce and detach from each other at t = 57.0 ms. Then the test piece enters the stage of elastic free vibration and the rebounding drop hammer moves upward at a speed of 1.6 m/s, which is about 1.63% of the initial input kinetic energy. Obviously, on this loading case, most of the impact energy is dissipated in the plastic deformation and fracture of the steel strands. On the other hand, the elastic rebound causes a complicated interaction between each wire of the test specimen which eliminates the “birdcage” knot formed at the end at the first stage.
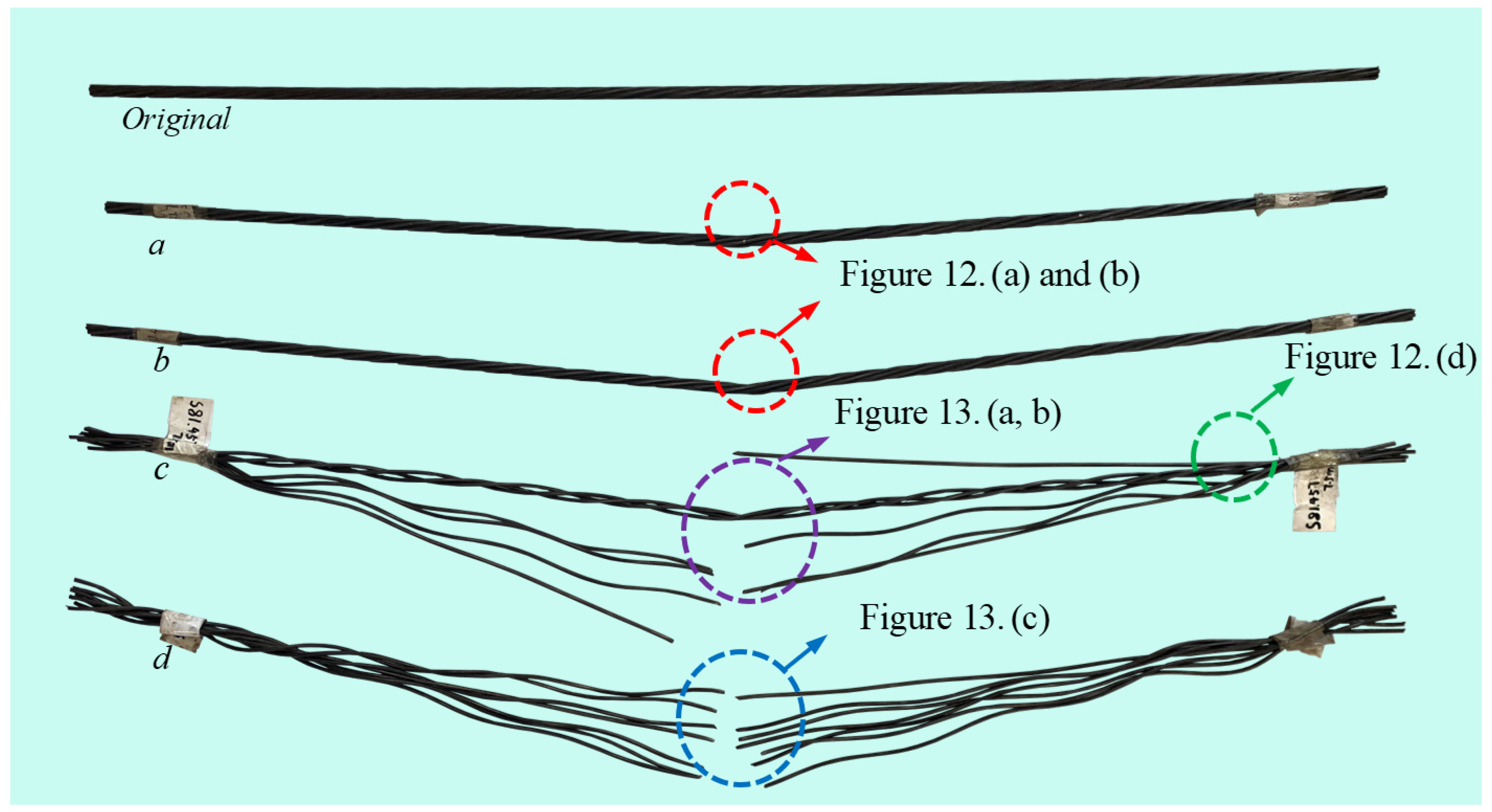
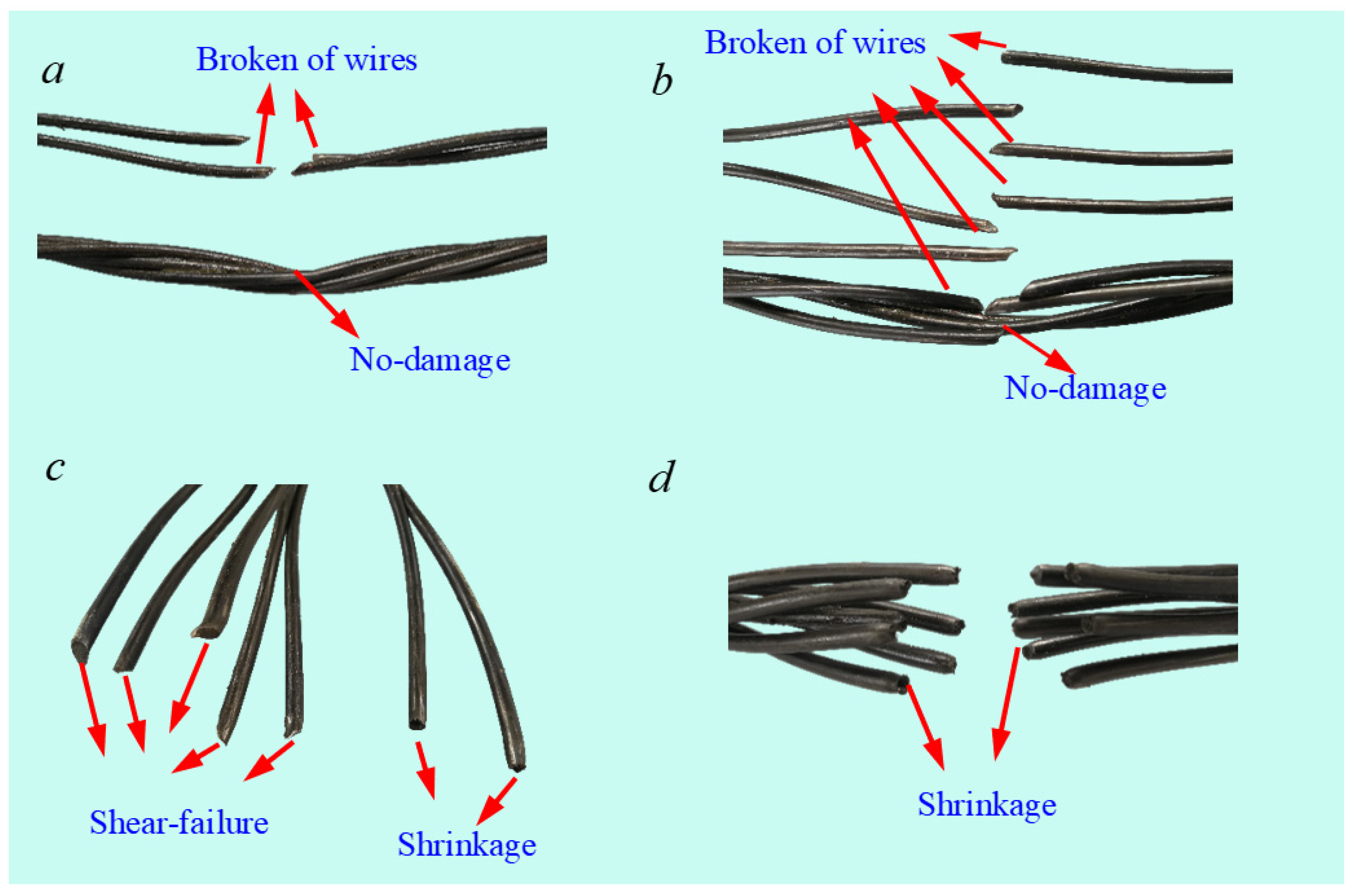
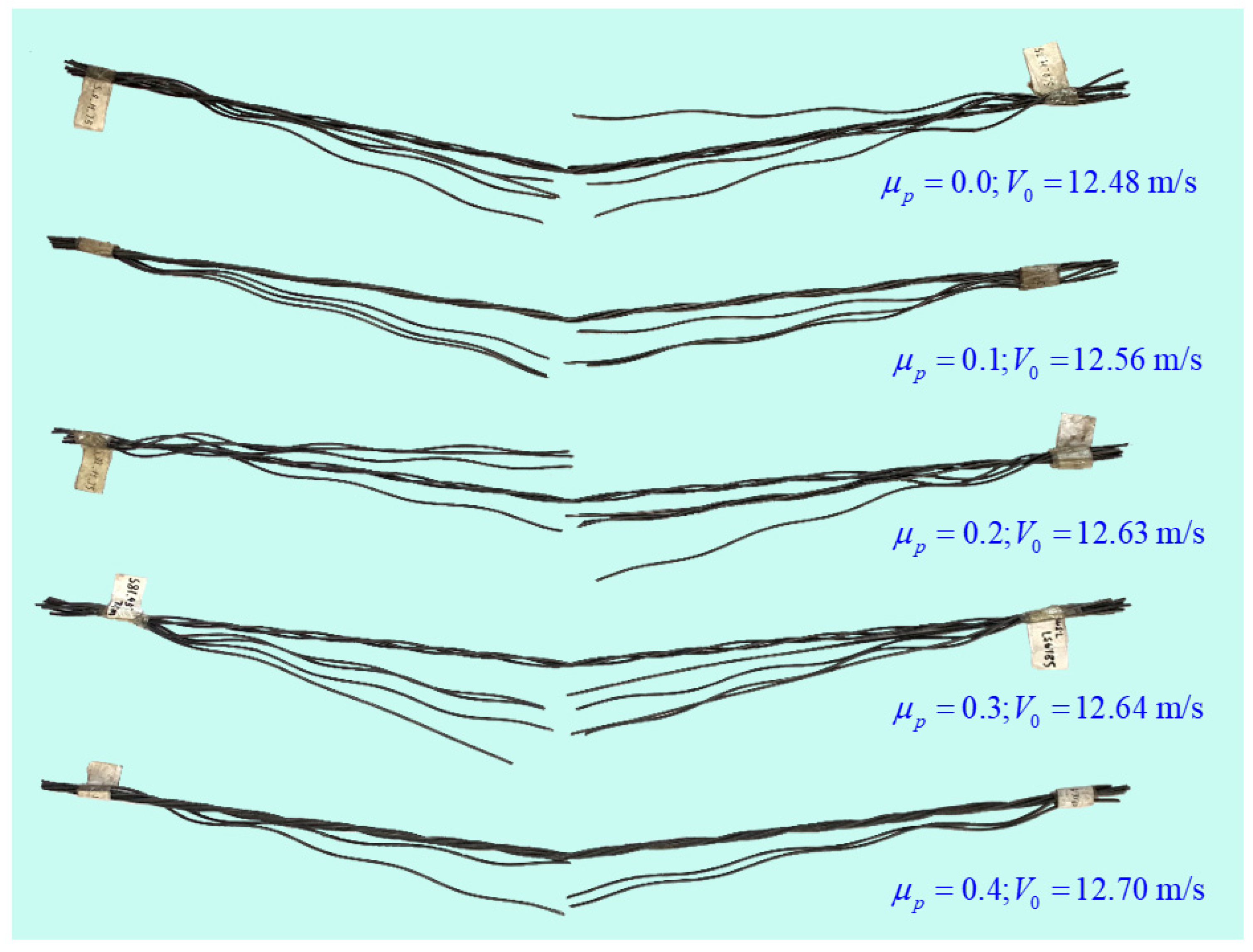
3.2. Failure Patterns
4. Discussion
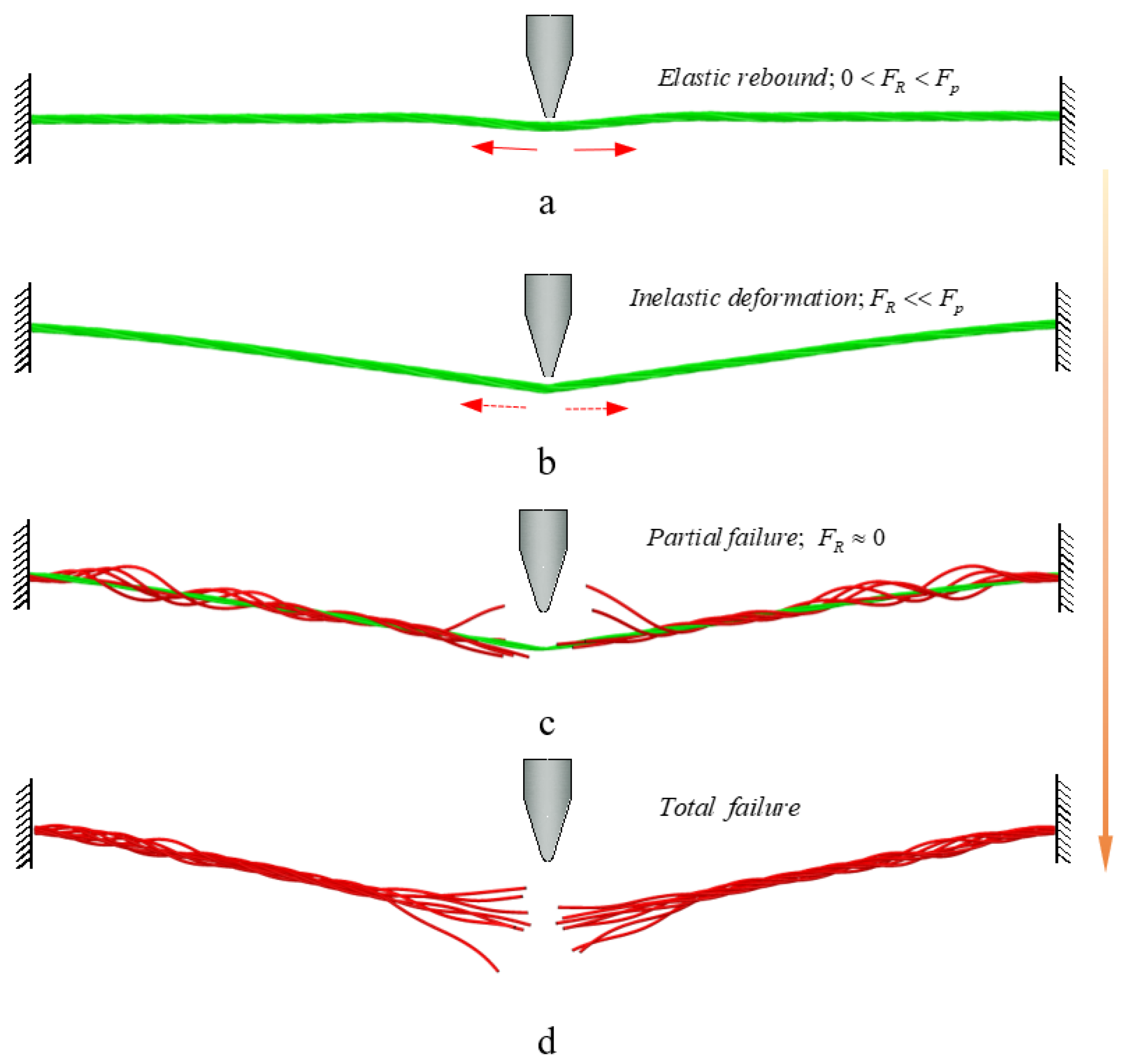
4.1. Response Modes
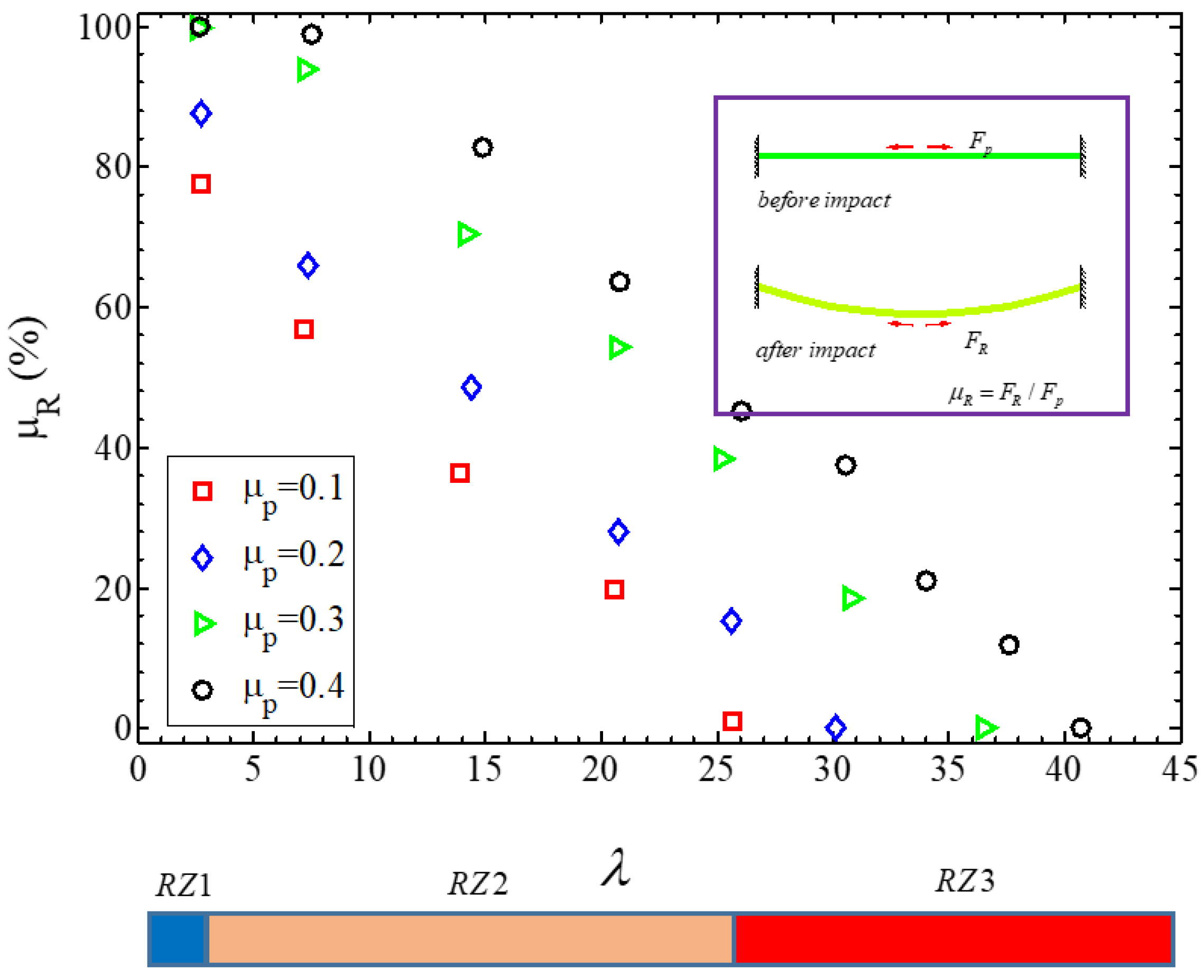
4.2. Plastic Displacement and Residual Stress
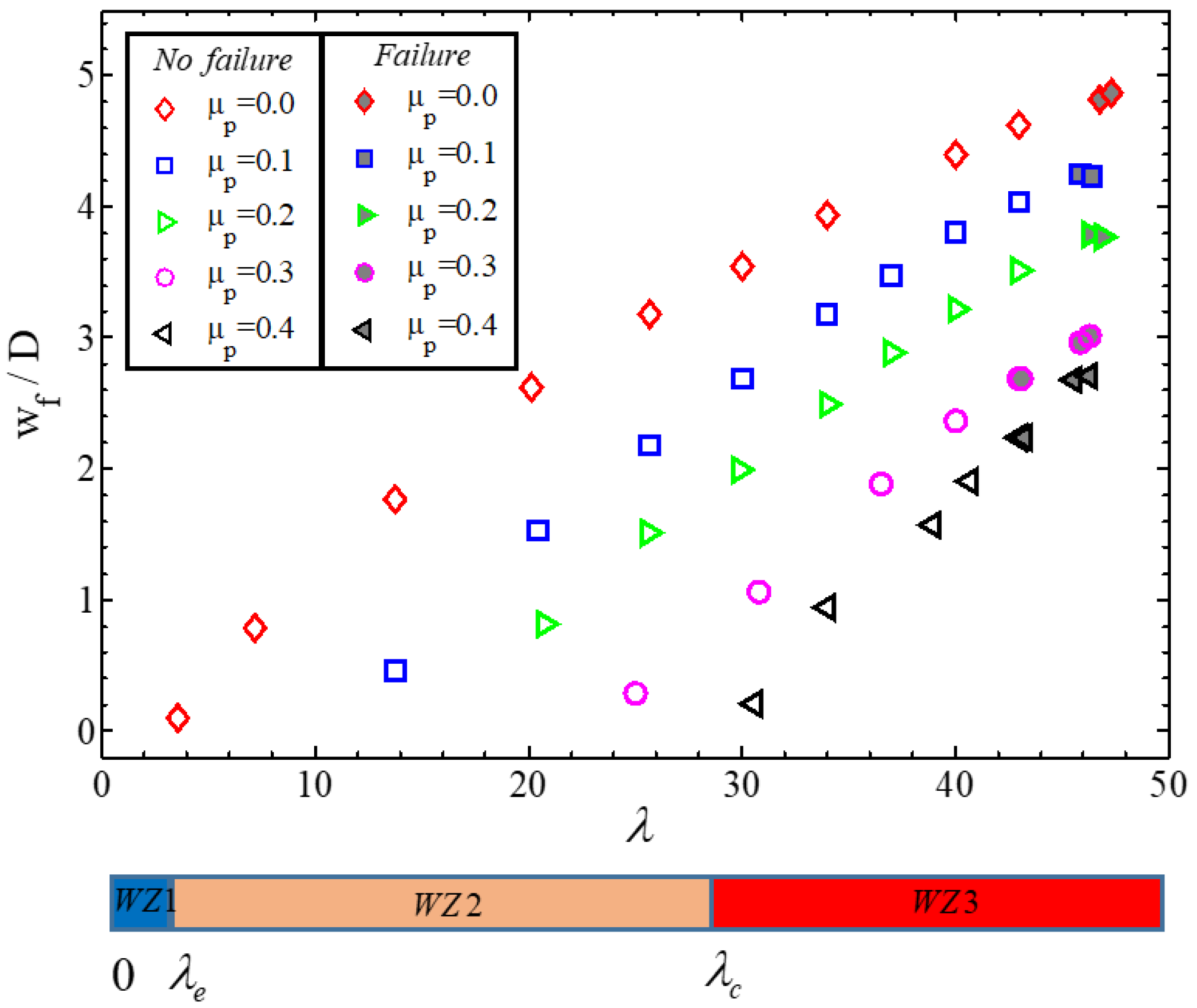
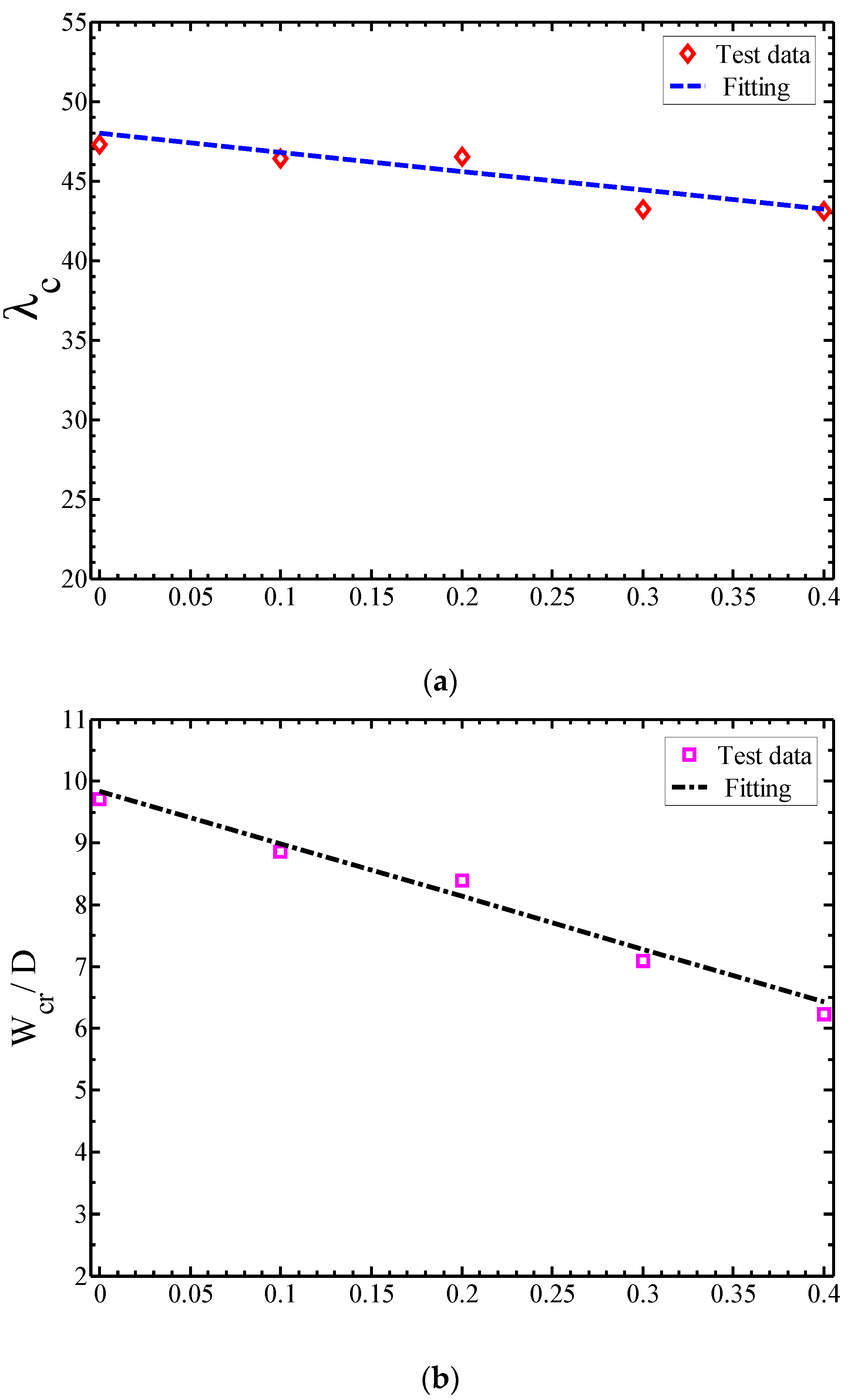
4.3. Critical Energy and Displacement
5. Conclusions
- (1)
- Under concentrated impact loading, the dynamic response of strands can be categorized into three modes: elastic bounce, plastic deformation and partial or full wire fracture, which corresponding to slight, partial and total loss of pre−tension, respectively.
- (2)
- The impact failure of steel cable is usually manifested as the unforeseen brittle fracture in the impact zone. The patterns include indentation−like damage of the upper steel wire, fracture of some or all steel wires under the multi−axial stress state which is the combination of compression, shear and tension. Under high−level of pre−tension, some steel wires may break under complicated stress state, and then the remaining steel wires undergo a process of tensile failure. Such failure modes suggest that engineers need to pay attention to at least the following two points in subsequent theoretical analysis: (1) Although the response of the steel strand under the impact load is mainly reflected as the axial tension mode, its failure would be controlled by the complicated stress state in the impact zone; (2) The material properties, especially the plastic behavior and failure criterion, are the key challenges to conquer to deeply understand the dynamic response and energy dissipation mechanism of such components.
- (3)
- For the same impact energy, the failure displacement decreases significantly with the increase of the pre−stress level. However, the failure energy of the cables is not sensitive to the initial pre−stress level.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| nominal diameter of strand | |
| span of strand | |
| elastic modulus | |
| proportional limit stress | |
| static ultimate tensile stress | |
| static uniaxial rupture strain | |
| indenter mass | |
| impact velocity of indenter | |
| initial kinetic energy | |
| pretension load | |
| maximum total permanent transverse displacement | |
| failure displacement | |
| initial stress level | |
| the classical static collapse load | |
| the dimensionless energy parameter | |
| no wire fracture energy | |
| the fracture at least one wire energy | |
| failure energy | |
| the critical energy |
References
- Chen, C.; Chen, J.; Zhao, X.; Shi, C. Experimental investigation on combustion characteristics of steel cable for cable-stayed bridge. J. Therm. Anal. Calorim. 2018, 134, 2317–2327. [Google Scholar] [CrossRef]
- Iordachescu, M.; Valiente, A.; De Abreu, M. Effect of environmentally assisted damage on fatigue resistance of tie-down cables after 30 years of service in a cable-stayed bridge. Eng. Fail. Anal. 2021, 126, 105455. [Google Scholar] [CrossRef]
- Du, Y.; Li, G.-Q. The Role of Tendons for Fire Safety Design of Pre-tensioned Steel Structures. ce/papers 2021, 4, 1488–1498. [Google Scholar] [CrossRef]
- Koh, C.H.; Low, K.; Li, L.; Zhao, Y.; Dend, C.; Tan, S.K.; Chen, Y.; Yeap, B.C.; Li, X. Weight threshold estimation of falling UAVs (Unmanned Aerial Vehicles) based on impact energy. Transp. Res. Part C 2018, 93, 228–255. [Google Scholar] [CrossRef]
- Lu, X.; Liu, X.; Li, Y.; Zhang, Y.; Zuo, H. Simulations of airborne collisions between drones and an aircraft windshield. Aerosp. Sci. Technol. 2020, 98, 105713. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Y.; Liang, K.; Cao, K.; Wang, Y.; Liu, X.; Guo, Y.; Wang, J. High-precision modeling and collision simulation of small rotor UAV. Aerosp. Sci. Technol. 2021, 118, 106977. [Google Scholar] [CrossRef]
- Utting, W.S.; Jones, N. The response of wire rope strands to axial tensile loads part I: Experimental results and theoretical pre-dictions. Int. J. Mech. Sci. 1987, 29, 605–619. [Google Scholar] [CrossRef]
- Ma, J.; Ge, S.; Zhang, D. Load distribution on the unit of the wire rope strand. J. Mech. Eng. 2009, 45, 259–264. [Google Scholar] [CrossRef]
- Kim, J.-K.; Yang, J.-M. Effect of design variables on deflected tensile performance of high-strength 7-wire steel strand for stay cable. Constr. Build. Mater. 2018, 188, 40–48. [Google Scholar] [CrossRef]
- Xing, X.; Li, Y.; Lei, Z.; Li, Q. Dynamic mechanical tensile properties and constitutive relationship of prestressed steel strand. Sci. Technol. Eng. 2018, 18, 228–233. (In Chinese) [Google Scholar]
- Brügger, A.; Lee, S.-Y.; Robinson, J.; Morgantini, M.; Betti, R.; Noyan, I.C. Internal Contact Mechanics of 61-Wire Cable Strands. Exp. Mech. 2022, 62, 1475–1488. [Google Scholar] [CrossRef]
- Xu, X.; Gao, H.; Ye, J.; Zhang, F.; Sheng, J. Study on initial tension load and load holding time of prestressed steel strand. J. Basic Sci. Eng. 2022, 30, 1014–1027. (In Chinese) [Google Scholar]
- Judge, R.; Yang, Z.; Jones, S.; Beattie, G. Full 3D finite element modelling of spiral strand cables. Constr. Build. Mater. 2012, 35, 452–459. [Google Scholar] [CrossRef]
- Chen, C.; Yuan, X.; Jiang, S.; Liang, X. Static model and cross section characteristic analysis of steel strand. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2016, 44, 13–17. (In Chinese) [Google Scholar]
- Qian, H.; Zong, Z.; Xie, G.; Liao, J.; Du, M. Refined simulation of elastic-plastic static behavior of grade 1860 strand wires. J. Southeast Univ. (Nat. Sci. Ed.) 2019, 49, 624–630. (In Chinese) [Google Scholar]
- Afshan, S.; Theofanous, M.; Wang, J.; Gkantou, M.; Gardner, L. Testing, numerical simulation and design of prestressed high strength steel arched trusses. Eng. Struct. 2019, 183, 510–522. [Google Scholar] [CrossRef]
- Minaei, A.; Daneshjoo, F.; Goicolea, J.M. Experimental and numerical study on cable breakage equivalent force in cable-stayed structures consisting of low-relaxation seven-wire steel strands. Structures 2020, 27, 595–606. [Google Scholar] [CrossRef]
- Kim, H.-J.; Lee, D.-H.; Yoon, K.; Lee, P.-S. A multi-director continuum beam finite element for efficient analysis of multi-layer strand cables. Comput. Struct. 2021, 256, 106621. [Google Scholar] [CrossRef]
- Ahmad, J.; Cheng, S.; Ghrib, F. Combined effect of external damper and cross-tie on the modal response of hybrid two-cable networks. J. Sound Vib. 2018, 417, 132–148. [Google Scholar] [CrossRef]
- Zhou, H.J.; Wu, Y.H.; Li, L.X.; Sun, L.M.; Xing, F. Free vibrations of a two-cable network inter-supported by cross-links extended to ground. Smart Struct. Syst. 2019, 23, 653–667. [Google Scholar]
- Chen, W.; Wang, R.; Zhou, H.; Zhen, X.; Zhang, Z. Research on natural vibration characteristics of coupling hangers considering bending stiffness. J. South China Univ. Technol. (Nat. Sci. Ed.) 2020, 48, 143–154. (In Chinese) [Google Scholar]
- Chen, W.; Zhang, Z.; Zhen, X.; Li, M. Effect of bending stiffness on the in-plane free vibration characteristics of a cable network. J. Mech. Sci. Technol. 2020, 34, 4439–4463. [Google Scholar] [CrossRef]
- Chen, C.-C.; Wu, W.-H.; Liu, Y.-T.; Lai, G. A convenient cable tension estimation method simply based on local vibration measurements to fit partial mode shapes. Eng. Struct. 2022, 272, 115008. [Google Scholar] [CrossRef]
- Utting, W.S.; Jones, N. The response of wire rope strands to axial tensile loads–part II: Comparison of experimental and theoretical predictions. Int. J. Mech. Sci. 1987, 29, 621–636. [Google Scholar] [CrossRef]
- Chen, Y.; Meng, F.; Gong, X. Full contact analysis of wire rope strand subjected to varying loads based on semi-analytical method. Int. J. Solids Struct. 2017, 117, 51–66. [Google Scholar] [CrossRef]
- Shi, K.; Wu, X.; Liu, Z.; Dai, S. Coupled calculation model for anchoring force loss in a slope reinforced by a frame beam and anchor cables. Eng. Geol. 2019, 260, 105245. [Google Scholar] [CrossRef]
- Shi, K.; Wu, X.; Tian, Y.; Xie, X. Analysis of Re-Tensioning Time of Anchor Cable Based on New Prestress Loss Model. Mathematics 2021, 9, 1094. [Google Scholar] [CrossRef]
- Qin, J.; Ju, Z.; Liu, F.; Zhang, Q. Cable Force Identification for Pre-Stressed Steel Structures Based on a Multi-Frequency Fitting Method. Buildings 2022, 12, 1689. [Google Scholar] [CrossRef]
- Gao, X.; Jia, J.; Mei, G.; Bao, X.; Zhang, L.; Liao, X. A New Prestress Loss Calculation Model of Anchor Cable in Pile–Anchor Structure. Mathematics 2022, 10, 1260. [Google Scholar] [CrossRef]
- Lu, Q.; Sun, Z.; Zhang, W. Nonlinear parametric vibration with different orders of small parameters for stayed cables. Eng. Struct. 2020, 224, 111198. [Google Scholar] [CrossRef]
- Xu, B.; Dan, D.; Yu, X. Real-time online intelligent perception of time-varying cable force based on vibration monitoring. Eng. Struct. 2022, 270, 114925. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, M.; Wang, X.; Zhao, L.; Bai, Y. Analytical investigation of the main cable bending stiffness effect on free flexural vibration of suspension bridges with a 3D cable system. Structures 2022, 41, 764–776. [Google Scholar] [CrossRef]
- Judge, R.; Yang, Z.; Jones, S.; Beattie, G.; Horsfall, I. Spiral strand cables subjected to high velocity fragment impact. Int. J. Impact Eng. 2017, 107, 58–79. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Zhang, Y.; Jiang, T.; Li, X.; Mao, A.; Wang, W.; Lin, X.; Yu, J.; Yan, C.; Xie, Z.; et al. GB/T 5224-2014; Steel Strand for Prestressed Concrete. Standards of the People’s Republic of China: Beijing, China, 2014. (In Chinese)
- Gao, Y.; Dong, L.; Liu, T.; Huang, X.; Luo, Y.; Long, J.; Wang, L.; Zhang, H.; Xu, L.; Yang, H.; et al. GB/T 228.1-2021; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. Standards of the People’s Republic of China: Beijing, China, 2021. (In Chinese)
- Reid, S.R.; Gui, X.G. On the elastic-plastic deformation of cantilever beams subjected to tip impact. Int. J. Impact Eng. 1987, 6, 109–127. [Google Scholar] [CrossRef]
- Yu, T.; Yang, J.; Reid, S. Interaction between reflected elastic flexural waves and a plastic ‘hinge’ in the dynamic response of pulse loaded beams. Int. J. Impact Eng. 1997, 19, 457–475. [Google Scholar] [CrossRef]
- Xi, F.; Liu, F.; Li, Q. Large deflection response of an elastic, perfectly plastic cantilever beam subjected to a step loading. Int. J. Impact Eng. 2012, 48, 33–45. [Google Scholar] [CrossRef]








| Component | Fe | C | Si | Mn | P | S | Cr | Ni | Cu |
|---|---|---|---|---|---|---|---|---|---|
| Mass % | >98.3 | 0.72 | 0.19 | 0.41 | <0.025 | <0.025 | <0.10 | <0.10 | <0.20 |
| No. | Nominal Area | Length | F_max | F_0.2 | E | Elongation | ||
|---|---|---|---|---|---|---|---|---|
| (mm2) | (mm) | (kN) | (kN) | (GPa) | (MPa) | (MPa) | (%) | |
| Specimen 1 | 140.0 | 607 | 279.7 | 254.5 | 202 | 1820 | 1998 | 6.59 |
| Specimen 2 | 140.0 | 604 | 279.8 | 257.8 | 198 | 1840 | 1999 | 6.47 |
| Specimen 3 | 140.0 | 611 | 277.3 | 254.1 | 200 | 1815 | 1981 | 6.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Yang, Y.; Hu, Y.; Liu, F. Response Characteristics of Pre-Stressed Strand Cables Subjected to Low-Velocity Impact: Experiment Test. Buildings 2023, 13, 330. https://doi.org/10.3390/buildings13020330
Wu Z, Yang Y, Hu Y, Liu F. Response Characteristics of Pre-Stressed Strand Cables Subjected to Low-Velocity Impact: Experiment Test. Buildings. 2023; 13(2):330. https://doi.org/10.3390/buildings13020330
Chicago/Turabian StyleWu, Zhijie, Yuchao Yang, Yachao Hu, and Feng Liu. 2023. "Response Characteristics of Pre-Stressed Strand Cables Subjected to Low-Velocity Impact: Experiment Test" Buildings 13, no. 2: 330. https://doi.org/10.3390/buildings13020330
APA StyleWu, Z., Yang, Y., Hu, Y., & Liu, F. (2023). Response Characteristics of Pre-Stressed Strand Cables Subjected to Low-Velocity Impact: Experiment Test. Buildings, 13(2), 330. https://doi.org/10.3390/buildings13020330







