Energy-Performance Evaluation with Revit Analysis of Mathematical-Model-Based Optimal Insulation Thickness
Abstract
:1. Introduction
2. Materials and Methods
2.1. Calculations for Building Performance with Sandwich Design
2.1.1. Calculating Heat Loss
2.1.2. Annual Energy Cost
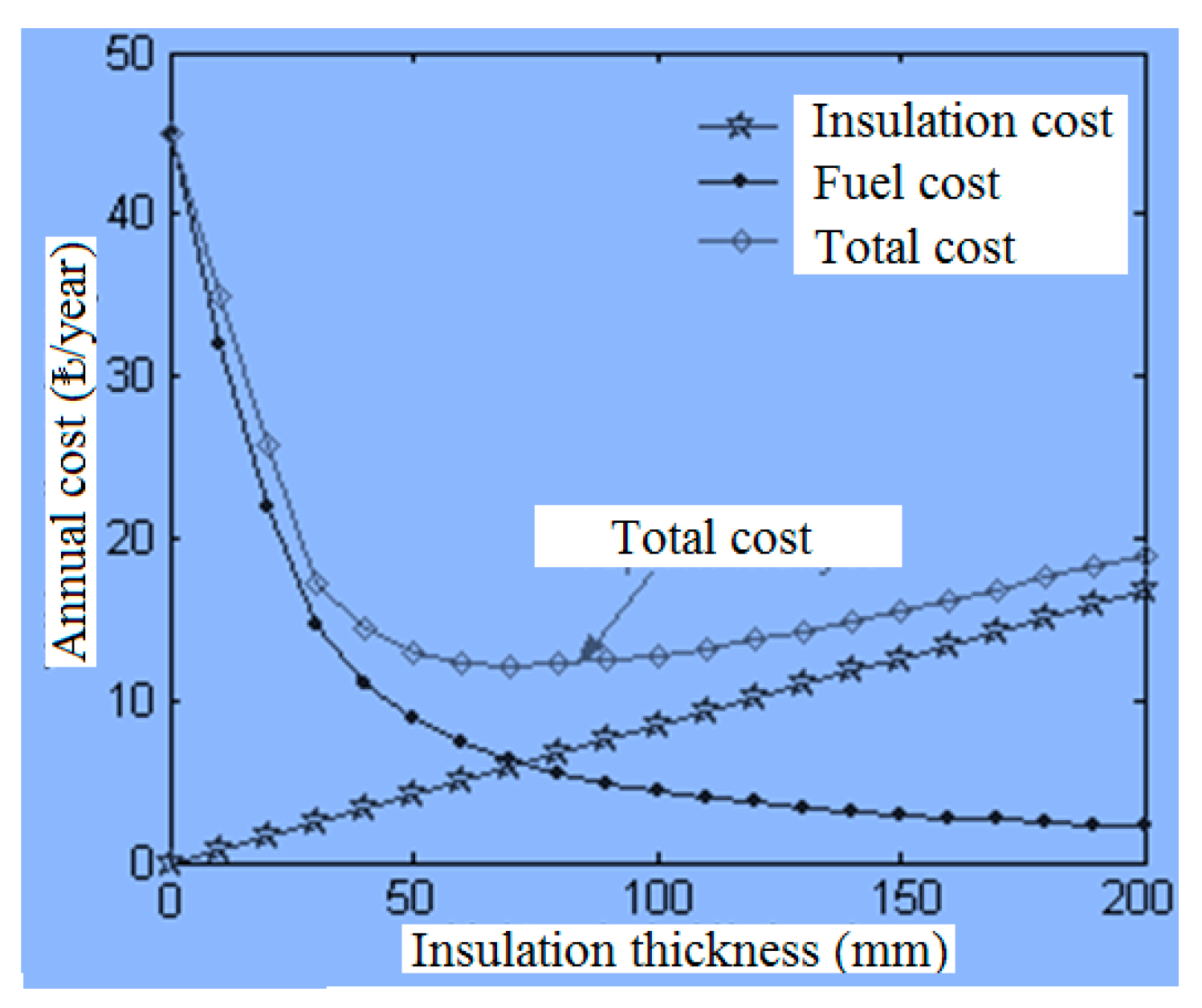
2.1.3. Optimization of Insulation Thickness
2.1.4. Calculation of the Fuel Consumption Process
2.2. Revit Analysis
3. Results and Discussion
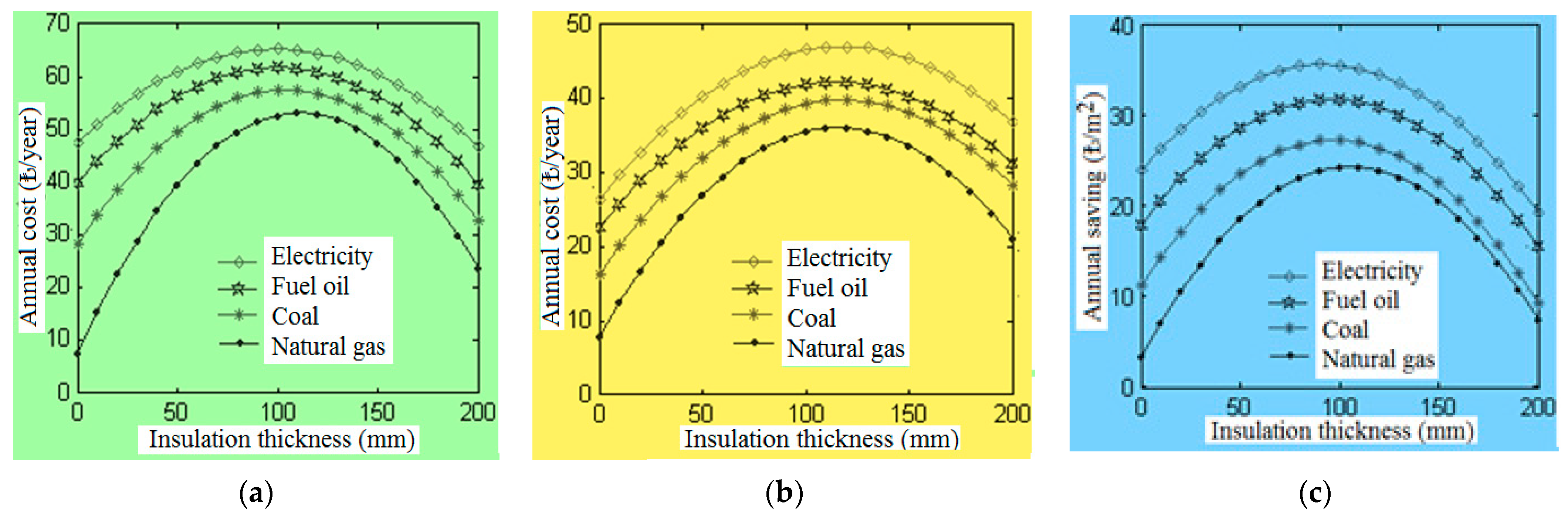
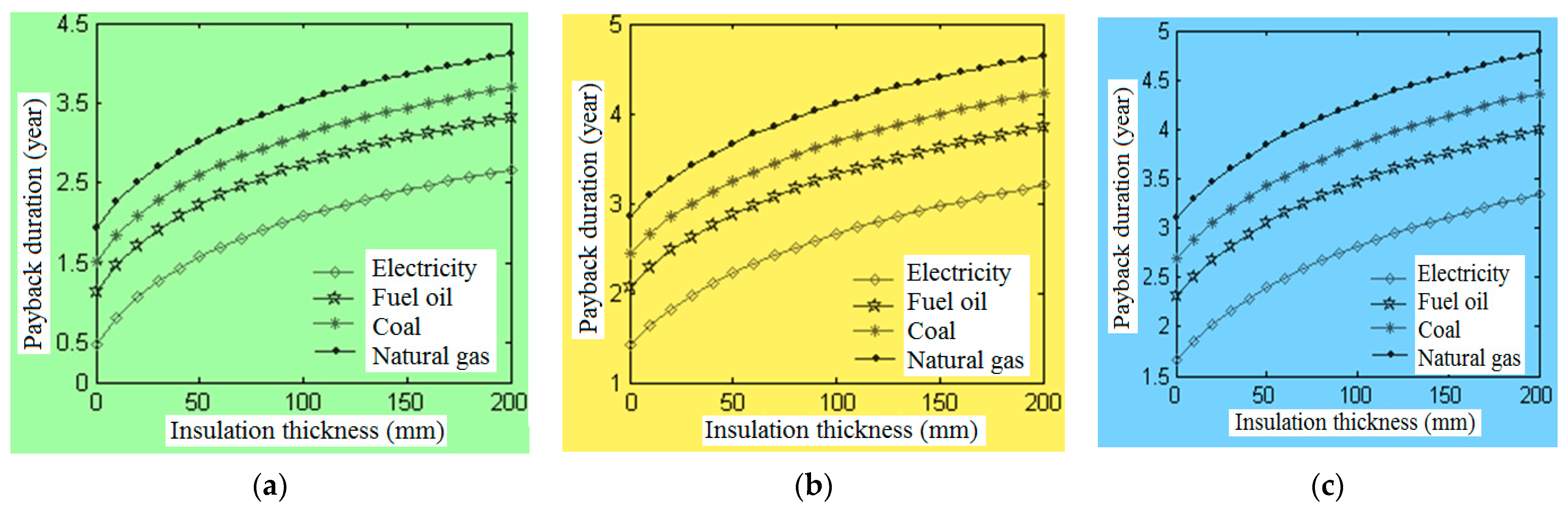
3.1. LCCA (Life-Cycle Cost Analysis)
3.2. Energy Consumption Analysis with Revit Simulation during One Year
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| As | Annual total cost difference [TRY/m2] |
| CA | Annual energy cost for hearing [TRY/m2-year] |
| Cf | Fuel cost [TRY/kg] |
| Cins | Insulation material cost [TRY/m2] |
| Ct | Total heating cost of non-insulated building [TRY/m2-year] |
| Ct, ins | Total heating cost of insulated building [TRY/m2-year] |
| DD | Degree-days [°C day] |
| EA | Annual energy required for heating [J/m2-year] |
| g | Inflation rate [%] |
| Hu | Thermal value [J/kg] |
| i | Interest rate [%] |
| U | Total heat-transfer coefficient [W/m2 K] |
| LCCA | Life-cycle cost analysis |
| N | Lifetime [year] |
| pp | Payback period [year] |
| PWF | Present-value factor |
| q | Thermal loss per unit field of external walls [W/m2] |
| qA | Annual heating loss [W/m2] |
| r | Real interest rate [%] |
| Rext | Outdoor thermal resistance coefficient [m2 K/W] |
| Rint | Indoor thermal resistance coefficient [m2 K/W] |
| Rins | Thermal resistance coefficient of the insulation material [m2 K/W] |
| Rt | Thermal resistance coefficient of the brick material [m2 K/W] |
| Rw | Thermal resistance coefficient of the non-insulated wall layer [m2 K/W] |
| Rtw | Total thermal resistance coefficient of the non-insulated wall layer [m2 K/W] |
| Rtw, ins | Total thermal resistance coefficient of the insulated wall layer |
| x | Insulation thickness [m] |
| xopt | Optimum insulation thickness [m] |
| k | Thermal conductivity of the insulation material [W/mK] |
| ŋ | Efficiency of burning system |
| D | Thickness [m] |
| M | Molecular weight of the fuel [kg/k mol] |
| MCO2 | Molecular weight of CO2 [kg CO2/kg fuel] |
| MSO2 | Molecular weight of SO2 [kg SO2/kg fuel] |
| mfa | Yearly energy cost of heating per unit field [TRY/year] |
| my | Yearly fuel consumption [kg/year] |
| T0 | Daily temperature [°C] |
| Tb | Base temperature [°C] |
References
- Balo, F. Energy and economic analyses of insulated exterior walls for four different city in Turkey. Energy Educ. Sci. Technol. Part A Energy Sci. Res. 2011, 26, 175–188. [Google Scholar]
- Regulation on Heat in Buildings; Ministry of Public Works and Housing: Ankara, Turkey, 2000.
- TS 825; Thermal İnsulation Requirements for Buildings. Turkish Standard Institute (TSE). Ministry of Public Works and Housing: Ankara, Turkey, 2008.
- TS 825; Thermal İnsulation Requirements for Buildings. Turkish Standard Institute (TSE). Ministry of Public Works and Housing: Ankara, Turkey, 2013.
- TS 825; Thermal İnsulation Requirements for Buildings, TS 825 Thermal Insulation Standard. Ministry of Public Works and Housing: Ankara, Turkey, 2000.
- Kaygusuz, K.; Kaygusuz, A. Energy and sustainable development in Turkey. Part I: Energy utilization and sustainability. Energy Sources 2002, 24, 483–498. [Google Scholar] [CrossRef]
- Abdullah, Y.; Gurlek, G.; Erkek, M.; Ozbalta, N. Economical and environmental analyses of thermal insulation thickness in buildings. J. Therm. Sci. Technol. 2008, 28, 25–34. [Google Scholar]
- Kaynakli, O.; Kaynakli, F. Determination of Optimum Thermal Insulation Thicknesses for External Walls Considering the Heating, Cooling and Annual Energy Requirement. Uludağ Univ. J. Fac. Eng. 2016, 21, 227–242. [Google Scholar] [CrossRef]
- Kon, O. Determination of optimum insulation thicknesses using economical analyse for exterior walls of buildings with different masses. Int. J. Optim. Control. Theor. Appl. (IJOCTA) 2017, 7, 149–157. [Google Scholar] [CrossRef]
- Comakli, K.; Yuksel, B. Optimum Insulation Thickness of External Walls for Energy Saving. Appl. Therm. Eng. 2003, 23, 473–479. [Google Scholar] [CrossRef]
- Balo, F.; Ucar, A.; Yucel, H. Development of The Insulation Materials From Coal Fly Ash, Perlite, Clay And Linseed Oil. Ceramics-Silikaty 2010, 54, 182–191. [Google Scholar]
- Öykü, D.; Koca, A.; Acet, R.C.; Çetin, M.G.; Gemici, Z. A study on optimum insulation thickness in walls and energy savings based on degree day approach for 3 different demo-sites in Europe. In Proceedings of the International Conference CISBAT 2015 Future Buildings and Districts Sustainability from Nano to Urban Scale, Lausanne, Switzerland, 9–11 September 2015; pp. 155–160. [Google Scholar]
- Thermal Insulation Benefits. Available online: https://www.teknopanel.com/en-us/product-detail/thermal-insulation-in-buildings-thermal-insulation-benefits (accessed on 31 July 2021).
- Cenker, A.; Atikol, U. Optimum Insulation Thickness for the Exterior Walls of Buildings in Turkey Based on Different Materials, Energy Sources and Climate Regions. Int. J. Eng. Technol.-IJET 2017, 3, 72–82. [Google Scholar]
- Nematchoua Kameni, M.; Ricciardi, P.; Reiter, S.; Yvon, A. A comparative study on optimum insulation thickness of walls and energy savings in equatorial and tropical climate. Int. J. Sustain. Built Environ. 2017, 6, 170–182. [Google Scholar] [CrossRef]
- Altan, D.Ö.; Ozturk, H.K.; Atalay, Ö.; Acar, Ş.G.; Ulu, E.Y. The impact of optimum insulation thickness of external walls to energy saving and emissions of CO2 and SO2 for Turkey different climate regions. Energy Power Eng. 2016, 8, 327–348. [Google Scholar]
- Alsayed, M.F.; Tayeh, R.A. Life cycle cost analysis for determining optimal insulation thickness in Palestinian buildings. Build Eng. 2019, 22, 101–112. [Google Scholar] [CrossRef]
- Hasan, A. Optimizing insulation thickness for buildings using life cycle cost. Appl. Energy 1999, 63, 115–124. [Google Scholar] [CrossRef]
- Khalid, E.; Younis, O.; Hamdan, A.M.; Hussein, A.K. A study on energy performance and optimum thickness of thermal insulation for building in different climatic regions in Sudan. J. Adv. Res. Fluid Mech. 2020, 73, 146–162. [Google Scholar]
- Axaopoulos, I.; Axaopoulos, P.; Gelegenis, J.; Fylladitakis, E.D. Optimum external wall insulation thickness considering the annual CO2 emissions. J. Build Phys. 2019, 42, 527–544. [Google Scholar] [CrossRef]
- Yu, J.; Yang, C.; Tian, L.; Liao, D. Evaluation on energy and thermal performance for residential envelopes in hot summer and cold winter zone of China. Appl. Energy 2009, 86, 1970–1985. [Google Scholar] [CrossRef]
- Ziapour, B.M.; Rahimi, M.; Yousefi Gendeshmin, M. Thermoeconomic analysis for determining optimal insulation thickness for new composite prefabricated wall block as an external wall member in buildings. J. Build Eng. 2020, 31, 101354. [Google Scholar] [CrossRef]
- Fohagui, V.; Cyrille, F.; Ghislain, T. The determination of the most economical combination between external wall and the optimum insulation material in Cameroonian’s buildings. J. Build. Eng. 2017, 9, 155–163. [Google Scholar]
- Shekarchian, M.; Moghavvemi, M.; Rismanchi, B.; Mahlia, T.; Olofsson, T. The cost benefit analysis and potential emission reduction evaluation of applying wall insulation for buildings in Malaysia. Renew. Sustain. Energy Rev. 2012, 16, 4708–4718. [Google Scholar] [CrossRef]
- Tzoulis, T.; Kontoleon, K. Thermal behaviour of concrete walls around all cardinal orientations and optimal thickness of insulation from an economic point of view. Procedia Environ. Sci. 2017, 38, 381–388. [Google Scholar] [CrossRef]
- Bolatturk, A. Optimum insulation thickness for building walls with respect to cooling and heating degree-hours in the warmest zone of Turkey. Build Environ. 2008, 43, 1055–1064. [Google Scholar] [CrossRef]
- Farhanieh, B.; Sattari, S. Simulation of energy saving in Iranian buildings using integrative modelling for insulation. Renew. Energy 2006, 31, 417–425. [Google Scholar] [CrossRef]
- Comakli, K.; Yuksel, B. Environmental impact of thermal insulation thickness in buildings. Appl. Therm. Eng. 2004, 24, 933–940. [Google Scholar] [CrossRef]
- Huanga, H.; Zhoub, Y.; Huanga, R.; Wua, H.; Sunc, Y.; Huangd, G.; Xua, T. Optimum insulation thicknesses and energy conservation of building thermal insulation materials in Chinese zone of humid subtropical climate. Sustain. Cities Soc. 2020, 52, 1018–1140. [Google Scholar] [CrossRef]
- Daouas, N. A study on optimum insulation thickness in walls and energy savings in Tunisian buildings based on analytical calculation of cooling and heating transmission loads. Appl. Energy 2011, 88, 156–164. [Google Scholar] [CrossRef]
- Al-Khawaja, M.J. Determination and selecting the optimum thickness of insulation for buildings in hot countries by accounting for solar radiation. Appl. Therm. Eng. 2004, 24, 2601–2610. [Google Scholar] [CrossRef]
- Mohsen, M.S.; Akash, B.A. Some prospects of energy savings in buildings. Energy Convers. Manag. 2001, 42, 1307–1315. [Google Scholar] [CrossRef]
- Murgul, V.; Pukhkal, V. Saving the Architectural Appearance of the Historical Buildings due to Heat Insulation of their External Walls. Procedia Eng. 2015, 117, 891. [Google Scholar] [CrossRef] [Green Version]
- Tettey, U.; Dodoo, A.; Gustavsson, L. Prımary Energy Implıcatıons of Dıfferent Wall Insulatıon Materıals for Buıldıngs in a Cold Clımate. Energy Procedia 2014, 2014, 1204. [Google Scholar] [CrossRef]
- Zhu, P.; Huckemann, V.; Fisch, M. The optimum thickness and energy saving potential of external wall insulation in different climate zones of China. Procedia Eng. 2011, 21, 608. [Google Scholar] [CrossRef]
- Nyers, J.; Kajtar, L.; Tomić, S.; Nyers, A. Investment-savings method for energy-economic optimization ofexternal wall thermal insulation thickness. Energy Build. 2015, 86, 268–274. [Google Scholar] [CrossRef]
- Singh, H.K.; Prakash, R.; Shukla, K.K. Economic and environmental benefits of roof insulation in composite climate of India. History 2015, 1, 397–403. [Google Scholar]
- Siddique, S.; Arif, S. Optimum Insulation Thickness for Walls and Roofs for Reducing Peak Cooling Loads in Residential Buildings in Lahore. Mehran Univ. Res. J. Eng. Technol. 2016, 35, 523–532. [Google Scholar] [CrossRef]
- Hamdan, M.; Malek, M.K. Optimization of insulation thickness for building’s external wall in Jordan. In Proceedings of the International Conference on Water, Energy and Environment, Sharjah, United Arab Emirates, 28 February–2 March 2017; Available online: https://www.researchgate.net/publication/314245931 (accessed on 29 January 2023).
- Nematchoua, M.K.; Raminosoa, C.R.R.; Mamiharijaona, R.; René, T.; Orosa, J.A.; Elvis, W.; Meukam, P. Study of the economical and optimum thermal insulation thickness for buildings in a wet and hot tropical climate: Case of Cameroon. Renew. Sustain. Energy Rev. 2015, 50, 1192–1202. [Google Scholar] [CrossRef]
- Jraida, K.; Farchi, A.; Mounir, B.; Mounir, I. A study on the optimum insulation thicknesses of building walls with respect to different zones in Morocco. Int. J. Ambient. Energy 2017, 38, 550–555. [Google Scholar] [CrossRef]
- Baniassadi, A.; Sayyaadi, H. Multivariate Optimization of PCM and Insulation Layer Thickness for a Residential Building- Case Study of Iran. In Proceedings of the Sixth International Conference on Heating, Ventilation and Air-Conditioning, Tehran, Iran, 26–28 May 2015. [Google Scholar]
- Liu, X.; Chen, Y.; Ge, H.; Fazio, P.; Chen, G.; Guo, X. Determination of optimum insulation thickness for building walls with moisture transfer in hot summer and cold winter zone of China. Energy Build. 2015, 109, 361–368. [Google Scholar] [CrossRef]
- Barrau, J.; Ibañez, M.; Badia, F. Impact of the optimization criteria on the determination of the insulation thickness. Energy Build. 2014, 76, 459–469. [Google Scholar] [CrossRef]
- Derradji, L.; Imessad, K.; Amara, M.; Boudali Errebai, F. A study on residential energy requirement and the effect of the glazing on the optimum insulation thickness. Appl. Therm. Eng. 2017, 112, 975–985. [Google Scholar] [CrossRef]
- Alghoul Samah, K.; Gwesha, A.O.; Abdurrauf, M.N. The effect of electricity price on saving energy transmitted from external building walls. Energy Res. J. 2016, 7, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Marif, Y.; Hammou, M.B.; Zerrouki, M.; Belhadj, M. Thermal performance of internal and external wall insulation in existing buildings in the South of Algeria. ISESCO J. Sci. Technol. 2013, 9, 53–59. [Google Scholar]
- Sagbansua, L.; Balo, F. Ecologıcal Impact & Fınancıal Feasıbılıty of Energy Recovery (EIFFER) Model for Natural Insulatıon Materıal Optımızatıon. Energy Build. 2017, 148, 1–14. [Google Scholar]
- Antipova, E.; Boer, D.; Guillén-Gosálbez, G.; Cabeza, L.F.; Jiménez, L. Multi-objective optimization coupled with life cycle assessment for retrofitting buildings. Energy Build. 2014, 82, 92–99. [Google Scholar] [CrossRef]
- Diakaki, C.; Grigoroudis, E.; Kololotsa, D.; Kalaitzakis, K.; Stavrakakis, G. Towards a multi-objective optimization approach for improving energy efficiency in buildings. Energy Build. 2008, 40, 1747–1754. [Google Scholar] [CrossRef]
- Ascione, F.; Rodriguez-Ubinas, E.; Bianco, N.; Masi, R.F.D.; Mauro, G.M.; Vanoli, G.P. Design of the building envelope: A novel multi-objective approach for the optimization of energy performance and thermal comfort. Sustainability 2015, 7, 10809–10836. [Google Scholar] [CrossRef]
- Cengel Yunus, A. Heat Transfer: A Practical Approach, 2nd ed.; McGrawHill: Boston, MA, USA, 2003. [Google Scholar]
- Dombayci, O.A. The environmental impact of optimum insulation thickness for external walls of buildings. Build Environ. 2007, 42, 3855–3859. [Google Scholar] [CrossRef]
- Onan, C. Determination of the Thermal Insulation for the Model Building Approach and the Global Effects in Turkey. Adv. Mech. Eng. 2014, 2014, 960278. [Google Scholar] [CrossRef]
- Gürel, A.; Daşdemir, A. Determination of Optimum Insulation Thickness for Heating and Cooling Loads in Four Different Climate Regions of Turkey. Erciyes Univ. J. Sci. Inst. 2011, 27, 346–352. [Google Scholar]
- Bolatturk, A. Determination of optimum insulation thickness for building walls with respect to various fuels and climate zones in Turkey. Appl. Therm. Eng. 2006, 26, 1301–1309. [Google Scholar] [CrossRef]
- Dombayci, O.A.; Golcu, M.; Pancar, Y. Optimization of insulation thickness for external walls using different energy-sources. Appl. Energy 2006, 83, 921–928. [Google Scholar] [CrossRef]
- Kaynakli, O. A study on residential heating energy requirement and optimum insulation thickness. Renew. Energy 2008, 33, 1164–1172. [Google Scholar] [CrossRef]
- Sisman, N.; Kahya, E.; Aras, N.; Aras, H. Determination of optimum insulation thicknesses of the external walls and roof (ceiling) for Turkey’s different degree-day regions. Energy Policy 2007, 35, 5151–5155. [Google Scholar] [CrossRef]
- Ucar, A.; Balo, F. Effect of fuel type on the optimum thickness of selected insulation materials for the four different climatic regions of Turkey. Appl. Energy 2009, 86, 730–736. [Google Scholar] [CrossRef]
- Ucar, A.; Balo, F. Determination of the energy savings and the optimum insulation thickness in the four different insulated exterior walls. Renew. Energy 2010, 35, 88–94. [Google Scholar] [CrossRef]
- Kallioğlu, M.A.; Ercan, U.; Avcı, A.S.; Fidan, C.; Karakaya, H. Empirical modeling between degree days and optimum insulation thickness for external wall. Energy Source Part A 2019, 42, 1–21. [Google Scholar] [CrossRef]
- Balo, F. Castor Oil-Based Building Materials Reinforced with Fly Ash, Clay, Expanded Perlite and Pumice Powder. Ceramics-Silikaty 2011, 55, 280–293. [Google Scholar]
- D’Agostino, D.; de’Rossi, F.; Marigliano, M.; Marino, C.; Minichiello, F. Evaluation of the optimal thermal insulation thickness for an office building in different climates by means of the basic and modified “cost-optimal” methodology. Build Eng. 2019, 24, 100743. [Google Scholar] [CrossRef]
- U-değeri / Yalitim Ölçümü. Available online: https://www.onurenerji.com.tr/olcumler/isi-yalitim-olcumu-isil-gecirgenlik-u-degeri-katsayisi/ (accessed on 31 July 2021).
- Gustafsson, S. Optimisation of Insulation Measures on Existing Buildings. Energy Build. 2000, 33, 49–55. [Google Scholar] [CrossRef]
- Doğal Gaz Piyasası Tarifeler Listesi. Available online: https://www.epdk.gov.tr/Detay/Icerik/3-0-96/tarifeler (accessed on 1 August 2021).
- National Energy Conservation Center. The Principles of Energy Management in Industry; Ministry of Public Works and Housing: Ankara, Turkey, 2006. [Google Scholar]
- Ucar, A.; Inalli, M.; Balo, F. Application of three different methods for determination of optimum insulation thickness in external walls. Environ. Prog. Sustain. Energy 2011, 30, 709–719. [Google Scholar] [CrossRef]
- Ucar, A.; Balo, F. Determination of Environmental Impact and Optimum Thickness of Insulation for Building Walls. Environ. Prog. Sustain. Energy 2011, 30, 113–122. [Google Scholar] [CrossRef]
- Aydin, N.; Biyikoglu, A. Determination of optimum insulation thickness by life cycle cost analysis for residential buildings in Turkey. Sci. Technol. Built Environ. 2021, 27, 2–13. [Google Scholar] [CrossRef]
- Altun, A.F. Determination of Optimum Building Envelope Parameters of a Room concerning Window-to-Wall Ratio, Orientation, Insulation Thickness and Window Type. Buildings 2022, 12, 383. [Google Scholar] [CrossRef]
- Yuan, J.; Farnham, C.; Emura, K. Optimum insulation thickness for building exterior walls in 32 regions of China to save energy and reduce CO2 emissions. Sustainability 2017, 9, 1711. [Google Scholar] [CrossRef]
- Yanga, C.; Choi, J.-H. Energy Use Intensity Estimation Method Based on Façade Features, International Conference on Sustainable Design, Engineering and Construction. Procedia Eng. 2015, 118, 842–852. [Google Scholar] [CrossRef] [Green Version]


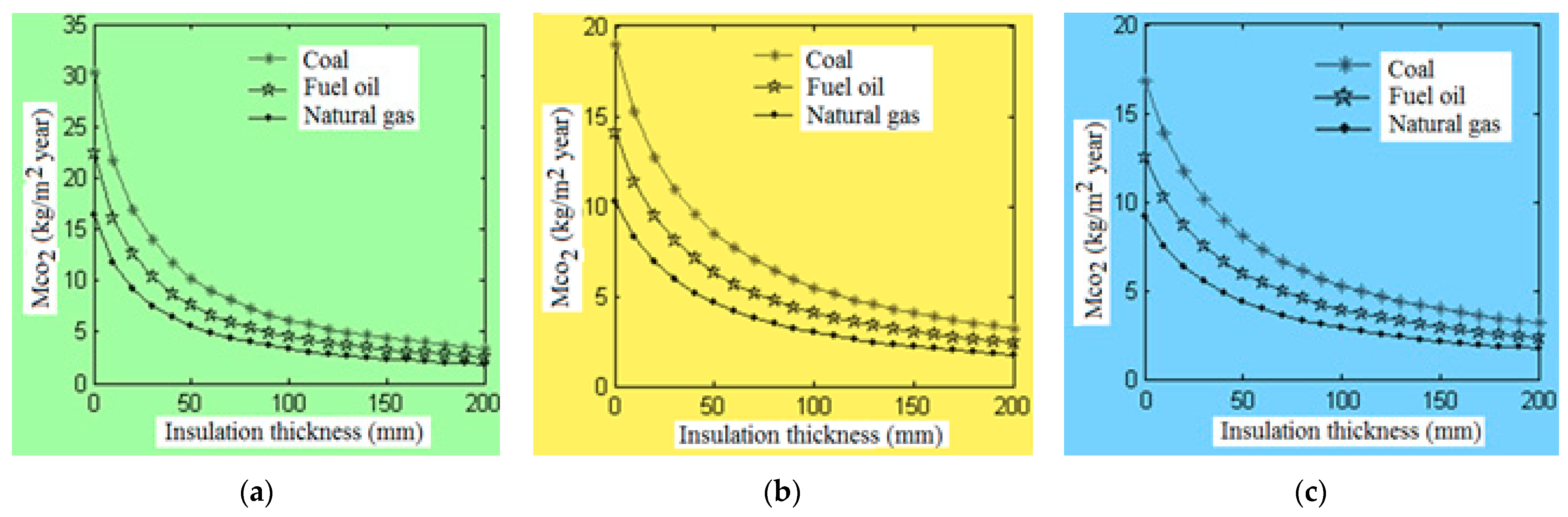

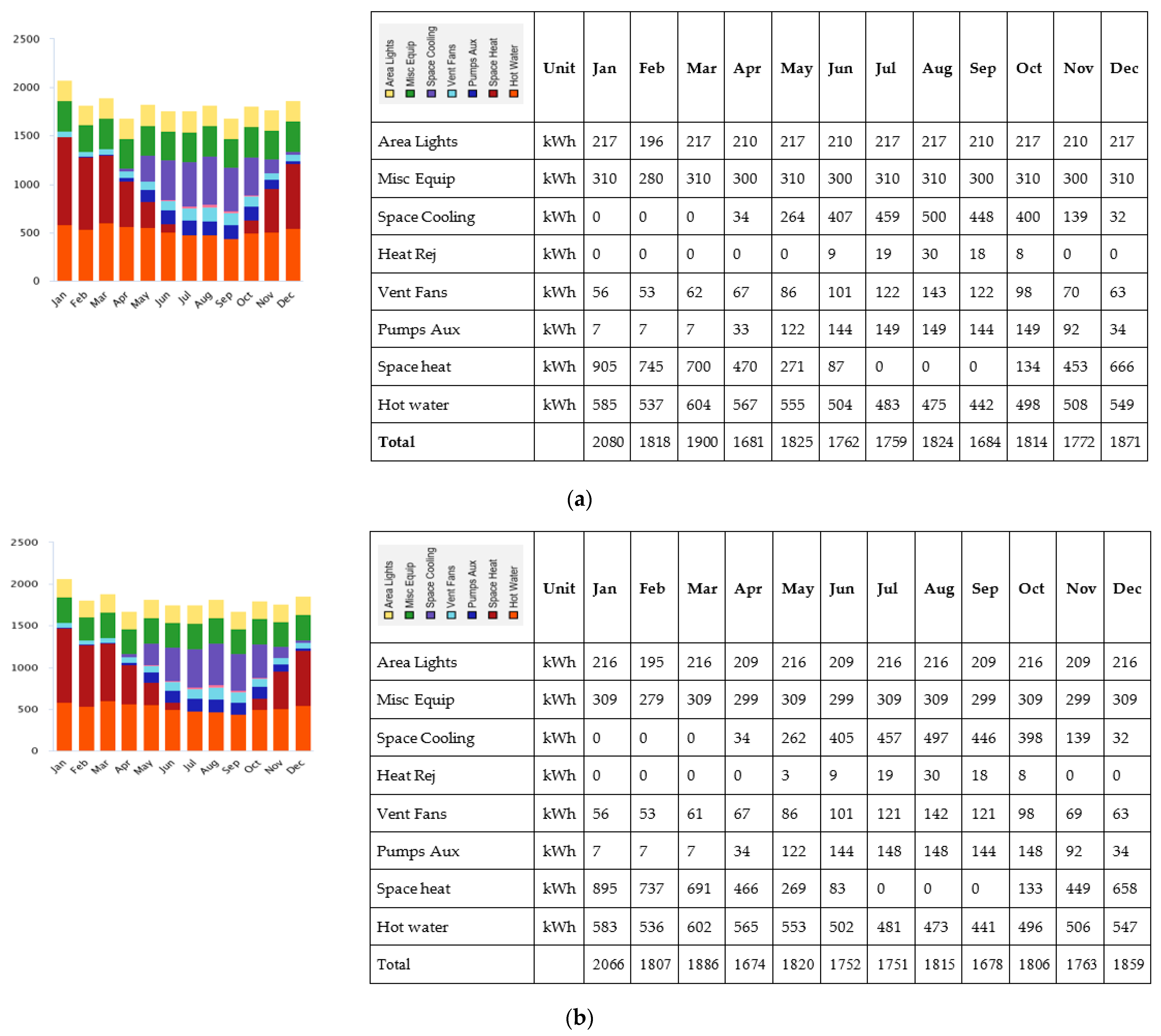

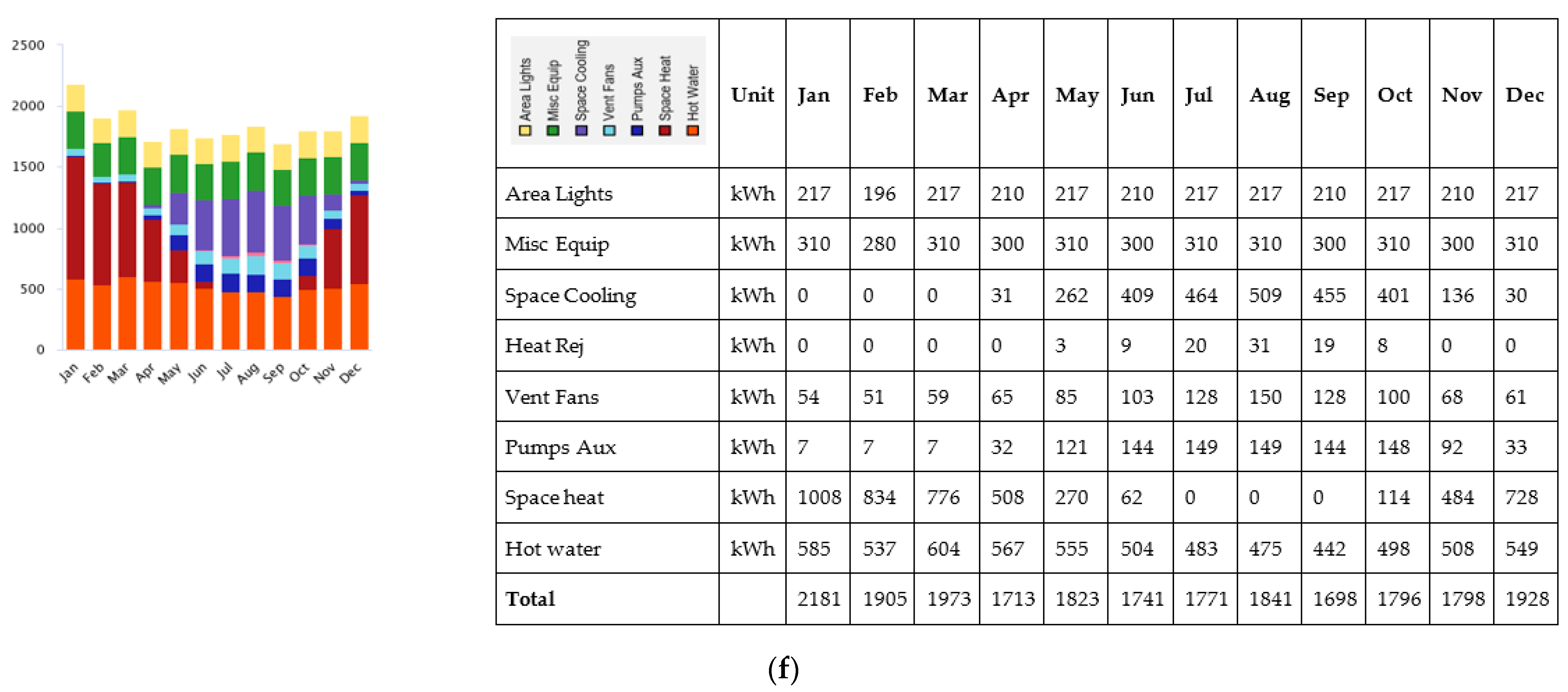
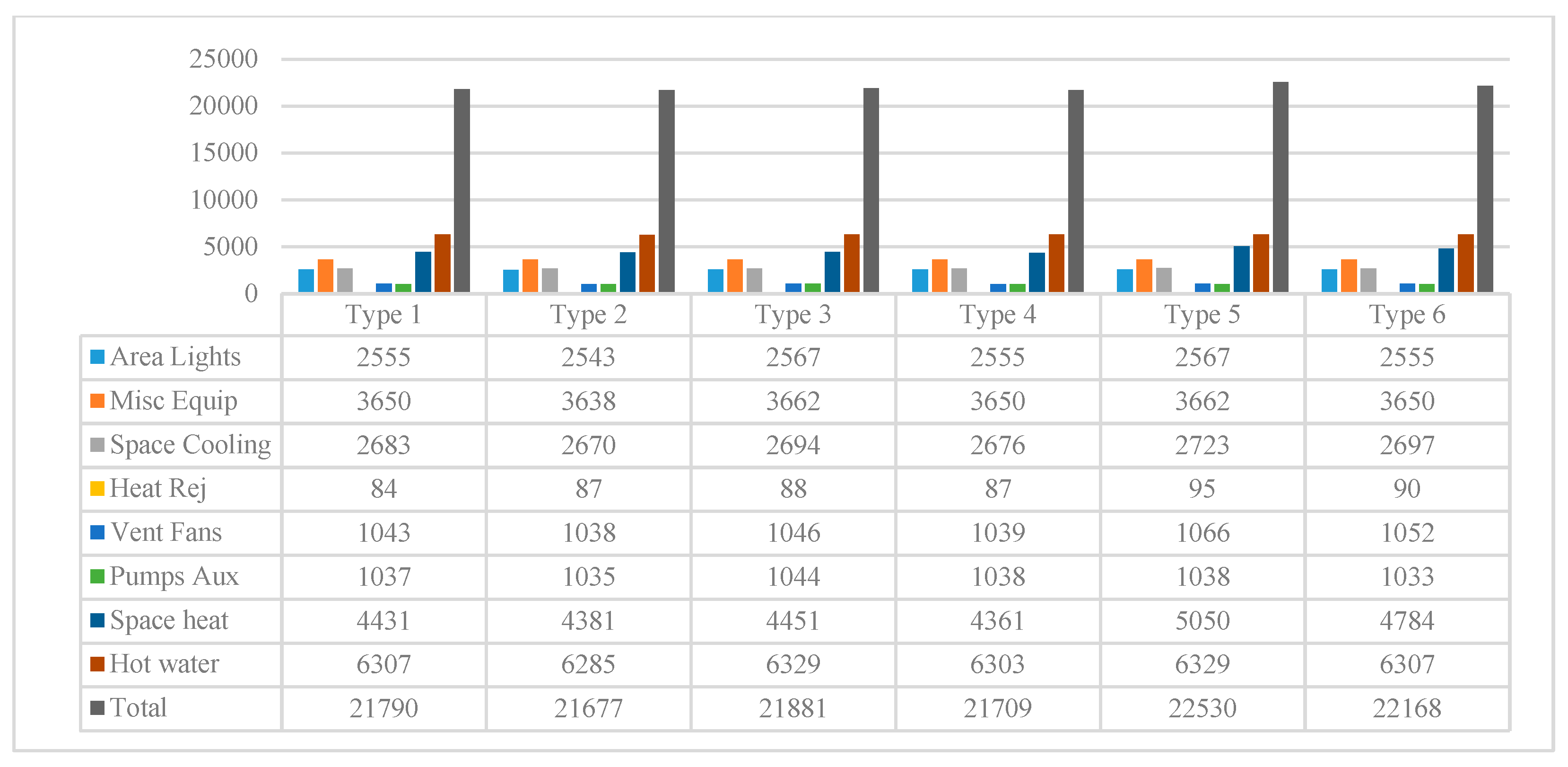
| Authors | Fuel Type | City in Turkey | Methodology | Insulation Material | Opt. Insulation Thickness |
|---|---|---|---|---|---|
| Yüksel and Comaklı [28] | Fuel oil | Erzurum | - | Styrofoam | 0.10 m calculated |
| Dombaycı [53] | Coal | Denizli | - | Expanded polystyrene | 0.095 m calculated |
| Onan [54] | Natural gas | İstanbul | P1–P2 | EPS | 0.0525 cm calculated |
| Gürel and Daşdemir [55] | Fuel oil, natural gas | Aydın, Edirne, Malatya and Sivas | LCC | EPS, XPS | 0.036–0.10 m calculated |
| Bolatturk [56] | LPG, electricity, fuel oil, coal, natural gas | Four cities for each of DD zones in Turkey (in total, 16 cities) | LCC | Polystyrene | For heating, they change in a broad range (between 0.019 and 0.172 m) relying on provinces and utilized energy source type |
| Dombayci et al. [57] | LPG, electricity, fuel oil, coal, natural gas | Denizli | LCC | Rock wool, Expanded polystyrene | For EPS, 0.259–0.076 m depending on fuel type For rock wool, 0.138–0.032 m depending on fuel type |
| Bolatturk [26] | For cooling, electricity For heating, natural gas | Mersin, Izmir, Iskenderun, Hatay, Antalya, Adana, Aydin, | P1–P2 | Extruded polystyrene | 0.016–0.027 m for HDHs and 0.032–0.038 m for CDHs |
| Yuksel and Comakli [10] | Coal | Erzincan Kars, Erzurum | LCC | Styrofoam | 0.085 m, 0.107 m, 0.105 m |
| Kaynakli [58] | LPG, fuel oil, coal, natural gas, electricity, | Bursa | Rock wool (for basement), fiberglass (for external walls and for ceiling) | 0.124 m and 0.053 m depending on fuel type | |
| Sisman et al. [59] | Coal | Erzurum, Izmir, Eskisehir, Bursa | LCC | Rock wool | 0.033, 0.047, 0.061, and 0.080 m (for walls) |
| Ucar and Balo [60] | LPG, natural gas, electricity, fuel oil, coal, | Elazig, Kocaeli, Agri, Aydin | P1–P2 | Extr. polystyrene, foamboard 3500, fiberglass, foamboard 1500 | 0.0764–0.0106 m depending on fuel type and city |
| Ucar and Balo [61] | Bitlis, Mersin, Elazig, Sanliurfa, | P1–P2 | Rock wool, nil siding, expanded and extruded polystyrene | 0.01 and 0.076 depending on CDDs or HDDs, fuel type, and insulation material | |
| Kallioglu [62] | Natural gas, fuel oil, coal | Diyarbakir | EPS and XPS | 0.068 and 0.083 m calculated |
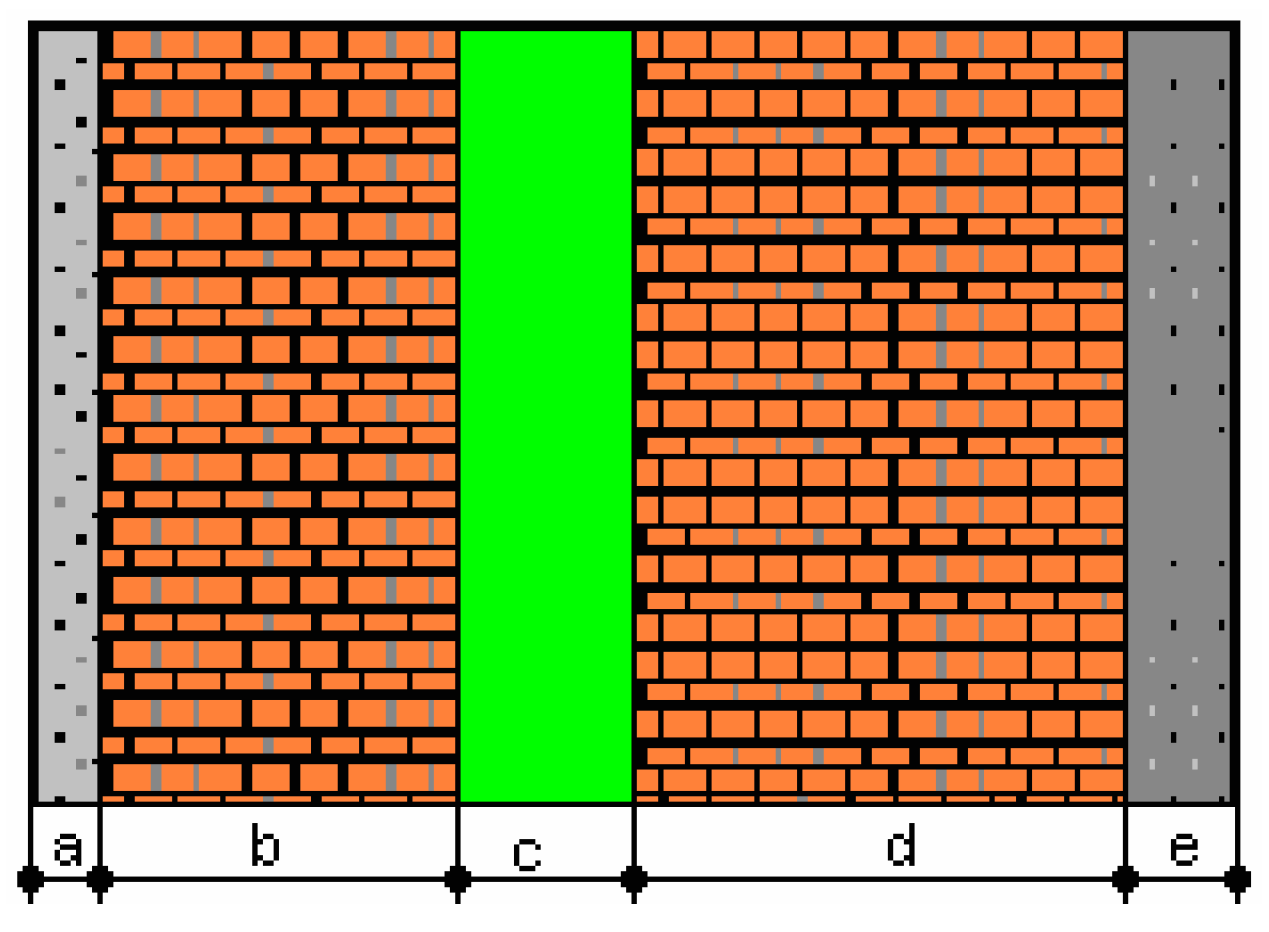
| Material | Thickness | Thermal Condictivity (W/m K) | R (m2 K/W) | |
|---|---|---|---|---|
| a | Internal plaster (lime-based) | 0.02 | 0.87 [4] | 0.023 |
| b | Construction materials (internal) | |||
| Porous light brick | 0.085 | 0.33 [4] | 0.257 | |
| Gas concrete | 0.085 | 0.18 [4] | 0.472 | |
| Bims block | 0.085 | 0.156 [4] | 0.544 | |
| Insulation materials | ||||
| c | XPS | * | 0.028 [4] | |
| Glass wool | * | 0.04 [4] | ||
| d | Construction materials (external) | |||
| Porous light brick | 0.13 | 0.33 [4] | 0.393 | |
| Gas concrete | 0.13 | 0.18 [4] | 0.722 | |
| Bims block | 0.13 | 0.156 [4] | 0.232 | |
| e | Exterior Plaster (cement-based) | 0.03 | 1.4 [4] | 0.021 |
| Energy Type | Hu × 106 (j/kg) | ηS | Unit Price [TRY/kWh] | Chemical Formula |
|---|---|---|---|---|
| Coal | 25.122 | 0.65 | 1.78 × 10−9 | |
| Natural gas | 34.542 | 0.93 | 4.19 | |
| Fuel oil | 40.614 | 0.80 | 4.36 × 10−9 | |
| Electricity | 3.6 | 0.99 | 24.01 | - |
| Building Information | |
|---|---|
| Carrier System: | Masonry Construction |
| Number of Floors: | Ground Floor |
| Story Height: | 3 m |
| Dimensions: | 10 m × 10 m |
| Gross Area: | 100 m2 |
| Net Area: | 87 m2 |
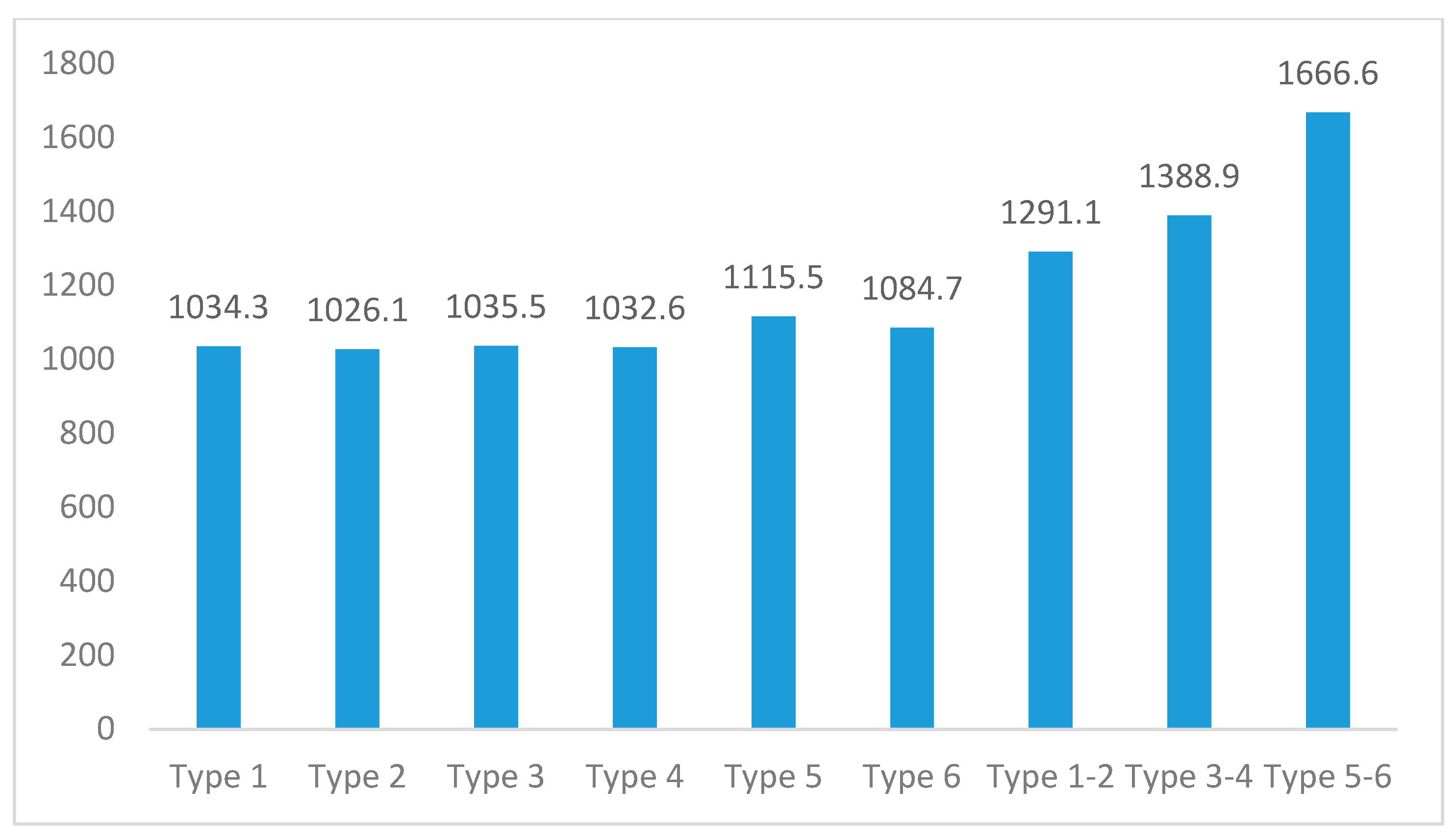
| Type 1 | Internal plaster (lime-based) | Porous light brick | XPS (0.04 m) | Porous light brick | Exterior Plaster (cement-based) |
| Type 2 | Internal plaster (lime-based) | Porous light brick | Glass wool (0.06 m) | Porous light brick | Exterior Plaster (cement-based) |
| Type 3 | Internal plaster (lime-based) | Gas concrete | XPS (0.03 m) | Gas-concrete | Exterior Plaster (cement-based) |
| Type 4 | Internal plaster (lime-based) | Gas concrete | Glass wool (0.05 m) | Gas-concrete | Exterior Plaster (cement-based) |
| Type 5 | Internal plaster (lime-based) | Bims block | XPS (0.02 m) | Bims block | Exterior Plaster (cement-based) |
| Type 6 | Internal plaster (lime-based) | Bims block | Glass wool (0.04 m) | Bims block | Exterior Plaster (cement-based) |
| Type 2 | Internal plaster (lime-based) | Porous light brick | Glass wool (0.06 m) | Porous light brick | Exterior Plaster (cement-based) |
| Optimal Insulating Thickness (m) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Extruded Polystyrene | Glass Wool | |||||||
| Coal | Natural Gas | Fuel Oil | Electricity | Coal | Natural Gas | Fuel Oil | Electricity | |
| Porous light brick | 0.05 | 0.04 | 0.07 | 0.11 | 0.08 | 0.06 | 0.10 | 0.16 |
| Gas concrete | 0.04 | 0.03 | 0.06 | 0.10 | 0.07 | 0.05 | 0.09 | 0.14 |
| Bims | 0.04 | 0.02 | 0.05 | 0.09 | 0.06 | 0.04 | 0.09 | 0.14 |
| Payback Period (Years) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Extruded Polystyrene | Glass Wool | |||||||
| Coal | Natural Gas | Fuel Oil | Electricity | Coal | Natural Gas | Fuel Oil | Electricity | |
| Porous light brick | 2.69 | 2.89 | 2.48 | 2.15 | 2.82 | 3.06 | 2.62 | 2.27 |
| Gas concrete | 3.17 | 3.38 | 2.97 | 2.63 | 3.37 | 3.60 | 3.15 | 2.78 |
| Bims | 3.29 | 3.51 | 3.09 | 2.75 | 3.51 | 3.76 | 3.28 | 2.91 |
| Energy Cost Savings (TRY/m2) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Extruded Polystyrene | Glass Wool | |||||||
| Coal | Natural Gas | Fuel Oil | Electricity | Coal | Natural Gas | Fuel Oil | Electricity | |
| Porous light brick | 8.74 | 7.66 | 9.95 | 12.84 | 9.43 | 8.11 | 10.86 | 14.12 |
| Gas concrete | 8.76 | 7.64 | 9.83 | 12.41 | 9.13 | 7.73 | 10.53 | 13.66 |
| Bims | 8.79 | 7.56 | 9.83 | 12.31 | 9.03 | 7.57 | 10.43 | 13.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balo, F.; Ulutaş, A. Energy-Performance Evaluation with Revit Analysis of Mathematical-Model-Based Optimal Insulation Thickness. Buildings 2023, 13, 408. https://doi.org/10.3390/buildings13020408
Balo F, Ulutaş A. Energy-Performance Evaluation with Revit Analysis of Mathematical-Model-Based Optimal Insulation Thickness. Buildings. 2023; 13(2):408. https://doi.org/10.3390/buildings13020408
Chicago/Turabian StyleBalo, Figen, and Alptekin Ulutaş. 2023. "Energy-Performance Evaluation with Revit Analysis of Mathematical-Model-Based Optimal Insulation Thickness" Buildings 13, no. 2: 408. https://doi.org/10.3390/buildings13020408
APA StyleBalo, F., & Ulutaş, A. (2023). Energy-Performance Evaluation with Revit Analysis of Mathematical-Model-Based Optimal Insulation Thickness. Buildings, 13(2), 408. https://doi.org/10.3390/buildings13020408






