Abstract
Headed shear studs are an essential interfacial connection for precast steel–concrete structures to ensure composite action; hence, the accurate prediction of the shear capacity of headed studs is of pivotal significance. This study first established a worldwide dataset with 428 push-out tests of headed shear studs embedded in concrete with varied strengths from 26 MPa to 200 MPa. Five advanced machine learning (ML) models and three widely used equations from design codes were comparatively employed to predict the shear resistance of the headed studs. Considering the inevitable data variation caused by material properties and load testing, the isolated forest algorithm was first used to detect the anomaly of data in the dataset. Then, the five ML models were established and trained, which exhibited higher prediction accuracy than three existing design codes that were widely used in the world. Compared with the equations from AASHTO (the one that has the best prediction accuracy among design specifications), the gradient boosting decision tree (GBDT) model showed an 80% lower root mean square error, 308% higher coefficient of determination, and 86% lower mean absolute percent error. Lastly, individual conditional expectation plots and partial dependence plots showed the relationship between the individual parameters and the predicted target based on the GBDT model. The results showed that the elastic modulus of concrete, the tensile strength of the studs, and the length–diameter ratio of the studs influenced most of the shear capacity of shear studs. Additionally, the effect of the length–diameter ratio has an upper limit which depends on the strength of the studs and concrete.
1. Introduction
Steel–concrete composite structures are efficient structural members that fully utilize the compressive strength of concrete and the tensile strength of steel in most loading scenarios [1]. Therefore, steel–concrete composite structures have been widely used in enormous buildings and bridges [2]. As steel parts are usually installed first as supports and form systems for concrete [3], steel–concrete composite structures show great potential for precast structures. For steel–concrete composite structures, the interfacial shear connection is a prerequisite to ensure the composite action between steel and concrete. Headed studs are one of the most popular and cost-effective interfacial shear connections for composite structures due to their fast installation, equal shear strength and stiffness in all directions normal to the axis of the stud, and little obstruction to the slab reinforcement ([4,5]).
Since the 1950s, numerous push-out tests have been carried out to investigate the mechanical performance of headed studs in steel–concrete composite structures under different loads and effects ([6,7,8]). Viest [6] identified three failure modes in push-out tests, including steel failures, concrete failures, and mixed failures that included the failure of both materials, and proposed the first equation for calculating the resistance of headed studs. Then, Ollgaard et al. [7] proposed an empirical equation for the shear resistance of headed studs based on the experimental tests on 48 push-out tests with headed studs embedded in both normal-weight and lightweight concrete. The equation later became the basis of the calculation equations for the design of headed stud shear connectors in many international design codes ([9,10,11]). In 1981, the first design code for steel–concrete composite structures adopted a design equation for the resistance of headed studs suggested by CEB-ECCS-FIP-IABSE [12]. In 2004, Lee and Shim [13] conducted static and fatigue tests on large-diameter headed stud connectors and found that the equations in Eurocode-4 [9] and AASHTO LRFD [10] underestimated the static and fatigue performances of large-size studs to a large extent. The following research focused on modifying the coefficients in existing design equations to achieve higher prediction accuracy [14] or developing new equations by fitting push-out tests ([15,16]). To summarize, traditional prediction equations provided limited accuracy based on parameters with physical meaning. Nevertheless, current design codes are based on limited test data and a lack of reliability beyond the range of the data. Additionally, ultra-high-performance concrete (UHPC) and high-performance concrete (HPC) have been proposed and applied to precast steel–concrete structures as a more durable and efficient solution in lieu of conventional concrete. However, studies have shown that using traditional equations, which were derived based on the experimental data of normal concrete specimens, to predict the shear capacity of headed studs in UHPC and HPC is questionable because the strength of normal concrete is much lower than that of UHPC and HPC ([16,17]). As a more efficient and accurate method to derive equations compared with physics-based equations in most cases, data-driven machine learning (ML) models have been widely used in engineering research in recent years, which can get rid of time-consuming and costly experimental tests.
ML has shown extremely high accuracy in many studies in predicting the interfacial behavior between steel and concrete, and there are many ML algorithms that have shown to be promising in modeling different civil engineering problems, namely, artificial neural network (ANN), multivariate adaptive regression splines, Gaussian process regression, minimax probability machine regression, random forest (RF), support vector machine (SVM), and least squares support vector machine (LS-SVM) available in the literature to develop models ([18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]). Esteghamati et al. [19] presented a framework to develop generalizable surrogate models to predict seismic vulnerability and environmental impacts of a cluster of buildings at a particular location and performed sensitivity assessments to evaluate the most important parameters and study assumptions. Avci-Karatas [21] presented regression methodologies to predict the resistance of headed studs by using the concepts of minimax probability machine regression and extreme ML methods. Wang et al. [25] predicted the stud shear stiffness and achieved automatic hyperparameter optimization with an auto-tuning deep forest. Mahjoubi et al. [26] presented a logic-guided neural network to predict the interfacial properties of steel–concrete composites. Additionally, accurate predictions made by ML models can serve as supplementary data, expanding the amount of data that can be exploited by empirical equations ([27,28,29]). However, most of the existing research focused on developing high-performance ML models or comparing the performance differences of several algorithms ([30,31,32,33]), which is limited by the datasets that need to extend the quantity and be updated in time, and they are still a kind of “black box” although these ML models have very high prediction accuracy. How to give explanatory analysis to these ML models with superior performance is very important, which is related to the better application of ML in engineering. Cakiroglu et al. [34] developed ensemble ML models to predict the axial compression capacity of rectangular concrete-filled steel tubular columns and the SHAP model for interpreting the ensemble learning models indicates that the side length of the cross-section has the highest impact on the predicted compressive load capacity. To quantify the contribution of each feature to the predictive ability of the model through feature importance is effective and widely used ([35,36]), but it cannot explain the complex influence of features and features on output variables. Several techniques have been developed to study the interpretability of ML models and visualize them, such as partial dependence plot (PDP) and individual conditional expectation (ICE) [37]. Setvati et al. [38] predicted the stud resistance based on six trained ML models and visualized relationships between the input variables within the predicted resistance, but the study is based on a dataset with 242 push-out specimens, which is rather few for training ML models, and no anomaly detection was performed on the dataset like most previous studies, although it is crucial in developing ML models. In comparison, this study is dedicated to establishing the largest, to the authors’ knowledge, dataset and to using isolation forests for anomaly detection to ensure prediction accuracy.
This study presents an interpretable ML method to predict the shear resistance of headed studs in steel–concrete structures. Five main contributions are made in this study: (1) a significantly larger database than used by many international design codes with 428 push-out test specimens was established; (2) an isolation forest algorithm is used to determine the presence of any anomaly in the dataset; (3) the performance of five advanced ML algorithms, namely ANN, SVM, RF, decision tree (DT), and gradient boosting decision tree (GBDT), was derived and compared; (4) three international design codes, namely GB50017–2017, Eurocode-4, and AASHTO LRFD Bridge Design Codes, were re-evaluated base on the established dataset; (5) an interpretable analysis of the GBDT model was performed by visualizing and evaluating the relationships between the characteristic parameters. The results from the present work demonstrate that interpretable ML models have a certain guiding significance and can be used as potential candidates in engineering design.
2. Physics-Based Equations
2.1. Eurocode-4
Eurocode-4 predicts the shear capacity of the headed studs based on two failure modes, namely, concrete failure and steel failure. On the basis of the research of Ollgaard et al. [7], Eurocode-4 [9] revised the equation through more push test data, together with additional rules when 3 ≤ ≤ 4 [17]:
where is the diameter of the headed stud; is the cylindrical compressive strength; is the partial factor for the design shear resistance of a headed stud, which is recommended in Eurocode-4 to have a value of 1.25; is the diameter of the stud shank; is the concrete elastic modulus; is the tensile strength of the headed studs; is a parameter related to the geometric shape of the headed stud, and is given by
where is the nominal height of the stud.
2.2. Chinese GB50017–2017 Code
According to the Chinese GB50017–2017 code [11], the capacity of headed studs themselves are the upper limit to determine the bearing capacity of the connector, and the cubic compressive strength is used to replace the cylindrical compressive strength . The design code is as follows:
where is the cross-sectional area of the headed studs; is the cubic compressive strength.
2.3. AASHTO LRFD Bridge Design Codes
In the AASHTO LRFD Bridge Design Codes [10], the resistance of the headed studs is calculated as follows:
where is the resistance coefficient of the stud, which is generally taken as 0.85 in steel–concrete composite constructions [39]. The AASHTO used the stud performance parameters to determine the upper limit of the resistance of the headed studs. The diameter of the stud, the compressive strength, and the elastic modulus of the concrete are selected as the decisive factors for the headed studs’ resistance.
3. Data
3.1. Dataset of Headed Studs Embedded in Concrete Push-Out Test Specimens
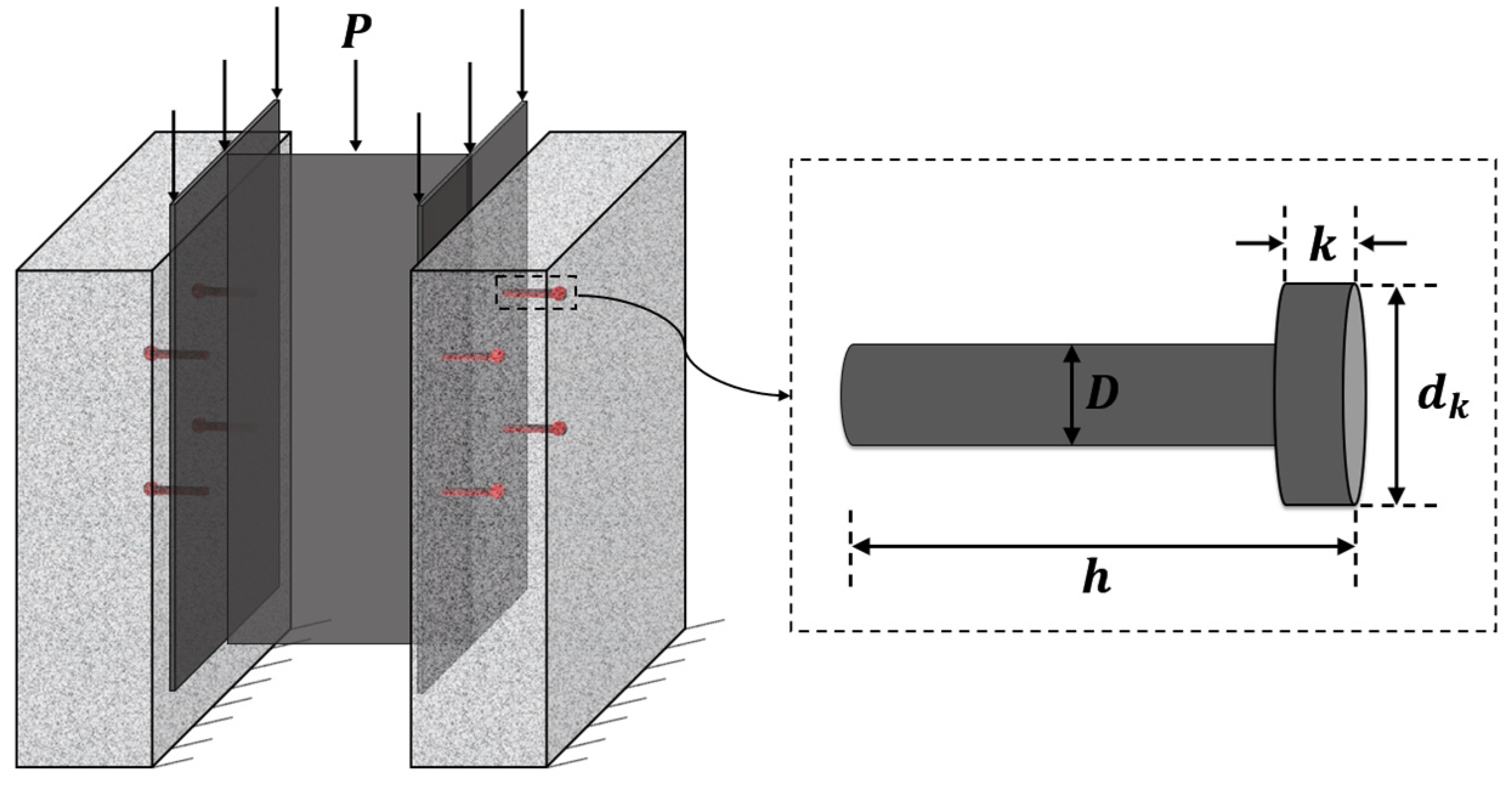
At present, beam tests and push-out tests are the most common methods to test the resistance of headed studs. Among them, the beam tests agree better with the actual loading situations but are also much more complicated than push-out tests. More importantly, the materials are more expensive, and the beam tests take much longer than push-out tests. The push-out tests are simpler and easier to implement and more convenient to carry out. As some research showed that the resistance of the headed studs obtained by the push-out test is lower than that of the beam test, which is more favored in code development [40]. Therefore, the international design codes for the resistance of shear connectors are proposed based on the push-out test results. Figure 1 shows the push-out tests; the diameter of the headed part and the shank are denoted by and , respectively. The depth of the headed part and the total length of the stud is denoted by and , respectively.
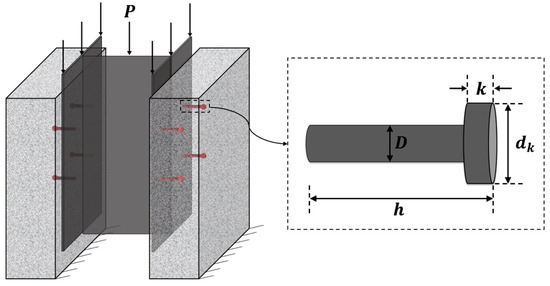
Figure 1.
Push-out test.
This study collects a total of 428 specimens from 37 references ([14,16,38,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74]) according to the following criteria:
- The test is a push-out test and uses two symmetrical concrete slabs;
- The connectors are headed studs, so specimens with bolts were discarded;
- The loading modes are monotonic loading and cyclic loading, which is closer to the actual engineering loading;
- The materials of the concrete slab are not limited to ordinary concrete, but UHPC and HPC are also collected.
In order to avoid the influence of the concrete material properties by the different sizes of the specimens, the compressive strength of concrete is uniformly converted into the compressive strength of the concrete cylinder according to GB 50010-2010 [75], and the conversion relationship is shown in Table 1. The details of the push-out test datasets are shown in Table 2.

Table 1.
Compressive strength conversion for concrete coupons with different sizes and shapes.

Table 2.
Dataset of headed studs embedded in concrete push-out test specimens.
3.2. Anomaly Detection
When we use ML algorithms to model datasets, the presence of noise and outliers tends to have a larger impact on the accuracy of the final model. The size of the dataset used in this article is 428. If there are several or more than a dozen outliers in these data, the proportion of outliers in the overall data set cannot be ignored, and the existence of outliers will affect the training of the model. At the same time, taking into account the possible human operation errors, literature hard brushing errors, or measurement errors that may occur during the experiment, it is necessary to perform anomaly detection on the established dataset to ensure the high quality of the data points of the data set and improve the final model. In this study, isolation forest [76] is used to detect and remove anomalous data.
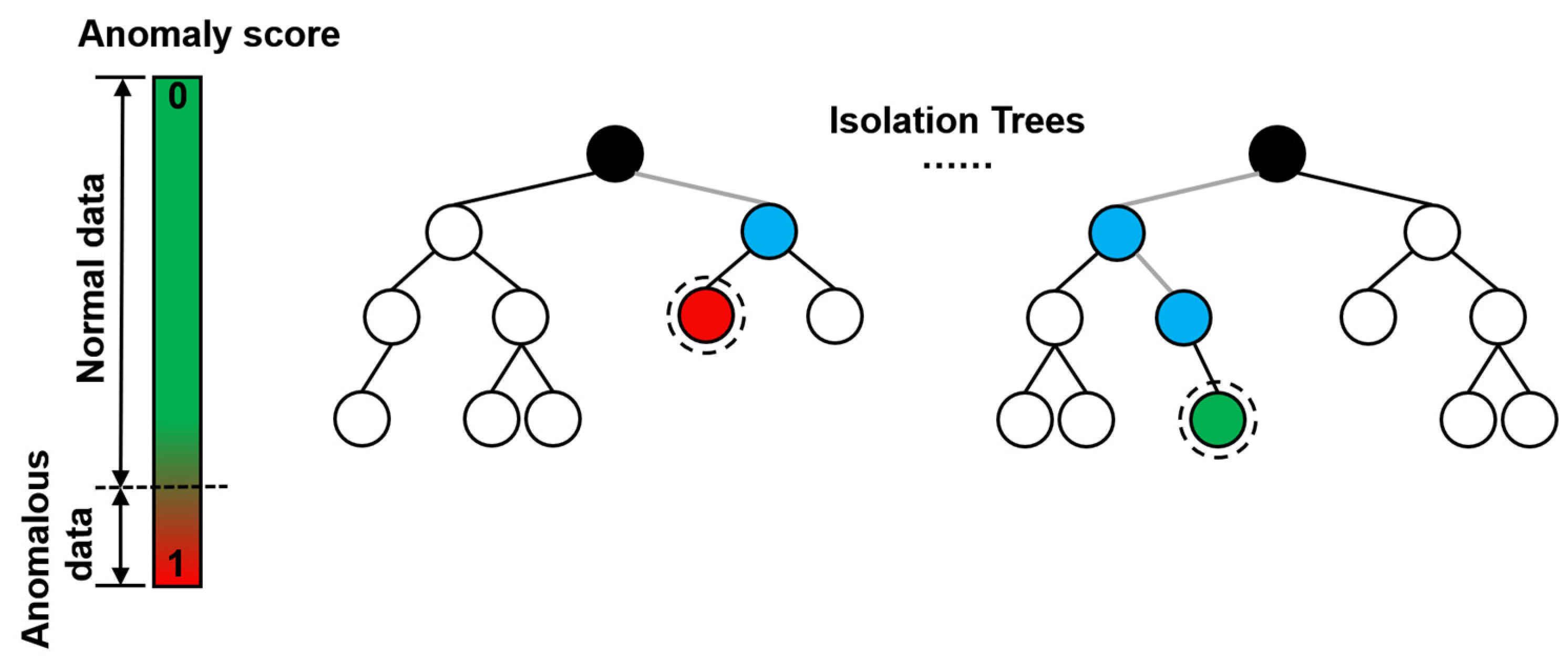
Isolation forest is an unsupervised algorithm that evaluates data through number of integrated decision trees and scores each data point in the interval of 0–1, which is shown in Figure 2. We use the following criteria to evaluate the datasets using the scores [76]:
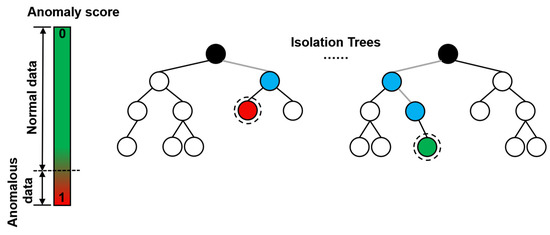
Figure 2.
Illustration of anomaly detection with isolation forest.
- 5.
- If instances return a score very close to 1, then they are highly likely to be anomalies;
- 6.
- If instances have a score much smaller than 0.5, then they are quite safe to be regarded as normal instances;
- 7.
- If all the instances return a score ≈ of 0.5, then the entire sample does not really have any distinct anomaly.
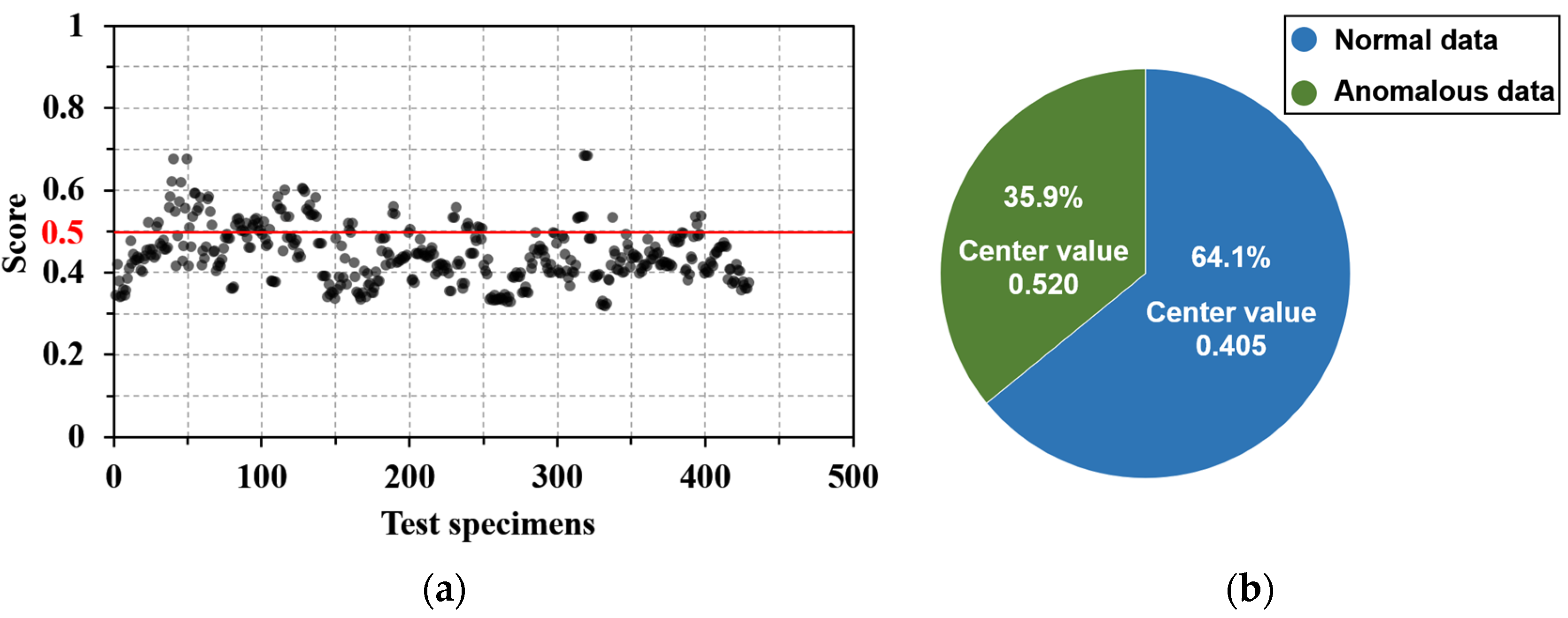
The isolation forest algorithm was implemented in the Statistics and Machine Learning Toolbox of MATLAB. The evaluation scores of all specimens are shown in Figure 3a. The minimum value of the score is 0.320, and the maximum value is 0.686, which is generally distributed around 0.5. There are no obvious outliers in the overall datasets according to the appeal evaluation criteria. In order to determine the quality of the datasets, this study uses the K-Means clustering method to analyze the score (K = 2). The specific method is to use the clustering method to calculate the center points of the two types of score and obtain the two class label centers (normal data and anomalous data), as shown in Figure 3b. The abnormal data category accounted for 35.9%, and the center value was 0.520; the anomalous data category accounted for 64.1%, and the center value was 0.405. According to No.3 of the above evaluation criteria, the difference between the central values of the two categories is very small, and both are around 0.5, especially the central value of the anomalous data category is only 0.520, which is far away from 1. Therefore, the datasets used in this study can be regarded as having no obvious abnormal data, and all 428 sets of data will be used in the following; 85% of the dataset (364 data instances) were randomly selected as the training set, and 15% of the dataset (64 data instances) were used as the test set.
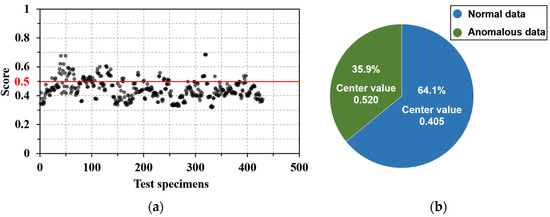
Figure 3.
Anomaly detection: (a) the score of datasets specimens and (b) K-means cluster analysis of score.
3.3. Pearson Correlation Coefficient Analysis
Data dimensions have a large impact on the efficiency and performance of ML model training. Therefore, parametric analysis of the data and consideration of dimensionality reduction is required before training ML models. Figure 4 shows the Pearson correlation coefficient analysis results for 5 parameters (, , , , and ). It is worth noting that the correlation coefficient between and is as high as 0.798, while we find that and are always put together in multinational design codes and represent the stiffness of concrete. Therefore, is used as the parameter to characterize the performance of concrete material to replace the original two parameters. The correlation coefficient between and is 0.560. Studies have shown that the length-to-diameter ratio of the stud has an impact on the shear strength [42], so this study considers the length-to-diameter ratio instead of the original two parameters and . In order to better reflect the influence of the parameters, the output representation becomes the stress form, namely . Finally, the original seven features are reduced to three. For each specimen sample, the input feature parameters of ML models are , and , the output result is .
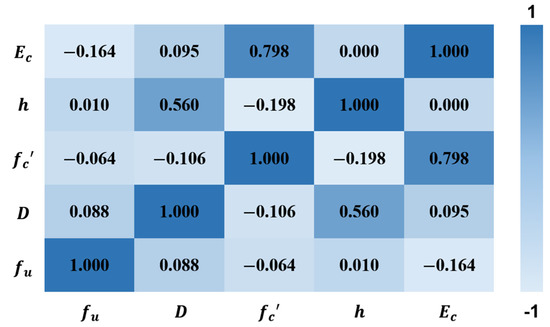
Figure 4.
Heatmap of correlation coefficient.
3.4. Performance Metrics
Three performance metrics are used to analyze the performance of the prediction model, namely, root mean square error (), coefficient of determination (), and mean absolute percent error (): is measured by is the deviation between the predicted value and the true value; is a statistical point of view that evaluates the goodness of fit of the model as a whole; is a relative error measure, which determines the scale as a percentage unit rather than a variable unit, and uses the absolute value to avoid positive and negative errors that cancel each other out. The mathematical expressions of the three indicators are as follows:
where and are the predicted and experimental values of the resistance of the studs, , respectively; and is the number of specimens considered.
4. ML Algorithms
In recent years, the ML algorithm has shown extremely strong prediction and fitting performance as a prediction method that can replace the traditional equation, and the application of ML in the field of civil engineering has shown considerable promise. This study selects five advanced and efficient ML algorithms: artificial neural network (ANN), support vector machines (SVM), decision tress (DT), random forest (RF), and gradient boosting decision tree (GBDT). These ML algorithms were chosen for this study because they are considered to be the most popular and widely used algorithms in structural engineering and have been shown to be reliable in predicting stud shear resistance ([38,77]). The five algorithms were elaborated on in reference [28]. The description of these algorithms is not duplicated in this study.
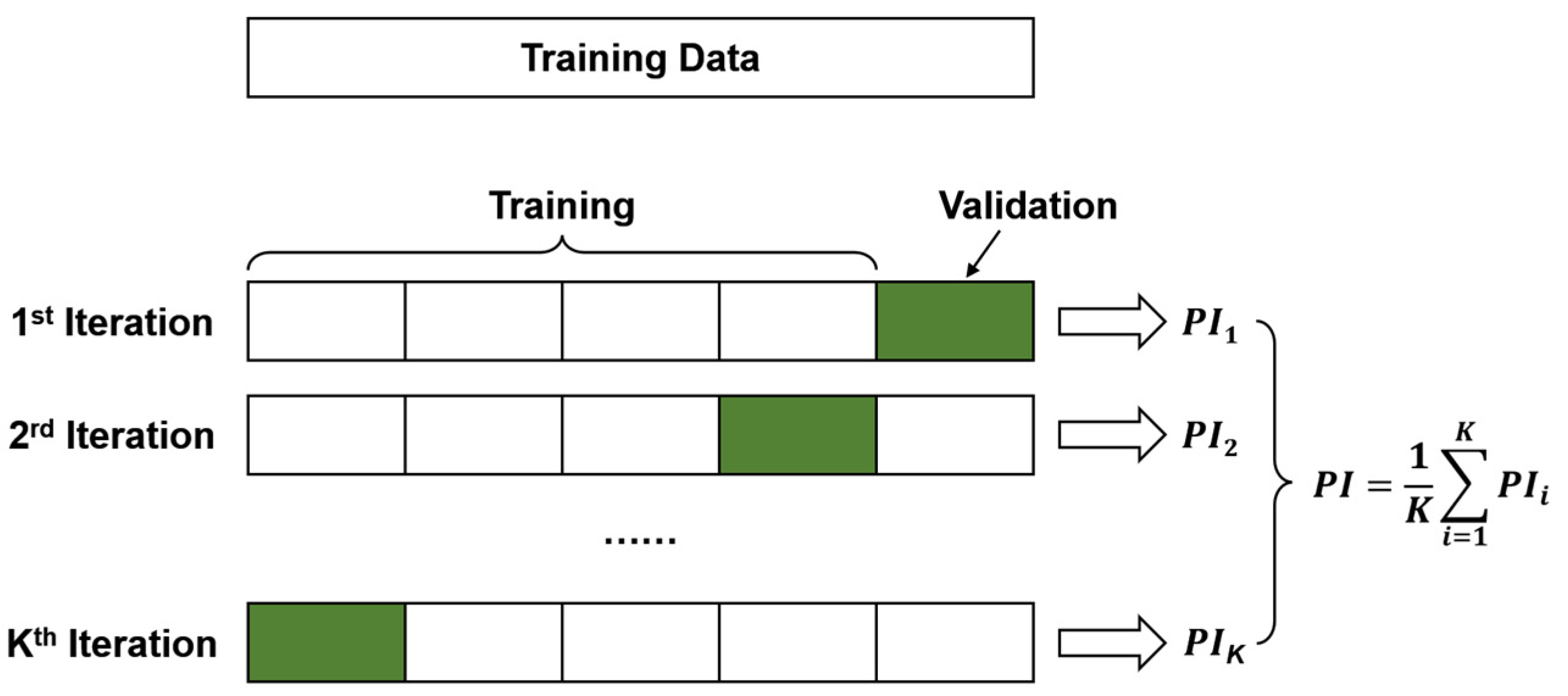
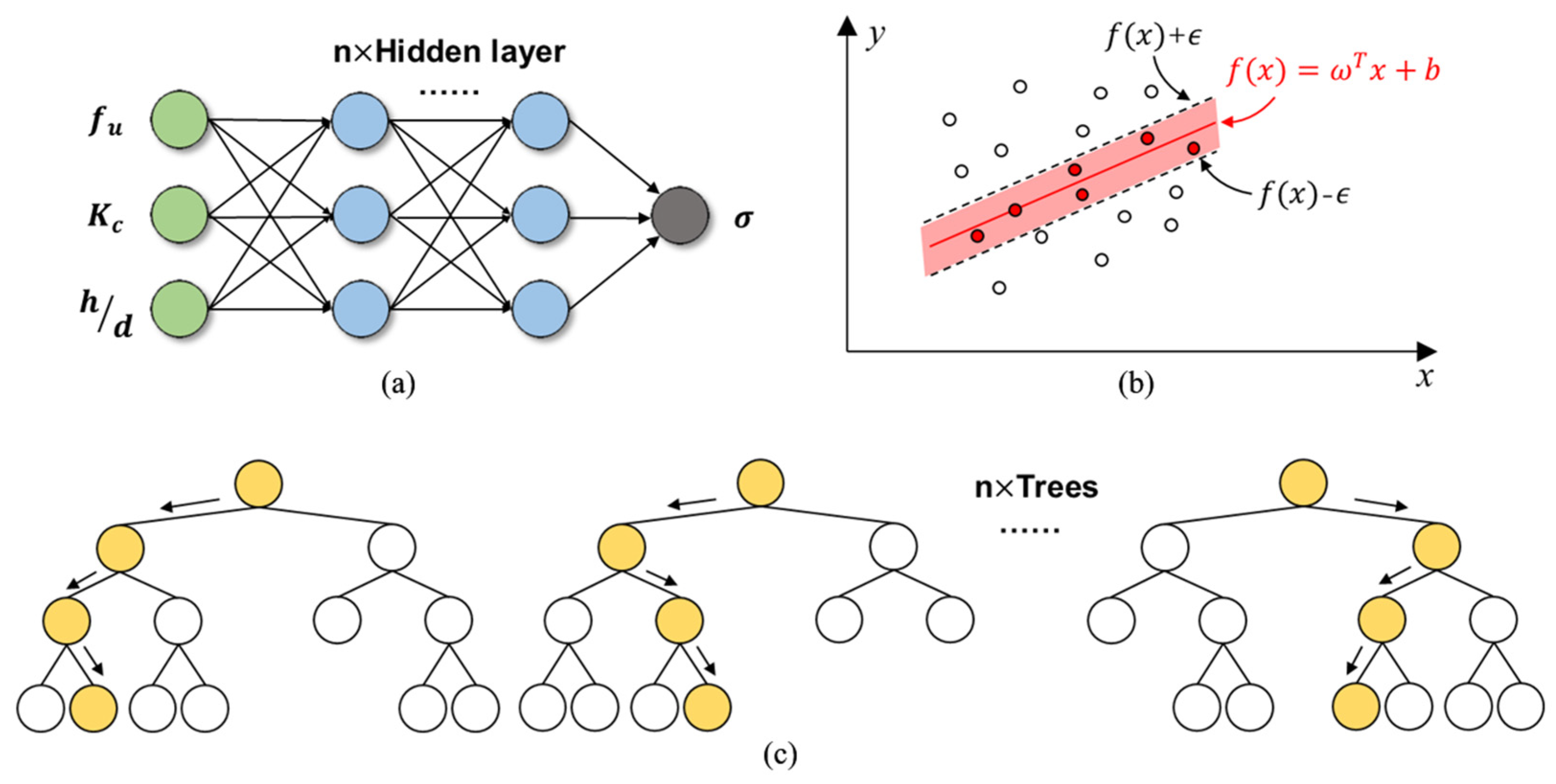
Hyperparameter optimization is a key step in developing ML models [78]. At present, the K-fold cross-validation method is mainly used to avoid overfitting in the training process. Additionally, the K-fold cross-validation method can be used together with grid search, random search, Bayesian optimization, and a manual search using the trial-and-error method to achieve hyperparameter tuning ([38,79,80,81]). K-fold cross-validation randomly splits the data into K groups of disjoint subsets of equal size, then traverses the K subsets in turn, each time using the current subset as the validation set and all the remaining samples as the training set for model training and evaluation; finally, the average value of K evaluation indicators is used as the final evaluation indicator, as shown in Figure 5. In this study, the 5-fold cross-validation was adopted to ensure that the resampled subset is large enough to represent the training dataset [38]. In the method of finding the best hyperparameter combination, the efficiency of grid search and random search is low. While Bayesian optimization can consider the previous parameter information, continuously update the prior, and has a small number of iterations and parameter adjustments. Therefore, 5-fold cross-validation combined with Bayesian optimization is selected for hyperparameter tuning in this study, as shown in Figure 6. ANN consists of an input layer (Input), a hidden layer, and an output layer (Output) [82], as shown in Figure 7a. It is found that the number of hidden layers of ANN is set to one layer, the number of hidden neurons is 60, and the activation function is the sigmoid function. Different from other ML algorithms, SVM regression is considered a nonparametric technique because it relies on kernel functions. SVM does not require the model output to be exactly the same as the real output when solving the regression problem. The loss is not calculated if the data are within the interval band, if and only if the absolute value of the gap between and is greater than . SVM optimizes the model by maximizing the width of the interval band and minimizing the total loss [83]; see Figure 7b. In this study, Radial Basis Function (RBF) is used as the kernel function of SVM, as considered that it can realize nonlinear mapping has fewer parameters which will affect the complexity of the model. In addition, this study adopts decision trees and two ensemble learning algorithms, namely RF and GBDT. DT is the base learner of RF and GBDT, which represents a mapping relationship between object attributes and object values. The DT model trained in this study has a depth of 14 layers, and the number of nodes is 14. On the basis of building a bagging ensemble with a decision tree as the base learner, RF further introduces random attribute selection in the training process of the decision tree and uses multiple decision tree models to obtain higher prediction accuracy than a single decision tree [84], see Figure 7c. The RF model consists of 10 decision trees and up to 20 layers. Unlike RF, GBDT optimizes by iterating over the residuals of the decision trees ([85,86]). In this study, we use 471 decision trees to build the GBDT model, the maximum depth is 5, and the learning rate is 0.3141. The gradient boosting decision tree algorithm was implemented in MATLAB, where more information can be found in the help menu of MATLAB [87].
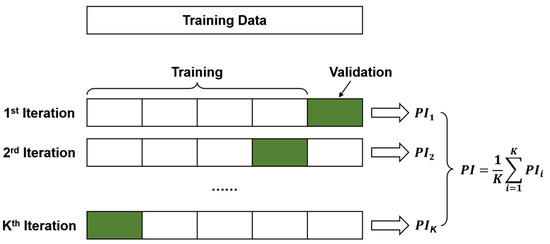
Figure 5.
K-fold cross-validation.
Figure 6.
Bayesian optimization approach.
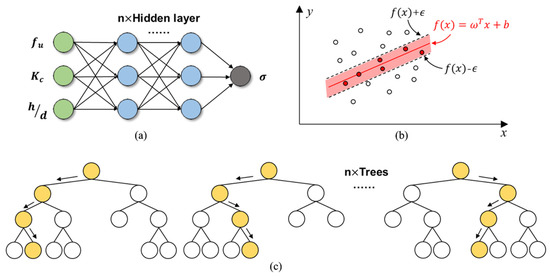
Figure 7.
Structural diagram of ML models: (a) ANN, (b) SVM, and (c) random forest.
5. Results and Discussion
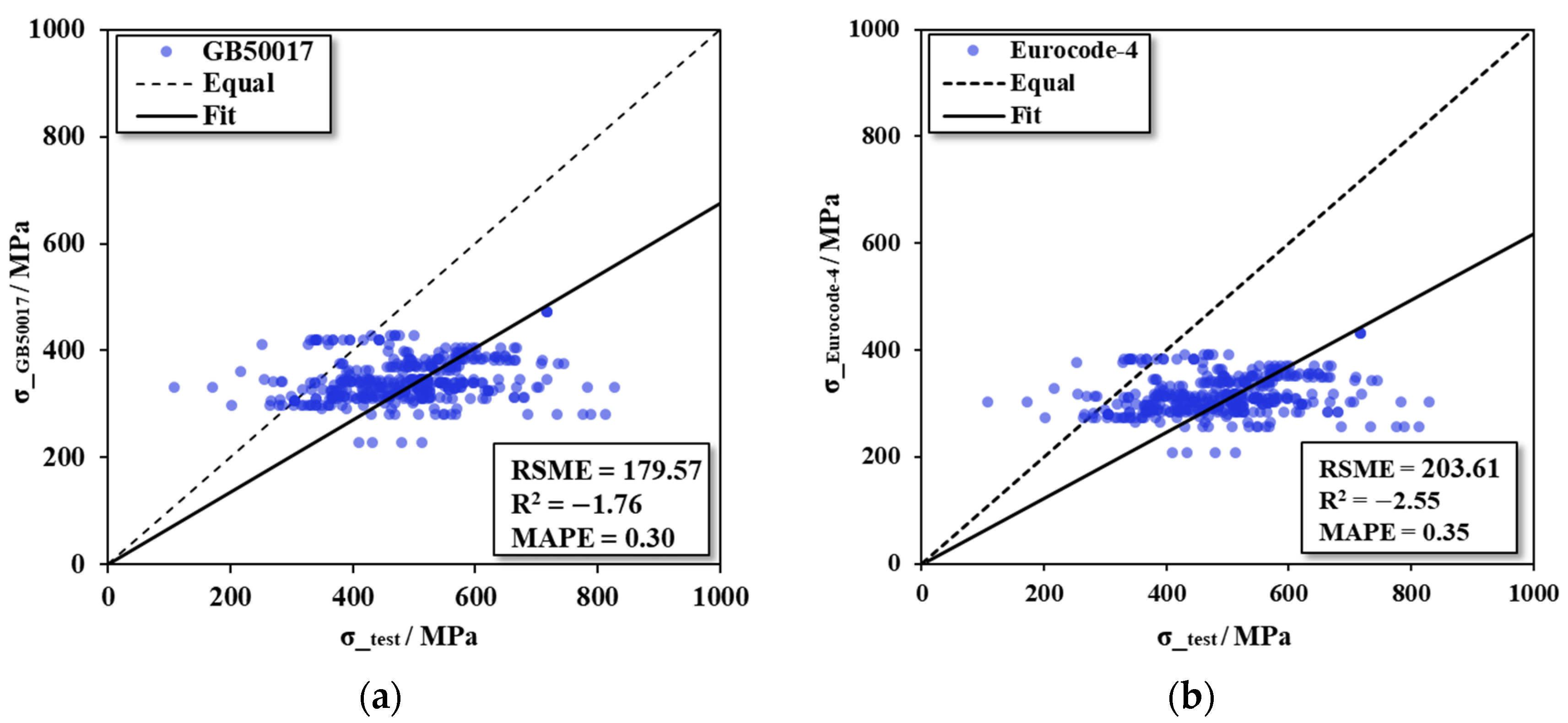
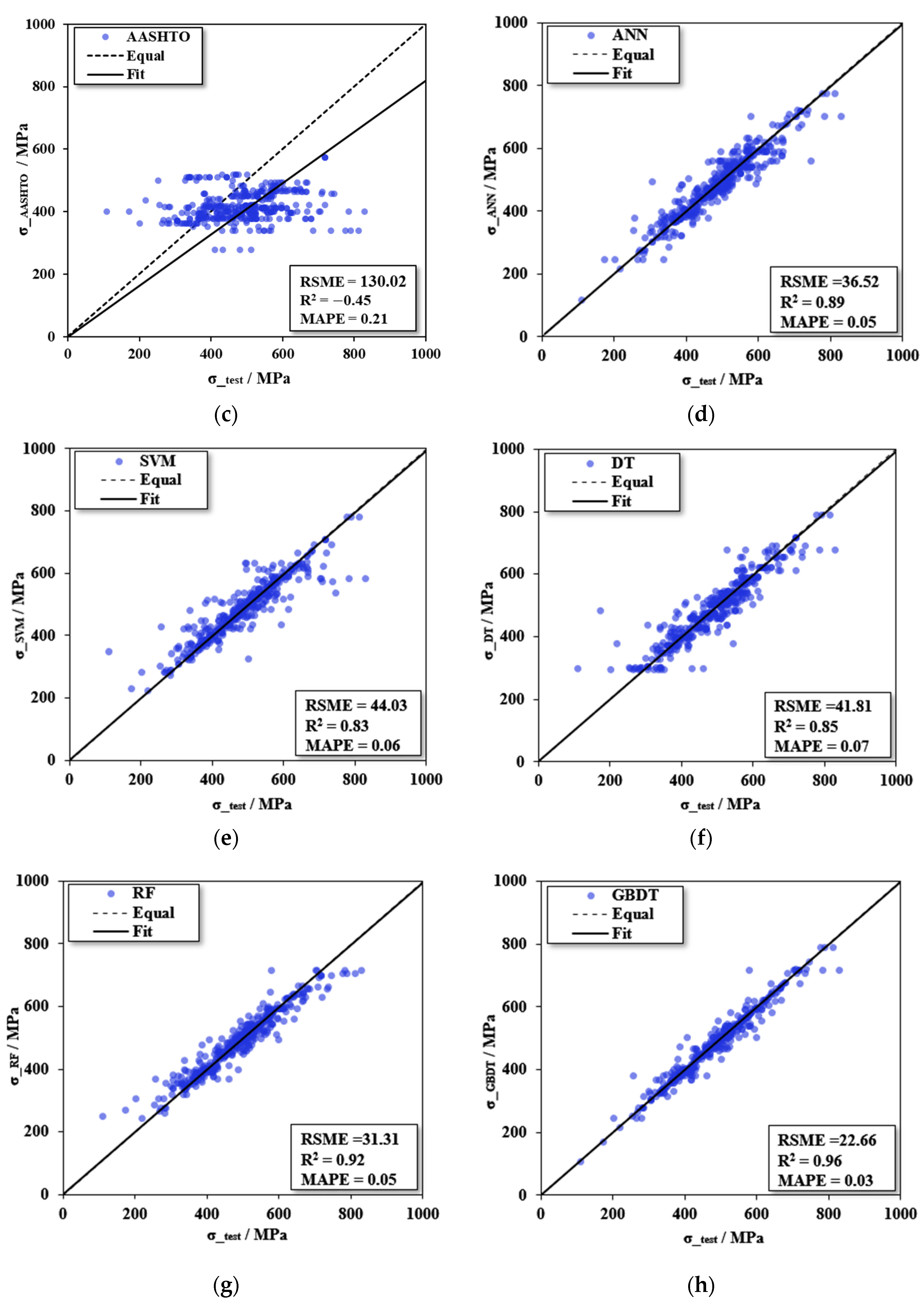
Figure 8 shows the prediction results of the collected 3 design codes and 5 ML models for 428 specimens. All points should lie on the diagonal dotted line when the predicted result is equal to the true value of the specimen sample. The vertical distance from the dotted line to a point is the prediction error of that point. The model in which the prediction points are scattered around the line indicates that the error is smaller and the prediction accuracy is higher. The black solid line represents the prediction trend of the model, and the smaller the angle between the solid line and the dotted line, the higher the prediction accuracy.
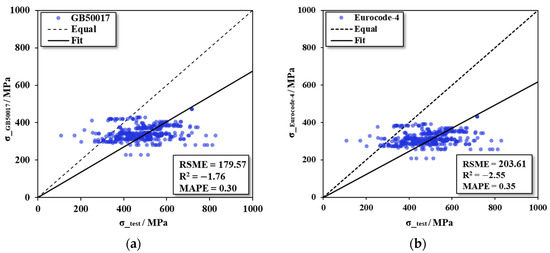
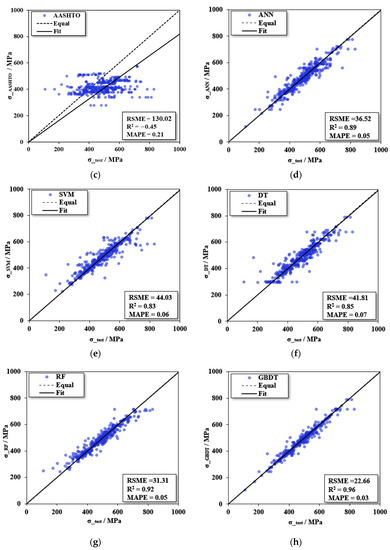
Figure 8.
Comparison between experimental results and prediction: (a) GB50017, (b) Eurocode-4, (c) AASHTO, (d) ANN, (e) SVM, (f) DT, (g) RF, and (h) GBDT.
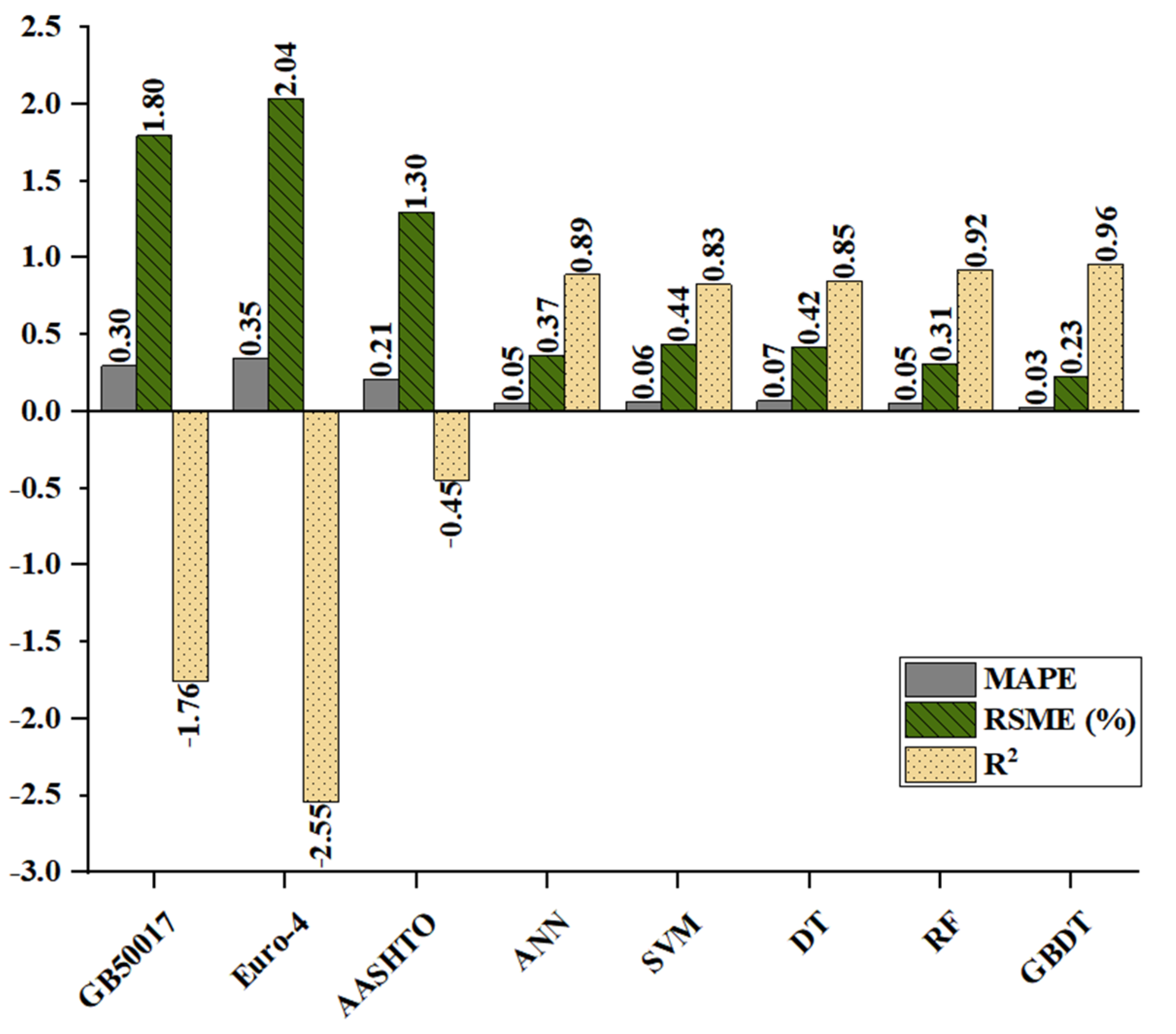
The in Figure 9 is percentageized in order to visually compare the other three performance metrics on the same order of magnitude. The results show that AASHTO has the highest accuracy among the three design codes, but the error is still very large: 30.02, 0.45, and .21, followed by GB50017: 79.57, 1.76, and .30. The error of Eurocode-4:03.61, 2.55, and .35. Most of the predicted values of Eurocode-4 and GB50017 are generally less than the test values, which is manifested in that the point is below the dotted line. It is worth noting that the of the three design codes are all negative, which means that their prediction accuracy is not as good as taking the average directly [38]. The results show that the prediction accuracy of the existing codes is insufficient, and there is a certain error compared with the real test results of the specimens. In the ML models, the GBDT model has the highest accuracy:2.66, .96, and .03, Figure 8g shows the prediction results are roughly distributed around the green line, and the error with the test results is effectively controlled, followed by the RF model:1.31, .92, and .05, while their base learner DT has lower prediction accuracy: 1.81, .85, and .07. The prediction accuracy of SVM is the lowest among ML models: 4.03, .83, and .06, but the accuracy is still much higher than the design codes. Among ML models, ensemble models that include the RF model and GBDT model have higher prediction accuracy than other types of ML models. Compared with the design codes, ML models show better prediction performance, and the error is greatly reduced. Compared with AASHTO, which with the highest accuracy, the GBDT model has an 82.57% decrease in , an increase in by 313.33%, and a decrease in by 85.71%. The comparison between ML models and the equation in AASHTO shows that the equation of the design codes is too conservative in giving accurate predictions, as most of the points lie below the diagonal dashed line. This may be because UHPC and HPC were not included in the data considered in the development of design codes. ML models can accurately predict the resistance of headed studs, and the dataset is of high quality and sufficient quantity to predict .
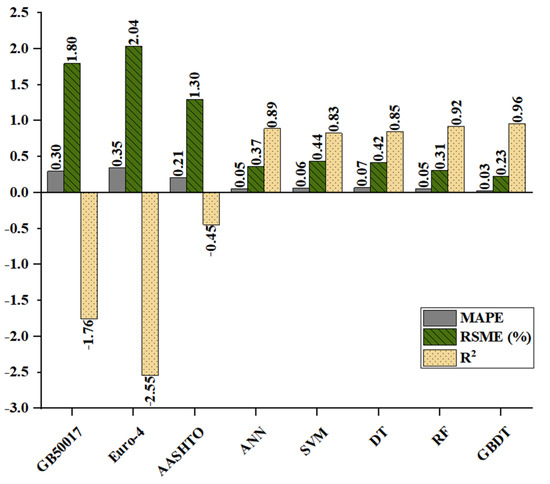
Figure 9.
Comparison between experimental and predicted results.
6. Visualization and Interpretation of GBDT Model
The ML models can predict the resistance of headed studs with high accuracy, and their accuracy is much higher than the design codes of various countries. However, we cannot fully understand the decisions of ML models from human thinking patterns, which makes most ML models a kind“of “black”box”. We can not know exactly when and why they will go wrong even though they show excellent predictive ability when dealing with large amounts of data, and it would be fatal if the error occurred in actual engineering. It is necessary to ensure that important decisions are made by humans rather than machines. The interpretability of the model is more important than the mere prediction of the results for decisions that ultimately need to be made by humans. Recently, shapley additive explanation (SHAP) [88], individual conditional expectation (ICE) plot, and partial dependence plot (PDP) [37] have shown great promise in interpreting the output of ML models and studying the importance of each factor and its interaction on the response variable, but SHAP may produce non-intuitive feature assignments. Therefore, in this study, individual conditional expectation (ICE) plots and partial dependence plots (PDP) are used to visualize and analyze the interpretability of the GBDT model, which has the highest accuracy.
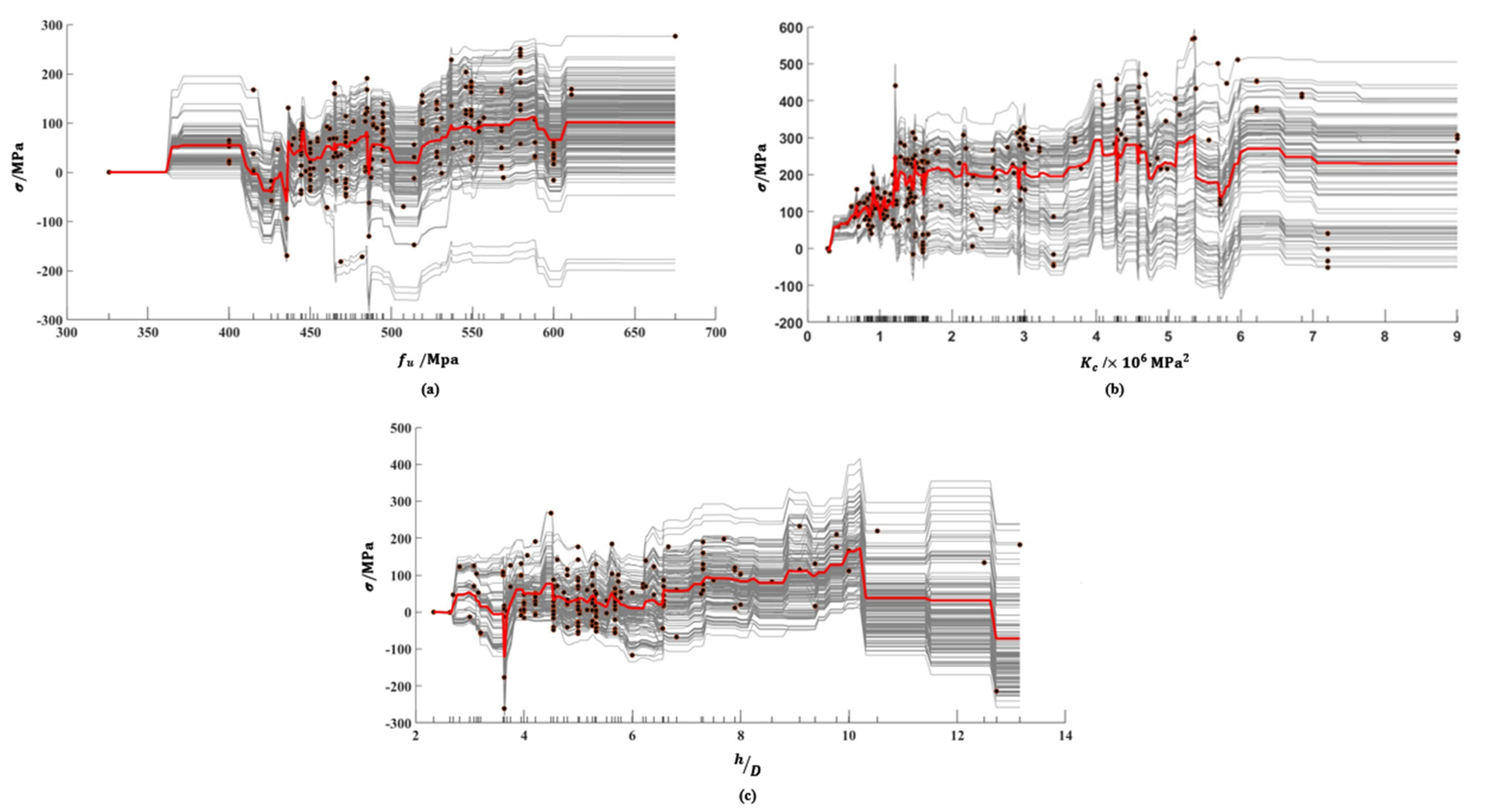
PDP can show the marginal effect of one or two features on the prediction results of ML models and visualize the relationship between the prediction target and the feature [34], such as a linear relationship, monotonic relationship, or more complex relationship, but PDP is a visualization of the average relationship between the prediction results and features. It may obscure the influence of features that are only shown on some samples as a global analysis that does not consider individuals. ICE is a refined analysis based on the PDP, showing the dependence of the prediction results on the features of each sample, eliminating the influence of non-uniform effects, and visualizing the dependence of the prediction results on the features for each sample separately, each sample one line. In order to compare the curves of each sample and observe the cumulative effect of each feature parameter, the central ICE (C-ICE) is used to fix the prediction starting point of different samples at zero. The PDP and C-ICE are computed and plotted for the GBDT model with the highest prediction accuracy and visualize the relationship between the characteristic parameters , , , and .
Figure 10 shows C-ICE plots of output for each of the three parameters , and . The dots in the figure represent each predicted value. Figure 10a show that the overall gradually increased with the increase in , but there was a brief decrease around 25 MPa. This may be due to the small amount of less than 425 MPa in the dataset, which leads to the larger prediction values of output . As shown in Figure 10b, The effect of on is similar to that of , and the trend is clearer: is positively correlated with , and the effect is obvious when is small. The growth of flattens and then starts to decline when is over . From Figure 10c, The influence of by is more obvious when the is small, reaches a peak when 0 and no longer increases significantly after that, but due to a lack of follow-up data, the trend is downward. The existence of a cap on the influence of may be because the increase in the length-to-diameter ratio of the stud will increase the stress-bearing area of the concrete, the force generated by the stud will also increase accordingly, and the degree of reduction of the stud pull-shear coupling will also increase. As the of the stud increases, the stud can be better anchored in the concrete, thereby reducing the separation phenomenon of the steel–concrete composite interface and making the stud closer to the pure shear state, which can give full play to the material properties of the stud and improve the stud resistance ([42,47,48]). However, since the shear strength of the stud will not exceed the shear strength of the material of the stud itself, there is an upper limit on the influence of the stud height on the shear strength of the stud. This is consistent, as shown in Figure 10c.
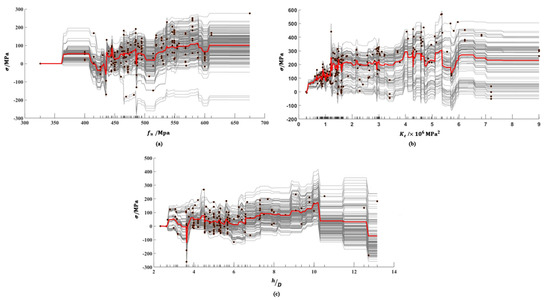
Figure 10.
C-ICE for three parameters: (a) , (b) , and (c) .
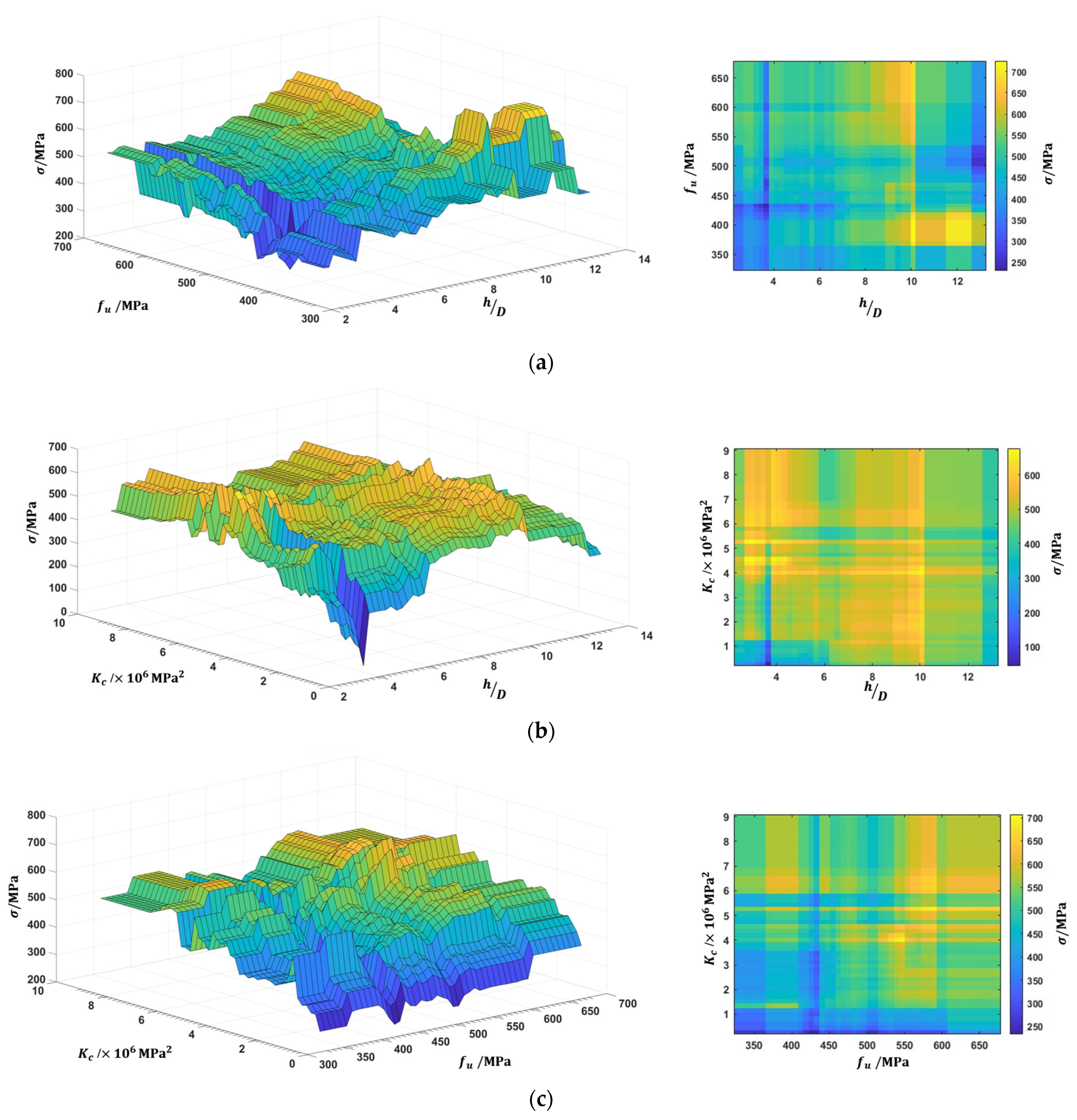
Figure 11 shows 3-D and 2-D PDP plots for three parameters, and the results show the interactions between every two features. It can be seen that, on the whole, is positively correlated with the three parameters. Figure 11a indicates the dependence of on the tensile strength of the stud and the length-to-diameter ratio of the stud, which represents the effect of the key material and geometric variable of the stud, respectively. For a of less than 10, increases and reaches its peak as increases, whereas for a of greater than 10, the tensile strength of stud between approximately 411 and 511 MPa has a negative correlation with . It can be seen from Figure 11b that and have apparent positive correlations with the resistance, but there is a clear upper limit on the effect of both.The stud resistance is relatively insensitive to the changes for of greater than and of greater than 10. As can be seen from Figure 11c, the stud resistance reaches its peak when is 610 MPa and is , and from around 400 to 425 MPa is negatively correlated with ; however, as can be seen from Figure 11a, most of the data lie in the range 425 MPa 610 MPa. In the Eurocode-4 [9], only affects the results when . However, the above results show that the stud aspect ratio could affect the resistance until 10, which may have implications in the development of future design models.
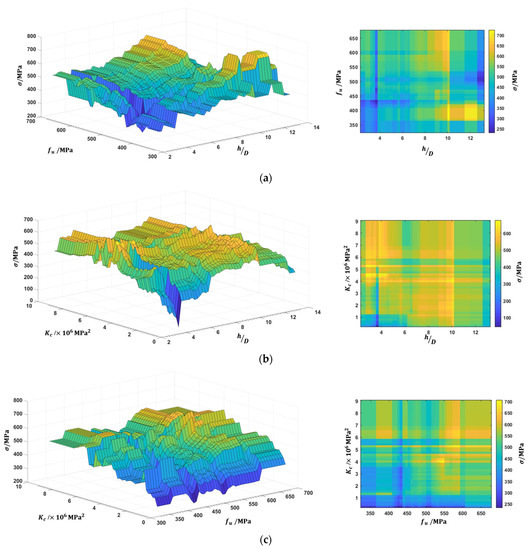
Figure 11.
Three-dimensional and two-dimensional PDP plots for (a) and , (b) and , and (c) and .
7. Conclusions
In this study, a total of 428 push-out test specimens were collected from 37 published pieces of literature. Five machine learning (ML) models are derived to predict the shear resistance of headed studs in steel–concrete structures. The following conclusions are drawn:
- The values of the equations from design codes of various countries were all negative when predicting datasets, including HPC and UHPC, which means these equations cannot be used for headed studs in HPC and UHPC.
- The prediction accuracy of ML models was much higher than the international design codes. The gradient boosting decision tree (GBDT) model had the overall highest accuracy and was compared with AASHTO, which had the highest accuracy among the three design codes. The values of and of the GBDT model were around 80% lower than that of the AASHTO equation.
- The visualization and interpretability analysis of the GBDT model showed that the length-to-diameter ratio of the stud had a substantial influence on the shear resistance of headed studs, which may be related to the effect of the length on the pull-out effect of the stud.
- The length-to-diameter ratio of the stud was suggested to be taken into account in the equations of future design codes, and there may be an upper limit on the positive effect of material properties on the shear resistance of headed studs, which requires future supplementation of high-strength material tests to determine.
Based on the research in this study, future research directions in this field are suggested to achieve better accuracy and to reveal more physical meaning behind parameters: it is expected that with the addition of new experimental data in the future, the prediction accuracy of ML models could be further improved. ML combined with data-driven analysis can provide a complementary research method to traditional experiments. This study investigated the prediction accuracy of limited to five ML models; there are many other ML algorithms that can be used to predict the stud shear resistance, including the simplest and most advanced ML algorithms, which are worth exploring in future research. Researchers can improve the design codes through the trained ML model. The dataset provided in this study, including UHPC and HPC, may be helpful in future studies to understand the influence of concrete types on the shear connection of headed studs.
Author Contributions
Conceptualization, F.Z. and X.Z.; methodology, F.Z. and X.Z.; validation, F.Z., C.W., and X.Z.; formal analysis, F.Z.; investigation, L.W. and X.Z.; resources, X.Z.; data curation, F.Z., C.W., and X.Z.; writing—original draft preparation, F.Z. and X.Z.; writing—review and editing, Q.W., D.C., Y.W., and X.Z.; visualization, F.Z.; supervision, L.W. and X.Z.; project administration, F.Z. and X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Basic Research Program from the Natural Science Foundation of Jiangsu Province, China (No. BK20210620); and Natural Science Research of Jiangsu Higher Education Institutions of China (No. 21KJB560007).
Data Availability Statement
Some or all data, models, or codes generated or used during this study are available from the corresponding author by request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nie, J.; Cai, C.S. Steel-concrete composite beams considering shear slip effects. J. Struct. Eng. 2003, 129, 495–506. [Google Scholar] [CrossRef]
- Nie, J.; Wang, J.; Gou, S.; Zhu, Y.; Fan, J. Technological development and engineering applications of novel steel-concrete composite structures. Front. Struct. Civ. Eng. 2019, 13, 1–14. [Google Scholar] [CrossRef]
- Ashraf, M.; Hasan, M.J.; Al-Deen, S. Semi-rigid behaviour of stainless steel beam-to-column bolted connections. Sustain. Struct. 2021, 1, 000002. [Google Scholar] [CrossRef]
- Qi, J.; Hu, Y.; Wang, J.; Li, W. Behavior and strength of headed stud shear connectors in ultra-high performance concrete of composite bridges. Front. Struct. Civ. Eng. 2019, 13, 1138–1149. [Google Scholar] [CrossRef]
- Johnson, R.P. Composite Structures of Steel and Concrete: Beams, Slabs, Columns and Frames for Buildings; John Wiley Sons: New York, NY, USA, 2018; 288p. [Google Scholar]
- Viest, I.M. Investigation of stud shear connectors for composite concrete and steel T.-beams. ACI J. 1956, 27, 875–981. [Google Scholar]
- Ollgaard, J.G.; Slutter, R.G.; Fisher, J.W. Shear strength of stud connectors in lightweight and normal weight concrete. AISC Eng. J. 1971, 71-10, 55-34. [Google Scholar]
- Civjan, S.A.; Singh, P. Behavior of shear studs subjected to fully reversed cyclic loading. J. Struct. Eng. 2003, 129, 1466–1474. [Google Scholar] [CrossRef]
- Eurocode-4; Design of Composite Steel and Concrete Structures. European Committee for Standardization: Brussels, Belgium, 2004.
- AASHTO. AASHTO LRFD Bridge Design Codes; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2012; p. 20001.
- GB50017–2017; Code for Design of Steel Structures. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2017. (In Chinese)
- Model Code. Joint Committee IASBSE/CEB/FIP/ECCS Composite Structures (Model Code); Construction Press: London, UK, 1981. [Google Scholar]
- Lee, P.G.; Shim, C.S.; Chang, S.P. Static and fatigue behavior of large stud shear connectors for steel–concrete composite bridges. J. Construct. Steel Res. 2005, 61, 1270–1285. [Google Scholar] [CrossRef]
- Hicks, S.J. Design shear resistance of headed studs embedded in solid slabs and encasements. J. Construct. Steel Res. 2017, 139, 339–352. [Google Scholar] [CrossRef]
- Oehlers, D.J.; Foley, L. The fatigue strength of stud shear connections in composite beams. Proc. Inst. Civ. Eng. 1985, 79, 349–364. [Google Scholar] [CrossRef]
- Lin, Z.F.; Liu, Y.Q. Experimental study on shear behavior of large stud connectors. J. Tongji 2015, 43, 1788–1793. (In Chinese) [Google Scholar]
- Duan, M.; Zou, X.; Bao, Y.; Li, G.; Chen, Y.; Li, Z. Experimental investigation of headed studs in steel-ultra-high performance concrete (UHPC) composite sections. Eng. Struct. 2022, 270, 114875. [Google Scholar] [CrossRef]
- Soleimani-Babakamali, M.H.; Esteghamati, M.Z. Estimating seismic demand models of a building inventory from nonlinear static analysis using deep learning methods. Eng. Struct. 2022, 266, 114576. [Google Scholar] [CrossRef]
- Esteghamati, M.Z.; Flint, M.M. Developing data-driven surrogate models for holistic performance-based assessment of mid-rise RC frame buildings at early design. Eng. Struct. 2021, 245, 112971. [Google Scholar] [CrossRef]
- Al-Bashiti, M.K.; Naser, M.Z. Machine learning for wildfire classification: Exploring blackbox, eXplainable, symbolic, and SMOTE methods. Nat. Hazard Res. 2022, 2, 154–165. [Google Scholar] [CrossRef]
- Avci-Karatas, C. Application of machine learning in prediction of shear capacity of headed steel studs in steel-concrete composite structures. Int. J. Steel Struct. 2022, 22, 539–556. [Google Scholar] [CrossRef]
- Cao, Y.; Wakil, K.; Alyousef, R.; Jermsittiparsert, K.; Ho, L.; Alabduljabbar, H.; Alaskar, A.; Alrshoudi, F.; Mohamed, A.M. Application of extreme learning machine in behavior of beam to column connections. Structures 2020, 25, 861–867. [Google Scholar] [CrossRef]
- Gholampour, A.; Mansouri, I.; Kisi, O.; Ozbakkaloglu, T. Evaluation of mechanical properties of concretes containing coarse recycled concrete aggregates using multivariate adaptive regression splines (MARS), M5 model tree (M5Tree), and least squares support vector regression (LSSVR) models. Neural Comput. Appl. 2020, 32, 295–308. [Google Scholar] [CrossRef]
- Huang, C.; Huang, S. Predicting capacity model and seismic fragility estimation for RC bridge based on artificial neural network. Structures 2020, 27, 1930–1939. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H.; Liu, Y. Auto-tuning deep forest for shear stiffness prediction of headed stud connectors. Structures 2022, 43, 1463–1477. [Google Scholar] [CrossRef]
- Mahjoubi, S.; Meng, W.; Bao, Y. Logic-guided neural network for predicting steel-concrete interfacial behaviors. Exp. Syst. Appl. 2022, 198, 116820. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Huang, Z.; Sui, L.; Chen, Y. Explicit neural network model for predicting FRP-concrete interfacial bond strength based on a large dataset. Compos. Struct. 2020, 240, 111998. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, C.; Liu, J.; Zou, X.; Sneed, L.H.; Bao, Y.; Wang, L. Prediction of FRP-concrete interfacial bond strength based on machine learning. Eng. Struct. 2023, 274, 115156. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C. Prediction of shear strength of FRP-reinforced concrete flexural members without stirrups using artificial neural networks. Eng. Struct. 2014, 61, 99–112. [Google Scholar] [CrossRef]
- Vinuesa, R.; Brunton, S.L. Enhancing computational fluid dynamics with machine learning. Nat. Comput. Sci. 2022, 2, 358–366. [Google Scholar] [CrossRef]
- Tran, V.Q.; Dang, V.Q.; Ho, L.S. Evaluating compressive strength of concrete made with recycled concrete aggregates using machine learning approach. Construct. Build. Mater. 2022, 323, 126578. [Google Scholar] [CrossRef]
- Yuan, X.; Tian, Y.; Ahmad, W.; Ahmad, A.; Usanova, K.I.; Mohamed, A.M.; Khallaf, R. Machine Learning Prediction Models to Evaluate the Strength of Recycled Aggregate Concrete. Materials 2022, 15, 2823. [Google Scholar] [CrossRef] [PubMed]
- Asteris, P.G.; Skentou, A.D.; Bardhan, A.; Samui, P.; Pilakoutas, K. Predicting concrete compressive strength using hybrid ensembling of surrogate machine learning models. Cem. Concr. Res. 2021, 145, 106449. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Islam, K.; Bekdaş, G.; Isikdag, U.; Mangalathu, S. Explainable machine learning models for predicting the axial compression capacity of concrete filled steel tubular columns. Construct. Build. Mater. 2022, 356, 129227. [Google Scholar] [CrossRef]
- Mangalathu, S.; Jeon, J.S. Machine learning–based failure mode recognition of circular reinforced concrete bridge columns: Comparative study. J. Struct. Eng. 2019, 145, 04019104. [Google Scholar] [CrossRef]
- Feng, D.C.; Liu, Z.T.; Wang, X.D.; Jiang, Z.M.; Liang, S.X. Failure mode classification and bearing capacity prediction for reinforced concrete columns based on ensemble machine learning algorithm. Adv. Eng. Inf. 2020, 45, 101126. [Google Scholar]
- Goldstein, A.; Kapelner, A.; Bleich, J.; Pitkin, E. Peeking inside the black box: Visualizing statistical learning with plots of individual conditional expectation. J. Comput. Graph. Stat. 2015, 24, 44–65. [Google Scholar] [CrossRef]
- Setvati, M.R.; Hicks, S.J. Machine learning models for predicting resistance of headed studs embedded in concrete. Eng. Struct. 2022, 254, 113803. [Google Scholar] [CrossRef]
- Hu, Y.; Qiu, M.; Chen, L.; Zhong, R.; Wang, J. Experimental and analytical study of the shear strength and stiffness of studs embedded in high strength concrete. Eng. Struct. 2021, 236, 111792. [Google Scholar] [CrossRef]
- Nie, J.; Sheng, J.; Yuan, Y.; Lin, W.; Wang, W. Study on actual bearing capacity of shear connectors in steel-concrete composite beams. J. Build. Struct. 1996, 17, 21–29. (In Chinese) [Google Scholar]
- Shim, C.S.; Lee, P.G.; Yoon, T.Y. Static behavior of large stud shear connectors. Eng. Struct. 2004, 26, 1853–1860. [Google Scholar] [CrossRef]
- Wang, W.H. Experimental and Analytical Study on Shear Properties of Headed Stud Connector; Zhejiang University: Hangzhou, China, 2018. (In Chinese) [Google Scholar]
- Wang, J.; Qi, J.; Tong, T.; Xu, Q.; Xiu, H. Static behavior of large stud shear connectors in steel-UHPC composite structures. Eng. Struct. 2019, 178, 534–542. [Google Scholar] [CrossRef]
- Han, Q.; Wang, Y.; Xu, J.; Xing, Y. Static behavior of stud shear connectors in elastic concrete–steel composite beams. J. Construct. Steel Res. 2015, 113, 115–126. [Google Scholar]
- Luo, Y.; Hoki, K.; Hayashi, K.; Nakashima, M. Behavior and strength of headed stud–SFRCC shear connection I: Experimental study. J. Struct. Eng. 2016, 142, 04015112. [Google Scholar] [CrossRef]
- Chen, Z. Research on Mechanical Properties and Bearing Capacity Analysis of Shear Connectors in Steel-UHPC Composite Structures; Changan University: Xian, China, 2021. (In Chinese) [Google Scholar]
- Kim, J.S.; Kwark, J.; Joh, C.; Yoo, S.W.; Lee, K.C. Headed stud shear connector for thin ultrahigh-performance concrete bridge deck. J. Construct. Steel Res. 2015, 108, 23–30. [Google Scholar]
- Kim, J.S.; Park, S.H.; Joh, C.B.; Kwark, J.D.; Choi, E.S. Push-out test on shear connectors embedded in UHPC. Appl. Mech. Mater. 2013, 351, 50–54. [Google Scholar] [CrossRef]
- Luo, Y.Z. Research on Bolted Shear Connections of Steel-Concrete Composite Beams; Central South University: Changsha, China, 2008. (In Chinese) [Google Scholar]
- Zeng, D.; Liu, Y.; Cao, L. Shear performance of innovative shear connectors in steel-UHPC composite structure. J. Zhejiang Univ. 2021, 55, 1714–1724+1771. (In Chinese) [Google Scholar]
- Lam, D.; El-Lobody, E. Behavior of headed stud shear connectors in composite beam. J. Struct. Eng. 2005, 131, 96–107. [Google Scholar] [CrossRef]
- Zhou, X.D. Experimental Study on Mechanical Properties of Large Diameter Shear Stud Connecters in Steel-UHPC Composite Structure; Nanjing Forestry University: Nanjing, China, 2018. (In Chinese) [Google Scholar]
- Wei, Z. Push-Out Tests on Stud Shear Connector of Prefabricated Steel-Concrete Composite Beams; Zhejiang University: Hangzhou, China, 2019. (In Chinese) [Google Scholar]
- Chen, L. Experimental Study of Static and Fatigue Properties of Interface Connection of Steel-Concrete Composite Beam Bridges; Southeast University: Nanjing, China, 2014. (In Chinese) [Google Scholar]
- Wang, W.F.; Chen, Z.J.; Zheng, X.H.; Xiong, Y. Experimental research on shear bearing capacity of Steel-RPC composite beam shear studs. Guangdong Archit. Civ. Eng. 2018, 25, 4. (In Chinese) [Google Scholar]
- Wang, Y. Experimental and Theoretical Research on Externally Prestressed Steel-Concrete Composite Beams; Tongji University: Shanghai, China, 2004. (In Chinese) [Google Scholar]
- Cao, J.; Shao, X.; Deng, L.; Gan, Y. Static and fatigue behavior of short-headed studs embedded in a thin ultrahigh-performance concrete layer. J. Bridge Eng. 2017, 22, 04017005. [Google Scholar] [CrossRef]
- An, L.; Cederwall, K. Push-out tests on studs in high strength and normal strength concrete. J. Construct. Steel Res. 1996, 36, 15–29. [Google Scholar] [CrossRef]
- Yamamoto, M.; Nakamura, S. The Study on Shear Connectors; The Public Works Research Institute, Construction Ministry Japan: Tokyo, Japan, 1962; Volume 5.
- Mainstone, R.J.; Menzies, J.B. Shear connectors in steel-concrete composite beams for bridges. Concrete 1967, 1, 291–302. [Google Scholar]
- Menzies, J.B. CP 117 and shear connectors in steel-concrete composite beams made with normal-density or lightweight concrete. Struct. Eng. 1971, 49, 137–154. [Google Scholar]
- Oehlers, D.J. Results on 101 Push-Specimens and Composite Beams; Research Report CE 8; Department of Civil Engineering, University of Warwick: Coventry, UK, 1981. [Google Scholar]
- Hiragi, H.; Miyoshi, E.; Kurita, A.; Ugai, M.; Akao, S. Static strength of Stud shear connectors in SRC Structures. Trans. Jpn. Concr. Inst. 1981, 3, 453–460. [Google Scholar]
- Roik, K.; Bürkner, K.E. Beitrag zur Tragfähigkeit von Kopfbolzendübeln in Verbundträgern mit Stahlprofilblechen. Bauingenieur 1981, 56, 97–101. (In German) [Google Scholar]
- Hicks, S.J. Longitudinal Shear Resistance of Steel and Concrete Composite Beams; University of Cambridge: Cambridge, UK, 1997. [Google Scholar]
- Easterling, W.S.; Murray, T.M.; Rambo-Roddenberry, M. Behaviour and Strength of Welded Stud Shear Connectors Data Report; Civil and Environmental Engineering, Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2002. [Google Scholar]
- Feldmann, M.; Hechler, O.; Hegger, J.; Rauscher, S. Neue Untersuchungen zum Ermüdungsverhalten von Verbundträgern aus hochfesten Werkstoffen mit Kopfbolzendübeln und Puzzleleiste. Stahlbau 2007, 76, 826–844. (In German) [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Y.; Luo, J.; Lebet, J.P. Experimental study on stud shear connectors with large diameter and high strength. In Proceedings of the 2011 International Conference on Electric Technology and Civil Engineering, Lushan, China, 22–24 April 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 340–343. [Google Scholar]
- Hanswille, G.; Jost, K.; Schmitt, C.; Trillmich, R. Experimentelle Untersuchungen zur Tragfähigkeit von Kopfbolzendübeln mit großen Schaftdurchmessern. Stahlbau 1998, 67, 555–560. (In German) [Google Scholar]
- Bullo, S.; Di Marco, R. Effects of high-performance concrete on stud shear connector behaviour. In Proceedings of the Nordic Steel Construction Conference, Malmö, Sweden, 19–21 June 1995; pp. 577–584. [Google Scholar]
- Döinghaus, P. Zum Zusammenwirken Hochfester Baustoffe in Verbundtragern; Technische Hochschule: Lübeck, Germany, 2002. (In German) [Google Scholar]
- Xue, D.; Liu, Y.; Yu, Z.; He, J. Static behavior of multi-stud shear connectors for steel-concrete composite bridge. J. Construct. Steel Res. 2012, 74, 1–7. [Google Scholar] [CrossRef]
- Jähring, A. Zum Tragverhalten von Kopfbolzendübeln in Hochfestem Beton; Technische Universität München: Munich, Germany, 2008. (In German) [Google Scholar]
- Hanswille, G.; Porsch, M.; Üstündag, C. Versuchsbericht über die Durchführung von 77 Push-Out-Versuchen. In Forschungsprojekt: Modellierung von Schädigungsmechanismen zur Beurteilung der Lebensdauer von Verbundkonstruktionen aus Stahl und Beton; Institut für Konstruktiven Ingenieurbau: Berlin, Germany, 2006; p. 7. (In German) [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. Building Industry Press: Beijing, China, 2010. (in Chinese)
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Northwest Washington, DC, USA, 15–19 December 2008; pp. 413–422. [Google Scholar]
- Degtyarev, V.; Hicks, S. Reliability-based design shear resistance of headed studs in solid slabs predicted by machine learning models. Archit. Struct. Construct. 2022. [Google Scholar] [CrossRef]
- Kutty, A.A.; Wakjira, T.G.; Kucukvar, M.; Abdella, G.M.; Onat, N.C. Urban resilience and livability performance of European smart cities: A novel machine learning approach. J. Clean. Prod. 2022, 378, 134203. [Google Scholar] [CrossRef]
- Abdella, G.M.; Kucukvar, M.; Kutty, A.A.; Abdelsalam, A.G.; Sen, B.; Bulak, M.E.; Onat, N.C. A novel approach for developing composite eco-efficiency indicators: The case for US food consumption. J. Clean. Prod. 2021, 299, 126931. [Google Scholar] [CrossRef]
- Abdella, G.M.; Shaaban, K. Modeling the impact of weather conditions on pedestrian injury counts using LASSO-based poisson model. Arab. J. Sci. Eng. 2021, 46, 4719–4730. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Alam, M.S.; Ebead, U. Plastic hinge length of rectangular RC columns using ensemble machine learning model. Eng. Struct. 2021, 244, 112808. [Google Scholar]
- Zhou, Z.H. Machine Learning; Tsinghua University Press: Beijing, China, 2016; pp. 138–139. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science and Business Media: Berlin, Germany, 1999; 188p. [Google Scholar]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- MATLAB Statistics and Machine Learning Toolbox. MathWorks. 2022. Available online: https://www.mathworks.com/products/statistics.html (accessed on 28 November 2022).
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Proc. Syst. 2017, 30, 4765–4774. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).