Characterization of Mechanical Behavior of Ultra-Small Clearance Tunnel Construction in Upper Soil and Lower Rock Composite Strata
Abstract
:1. Introduction
2. Research Background and Automated Monitoring Program
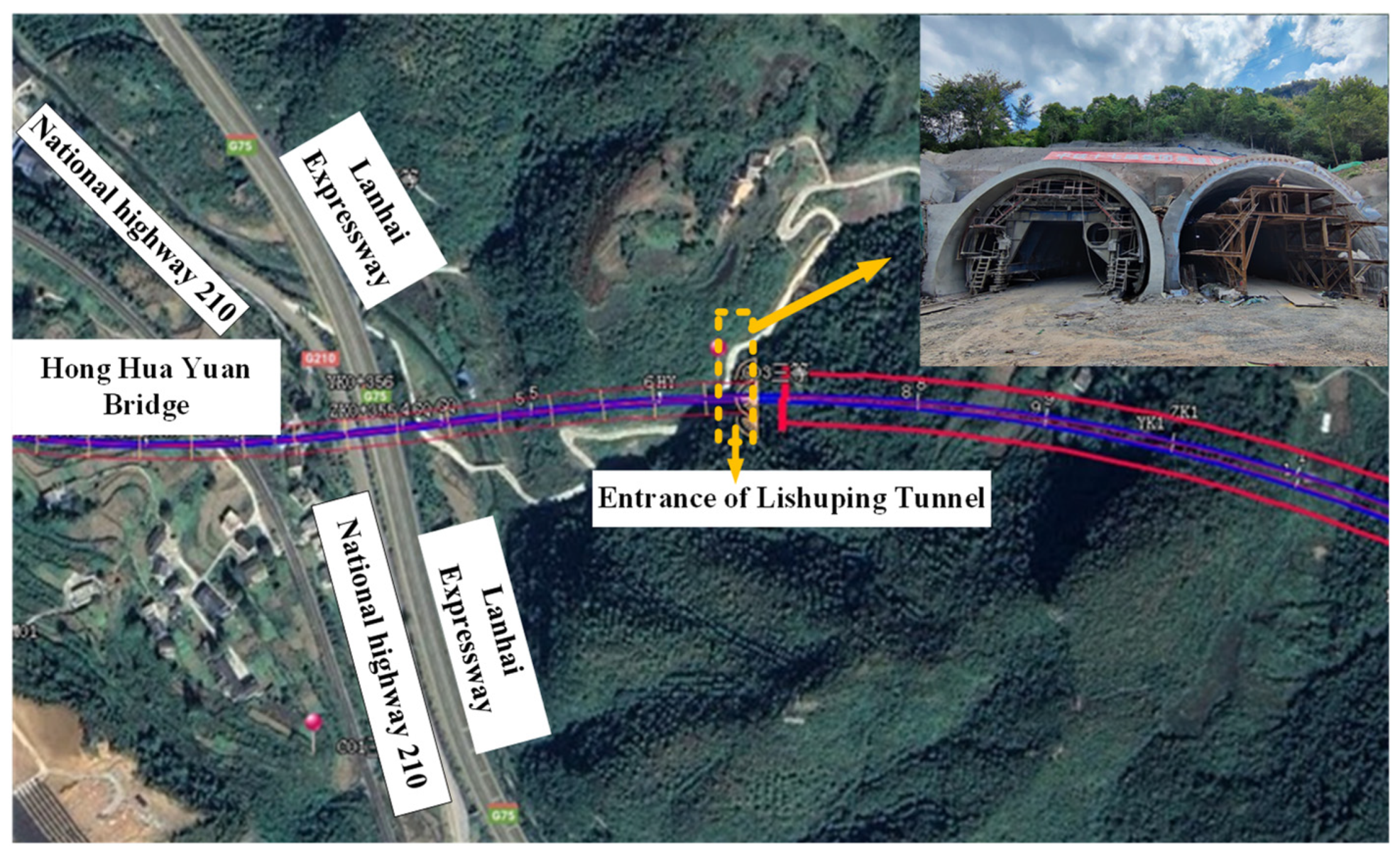
2.1. Project Background
2.2. Construction and Automation Monitoring Program
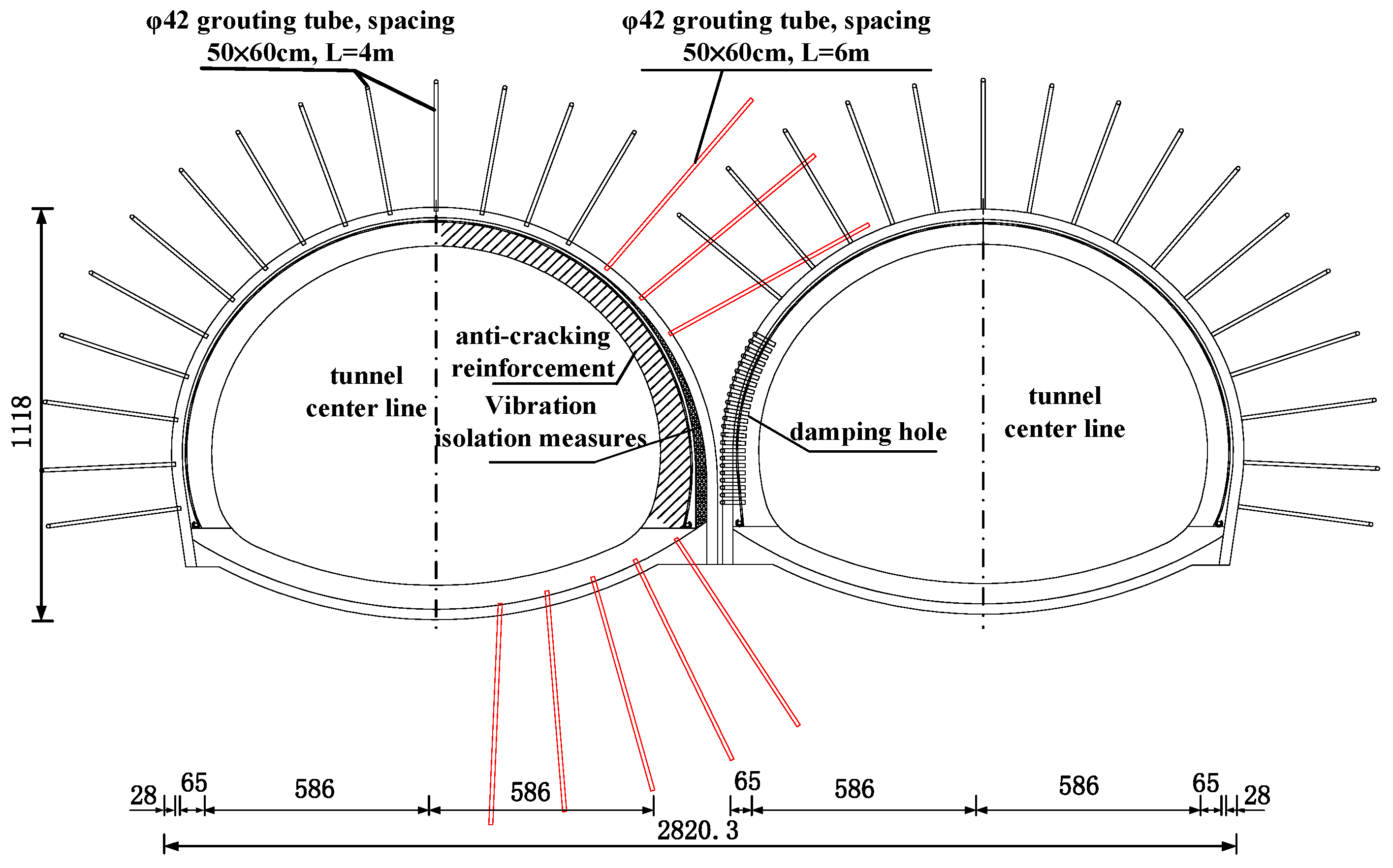
2.2.1. Construction and Support Parameters
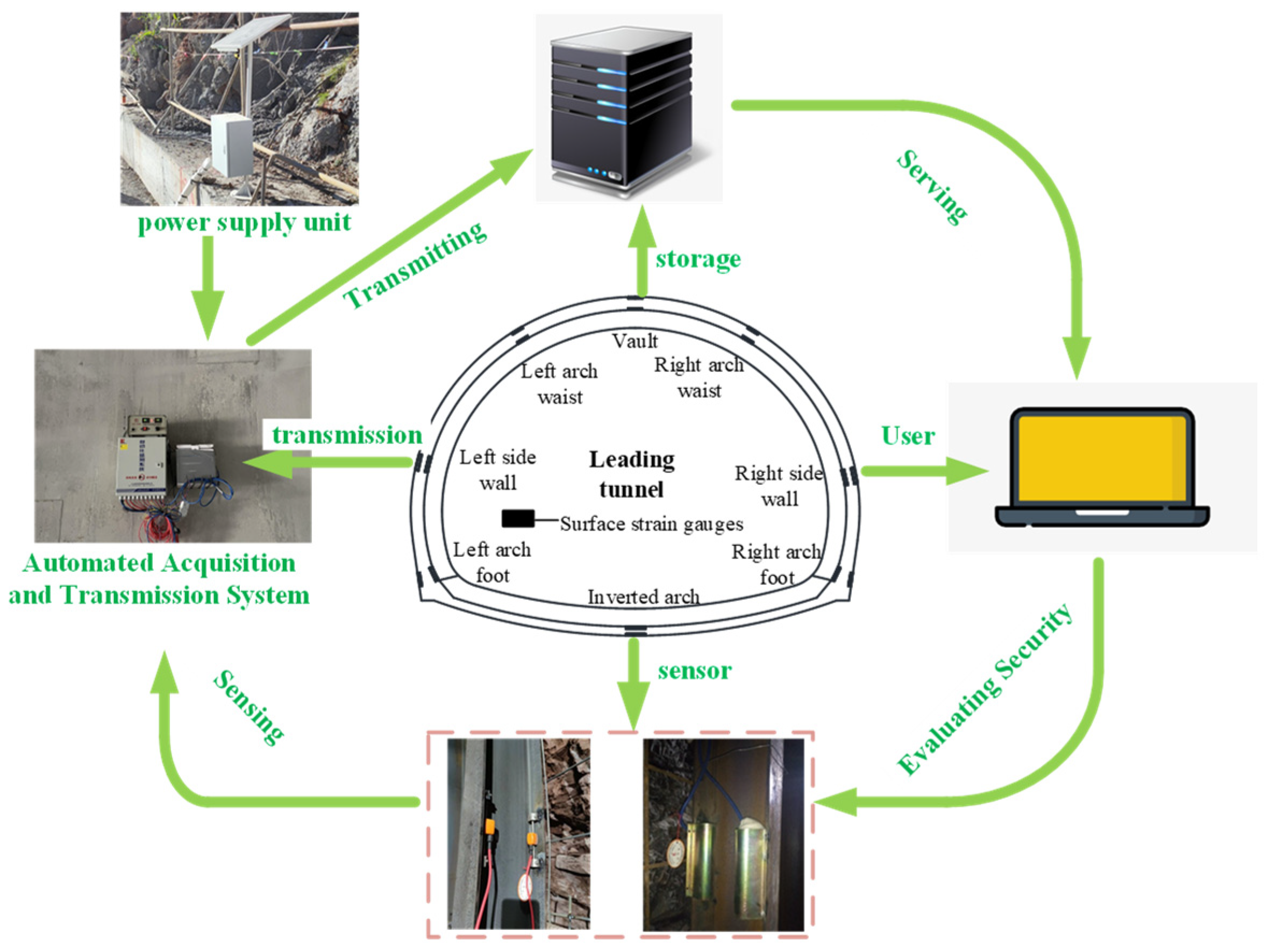
2.2.2. Automated Monitoring and Acquisition System
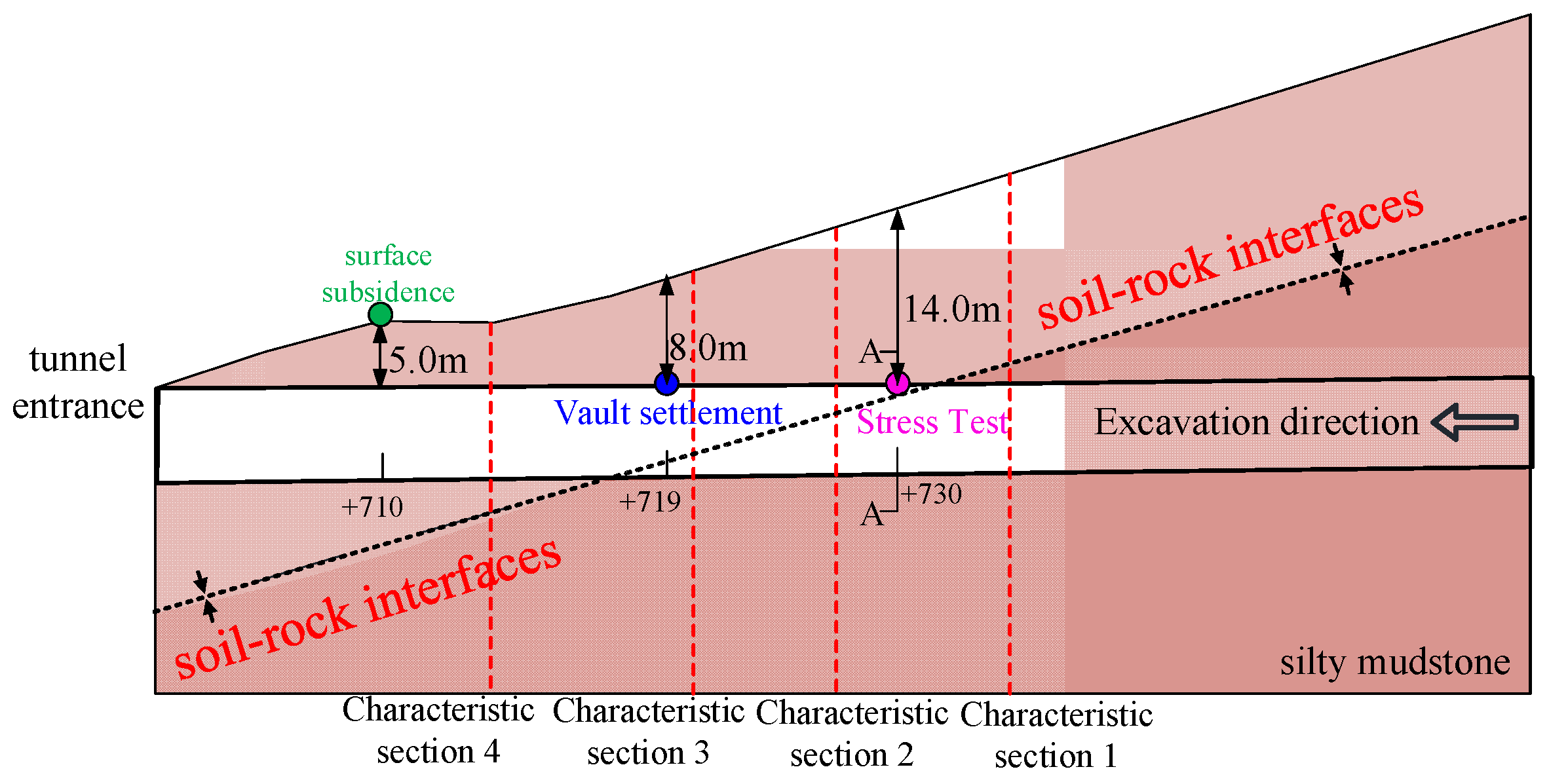
2.2.3. Deformation and Stress Test Program
3. Field Test
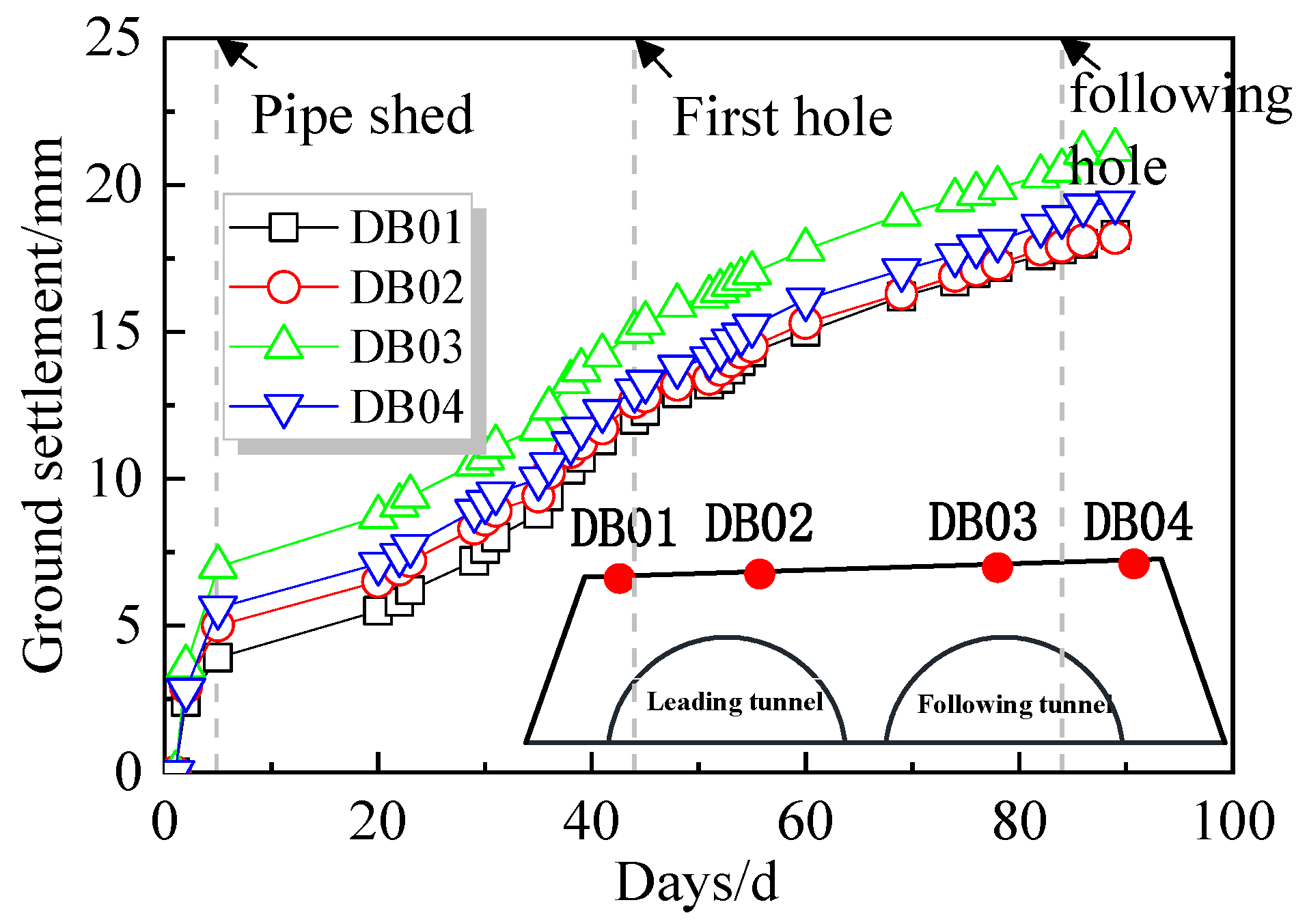
3.1. Ground Settlement
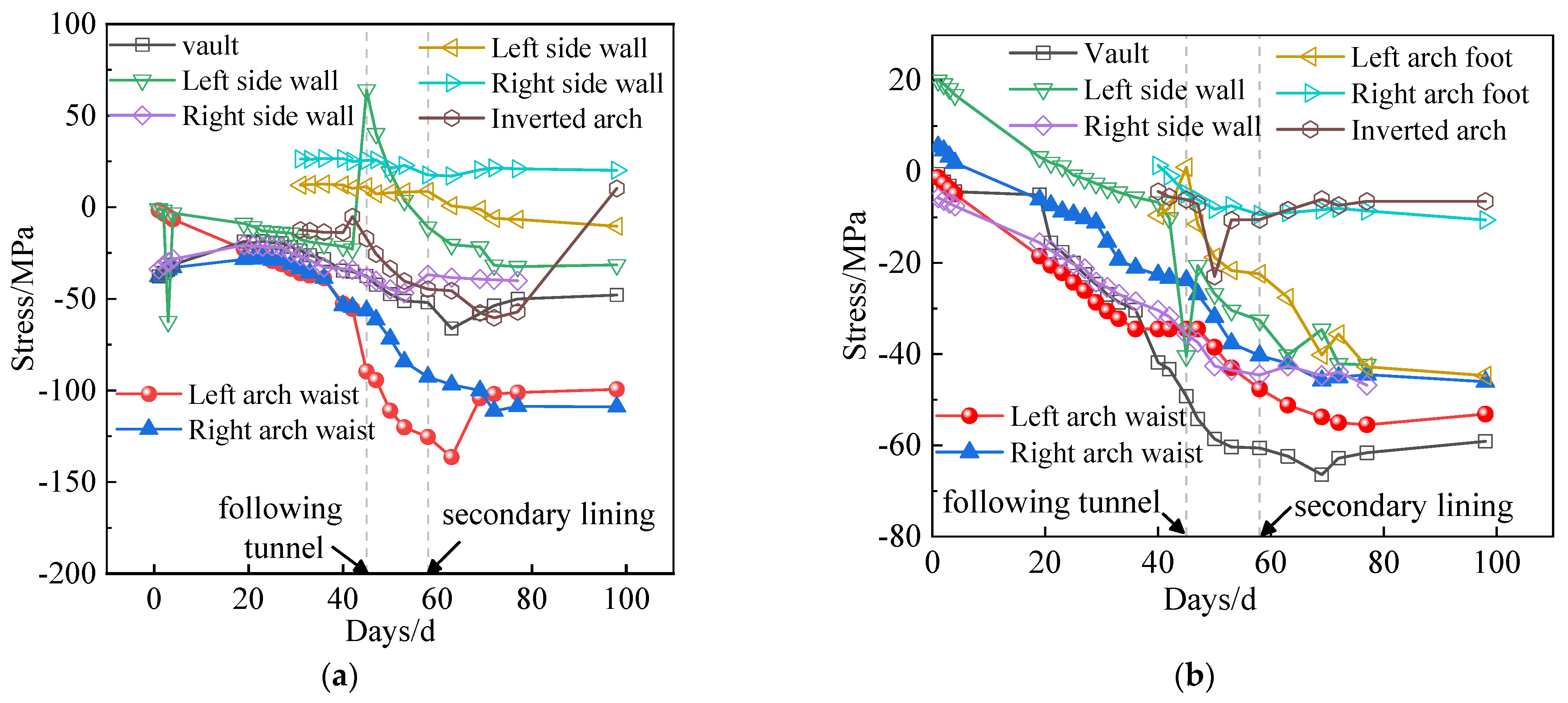
3.2. Time Variation of Stress in Primary Support Steel Frame
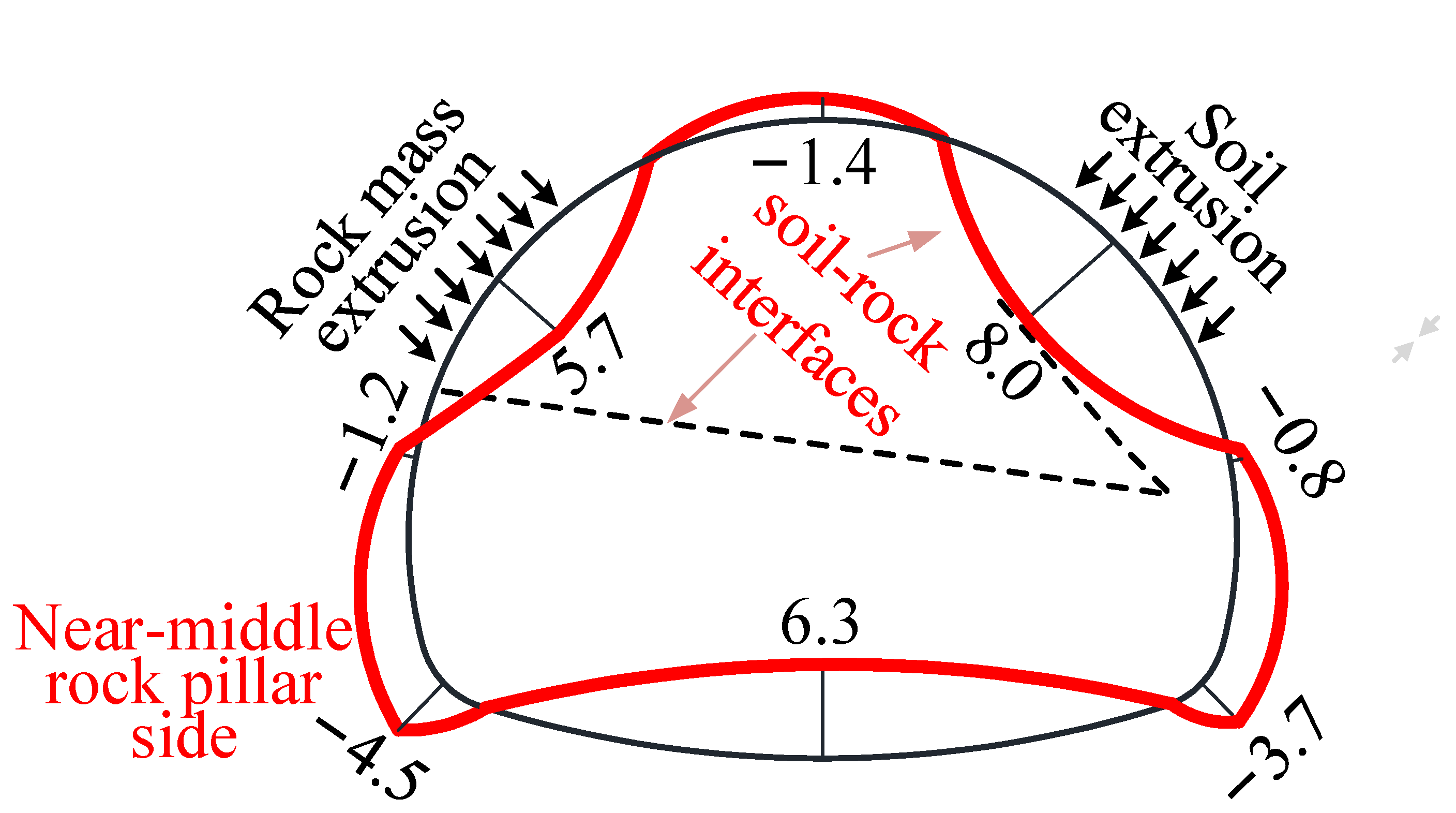
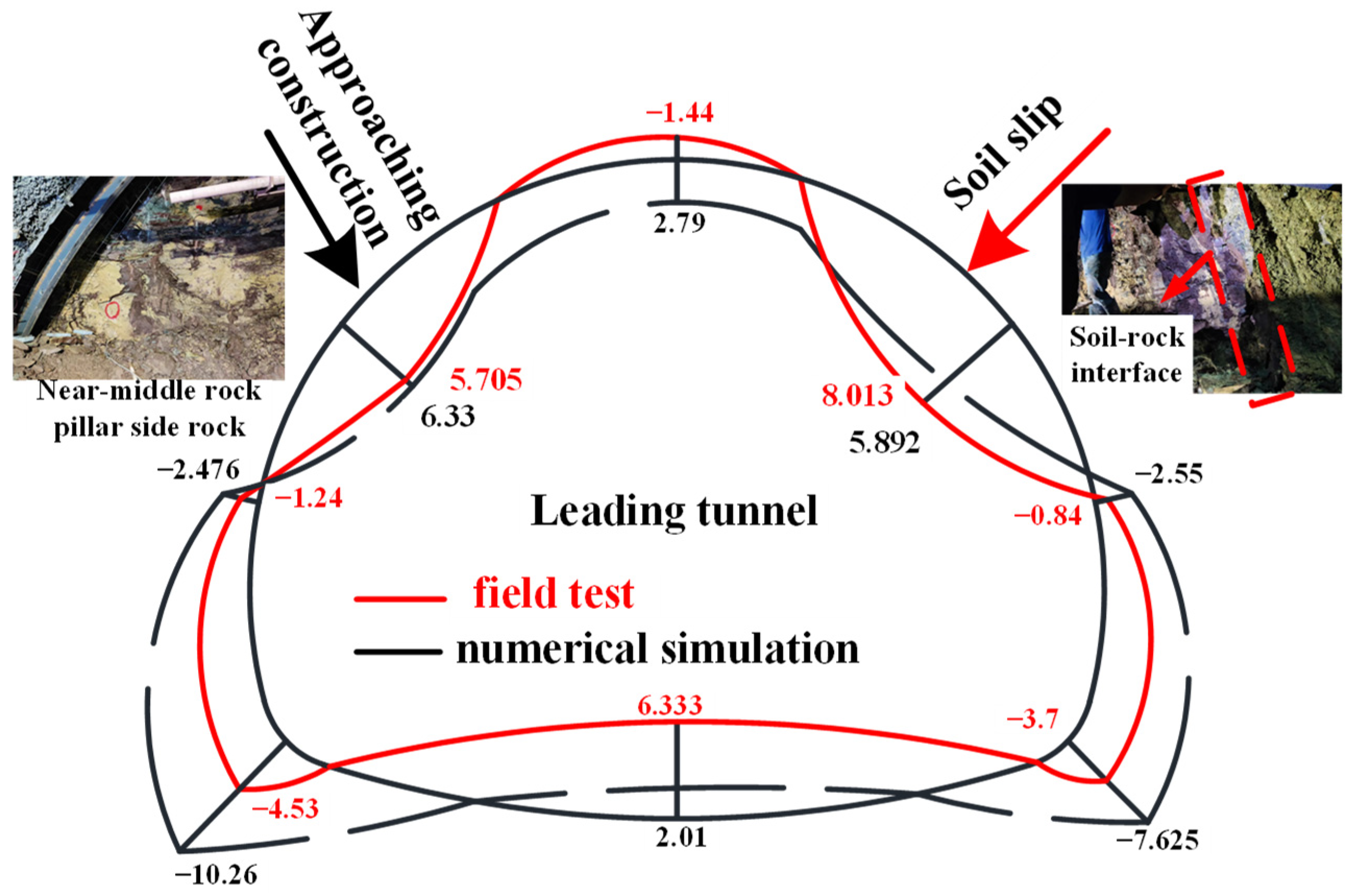
3.3. Measured Bending Moment Distribution of Primary Support Steel Frame
4. Analysis of the Influence of Soil-Rock Partition Location on Tunnel Structure
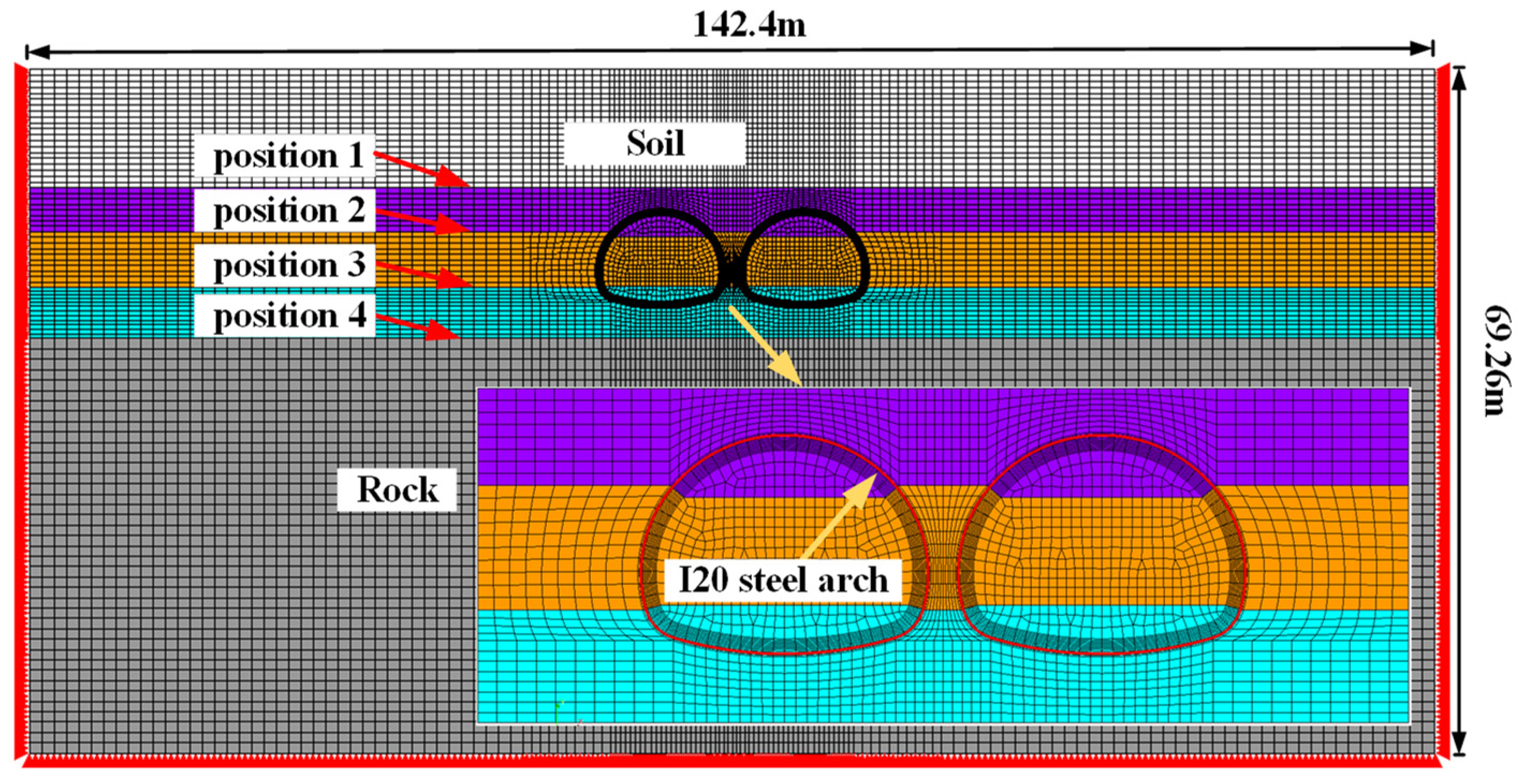
4.1. Numerical Model
4.2. Numerical Simulation of Working Conditions
4.3. Model Reasonableness Verification
4.4. Analysis of Calculation Results
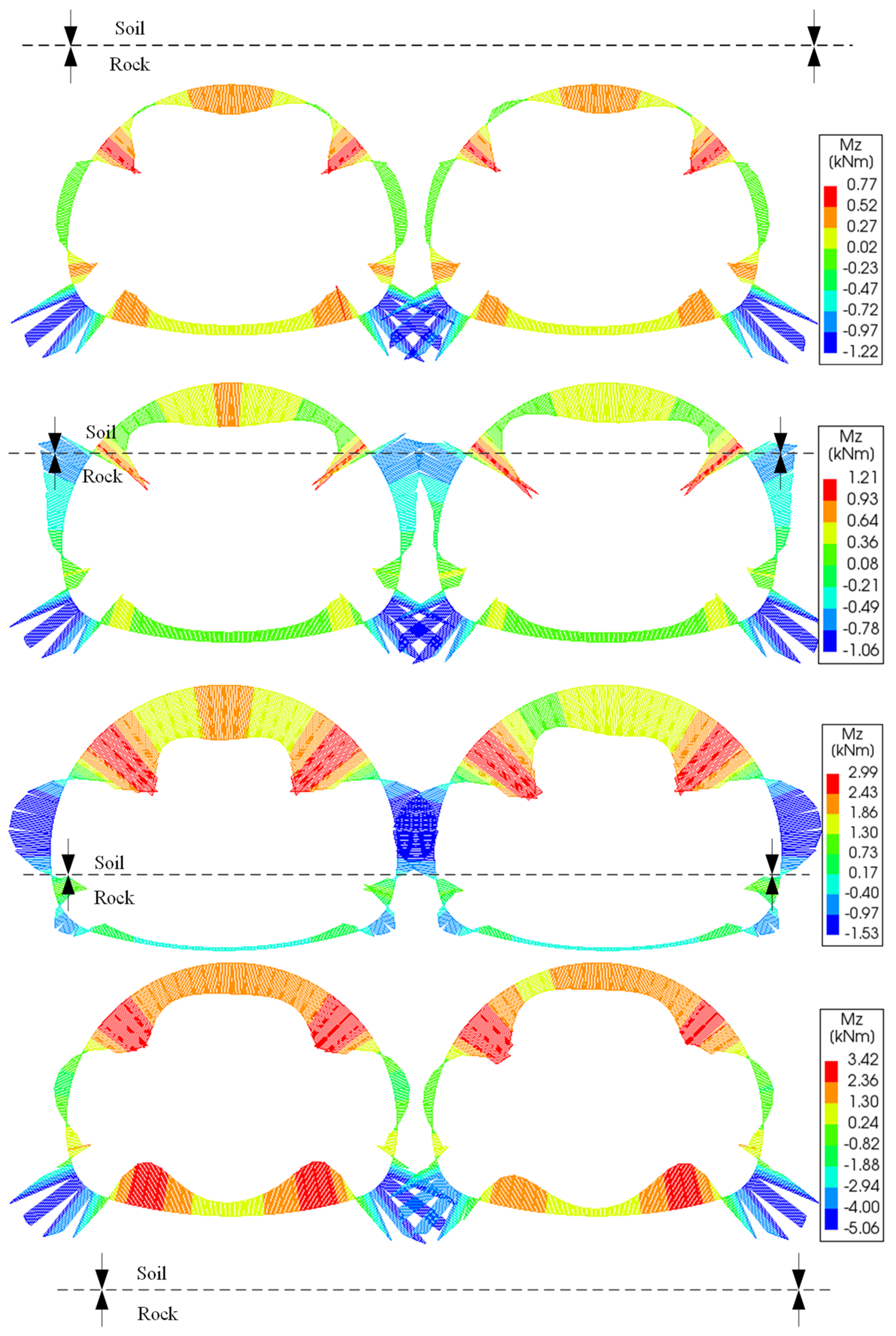
4.4.1. Primary Support Force Characteristics
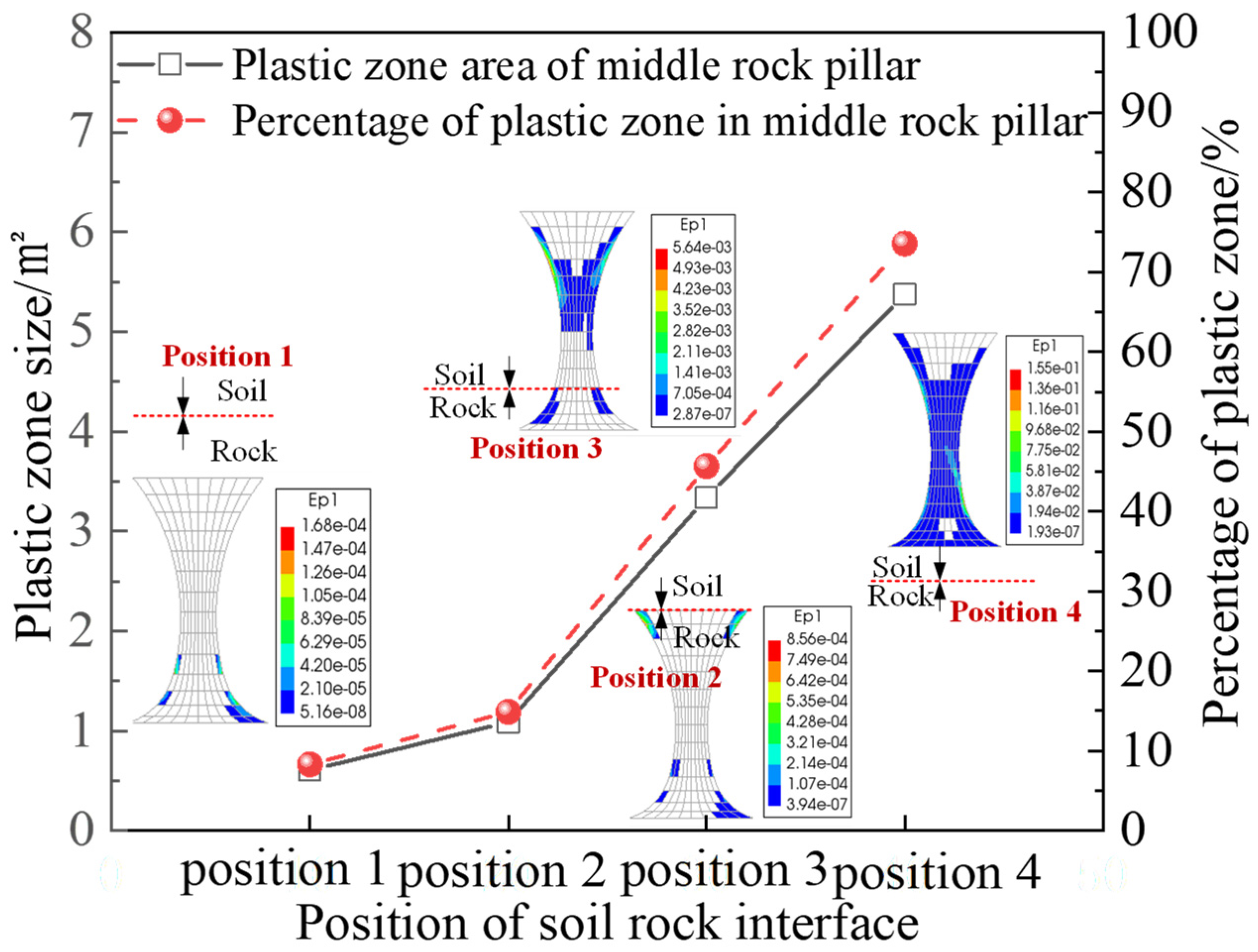
4.4.2. Variation of the Plastic Zone in the Middle Rock Pillar
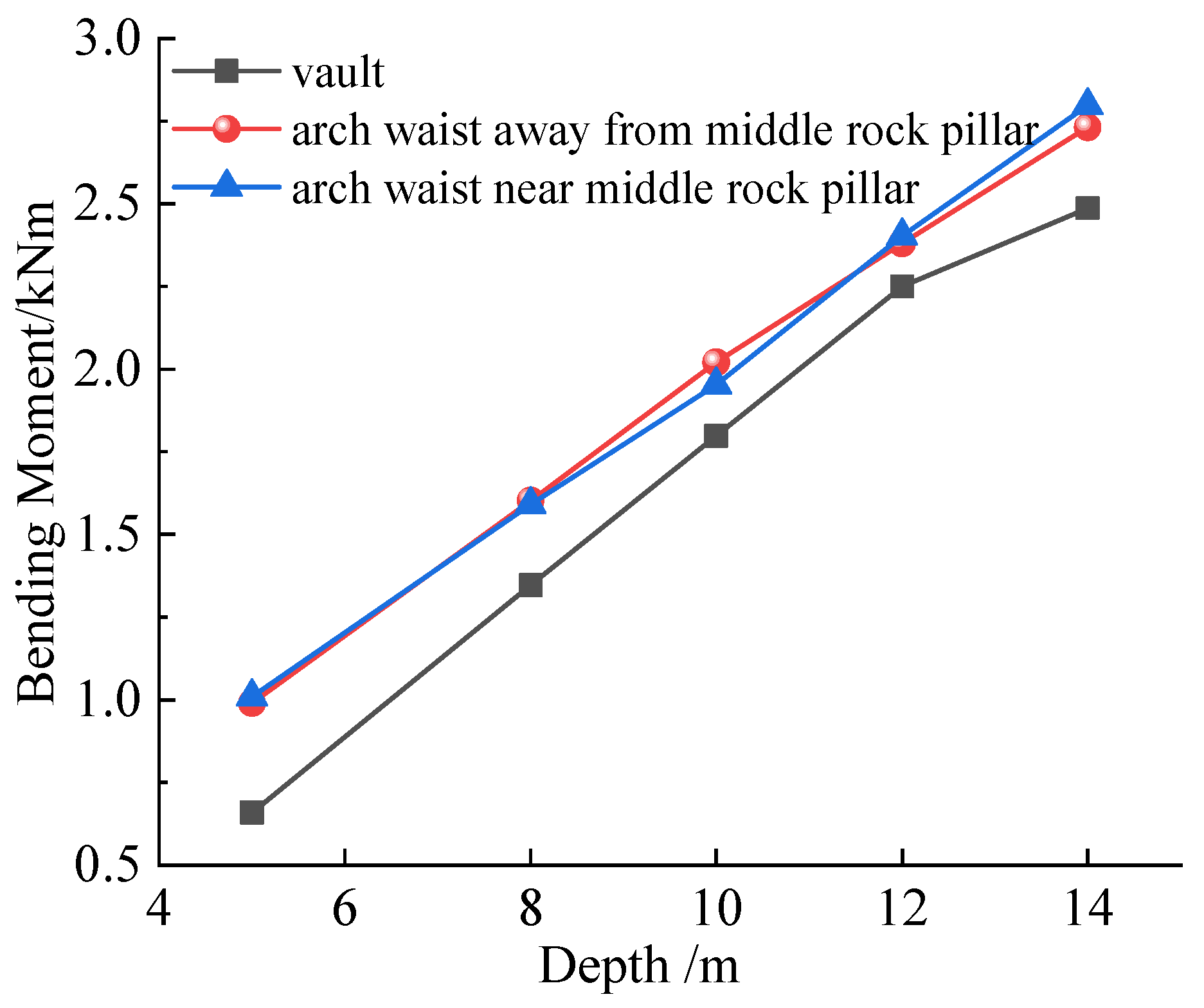
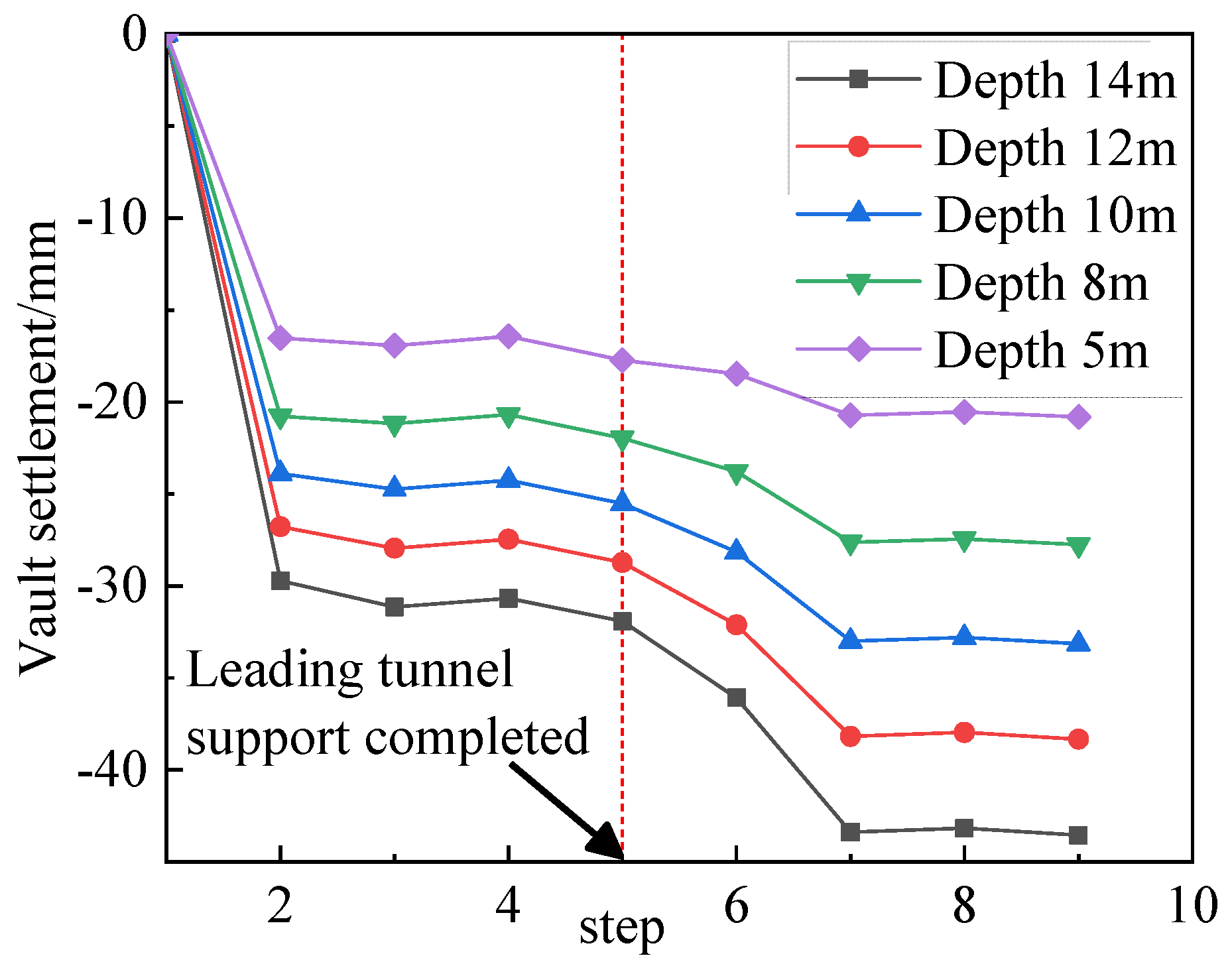
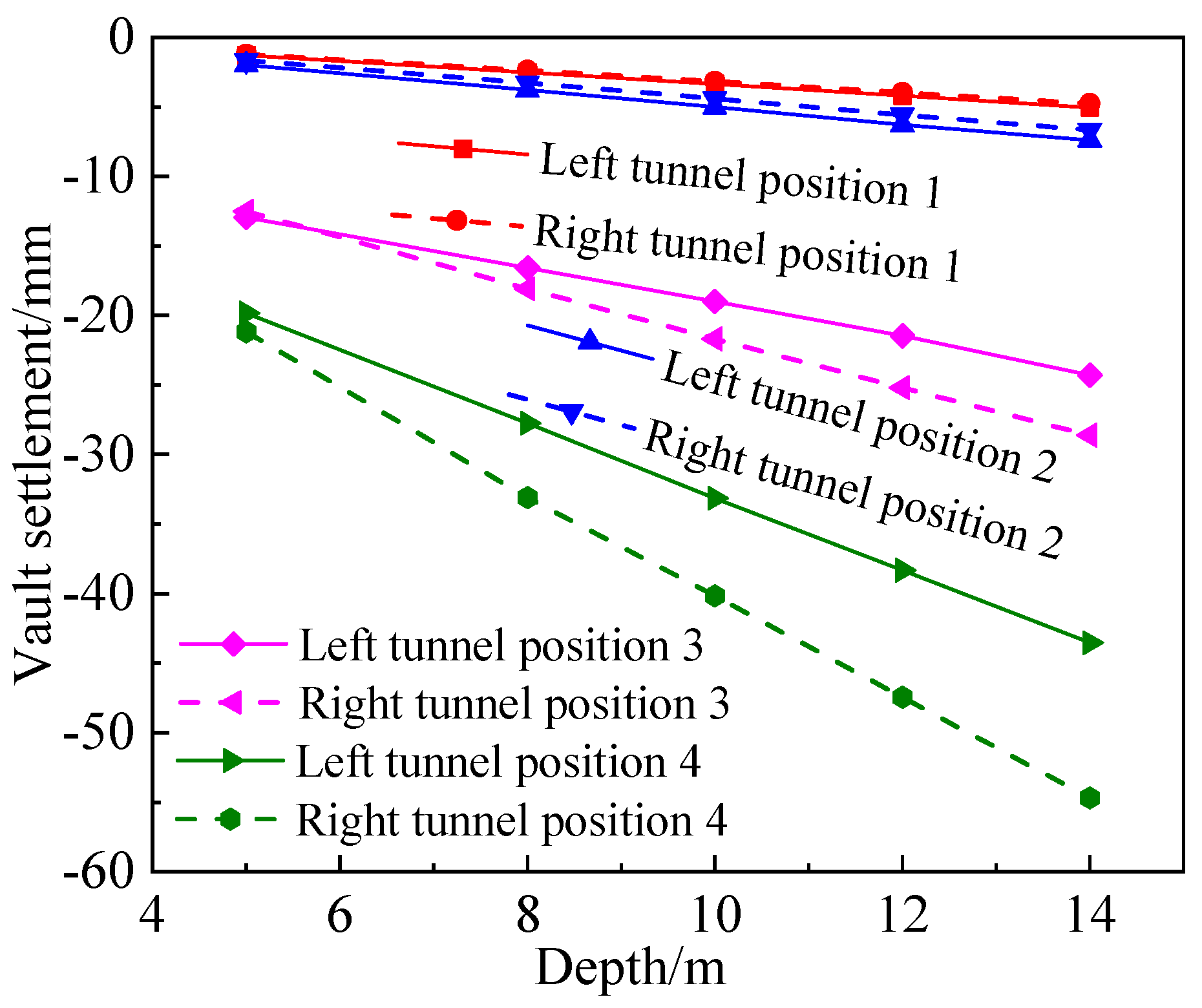
4.4.3. Effect of Burial Depth on Surrounding Rock Deformation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, A.Z.; Zhang, L.Q. Complex Function Method on Mechanical Analysis of Underground Tunnel; Science Press: Beijing, China, 2007. [Google Scholar]
- Chen, Z.Y. Analytical Method of Rock Mechanics Analysis; China Coal Industry Publishing House: Beijing, China, 1994. [Google Scholar]
- Lu, A.; Xu, Z.; Zhang, N. Stress analytical solution for an infinite plane containing two tunnels. Int. J. Mech. Sci. 2017, 128, 224–234. [Google Scholar] [CrossRef]
- Zeng, X.; Lu, A.; Zhang, N. Analytical stress sol ution for an infinite plate containing two oval tunnels. Eur. J. Mech.-A/Solids 2018, 67, 291–304. [Google Scholar] [CrossRef]
- Wang, H.N.; Zeng, G.S.; Utili, S.; Jiang, M.J.; Wu, L. Analytical solutions of stresses and displacements for deeply buried twin tunnels in viscoelastic rock. Int. J. Rock Mech. Min. Sci. 2017, 93, 13–29. [Google Scholar] [CrossRef]
- Chen, F.; Lin, L.; Li, D. Analytic solutions for twin tunneling at great depth considering liner installation and mutual interaction between geomaterial and liners. Appl. Math. Model. 2019, 73, 412–441. [Google Scholar] [CrossRef]
- Yanqing, L.; Shihang, Z.; Rusui, L.; Rongtian, M. Experimental study on mechanical characteristics of twin tunnels with small spacing. Chin. J. Rock Mech. Eng. 2000, 19, 590–594. [Google Scholar]
- Gong, J.W.; Xia, C.C.; Lei, X.W. Calculation and monitoring analysis of surrounding rock pressure of shallow buried small clearance tunnel. Chin. J. Rock Mech. Eng. 2010, 29 (Suppl. S2), 4139–4145. [Google Scholar]
- Mingqing, X.; Chen, X. Discussion on the representative value of surrounding rock pressure of deep buried small clearance tunnel. J. Railw. Eng. Soc. 2020, 37, 83–89. [Google Scholar]
- Jia, L. Calculation method and stress characteristics of surrounding rock in small clearance tunnel with weak geology. Tunn. Constr. (Chin.-Engl.) 2021, 41 (Suppl. S1), 174–180. [Google Scholar]
- Fang, Q.; Tai, Q.; Zhang, D.; Wong, L.N.Y. Ground surface settlements due to construction of closely-spaced twin tunnels with different geometric arrangements. Tunn. Undergr. Space Technol. 2016, 51, 144–151. [Google Scholar] [CrossRef]
- Acun, S.; Bilgin, N.; Erboylu, U. Contribution on the understanding of EPB-TBM drives in complex geologic structures. Tunn. Undergr. Space Technol. 2021, 107, 103646. [Google Scholar] [CrossRef]
- Fang, H.; Zhang, D.; Fang, Q.; Wen, M. A generalized complex variable method for multiple tunnels at great depth considering the interaction between linings and surrounding rock. Comput. Geotech. 2021, 129, 103891. [Google Scholar] [CrossRef]
- Shivaei, S.; Hataf, N.; Pirastehfar, K. 3D numerical investigation of the coupled interaction behavior between mechanized twin tunnels and groundwater—A case study: Shiraz metro line 2. Tunn. Undergr. Space Technol. 2020, 103, 103458. [Google Scholar] [CrossRef]
- Rahaman, O.; Kumar, J. Stability analysis of twin horse-shoe shaped tunnels in rock mass. Tunn. Undergr. Space Technol. 2020, 98, 103354. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Ranken, R.E. Interaction between two parallel tunnels. Int. J. Numer. Anal. Methods Geomech. 1977, 1, 75–103. [Google Scholar] [CrossRef]
- Costamagna, E.; Oggeri, C.; Vinai, R. Damage and contour quality in rock excavations for quarrying and tunnelling: Assessment for properties and solutions for stability. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 833, p. 012137. [Google Scholar]
- Shirinabadi, R.; Moosavi, E. Twin tunnel behavior under static and dynamic loads of Shiraz metro, Iran. J. Min. Sci. 2016, 52, 461–472. [Google Scholar] [CrossRef]
- El Omari, A.; Chourak, M.; Echebba, E.M.; Cherif, S.E.; Navarro Ugena, C.; Rougui, M.; Chehade, F.H.; Fernández, F.L.; Chaaraoui, A. Numerical analysis of twin tunnels lining under different seismic conditions. Infrastructures 2021, 6, 29. [Google Scholar] [CrossRef]
- Guijun, W.; Chundu, L.; Switzerland, G.; Junhua, H.; Qi, Z. Excavation deformation and stress analysis of soft interlayer section of shallow buried small clearance tunnel. J. Highw. Transp. Sci. Technol. 2022, 39, 131–138. [Google Scholar]
- Jingang, L. Study on the Influence of Construction Sequence on Ultra-Small Clearance Cross Tunnel. Modern TunnelTechnology: 1–7. Available online: http://kns.cnki.net/kcms/detail/51.1600.U.20220309.1521.002.html (accessed on 17 November 2022).
- Yi, F. Model test study of large-span and small-clearance highway tunnel. Chin. J. Undergr. Space Eng. 2016, 12 (Suppl. S1), 18–23+31. [Google Scholar]
- Zhiyu, T.; Guojin, L.; Jinlong, Z.; Lian, W. Study on Failure Mode of Small Clear Distance Tunnel. Mod. Tunn. Technol. 2019, 56 (Suppl. S2), 202–208. [Google Scholar] [CrossRef]
- Ou, Y.; Tian, G.; Chen, J.; Chen, G.; Chen, X.; Li, H.; Liu, B.; Huang, T.; Qiang, M.; Satyanaga, A.; et al. Feasibility Studies on the Utilization of Recycled Slag in Grouting Material for Tunneling Engineering. Sustainability 2022, 14, 11013. [Google Scholar] [CrossRef]
- Zhenhu, Y.; Kai, W.; Kun, T.; Bin, L.; Wenjie, L. Study on stability and reinforcement scheme of rock column in shallow buried small clearance tunnel. J. Yangtze River Res. Inst. 2022, 39, 126–134. [Google Scholar]
- Li, P.X.; Chen, B.R.; Xiao, Y.X.; Feng, G.L.; Zhou, Y.Y.; Zhao, J.S. Rockburst and microseismic activity in a lagging tunnel as the spacing between twin TBM excavated tunnels changes: A case from the Neelum-Jhelum hydropower project. Tunn. Undergr. Space Technol. 2023, 132, 104884. [Google Scholar] [CrossRef]
- Fu, J.; Zhao, N.; Qu, Y.; Yang, J.; Wang, S. Effects of twin tunnel undercrossing excavation on the operational high speed railway tunnel with ballastless track. Tunn. Undergr. Space Technol. 2022, 124, 104470. [Google Scholar] [CrossRef]
- Zhou, Z.; Ding, H.; Miao, L.; Gong, C. Predictive model for the surface settlement caused by the excavation of twin tunnels. Tunn. Undergr. Space Technol. 2021, 114, 104014. [Google Scholar] [CrossRef]
- Qi-Xiang, Y.; Chuan, H.E.; Yong, Y.A.O. Study on construction characteristics and dynamic mechanical behavior of soft rock tunnel. Chin. J. Rock Mech. Eng. 2006, 25, 572–577. [Google Scholar]
- Kun, J.; Caichu, X. Monitoring measurement analysis of two-way eight-lane small clearance highway tunnel. Chin. J. Rock Mech. Eng. 2010, 29 (Suppl. S2), 3755–3761. [Google Scholar]
- Songtao, L.; Zhongsheng, T.; Wentao, D. Mechanical effect analysis of small clearance highway tunnel with extra la-rge section. China Civ. Eng. J. 2017, 50 (Suppl. S2), 292–296. [Google Scholar] [CrossRef]
- Yunliang, Z.; Changsheng, W.; Ping, L.; Fengxiang, L. Small clearance tunnel construction monitoring measurement and numerical analysis. J. Railw. Sci. Eng. 2011, 8, 50–53. [Google Scholar] [CrossRef]
- Ran, L.; Shengtao, W.; Dingli, Z.; Ping, C.; Honggui, P.; Ao, L. Control Mechanism and Engineering Application of Rock-interbed Tension Anchor in Small Clear Distance Tunnel. Rock Soil Mech. 2022, 43, 1865–1876. [Google Scholar] [CrossRef]
- Oggeri, C.; Oreste, P. Tunnel static behavior assessed by a probabilistic approach to the back-analysis. Am. J. Appl. Sci. 2012, 9, 1137. [Google Scholar]
- Greco, O.; Ferrero, A.M.; Oggeri, C. Experimental and analytical interpretation of the behaviour of laboratory tests on composite specimens. Int. J. Rock. Mech. Min. Sci. 1993, 30, 1539–1543. [Google Scholar] [CrossRef]


| Materials | Density (kg·m−3) | Elastic Modulus (GPa) | Poisson Ratio | Cohesion (Mpa) | Friction Angle (°) |
|---|---|---|---|---|---|
| Surrounding rock | 1800 | 1.2 | 0.35 | 0.16 | 27 |
| Silty clay | 1800 | 0.03 | 0.35 | 0.016 | 20 |
| C25 | 2200 | 28 | 0.2 | / | / |
| Secondary lining | 2500 | 30 | 0.2 | / | / |
| Depth/m | Position 1 | Position 2 | Position 3 | Position 4 |
|---|---|---|---|---|
| 5.0 | 1 | 2 | 3 | 4 |
| 8.0 | 5 | 6 | 7 | 8 |
| 10.0 | 9 | 10 | 11 | 12 |
| 12.0 | 13 | 14 | 15 | 16 |
| 14.0 | 17 | 18 | 19 | 20 |
| Case 4 | Field Test | |
|---|---|---|
| Left tunnel | 18.3454 mm | 18.2 mm |
| Right tunnel | 19.6324 mm | 21.2 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Fu, D.; Zhou, X.; Han, Y. Characterization of Mechanical Behavior of Ultra-Small Clearance Tunnel Construction in Upper Soil and Lower Rock Composite Strata. Buildings 2023, 13, 559. https://doi.org/10.3390/buildings13020559
Zhang X, Fu D, Zhou X, Han Y. Characterization of Mechanical Behavior of Ultra-Small Clearance Tunnel Construction in Upper Soil and Lower Rock Composite Strata. Buildings. 2023; 13(2):559. https://doi.org/10.3390/buildings13020559
Chicago/Turabian StyleZhang, Xuemin, Dong Fu, Xianshun Zhou, and Yuanyuan Han. 2023. "Characterization of Mechanical Behavior of Ultra-Small Clearance Tunnel Construction in Upper Soil and Lower Rock Composite Strata" Buildings 13, no. 2: 559. https://doi.org/10.3390/buildings13020559
APA StyleZhang, X., Fu, D., Zhou, X., & Han, Y. (2023). Characterization of Mechanical Behavior of Ultra-Small Clearance Tunnel Construction in Upper Soil and Lower Rock Composite Strata. Buildings, 13(2), 559. https://doi.org/10.3390/buildings13020559






