1. Introduction
Stairways, the primary vertical emergency exit routes in most buildings, are critically significant for building accessibility and survivability in emergency events. They should remain operable following even a severe earthquake and the ensuing post-earthquake disaster in order to support the occupant evacuation and recovery response [
1]. However, the seismic behavior of stairways is complicated, and staircases have performed poorly in prior earthquakes [
2,
3,
4,
5]. In some cases, stairways were damaged more severely than the main structures, such as in the observations made following the 2003 Algeria earthquake, where the presence of short columns near the staircase was one of the main causes of severe stair damage [
6]. In the 2008 Wenchuan earthquake [
2], the damages to buildings, especially stairwells with reinforced concrete frames, were severe. The majority of deaths and injuries were caused by collapsed stairways. In the 2011 Christchurch earthquake [
3,
4], many stairways exhibited significant damage in buildings where inter-story movements of the stairs were restrained. Seismically damaged stairways, in short, caused disruptions to the building functionality, delayed rescue operations, and threatened safety, as shown in
Figure 1 and
Figure 2.
Despite such proof of the vulnerability of stairs as well as the implications related to stair damage, studies on the seismic behavior of stair systems have been only occasionally conducted. In the work of Li et al. [
2], the seismic behavior of reinforced-concrete stairs during the 2008 Wenchuan earthquake was studied. This research indicated that various types of seismic damage to the stair components or the major structures occurred because of the interaction between the primary structural systems and stairways. Cosenza et al. [
7] investigated the seismic behavior of stairs in existing RC buildings and suggested that the stairs increase the stiffness and strength of the structure, which results in a reduction in the natural vibration period and the attraction of seismic forces. In addition, Tegos et al. [
8] attempted to quantify the influence of a stair system on the structure response with the numerical simulation method. Thus far, limited experimental data are available to validate the findings of these and other numerical studies. For complementing these studies, tests on the seismic performance of stair systems are required. Simmons and Bull [
9] conducted quasi-static cyclic tests of three full-height reinforced concrete straight-run stair flights conforming to the New Zealand design code. Higgins [
10] performed tests of two full-sized prefabricated steel scissor stairs constructed in accordance with the US design standards, to assess the seismic inter-story drift response combined with the factored gravity loads. These experimental studies promoted the understanding regarding the seismic performance of stair systems. However, they were both conducted in an isolated configuration, using cyclic loading to replicate earthquake floor drifts.
In the design practice, stairways are typically attached to their major structure and span as a floor-to-floor system. Nevertheless, the seismic design forces for stairways can be easily determined from code provisions [
11], detailing why it is difficult to keep these floor-to-floor systems damage-free with relative deformation between their lower and upper floors. The current condition of practice often imposes specific provisions to one end of the stairways (e.g., slotted or ductile connections and seismic gaps) to provide the desired floor-to-floor relative drift. However, more commonly, the designers simply fix both the bottom and top of the stair system to the lower and upper floors of the supporting structure. This practice has demonstrated catastrophic results, as the stairways lack protection from the large floor-to-floor relative displacements [
11,
12].
Feng et al. [
13] and Zhao et al. [
14] proposed a design to separate the staircase from the overall structure and suggested cutting off the transfer path of horizontal load in the staircase. In addition, Jiang et al. [
15] put forward detailed requirements to separate the staircase from the overall structure, and the sliding support installed in the staircase was also proposed. Subsequently, shaking table tests of a reinforced concrete stair with sliding bearing were conducted by Zhao et al. [
16]. The test results showed that the presence of sliding bearing can improve the seismic performance of staircases, however, several vertical detachment and horizontal sways occurred between the lower end of the flight and the sliding bearing, and there existed a risk of falling off the flight during a strong earthquake.
Seismic isolation is the separation of the superstructure from its base to negotiate the destructive movement of the ground [
17,
18]. By comparison with the conventional seismic design approach, which is based on an increased strengthening of the structures, the seismic isolation concept is aimed at a significant reduction in dynamic response induced by the earthquake. To date, extensive isolation devices, including rubber bearings (RB), lead plug rubber bearings (LRB), frictional-sliding bearings, and roller bearings, have been developed [
19,
20,
21,
22,
23]. Though those isolation bearings have been applied to the area of base isolation, the application of the seismic isolation devices into the staircases is still rare. Compared to LRB and rolling bearings, the RB has the advantages of simpler construction and lower cost. Additionally, as shown in the following
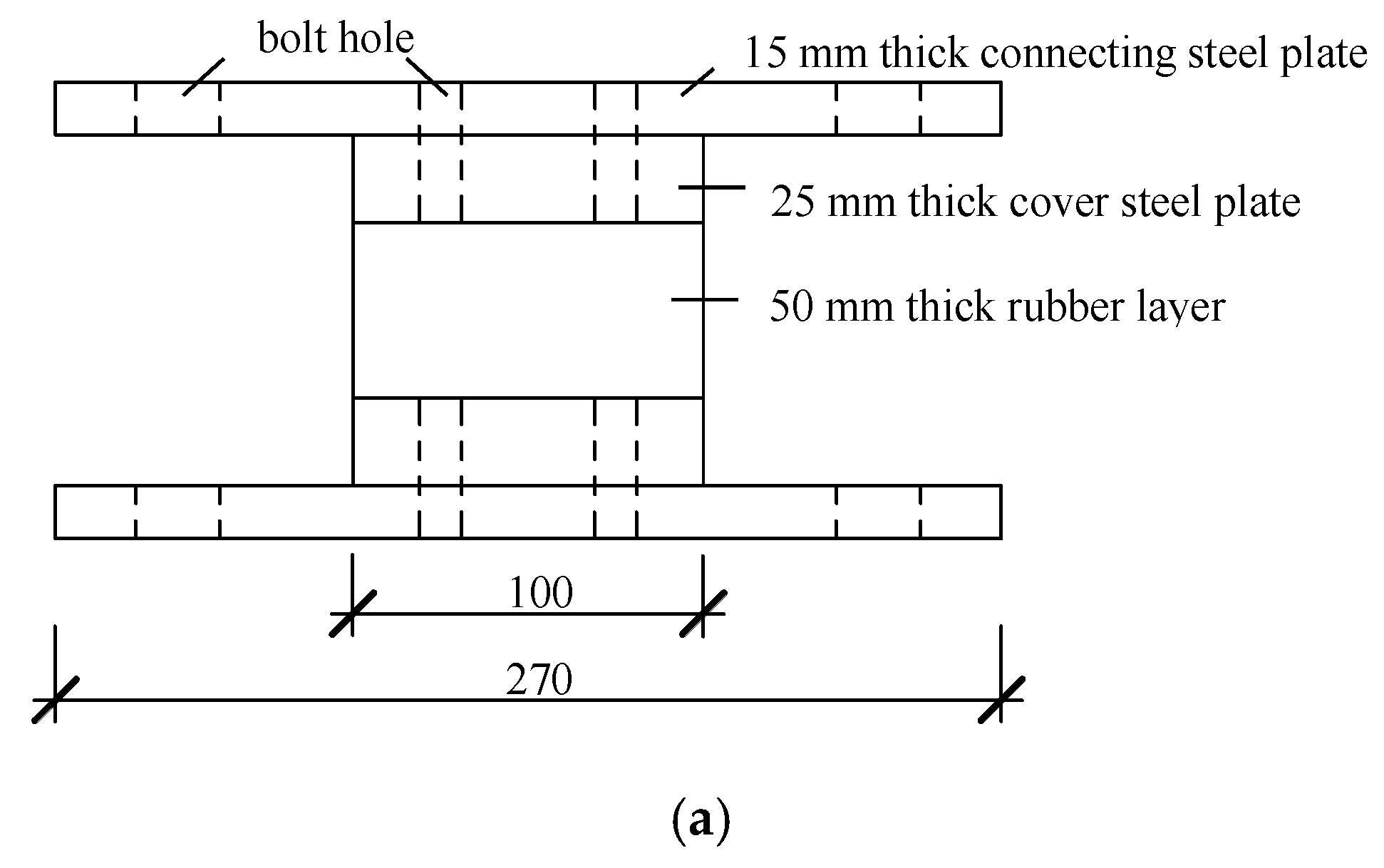
Figure 3a, the isolation bearings are set between the flight and the landing beam, and the space for installation is limited. The application of RB could solve this problem and is more convenient to install in staircases. To mitigate seismic damages to the component of staircases and improve their seismic performance, this work introduces a rubber isolation bearing installed in a staircase (RBS), as shown in
Figure 3a, which is composed of a rubber layer, connecting steel plate, cover steel plate, and anchor bolts. The rubber layer was vulcanized to the cover steel plate. The connecting steel plate and cover steel plate were connected by sunken bolts.
Figure 3b,c depict the specific layout and detailed view of the RBS, respectively. As seen in
Figure 3b, the RBS is set between the flight and the landing beam, and the flight and landing beam are connected by anchor bolts with the RBS. When under a horizontal seismic action, the RBS will generate relative deformation, which could accommodate the desired floor-to-floor relative drift, effectively weaken the diagonal strut effect of the flight, and mitigate the effect of the staircase on the whole structure, consequently protecting the staircase from damage.
In this study, the horizontal and vertical mechanical properties of RBS were determined through experimental study, and numerical modeling was validated with the experimental result. Subsequently, finite element models of three types of reinforced concrete frames (without stairs, with cast-in-place reinforced concrete stairs, and with RBS stairs) were established in order to assess the seismic performance of the proposed RBS. Response spectrum and non-linear time–history analyses were conducted to analyze the effect of the RBS on the dynamic characteristics of the whole structure. The dynamic responses (i.e., natural vibration period, base shear, story shear, story drift angle, and vertex acceleration) were obtained for each model, and the inner forces of stair components were deeply analyzed.
3. Numerical Modeling and Verification of RBS Bearings
The general-purpose software package for finite element analysis, ABAQUS/CAE6.10-1 [
26], was employed to simulate the shear behavior of the RBS bearings tested in this study, and the experimental results are used to calibrate the model.
The existing studies [
27,
28] demonstrated that the strength degradation of LRB under cyclic loading should be considered when modeling the behavior of LRB. In comparison, the rubber materials were characterized by their isotropic property and nonlinear elastic and incompressible behavior; therefore, the strength degradation of rubber materials under cyclic loading was not involved. The Mooney–Rivlin model [
29] was used to simulate the mechanical properties of rubber materials in this study which considers the aging effect of the rubber materials.
The rubber components of the bearings were simulated with eight-node continuum elements (C3D8H) that use a first order hybrid formulation in which the displacement and pressure fields are integrated independently to prevent the volumetric locking caused by the nearly incompressible behavior of rubber. The Mooney-Rivlin [
29] model was adopted for the rubber material because of the direct relationship between the engineering properties of the rubber and the model parameters. The Mooney-Rivlin model assumes that rubber is isotropic, nonlinear elastic, and incompressible or nearly incompressible and is stated by the strain energy potential
W, that is
In which I1 = the first stress invariant, I2 = the second stress invariant, and C10 and C01 = material parameters. The material parameters which were input into the ABAQUS program were calculated as C10 = 0.32 MPa and C01 = 0.08 MPa, based on the following Equations (2)–(5).
According to the incompressibility of the rubber material, the Poisson’s ratio of rubber is obtained, where
ν = 0.5; hence, the relation between
C10,
C01, and elastic modulus
E0 can be obtained as follows:
An empirical equation between
C01 and
C10:
C01 = 0.25
C10 is proposed in the literature of Gent [
30]. The following Equation (3) can be obtained.
The relation between hardness (
Hr) and the elastic moduli (
E0) of the rubber material is proposed according to the experimental data [
31].
Substituting Equation (3) into Equation (4), the relation between
Hr and
C10 can be obtained as follows:
where
Hr was determined to be 58 in the above experiment. Substituting
Hr into Equation (5),
C10 can be obtained; furthermore,
C01 is also obtained by the equation
C01 = 0.25
C10.
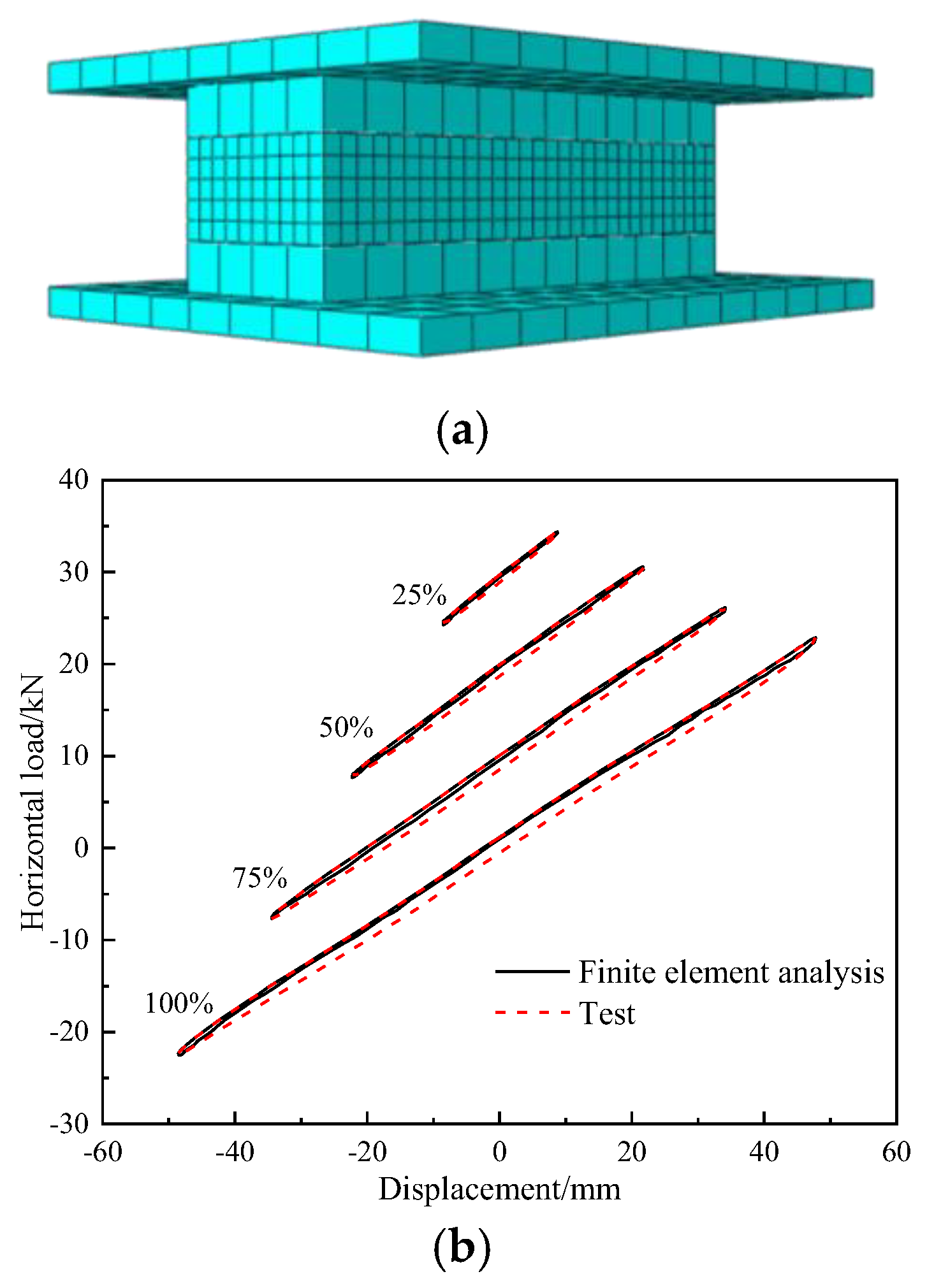
Figure 9a showed three−dimensional views of the mesh for the RBS bearing, which was selected as the mesh with the fewest number of elements that provided a converged solution from a mesh sensitivity analysis.
The finite element model of the RBS was used to simulate the horizontal shearing performance of the bearing. The comparisons of horizontal load-displacement curves between finite element analysis and test were shown in
Figure 9b. The results indicated the comparison between the numerical performance parameters of RBS under varying shear strains and the experimental results. Comparing the finite element analysis results with the experimental results, the error rate is within 0.2%, which indicates that the finite element analysis is in good agreement with the experimental results.