An Experimental Study of Non-Gaussian Properties of Tornado-like Loads on a Low-Rise Building Model
Abstract
:1. Introduction
2. Experimental Setup
2.1. Tornado Simulator
2.2. Building Model and Test Configurations
2.3. Measurements and Data Processing
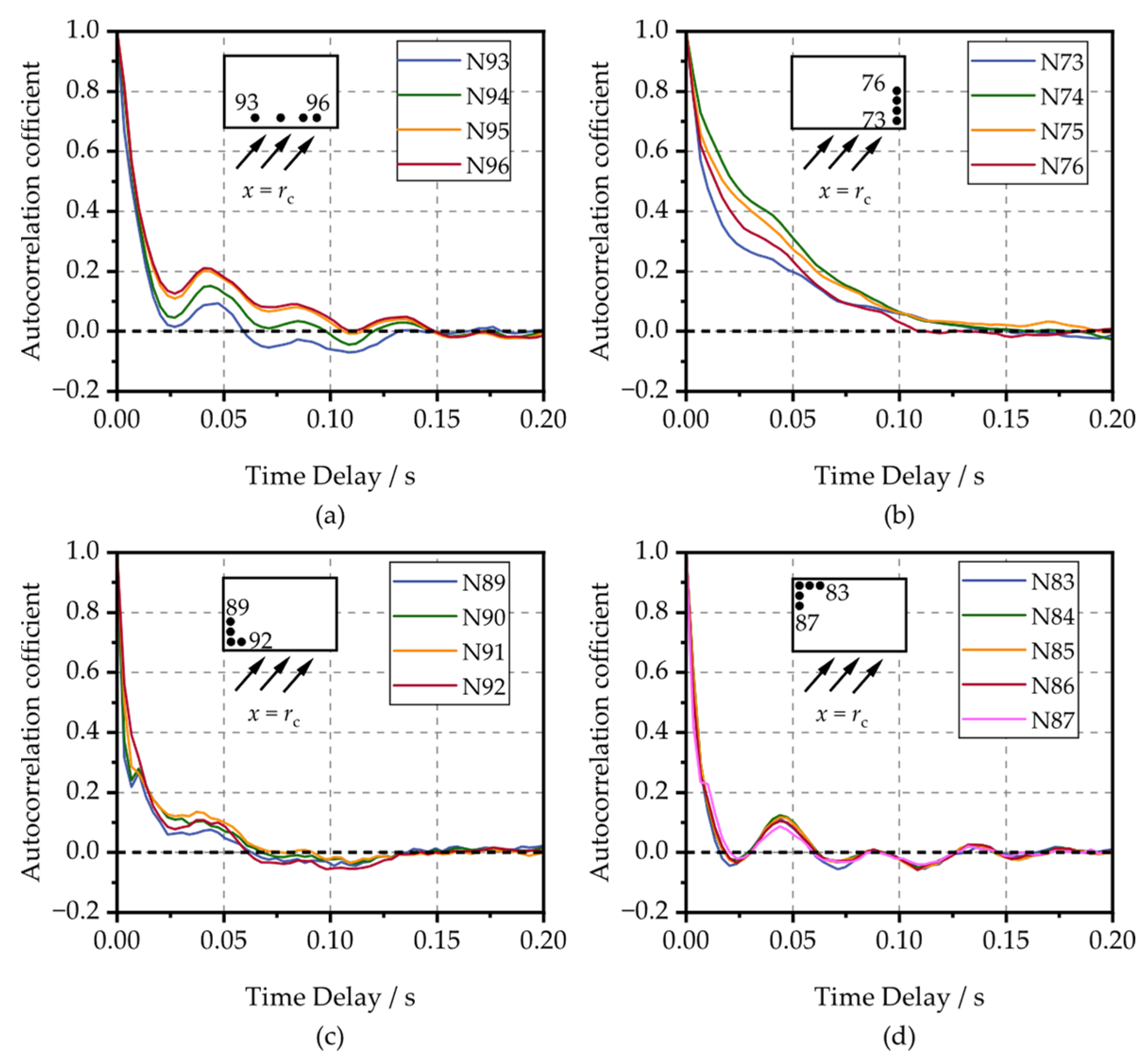
3. Tornado-like Vortex
4. Results and Discussion
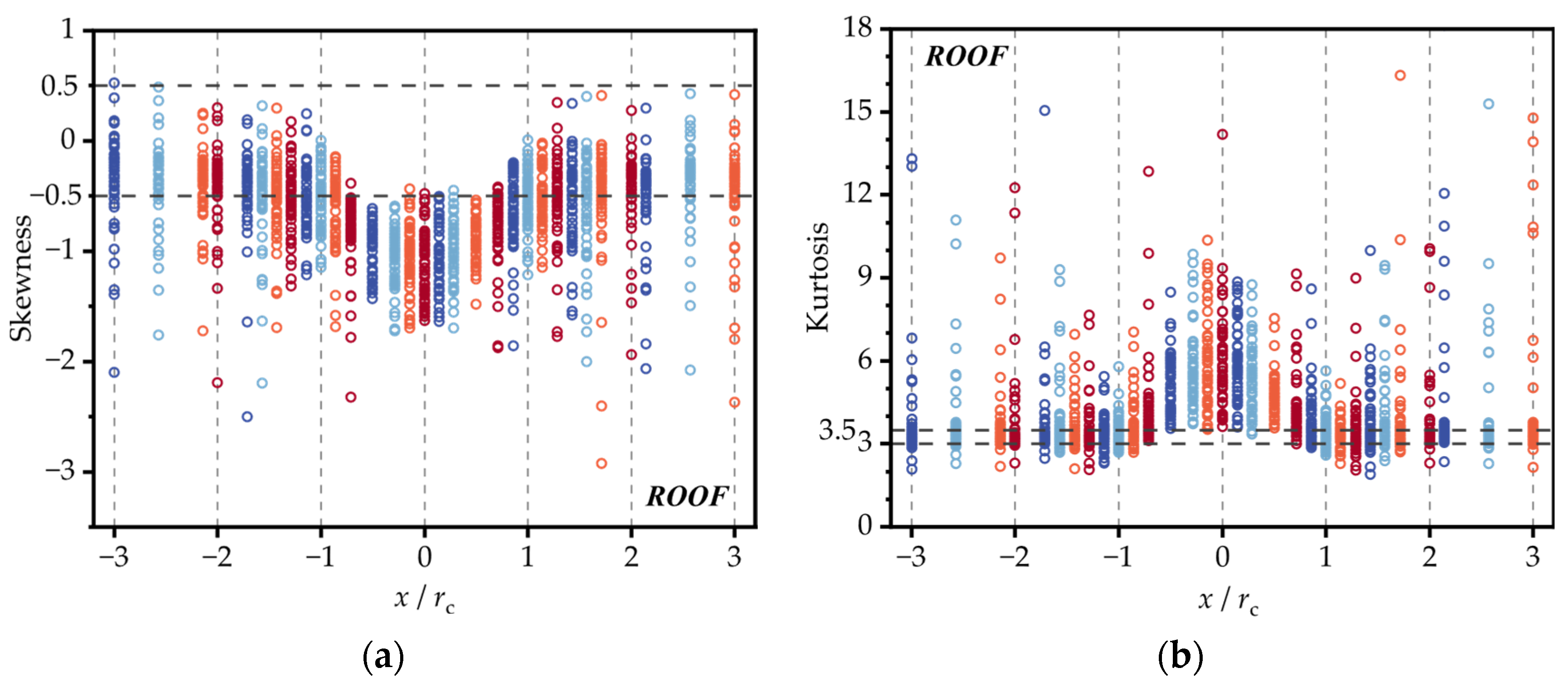
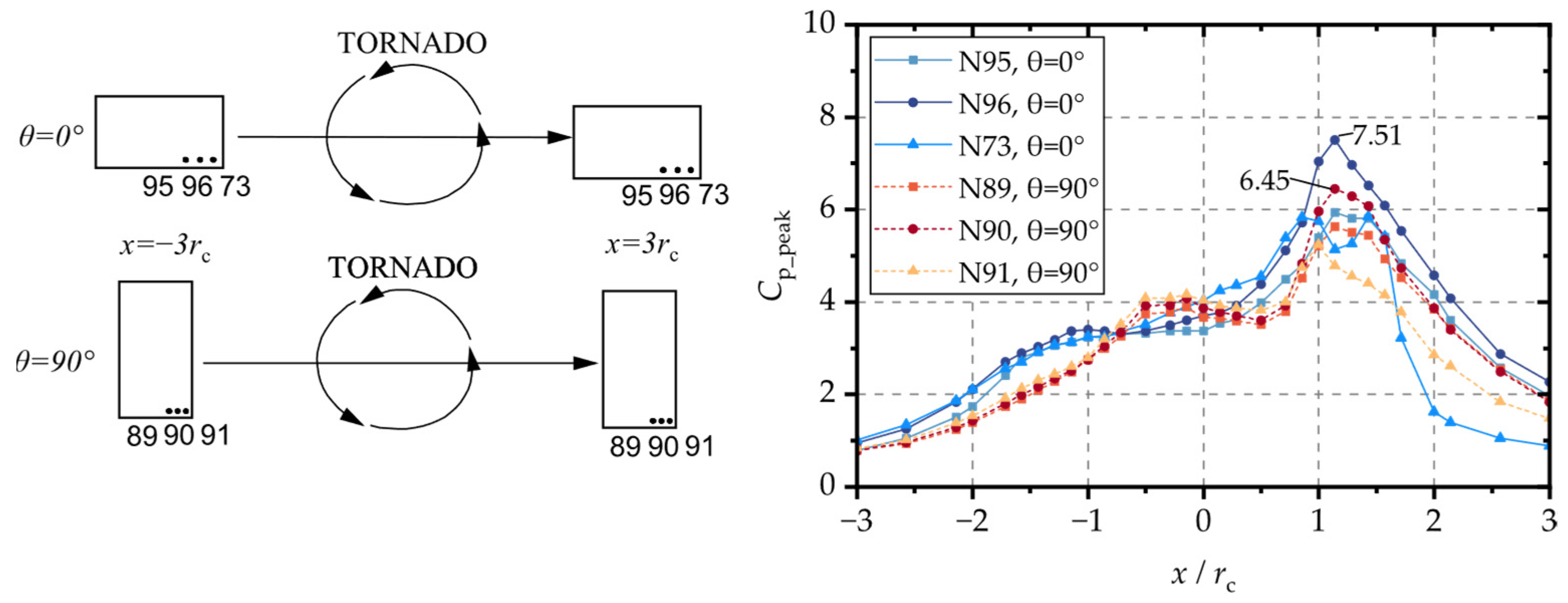
4.1. Non-Gaussian Zone
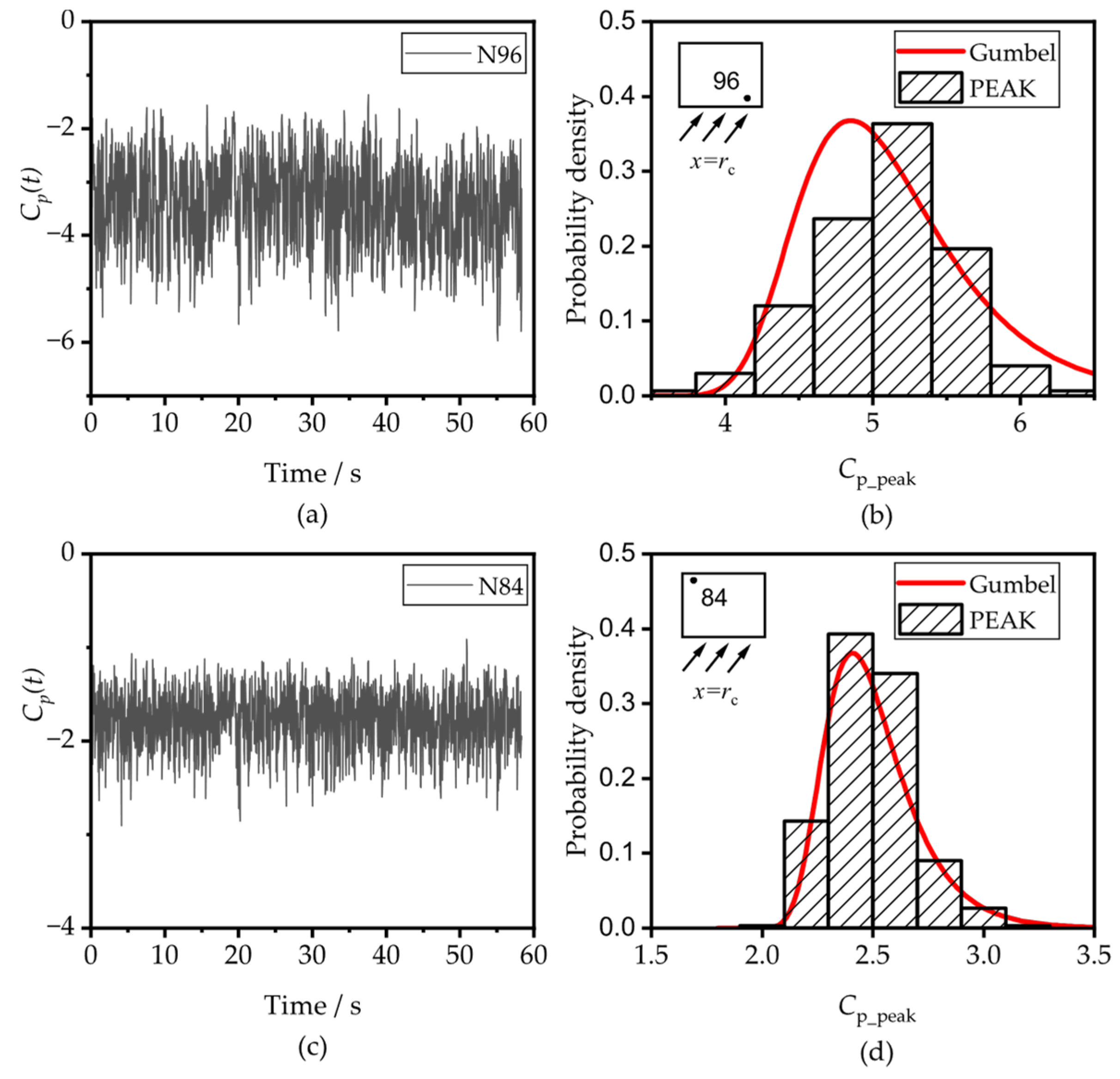
4.2. Extreme Value Estimating of Tornado-like Pressure
- Analyze the autocorrelation function of the original sample and find the time delay when the autocorrelation coefficient drops from 1 to near 0;
- Determine an appropriate time interval t2 and divide the original sample into subsamples at intervals of t2;
- Utilize the Gumbel distribution to fit the distribution of the maximum values of the subsamples and obtain parameters and ;
- Convert and into and using Equations (6) and (7);
- Calculate the expectation of extreme values using Equation (4) with parameters and .
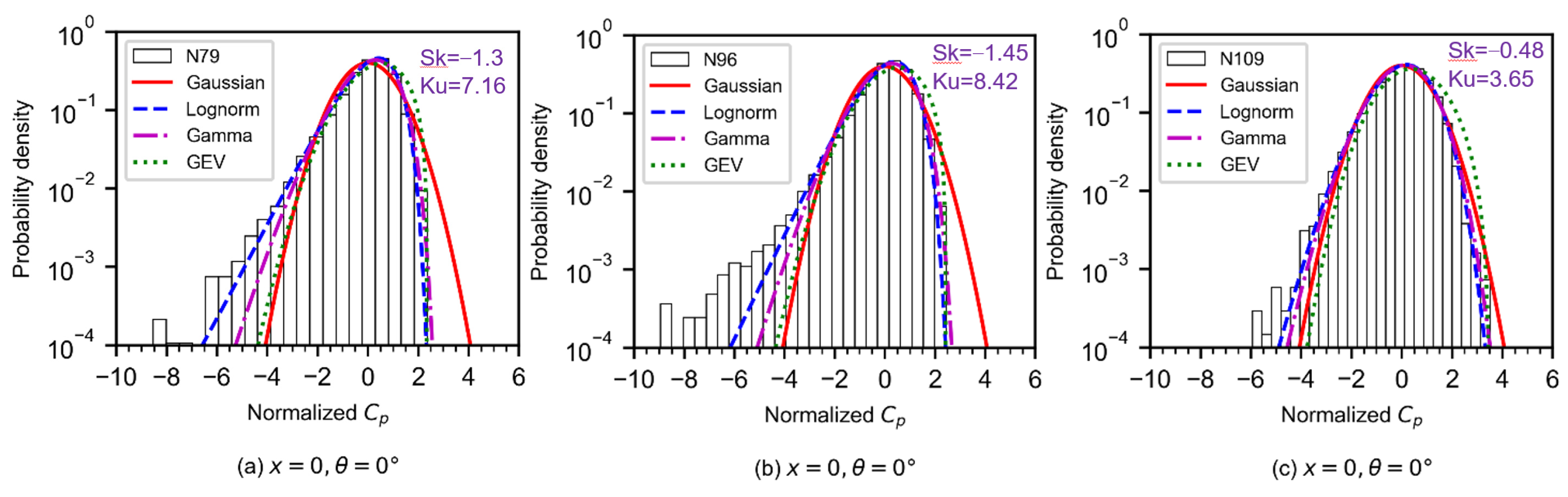
4.3. Probability Density Function of Tornado Pressure Time Series
- The Gaussian distribution:
- The 3-parameter lognormal distribution:
- The 3-parameter gamma distribution:
- The GEV (generalized extreme value) distribution:
4.4. Comparison of Different Peak Factor Methods
5. Conclusions
- At the center of the tornado vortex, the skewness and kurtosis of roof taps are uniformly distributed in a small range, and almost all of the model’s surface is subject to non-Gaussian fluctuations. At the core radius of the tornado vortex, for taps with different spatial locations, their skewness and kurtosis vary greatly from each other. The windward walls and eaves are subject to Gaussian fluctuations, while the middle portion of the roof is subject to non-Gaussian fluctuations.
- The PDF of tornado pressure time series on the surfaces of the buildings cannot be fitted by one certain exponential distribution, especially in the regions of strong non-Gaussianity. Compared with Gaussian distribution and lognormal distribution, the GEV distribution and gamma distribution are the better mathematical models to describe the probability density of tornado pressures at the most unfavorable load position.
- The skewness-dependent peak factor method is the better way to estimate the tornado loads. For a TTU building model in a tornado-like vortex with a swirl ratio of 0.74, the most unfavorable load position is near the end of windward eaves, and the tornado peak factor can be relatively safely taken as 5.6.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, K.S.; Stathopoulos, T. Wind Loads on Low Building Roofs: A Stochastic Perspective. J. Struct. Eng. 2000, 126, 944–956. [Google Scholar] [CrossRef]
- Caracoglia, L.; Jones, N.P. Analysis of Full-Scale Wind and Pressure Measurements on a Low-Rise Building. J. Wind Eng. Ind. Aerodyn. 2009, 97, 157–173. [Google Scholar] [CrossRef]
- Liu, Z.; Prevatt, D.O.; Aponte-Bermudez, L.D.; Gurley, K.R.; Reinhold, T.A.; Akins, R.E. Field Measurement and Wind Tunnel Simulation of Hurricane Wind Loads on a Single Family Dwelling. Eng. Struct. 2009, 31, 2265–2274. [Google Scholar] [CrossRef]
- Tieleman, H.W.; Reinhold, T.A. Wind Tunnel Model Investigation for Basic Dwelling Geometries; Department of Engineering Science & Mechanics: Virginia Polytechnic, VA, USA, 1976. [Google Scholar]
- Gioffrè, M.; Gusella, V.; Grigoriu, M. Non-Gaussian Wind Pressure on Prismatic Buildings. II: Numerical Simulation. J. Struct. Eng. 2001, 127, 990–995. [Google Scholar] [CrossRef]
- Sadek, F.; Simiu, E. Peak Non-Gaussian Wind Effects for Database-Assisted Low-Rise Building Design. J. Eng. Mech. 2002, 128, 530–539. [Google Scholar] [CrossRef] [Green Version]
- Quan, Y.; Wang, F.; Gu, M. A Method for Estimation of Extreme Values of Wind Pressure on Buildings Based on the Generalized Extreme-Value Theory. Math. Probl. Eng. 2014, 2014, e926253. [Google Scholar] [CrossRef] [Green Version]
- Wint’erstein, S.R. Nonlinear Vibration Models for Extremes and Fatigue. J. Eng. Mech. 1988, 114, 1772–1790. [Google Scholar] [CrossRef]
- Yang, L.; Gurley, K.R.; Prevatt, D.O. Probabilistic Modeling of Wind Pressure on Low-Rise Buildings. J. Wind Eng. Ind. Aerodyn. 2013, 114, 18–26. [Google Scholar] [CrossRef]
- Peng, X.; Yang, L.; Gavanski, E.; Gurley, K.; Prevatt, D. A Comparison of Methods to Estimate Peak Wind Loads on Buildings. J. Wind Eng. Ind. Aerodyn. 2014, 126, 11–23. [Google Scholar] [CrossRef]
- Davenport, A.G. The application of statistical concepts to the wind loading of structures. Proc. Inst. Civ. Eng. 1961, 19, 449–472. [Google Scholar] [CrossRef]
- Kareem, A.; Zhao, J. Analysis of Non-Gaussian Surge Response of Tension Leg Platforms Under Wind Loads. J. Offshore Mech. Arct. Eng. 1994, 116, 137–144. [Google Scholar] [CrossRef]
- Huang, M.F.; Chan, C.M.; Kwok, K.C.S.; Lou, W. A Peak Factor for Predicting Non-Gaussian Peak Resultant Response of Wind-Excited Tall Buildings. In Proceedings of the 7th Asia-Pacific Conference on Wind Engineering, Taipei, China, 12 August 2009. [Google Scholar]
- Huang, M.; Lou, W.; Chan, C.-M.; Bao, S. Peak Factors of Non-Gaussian Wind Forces on a Complex-Shaped Tall Building. Struct. Des. Tall Spec. Build. 2013, 22, 1105–1118. [Google Scholar] [CrossRef]
- Lin, W.; Huang, M.F.; Lou, W.J. Peak factor method for non-Gaussian fluctuating pressures on long-span roofs. Build. Struct. 2013, 43, 83–87+14. [Google Scholar] [CrossRef]
- Gao, R. Tornado Characteristics Statistical Analysis and Post-Disaster Investigations in China. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2018. [Google Scholar]
- Ruggieri, S.; Chatzidaki, A.; Vamvatsikos, D.; Uva, G. Reduced-Order Models for the Seismic Assessment of Plan-Irregular Low-Rise Frame Buildings. Earthq. Eng. Struct. Dyn. 2022, 51, 3327–3346. [Google Scholar] [CrossRef]
- Wang, M.; Cao, S.; Cao, J. Tornado-like-Vortex-Induced Wind Pressure on a Low-Rise Building with Opening in Roof Corner. J. Wind Eng. Ind. Aerodyn. 2020, 205, 104308. [Google Scholar] [CrossRef]
- Cao, S.; Wang, J.; Cao, J.; Zhao, L.; Chen, X. Experimental Study of Wind Pressures Acting on a Cooling Tower Exposed to Stationary Tornado-like Vortices. J. Wind Eng. Ind. Aerodyn. 2015, 145, 75–86. [Google Scholar] [CrossRef]
- Case, J.; Sarkar, P.; Sritharan, S. Effect of Low-Rise Building Geometry on Tornado-Induced Loads. J. Wind Eng. Ind. Aerodyn. 2014, 133, 124–134. [Google Scholar] [CrossRef] [Green Version]
- Lewellen, D.C.; Lewellen, W.S.; Xia, J. The Influence of a Local Swirl Ratio on Tornado Intensification near the Surface. J. Atmos. Sci. 2000, 57, 527–544. [Google Scholar] [CrossRef]
- Wang, J. 3D Tornado Wind Field Model and Risk Assessment of Tornado Damage. Ph.D. Thesis, Clemson University, Clemson, SC, USA, 2017. [Google Scholar]
- Tang, Z.; Zuo, D.; James, D.; Eguchi, Y.; Hattori, Y. Experimental Study of Tornado-like Loading on Rectangular Prisms. J. Fluids Struct. 2022, 113, 103672. [Google Scholar] [CrossRef]
- Haan, F.L.; Sarkar, P.P.; Gallus, W.A. Design, Construction and Performance of a Large Tornado Simulator for Wind Engineering Applications. Eng. Struct. 2008, 30, 1146–1159. [Google Scholar] [CrossRef]
- Wang, M.; Cao, S.; Cao, J. Numerical study of tornado-like flow. J. Tongji Univ. (Nat. Sci.) 2019, 47, 1548–1556. [Google Scholar]
- Levitan, M.L.; Mehta, K.C.; Vann, W.P.; Holmes, J.D. Field Measurements of Pressures on the Texas Tech Building. J. Wind Eng. Ind. Aerodyn. 1991, 38, 227–234. [Google Scholar] [CrossRef]
- Quan, Y.; Gu, M.; Chen, B.; Tamura, Y. Study on the extreme value estimating method of non-Gaussian wind pressure. Chin. J. Theor. Appl. Mech. 2010, 42, 560–566. [Google Scholar]

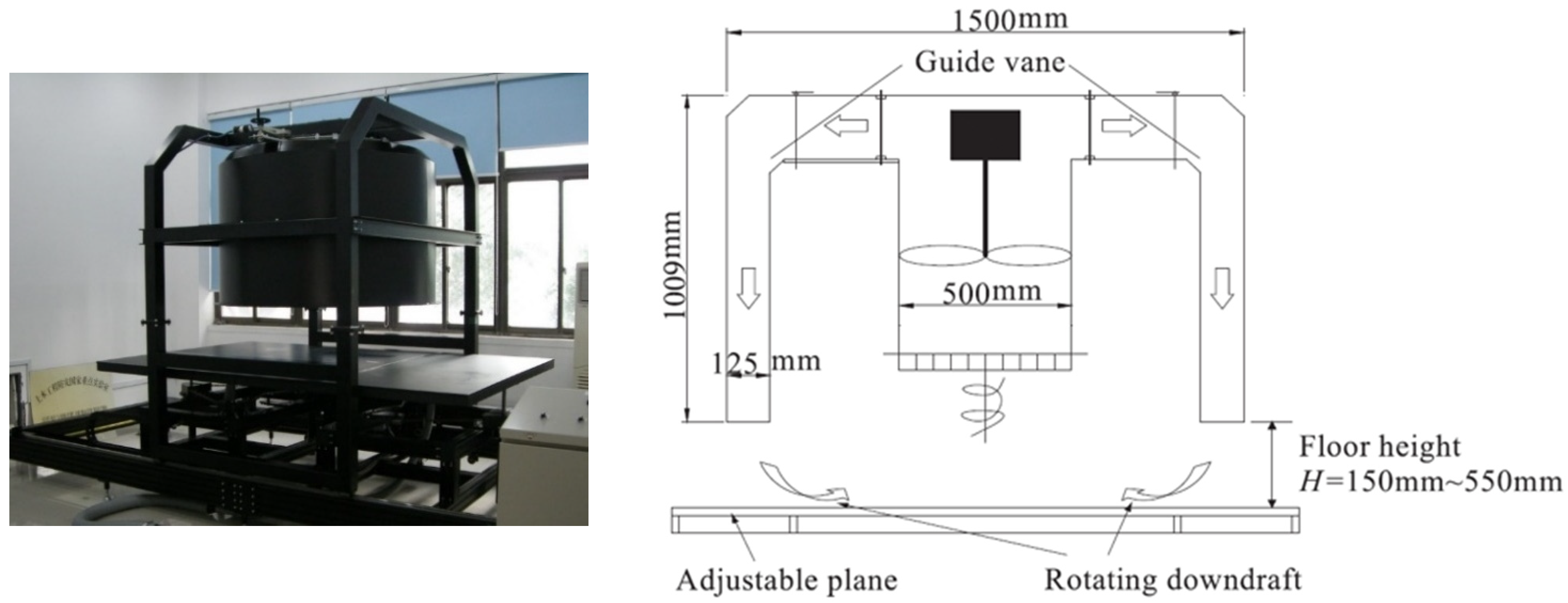
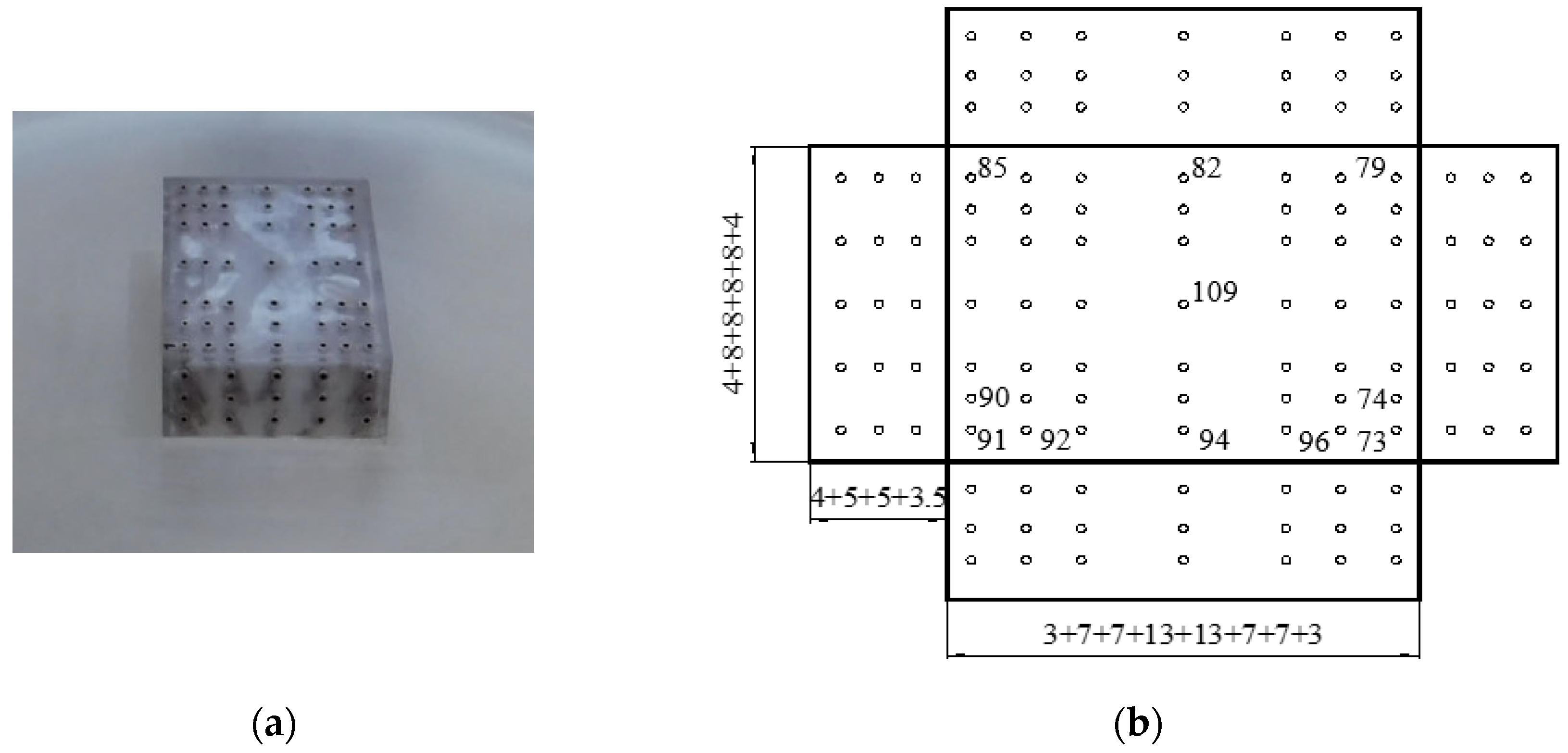
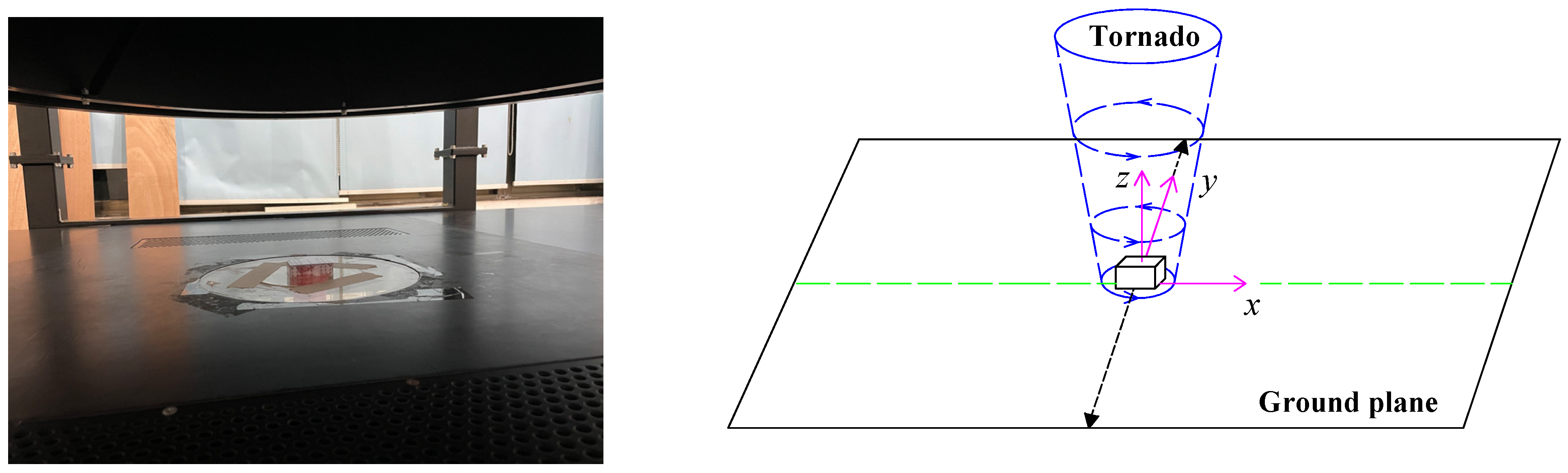







| Parameter | Value |
|---|---|
| Roof type | Flat 1 |
| Length | 60 mm |
| Width | 40 mm |
| Depth | 17.5 mm |
| Length scale | 1:300 |
| Velocity scale | 1:5 |
| Time scale | 1:60 |
| EF Scale | EF0 | EF1 | EF2 | EF3 | EF4 | EF5 |
|---|---|---|---|---|---|---|
| Wind velocity (m/s) | 29–38 | 39–49 | 50–60 | 61–74 | 75–89 | >89 |
| Parameter | Value |
|---|---|
| x/mm | 0, ±10, ±20, ±35, ±50, ±60, ±70, ±80, ±90, ±100, ±110, ±120, ±140, ±160, ±180, ±210 |
| θ/° | 0, 90 |
| Parameter | Value |
|---|---|
| Swirl ratio Sr | 0.74 |
| Maximum tangential velocity Ut, max | 13.4 m/s |
| Height at which Ut, max occurs hc | 15 mm |
| Radius at which Ut, max occurs rc | 70 mm |
| Model Position | Tap Number | Method | Value |
|---|---|---|---|
| x = rc | N96 | Improved Gumbel Method | 5.6 |
| x = rc | N96 | Gaussian Peak Factor Method | 3.6 |
| x = rc | N96 | Sadek–Simiu Method | 4.4 |
| x = rc | N96 | Kareem–Zhao Method | 5.2 |
| x = rc | N96 | Lin Method | 5.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Cao, S. An Experimental Study of Non-Gaussian Properties of Tornado-like Loads on a Low-Rise Building Model. Buildings 2023, 13, 748. https://doi.org/10.3390/buildings13030748
Yang H, Cao S. An Experimental Study of Non-Gaussian Properties of Tornado-like Loads on a Low-Rise Building Model. Buildings. 2023; 13(3):748. https://doi.org/10.3390/buildings13030748
Chicago/Turabian StyleYang, Hanzhang, and Shuyang Cao. 2023. "An Experimental Study of Non-Gaussian Properties of Tornado-like Loads on a Low-Rise Building Model" Buildings 13, no. 3: 748. https://doi.org/10.3390/buildings13030748





