Optimal Design of Segment Storage and Hoisting of Precast Segmental Composite Box Girders with Corrugated Steel Webs
Abstract
:1. Introduction
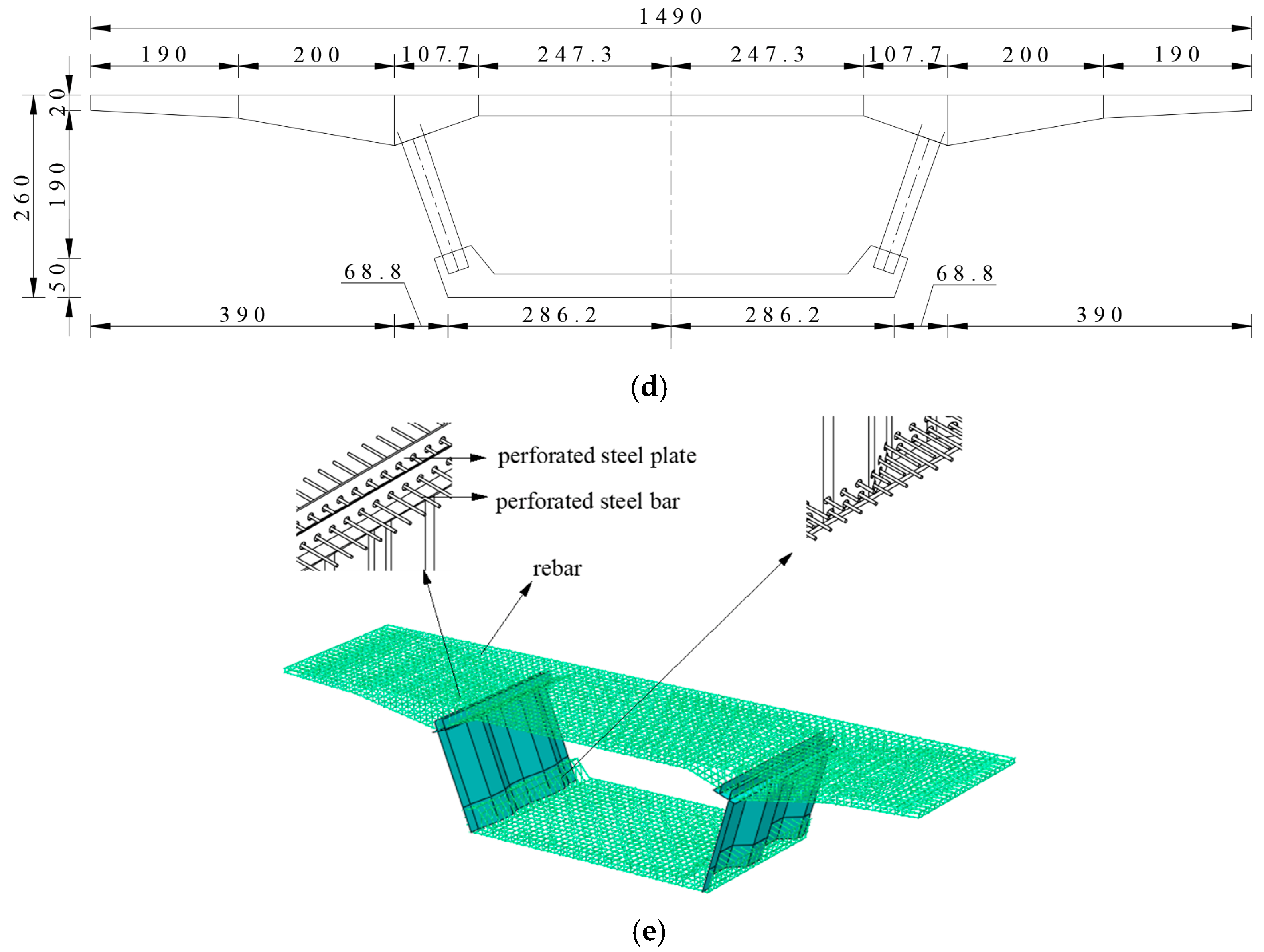
2. Practical Bridge Project
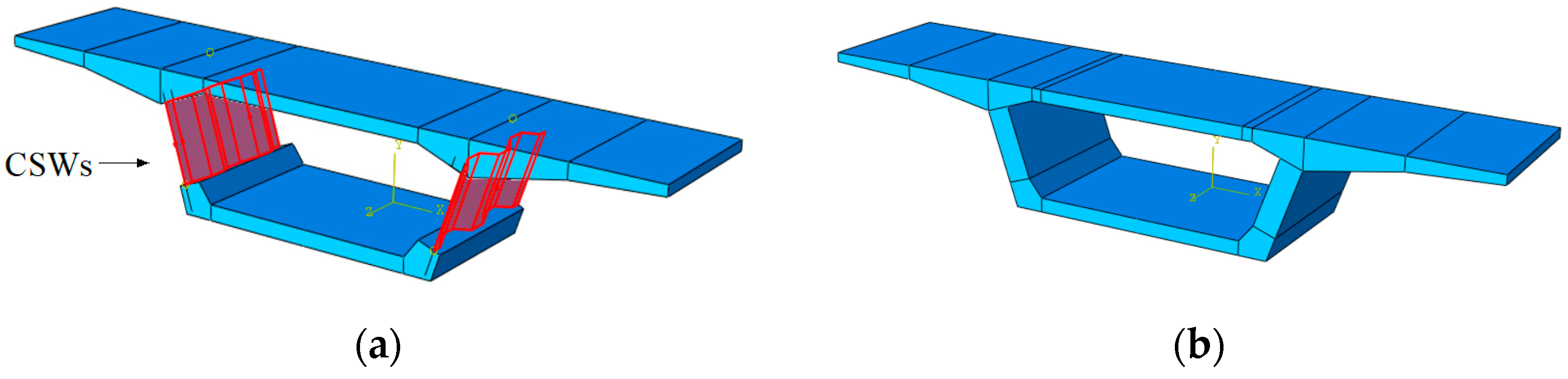
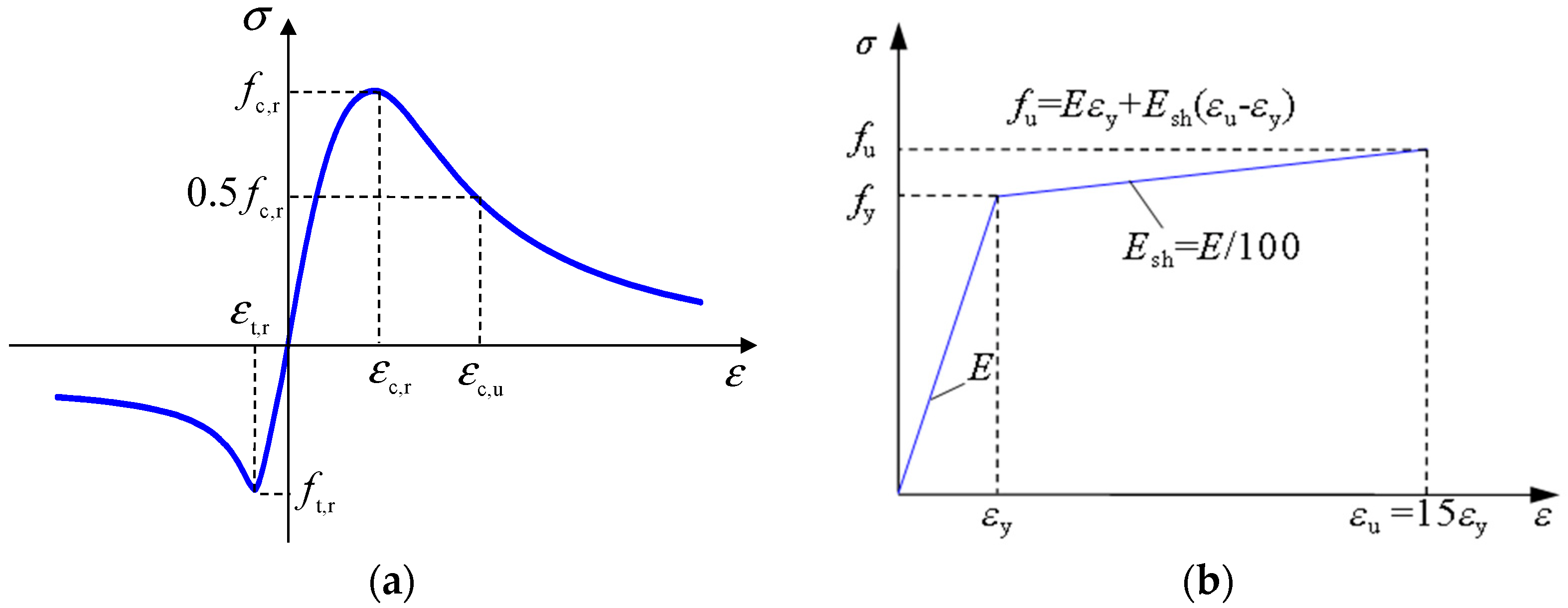
3. Finite Element Model
3.1. Storage Period
3.2. Hoisting Period
4. Comparison of the Mechanical Properties of the Box Girder Segments with Different Webs
5. Analysis of the Mechanical Performance of the Single Segment of a Precast Segmental Composite Box Girder with Corrugated Steel Webs during Storage
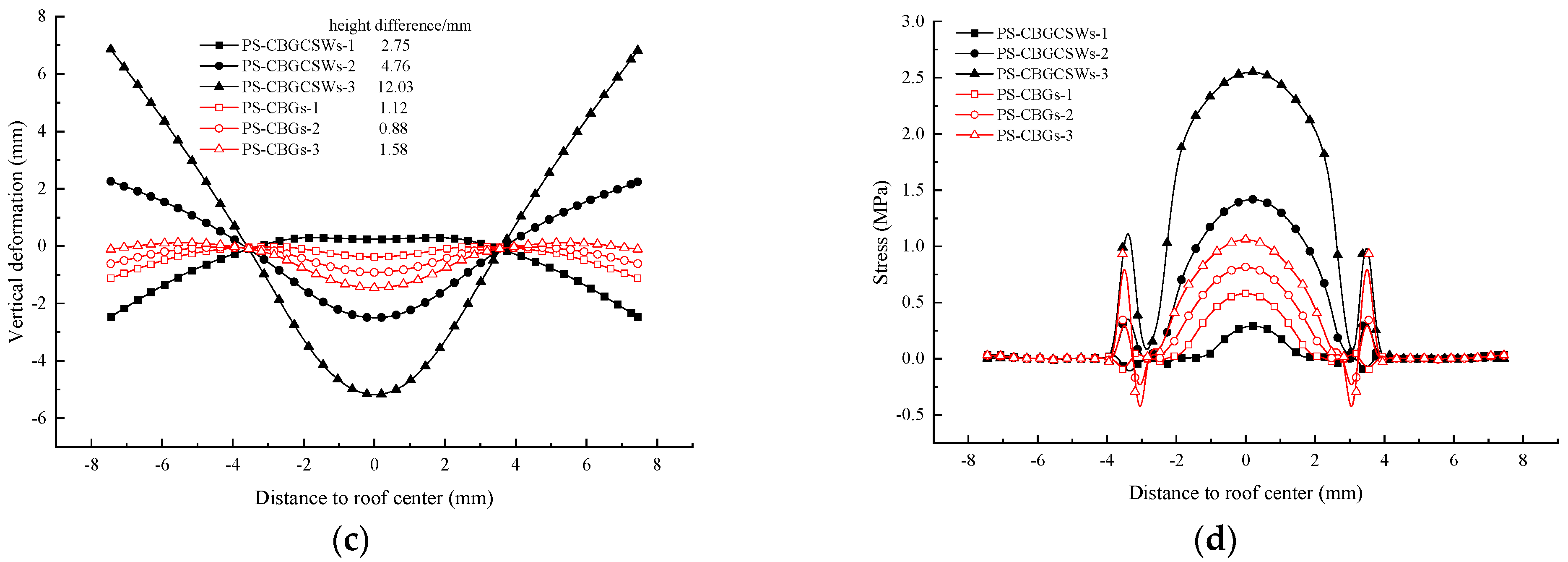
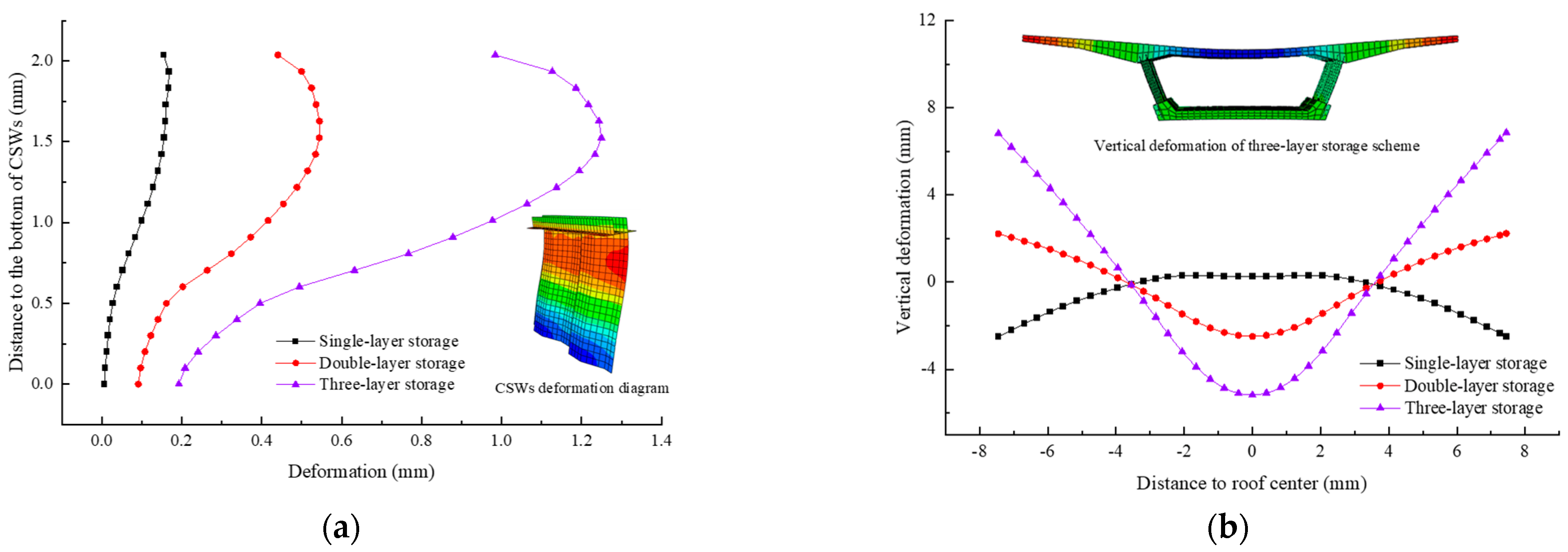
5.1. Number of Storage Layers
5.2. Temporary Support
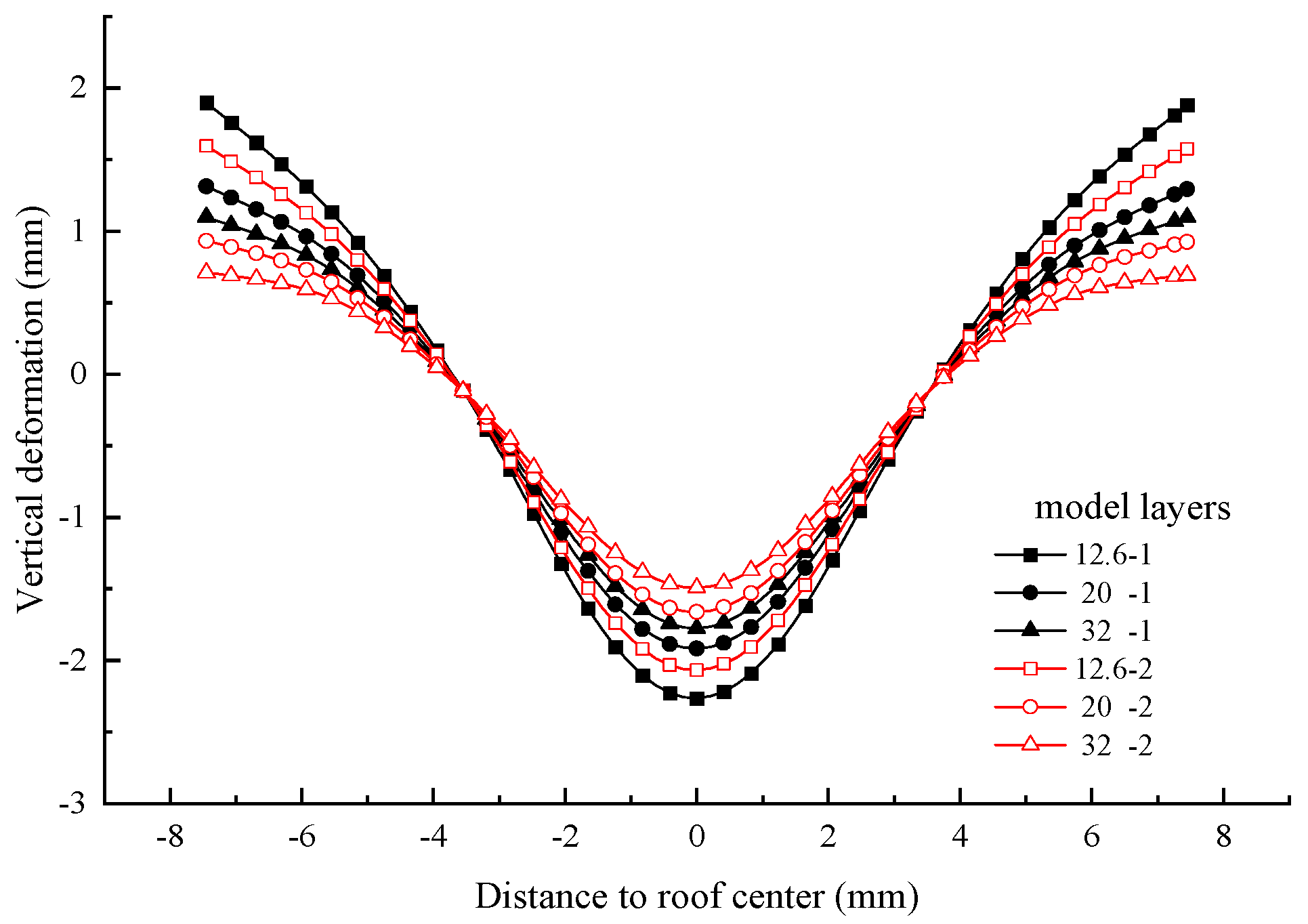
5.3. Segment Length
6. Analysis of the Mechanical Performance of a Single Segment of a Precast Segmental Composite Box Girder with Corrugated Steel Webs during Hoisting
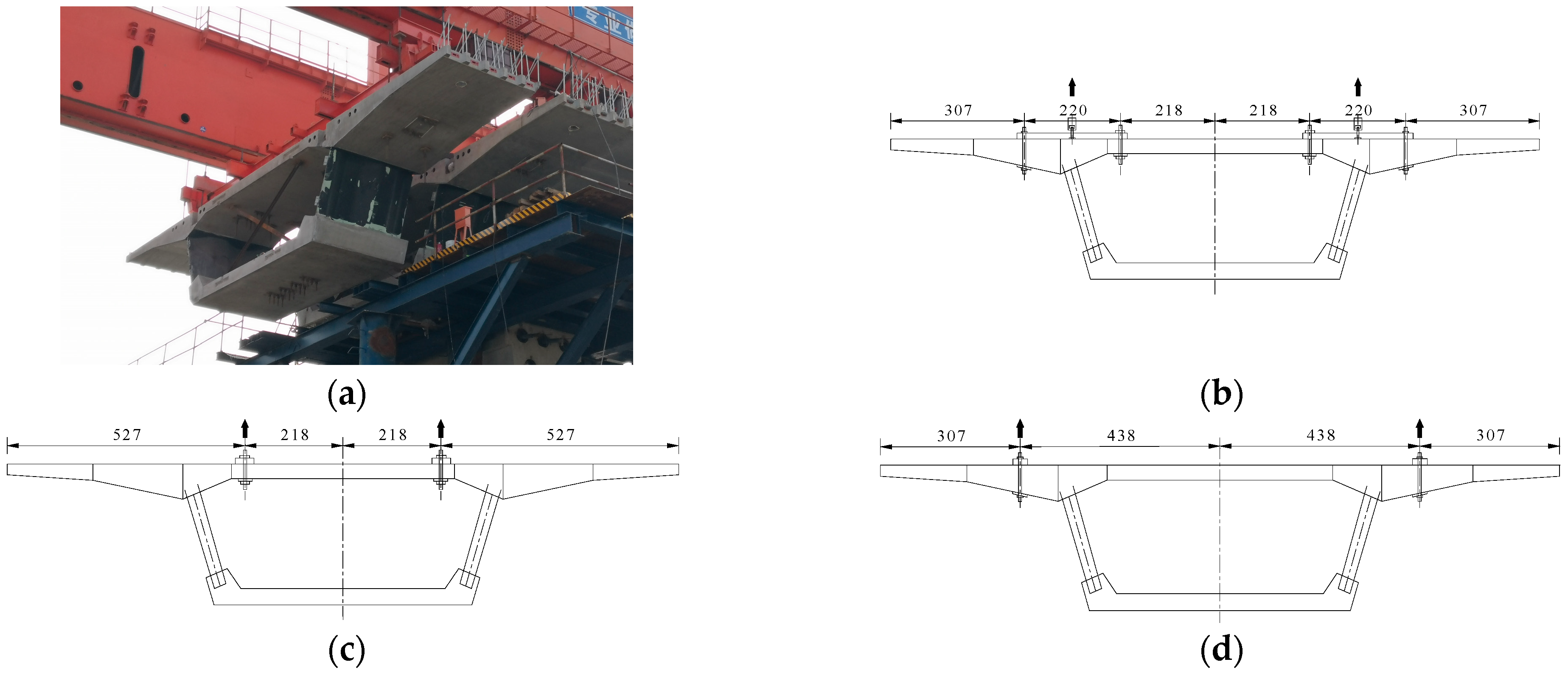
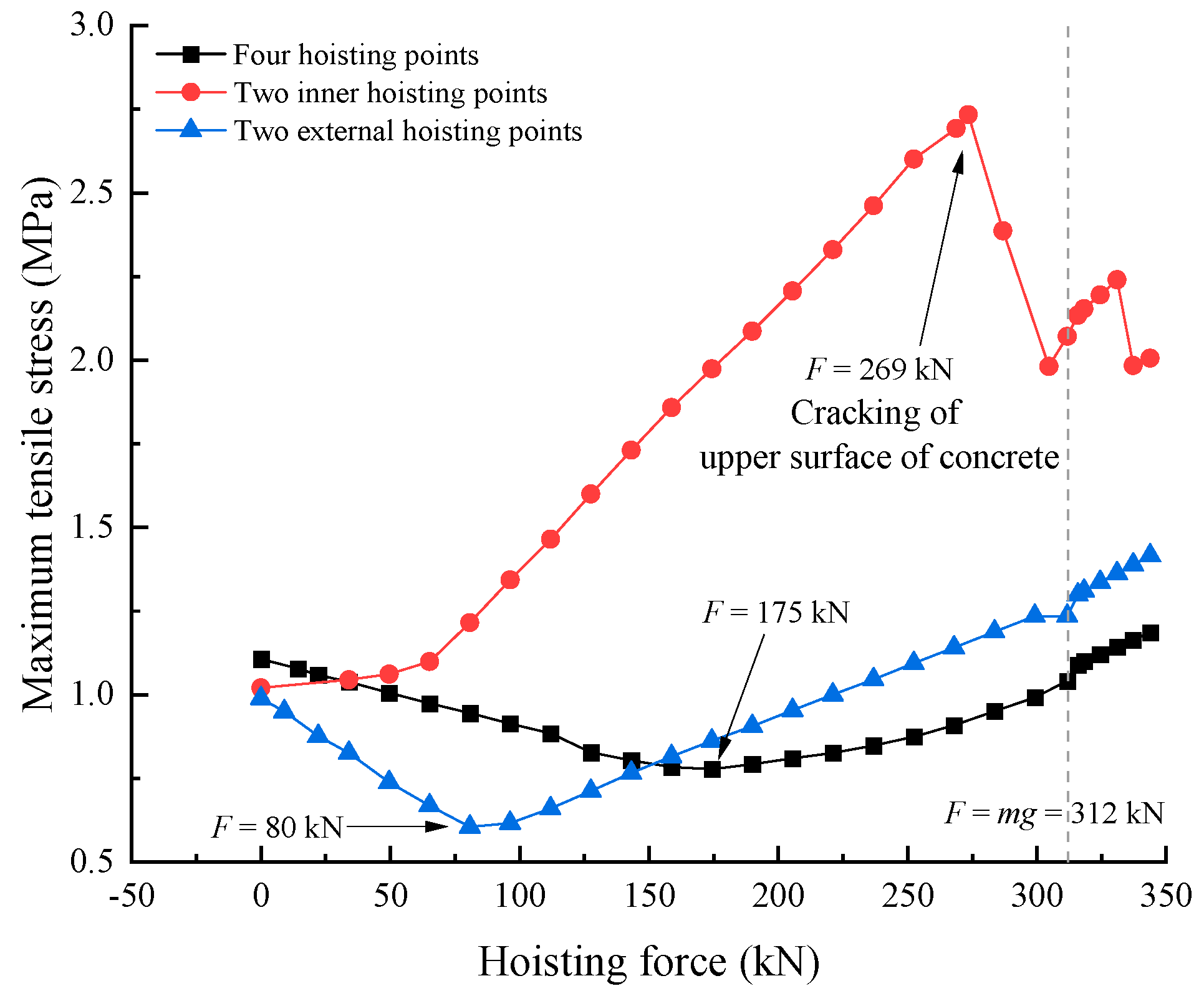
6.1. Number and Location of Hoisting Points
6.2. Temporary Support
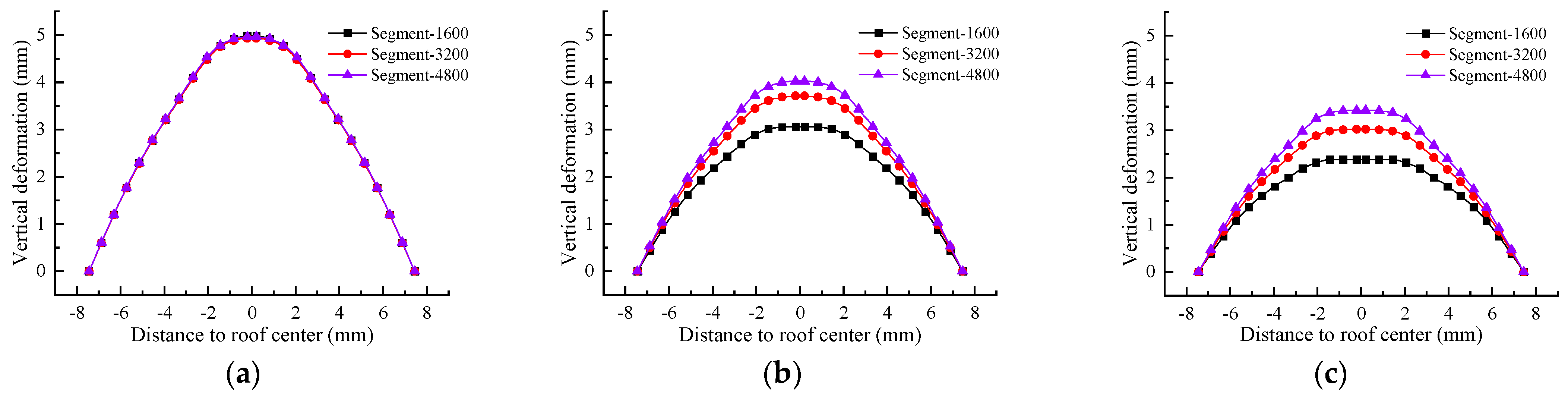
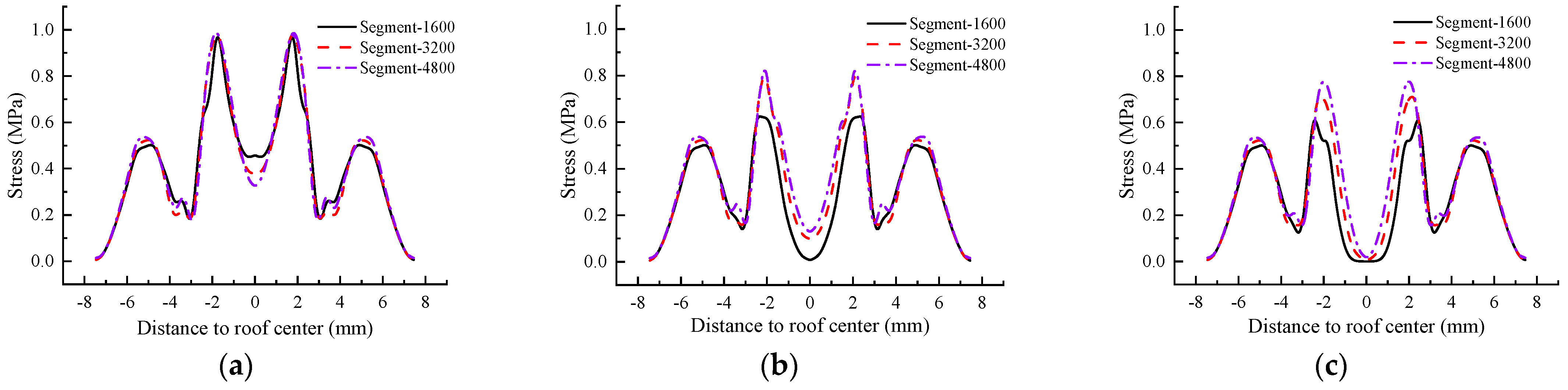
6.3. Segment Length
7. Conclusions
- Compared with precast segmental concrete box girders, due to the weaker torsional and lateral stiffness of the precast segmental composite box girders with corrugated steel webs, regardless of the storage period or the hoisting period, the roof stress and deformation are larger. In particular, the roof deformation of the precast segmental composite box girders with corrugated steel webs is much larger than that of the precast segmental concrete box girders, and the amplitude is approximately 70–80%;
- Due to the low rigidity of CSWs, it is recommended that precast segmental composite box girders with corrugated steel webs should be stored in double layers and should not exceed two layers. Temporary rigid supports should be set between the top and bottom plates of segment girders, the channel steel type should not be less than 20, and one to two supports can be used;
- The four-hoisting point scheme should be adopted for the hoisting of the precast segmental composite box girders with corrugated steel webs segment, that is, four hoisting points should be set near the web to meet the force requirements during the structural hoisting process. We set one to two channels of not less than 20 type channel steel supports between the top and bottom plates (two for 4.8 m segment girders) to prevent the box girders from becoming deformed too much during the hoisting process;
- With the increase in the segment length, the deformation and stress of the roof will increase to a certain extent regardless of the storage period and the hoisting period. To simplify the process, 20 grade channel steel and above can be selected regardless of the length of the segment, and one or two supports are selected according to the importance of the segment girder (two supports are required for the 4.8 m segment girder during the hoisting period). If the safety factor needs to be increased, when the segment length is short (1.6–3.2 m), increasing the support size is recommended. When the segment length is longer (4.0 m, 4.8 m), increasing the number of supports is recommended.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saleem, M.A.; Zafar, M.N.; Saleem, M.M.; Xia, J. Recent developments in the prefabricated bridge deck systems. Case Stud. Constr. Mater. 2021, 15, e00750. [Google Scholar] [CrossRef]
- Wang, X.; Du, Q.; Lu, C.; Li, J. Exploration in carbon emission reduction effect of low-carbon practices in prefabricated building supply chain. J. Clean. Prod. 2022, 368, 133153. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Y.; Ren, D. Quantitative study on external benefits of prefabricated buildings: From perspectives of economy, environment, and society. Sustain. Cities Soc. 2022, 86, 104132. [Google Scholar] [CrossRef]
- Aghasizadeh, S.; Tabadkani, A.; Hajirasouli, A.; Banihashemi, S. Environmental and economic performance of prefabricated construction: A review. Environ. Impact Assess. Rev. 2022, 97, 106897. [Google Scholar] [CrossRef]
- He, Z.Q.; Li, Y.; Xu, T.; Ma, Z.J. Crack-based serviceability assessment of post-tensioned segmental concrete box-girder bridges. Struct. Elsevier 2021, 30, 1097–1108. [Google Scholar] [CrossRef]
- Yan, W.T.; Han, B.; Xie, H.B.; Li, P.F.; Zhu, L. Research on numerical model for flexural behaviors analysis of precast concrete segmental box girders. Eng. Struct. 2020, 219, 110733. [Google Scholar] [CrossRef]
- Sheng, X.; Zhou, T.; Huang, S.; Cai, C.; Shi, T. Prediction of vertical temperature gradient on concrete box-girder considering different locations in China. Case Stud. Constr. Mater. 2022, 16, e01026. [Google Scholar] [CrossRef]
- Yuan, M.; Yan, D.; Zhong, H.; Liu, Y. Experimental investigation of high-cycle fatigue behavior for prestressed concrete box-girders. Constr. Build. Mater. 2017, 157, 424–437. [Google Scholar] [CrossRef]
- Ahmed, G.H.; Aziz, O.Q. Shear behavior of dry and epoxied joints in precast concrete segmental box girder bridges under direct shear loading. Eng. Struct. 2019, 182, 89–100. [Google Scholar] [CrossRef]
- Huang, L.; Hikosaka, H.; Komine, K. Simulation of accordion effect in corrugated steel web with concrete flanges. Comput. Struct. 2004, 82, 2061–2069. [Google Scholar] [CrossRef]
- Oh, J.Y.; Lee, D.H.; Kim, K.S. Accordion effect of prestressed steel beams with corrugated webs. Thin-Walled Struct. 2012, 57, 49–61. [Google Scholar] [CrossRef]
- Inaam, Q.; Upadhyay, A. Accordion effect in bridge girders with corrugated webs. J. Constr. Steel Res. 2022, 188, 107040. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, Z.; Zhang, J.; An, L.; He, Z. Equivalent computational models and deflection calculation methods of box girders with corrugated steel webs. Eng. Struct. 2016, 127, 615–634. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.S.; Lee, D.H.; Choi, S.M.; Choi, Y.H.; Jung, S.H. Flexural behavior of prestressed composite beams with corrugated web: Part I. Development and analysis. Compos. Part B Eng. 2011, 42, 1603–1616. [Google Scholar] [CrossRef]
- Kim, K.S.; Lee, D.H. Flexural behavior of prestressed composite beams with corrugated web: Part II. Experiment and verification. Compos. Part B Eng. 2011, 42, 1617–1629. [Google Scholar] [CrossRef]
- He, J.; Liu, Y.; Chen, A.; Yoda, T. Mechanical behavior and analysis of composite bridges with corrugated steel webs: State-of-the-art. Int. J. Steel Struct. 2012, 12, 321–338. [Google Scholar] [CrossRef]
- Chen, Y.; Dong, J.; Tong, Z.; Jiang, R.; Yue, Y. Flexural behavior of composite box girders with corrugated steel webs and trusses. Eng. Struct. 2020, 209, 110275. [Google Scholar] [CrossRef]
- Shi, F.; Wang, D.; Chen, L. Study of flexural vibration of variable cross-section box-girder bridges with corrugated steel webs. Struct. Elsevier 2021, 33, 1107–1118. [Google Scholar] [CrossRef]
- Zhu, Y.; Shen, K.; Wan, S.; Brigham, J.C.; Fascetti, A.; Zhou, P. Torsional repair of damaged single-box multi-cell composite box-girder with corrugated steel webs using CFRP. Part I: Experimental investigation. Compos. Struct. 2022, 296, 115920. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, Y.; Li, J.; Hai, L.T. Torsional behavior of box-girder with corrugated web and steel bottom flange. J. Constr. Steel Res. 2020, 167, 105855. [Google Scholar] [CrossRef]
- Zhu, Y.; Wan, S.; Shen, K.; Su, Q.; Huang, M. Experimental and numerical study on the nonlinear performance of single-box multi-cell composite box-girder with corrugated steel webs under pure torsion. J. Constr. Steel Res. 2020, 168, 106005. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Zhang, X.; Li, Y.; Wei, X. Coupled bending-torsion behaviour of single-box multi-cell curved composite box-girders with corrugated-steel-webs. J. Constr. Steel Res. 2022, 196, 107411. [Google Scholar] [CrossRef]
- Zhu, Y.; Meng, D.; Zhang, Y.; Hussein, H.H.; He, S. Long-term performance of a continuous box-girder bridge constructed using precast segments with wet ultra-high-performance concrete (UHPC) joints. Case Stud. Constr. Mater. 2022, 17, e01285. [Google Scholar] [CrossRef]
- Do, T.A.; Verdugo, D.; Tia, M.; Hoang, T.T. Effect of volume-to-surface area ratio and heat of hydration on early-age thermal behavior of precast concrete segmental box girders. Case Stud. Therm. Eng. 2021, 28, 101448. [Google Scholar] [CrossRef]
- Ahmed, G.H.; Aziz, O.Q. Stresses, deformations and damages of various joints in precast concrete segmental box girder bridges subjected to direct shear loading. Eng. Struct. 2020, 206, 110151. [Google Scholar] [CrossRef]
- Ahmed, G.H.; Aziz, O.Q. Shear strength of joints in precast posttensioned segmental bridges during 1959-2019, review and analysis. Struct. Elsevier 2019, 20, 527–542. [Google Scholar] [CrossRef]
- Ahmed, G.H.; Aziz, O.Q. Influence of intensity & eccentricity of posttensioning force and concrete strength on shear behavior of epoxied joints in segmental box girder bridges. Constr. Build. Mater. 2019, 197, 117–129. [Google Scholar]
- Zhang, Z.; Zou, P.; Deng, E.F.; Ye, Z.; Tang, Y.; Li, F.R. Experimental study on prefabricated composite box girder bridge with corrugated steel webs. J. Constr. Steel Res. 2023, 201, 107753. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Liu, X.L.; Hu, L.Y.; Wang, Y.; Chen, W.Q.; Xu, R.Q. Zig-zag theory for concrete beams with corrugated steel webs. Eng. Struct. 2022, 258, 114100. [Google Scholar] [CrossRef]
- Wang, T.; Ma, J. Shear buckling stress and normalized shear strength of trapezoidal corrugated steel web. J. Build. Eng. 2022, 57, 104807. [Google Scholar] [CrossRef]
- Chan, C.L.; Khalid, Y.A.; Sahari, B.B.; Hamouda, A.M.S. Finite element analysis of corrugated web beams under bending. J. Constr. Steel Res. 2002, 58, 1391–1406. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Kharoob, O.F. Behavior of bridge girders with corrugated webs: (I) Real boundary condition at the juncture of the web and flanges. Eng. Struct. 2013, 57, 554–564. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Kharoob, O.F. Behavior of bridge girders with corrugated webs: (II) Shear strength and design. Eng. Struct. 2013, 57, 544–553. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Kharoob, O.F. Shear buckling behavior of tapered bridge girders with steel corrugated webs. Eng. Struct. 2014, 74, 157–169. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Elkawas, A.A.; El Hadidy, A.M.; Elchalakani, M. Shear analysis and design of high-strength steel corrugated web girders for bridge design. Eng. Struct. 2017, 146, 18–33. [Google Scholar] [CrossRef]
- Mo, Y.L.; Fan, Y.L. Torsional design of hybrid concrete box girders. J. Bridge Eng. 2006, 11, 329–339. [Google Scholar] [CrossRef]
- Ding, Y.; Jiang, K.B.; Liu, Y.W. Nonlinear analysis for PC box-girder with corrugated steel webs under pure torsion. Thin-Walled Struct. 2012, 51, 167–173. [Google Scholar] [CrossRef]
- Shen, K.; Wan, S.; Mo, Y.L.; Li, X.; Song, A. A softened membrane model for composite box-girders with corrugated steel webs under pure torsion. Eng. Struct. 2018, 173, 357–371. [Google Scholar] [CrossRef]
- Zhou, C.; Li, L.; Wang, L. Improved softened membrane model for prestressed composite box girders with corrugated steel webs under pure torsion. J. Constr. Steel Res. 2019, 153, 372–384. [Google Scholar] [CrossRef]
- Li, L.; Zhou, C.; Wang, L. Distortion analysis of non-prismatic composite box girders with corrugated steel webs. J. Constr. Steel Res. 2018, 147, 74–86. [Google Scholar] [CrossRef]
- Zhou, M.; Liu, Y.; Deng, W.Q.; Hassanein, M.F.; Zhang, H. Transverse analysis of full-scale precast segmental box girder segments with corrugated steel webs: Experimental tests and FE modelling. Eng. Struct. 2019, 187, 231–241. [Google Scholar] [CrossRef]



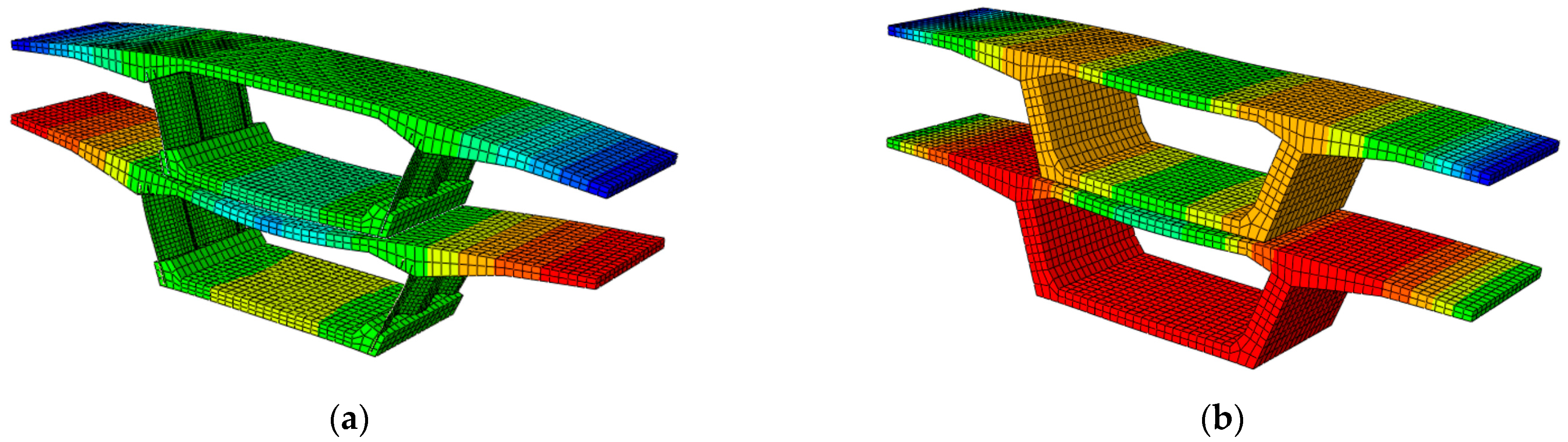





| Component | Material | Elastic Modulus (MPa) | Poisson Ratio | Density (t/mm3) |
|---|---|---|---|---|
| Concrete slabs | C50 | 3.45 × 104 | 0.2 | 2.5 × 10−9 |
| Rebar | HRB400 | 2 × 105 | 0.3 | 7.85 × 10−9 |
| Steel plate | Q345 | 2 × 105 | 0.3 | 7.85 × 10−9 |
| Scissor support | Q235 | 2 × 105 | 0.3 | 7.85 × 10−9 |
| Scheme | Roof Max Principal Stress (MPa) | CSWs Max Stress (MPa) | Roof Deformation (mm) |
|---|---|---|---|
| Single-layer storage | 1.01 | 21.02 | 2.804 |
| Double-layer storage | 1.44 | 62.49 | 4.829 |
| Triple-layer storage | 2.58 | 132.10 | 12.000 |
| Channel Steel Model | Double-Layer Storage | Triple-Layer Storage | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 Support | 2 Supports | 1 Support | 2 Supports | |||||
| Stress (MPa) | Deformation (mm) | Stress (MPa) | Deformation (mm) | Stress (MPa) | Deformation (mm) | Stress (MPa) | Deformation (mm) | |
| 12.6 | 1.347 | 4.265 | 1.274 | 3.755 | 2.407 | 11.140 | 2.257 | 10.181 |
| 20 | 1.225 | 3.330 | 1.119 | 2.672 | 2.286 | 9.528 | 2.206 | 8.644 |
| 32 | 1.179 | 2.974 | 1.058 | 2.278 | 2.431 | 9.264 | 1.849 | 6.660 |
| Segment Length (m) | 0 Support | 1 Support | 2 Supports | ||||
|---|---|---|---|---|---|---|---|
| 12.6 | 20 | 32 | 12.6 | 20 | 32 | ||
| 1.6 | 4.496 | 3.502 | 2.553 | 2.118 | 2.829 | 1.854 | 1.476 |
| 3.2 | 4.829 | 4.265 | 3.330 | 2.974 | 3.755 | 2.672 | 2.278 |
| 4.8 | 4.808 | 4.445 | 3.750 | 3.336 | 4.055 | 3.020 | 2.745 |
| Segment Length (m) | 0 Support | 1 Support | 2 Supports | ||||
|---|---|---|---|---|---|---|---|
| 12.6 | 20 | 32 | 12.6 | 20 | 32 | ||
| 1.6 | 1.376 | 1.233 | 1.098 | 1.033 | 1.140 | 1.007 | 0.936 |
| 3.2 | 1.431 | 1.347 | 1.225 | 1.179 | 1.274 | 1.119 | 1.058 |
| 4.8 | 1.451 | 1.412 | 1.327 | 1.274 | 1.338 | 1.188 | 1.143 |
| Hoisting Force (kN) | Four Hoisting Points | Two Inner Hoisting Points | Two External Hoisting Points | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Roof Stress (MPa) | Roof Deformation (mm) | CSWs Deformation (mm) | Roof Stress (MPa) | Roof Deformation (mm) | CSWs Deformation (mm) | Roof Stress (MPa) | Roof Deformation (mm) | CSWs Deformation (mm) | |
| 0 | 1.02 | 2.67 | 0.17 | 1.02 | 2.67 | 0.17 | 1.02 | 2.67 | 0.17 |
| 175/269/80 1 | 0.78 | 3.09 | 0.22 | 2.71 | 12.90 | 1.19 | 0.61 | 0.76 | −0.03 |
| 312 | 1.04 | 4.49 | 0.44 | 2.07 | 16.62 | 1.60 | 1.24 | −5.99 | −0.56 |
| 318 | 1.10 | 4.67 | 0.45 | 2.15 | 17.15 | 1.66 | 1.31 | −6.11 | −0.57 |
| 331 | 1.14 | 4.75 | 0.47 | 2.24 | 17.83 | 1.72 | 1.36 | −6.36 | −0.60 |
| 344 | 1.18 | 4.93 | 0.49 | 2.01 | 18.60 | 1.79 | 1.42 | −6.60 | −0.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Q.; Deng, W.; Liu, D.; Pei, H.; Peng, Z.; Zhang, J. Optimal Design of Segment Storage and Hoisting of Precast Segmental Composite Box Girders with Corrugated Steel Webs. Buildings 2023, 13, 801. https://doi.org/10.3390/buildings13030801
Song Q, Deng W, Liu D, Pei H, Peng Z, Zhang J. Optimal Design of Segment Storage and Hoisting of Precast Segmental Composite Box Girders with Corrugated Steel Webs. Buildings. 2023; 13(3):801. https://doi.org/10.3390/buildings13030801
Chicago/Turabian StyleSong, Qigang, Wenqin Deng, Duo Liu, Huiteng Pei, Zongqing Peng, and Jiandong Zhang. 2023. "Optimal Design of Segment Storage and Hoisting of Precast Segmental Composite Box Girders with Corrugated Steel Webs" Buildings 13, no. 3: 801. https://doi.org/10.3390/buildings13030801
APA StyleSong, Q., Deng, W., Liu, D., Pei, H., Peng, Z., & Zhang, J. (2023). Optimal Design of Segment Storage and Hoisting of Precast Segmental Composite Box Girders with Corrugated Steel Webs. Buildings, 13(3), 801. https://doi.org/10.3390/buildings13030801





