Lateral Distortional Buckling Resistance Predictions of Composite Alveolar Beams: A Review

Abstract

Few studies have investigated the structural behavior of steel-concrete composite alveolar beams in hogging bending regions. Their resistance can be reached by lateral distortional buckling (LDB), coupling LDB and local failure modes, or limit states of cracking or crushing in the concrete slab. This case is characteristic of continuous or cantilever elements. Another critical issue is that the design and calculation recommendations only address the LDB verification on steel-concrete composite beams without web openings, thus disregarding the interaction between the buckling modes. Furthermore, it is necessary to use adaptations of these formulations for beams with web openings. This review paper aims to evaluate the different approaches for standard code adaptations to verify the LDB resistance of the beams in question and to highlight the investigations that addressed this issue. The addressed adaptations consist of different approaches which determine the cross-section geometric properties in the central region of the openings, the so-called double T section, in the region of the web posts (solid section), and the averages between the solid section and double T section. The accuracy of the formulations in question is verified against experimental results from the literature. Furthermore, discussions and suggestions for further studies are presented.

1. Introduction

Steel profiles generally meet the resistance needs obtained in the structural pre-dimensioning of beams with large spans and relatively low loads. However, there is difficulty in meeting the service requirements. In this case, there is a need for beams with greater height and, consequently, greater stiffness. This kind of situation usually occurs in roof structures (sports halls, industrial sheds, supermarkets, theaters), parking buildings, bridges, walkways, and bus station floors [1].

The use of steel profiles with sequential web openings is an adequate solution to this problem. These profiles have greater flexural stiffness when compared to the parent profile used for its manufacturing. Moreover, beams with web openings allow the passage of ducts that favor integration between services [2].

The first kind of steel profiles with sequential web openings were the ones with hexagonal opening geometry. These beams received the nomenclature of castellated beams, as their geometry is similar to the walls of medieval castles [3]. As an alternative to castellated beams, the steel beams with circular web openings, known as cellular beams, were consolidated. Castellated beams require only one cut with a zig-zag pattern along their web (Figure 1), and cellular beams require two cuts in a semicircular pattern (Figure 2). Although cellular beams were developed primarily for architectural application, being considered aesthetically pleasing, they produce an efficient and economical solution due to their geometry [4]. Figure 3 shows the geometric parameters of castellated and cellular beams.

The considerable gain in the resistant capacity of the floor system justifies the use of alveolar profiles in steel-concrete composite beams. Thus, these beams can be designed to cover spans from 12 to 20 m [8,9]. However, the behavior of steel alveolar beams becomes more complex than steel profiles without sequential web openings [10]. Alveolar profiles are susceptible to different types of buckling modes or their interaction [10,11,12]. The increase in the composite alveolar beam resistance over non-composite beams is more evident in long spans [13]. Figure 4a,b show examples of composite castellated and cellular beams with steel deck slab, respectively.

Steel-concrete composite beams subjected to hogging moment are characteristics of continuous or cantilever elements. Continuous composite beams present hogging moments near to supports. On the other hand, cantilever composite beams are submitted to hogging moment in all their span.

The steel I-section is compressed in hogging moment regions of steel-concrete composite beams, and the concrete slab is tensioned [15]. Due to this, these beams can reach failure by lateral distortional buckling (LDB), an instability mode characterized by a lateral displacement and rotation of the lower flange accompanied by web distortion (Figure 5a) [16]. Since the steel profile is subjected to compressive stress, the lower flange tends to move laterally out of the bending plane. When the profile web does not have enough flexural stiffness to contain this lower flange lateral displacement, the LDB can occur [17], as shown in Figure 5b. The LDB behavior of the steel-concrete composite beams without web openings was considerably investigated. Elastic numerical analyses [18,19,20,21,22,23], inelastic numerical analyses [16,24,25,26,27,28,29,30,31], and experimental tests [32,33,34,35,36,37,38,39,40] were conducted. In addition to LDB, web local buckling has also been addressed by experimental and numerical investigations [41,42,43,44,45]. Additionally, studies have assessed ways to improve the cracking of the concrete slab of these beams, such as the use of high-performance concrete (HPC) [46], ultra-high-performance concrete (UHPC) [47,48,49], engineered cementitious composite (ECC) [49,50], prestressed concrete slabs [51], and carbon fiber-reinforced polymer (CFRP) [52]. Other issues, such as the shear interaction steel beam-concrete slab [53,54,55], beam-to-column joints [56], and residual deflections [57], have also been studied for the beams in question.

Among the few experimental studies that evaluated the behavior of composite alveolar beams under hogging bending [58,59,60], Salah [58] and Gizejowski and Salah [59] present the only tests in which the beams showed instability modes by the LDB (Figure 6). In all, only five investigations that analyzed the LDB in composite alveolar beams were found; the main focus of each is summarized in

Table 1. Investigations on the LDB behavior of composite alveolar beam.

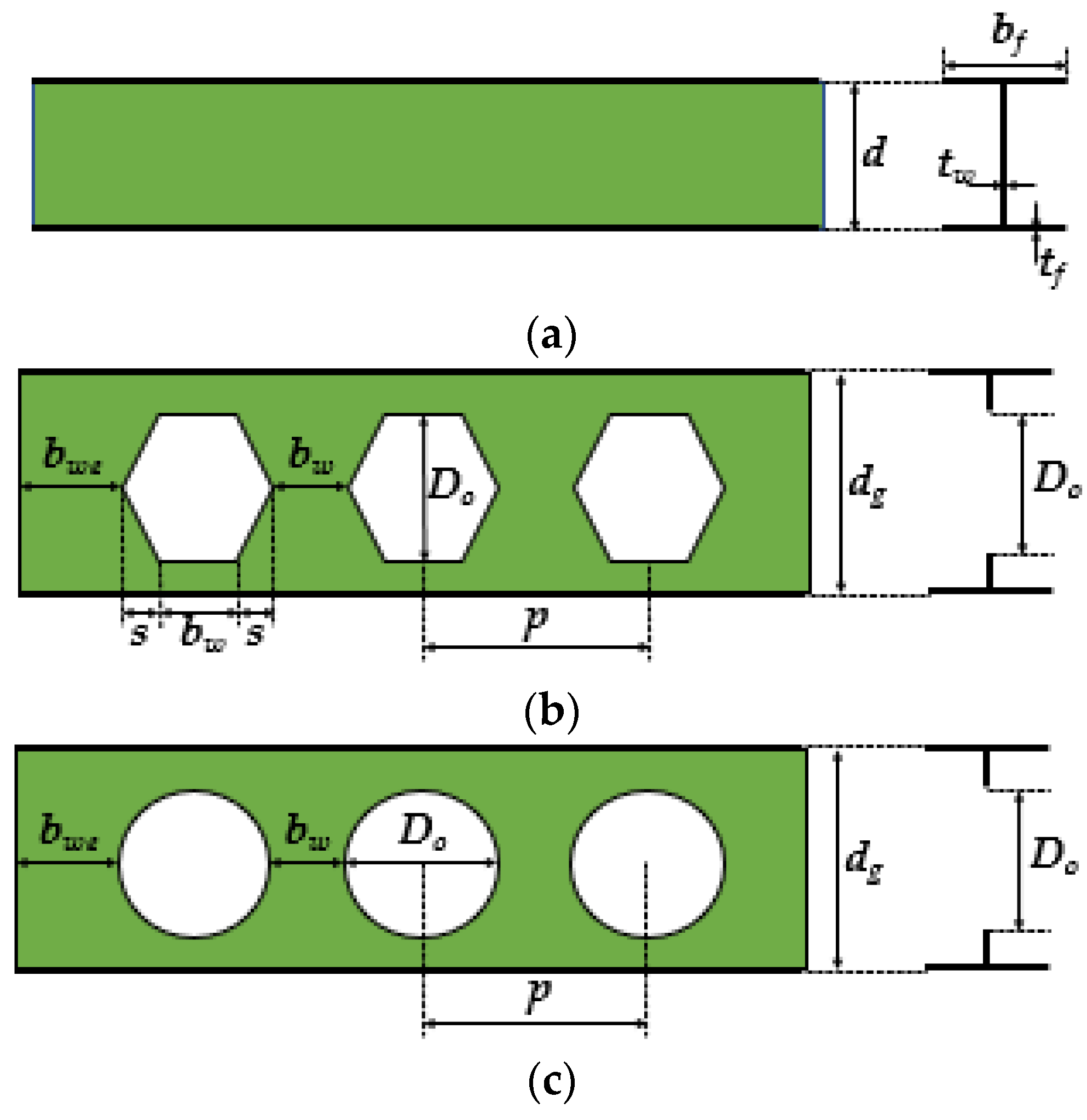
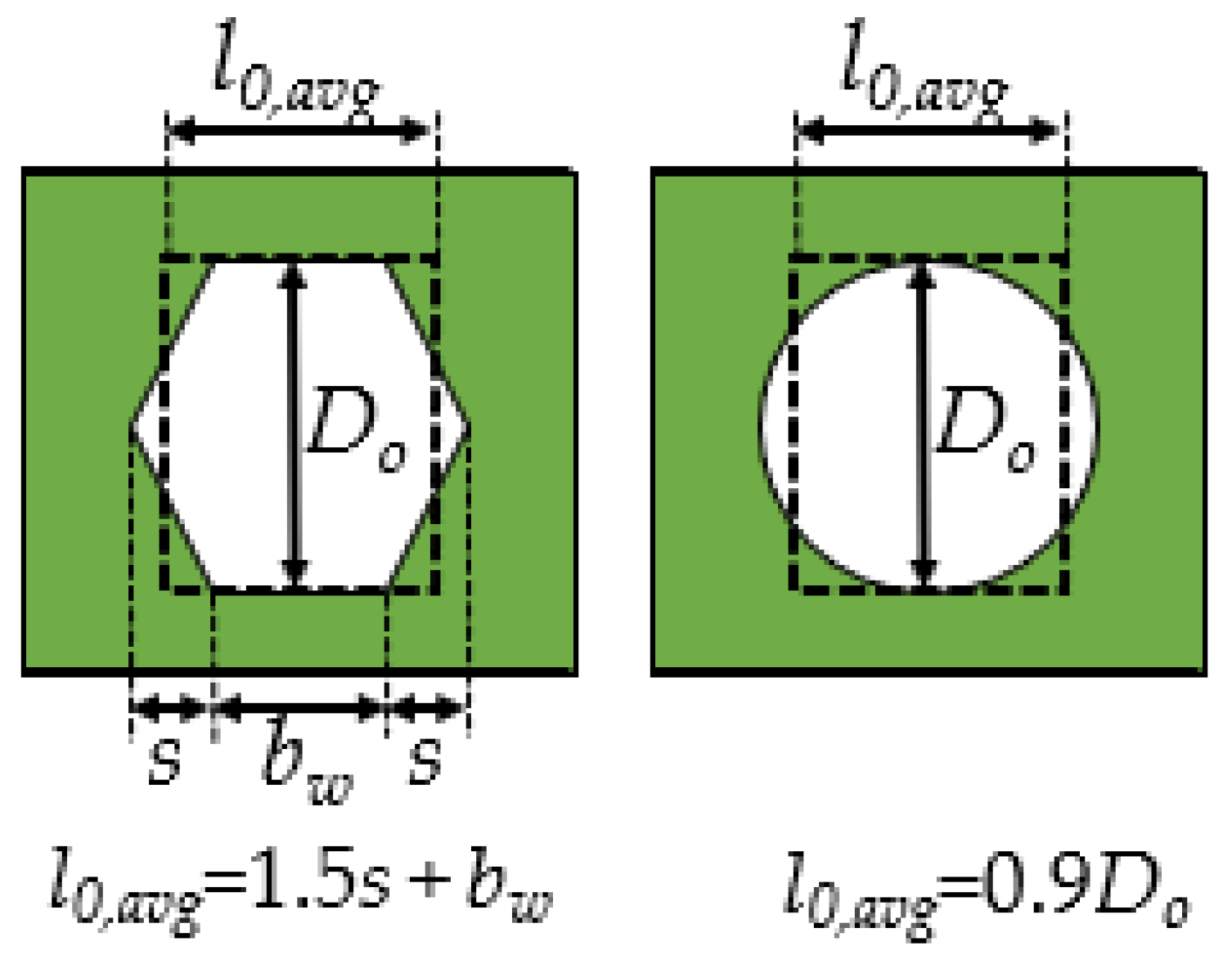
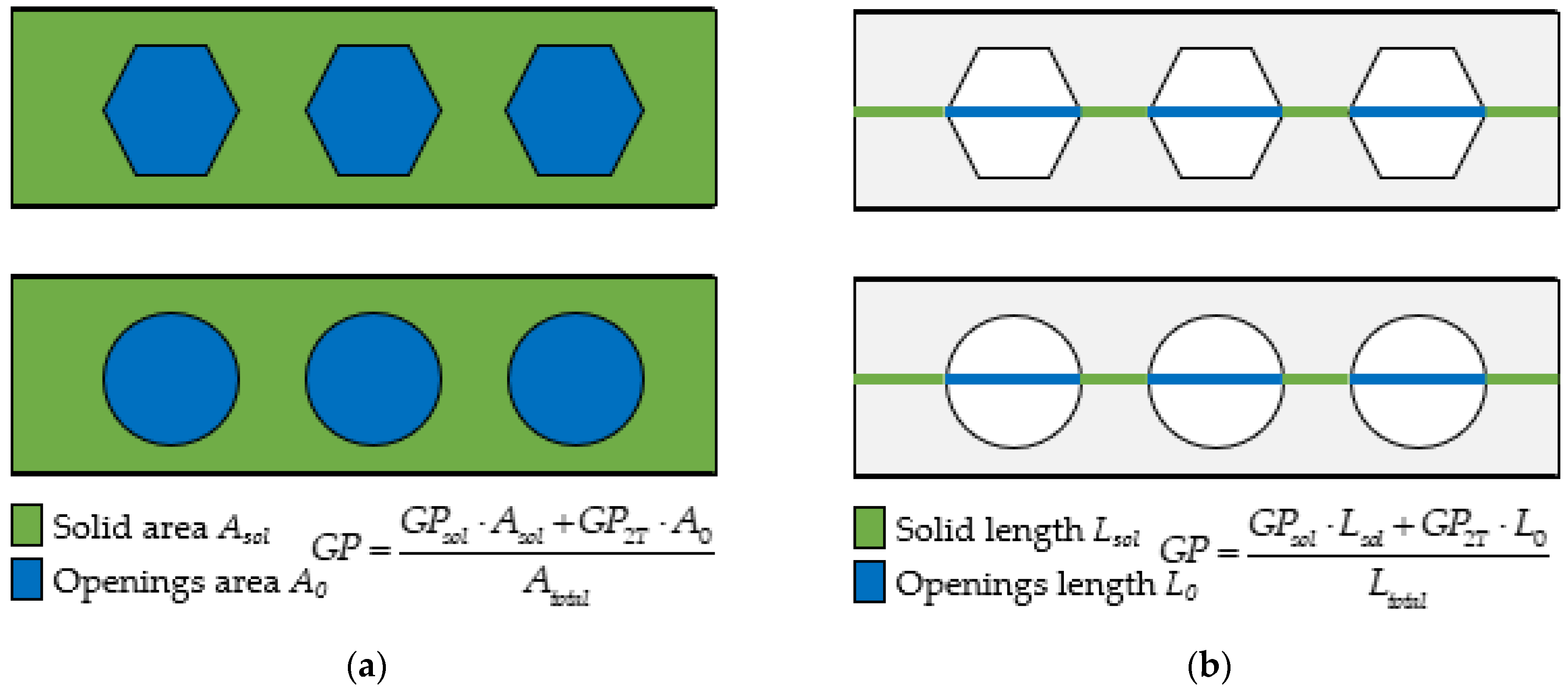
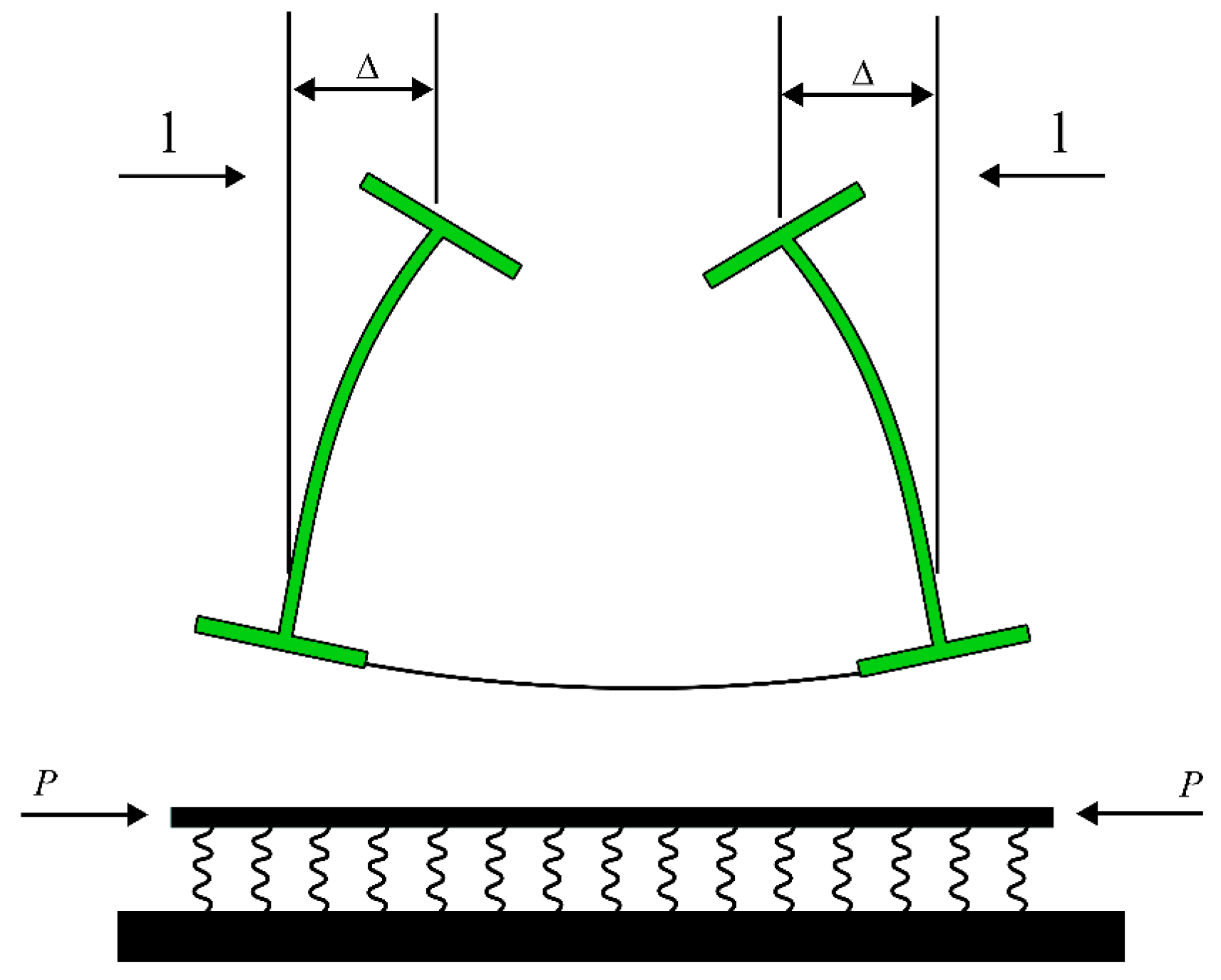
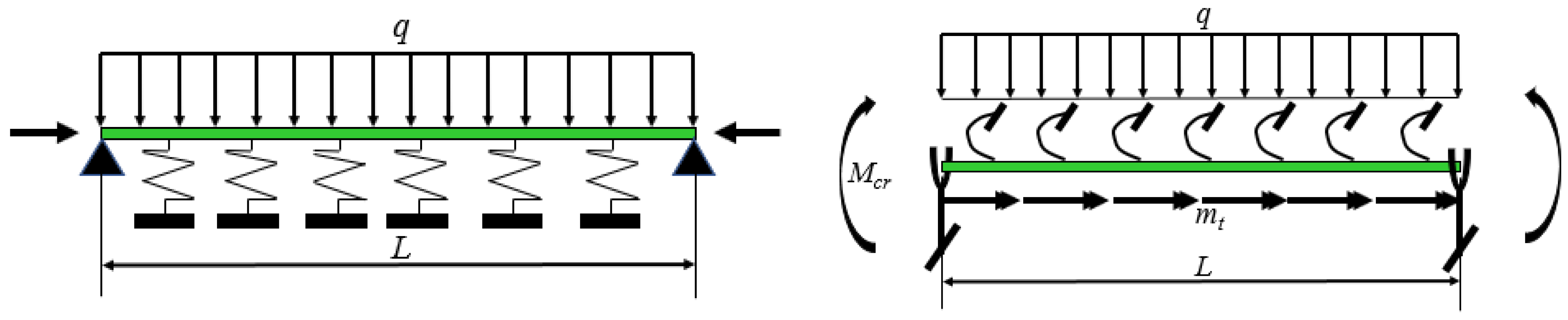
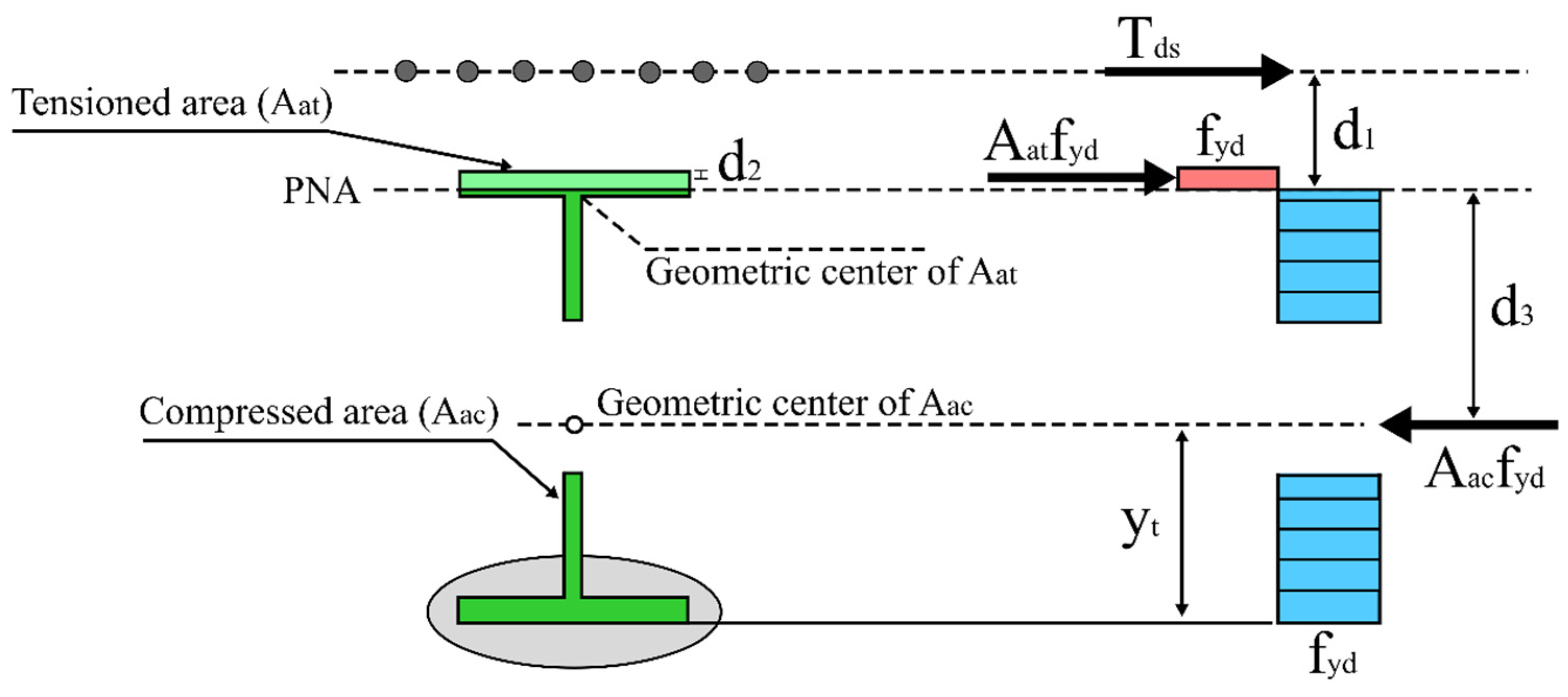
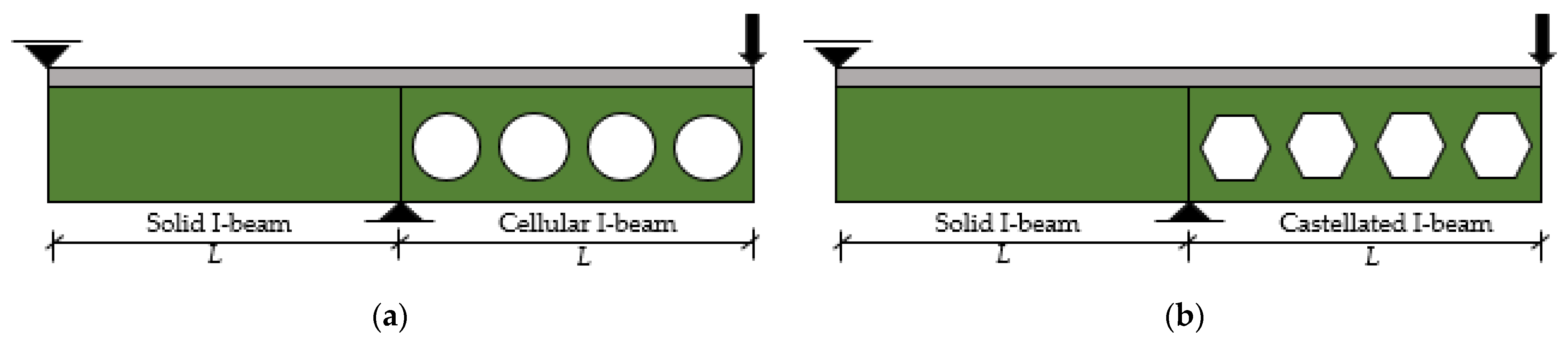
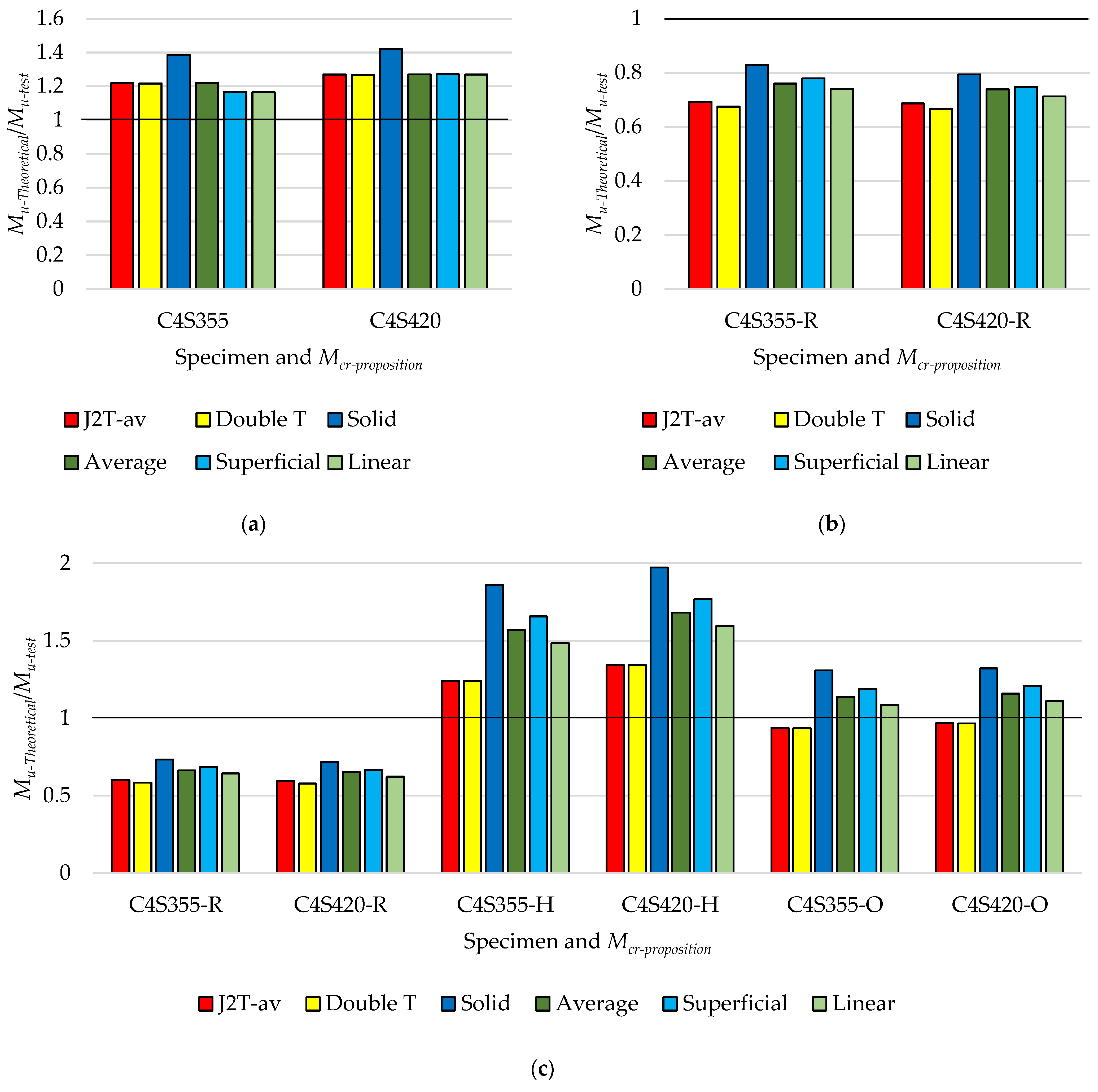
Model	Reference	Highlight
Experimental	Salah [58] and Gizejowski and Salah [59]	Performed tests with steel-concrete composite beams with circular, hexagonal, and rectangular web openings
Numerical	Salah [58] and Gizejowski and Salah [59]	Carried out sensitivity analysis with geometrical and physical nonlinear finite element models
	Gizejowski and Salah [97]	Used geometrical nonlinear finite element models to analyze the stability behavior of continuous composite cellular beams
	Oliveira et al. [98]	Conducted nonlinear analysis to investigate the effect of the opening diameter, web post width, I-section dimensions, free span, and hogging moment distribution
	Oliveira et al. [99]	Analyzed the elastic behavior of the same beams investigated by Oliveira et al. [98]

. The papers in question are discussed in Section 2.3. Thus, it is clear that steel-concrete composite beams with solid web are significantly more studied than those with web openings. However, due to the alveolus, the behavior of the composite alveolar beams becomes more complex than the composite beams without openings. The alveolar profiles are susceptible to local failure modes that do not occur in I-sections with solid web [4,10,61,62,63]. These local failure modes are web post buckling (WPB) and the Vierendeel mechanism (VM) due to shear force and tee local buckling (TLB) caused by bending moment, which has been investigated in steel castellated beams [64,65,66,67,68], steel cellular beams [12,69,70,71,72,73,74,75], steel beams with sequential sinusoidal web openings [76,77], and steel-concrete composite cellular beams under positive bending [13,78,79,80,81]. In addition, the lateral torsional buckling (LTB) and its interaction with local failure modes has also been assessed in steel alveolar beams, with studies concentrated on steel castellated beams [65,66,82,83,84,85], steel cellular beams [86,87,88,89,90,91,92,93], and steel beams with sequential sinusoidal web openings [94,95,96].

According to Bradford [20], web distortion causes different effects on the elastic critical moment depending on the structure type. In steel I-sections, web distortion is responsible for reducing the elastic critical moment compared to the classical theories of LTB [20,100,101]. However, Bradford [20] states that in the case of steel-concrete composite beams, the LDB elastic critical moment is higher than that obtained by analytical formulations that do not consider the possibility of cross-section distortion. The classical LTB theories consider Vlasov’s hypothesis [102].

AISC 360-16 [103], AASHTO 2017 [104], AS: 1998 R2016 [105], AS/NZS2327-2017 [106], EN 1994-1-1: 2004 [107], and ABNT NBR 8800: 2008 [108] are codes that address the LDB resistance prediction of steel-concrete composite beams with full web. As these codes do not include composite alveolar beams, it is necessary to make adaptations for the beams in question to predict their bearing capacity to LDB. The resistance of composite alveolar beams can be reached by an interaction between LDB and local failure modes, such as WPB and the formation of plastic mechanisms [58,59,97,98,99]. These interactions are disregarded in the analytical procedures for the LDB resistance prediction analyzed in the present paper. This is because the cited codes’ formulations were not developed for beams with web openings. SCI P355 [109] and Steel Design Guide 31 [110] provide methodologies to evaluate the resistance to WPB and VM of composite and non-composite alveolar beams. However, they do not present approaches for LDB.

The present review paper focuses on two issues: the gap in the investigations of the LDB behavior in composite alveolar beams and the need for codes procedures for these structures. Furthermore, this work discusses the parameters that need further assessment and describes some approaches for adapting the LDB resistance predictions developed for beams without web openings. The accuracy of these approaches is assessed with experimental results from Salah [58]. Therefore, this paper can support future investigations of the LDB resistance of composite alveolar beams.

2. LDB Standard Codes, Analytical Methodologies, and Investigations

The standard procedures presented in this section do not address the LDB verification on continuous steel-concrete composite beams with web openings. However, some authors give adaptations of these standards [111,112,113]. In addition, assessments on the lateral-torsional buckling behavior of steel cellular beams show that the methodologies developed for solid I-beams can be adapted to cellular I-beams, which must determine the cross-section geometric properties in the central region of the openings, the so-called double T section [94,95,96,114,115]. On the other hand, Sonck and Belis [114,115] recommend that the torsional constant (J) must be obtained by an average (J_2T,_Average) between the J of the I-section (J_solid) and the J of the double T section (J_2T) obtained through Equation (1), where the parameters are: number of openings (n), equivalent opening length for the adapted torsion constant (l_0,avg), and I-section unrestrained length (L). The opening equivalent length (l_0,avg) for the castellated and cellular I-sections are determined as shown in Figure 7 [114,115].

$$J_{2T,Average}=\frac{n{l}_{0,avg}}{L}{J}_{2T}+\left(1-\frac{n{l}_{0,avg}}{L}\right)J_{solid}$$

(1)

Other approaches were presented by Carvalho, Rossi, and Martins [94], which cover different methods in the determination of geometric properties: without web openings (solid section); the calculation of properties at the center of the opening (double T); and three approaches using average values between the properties of the solid section and the double T section, the so-called “average section”, “linear weighting section”, and “superficial weighting section”. The mean value between the properties is used in the “average section”. In addition, the weighting of the values, the total length of the web post, and the total length of the openings, are utilized in the “linear weighting section”. Finally, the weighting of the values, the total area of steel in the web, and the total area of the web openings, are adopted in the “superficial weighting section”. The last two approaches are detailed in Figure 8, where the parameters are: arbitrary geometric property (GP), arbitrary geometric property calculated at plain section web (GP_sol), and the arbitrary geometric property calculated at the middle of the opening (double T section).

The resistance predictions of LDB addressed in the present paper are based on the calculus of the elastic critical moment. This way, design curves are applicated to obtain the ultimate moment. Thus, the elastic and ultimate moment formulations found in the literature are described in Section 2.1 and Section 2.2, respectively. In Section 3, a comparison between the methods is discussed.

2.1. LDB Elastic Critical Moment

The standard procedures that address the LDB verification in steel-concrete composite beams use the conventional LTB theories of partially constrained beams or the U-frame model [116]. These methodologies are illustrated in Figure 9.

The European standard (EN 1994-1-1: 2004 [107]) and Brazilian standard (ABNT NBR 8800: 2008 [108]) use the inverted U-frame model to determine the elastic critical moment to LDB (M_cr). The U-frame model (Figure 9b) considers the composite beam cross-section as an I-section with its upper flange with lateral displacement completely prevented and rotation partially prevented by a rotational stiffness spring (k_s). The rotational stiffness k_s, given by Equation (2), is composed of the bending stiffness of the slab (k₁, Equation (3)) per unit of beam length and the bending stiffness of the web I-section (k₂, Equation (4)):

$$k_s=\frac{k_1{k}_2}{k_1+k_2}$$

(2)

$$k_1=\frac{\alpha {\left(E{I}_c\right)}_2}{a}$$

(3)

$$k_2=\frac{E{t}_w^3}{4\left(1-v_{}^2\right)h_0}$$

(4)

where the parameters are: coefficient related to the I-section position (α), being equal to 2 for end beams, 3 for intermediate beams, and 4 for internal beams having four or more similar neighboring sections [17]; flexural stiffness of the reinforced concrete slab with homogenized composite section per unit of beam length (EI_c2); distance between the I-sections; I-section elasticity modulus (E); web thickness (t_w); I-section Poisson ratio (n); and distance between the flanges centroids (h₀).

The study by Müller et al. [111] was one of the first found in the literature that addressed the verification of resistance to LDB in composite beams with web openings. The authors presented an adaptation of the European standard (EN 1994-1-1-2004 [107]), contemplating the calculation of k₂ for composite cellular beams and composite beams with only one rectangular opening in the web. To calculate the M_cr, the authors suggest using the proposition by Hanswille et al. [117]. According to Müller et al. [111], it can be taken as shown in Equations (5) and (6).

$$k_2=\frac{E{t}_w^3}{4\left(1-v_{}^2\right)h_0}{k}_{hole}^{*}$$

(5)

$$k_{hole}^{*}=1-\frac{3D_0}{4p} \mathrm{for}\mathrm{cellular}\mathrm{beams}.$$

(6)

Studies of LDB in composite castellated beams also presented adaptations of k₂ rotational stiffness [112,113]. Basically, these propositions approach the k₂ rotational stiffness determination of a composite alveolar beam from the adaptation of the k₂ of a composite beam without web opening, applying a reduction factor referring to the web openings. Silva et al. [113] presented a reduction factor equal to 0.51, and the method by Müller et al. [111], for the experimental models of Salah [58], provided a reduction factor equal to 0.524.

Silva et al. [112] presented an analytical formulation for calculating the rotational stiffness of castellated composite beams. For this, the authors performed numerical simulations of composite beams using castellated beams with Anglo-Saxon, Litzka, and Peiner opening patterns. According to the authors, rotational stiffness strongly depends on the web’s rotational stiffness (k₂), which can be determined by considering the web as a cantilever plate in the centroid of the upper flange and free in the centroid of the lower flange [112]. Thus, a simplified numerical slab model was developed to determine the web stiffness of the castellated profiles. Silva et al. [112] verified a linear relationship between the k₂ results obtained by the numerical models of the plates with hexagonal openings and the results obtained by the analytical formulations provided by the Brazilian standards (ABNT NBR 8800: 2008 [108]) and European standards (EN 1994-1-1-2004 [107]) of the web without openings adopting the same dimensions as the plates with hexagonal openings. The relationship between the numerical/analytical results was 0.53, 0.54, and 0.55 for the Anglo-Saxon, Litzka, and Peiner opening patterns, respectively. Thus, the authors proposed an adjustment coefficient (β) whose value is equal to the relationship between the numerical/analytical results of each type of opening. According to the authors, the determination of the rotational stiffness of castellated profiles, considering the total height of the expanded I-section, d_g, can be taken as:

$$k_2=\beta \frac{E t_w{}^3}{4d_g\left(1-{\nu }^2\right)}$$

(7)

Subsequently, Silva et al. [113] presented a new equation for calculating k₂ very similar to the one shown by Silva et al. [112]. However, to maintain the same parameters used in the standard prescriptions, they adopted the distance between the flanges centroids (h₀), instead of the total height of the section (d_g). The equation proposed by Silva et al. [113] is limited only to the castellated composite beams with Anglo-Saxon pattern openings. Equation (8) presents the expression proposed by the authors to calculate the rotational stiffness of the web of castellated composite beams:

$$k_2=0.51\frac{E t_w{}^3}{4h_0\left(1-{\nu }^2\right)}$$

(8)

The procedure proposed by Silva et al. [113] was verified from the results obtained by numerical simulations using ANSYS software. According to the authors, with the statistical treatment of the results, it was observed that the proposed procedure is suitable for evaluating the LDB behavior of castellated composite beams. In addition, the authors also observed that the procedure remains valid when the stiffness of the slab is varied.

According to Fan [37], the inverted U-frame model is more appropriate to evaluate the LDB in steel-concrete composite beams than the T section, which is composed of only one I-section associated with the slab. Given that the U-frame model better represents the slab’s collaboration in the LDB strength, it is possible to analyze the lateral displacement and torsional restrictions imposed on the steel I-section by the concrete slab and by the shear connector. The U-frame model also relates to typical situations since most constructions use floor systems of parallel steel beams equally spaced under the concrete slab [112]. However, Rossi et al. [116] explain that the inverted U-frame model consists of the simplified consideration of a beam uniformly compressed by the maximum bending stress and restricted by springs along its length. Thus, the compressed beam represents the I-section lower flange, and the springs represent the rigidity imposed by the web I-section, as shown in Figure 10. In most cases, the steel-concrete composite beams under hogging moment present a significant moment gradient, which makes the procedure based on the inverted U-frame model highly conservative in most cases [116].

Currently, the Brazilian standard (ABNT NBR 8800: 2008 [108]) uses the methodology proposed by Roik et al. [118] to determine the M_cr based on the inverted U-frame model. That method was also presented in the previous version of EC4 (ENV 1994-1-1: 1992 [119]). The current version of EC4 (EN 1994-1-1: 2004 [107]) does not present equations for determining the M_cr. However, it proposes the use of calculation methodologies based on the inverted U-frame model. In the literature, calculation propositions based on this model are also presented in the works by Hanswille et al. [117] and Dias et al. [120].

According to Rossi et al. [116], the LDB research methods for the elastic critical moment determination generally fall into two categories: studies based on the energy method (Galerkin method) or those based on the elastic foundation-beams theory. The formulations of Roik et al. [118] and Dias et al. [120] are within the methodologies developed using the energy method as well as the propositions of Svensson [121] and Williams and Jemah [122]. On the other hand, Hanswille et al. [117] utilized the elastic foundation-beams theory in their prediction procedure. The methods in question are objectively described below.

2.1.1. Svensson [121]

The first procedures found in the literature are based on the energy method, such as the works of Svensson [121] and Williams and Jemah [122], and the methodologies proposed in these works are very similar. Starting with the method proposed by Svensson [121], the author adopted the T section model (considers only an I-section associated with the slab) to evaluate the structure, in which it was considered that the I-section compressed flange could be treated as a column subjected to axial compressive loads. The author proposed a method that can be applied to several bending moment distributions. Svensson’s formulation [121] is described in Equations (9)–(12), where W_x is the elastic section modulus taken about the strong axis. Equation (12) and

Table 2. λ values for different bending moments [121]. Adapted from Svensson [121].

	λ Values
	Case
βL	1	2	3	4	5	6	7	8	9
0	1.000	1.881	2.355	5.824	2.835	4.518	10.83	5.824	0.377
1	1.010	1.889	2.376	5.856	2.860	4.538	10.84	5.856	0.438
2	1.164	2.166	2.694	6.309	3.235	4.827	11.02	6.309	1.332
3	1.832	3.240	3.944	7.952	4.732	5.884	11.72	7.952	4.543
4	3.628	5.472	6.450	11.06	8.044	7.875	13.26	11.06	6.775
5	5.604	8.110	9.537	15.24	13.16	10.41	15.65	15.24	9.135
6	7.326	10.91	12.86	20.06	19.48	13.20	18.67	20.06	12.48
8	13.67	18.06	20.91	30.99	33.16	20.28	25.23	30.99	20.26
10	20.41	26.92	30.75	43.62	47.21	29.27	34.17	43.62	29.18
12.5	31.66	40.41	45.51	61.89	66.65	42.74	47.83	61.89	42.73
15	45.79	56.56	63.00	82.97	88.86	58.73	64.10	82.97	58.73
17.5	62.75	75.35	83.20	106.8	113.9	77.21	82.96	106.8	77.20
20	81.63	96.78	106.1	133.5	141.7	98.18	104.4	133.5	98.18
Legend
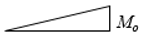	Case 1			Case 2			Case 3
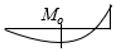	Case 4			Case 5			Case 6
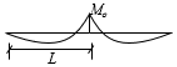	Case 7			Case 8			Case 9

describe the formulation to obtain the slenderness parameter (λ).

$$M_{cr}=\frac{{\pi }^{2}E}{{\lambda }_{el}^2}{W}_x$$

(9)

$${\lambda }_{el}=\frac{L_{el}}{b_f/\sqrt{12}}$$

(10)

$$L_{el}=L\cdot {\lambda }^{-0.5}$$

(11)

$$\beta L=1.35{\left(\frac{t_w{}^3{L}^4}{d_g{}^3{t}_f{b}_f}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}$$

(12)

2.1.2. Williams and Jemah [122]

Williams and Jemah [122] presented a proposal based on Svensson’s method [121]. The authors considered that in addition to the compressed flange, a 15% portion of the web could also be analyzed as a column under compression (Figure 11). The proposition of Williams and Jemah [122] is presented in Equation (13). The slenderness parameter (λ_el) is obtained as described in Section 2.1.1.

$$M_{cr}=\frac{\frac{{\pi }^{2}E}{{\lambda }_{el}^2}{W}_x}{\left(1+0.15\frac{b_f{t}_f}{h_0{t}_w}\right)}$$

(13)

2.1.3. Roik et al. [118]

The formulation proposed by Roik et al. [118] is presented in Equations (14)–(16), where the parameters are: coefficient referring to the hogging moment distribution (C_dist), as described in

Table 3. C_dist coefficient for continuous beams with loading on the analyzed span (L). Adapted from ABNT NBR 8800:2008 [108].

* Moment Distribution	ψ
	0.50	0.75	1.00	1.25	1.50	1.75	2.00	2.25	2.50
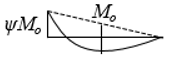	41.5	30.2	24.5	21.1	19.0	17.5	16.5	15.7	15.2
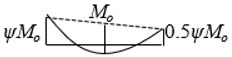	33.9	22.7	17.3	14.1	13.0	12.0	11.4	10.9	10.6
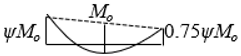	28.2	18.0	13.7	11.7	10.6	10.0	9.5	9.1	8.9
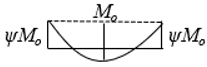	21.9	13.9	11.0	9.6	8.8	8.3	8.0	7.8	7.6
	28.4	21.8	18.6	16.7	15.6	14.8	14.2	13.8	13.5
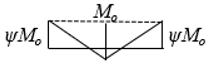	12.7	9.89	8.6	8.0	7.7	7.4	7.2	7.1	7.0

* M_o is the maximum moment, considering the analyzed span as simply supported.

and

Table 4. C_dist coefficient for continuous beams without loading on the analyzed span (L). Adapted from ABNT NBR 8800:2008 [108].

* Moment Distribution	ψ
	0.00	0.25	0.50	0.75	1.00
	11.1	9.5	8.2	7.1	6.2
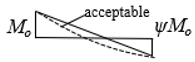	11.1	12.8	14.6	16.3	18.1

* M_o is the higher moment, in modulus, in the analyzed span, in which ψ values higher than 1.00 must be taken as 1.00.

; I-section shear modulus (G); flange inertia moment about the weak axis (I_af,y); composite cross-section inertia moment about the strong axis (I_x); I-section inertia moment about the strong axis (I_ax); I-section inertia moment about the weak axis (I_ay); I-section sectional area (A_a); composite cross-section sectional area (A).

$$M_{cr}={\alpha }_g\frac{C_{dist}}{L}\sqrt{\left(GJ+\frac{k_s{L}^2}{{\pi }^2}\right)E{I}_{af,y}}$$

(14)

$${\alpha }_g=\frac{h_0{I}_x/I_{ax}}{\frac{h_0^2/4+\frac{\left(I_{ax}+I_{ay}\right)}{A_a}}{e}+h_0}$$

(15)

$$e=\frac{A{I}_{ax}}{A_a{y}_c\left(A-A_a\right)}$$

(16)

2.1.4. Hanswille et al. [117]

In the search for a new strategy for determining the LDB elastic critical moment, Hanswille et al. [117] developed a proposal similar to Roik et al. [118] using the inverted U-frame model to represent the composite beam. However, the authors deduced their procedure through the elastic foundation-beams theory (Figure 12).

The formulation for M_cr proposed by Hanswille et al. [117] is presented in Equation (17).

$$M_{cr}=\frac{1}{k_z}\left(\frac{\left({\pi }^{2}E{C}_{w,d}\right)}{{\left({\beta }_{b}L\right)}^2}+G{J}_{ef}\right)$$

(17)

where the parameters are the cross-section geometric parameters described by Equation (18) (k_z, y_f and e), the distance between the I-section centroid and the composite section (reinforcement bar and I-section) centroid (y*),

$$k_z=\frac{I_{ax}}{I_x}\left(2y_f-\frac{1}{e}\left(y_f^2+\frac{I_{ax}+I_{ay}}{A_a}\right)\right) ; y_f=\frac{d_g-b_f}{2} ;e=\frac{I_{ax}}{y*A_a}$$

(18)

where the warping constant calculated with the pole in the center of the profile upper flange had by Equation (19) (C_w,d),

$$C_{w,d}=I_{af,y}{h}_0{}^2$$

(19)

where the effective length factor determined by Equation (20) (β_B),

$${\beta }_B={\beta }_{0B}{\left(\frac{1}{1+{\left(a\frac{{\sqrt{\eta }}_b}{\pi }\right)}^{n_1}}\right)}^{1/n_2}$$

(20)

where the stiffness factor presented in Equation (21) (η_b), and the effective Saint Venant torsion stiffness (GJ_ef), as shown in Equation (22).

$${\eta }_b=\sqrt{\frac{k_s{L}^4}{E{C}_{w,d}}}$$

(21)

$$G{J}_{ef}=A\left(1.5-0.5\psi \right)GJ$$

(22)

To calculate the parameters B_B and GJ_ef it is necessary to obtain the coefficients A, a, η₁, and η₂, which are dependent on the hogging moment factors: the relationship between the end moment and the maximum moment (ψ); and the relationship between the smaller end moment and the higher end moment. The parameters A, a, η₁, and η₁ are given according to the load configurations, which are detailed in

Table 5. Approximate determination of the elastic critical moment for members with end moments. Adapted from Hanswille et al. [117].

* Moment Distribution
β0B = –0.11ψ2 − 0.37ψ + 0.74
ψ	a	η1	η2
1.0	1.48	9.10	9.30
0.5	1.45	8.30	8.80
0.0	1.40	6.40	7.30
–0.5	1.25	4.70	5.70
–1.0	1.00	4.20	5.10

* M_o is the maximum moment, considering the analyzed span as simply supported.

(for members with end moments),

Table 6. Approximate determination of the elastic critical moment for members with concentrated load and end moments. Adapted from Hanswille et al. [117].

* Moment Distribution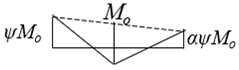
	β0B = 0.320ψ + 0.53			β0B = 0.075ψ2 + 0.25ψ + 0.35			β0B = 0.116ψ2 + 0.06ψ + 0.21
	α = 1 A = 1.25			α = 0.5 A = 1.5			α = 0.25 A = 1.6
	a	η1	η2	a	η1	η2	a	η1	η2
ψ = 1.0	1.46	9.85	9.55	1.35	7.10	6.85	0.95	4.90	4.50
ψ = 0.5	1.45	9.00	9.75	1.30	5.75	6.80	0.85	4.50	5.60
ψ = 0.0	1.35	5.95	7.75	1.05	4.60	6.30	0.70	4.15	6.10

* M_o is the maximum moment, considering the analyzed span as simply supported.

(for members with concentrated load and end moments), and

Table 7. Approximate determination of the elastic critical moment for members with uniformly distributed load and end moments. Adapted from Hanswille et al. [117].

* Moment Distribution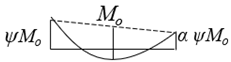
	β0B = 0.037ψ2 + 0.30ψ + 0.4			β0B = 0.16ψ2 + 0.05ψ + 0.24			β0B = 0.07ψ2 + 0.01ψ + 0.13
	α = 1 A = 1.25			α = 0.5 A = 1.5			α = 0.25 A = 1.75
	a	η1	η2	a	η1	η2	a	η1	η2
ψ = 1.0	1.45	8.80	8.95	1.15	4.90	5.15	0.65	4.05	4.50
ψ = 0.5	1.37	5.95	6.70	0.95	4.50	5.90	0.55	4.00	5.70
ψ = 0.0	1.13	4.50	5.75	0.77	4.20	5.95	0.48	3.95	6.15

* M_o is the maximum moment, considering the analyzed span as simply supported.

(members with uniformly distributed load and end moments).

2.1.5. Dias et al. [120] and Oliveira [123]

The methodology proposed by Dias et al. [120] and Dias [124] only covers steel-concrete composite beams under uniform hogging moment and is shown in Equation (23).

$$M_{cr}=\frac{k_g}{h_0}\left\{GJ+\frac{E{C}_{w,d}}{L^2}\left[{\left(n\pi \right)}^2+{\left(\frac{{\eta }_b}{n\pi }\right)}^2\right]\right\}$$

(23)

The k_g coefficient considers the elastic neutral axis and moment portion absorbed by the reinforcement bars.

$$k_g=\frac{I_x}{I_{ax}}\left(0.31+0.69\cdot {0.05}^{y*/h_0}\right)$$

(24)

As in the proposition of Hanswille et al. [117], η_b is the stiffness factor (Equation (25)), and C_w,d is the warping constant calculated with the pole in the center of the profile upper flange (Equation (26)).

$${\eta }_b=\sqrt{\frac{k_s{L}^4}{E{C}_{w,d}}}$$

(25)

$$C_{w,d}=I_{af,y}{h}_0{}^2$$

(26)

According to Dias et al. [120], the number of waves (n) must be an integer to fulfill essential boundary conditions. Thus, one may calculate the M_cr value for the two integers n₁ and n₂ nearest to n_id (Equation (27)) and adopt the smallest value of the critical moment obtained.

$$n_{id}=\frac{\sqrt{{\eta }_b}}{\pi }$$

(27)

Oliveira [123] presented an adaptation based on the methodology of Dias [124] to verify beams subjected to non-uniform moment, according to Equation (28).

$$M_{cr}=\frac{k_g}{h_0}\left\{GJ+\frac{E{C}_{w,d}}{L_{neg}^2}\left[{\left(n\pi \right)}^2+{\left(\frac{{\eta }_b}{n\pi }\right)}^2\right]\right\}\left\{2.13\beta {\left(\frac{L_{neg}}{h_0}\right)}^{-0.1}\right\}$$

(28)

Oliveira’s proposition [123] imposed a reduction factor equal to 1/4 in the stiffness factor (η_b), determined according to Equation (29).

$${\eta }_b=\frac{1}{4}\sqrt{\frac{k_s{L}_{neg}^4}{E{C}_{w,d}}}$$

(29)

Equation (30) describes the conditions to determine the β coefficient related to the positions of supports for different hogging moment diagrams. The parameters of Equation (30) are the smallest length of the negative moment stretch (L₁); and the critical length of the composite beam (L_cr) had by Equation (31), in which h_w is the web depth. The lengths L_neg and L₁ are determined as shown in Figure 13.

$$\beta =\{\begin{array}{l}\beta =1.0,if \frac{L_1}{L_{cr}}\ge 1.0\\ \beta =-0.16\left(\frac{L_1}{L_{cr}}\right)+1.15,if\frac{L_1}{L_{cr}}<1.0\end{array}$$

(30)

$$L_{cr}=2.4h_w{\left[\frac{b_f{}^3{t}_f\left(1-v^2\right)}{t_w{}^3{h}_w}\right]}^{0.25}$$

(31)

2.2. LDB Ultimate Moment

The standards address the LDB in continuous composite beams by applying a reduction factor in the plastic moment (M_pl) of the analyzed section under hogging moment. For this, these standards use curves expressed in terms of the slenderness ratio and the reduction factor determined by full-scale tests of steel elements with initial geometric imperfections and residual stress.

European codes (EN 1994-1-1: 2004 [107]) and Brazilian codes (ABNT NBR 8800: 2008 [108]) present analogous formulations to determine the cross-section plastic moment (M_pl-C.beam), which are composed of steel I-beam and reinforcement bars (composite section). According to the codes in question, the plastic theory (full plastic rectangular distribution stress) must be used, and M_pl-C.beam is obtained with Equation (32), where the parameters are: longitudinal reinforcement area (A_bar); reinforcement bars yield strength (f_y,bar); I-section tensioned area (A_at); I-section compressed area (A_ac); steel I-section yield strength (f_y); distance between the geometric centers of the composite cross-section and reinforcement bars (d₃); distance between the geometric centers of the composite cross-section and I-section tensioned area (d₄); and distance between the geometric centers of the composite cross-section and I-section compressed area (d₅).

$$M_{pl-C.beam}=A_{bar}{f}_{y,bar}{d}_3+A_{at}{f}_y{d}_4+A_{ac}{f}_y{d}_5$$

(32)

The parameters which compose Equation (32) depend on the composite section geometry, materials yield strength, and plastic neutral axis (PNA) position. This way, two cases of PNA position usually occur in steel-concrete composite beams in hogging moment regions: PNA on the I-section web and PNA on the I-section upper flange. In the present paper, the M_pl-C.beam formulations are developed considering the composite section in the center region of the opening. Thus, to calculate M_pl-C.beam in the region with solid web, D_o equal to zero must be adopted. The cases in question are detailed below.

I—PNA on the I-section web is true if “(A_a − A_f) * f_y ≥ A_f * f_y + T_ds”, which can have PNA position (y_PNA) defined in relation to the I-section upper face, as shown in Figure 14. The parameters are A_f, which is the flange area, and T_ds, which is the calculation tensile strength of the reinforment bars (A_bar * f_y,bar).

As the PNA position is on the web, the steel I-section’s tensioned area (A_at) and compressed area (A_ac) are defined as presented in Equations (33) and (34), respectively.

$$A_{at}=b_f{t}_f+\left(y_{PNA}-t_f\right)t_w$$

(33)

$$A_{ac}=A_a-A_{at}-D_o{t}_w$$

(34)

This way, the PNA position is obtained with the equilibrium of resulting forces. These resulting forces are equivalent to full plastic rectangular distribution stress on reinforcement bars and the I-section’s tensioned and compressed area. Thus, the PNA position in relation to the I-section upper face is determined by Equation (35).

$$y_{PNA}=t_f+\frac{-A_{bar}{f}_{y,bar}+f_y\left(A_a-2b_f{t}_f\right)-D_o{t}_w}{2f_y{t}_w}$$

(35)

To calculate the distances d₂ and d₃ of Equation (32), the geometric center positions of the I-section’s tensioned (y*_at) and compressed area (y*_ac) are necessary. Equation (36) shows the formulation for the tensioned area with the origin on the I-section upper face. On the other hand, Equation (37) presents the calculus for the compressed area with the origin on the I-section lower face.

$$y_{at}^{*}=\frac{0.5b_f{t}_f{}^2+t_w\left(y_{PNA}-t_f\right)\left[0.5\left(y_{PNA}-t_f\right)+t_f\right]}{A_{at}}$$

(36)

$$y_{ac}^{*}=\frac{0.5b_f{t}_f{}^2+t_w\left[0.5{\left(d_g-y_{PNA}-t_f-D_o\right)}^2+t_f\right]}{A_{ac}}$$

(37)

Finally, the distances d₁, d₂, and d₃ are obtained according to Equations (38)–(40), in which c is the distance between the geometric center of the reinforcement bars and the I-section upper face.

$$d_1=y_{PNA}+c$$

(38)

$$d_2=y_{PNA}-y_{at}^{*}$$

(39)

$$d_3=d_g-y_{PNA}-y_{ac}^{*}$$

(40)

II—PNA on the I-section upper flange is true if “(A_a − A_f)*f_y < A_f * f_y + T_ds” and “A_a * f_y ≥ T_ds”, which can also have the PNA position (y_PNA) defined in relation to the I-section upper face. Figure 15 illustrates this case.

As the PNA position is on the upper flange, the steel I-section’s tensioned area (A_at) and compressed area (A_ac) are obtained by Equations (41) and (42), respectively.

$$A_{at}=b_f{y}_{PNA}$$

(41)

$$A_{ac}=b_f{t}_f+t_w\left(d_g-2t_f-D_o\right)+b_f\left(t_f-y_{PNA}\right)$$

(42)

Thus, the PNA position in relation to the I-section upper face is determined by Equation (43).

$$y_{PNA}=\frac{-A_{bar}{f}_{y,bar}+f_y\left[2b_f{t}_f+t_w\left(d_g-2t_f-D_o\right)\right]}{2f_y{b}_f}$$

(43)

Like the case I, the formulation for the center position of the tensioned area is developed with the origin on the I-section upper face, and for the compressed area, the origin is on the I-section lower face. Equations (44) and (45) describe the calculus of the center positions y*_at and y*_ac. Equations (38)–(40) must be used to obtain the distances d₁, d₂, and d₃.

$${\overline{y}}_{at}=\frac{y_{PNA}}{2}$$

(44)

$${\overline{y}}_{ac}=\frac{0.5b_f{t}_f{}^2+t_w\left(d_g-D_o-2t_f\right)0.5d_g+b_f\left(t_f-y_{PNA}\right)\left[d_g-y_{PNA}-0.5\left(t_f-y_{PNA}\right)\right]}{A_{ac}}$$

(45)

EN 1994-1-1: 2004 [107] uses multiple Perry–Robertson design curves that constitute the ECCS (European Convention for Constructional Steelwork) curves [125], while ABNT NBR 8800:2008 [108] uses the 2P design curve provided by the SSRC (Structural Stability Research Council) [116]. However, according to Rossi et al. [116], the Perry–Robertson curves were developed considering only steel elements under bending. This situation can lead to an inaccurate determination of the LDB strength in steel-concrete composite beams. On the other hand, the 2P curve provided by SSRC is the result of experimental tests of steel elements under compression.

Differently from the standards that are fundamental in the inverted U-frame model, the North American standards (AISC 360-16 [103] and AASHTO 2017 [104]) and Australian standards (AS4100: 1998 R2016 [105] and AS/NZS2327-2017 [106]) present adaptations of the classic lateral-torsional buckling theories of partially constrained beams. These methodologies consider only the steel I-beam as a resistant cross-section against LDB. Equation (46) determines the I-section plastic moment (M_pl.I.-beam).

$$M_{p{l}_{I-beam}}=2b_f{t}_f\left(\frac{t_f+h_w}{2}\right)+\frac{t_w\left(h_w^2-D_0^2\right)}{4}$$

(46)

AASHTO [104] proposes modifications to the LTB formulation of steel I-beams present in AISC [103]. On the other hand, the Australian standards (AS4100: 1998 R2016 [105] and AS/NZS2327-2017 [106]) present a method that evaluates the so-called critical flange that is not restricted against instability phenomena [116]. According to the above, there are differences between the standard procedures.

Table 8. Procedures for determining the LDB strength in SCCB. Adapted from Rossi et al. [29].

Source	EN 1994-1-1: 2004 [107]	NBR 8800: 2008 [108]	Australian Standards [105,106]
Mu	$\begin{array}{l}{M}_{u,dist}={\chi }_{LT}{M}_{pl-C.beam}\\ {\chi }_{LT}={\left[{\varphi }_{LT}+\sqrt{{\varphi }_{LT}^2-{\overline{\lambda }}_{LT}^2}\right]}^{-1}\le 1\\ {\varphi }_{LT}=0.5\left[1+{\alpha }_{LT}\left({\overline{\lambda }}_{LT}-0.2\right)+{\overline{\lambda }}_{LT}^2\right]\\ {\overline{\lambda }}_{LT}=\sqrt{\frac{M_{pl-C.beam}}{M_{cr}}}\end{array}$	$\begin{array}{l}{M}_{u,dist}=\chi M_{pl-C.beam}\\ {\lambda }_0\le 1.5:\chi ={0.658}^{{\lambda }_0^2}\\ {\lambda }_0>1.5:\chi =0.877/{\lambda }_0^2\\ {\overline{\lambda }}_0=\sqrt{\frac{M_{pl-C.beam}}{M_{cr}}}\end{array}$	$\begin{array}{l}{M}_{u,dist}={\alpha }_m{\alpha }_s{M}_{p{l}_{I-beam}}\le M_{p{l}_{I-beam}}\\ {\alpha }_m=\frac{1.7M_{m\wedge x}}{\sqrt{\left[{\left(M_2\right)}^2+{\left(M_3\right)}^2+{\left(M_4\right)}^2\right]}}\le 2.5\\ {\alpha }_s=0.6\left\{\sqrt{\left[{\left(\frac{M_{p{l}_{I-beam}}}{M_{cr}}\right)}^2+3\right]}-\left(\frac{M_{p{l}_{I-beam}}}{M_{cr}}\right)\right\}\end{array}$
Mcr	Formulations developed based on the U-frame model (Section 2.1.3, Section 2.1.4 and Section 2.1.5)	Formulation proposed by Roik et al. [118] (Section 2.1.3)	$M_{cr}=\sqrt{\left\{\left(\frac{{\pi }^{2}E{I}_y}{l_e^2}\right)\left[GJ+\left(\frac{{\pi }^{2}E{C}_w}{l_e^2}\right)\right]\right\}}$

presents the formulations for determining the LDB ultimate moment present in the mentioned standards, except the North American standards (AISC 360-16 [103] and AASHTO 2017 [104]), as they will not be covered in this work. In Table 8, l_e is the effective length according to the codes [105,106].

Salah [58] performed experimental tests on twelve composite beams with web openings under hogging bending. The author also numerically investigated the behavior of the models tested using the ABAQUS software. Salah [58] used the results of these investigations to validate the direct strength equation developed to verify the M_u to LDB. According to Gizejowski and Salah [126], calculations were performed to predict the relative slenderness λ in terms of the elastic buckling load factor Λ_cr and the limit load factor Λ_pl. For each tested beam, the dimensionless distortion buckling load Λ_b,exp/Λ_pl was calculated, where Λ_b,exp is the experimentally obtained distortional buckling load factor. The results were compared with the predictions of the Λ_b,dsm/Λ_pl direct strength method, according to Equations (47) and (48).

$$\frac{{\mathsf{\Lambda }}_{b,dsm}}{{\mathsf{\Lambda }}_{pl}}=\left({\alpha }_1-{\alpha }_2\frac{1}{{\overline{\lambda }}^k}\right)\frac{1}{{\overline{\lambda }}^k}$$

(47)

$$\overline{\lambda }=\sqrt{\frac{{\mathsf{\Lambda }}_{pl}}{{\mathsf{\Lambda }}_{cr}}}$$

(48)

From the parametric study of Salah [58], the author obtained the following constants for Equation (47): α₁ = 0.75, α₂ = 0.11, and k = 1. The proposed methodology was compared with the results of the experimental tests. The authors concluded that the proposed method provides safe results of the LDB-resistant capacity of the composite beams with web openings.

2.3. LDB Experimental and Numerical Investigations

Salah [58] and Gizejowski and Salah [59] performed experimental investigations on twelve beams. Two sets of specimens were assessed, six with long spans to represent the cases where bending is predominant in the behavior of composite beams and another six short spans to the instances where shear is dominant. The specimens had rectangular, circular, and hexagonal openings, and for a beam with equal geometry, the steel was varied (S355 and S420). The authors observed the lateral distortional mode predominance (LDB) in the long-span beams with circular and hexagonal openings, showing a significant lateral displacement in the I-section lower flange and a small deformation with web distortion (Figure 16a). This failure occurred due to the significantly hogging moment and because these beams have longer unrestrained lengths than those with a short span, which favors global lateral instability. On the other hand, in the short-span beams there occurred a torsional-distortional mode (WPB) with a not significant contribution of lateral lower flange deformations (Figure 16b). This failure mode is characteristic of beams with a predominance of shear forces, the case of the short-span beams, in which the shear force was more critical than the hogging moment. In addition, this behavior was also noted in the beams with rectangular openings and long spans, as, due to the lower web post area than the ones with circular and rectangular openings, these beams are more susceptible to the local web post-failure modes.

Salah [58] also performed a sensitivity analysis of the numerical models developed in the ABAQUS software, which was verified with the experimental results obtained by the author. Furthermore, the author conducted a parametric study using validated numerical models. Salah [58] observed, by the deformations obtained numerically, that the slender sections of composite beams fail by excessive bending, presenting the LDB before reaching the load of the Vierendeel mechanism in the beam plane.

Gizejowski and Salah [97] analyzed the continuous composite cellular beams behavior via geometrically nonlinear analysis. The authors noted that the buckling mode in short-span beams is characterized by the interaction between LDB and WPB. On the other hand, in long-span beams, the instability mode changes to LDB.

Oliveira et al. [98] carried out numerical investigations on the behavior of composite cellular beams subjected to hogging moment. The authors observed that models subjected to uniform hogging moment distribution (without shear loads) reached failure by LDB or its interaction with compression tee yielding (CTY). In contrast, the models subjected to linear hogging moment distribution (with shear loads) reached failure by WPB with the formation of plastic mechanism (PM), LDB, LDB+CTY, LDB+WPB+PM, LDB+WPB+PM+CTY, and LDB+WPB+CTY. According to the authors, in many models with lower global slenderness (L/r_y) and subjected to linear hogging moment, the ultimate moment to LDB reached values above the plastic moment of the composite section. Oliveira et al. [98] concluded that the I-section dimensions were the parameters that had the most significant influence on the load-carrying capacity of the models.

Oliveira et al. [99] conducted elastic analyses and compared them with the inelastic assessments previously performed by Oliveira et al. [98]. Analyzing the first positive eigenvector of the beams, the authors observed buckling modes characterized by LDB, WPB, TLB, web local buckling (WLB), and the interaction between them. Furthermore, Oliveira et al. [99] verified that the instability modes by TLB and WLB did not occur in the inelastic analysis.

According to the above, the behavior of composite cellular beams under hogging bending requires further investigation. There is still no knowledge about the influence of composite cellular beam parameters, such as the dimensions of the slab cross-section (height and width), slab typology, the longitudinal reinforcement ratio, shear interaction degree, expansion ratio of the cellular profile, mechanical properties of structural steel (E, f_y, f_u), and the use of asymmetric I-sections.

As described in this section, there are many possibilities to calculate the ultimate moment to LDB of steel-concrete composite alveolar beams. Most of these approaches still need to have their precisions measured for the beams in question, mainly for composite castellated beams, in which there is no assessment present in the bibliography. This way, Section 3 deals with the accuracy verification of all approaches shown in this section for composite castellated and cellular beams.

3. Accuracy Obtained by LDB Resistance Formulations

To verify the accuracy of the calculation procedures presented in Section 2.1 and Section 2.2, the results obtained by these procedures were compared to the experimental results of Salah [58]. Four composite alveolar beams which reached the failure by LDB were used, two with cellular I-section (C4S355 and C4S420) and two with castellated I-section (H4S355 and H4S420), as illustrated in Figure 17.

Table 9. Geometric parameters of the specimens (in mm and mm²).

Specimen	L	dg	bf	tf	tw	D0	bw	s	p	*n	Abar	c
C4S355	2116	480	100	6	4	336	193	92	529	4	1256.64	50
C4S420	2116	480	100	6	4	336	193	92	529	4	1256.64	50
H4S355	2116	480	100	6	4	321	193	92	529	4	1256.64	50
H4S420	2116	480	100	6	4	321	193	92	529	4	1256.64	50

* n is the number of openings.

describes the geometric parameters of the specimens, and

Table 10. Mechanical properties and ultimate load of the specimens.

Specimen	E (GPa)	fy (MPa)	fy,bar (MPa)	Pu (kN)
C4S355	200	355	459.6	59.56
C4S420	200	420	459.6	62.26
H4S355	200	355	459.6	62.03
H4S420	200	420	459.6	62.55

presents their mechanical properties and ultimate load (P_u). As these specimens are the only ones in the literature with the instability mode characterized by LDB, there are no experimental results of other composite alveolar beams to use in this study to verify the accuracy of the analytical formulations from Section 2.1 and Section 2.2.

The used methodologies are adaptations of procedures developed to verify the LDB in composite beams without web openings, so it was necessary to adopt geometric properties that were adapted to sections of the alveolar beams, as presented in Section 2. The approaches presented by Sonck and Belis (J_2T,Average) [114,115] and Carvalho, Rossi, and Martins (solid, double T, average, superficial, and linear weighting section) [94] were utilized. To determine the rotational stiffness of the web (k₂), the adaptation proposed by Müller et al. [111] and Silva et al. [113] was adopted for cellular and castellated beams, respectively.

The graphs below show the comparison of the experimental results of Salah [58] with the following calculation procedures to determine the M_u,dist to the LDB: AS4100: 1998 R2016 [105] and AS/NZS2327-2017 [106], EN 1994- 1-1: 2004 [107], ABNT NBR 8800: 2008 [108] and Salah [58]. The proposition of Roik et al. [118] is described in the Brazilian code (ABNT NBR 8800: 2008 [108]) to calculate the M_cr. On the other hand, Eurocode 4 (EN 1994- 1-1: 2004 [107]) does not specify a formulation to obtain the M_cr. However, this code proposes calculation methodologies based on the inverted-U frame model. The equations of Roik et al. [118], Hanswille et al. [117], and Dias et al. [120] are based on the model in question. These methodologies and those proposed by Svensson [121] and Williams and Jemah [122] to determine M_cr were also used in the calculation of Salah’s proposition [58] for the determination of M_u,dist. The proposition by Dias et al. [120] considers only the uniform hogging moment configuration. However, the procedure by Oliveira [123] was used, which adopted the proposal by Dias et al. [120] for other loading settings. In the graphs below, the capital letters S, W, R, H, and O mean that the procedure for determining the M_u,dist is the calculation of the M_cr from the propositions of Svensson [121], Williams and Jemah [122], Roik et al. [118], Hanswille et al. [117], and Oliveira [123], respectively. The ratio between the ultimate moment theoretical and the ultimate moment of the tests (M_{u-Theoretical}/M_u-test) with values above 1 represent unsafe results.

From Figure 18 and Figure 19, it is noted that most code’s adaptation methods provided unsafe results. The procedures that had conservative results were: ABNT NBR 8800: 2008 [108] for all geometric properties approaches (Figure 18b and Figure 19b); and EN 1994-1-1: 2004 [107], from M_cr determination by Roik et al. [118] for all approaches, and M_cr by Oliveira [123] for J_2T,Average and double T (Figure 18c and Figure 19c). Among these formulations, EN 1994-1-1: 2004 [107] with M_cr by Oliveira [123] and J_2T,Average was the formulation that had the highest average of the ratio (M_{u-Theoretical}/M_u-test = 0.951), followed by the same equations with double T geometric properties (M_{u-Theoretical}/M_u-test = 0.949). For ABNT NBR 8800: 2008 [108], the highest M_{u-Theoretical}/M_u-test value (0.83) was obtained with the solid section (Figure 18b). The methods that had non-conservative results were: AS4100:1998 R2016 [105] for all geometric properties approaches (Figure 18a and Figure 19a); EN 1994-1-1: 2004 [107] with M_cr by Hanswille et al. [117] for all geometric properties approaches; and EN 1994-1-1: 2004 [107] with M_cr by Oliveira [123] for the solid, average, superficial, and linear weighting section (Figure 18c and Figure 19c). EN 1994-1-1: 2004 [107] with M_cr by Hanswille et al. [117] and solid section obtained the most unsafe results within the code’s adaptations, having the highest M_{u-Theoretical}/M_u-test value equal to 1.97. For EN 1994-1-1: 2004 [107] with M_cr by Hanswille et al. [117], the solid, average, superficial, and linear weighting section provided M_{u-Theoretical}/M_u-test values above 1.5, which shows the significant non-conservatism of then. Within the other combinations of M_u and M_cr equations with unsafe results, the M_{u-Theoretical}/M_u-test values were: AS4100:1998 R2016 [105] for solid section (1.42); and EN 1994-1-1: 2004 [107] with M_cr by Oliveira [123] for solid section (1.32). Another issue is that no significant differences were observed between the accuracies obtained for the models with circular and hexagonal openings considering the same calculation method. For the Australian code (AS4100:1998 R2016 [105]), the geometric properties considering J_2T,Average, double T and average section had similar values to M_{u-Theoretical}/M_u-test (Figure 18a and Figure 19a), which also occurred with superficial and linear weighting sections in the composite cellular beams (Figure 18a). On the other hand, superficial and linear weighting section provided lower values of M_{u-Theoretical}/M_u-test than J_2T,Average, double T, and average section in the composite castellated beams (Figure 19a). In addition, these geometric properties approaches presented a trend for the other procedures, shown in Figure 18 and Figure 19. This trend is double T, J_2T,Average, linear weighting, average, superficial weighting, and solid section from the smallest to highest values of M_{u-Theoretical}/M_u-test (Figure 18 and Figure 19). Finally, the only methodologies that obtained safe results for all section approaches were EN 1994-1-1: 2004 [107] and ABNT NBR 8800: 2008 [108] with M_cr by Roik et al. [118].

Figure 20 and Figure 21 show that most approaches with Salah’s M_u proposition [58] provided unsafe results. This M_u formulation with M_cr by Roik et al. [118] for J_2T,Average, double T, average section, superficial, and linear weighting section were the procedures that had conservative results (Figure 20a and Figure 21a). Among these calculation methodologies, the one with the superficial weighting section had the highest average of the ratio (M_{u-Theoretical}/M_u-test = 0.902), followed by the average section (M_{u-Theoretical}/M_u-test = 0.863). The use of M_cr, proposed by Roik et al. [118], with solid section and M_cr by Oliveira [123] with the J_2T,Averange, and double T section provided the most similar results against the tests. However, the results of the models C4S420 and H4S420 were non-conservative (Figure 20a and Figure 21a). The methods that obtained non-conservative results were: M_cr by Roik et al. [118] with solid section; and M_cr by Hanswille et al. [117], Oliveira [123], Svensson [121], and Williams and Jemah [122] for all geometric properties approaches. Some methodologies fall into a high level of non-conservatism with M_{u-Theoretical}/M_u-test values above 2, such as M_cr by Hanswille et al. [117] with solid section; M_cr by Svensson [121] and Williams and Jemah [122] with solid, average, superficial, and linear weighting section. Within these methods, M_cr by Svensson [121] and Williams and Jemah [122] with solid section presented M_{u-Theoretical}/M_u-test values above 2.5. The most unsafe result was observed in M_cr by Svensson [121] and solid section, having a M_{u-Theoretical}/M_u-test value equal to 2.65 for the specimen C4S420 (Figure 20b). Other formulations with significant non-conservatism provided M_{u-Theoretical}/M_u-test values above 1.5, such as M_cr by Hanswille et al. [117] with J_2T,Average, double T, superficial, and linear weighting; and M_cr by Svensson [121] and Williams and Jemah [122], with double T section. As well as for the code’s adaptation methods (Figure 18 and Figure 19), significant differences were not observed between the accuracies obtained for the models with circular and hexagonal openings considering the same calculation method (Figure 20a and Figure 21a). Finally, the same trend of the geometric section approaches in Figure 18 and Figure 19 are noted in Figure 20 and Figure 21, in which, from the smallest to the highest values of M_{u-Theoretical}/M_u-test, is double T, J_2T,Average, linear weighting, average, superficial weighting, and solid section.

Table 11. M_{u-Theoretical}/M_u-test obtained by the calculation procedure of AS4100:1998 R2016 [105].

Model	Geometric Properties Approach
	J2T-Average	Double T	Solid	Average	Superficial	Linear
C4S355	1.22	1.22	1.38	1.22	1.17	1.17
C4S420	1.27	1.27	1.42	1.27	1.27	1.27
H4S355	1.18	1.18	1.32	1.18	1.18	1.18
H4S420	1.28	1.28	1.42	1.29	1.29	1.28
Avg.	1.24	1.24	1.39	1.24	1.23	1.23
SD. (%)	4.77	4.75	4.52	4.78	6.09	6.07
Var. (%)	0.23	0.23	0.20	0.23	0.37	0.37

shows the M_{u-Theoretical}/M_u-test values obtained by the calculation procedure of AS4100:1998 R2016 [105]. As noted, all geometric property approaches provide significantly unsafe results, with M_{u-Theoretical}/M_u-test values above 1.23. This may occur because the code disregards some factors that occurred in the specimens, such as the web distortion and the interaction with local failure modes (WPB). On the other hand, ABNT NBR 8800: 2008 [108] provides only safe results as described in

Table 12. M_{u-Theoretical}/M_u-test obtained by the calculation procedure of ABNT NBR 8800: 2008 [108].

Model	Geometric Properties Approach
	J2T-Average	Double T	Solid	Average	Superficial	Linear
C4S355	0.69	0.67	0.83	0.76	0.78	0.74
C4S420	0.69	0.67	0.79	0.74	0.75	0.71
H4S355	0.67	0.65	0.79	0.73	0.75	0.71
H4S420	0.68	0.67	0.79	0.73	0.75	0.72
Avg.	0.68	0.66	0.80	0.74	0.76	0.72
SD. (%)	1.05	0.92	2.01	1.42	1.51	1.36
Var. (%)	0.01	0.01	0.04	0.02	0.02	0.02

, in which the highest average of the ratio (M_{u-Theoretical}/M_u-test = 0.80) was obtained with the solid section approach. In addition, the double T section had the most conservative result (M_{u-Theoretical}/M_u-test average = 0.66).

Table 13. M_{u-Theoretical}/M_u-test obtained by the calculation procedure of EN 1994- 1-1: 2004 [107].

Model	Mcr Proposition/* Geometric Properties Approach
	Roik et al. [118]						Hanswille et al. [117]						Oliveira [123]
	J2T-Avg	Db. T	Solid	Avg.	Sup.	Lin.	J2T-Avg	Db. T	Solid	Avg.	Sup.	Lin.	J2T-Avg	Db. T	Solid	Avg.	Sup.	Lin.
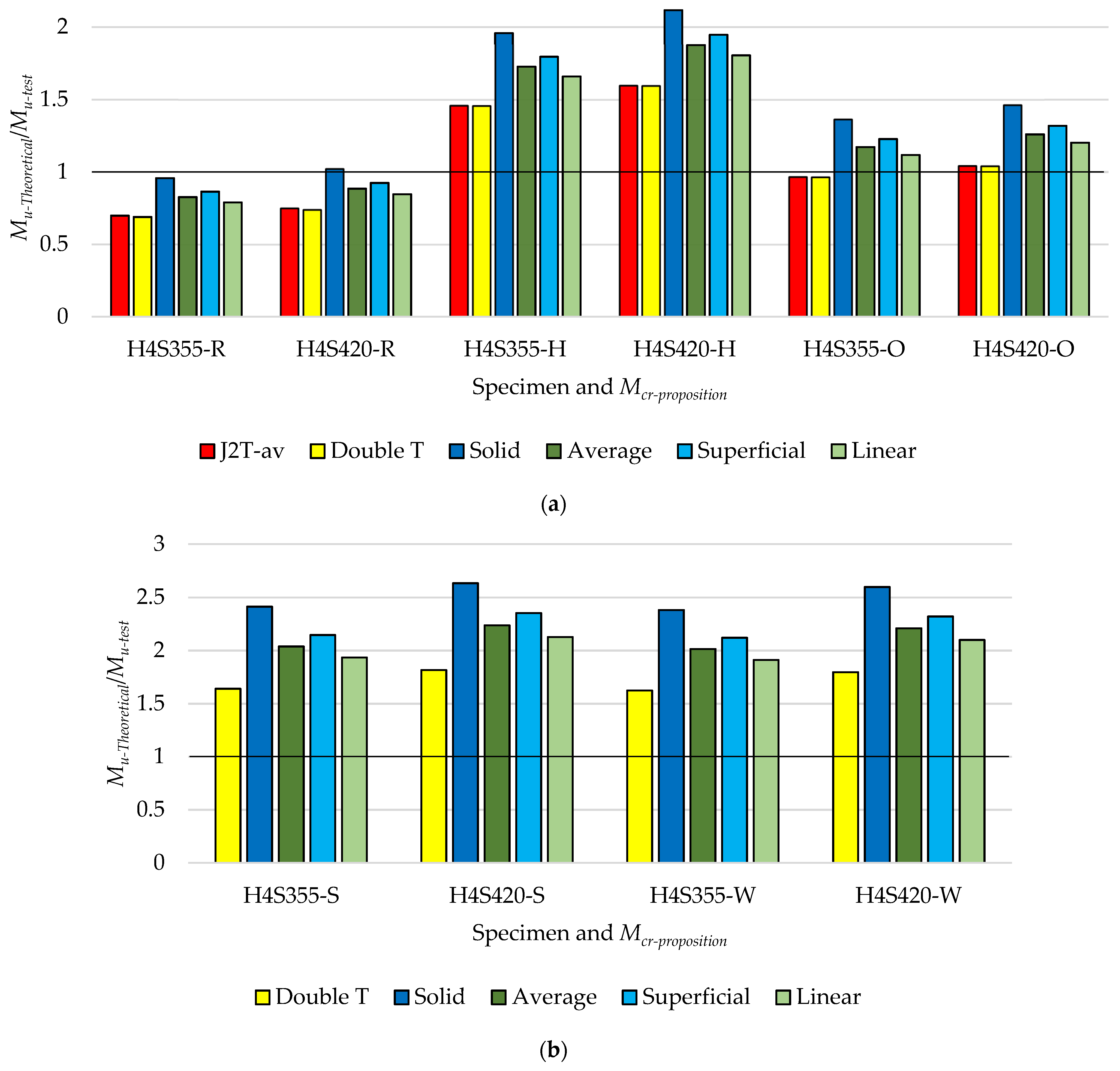
C4S355	0.60	0.58	0.73	0.66	0.68	0.64	1.24	1.24	1.86	1.57	1.66	1.48	0.94	0.93	1.31	1.14	1.19	1.09
C4S420	0.59	0.58	0.72	0.65	0.67	0.62	1.34	1.34	1.97	1.68	1.77	1.59	0.97	0.97	1.32	1.16	1.21	1.11
H4S355	0.58	0.56	0.70	0.64	0.65	0.62	1.22	1.22	1.79	1.52	1.60	1.44	0.92	0.91	1.26	1.10	1.15	1.05
H4S420	0.59	0.58	0.71	0.65	0.67	0.63	1.37	1.37	1.96	1.69	1.77	1.60	0.98	0.98	1.31	1.16	1.21	1.11
Avg.	0.59	0.58	0.71	0.65	0.67	0.63	1.29	1.29	1.90	1.61	1.70	1.53	0.95	0.95	1.30	1.14	1.19	1.09
SD. (%)	0.94	0.83	1.39	1.11	1.19	1.09	7.35	7.35	8.89	8.30	8.51	8.07	2.93	2.91	2.96	2.88	2.89	2.87
Var.(%)	0.01	0.01	0.02	0.01	0.01	0.01	0.54	0.54	0.79	0.69	0.72	0.65	0.09	0.08	0.09	0.08	0.08	0.08

* Db. T is the double T, Avg. is the Average, Sup. is the Superficial, and Lin. is the Linear weighting section approaches.

presents the M_{u-Theoretical}/M_u-test values provided by the standard recommendation of EN 1994-1-1: 2004 [107]. As observed, utilizing the M_cr calculation proposed by Roik et al. [118], this code obtained safe results for all geometric property approaches, with the highest average of the ratio (M_{u-Theoretical}/M_u-test = 0.71) obtained with the solid section approach. In addition, considering all the results in Table 13, the M_cr proposition by Hanswille et al. [117], with the solid section, had the most unsafe M_{u-Theoretical}/M_u-test values, having an average equal to 1.90. As previously stated, using M_cr by Oliveira [123] and J_2T,Average, EN 1994-1-1: 2004 [107] formulation had the highest average of the ratio (M_{u-Theoretical}/M_u-test = 0.951) considering only the safe values, followed by the double T section approach (M_{u-Theoretical}/M_u-test = 0.949). Finally, within all methods analyzed in this study, the most conservative results were obtained by EN 1994-1-1: 2004 [107] recommendation with M_cr by Roik et al. [118] and the double T section (M_{u-Theoretical}/M_u-test average = 0.58).

Within all formulations analyzed in this work, Salah’s M_u proposition [58] with M_cr by Roik et al. [118] and solid section, as well as with Oliveira [123] and the double T section, had the better average of the ratio (M_{u-Theoretical}/M_u-test = 1.00), as shown in

Table 14. M_{u-Theoretical}/M_u-test obtained by the calculation procedure of Salah’s M_u proposition [58] with M_cr calculation based on the U-frame model.

Model	Mcr Proposition/*Geometric Properties Approach
	Roik et al. [118]						Hanswille et al. [117]						Oliveira [123]
	J2T-Avg	Db. T	Solid	Avg.	Sup.	Lin.	J2T-Avg	Db. T	Solid	Avg.	Sup.	Lin.	J2T-Avg	Db. T	Solid	Avg.	Sup.	Lin.
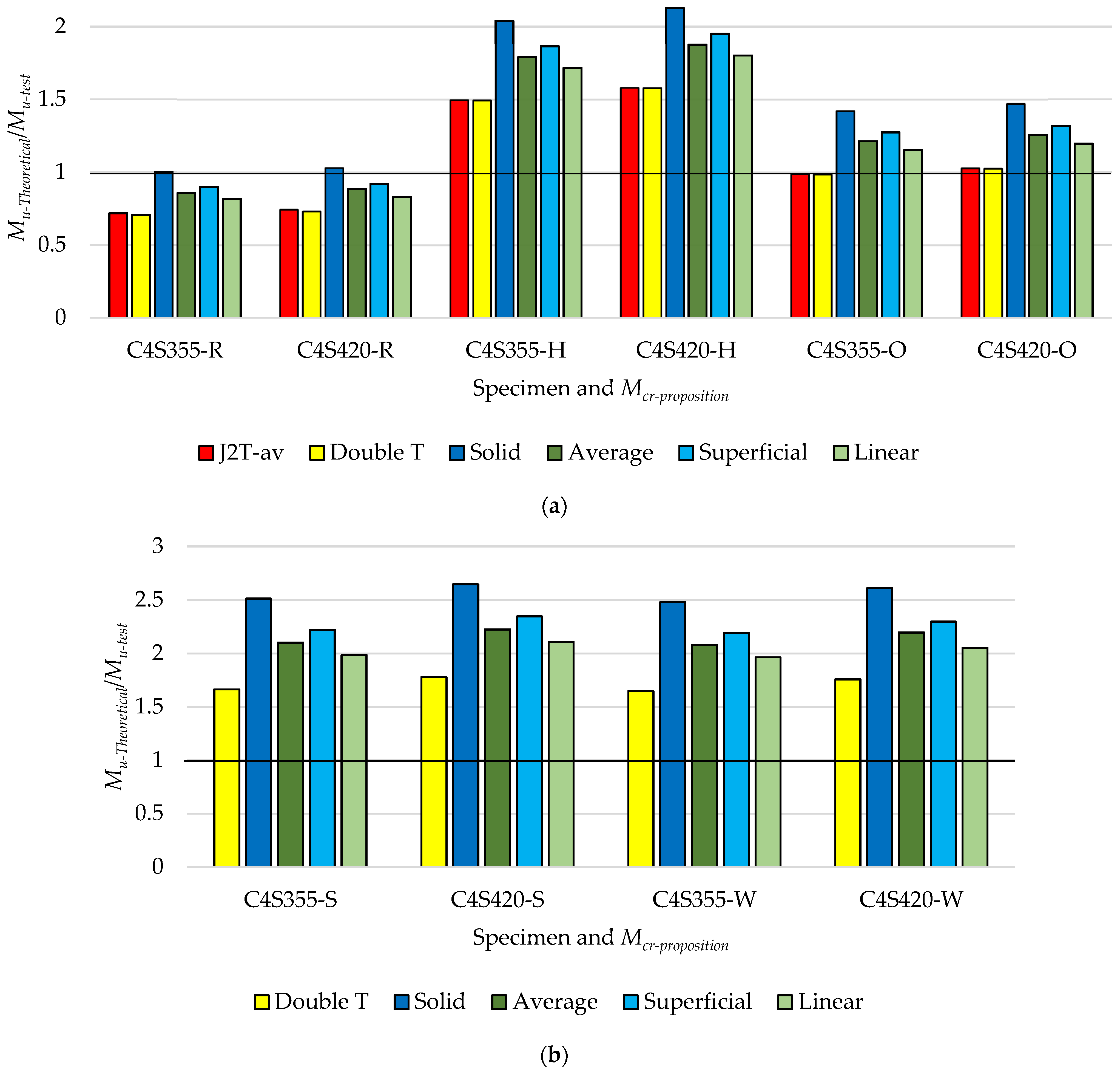
C4S355	0.72	0.71	1.00	0.86	0.90	0.82	1.50	1.49	2.04	1.79	1.86	1.72	0.99	0.99	1.42	1.21	1.27	1.15
C4S420	0.74	0.73	1.03	0.88	0.92	0.83	1.58	1.58	2.13	1.88	1.95	1.80	1.03	1.03	1.47	1.26	1.32	1.20
H4S355	0.70	0.69	0.96	0.83	0.86	0.79	1.46	1.46	1.96	1.73	1.80	1.66	0.97	0.97	1.36	1.17	1.23	1.12
H4S420	0.75	0.74	1.02	0.88	0.92	0.85	1.60	1.60	2.12	1.88	1.95	1.80	1.04	1.04	1.46	1.26	1.32	1.20
Avg.	0.73	0.72	1.00	0.86	0.90	0.82	1.53	1.53	2.06	1.82	1.89	1.74	1.01	1.00	1.43	1.23	1.28	1.17
SD. (%)	2.39	2.34	3.28	2.78	2.75	2.40	6.67	6.66	7.84	7.25	7.42	7.08	3.54	3.53	4.86	4.16	4.36	3.98
Var.(%)	0.06	0.05	0.11	0.08	0.08	0.06	0.44	0.44	0.61	0.52	0.55	0.50	0.13	0.12	0.24	0.17	0.19	0.16

* Db. T is the double T, Avg. is the Average, Sup. is the Superficial, and Lin. is the Linear weighting section approaches.

. However, these formulations provided unsafe results for the specimens C4S420 and H4S420. On the other hand, among the results presented in Table 14, the most unsafe results were obtained using M_cr by Hanswille et al. [117] and solid section (M_{u-Theoretical}/M_u-test average = 2.06).

As noted, all results presented in Table 14 were significantly unsafe. Within all formulations analyzed in the present review paper, Salah’s M_u proposition [58] with M_cr by Svensson [121] and the solid section provided the most unsafe results, in which the average M_{u-Theoretical}/M_u-test ratio was 2.55 (

Table 15. M_{u-Theoretical}/M_u-test obtained by the calculation procedure of Salah’s M_u proposition [58] with M_cr calculation proposed by Svensson [121] and Williams and Jemah [122].

Model	Mcr Proposition/Geometric Properties Approach
	Svensson [121]					Williams and Jemah [122]
	Double T	Solid	Average	Superficial	Linear	Double T	Solid	Average	Superficial	Linear
C4S355	1.66	2.51	2.10	2.22	1.99	1.65	2.48	2.08	2.19	1.96
C4S420	1.78	2.65	2.23	2.35	2.11	1.76	2.61	2.20	2.30	2.05
H4S355	1.64	2.41	2.04	2.15	1.93	1.62	2.38	2.02	2.12	1.91
H4S420	1.82	2.64	2.24	2.35	2.13	1.80	2.60	2.21	2.32	2.10
Avg.	1.72	2.55	2.15	2.27	2.04	1.71	2.52	2.12	2.23	2.01
SD. (%)	8.57	11.06	9.68	10.05	9.34	8.34	10.78	9.43	9.36	8.45
Var. (%)	0.73	1.22	0.94	1.01	0.87	0.70	1.16	0.89	0.88	0.71

). This way, one must have a critical eye when adopting the propositions of Svensson [121] and Williams and Jemah [122] to determine the M_cr.

4. Discussion

Due to a gap in the studies that investigated composite alveolar beams under hogging bending, there are no studies that investigated all possible failure modes in these structures. However, based on the main observations by the works presented in this literature review, it was observed that the composite alveolar beams subjected to hogging bending could reach failure by LDB, WPB, the formation of plastic mechanisms, and their interactions.

It is noted that the assessment presented in Section 3 is limited, as it addresses only four specimens (C4S355, C4S420, H4S355, and H4S420). Furthermore, when verifying the same formulations addressed in this study for beams with other geometries and materials, the calculation procedures can obtain different precisions from those presented in Section 3. Salah [58] tested the other four composite cellular and castellated beams with short spans (C2S355, C2S420, C2S355, and C2S420). However, these beams reach failure predominantly by WPB. This way, formulations for WPB resistance must be verified.

Furthermore, it is also essential to investigate the influence of other parameters not assessed in Salah’s experimental tests [58]. According to the LDB studies discussed in Section 2.3, the only parameters that have already been analyzed are the unrestrained length, the web openings pattern, the strength of the steel I-beam, the I-section dimensions, hogging moment distribution, the opening diameter of composite cellular beams, and the web post width of composite cellular beams. This way, suggestions for future investigations are stated in Section 5.

LDB resistance predictions provided by the standard codes do not comprehend composite alveolar beams, having only the formulations for composite beams with solid webs. This way, it is necessary to use adaptation approaches for beams with web openings. Another critical point is that calculation propositions directly developed to verify the M_cr to LDB of the composite alveolar beams were not found in the literature. Only adaptations made by authors who proposed changes to the methodologies that consider the verification of the M_cr of composite beams without web openings were found. From these adaptations, it is possible to obtain the M_u to LDB by the methodologies presented by Salah [58] and the European standards (EN 1994-1-1: 2004 [107]) and Brazilian standards (ABNT NBR 8800: 2008 [108]). In addition to these methodologies, using the geometric properties of alveolar sections presented by Sonck and Belis [114,115] and Carvalho, Rossi, and Martins [94], it is also possible to verify the M_u to LDB using the Australian standards procedure (AS4100: 1998 R2016 [105] and AS/NZS2327-2017 [106]). The accuracy of these procedures was verified by comparing their results with the experimental results of Salah [58]. Through this analysis, it was observed that many analyzed approaches provided unsafe results. Among the formulations that had only safe results, the combination of EN 1994-1-1: 2004 [107] with M_cr by Oliveira [123] and J_2T,Average obtained the highest average of the ratio (M_{u-Theoretical}/M_u-test = 0.951). Additionally, EN 1994-1-1: 2004 [107] and ABNT NBR 8800: 2008 [108] with M_cr by Roik et al. [118] were the only methodologies that provided conservative results for all section approaches.

As discussed, the procedures assessed in the present study are adaptations of methodologies for checking the LDB in steel-concrete composite beams without web openings. Therefore, specific development design calculation for composite alveolar beams is necessary to consider the possibility of WPB. However, it is a complex study to be carried out due to the significant influence of many parameters. This way, some authors have been using artificial intelligence algorithms, in which a reliable database with information on the behavior of alveolar beams is adopted to generate mathematical formulations for the beams resistance prediction [83,127,128,129,130,131,132,133]. These techniques were also used for the LDB resistance prediction of beams without web openings [134,135,136,137].

5. Conclusions

The investigations on the LDB behavior of composite alveolar have few studies, in which the assessments by Salah [58] and Gizejowski and Salah [59] are the only ones that present experimental results. However, few parameters were evaluated in the Salah tests [58]. These parameters were the free span under hogging bending, the opening pattern, and the strength of the steel. According to the above, it is concluded that further investigations are necessary to understand the LDB behavior of steel-concrete composite alveolar beams. Many parameters that have a significant influence on the resistance capacity of these structures need to be clarified. Therefore, some guidelines for the development of future investigations are:

• Investigations on the influence of the concrete slab and the longitudinal reinforcement ratio in elastic stability analysis and the LDB inelastic behavior;
• Assessments of composite beams with high-strength steel alveolar I-section and ultra-high-performance concrete;
• The influence of the expansion factor (d_g/d) of the alveolar profile;
• The influence of the presence of transverse stiffeners in the web of the alveolar profile on the LDB behavior;
• Investigations into the influence of the use of asymmetrical alveolar profiles;
• Investigations on the LDB behavior of steel-concrete alveolar composite beams with sinusoidal web openings;
• Investigations via experimental tests of the LDB behavior of composite alveolar beams subjected to uniform hogging moment distribution, and others’ moment distribution;
• Calculation propositions that are directly developed for LDB verification in steel-concrete composite alveolar beams. One option is to use artificial intelligence algorithms to determine the LDB ultimate moment using a set of input parameters.