Lateral Distortional Buckling Resistance Predictions of Composite Alveolar Beams: A Review
Abstract
1. Introduction
2. LDB Standard Codes, Analytical Methodologies, and Investigations
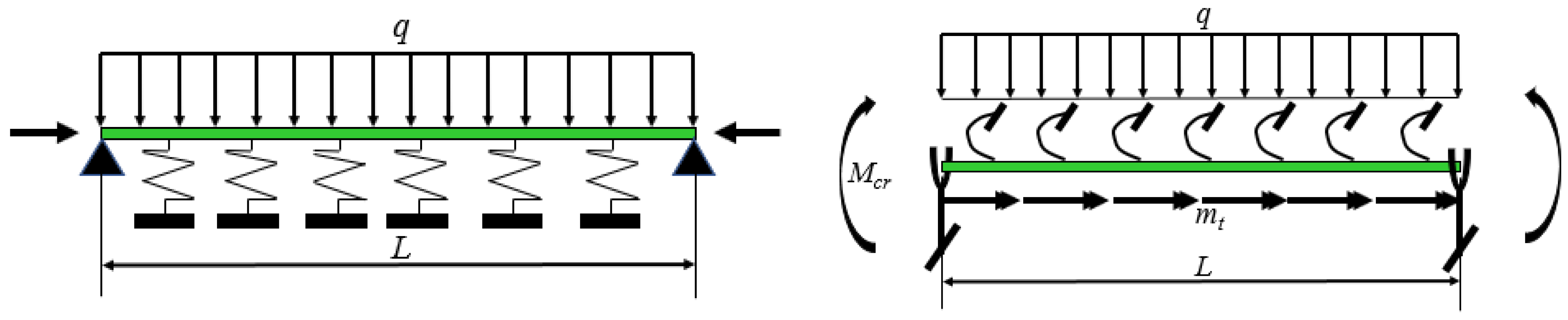
2.1. LDB Elastic Critical Moment
2.1.1. Svensson [121]
2.1.2. Williams and Jemah [122]
2.1.3. Roik et al. [118]
2.1.4. Hanswille et al. [117]
2.1.5. Dias et al. [120] and Oliveira [123]
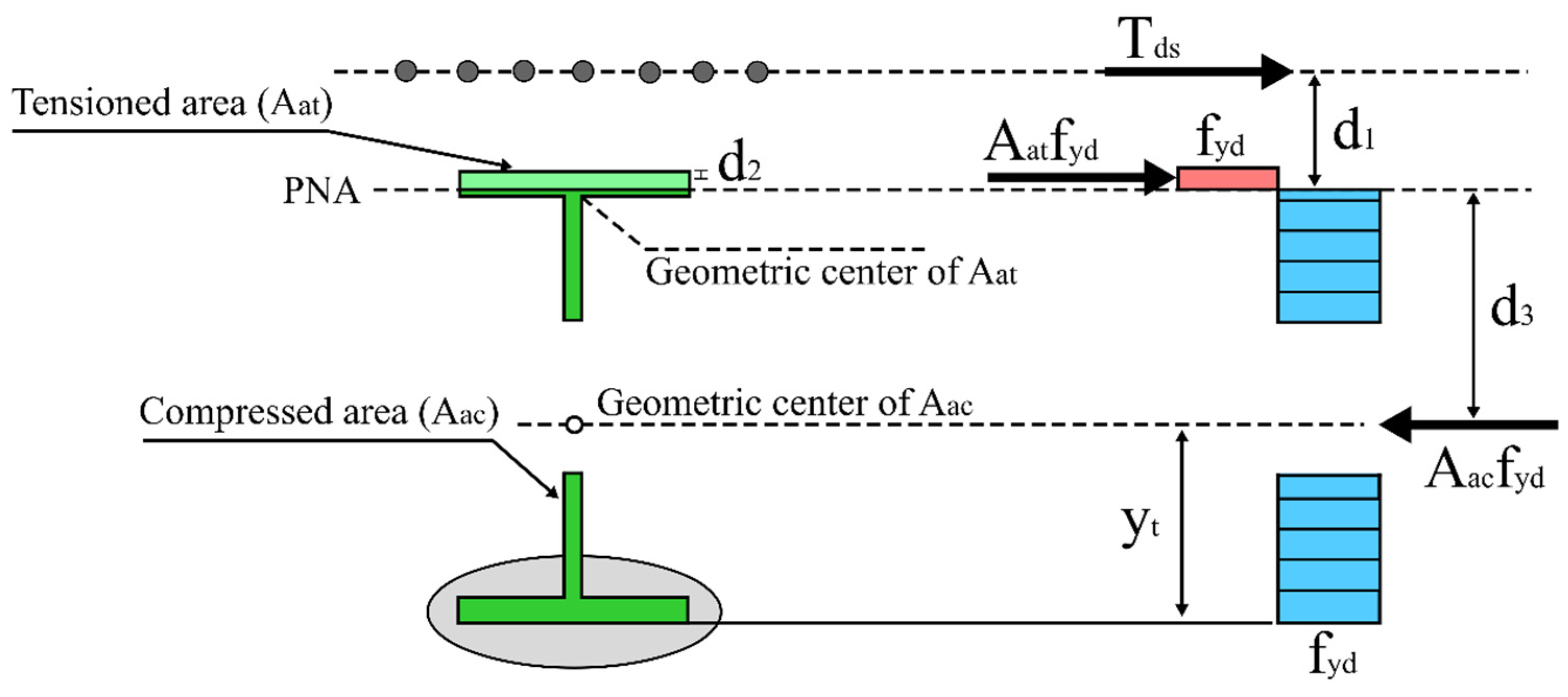
2.2. LDB Ultimate Moment
2.3. LDB Experimental and Numerical Investigations
3. Accuracy Obtained by LDB Resistance Formulations
4. Discussion
5. Conclusions
- Investigations on the influence of the concrete slab and the longitudinal reinforcement ratio in elastic stability analysis and the LDB inelastic behavior;
- Assessments of composite beams with high-strength steel alveolar I-section and ultra-high-performance concrete;
- The influence of the expansion factor (dg/d) of the alveolar profile;
- The influence of the presence of transverse stiffeners in the web of the alveolar profile on the LDB behavior;
- Investigations into the influence of the use of asymmetrical alveolar profiles;
- Investigations on the LDB behavior of steel-concrete alveolar composite beams with sinusoidal web openings;
- Investigations via experimental tests of the LDB behavior of composite alveolar beams subjected to uniform hogging moment distribution, and others’ moment distribution;
- Calculation propositions that are directly developed for LDB verification in steel-concrete composite alveolar beams. One option is to use artificial intelligence algorithms to determine the LDB ultimate moment using a set of input parameters.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vieira, H.C. Numerical Analysis of Web Post Buckling Due to Shear in Cellular Steel Beams [in Portuguese]. Ph.D. Thesis, Federal University of Minas Gerais, Belo Horizonte, Brazil, 2014. [Google Scholar]
- Ferreira, F.P.V.; Martins, C.H.; Nardin, S. Advances in Composite Beams with Web Openings and Composite Cellular Beams. J. Constr. Steel Res. 2020, 172, 106182. [Google Scholar] [CrossRef]
- Oliveira, L.B. De Procedures to Define the Geometric Characteristics of Alveolar Steel Beams to Floor Systems and Roof Systems [in Portuguese]. Master’s Thesis, Ferderal University of Viçosa, Viçosa, Brazil, 2012. [Google Scholar]
- Erdal, F.; Saka, M.P. Ultimate Load Carrying Capacity of Optimally Designed Steel Cellular Beams. J. Constr. Steel Res. 2013, 80, 355–368. [Google Scholar] [CrossRef]
- Grunbauer. Available online: http://www.grunbauer.nl/ (accessed on 27 February 2023).
- AcelorMittal ACB Cellular Beams. Available online: https://constructalia.arcelormittal.com/en/products/acb (accessed on 27 February 2023).
- UK Kloeckner Metals. Available online: https://www.kloecknermetalsuk.com/ (accessed on 27 February 2023).
- Lawson, R.M.; Lim, J.; Hicks, S.J.; Simms, W.I. Design of Composite Asymmetric Cellular Beams and Beams with Large Web Openings. J. Constr. Steel Res. 2006, 62, 614–629. [Google Scholar] [CrossRef]
- Lawson, R.M.; Saverirajan, A.H.A. Simplified Elasto-Plastic Analysis of Composite Beams and Cellular Beams to Eurocode 4. J. Constr. Steel Res. 2011, 67, 1426–1434. [Google Scholar] [CrossRef]
- Grilo, L.F.; Fakury, R.H.; de Castro e Silva, A.L.R.; de Souza Veríssimo, G. Design Procedure for the Web-Post Buckling of Steel Cellular Beams. J. Constr. Steel Res. 2018, 148, 525–541. [Google Scholar] [CrossRef]
- Tsavdaridis, K.D.; Mello, C.D. Web Buckling Study of the Behaviour and Strength of Perforated Steel Beams with Different Novel Web Opening Shapes. J. Constr. Steel Res. 2011, 67, 1605–1620. [Google Scholar] [CrossRef]
- Shamass, R.; Guarracino, F. Numerical and Analytical Analyses of High-Strength Steel Cellular Beams: A Discerning Approach. J. Constr. Steel Res. 2020, 166, 105911. [Google Scholar] [CrossRef]
- Benincá, M.E.; Morsch, I.B. Numerical Simulation of Composite Steel-Concrete Alveolar Beams: Web-Post Buckling, Vierendeel and Flexural Mechanisms. Lat. Am. J. Solids Struct. 2020, 17, 1–28. [Google Scholar] [CrossRef]
- C-Beams. Available online: https://www.c-beams.com/ (accessed on 27 February 2023).
- De Angelis, A.; Pecce, M.R.; Logorano, G. Evaluation of the Plastic Hinge Length of Steel-Concrete Composite Beams under Hogging Moment. Eng. Struct. 2019, 191, 674–685. [Google Scholar] [CrossRef]
- Rossi, A.; Nicoletti, R.S.; de Souza, A.S.C.; Martins, C.H. Numerical Assessment of Lateral Distortional Buckling in Steel-Concrete Composite Beams. J. Constr. Steel Res. 2020, 172, 106192. [Google Scholar] [CrossRef]
- Amaral, T.V.; Oliveira, J.P.S.; Calenzani, A.F.G.; Teixeira, F.B. Lateral-Distortional Buckling of Continuous Steel-Concrete Composite Beam. IBRACON Struct. Mater. J. 2018, 11, 719–737. [Google Scholar] [CrossRef]
- Dekker, N.W.; Kemp, A.R.; Trinchero, P. Factors Influencing the Strength of Continuous Composite Beams in Negative Bending. J. Constr. Steel Res. 1995, 34, 161–185. [Google Scholar] [CrossRef]
- Bradford, M.A.; Gao, Z. Distortional Buckling Solutions for Restraint by Slab Distortion of Web Flange Remains Rigid. J. Struct. Eng. 1992, 118, 73–89. [Google Scholar] [CrossRef]
- Bradford, M.A. Distortional Buckling of Elastically Restrained Cantilevers. J. Constr. Steel Res. 1998, 47, 3–18. [Google Scholar] [CrossRef]
- Vrcelj, Z.; Bradford, M.A. Elastic Bubble Augmented Spline Finite Strip Method in Analysis of Continuous Composite Beams. Aust. J. Struct. Eng. 2007, 7, 75–84. [Google Scholar] [CrossRef]
- Rossi, A.; Nicoletti, R.S.; de Souza, A.S.C.; Martins, C.H. Numerical Analysis of the Elastic Critical Moment to Lateral Distortional Buckling of Steel-Concrete Composite Beams. Holos 2021, 8800, 1–28. [Google Scholar] [CrossRef]
- Araujo, H.F.; Andrade, C.M.; Basaglia, C.; Camotim, D. Lateral-Distortional Buckling of Steel-Concrete Composite Beams: Kinematics, Constrained-Mode GBT and Analytical Formulae. J. Constr. Steel Res. 2022, 192, 107210. [Google Scholar] [CrossRef]
- Bradford, M.A.; Johnson, R.P. Inelastic Buckling of Composite Bridge Girders Near Internal Supports. Proc. Inst. Civ. Eng. 1987, 83, 143–159. [Google Scholar] [CrossRef]
- Bradford, M.A. Strength of Compact Steel Beams with Partial Restraint. J. Constr. Steel Res. 2000, 53, 183–200. [Google Scholar] [CrossRef]
- Vrcelj, Z.; Bradford, M.A. Inelastic Restrained Distortional Buckling of Continuous Composite T-Beams. J. Constr. Steel Res. 2009, 65, 850–859. [Google Scholar] [CrossRef]
- Chen, S.; Jia, Y. Numerical Investigation of Inelastic Buckling of Steel–Concrete Composite Beams Prestressed with External Tendons. Thin-Walled Struct. 2010, 48, 233–242. [Google Scholar] [CrossRef]
- Chen, S.; Wang, X. Finite Element Analysis of Distortional Lateral Buckling of Continuous Composite Beams with Transverse Web Stiffeners. Adv. Struct. Eng. 2012, 15, 1607–1616. [Google Scholar] [CrossRef]
- Rossi, A.; de Souza, A.S.C.; Nicoletti, R.S.; Martins, C.H. Stability Behavior of Steel–Concrete Composite Beams Subjected to Hogging Moment. Thin-Walled Struct. 2021, 167, 108193. [Google Scholar] [CrossRef]
- de Oliveira, J.P.S.; Dias, J.V.F.; Fakury, R.H.; Calenzani, A.F.G. Resistant Bending Moment to Lateral-Torsional Buckling of Continuous Steel and Concrete Composite Beams with Transverse Stiffeners. Rev. IBRACON Estruturas e Mater. 2021, 14, 1–18. [Google Scholar] [CrossRef]
- Rossi, A.; Sander, A.; De Souza, C.; Silva, R.; Humberto, C. The Influence of Structural and Geometric Imperfections on the LDB Strength of Steel—Concrete Composite Beams. Thin-Walled Struct. 2021, 162, 107542. [Google Scholar] [CrossRef]
- Hope-Gill, M.C.; Johnson, R.P. Tests on Three-Span Continuous Composite Beams. Proc. Instn Civ. Engrs 1976, 61, 367–381. [Google Scholar] [CrossRef]
- Johnson, R.P.; Fan, C.K.R. Distortional Lateral Buckling of Continuous Composite Beams. Proc.—Inst. Civ. Eng. Part 2 Res. Theory 1991, 91, 131–161. [Google Scholar] [CrossRef]
- Johnson, R.P.; Chen, S. Stability of Continuous Composite Plate Girders with U-Frame Action. Proc. Inst. Civ. Eng. Struct. Build. 1993, 99, 187–197. [Google Scholar] [CrossRef]
- Kitaoka, S.; Kanno, R.; Hiroshima, S.; Hanya, K.; Takada, K.; Yoshida, F. Strength of Lateral-Torsional Buckling of a Composite Steel Beam Subjected to Reverse Curvature Bending. In Proceedings of the Eighth International Conference on Composite Construction in Steel and Concrete, Jackson, WY, USA, 29 July–2 August 2017; pp. 334–345. [Google Scholar]
- Tong, L.; Liu, Y.; Sun, B.; Chen, Y.; Zhou, F.; Tian, H.; Sun, X. Experimental Investigation on Mechanical Behavior of Steel-Concrete Composite Beams under Negative Bending. J. Build. Struct. 2014, 35, 1–10. [Google Scholar] [CrossRef]
- Fan, C.X.R. Buckling in Continuous Composite Beams. Ph.D. Thesis, University of Warwick, Warwick, UK, 1990. [Google Scholar]
- Chen, S. Instability of Composite Beams in Hogging Bending. Ph.D. Thesis, University of Warwick, Warwick, UK, 1992. [Google Scholar]
- Vasdravellis, G.; Uy, B.; Tan, E.L.; Kirkland, B. Behaviour and Design of Composite Beams Subjected to Negative Bending and Compression. J. Constr. Steel Res. 2012, 79, 34–47. [Google Scholar] [CrossRef]
- Vasdravellis, G.; Uy, B.; Tan, E.L.; Kirkland, B. The Effects of Axial Tension on the Hogging-Moment Regions of Composite Beams. J. Constr. Steel Res. 2012, 68, 20–33. [Google Scholar] [CrossRef]
- Bui, V.T.; Truong, V.H.; Trinh, M.C.; Kim, S.E. Fully Nonlinear Analysis of Steel-Concrete Composite Girder with Web Local Buckling Effects. Int. J. Mech. Sci. 2020, 184, 105729. [Google Scholar] [CrossRef]
- Zhou, X.; Men, P.; Di, J.; Qin, F. Experimental Investigation of the Vertical Shear Performance of Steel–Concrete Composite Girders under Negative Moment. Eng. Struct. 2021, 228, 111487. [Google Scholar] [CrossRef]
- Men, P.; Zhou, X.; Zhang, Z.; Di, J.; Qin, F. Behaviour of Steel–Concrete Composite Girders under Combined Negative Moment and Shear. J. Constr. Steel Res. 2021, 179, 106508. [Google Scholar] [CrossRef]
- Men, P.; Di, J.; Jiang, H.; Zhou, X.; Qin, F. Web Shear Buckling of Steel–Concrete Composite Girders in Negative-Moment Regions. Eng. Struct. 2021, 237, 112210. [Google Scholar] [CrossRef]
- Men, P.; Di, J.; Qin, F.; Su, Y. Experimental Investigation of the Shear Behavior of Slender Continuous Steel–Concrete Composite Girders in Hogging Moment. J. Struct. Eng. 2023, 149, 04022218. [Google Scholar] [CrossRef]
- Hamoda, A.; Hossain, K.M.A.; Sennah, K.; Shoukry, M.; Mahmoud, Z. Behaviour of Composite High Performance Concrete Slab on Steel I-Beams Subjected to Static Hogging Moment. Eng. Struct. 2017, 140, 51–65. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, S.; Zhu, Y.; Fan, L.; Shao, X. Flexural Responses of Steel-UHPC Composite Beams under Hogging Moment. Eng. Struct. 2020, 206, 110134. [Google Scholar] [CrossRef]
- Qi, J.; Cheng, Z.; Wang, J.; Tang, Y. Flexural Behavior of Steel-UHPFRC Composite Beams under Negative Moment. Structures 2020, 24, 640–649. [Google Scholar] [CrossRef]
- Wu, F.; Fan, Z.; He, L.; Liu, S.; Zuo, J.; Yang, F. Comparative Study of the Negative Bending Behaviour of Corrugated Web Steel—Concrete Composite Beams Using NC, ECC and UHPC. Eng. Struct. 2023, 283, 115925. [Google Scholar] [CrossRef]
- Fan, J.; Gou, S.; Ding, R.; Zhang, J.; Shi, Z. Experimental and Analytical Research on the Flexural Behaviour of Steel–ECC Composite Beams under Negative Bending Moments. Eng. Struct. 2020, 210, 110309. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Yu, J.; Liu, J.-P.; Zhou, B.-X.; Chen, Y.F. Experimental Study on Assembled Monolithic Steel-Prestressed Concrete Composite Beam in Negative Moment. J. Constr. Steel Res. 2020, 167, 105667. [Google Scholar] [CrossRef]
- Liu, X.; Tang, L.; Jing, Y.; Xiang, J.; Tian, X.; Liu, W.; Huang, Y.; Zhang, G.; Zhao, W.; Yang, G. Behaviour of Continuous Steel–Concrete Composite Beams Strengthened with CFRP Sheets at Hogging-Moment Region. Compos. Struct. 2022, 291, 115695. [Google Scholar] [CrossRef]
- Jurkiewiez, B.; Tout, F.; Ferrier, E. Push-out and Bending Tests of Steel-Concrete Adhesively Bonded Composite Elements. Eng. Struct. 2021, 231, 111717. [Google Scholar] [CrossRef]
- Ding, J.; Li, Y.; Xing, W.; Ren, P.; Kong, Q.; Yuan, C. Mechanical Properties and Engineering Application of Single-Span Steel-Concrete Double-Sided Composite Beams. J. Build. Eng. 2021, 40, 102644. [Google Scholar] [CrossRef]
- Fang, J.; Bao, W.; Ren, F.; Pang, L.; Jiang, J. Behaviour of Composite Beams with Beam-to-Girder End-Plate Connection under Hogging Moments. Eng. Struct. 2021, 235, 112030. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.; Uy, B.; Li, D. Behaviour and Design of Stainless Steel-Concrete Composite Beam-to-Column Joints. J. Constr. Steel Res. 2021, 184, 106800. [Google Scholar] [CrossRef]
- Song, A.; Wan, S.; Jiang, Z.; Xu, J. Residual Deflection Analysis in Negative Moment Regions of Steel-Concrete Composite Beams under Fatigue Loading. Constr. Build. Mater. 2018, 158, 50–60. [Google Scholar] [CrossRef]
- Salah, W.A. Modelling of Instability Behavior in Hogging Moment Regions of Steel-Concrete Composite Beams. Ph.D. Theis, Warsaw University of Technology, Warsaw, UK, 2009. [Google Scholar]
- Gizejowski, M.A.; Salah, W.A. Stability and Ductility of Castellated Composite Beams Subjected to Hogging Bending. In Proceedings of the SDSS’ Rio 2010: International Colloquium Stability and Ductility of Steel Structures, Rio de Janeiro, Brazil, 8–10 September 2010; Volume 2, pp. 839–846. [Google Scholar]
- Geng, K.; Jia, L.; Xu, F.; Li, Q. Experimental Study on the Mechanical Behaviour of Castellated Composite Beams under a Negative Bending Moment. Structures 2023, 47, 953–965. [Google Scholar] [CrossRef]
- Kerdal, D.; Nethercot, D.A. Failure Modes for Castellated Beams. J. Constr. Steel Res. 1984, 4, 295–315. [Google Scholar] [CrossRef]
- Warren, J. Ultimate Load and Deflection Behaviour of Cellular Beams. Master’s Thesis, University of Natal, Durban, South Africa, 2001. [Google Scholar]
- Panedpojaman, P.; Thepchatri, T.; Limkatanyu, S. Novel Design Equations for Shear Strength of Local Web-Post Buckling in Cellular Beams. Thin-Walled Struct. 2014, 76, 92–104. [Google Scholar] [CrossRef]
- Deepha, R.; Jayalekshmi, S.; Jagadeesan, K. Nonlinear Analysis of Castellated ISMB150—I Beam with Hexagonal Openings—A Finite Element Approach. Mater. Today Proc. 2020, 27, A8–A16. [Google Scholar] [CrossRef]
- Weidlich, C.M.; Sotelino, E.D.; Cardoso, D.C.T. An Application of the Direct Strength Method to the Design of Castellated Beams Subject to Flexure. Eng. Struct. 2021, 243, 112646. [Google Scholar] [CrossRef]
- de Oliveira, J.P.; Cardoso, D.C.T.; Sotelino, E.D. Elastic Flexural Local Buckling of Litzka Castellated Beams: Explicit Equations and FE Parametric Study. Eng. Struct. 2019, 186, 436–445. [Google Scholar] [CrossRef]
- Braga, J.J.V.; Linhares, D.A.; Cardoso, D.C.T.; Sotelino, E.D. Failure Mode and Strength Prediction of Laterally Braced Litzka-Type Castellated Beams. J. Constr. Steel Res. 2021, 184, 106796. [Google Scholar] [CrossRef]
- Liu, M.; Liang, M.; Ma, Q.; Wang, P.; Ma, C. Web-Post Buckling of Bolted Castellated Steel Beam with Octagonal Web Openings. J. Constr. Steel Res. 2020, 164, 105794. [Google Scholar] [CrossRef]
- Mohebkhah, A.; Azandariani, M.G. Shear Resistance of Retrofitted Castellated Link Beams: Numerical and Limit Analysis Approaches. Eng. Struct. 2020, 203, 109864. [Google Scholar] [CrossRef]
- Kang, L.; Hong, S.; Liu, X. Shear Behaviour and Strength Design of Cellular Beams with Circular or Elongated Openings. Thin-Walled Struct. 2021, 160, 107353. [Google Scholar] [CrossRef]
- Limbachiya, V.; Shamass, R. Application of Artificial Neural Networks for Web-Post Shear Resistance of Cellular Steel Beams. Thin-Walled Struct. 2021, 161, 107414. [Google Scholar] [CrossRef]
- Zaher, O.F.; Yossef, N.M.; El-Boghdadi, M.H.; Dabaon, M.A. Structural Behaviour of Arched Steel Beams with Cellular Openings. J. Constr. Steel Res. 2018, 148, 756–767. [Google Scholar] [CrossRef]
- Zewudie, B.B. Nonlinear Finite Element Analysis and Comparison of In-Plane Strength of Circular and Parabolic Arched I-Section Cellular Steel Beam. Adv. Civ. Eng. 2022, 2022, 13. [Google Scholar] [CrossRef]
- Morkhade, S.G.; Gupta, L.M.; Martins, C.H. Effect of Web Post Width on Strength Capacity of Steel Beams with Web Openings: Experimental and Analytical Investigation. Pract. Period. Struct. Des. Constr. 2022, 27, 1–9. [Google Scholar] [CrossRef]
- Qiao, H.; Guo, Z.; Chen, Y. Experimental Investigation of a Substructure in a Frame with Castellated Steel Beams in Case of a Column Loss. Eng. Struct. 2022, 255, 113926. [Google Scholar] [CrossRef]
- Nawar, M.T.; Arafa, I.T.; Elhosseiny, O. Numerical Investigation on e Ff Ective Spans Ranges of Perforated Steel Beams. Structures 2020, 25, 398–410. [Google Scholar] [CrossRef]
- França, G.M.; Weidlich, C.M.; Sotelino, E.D.; Cardoso, D.C.T. An Appraisal of the Vierendeel Mechanism Capacity of Cellular Beams with Sinusoidal Openings. J. Constr. Steel Res. 2022, 198, 107539. [Google Scholar] [CrossRef]
- Ferreira, F.P.V.; Martins, C.H.; Nardin, S. Assessment of Web Post Buckling Resistance in Steel-Concrete Composite Cellular Beams. Thin-Walled Struct. 2021, 158, 106969. [Google Scholar] [CrossRef]
- Ferreira, F.P.V.; Tsavdaridis, K.D.; Martins, C.H.; De Nardin, S. Buckling and Post-Buckling Analyses of Composite Cellular Beams. Compos. Struct. 2021, 262, 113616. [Google Scholar] [CrossRef]
- Ferreira, F.P.V.; Tsavdaridis, K.D.; Martins, C.H.; Nardin, S. De Composite Action on Web-Post Buckling Shear Resistance of Composite Cellular Beams with PCHCS and PCHCSCT. Eng. Struct. 2021, 246, 113065. [Google Scholar] [CrossRef]
- Ferreira, F.P.V.; Tsavdaridis, K.D.; Martins, C.H.; De Nardin, S. Ultimate Strength Prediction of Steel–Concrete Composite Cellular Beams with PCHCS. Eng. Struct. 2021, 236, 112082. [Google Scholar] [CrossRef]
- Ponsorn, P.; Phuvoravan, K. Efficiency of Castellated and Cellular Beam Utilization Based on Design Guidelines. Pract. Period. Struct. Des. Constr. 2020, 25, 1–11. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Sharifi, Y. Finite Element Modelling of Castellated Steel Beams under Lateral-Distortional Buckling Mode. Structures 2021, 29, 1507–1521. [Google Scholar] [CrossRef]
- Muhammed Jasir, T.; Raj, M.P. Numerical Investigation on Behaviour of Castellated Steel Beam in Lateral Distortional Buckling. Mater. Today Proc. 2022, 65, 3874–3880. [Google Scholar] [CrossRef]
- Salah, W.A. Performance of Hybrid Castellated Beams Prediction Using Finite Element Modeling. Technol. Appl. Sci. Res. 2022, 12, 8444–8451. [Google Scholar] [CrossRef]
- Ferreira, F.P.V.; Rossi, A.; Martins, C.H. Lateral-Torsional Buckling of Cellular Beams According to the Possible Updating of EC3. J. Constr. Steel Res. 2019, 153, 222–242. [Google Scholar] [CrossRef]
- Ferreira, F.P.V.; Martins, C.H. LRFD for Lateral-Torsional Buckling Resistance of Cellular Beams. Int. J. Civ. Eng. 2020, 18, 303–323. [Google Scholar] [CrossRef]
- Sehwail, M.M.; Celikag, M. Load Carrying Capacity of Hot-Rolled Hybrid Cellular Steel Beams: Experimental Investigations. Arab. J. Sci. Eng. 2022, 47, 12633–12648. [Google Scholar] [CrossRef]
- Salah, W.A. Lateral Torsional Buckling Capacity Assessment of Cellular Steel Beams. Pract. Period. Struct. Des. Constr. 2023, 28, 1–15. [Google Scholar] [CrossRef]
- Ertenli, M.F.; Erdal, E.; Buyukkaragoz, A.; Kalkan, I.; Aksoylu, C.; Özkılıç, Y.O. Lateral Torsional Buckling of Doubly—Symmetric Steel Cellular I—Beams. Steel Compos. Struct. 2023, 5, 10. [Google Scholar] [CrossRef]
- Bhat, R.A.; Gupta, L.M. Moment-Gradient Factor for Perforated Cellular Steel Beams Under Lateral Torsional Buckling. Arab. J. Sci. Eng. 2020, 45, 8727–8743. [Google Scholar] [CrossRef]
- Bhat, R.A.; Gupta, L.M. Interaction of Buckling Modes for Cellular Steel Beams Under Flexure. Int. J. Steel Struct. 2021, 21, 260–273. [Google Scholar] [CrossRef]
- Khatri, A.P.; Katikala, S.R.; Kotapati, V.K. Effect of Load Height on Elastic Buckling Behavior of I-Shaped Cellular Beams. Structures 2021, 33, 1923–1935. [Google Scholar] [CrossRef]
- de Carvalho, A.S.; Rossi, A.; Martins, C.H. Assessment of Lateral–Torsional Buckling in Steel I-Beams with Sinusoidal Web Openings. Thin-Walled Struct. 2022, 175, 109242. [Google Scholar] [CrossRef]
- de Carvalho, A.S.; de Oliveira, V.M.; Rossi, A.; Martins, C.H. Elastic Lateral-Torsional Buckling Behavior of Steel I-Beams with Sinusoidal Web Openings. Structures 2023, 47, 23–36. [Google Scholar] [CrossRef]
- de Carvalho, A.S.; Martins, C.H.; Rossi, A.; de Oliveira, V.M.; Morkhade, S.G. Moment Gradient Factor for Steel I-Beams with Sinusoidal Web Openings. J. Constr. Steel Res. 2023, 202, 107775. [Google Scholar] [CrossRef]
- Gizejowski, M.A.; Salah, W.A. Numerical Modeling of Composite Castellated Beams. In Proceedings of the International Conference on Composite Construction in Steel and Concrete 2008, Tabernash, CO, USA, 20–24 July 2008; pp. 554–565. [Google Scholar] [CrossRef]
- de Oliveira, V.M.; Rossi, A.; Ferreira, F.P.V.; Martins, C.H. Stability Behavior of Steel—Concrete Composite Cellular Beams Subjected to Hogging Moment. Thin-Walled Struct. 2022, 173, 108987. [Google Scholar] [CrossRef]
- de Oliveira, V.M.; Carvalho, d.A.S.; Rossi, A.; Ferreira, F.P.V.; Martins, C.H. Elastic and Inelastic Analyses of Composite Cellular Beams in Hogging Moment Regions. Thin-Walled Struct. 2023, 184, 110513. [Google Scholar] [CrossRef]
- Rossi, A.; Ferreira, F.P.V.; Martins, C.H.; Mesacasa Júnior, E.C. Assessment of Lateral Distortional Buckling Resistance in Welded I-Beams. J. Constr. Steel Res. 2020, 166, 105924. [Google Scholar] [CrossRef]
- Rossi, A.; Martins, C.H.; Nicoletti, R.S.; de Souza, A.S.C. Reassesment of Lateral Torsional Buckling in Hot-Holled I-Beams. Structures 2020, 26, 524–536. [Google Scholar] [CrossRef]
- Vlasov, V.Z. Thin Walled Elastic Beams; Isr. Progr. Sci. Transl.; National Science Foundation: Washington, DC, USA, 1961. [Google Scholar]
- AISC Specification for Structural Steel Buildings; ANSI/AISC 360-16; Institute of Steel Construction: Chicago, IL, USA, 2016.
- American Association of State and Highway Transportation Officials (AASHTO). AASHTO LRFD Bridge Design Specifications, 8th ed.; With 2017 Interim Provisions; AASHTO: Washington, DC, USA, 2017. [Google Scholar]
- Standards Association of Australia. AS 4100 Steel Structures. Sydney Australia, 1998; Standards Association of Australia: Sydney, Australia, 2016. [Google Scholar]
- Standard Association of Australia Standard Association of New Zealand. AS/NZS 2327 Composite Structures—Composite Steel Concrete Construction in Buildings Sydney (Australia); Standards Australia: Sydney, Australia, 2017. [Google Scholar]
- Eurocode 4 Design of Composite Steel and Concrete Structures—Part 1-1: General Rules and Rules for Buildings, Standard; Comite Europeen de Normalisation: Brussels, Belgium, 1994.
- Associação Brasileira de Normas Técnicas ABNT NBR 8800; Projeto de Estruturas de Aço e de Estruturas Mistas de Aço e Concreto de Edifícios, Standard; Associação Brasileira de Normas Técnicas: São Paulo, Brazil, 2008.
- Lawson, H. Design of Composite Beams with Large Web Openings; The Steel Constrution Institute, 2011; ISBN 0-9679749-0-9. Available online: https://www.steelconstruction.info/images/e/e7/SCI_P355.pdf (accessed on 27 February 2023).
- Fares, S.; Coulson, J.; Dinehart, D. Dinehart Castellated and Cellular Beam Design 31. Am. Inst. Steel Constr. 2016, 1–116. [Google Scholar]
- Müller, C.; Hechler, O.; Bureau, A.; Bitar, D.; Joyeux, D.; Cajot, L.G.; Demarco, T.; Lawson, R.M.; Hicks, S.; Devine, P.; et al. Large Web Openings for Service Integration in Composite Floors; Technical Steel Research. European Comission, Contract No 7210-PR/315. Final Report; European Comission: Brussels, Belgium, 2006; ISBN 9279017233. [Google Scholar]
- Silva, C.C.; Caldas, R.B.; Fakury, R.H.; Carvalho, H.; Dias, J.V.F. Web Rotational Stiffness of Continuous Steel-Concrete Composite Castellated Beams. Frat. Ed Integrita Strutt. 2019, 13, 264–275. [Google Scholar] [CrossRef]
- Silva, C.C.; Caldas, R.B.; Fakury, R.H.; Dias, J.V.F.; Carvalho, H. Elastic Critical Moment of Lateral Distortional Buckling of Castellated Composite Beams under Uniform Hogging Moment. Pract. Period. Struct. Des. Constr. 2020, 25, 04020032. [Google Scholar] [CrossRef]
- Sonck, D.; Belis, J. Lateral-Torsional Buckling Resistance of Cellular Beams. J. Constr. Steel Res. 2015, 105, 119–128. [Google Scholar] [CrossRef]
- Sonck, D.; Belis, J. Lateral-Torsional Buckling Resistance of Castellated Beams. J. Struct. Eng. 2017, 143, 1–9. [Google Scholar] [CrossRef]
- Rossi, A.; Nicoletti, R.S.; de Souza, A.S.C.; Humberto Martins, C. Lateral Distortional Buckling in Steel-Concrete Composite Beams: A Review. Structures 2020, 27, 1299–1312. [Google Scholar] [CrossRef]
- Hanswille, G.; Lindner, J.; Münich, D. Lateral Torsional Buckling of Composite Beams [in German]. Stahlbau 1998, 67, 525–535. [Google Scholar] [CrossRef]
- Roik, K.; Hanswille, G.; Kina, J. Solution for the Lateral Torsional Buckling Prob Lem of Composite Beams [in German]. Stahlbau 1990, 59, 327–332. [Google Scholar]
- Eurocode 4 Design of Composite Steel and Concrete Structures—Part 1-1: General Rules and Rules for Buildings, Standard; Comite Europeen de Normalisation: Brussels, Belgium, 1992.
- Dias, J.V.F.; Oliveira, J.P.S.; Calenzani, A.F.G.; Fakury, R.H. Elastic Critical Moment of Lateral-Distortional Buckling of Steel-Concrete Composite Beams under Uniform Hogging Moment. Int. J. Struct. Stab. Dyn. 2019, 19. [Google Scholar] [CrossRef]
- Svensson, S.E. Lateral Buckling of Beams Analysed as Elastically Supported Columns Subject to a Varying Axial Force. J. Constr. Steel Res. 1985, 5, 179–193. [Google Scholar] [CrossRef]
- Williams, F.W.; Jemah, A.K. Buckling Curves for Elastically Supported Columns with Varying Axial Force, to Predict Lateral Buckling of Beams. J. Constr. Steel Res. 1987, 7, 133–147. [Google Scholar] [CrossRef]
- Oliveira, J.P.S. New Proposition for Verification of Lateral Distortional Buckling of Steel-Concrete Composite Beams [in Portuguese]. Ph.D. Thesis, Federal University of Minas Gerais, Belo Horizonte, Brazil, 2018. [Google Scholar]
- Dias, J.V.F. Determination of the Elastic Critical Moment to Lateral Distortional Buckling of Continuous and Semicontinuous Composite Beams [in Portuguese]. Master’s Thesis, Federal University of Minas Gerais, Belo Horizonte, Brazil, 2018. [Google Scholar]
- Zhou, W.-B.; Yan, W.-J. Refined Nonlinear Finite Element Modelling towards Ultimate Bending Moment Calculation for Concrete Composite Beams under Negative Moment. Thin-Walled Struct. 2017, 116, 201–211. [Google Scholar] [CrossRef]
- Gizejowski, M.A.; Salah, W.A. Restrained Distortional Buckling Strength of Steel-Concrete Composite Beams—A Review of Current Practice and New Developments. In Proceedings of the 10th International Conference Modern Building Materials, Structures and Techniques, Vilnius, Lithuania, 19–21 May 2010; pp. 604–612. [Google Scholar]
- Hosseinpour, M.; Shari, Y.; Shari, H.; Sharifi, Y.; Moghbeli, A.; Sharifi, Y.; Moghbeli, A.; Hosseinpour, M.; Sharifi, H. Neural Network Application for Distortional Buckling Capacity Assessment of Castellated Steel Beams. Structures 2020, 29, 1174–1183. [Google Scholar] [CrossRef]
- Sharifi, Y.; Moghbeli, A.; Hosseinpour, M.; Sharifi, H. Study of Neural Network Models for the Ultimate Capacities of Cellular Steel Beams. Iran. J. Sci. Technol.—Trans. Civ. Eng. 2020, 44, 579–589. [Google Scholar] [CrossRef]
- Moghbeli, A.; Sharifi, Y. New Predictive Equations for Lateral-Distortional Buckling Capacity Assessment of Cellular Steel Beams. Structures 2021, 29, 911–923. [Google Scholar] [CrossRef]
- Rajana, K.; Tsavdaridis, K.D.; Koltsakis, E. Elastic and Inelastic Buckling of Steel Cellular Beams under Strong-Axis Bending. Thin-Walled Struct. 2020, 156, 106955. [Google Scholar] [CrossRef]
- Ferreira, F.P.V.; Shamass, R.; Limbachiya, V.; Tsavdaridis, K.D.; Martins, C.H. Lateral–Torsional Buckling Resistance Prediction Model for Steel Cellular Beams Generated by Artificial Neural Networks (ANN). Thin-Walled Struct. 2022, 170, 108592. [Google Scholar] [CrossRef]
- Shamass, R.; Ferreira, F.P.V.; Limbachiya, V.; Santos, L.F.P.; Tsavdaridis, K.D. Web-Post Buckling Prediction Resistance of Steel Beams with Elliptically-Based Web Openings Using Artificial Neural Networks (ANN). Thin-Walled Struct. 2022, 180, 109959. [Google Scholar] [CrossRef]
- de Carvalho, A.S.; Hosseinpour, M.; Rossi, A.; Martins, C.H.; Sharifi, Y. New Formulas for Predicting the Lateral–Torsional Buckling Strength of Steel I-Beams with Sinusoidal Web Openings. Thin-Walled Struct. 2022, 181, 110067. [Google Scholar] [CrossRef]
- Tohidi, S.; Sharifi, Y. Neural Networks for Inelastic Distortional Buckling Capacity Assessment of Steel I-Beams. Thin-Walled Struct. 2015, 94, 359–371. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Rossi, A.; Sander Clemente de Souza, A.; Sharifi, Y. New Predictive Equations for LDB Strength Assessment of Steel–Concrete Composite Beams. Eng. Struct. 2022, 258, 114121. [Google Scholar] [CrossRef]
- Rossi, A.; Hosseinpour, M.; Martins, C.H.; Sharifi, Y. A New Formula for Predicting Lateral Distortional Buckling Strength of I-Beams Subjected to Different Loading Conditions. Int. J. Struct. Stab. Dyn. 2022, 2250129, 1–29. [Google Scholar] [CrossRef]
- Couto, C. Neural Network Models for the Critical Bending Moment of Uniform and Tapered Beams. Structures 2022, 41, 1746–1762. [Google Scholar] [CrossRef]









| Model | Reference | Highlight |
|---|---|---|
| Experimental | Salah [58] and Gizejowski and Salah [59] | Performed tests with steel-concrete composite beams with circular, hexagonal, and rectangular web openings |
| Numerical | Salah [58] and Gizejowski and Salah [59] | Carried out sensitivity analysis with geometrical and physical nonlinear finite element models |
| Gizejowski and Salah [97] | Used geometrical nonlinear finite element models to analyze the stability behavior of continuous composite cellular beams | |
| Oliveira et al. [98] | Conducted nonlinear analysis to investigate the effect of the opening diameter, web post width, I-section dimensions, free span, and hogging moment distribution | |
| Oliveira et al. [99] | Analyzed the elastic behavior of the same beams investigated by Oliveira et al. [98] |
| λ Values | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Case | |||||||||
| βL | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 1.000 | 1.881 | 2.355 | 5.824 | 2.835 | 4.518 | 10.83 | 5.824 | 0.377 |
| 1 | 1.010 | 1.889 | 2.376 | 5.856 | 2.860 | 4.538 | 10.84 | 5.856 | 0.438 |
| 2 | 1.164 | 2.166 | 2.694 | 6.309 | 3.235 | 4.827 | 11.02 | 6.309 | 1.332 |
| 3 | 1.832 | 3.240 | 3.944 | 7.952 | 4.732 | 5.884 | 11.72 | 7.952 | 4.543 |
| 4 | 3.628 | 5.472 | 6.450 | 11.06 | 8.044 | 7.875 | 13.26 | 11.06 | 6.775 |
| 5 | 5.604 | 8.110 | 9.537 | 15.24 | 13.16 | 10.41 | 15.65 | 15.24 | 9.135 |
| 6 | 7.326 | 10.91 | 12.86 | 20.06 | 19.48 | 13.20 | 18.67 | 20.06 | 12.48 |
| 8 | 13.67 | 18.06 | 20.91 | 30.99 | 33.16 | 20.28 | 25.23 | 30.99 | 20.26 |
| 10 | 20.41 | 26.92 | 30.75 | 43.62 | 47.21 | 29.27 | 34.17 | 43.62 | 29.18 |
| 12.5 | 31.66 | 40.41 | 45.51 | 61.89 | 66.65 | 42.74 | 47.83 | 61.89 | 42.73 |
| 15 | 45.79 | 56.56 | 63.00 | 82.97 | 88.86 | 58.73 | 64.10 | 82.97 | 58.73 |
| 17.5 | 62.75 | 75.35 | 83.20 | 106.8 | 113.9 | 77.21 | 82.96 | 106.8 | 77.20 |
| 20 | 81.63 | 96.78 | 106.1 | 133.5 | 141.7 | 98.18 | 104.4 | 133.5 | 98.18 |
| Legend | |||||||||
 | 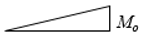 |  | |||||||
| Case 1 | Case 2 | Case 3 | |||||||
 |  | 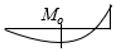 | |||||||
| Case 4 | Case 5 | Case 6 | |||||||
 | 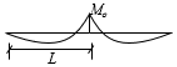 |  | |||||||
| Case 7 | Case 8 | Case 9 | |||||||
| * Moment Distribution | ψ | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 2.00 | 2.25 | 2.50 | |
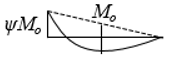 | 41.5 | 30.2 | 24.5 | 21.1 | 19.0 | 17.5 | 16.5 | 15.7 | 15.2 |
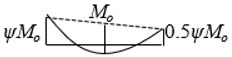 | 33.9 | 22.7 | 17.3 | 14.1 | 13.0 | 12.0 | 11.4 | 10.9 | 10.6 |
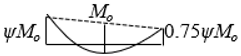 | 28.2 | 18.0 | 13.7 | 11.7 | 10.6 | 10.0 | 9.5 | 9.1 | 8.9 |
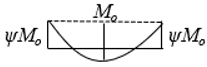 | 21.9 | 13.9 | 11.0 | 9.6 | 8.8 | 8.3 | 8.0 | 7.8 | 7.6 |
 | 28.4 | 21.8 | 18.6 | 16.7 | 15.6 | 14.8 | 14.2 | 13.8 | 13.5 |
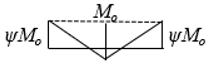 | 12.7 | 9.89 | 8.6 | 8.0 | 7.7 | 7.4 | 7.2 | 7.1 | 7.0 |
| * Moment Distribution | ψ | ||||
|---|---|---|---|---|---|
| 0.00 | 0.25 | 0.50 | 0.75 | 1.00 | |
 | 11.1 | 9.5 | 8.2 | 7.1 | 6.2 |
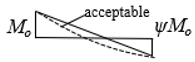 | 11.1 | 12.8 | 14.6 | 16.3 | 18.1 |
* Moment Distribution | |||
| β0B = –0.11ψ2 − 0.37ψ + 0.74 | |||
| ψ | a | η1 | η2 |
| 1.0 | 1.48 | 9.10 | 9.30 |
| 0.5 | 1.45 | 8.30 | 8.80 |
| 0.0 | 1.40 | 6.40 | 7.30 |
| –0.5 | 1.25 | 4.70 | 5.70 |
| –1.0 | 1.00 | 4.20 | 5.10 |
* Moment Distribution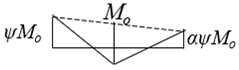 | |||||||||
| β0B = 0.320ψ + 0.53 | β0B = 0.075ψ2 + 0.25ψ + 0.35 | β0B = 0.116ψ2 + 0.06ψ + 0.21 | |||||||
| α = 1 A = 1.25 | α = 0.5 A = 1.5 | α = 0.25 A = 1.6 | |||||||
| a | η1 | η2 | a | η1 | η2 | a | η1 | η2 | |
| ψ = 1.0 | 1.46 | 9.85 | 9.55 | 1.35 | 7.10 | 6.85 | 0.95 | 4.90 | 4.50 |
| ψ = 0.5 | 1.45 | 9.00 | 9.75 | 1.30 | 5.75 | 6.80 | 0.85 | 4.50 | 5.60 |
| ψ = 0.0 | 1.35 | 5.95 | 7.75 | 1.05 | 4.60 | 6.30 | 0.70 | 4.15 | 6.10 |
* Moment Distribution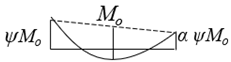 | |||||||||
| β0B = 0.037ψ2 + 0.30ψ + 0.4 | β0B = 0.16ψ2 + 0.05ψ + 0.24 | β0B = 0.07ψ2 + 0.01ψ + 0.13 | |||||||
| α = 1 A = 1.25 | α = 0.5 A = 1.5 | α = 0.25 A = 1.75 | |||||||
| a | η1 | η2 | a | η1 | η2 | a | η1 | η2 | |
| ψ = 1.0 | 1.45 | 8.80 | 8.95 | 1.15 | 4.90 | 5.15 | 0.65 | 4.05 | 4.50 |
| ψ = 0.5 | 1.37 | 5.95 | 6.70 | 0.95 | 4.50 | 5.90 | 0.55 | 4.00 | 5.70 |
| ψ = 0.0 | 1.13 | 4.50 | 5.75 | 0.77 | 4.20 | 5.95 | 0.48 | 3.95 | 6.15 |
| Source | EN 1994-1-1: 2004 [107] | NBR 8800: 2008 [108] | Australian Standards [105,106] |
|---|---|---|---|
| Mu | |||
| Mcr | Formulations developed based on the U-frame model (Section 2.1.3, Section 2.1.4 and Section 2.1.5) | Formulation proposed by Roik et al. [118] (Section 2.1.3) |
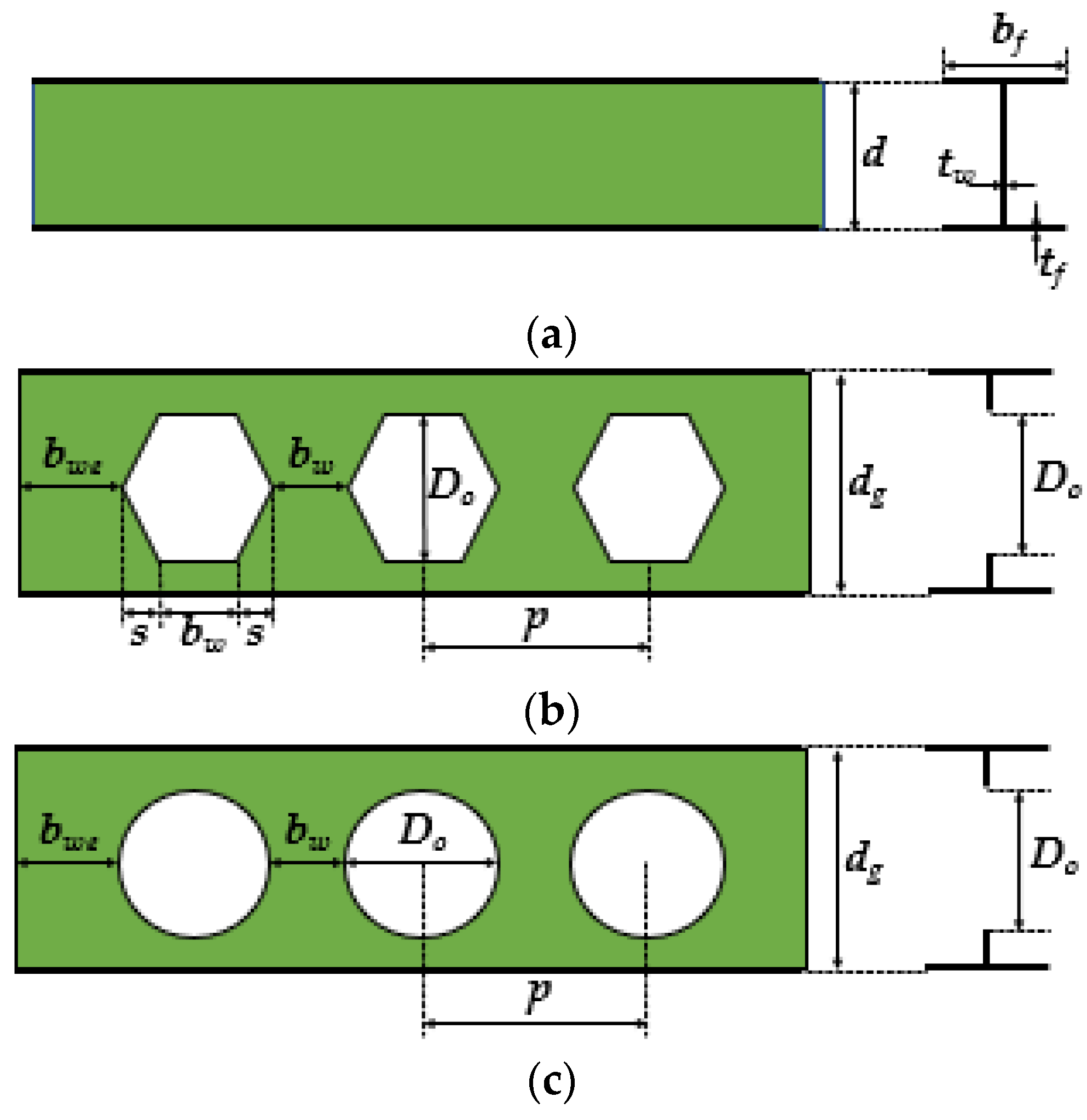
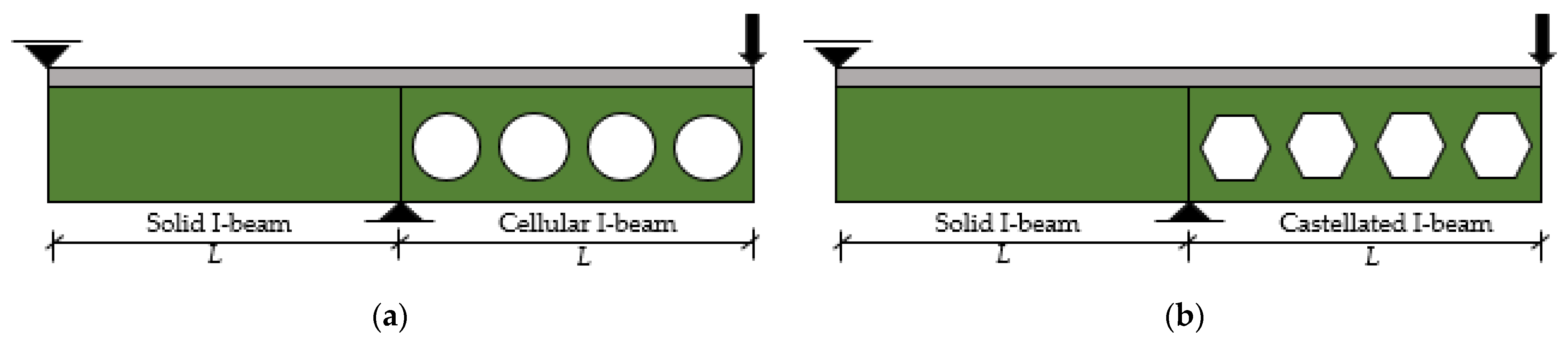
| Specimen | L | dg | bf | tf | tw | D0 | bw | s | p | *n | Abar | c |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C4S355 | 2116 | 480 | 100 | 6 | 4 | 336 | 193 | 92 | 529 | 4 | 1256.64 | 50 |
| C4S420 | 2116 | 480 | 100 | 6 | 4 | 336 | 193 | 92 | 529 | 4 | 1256.64 | 50 |
| H4S355 | 2116 | 480 | 100 | 6 | 4 | 321 | 193 | 92 | 529 | 4 | 1256.64 | 50 |
| H4S420 | 2116 | 480 | 100 | 6 | 4 | 321 | 193 | 92 | 529 | 4 | 1256.64 | 50 |
| Specimen | E (GPa) | fy (MPa) | fy,bar (MPa) | Pu (kN) |
|---|---|---|---|---|
| C4S355 | 200 | 355 | 459.6 | 59.56 |
| C4S420 | 200 | 420 | 459.6 | 62.26 |
| H4S355 | 200 | 355 | 459.6 | 62.03 |
| H4S420 | 200 | 420 | 459.6 | 62.55 |
| Model | Geometric Properties Approach | |||||
|---|---|---|---|---|---|---|
| J2T-Average | Double T | Solid | Average | Superficial | Linear | |
| C4S355 | 1.22 | 1.22 | 1.38 | 1.22 | 1.17 | 1.17 |
| C4S420 | 1.27 | 1.27 | 1.42 | 1.27 | 1.27 | 1.27 |
| H4S355 | 1.18 | 1.18 | 1.32 | 1.18 | 1.18 | 1.18 |
| H4S420 | 1.28 | 1.28 | 1.42 | 1.29 | 1.29 | 1.28 |
| Avg. | 1.24 | 1.24 | 1.39 | 1.24 | 1.23 | 1.23 |
| SD. (%) | 4.77 | 4.75 | 4.52 | 4.78 | 6.09 | 6.07 |
| Var. (%) | 0.23 | 0.23 | 0.20 | 0.23 | 0.37 | 0.37 |
| Model | Geometric Properties Approach | |||||
|---|---|---|---|---|---|---|
| J2T-Average | Double T | Solid | Average | Superficial | Linear | |
| C4S355 | 0.69 | 0.67 | 0.83 | 0.76 | 0.78 | 0.74 |
| C4S420 | 0.69 | 0.67 | 0.79 | 0.74 | 0.75 | 0.71 |
| H4S355 | 0.67 | 0.65 | 0.79 | 0.73 | 0.75 | 0.71 |
| H4S420 | 0.68 | 0.67 | 0.79 | 0.73 | 0.75 | 0.72 |
| Avg. | 0.68 | 0.66 | 0.80 | 0.74 | 0.76 | 0.72 |
| SD. (%) | 1.05 | 0.92 | 2.01 | 1.42 | 1.51 | 1.36 |
| Var. (%) | 0.01 | 0.01 | 0.04 | 0.02 | 0.02 | 0.02 |
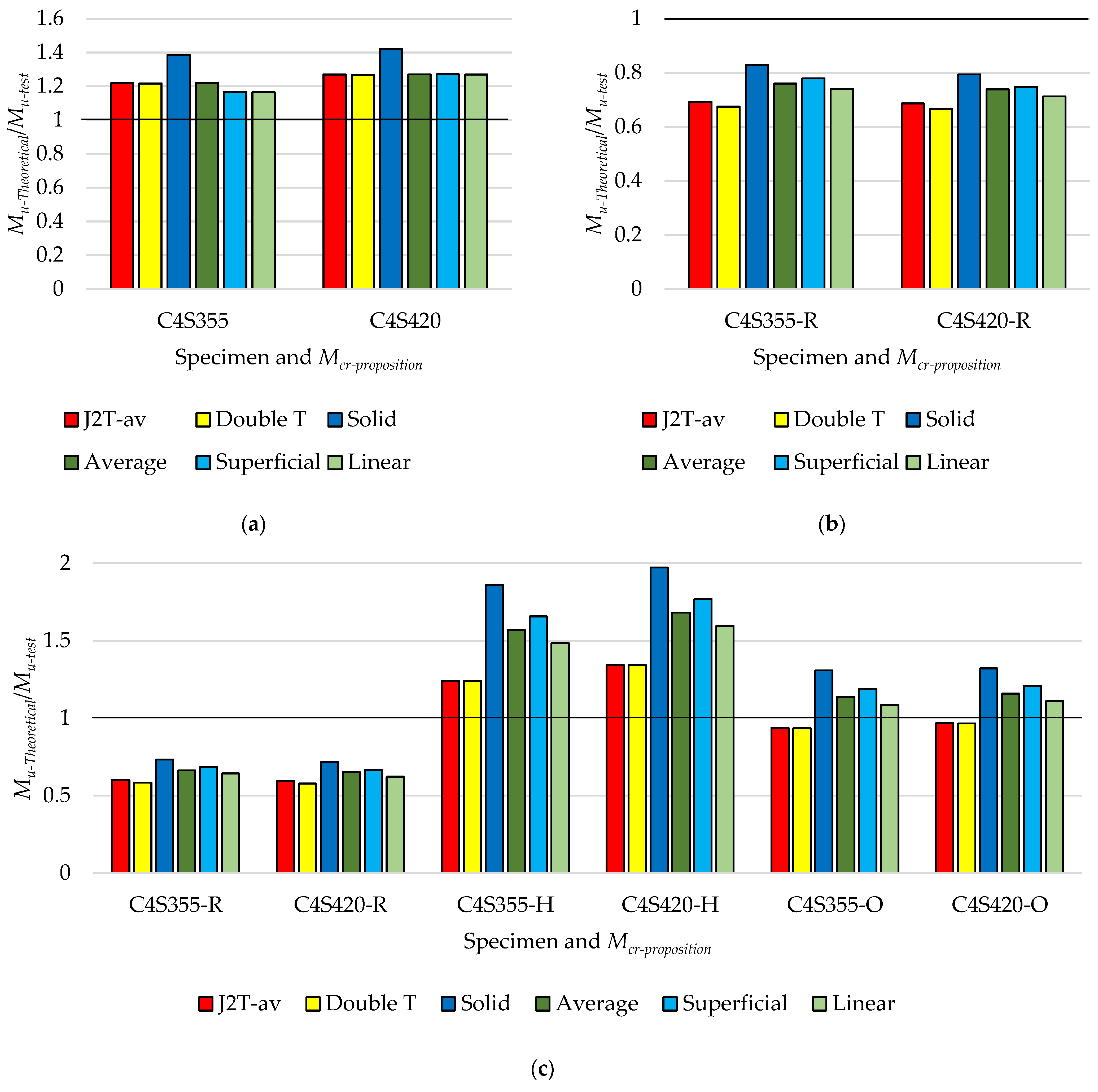
| Model | Mcr Proposition/* Geometric Properties Approach | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Roik et al. [118] | Hanswille et al. [117] | Oliveira [123] | ||||||||||||||||
| J2T-Avg | Db. T | Solid | Avg. | Sup. | Lin. | J2T-Avg | Db. T | Solid | Avg. | Sup. | Lin. | J2T-Avg | Db. T | Solid | Avg. | Sup. | Lin. | |
| C4S355 | 0.60 | 0.58 | 0.73 | 0.66 | 0.68 | 0.64 | 1.24 | 1.24 | 1.86 | 1.57 | 1.66 | 1.48 | 0.94 | 0.93 | 1.31 | 1.14 | 1.19 | 1.09 |
| C4S420 | 0.59 | 0.58 | 0.72 | 0.65 | 0.67 | 0.62 | 1.34 | 1.34 | 1.97 | 1.68 | 1.77 | 1.59 | 0.97 | 0.97 | 1.32 | 1.16 | 1.21 | 1.11 |
| H4S355 | 0.58 | 0.56 | 0.70 | 0.64 | 0.65 | 0.62 | 1.22 | 1.22 | 1.79 | 1.52 | 1.60 | 1.44 | 0.92 | 0.91 | 1.26 | 1.10 | 1.15 | 1.05 |
| H4S420 | 0.59 | 0.58 | 0.71 | 0.65 | 0.67 | 0.63 | 1.37 | 1.37 | 1.96 | 1.69 | 1.77 | 1.60 | 0.98 | 0.98 | 1.31 | 1.16 | 1.21 | 1.11 |
| Avg. | 0.59 | 0.58 | 0.71 | 0.65 | 0.67 | 0.63 | 1.29 | 1.29 | 1.90 | 1.61 | 1.70 | 1.53 | 0.95 | 0.95 | 1.30 | 1.14 | 1.19 | 1.09 |
| SD. (%) | 0.94 | 0.83 | 1.39 | 1.11 | 1.19 | 1.09 | 7.35 | 7.35 | 8.89 | 8.30 | 8.51 | 8.07 | 2.93 | 2.91 | 2.96 | 2.88 | 2.89 | 2.87 |
| Var.(%) | 0.01 | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 | 0.54 | 0.54 | 0.79 | 0.69 | 0.72 | 0.65 | 0.09 | 0.08 | 0.09 | 0.08 | 0.08 | 0.08 |
| Model | Mcr Proposition/*Geometric Properties Approach | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Roik et al. [118] | Hanswille et al. [117] | Oliveira [123] | ||||||||||||||||
| J2T-Avg | Db. T | Solid | Avg. | Sup. | Lin. | J2T-Avg | Db. T | Solid | Avg. | Sup. | Lin. | J2T-Avg | Db. T | Solid | Avg. | Sup. | Lin. | |
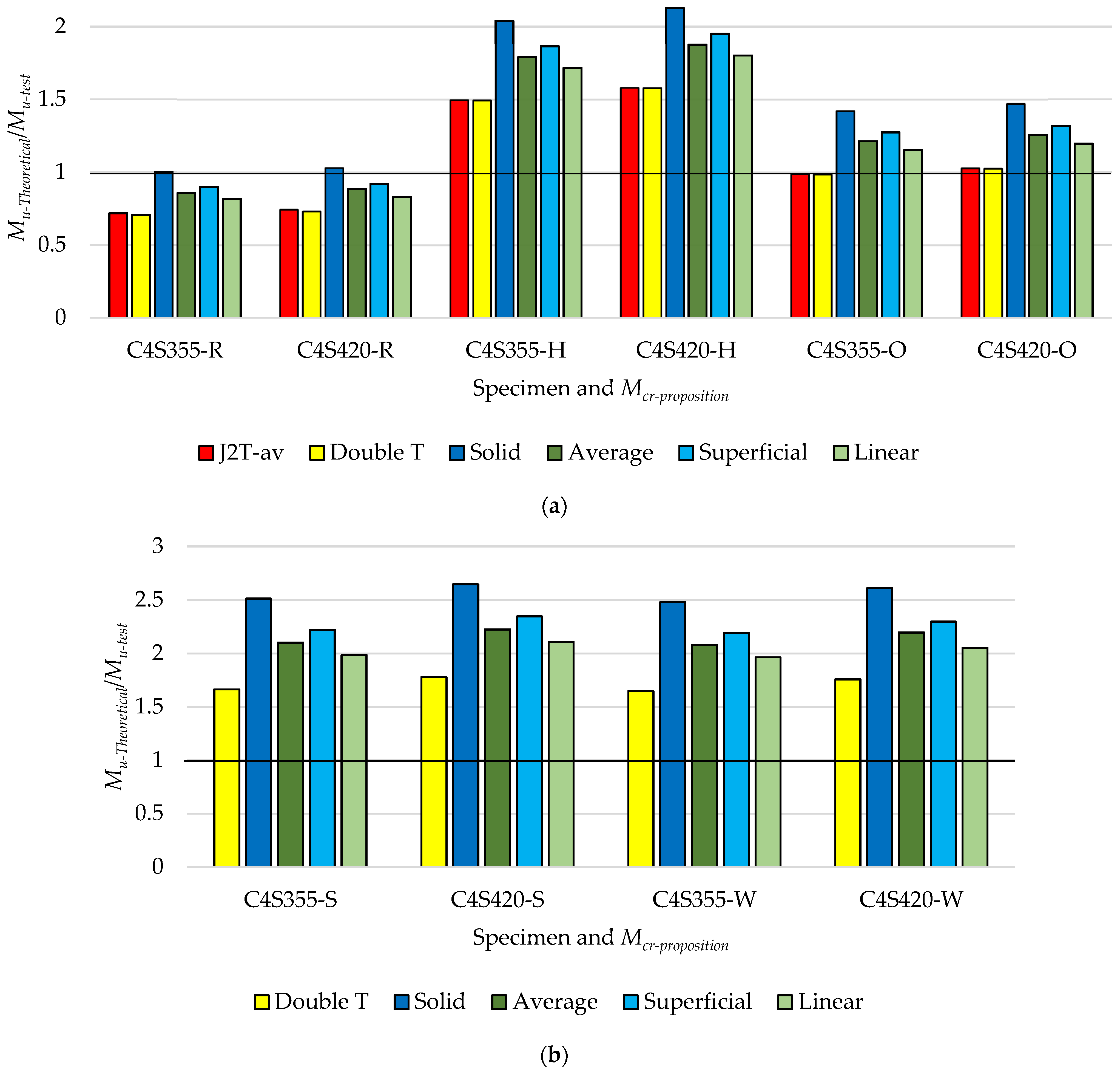
| C4S355 | 0.72 | 0.71 | 1.00 | 0.86 | 0.90 | 0.82 | 1.50 | 1.49 | 2.04 | 1.79 | 1.86 | 1.72 | 0.99 | 0.99 | 1.42 | 1.21 | 1.27 | 1.15 |
| C4S420 | 0.74 | 0.73 | 1.03 | 0.88 | 0.92 | 0.83 | 1.58 | 1.58 | 2.13 | 1.88 | 1.95 | 1.80 | 1.03 | 1.03 | 1.47 | 1.26 | 1.32 | 1.20 |
| H4S355 | 0.70 | 0.69 | 0.96 | 0.83 | 0.86 | 0.79 | 1.46 | 1.46 | 1.96 | 1.73 | 1.80 | 1.66 | 0.97 | 0.97 | 1.36 | 1.17 | 1.23 | 1.12 |
| H4S420 | 0.75 | 0.74 | 1.02 | 0.88 | 0.92 | 0.85 | 1.60 | 1.60 | 2.12 | 1.88 | 1.95 | 1.80 | 1.04 | 1.04 | 1.46 | 1.26 | 1.32 | 1.20 |
| Avg. | 0.73 | 0.72 | 1.00 | 0.86 | 0.90 | 0.82 | 1.53 | 1.53 | 2.06 | 1.82 | 1.89 | 1.74 | 1.01 | 1.00 | 1.43 | 1.23 | 1.28 | 1.17 |
| SD. (%) | 2.39 | 2.34 | 3.28 | 2.78 | 2.75 | 2.40 | 6.67 | 6.66 | 7.84 | 7.25 | 7.42 | 7.08 | 3.54 | 3.53 | 4.86 | 4.16 | 4.36 | 3.98 |
| Var.(%) | 0.06 | 0.05 | 0.11 | 0.08 | 0.08 | 0.06 | 0.44 | 0.44 | 0.61 | 0.52 | 0.55 | 0.50 | 0.13 | 0.12 | 0.24 | 0.17 | 0.19 | 0.16 |
| Model | Mcr Proposition/Geometric Properties Approach | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Svensson [121] | Williams and Jemah [122] | |||||||||
| Double T | Solid | Average | Superficial | Linear | Double T | Solid | Average | Superficial | Linear | |
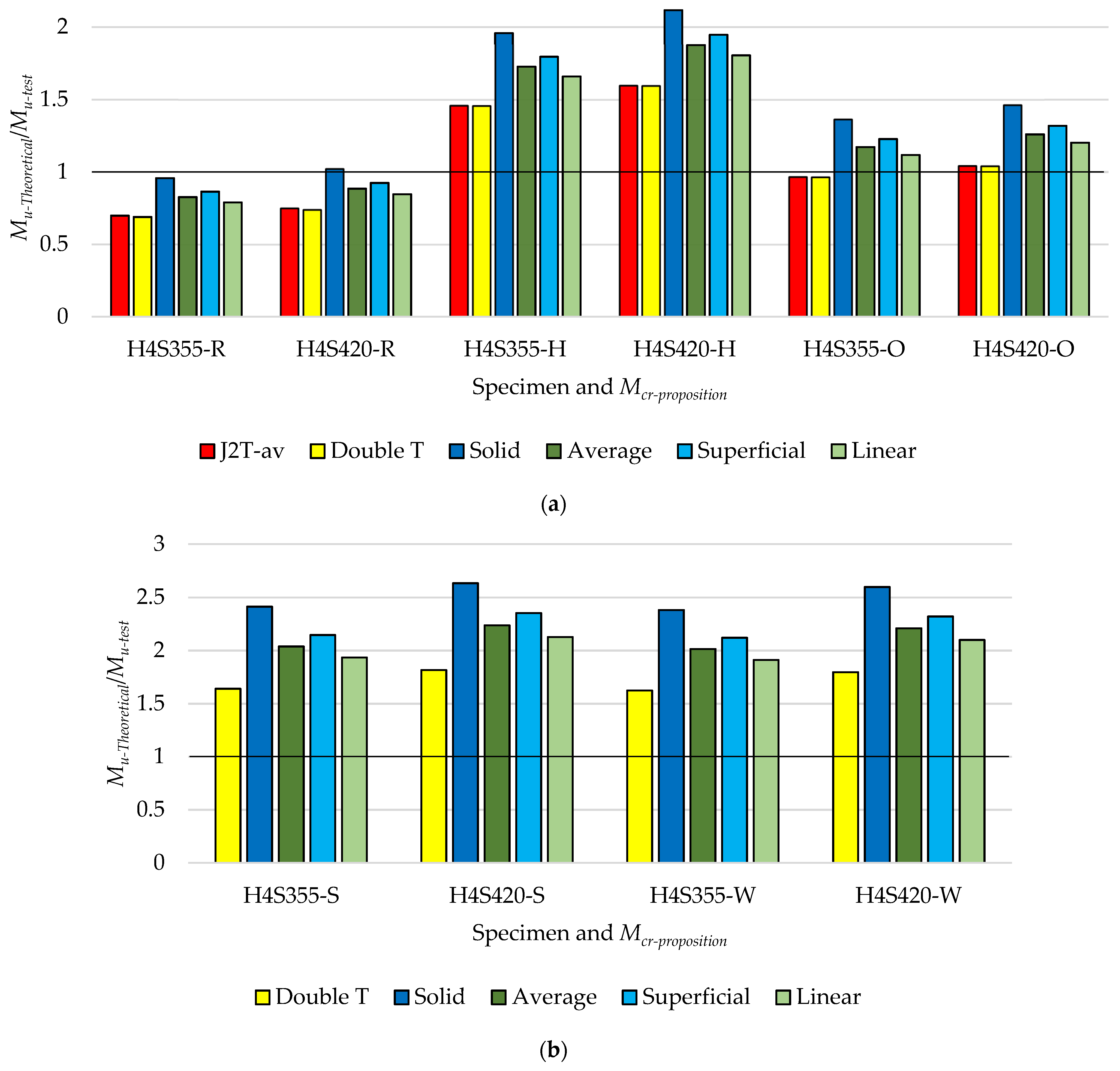
| C4S355 | 1.66 | 2.51 | 2.10 | 2.22 | 1.99 | 1.65 | 2.48 | 2.08 | 2.19 | 1.96 |
| C4S420 | 1.78 | 2.65 | 2.23 | 2.35 | 2.11 | 1.76 | 2.61 | 2.20 | 2.30 | 2.05 |
| H4S355 | 1.64 | 2.41 | 2.04 | 2.15 | 1.93 | 1.62 | 2.38 | 2.02 | 2.12 | 1.91 |
| H4S420 | 1.82 | 2.64 | 2.24 | 2.35 | 2.13 | 1.80 | 2.60 | 2.21 | 2.32 | 2.10 |
| Avg. | 1.72 | 2.55 | 2.15 | 2.27 | 2.04 | 1.71 | 2.52 | 2.12 | 2.23 | 2.01 |
| SD. (%) | 8.57 | 11.06 | 9.68 | 10.05 | 9.34 | 8.34 | 10.78 | 9.43 | 9.36 | 8.45 |
| Var. (%) | 0.73 | 1.22 | 0.94 | 1.01 | 0.87 | 0.70 | 1.16 | 0.89 | 0.88 | 0.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Oliveira, V.M.; Rossi, A.; Ferreira, F.P.V.; de Carvalho, A.S.; Martins, C.H. Lateral Distortional Buckling Resistance Predictions of Composite Alveolar Beams: A Review. Buildings 2023, 13, 808. https://doi.org/10.3390/buildings13030808
de Oliveira VM, Rossi A, Ferreira FPV, de Carvalho AS, Martins CH. Lateral Distortional Buckling Resistance Predictions of Composite Alveolar Beams: A Review. Buildings. 2023; 13(3):808. https://doi.org/10.3390/buildings13030808
Chicago/Turabian Stylede Oliveira, Vinicius Moura, Alexandre Rossi, Felipe Piana Vendramell Ferreira, Adriano Silva de Carvalho, and Carlos Humberto Martins. 2023. "Lateral Distortional Buckling Resistance Predictions of Composite Alveolar Beams: A Review" Buildings 13, no. 3: 808. https://doi.org/10.3390/buildings13030808
APA Stylede Oliveira, V. M., Rossi, A., Ferreira, F. P. V., de Carvalho, A. S., & Martins, C. H. (2023). Lateral Distortional Buckling Resistance Predictions of Composite Alveolar Beams: A Review. Buildings, 13(3), 808. https://doi.org/10.3390/buildings13030808












