Seismic Damage “Semaphore” Based on the Fundamental Period Variation: A Probabilistic Seismic Demand Assessment of Steel Moment-Resisting Frames
Abstract
:1. Introduction
2. Buildings
3. Probabilistic Variables
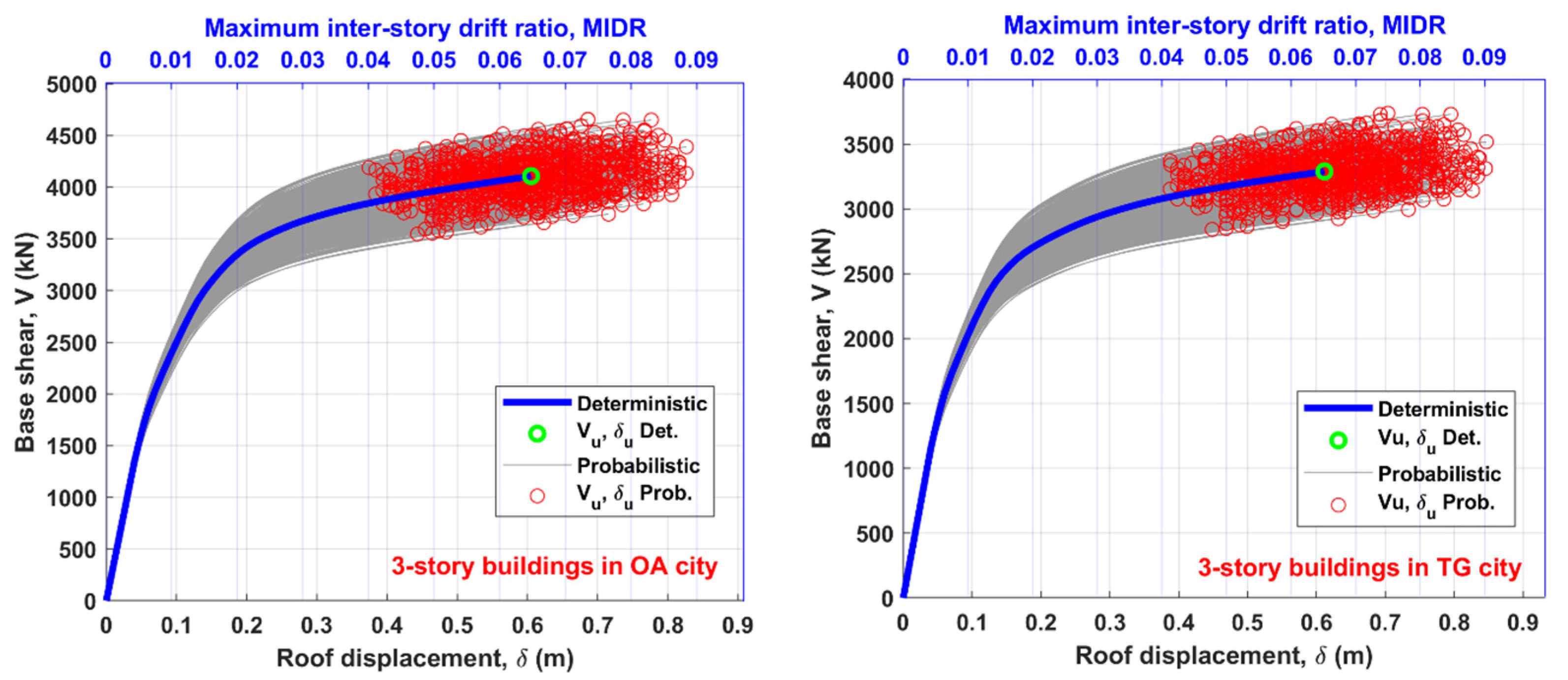
4. Nonlinear Static Analysis
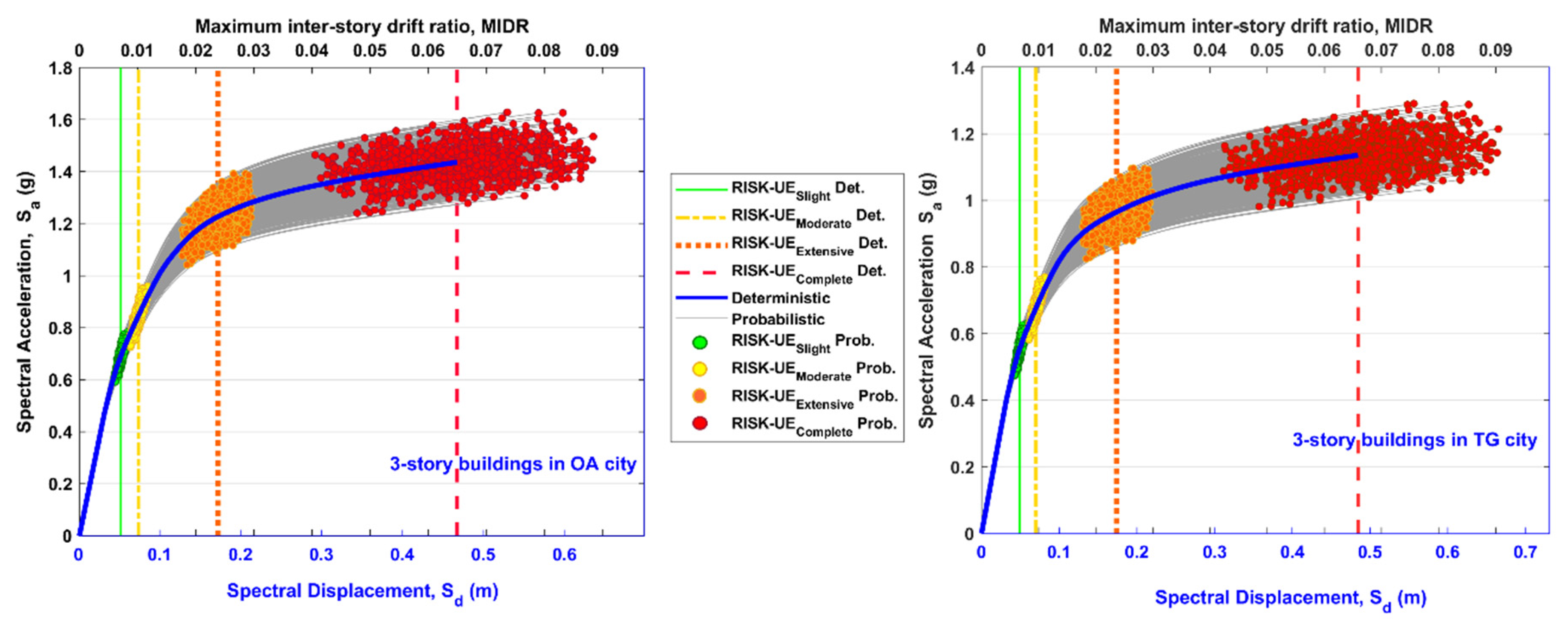
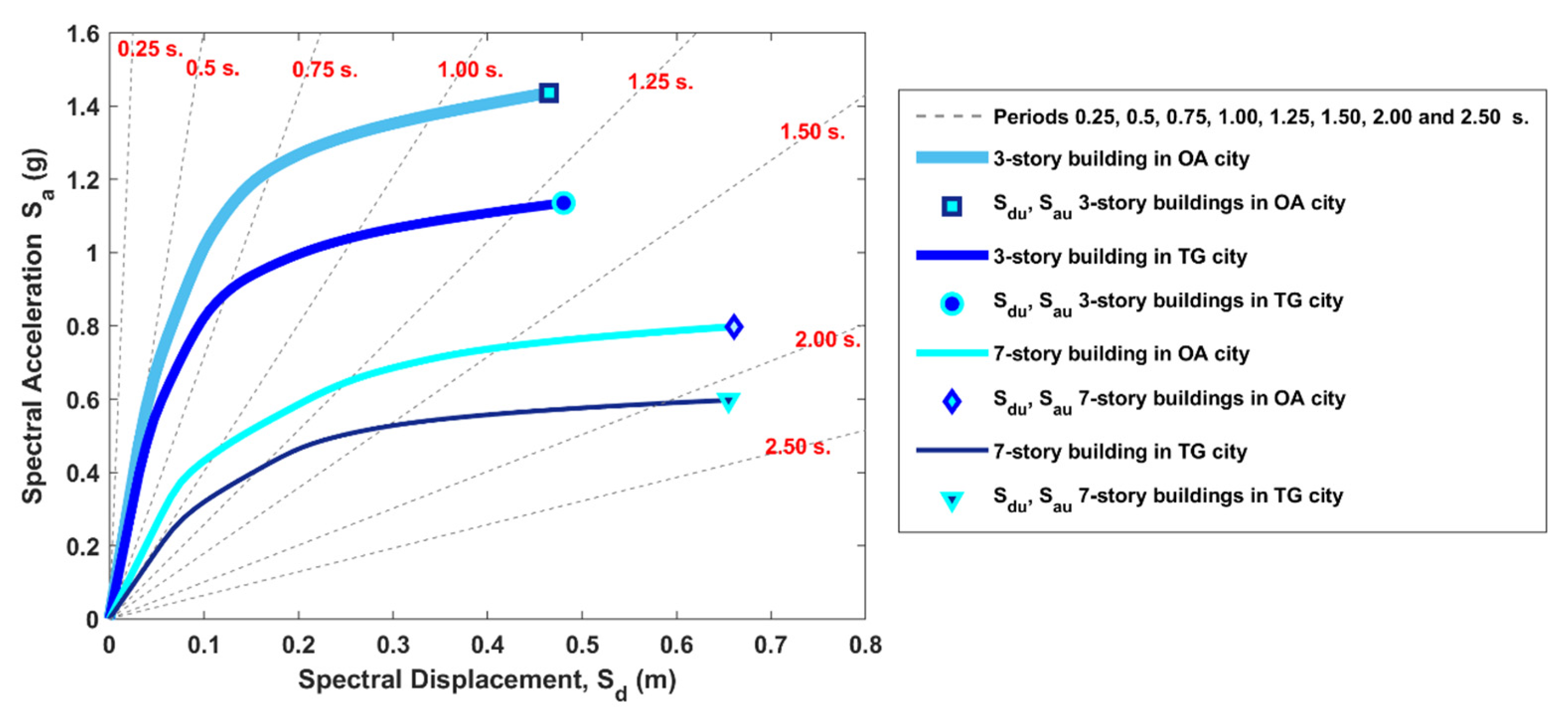
5. Capacity Spectra and Damage States
| City | Stories | MIDR (DSSlight) | MIDR (DSModerate) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Det. | Min | Max | Mean | Det. | ||
| Oaxaca (OA) | 3 | 0.0060 | 0.0083 | 0.0071 | 0.0070 | 0.0085 | 0.0118 | 0.0101 | 0.0102 |
| 7 | 0.0054 | 0.0074 | 0.0063 | 0.0063 | 0.0078 | 0.0106 | 0.0089 | 0.0090 | |
| Tuxtla Gutiérrez (TG) | 3 | 0.0056 | 0.0078 | 0.0067 | 0.0067 | 0.0080 | 0.0112 | 0.0095 | 0.0095 |
| 7 | 0.0066 | 0.0089 | 0.0076 | 0.0076 | 0.0094 | 0.0128 | 0.0108 | 0.0108 | |
| City | Stories | MIDR (DSExtensive) | MIDR (DSComplete) | ||||||
| Min | Max | Mean | Det. | Min | Max | Mean | Det. | ||
| Oaxaca (OA) | 3 | 0.0176 | 0.0298 | 0.0237 | 0.0239 | 0.0406 | 0.0884 | 0.0647 | 0.0650 |
| 7 | 0.0168 | 0.0276 | 0.0219 | 0.0199 | 0.0399 | 0.0832 | 0.0610 | 0.0527 | |
| Tuxtla Gutiérrez (TG) | 3 | 0.0175 | 0.0298 | 0.0237 | 0.0236 | 0.0424 | 0.0905 | 0.0662 | 0.0659 |
| 7 | 0.0184 | 0.0311 | 0.0224 | 0.0247 | 0.0412 | 0.0909 | 0.0664 | 0.0572 | |
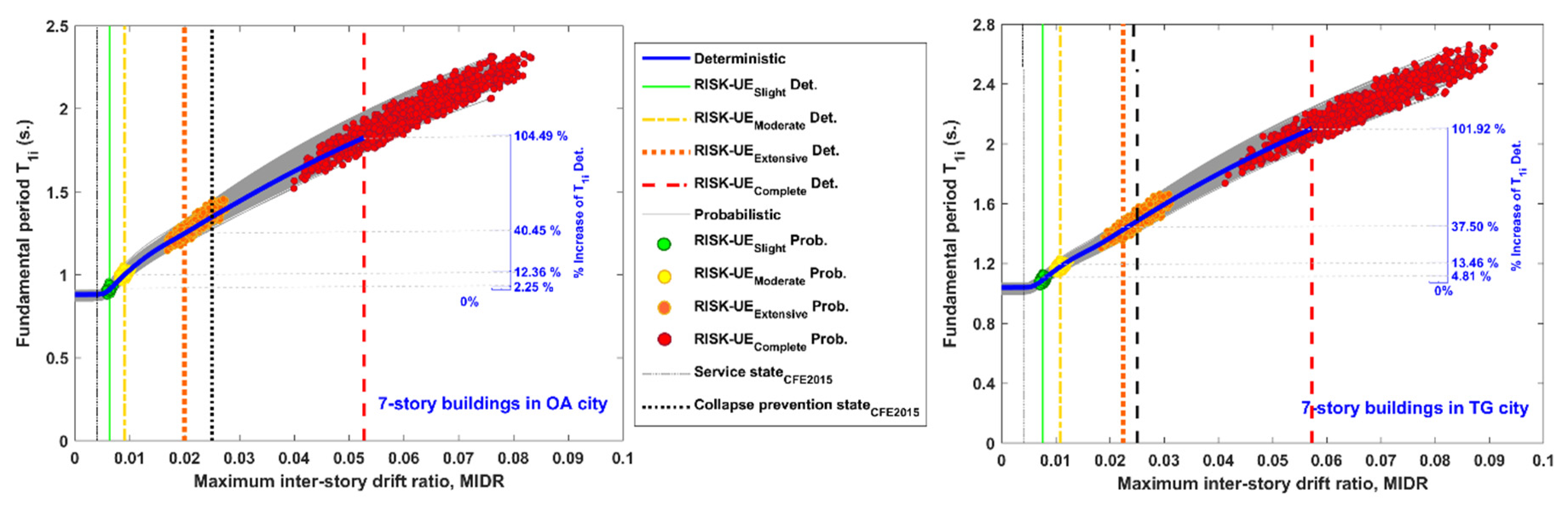
6. T1 Variation
| City | Stories | T1i (DSSlight) | T1i (DSModerate) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Det. | Min | Max | Mean | Det. | ||
| Oaxaca (OA) | 3 | 0.52 | 0.57 | 0.54 | 0.54 | 0.56 | 0.61 | 0.59 | 0.59 |
| 7 | 0.90 | 0.96 | 0.91 | 0.91 | 0.95 | 1.05 | 1.00 | 1.00 | |
| Tuxtla Gutiérrez (TG) | 3 | 0.57 | 0.62 | 0.59 | 0.59 | 0.61 | 0.67 | 0.64 | 0.64 |
| 7 | 1.05 | 1.14 | 1.09 | 1.09 | 1.13 | 1.23 | 1.18 | 1.18 | |
| City | Stories | T1i (DSExtensive) | T1i (DSComplete) | ||||||
| Min | Max | Mean | Det. | Min | Max | Mean | Det. | ||
| Oaxaca (OA) | 3 | 0.65 | 0.85 | 0.75 | 0.75 | 0.89 | 1.35 | 1.14 | 1.14 |
| 7 | 1.14 | 1.46 | 1.30 | 1.25 | 1.52 | 2.33 | 1.96 | 1.82 | |
| Tuxtla Gutiérrez (TG) | 3 | 0.73 | 0.96 | 0.85 | 0.85 | 1.03 | 1.55 | 1.30 | 1.30 |
| 7 | 1.30 | 1.66 | 1.48 | 1.43 | 1.74 | 2.66 | 2.24 | 2.10 | |
7. Preventive “Semaphore” for Seismic Damage
| City | Stories | %T1i (DSSlight) | %T1i (DSModerate) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Det. | Min | Max | Mean | Det. | ||
| Oaxaca (OA) | 3 | 3.62 | 8.10 | 6.11 | 5.88 | 11.14 | 16.70 | 14.44 | 15.69 |
| 7 | 3.98 | 7.33 | 4.52 | 2.25 | 9.28 | 18.49 | 15.01 | 12.36 | |
| Tuxtla Gutiérrez (TG) | 3 | 3.29 | 7.24 | 5.50 | 5.36 | 11.12 | 16.38 | 14.03 | 14.29 |
| 7 | 3.02 | 8.64 | 5.96 | 4.81 | 10.70 | 17.41 | 14.62 | 13.46 | |
| Average | 3.48 | 7.83 | 5.52 | 4.57 | 10.56 | 17.25 | 14.53 | 13.95 | |
| City | Stories | %T1i (DSExtensive) | %T1i (DSComplete) | ||||||
| Min | Max | Mean | Det. | Min | Max | Mean | Det. | ||
| Oaxaca (OA) | 3 | 25.94 | 64.59 | 45.79 | 47.06 | 70.79 | 162.16 | 121.65 | 123.53 |
| 7 | 29.55 | 69.48 | 48.77 | 40.45 | 72.00 | 172.17 | 124.97 | 104.49 | |
| Tuxtla Gutiérrez (TG) | 3 | 28.65 | 70.37 | 50.66 | 51.79 | 79.60 | 174.49 | 131.76 | 132.14 |
| 7 | 24.87 | 63.89 | 43.82 | 37.50 | 66.55 | 162.61 | 118.09 | 101.92 | |
| Average | 27.25 | 67.08 | 47.26 | 44.20 | 72.24 | 167.86 | 124.12 | 115.52 | |
- Null damage ≈ Operational Limit (OL)
- Slight damage (green color) ≈ Immediate Occupancy (IO)
- Moderate damage (yellow color) ≈ Life Safety (LS)
- Extensive damage (orange color) ≈ Collapse Prevention (CP)
- Complete damage (red color) ≈ Complete Collapse (CC)
| PSSD (Risk-UE Guideline) | Null Damage | Slight Damage | Moderate Damage | Extensive Damage | Complete Damage | |
|---|---|---|---|---|---|---|
| PSSD (Vision 2000 Report) | Operational Limit (OL) | Immediate Occupancy (IO) | Life Safety (LS) | Collapse Prevention (CP) | Complete Collapse (CC) | |
| Minimum values | %T1i | <3.48% | ≥3.48% | ≥10.56% | ≥27.25% | ≥72.24% |
| Mean values | <5.52% | ≥5.52% | ≥14.53% | ≥47.26% | ≥124.12% | |
| Maximum values | <7.83% | ≥7.83% | ≥17.25% | ≥67.08% | ≥167.86% | |
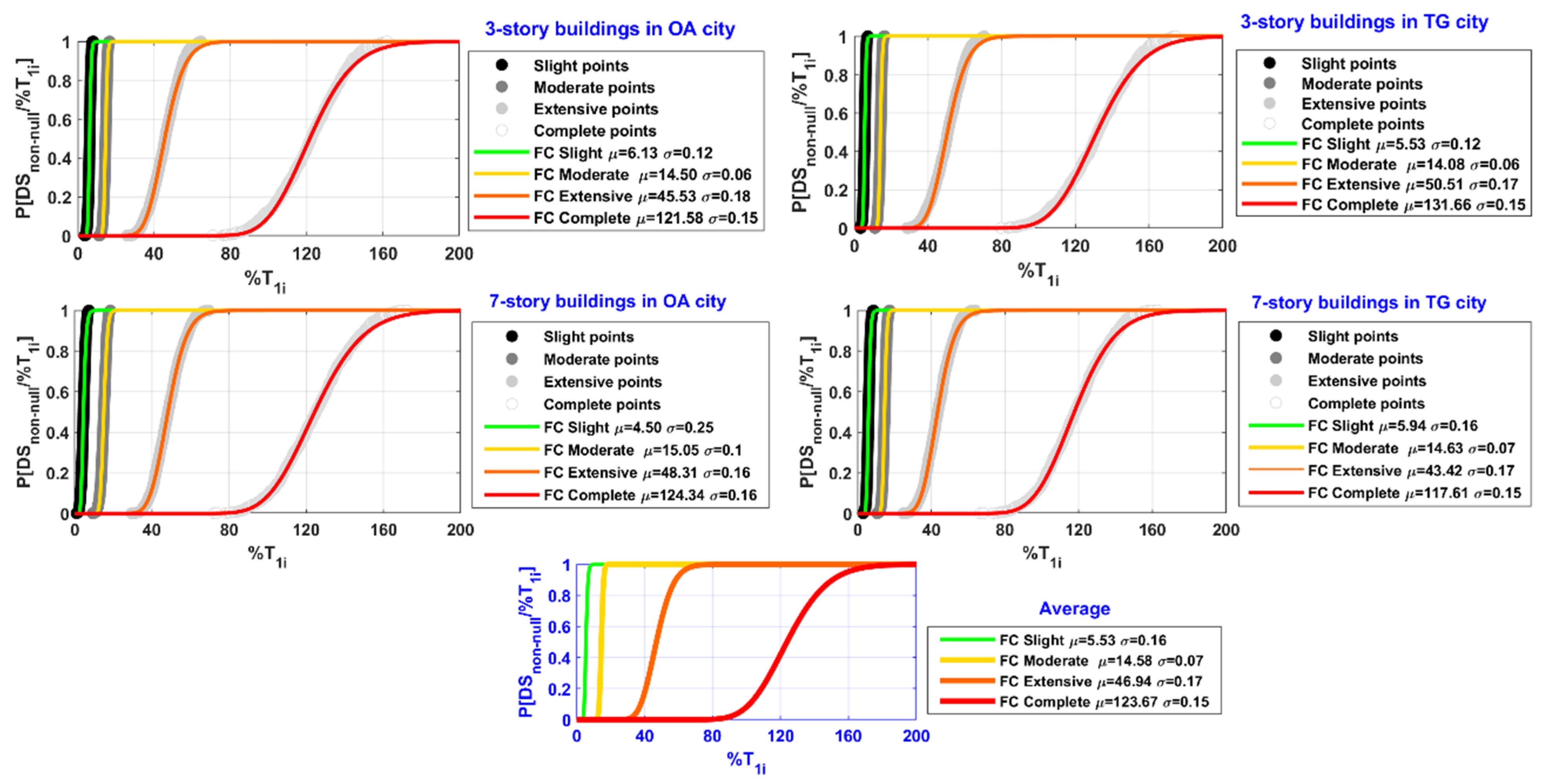
8. Fragility Curves
| City | Stories | FCSlight | FCModerate | FCExtensive | FCComplete | ||||
|---|---|---|---|---|---|---|---|---|---|
| μ (%T1i) | σ | μ (%T1i) | σ | μ (%T1i) | σ | μ (%T1i) | σ | ||
| Oaxaca (OA) | 3 | 6.13 | 0.12 | 14.50 | 0.06 | 45.53 | 0.18 | 121.58 | 0.15 |
| 7 | 4.50 | 0.25 | 15.05 | 0.10 | 48.31 | 0.16 | 124.34 | 0.16 | |
| Tuxtla Gutiérrez (TG) | 3 | 5.53 | 0.12 | 14.08 | 0.06 | 50.51 | 0.17 | 131.16 | 0.15 |
| 7 | 5.94 | 0.16 | 14.67 | 0.07 | 43.42 | 0.17 | 117.61 | 0.15 | |
| Average | 5.53 | 0.16 | 14.58 | 0.07 | 46.94 | 0.17 | 123.67 | 0.15 | |
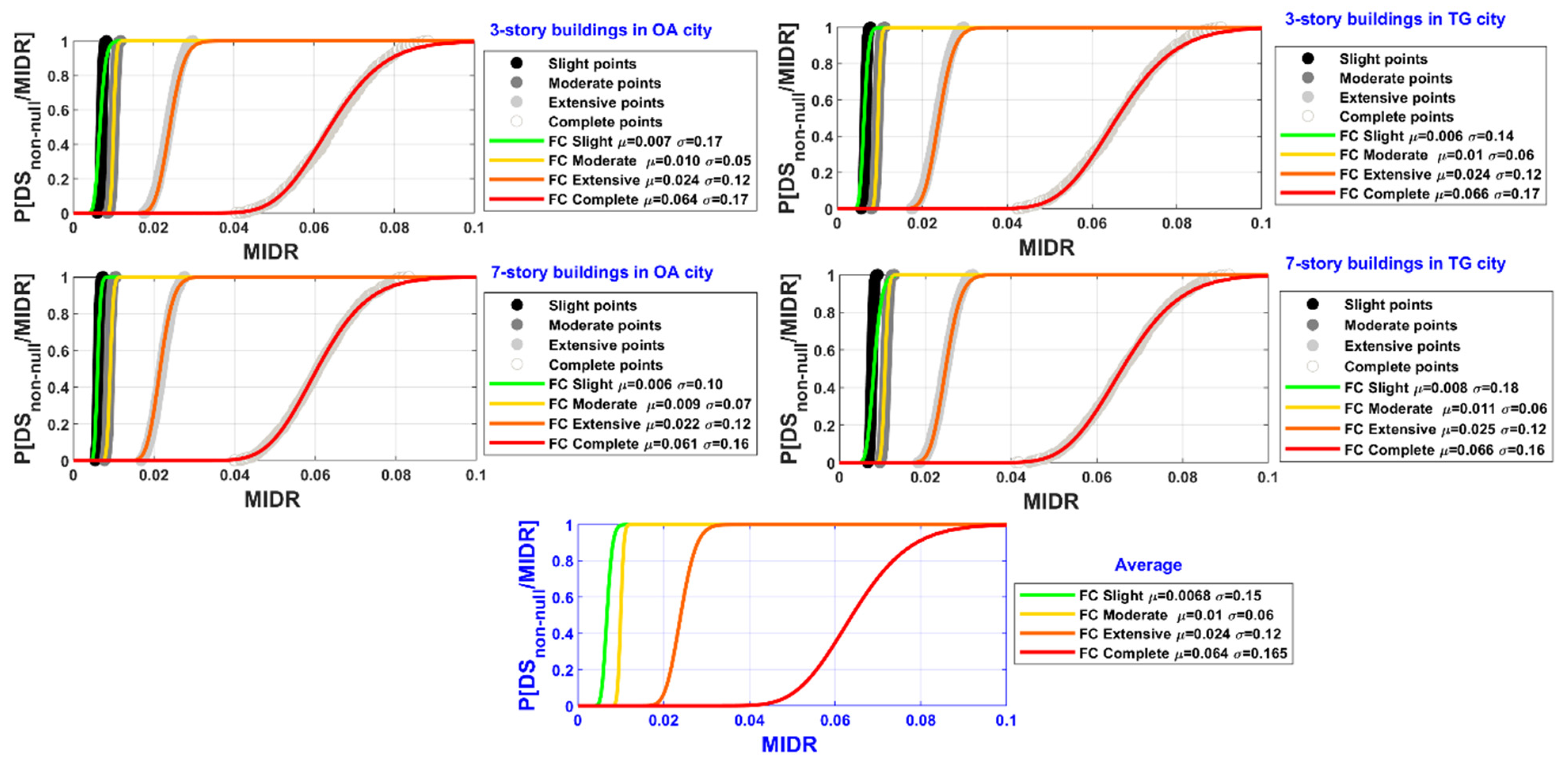
| City | Stories | FCSlight | FCModerate | FCExtensive | FCComplete | ||||
|---|---|---|---|---|---|---|---|---|---|
| μ (MIDR) | σ | μ (MIDR) | σ | μ (MIDR) | σ | μ (MIDR) | σ | ||
| Oaxaca (OA) | 3 | 0.007 | 0.17 | 0.010 | 0.05 | 0.024 | 0.12 | 0.064 | 0.17 |
| 7 | 0.006 | 0.10 | 0.009 | 0.07 | 0.022 | 0.12 | 0.061 | 0.16 | |
| Tuxtla Gutiérrez (TG) | 3 | 0.006 | 0.14 | 0.010 | 0.06 | 0.024 | 0.12 | 0.066 | 0.17 |
| 7 | 0.008 | 0.18 | 0.011 | 0.06 | 0.025 | 0.12 | 0.066 | 0.16 | |
| Average | 0.0068 | 0.15 | 0.010 | 0.06 | 0.024 | 0.12 | 0.064 | 0.165 | |
9. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aguilar-Meléndez, A.; Pujades, L.G.; Barbat, A.H.; Ordaz, M.G.; De la Puente, J.; Lantada, N.; Rodríguez-Lozoya, H.E. A probabilistic approach for seismic risk assessment based on vulnerability functions. Application to Barcelona. Bull. Earthq. Eng. 2019, 17, 1863–1890. [Google Scholar] [CrossRef] [Green Version]
- Romero, D.Z.; Akbas, B.; Budiman, J.; Shen, J. Consideration of economic vulnerability in seismic performance evaluation of structures. Bull. Earthq. Eng. 2020, 18, 3351–3381. [Google Scholar] [CrossRef]
- Ramírez-Eudave, R.; Ferreira, T.M.; Vicente, R. Parameter-based seismic vulnerability assessment of Mexican historical buildings: Insights, suitability, and uncertainty treatment. Int. J. Disaster Risk Reduct. 2022, 74, 102909. [Google Scholar] [CrossRef]
- Ferreira, T.; Rodrigues, H. Seismic Vulnerability Assessment of Civil Engineering Structures at Multiple Scales. From Single Buildings to Large-Scale Assessment; A volume in Woodhead Publishing Series in Civil and Structural Engineering; Woodhead Publishing: Sawston, UK, 2022; pp. 1–383. [Google Scholar] [CrossRef]
- Li, S.Q.; Liu, H.B. Vulnerability prediction model of typical structures considering empirical seismic damage observation data. Bull. Earthq. Eng. 2022, 20, 5161–5203. [Google Scholar] [CrossRef]
- Barbat, A.H.; Carreño, M.L.; Pujades, L.G.; Lantada, N.; Cardona, O.D.; Marulanda, M.C. Seismic vulnerability and risk evaluation methods for urban areas. A review with application to a pilot area. Struct. Infrastruct. Eng. 2010, 6, 17–38. [Google Scholar] [CrossRef]
- Díaz, S.A.; Pujades, L.G.; Barbat, A.H.; Hidalgo-Leiva, D.A.; Vargas, Y.F. Capacity, damage and fragility models for steel buildings. A probabilistic approach. Bull. Earthq. Eng. 2018, 16, 1209–1243. [Google Scholar] [CrossRef] [Green Version]
- Roghaei, M.; Zabihollah, A. An Efficient and Reliable Structural Health Monitoring System for Buildings after Earthquake. APCBEE Procedia 2014, 9, 309–316. [Google Scholar] [CrossRef] [Green Version]
- Fujino, Y.; Siringoringo, D.M.; Ikeda, Y.; Nagayama, T.; Mizutani, T. Research and Imple-mentations of Structural Monitoring for Bridges and Buildings in Japan. Engineering 2019, 5, 1093–1119. [Google Scholar] [CrossRef]
- Alva, R.E.; Pujades, L.G.; González-Drigo, R.; Luzi, G.; Caselles, O.; Pinzón, L.A. Dynamic Monitoring of a Mid-Rise Building by Real-Aperture Radar Interferometer: Advantages and Limitations. Remote Sens. 2020, 12, 1025. [Google Scholar] [CrossRef] [Green Version]
- Gopinath, V.K.; Ramadoss, R. Review on structural health monitoring for restoration of heritage buildings. Mater. Today Proc. 2021, 43, 1534–1538. [Google Scholar] [CrossRef]
- Vargas-Alzate, Y.F.; Pujades, L.G.; Barbat, A.H.; Hurtado, J.E. An efficient methodology to estimate probabilistic seismic damage curves. J. Struct. Eng. ASCE 2019, 145, 04019010. [Google Scholar] [CrossRef] [Green Version]
- Vamvatsikos, D.; Fragiadakis, M. Incremental dynamic analysis for estimating seismic performance sensitivity and uncertainty. Earthq. Eng. Struct. Dyn. 2010, 39, 141–163. [Google Scholar] [CrossRef]
- Kazantzi, A.K.; Vamvatsikos, D.; Lignos, D.G. Seismic performance of a steel moment-resisting frame subject to strength and ductility uncertainty. Eng. Struct. 2014, 78, 69–77. [Google Scholar] [CrossRef] [Green Version]
- Díaz, S.A.; Pujades, L.G.; Barbat, A.H.; Vargas, Y.F.; Hidalgo-Leiva, D.A. Energy damage index based on capacity and response spectra. Eng. Struct. 2017, 152, 424–436. [Google Scholar] [CrossRef]
- Vargas-Alzate, Y.F.; Lantada, N.; González-Drigo, R.; Pujades, L.G. Seismic Risk Assessment Using Stochastic Nonlinear Models. Sustainability 2020, 12, 1308. [Google Scholar] [CrossRef] [Green Version]
- Pinzón, L.A.; Vargas-Alzate, Y.F.; Pujades, L.G.; Diaz, S.A. A drift-correlated ground motion intensity measure: Application to steel frame buildings. Soil Dyn. Earthq. Eng. 2020, 132, 106096. [Google Scholar] [CrossRef]
- Wang, F.; Shi, Q.X.; Wang, P. Research on the Physical Inter-story Drift Ratio and the Damage Evaluation of RC Shear Wall Structures. KSCE J. Civ. Eng. 2021, 25, 2121–2133. [Google Scholar] [CrossRef]
- Kenari, M.S.; Celikag, M. Correlation of Ground Motion Intensity Measures and Seismic Damage Indices of Masonry-Infilled Steel Frames. Arab. J. Sci. Eng. 2019, 44, 5131–5150. [Google Scholar] [CrossRef]
- Aljawhari, K.; Gentile, R.; Freddi, F.; Galasso, C. Effects of ground-motion sequences on fragility and vulnerability of case-study reinforced concrete frames. Bull. Earthq. Eng. 2021, 1, 6329–6359. [Google Scholar] [CrossRef]
- Vargas-Alzate, Y.F.; Hurtado, J.E.; Pujades, L.G. New insights into the relationship between seismic intensity measures and nonlinear structural response. Bull. Earthq. Eng. 2022, 20, 2329–2365. [Google Scholar] [CrossRef]
- Masi, A.; Vona, M. Experimental and numerical evaluation of the fundamental period of undamaged and damaged RC framed buildings. Bull. Earthq. Eng. 2010, 8, 643–656. [Google Scholar] [CrossRef]
- Anastasia, K.E.; Athanasios, I.K. Correlation of Structural Seismic Damage with Fundamental Period of RC Buildings. Open J. Civ. Eng. 2013, 3, 5–67. [Google Scholar] [CrossRef] [Green Version]
- Ditommaso, R.; Vona, M.; Gallipoli, M.R.; Mucciarelli, M. Evaluation and considerations about fundamental periods of damaged reinforced concrete buildings. Nat. Hazards Earth Syst. Sci. 2013, 13, 1903–1912. [Google Scholar] [CrossRef] [Green Version]
- Aninthaneni, P.V.; Dhakal, R.P. Prediction of Fundamental Period of Regular Frame Buildings. Bull. N. Z. Soc. Earthq. Eng. 2016, 49, 175–189. [Google Scholar] [CrossRef]
- Lu, W.-T.; Phillips, B.M. A fundamental-period-preserving seismic retrofit methodology for low-rise buildings with supplemental inerters. Eng. Struct. 2022, 266, 114583. [Google Scholar] [CrossRef]
- Sarma, S.; Sundar Das, T.; Bora, A.; Bharadwaj, K. Parametric Study on the Variation of Time Period of RC MRF Buildings. In Recent Advances in Earthquake Engineering; Lecture Notes in Civil Engineering; Kolathayar, S., Chian, S.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; Volume 175, pp. 415–426. [Google Scholar] [CrossRef]
- Harris, J.L.; Michel, J.J.L. Approximate Fundamental Period for Seismic Design of Steel Buildings Assigned to High-Risk Categories. Pract. Period. Struct. Des. Constr. 2019, 24, 04019023. [Google Scholar] [CrossRef]
- Gallipoli, M.R.; Stabile, T.A.; Guéguen, P.; Mucciarelli, M.; Comelli, P.; Bertoni, M. Fundamental period elongation of a RC building during the Pollino seismic swarm sequence. Case Stud. Struct. Eng. 2016, 6, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Comisión Nacional de Electricidad (CFE). MDOC-CFE. Manual de Diseño de Obras Civiles. Diseño por Sismos. 2015, pp. 1–745. Available online: https://www.gob.mx/ineel/articulos/manual-de-diseno-de-obras-civiles-diseno-por-sismo-logro-de-la-ingenieria-de-mexico (accessed on 3 April 2023).
- Milutinovic, Z.V.; Trendafiloski, G.S. Risk-UE An Advanced Approach to Earthquake Risk Scenarios with Applications to Different European Towns. 2003. Available online: https://cordis.europa.eu/project/id/EVK4-CT-2000-00014 (accessed on 3 April 2023).
- Arcos-Díaz, D.; Díaz, S.A.; Pinzón, L.A.; Jesús, H.; Mora-Ortiz, R.S. Seismic performance assessment based on the interstory drift of steel buildings. Lat. Am. J. Solids Struct. 2022, 19, e431. [Google Scholar] [CrossRef]
- Gaceta Oficial del Gobierno de México. NTCDS-RCDF. Norma Técnica Complementaria para la Revisión de la Seguridad Estructural de las Edificaciones de la Ciudad de México. 2017, pp. 1–712. Available online: https://smie.com.mx/smie-2022/informacion-tecnica/normas-tecnicas-complementarias.php (accessed on 3 April 2023).
- American Institute of Steel Construction. ANSI/AISC 360-16. Specification for Structural Steel Buildings. 2016. Available online: https://www.aisc.org/Specification-for-Structural-Steel-Buildings-ANSIAISC-360-16-Download (accessed on 3 April 2023).
- Seismosoft. SeismoStruct. Civil Engineering Software for Structural Assessment and Structural Retrofitting. 2021. Available online: https://seismosoft.com/products/seismostruct/ (accessed on 3 April 2023).
- Fernández, R.; Yamin, L.; D’Ayala, D.; Adhikari, R.; Reyes, J.C.; Juan Echeverry, J.; Fuentes, G. A simplified component-based methodology for the seismic vulnerability assessment of school buildings using nonlinear static procedures: Application to RC school buildings. Bull. Earthq. Eng. 2022, 20, 6555–6585. [Google Scholar] [CrossRef]
- Applied Technology Council. ATC-40. Seismic Evaluation and Retrofit of Concrete Buildings. 1996. Available online: https://www.atcouncil.org/pdfs/atc40toc.pdf (accessed on 3 April 2023).
- Pujades, L.G.; Vargas-Alzate, Y.F.; Barbat, A.H.; González-Drigo, J.R. Parametric model for capacity curves. Bull. Earthq Eng. 2015, 13, 1347–1376. [Google Scholar] [CrossRef] [Green Version]
- Jalayer, F.; De Risi, R.; Manfredi, G. Bayesian Cloud Analysis: Efficient structural fragility assessment using linear regression. Bull. Earthq. Eng. 2015, 13, 1183–1203. [Google Scholar] [CrossRef]
- Hurtado, J.E.; Barbat, A.H. Monte Carlo techniques in computational stochastic mechanics. Arch. Comput. Methods Eng. 1998, 5, 3–29. [Google Scholar] [CrossRef]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2016; pp. 1–414. Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/9781118631980 (accessed on 3 April 2023).
- Schmidt, B.J.; Bartlett, F.M. Review of resistance factor for steel: Data collection. Can. J. Civ. Eng. 2002, 29, 98–108. [Google Scholar] [CrossRef]
- Bartlett, F.M.; Dexter, R.J.; Graeser, M.D.; Jelinek, J.J.; Schmidt, B.J.; Galambos, T.V. Updating standard shape material properties database for design and reliability. ASCI Eng. J. 2003, 40, 1–14. Available online: https://www.aisc.org/Updating-Standard-Shape-Material-Properties-Database-for-Design-and-Reliability (accessed on 3 April 2023).
- Iman, R.L. Appendix A: Latin hypercube sampling. In Encyclopedia of Statistical Sciences; Wiley: New York, NY, USA, 1999; Volume 3, pp. 408–411. [Google Scholar]
- Structural Engineers Association of California. SEAOC. Vision 2000: Performance Based Seismic Engineering of Buildings. 1995. Available online: https://www.seaoc.org/store/ViewProduct.aspx?id=11238558 (accessed on 3 April 2023).
- Aldama, B.D. Proceso Automatizado Para Determinar el Estado Estructural en Edificios Instrumentados. Master’s Thesis, Universidad Nacional Autónoma de México (UNAM), Ciudad de México, México, 2009. (In Spanish). [Google Scholar]
- Murià-Vila, D.; Aldama, B.D.; Loera, S. Structural warning for instrumented buildings. In Proceedings of the 14th European Conference on Earthquake Engineering, Ohrid, North Macedonia, 30 August–3 September 2010; Volume 2. Available online: https://www.tib.eu/en/search/id/TIBKAT:667434461/14th-European-Conference-on-Earthquake-Engineering?cHash=1727db18b7fdcc71af94e1729c032324 (accessed on 3 April 2023).
- Murià-Vila, D.; Aldama-Sánchez, B.D.; García-Illescas, M.Á.; Rodríguez Gutiérrez, G. Monitoring of a rehabilitated building in soft soil in Mexico and structural response to the September 2017 earthquakes: Part 1: Structural health monitoring system. Earthq. Spectra 2021, 37, 2737–2766. [Google Scholar] [CrossRef]
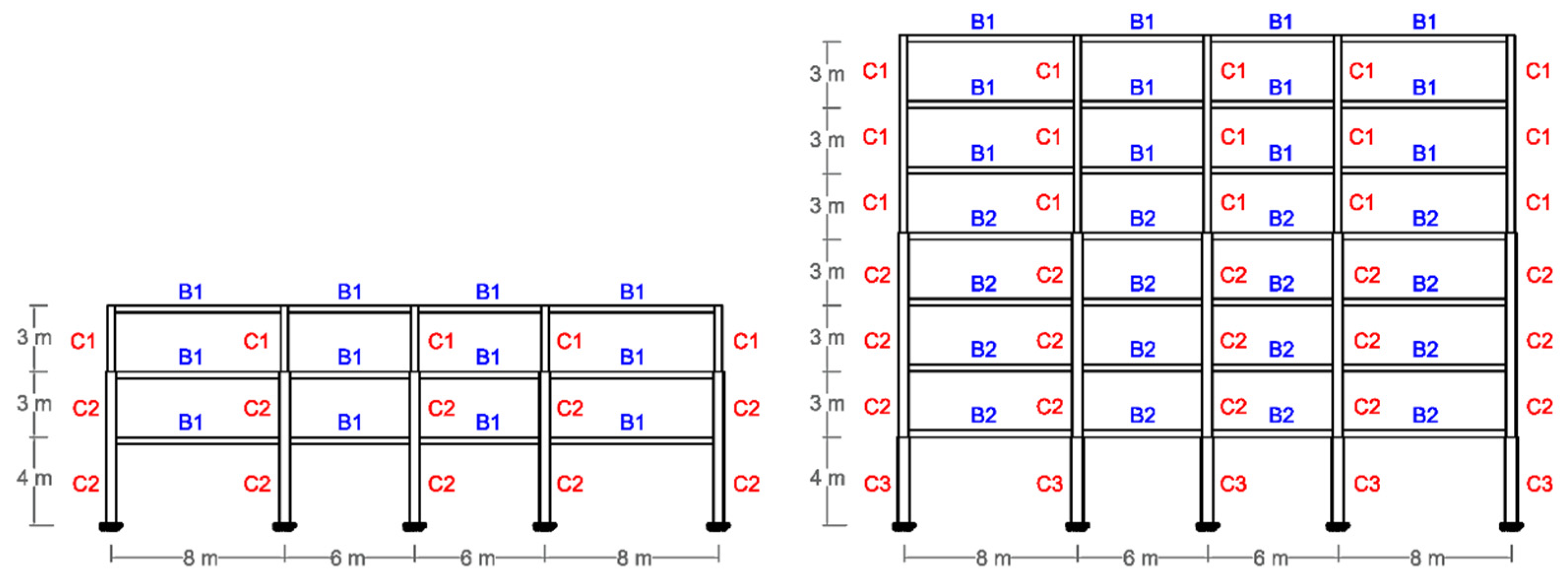




| Load Types | Story | Load (kN/m2) |
|---|---|---|
| Dead Load (DL) | Inter-story | 6.5 |
| Roof | 5.0 | |
| Live Load (LL) (Office building) | Inter-story | 2.5 |
| Roof | 1.0 |
| City | Columns | Beams | |
|---|---|---|---|
| C1 | C2 | B1 | |
| Oaxaca (OA) | W14 × 74 | W18 × 119 | W12 × 72 |
| Tuxtla Gutiérrez (TG) | W16 × 67 | W18 × 97 | W14 × 48 |
| City | Columns | Beams | |||
|---|---|---|---|---|---|
| C1 | C2 | C3 | B1 | B2 | |
| Oaxaca (OA) | W16 × 100 | W18 × 192 | W21 × 201 | W12 × 53 | W14 × 61 |
| Tuxtla Gutiérrez (TG) | W16 × 89 | W18 × 119 | W21 × 147 | W14 × 61 | W16 × 57 |
| City | Stories | T1 (s) * | PF1 * | α1 * | W (kN) * |
|---|---|---|---|---|---|
| Oaxaca (OA) | 3 | 0.51 | 1.30 | 0.89 | 327.38 |
| 7 | 0.89 | 1.39 | 0.82 | 831.04 | |
| Tuxtla Gutiérrez (TG) | 3 | 0.56 | 1.27 | 0.91 | 325.89 |
| 7 | 1.04 | 1.33 | 0.84 | 823.95 |
| Variable | Coefficients of Variation (CV) * | ||
|---|---|---|---|
| Yield strength, fy (kN/m2) | 396,448.54 | 0.066 | 26,165.60 |
| Modulus of elasticity, Es (kN/m2) | 200,000,000 | 0.039 | 7,800,000 |
| Fracture strain, εu | 0.06 | 0.155 | 0.0093 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz, S.A.; Pinzón, L.A.; Vargas-Alzate, Y.F.; Mora-Ortiz, R.S. Seismic Damage “Semaphore” Based on the Fundamental Period Variation: A Probabilistic Seismic Demand Assessment of Steel Moment-Resisting Frames. Buildings 2023, 13, 1009. https://doi.org/10.3390/buildings13041009
Díaz SA, Pinzón LA, Vargas-Alzate YF, Mora-Ortiz RS. Seismic Damage “Semaphore” Based on the Fundamental Period Variation: A Probabilistic Seismic Demand Assessment of Steel Moment-Resisting Frames. Buildings. 2023; 13(4):1009. https://doi.org/10.3390/buildings13041009
Chicago/Turabian StyleDíaz, Sergio A., Luis A. Pinzón, Yeudy F. Vargas-Alzate, and René S. Mora-Ortiz. 2023. "Seismic Damage “Semaphore” Based on the Fundamental Period Variation: A Probabilistic Seismic Demand Assessment of Steel Moment-Resisting Frames" Buildings 13, no. 4: 1009. https://doi.org/10.3390/buildings13041009
APA StyleDíaz, S. A., Pinzón, L. A., Vargas-Alzate, Y. F., & Mora-Ortiz, R. S. (2023). Seismic Damage “Semaphore” Based on the Fundamental Period Variation: A Probabilistic Seismic Demand Assessment of Steel Moment-Resisting Frames. Buildings, 13(4), 1009. https://doi.org/10.3390/buildings13041009











