Seismic Behavior of UHPC-Filled Rectangular Steel Tube Columns Incorporating Local Buckling
Abstract
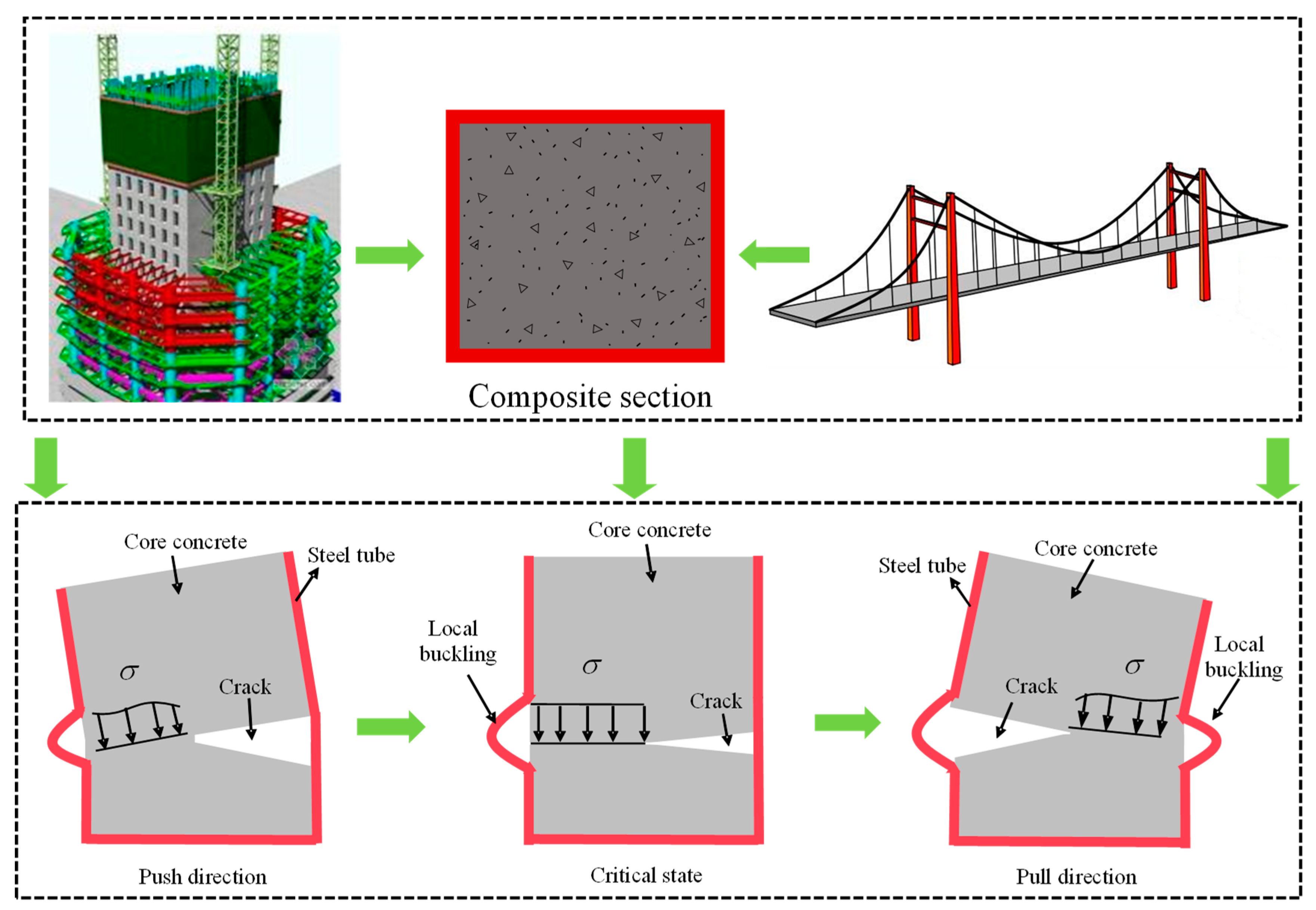
:1. Introduction
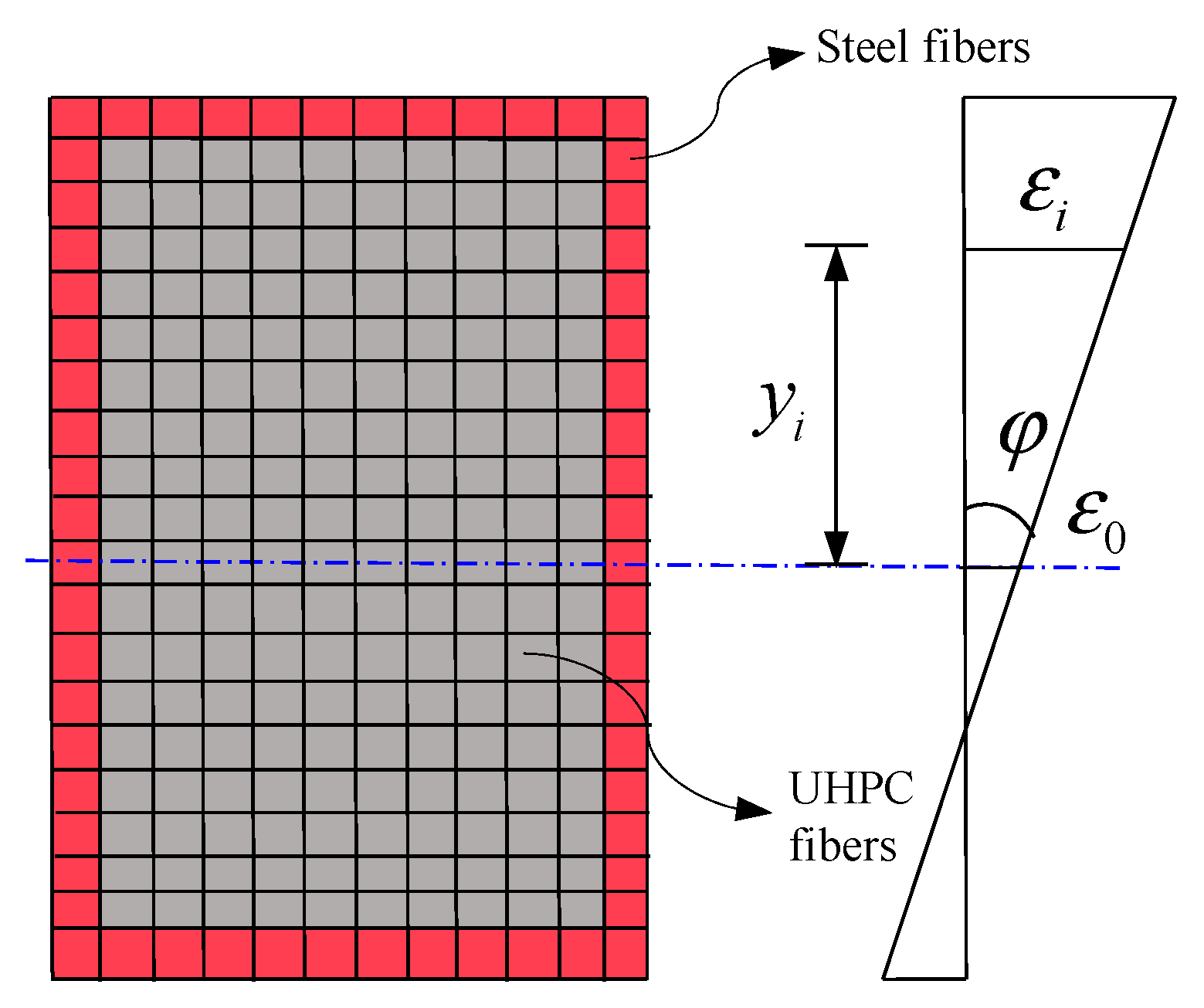
2. Fiber Element Model
- (1)
- Plane-section assumption.
- (2)
- The strains are the same in each individual fiber of the same height of the cross-section.
- (3)
- The bond-slip at the interface between the two materials is neglected.
- (4)
- The lateral deflection curve of the member presents the sine curve with half a wave.
2.1. Constitutive Model of Materials
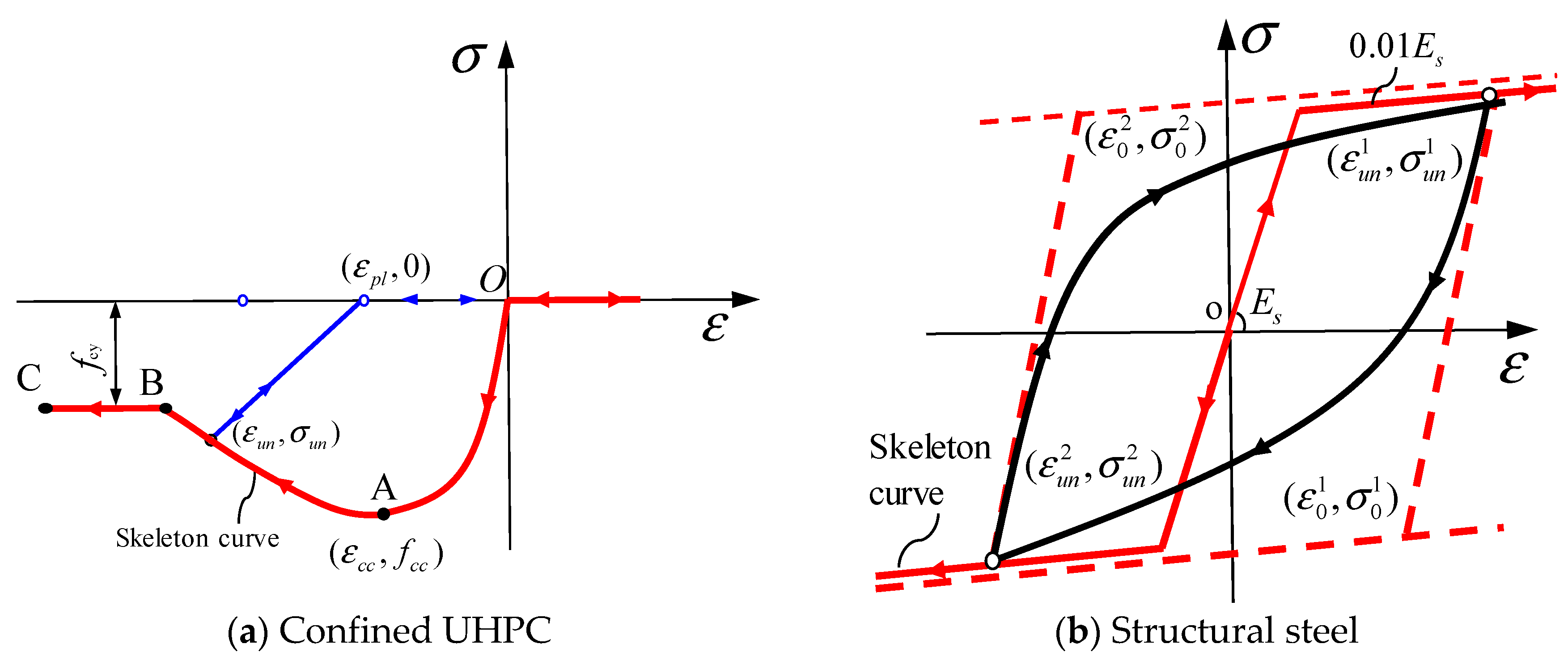
2.1.1. Concrete
2.1.2. Steel
3. Model Verification
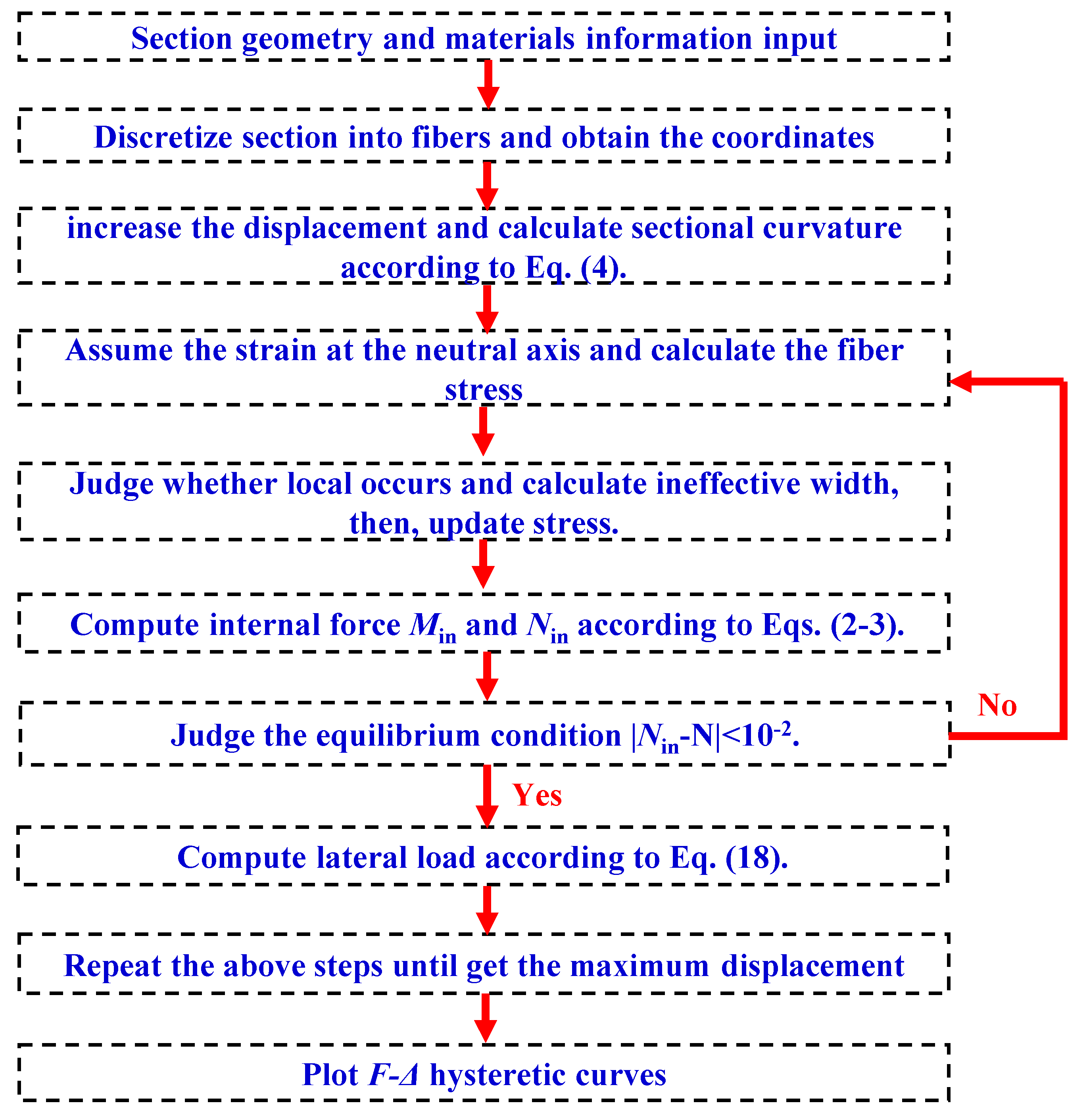
- (1)
- Input data.
- (2)
- Discretize section into fibers and obtain the coordinates.
- (3)
- Gradually increase the displacement and calculate sectional curvature according to Equation (4).
- (4)
- Assume the strain at the neutral axis and calculate the fiber stress σci and σsi according to loading history.
- (5)
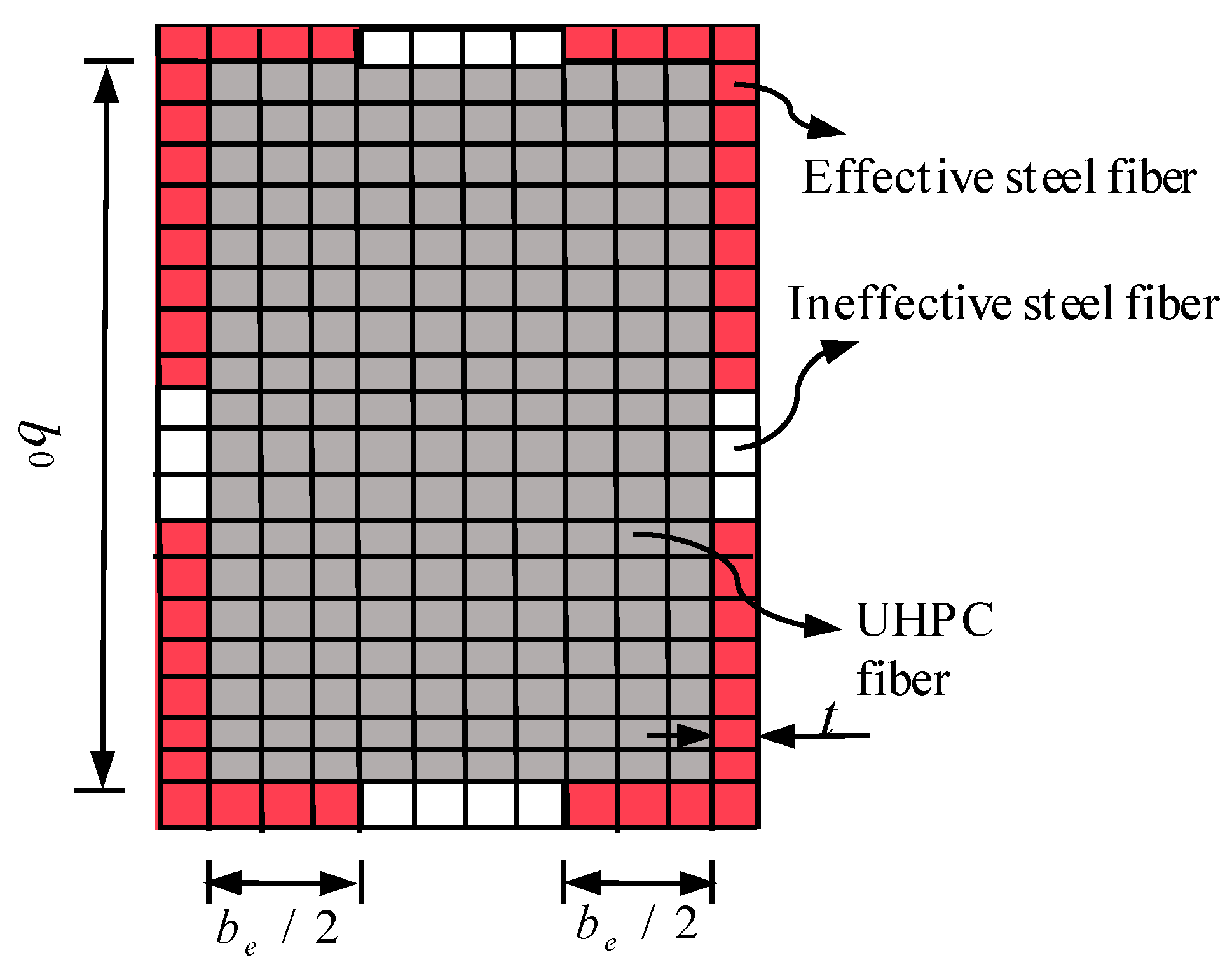
- Judge whether the local buckling of steel tubes occurs and calculate the ineffective width; then, update the stress.
- (6)
- Compute internal force according to Equations (2) and (3), including Min and Nin.
- (7)
- Judge whether the axial compression load satisfies the equilibrium condition |Nin−N| < 10−2. If not, return to step (4) until the equilibrium condition is satisfied.
- (8)
- Compute the lateral load according to Equation (18).
- (9)
- Repeat steps (3–8) until the maximum lateral displacement is achieved.
- (10)
- Plot F-Δ hysteretic curves.
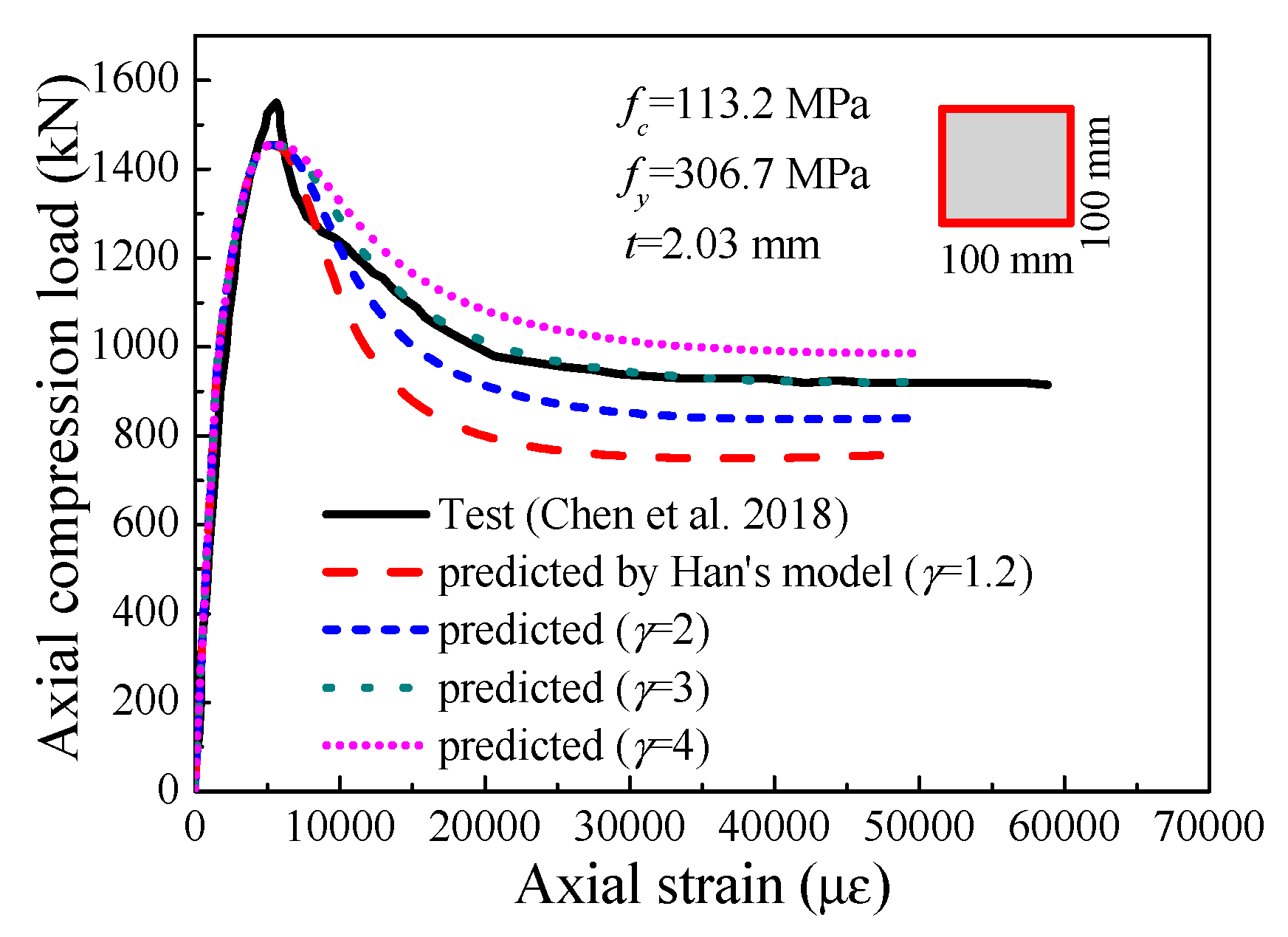
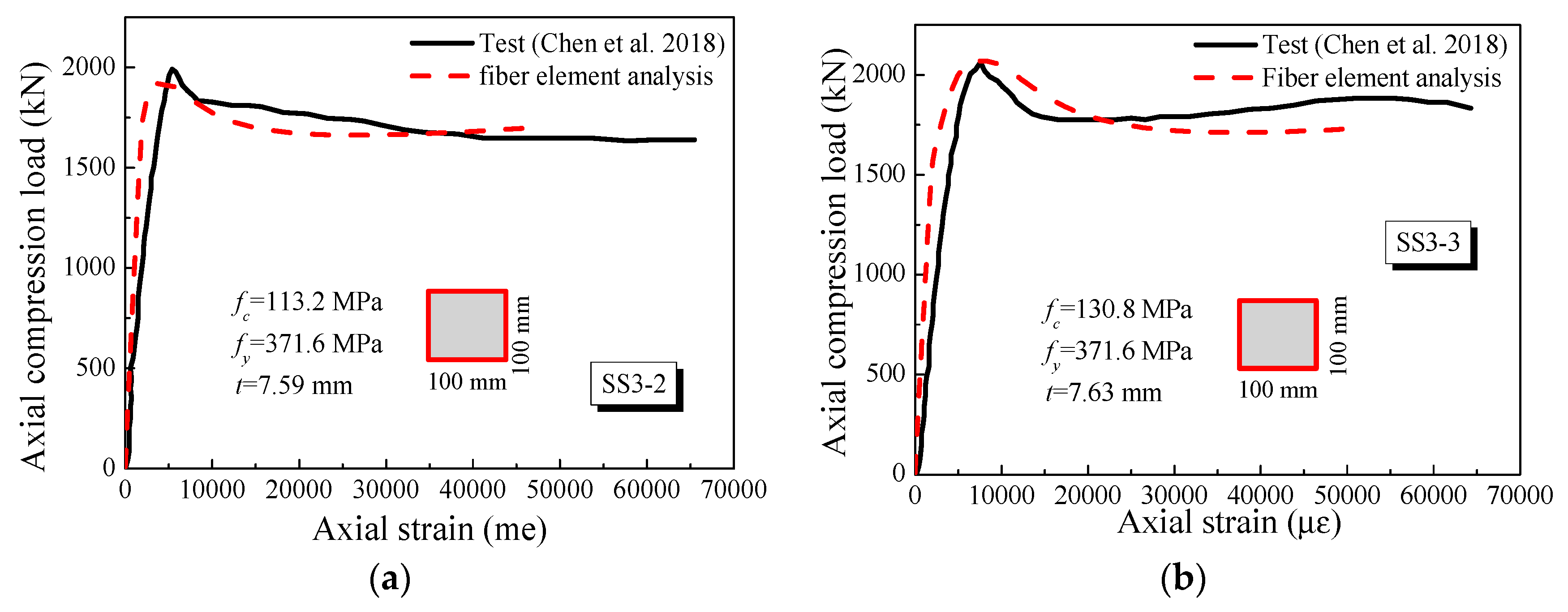
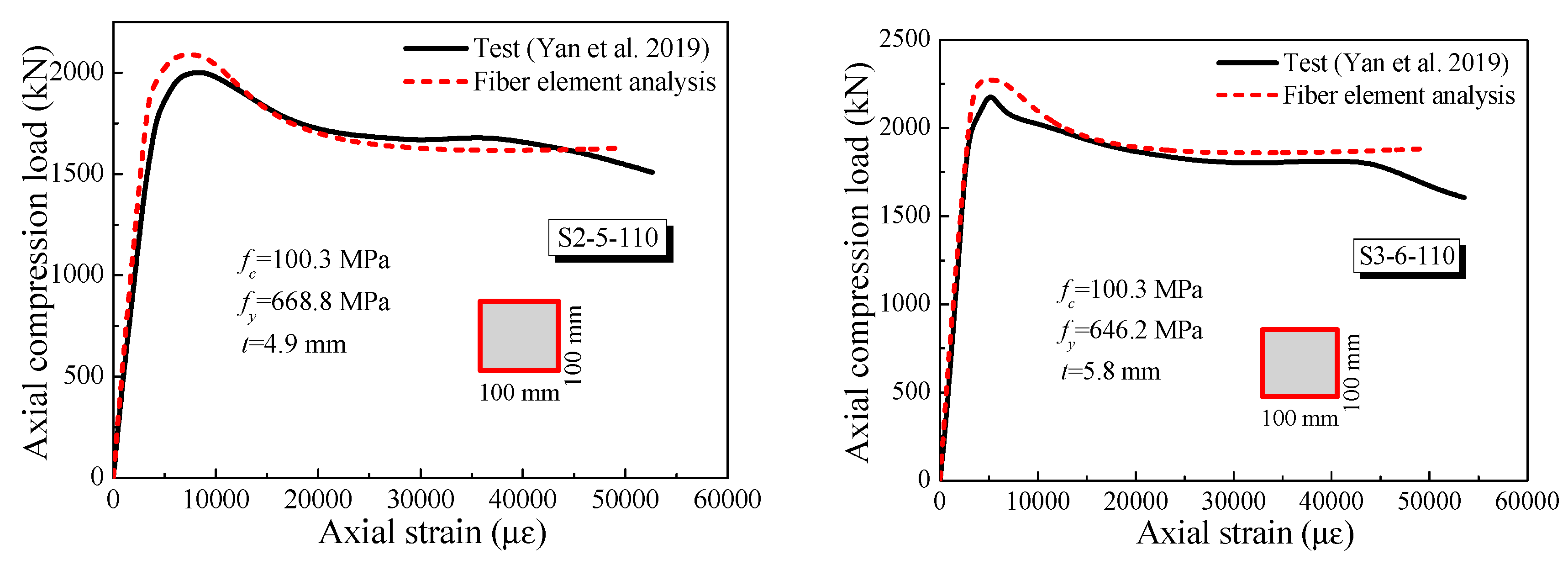
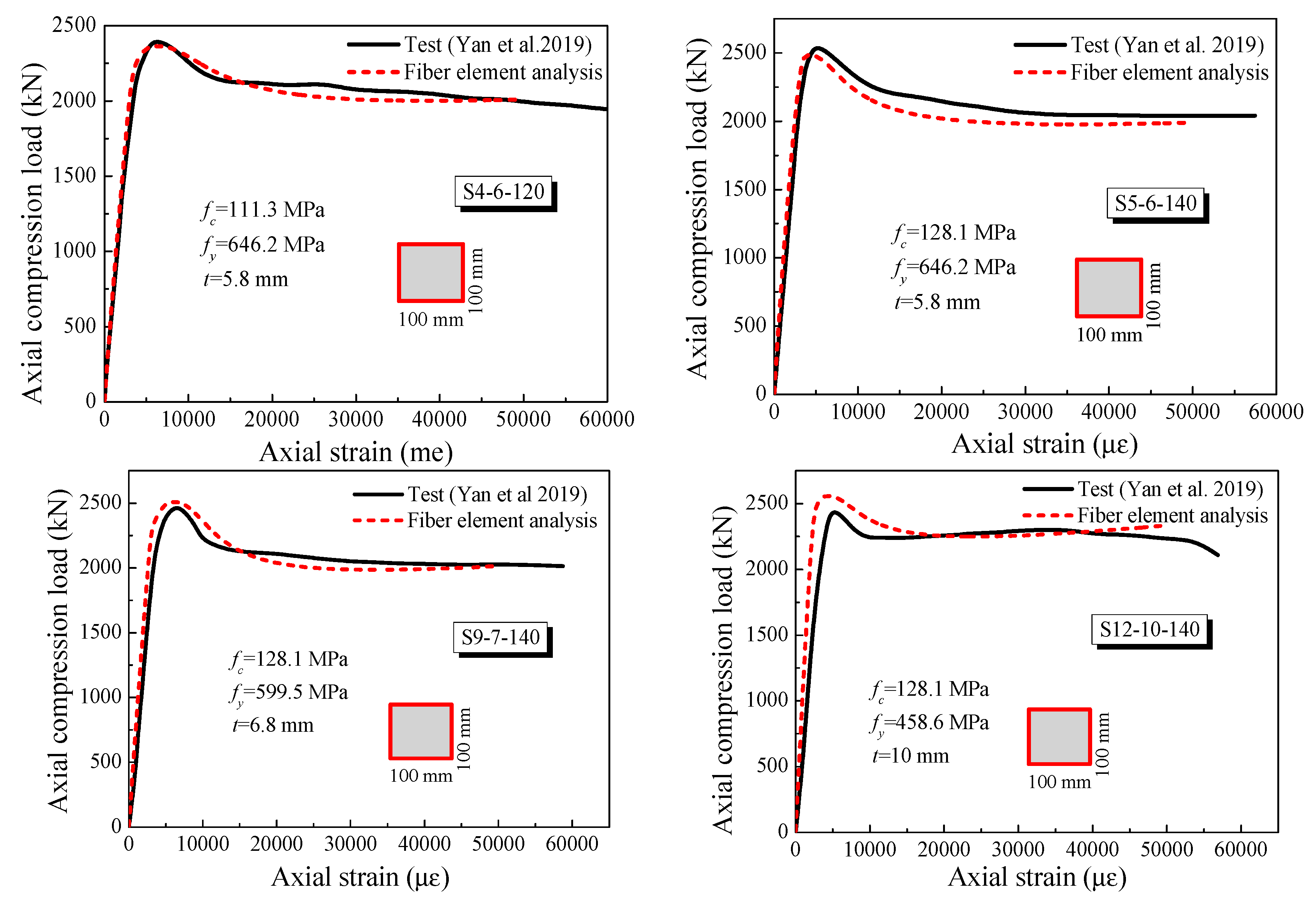
3.1. Stub UHPCFST Columns under Axial Compressive Load
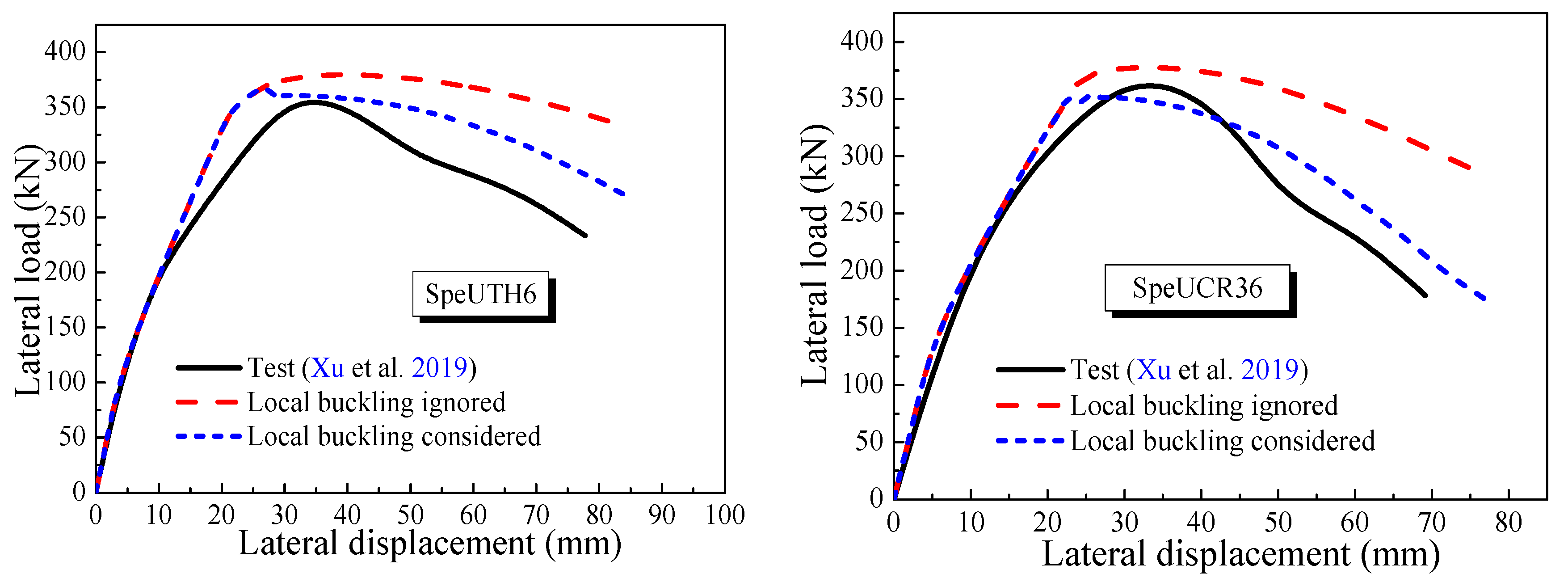
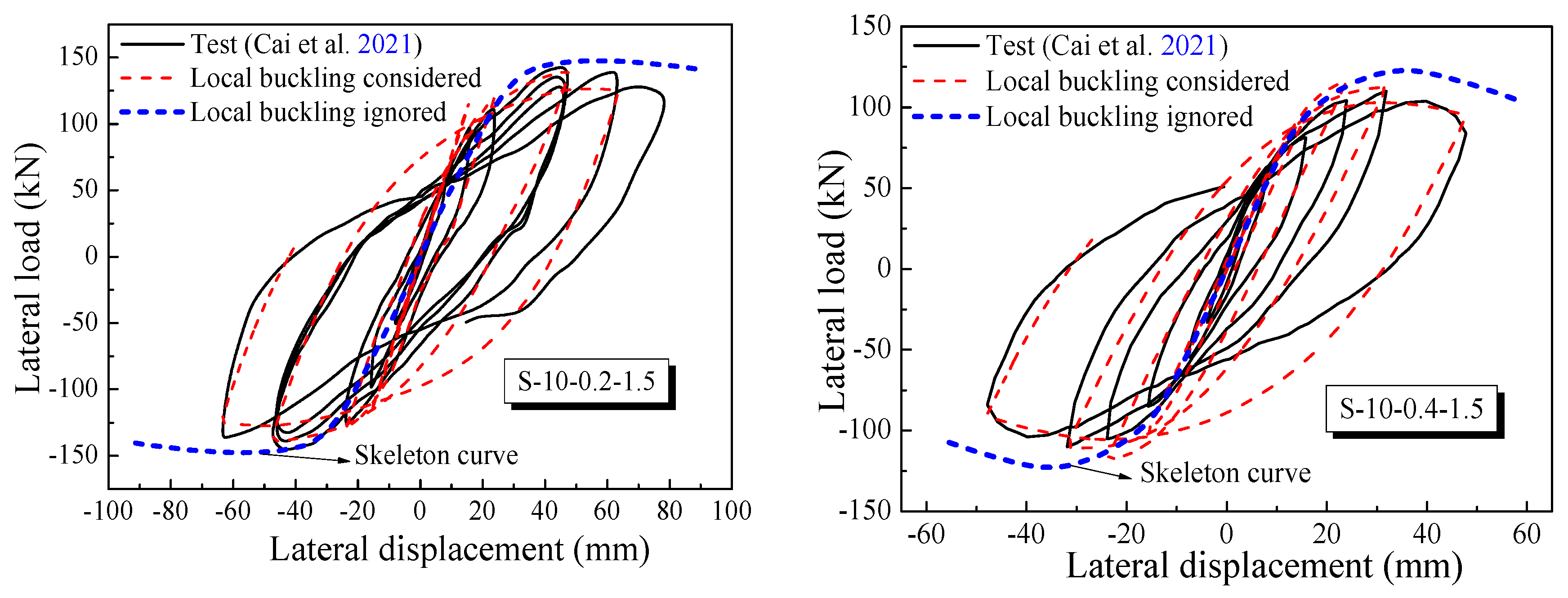
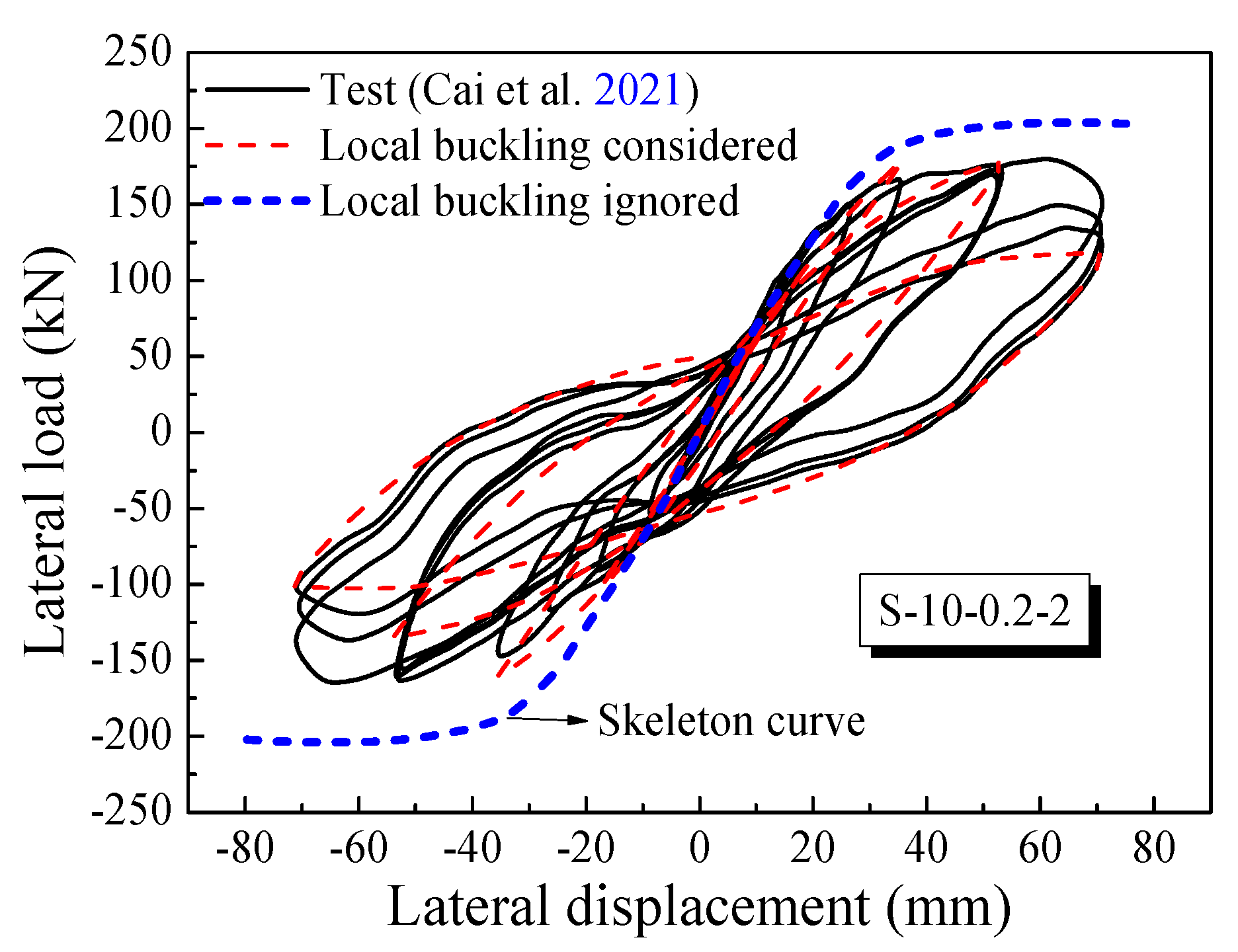
3.2. UHPCFST Columns under Cyclic Loading
4. Parametric Analysis
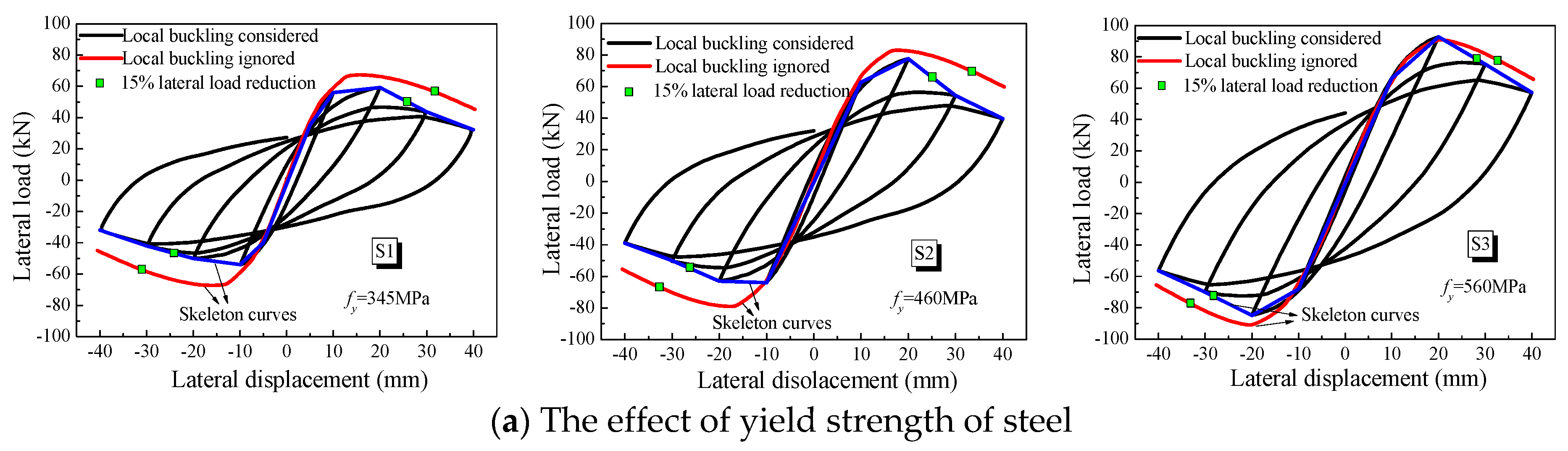
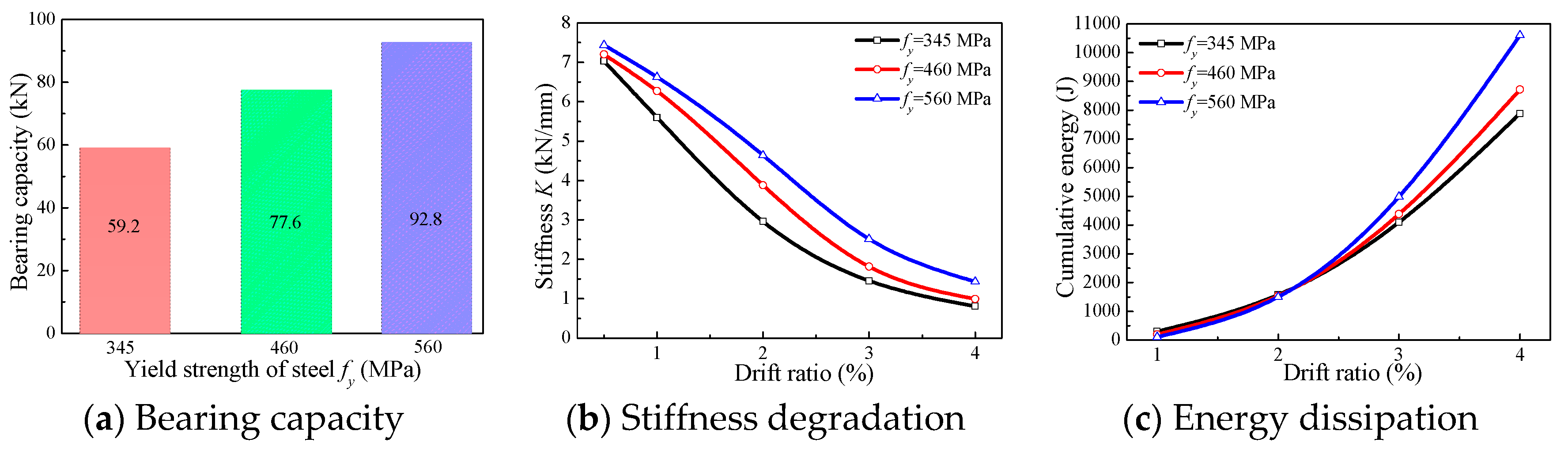
4.1. The Effect of the Strength of Steel
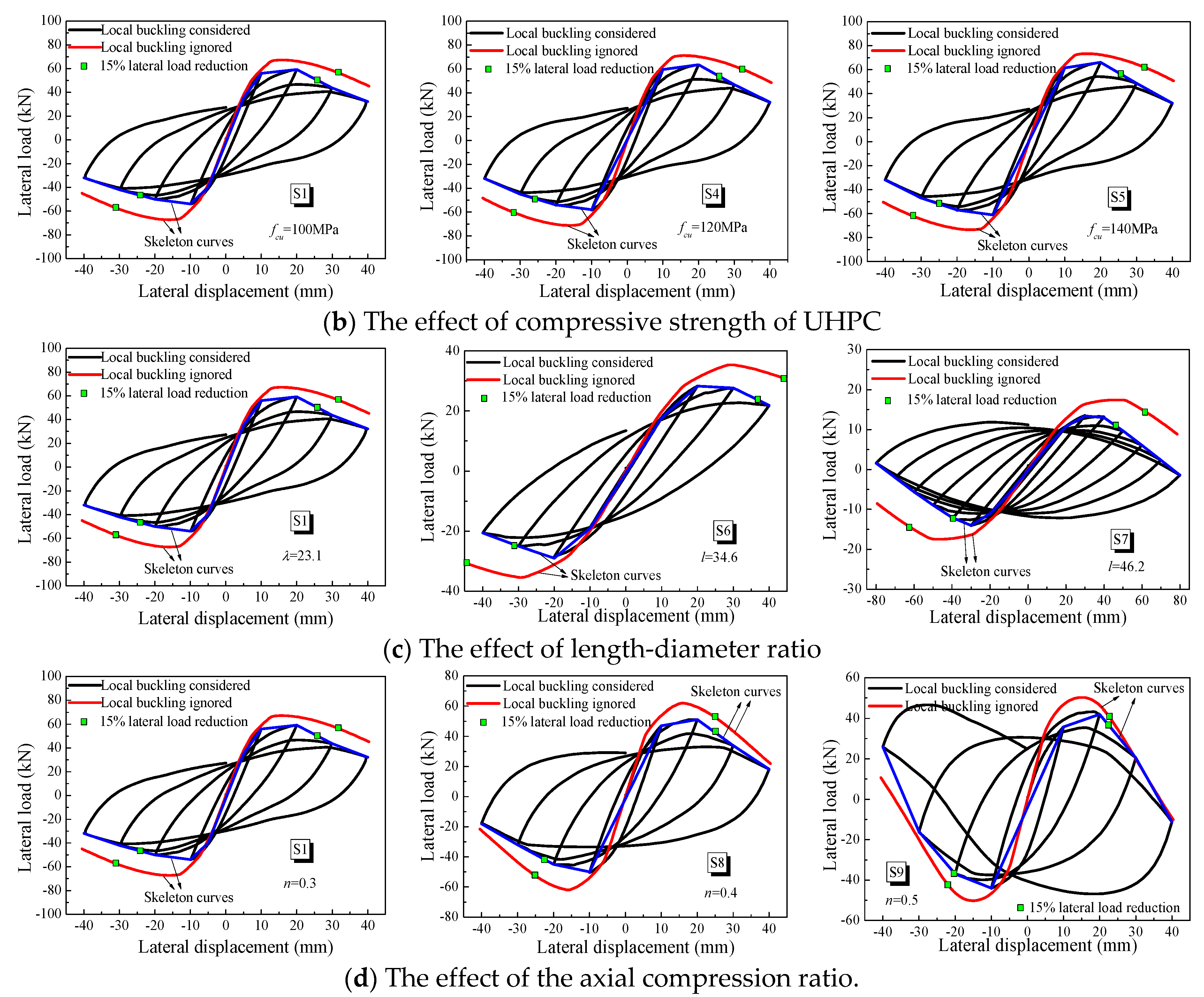
4.2. The Effect of the UHPC Strength
4.3. The Effect of the Length–Diameter Ratio
4.4. The Effect of the Axial Compression Ratio
5. Conclusions
- (1)
- For the stress–strain model for the confined UHPC, satisfactory results are obtained when the parameter γ is taken as 3.0.
- (2)
- The proposed fiber element model can predict the nonlinear static and cyclic behavior of UHPCFST columns well.
- (3)
- Neglecting the local buckling of the thin-walled steel tubes can bring about the overestimation of the bearing capacity and the post-peak ductility of UHPCFST columns.
- (4)
- The errors caused by the local buckling of the steel tube are increased with the increasing in the length–diameter ratio. The errors in terms of bearing capacity, induced by the local buckling, are decreased with the increasing of the yield strength of steel. A higher axial compression ratio causes an overestimation of the maximum value rather than the post-peak ductility.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, L.H. Concrete Filled Steel Tubular Structures from Theory to Practices; Science Press: Beijing, China, 2016. [Google Scholar]
- Ahmed, M.; Liang, Q.Q.; Patel, V.I. Nonlinear analysis of rectangular concrete-filled double steel tubular short columns incorporating local buckling. Eng. Struct. 2018, 175, 13–26. [Google Scholar] [CrossRef]
- Zubydan, A.H.; ElSabbagh, A.I. Monotonic and cyclic behavior of concrete-filled steel-tube beam-columns considering local buckling effect. Thin-Walled Struct. 2011, 49, 465–481. [Google Scholar] [CrossRef]
- Ahmed, M.; Liang, Q.Q.; Patel, V.I.; Hadi, M.N.S. Nonlinear analysis of square concrete-filled double steel tubular slender columns incorporating preload effects. Eng. Struct. 2020, 207, 110272. [Google Scholar] [CrossRef]
- Vrcelj, Z.; Uy, B. Strength of slender concrete-filled steel box columns incorporating local buckling. J. Constr. Steel. Res. 2002, 58, 275–300. [Google Scholar] [CrossRef]
- Uy, B. Strength of concrete filled steel box columns incorporating local buckling. J. Struct. Eng. 2000, 126, 341–352. [Google Scholar] [CrossRef]
- Valipour, H.R.; Foster, S.J. Nonlinear static and cyclic analysis of concrete-filled steel columns. J. Constr. Steel. Res. 2010, 66, 793–802. [Google Scholar] [CrossRef]
- Varma, A.H.; Ricles, J.M.; Sause, R. Seismic behavior and modeling of high-strength composite concrete-filled steel tube (CFT) beam–columns. J. Constr. Steel. Res. 2002, 58, 725–758. [Google Scholar] [CrossRef]
- Kamila, G.M.; Liang, Q.Q.; Hadi, M.N.S. Fiber element simulation of interaction behavior of local and global buckling in axially loaded rectangular concrete-filled steel tubular slender columns under fire exposure. Thin-Walled Struct. 2019, 145, 106403. [Google Scholar] [CrossRef]
- Chung, K.; Chung, J.; Choib, S. Prediction of pre- and post-peak behavior of concrete-filled square steel tube columns under cyclic loads using fiber element method. Thin-Walled Struct. 2007, 45, 747–758. [Google Scholar] [CrossRef]
- Richard, P.; Cheyrezy, M. Composition of reactive powder concretes. Cem. Concr. Res. 1995, 25, 1501–1511. [Google Scholar] [CrossRef]
- Xu, L.Y.; Huang, B.T.; Lao, J.C. Tensile over-saturated cracking of Ultra-high-strength engineered cementitious composites (UHS-ECC) with artificial geopolymer aggregates. Cem. Concr. Comp. 2023, 136, 104896. [Google Scholar] [CrossRef]
- Su, Y.; Wu, C.Q.; Li, J. Development of novel ultra-high performance concrete: From material to structure. Constr. Build. Mater. 2017, 135, 517–528. [Google Scholar] [CrossRef]
- Deng, E.F.; Zhang, Z.; Zhang, C.X. Experimental study on flexural behavior of UHPC wet joint in prefabricated multi-girder bridge. Eng. Struct. 2023, 275, 115314. [Google Scholar] [CrossRef]
- Kang, S.T.; Chio, J.I.; Koh, K.T. Hybrid effects of steel fiber and microfiber on the tensile behavior of ultra-high performance concrete. Compos. Struct. 2016, 145, 37–42. [Google Scholar] [CrossRef]
- Park, S.H.; Kim, D.J.; Ryu, G.S. Tensile behavior of ultra high performance hybrid fiber reinforced concrete. Cem. Concr. Compos. 2012, 34, 172–184. [Google Scholar] [CrossRef]
- Montuori, R.; Piluso, V.; Tisi, A. Ultimate behavior of FRP wrapped sections under axial force and bending: Influence of stress-strain confinement model. Compos. Part B-Eng. 2013, 54, 85–96. [Google Scholar] [CrossRef]
- Cavaleri, L.; Trapani, F.D.; Ferrotto, M.F. Stress-strain models for normal and high strength confined concrete: Test and comparison of literature models reliability in reproducing experimental results. Ing. Sismica-ital. 2017, 34, 114–137. [Google Scholar]
- Le´geron, F.; Paultre, P. Uniaxial confinement model for normal- and high-strength concrete columns. J. Struct. Eng. 2003, 129, 241–252. [Google Scholar] [CrossRef]
- An, L.H.; Fehling, E. Assessment of stress-strain model for UHPC confined by steel tube stub columns. Struct. Eng. Mech. 2017, 63, 371–384. [Google Scholar]
- Li, G.C.; Liu, D.; Yang, Z.J.; Zhang, C.Y. Flexural behavior of high strength concrete filled high strength square steel tube. J. Constr. Steel. Res. 2017, 128, 732–744. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestly, M.N.J.; Park, R. Theoretical stress–strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Menegotto, M.; Paolo, E. Method of analysis for cyclically loaded R.C. plane frames including change in geometry and non-elastic behavior of elements under combines normal force and bending. In Proceedings of the IABSE Symposium on Resistance and Ultimate Deformability of Structures, Lisbon, Portugal, 12–14 September 1973; pp. 15–22. [Google Scholar]
- AIJ. Recommendations for Design and Construction of Concrete Filled Steel Tubular Structures; Architectural Institute of Japan: Tokyo, Japan, 2001. [Google Scholar]
- AISC. Load and Resistance Factor Design (LRFD) Specification for Structural Steel Buildings; American Institute of Steel Construction: Chicago, IL, USA, 1999. [Google Scholar]
- EC4. Design of Composite Steel and Concrete Structures; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Liang, Q.Q.; Uy, B.; Liew, J.Y.R. Local buckling of steel plates in concrete filled thin-walled steel tubular beam-columns. J. Constr. Steel. Res. 2007, 63, 396–405. [Google Scholar] [CrossRef] [Green Version]
- Liang, Q.Q.; Uy, B. Theoretical study on the post-local buckling of steel plates in concrete filled thin-walled steel box columns. Comput. Struct. 2000, 75, 479–490. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.M.; Zhang, R.; Jia, L.J. Structural behavior of UHPC filled steel tube columns under axial loading. Thin-Walled Struct. 2018, 130, 550–563. [Google Scholar] [CrossRef]
- Yan, Y.X.; Xu, L.H.; Li, B. Axial behavior of ultra-high performance concrete (UHPC) filled stocky steel tubes with square sections. J. Constr. Steel. Res. 2019, 158, 417–428. [Google Scholar] [CrossRef]
- Xu, S.C.; Wu, C.Q.; Liu, Z.X. Experimental investigation on the cyclic behaviors of ultra-high performance steel fiber reinforced concrete filled thin-walled steel tubular columns. Thin-Walled Struct. 2019, 140, 1–20. [Google Scholar] [CrossRef]
- Cai, H.; Xu, L.H.; Chi, Y. Seismic performance of rectangular ultra-high performance concrete filled steel tube (UHPCFST) columns. Compos. Struct. 2021, 259, 113242. [Google Scholar] [CrossRef]




| Origin | Specimen Name | B × h (mm) | t (mm) | L (mm) | fy (MPa) | fc (MPa) | Nc (kN) | Nt (kN) | Nc/Nt |
|---|---|---|---|---|---|---|---|---|---|
| Chen et al. [29] | SS1-2 | 100 × 100 | 2.03 | 300 | 348.7 | 113.2 | 1340 | 1406 | 0.95 |
| SS1-3 | 100 × 100 | 2.05 | 300 | 348.7 | 130.8 | 1503 | 1575 | 0.95 | |
| SS2-2 | 100 × 100 | 3.83 | 300 | 306.7 | 113.2 | 1454 | 1544 | 0.94 | |
| SS2-3 | 100 × 100 | 3.79 | 300 | 306.7 | 130.8 | 1595 | 1676 | 0.95 | |
| SS3-2 | 100 × 100 | 7.59 | 300 | 371.6 | 113.2 | 1921 | 1976 | 0.97 | |
| SS3-3 | 100 × 100 | 7.63 | 300 | 371.6 | 130.8 | 2069 | 2051 | 1.01 | |
| Yan et al. [30] | S1-5-100 | 100 × 100 | 4.9 | 300 | 668.8 | 89.2 | 2038 | 1800 | 1.13 |
| S2-5-110 | 100 × 100 | 4.9 | 300 | 668.8 | 100.3 | 2128 | 2004 | 1.06 | |
| S3-6-110 | 100 × 100 | 5.8 | 300 | 646.2 | 100.3 | 2274 | 2220 | 1.02 | |
| S4-6-120 | 100 × 100 | 5.8 | 300 | 646.2 | 111.3 | 2364 | 2391 | 0.99 | |
| S5-6-140 | 100 × 100 | 5.8 | 300 | 646.2 | 128.1 | 2484 | 2573 | 0.97 | |
| S6-7-100 | 100 × 100 | 6.8 | 300 | 599.5 | 89.2 | 2262 | 2209 | 1.02 | |
| S7-7-110 | 100 × 100 | 6.8 | 300 | 599.5 | 100.3 | 2345 | 2295 | 1.02 | |
| S8-7-120 | 100 × 100 | 6.8 | 300 | 599.5 | 111.3 | 2427 | 2369 | 1.02 | |
| S9-7-140 | 100 × 100 | 6.8 | 300 | 599.5 | 128.1 | 2552 | 2492 | 1.02 | |
| S10-10-100 | 100 × 100 | 10 | 300 | 458.6 | 89.2 | 2305 | 2206 | 1.04 | |
| S11-10-120 | 100 × 100 | 10 | 300 | 458.6 | 111.3 | 2449 | 2298 | 1.07 | |
| S12-10-140 | 100 × 100 | 10 | 300 | 458.6 | 128.1 | 2558 | 2499 | 1.04 | |
| S13-14-100 | 100 × 100 | 14.2 | 300 | 468.6 | 89.2 | 2867 | 3107 | 0.92 | |
| S14-14-120 | 100 × 100 | 14.2 | 300 | 468.6 | 111.3 | 2933 | 3120 | 0.94 | |
| S15-14-140 | 100 × 100 | 14.2 | 300 | 468.6 | 128.1 | 2986 | 3274 | 0.91 | |
| S16-18-140 | 100 × 100 | 18.5 | 300 | 444.6 | 128.1 | 3382 | 3441 | 0.98 |
| Source | Specimen Name | B × h (mm) | t (mm) | L (mm) | fy (MPa) | fcu (MPa) | n | N (kN) | Pc (kN) | Pt (kN) | Pc/Pt |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Xu et al. [31] | SpeUTH4 | 250 × 250 | 4 | 1250 | 360 | 152.6 | 0.24 | 1736 | 275 | 288 | 1.05 |
| SpeUTH5 | 250 × 250 | 5 | 1250 | 360 | 155.4 | 0.24 | 1798 | 307 | 331 | 1.08 | |
| SpeUTH6 | 250 × 250 | 6 | 1250 | 360 | 152.2 | 0.24 | 1854 | 357 | 369 | 1.03 | |
| SpeUCR12 | 250 × 250 | 5 | 1250 | 360 | 150.4 | 0.12 | 899 | 272 | 294 | 1.08 | |
| SpeUCR36 | 250 × 250 | 5 | 1250 | 360 | 151.3 | 0.36 | 2697 | 360 | 352 | 0.98 | |
| Cai et al. [32] | S-10-0.2-1.5 | 100 × 150 | 10 | 800 | 460 | 140 | 0.2 | 690 | 139 | 143 | 0.97 |
| S-10-0.4-1.5 | 100 × 150 | 10 | 800 | 460 | 140 | 0.4 | 1380 | 116 | 110 | 1.05 | |
| S-10-0.2-2 | 100 × 200 | 10 | 900 | 460 | 140 | 0.2 | 884 | 169 | 173 | 0.98 |
| Specimen | fy (MPa) | fcu (MPa) | L (mm) | B × h (mm) | t (mm) | λ | w | n | N (kN) |
|---|---|---|---|---|---|---|---|---|---|
| S1 | 345 | 100 | 1000 | 150 × 150 | 5 | 23.1 | 30 | 0.3 | 823 |
| S2 | 460 | 100 | 1000 | 150 × 150 | 5 | 23.1 | 30 | 0.3 | 924 |
| S3 | 560 | 100 | 1000 | 150 × 150 | 5 | 23.1 | 30 | 0.3 | 1010 |
| S4 | 345 | 120 | 1000 | 150 × 150 | 5 | 23.1 | 30 | 0.3 | 965 |
| S5 | 345 | 140 | 1000 | 150 × 150 | 5 | 23.1 | 30 | 0.3 | 1053 |
| S6 | 345 | 100 | 1500 | 150 × 150 | 5 | 34.6 | 30 | 0.3 | 823 |
| S7 | 345 | 100 | 2000 | 150 × 150 | 5 | 46.2 | 30 | 0.3 | 823 |
| S8 | 345 | 100 | 1000 | 150 × 150 | 5 | 23.1 | 30 | 0.4 | 1098 |
| S9 | 345 | 100 | 1000 | 150 × 150 | 5 | 23.1 | 30 | 0.5 | 1372 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Yan, Y.; Wang, Y.; Cai, H.; Zhu, Y. Seismic Behavior of UHPC-Filled Rectangular Steel Tube Columns Incorporating Local Buckling. Buildings 2023, 13, 1028. https://doi.org/10.3390/buildings13041028
Yan Y, Yan Y, Wang Y, Cai H, Zhu Y. Seismic Behavior of UHPC-Filled Rectangular Steel Tube Columns Incorporating Local Buckling. Buildings. 2023; 13(4):1028. https://doi.org/10.3390/buildings13041028
Chicago/Turabian StyleYan, Yanxiang, Yu Yan, Yansong Wang, Heng Cai, and Yaorui Zhu. 2023. "Seismic Behavior of UHPC-Filled Rectangular Steel Tube Columns Incorporating Local Buckling" Buildings 13, no. 4: 1028. https://doi.org/10.3390/buildings13041028
APA StyleYan, Y., Yan, Y., Wang, Y., Cai, H., & Zhu, Y. (2023). Seismic Behavior of UHPC-Filled Rectangular Steel Tube Columns Incorporating Local Buckling. Buildings, 13(4), 1028. https://doi.org/10.3390/buildings13041028





