An Integrated Multi-Criteria Decision Model to Select Sustainable Construction Projects under Intuitionistic Fuzzy Conditions
Abstract
:1. Introduction
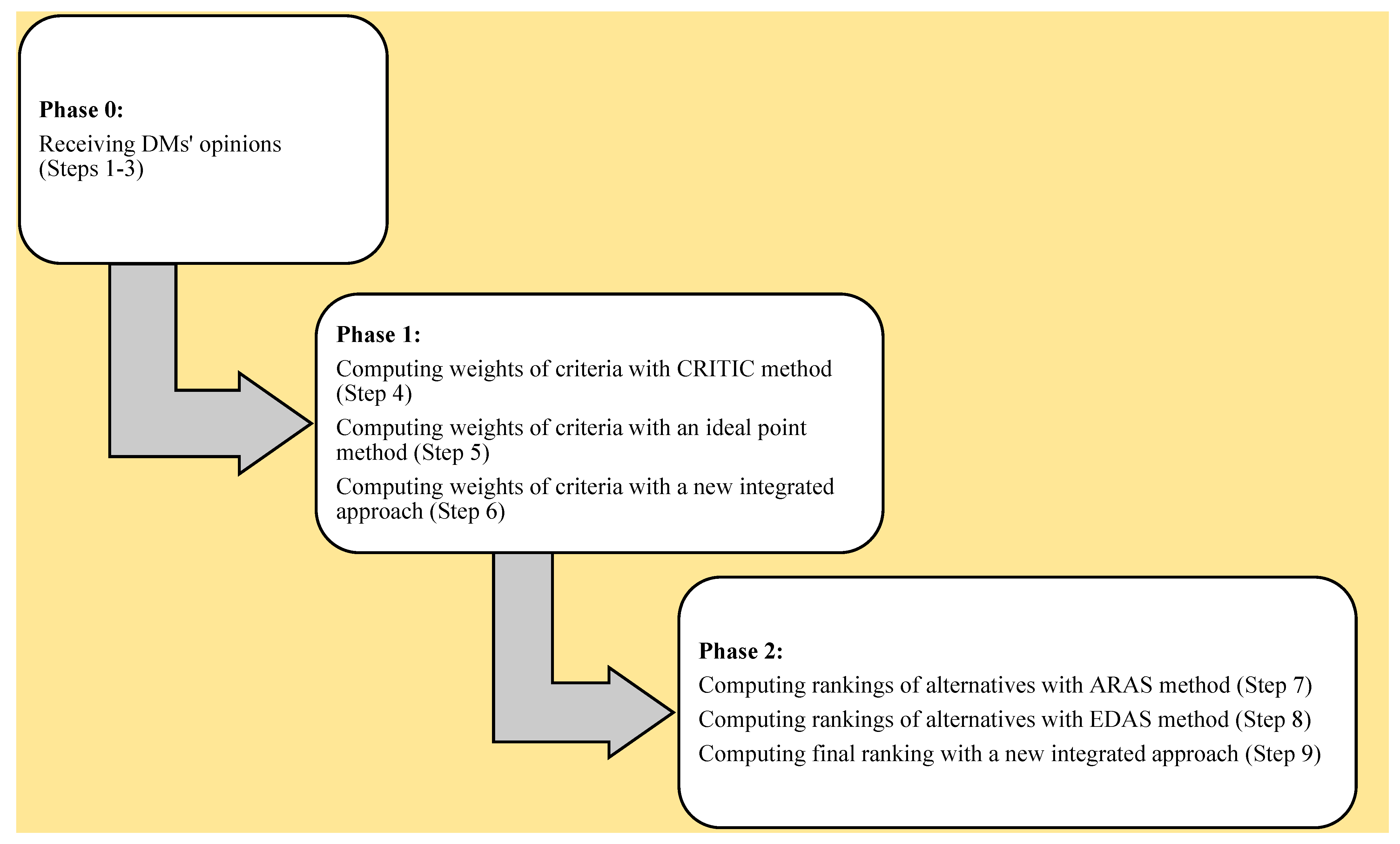
- Introducing a new integrated weighting method based on the CRITIC and ideal point approaches under uncertainty.
- Extending an ideal point approach for weighting criteria in an IF environment.
- Proposing a new combined ranking method based on the ARAS and EDAS approaches under uncertainty.
- Expanding an MCDM problem for the weighting and ranking of IFS situations.
2. Preliminaries
3. Proposed New Integrated Soft Computing Model
- IFSs evaluate both benefits (memberships) and weaknesses (non-memberships) of a considered answer, and the ambiguous area is taken into account, as well [59].
- IFSs transform an unclear practice unit problem into a specific and well-described optimization problem.
- IFSs, unlike ordinary fuzzy sets, keep a metric degree of uncertainty [60].
- The IFS separates the positive and negative information for membership of an element in the set [61].
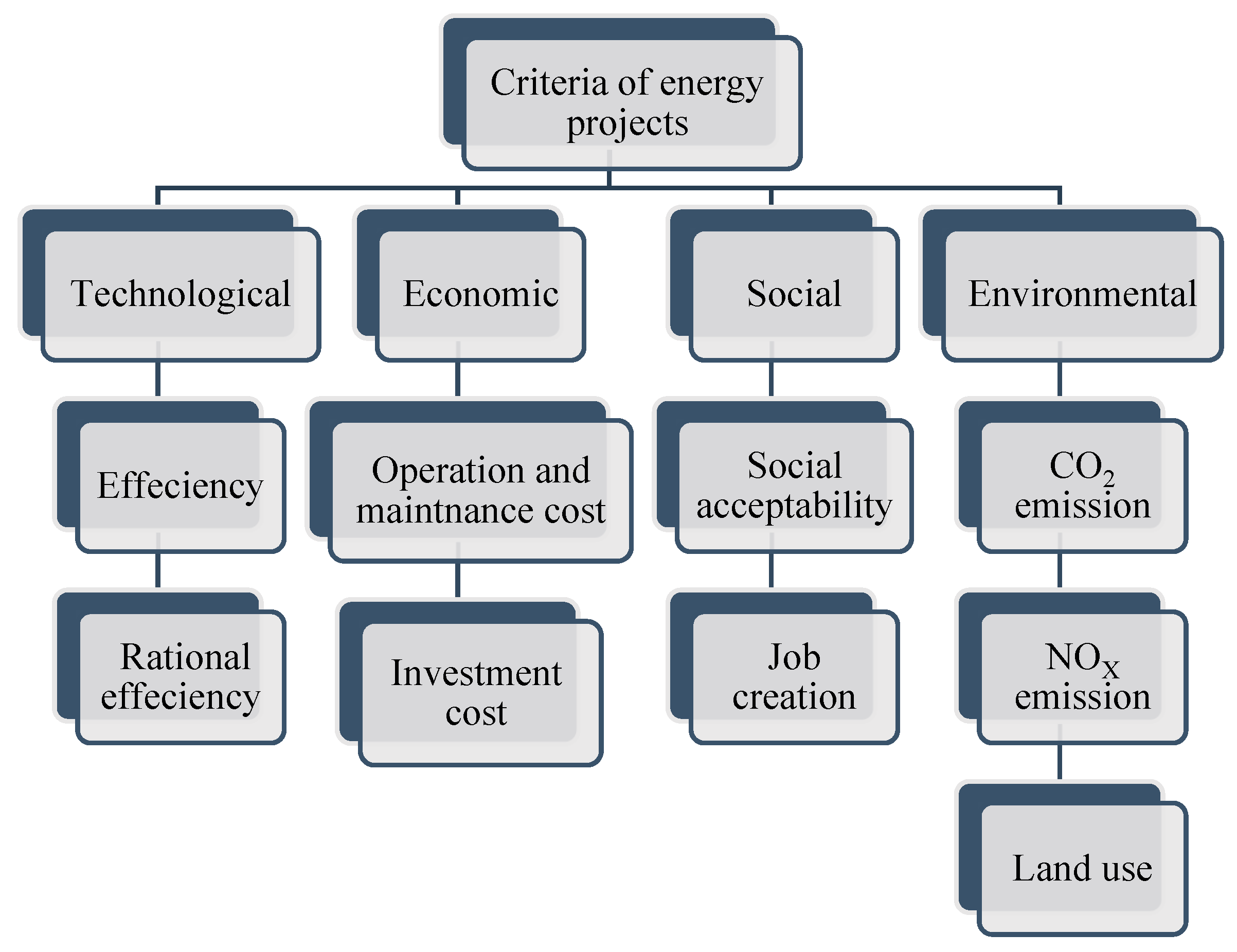
4. Case Study
5. Discussion of Results
5.1. Sensitivity Analysis
5.2. Comparative Analysis
6. Conclusions and Future Suggestions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akram, R.; Thaheem, M.J.; Nasir, A.R.; Ali, T.H.; Khan, S. Exploring the role of building information modeling in construction safety through science mapping. Saf. Sci. 2019, 120, 456–470. [Google Scholar] [CrossRef]
- Ding, G.; Langston, C. Multiple Criteria Sustainability Modelling: Case Study on School Buildings. Int. J. Constr. Manag. 2004, 4, 13–26. [Google Scholar] [CrossRef]
- Griffith, A.; Stephenson, P.; Bhutto, K. An Integrated Management System for Construction Quality, Safety and Environment: A Framework for IMS. Int. J. Constr. Manag. 2005, 5, 51–60. [Google Scholar] [CrossRef]
- Tupenaite, L.; Zilenaite, V.; Kanapeckiene, L.; Gecys, T.; Geipele, I. Sustainability Assessment of Modern High-Rise Timber Buildings. Sustainability 2021, 13, 8719. [Google Scholar] [CrossRef]
- Brundtland, G.H. Our Common Future—Call for Action. Environ. Conserv. 1987, 14, 291–294. [Google Scholar] [CrossRef]
- Van Zeijl-Rozema, A.; Martens, P. An adaptive indicator framework for monitoring regional sustainable development: A case study of the INSURE project in Limburg, The Netherlands. Sustain. Sci. Pract. Policy 2010, 6, 6–17. [Google Scholar] [CrossRef] [Green Version]
- Zadeh, L.A.; Klir, G.J.; Yuan, B. Fuzzy sets, fuzzy logic, and fuzzy systems. Selected papers by Lotfi A Zadeh. In Advances in Fuzzy Systems—Applications and Theory; World Scientific: Tokyo, Japan, 1996; Volume 6. [Google Scholar]
- Wang, W.; Liu, X.; Qin, Y. Multi-attribute group decision making models under interval type-2 fuzzy environment. Knowl.-Based Syst. 2012, 30, 121–128. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets; Springer: Berlin/Heidelberg, Germany, 1999; pp. 1–137. [Google Scholar] [CrossRef]
- Mousavi, S.; Mirdamadi, S.; Siadat, A.; Dantan, J.; Tavakkoli-Moghaddam, R. An intuitionistic fuzzy grey model for selection problems with an application to the inspection planning in manufacturing firms. Eng. Appl. Artif. Intell. 2015, 39, 157–167. [Google Scholar] [CrossRef] [Green Version]
- Plebankiewicz, E.; Zima, K.; Wieczorek, D. Modelling of time, cost and risk of construction with using fuzzy logic. J. Civ. Eng. Manag. 2021, 27, 412–426. [Google Scholar] [CrossRef]
- Florez, L.; Castro, D.; Irizarry, J. Impact of sustainability perceptions on optimal material selection in con-struction projects. In Proceedings of the Second International Conference on Sustainable Construction Materials and Technologies, Ancona, Italy, 28–30 June 2010; pp. 719–727. [Google Scholar]
- Ebrahimnejad, S.; Mousavi, S.; Tavakkoli-Moghaddam, R.; Hashemi, H.; Vahdani, B. A novel two-phase group decision making approach for construction project selection in a fuzzy environment. Appl. Math. Model. 2012, 36, 4197–4217. [Google Scholar] [CrossRef]
- Rezakhani, P. Fuzzy MCDM Model for Risk Factor Selection in Construction Projects. Eng. J. 2012, 16, 79–94. [Google Scholar] [CrossRef]
- Tsai, W.-H.; Lin, S.-J.; Lee, Y.-F.; Chang, Y.-C.; Hsu, J.-L. Construction method selection for green building projects to improve environmental sustainability by using an MCDM approach. J. Environ. Plan. Manag. 2013, 56, 1487–1510. [Google Scholar] [CrossRef]
- Dėjus, T.; Antuchevičienė, J. Assessment of health and safety solutions at a construction site. J. Civ. Eng. Manag. 2013, 19, 728–737. [Google Scholar] [CrossRef]
- Tamošaitienė, J.; Zavadskas, E.K.; Turskis, Z. Multi-criteria Risk Assessment of a Construction Project. Procedia Comput. Sci. 2013, 17, 129–133. [Google Scholar] [CrossRef] [Green Version]
- Taylan, O.; Bafail, A.O.; Abdulaal, R.M.; Kabli, M.R. Construction projects selection and risk assessment by fuzzy AHP and fuzzy TOPSIS methodologies. Appl. Soft Comput. 2014, 17, 105–116. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Gitinavard, H.; Vahdani, B. Evaluating Construction Projects by a New Group Decision-Making Model Based on Intuitionistic Fuzzy Logic Concepts. Int. J. Eng. 2015, 28, 1312–1319. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Vahdani, B. Cross-docking Location Selection in Distribution Systems: A New Intuitionistic Fuzzy Hierarchical Decision Model. Int. J. Comput. Intell. Syst. 2016, 9, 91–109. [Google Scholar] [CrossRef] [Green Version]
- Prascevic, N.; Prascevic, Z. Application of fuzzy ahp for ranking and selection of alternatives in construction project management. J. Civ. Eng. Manag. 2017, 23, 1123–1135. [Google Scholar] [CrossRef] [Green Version]
- Pavlovskis, M.; Antucheviciene, J.; Migilinskas, D. Assessment of Buildings Redevelopment Possibilities using MCDM and BIM Techniques. Procedia Eng. 2017, 172, 846–850. [Google Scholar] [CrossRef]
- Chatterjee, K.; Zavadskas, E.K.; Tamošaitienė, J.; Adhikary, K.; Kar, S. A Hybrid MCDM Technique for Risk Management in Construction Projects. Symmetry 2018, 10, 46. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Zhang, H.-Y.; Wang, J.-Q.; Li, L. Picture fuzzy normalized projection-based VIKOR method for the risk evaluation of construction project. Appl. Soft Comput. 2018, 64, 216–226. [Google Scholar] [CrossRef]
- Dahooie, J.H.; Zavadskas, E.K.; Abolhasani, M.; Vanaki, A.; Turskis, Z. A Novel Approach for Evaluation of Projects Using an Interval–Valued Fuzzy Additive Ratio Assessment (ARAS) Method: A Case Study of Oil and Gas Well Drilling Projects. Symmetry 2018, 10, 45. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K.; Sotirova, E.; Andonov, V. Generalized Net Model of Multicriteria Decision Making Procedure Using Intercriteria Analysis. In Advances in Fuzzy Logic and Technology 2017: Proceedings of: EUSFLAT-2017–The 10th Conference of the European Society for Fuzzy Logic and Technology, September 11–15, 2017, Warsaw, Poland IWIFSGN’2017–The Sixteenth International Workshop on Intuitionistic Fuzzy Sets and Generalized Nets, September 13–15, 2017, Warsaw, Poland; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Chalekaee, A.; Turskis, Z.; Khanzadi, M.; Ghodrati Amiri, G.; Keršulienė, V. A New Hybrid MCDM Model with Grey Numbers for the Construction Delay Change Response Problem. Sustainability 2019, 11, 776. [Google Scholar] [CrossRef] [Green Version]
- Davoudabadi, R.; Mousavi, S.M.; Šaparauskas, J.; Gitinavard, H. Solving construction project selection problem by a new uncertain weighting and ranking based on compromise solution with linear assignment approach. J. Civ. Eng. Manag. 2019, 25, 241–251. [Google Scholar] [CrossRef] [Green Version]
- Gunduz, M.; Khader, B.K. Construction Project Safety Performance Management Using Analytic Network Process (ANP) as a Multicriteria Decision-Making (MCDM) Tool. Comput. Intell. Neurosci. 2020, 2020, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohandes, S.R.; Sadeghi, H.; Mahdiyar, A.; Durdyev, S.; Banaitis, A.; Yahya, K.; Ismail, S. Assessing construction labours’ safety level: A fuzzy mcdm approach. J. Civ. Eng. Manag. 2020, 26, 175–188. [Google Scholar] [CrossRef] [Green Version]
- Fallahpour, A.; Wong, K.Y.; Rajoo, S.; Olugu, E.U.; Nilashi, M.; Turskis, Z. A fuzzy decision support system for sustainable construction project selection: An integrated fpp-fis model. J. Civ. Eng. Manag. 2020, 26, 247–258. [Google Scholar] [CrossRef]
- Zhang, Z.; Liao, H.; Al-Barakati, A.; Zavadskas, E.K.; Antuchevičienė, J. Supplier selection for housing development by an integrated method with interval rough boundaries. Int. J. Strat. Prop. Manag. 2020, 24, 269–284. [Google Scholar] [CrossRef]
- Peng, J.-J.; Tian, C.; Zhang, W.-Y.; Zhang, S.; Wang, J.-Q. An integrated multi-criteria decision-making framework for sustainable supplier selection under picture fuzzy environment. Technol. Econ. Dev. Econ. 2020, 26, 573–598. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.M.; Gitinavard, H.; Vahdani, B. ELECTRE I-based group decision methodology with risk preferences in an imprecise setting for flexible manufacturing systems. J. Optim. Ind. Eng. 2021, 14, 239–253. [Google Scholar] [CrossRef]
- Banihashemi, S.A.; Khalilzadeh, M.; Antucheviciene, J.; Šaparauskas, J. Trading off Time–Cost–Quality in Construction Project Scheduling Problems with Fuzzy SWARA–TOPSIS Approach. Buildings 2021, 11, 387. [Google Scholar] [CrossRef]
- Tamošaitienė, J.; Sarvari, H.; Cristofaro, M.; Chan, D.W.M. Identifying and prioritizing the selection criteria of appropriate repair and maintenance methods for commercial buildings. Int. J. Strat. Prop. Manag. 2021, 25, 413–431. [Google Scholar] [CrossRef]
- Naik, G.; Kishore, R.; Dehmourdi, S.A.M. Modeling a Multi-Criteria Decision Support System for Prequalification Assessment of Construction Contractors using CRITIC and EDAS Models. Oper. Res. Eng. Sci. Theory Appl. 2021, 4, 79–101. [Google Scholar] [CrossRef]
- Kao, J.C.; Wang, C.N.; Nguyen, V.T.; Husain, S.T. A Fuzzy MCDM Model of Supplier Selection in Supply Chain Management. Intell. Autom. Soft Comput. 2022, 31. [Google Scholar] [CrossRef]
- Li, J.; He, R.; Wang, T. A data-driven decision-making framework for personnel selection based on LGBWM and IFNs. Appl. Soft Comput. 2022, 126, 109227. [Google Scholar] [CrossRef]
- Seker, S.; Kahraman, C. A Pythagorean cubic fuzzy methodology based on TOPSIS and TODIM methods and its application to software selection problem. Soft Comput. 2021, 26, 2437–2450. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, W. Multi-criteria group decision-making with cloud model and TOPSIS for alternative selection under uncertainty. Soft Comput. 2022, 26, 12509–12529. [Google Scholar] [CrossRef]
- Salimian, S.; Mousavi, S.M.; Antucheviciene, J. An Interval-Valued Intuitionistic Fuzzy Model Based on Extended VIKOR and MARCOS for Sustainable Supplier Selection in Organ Transplantation Networks for Healthcare Devices. Sustainability 2022, 14, 3795. [Google Scholar] [CrossRef]
- Salimian, S.; Mousavi, S.M.; Antuchevičienė, J. Evaluation of infrastructure projects by a decision model based on rpr, mabac, and waspas methods with interval-valued intuitionistic fuzzy sets. Int. J. Strat. Prop. Manag. 2022, 26, 106–118. [Google Scholar] [CrossRef]
- Ghorui, N.; Mondal, S.P.; Chatterjee, B.; Ghosh, A.; Pal, A.; De, D.; Giri, B.C. Selection of cloud service providers using MCDM methodology under intuitionistic fuzzy uncertainty. Soft Comput. 2023, 27, 2403–2423. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T. New operations defined over the intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994, 61, 137–142. [Google Scholar] [CrossRef]
- Xu, Z.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Feng, F.; Yan, M.; Liu, X. Intuitionistic fuzzy soft decision-making method based on expectation score functions. J. Jilin Univ. 2018, 56, 1084–1090. [Google Scholar]
- Szmidt, E.; Kacprzyk, J. Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 114, 505–518. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z. A new additive ratio assessment (aras) method in multicriteria decision-making/naujas adityvinis kriterijų santykių įvertinimo metodas (aras) daugiakriteriniams uždaviniams spręsti. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
- Kahraman, C.; Ghorabaee, M.K.; Zavadskas, E.K.; Onar, S.C.; Yazdani, M.; Oztaysi, B. Intuitionistic fuzzy edas method: An application to solid waste disposal site selection. J. Environ. Eng. Landsc. Manag. 2017, 25, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Li, M.; Luo, H.; Huang, G.Q. Industrial robot selection using stochastic multicriteria acceptability analysis for group decision making. Robot. Auton. Syst. 2019, 122, 103304. [Google Scholar] [CrossRef]
- Peng, X.; Garg, H. Intuitionistic fuzzy soft decision making method based on CoCoSo and CRITIC for CCN cache placement strategy selection. Artif. Intell. Rev. 2021, 55, 1567–1604. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, X.; Luo, Z. Pythagorean fuzzy MCDM method based on CoCoSo and CRITIC with score function for 5G industry evaluation. Artif. Intell. Rev. 2019, 53, 3813–3847. [Google Scholar] [CrossRef]
- Elaalem, M.; Comber, A.; Fisher, P. A Comparison of Fuzzy AHP and Ideal Point Methods for Evaluating Land Suitability. Trans. GIS 2011, 15, 329–346. [Google Scholar] [CrossRef]
- Mishra, D.; Satapathy, S. MCDM Approach for Mitigation of Flooding Risks in Odisha (India) Based on Information Retrieval. Int. J. Cogn. Inform. Nat. Intell. 2020, 14, 77–91. [Google Scholar] [CrossRef]
- Zamani, M.; Rabbani, A.; Yazdani-Chamzini, A.; Turskis, Z. An integrated model for extending brand based on fuzzy aras and anp methods. J. Bus. Econ. Manag. 2014, 15, 403–423. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Lei, F.; Wei, G.; Wang, R.; Wu, J.; Wei, C. EDAS Method for Multiple Attribute Group Decision Making with Probabilistic Uncertain Linguistic Information and Its Application to Green Supplier Selection. Int. J. Comput. Intell. Syst. 2019, 12, 1361. [Google Scholar] [CrossRef] [Green Version]
- Szmidt, E.; Baldwin, J. Intuitionistic Fuzzy Set Functions, Mass Assignment Theory, Possibility Theory and Histograms. In Proceedings of the 2006 IEEE International Conference on Fuzzy Systems, Vancouver, BC, Canada, 16–21 July 2006; pp. 35–41. [Google Scholar] [CrossRef]
- Khatibi, V.; Montazer, G.A. Intuitionistic fuzzy set vs. fuzzy set application in medical pattern recognition. Artif. Intell. Med. 2009, 47, 43–52. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Yadav, S.P.; Kumar, S. Fuzzy system reliability evaluation using time-dependent intuitionistic fuzzy set. Int. J. Syst. Sci. 2013, 44, 50–66. [Google Scholar] [CrossRef]
- Kaya, T.; Kahraman, C. Multicriteria decision making in energy planning using a modified fuzzy TOPSIS methodology. Expert Syst. Appl. 2011, 38, 6577–6585. [Google Scholar] [CrossRef]
- Park, J.H.; Park, I.Y.; Kwun, Y.C.; Tan, X. Extension of the TOPSIS method for decision making problems under interval-valued intuitionistic fuzzy environment. Appl. Math. Model. 2011, 35, 2544–2556. [Google Scholar] [CrossRef]
- Dorfeshan, Y.; Tavakkoli-Moghaddam, R.; Mousavi, S.; Vahedi-Nouri, B. A new weighted distance-based approximation methodology for flow shop scheduling group decisions under the interval-valued fuzzy processing time. Appl. Soft Comput. 2020, 91, 106248. [Google Scholar] [CrossRef]

| Linguistic Variables | Intuitionistic Fuzzy Values |
|---|---|
| Extremely high (EH) | |
| Very very high (VVH) | |
| Very high (VH) | |
| High (H) | |
| Medium high (MH) | |
| Medium (M) | |
| Medium low (ML) | |
| Low (L) | |
| Very low (VL) | |
| Very very low (VVL) |
| Criteria | Alternatives | ||||||
|---|---|---|---|---|---|---|---|
| H | VH | M | ML | MH | M | M | |
| H | M | M | MH | H | MH | MH | |
| MH | VL | M | H | MH | M | M | |
| MH | VH | M | H | M | M | ML | |
| VL | ML | VH | H | ML | H | M | |
| VL | ML | H | VH | L | H | M | |
| L | ML | VH | VH | ML | MH | MH | |
| ML | L | H | VH | M | H | H | |
| MH | L | M | M | H | H | MH | |
| Criteria | Alternatives | ||||||
|---|---|---|---|---|---|---|---|
| VH | H | ML | M | M | M | MH | |
| MH | VH | M | MH | H | M | M | |
| H | ML | MH | H | MH | MH | M | |
| M | VH | M | H | M | M | ML | |
| VL | ML | VH | H | ML | H | M | |
| ML | ML | H | VH | L | H | M | |
| VL | VL | H | H | ML | MH | H | |
| L | ML | H | VH | M | H | MH | |
| H | H | MH | M | MH | H | MH | |
| Criteria | Alternatives | ||||||
|---|---|---|---|---|---|---|---|
| VH | VH | M | L | H | M | MH | |
| VH | VH | M | MH | H | MH | M | |
| MH | VL | M | H | MH | M | MH | |
| MH | VH | M | VH | M | MH | M | |
| ML | L | H | VH | ML | H | M | |
| ML | ML | H | VH | L | H | M | |
| L | ML | H | H | ML | MH | MH | |
| ML | ML | H | VH | M | H | H | |
| MH | H | M | M | H | MH | MH | |
| Criteria | Alternatives | ||||||
|---|---|---|---|---|---|---|---|
| [0.76436 0.13564] | [0.76931 0.13069] | [0.46931 0.43069] | [0.38020 0.50297] | [0.60297 0.29703] | [0.50000 0.40000] | [0.56436 0.33564] | |
| [0.70297 0.19703] | [0.69307 0.20693] | [0.50000 0.40000] | [0.60000 0.30000] | [0.70000 0.20000] | [0.56931 0.33069] | [0.53564 0.36436] | |
| [0.36931 0.73069] | [0.80792 0.32673] | [0.46931 0.63069] | [0.30000 0.80000] | [0.40000 0.70000] | [0.46931 0.63069] | [0.46634 0.63366] | |
| [0.43069 0.66931] | [0.20000 0.90000] | [0.50000 0.60000] | [0.26634 0.83366] | [0.50000 0.60000] | [0.46634 0.63366] | [0.56634 0.53366] | |
| [0.20099 0.66584] | [0.34950 0.53366] | [0.76634 0.13366] | [0.73366 0.16634] | [0.40000 0.50000] | [0.70000 0.20000] | [0.50000 0.40000] | |
| [0.29307 0.58911] | [0.40000 0.50000] | [0.70000 0.20000] | [0.80000 0.10000] | [0.25000 0.60000] | [0.70000 0.20000] | [0.50000 0.40000] | |
| [0.79604 0.35396] | [0.69208 0.42327] | [0.26436 0.83564] | [0.26436 0.83564] | [0.60000 0.50000] | [0.40000 0.70000] | [0.36931 0.73069] | |
| [0.64604 0.46931] | [0.65347 0.46436] | [0.30000 0.80000] | [0.20000 0.90000] | [0.50000 0.60000] | [0.30000 0.80000] | [0.33069 0.76931] | |
| [0.63069 0.26931] | [0.53960 0.34257] | [0.53069 0.36931] | [0.50000 0.40000] | [0.66931 0.23069] | [0.66634 0.23366] | [0.60000 0.30000] | |
| Criteria | Alternatives | ||||||
|---|---|---|---|---|---|---|---|
| 0.81436 | 0.18317 | 0.81931 | 0.33069 | 0.51931 | 0.52525 | 0.43861 | |
| 0.75297 | 0.25198 | 0.74307 | 0.35347 | 0.55000 | 0.40000 | 0.65000 | |
| 0.31931 | 0.46139 | 0.74059 | 0.42871 | 0.41931 | 0.66535 | 0.25000 | |
| 0.38069 | 0.73465 | 0.15000 | 0.70000 | 0.45000 | 0.66683 | 0.21634 | |
| 0.26757 | 0.65817 | 0.40792 | 0.38366 | 0.81634 | 0.20000 | 0.78366 | |
| 0.35198 | 0.59455 | 0.45000 | 0.40000 | 0.75000 | 0.20000 | 0.85000 | |
| 0.72104 | 0.33094 | 0.63441 | 0.57946 | 0.21436 | 0.78564 | 0.21436 | |
| 0.58837 | 0.40792 | 0.59455 | 0.58218 | 0.25000 | 0.80000 | 0.15000 | |
| 0.68069 | 0.36485 | 0.59851 | 0.40594 | 0.58069 | 0.43465 | 0.55000 | |
| Criteria | Alternatives | ||||||
|---|---|---|---|---|---|---|---|
| 0.81436 | 0.18317 | 0.81931 | 0.33069 | 0.51931 | 0.52525 | 0.43861 | |
| 0.75297 | 0.25198 | 0.74307 | 0.35347 | 0.55000 | 0.40000 | 0.65000 | |
| 0.31931 | 0.46139 | 0.74059 | 0.42871 | 0.41931 | 0.66535 | 0.25000 | |
| 0.38069 | 0.73465 | 0.15000 | 0.70000 | 0.45000 | 0.66683 | 0.21634 | |
| 0.26757 | 0.65817 | 0.40792 | 0.38366 | 0.81634 | 0.20000 | 0.78366 | |
| 0.35198 | 0.59455 | 0.45000 | 0.40000 | 0.75000 | 0.20000 | 0.85000 | |
| 0.72104 | 0.33094 | 0.63441 | 0.57946 | 0.21436 | 0.78564 | 0.21436 | |
| Criteria | ||||
|---|---|---|---|---|
| 0.51867 | 0.57634 | 0.51867 | 0.57634 | |
| 0.52878 | 0.48504 | 0.52878 | 0.48504 | |
| 0.46924 | 0.43224 | 0.46924 | 0.43224 | |
| 0.47122 | 0.58034 | 0.47122 | 0.58034 | |
| 0.50248 | 0.60954 | 0.50248 | 0.60954 | |
| 0.51379 | 0.56304 | 0.51379 | 0.56304 | |
| 0.49717 | 0.58868 | 0.49717 | 0.58868 |
| Criteria | ||
|---|---|---|
| [0.01171 0.00766] | 0.04459 | |
| [0.00758 0.00431] | 0.03912 | |
| [0.00692 0.00685] | 0.04134 | |
| [0.00874 0.01389] | 0.05349 | |
| [0.01305 0.01134] | 0.04717 | |
| [0.01162 0.00872] | 0.04410 | |
| [0.01264 0.01327] | 0.05501 | |
| [0.00912 0.01257] | 0.05246 | |
| [0.00248 0.00148] | 0.02371 |
| Alternative | |
|---|---|
| 0.05246 | |
| 0.05258 | |
| 0.05208 | |
| 0.05520 | |
| 0.04879 | |
| 0.05074 | |
| 0.04866 |
| Criteria | CRITIC Method | Ideal Point Method | Final Weights |
|---|---|---|---|
| 0.12337 | 0.11121 | 0.11135 | |
| 0.10383 | 0.09755 | 0.09762 | |
| 0.09253 | 0.10308 | 0.10296 | |
| 0.12423 | 0.13339 | 0.13329 | |
| 0.13048 | 0.11764 | 0.11779 | |
| 0.12053 | 0.10998 | 0.11011 | |
| 0.12601 | 0.13718 | 0.13706 | |
| 0.11816 | 0.13083 | 0.13068 | |
| 0.06087 | 0.05912 | 0.05914 |
| Criteria | Alternatives | ||||||
|---|---|---|---|---|---|---|---|
| 0.53687 | 0.53745 | 0.50226 | 0.49280 | 0.51794 | 0.50586 | 0.51341 | |
| 0.52547 | 0.52447 | 0.50503 | 0.51510 | 0.52517 | 0.51201 | 0.50862 | |
| 0.48233 | 0.52353 | 0.49211 | 0.47555 | 0.48533 | 0.49211 | 0.49182 | |
| 0.48463 | 0.45492 | 0.49356 | 0.46346 | 0.49356 | 0.48922 | 0.50210 | |
| 0.47116 | 0.48858 | 0.53925 | 0.53519 | 0.49380 | 0.53102 | 0.50620 | |
| 0.48294 | 0.49424 | 0.52881 | 0.54034 | 0.47983 | 0.52881 | 0.50576 | |
| 0.52909 | 0.51769 | 0.46241 | 0.46241 | 0.50658 | 0.48026 | 0.47622 | |
| 0.51100 | 0.51177 | 0.46888 | 0.45643 | 0.49378 | 0.46888 | 0.47270 | |
| 0.51084 | 0.50591 | 0.50484 | 0.50300 | 0.51316 | 0.51298 | 0.50900 | |
| Alternative | ||
|---|---|---|
| 4.53434 | 0.46526 | |
| 4.55856 | 0.50944 | |
| 4.49715 | 0.35180 | |
| 4.44428 | 0.36535 | |
| 4.50914 | 0.41516 | |
| 4.52115 | 0.34387 | |
| 4.48584 | 0.45025 |
| Alternative | ARAS Method | EDAS Method | Integration Approach | Final Rank |
|---|---|---|---|---|
| 8.96086 | 0.46526 | 4.71306 | 2 | |
| 9.00872 | 0.50944 | 4.75908 | 1 | |
| 8.88737 | 0.35180 | 4.61959 | 6 | |
| 8.78289 | 0.36535 | 4.57412 | 7 | |
| 8.91107 | 0.41516 | 4.66311 | 3 | |
| 8.93480 | 0.34387 | 4.63934 | 5 | |
| 8.86502 | 0.45025 | 4.65764 | 4 |
| 0.1 | 8.11130 | 8.15879 | 8.03382 | 7.94113 | 8.06148 | 8.07571 | 8.02354 |
| 0.2 | 7.26174 | 7.30887 | 7.18026 | 7.09938 | 7.21189 | 7.21662 | 7.18207 |
| 0.3 | 6.41218 | 6.45894 | 6.32670 | 6.25763 | 6.36230 | 6.35752 | 6.34059 |
| 0.4 | 5.56262 | 5.60901 | 5.47314 | 5.41587 | 5.51270 | 5.49843 | 5.49911 |
| 0.5 | 4.71306 | 4.75908 | 4.61959 | 4.57412 | 4.66311 | 4.63934 | 4.65764 |
| 0.6 | 3.86350 | 3.90915 | 3.76603 | 3.73236 | 3.81352 | 3.78024 | 3.81616 |
| 0.7 | 3.01394 | 3.05923 | 2.91247 | 2.89061 | 2.96393 | 2.92115 | 2.97468 |
| 0.8 | 2.16438 | 2.20930 | 2.05891 | 2.04886 | 2.11434 | 2.06205 | 2.13321 |
| 0.9 | 1.31482 | 1.35937 | 1.20535 | 1.20710 | 1.26475 | 1.20296 | 1.29173 |
| Alternative | IF-TOPSIS Method | IF-TOPSIS rank | Proposed Approach | Final Rank |
|---|---|---|---|---|
| 0.50078 | 2 | 4.71306 | 2 | |
| 0.50633 | 1 | 4.75908 | 1 | |
| 0.49654 | 6 | 4.61959 | 6 | |
| 0.49060 | 7 | 4.57412 | 7 | |
| 0.49964 | 3 | 4.66311 | 3 | |
| 0.49783 | 5 | 4.63934 | 5 | |
| 0.49958 | 4 | 4.65764 | 4 |
| Alternative | IF-TOPSIS Method | IF-TOPSIS DD Value | IVIF-TOPSIS Rank | Proposed Approach | Proposed Approach DD Value | Final Rank |
|---|---|---|---|---|---|---|
| 0.49060 | 1.21248 | 7 | 4.57412 | 0.99407 | 7 | |
| 0.49654 | 0.25792 | 6 | 4.61959 | 0.42752 | 6 | |
| 0.49783 | 0.35275 | 5 | 4.63934 | 0.39445 | 5 | |
| 0.49958 | 0.01256 | 4 | 4.65764 | 0.11744 | 4 | |
| 0.49964 | 0.22662 | 3 | 4.66311 | 1.07117 | 3 | |
| 0.50078 | 1.10979 | 2 | 4.71306 | 0.97579 | 2 | |
| 0.50633 | 1 | 4.75905 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salimian, S.; Mousavi, S.M.; Tupenaite, L.; Antucheviciene, J. An Integrated Multi-Criteria Decision Model to Select Sustainable Construction Projects under Intuitionistic Fuzzy Conditions. Buildings 2023, 13, 848. https://doi.org/10.3390/buildings13040848
Salimian S, Mousavi SM, Tupenaite L, Antucheviciene J. An Integrated Multi-Criteria Decision Model to Select Sustainable Construction Projects under Intuitionistic Fuzzy Conditions. Buildings. 2023; 13(4):848. https://doi.org/10.3390/buildings13040848
Chicago/Turabian StyleSalimian, Sina, Seyed Meysam Mousavi, Laura Tupenaite, and Jurgita Antucheviciene. 2023. "An Integrated Multi-Criteria Decision Model to Select Sustainable Construction Projects under Intuitionistic Fuzzy Conditions" Buildings 13, no. 4: 848. https://doi.org/10.3390/buildings13040848
APA StyleSalimian, S., Mousavi, S. M., Tupenaite, L., & Antucheviciene, J. (2023). An Integrated Multi-Criteria Decision Model to Select Sustainable Construction Projects under Intuitionistic Fuzzy Conditions. Buildings, 13(4), 848. https://doi.org/10.3390/buildings13040848








