Effects of Geogrid Reinforcement on the Backfill of Integral Bridge Abutments
Abstract
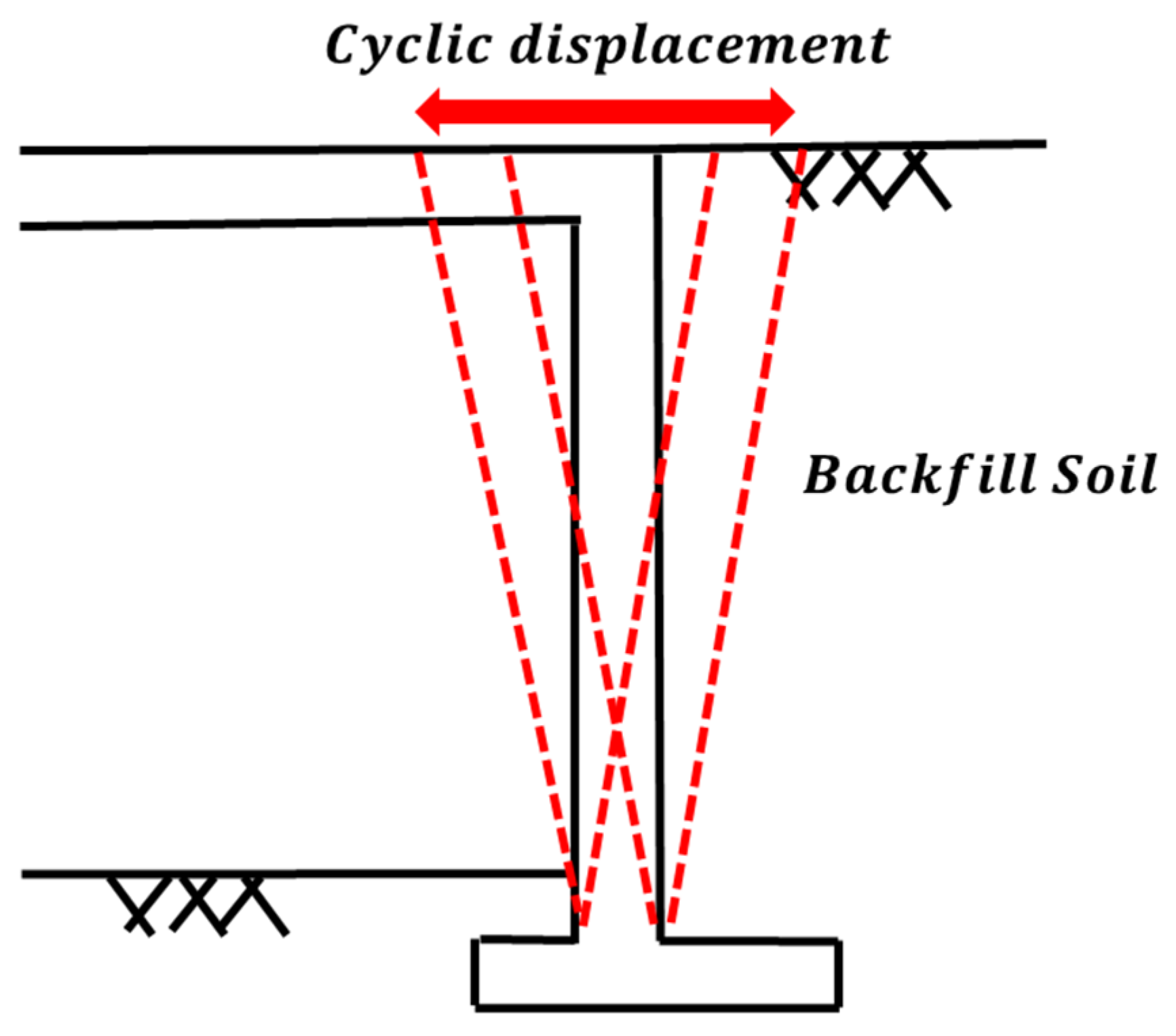
:1. Introduction
2. Equipment and Materials
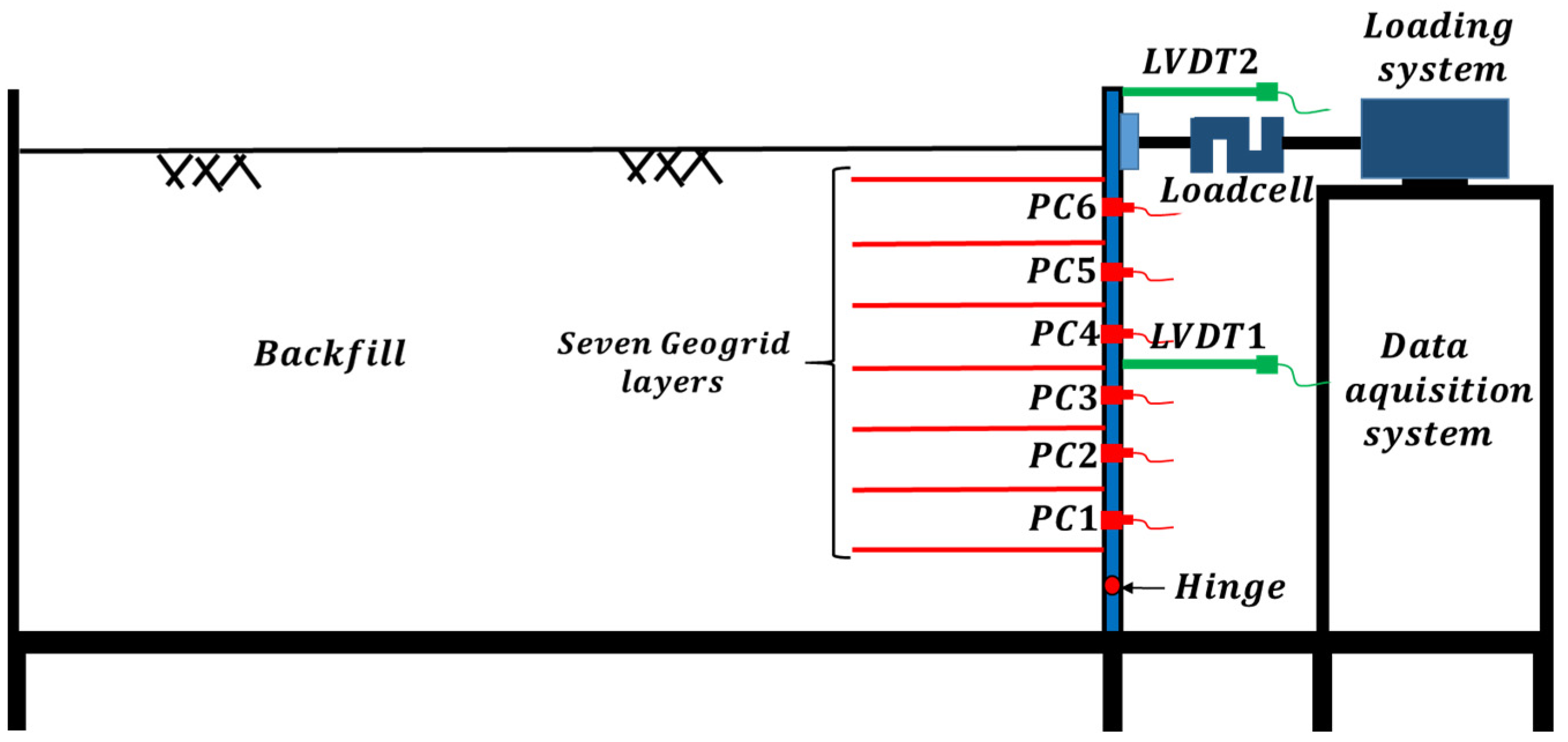
2.1. Model Box
2.2. Sand Pluviator
2.3. Instruments and Measurement
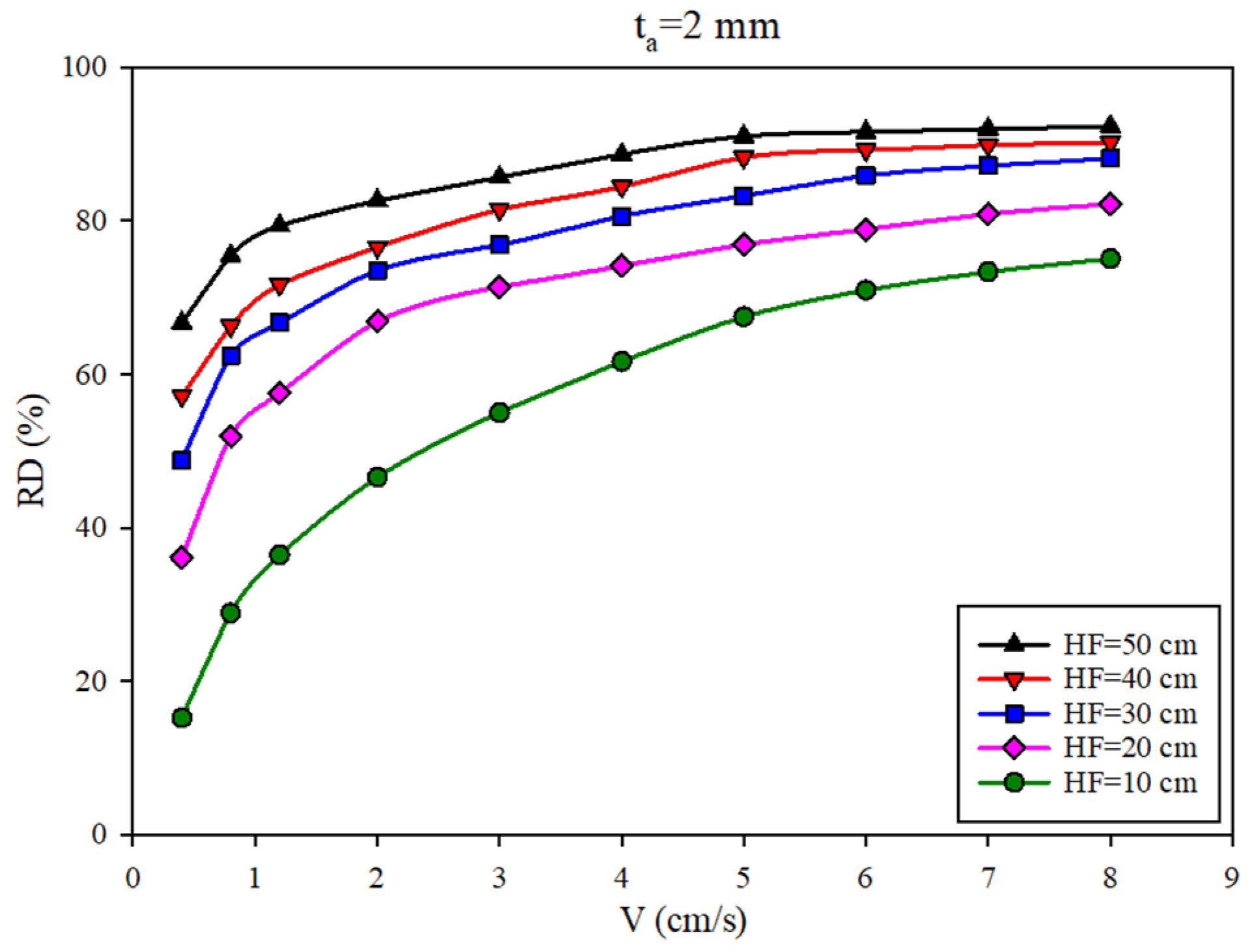
2.4. Soil
2.5. Geogrid
3. Model Similarity of Law
4. Test Program and Model Preparation
Lateral Soil Pressure Coefficients
5. Results and Discussion
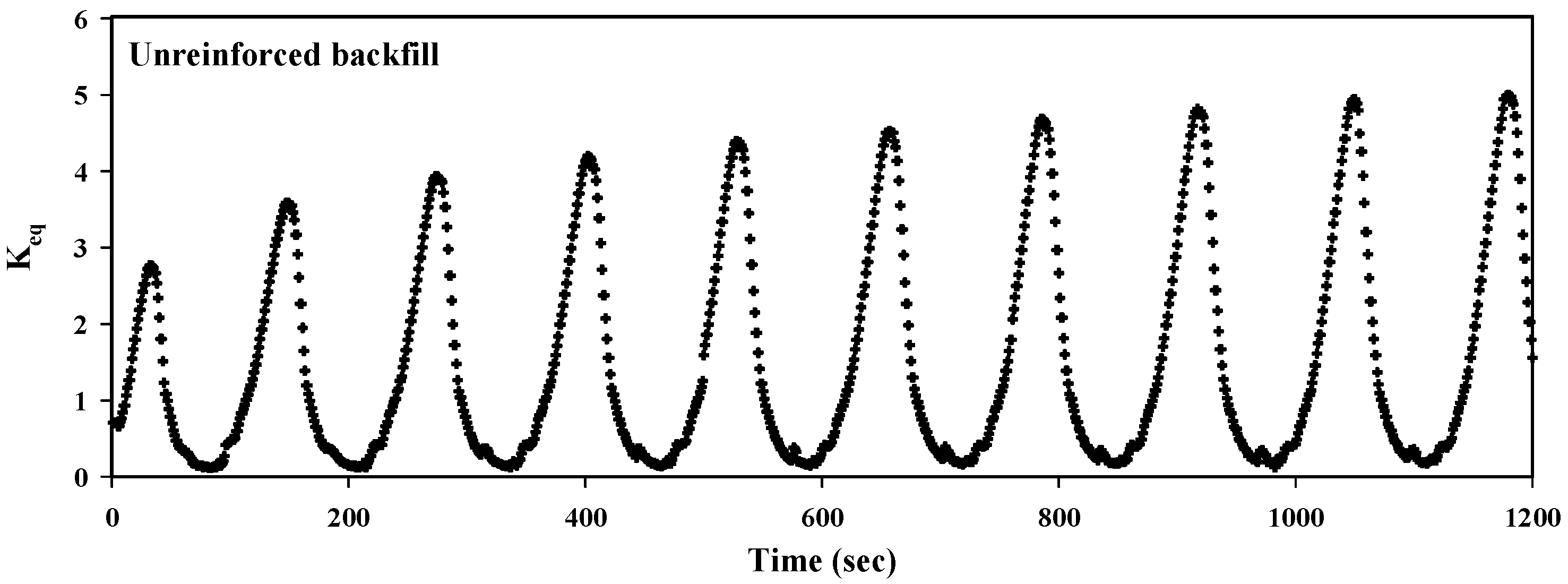
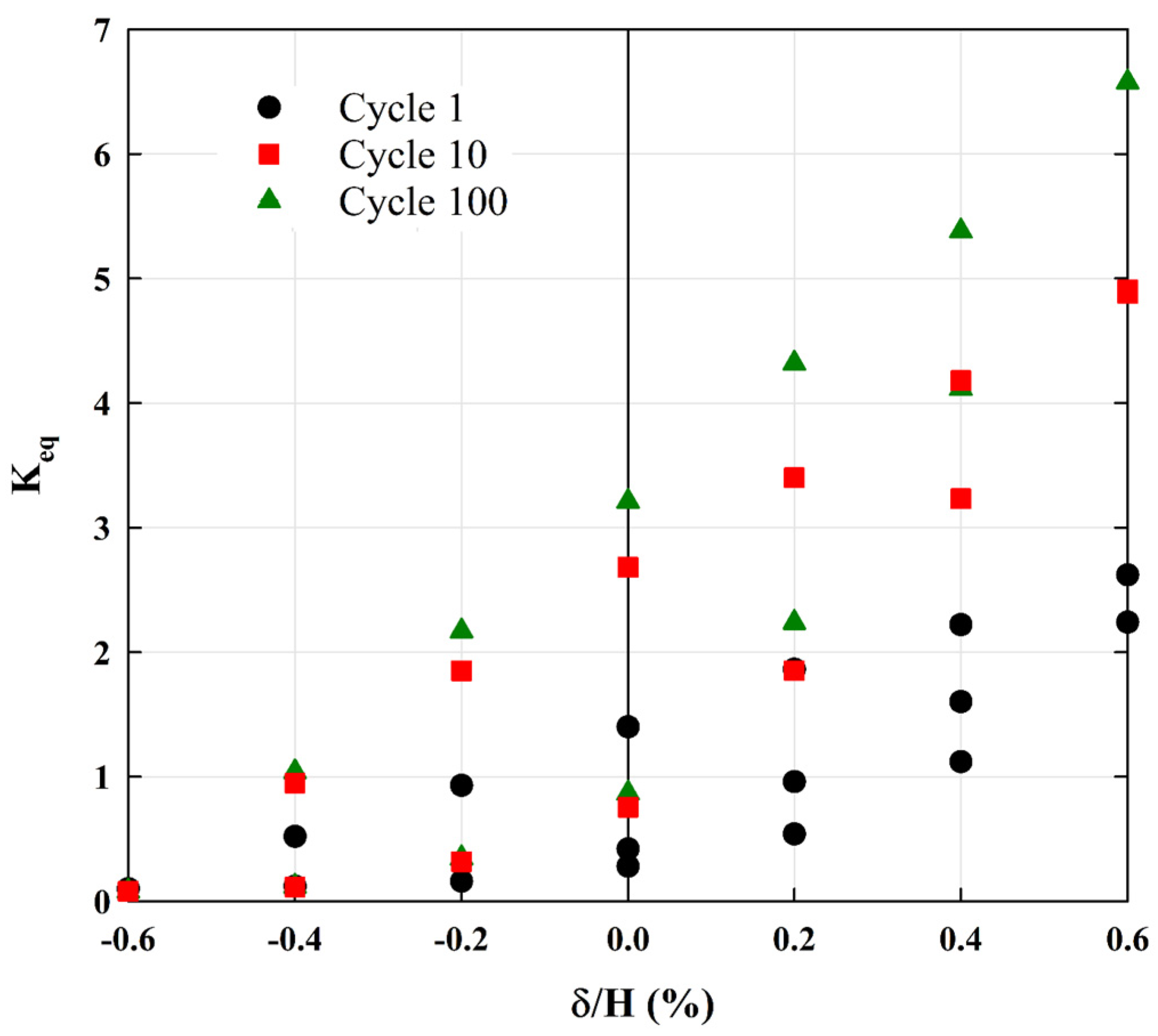
5.1. Equivalent Lateral Earth Pressure Coefficient (Keq)
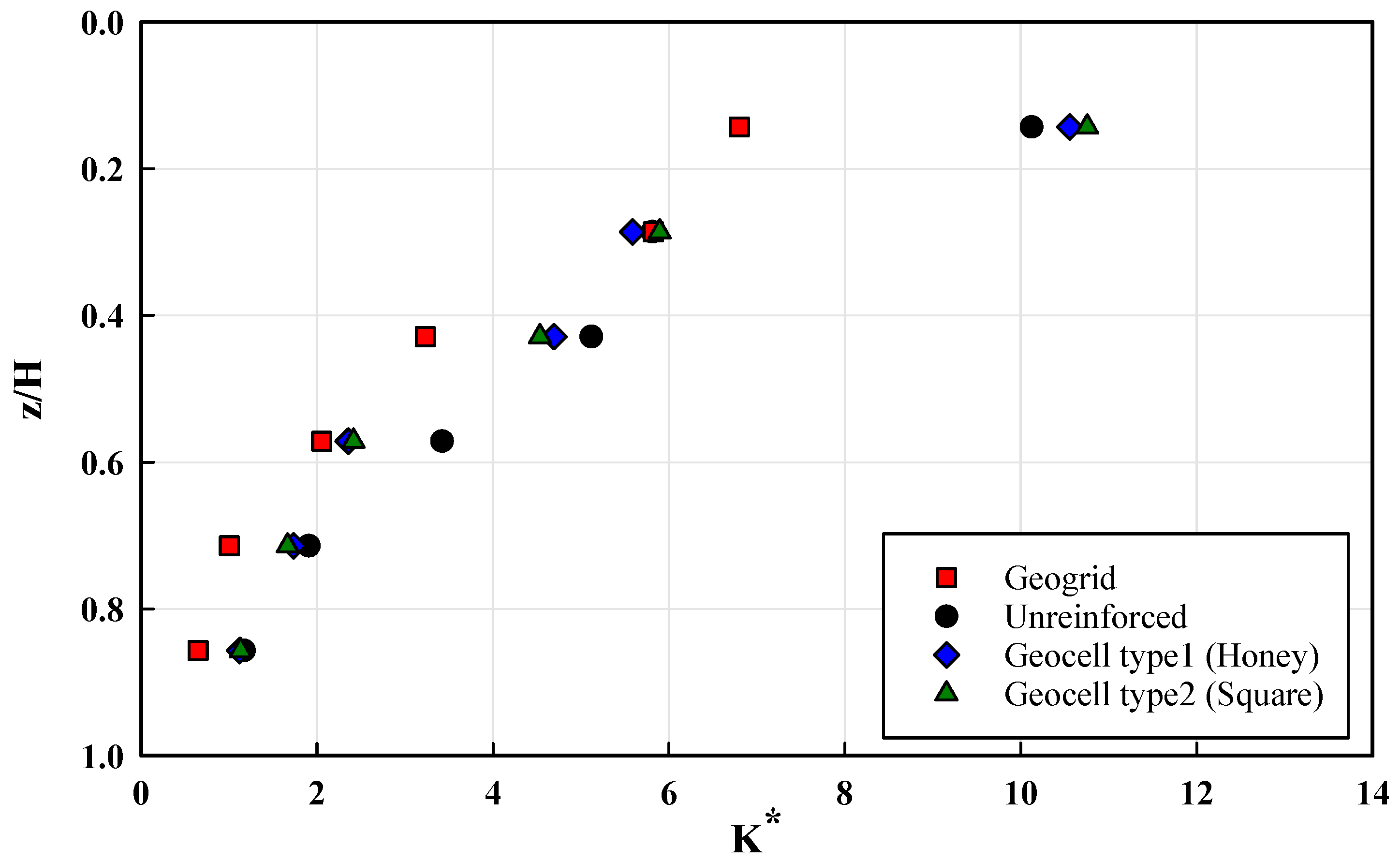
5.2. Lateral Earth Pressure Coefficient
5.3. Settlements
6. Conclusions
- Geogrid reinforcement effectively reduced the excessive pressure and settlement behind abutments, problems associated with the cyclic movements of the abutments of integral bridges.
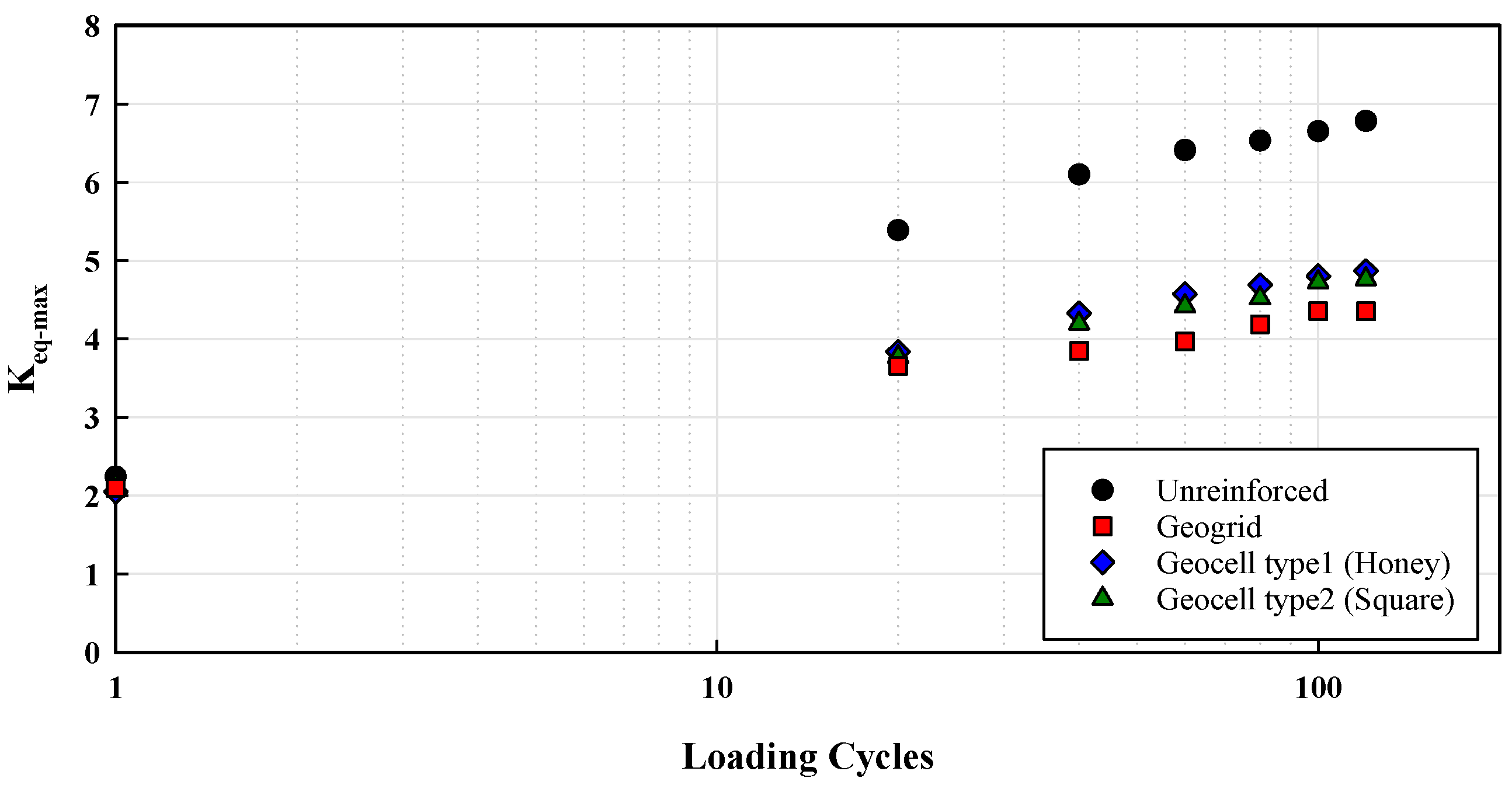
- Geogrid reinforcement reduced the maximum lateral earth pressure coefficient (Keq,max) by 36 percent compared to unreinforced backfill. This reduction in lateral earth pressure coefficient can be attributed to the mechanical interaction between the geogrid and the surrounding soil. In addition, geogrids can improve the soil’s shear strength and increase its overall stability, which further contributes to the reduction in lateral earth pressures.
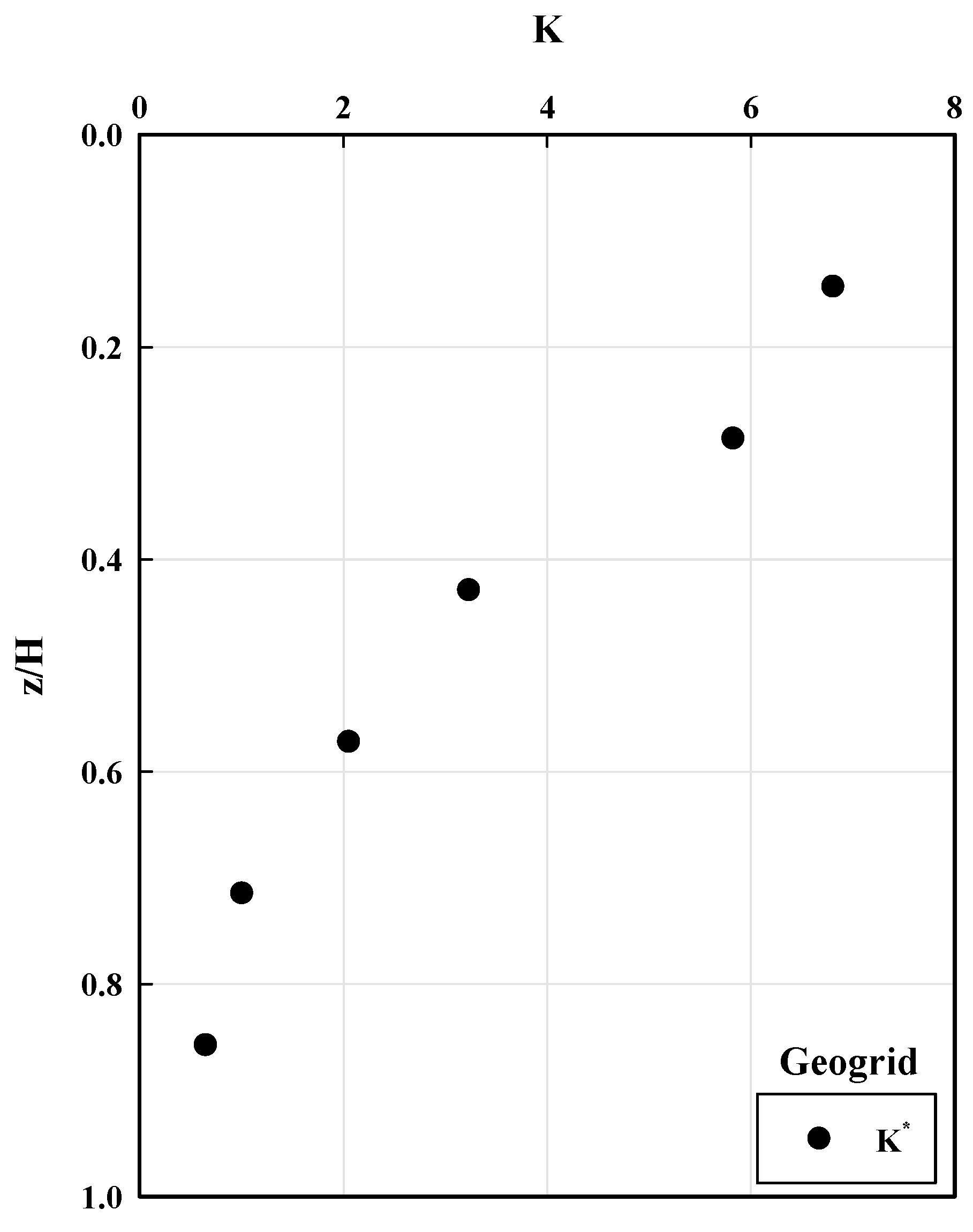
- The derived K* are larger than Keq,max at upper parts of the wall, and smaller at lower parts, suggesting the value of considering different lateral earth pressure coefficient values for design at the wall height. This difference can be attributed to the variation in wall displacement at different heights of the wall.
- Geogrid reinforcement significantly reduced the settlement behind the wall (62%) by preventing the formation of active shear zones. This reduction can be attributed to the improved mechanical interaction between the geogrid and the surrounding soil and the soil’s shear strength, which helps distribute loads and reduce stress concentrations in the soil, prevents the formation of slip lines in soil behind the wall. However, a small bump behind the reinforced zone suggests that cyclic movement is not entirely attenuated in the geogrid-reinforced zone.
- Geogrid reinforcement shows better performance than the two types of geocell. The calculated Keq,max for the geogrid-reinforced backfill test is 10% lower than the Keq, which is calculated for the geocell-reinforced backfill tests. The settlements are quite similar for geogrid- and geocell-reinforced backfill tests. Overall, the findings of this study suggest that geogrid reinforcement may be a more effective and efficient solution for retaining walls compared to geocell reinforcement. However, it is important to note that the performance of geogrid and geocell reinforcement can vary depending on various factors such as soil type, slope angle, and groundwater conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | |
| LVDT | linear variable differential transformer |
| HDPE | high-density polyethylene |
| PC | Pressure Cell |
| GRS | Geosynthetic-Reinforced Structure |
| EPS | Expanded Poly Styrene |
| Nomenclature | |
| Soil density | |
| g | Gravity acceleration |
| Elastic modulus of soil | |
| Poisson’s ratio of soil | |
| Internal friction angle of soil (degrees) | |
| H | Height of soil behind the wall |
| D | Distance between two geogrid layers |
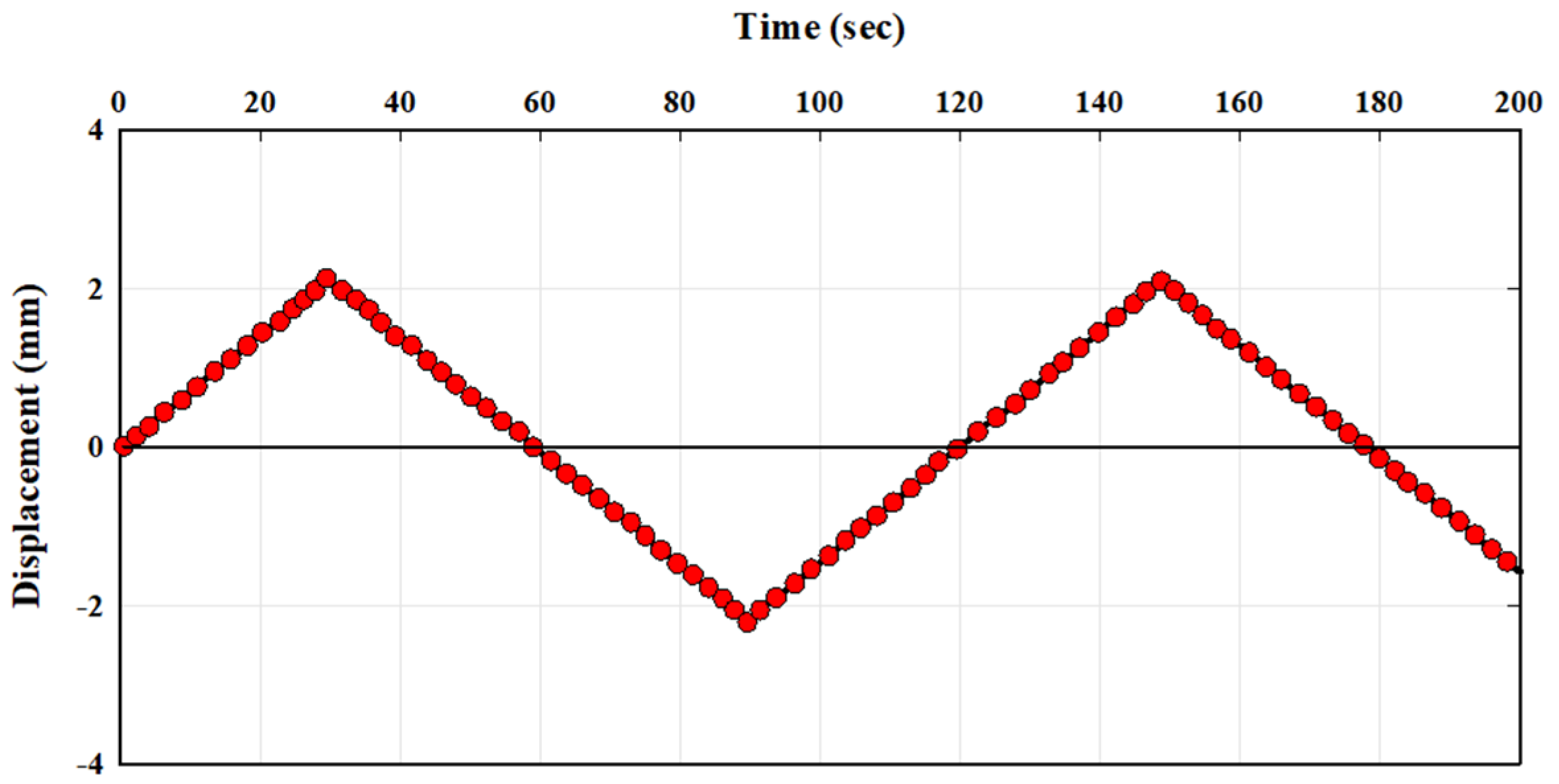
| Wall displacement at its top during one cycle | |
| Length of geogrid | |
| Tensile strength of geocell material (kN/m) | |
| Dimensionless factors | |
| RD | Relative Density (%) |
| Cc | Coefficient of curvature |
| Cu | Coefficient of uniformity |
| emax | Maximum void ratio |
| emin | Minimum void ratio |
| Gs | The specific gravity of soil |
| Maximum lateral pressure measured by a pressure cell | |
| Initial vertical stress | |
| Initial horizontal stress | |
| Lateral soil coefficient (calculated by dividing maximum lateralpressure cell to initial vertical stress) | |
| eq | Lateral soil coefficient (calculated by load cell force) |
| Lateral force measured by the load cell | |
| Soil moist unit weight (KN/m3) | |
| Keq,max | Maximum lateral soil coefficient in all cycles |
| z | Distance from the surface |
| x | Distance from the wall |
References
- Karakouzian, M.; Farhangi, V.; Farani, M.R.; Joshaghani, A.; Zadehmohamad, M.; Ahmadzadeh, M. Mechanical Characteristics of Cement Paste in the Presence of Carbon Nanotubes and Silica Oxide Nanoparticles: An Experimental Study. Materials 2021, 14, 1347. [Google Scholar] [PubMed]
- Zadehmohamad, M.; Moradi, M.; Ghalandarzadeh, A. Seismic behavior of pile group in soil slope. engrXiv 2021. [Google Scholar] [CrossRef]
- Zadehmohamad, M.; Moradi, M.; Ghalandarzadeh, A. The effect of pile group location in slope on its seismic behavior. engrXiv 2021. [Google Scholar] [CrossRef]
- Zadehmohamad, M.; Luo, N.; Abu-Farsakh, M.; Voyiadjis, G. Evaluating long-term benefits of geosynthetics in flexible pavements built over weak subgrades by finite element and Mechanistic-Empirical analyses. Geotext. Geomembr. 2022, 50, 455–469. [Google Scholar]
- Abu-Farsakh, M.; Zadehmohamad, M.; Voyiadjis, G.Z. Incorporating the Benefits of Geosynthetic into MEPDG. Infrastructures 2023, 8, 35. [Google Scholar] [CrossRef]
- Momeni, E.; Poormoosavian, M.; Salmani Tehrani, H.; Fakher, A. Reliability analysis and risk assessment of deep excavations using random-set finite element method and event tree technique. Transp. Geotech. 2021, 29, 100560. [Google Scholar] [CrossRef]
- Krier, D. Modeling of Integral Abutment Bridges Considering Soil-Structure Interaction Effects; The University of Oklahoma: Norman, OK, USA, 2009. [Google Scholar]
- Wallbank, E. The Performance of Concrete in Bridges. A Survey of 200 Highway Bridges; National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1989. [Google Scholar]
- Wolde-Tinsae, A.M.; Klinger, J.E. Integral Abutment Bridge Design and Construction; National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1987. [Google Scholar]
- Cosgrove, E.F.; Lehane, B.M. Cyclic loading of loose backfill placed adjacent to integral bridge abutments. Int. J. Phys. Model. Geotech. 2003, 3, 9–16. [Google Scholar]
- Horvath, J.S. Integral-Abutment Bridges: Problems and Innovative Solutions Using EPS Geofoam and Other Geosynthetics; Res. Rpt. No. CE/GE-00, 2; Manhattan College: Bronx, NY, USA, 2000. [Google Scholar]
- Zadehmohamad, M. Evaluation of Cyclic Displacement Amplitude of Integral Bridge Abutment on Backfill Soil Pressure and Settlements. J. Transp. Res. 2020. Available online: http://www.trijournal.ir/article_119193.html?lang=en (accessed on 5 March 2022).
- Khodair, Y.; Hassiotis, S. Numerical and experimental analyses of an integral bridge. Int. J. Adv. Struct. Eng. 2013, 5, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Fiorentino, G.; Cengiz, C.; De Luca, F.; Mylonakis, G.; Karamitros, D.; Dietz, M.; Dihoru, L.; Lavorato, D.; Briseghella, B.; Isakovic, T. Integral abutment bridges: Investigation of seismic soil-structure interaction effects by shaking table testing. Earthq. Eng. Struct. Dyn. 2021, 50, 1517–1538. [Google Scholar]
- Hirakawa, D.; Nojiri, M.; Aizawa, H.; Nishikiori, H.; Tatsuoka, F.; Watanabe, K.; Tateyama, M. Effects of the tensile resistance of reinforcement in the backfill on seismic stability of GRS integral bridge. New Horiz. Earth Reinf. 2007, 811–817. [Google Scholar]
- Mitoulis, S.A. Challenges and opportunities for the application of integral abutment bridges in earthquake-prone areas: A review. Soil Dyn. Earthq. Eng. 2020, 135, 106183. [Google Scholar]
- Kawabe, S.; Kikuchi, Y.; Watanabe, K.; Tatsuoka, F. Model tests on the stability of GRS integral bridge against tsunami load. Jpn. Geotech. Soc. Spec. Publ. 2016, 2, 2313–2318. [Google Scholar] [CrossRef] [Green Version]
- Tatsuoka, F.; Tateyama, M.; Koda, M.; Kojima, K.-I.; Yonezawa, T.; Shindo, Y.; Tamai, S.-I. Research and construction of geosynthetic-reinforced soil integral bridges. Transp. Geotech. 2016, 8, 4–25. [Google Scholar]
- Wasserman, E.P.; Walker, J.H. Integral Abutments for Steel Bridges; National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1996. [Google Scholar]
- Al-Qarawi, A.; Leo, C.; Liyanapathirana, D. Effects of wall movements on performance of integral abutment bridges. Int. J. Geomech. 2020, 20, 04019157. [Google Scholar]
- Arsoy, S.; Barker, R.M.; Duncan, J.M. The Behavior of Integral Abutment Bridges; Virginia Transportation Research Council: Charlottesville, VA, USA, 1999. [Google Scholar]
- LaFave, J.M.; Brambila, G.; Kode, U.; Liu, G.; Fahnestock, L.A. Field Behavior of Integral Abutment Bridges under Thermal Loading. J. Bridge Eng. 2021, 26, 04021013. [Google Scholar] [CrossRef]
- Huang, F.; Shan, Y.; Chen, G.; Lin, Y.; Tabatabai, H.; Briseghella, B. Experiment on Interaction of Abutment, Steel H-Pile and Soil in Integral Abutment Jonitless Bridges (IAJBs) under Low-Cycle Pseudo-Static Displacement Loads. Appl. Sci. 2020, 10, 1358. [Google Scholar] [CrossRef] [Green Version]
- Perić, D.; Miletić, M.; Shah, B.R.; Esmaeily, A.; Wang, H. Thermally induced soil structure interaction in the existing integral bridge. Eng. Struct. 2016, 106, 484–494. [Google Scholar]
- England, G.; Tsang, N. Towards the Design of Soil Loading for Integral Bridges-Experimental Evaluation; Department of Civil and Environmental Engineering, Imperial College: London, UK, 2001. [Google Scholar]
- Tatsuoka, F.; Hirakawa, D.; Nojiri, M.; Aizawa, H.; Nishikiori, H.; Soma, R.; Tateyama, M.; Watanabe, K. A new type of integral bridge comprising geosynthetic-reinforced soil walls. Geosynth. Int. 2009, 16, 301–326. [Google Scholar]
- Liu, H.; Han, J.; Parsons, R.L. Reduction of lateral earth pressures behind retaining walls using EPS and geosynthetic reinforcement. In Proceedings of the Geosynthetics Conference 2021, Kansas City, MO, USA, 5–8 February 2021; pp. 561–569. [Google Scholar]
- Liu, H.; Han, J.; Parsons, R.L. Mitigation of seasonal temperature change-induced problems with integral bridge abutments using EPS foam and geogrid. Geotext. Geomembr. 2021, 49, 1380–1392. [Google Scholar]
- Xie, M.; Zheng, J.; Shao, A.; Miao, C.; Zhang, J. Study of lateral earth pressures on nonyielding retaining walls with deformable geofoam inclusions. Geotext. Geomembr. 2020, 49, 684–690. [Google Scholar]
- Kim, H.; Witthoeft, A.F.; Kim, D. Numerical study of earth pressure reduction on rigid walls using EPS geofoam inclusions. Geosynth. Int. 2018, 25, 180–199. [Google Scholar]
- Hazarika, H.; Kohama, E.; Sugano, T. Underwater shake table tests on waterfront structures protected with tire chips cushion. J. Geotech. Geoenviron. Eng. 2008, 134, 1706–1719. [Google Scholar]
- Horvath, J.S. Lateral pressure reduction on earth-retaining structures using geofoams: Correcting some misunderstandings. In Proceedings of the Earth Retention Conference 3; ASCE: Reston, VA, USA, 2010; pp. 862–869. [Google Scholar]
- Horvath, J.S. Geofoam compressible inclusions: The new frontier in earth retaining structures. In Geotechnical Engineering for Transportation Projects; ASCE: Reston, VA, USA, 2004; pp. 1925–1934. [Google Scholar]
- Horvath, J.S. The compressible inclusion function of EPS geofoam. Geotext. Geomembr. 1997, 15, 77–120. [Google Scholar] [CrossRef]
- Tweedie, J.; Humphrey, D.; Sandford, T. Tire shreds as lightweight retaining wall backfill: Active conditions. J. Geotech. Geoenviron. Eng. 1998, 124, 1061–1070. [Google Scholar]
- Carder, D.; Card, G. Innovative Structural Backfills to Integral Bridge Abutments; TRL REPORT NO. 290; Transport Research Laboratory: Crawthorne, UK, 1997. [Google Scholar]
- Lutenegger, A.J.; Ciufetti, M. Full-Scale Pilot Study to Reduce Lateral Stresses in Retaining Structures Using Geofoam; Final Report, Project No. RSCH010-983 Vermont DOT; University of Massachusetts: Amherst, MA, USA, 2009. [Google Scholar]
- Hoppe, E.J. Field Study of Integral Backwall with Elastic Inclusion; Virginia Transportation Research Council: Charlottesville, VA, USA, 2005. [Google Scholar]
- Cecich, V.; Gonzales, L.; Hoisaeter, A.; Williams, J.; Reddy, K. Use of shredded tires as lightweight backfill material for retaining structures. Waste Manag. Res. 1996, 14, 433–451. [Google Scholar] [CrossRef]
- Lee, H.J.; Roh, H.S. The use of recycled tire chips to minimize dynamic earth pressure during compaction of backfill. Constr. Build. Mater. 2007, 21, 1016–1026. [Google Scholar]
- Zadehmohamad, M.; Bazaz, J.B.; Riahipour, R.; Farhangi, V. Physical modelling of the longterm behavior of integral abutment bridge backfill reinforced with tire-rubber. Int. J. Geo-Eng. 2021, 12, 1–19. [Google Scholar]
- Yonezawa, T.; Yamazaki, T.; Tateyama, M.; Tatsuoka, F. Design and construction of geosynthetic-reinforced soil structures for Hokkaido high-speed train line. Transp. Geotech. 2014, 1, 3–20. [Google Scholar]
- Munoz, H.; Tatsuoka, F.; Hirakawa, D.; Nishikiori, H.; Soma, R.; Tateyama, M.; Watanabe, K. Dynamic stability of geosynthetic-reinforced soil integral bridge. Geosynth. Int. 2012, 19, 11–38. [Google Scholar] [CrossRef]
- Zadehmohamad, M.; Bazaz, J.B. Cyclic behaviour of geocell-reinforced backfill behind integral bridge abutment. Int. J. Geotech. Eng. 2017, 13, 438–450. [Google Scholar] [CrossRef]
- Bolouri Bazaz, J.; Zadehmohamad, M.; Hashemi, S.S. Developing a Portable Curtain Sand Pluviator for Reconstitution of Soil Models. Modares Civ. Eng. J. 2018, 18, 231–242. [Google Scholar]
- Lehane, B. Lateral soil stiffness adjacent to deep integral bridge abutments. Géotechnique 2011, 61, 593–603. [Google Scholar] [CrossRef]








| Sand | D10 (mm) | D30 (mm) | D60 (mm) | Cu | Cc | emax | emin | Gs |
|---|---|---|---|---|---|---|---|---|
| Firuzkooh NO.161 | 0.16 | 0.21 | 0.28 | 1.87 | 0.88 | 0.943 | 0.548 | 2.65 |
| Geogrid Material | Prototype | Model (kN/m) |
|---|---|---|
| Tensile Strength (T) | 52 (kN/m) | 1.02 (kN/m) |
| Height of wall (H) | 5 m | 0.7 |
| 15.93 (kN/m3) | 15.93 (kN/m3) | |
| 0.13 | 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhangi, V.; Zadehmohamad, M.; Monshizadegan, A.; Izadifar, M.; Moradi, M.J.; Dabiri, H. Effects of Geogrid Reinforcement on the Backfill of Integral Bridge Abutments. Buildings 2023, 13, 853. https://doi.org/10.3390/buildings13040853
Farhangi V, Zadehmohamad M, Monshizadegan A, Izadifar M, Moradi MJ, Dabiri H. Effects of Geogrid Reinforcement on the Backfill of Integral Bridge Abutments. Buildings. 2023; 13(4):853. https://doi.org/10.3390/buildings13040853
Chicago/Turabian StyleFarhangi, Visar, Mehdi Zadehmohamad, Armaghan Monshizadegan, MohammadAli Izadifar, Mohammad Javad Moradi, and Hamed Dabiri. 2023. "Effects of Geogrid Reinforcement on the Backfill of Integral Bridge Abutments" Buildings 13, no. 4: 853. https://doi.org/10.3390/buildings13040853
APA StyleFarhangi, V., Zadehmohamad, M., Monshizadegan, A., Izadifar, M., Moradi, M. J., & Dabiri, H. (2023). Effects of Geogrid Reinforcement on the Backfill of Integral Bridge Abutments. Buildings, 13(4), 853. https://doi.org/10.3390/buildings13040853






