Stress–Strain Model of High-Strength Concrete Confined by Lateral Ties under Axial Compression

Abstract

High-strength concrete can effectively reduce the cross-sectional size, increase space usage, and cut material costs. To analyze the mechanical properties of high-strength concrete vertical members, various confinement models have been proposed to define the ties-confined concrete stress–strain relationship. However, most existing models are divided into ascending and descending segments. These are continuous but not derivable at the peak point, which does not facilitate numerical calculations. Moreover, these models have a large number of parameters that are mostly obtained based on the fitting of experimental data, which may also lead to the limited applicability of the models. In this study, existing confinement models for high-strength concrete under axial compression are reviewed, and the differences between the models are discussed. Based on the results of normal triaxial experiments on high-strength concrete and the test data from other studies on ties-confined concrete columns, the effective confinement coefficient and empirical formula of ties strain at the peak stress of confined concrete are proposed. A confinement model is proposed based on the continuous derivable function, and it is validated based on the available experimental data. Results show that the proposed model can reflect the stress–strain relationship of the test specimens more simply while keeping the basic accuracy with other models.

1. Introduction

Concrete is a widely used building material, and the application of high-strength concrete is gradually on the rise. When high-strength concrete is used for vertical members of high-rise structures, it can effectively reduce the cross-sectional size, increase space usage, and cut material costs. Ties-confined concrete is the most widely used form in engineering practice. To analyze the mechanical properties of high-strength concrete vertical members, the ties-confined concrete stress–strain relationship is considered.

In 1903, Considere [1] first proposed that the use of spiral bars could effectively confine the axially compressed column; since then, the research on confined concrete has spanned a century. In the 1920s, Richart et al. [2] quantitatively studied the mechanical properties of confined normal-strength concrete and established the classical Richart formula. Subsequently, the different influencing parameters (e.g., strength, number and form of ties, cross-sectional form, number of longitudinal bars, loading rate) for confined normal-strength concrete have been considered, and different stress–strain models for confined normal-strength concrete have been established empirically. With the increased application of high-strength concrete, the models based on normal-strength concrete are no longer applicable, owing to the fact that these models overestimate the descending section curve. Ahmad and Shah [3] first developed a stress–strain model for confined high-strength concrete based on experimental results, where the cylindrical concrete strength was up to 69 MPa. Martinez [4] and Fafitis [5] also proposed corresponding models with maximum strengths of 69 MPa and 62 MPa, respectively, for cylindrical concrete. With the sustainable development of concrete technology, higher-strength concrete has been gradually used in practical projects; for example, the maximum compressive strengths of Two Union Square (1989) in Seattle and 311 South Wacker (1990) column in Chicago were 131 MPa and 83 MPa, respectively. To promote the application of higher concrete strengths, Yong et al. [6], Muguruma et al. [7], Nagashima et al. [8], Cusson et al. [9], EI-Dash et al. [10], Han et al. [11], and Shi et al. [12] developed models based on experimental results applicable to square columns; Bjerkli et al. [13], Mander et al. [14], Li et al. [15], and Umesh et al. [16] proposed models based on experimental results applicable to both circular and square columns. Suzuki et al. [17] found that ties generally may not yield using high-strength concrete or ties and proposed a method to compute the ties stress at maximum concrete strength. Chung et al. [18] and Van et al. [19] proposed an empirical formula for ties stress based on the regression of experimental results. To develop a more general stress–strain model for confined concrete, Razvi et al. [20] and Légeron et al. [21] developed a confinement model applicable to both normal-strength and high-strength concrete based on their experimental results and those of other scholars. To provide more accurate stress–strain relationships for confined concrete, Montoya et al. [22] investigated the three-dimensional behavior of confined concrete and proposed a new set of constitutive material models for concrete in confined compression. Koksal et al. [23] introduced the concept of least confined volume in the damage localization zone at the middle of the concrete core to determine the confinement stress distribution of lateral ties and developed a stress–strain model of high-strength concrete for tied square columns.

However, most existing models [6,7,8,9,11,12,13,14,15,17,18,19,20,21] are continuous at the peak but not derivable, and they have a large number of correction parameters, which may not be convenient for numerical calculations and engineering applications. The purpose of this paper is to establish a stress–strain model for convenient numerical calculation. To this end, this study first reviews existing models for axial compressive stress–strain in ties-confined high-strength concrete and discusses the differences between existing models. Then, based on the test data of the normal triaxial compression of high-strength concrete and axial compression of ties-confined concrete columns obtained from other studies, a new stress–strain model for ties-confined high-strength concrete is proposed that would serve as a reference for the application and development of high-strength concrete in which the applicable ranges for concrete and ties are 60–115 MPa and 400–1387 MPa, respectively.

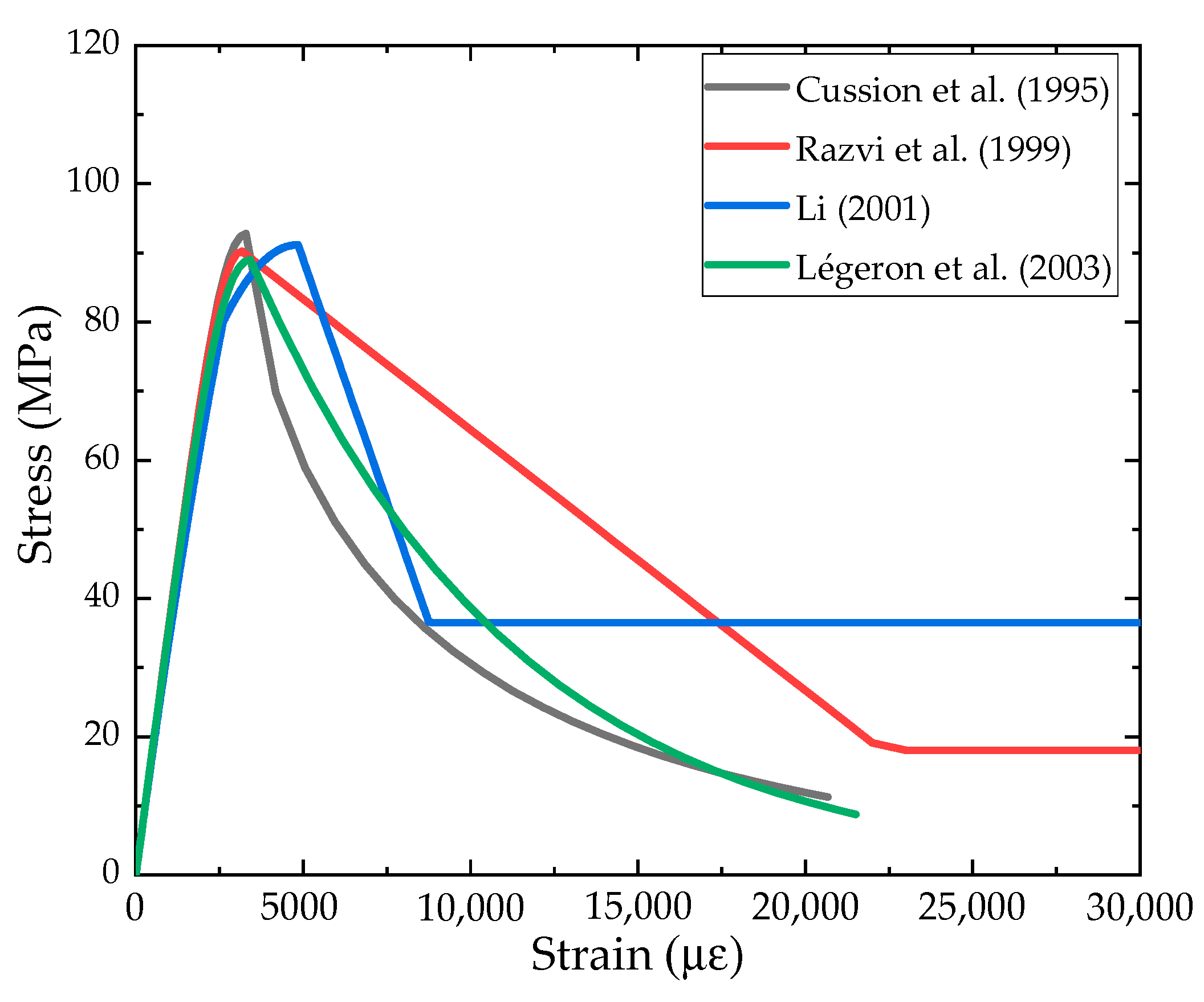
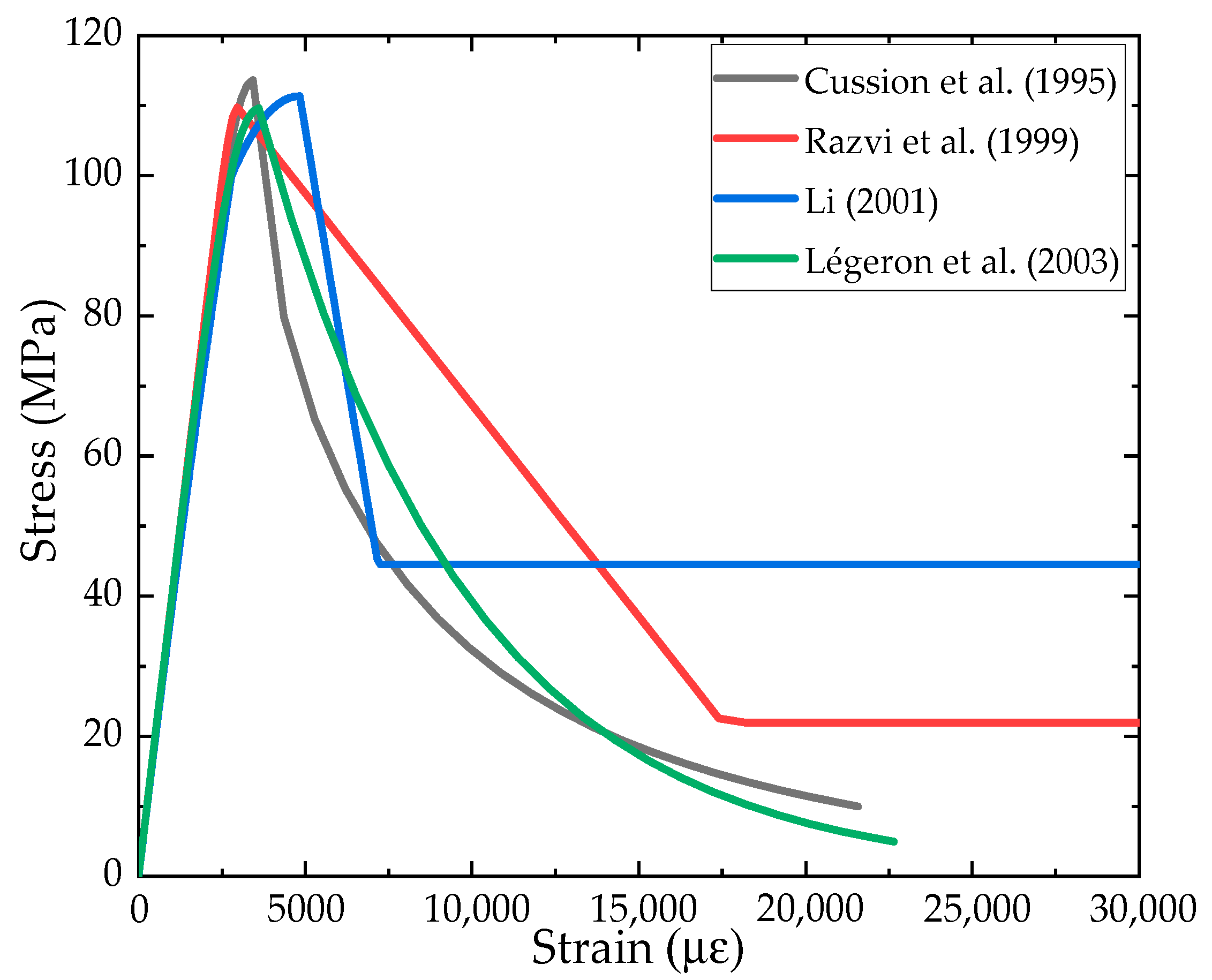
2. Existing Models

There are currently many ties-confined high-strength concrete stress–strain models. The range of application of concrete strength varies per study, for example, 84–94 MPa for Yong et al. [6], 20–160 MPa for Muguruma et al. [7], 60–118 MPa for Nagashima et al. [8], 52–118 MPa for Cussion et al. [9], 45–90 MPa for Bjerkli et al. [13], 30–130 MPa for Razvi et al. [20], and 20–140 MPa for Légeron et al. [21]. Currently, Cussion’s, Razvi’s, Li’s, and Légeron’s models are mostly used, as shown in Table 1.

Table 1. Ties-confined high-strength axial compressive stress–strain models.

Proposed by	Complete Curve Equation	Model Parameters
Cussion et al. [9] (1995)	$\left(1\right)0\le \epsilon \le {\epsilon }_{\mathit{cc}}$ ${\sigma =f}_{\mathit{cc}}\frac{k\left({\epsilon /\epsilon }_{\mathit{cc}}\right)}{k-1+{({\epsilon /\epsilon }_{\mathit{cc}})}^k}$ $\left(2\right){\epsilon }_{\mathit{cc}}\le \epsilon$ ${\sigma =f}_{\mathit{cc}}\mathit{exp}{[k_1({\epsilon /\epsilon }_{\mathit{cc}})]}^{k_2}$	$f_l{=f}_{\mathit{yv}}({\displaystyle \sum _{i=1}^o{A}_{\mathit{sbi}}}+{\displaystyle \sum _{i=1}^p{A}_{\mathit{sbi}}})/[s(b_c{+h}_c)]$$;{k=E}_c/(E_c-f_{\mathit{cc}}{/\epsilon }_{\mathit{cc}})$ $k_{e,\mathit{mander}}=[1-{\displaystyle \sum _{i=1}^n{\omega }_i^2/(6}{b}_c{h}_c)][1-(s^{\prime }/2b_c)][1-(s^{\prime }/2h_c)]/(1{-\rho }_{\mathit{cc}})$ $f_{\mathit{le}}{=k}_{e,\mathit{mander}}{f}_l$$;f_{\mathit{cc}}{/f}_c=1+2.1{(f_{\mathit{le}}{/f}_c)}^{0.7}$$;{\epsilon }_{\mathit{cc}}/{\epsilon }_c=1+0.21{(f_{\mathit{le}}{/f}_c)}^{1.7}$ $\mathrm{If}\mathrm{no}\mathrm{test}\mathrm{data}\mathrm{is}\mathrm{available},{\epsilon }_{c50}$$\mathrm{takes}0.004;{\epsilon }_{\mathit{cc}50}={\epsilon }_{c50}+0.15{(f_{\mathit{le}}{/f}_c)}^{1.1}$ $k_1=\mathit{ln}(0.5)/{({\epsilon }_{\mathit{cc}50}{-\epsilon }_{\mathit{cc}})}^{k_2}$$;k_2=0.58+16{(f_{\mathit{le}}{/f}_c)}^{1.4}$
Razvi et al. [20] (1999)	$\left(1\right)0\le \epsilon \le {\epsilon }_{\mathit{cc}}$ Same as the ascending portion of the Cussion model. $\left(2\right){\epsilon }_{\mathit{cc}}\le \epsilon \le {\epsilon }_{\mathit{cc}20}$ ${\sigma =f}_{\mathit{cc}}[1-0.15({\epsilon /\epsilon }_{\mathit{cc}})/({\epsilon }_{c85}{-\epsilon }_{\mathit{cc}})]$ $\left(3\right){\epsilon }_{\mathit{cc}20}\le \epsilon$$\sigma =0.2f_{\mathit{cc}}$	$m_1=6.7{(f_{\mathit{le}})}^{0.17}$$;m_2=0.15\sqrt{(b_c/s)(h_c{/s}_l)}$$;m_3=40{/f}_c\le 1.0$ $m_4{=f}_{\mathit{ys}}/500\ge 1.0$$;f_{\mathit{cc}}{=f}_c+0.5m_1{\rho }_{\mathit{sv}}{f}_{\mathit{ys}}$$;{\epsilon }_c=0.0028-0.008m_3$ ${\epsilon }_{c85}{=\epsilon }_c+0.0018m_3^2$$;{\epsilon }_{\mathit{cc}}{/\epsilon }_c=1+5m_1{m}_3{f}_{\mathit{le}}{/f}_c$ ${\epsilon }_{\mathit{cc}85}=260m_3{\rho }_c{\epsilon }_{\mathit{cc}}[1+0.5m_2(m_4-1)]{+\epsilon }_{c85}$ $E_c=3320\sqrt{f_c}+6900$ $f_{\mathit{ys}}$$,{\rho }_c$ Calculation formulae are shown in Table 2
Li et al. [15] (2001)	$\left(1\right)0\le \epsilon \le {\epsilon }_c$ ${\sigma =E}_c\epsilon +\frac{\left(f_c{-E}_c{\epsilon }_c\right)\epsilon }{{\epsilon }_c^2}$ $\left(2\right){\epsilon }_c\le \epsilon \le {\epsilon }_{\mathit{cc}}$ ${\sigma =f}_{\mathit{cc}}-\frac{(f_{\mathit{cc}}{-f}_c\left)\right(\epsilon -{\epsilon }_{\mathit{cc}}{)}^2}{{({\epsilon }_{\mathit{cc}}-{\epsilon }_c)}^2}$ $\left(3\right){\epsilon }_{\mathit{cc}}\le \epsilon$ ${\sigma =f}_{\mathit{cc}}-\beta \frac{f_{\mathit{cc}}\left({\epsilon -\epsilon }_{\mathit{cc}}\right)}{{\epsilon }_{\mathit{cc}}}\ge 0.4f_{\mathit{cc}}$	$f_{\mathit{le}}$$,k_{e,\mathit{mander}}$$\mathrm{are}\mathrm{the}\mathrm{same}\mathrm{as}\mathrm{the}\mathrm{Cussion}\mathrm{model};E_c=3320\sqrt{f_c}+6900$ $f_{\mathit{cc}}{=f}_c(-0.413+1.413\sqrt{1+11.4f_{\mathit{le}}{/f}_c}-2f_{\mathit{le}}{/f}_c)$ (For high-strength concrete) ${\epsilon }_{\mathit{cc}}/{\epsilon }_c=1+11.3f_{\mathit{le}}{/f}_c{)}^{0.7}$$(f_{\mathit{yv}}\le 550$$\mathrm{MPa});{\epsilon }_c=0.0007{(f_c)}^{0.3}$ $\beta =(0.048f_c-2.14)-(0.098f_c-4.57\left)\right(f_{\mathit{le}}{/f}_c{)}^{1/3}$$(f_{\mathit{yv}}\le 550$$\mathrm{MPa}\mathrm{and}{f}_c>75$ MPa)
Légeron et al. [21] (2003)	$\left(1\right)0\le \epsilon \le {\epsilon }_c$ Similar to the ascending portion of the Cussion model. $\left(2\right){\epsilon }_{\mathit{cc}}\le \epsilon$ Same as the descending portion of the Cussion model.	${\rho }_{\mathit{sey}}$, $\kappa$ Calculation formulae are shown in Table 2 $k_{e,\mathit{mander}}$$\mathrm{is}\mathrm{similar}\mathrm{to}\mathrm{the}\mathrm{Cussion}\mathrm{model};{\epsilon }_c=0.0005{(f_c)}^{0.4}$ $I_e^{\prime }{=f}_{\mathit{le}}{/f}_c$$;I_{e50}{=\rho }_{\mathit{sey}}{f}_{\mathit{ys}}{/f}_c$$;f_{\mathit{cc}}{/f}_c=1+2.4{(I_e^{\prime })}^{0.7}$ ${\epsilon }_{\mathit{cc}}{/\epsilon }_c=1+35({I^{\prime }}_e{)}^{1.2}$$;{\epsilon }_{\mathit{cc}50}{/\epsilon }_{c50}=1+60I_{e50}$ $k_1$$\mathrm{is}\mathrm{the}\mathrm{same}\mathrm{as}\mathrm{the}\mathrm{Cussion}\mathrm{model};k_2=1+25(I_{e50}{)}^2$

Table 1. Ties-confined high-strength axial compressive stress–strain models.

Proposed by	Complete Curve Equation	Model Parameters
Cussion et al. [9] (1995)	$\left(1\right)0\le \epsilon \le {\epsilon }_{\mathit{cc}}$ ${\sigma =f}_{\mathit{cc}}\frac{k\left({\epsilon /\epsilon }_{\mathit{cc}}\right)}{k-1+{({\epsilon /\epsilon }_{\mathit{cc}})}^k}$ $\left(2\right){\epsilon }_{\mathit{cc}}\le \epsilon$ ${\sigma =f}_{\mathit{cc}}\mathit{exp}{[k_1({\epsilon /\epsilon }_{\mathit{cc}})]}^{k_2}$	$f_l{=f}_{\mathit{yv}}({\displaystyle \sum _{i=1}^o{A}_{\mathit{sbi}}}+{\displaystyle \sum _{i=1}^p{A}_{\mathit{sbi}}})/[s(b_c{+h}_c)]$$;{k=E}_c/(E_c-f_{\mathit{cc}}{/\epsilon }_{\mathit{cc}})$ $k_{e,\mathit{mander}}=[1-{\displaystyle \sum _{i=1}^n{\omega }_i^2/(6}{b}_c{h}_c)][1-(s^{\prime }/2b_c)][1-(s^{\prime }/2h_c)]/(1{-\rho }_{\mathit{cc}})$ $f_{\mathit{le}}{=k}_{e,\mathit{mander}}{f}_l$$;f_{\mathit{cc}}{/f}_c=1+2.1{(f_{\mathit{le}}{/f}_c)}^{0.7}$$;{\epsilon }_{\mathit{cc}}/{\epsilon }_c=1+0.21{(f_{\mathit{le}}{/f}_c)}^{1.7}$ $\mathrm{If}\mathrm{no}\mathrm{test}\mathrm{data}\mathrm{is}\mathrm{available},{\epsilon }_{c50}$$\mathrm{takes}0.004;{\epsilon }_{\mathit{cc}50}={\epsilon }_{c50}+0.15{(f_{\mathit{le}}{/f}_c)}^{1.1}$ $k_1=\mathit{ln}(0.5)/{({\epsilon }_{\mathit{cc}50}{-\epsilon }_{\mathit{cc}})}^{k_2}$$;k_2=0.58+16{(f_{\mathit{le}}{/f}_c)}^{1.4}$
Razvi et al. [20] (1999)	$\left(1\right)0\le \epsilon \le {\epsilon }_{\mathit{cc}}$ Same as the ascending portion of the Cussion model. $\left(2\right){\epsilon }_{\mathit{cc}}\le \epsilon \le {\epsilon }_{\mathit{cc}20}$ ${\sigma =f}_{\mathit{cc}}[1-0.15({\epsilon /\epsilon }_{\mathit{cc}})/({\epsilon }_{c85}{-\epsilon }_{\mathit{cc}})]$ $\left(3\right){\epsilon }_{\mathit{cc}20}\le \epsilon$$\sigma =0.2f_{\mathit{cc}}$	$m_1=6.7{(f_{\mathit{le}})}^{0.17}$$;m_2=0.15\sqrt{(b_c/s)(h_c{/s}_l)}$$;m_3=40{/f}_c\le 1.0$ $m_4{=f}_{\mathit{ys}}/500\ge 1.0$$;f_{\mathit{cc}}{=f}_c+0.5m_1{\rho }_{\mathit{sv}}{f}_{\mathit{ys}}$$;{\epsilon }_c=0.0028-0.008m_3$ ${\epsilon }_{c85}{=\epsilon }_c+0.0018m_3^2$$;{\epsilon }_{\mathit{cc}}{/\epsilon }_c=1+5m_1{m}_3{f}_{\mathit{le}}{/f}_c$ ${\epsilon }_{\mathit{cc}85}=260m_3{\rho }_c{\epsilon }_{\mathit{cc}}[1+0.5m_2(m_4-1)]{+\epsilon }_{c85}$ $E_c=3320\sqrt{f_c}+6900$ $f_{\mathit{ys}}$$,{\rho }_c$ Calculation formulae are shown in Table 2
Li et al. [15] (2001)	$\left(1\right)0\le \epsilon \le {\epsilon }_c$ ${\sigma =E}_c\epsilon +\frac{\left(f_c{-E}_c{\epsilon }_c\right)\epsilon }{{\epsilon }_c^2}$ $\left(2\right){\epsilon }_c\le \epsilon \le {\epsilon }_{\mathit{cc}}$ ${\sigma =f}_{\mathit{cc}}-\frac{(f_{\mathit{cc}}{-f}_c\left)\right(\epsilon -{\epsilon }_{\mathit{cc}}{)}^2}{{({\epsilon }_{\mathit{cc}}-{\epsilon }_c)}^2}$ $\left(3\right){\epsilon }_{\mathit{cc}}\le \epsilon$ ${\sigma =f}_{\mathit{cc}}-\beta \frac{f_{\mathit{cc}}\left({\epsilon -\epsilon }_{\mathit{cc}}\right)}{{\epsilon }_{\mathit{cc}}}\ge 0.4f_{\mathit{cc}}$	$f_{\mathit{le}}$$,k_{e,\mathit{mander}}$$\mathrm{are}\mathrm{the}\mathrm{same}\mathrm{as}\mathrm{the}\mathrm{Cussion}\mathrm{model};E_c=3320\sqrt{f_c}+6900$ $f_{\mathit{cc}}{=f}_c(-0.413+1.413\sqrt{1+11.4f_{\mathit{le}}{/f}_c}-2f_{\mathit{le}}{/f}_c)$ (For high-strength concrete) ${\epsilon }_{\mathit{cc}}/{\epsilon }_c=1+11.3f_{\mathit{le}}{/f}_c{)}^{0.7}$$(f_{\mathit{yv}}\le 550$$\mathrm{MPa});{\epsilon }_c=0.0007{(f_c)}^{0.3}$ $\beta =(0.048f_c-2.14)-(0.098f_c-4.57\left)\right(f_{\mathit{le}}{/f}_c{)}^{1/3}$$(f_{\mathit{yv}}\le 550$$\mathrm{MPa}\mathrm{and}{f}_c>75$ MPa)
Légeron et al. [21] (2003)	$\left(1\right)0\le \epsilon \le {\epsilon }_c$ Similar to the ascending portion of the Cussion model. $\left(2\right){\epsilon }_{\mathit{cc}}\le \epsilon$ Same as the descending portion of the Cussion model.	${\rho }_{\mathit{sey}}$, $\kappa$ Calculation formulae are shown in Table 2 $k_{e,\mathit{mander}}$$\mathrm{is}\mathrm{similar}\mathrm{to}\mathrm{the}\mathrm{Cussion}\mathrm{model};{\epsilon }_c=0.0005{(f_c)}^{0.4}$ $I_e^{\prime }{=f}_{\mathit{le}}{/f}_c$$;I_{e50}{=\rho }_{\mathit{sey}}{f}_{\mathit{ys}}{/f}_c$$;f_{\mathit{cc}}{/f}_c=1+2.4{(I_e^{\prime })}^{0.7}$ ${\epsilon }_{\mathit{cc}}{/\epsilon }_c=1+35({I^{\prime }}_e{)}^{1.2}$$;{\epsilon }_{\mathit{cc}50}{/\epsilon }_{c50}=1+60I_{e50}$ $k_1$$\mathrm{is}\mathrm{the}\mathrm{same}\mathrm{as}\mathrm{the}\mathrm{Cussion}\mathrm{model};k_2=1+25(I_{e50}{)}^2$

Table 2. Empirical formulae for ties strain when confined concrete is at peak stress.

Proposed by	Empirical Formulae	Parameters
Razvi et al. [20] (1999)	$f_y{=E}_s(0.0025+0.04\sqrt[3]{k_e{\rho }_c{/f}_c})\le f_y$	${\rho }_c=\frac{{\displaystyle \sum _{i=1}^n{(A_{\mathit{sb}})}_i}+{\displaystyle \sum _{i=1}^n{(A_{\mathit{sh}})}_i}}{s(b_c{+h}_c)}$
Légeron et al. [21] (2003)	$f_{\mathit{ys}}=0.25f_c/[{\rho }_{\mathit{sey}}(\kappa -10)]\ge 0.43{\epsilon }_c{E}_s{f}_{\mathit{ys}}{,f}_{\mathit{ys}}\le f_{\mathit{yv}}$	${\rho }_{\mathit{sey}}{=k}_e{A}_{\mathit{sh}}/({\mathit{sh}}_c)$, ${\kappa =f}_c/({\rho }_{\mathit{sey}}{E}_s{\epsilon }_c)$

Table 2. Empirical formulae for ties strain when confined concrete is at peak stress.

Proposed by	Empirical Formulae	Parameters
Razvi et al. [20] (1999)	$f_y{=E}_s(0.0025+0.04\sqrt[3]{k_e{\rho }_c{/f}_c})\le f_y$	${\rho }_c=\frac{{\displaystyle \sum _{i=1}^n{(A_{\mathit{sb}})}_i}+{\displaystyle \sum _{i=1}^n{(A_{\mathit{sh}})}_i}}{s(b_c{+h}_c)}$
Légeron et al. [21] (2003)	$f_{\mathit{ys}}=0.25f_c/[{\rho }_{\mathit{sey}}(\kappa -10)]\ge 0.43{\epsilon }_c{E}_s{f}_{\mathit{ys}}{,f}_{\mathit{ys}}\le f_{\mathit{yv}}$	${\rho }_{\mathit{sey}}{=k}_e{A}_{\mathit{sh}}/({\mathit{sh}}_c)$, ${\kappa =f}_c/({\rho }_{\mathit{sey}}{E}_s{\epsilon }_c)$

To present the differences between each model, this study takes a $f_c$ of 80 MPa and 100 MPa, section size of 250 mm × 250 mm, concrete cover thickness of 15 mm, longitu-dinal symmetrical uniform reinforcement of 12φ12 ($f_{yv}$: 400 MPa), and ties reinforcement φ8@100 (4 legs,$f_{yv}$: 400 MPa) short column as examples. The formulae for the elastic modulus and concrete in Cussion’s and Légeron’s models are the same as those of Razvi’s and Li’s models. Moreover, the formula for the peak strain of concrete in Cussion’s model is the same as that of Légeron’s model. The comparison results of each model are shown in Figure 1 and Figure 2.

Figure 1 and Figure 2 show that the ascending portion of each model is basically similar, which is mainly because the same ascending portion function is adopted for Cussion’s, Razvi’s, and Légeron’s models. However, the nonlinearity before peak stress in Li’s model is more obvious than that in the other models. For the descending section, the differences among the models are significant; the residual platform value of Li’s model is higher than that of the other models. The descending portion of Razvi’s model is the slowest, and that of Li’s model is the steepest.

3. Details of the Proposed Model

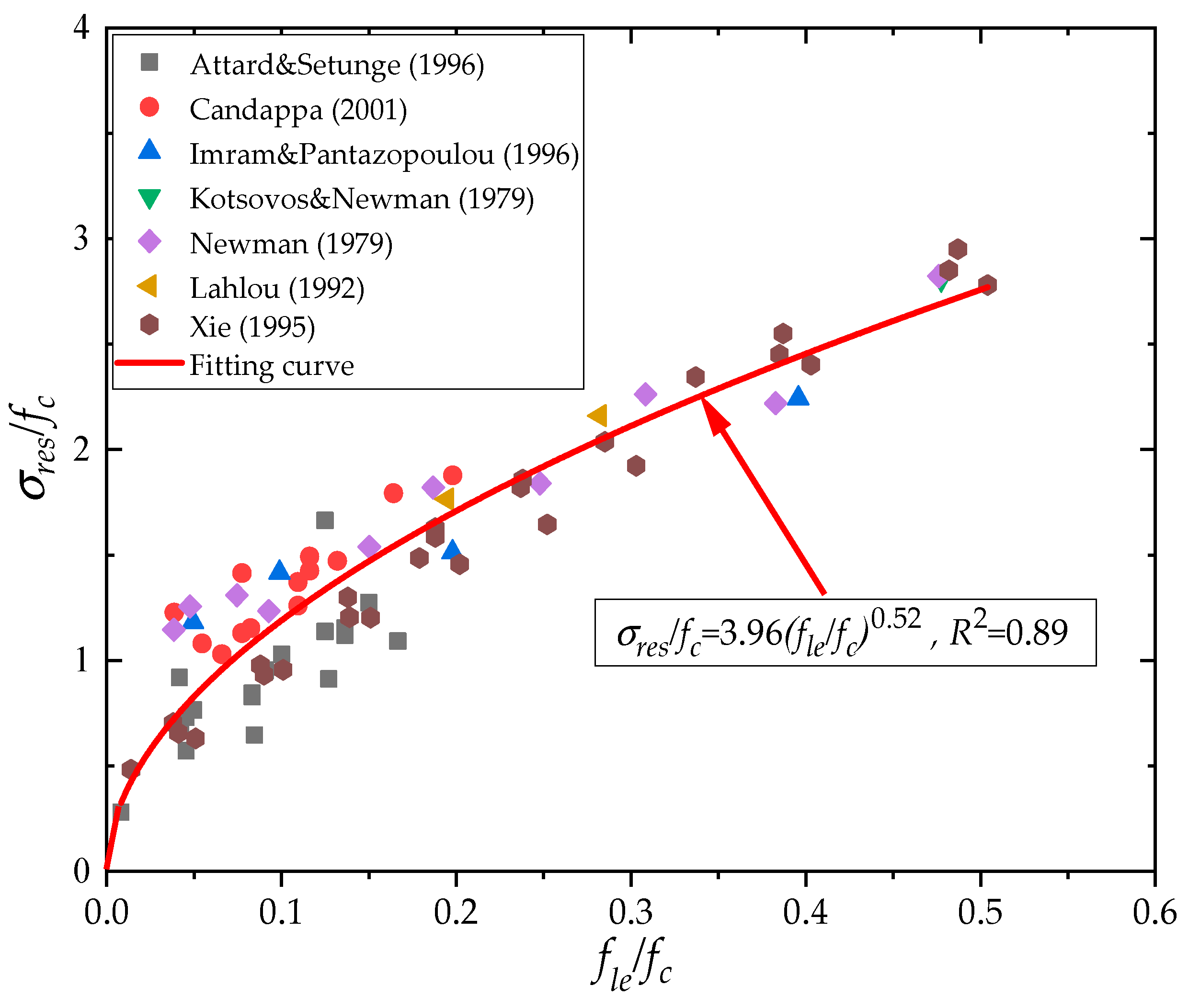
3.1. Normal Triaxial Compression Model

To establish a ties-confined high-strength concrete stress–strain model, the law of strength and deformation of high-strength concrete under uniform lateral confinement needs to be determined first. In this study, we used the results of normal triaxial experiments on high-strength concrete from related studies [24,25,26,27,28,29,30,31,32,33] to establish the relationship between the peak stress, peak strain, and lateral confinement ratio ($f_{le}/f_c$) under uniform lateral confinement. The cylindrical compressive strength ranges from 60 MPa to 120 MPa, and the lateral confinement ratio is in the range 0–0.5. The test data are shown in Figure 3 and Figure 4.

By doing regression analysis on the test data, the relationship between the peak stress, peak-strain enhancement coefficient, and lateral confinement ratio is obtained as

$$f_{\mathit{cc}}{/f}_c=1+3.32(f_{\mathit{le}}{/f}_c{)}^{0.76}{,R}^2=0.92$$

(1)

$${\epsilon }_{\mathit{cc}}{/\epsilon }_c=1+11.92f_{\mathit{le}}{/f}_c{,R}^2=0.96$$

(2)

From Figure 3 and Figure 4, Equations (1) and (2) can better reflect the law of the test data. The dispersion of the peak-stress improvement coefficient is relatively small over the whole lateral confinement ratio. Conversely, the dispersion of the peak-strain improvement coefficient is small when the lateral confinement ratio is 0–0.2 and becomes relatively large as the lateral confinement ratio increases.

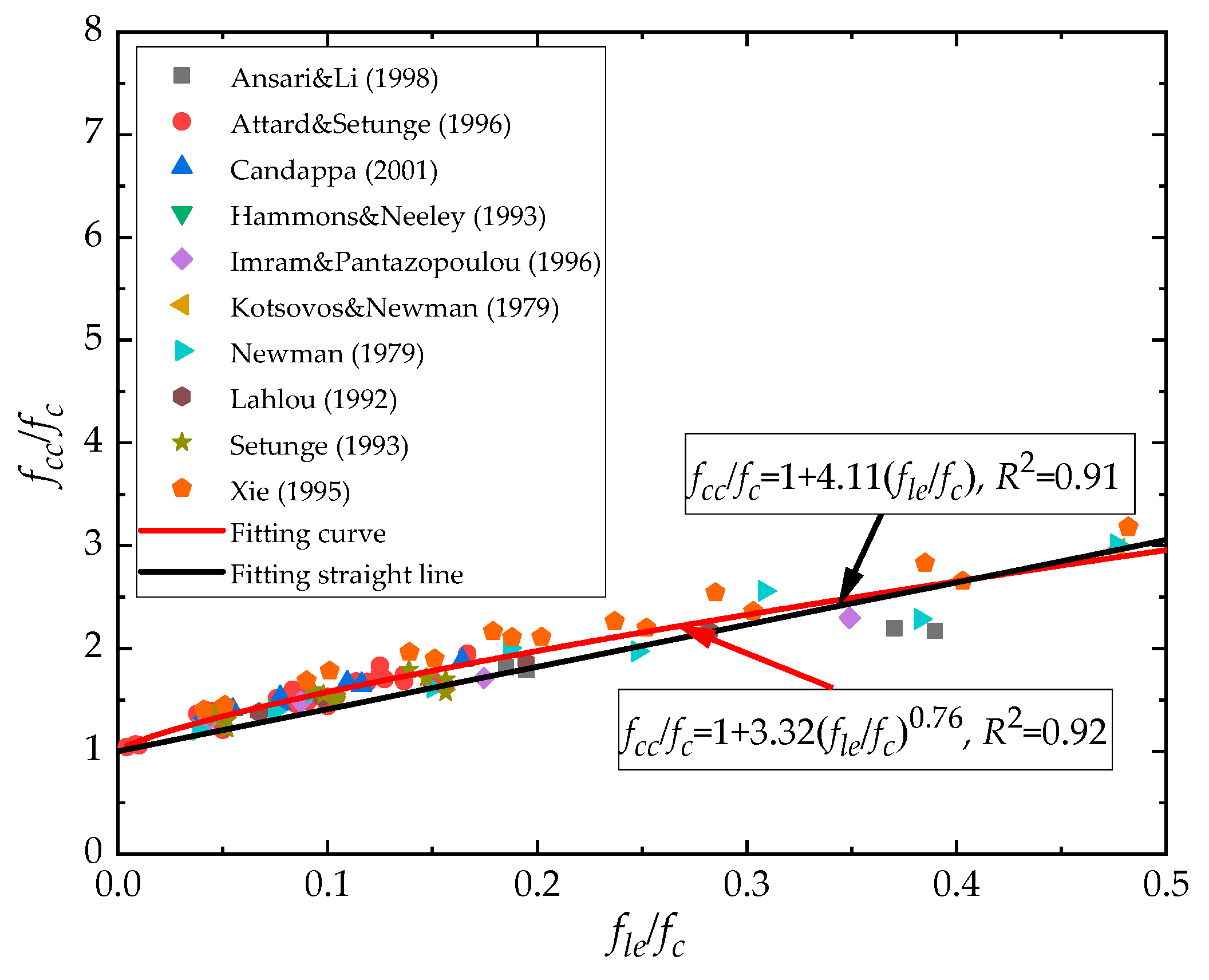
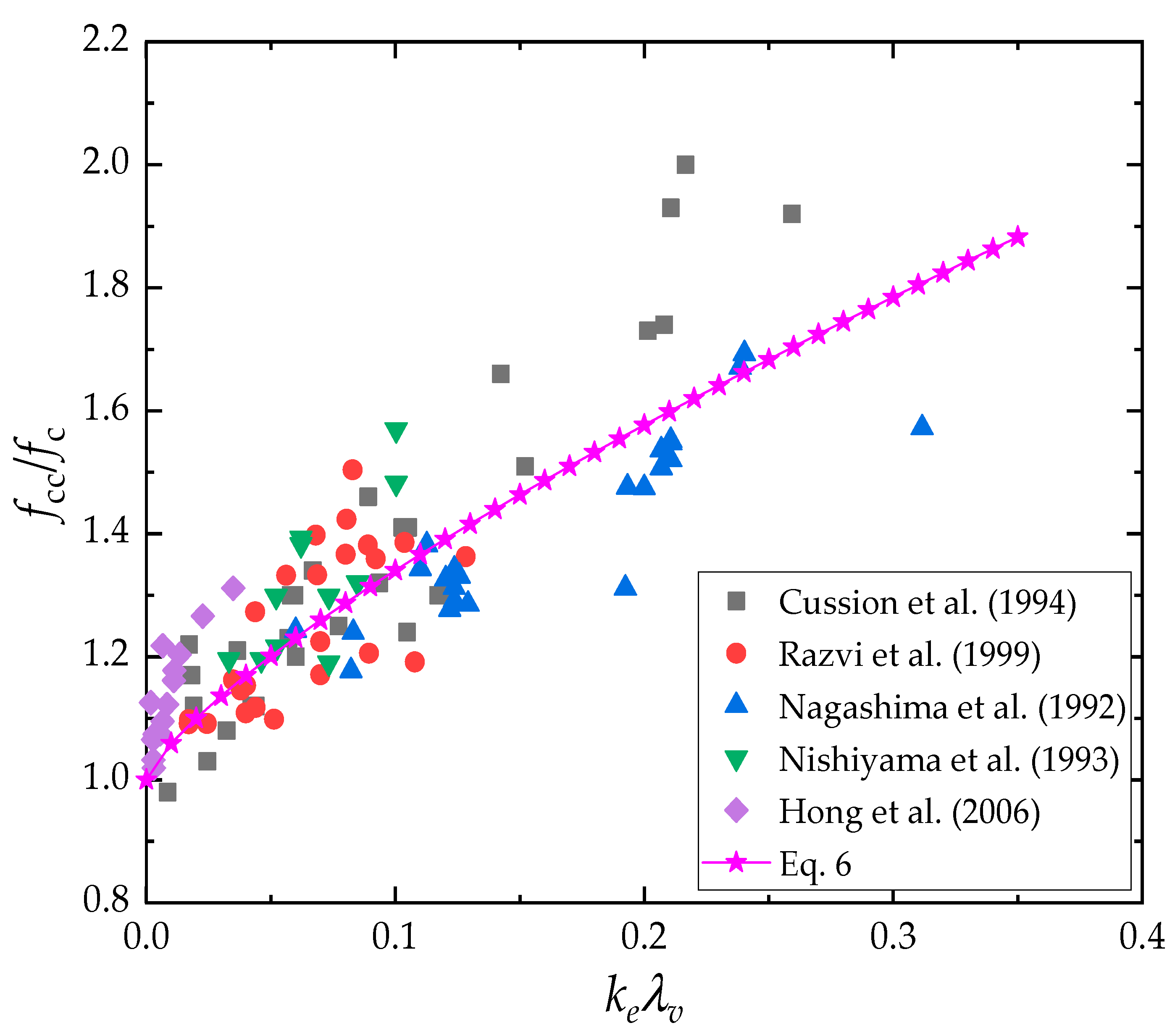
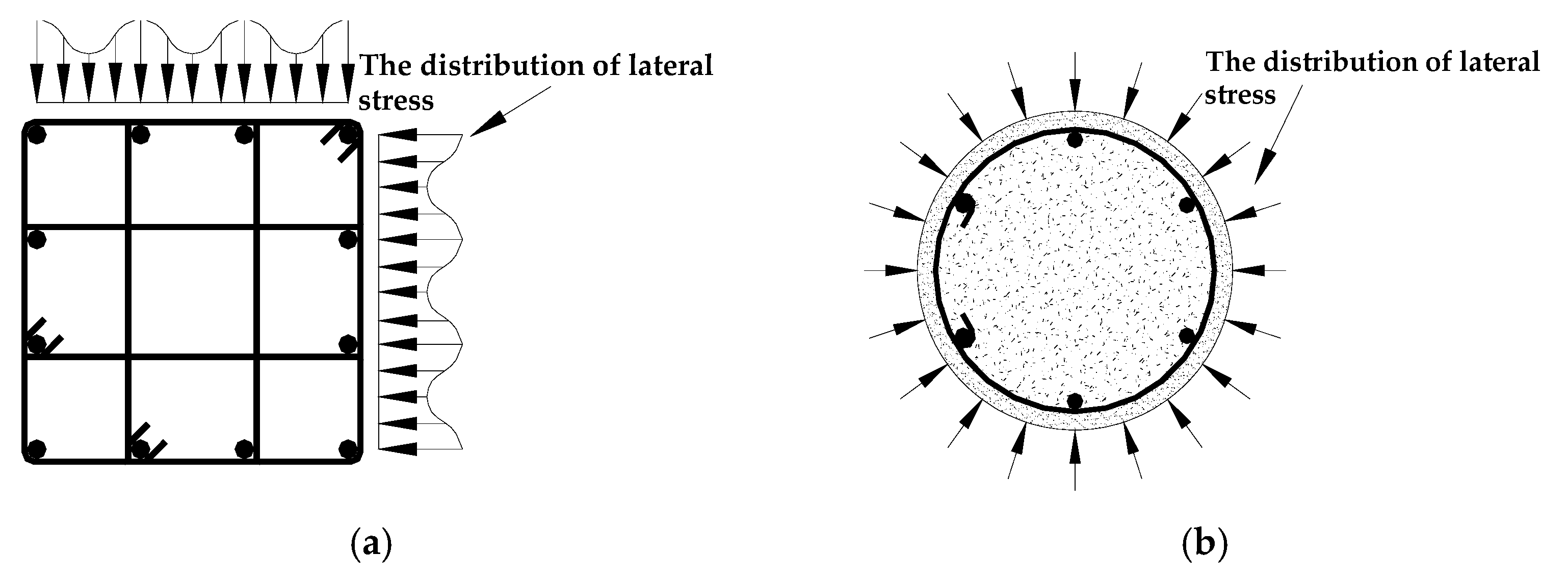
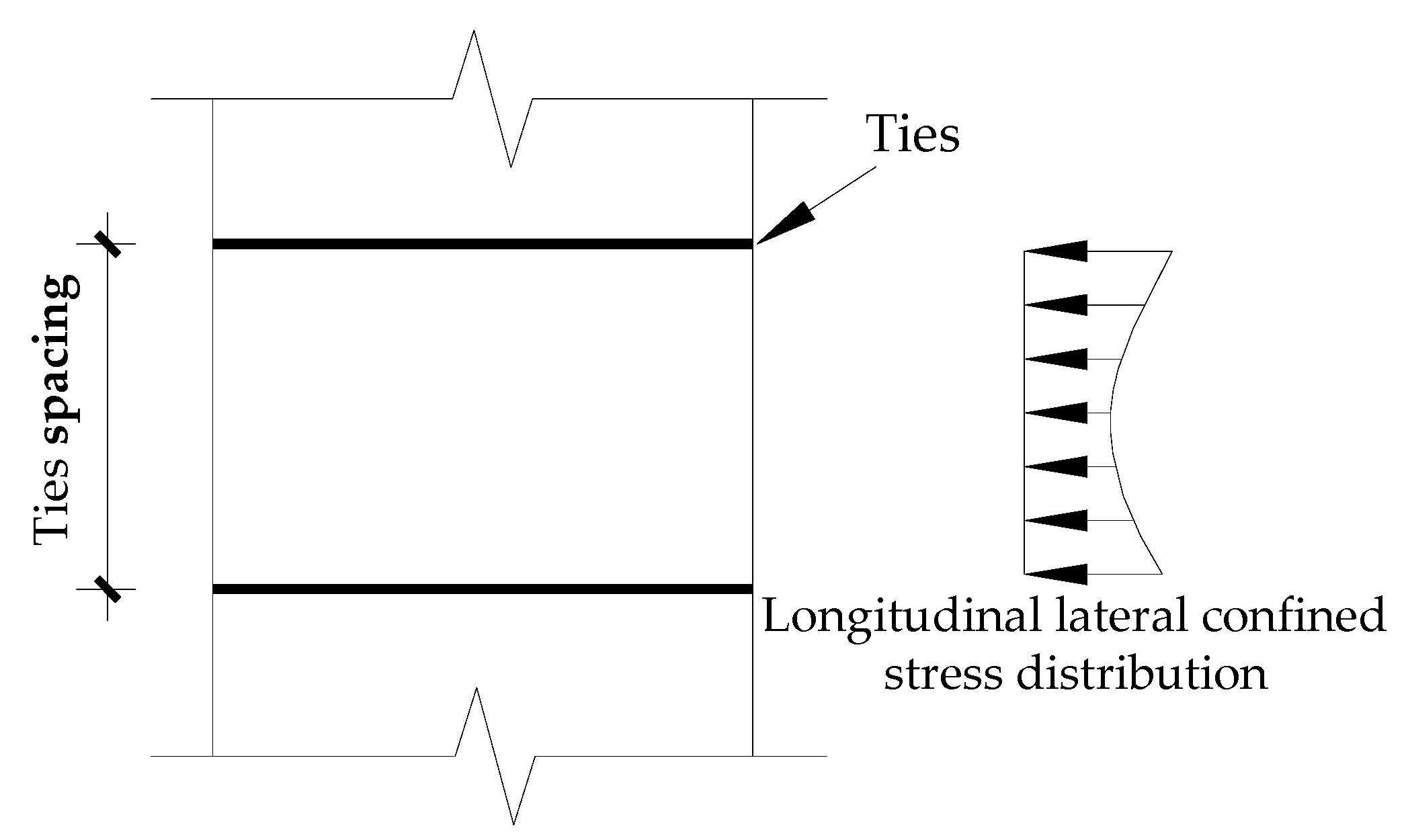
3.2. Effective Confinement Coefficient

For ties-confined concrete, the passive lateral stress generated by laterally expanding concrete and the passive confined stress provided by the ties are nonuniformly distributed. The form of the confined stress distribution varies with the ties arrangements and cross-sectional shapes. The passive confined stress that develops in the sections with different ties arrangements is shown in Figure 5. The square and rectangular sections, confined by rectilinear ties, develop nonuniform lateral stress that peaks near the longitudinal bars. For circular sections, the lateral confined stress can be approximated as uniform.

Because rectangular and square columns are common forms in engineering and the lateral confining stress of circular columns can be approximately considered uniform (especially when spiral reinforcements are used), this study mainly focuses on rectangular columns. Rectangular ties sections can be divided into three main regions according to the degree of ties confinement, as shown in Figure 6:

(1)

unconfined zone: the concrete is outside the ties without any confined effect in this region;

(2)

weakly confined zone: the concrete is near the inner side of the ties reinforcement with a weak triaxial compressive stress state in this region;

(3)

heavily confined zone: the remaining part of the concrete is in the core region with a strong triaxial compressive stress state in this region.

The longitudinal lateral confined stress along the column is also unevenly distributed with the strongest lateral confined effect at the ties plane and the weakest at the center of the adjacent ties plane. The approximate distribution of the lateral confined stress is shown in Figure 7.

There are many factors affecting the lateral confined-stress distribution; however, the main factors are the ties spacing, ties form, average lateral confined stress, and compressive concrete strength. To simplify the calculation, the effective confinement coefficients of the ties reinforcement in the existing models are mainly obtained based on experimental or empirical formulae, which can mainly be divided into the effective confined zone and experimental fitting methods.

Sheikh and Uzumeri [34] first proposed the concept of the “effective confinement core” in 1982, assuming that the shape of the weakly confined area is a quadratic parabola. Ignoring the difference in the effective confined area between the ties planes and adjacent ties planes, they finally determined the effective confined area of the ties. Mander et al. [14] introduced the concept of the effective confinement core for rectangular ties by assuming that the end inclination of the weakly confined zone is π/4. Saatcioglu and Razvi [35] proposed that the effective confinement coefficient is inversely proportional to the ties spacing, longitudinal reinforcement spacing, and average confined stress based on the experimental results. They regressed the test data to obtain the empirical formula for the effective stress coefficient. The empirical formula was later modified based on the experimental results for high-strength concrete.

Taking the cross-sectional size of 400 mm × 400 mm, longitudinal reinforcement uniformly arranged 12φ16 ($f_{yv}$: 400 MPa), ties reinforcement φ8@100 (4 legs, $f_{yv}$: 400 MPa), and concrete cover thickness of 25 mm for a column as an example, the effective confinement coefficients calculated using Razvi’s and Mander’s empirical formulae are 0.49 and 0.64, respectively. The absolute error is 0.15, and the relative error is 30 %, which is large. Because the high-strength concrete material is brittle, the number of confined ties should increase such that the average confined stress increases to ensure that the ductility requirements of high-strength concrete columns are met. Furthermore, the equivalent uniform confined stress varies significantly when different effective confined factors are used. Therefore, this study proposes an empirical formula for the effective confinement coefficient based on the test data of the normal triaxial compression of high-strength concrete from this study and other studies with reference to the influence parameters of existing models.

The effective confinement coefficient is obtained using the inverse of Equation (1):

$$k_e=\frac{f_c}{f_l}{\left[\left(\frac{f_{\mathit{cc}}}{f_c}-1\right)/3.32\right]}^{1.32}$$

(3)

From Equation (3), the effective confinement coefficient is related to the concrete strength, average confined stress, and peak-stress improvement coefficient. The peak-stress improvement coefficient is related to numerous parameters, such as concrete strength, ties yield strength, and volumetric ties ratio. The influencing factors of the effective confinement coefficient are coupled with each other. However, the effective confinement coefficient has been shown to decrease when the average confined stress increases. The elastic range increases with the concrete strength increase (similar to an elastic foundation beam), such that the area of the weakly confined zone decreases, and the effective confinement coefficient increases. In addition, the effective confinement coefficient is influenced by the specific arrangement of the ties reinforcement (e.g., the spacing between longitudinal bars), which is approximated by the dimensionless parameter $\sqrt{(b_c/s)(h_c{/s}_l)}$, characterized in this paper with reference to Mander’s and Razvi’s models. The final expression of the effective confinement coefficient is taken as

$$k_e=a{\left(\frac{f_c}{f_l}\right)}^b{\left(\sqrt{\frac{b_c}{s}\frac{h_c}{s_l}}\right)}^c$$

(4)

where a, b, and c are the model parameters.

Not all the influencing factors are considered in the construction of Equation (4), i.e., the randomness is ignored, which will inevitably result in a difference between the theoretical and experimental values. To identify the model parameters, the ratio of the calculated value of the effective confinement coefficient to the test value is considered as a random variable X; when the probability distribution of the random variable is known, the model parameters are obtained. Because the concrete strength, spacing between the ties, longitudinal bars, and average confining stress are not independent of each other, the random variable X can be assumed to obey a lognormal distribution. By adjusting the model parameters, the effective confinement coefficient is finally obtained as

$$k_e=0.06{\left(\frac{f_c}{f_l}\right)}^{0.21}{\left(\sqrt{\frac{b_c}{s}\frac{h_c}{s_l}}\right)}^{1.32}$$

(5)

To verify the rationality of Equation (5), let $f_l=0.5{\rho }_{\mathit{sv}}{f}_{\mathit{ys}}$ and substitute it into Equation (3) to obtain

$$\frac{f_{\mathit{cc}}}{f_c}=1+1.96{(k_e{\lambda }_v)}^{0.76}$$

(6)

where ${\lambda }_v{=\rho }_{\mathit{sv}}{f}_{\mathit{ys}}{/f}_c$.

In this study, the relevant experimental data from other studies [20,36,37,38] were used to calculate the effective confinement coefficient using Equation (5). The relationship between $f_{\mathit{cc}}{/f}_c$ and $k_e{\lambda }_v$ was obtained based on the test results of the peak-stress improvement factor and ties characteristic value. The results were compared with the theoretical results of Equation (6), as shown in Figure 8.

Figure 8 shows that the relationship between $f_{\mathit{cc}}{/f}_c$ and $k_e{\lambda }_v$, calculated using Equation (5), is consistent with that of Equation (6). However, Equation (6) has a certain dispersion; on the whole, Equation (5) can better reflect the degree of ties confined inhomogeneity.

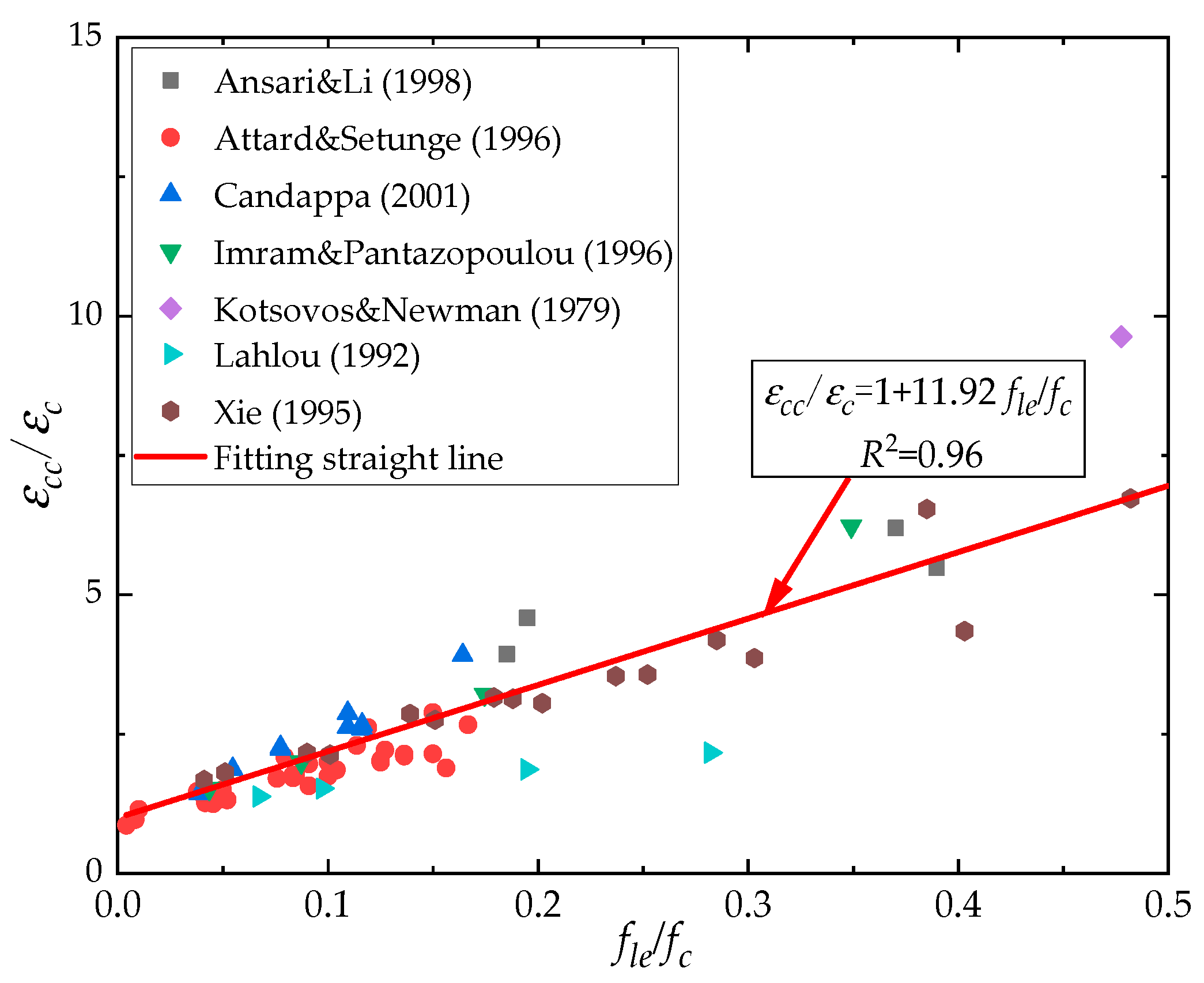
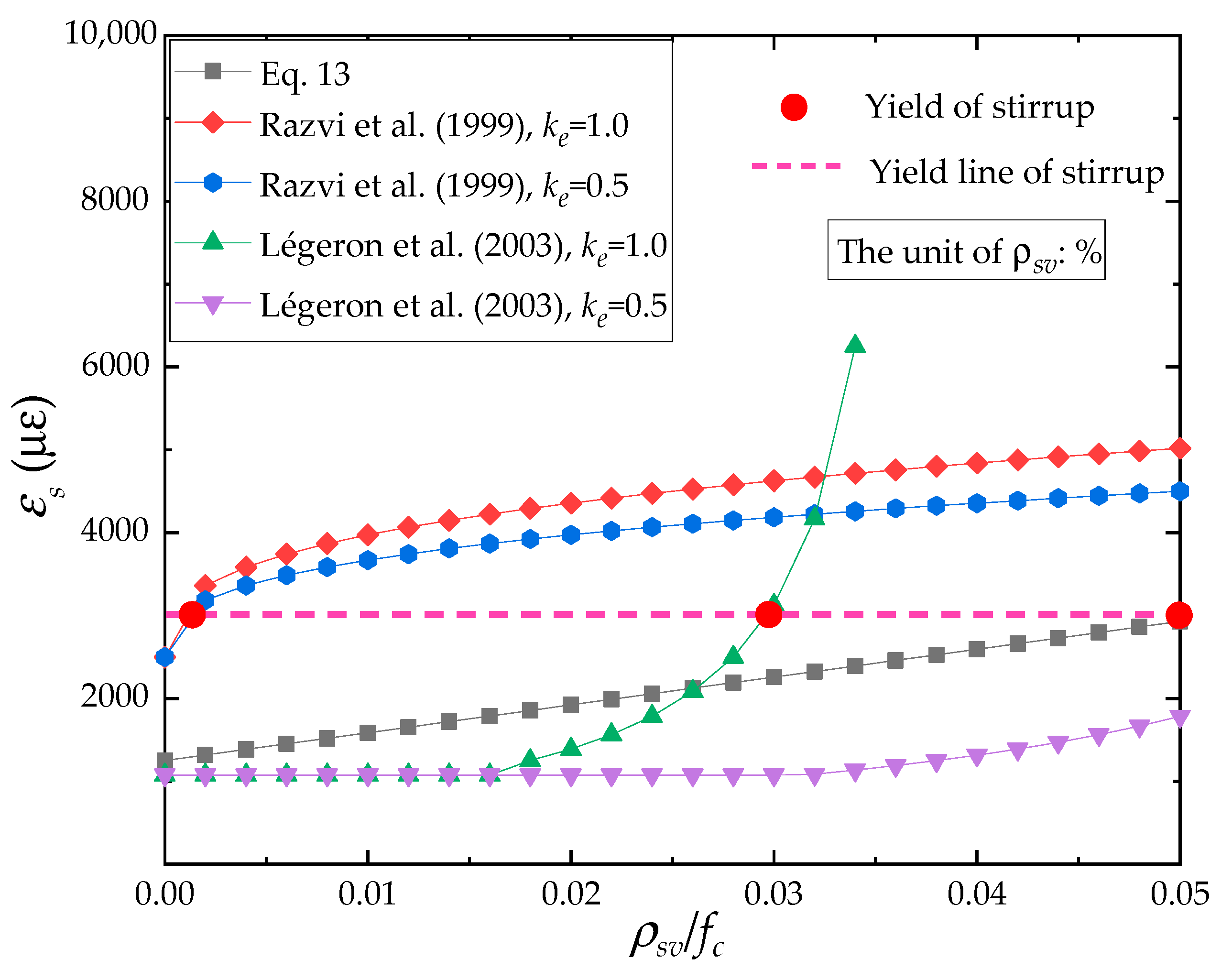
3.3. Ties Strain at the Peak Stress in Confined Concrete

When the yield strength of the ties is high, it may not yield when the concrete reaches the peak stress. To determine the main influencing factors of ties strain at this time, the confined concrete is assumed to be an elastic homogeneous material. Poisson’s ratio is approximated to be 0.5 when the confined concrete reaches the peak stress. Using the generalized Hooke’s law, we can obtain

$${\epsilon }_s=0.5{\epsilon }_{\mathit{cc}}(1{-k}_e{f}_l{/f}_{\mathit{cc}})$$

(7)

Based on the relationship between the peak-stress enhancement factor and lateral confinement ratio in Section 3.1, Equation (7) can be further simplified. To facilitate the derivation, the relationship between the peak-stress improvement coefficient and lateral confinement ratio is approximately linear:

$$\frac{f_{\mathit{cc}}}{f_c}=1+4.11\frac{k_e{f}_l}{f_c},R^2=0.91$$

(8)

Substituting Equation (8) into Equation (7), we get

$${\epsilon }_s=0.5{\epsilon }_c\left(1+11.92\frac{k_e{f}_l}{f_c}\right)\left(1-\frac{k_e{f}_l{/f}_c}{1+4.11k_e{f}_l{/f}_c}\right)$$

(9)

From Equation (9), the ties strain, when confined concrete is at peak stress, is related to the effective confinement coefficient, average confined stress, and strength of unconfined concrete. When the lateral confinement ratio is 0–0.5, the ties strain increases with an increase in the lateral confinement ratio. However, the lateral confinement ratio is still related to the ties strain; therefore, Equation (9) is an implicit function with the ties strain as the independent variable, and at this time, we can let

$$g(x)=1-\frac{x}{1+4.11x}$$

(10)

where ${x=k}_e{f}_l{/f}_c$.

The lateral confinement ratio of ties reinforcement in engineering is generally not greater than 0.2. Hence, when the lateral confinement ratio is 0–0.2, the value domain of $g\left(x\right)$ is [1, 0.89], and it is a monotonically decreasing function; $g\left(x\right)$ can be conservatively taken as 0.89, and Equation (9) can be further simplified as

$${\epsilon }_s=0.45{\epsilon }_c\left(1+\frac{11.92k_e{f}_l}{f_c}\right)$$

(11)

When the rectangular ties arrangement, $f_l=0.5{\rho }_{\mathit{sv}}{f}_{\mathit{yv}}$, we can substitute this value into Equation (11):

$${\epsilon }_s=\frac{0.45{\epsilon }_c}{1-2.68k_e{E}_s{\epsilon }_c{\rho }_{\mathit{sv}}{/f}_c}$$

(12)

From Equation (12), the ties strain of confined concrete at peak stress is related to ${\epsilon }_c$ and $k_e{\rho }_{\mathit{sv}}{/f}_c$; it increases with an increase in ${\epsilon }_c$ and $k_e{\rho }_{\mathit{sv}}{/f}_c$. To this end, this study collects experimental data from relevant studies [8,20,36,38], as shown in Figure 9.

Using ${\epsilon }_c$ and $k_e{\rho }_{\mathit{sv}}{/f}_c$ as the basic parameters, the empirical formulae for the ties strain were obtained using regression analysis in which the concrete and ties yield strength ranges were 50–115 MPa and 392–1387 MPa, respectively.

By using regression analysis on the test data, the relationship between the relative strain ${\epsilon }_c$ and $k_e{\rho }_{\mathit{sv}}{/f}_c$ of the ties reinforcement is obtained as

$$\frac{{\epsilon }_s}{{\epsilon }_c}=0.5+13.44\frac{{\rho }_{\mathit{sv}}}{f_c}{,R}^2=0.83$$

(13)

where the unit of ${\rho }_{\mathit{sv}}$ is %.

Razvi et al. [20] and Légeron et al. [21] also proposed empirical formulae for ties strains when confined concrete is at peak stresses based on the experimental results, as shown in Table 2.

For rectangular-ties square columns, ${\rho }_c{=\rho }_{\mathit{sv}}/2$ and ${\rho }_{\mathit{sey}}{=k}_e{\rho }_{\mathit{sv}}/2$; let ${\epsilon }_c=2500\mu \epsilon$, $E_s=2\times 10^5$ MPa, $f_{\mathit{yv}}=600$ MPa, and $k_e=$1.0 and 0.5. The relationship between ties strain and ${\rho }_{\mathit{sv}}{/f}_c$ is shown in Figure 10.

From Figure 10, the ties strain in Razvi’s model increases with an increase in the effective confinement coefficient; however, the rate of increase gradually slows down. The ties strain tends to infinity when ${\rho }_{\mathit{sv}}{/f}_c$ increases to a certain value in Légeron’s model. The ties strain predicted by the proposed model is between that of Razvi’s and Légeron’s models, which can better reflect the relationship between ties strain and ${\rho }_{\mathit{sv}}{/f}_c$. When ${\rho }_{\mathit{sv}}{/f}_c=0$ and ${\epsilon }_s{/\epsilon }_c=0.5$, it is in general agreement with the results of Candappa et al. [26] for Poisson’s ratio tests on high-strength concrete.

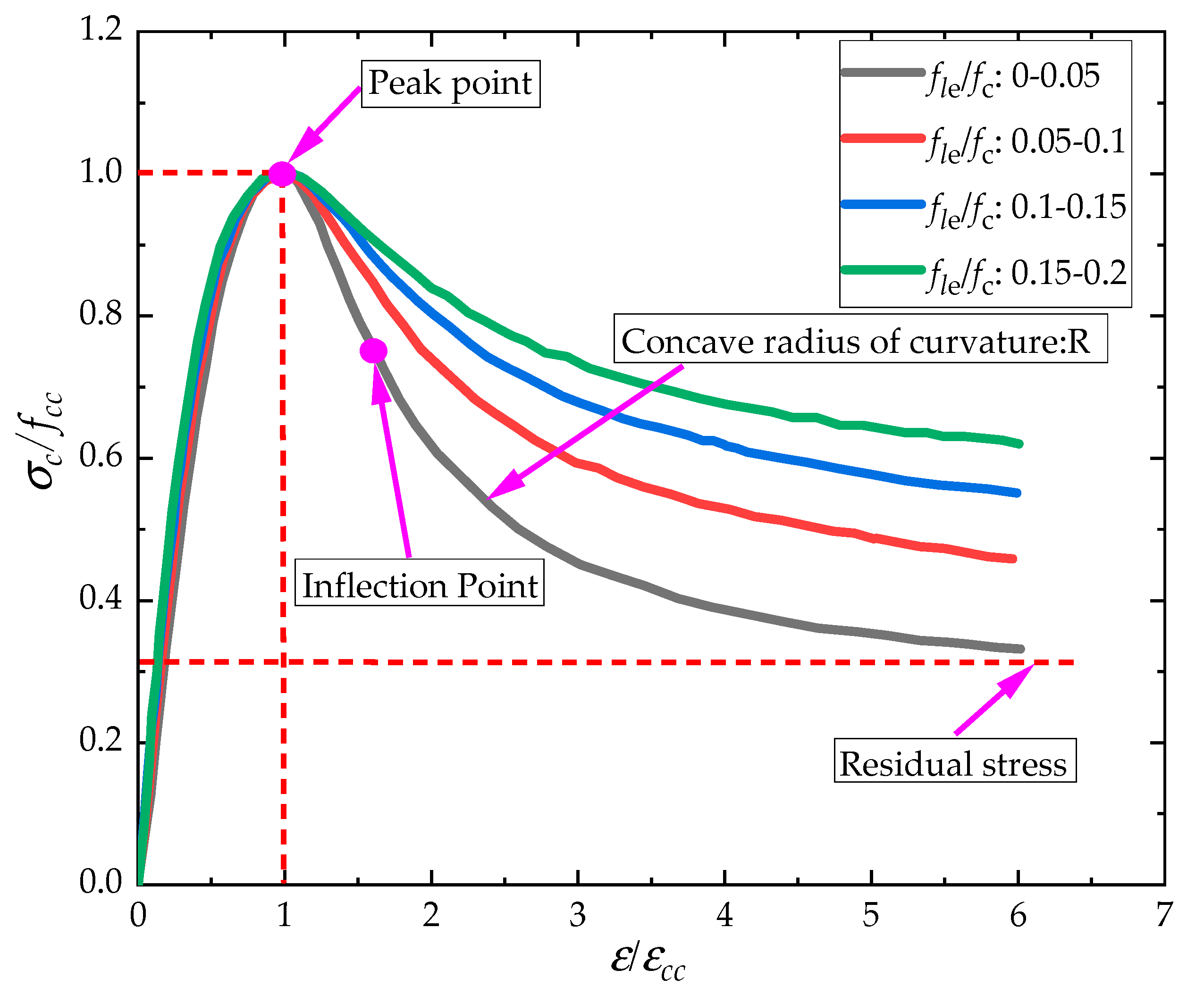
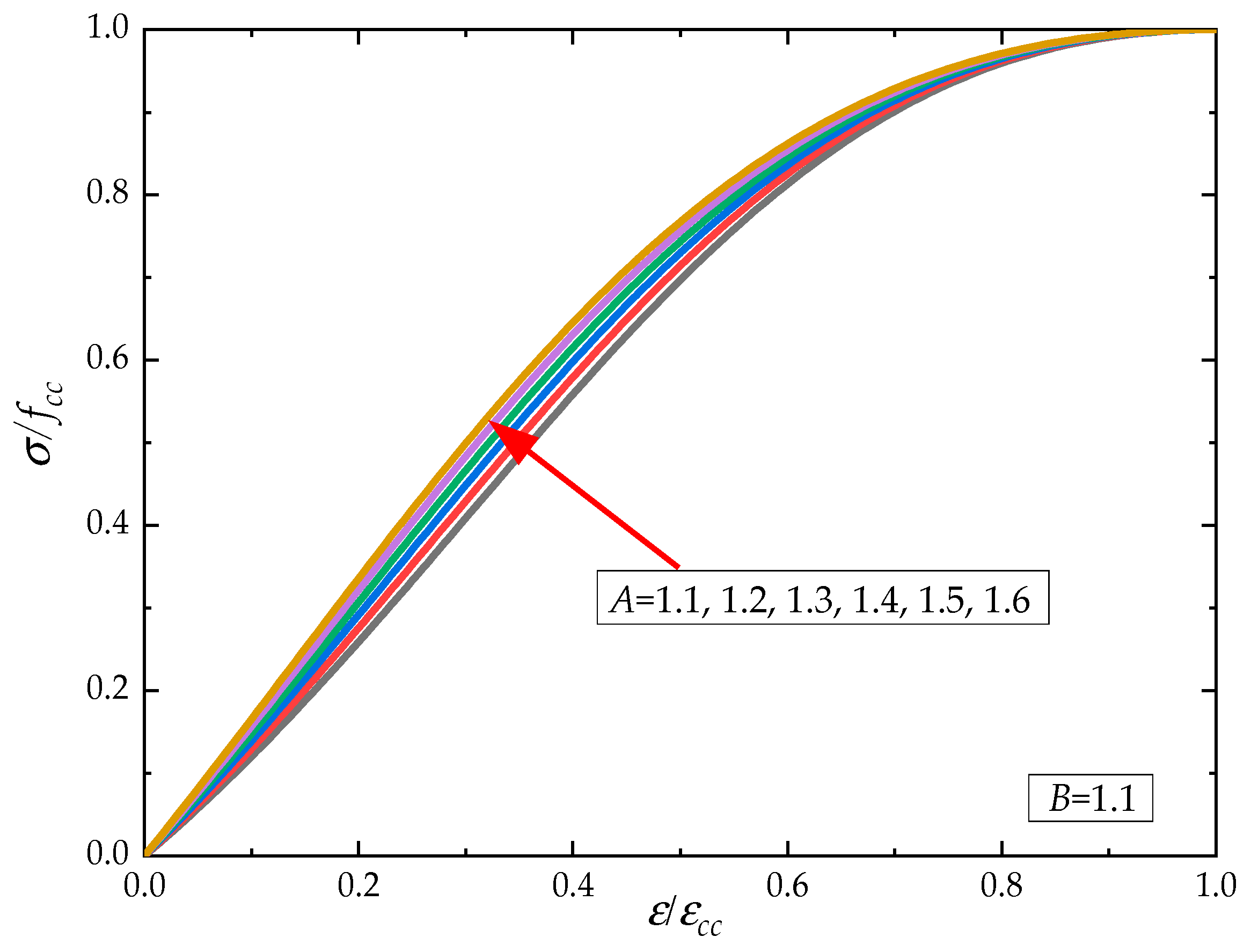
3.4. Stress–Strain Model

The geometry of the complete curve of the axially compressed stress–strain relationship in confined high-strength concrete is closely related to the degree of lateral confinement. The ascending portion is weakly influenced by the degree of lateral confinement; however, the impact on the descending portion is significant. With an increase in the lateral confinement degree, the concavity of the descending section of the complete curve gradually decreases, and the radius of curvature at the corresponding concave point gradually increases. The complete curve geometry with different lateral confinement ratios is shown in Figure 11. The complete geometric characteristics of the curve of confined high-strength concrete are essentially similar to those of unconfined concrete. However, there is a clearer residual stress plateau in the later part of the full stress–strain curve due to the confined effect.

There are different functional forms of the complete curve equation for the stress–strain relationship of the confined concrete. It can be mainly divided into segmental non-derivative and continuous derivative functions based on the derivability of the function; in this study, based on the reference of existing models, the continuous derivative function form is suggested, and the expression is

$$y=\frac{\mathit{Ax}+(B-1)x^2}{1-(A-2){x+\mathit{Bx}}^2}$$

(14)

where ${x=\epsilon /\epsilon }_c$ and ${y=\sigma /f}_{\mathit{cc}}$; A and B are model parameters.

When the model parameters are all greater than 1.0, Equation (14) can satisfy the full curve equation geometry condition:

(1)

$y\left(0\right)=0,y\left(1\right)=1$;

(2)

$y^{\prime }\left(0\right)=A,y^{\prime }\left(1\right)=0$;

(3)

When $x\to +\infty$, $y\to (B-1)/B$;

(4)

The ascending portion is a convex function, and the descending portion has an inflection point.

The model parameters control the initial slope and residual stress of the complete curve equation. The effects of A and B on the ascending and descending sections of Equation (14) are shown in Figure 12 and Figure 13, respectively.

Based on the geometric conditions of the complete curve equation, ${A=E}_c{\epsilon }_{\mathit{cc}}{/f}_{\mathit{cc}}$; the model parameter B depends on the value of the residual stress in the descending portion, which is mainly related to the concrete strength and lateral confining stresses. In this study, the experimental results of related studies [24,25,26,27,28,29,30,31,32,33] were collected to establish the empirical formula of residual stress. Here, the unconfined concrete strength ranges from 60 MPa to 120 MPa, and the lateral confinement ratio is 0–0.5. The relationship between residual stress, concrete strength, and peak strength of confined concrete is shown in Figure 14 and Figure 15.

From Figure 14 and Figure 15, the dispersion of ${\sigma }_{\mathrm{res}}{/f}_c$ and lateral confinement ratio is relatively small and has a more evident law compared to that of ${\sigma }_{\mathrm{res}}{/f}_{\mathit{cc}}$; therefore, the latter is used to calculate the residual stress in this study. From the regression analysis results of the test data, we obtain

$$\frac{{\sigma }_{\mathit{res}}}{f_c}=3.96{\left(\frac{f_{\mathit{le}}}{f_c}\right)}^{0.52}$$

(15)

Substituting Equation (15) into Equation (1), we obtain

$$\frac{{\sigma }_{\mathit{res}}}{f_{\mathit{cc}}}=\frac{3.96{(f_{\mathit{le}}{/f}_c)}^{0.52}}{1+3.22{(f_{\mathit{le}}{/f}_c)}^{0.76}}$$

(16)

The ties-confined concrete is different from that in normal triaxial experiments because there is no lateral confinement in the adjacent ties plane. Hence, the concrete will keep spalling in the late loading stage, and the residual stress is lower than that in the normal triaxial experiments. For this purpose, this research refers to the effective confinement core concept proposed by Sheikh et al. [34] and defines the residual stress reduction factor $\beta$ as

$$\beta =1-\frac{A_{\mathit{ce}}}{A_{\mathit{ce}0}}$$

(17)

For calculation purposes, using the same assumptions as Mander [14] for the effective confinement coefficients, Equation (17) is expressed as

$$\beta =1-\left[1-{\displaystyle \sum _{i=1}^n{\omega }_i^2}/\left(6b_c{h}_c\right)\right]\left(1-\frac{s^{\prime }}{2b_c}\right)\left(1-\frac{s^{\prime }}{2h_c}\right)$$

(18)

Considering the nonuniformity of lateral confined stresses, this study approximates the equivalent lateral uniform stresses using Equation (5). Using $k_e\beta$ to correct the residual stress of the normal uniaxial experiment, the model parameter B is obtained by combining the complete curve geometry condition:

$$B=\frac{1}{1{-k}_e{\beta \sigma }_{\mathit{res}}{/f}_{\mathit{cc}}}$$

(19)

The calculation steps of the complete stress–strain curve of ties-confined concrete under axial compression are as follows:

(1)

The peak stress and peak strain of unconfined concrete under compression are obtained with experiments or empirical formulae;

(2)

Equation (13) is used to calculate the ties strain when confined concrete experiences the peak stress;

(3)

Equation (5) is used to calculate the effective confinement coefficient based on the arrangement form of the ties reinforcement;

(4)

The equivalent uniform lateral confined stress is calculated; and Equations (1), (2), (14), (16), (18), and (19) are used to obtain the complete curve equation model parameters A and B.

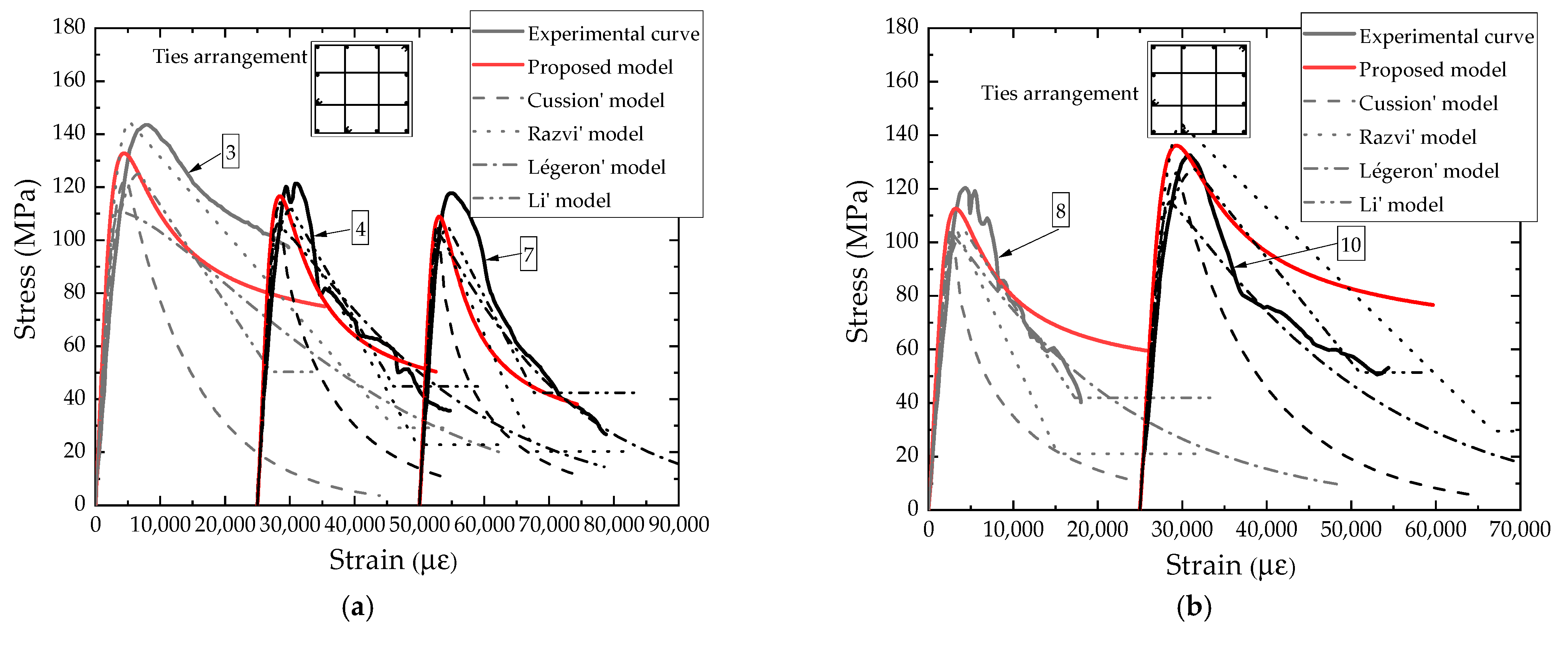
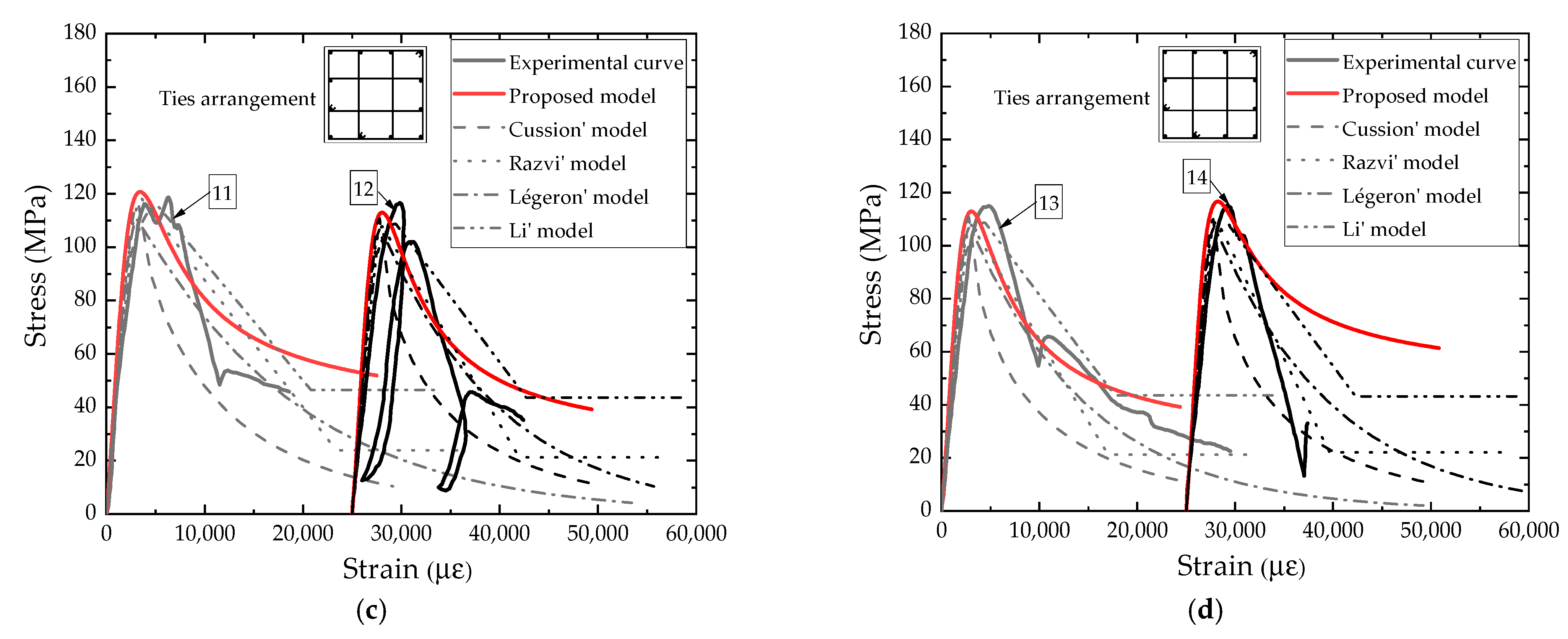
4. Model Evaluation

To verify the model integrity, the experimental data from relevant studies [8,20,37] were collected, as shown in

Table 3. Database for model verification.

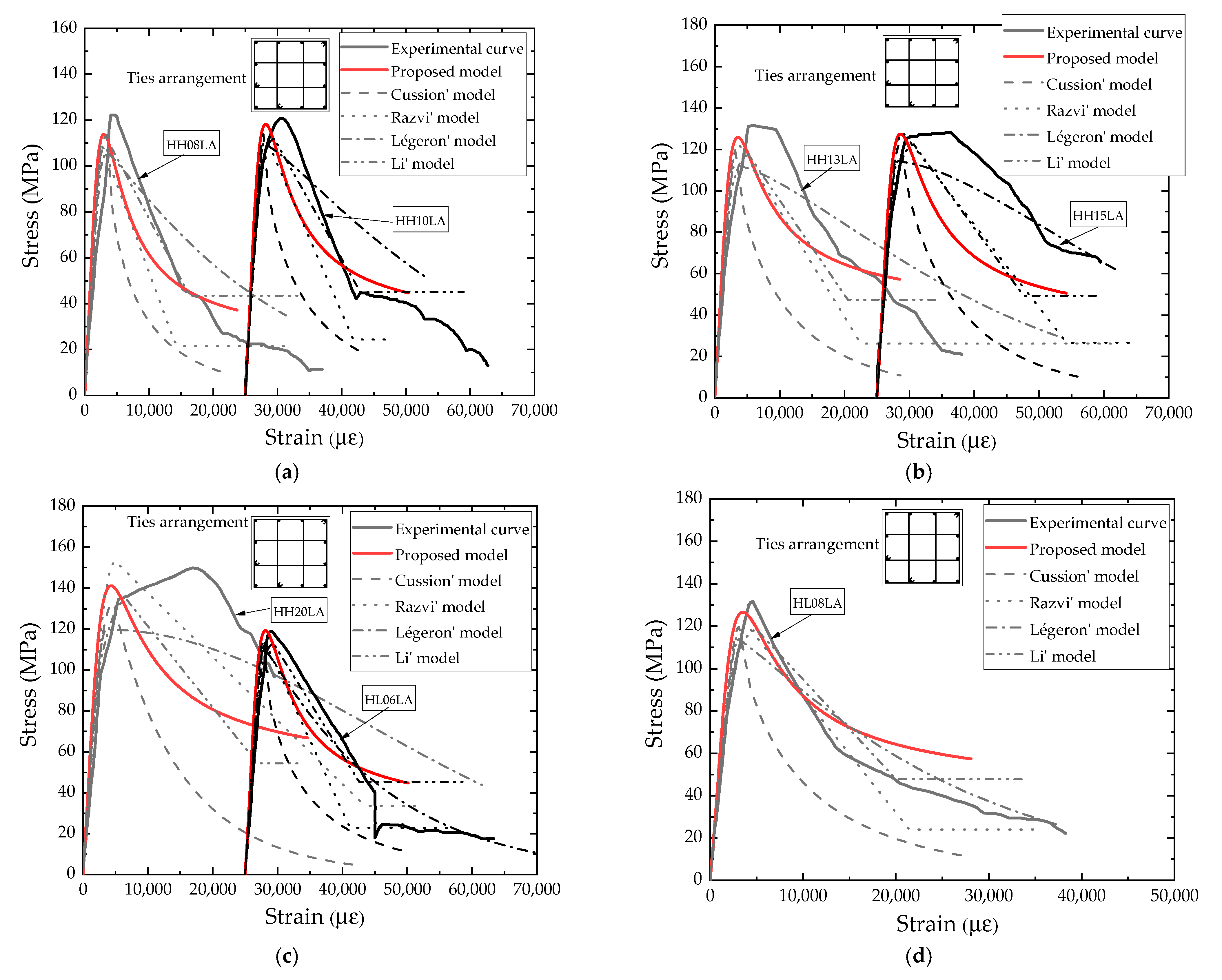
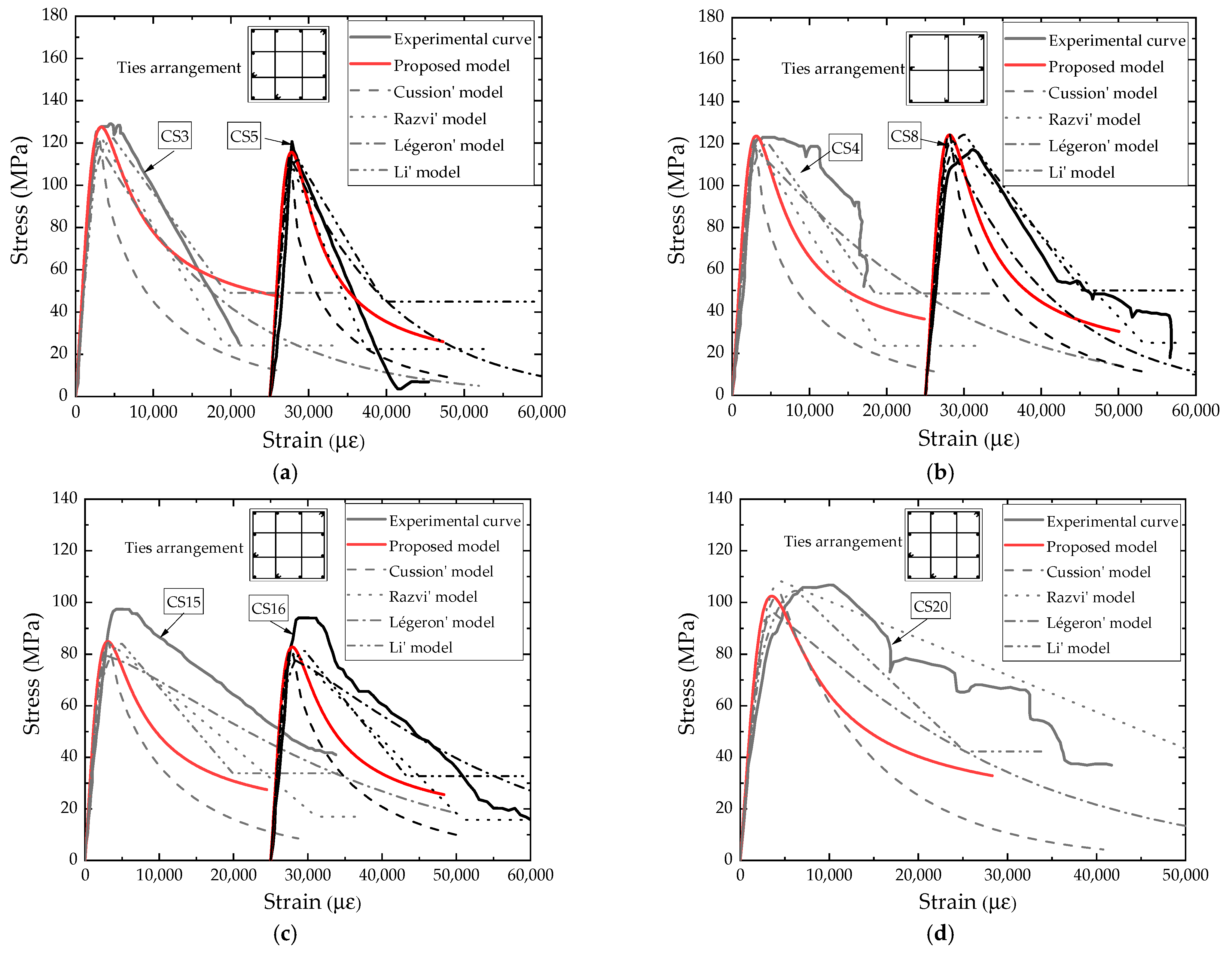
Source	ID	Cross-Section		Longitudinal Bars			Ties		Concrete			${{\mathit{f}}^{\prime }}_{\mathit{cc}}$ (MPa)
		$\mathit{B}$ (mm)	$\mathit{H}$ (mm)	$\mathit{n}$	$\mathit{d}$ (mm)	${\mathit{d}}_{\mathit{s}}$ (mm)	$\mathit{s}$ (mm)	${\mathit{f}}_{\mathit{yv}}$ (MPa)	${{\mathit{f}}^{\prime }}_{\mathit{c}}$(MPa)	${\mathsf{\epsilon }}_{\mathit{c}}$$\left(\mathsf{\mu }\mathsf{\epsilon }\right)$	${\mathit{E}}_{\mathit{c}}$ (MPa)
Nagashima et al. [7] (1992)	HH08LA	225	225	12	10	5.1	55	1387	98.8	2459.1	47154.1	122.8
	HH10LA	225	225	12	10	5.1	45	1387	98.8	2459.1	47154.1	122.5
	HH13LA	225	225	12	10	5.1	35	1387	98.8	2459.1	47154.1	131.5
	HH15LA	225	225	12	10	6.4	45	1368	98.8	2459.1	47154.1	127.0
	HH20LA	225	225	12	10	6.4	35	1368	100.4	2469.0	47407.2	148.2
	HL06LA	225	225	12	10	5	45	807	100.4	2469.0	47407.2	118.2
	HL08LA	225	225	12	10	5	35	807	100.4	2469.0	47407.2	133.2
	3	250	250	12	16	6	31	813	92.4	2418.3	46113.1	145.0
	4	250	250	12	16	6	45	813	92.4	2418.3	46113.1	122.0
Nishiyama et al. [27] (1993)	7	250	250	12	16	6	60	813	92.4	2418.3	46113.1	120.0
	8	250	250	12	16	4	31	840	92.4	2418.3	46113.1	120.0
	10	250	250	12	16	6	31	462	96.2	2442.8	46736.8	133.0
	11	250	250	12	16	6	45	462	96.2	2442.8	46736.8	117.0
	12	250	250	12	16	6	60	462	96.2	2442.8	46736.8	115.0
	13	250	250	12	16	6	60	462	96.2	2442.8	46736.8	115.0
Razvi et al. [11] (1999)	14	250	250	12	16	4	31	481	96.2	2442.8	46736.8	115.0
	CS-3	250	250	12	16	6.5	55	570	105.4	2499.2	48181.5	129.1
	CS-4	250	250	8	16	7.5	55	1000	105.4	2499.2	48181.5	123.4
	CS-5	250	250	12	16	7.5	120	1000	105.4	2499.2	48181.5	122.5
	CS-7	250	250	12	16	6.5	120	400	105.4	2499.2	48181.5	115.0
	CS-8	250	250	8	16	11.3	85	400	105.4	2499.2	48181.5	117.8
	CS-15	250	250	8	16	7.5	55	1000	68.9	2247.2	41815.8	95.5
	CS-16	250	250	12	16	7.5	85	1000	68.9	2247.2	41815.8	95.2
	CS-20	250	250	12	16	11.3	85	400	78.2	2319.5	43618.3	106.3

. Owing to the lack of unconfined concrete modulus of elasticity and peak strain in the test results, this study referred to the empirical formula proposed by Wee et al. [39] for the calculations:

$$E_c=\mathrm{10,200}{(f_c^{\prime })}^{1/3}$$

(20)

$${\epsilon }_c=780{(f_c^{\prime })}^{1/4}$$

(21)

According to the basic parameters in Table 3, the stress–strain relationships of different specimens were calculated using the stress–strain model established in Section 3.4. The comparisons between different experimental curves and analytical models are shown in Figure 16, Figure 17 and Figure 18.

Although there are some differences in the descending portion of the curve, the normal triaxial experimental study of high-strength concrete indicated that the descending portion of the curve has considerable dispersion, and different test conditions may produce different results. Therefore, a model that fits every test specimen completely is still difficult to obtain. Overall, the proposed model can reflect the whole stress–strain process in the test specimens, and its accuracy is basically comparable with other models. However, fewer model parameters and continuously derivable functional form are more convenient for the nonlinear calculation of the members, which is more beneficial in engineering applications.

The dispersion of the calculated peak strain was large, which is mainly because the test in Table 3 lacks the test value of the peak concrete strain. Furthermore, the estimation of the peak concrete strain using Equation (21) will result in certain errors. The calculated peak stress was compared with the test results, as shown in Figure 19. The frequency statistics of the relative error between the calculated $f_{\mathit{cc}}$ and tested $f_{\mathit{cc}}$ are shown in Figure 20.

From Figure 19 and Figure 20, the calculated peak stress is slightly lower than the test value, and the relative error is within 10%, which accounts for 92% of the test data. Considering the existence of randomness in the test process of the specimen, the proposed model can predict the peak stress of ties-confined concrete better than existing models.

5. Conclusions

This paper aims to establish a stress–strain model for high-strength concrete confined by lateral ties for facilitating engineering applications. The effective confinement coefficient and the empirical formula of ties strain at the peak stress of confined concrete were proposed. The stress-strain model used continuously derivable functions, which is convenient for numerical calculations. Based on the results and discussions in this paper, the following conclusions can be drawn:

(1)

The existing models of ties-confined concrete stress–strain were compared; the differences between different empirical models were evident, particularly because the dispersion of the descending portion was large.

(2)

The effective confinement coefficient and empirical formula for the ties strain when confined concrete experienced the peak stress were established. The stress–strain model was proposed using a continuous derivable function, which has fewer model parameters and facilitates numerical calculations.

(3)

The proposed model is in good agreement with the test curve, and the predicted peak stress is slightly lower than the test results. The relative error is within 10%, which accounts for 92% of the test data; overall, the prediction accuracy of the proposed model for the stress–strain relationship for the specimens with fewer parameters and simpler functional form is generally comparable to other models.