3-D Numerical Simulation of Seismic Response of the Induced Joint of a Subway Station
Abstract
:1. Introduction
2. Shaking Table Test and Numerical Simulation Method
2.1. Information Related to Previous Shaking Table Test
2.2. Numerical Simulation of the Shaking Table Test
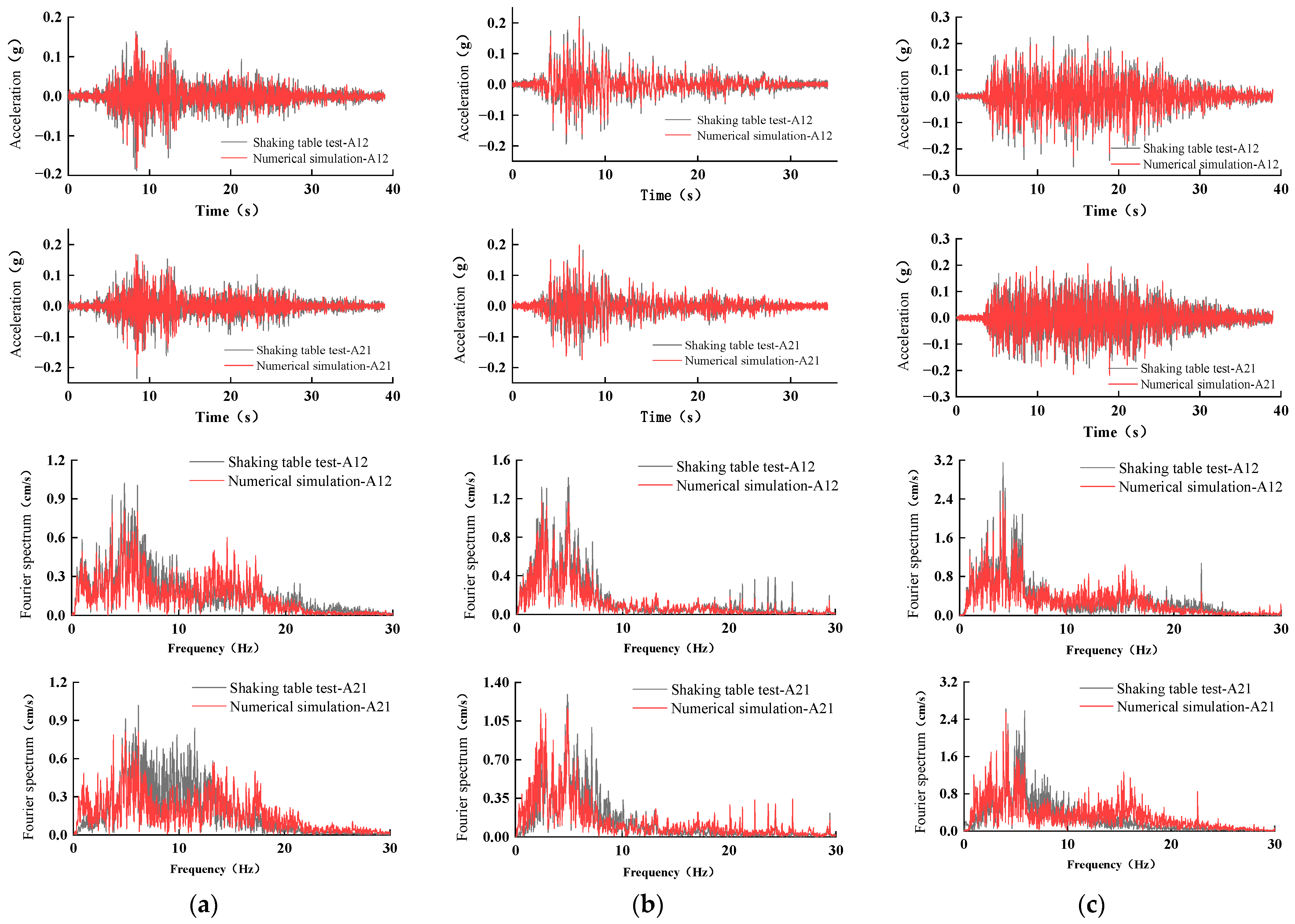
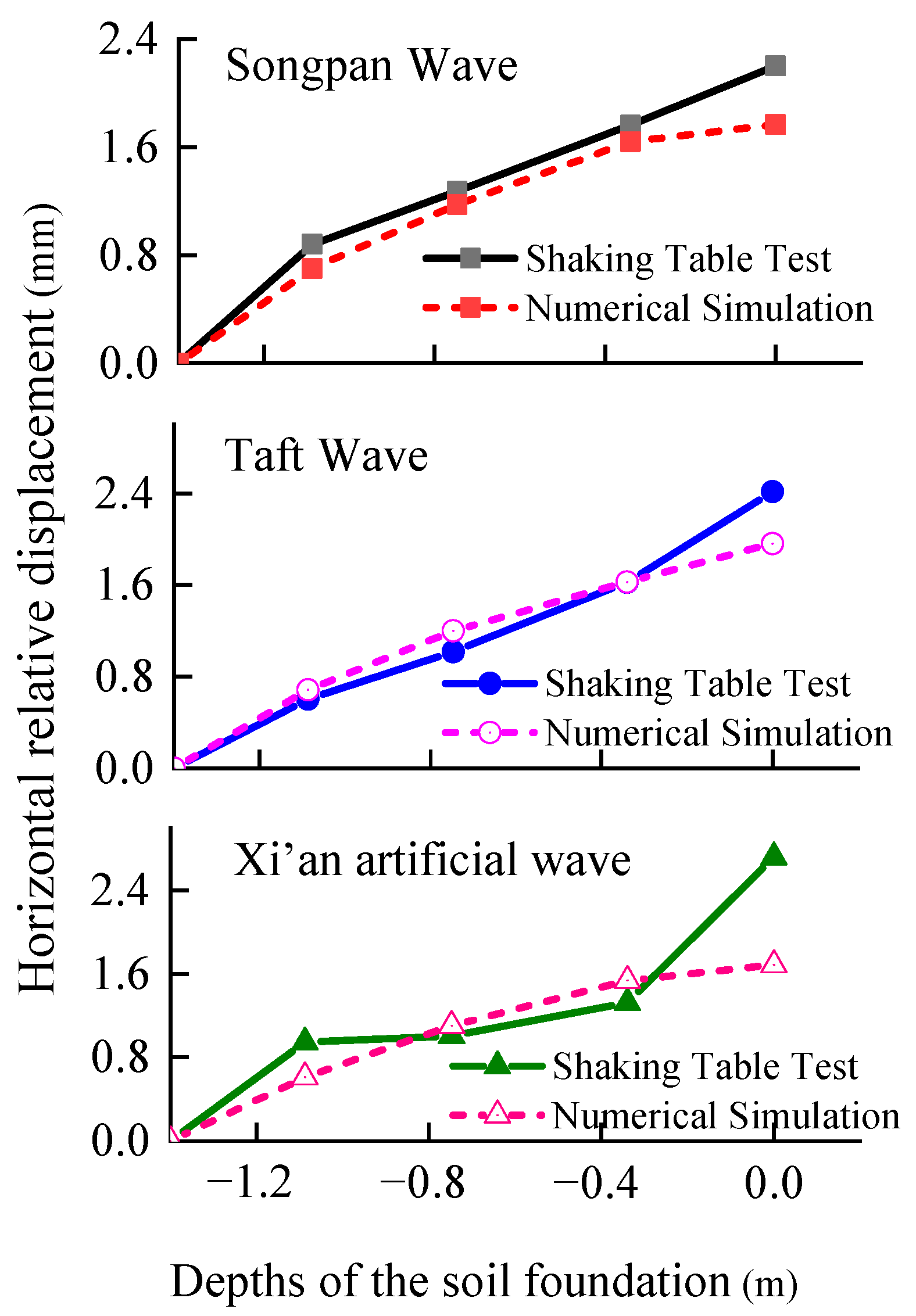
2.3. Acceleration Response Comparison
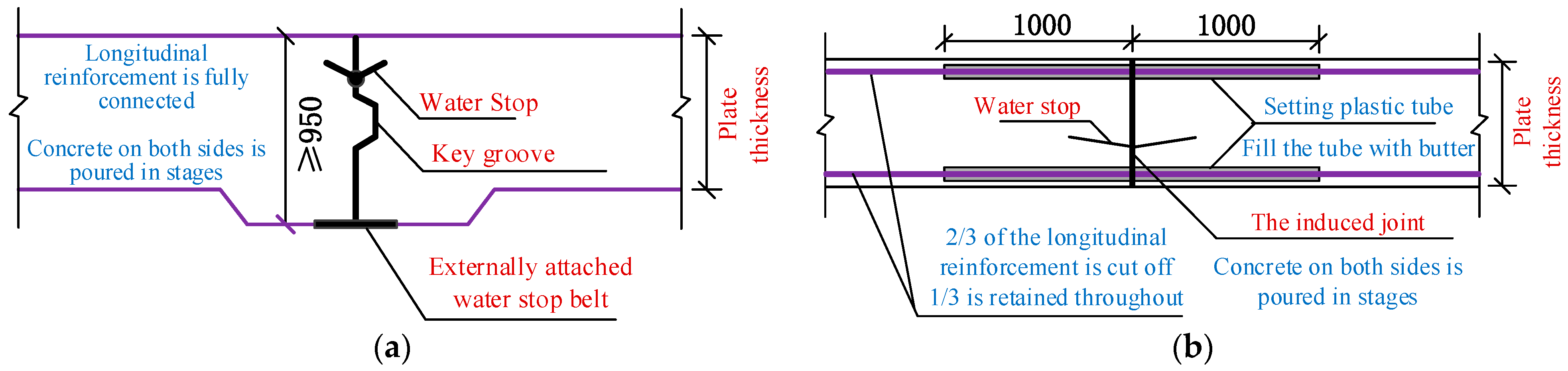
3. Numerical Model of the Induced Joint of the Subway Station Structure
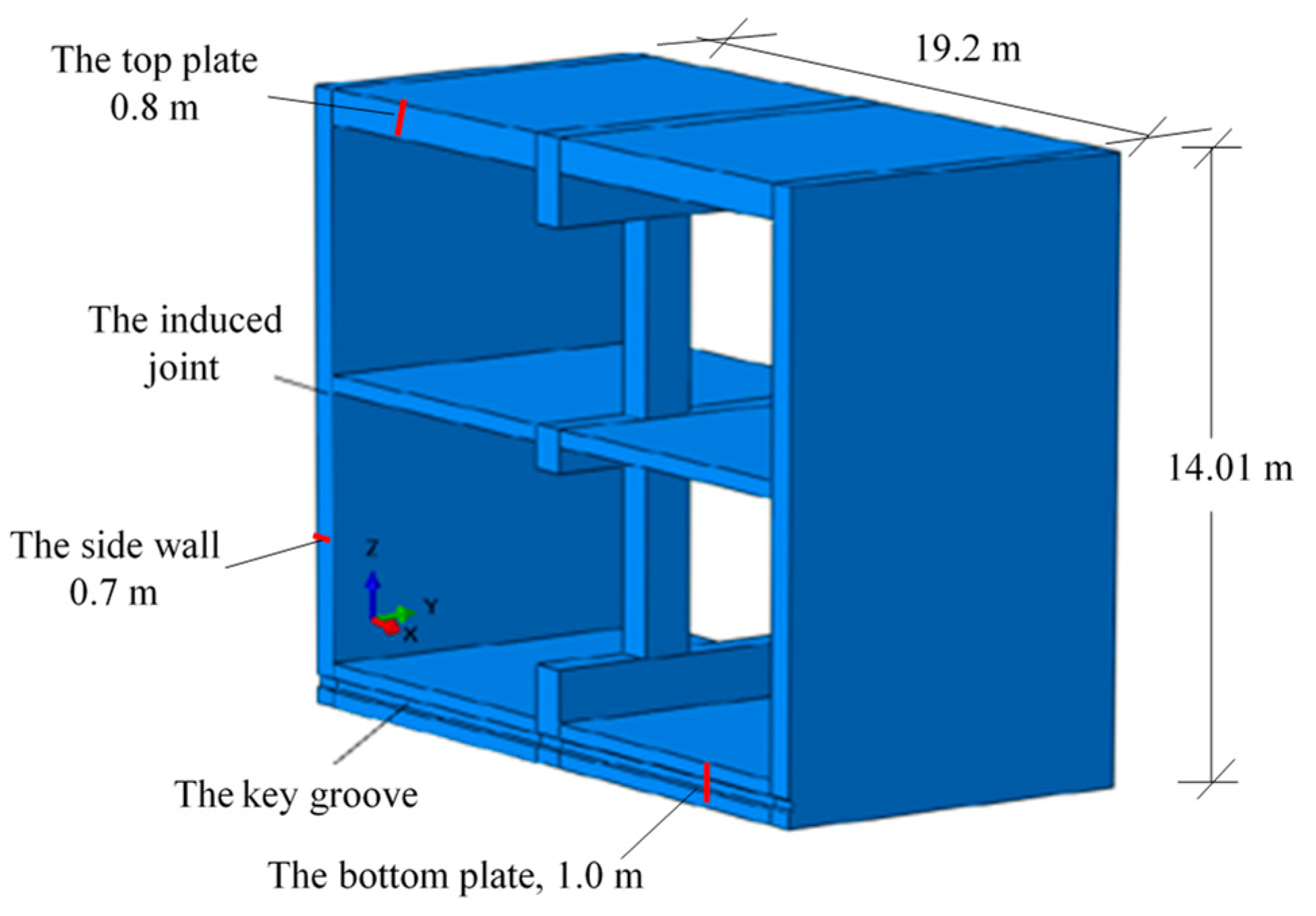
3.1. Model Design and Boundary Setting
3.2. Material Parameters and Seismic Wave Setting
3.3. Location of Observation Section and Test Point
3.4. Dynamic Damage of the Subway Station Structure
4. Seismic Response of the Induced Joint in the Subway Station Structure
4.1. Influence of Seismic Waves with Different Spectral Characteristics
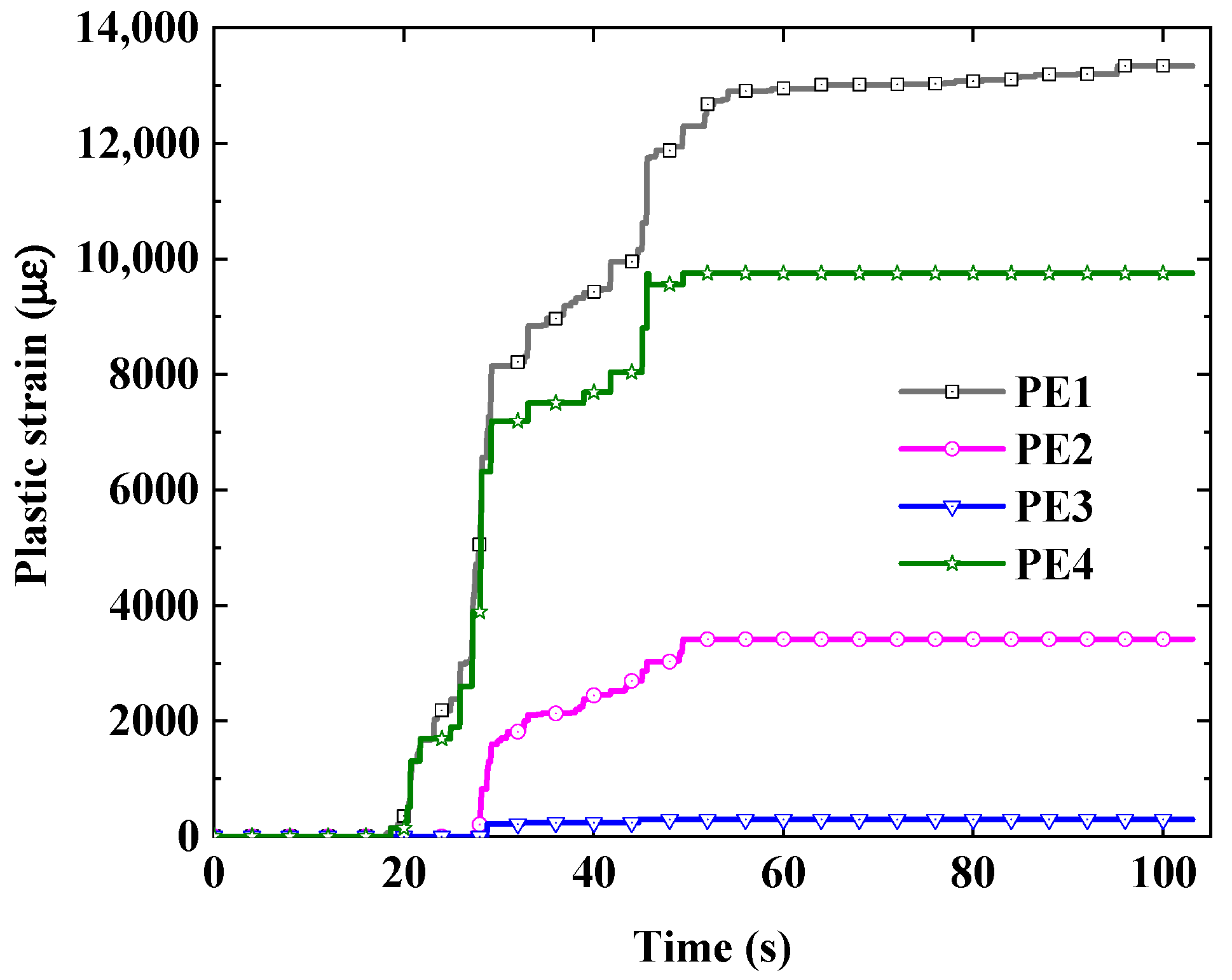
4.1.1. Strain of Remaining Longitudinal Reinforcement at Induced Joint
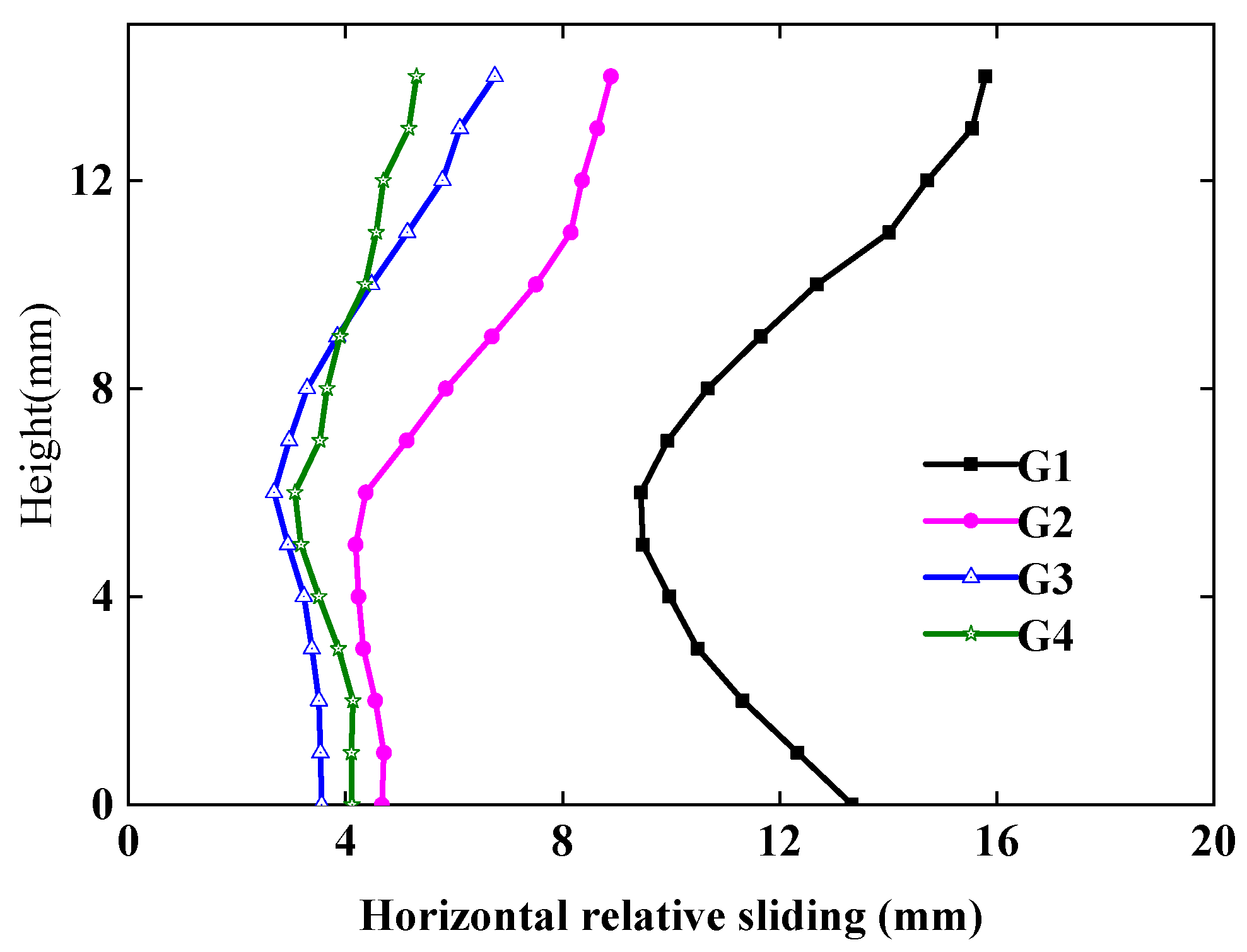
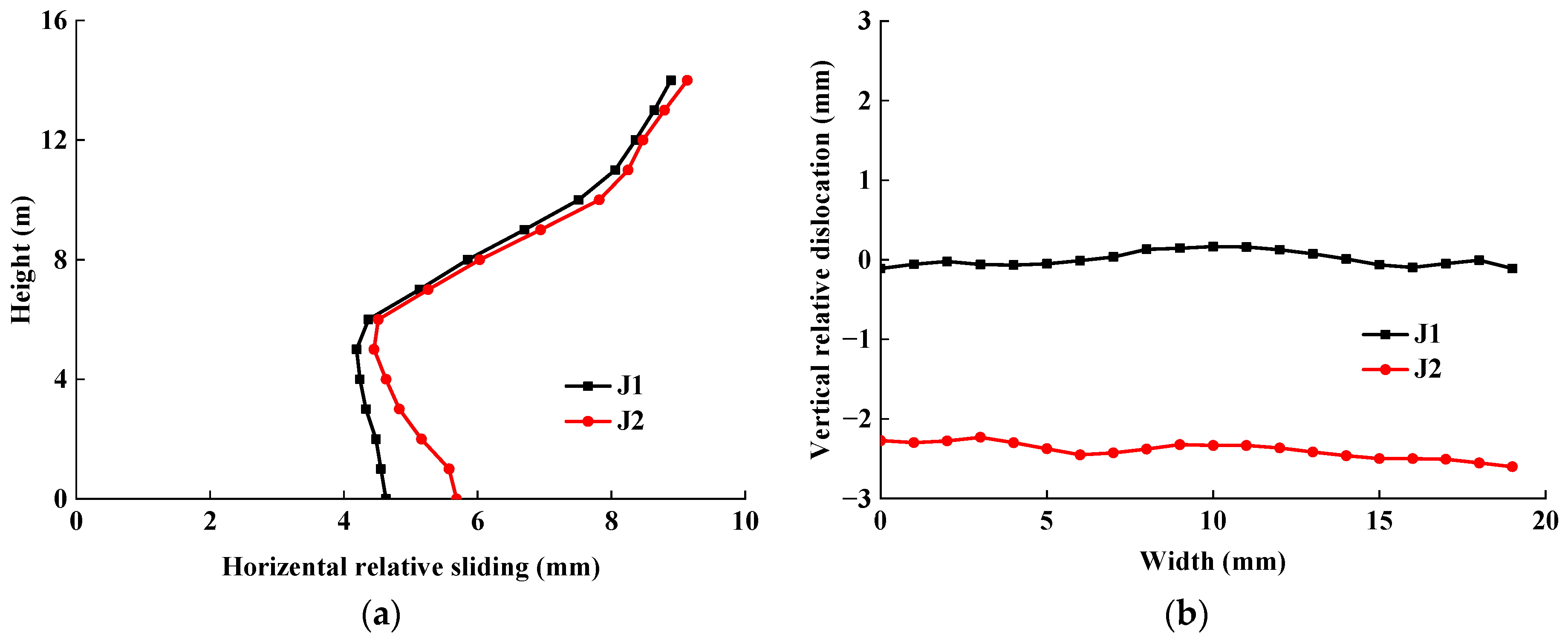
4.1.2. Horizontal Relative Sliding of Structure on Both Sides of Induced Joint
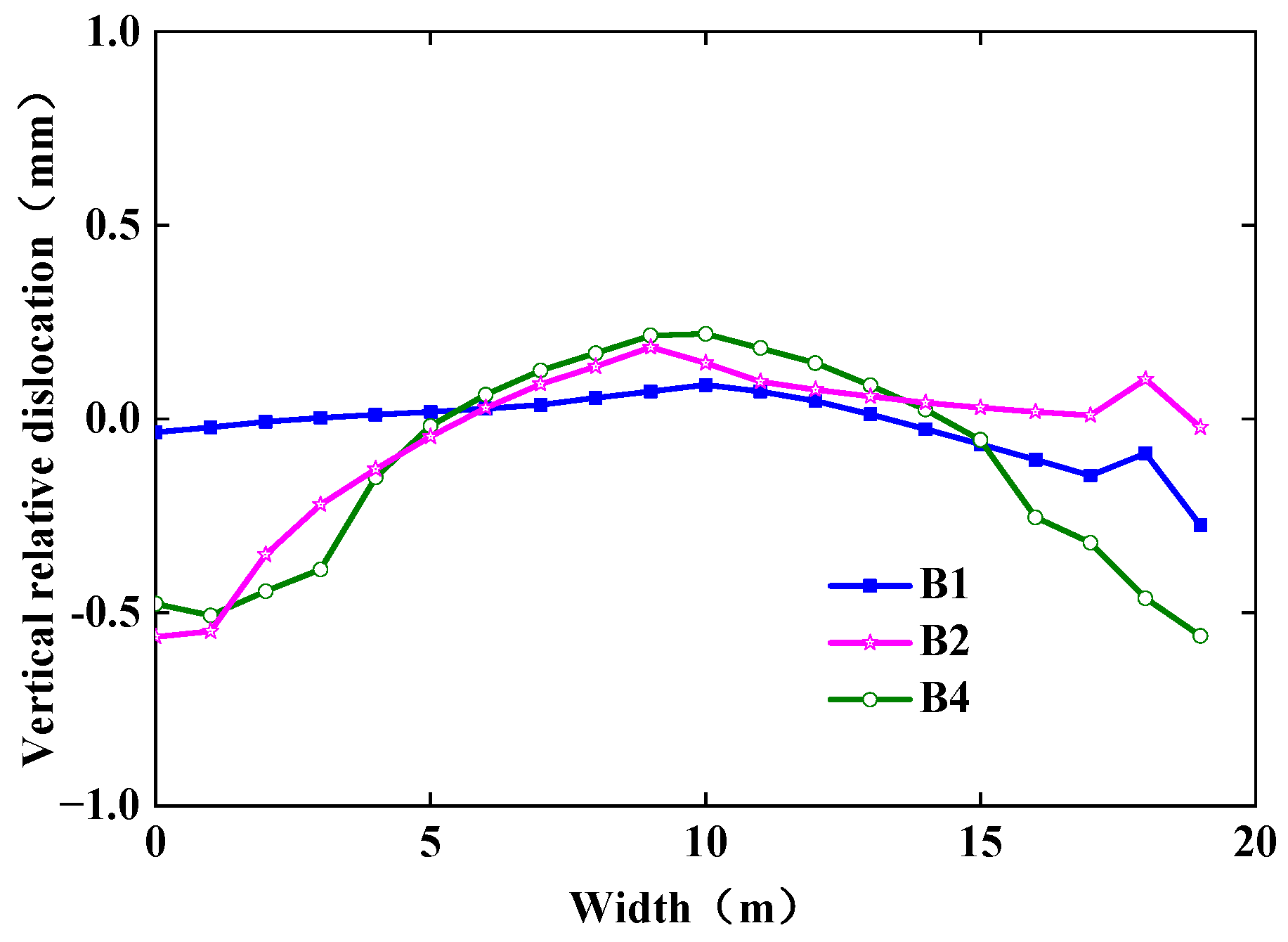
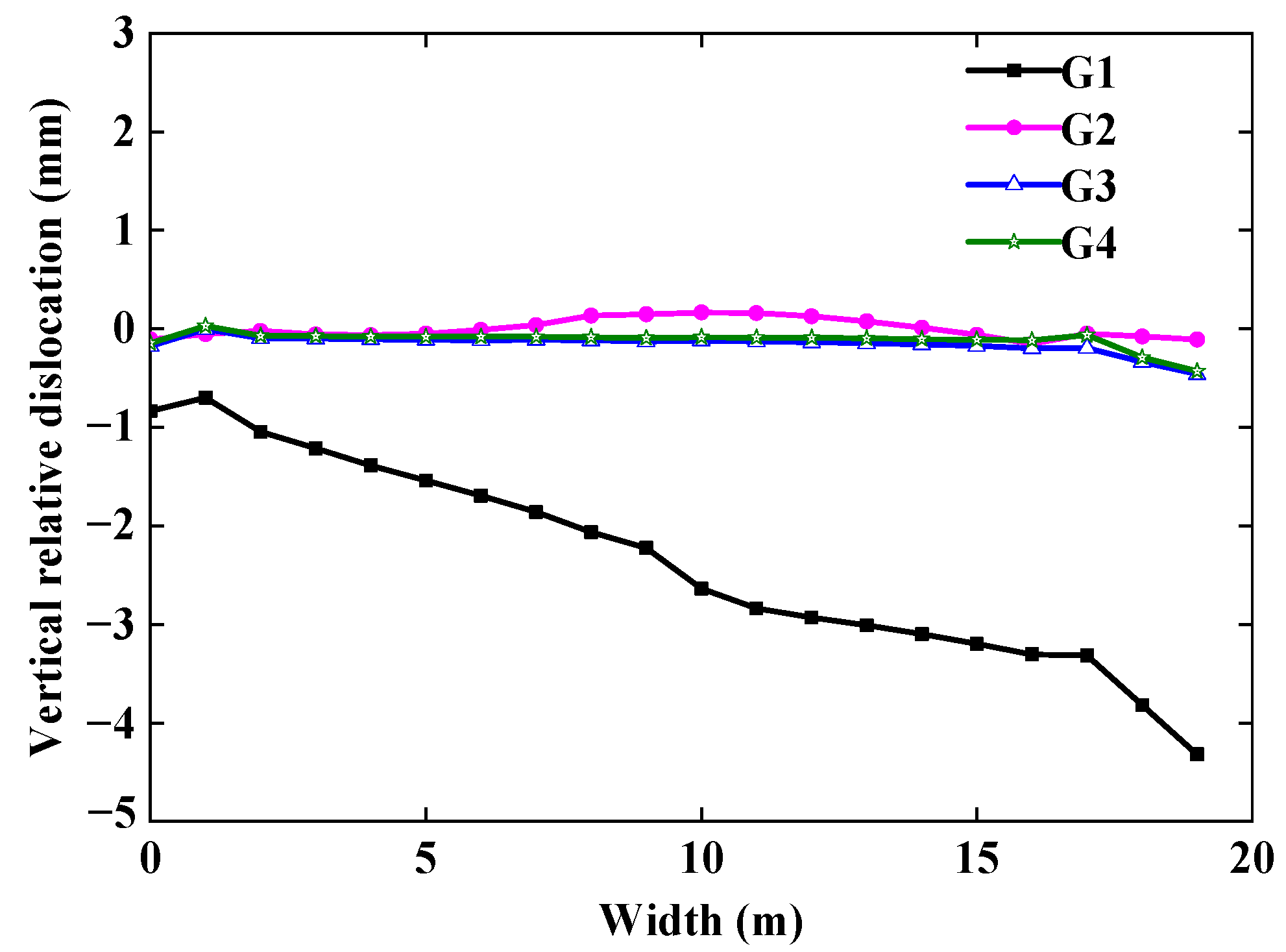
4.1.3. Vertical Relative Dislocation of Structures on Both Sides of Induced Joint
4.2. Influence of Seismic Waves with Different Peak Acceleration
4.2.1. Strain of Remaining Longitudinal Reinforcement at Induced Joint
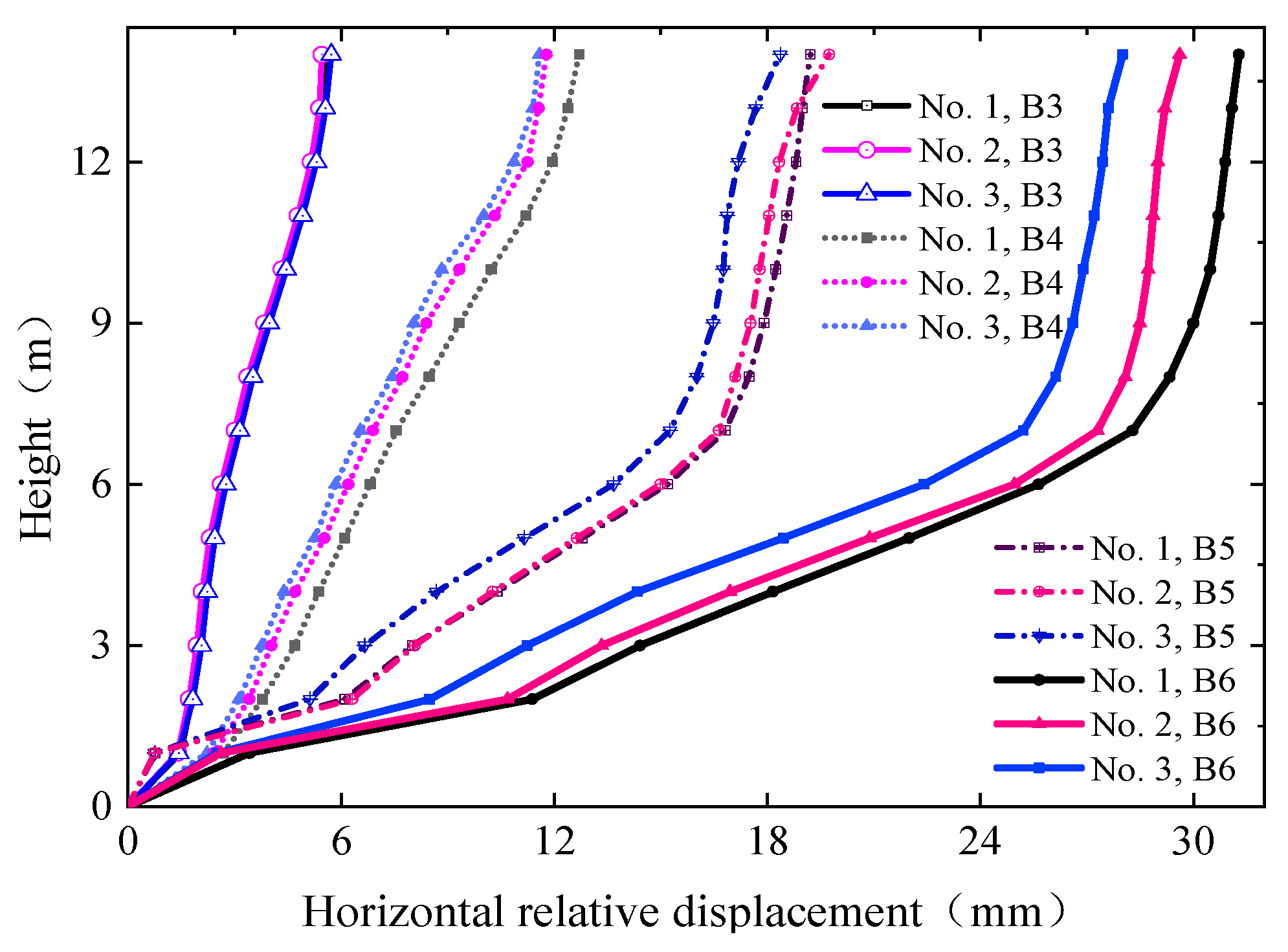
4.2.2. Horizontal Relative Sliding of Structures on Both Sides of Induced Joint
4.3. Influence of Remaining Longitudinal Reinforcement
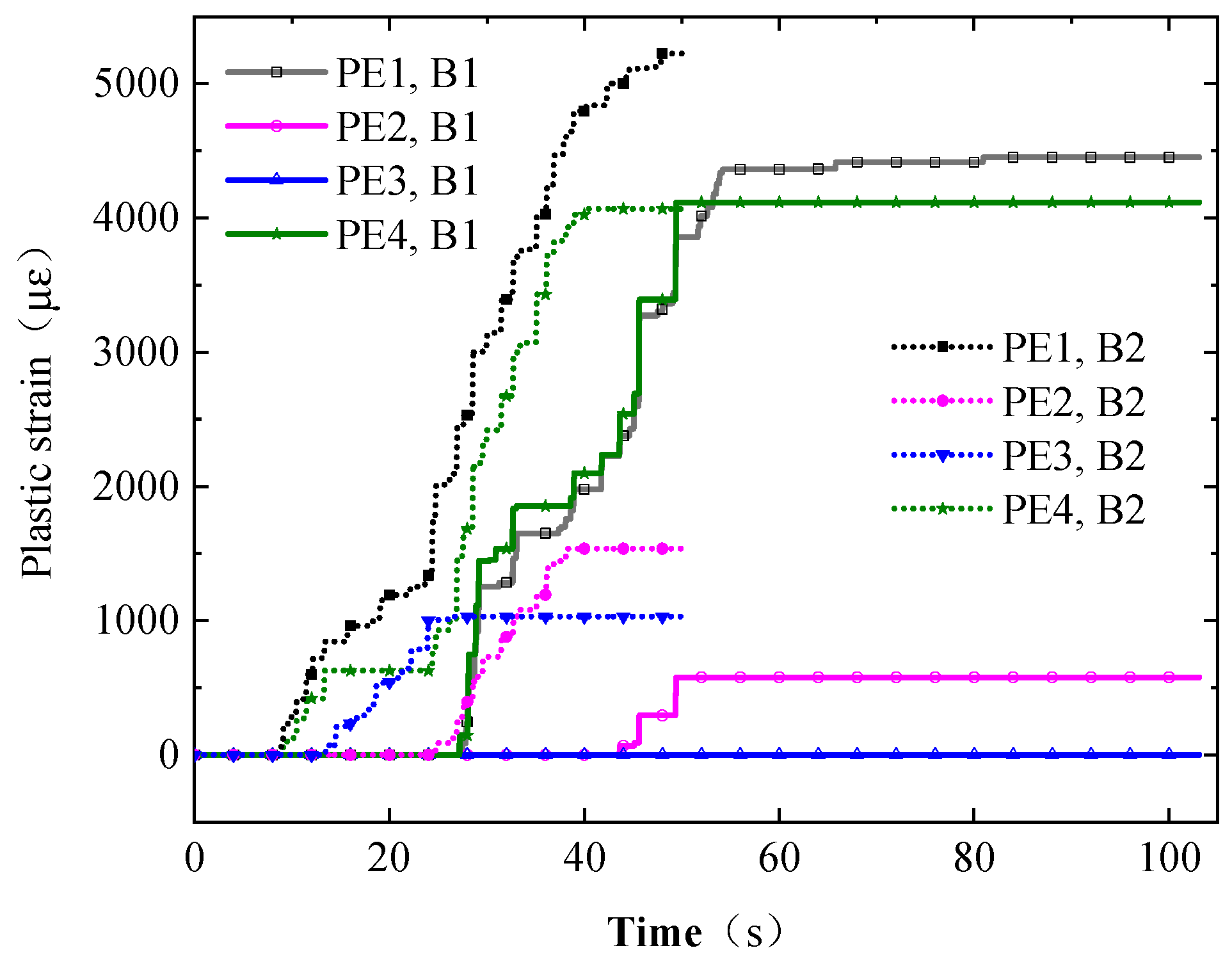
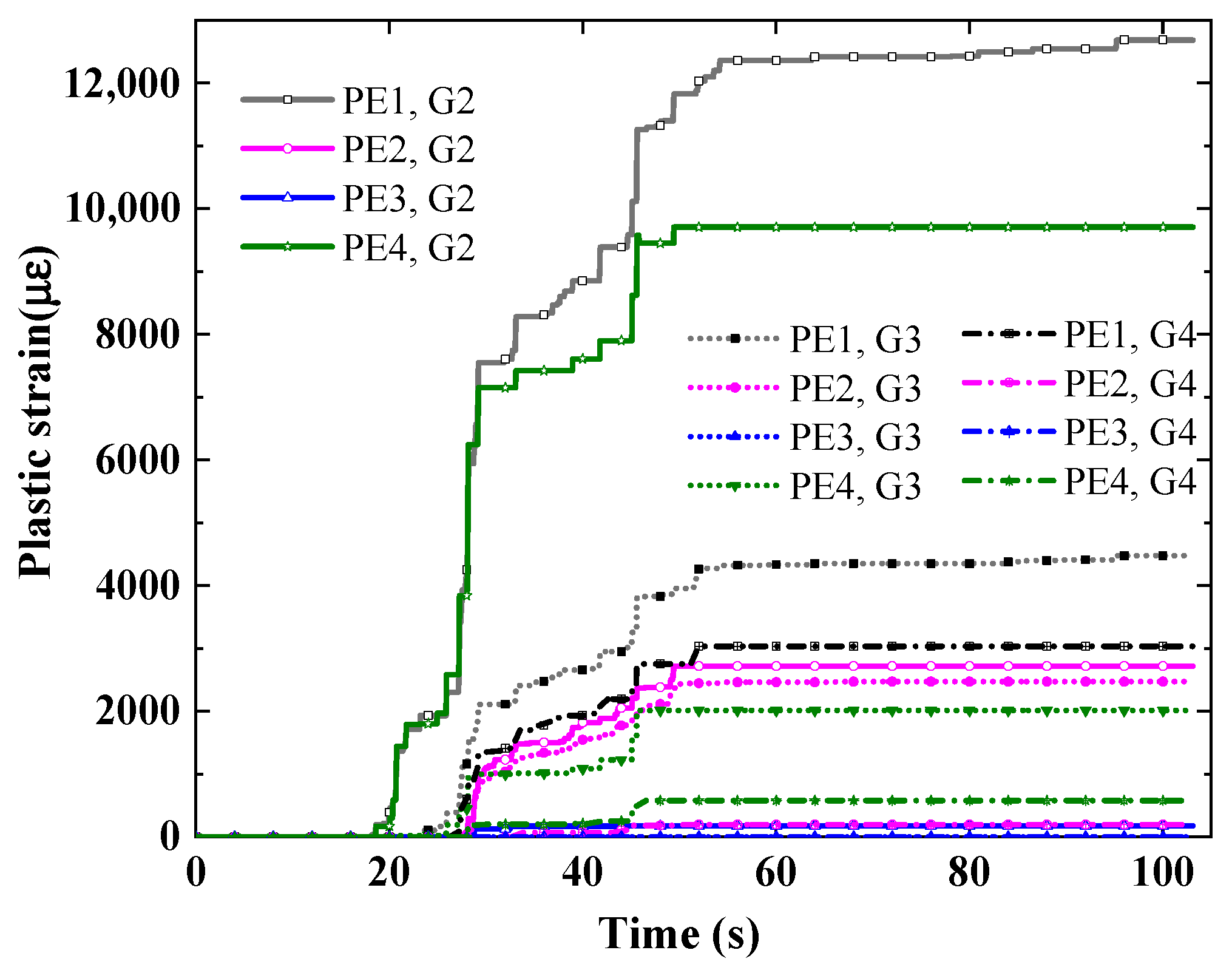
4.3.1. Strain Analysis of Remaining Longitudinal Reinforcement at Induced Joint
4.3.2. Horizontal Relative Sliding of Structures on Both Sides of Induced Joint
4.3.3. Vertical Relative Dislocation of Structures on Both Sides of Induced Joint
4.4. Influence of the Key Groove
5. Conclusions and Suggestions
- (1)
- The structure at the induced joint section is more likely to be damaged due to large horizontal relative displacement and is the weak section of the subway station structure. The horizontal relative sliding of the structures on both sides of the induced joint gradually increases from bottom to top along the subway station structure. With an increase in earthquake intensity, the horizontal relative sliding of the structures on both sides of the induced joint becomes larger, and the horizontal relative sliding of the top structure at the section of the induced joint of the subway station is more obvious.
- (2)
- The horizontal relative sliding and vertical relative misalignment of the structures on both sides of the induced joint can be reduced by increasing the reinforcement ratio of the remaining longitudinal reinforcement in the induced joint.
- (3)
- The vertical relative dislocation of structures on both sides of the induced joint along the width direction of the subway station section is generally larger at both ends and smaller in the middle. With an increase in earthquake intensity, the vertical relative dislocation is smaller.
- (4)
- Under the action of Songpan and Taft waves, the plastic deformation of the remaining longitudinal reinforcement at the induced joint is mainly concentrated in the duration of strong earthquake action. However, under the action of Xi’an artificial waves, the plastic deformation of the remaining longitudinal reinforcement at the induced joint runs through the whole process of earthquake action, and the cumulative effect of plastic strain is significant. With an increase in earthquake intensity, the plastic deformation of the remaining longitudinal reinforcement at the induced joint increases.
- (5)
- The key groove on the bottom plate has little effect on the horizontal relative sliding of the structures on both sides of the induced joint at the bottom layer but has a significant effect on controlling the vertical relative dislocation of the structures on both sides of the induced joint.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hashash, Y.M.A.; Hook, J.J.; Schmidt, B.; Yao, J.I. Seismic design and analysis of underground structures. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2001, 16, 247–293. [Google Scholar] [CrossRef]
- Smerzini, C.; Avilés, J.; Sánchezlogesma, F.J.; Paolucci, R. Analytical solutions for the seismic response of underground structures under SH wave propagation. Aip Conf. Am. Inst. Phys. 2008, 1020, 674–683. [Google Scholar]
- Naggar, H.E.; Hinchberger, S.D.; Naggar, M. Simplified analysis of seismic in-plane stresses in composite and jointed tunnel linings. Soil Dyn. Earthq. Eng. 2008, 28, 1063–1077. [Google Scholar] [CrossRef]
- Kazemeini, M.J.; Haghshenas, E.; Kamalian, M. Experimental evaluation of seismic site response over and nearby underground cavities (study of subway tunnel in city of Karaj, Iran). Iran. J. Sci. Technol. Trans. Civ. Eng. 2015, 39, 319–322. [Google Scholar]
- Dadfar, B.; Naggar, M.E.; Nastev, M. Experimental and analytical study of seismic site response of discontinuous permafrost. Can. Geotech. J. 2016, 53, 1363–1375. [Google Scholar] [CrossRef]
- Hushmand, A.; Dashti, S.; Davis, C.; McCartney, J.S.; Hushmand, B. A centrifuge study of the influence of site response, relative stiffness, and kinematic constraints on the seismic performance of buried reservoir structures. Soil Dyn. Earthq. Eng. 2016, 88, 427–438. [Google Scholar] [CrossRef]
- Amorosi, A.; Boldini, R.; Elia, R. Parametric study on seismic ground response by finite element modelling. Comput. Geotech. 2010, 37, 515–528. [Google Scholar] [CrossRef]
- Ichimura, T.; Tanaka, S.; Hori, M.; Yamamoto, Y.; Dobashi, H.; Osada, M.; Ohbo, N.; Yamada, T. Full three-dimensional seismic response analysis of underground structures with large complex cross sections and two-step analysis method for reducing the computational costs. J. Earthq. Tsunami 2016, 10, 1640016. [Google Scholar] [CrossRef]
- Schanze, E.; Schanze, E.; Gomez, M.; Lopez, A. Numerical study of the seismic response of an instrumented building with underground stories. Appl. Sci. 2021, 11, 3190. [Google Scholar] [CrossRef]
- Jeng, D.S.; Lu, J.F. Vibration analysis of a circular tunnel with jointed liners embedded in an elastic medium subjected to seismic waves. J. Vib. Acoust. Trans. ASME 2009, 131, 021005. [Google Scholar] [CrossRef]
- Lin, G.; Lu, S.; Liu, J. Transmitting boundary for transient analysis of wave propagation in layered media formulated based on acceleration unit-impulse response. Soil Dyn. Earthq. Eng. 2016, 90, 494–509. [Google Scholar] [CrossRef]
- Carlos, G.M.; Jesus, G.G.; Claudio, O.M. Enhanced simplified method for pseudostatic analysis of seismic internal forces in rectangular underground structures. J. Geotech. Geoenviron. Eng. 2021, 147, 04021090. [Google Scholar]
- Mehdi, P.; Saeed, M.H.; Amirabbas, F. Seismic response of the ground surface including underground horseshoe-shaped cavity. Transp. Infrastruct. Geotechnol. 2021, 9, 338–355. [Google Scholar]
- Zhao, M.; Gao, Z.D.; Du, X.L.; Wang, J.J.; Zhong, Z.L. Response spectrum method for seismic soil-structure interaction analysis of underground structure. Bull. Earthq. Eng. 2019, 17, 5339–5363. [Google Scholar] [CrossRef]
- Iwatate, T.; Kobayashi, Y.; Kusu, H.; Rin, K. Investigation and shaking table tests of subway structures of the Hyogoken-Nanbu earthquake. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; New Zealand Society for Earthquake Engineering: Wellington, New Zealand, 2000. [Google Scholar]
- Chou, J.C.; Kutter, B.L.; Travasarou, T.; Chacko, J.M. Centrifuge modeling of seismically induced uplift for the BART Transbay Tube. J. Geotech. Geoenviron. Eng. ASCE 2011, 137, 754–765. [Google Scholar] [CrossRef]
- Cilingir, U.; Madabhushi, S.P.G. A model study on the effects of input motion on the seismic behaviour of tunnels. Soil Dyn. Earthq. Eng. 2011, 31, 452–462. [Google Scholar] [CrossRef]
- Baziar, M.H.; Moghadam, M.R.; Kim, D.S.; Choo, Y.W. Effect of underground tunnel on the ground surface accelerationl. Tunn. Undergr. Space Technol. 2014, 44, 10–22. [Google Scholar] [CrossRef]
- Ulgen, D.; Saglam, S.; Ozkan, M.Y. Dynamic response of a flexible rectangular underground structure in sand: Centrifuge modeling. Bull. Earthq. Eng. 2015, 13, 2547–2566. [Google Scholar] [CrossRef]
- Dashti, S.; Hashash, Y.M.A.; Gillis, K.; Musgrove, M.; Walker, M. Development of dynamic centrifuge models of underground structures near tall buildings. Soil Dyn. Earthq. Eng. 2016, 86, 89–105. [Google Scholar] [CrossRef]
- Masoud, R.M.; Mohammad, H.B. Seismic ground motion amplification pattern induced by a subway tunnel: Shaking table testing and numerical simulation. Soil Dyn. Earthq. Eng. 2016, 83, 81–97. [Google Scholar]
- Quan, D.Z.; Chai, S.B.; Chen, S.; Wang, Y.H. Experimental study on seismic response of subway station built in loess. Lat. Am. J. Solids Struct. 2020, 17, e282. [Google Scholar] [CrossRef]
- Moss, R.; Crosariol, V.A. Scale model shake table testing of an underground tunnel cross section in soft clay. Earthq. Spectra 2013, 29, 1413–1440. [Google Scholar] [CrossRef]
- Tabatabaiefar, H.R. Development of synthetic soil mixture for experimental shaking table tests on building frames resting on soft soils. Geomech. Geoengin. 2016, 12, 28–35. [Google Scholar] [CrossRef]
- Zhuang, H.Y.; Wang, X.; Miao, Y.; Yao, E.; Chen, S.; Ruan, B.; Chen, G.X. Seismic responses of a subway station and tunnel in a slightly inclined liquefiable ground through shaking table test. Soil Dyn. Earthq. Eng. 2019, 116, 371–385. [Google Scholar]
- Adampira, M.; Derakhshandi, M.; Ghalandarzadeh, A. Experimental study on seismic response characteristics of liquefiable soil layers. J. Earthq. Eng. 2021, 25, 1287–1315. [Google Scholar] [CrossRef]
- Wang, J.N.; Yang, J.; Zhuang, H.Y.; Ma, G.W.; Sun, Y.J. Seismic responses of a large unequal-span underground subway station in liquefiable soil using shaking table test. J. Earthq. Eng. 2022, 26, 8446–8467. [Google Scholar] [CrossRef]
- Parra, M.G.J.; Bobet, A.; Ramirez, J.A. Evaluation of soil-structure interaction and structural collapse in Daikai subway station during Kobe earthquake. ACI Struct. J. Am. Concr. Inst. 2006, 103, 113–122. [Google Scholar]
- Abate, G.; Massimino, M.R.; Maugeri, M.; Muir Wood, D. Numerical modelling of a shaking table test for soil-foundation-superstructure interaction by means of a soil constitutive model implemented in a FEM code. Geotech. Geol. Eng. 2010, 28, 37–59. [Google Scholar] [CrossRef]
- Long, H.; Chen, G.X.; Zhuang, H.Y. Analysis of seismic response influence of high rise building nearby subway station in soft site. Appl. Mech. Mater. 2012, 166–169, 2105–2111. [Google Scholar] [CrossRef]
- Conti, R.; Viggiani, G.M.; Perugini, F. Numerical modelling of centrifuge dynamic tests of circular tunnels in dry sand. Acta Geotech. 2014, 9, 597–612. [Google Scholar] [CrossRef]
- Abate, G.; Massimino, M.; Maugeri, M. Numerical modelling of centrifuge tests on tunnel–soil systems. Bull. Earthq. Eng. 2015, 13, 1927–1951. [Google Scholar] [CrossRef]
- Keykhosropour, L.; Lemnitzer, A. Seismic response behavior of deep flexible underground structures in sand-insights from an experimental-numerical investigation. Bull. Earthq. Eng. 2022, 20, 5205–5231. [Google Scholar] [CrossRef]
- Yoo, M.; Kwon, S.Y.; Hong, S. Dynamic response evaluation of deep underground structures based on numerical simulation. Geomech. Eng. 2022, 29, 269–279. [Google Scholar]
- Sun, Q.Q.; Peng, D.; Dias, D. Seismic performances of three- and four-sided box culverts: A comparative study. Geomech. Eng. 2020, 22, 49–63. [Google Scholar]
- Wang, Q.; Geng, P.; Guo, X.Y.; Wang, X.; Li, P.; Zhao, B. Case study on the seismic response of a subway station combined with a flyover. Undergr. Space 2021, 6, 665–677. [Google Scholar] [CrossRef]
- Alejandro, R.C.; Victor, M.C.; Fabian, I.P. Seismic response of underground and floating tunnels. Pure Appl. Geophsics 2022, 179, 973–992. [Google Scholar]
- GB 50909-2014; Code for Seismic Design of Urban Rail Transit Structures. China Planning Publishing House: Beijing, China, 2014.
- Du, X.L.; Zhao, M.; Wang, J.T. Artificial stress boundary conditions for near field wave simulation. J. Mech. 2006, 1, 49–56. [Google Scholar]
- Du, X.L.; Zhao, M. Seismic response analysis method of arch dam based on viscoelastic boundary. J. Water Conserv. 2006, 9, 1063–1069. [Google Scholar]



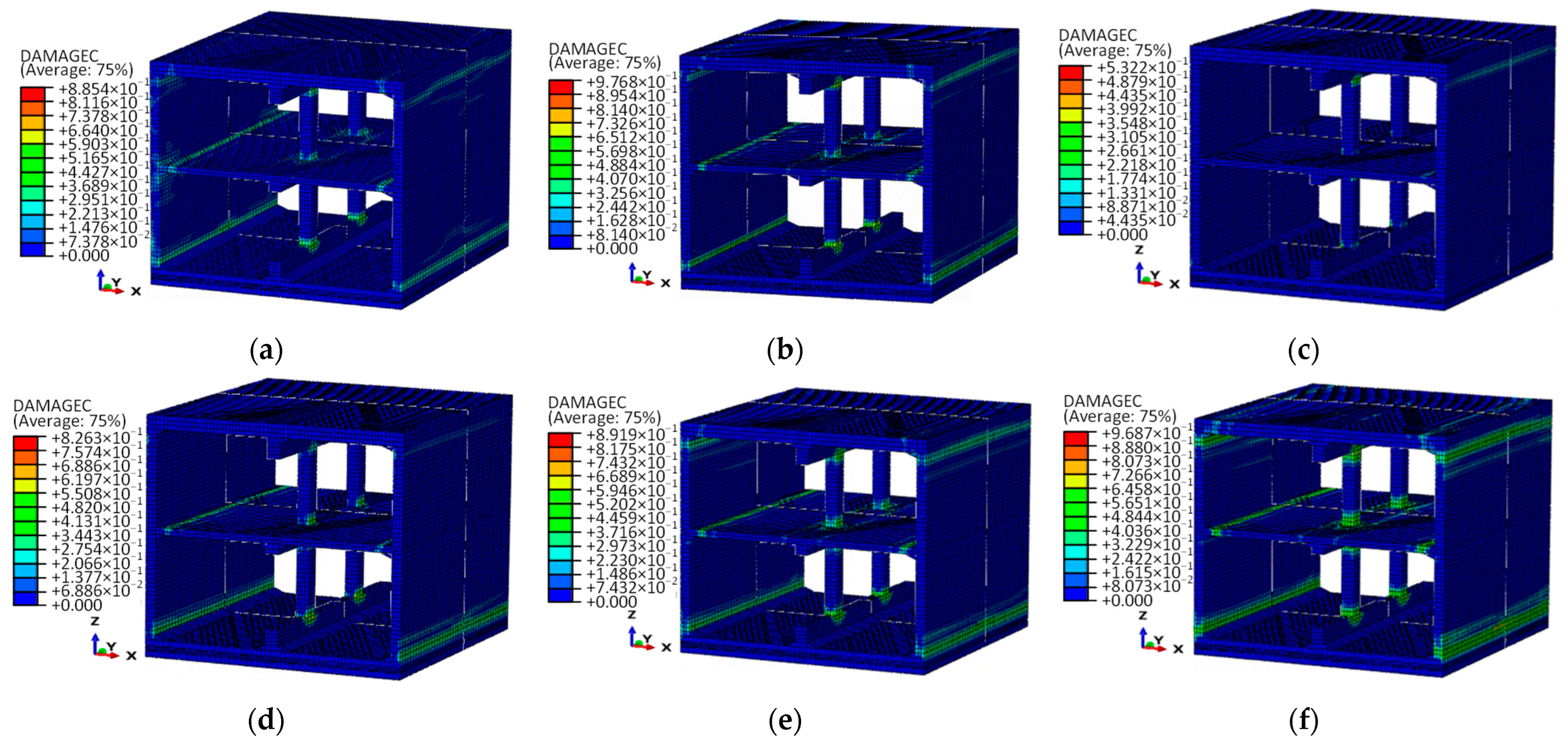
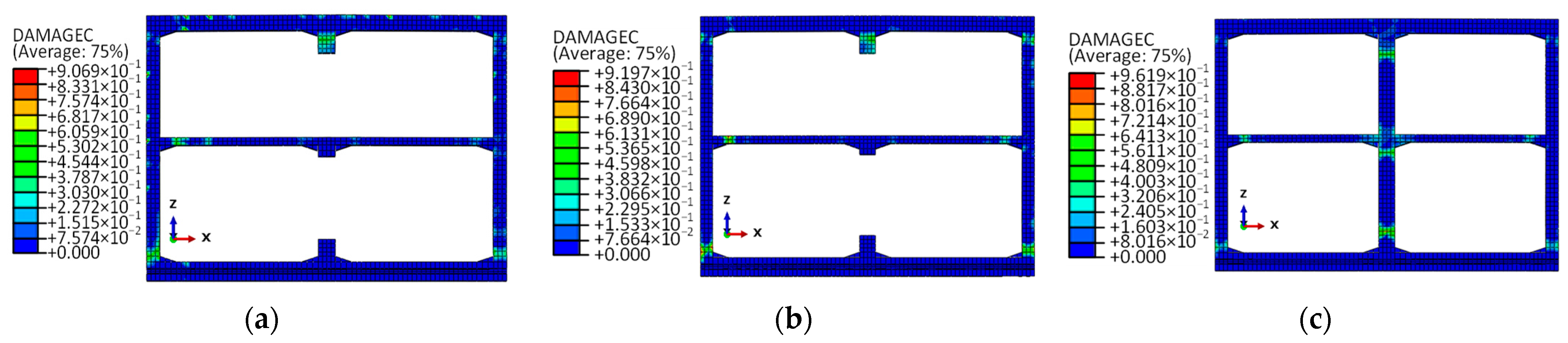



| Layer | Thickness h (m) | Density ρ (g/cm3) | Poisson’s Ratio | Gmax (MPa) |
|---|---|---|---|---|
| 1 | 0.15 | 1.67 | 0.31 | 6.8 |
| 2~6 | 0.25 | 1.67 | 0.31 | 6.8 |
| Model Parameter | Values | Model Parameter | Values |
|---|---|---|---|
| Density (kg/m3) | 2500 | Dilatancy angle Ψ (°) | 30 |
| Elastic modulus E (MPa) | 0.66 × 104 | Viscosity coefficient µ | 0.0005 |
| Poisson’s ratio υ | 0.2 | Invariant stress ratio Kc | 0.6667 |
| Ultimate compressive stress | 5.39 | Damping ratio ξ | 0.1 |
| Layer | Thickness (m) | Density (g/cm3) | Poisson’s Ratio | Shear Wave Velocity (m/s) | Gmax (MPa) | γγ (103) | λmax | β |
|---|---|---|---|---|---|---|---|---|
| New loess | 0~6 | 1960 | 0.26 | 205 | 43.6 | 2.060 | 0.100 | 0.2720 |
| New loess | 6~13 | 2010 | 0.26 | 241 | 48.7 | 3.772 | 0.058 | 0.2420 |
| ancient soil | 13~17 | 1540 | 0.26 | 271 | 82.3 | 2.258 | 0.137 | 0.3963 |
| ancient loess | 17~24 | 1670 | 0.29 | 298 | 97.5 | 2.364 | 0.156 | 0.5951 |
| ancient soil | 24~36 | 1760 | 0.29 | 317 | 123.5 | 2.872 | 0.109 | 0.4829 |
| ancient loess | 36~44 | 2060 | 0.30 | 339 | 63.9 | 3.764 | 0.130 | 0.2428 |
| ancient soil | 44~56 | 2000 | 0.29 | 383 | 95.0 | 1.531 | 0.175 | 0.4751 |
| ancient loess | 56~64 | 1970 | 0.31 | 434 | 95.0 | 2.309 | 0.135 | 0.4318 |
| ancient loess | 64~70 | 1980 | 0.31 | 466 | 92.6 | 2.000 | 0.150 | 0.5401 |
| Model Parameter | Values | Model Parameter | Values |
|---|---|---|---|
| Density (kg/m3) | 2500 | Dilatancy angle Ψ (°) | 36 |
| Elastic modulus E (MPa) | 3.25 × 104 | Viscosity coefficient µ | 0.0005 |
| Poisson’s ratio υ | 0.2 | Invariant stress ratio Kc | 0.6667 |
| Ultimate compressive stress | 26.8 | Damping ratio ξ | 0.1 |
| Working Condition | Seismic Wave | Peak Accelerations | Working Condition | Seismic Wave | Peak Accelerations |
|---|---|---|---|---|---|
| B1 | Songpan wave | 0.2 g | B4 | Taft Wave | 0.2 g |
| B2 | Xi’an artificial wave | 0.2 g | B5 | Taft Wave | 0.4 g |
| B3 | Taft Wave | 0.1 g | B6 | Taft Wave | 0.6 g |
| Working Conditions | Maximum Plastic Strain (με) | |||
|---|---|---|---|---|
| PE1 | PE2 | PE3 | PE4 | |
| B1 | 4450 | 578 | 0 | 4116 |
| B2 | 5226 | 1536 | 1030 | 4068 |
| B4 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, D.; Chai, S.; Wang, Y.; Fan, Z.; Bu, Y. 3-D Numerical Simulation of Seismic Response of the Induced Joint of a Subway Station. Buildings 2023, 13, 1244. https://doi.org/10.3390/buildings13051244
Quan D, Chai S, Wang Y, Fan Z, Bu Y. 3-D Numerical Simulation of Seismic Response of the Induced Joint of a Subway Station. Buildings. 2023; 13(5):1244. https://doi.org/10.3390/buildings13051244
Chicago/Turabian StyleQuan, Dengzhou, Shaobo Chai, Yuling Wang, Zhishuang Fan, and Yonghong Bu. 2023. "3-D Numerical Simulation of Seismic Response of the Induced Joint of a Subway Station" Buildings 13, no. 5: 1244. https://doi.org/10.3390/buildings13051244
APA StyleQuan, D., Chai, S., Wang, Y., Fan, Z., & Bu, Y. (2023). 3-D Numerical Simulation of Seismic Response of the Induced Joint of a Subway Station. Buildings, 13(5), 1244. https://doi.org/10.3390/buildings13051244







