Experimental Study on the Coefficient of Earth Pressure at Rest for Sand
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Sand
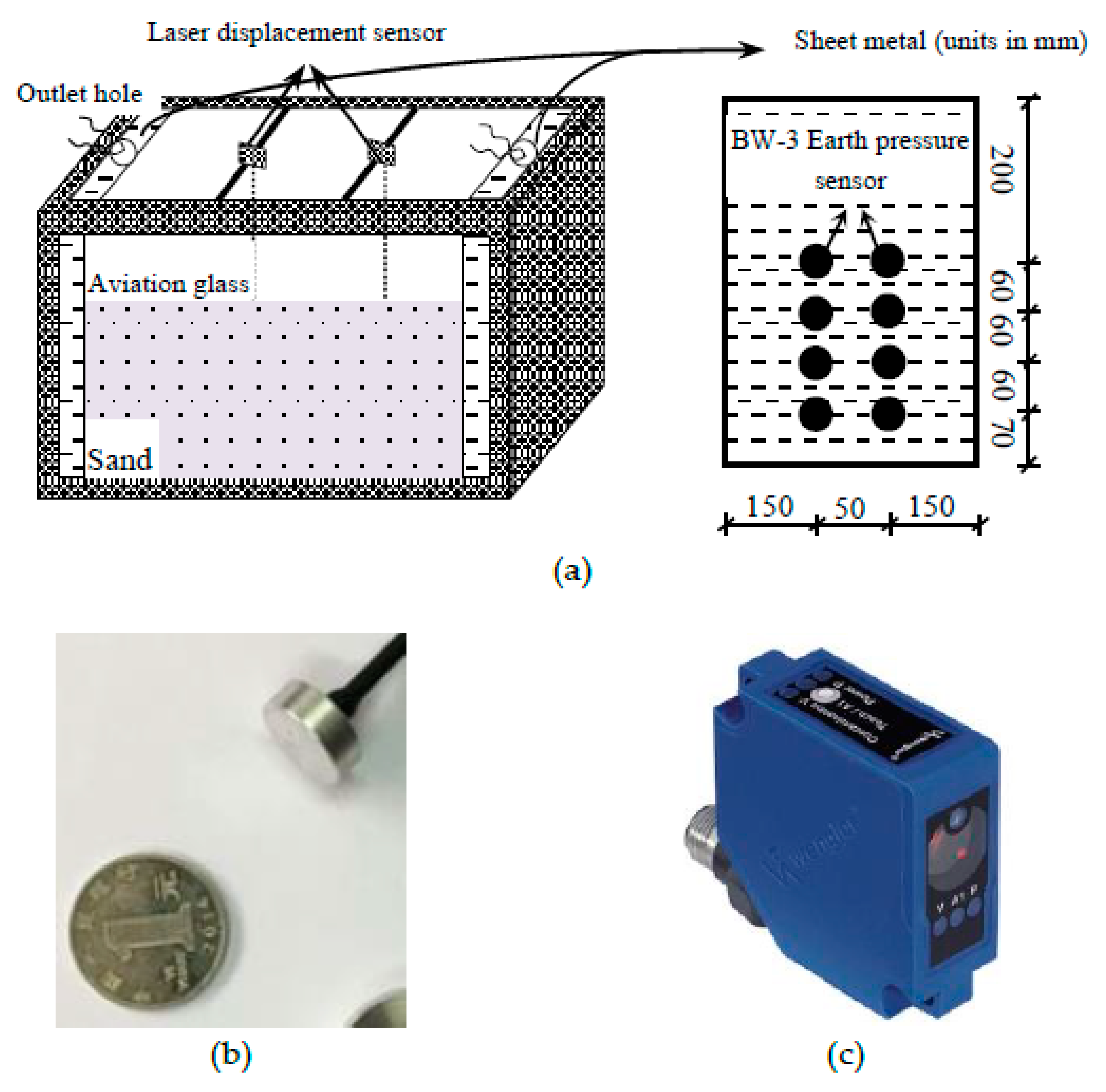
2.2. Test Equipment
2.3. Test Program
3. Results
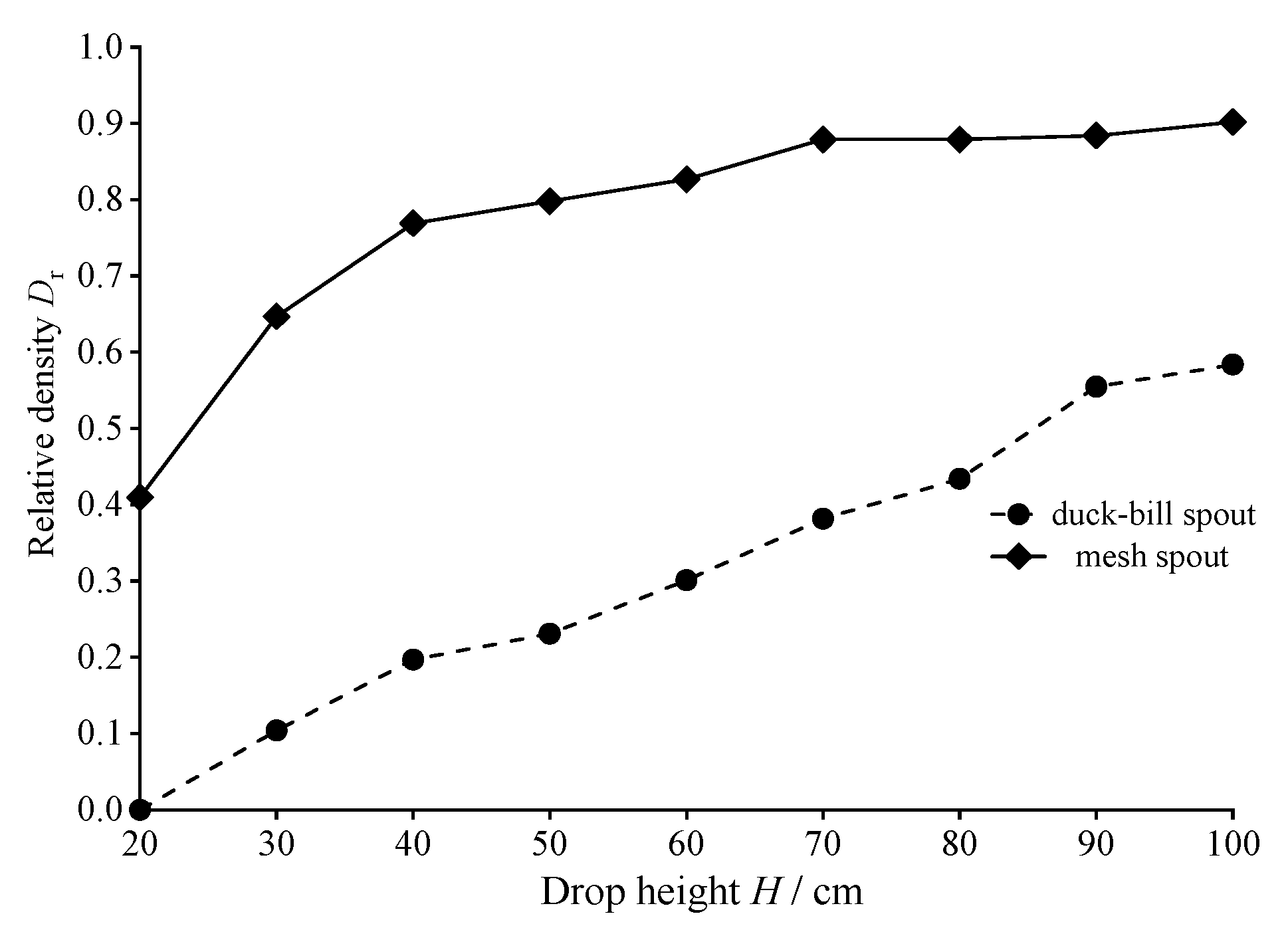
3.1. The Relationship between Drop Distance and Relative Density from the Sand Pluviation Test
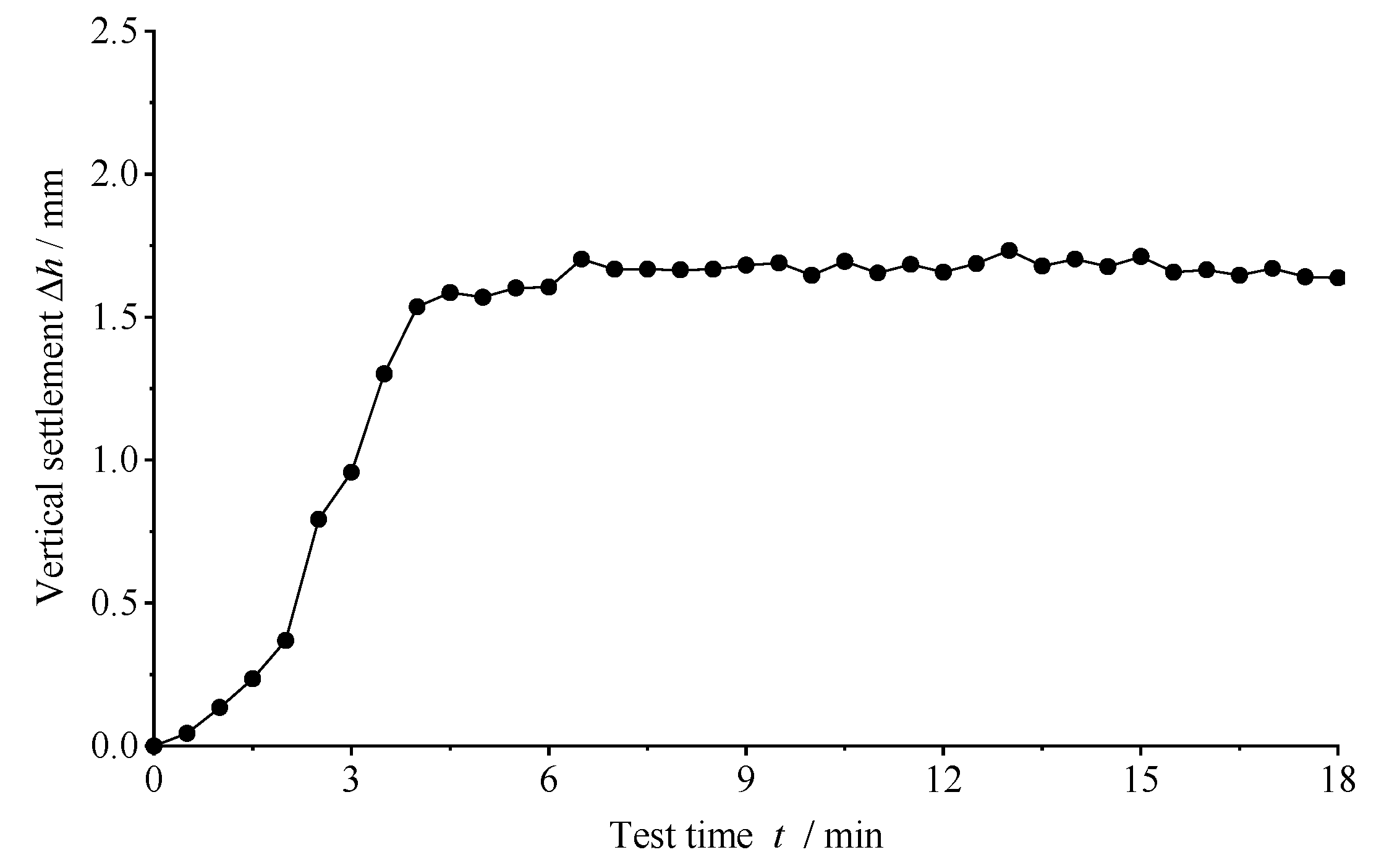
3.2. Analysis of Soil Sample Settlement
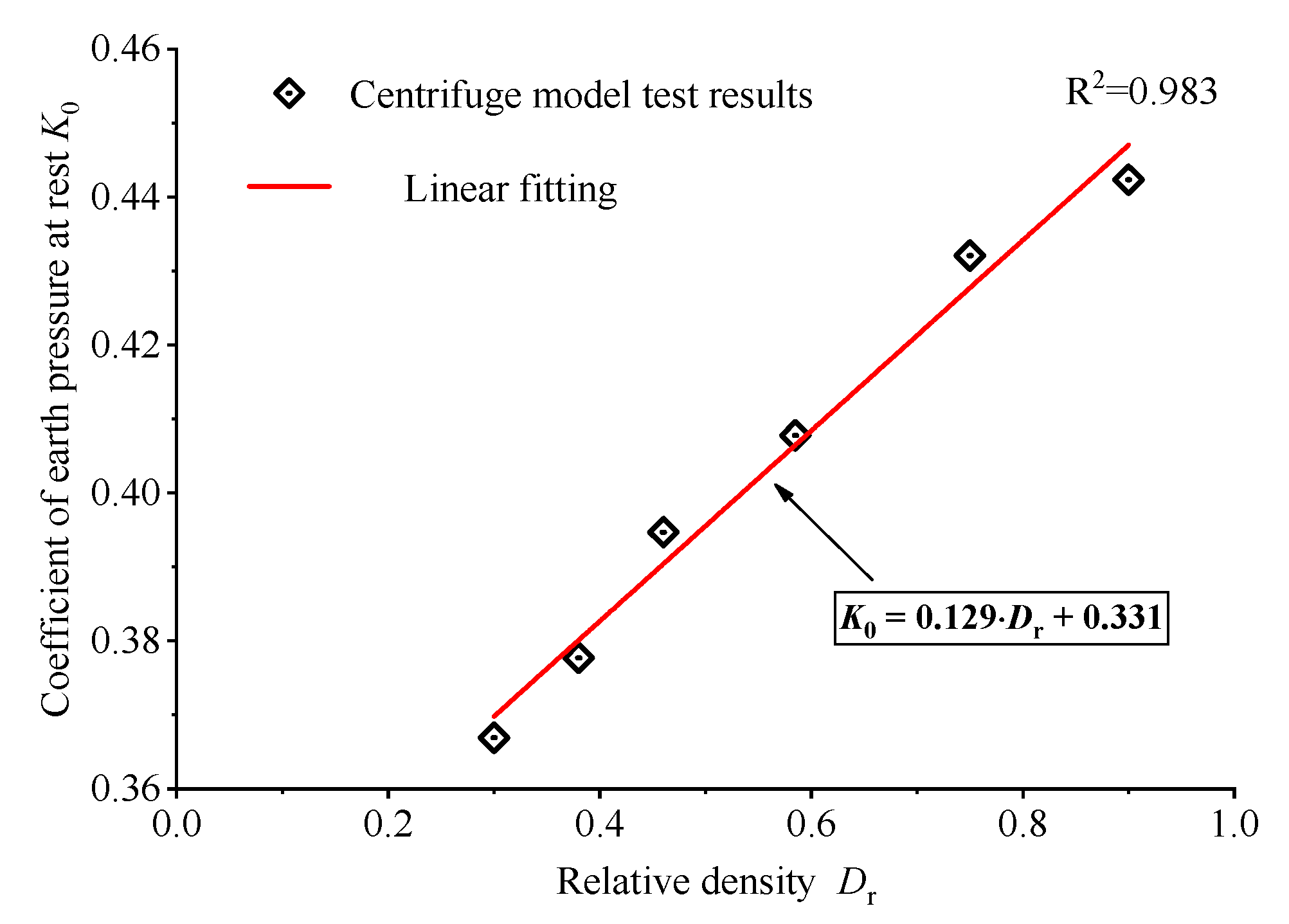
3.3. Effect of Relative Density on the Coefficient of Earth Pressure at Rest
4. Analysis and Discussion
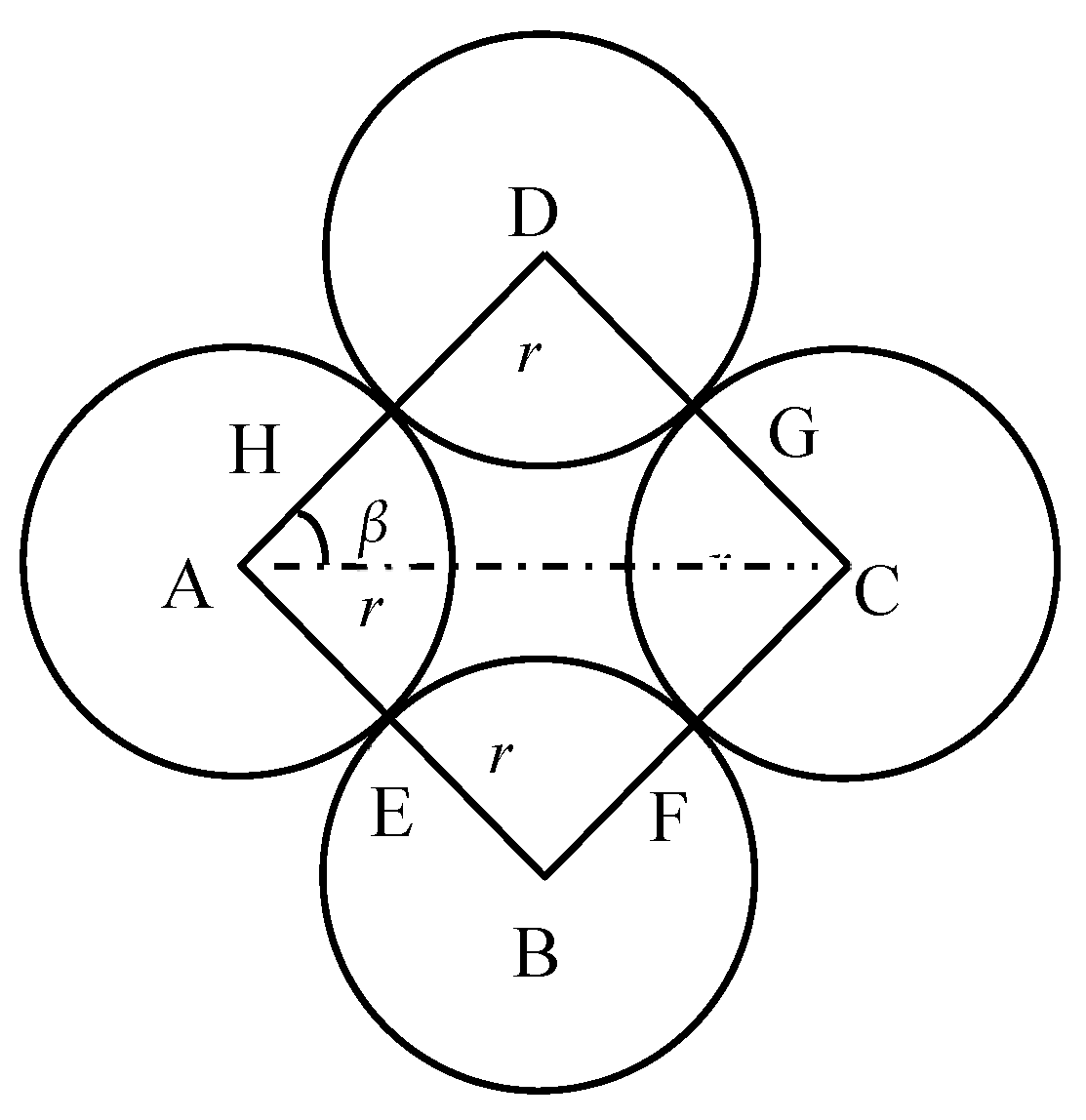
4.1. Mechanism Analysis of the Coefficient of Lateral Pressure at Rest
4.2. Discussion
5. Conclusions
- (1)
- It is simpler to prepare soil samples with relatively loose densities using the duck-bill sand spout, while the mesh sand spout is more suited for denser soil samples. Moreover, when the drop height of the two sand spouts is minimal, the relative density of the soil samples gradually increases with drop height. Once the drop height reaches a certain level, the relative density of the soil samples shows minimal changes.
- (2)
- In the centrifugal model test, where the K0 value of sand was determined, the maximum settlement of the sand layer was 1.74 mm. For the sand specimens with a height of 320 mm, the change in the self-weight stress of the sand caused by the centrifugal acceleration had a negligible effect on its vertical deformation and could be disregarded.
- (3)
- The results of the centrifugal model test showed that the coefficient K0 demonstrated a good linear increasing trend with an increase in the initial Dr of sand. Therefore, the following formula was proposed for the relationship between K0 and relative density Dr: K0 = 0.129 Dr + 0.331.
- (4)
- The meso-evolution analysis model of the pressure coefficient on the stationary side of sand was improved, and the relationship between K0, the displacement deflection angle θ, and the friction offset angle μ was obtained. The relationship between the coefficient K0 and the volume fraction of meso-particles ψ was established. Lastly, the influence mechanism of Dr on the coefficient K0 was shown from the meso-level.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| φ | Effective internal friction angle. |
| ν | Poisson’s ratio. |
| γd | Unit weight of soil. |
| γdmin | Minimum weight of the soil. |
| OCR | Over-consolidation ratio. |
| Dr | Relative density. |
| K0 | Coefficient of earth pressure at rest. |
| σz | Vertical stress. |
| z | Depth of the soil layer. |
| n | Acceleration. |
| σx | Minor principal stress. |
| σy | Major principal stress. |
| f0 | Particle contact force |
| Fx | Horizontal force |
| Fy | Vertical force |
| fx | Horizontal component of contact force |
| fy | Vertical component of the contact force |
| μ | Coefficient of friction |
| r | Radius |
| ψ | Volume fraction |
| εx | Horizontal strain |
| εy | Vertical strain |
References
- Terzaghi, K.; Peck, R.B. Soil Mechanics Engineering Practice, 2nd ed.; Wiley: New York, NY, USA, 1967; p. 729. [Google Scholar] [CrossRef]
- Nguyen, N.; Hanna, A. At-Rest Earth Pressure of Over consolidated Collapsible Soil Subjected to Full Inundation. Geotech. Geol. Eng. 2021, 39, 2019–2027. [Google Scholar] [CrossRef]
- Wang, L.; Nagarajaiah, S.; Zhou, Y.; Shi, W. Experimental Study on Adaptive-passive Tuned Mass Damper with Variable Stiffness for Vertical Human-induced Vibration Control. Eng. Struct. 2023, 280, 115714. [Google Scholar] [CrossRef]
- Wang, L.; Shi, W.; Zhou, Y. Adaptive-Passive Tuned Mass Damper for Structural Aseismic Protection Including Soil–Structure Interaction. Soil. Dyn. Earthq. Eng. 2022, 158, 107298. [Google Scholar] [CrossRef]
- Xu, H.; Cai, X.; Wang, H.; Li, S.; Huang, X.; Zhang, S. Analysis of the Working Response Mechanism of Wrapped Face Reinforced Soil Retaining Wall under Strong Vibration. Sustainability 2022, 14, 9741. [Google Scholar] [CrossRef]
- Lee, J.; Lee, D.; Park, D. Experimental Investigation on the Coefficient of Lateral Earth Pressure at Rest of Silty Sands: Effect of Fines. Geotech. Test. J. 2014, 37, 20130204. [Google Scholar] [CrossRef]
- Jaky, J. The coefficient of earth pressure at rest. J. Soc. Hung. Archit. Eng. 1944, 78, 355–357. [Google Scholar] [CrossRef]
- Northcutt, S.; Wijewickreme, D. Effect of Particle Fabric on the Coefficient of Lateral Earth Pressure Observed during One-dimensional Compression of Sand. Can. Geotech. J. 2013, 50, 457–466. [Google Scholar] [CrossRef]
- Mesri, G.; Hayat, T. The coefficient of earth pressure at rest. Can. Geotech. J. 1993, 30, 647–666. [Google Scholar] [CrossRef]
- Yang, K.; Hou, T.; Sun, C. Coefficient of Earth Pressure at Rest of Light Weight Soil Under Complex Loading. Geotech. Geol. Eng. 2023, 41, 2713–2726. [Google Scholar] [CrossRef]
- Wanatowski, D.; Chu, J. Effect of specimen preparation method on the stress-strain behavior of sand in plane-strain compression tests. Geotech. Test. J. 2008, 31, 1–13. [Google Scholar] [CrossRef]
- Oda, M.; Koishikawa, I.; Higuchi, T. Experimental Study of Anisotropic Shear Strength of Sand by Plane Strain Test. Soils Found. 1978, 18, 25–38. [Google Scholar] [CrossRef]
- Sherif, M.A.; Fang, Y.S.; Sherif, R.I. KA and K0 behind Rotating and Non-Yielding Walls. J. Geotech. Eng. 1985, 110, 41–56. [Google Scholar] [CrossRef]
- Matsuoka, H.; Sakakibara, K. A Constitutive Model for Sands and Clays Evaluating Principal Stress Rotation. Soils Found. 1987, 27, 73–88. [Google Scholar] [CrossRef] [PubMed]
- Szepeshazi, R. On the K0 Factor. Period. Polytech. Civ. Eng. 1994, 38, 127–135. [Google Scholar] [CrossRef]
- Sharif, E.I.; Abdel, A.; Yehia, K.T.; Eweada, S.N. Theoretical Study of Earth Pressure at-rest for Sandy Soils. JES 2011, 39, 1–13. [Google Scholar] [CrossRef]
- Chen, C.L.; Jia, Y.J.; Jin, J.; Zhang, D.F.; Sun, Y.R.; Li, F.L. Influences of Water Content and Stress on Coefficient of Lateral Pressure at Rest of Undisturbed Loess. Chin. J. Rock Mech. Eng. 2017, 36, 3535–3542. [Google Scholar] [CrossRef]
- Schnaid, F.; Odebrecht, E.; Sosnoski, J.; Robertson, P.K. Effects of Test Procedure on Flat Dilatometer Test (DMT) Results in Intermediate Soils. Can. Geotech. J. 2016, 53, 1270–1280. [Google Scholar] [CrossRef]
- Deng, S.; Zhang, Y.; Han, J.; Wang, K.; Tian, Z.; Liu, T. An Analytical Study on Penetration and Pore Pressure Dissipation of Piezocone Test in Typical Normally and Over-Consolidated Silty Clays. Appl. Sci. 2023, 13, 3797. [Google Scholar] [CrossRef]
- Reid, D.; Urbina, F.; Tiwari, B.; Fanni, R.; Smith, K.; Fourie, A. Effect of Saturation Confining Pressure on Accessible Densities and Shear Behaviour of a Sandy Silt Tailings. Geotech. Lett. 2023, 13, 1–17. [Google Scholar] [CrossRef]
- Marsland, A.; Randolph, M.F. Comparisons of the Results from Pressure Meter Tests and Large in Situ Plate Tests in London Clay. Géotechnique 1977, 27, 217–243. [Google Scholar] [CrossRef]
- Okochi, Y.; Tatsuoka, F. Some Factors Affecting K0-values of Sand Measured in Triaxial Cell. Soils Found. 1984, 24, 52–68. [Google Scholar] [CrossRef] [PubMed]
- Federico, A.; Elia, G.; Germano, V. A Short Note on the Earth Pressure and Mobilized Angle of Internal Friction in One-Dimensional Compression of Soils. J. Geoeng. 2008, 3, 41–46. [Google Scholar] [CrossRef]
- Chen, S.F.; Kong, L.W.; Luo, T. Lateral Stress Release Characteristics of Over-Consolidated Silty Clay and Calculation Method for Lateral Earth Pressure Coefficient at Rest. Rock Soil Mech. 2022, 43, 160–168. [Google Scholar] [CrossRef]
- Grønbech, G.L.; Ibsen, L.B.; Nielsen, B.N. Earth Pressure at Rest of Søvind Marl—A Highly Over-Consolidated Eocene Clay. Eng. Geol. 2016, 200, 66–74. [Google Scholar] [CrossRef]
- Lee, K.; Kim, J.; Woo, S.I. Analysis of Horizontal Earth Pressure Acting on Box Culverts through Centrifuge Model Test. Appl. Sci. 2022, 12, 1993. [Google Scholar] [CrossRef]
- Cho, H.I.; Park, H.J.; Kim, D.S.; Choo, Y.W. Evaluation of Ko in Centrifuge Model Using Shear Wave Velocity. Geotech. Test. J. 2014, 37, 255–267. [Google Scholar] [CrossRef]
- Abdoun, T.H.; El-Sekelly, W.; Dobry, R. Effect of Overconsolidation on K0 in Centrifuge Models Using Cpt and Tactile Pressure Sensor. Geotech. Test. J. 2015, 38, 150–165. [Google Scholar] [CrossRef]
- Gaudin, C.; Schnaid, F.; Garnier, J. Sand Characterization by Combined Centrifuge and Laboratory Tests. Int. J. Phys. Model. Geotech. 2005, 5, 42–56. [Google Scholar] [CrossRef]
- Xu, G.M.; Chen, A.Z.; Zeng, Y.J.; Gu, X.W.; Cai, Z.Y. Measurement of Boundary Total Stress in a Multi-gravity Environment. Rock Soil Mech. 2007, 9, 2671–2674. [Google Scholar] [CrossRef]
- Cai, Z.Y.; Dai, Z.Y.; Xu, G.M.; Ren, G.F. Study on Calibration Method of Interface Soil Pressure Sensor in Centrifugal Model Test. J. Hydraul. Eng. 2020, 51, 695–704. [Google Scholar] [CrossRef]
- Vahidi-Nia, F.; Bayesteh, H.; Khodaparast, M. Effect of Initial Packing Density, Stress Level and Particle Size Ratio on the Behavior of Binary Granular Material: A Micromechanical Approach. Granul. Matter 2020, 22, 68. [Google Scholar] [CrossRef]
- Wang, L.; Nagarajaiah, S.; Shi, W.; Zhou, Y. Seismic Performance Improvement of Base-Isolated Structures Using a Semi-Active Tuned Mass Damper. Eng. Struct. 2022, 271, 114963. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, G.; Wang, Z.; Yuan, S. Research on the Effect of Particle Size on the Interface Friction between Geogrid Reinforcement and Soil. Sustainability 2022, 14, 15443. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, S.; Zhao, J.; Zhou, X. The Microscopic Origin of K0 on Granular Soils: The Role of Particle Shape. Acta Geotech. 2021, 16, 2089–2109. [Google Scholar] [CrossRef]
- Sun, Q.C.; Jin, F.; Wang, G.Q.; Zhang, G.H. Force Chains in a Uniaxially Compressed Static Granular Matter in 2D. Acta Phys. Sin. 2010, 59, 30–37. [Google Scholar] [CrossRef]
- Li, X.; Li, X.S. Micro-Macro Quantification of the Internal Structure of Granular Materials. J. Eng. Mech. 2009, 135, 641–656. [Google Scholar] [CrossRef]
- Michalowski, R.L. Coefficient of Earth Pressure at Rest. J. Geotech. Geoenviron. 2005, 131, 1429–1433. [Google Scholar] [CrossRef]
- Bowles, J.E. Foundation Analysis and Design, 5th ed.; The McGraw-Hill Companies: New York, NY, USA, 2004; pp. 107–108. [Google Scholar]
- Sun, Y.Z.; Shao, L.T.; Fan, Z.Q.; Tian, S.L. Experimental Research on Poisson’s Ratio of Sandy Soil. Rock Soil Mech. 2009, 30, 63–68. [Google Scholar] [CrossRef]
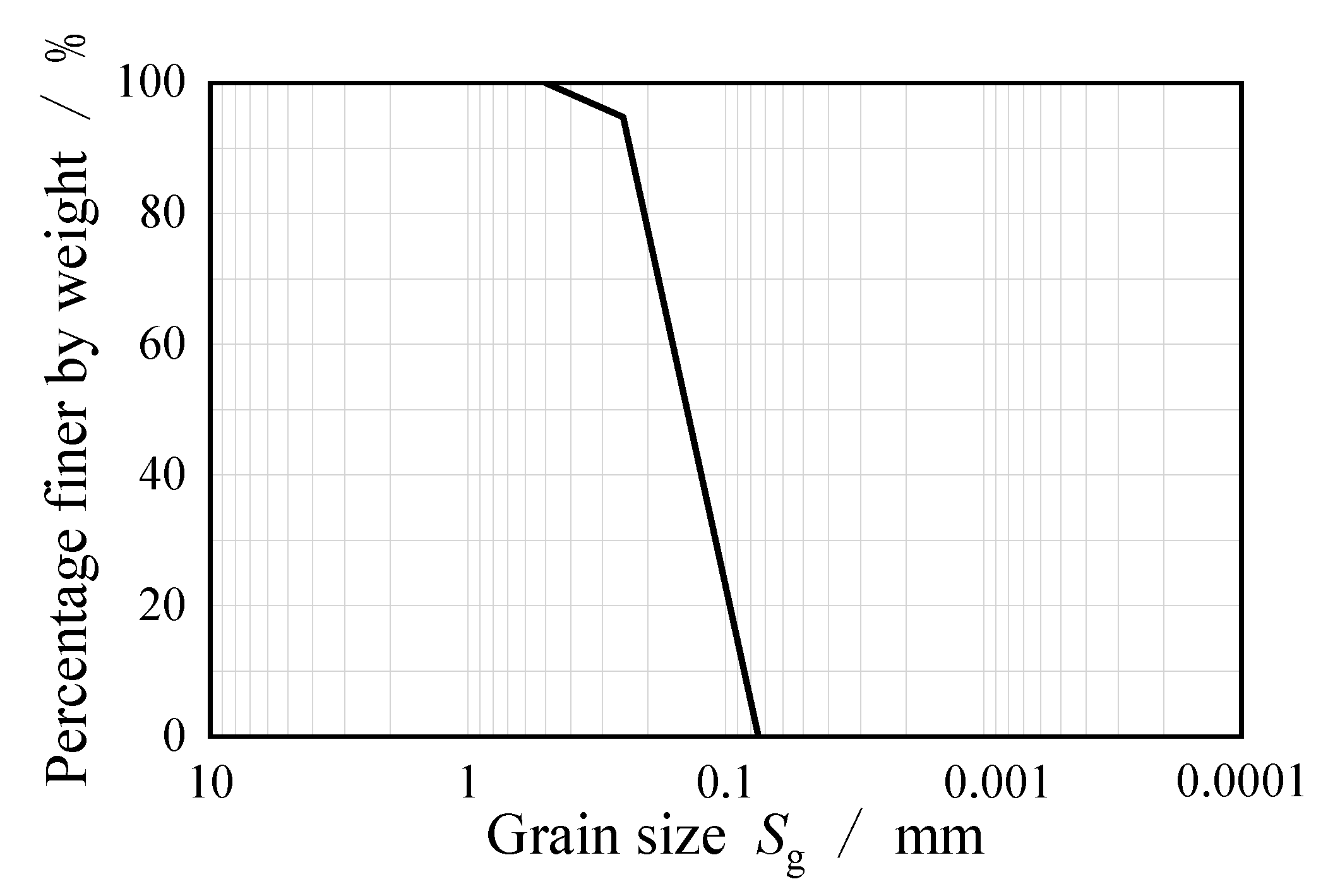





| Specific Gravity Gs | Min. Mass Density ρmin/(g/cm3) | Max. Mass Density ρmax/(g/cm3) | Median Size D50/mm | Coefficient of Uniformity Cu | Coefficient of Curvature Cc |
|---|---|---|---|---|---|
| 2.65 | 1.36 | 1.60 | 0.183 | 1.58 | 0.99 |
| Sand Outlet Type | Drop Height H/cm | Relative Density Dr | Sand Outlet Type | Drop Height H/cm | Relative Density Dr |
|---|---|---|---|---|---|
| duck-bill spout | 60 | 0.30 | mesh spout | 40 | 0.77 |
| 70 | 0.38 | ||||
| 85 | 0.46 | 100 | 0.89 | ||
| 100 | 0.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Dai, Z.; Liu, R.; Jian, F. Experimental Study on the Coefficient of Earth Pressure at Rest for Sand. Buildings 2023, 13, 1276. https://doi.org/10.3390/buildings13051276
Li L, Dai Z, Liu R, Jian F. Experimental Study on the Coefficient of Earth Pressure at Rest for Sand. Buildings. 2023; 13(5):1276. https://doi.org/10.3390/buildings13051276
Chicago/Turabian StyleLi, Libing, Zhiyu Dai, Ruiming Liu, and Fuxian Jian. 2023. "Experimental Study on the Coefficient of Earth Pressure at Rest for Sand" Buildings 13, no. 5: 1276. https://doi.org/10.3390/buildings13051276
APA StyleLi, L., Dai, Z., Liu, R., & Jian, F. (2023). Experimental Study on the Coefficient of Earth Pressure at Rest for Sand. Buildings, 13(5), 1276. https://doi.org/10.3390/buildings13051276




