Passive Control of Ultra-Span Twin-Box Girder Suspension Bridges under Vortex-Induced Vibration Using Tuned Mass Dampers: A Sensitivity Analysis
Abstract
:1. Introduction
- Prevent vortex shedding by refining the bridge deck’s aerodynamic design, utilizing distinct streamlined box girders.
- Modify the bridge’s dynamic properties by changing its structural layout.
- Enhance stability by incorporating additional attachments such as spoilers, guide vanes, or flapping plates.
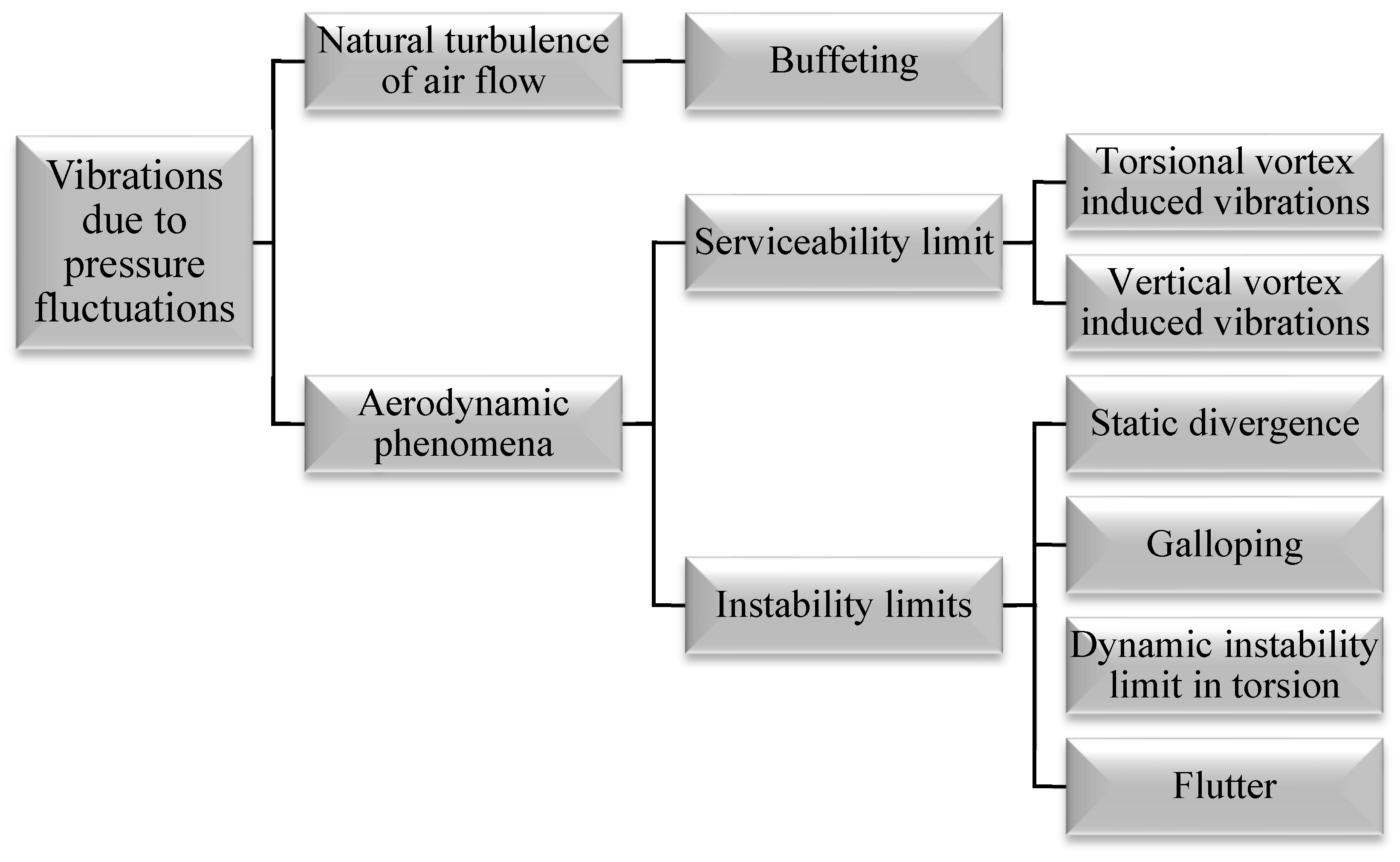
2. Aerodynamic Phenomena
- Oncoming airflow inherently includes turbulence, i.e., it is fluctuating in time and space.
- The flow separates at the body’s sharp edges because of the friction that causes further turbulence and vortex development on the surface. As a result, there is vortex shedding in the body’s wake since the flow past the body is unstable, with a variable fraction alternating from side to side.
- The flexible body will be vibrated by fluctuating forces. In this condition, the interaction between the oscillating body and alternation flow will cause additional forces.
3. Vortex Shedding Vibration
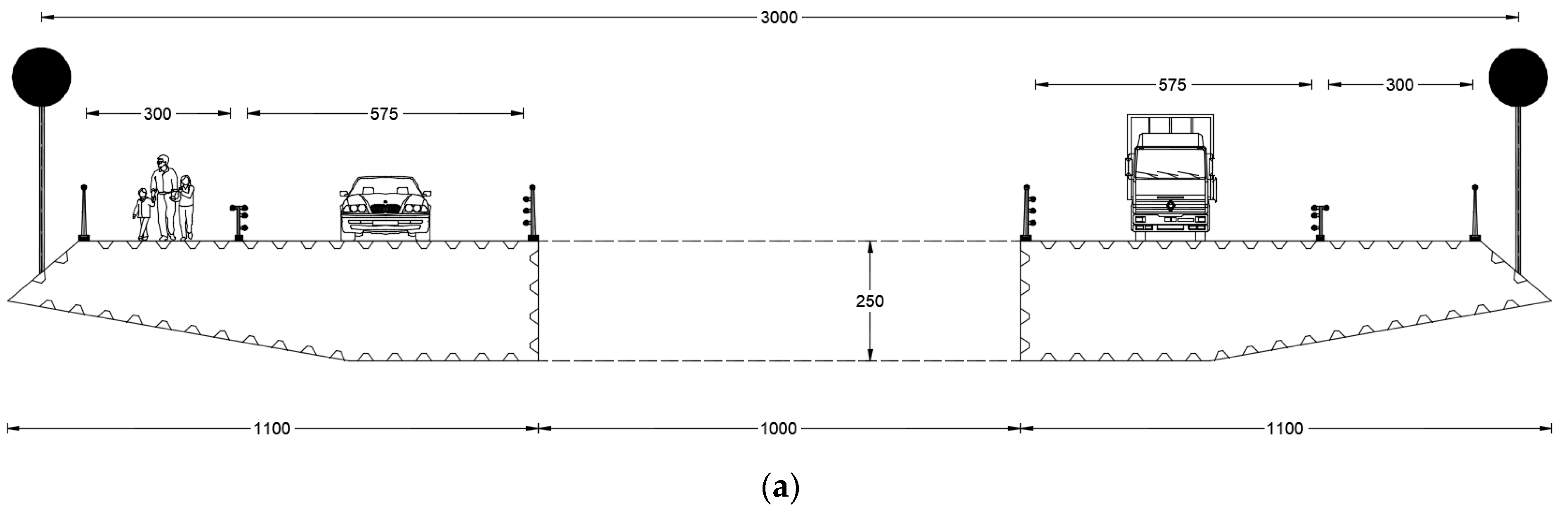
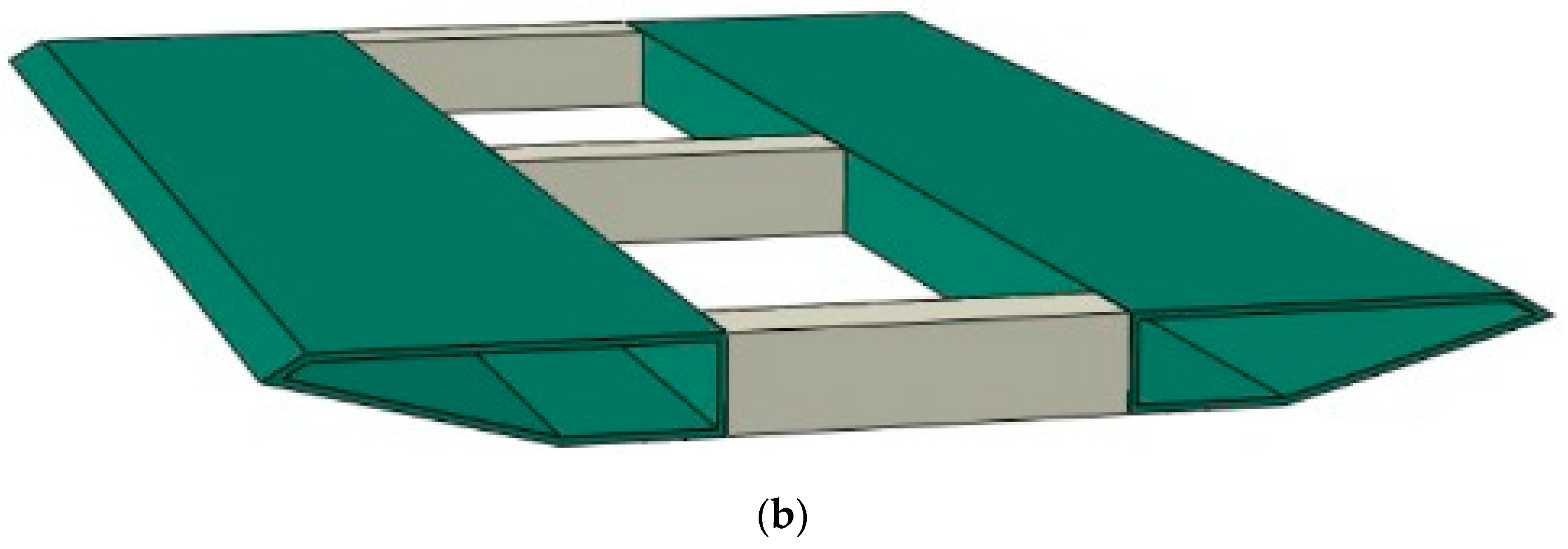
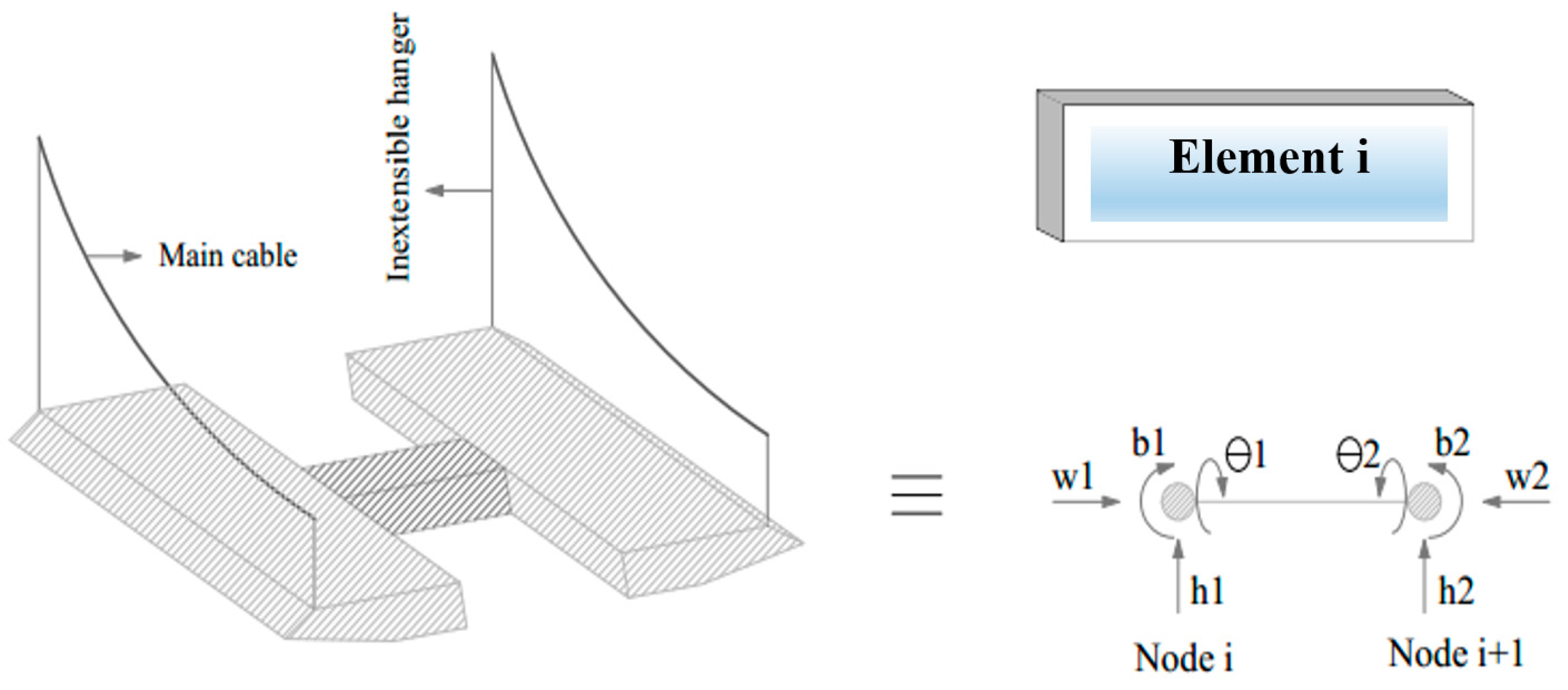
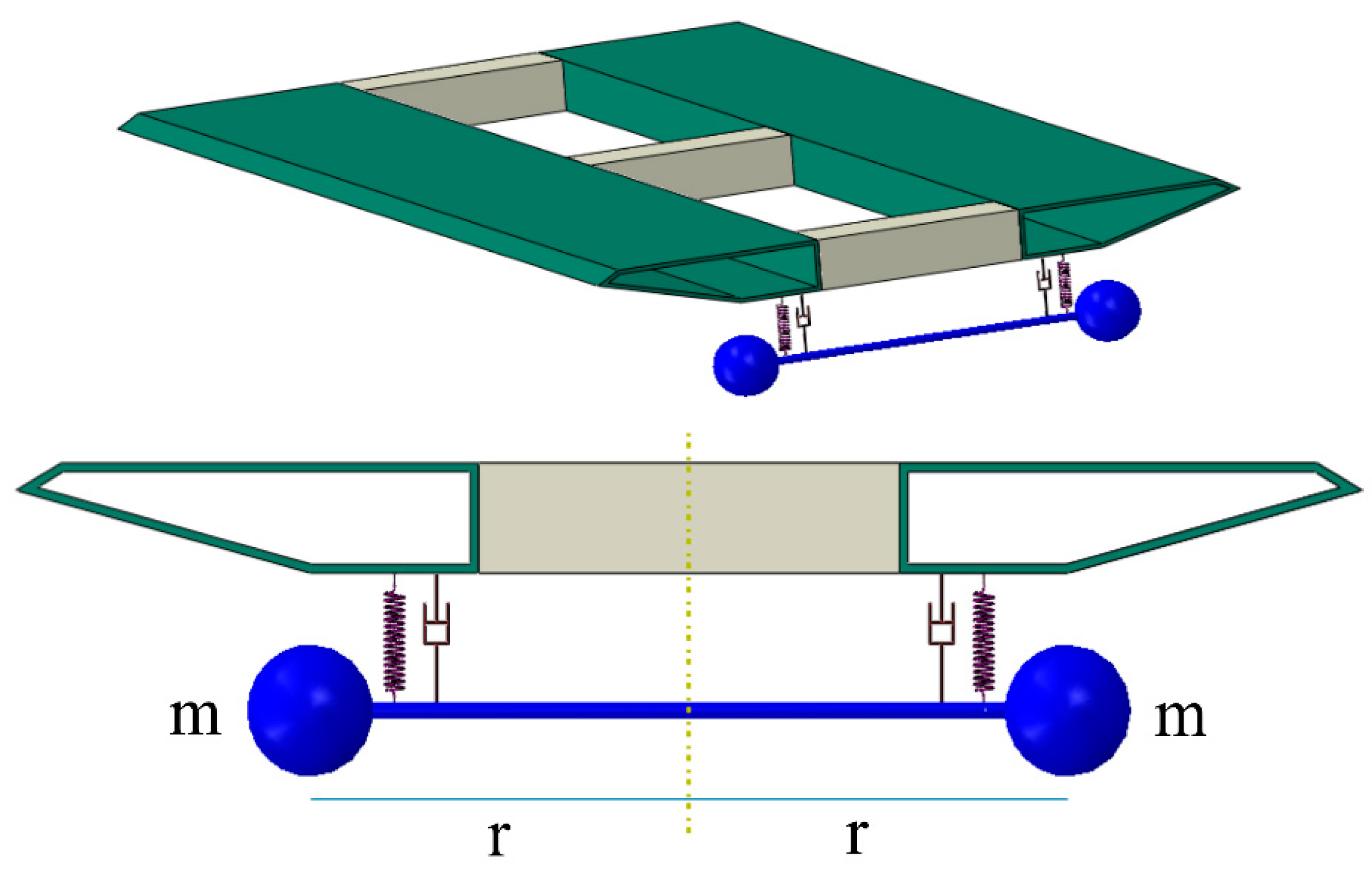
4. The Considered Bridge
TMD Device
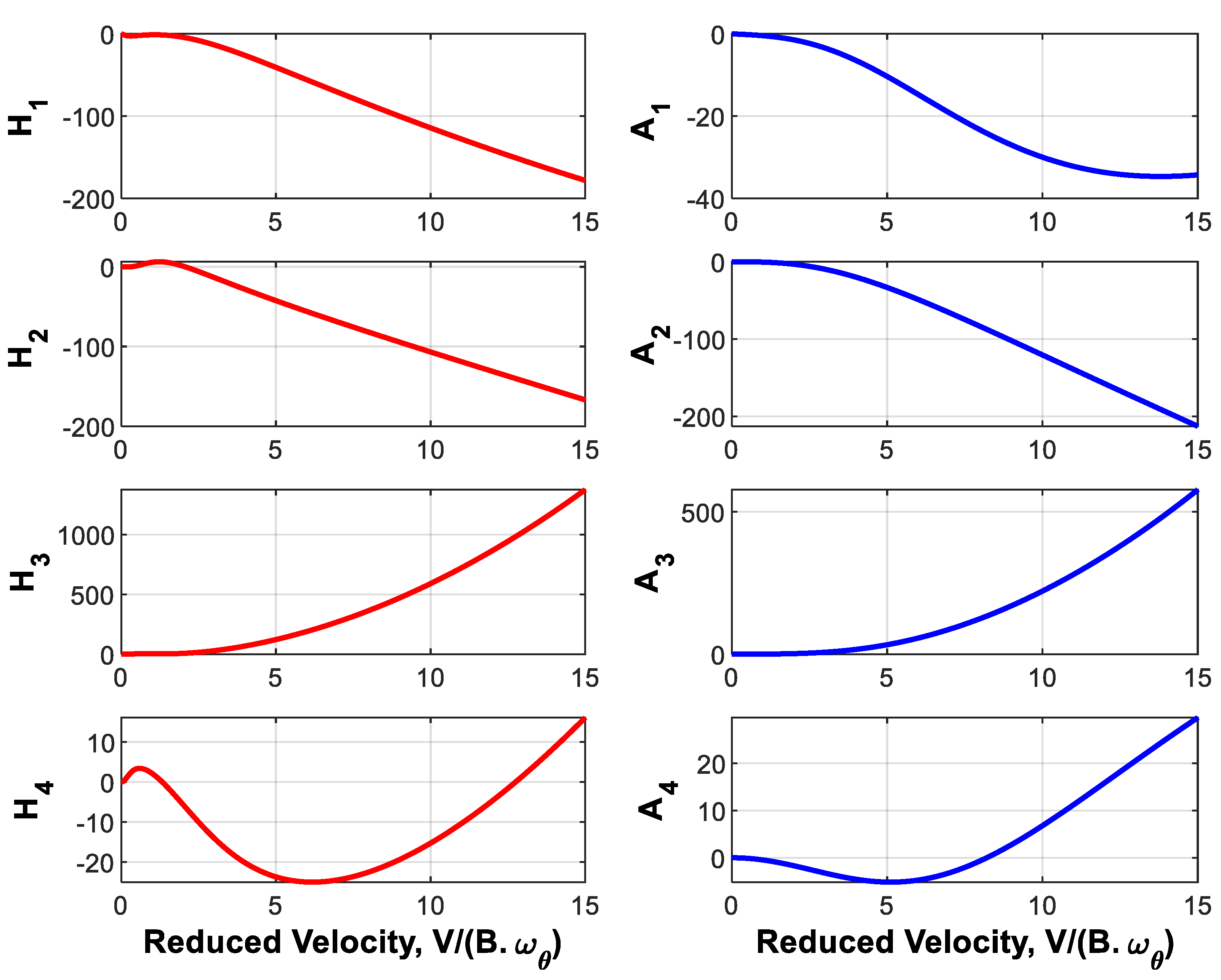
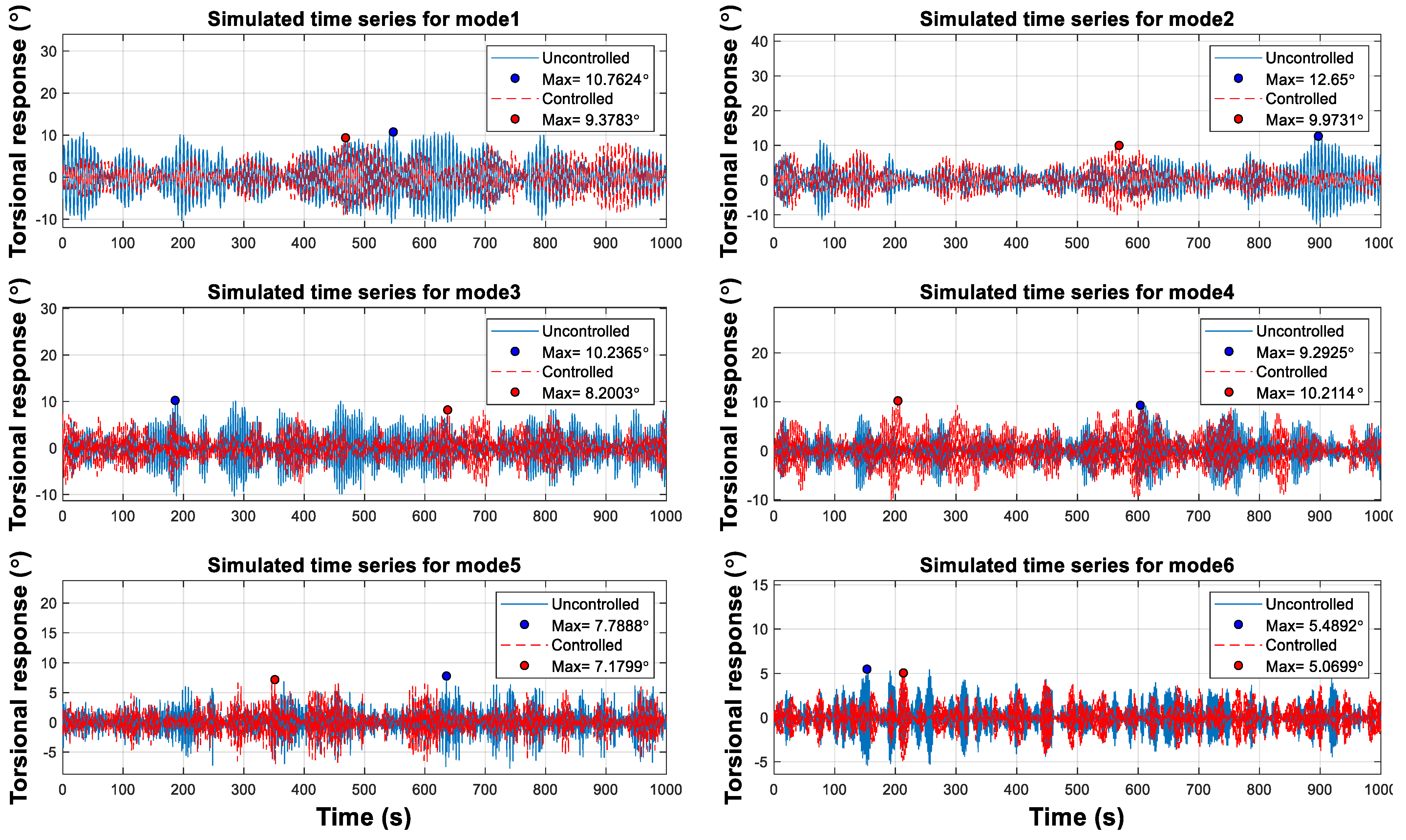
5. Numerical Analysis
- (a)
- One TMD is placed at the middle point.
- (b)
- Two TMDs are placed at the and points.
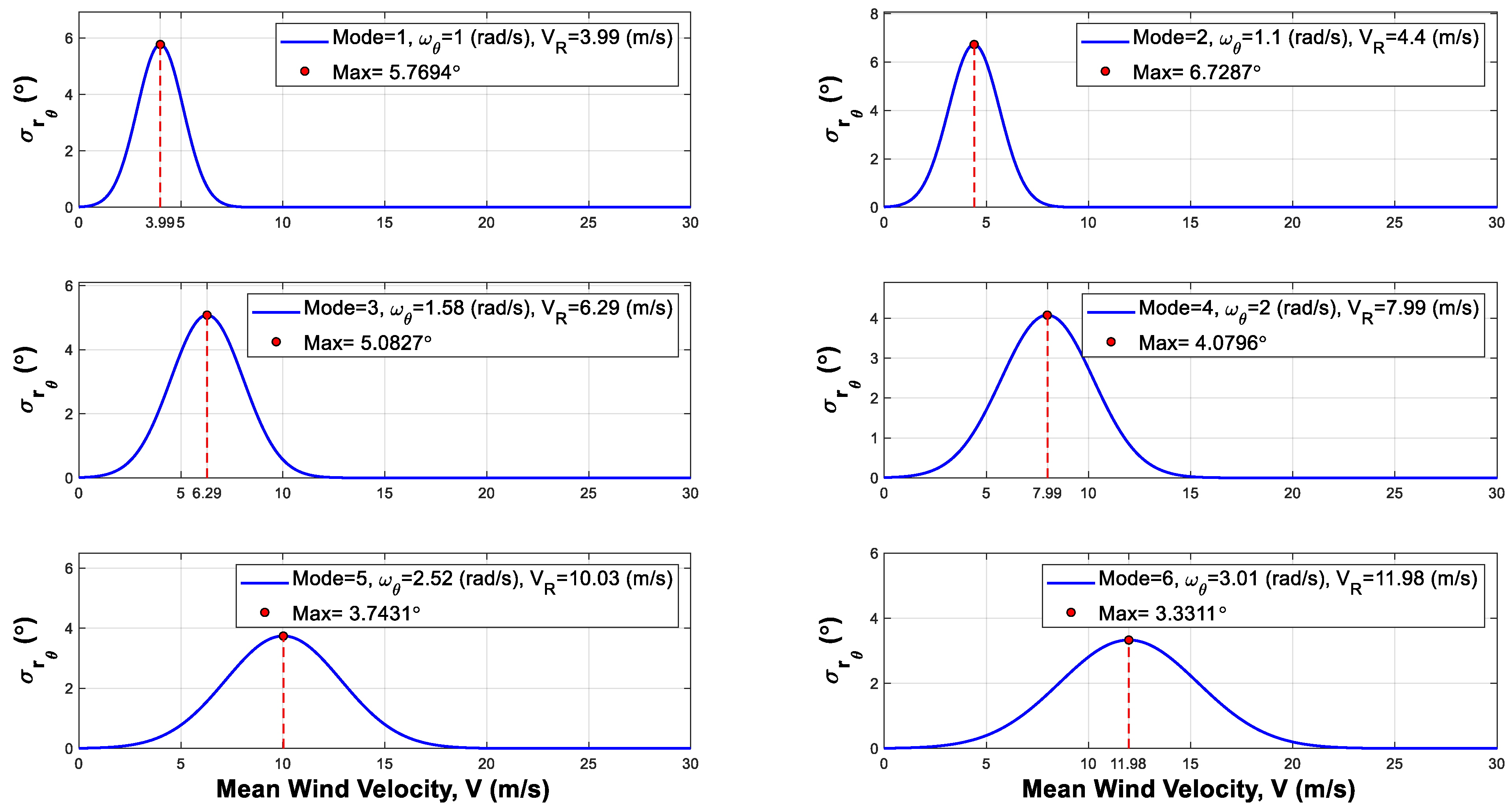
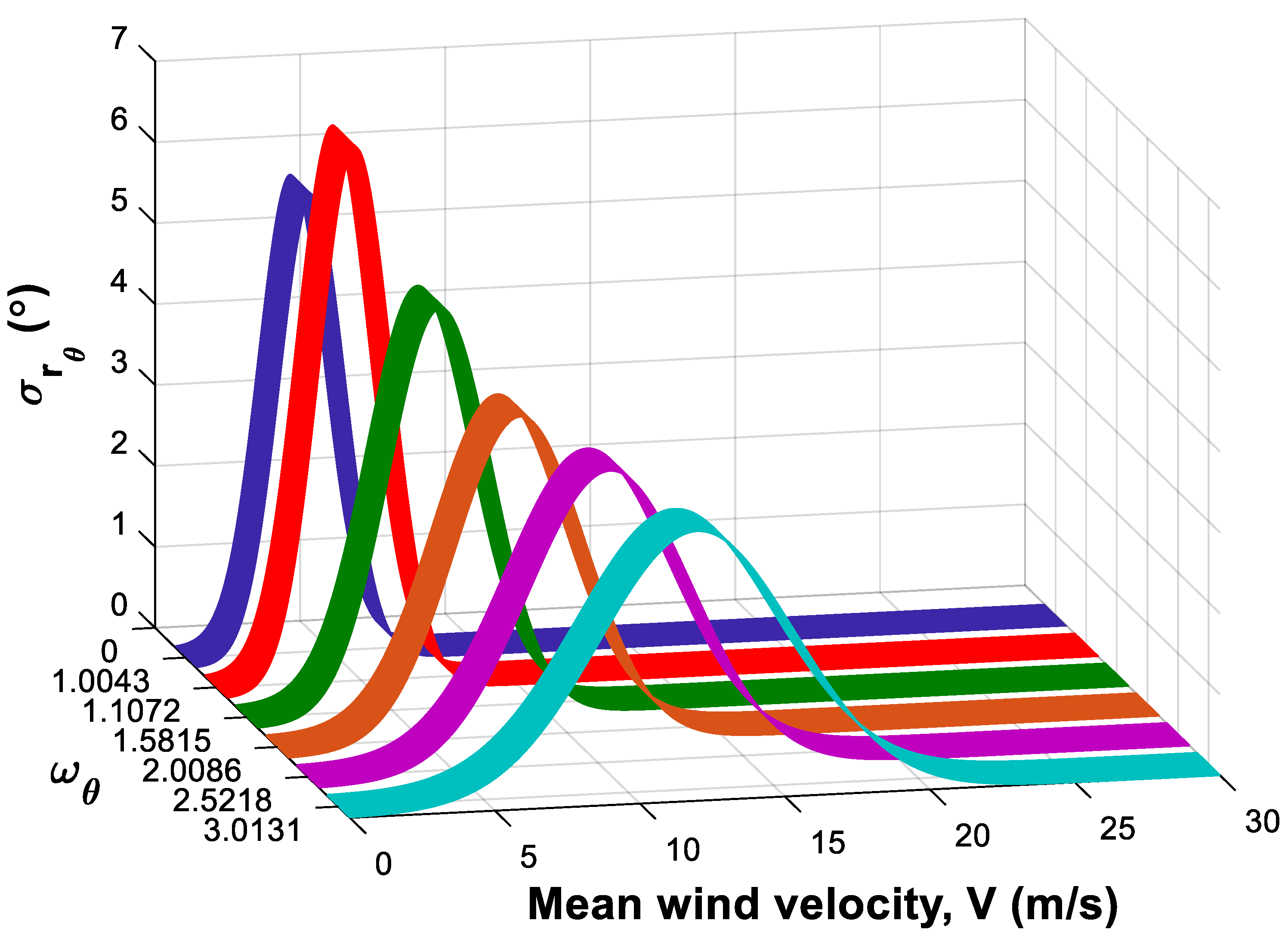
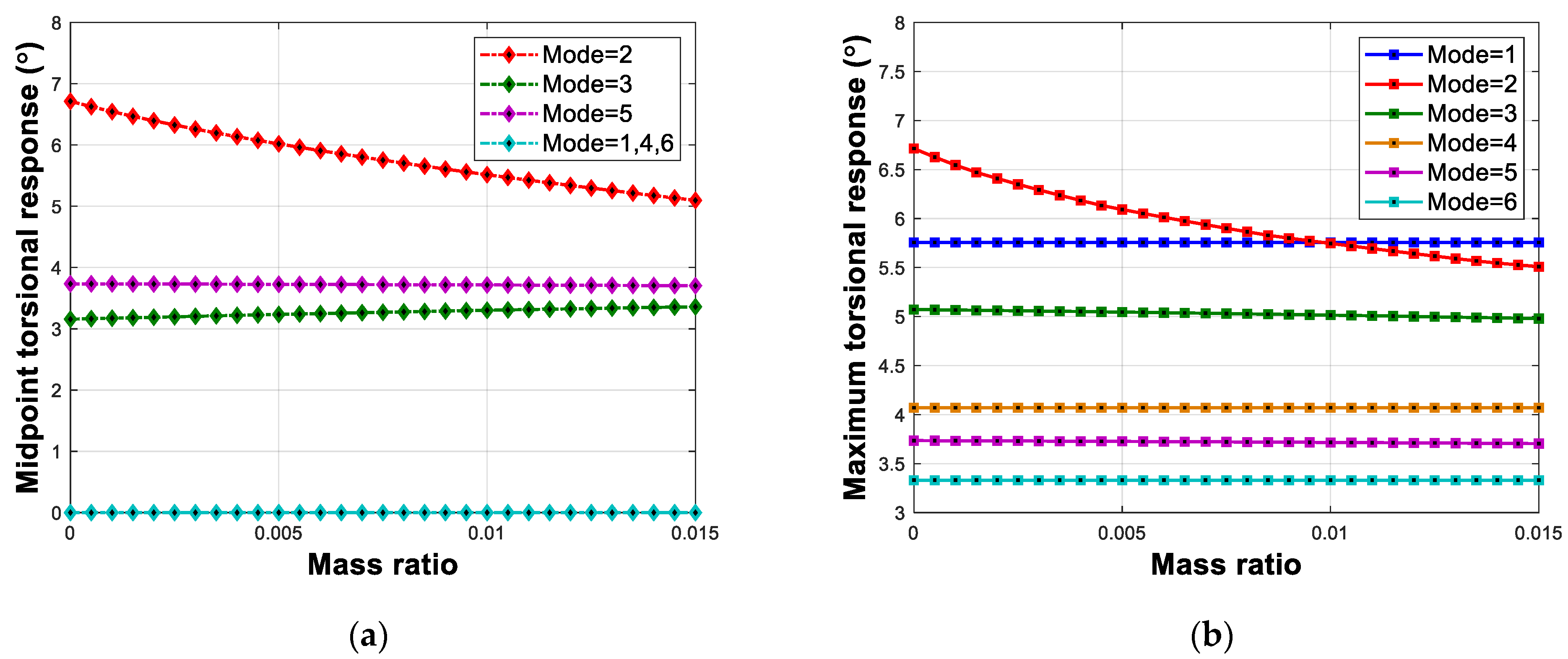
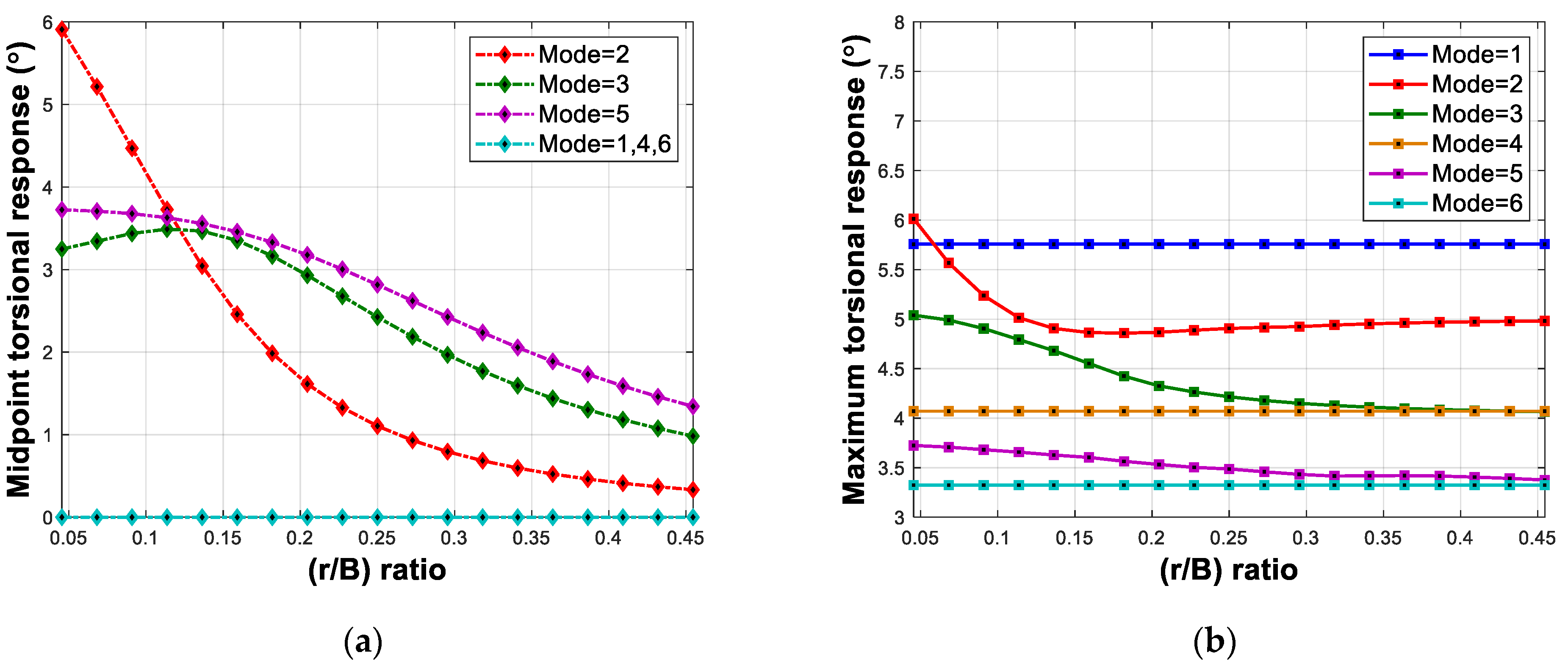
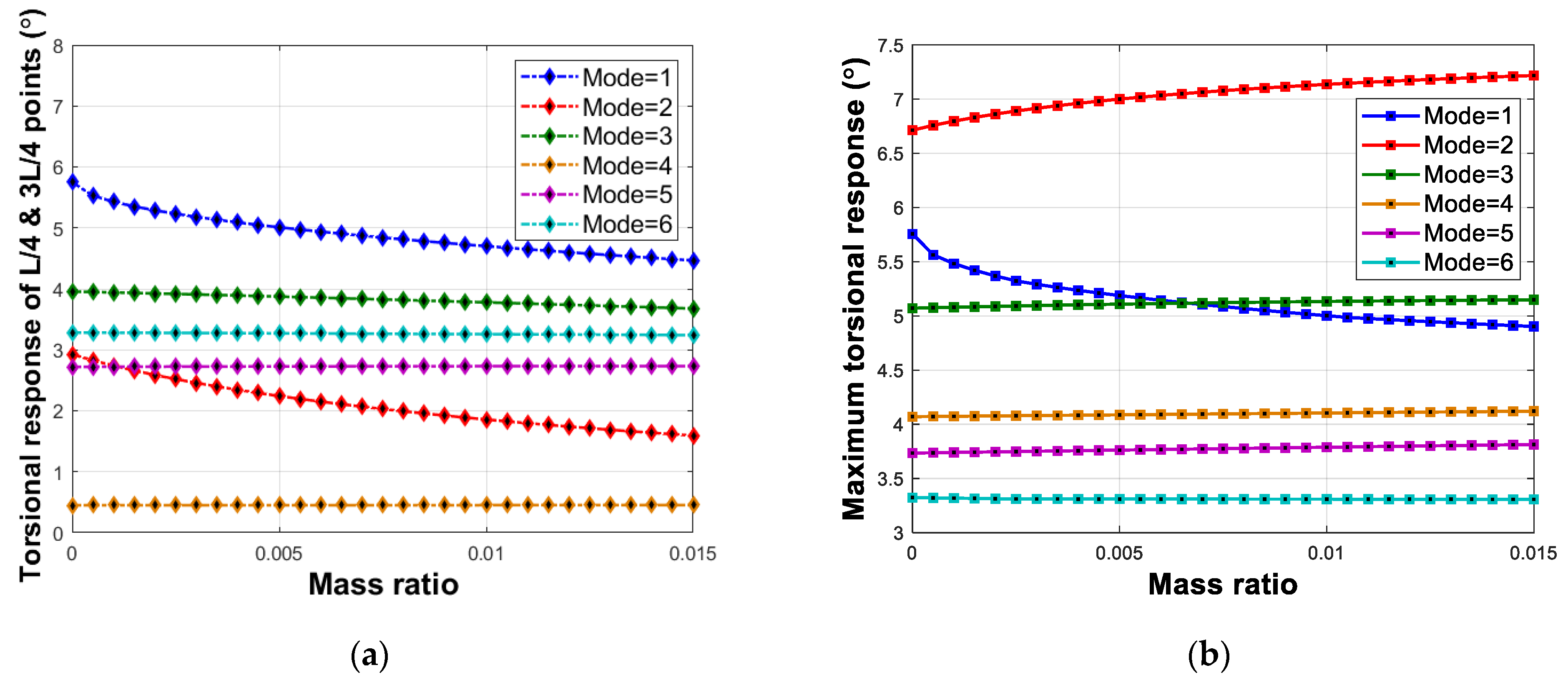
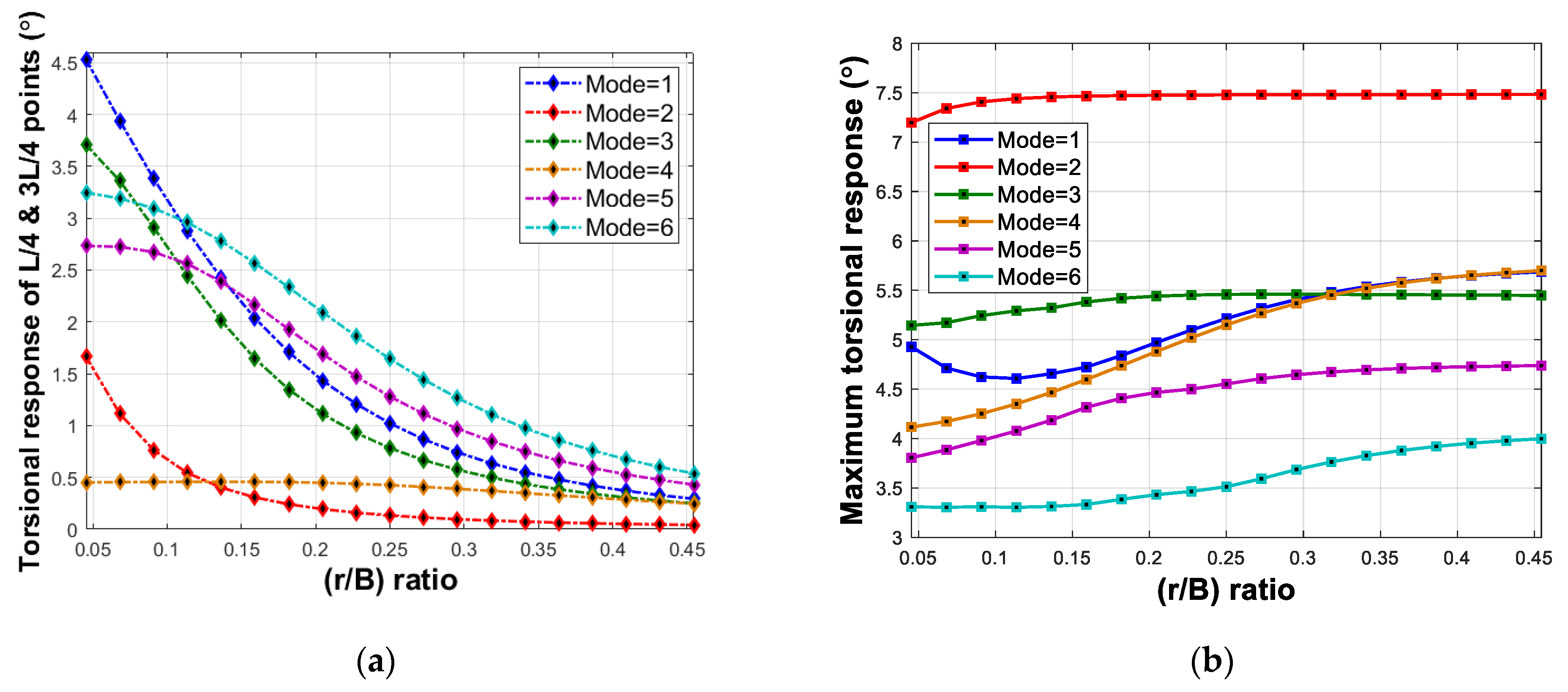
5.1. Mass Polar Moment of Inertia
5.2. Damping Ratio
5.3. Frequency Ratio
5.4. Combined Condition
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alizadeh, H.; Lavassani, S.H.H. Flutter Control of Long Span Suspension Bridges in Time Domain Using Optimized TMD. Int. J. Steel Struct. 2021, 21, 731–742. [Google Scholar] [CrossRef]
- Alizadeh, H.; Hosseini Lavassani, S.H. The effect of soil-structure interaction on longitudinal seismic responses of suspension bridges controlled by optimal TMD. J. Struct. Constr. Eng. 2022, 8, 439–458. [Google Scholar] [CrossRef]
- Hosseini Lavassani, S.H.; Alizadeh, H.; Doroudi, R.; Homami, P. Vibration control of suspension bridge due to vertical ground motions. Adv. Struct. Eng. 2020, 23, 2626–2641. [Google Scholar] [CrossRef]
- Basu, R.; Vickery, B. Across-wind vibrations of structure of circular cross-section. Part II. Development of a mathematical model for full-scale application. J. Wind Eng. Ind. Aerodyn. 1983, 12, 75–97. [Google Scholar] [CrossRef]
- Fujino, Y.; Yoshida, Y. Wind-induced vibration and control of Trans-Tokyo Bay crossing bridge. J. Struct. Eng. 2002, 128, 1012–1025. [Google Scholar] [CrossRef]
- Weber, F.; Maślanka, M. Frequency and damping adaptation of a TMD with controlled MR damper. Smart Mater. Struct. 2012, 21, 055011. [Google Scholar] [CrossRef]
- Gao, D.; Deng, Z.; Yang, W.; Chen, W. Review of the excitation mechanism and aerodynamic flow control of vortex-induced vibration of the main girder for long-span bridges: A vortex-dynamics approach. J. Fluids Struct. 2021, 105, 103348. [Google Scholar] [CrossRef]
- Park, J.; Kim, S.; Kim, H.-K. Effect of gap distance on vortex-induced vibration in two parallel cable-stayed bridges. J. Wind Eng. Ind. Aerodyn. 2017, 162, 35–44. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Hua, X.; Song, G.; Chen, Z. Vibration control of vortex-induced vibrations of a bridge deck by a single-side pounding tuned mass damper. Eng. Struct. 2018, 173, 61–75. [Google Scholar] [CrossRef]
- Xue, Z.; Han, B.; Zhang, H.; Xin, D.; Zhan, J.; Wang, R. External suction-blowing method for controlling vortex-induced vibration of a bridge. J. Wind Eng. Ind. Aerodyn. 2021, 215, 104661. [Google Scholar] [CrossRef]
- Li, K.; Ge, Y.; Guo, Z.; Zhao, L. Theoretical framework of feedback aerodynamic control of flutter oscillation for long-span suspension bridges by the twin-winglet system. J. Wind Eng. Ind. Aerodyn. 2015, 145, 166–177. [Google Scholar] [CrossRef]
- Bai, H.; Ji, N.; Xu, G.; Li, J. An alternative aerodynamic mitigation measure for improving bridge flutter and vortex induced vibration (VIV) stability: Sealed traffic barrier. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104302. [Google Scholar] [CrossRef]
- Zhou, R.; Ge, Y.; Liu, Q.; Yang, Y.; Zhang, L. Experimental and numerical studies of wind-resistance performance of twin-box girder bridges with various grid plates. Thin-Walled Struct. 2021, 166, 108088. [Google Scholar] [CrossRef]
- Hosseini Lavassani, S.H.; Alizadeh, H.; Homami, P. Optimizing tuned mass damper parameters to mitigate the torsional vibration of a suspension bridge under pulse-type ground motion: A sensitivity analysis. J. Vib. Control 2020, 26, 1054–1067. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Research developments in vibration control of structures using passive tuned mass dampers. Annu. Rev. Control. 2017, 44, 129–156. [Google Scholar] [CrossRef]
- Frahm, H. Device for Damping Vibrations of Bodies. US Patent US989958A, 30 October 1909. [Google Scholar]
- Den Hartog, J.; Ormondroyd, J. Theory of the dynamic vibration absorber. ASME J. Appl. Mech. 1928, 50, 11–22. [Google Scholar]
- Kwon, S.-D.; Jung, M.S.; Chang, S.-P. A new passive aerodynamic control method for bridge flutter. J. Wind Eng. Ind. Aerodyn. 2000, 86, 187–202. [Google Scholar] [CrossRef]
- Gu, M.; Chen, S.; Chang, C. Control of wind-induced vibrations of long-span bridges by semi-active lever-type TMD. J. Wind Eng. Ind. Aerodyn. 2002, 90, 111–126. [Google Scholar] [CrossRef]
- Pourzeynali, S.; Datta, T. Control of flutter of suspension bridge deck using TMD. Wind Struct. 2002, 5, 407–422. [Google Scholar] [CrossRef]
- Chen, X.; Kareem, A. Efficacy of tuned mass dampers for bridge flutter control. J. Struct. Eng. 2003, 129, 1291–1300. [Google Scholar] [CrossRef]
- Chen, S.; Cai, C. Coupled vibration control with tuned mass damper for long-span bridges. J. Sound Vib. 2004, 1, 449–459. [Google Scholar] [CrossRef]
- Abdel-Rohman, M.; John, M.J. Control of wind-induced nonlinear oscillations in suspension bridges using a semi-active tuned mass damper. J. Vib. Control 2006, 12, 1049–1080. [Google Scholar] [CrossRef]
- Domaneschi, M.; Martinelli, L.; Po, E. Control of wind buffeting vibrations in a suspension bridge by TMD: Hybridization and robustness issues. Comput. Struct. 2015, 155, 3–17. [Google Scholar] [CrossRef]
- Alizadeh, H.; Lavassani, S.H.H.; Pourzeynali, S. Flutter Instability Control in Suspension Bridge by TMD. In Proceedings of the 11th International Congress on Civil Engineering, Tehran, Iran, 8–10 May 2018. [Google Scholar]
- Kontoni, D.-P.N.; Farghaly, A.A. Mitigation of the seismic response of a cable-stayed bridge with soil-structure-interaction effect using tuned mass dampers. Struct. Eng. Mech. 2019, 69, 699–712. [Google Scholar] [CrossRef]
- Mansouri, S.; Kontoni, D.-P.N.; Pouraminian, M. The effects of the duration, intensity and magnitude of far-fault earthquakes on the seismic response of RC bridges retrofitted with seismic bearings. Adv. Bridge Eng. 2022, 3, 19. [Google Scholar] [CrossRef]
- Patil, V.B.; Jangid, R.S. Optimum multiple tuned mass dampers for the wind excited benchmark building. J. Civ. Eng. Manag. 2011, 17, 540–557. [Google Scholar] [CrossRef]
- Bandivadekar, T.; Jangid, R. Optimization of multiple tuned mass dampers for vibration control of system under external excitation. J. Vib. Control 2013, 19, 1854–1871. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Chen, S. Damping effects of linear and nonlinear tuned mass dampers on nonlinear hinged-hinged beam. J. Sound Vib. 2018, 430, 150–173. [Google Scholar] [CrossRef]
- Shi, W.; Wang, L.; Lu, Z.; Wang, H. Experimental and numerical study on adaptive-passive variable mass tuned mass damper. J. Sound Vib. 2019, 452, 97–111. [Google Scholar] [CrossRef]
- Dai, J.; Xu, Z.-D.; Gai, P.-P.; Xu, Y.W. Mitigation of vortex-induced vibration in bridges using semi active tuned mass dampers. J. Bridge Eng. 2021, 26, 05021003. [Google Scholar] [CrossRef]
- Ubertini, F.; Comanducci, G.; Laflamme, S. A parametric study on reliability-based tuned-mass damper design against bridge flutter. J. Vib. Control 2015, 23, 1518–1534. [Google Scholar] [CrossRef]
- Pisal, A.Y.; Jangid, R.S. Vibration control of bridge subjected to multiaxle vehicle using multiple tuned mass friction dampers. Int. J. Adv. Struct. Eng. 2016, 8, 213–227. [Google Scholar] [CrossRef]
- Tao, T.; Wang, H.; Yao, C.; He, X. Parametric sensitivity analysis on the buffeting control of a long-span tripletower suspension bridge with MTMD. Appl. Sci. 2017, 7, 395. [Google Scholar] [CrossRef]
- Strømmen, E. Theory of Bridge Aerodynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Amini, F.; Doroudi, R. Control of a building complex with magneto-rheological dampers and tuned mass damper. Struct. Eng. Mech. 2010, 36, 181–195. [Google Scholar] [CrossRef]
- Bortoluzzi, D.; Casciati, S.; Elia, L.; Faravelli, L. Design of a TMD solution to mitigate wind-induced local vibrations in an existing timber footbridge. Smart Struct. Syst. 2015, 16, 459–478. [Google Scholar] [CrossRef]
- Debbarma, R.; Das, D. Vibration control of building using multiple tuned mass dampers considering real earthquake time history. Int. J. Civ. Environ. Eng. 2016, 10, 694–704. [Google Scholar]
- Kontoni, D.-P.N.; Farghaly, A.A. Enhancing the earthquake resistance of RC and steel high-rise buildings by bracings, shear walls and TMDs considering SSI. Asian J. Civ. Eng. 2023. [Google Scholar] [CrossRef]
- Kontoni, D.-P.N.; Farghaly, A.A. The effect of base isolation and tuned mass dampers on the seismic response of RC high-rise buildings considering soil-structure interaction. Earthq. Struct. 2019, 17, 425–434. [Google Scholar] [CrossRef]
- Kontoni, D.-P.N.; Farghaly, A.A. TMD effectiveness for steel high-rise building subjected to wind or earthquake including soil-structure interaction. Wind Struct. 2020, 30, 423–432. [Google Scholar] [CrossRef]
- Hosseini Lavassani, S.H.; Shangapour, S.; Homami, P.; Gharehbaghi, V.; Farsangi, E.N.; Yang, T.Y. An innovative methodology for hybrid vibration control (MR + TMD) of buildings under seismic excitations. Soil Dyn. Earthq. Eng. 2022, 155, 107175. [Google Scholar] [CrossRef]



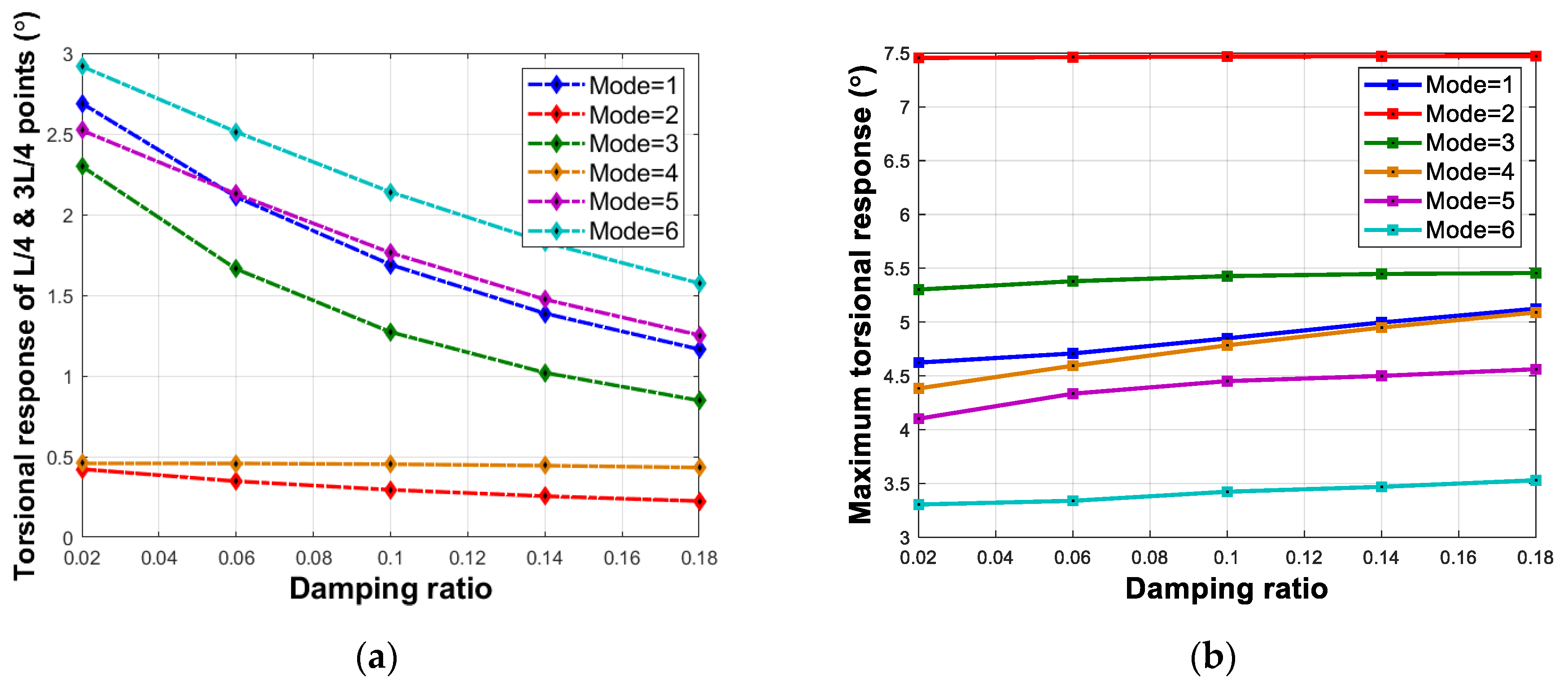

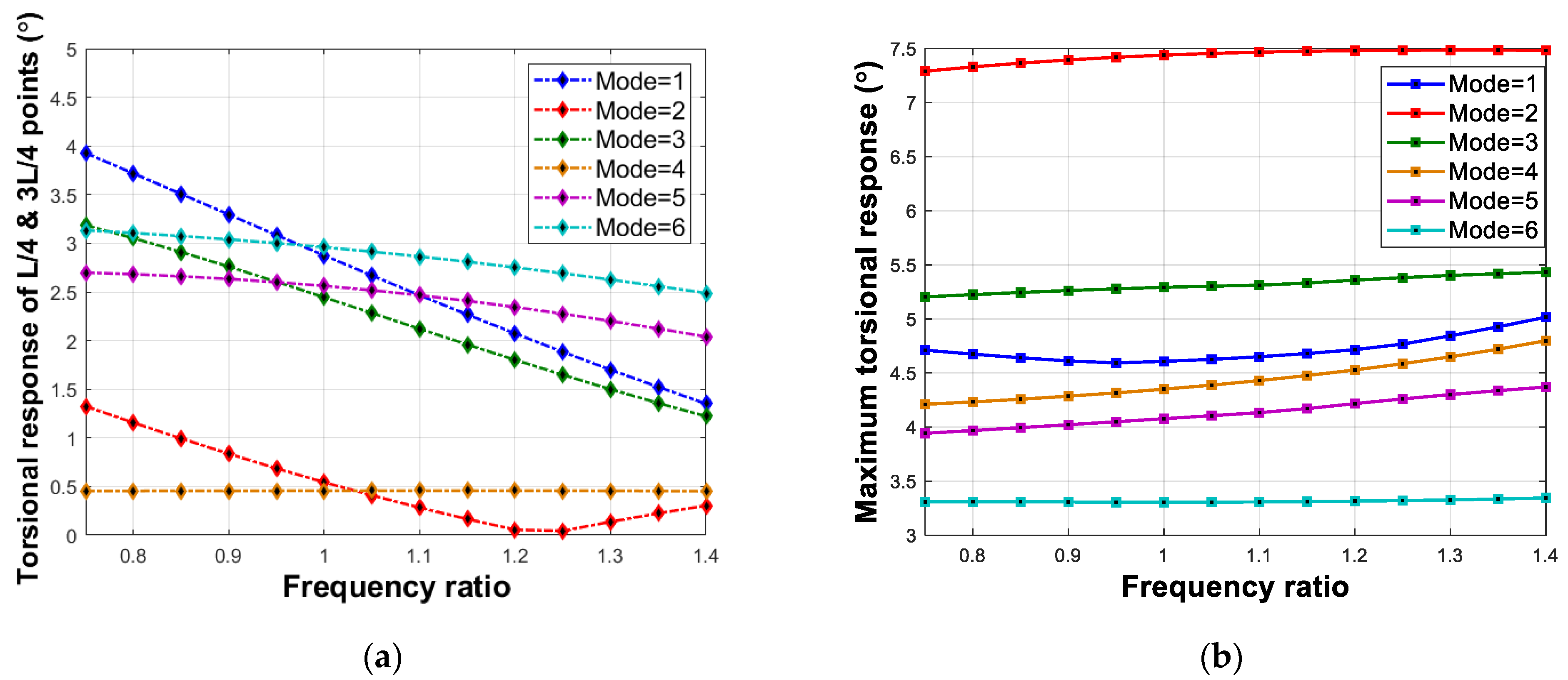
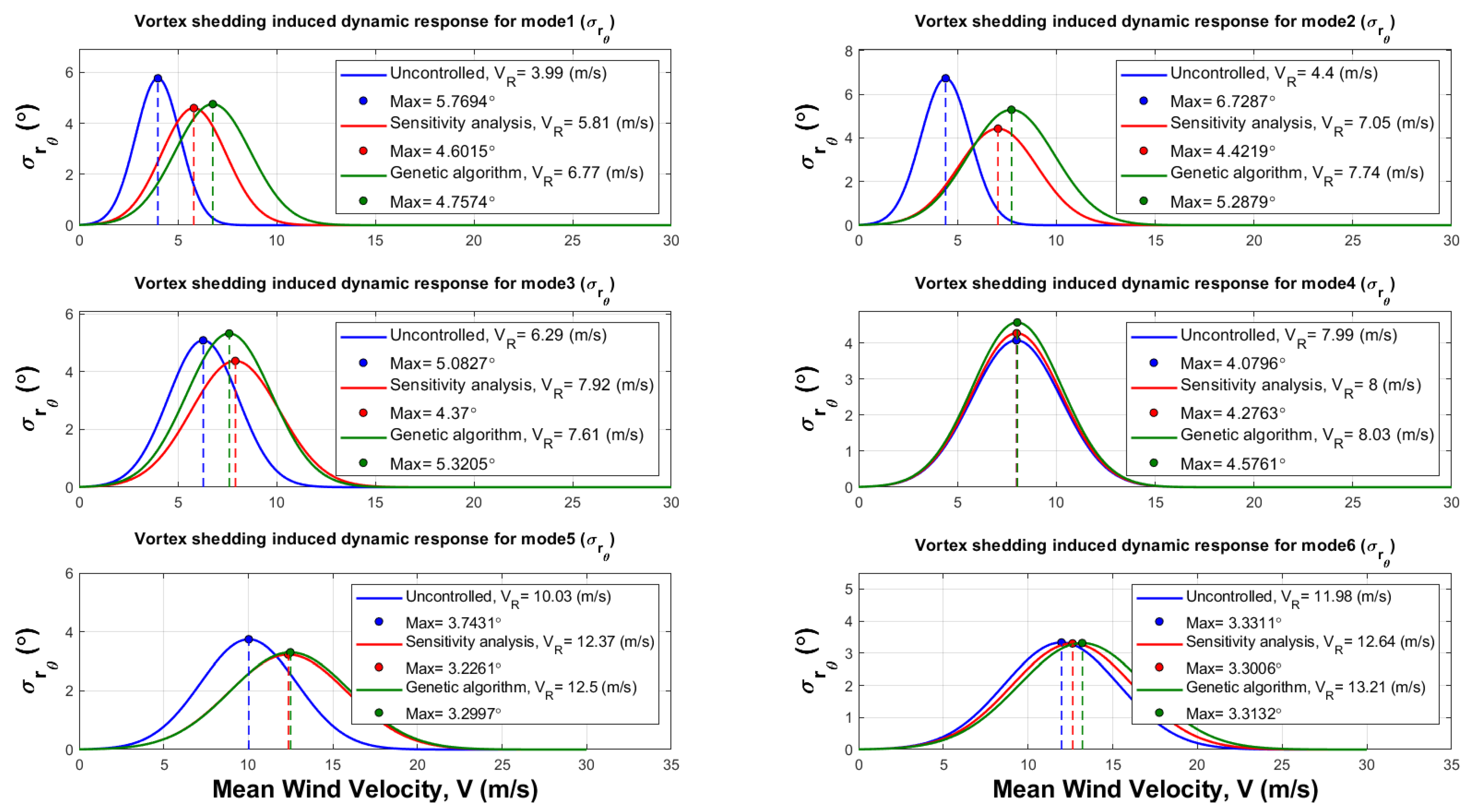

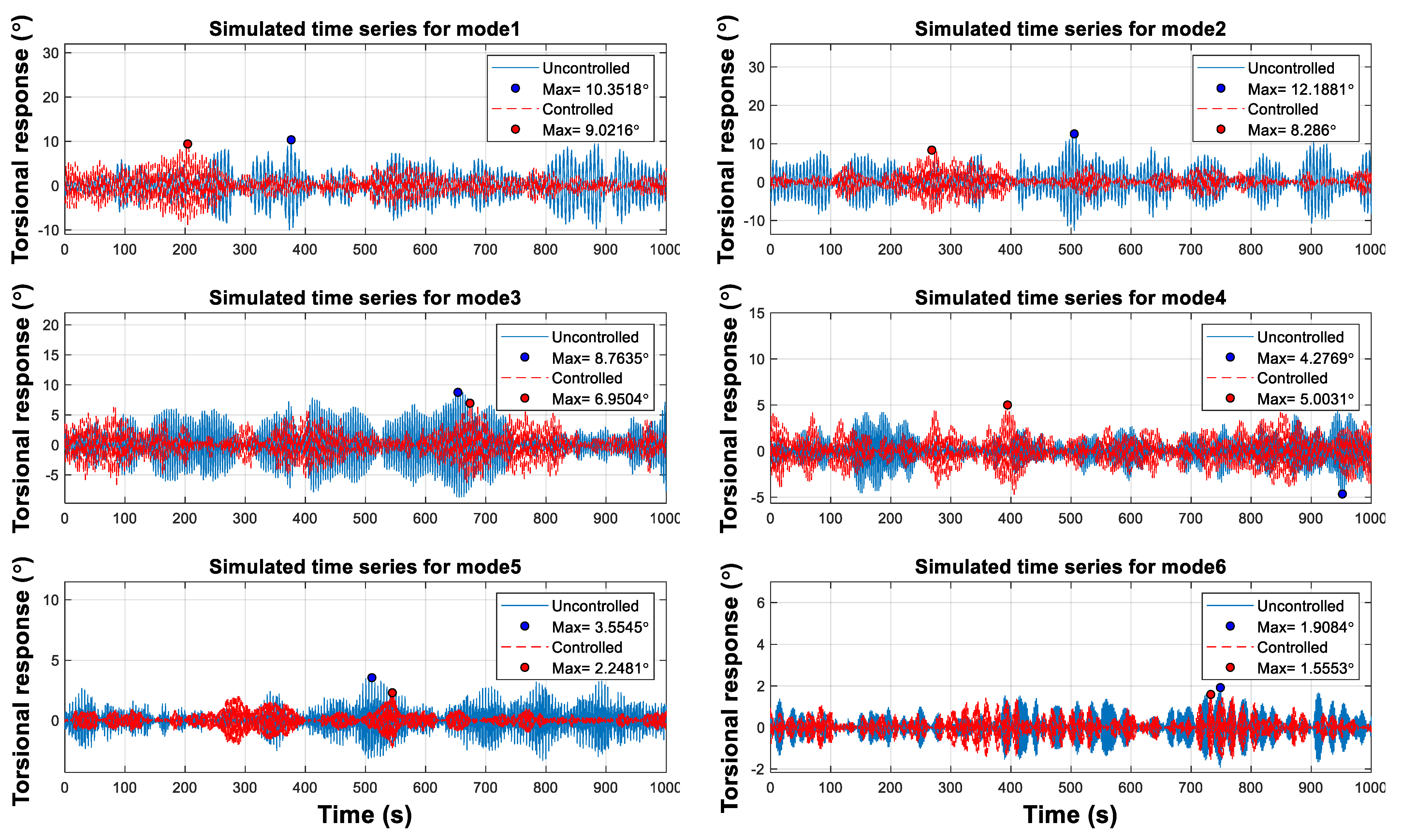
| No. | Parameters | Value |
|---|---|---|
| 1 | Length of span, | 2050 |
| 2 | Virtual length of cable, | 3160 |
| 3 | Width of deck, | 32 |
| 4 | Depth of deck, | 2.5 |
| 5 | Gyration radius, | 0.62 |
| 6 | Cross section of main cable, | 375 |
| 7 | Modulus of elasticity of girder, | 2.00 × 1011 |
| 8 | Shear modulus of elasticity of girder, | 8.0 × 1010 |
| 9 | Warping constant, | 1.712 |
| 10 | Second moment of inertia, | 0.4414 |
| 11 | Modulus of elasticity of main cable, | 2.00 × 1011 |
| 12 | Horizontal tension of main cable, | 248,050 |
| 13 | Dead weight of main cable, | 9825 |
| Mode Shape | |||
|---|---|---|---|
| TA1 |  | 1.0043 | 6.28 |
| TS1 |  | 1.1072 | 5.71 |
| TS2 |  | 1.5815 | 3.98 |
| TA2 |  | 2.0086 | 3.14 |
| TS3 |  | 2.5218 | 2.50 |
| TA3 |  | 3.0131 | 2.09 |
| 1.25 | 0.1 | 0.3 | 0.2 |
| TMDs | Mass Ratio (%) | Frequency Ratio | Damping Ratio (%) | |
|---|---|---|---|---|
| Middle one | 0.6 | 5.21 | 1.2 | 11.35 |
| Side ones | 1.35 | 2.5 | 1.25 | 12.65 |
| TMDs | Mass Ratio (%) [0.5, 1.5] | [4.04, 5.4] | Frequency Ratio [1, 1.25] | Damping Ratio (%) [5, 12.5] |
|---|---|---|---|---|
| Middle one | 1 | 4.8 | 1.25 | 10 |
| Side ones | 1 | 4.8 | 1.25 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseini Lavassani, S.H.; Kontoni, D.-P.N.; Alizadeh, H.; Gharehbaghi, V. Passive Control of Ultra-Span Twin-Box Girder Suspension Bridges under Vortex-Induced Vibration Using Tuned Mass Dampers: A Sensitivity Analysis. Buildings 2023, 13, 1279. https://doi.org/10.3390/buildings13051279
Hosseini Lavassani SH, Kontoni D-PN, Alizadeh H, Gharehbaghi V. Passive Control of Ultra-Span Twin-Box Girder Suspension Bridges under Vortex-Induced Vibration Using Tuned Mass Dampers: A Sensitivity Analysis. Buildings. 2023; 13(5):1279. https://doi.org/10.3390/buildings13051279
Chicago/Turabian StyleHosseini Lavassani, Seyed Hossein, Denise-Penelope N. Kontoni, Hamed Alizadeh, and Vahidreza Gharehbaghi. 2023. "Passive Control of Ultra-Span Twin-Box Girder Suspension Bridges under Vortex-Induced Vibration Using Tuned Mass Dampers: A Sensitivity Analysis" Buildings 13, no. 5: 1279. https://doi.org/10.3390/buildings13051279
APA StyleHosseini Lavassani, S. H., Kontoni, D.-P. N., Alizadeh, H., & Gharehbaghi, V. (2023). Passive Control of Ultra-Span Twin-Box Girder Suspension Bridges under Vortex-Induced Vibration Using Tuned Mass Dampers: A Sensitivity Analysis. Buildings, 13(5), 1279. https://doi.org/10.3390/buildings13051279










