Bayesian RC-Frame Finite Element Model Updating and Damage Estimation Using Nested Sampling with Nonlinear Time History
Abstract
:1. Introduction
2. Theory Background
2.1. Bayesian Method Based on Nonlinear Time History
2.2. Nested Sampling
- “Slicing” the posterior into many simpler distributions.
- Sampling from each of those in turn.
- Re-combining the results afterwards.
2.2.1. Basic Overview of Nested Sampling
2.2.2. Stopping Criterion
2.2.3. Sampling Flow
- Draw K “live” points from the prior , live points distribution is the same as prior. In this paper, because prior is a uniform distribution, samples will be selected randomly.
- Compute the minimum likelihood among the current set of live points. Record it as , accumulate Z, and record these K “live” points into samples.
- Add a new point , which is subject to the constraint , and replace the point of in step 2. Treat the new set of “live” points as .
- Compute whether it meets the stopping criterion. If it does, end this flow. If it does not, continue this flow.
- Replace the original by in step 1, and go back to step 1.
2.2.4. Re-Combine Samples
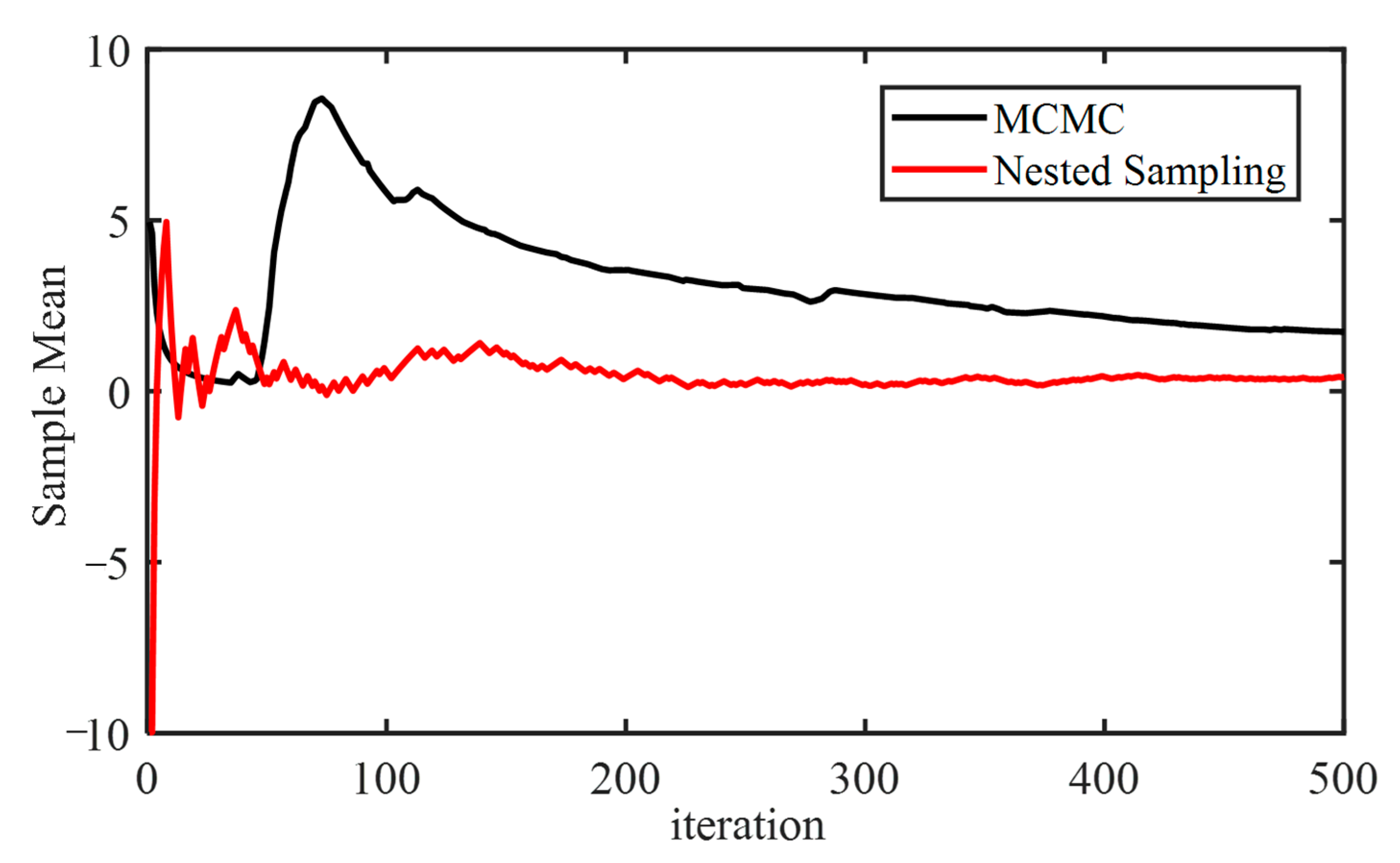
2.2.5. Comparison of Nested Sampling and MCMC in Efficiency
3. Numerical Example
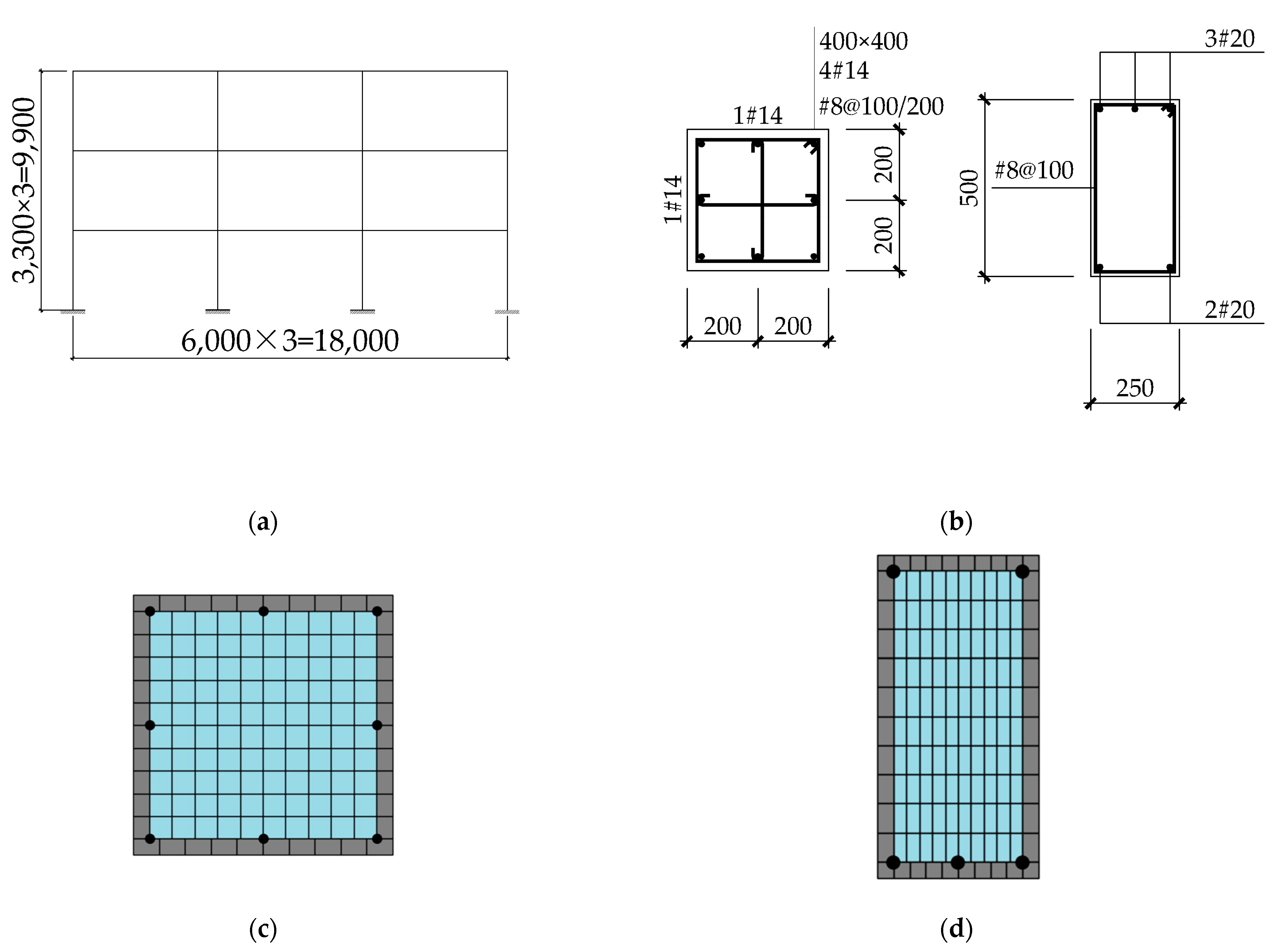
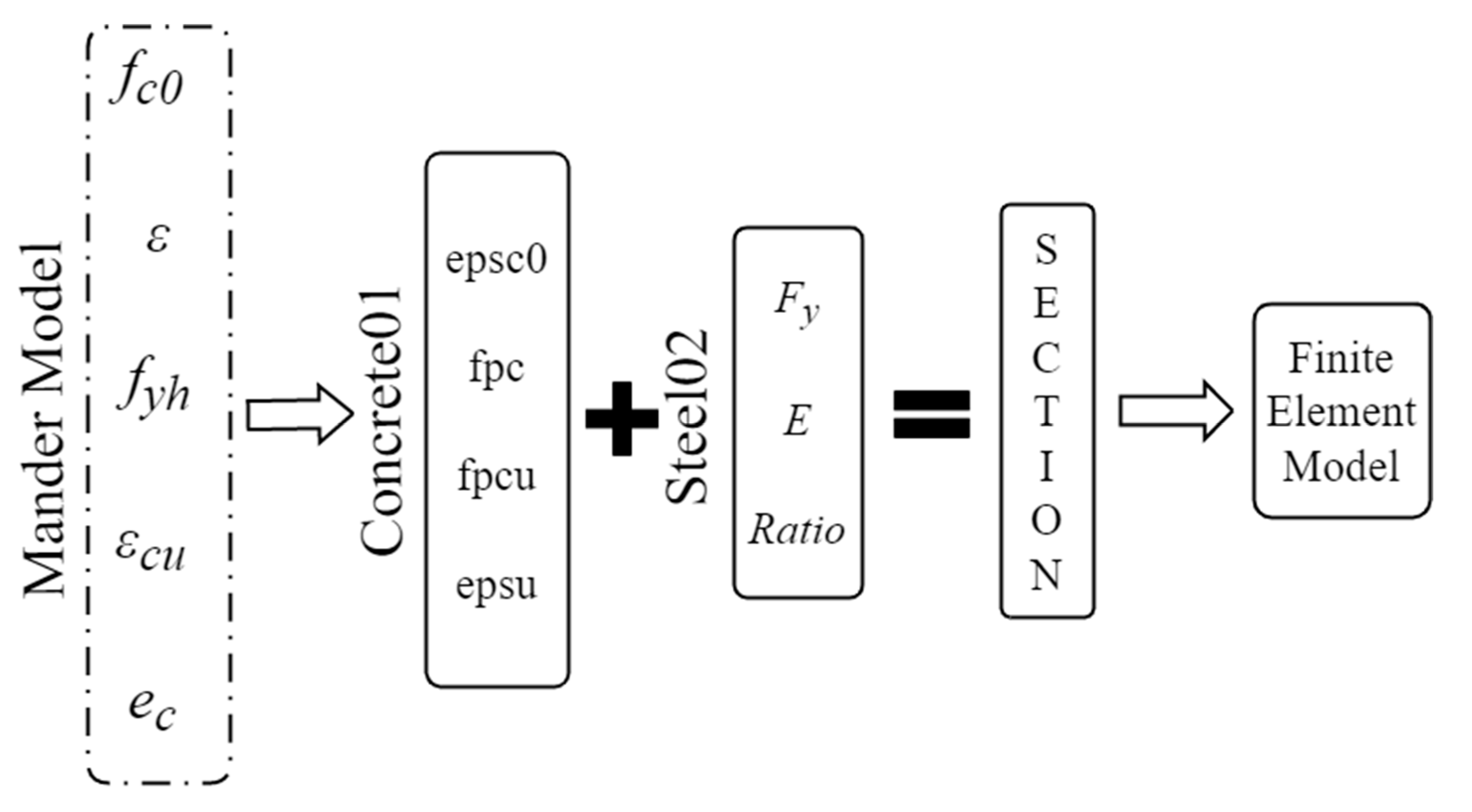
3.1. Two-Dimensional RC-Frame Finite Element Model
3.2. Structural Parameter Identification based on Nested Sampling
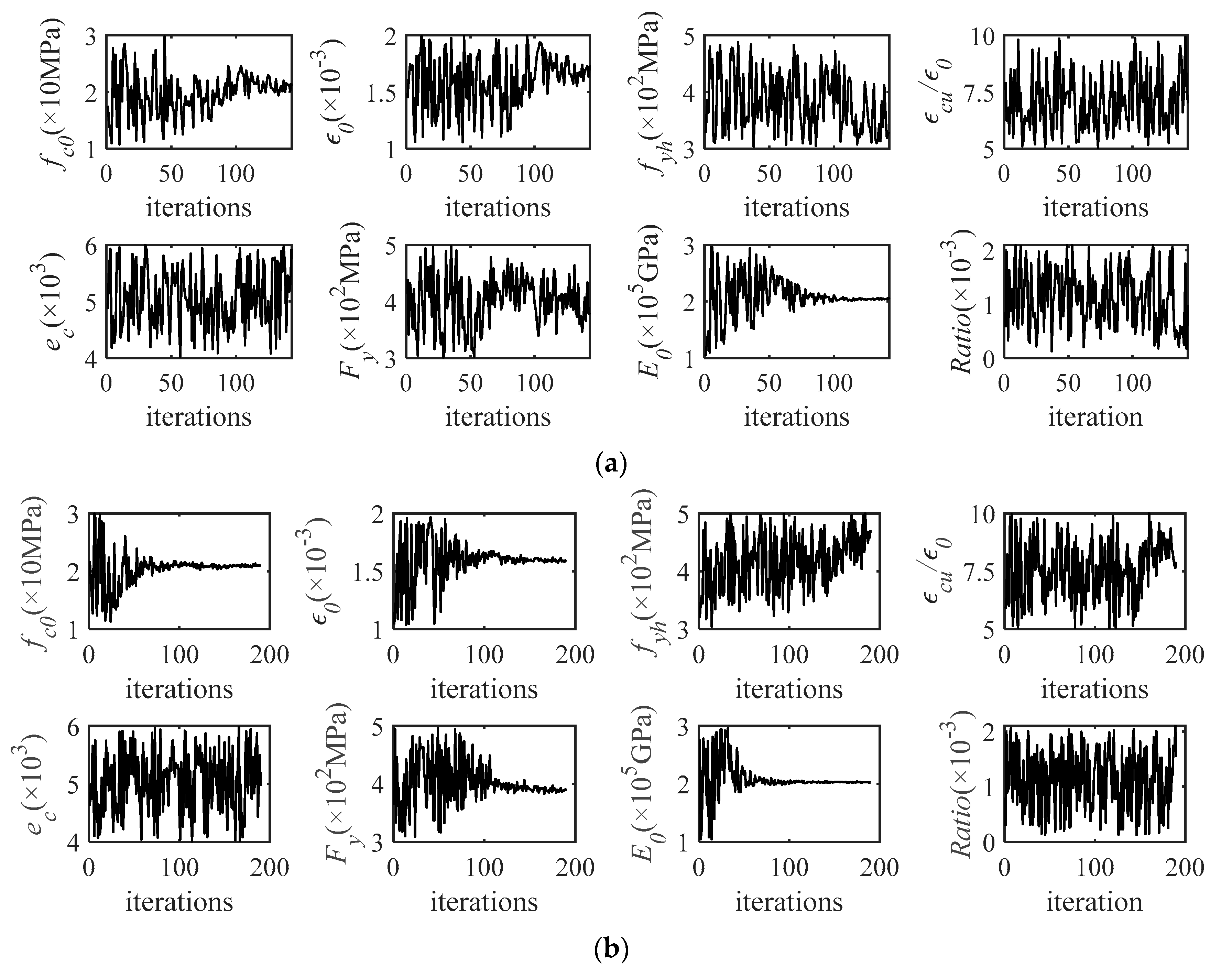
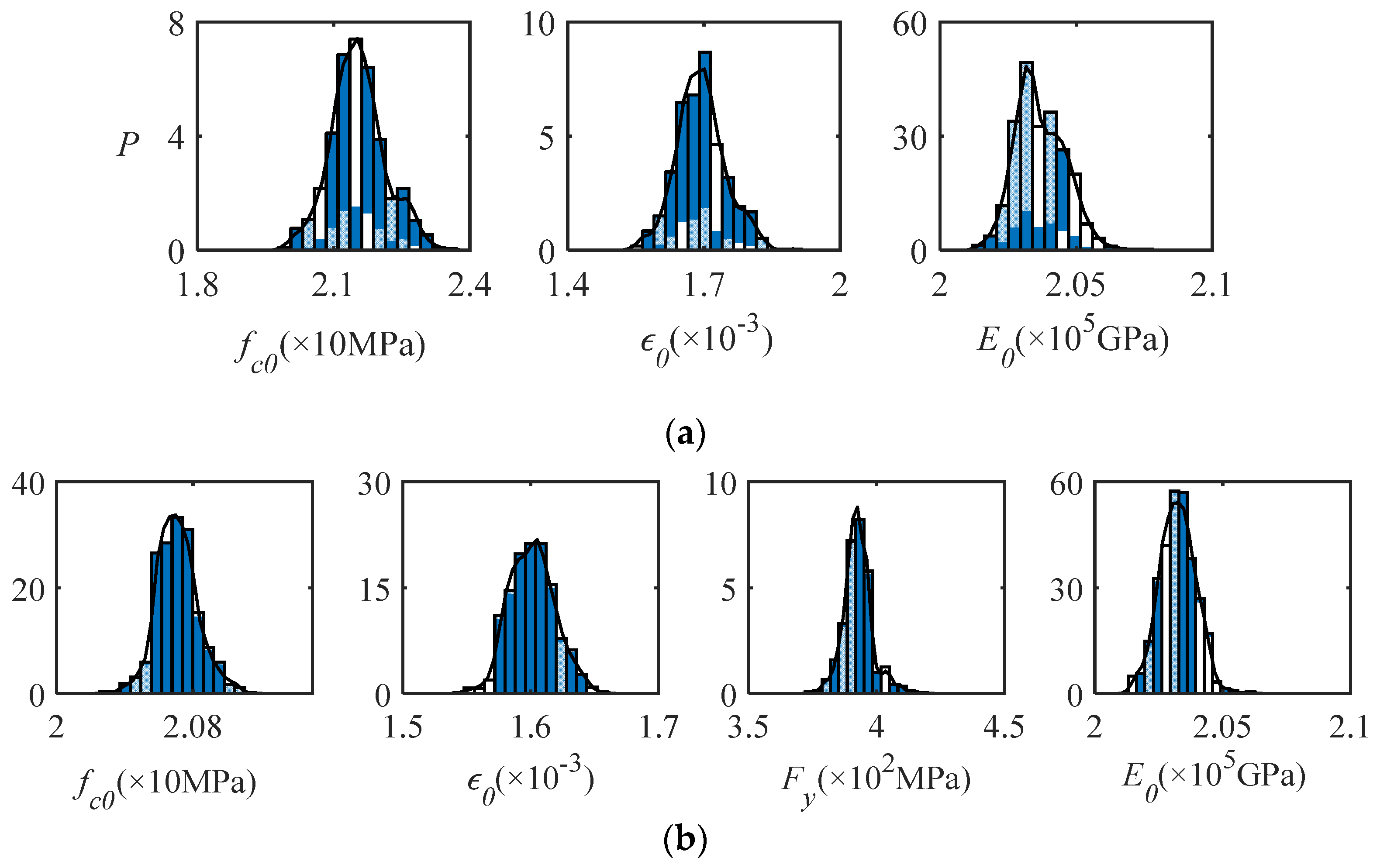
3.2.1. Initial Sampling and Structural Parameters Selection
3.2.2. Secondary Sampling
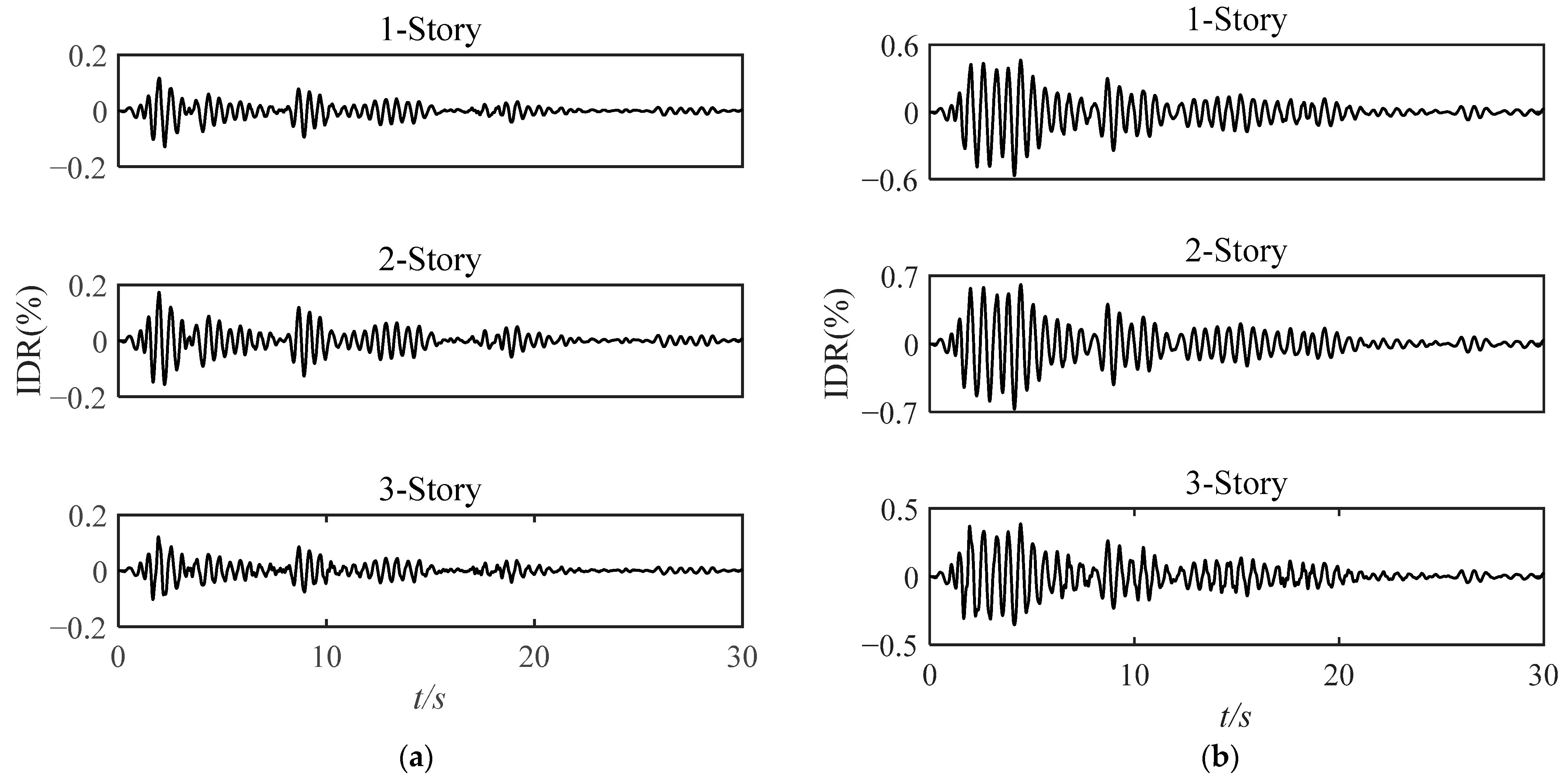
3.3. Damage State Estimation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 561–582. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Applied incremental dynamic analysis. Earthq. Spectra 2004, 20, 523–553. [Google Scholar] [CrossRef]
- Mander, J.B.; Dhakal, R.P.; Mashiko, N.; Solberg, K.M. Incremental dynamic analysis applied to seismic financial risk assessment of bridges. Eng. Struct. 2007, 29, 2662–2672. [Google Scholar] [CrossRef]
- Farrar, C.R.; Duffey, T.A. Bridge modal properties using simplified finite element analysis. J. Bridge Eng. 1998, 3, 38–46. [Google Scholar] [CrossRef]
- Friswell, M.; Mottershead, J.E. Finite Element Model Updating in Structural Dynamics; Springer Science & Business Media: BerlinHeidelberg, Germany, 1995; p. 5. [Google Scholar]
- Imregun, M.; Visser, W.J.; Ewins, D.J. Finite element model updating using frequency response function data: I. Theory and initial investigation. Mech. Syst. Signal Process. 1995, 9, 187–202. [Google Scholar] [CrossRef]
- Jaishi, B.; Ren, W.X. Structural finite element model updating using ambient vibration test results. J. Struct. Eng. 2005, 131, 617–628. [Google Scholar] [CrossRef]
- Marwala, T. Finite-Element-Model Updating Using Computational Intelligence Techniques: Applications to Structural Dynamics; Springer: London, UK, 2010; pp. 225–231. [Google Scholar]
- Ren, W.X.; Chen, H.B. Finite element model updating in structural dynamics by using the response surface method. Eng. Struct. 2010, 32, 2455–2465. [Google Scholar] [CrossRef]
- Abedin, M.; y Basalo, F.J.D.C.; Kiani, N.; Mehrabi, A.B.; Nanni, A. Bridge load testing and damage evaluation using model updating method. Eng. Struct. 2022, 252, 113648. [Google Scholar] [CrossRef]
- Li, W.; Yong, H.; Zikai, X. Machine Learning-Based Probabilistic Seismic Demand Model of Continuous Girder Bridges. Adv. Civ. Eng. 2022, 2022, 3867782. [Google Scholar] [CrossRef]
- Atalla, M.J.; Inman, D.J. On model updating using neural networks. Mech. Syst. Signal Process. 1998, 12, 135–161. [Google Scholar] [CrossRef]
- Levin, R.I.; Lieven, N.A.J. Dynamic finite element model updating using neural networks. J. Sound Vib. 1998, 210, 593–607. [Google Scholar] [CrossRef]
- Astroza, R.; Alessandri, A.; Conte, J.P. A dual adaptive filtering approach for nonlinear finite element model updating accounting for modeling uncertainty. Mech. Syst. Signal Process. 2019, 115, 782–800. [Google Scholar] [CrossRef]
- Behmanesh, I.; Moaveni, B.; Lombaert, G.; Papadimitriou, C. Hierarchical Bayesian model updating for structural identification. Mech. Syst. Signal Process. 2015, 64, 360–376. [Google Scholar] [CrossRef]
- Beck, J.L.; Katafygiotis, L.S. Updating models and their uncertainties. I: Bayesian statistical framework. J. Eng. Mech. 1998, 124, 455–461. [Google Scholar] [CrossRef]
- Li, X.; Kurata, M. Probabilistic updating of fishbone model for assessing seismic damage to beam–column connections in steel moment-resisting frames. Comput. Aided Civ. Infrastruct. Eng. 2019, 34, 790–805. [Google Scholar] [CrossRef]
- Lam, H.F.; Yang, J.H.; Beck, J.L. Bayesian operational modal analysis and assessment of a full-scale coupled structural system using the Bayes-Mode-ID method. Eng. Struct. 2019, 186, 183–202. [Google Scholar] [CrossRef]
- Jensen, H.A.; Millas, E.; Kusanovic, D.; Papadimitriou, C. Model-reduction techniques for Bayesian finite element model updating using dynamic response data. Comput. Methods Appl. Mech. Eng. 2014, 279, 301–324. [Google Scholar] [CrossRef]
- Beck, J.L.; Siu-Kui, A. Bayesian Updating of Structural Models and Reliability using Markov Chain Monte Carlo Simulation. J. Eng. Mech. 2002, 128, 380–391. [Google Scholar] [CrossRef]
- Ching, J.; Muto, M.; Beck, J.L. Bayesian Linear Structural Model Updating using Gibbs Sampler with Modal Data. In Proceedings of the 9th International Conference on Structural Safety and Reliability, Rome, Italy, 19–23 June 2005; Millpress: Rotterdam, The Netherlands, 2005; pp. 2609–2616. [Google Scholar]
- Cheung, S.H.; Beck, J.L. Bayesian Model Updating Using Hybrid Monte Carlo Simulation with Application to Structural Dynamic Models with Many Uncertain Parameters. J. Eng. Mech. 2009, 135, 243–255. [Google Scholar] [CrossRef]
- Boulkaibet, I.; Mthembu, L.; Marwala, T.; Friswell, M.I.; Adhikari, S. Finite element model updating using the separable shadow hybrid Monte Carlo technique. Top. Modal Anal. II 2014, 8, 267–275. [Google Scholar]
- Boulkaibet, I.; Mthembu, L.; Marwala, T.; Friswell, M.I.; Adhikari, S. Finite element model updating using the shadow hybrid Monte Carlo technique. Mech. Syst. Signal Process. 2015, 52–53, 115–132. [Google Scholar] [CrossRef]
- Lam, H.F.; Yang, J.H.; Au, S.K. Bayesian model updating of a coupled-slab system using field test data utilizing an enhanced Markov chain Monte Carlo simulation algorithm. Eng. Struct. 2015, 102, 144–155. [Google Scholar] [CrossRef]
- Zhao, Y.; Gong, M.; Zuo, Z.; Gao, Y. Bayesian estimation approach based on modified SCAM algorithm and its application in structural damage identification. Struct. Control Health Monit. 2021, 28, e2654. [Google Scholar] [CrossRef]
- Yuen, K.-V. Bayesian Methods for Structural Dynamics and Civil Engineering; John Wiley & Sons: New York, NY, USA, 2010. [Google Scholar]
- Skilling, J. Nested sampling. AIP Conference Proceedings. Am. Inst. Phys. 2004, 735, 395–405. [Google Scholar]
- Keeton, C.R. On statistical uncertainty in nested sampling. Mon. Not. R. Astron. Soc. 2011, 414, 1418–1426. [Google Scholar] [CrossRef]
- Speagle, J.S. Dynesty: A dynamic nested sampling package for estimating Bayesian posteriors and evidences. Mon. Not. R. Astron. Soc. 2020, 493, 3132–3158. [Google Scholar] [CrossRef]
- Jaynes, E.T. Prior probabilities. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 227–241. [Google Scholar] [CrossRef]
- Xin, Y.; Hao, H.; Li, J.; Wang, Z.C.; Wan, H.P.; Ren, W.X. Bayesian based nonlinear model updating using instantaneous characteristics of structural dynamic responses. Eng. Struct. 2019, 183, 459–474. [Google Scholar] [CrossRef]
- Beck, J.L.; Yuen, K.V. Model selection using response measurements: Bayesian probabilistic approach. J. Eng. Mech. 2004, 130, 192–203. [Google Scholar] [CrossRef]
- Cao, T.; Zeng, X.; Wu, J. An arithmetic example study of nested sampling algorithm for groundwater model evaluation. Hydrogeol. Eng. Geol. 2017, 44, 69–76. (In Chinese) [Google Scholar]
- Myung, I.J. Tutorial on maximum likelihood estimation. J. Math. Psychol. 2003, 47, 90–100. [Google Scholar] [CrossRef]
- Terrell, G.R.; Scott, D.W. Variable kernel density estimation. Ann. Stat. 1992, 20, 1236–1265. [Google Scholar] [CrossRef]
- Douc, R.; Cappé, O. Comparison of resampling schemes for particle filtering Ispa 2005. In Proceedings of the 4th International Symposium on Image and Signal Processing and Analysis, Zagreb, Croatia, 15–17 September 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 64–69. [Google Scholar]
- McKenna, F. OpenSees: A framework for earthquake engineering simulation. Comput. Sci. Eng. 2011, 13, 58–66. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Y.Q.; Zhao, Y.N. Comparative analysis of seismic capacity of RC frame structures based on different damage models. Earthq. Eng. Eng. Vib. 2020, 40, 118–126. (In Chinese) [Google Scholar]
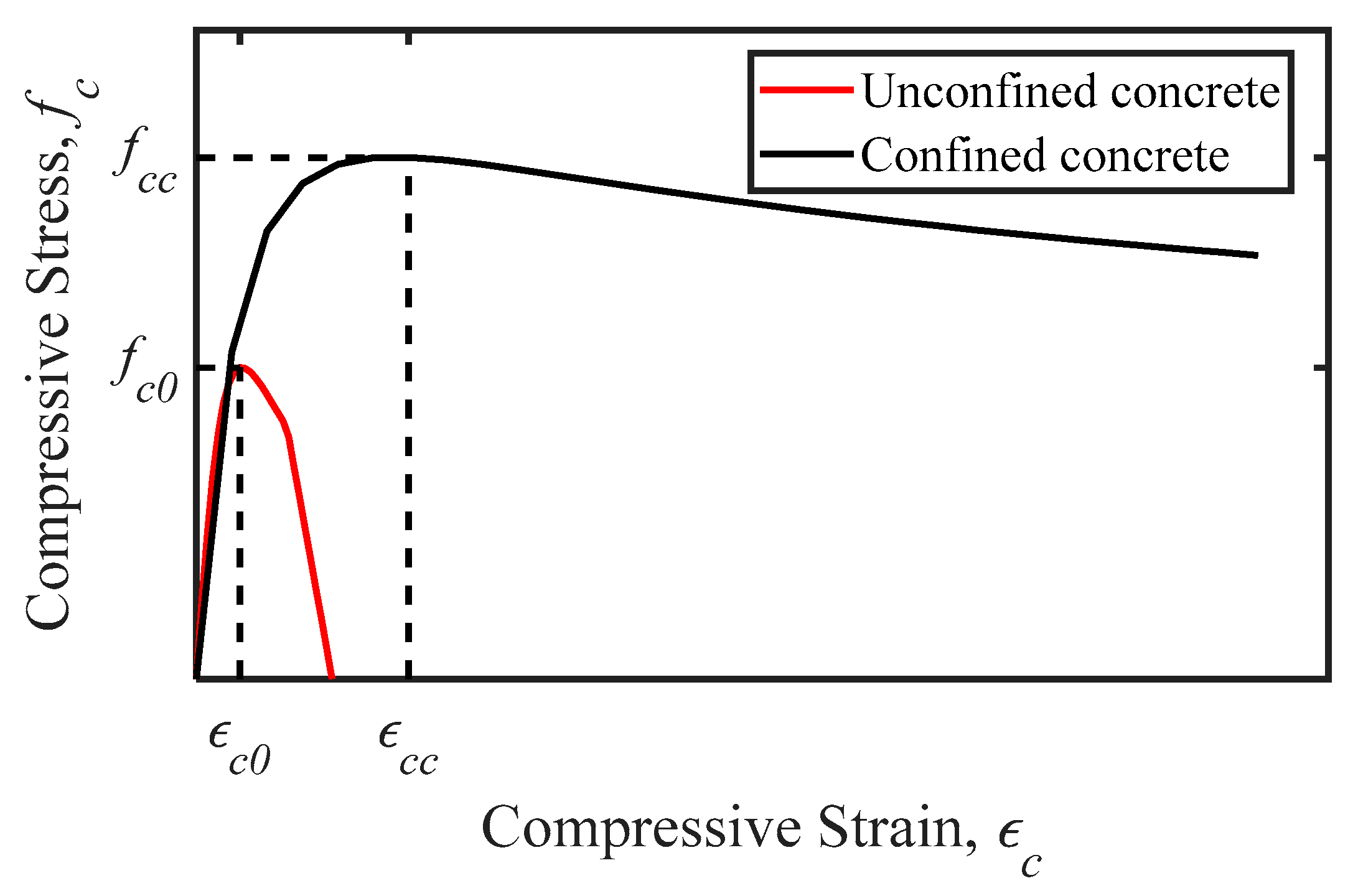
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Filippou, F.C.; Popov, E.P.; Bertero, V.V. Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints; Report EERC 83–19; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1983. [Google Scholar]
- Gasparini, D.A.; DebChaudhury, A. Dynamic response to nonstationary nonwhite excitation. J. Eng. Mech. Div. 1980, 106, 1233–1248. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Z.; Zuo, X.; Du, X.; Gao, H. Shaking table test on the seismic failure characteristics of a subway station structure on liquefiable ground. Earthq. Eng. Struct. Dyn. 2013, 42, 1489–1507. [Google Scholar] [CrossRef]
- Zhang, S.; Gaohui, W. Effects of near-fault and far-fault ground motions on nonlinear dynamic response and seismic damage of concrete gravity dams. Soil Dyn. Earthq. Eng. 2013, 53, 217–229. [Google Scholar] [CrossRef]
- Zhong, Z.; Wang, Z.; Zhao, M.; Du, X. Structural damage assessment of mountain tunnels in fault fracture zone subjected to multiple strike-slip fault movement. Tunn. Undergr. Space Technol. 2020, 104, 103527. [Google Scholar] [CrossRef]
- Naeim, F. The Seismic Design Handbook, 2nd ed.; Kluwer Academic: Boston, MA, USA, 2011. [Google Scholar]
- Masi, A.; Vona, M.; Mucciarelli, M. Selection of natural and synthetic accelero- grams for seismic vulnerability studies on reinforced concrete frames. J. Struct. Eng. 2011, 137, 367–378. [Google Scholar] [CrossRef]
- Morfidis, K.; Kostinakis, K. Seismic parameters’ combinations for the optimum prediction of the damage state of R/C buildings using neural networks. Adv. Eng. Softw. 2017, 106, 1–16. [Google Scholar] [CrossRef]



| Parameters | Suggested Value |
|---|---|
| (×10 MPa) | 2.01 |
| (×10−3) | 1.64 |
| (×102 MPa) | 4.00 |
| / | 7.00 |
| (×103) | 5.00 |
| (×102 MPa) | 4.00 |
| (×105 GPa) | 2.06 |
| Ratio (×103) | 1.00 |
| STD | Estimated | True | Error (%) |
|---|---|---|---|
| (PGA = 0.1 g) | 0.0695 | 0.0697 | 0.29 |
| (PGA = 0.3 g) | 0.2537 | 0.2535 | 0.08 |
| Case | Parameters | Estimate | True | Error (%) |
|---|---|---|---|---|
| PGA = 0.1 g | 2.01 | 2.13 | 5.97 | |
| 1.64 | 1.66 | 1.22 | ||
| 2.06 | 2.03 | 1.46 | ||
| PGA = 0.3 g | 2.01 | 2.07 | 2.99 | |
| 1.64 | 1.61 | 1.83 | ||
| 4.00 | 3.95 | 1.25 | ||
| 2.06 | 2.04 | 0.97 |
| MIDR (%) | <0.25 | 0.25–0.50 | 0.50–1.00 | 1.00–1.50 | >1.50 |
|---|---|---|---|---|---|
| Degree of damage | Null | Slight | Moderate | Heavy | Destruction |
| Case | MIDR | Damage State |
|---|---|---|
| PGA = 0.1 g | 0.17 | Null |
| PGA = 0.3 g | 0.67 | Moderate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Kajita, Y.; Yang, Y. Bayesian RC-Frame Finite Element Model Updating and Damage Estimation Using Nested Sampling with Nonlinear Time History. Buildings 2023, 13, 1281. https://doi.org/10.3390/buildings13051281
Wang K, Kajita Y, Yang Y. Bayesian RC-Frame Finite Element Model Updating and Damage Estimation Using Nested Sampling with Nonlinear Time History. Buildings. 2023; 13(5):1281. https://doi.org/10.3390/buildings13051281
Chicago/Turabian StyleWang, Kunyang, Yukihide Kajita, and Yaoxin Yang. 2023. "Bayesian RC-Frame Finite Element Model Updating and Damage Estimation Using Nested Sampling with Nonlinear Time History" Buildings 13, no. 5: 1281. https://doi.org/10.3390/buildings13051281
APA StyleWang, K., Kajita, Y., & Yang, Y. (2023). Bayesian RC-Frame Finite Element Model Updating and Damage Estimation Using Nested Sampling with Nonlinear Time History. Buildings, 13(5), 1281. https://doi.org/10.3390/buildings13051281





_Mei.png)


