Analysis of the Ultimate Load-Bearing Capacity of Steel-Clad Concrete-Filled Steel Tube Arched Protective Doors under Blast Shock Waves
Abstract
:1. Introduction
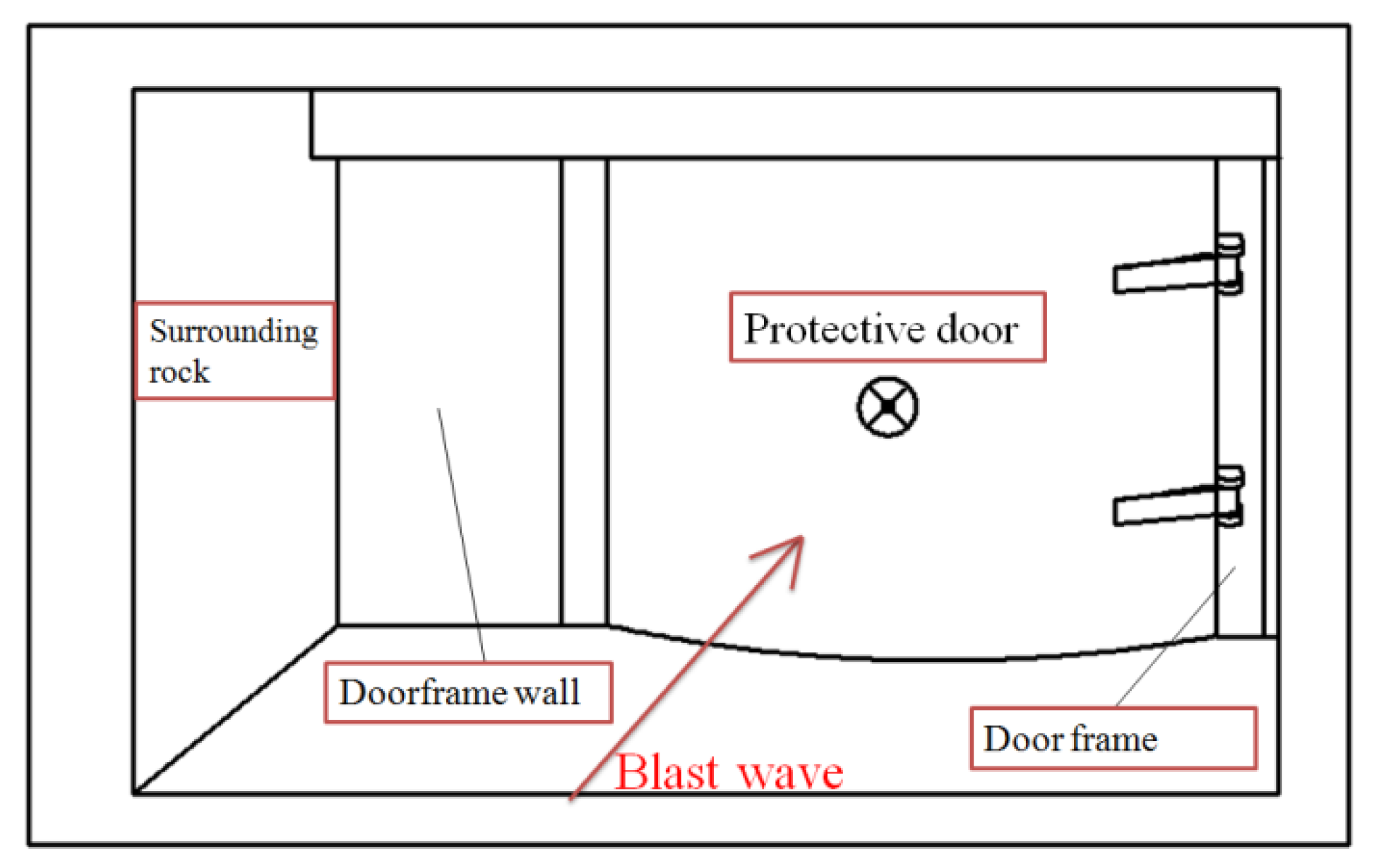
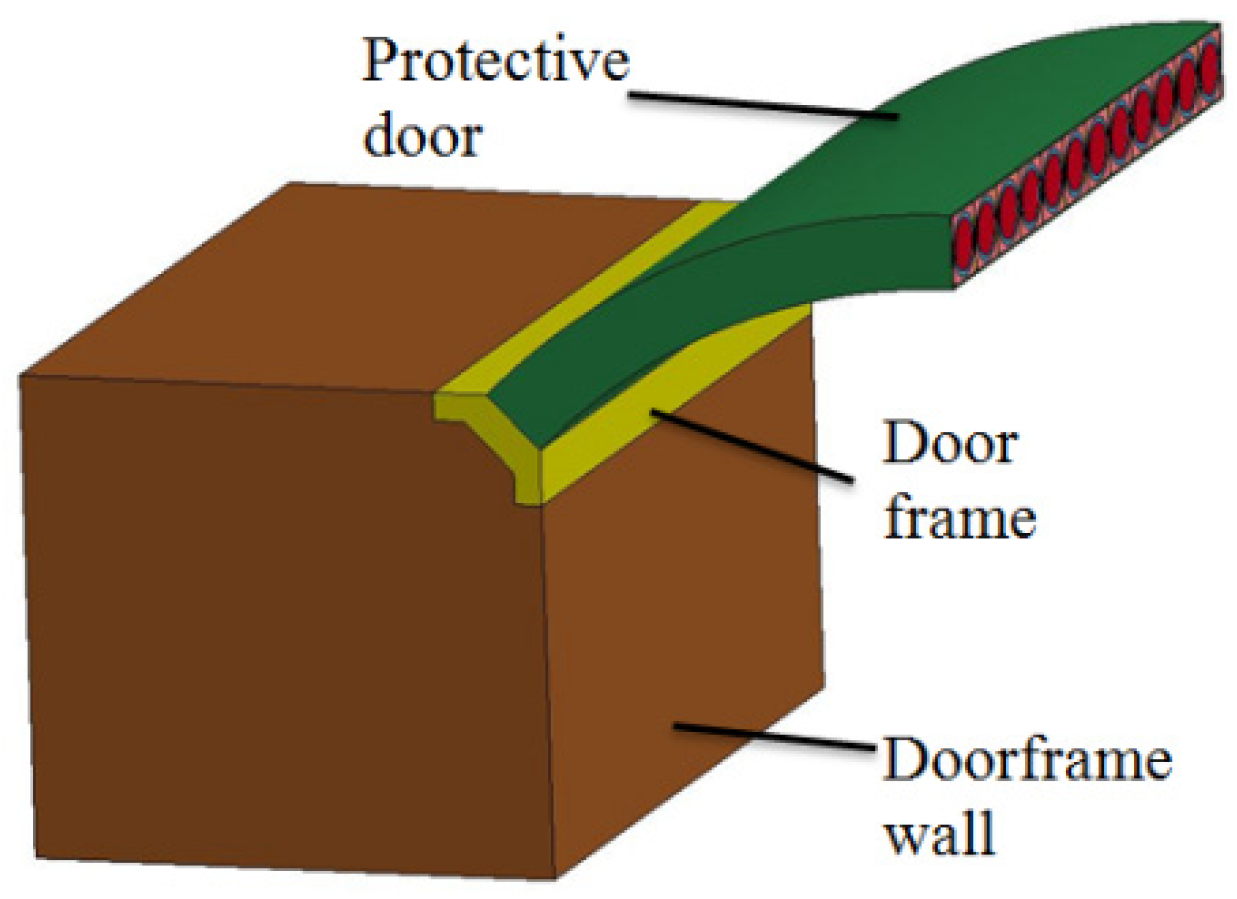
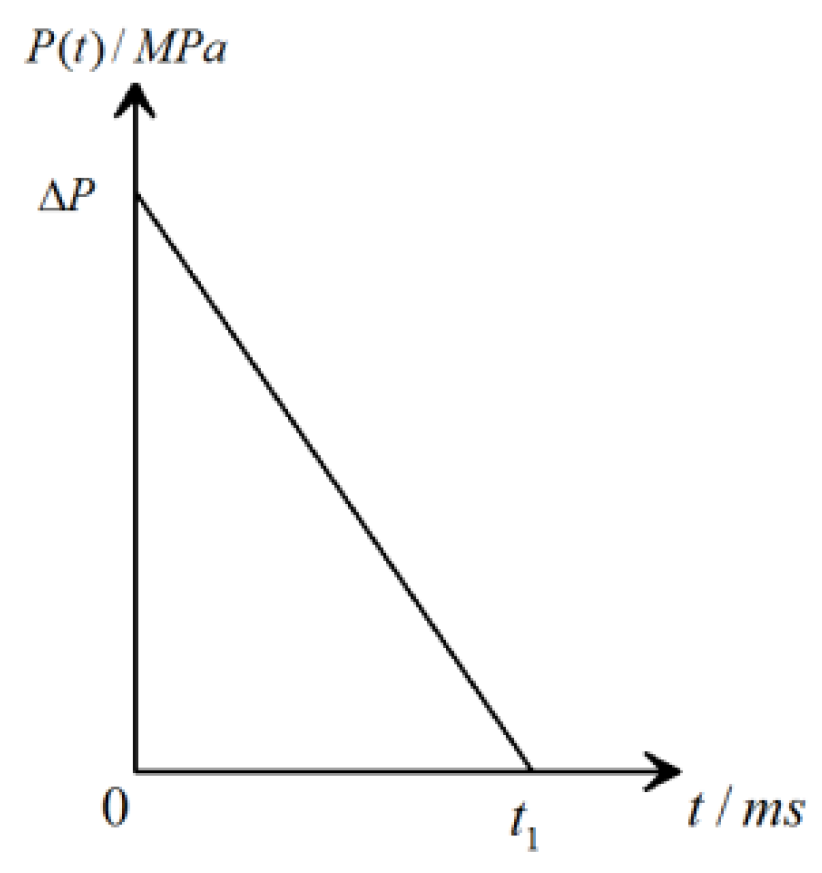
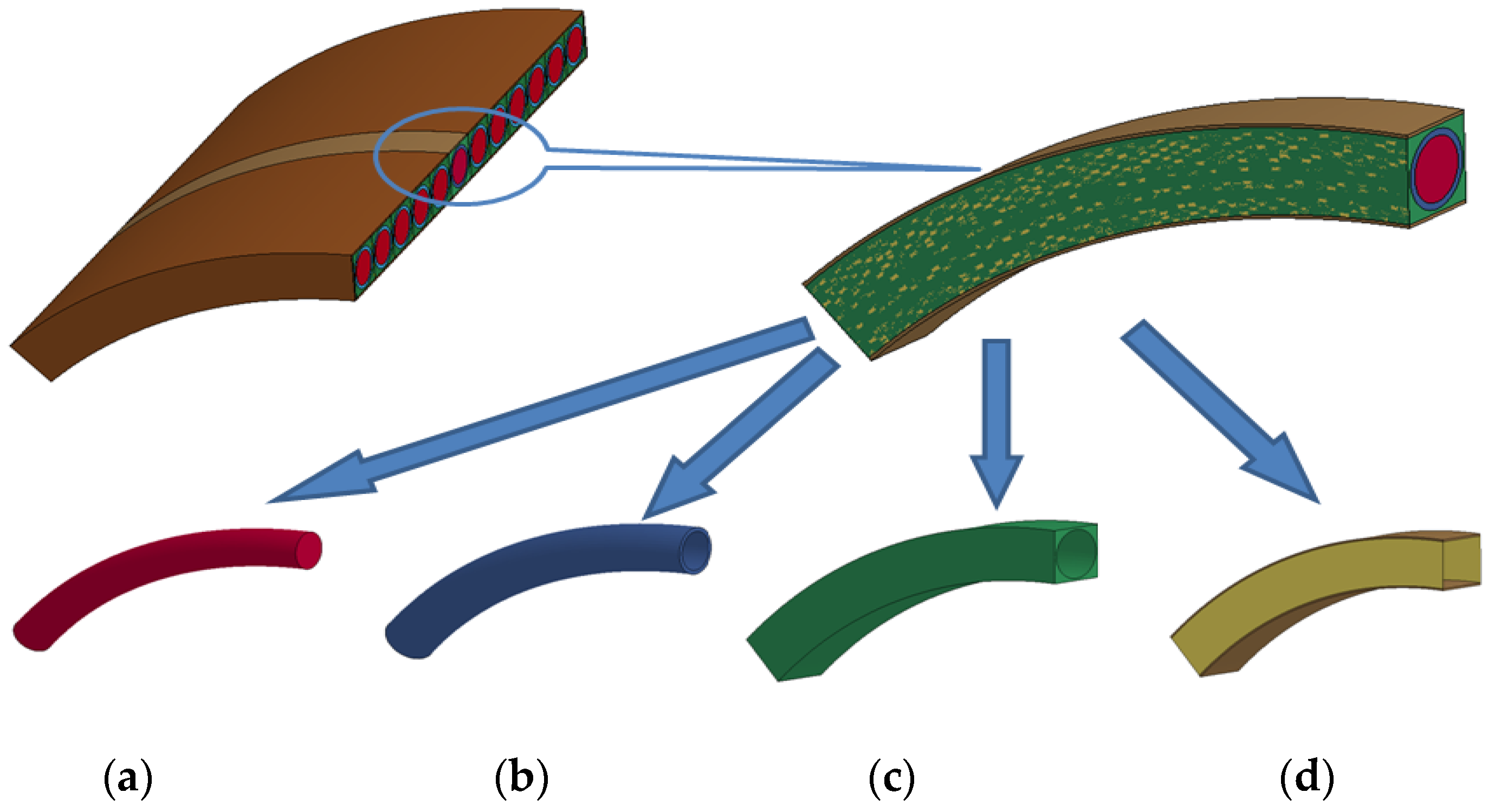
2. Problem Formulation and Computational Model
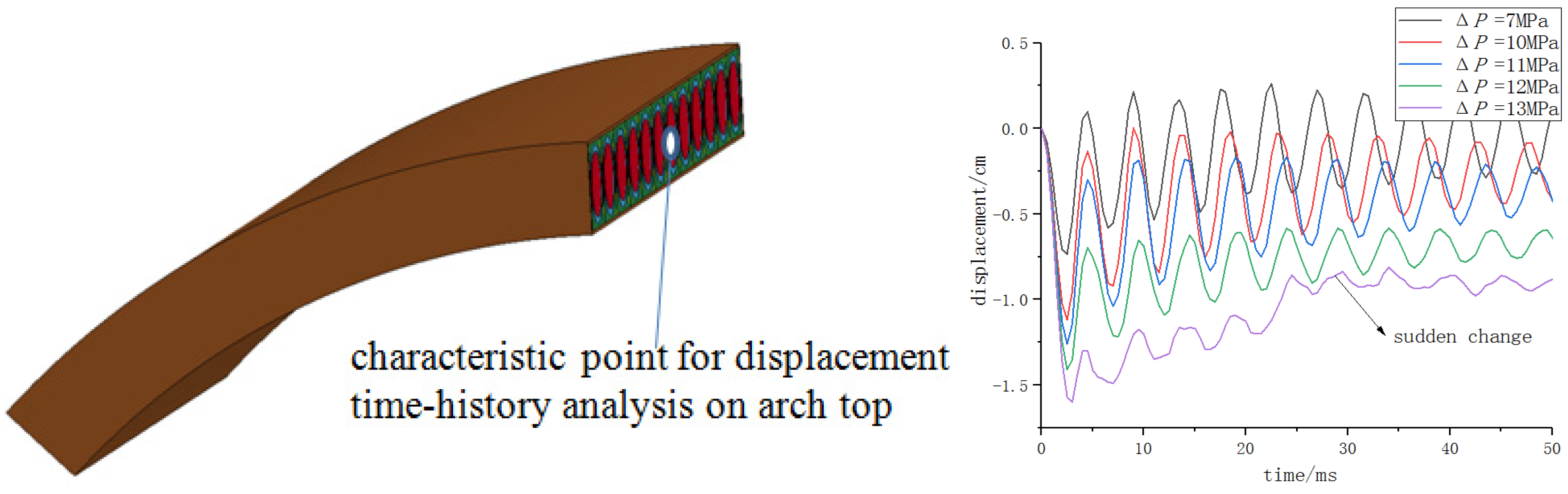
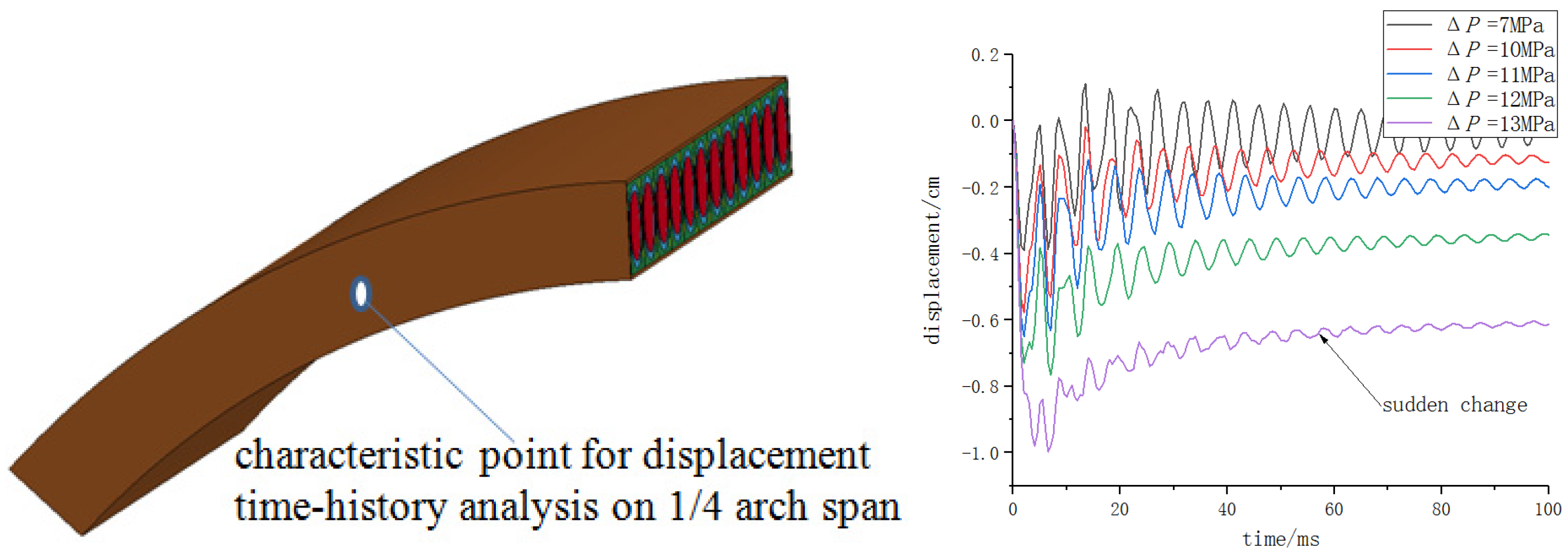
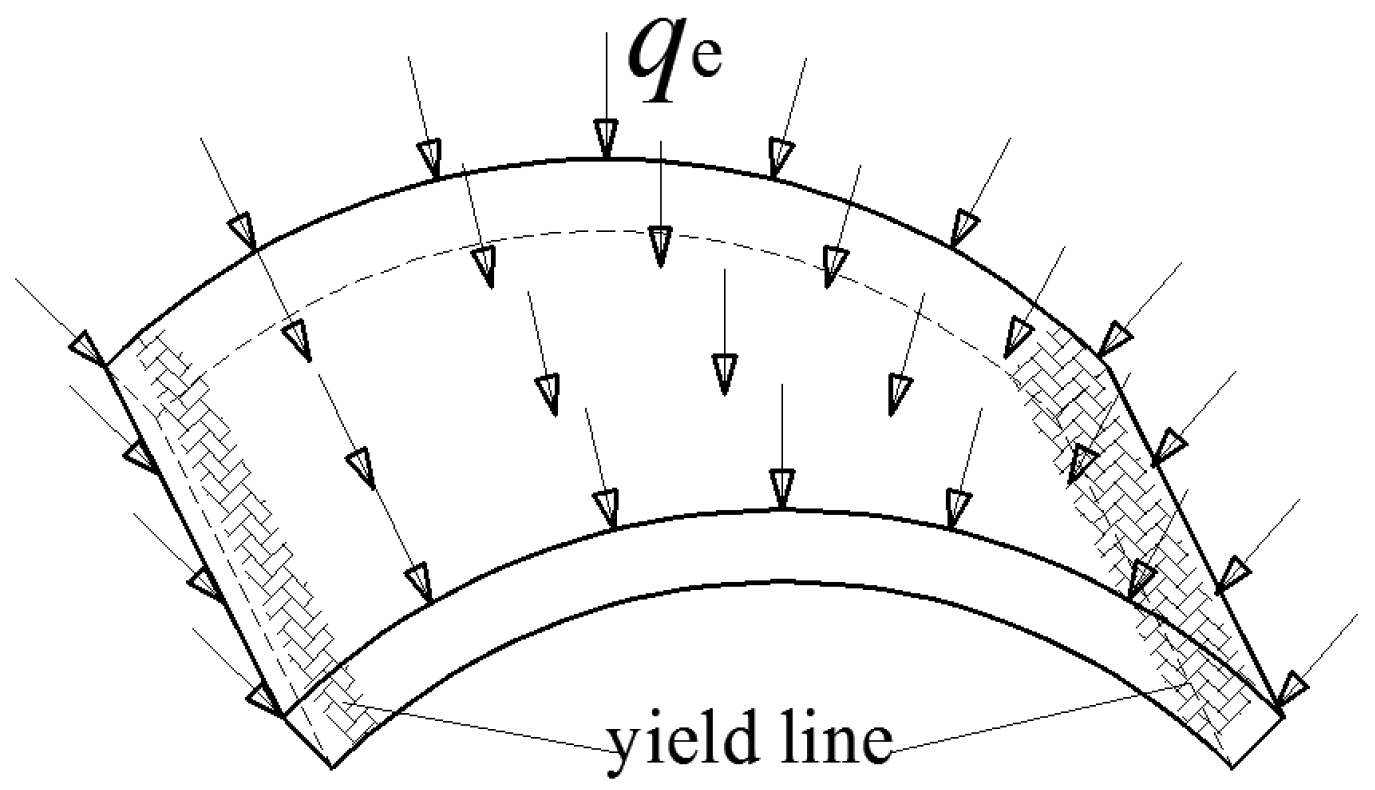
3. Dynamic Response Law and Damage Mode of the Protective Door under Blast Load
3.1. Dynamic Response Law of Protective Door
3.2. Damage Mode of the Protective Door
3.3. Damage Mechanism of the Protective Door
4. Theoretical Calculation of Ultimate Blast Resistance-Bearing Capacity of the Protective Door
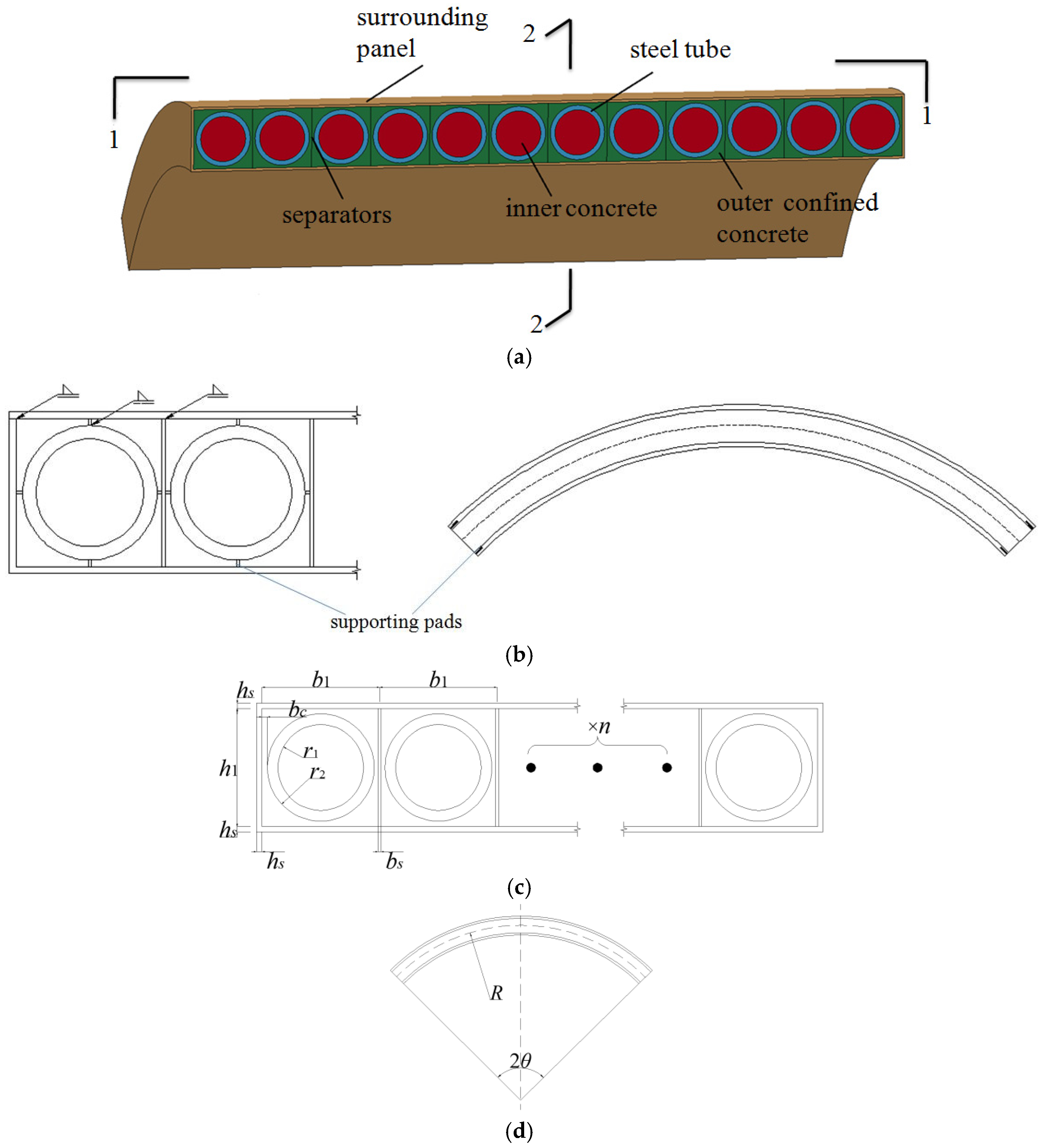
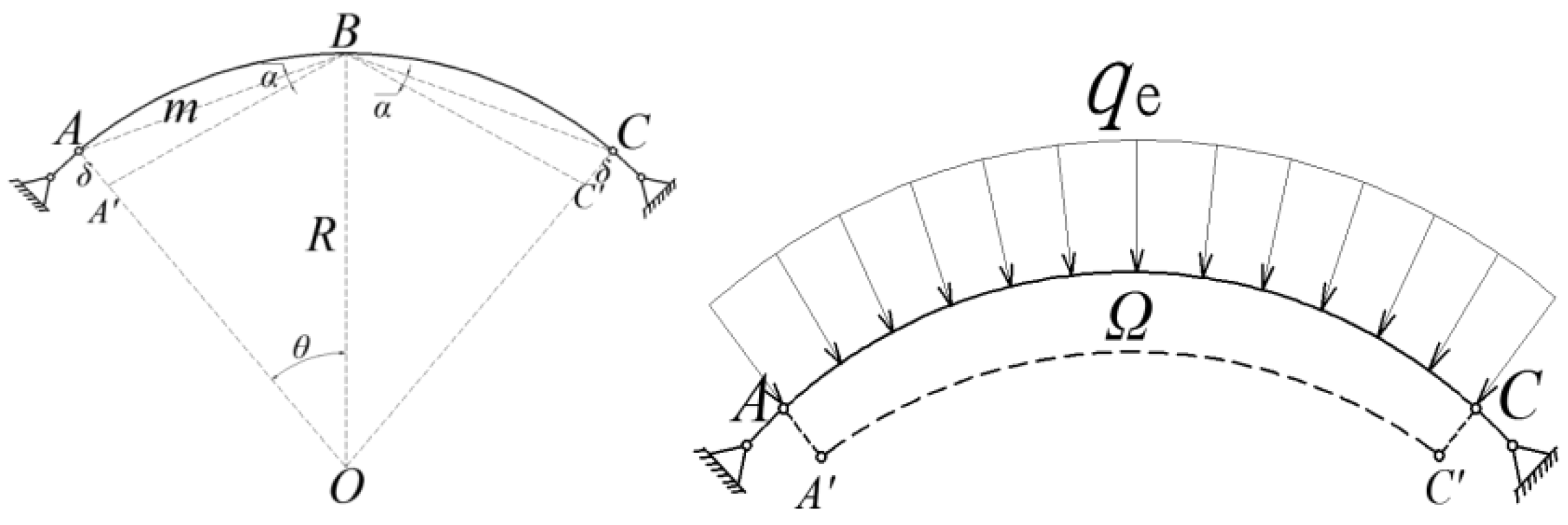
4.1. Mechanical Model
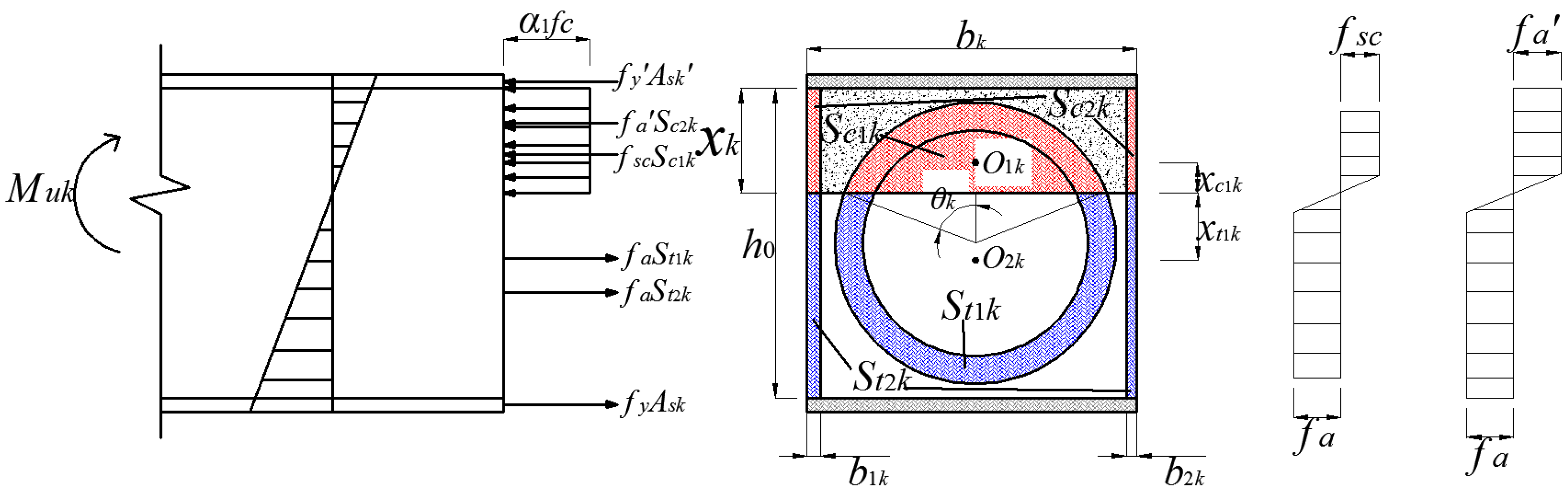
4.2. Ultimate Bending Moment of Cross-Sectional
- (1)
- Steel and concrete have flat sections with respect to deformation;
- (2)
- The plot of stresses in the compressed zone within the concrete can be simplified to an equivalent rectangle;
- (3)
- The plots of tensile and compressive stresses in the steel bones are trapezoidal, which can be simplified to an equivalent rectangle in calculation;
- (4)
- The tensile strength of the concrete is ignored.
4.3. Analysis of Calculation Results
5. Analysis of the Impact of Design Parameters on the Ultimate Blast Resistance-Bearing Capacity
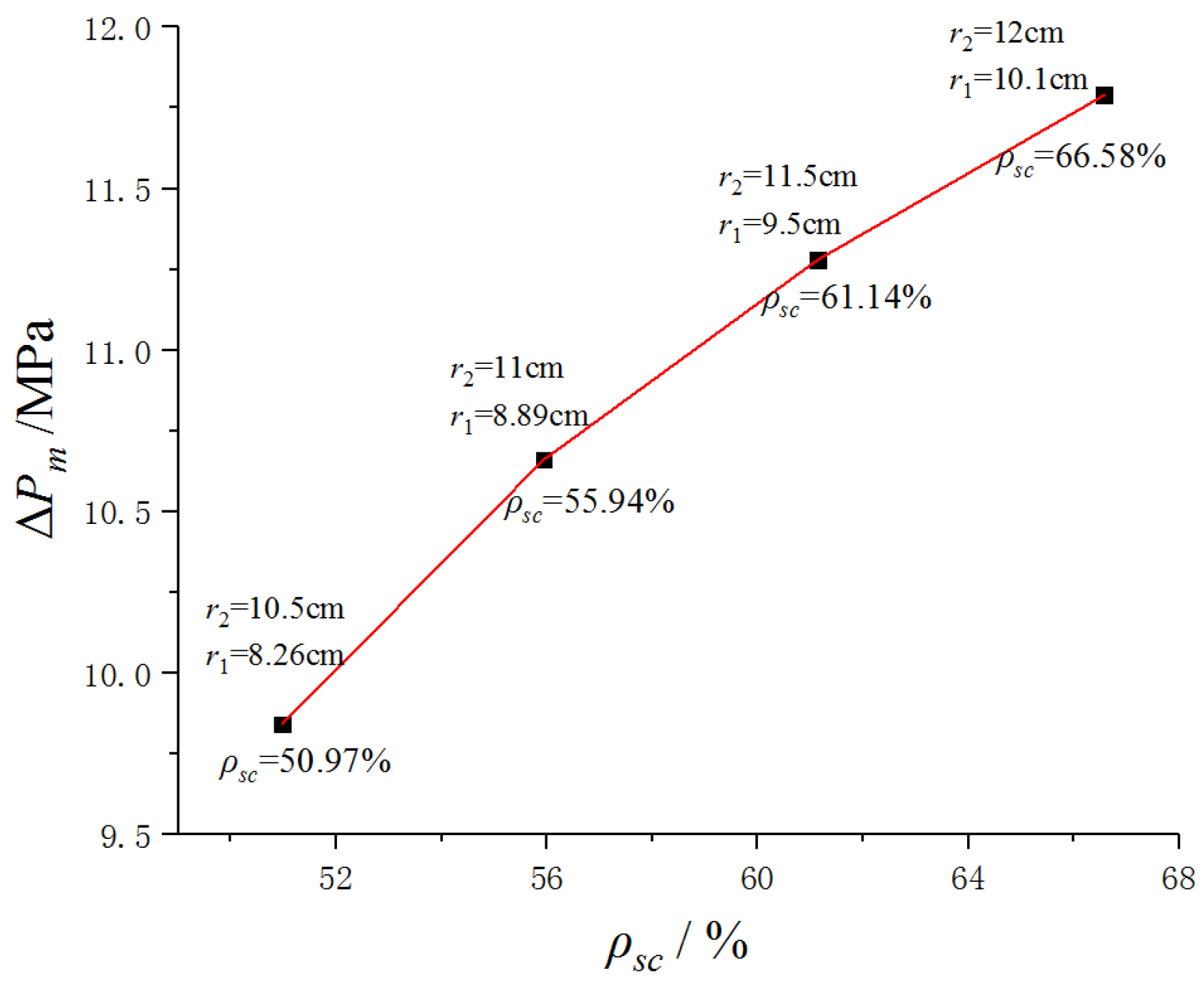
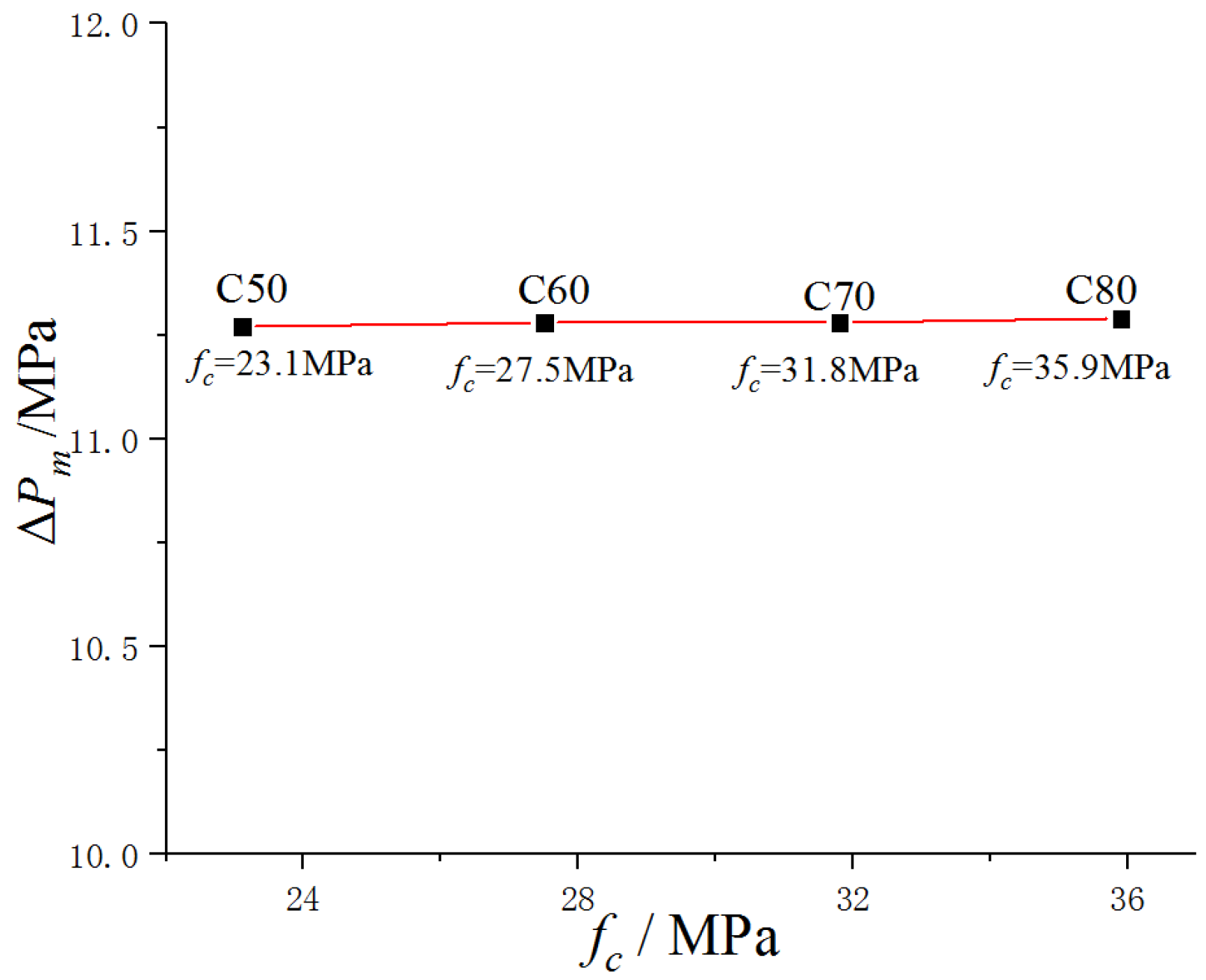
5.1. Influence of Concrete-Filled Steel Tube Design Parameters
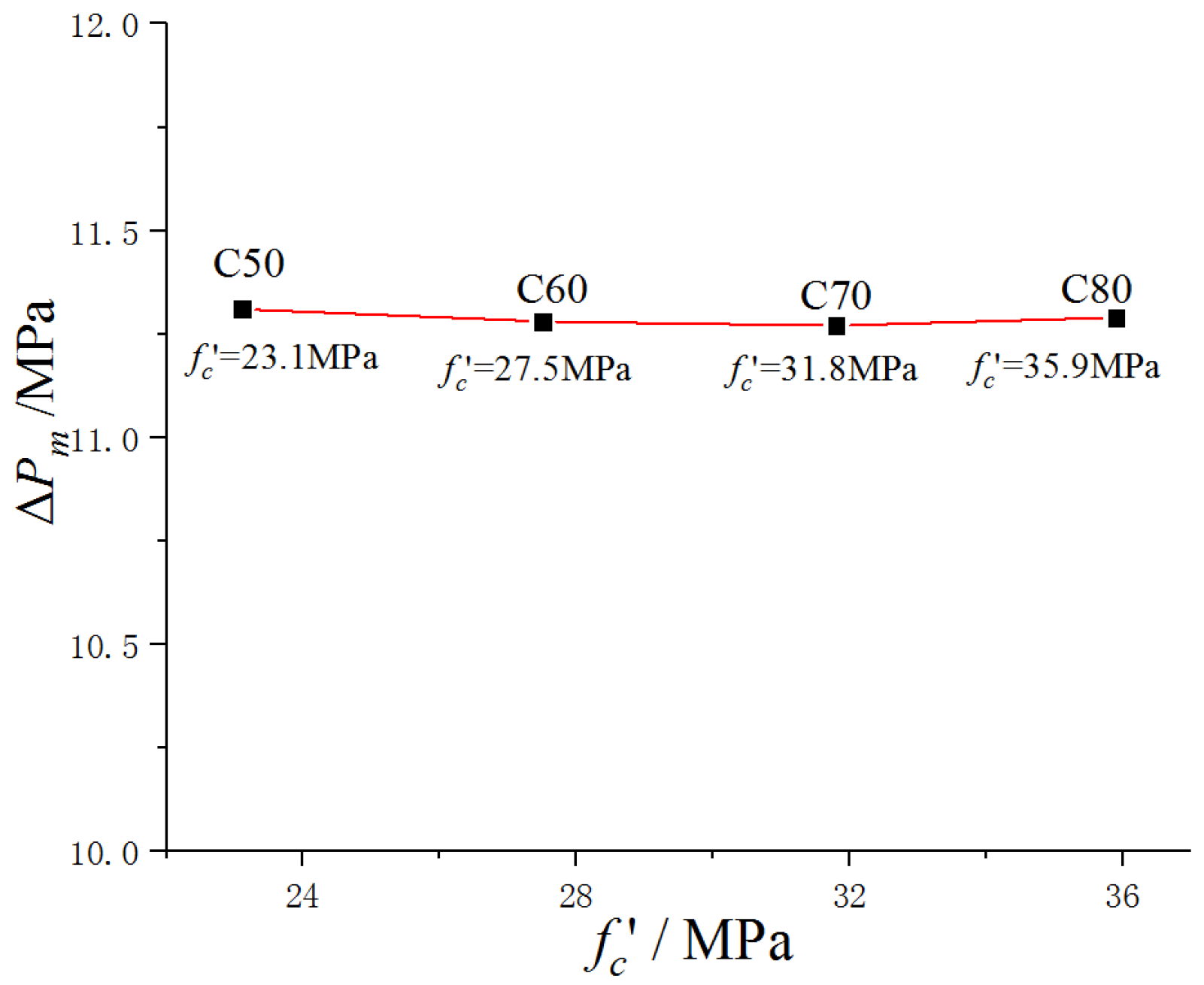
5.2. Influence of Design Parameters of Confined Concrete
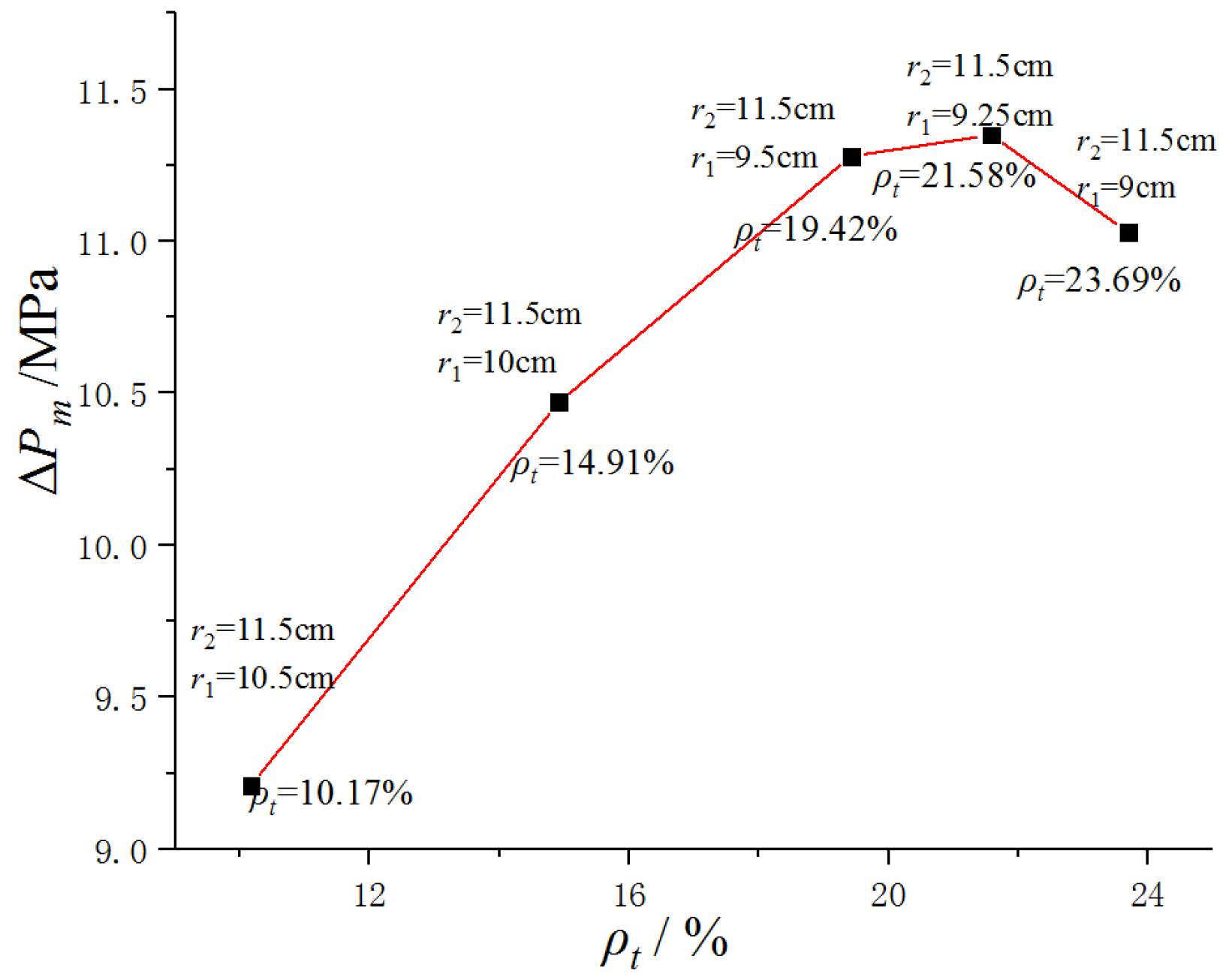
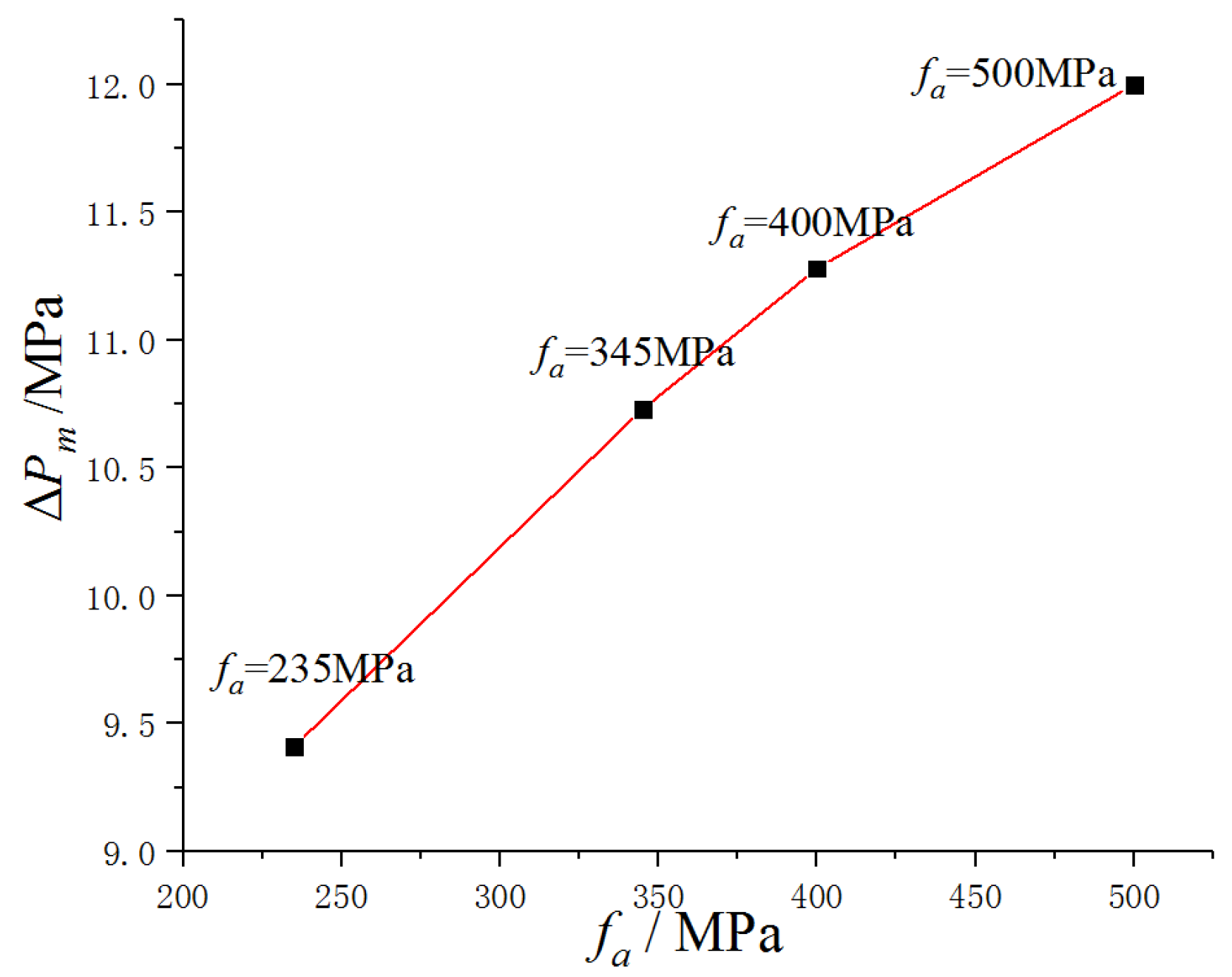
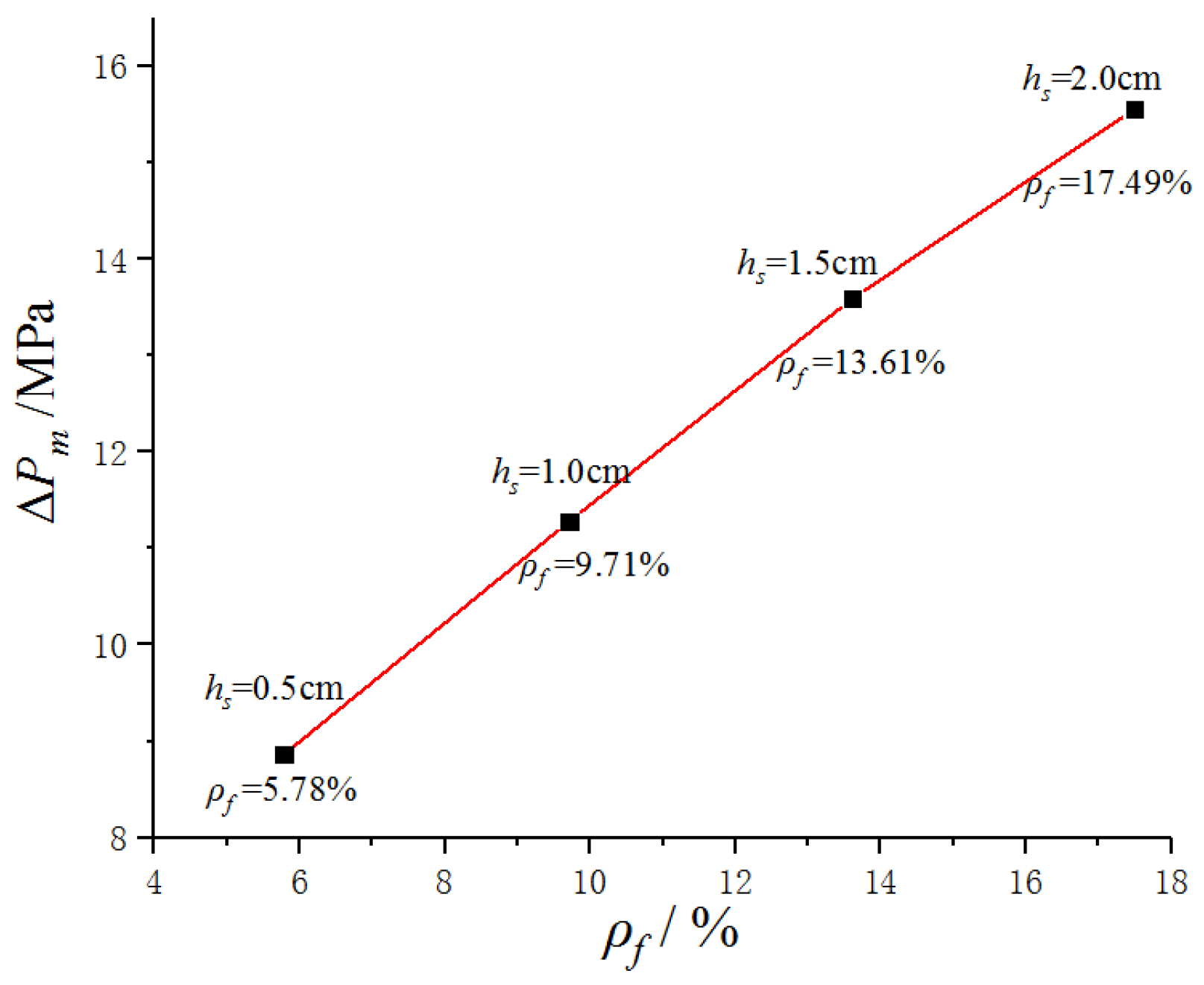
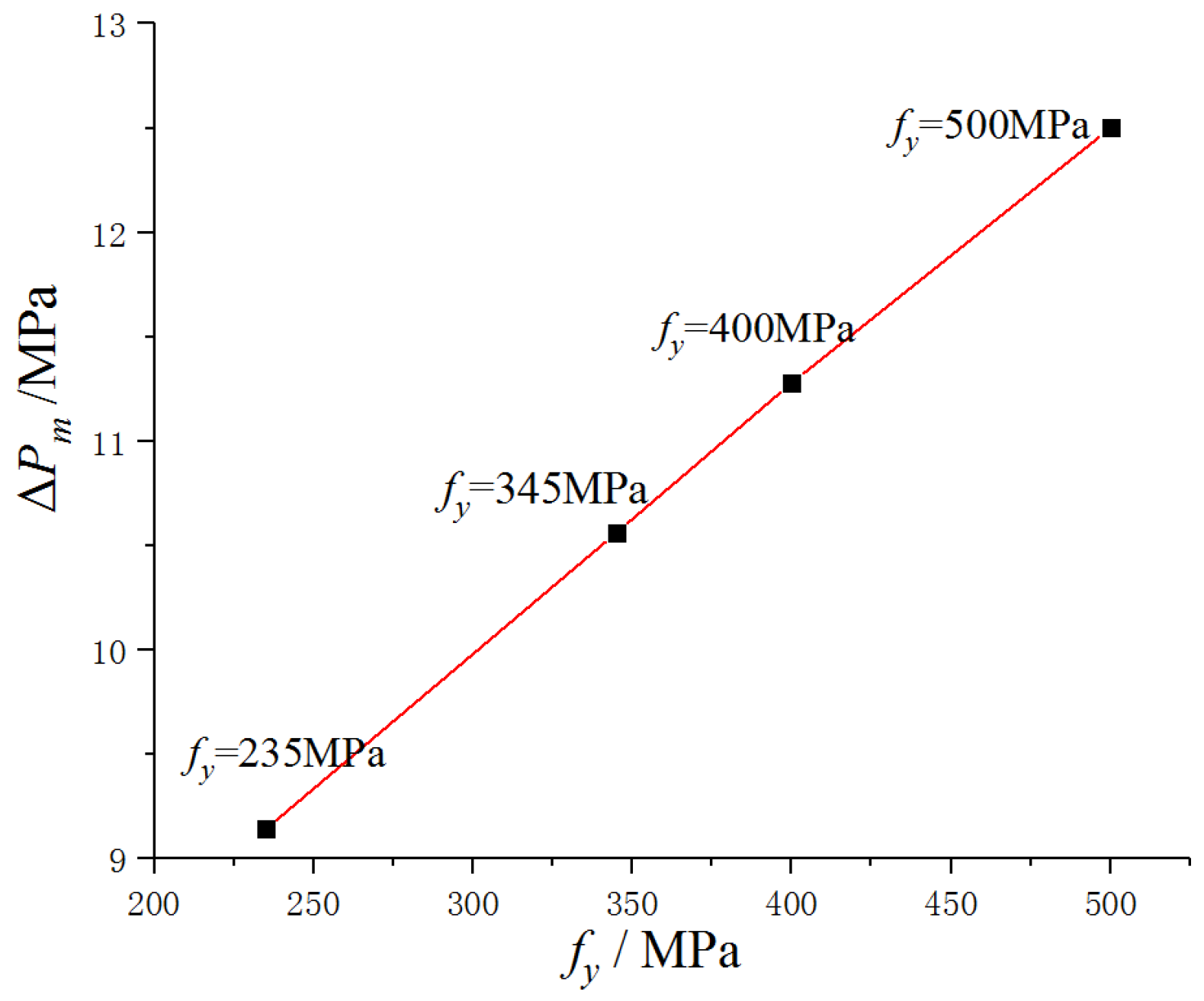
5.3. Influence of Design Parameters of the Surrounding Panel and Its Separators
6. Conclusions
- (1)
- Under a radially uniform load on the outer surface, as the load increases, the SCCFST arched protective door supported on both sides shifts from the overall deformation reaction mode into the development of a plastic hinge line at the foot of the two arches, resulting in dynamic instability. The protective door becomes a geometrically unstable system and eventually fails due to slip fracture damage.
- (2)
- This paper proposes a method for calculating the ultimate blast resistance of the SCCFST arched protective door based on the motorized hinge method of ultimate analysis. This method considers the geometric relationship between the “plastic hinge” damage mode of the door and the coordinated action of the components of the door section and can be used for the design and analysis of protective doors against blast load.
- (3)
- The impact of the design parameters of each part of the SCCFST arched protective door on the ultimate blast resistance-bearing capacity has a clear pattern: (A) The primary factor influencing the ultimate blast resistance is the surrounding panel and its separators. Hence, increasing the steel ratio and steel strength can significantly increase the ultimate blast resistance load capacity. (B) The concrete-filled steel tube contributes to the ultimate blast resistance to a lesser extent. Enhancing the steel ratio and strength of the steel tube within a certain range can moderately improve the ultimate blast resistance. (C) While confined concrete plays a role in the ultimate blast resistance capacity, the impact of increasing the concrete class on the load-bearing capacity is not particularly pronounced.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jacques, E.; Lloyd, A.; Berry, T.; Saatcioglu, M.; Shinder, J. Development of blast resistant steel doors. In Proceedings of the 11th International Conference on Shock & Impact Loads on Structures, Ottawa, ON, Canada, 14–15 May 2015; pp. 14–15. [Google Scholar]
- Meng, Y.; Li, B.; Wang, Y. Structure design of new airtight blast door based on topology and shape optimization method. Geotech. Geol. Eng. 2016, 34, 703–711. [Google Scholar] [CrossRef]
- Veeredhi, L.S.B.; Ramana Rao, N.V. Studies on the impact of explosion on blast resistant stiffened door structures. J. Inst. Eng. Ser. A 2015, 96, 11–20. [Google Scholar] [CrossRef]
- Thimmesh, T.; Shirbhate, P.; Mandal, J.; Sandhu, I.; Goel, M. Numerical investigation on the blast resistance of a door panel. Mater. Today Proc. 2021, 44, 659–666. [Google Scholar] [CrossRef]
- He, H.; Zhang, B.; Zheng, Q.; Fan, H. Anisotropic dynamic theory to predict blast responses of composite fluted-core sandwich protective door panels. Thin-Walled Struct. 2021, 161, 107436. [Google Scholar] [CrossRef]
- Li, X.; Miao, C.; Wang, Q.; Geng, Z. Antiknock performance of interlayered high-damping-rubber blast door under thermobaric shock wave. Shock. Vib. 2016, 2016, 2420893. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, H.; Zhao, Z.; Fan, H.; Jin, F. Blast response of hierarchical anisogrid stiffened composite panel: Considering the damping effect. Int. J. Mech. Sci. 2018, 140, 250–259. [Google Scholar] [CrossRef]
- Meng, F.; Zhang, B.; Zhao, Z.; Xu, Y.; Fan, H.; Jin, F. A novel all-composite blast-resistant door structure with hierarchical stiffeners. Compos. Struct. 2016, 148, 113–126. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, J.; Tao, J.; Jia, X.; Huang, Z.; Liu, X.; Liang, S.; Zhao, Y.; Bai, X. A sutdy on impact resistance performance of a blast door with POZD coating. J. Vib. Shock. 2022, 4, 231–238. (In Chinese) [Google Scholar]
- Shi, S.; Zhang, X.; Yin, P. Static Analysis of the New Defensive Structure under Explosive Loading. Undergr. Space 2003, 23, 66–68+109. (In Chinese) [Google Scholar]
- Ganorkar, K.; Goel, M.D.; Chakraborty, T. Numerical Analysis of Double-Leaf Composite Stiffened Door Subjected to Blast Loading. J. Perform. Constr. Facil. 2023, 37, 04022067. [Google Scholar] [CrossRef]
- Tan, Z. The Dynamic Response and Optimum Design of Vaulted Blast Resistant Door; Chang’an University: Xi’an, China, 2015. [Google Scholar]
- Manojkumar, V.C.; Mattur, C.N.; Kulkarni, S.M. Axial strength of circular concrete-filled steel tube columns-DOE approach. J. Constr. Steel Res. 2010, 66, 1248–1260. [Google Scholar]
- Chung, K.; Park, S.; Choi, S. Material effect for predicting the fire resistance of concrete-filled square steel tube column under constant axial load. J. Constr. Steel Res. 2008, 64, 1505–1515. [Google Scholar] [CrossRef]
- Jiang, Z.; Sun, S.; Lu, H.; Yu, S. Analysis of dynamic response and influence factors of concrete-filled steel and steel tube blast doors. J. Ordnance Equip. Eng. 2022, 43, 41–47. (In Chinese) [Google Scholar]
- Li, E.; Sheng, X.; Wang, J. Dynamic analysis of vaulted protective doors under nuclear and conventional blast loadings. Prot. Eng. 2011, 33, 16–21. (In Chinese) [Google Scholar]
- Chen, W.; Hao, H. Numerical study of a new multi-arch double-layered blast-resistance door panel. Int. J. Impact Eng. 2012, 43, 16–28. [Google Scholar]
- Li, C.; Qin, F.; Zhang, Y.-D.; Zhang, Y.; Fan, J.-Y. Numerical and Experimental Investigations on the blast-resistant properties of arched RC blast doors. Int. J. Prot. Struct. 2010, 1, 425–441. [Google Scholar]
- Guo, D.; Li, Z.; Wang, Q.; Hou, X. Research on blast-resistant properties of concrete-filled steel and steel tube blast doors. Prot. Eng. 2013, 35, 38–43. (In Chinese) [Google Scholar]
- LS-DYNA Keyword User’s Manual; LSTC: San Francisco, CA, USA, 2017.
- Xu, Y.; Hu, S. A study on the dynamic ultimate capacity of CFST arch bridges. China Civ. Eng. J. 2006, 39, 68–73. (In Chinese) [Google Scholar]
- Budiansky, B.; Roth, R.S. Axisymmetric Dynamic Buckling of Clamped Shallow Spherical Shells. NASA TN 1962, 510, 597–606. [Google Scholar]
- Shen, J.; Wang, C.; Jiang, J. Finite Element of Reinforced Concrete and Limit Analysis of Shell; Tsinghua University Press: Beijing, China, 1993. [Google Scholar]
- US Department of the Army. TM5-1300 Structures to Resist the Effects of Accidental Explosions; US Department of the Army: Washington, DC, USA, 1990. [Google Scholar]
- Ma, H.; Wang, T. Combination Structure of Steel-Concrete; Building Materials Industry Press: Beijing, China, 2006. [Google Scholar]
- DL/T5085-2021; Code for Design of Steel-Comcrete Composite Structure. Department of Transportation: Beijing, China, 2021.
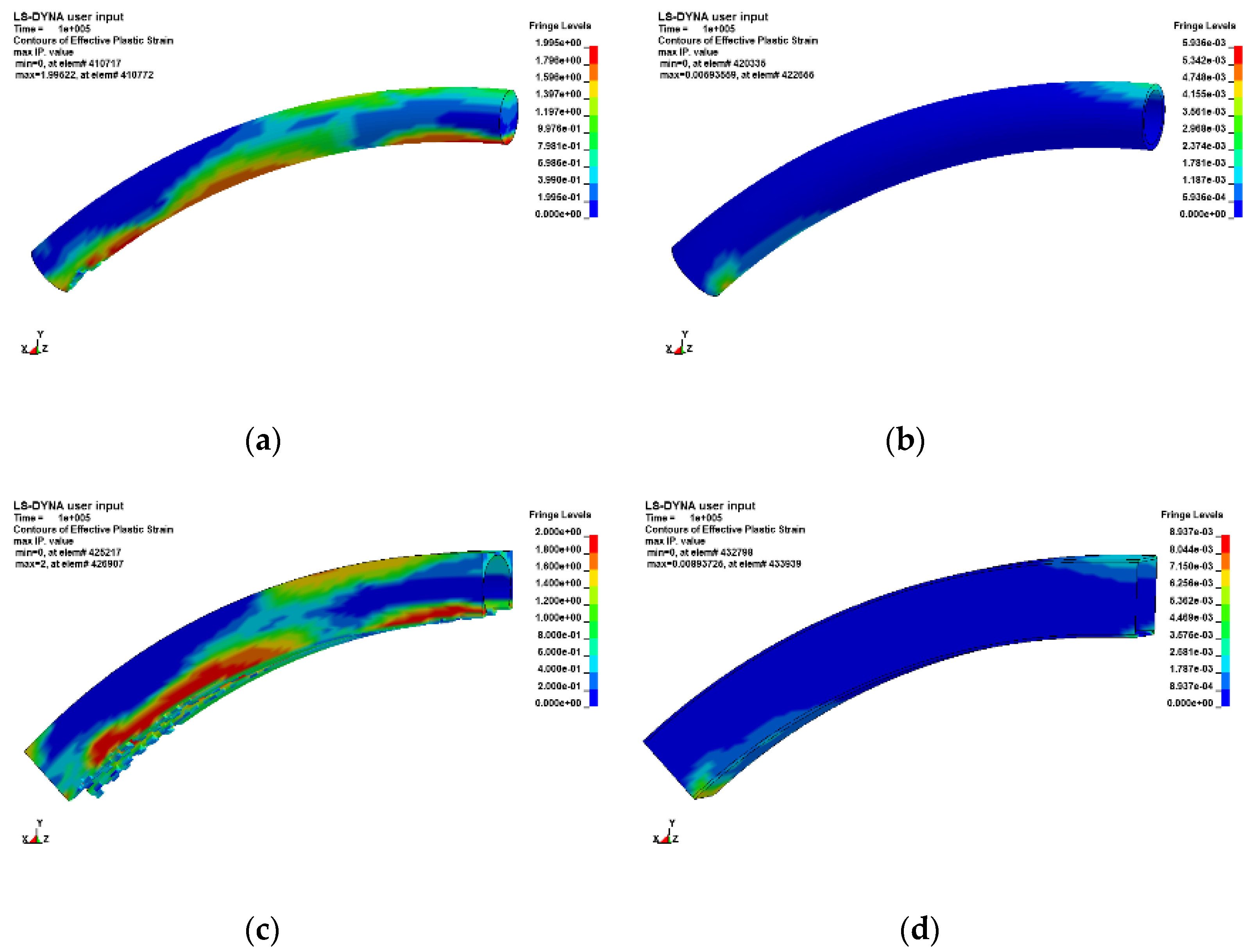
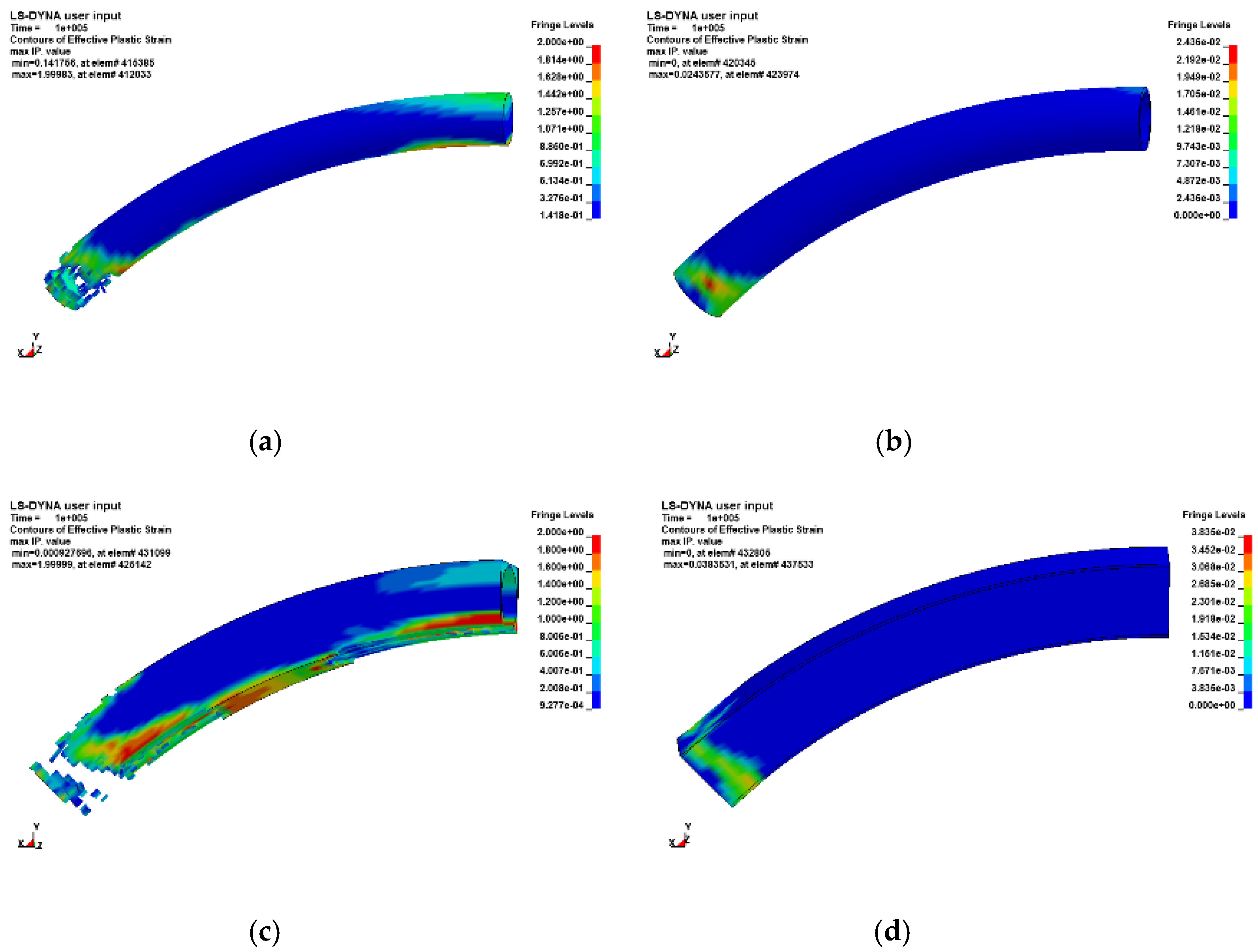
| Distribution Diagram of Plastic Strain | Description of Damage Characteristics | |
|---|---|---|
| 7 |  | The protective door shows overall deformation response characteristics; the plastic strains appear at the top and foot of the arch, but the distribution of the plastic zone is not large, and the plastic zone at the foot of the arch is smaller. |
| 10 |  | |
| 11 | 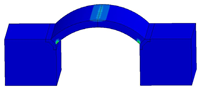 | The protective door still shows the overall deformation response characteristics, and the plastic strains appear at both the top and foot of the arch. However, compared to the case of = 10 MPa, the range of plastic strain distribution at the top of the arch is reduced, while the range of plastic strain at the foot of the arch is increased. |
| 12 | 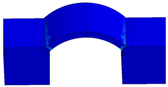 | The protective door shows local damage characteristics, plastic strains are concentrated at the foot of the arch, the concrete in this position shows “fracture,” and the steel is about to enter or has entered the situation of full section yielding. |
| 13 |  | |
| 14 |  | A slip fracture appears at the foot of the arch, and the protective door becomes unstable and collapses. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, S.; Tian, Z.; Cao, X.; Tian, C.; Wang, Z. Analysis of the Ultimate Load-Bearing Capacity of Steel-Clad Concrete-Filled Steel Tube Arched Protective Doors under Blast Shock Waves. Buildings 2023, 13, 1424. https://doi.org/10.3390/buildings13061424
Dong S, Tian Z, Cao X, Tian C, Wang Z. Analysis of the Ultimate Load-Bearing Capacity of Steel-Clad Concrete-Filled Steel Tube Arched Protective Doors under Blast Shock Waves. Buildings. 2023; 13(6):1424. https://doi.org/10.3390/buildings13061424
Chicago/Turabian StyleDong, Shangwei, Zhimin Tian, Xingwei Cao, Ce Tian, and Zhenyu Wang. 2023. "Analysis of the Ultimate Load-Bearing Capacity of Steel-Clad Concrete-Filled Steel Tube Arched Protective Doors under Blast Shock Waves" Buildings 13, no. 6: 1424. https://doi.org/10.3390/buildings13061424





