Optimal Shape Design of Concrete Sleepers under Lateral Loading Using DEM
Abstract
:1. Introduction
2. Material Specifications and DEM Simulations
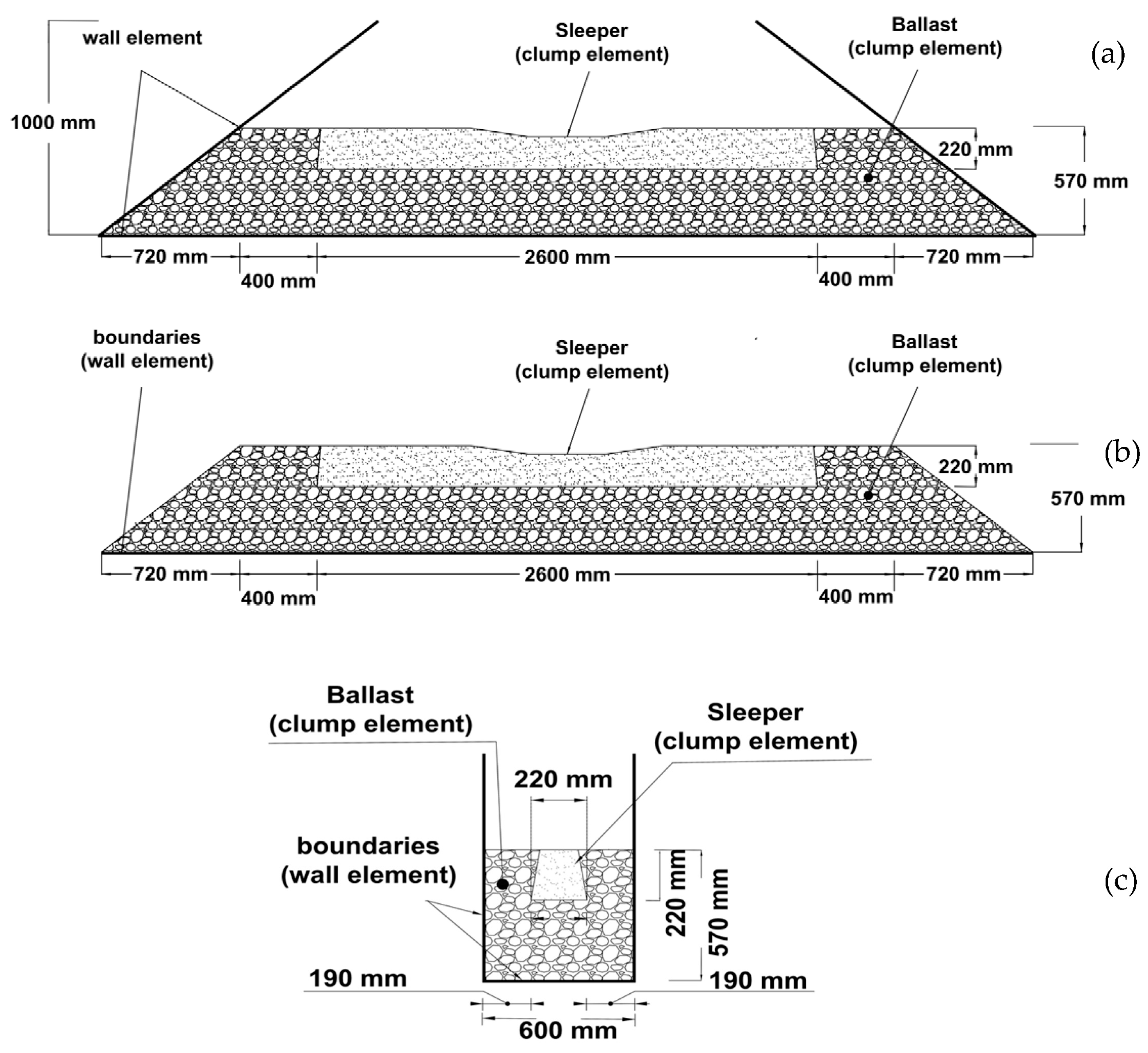
2.1. Model Geometry
2.2. Simulation of Sleeper
2.3. Simulation of Ballast Particles
2.4. Contact Model
2.5. Simulation of the STPT Process
3. Numerical Simulation and Optimization Algorithm
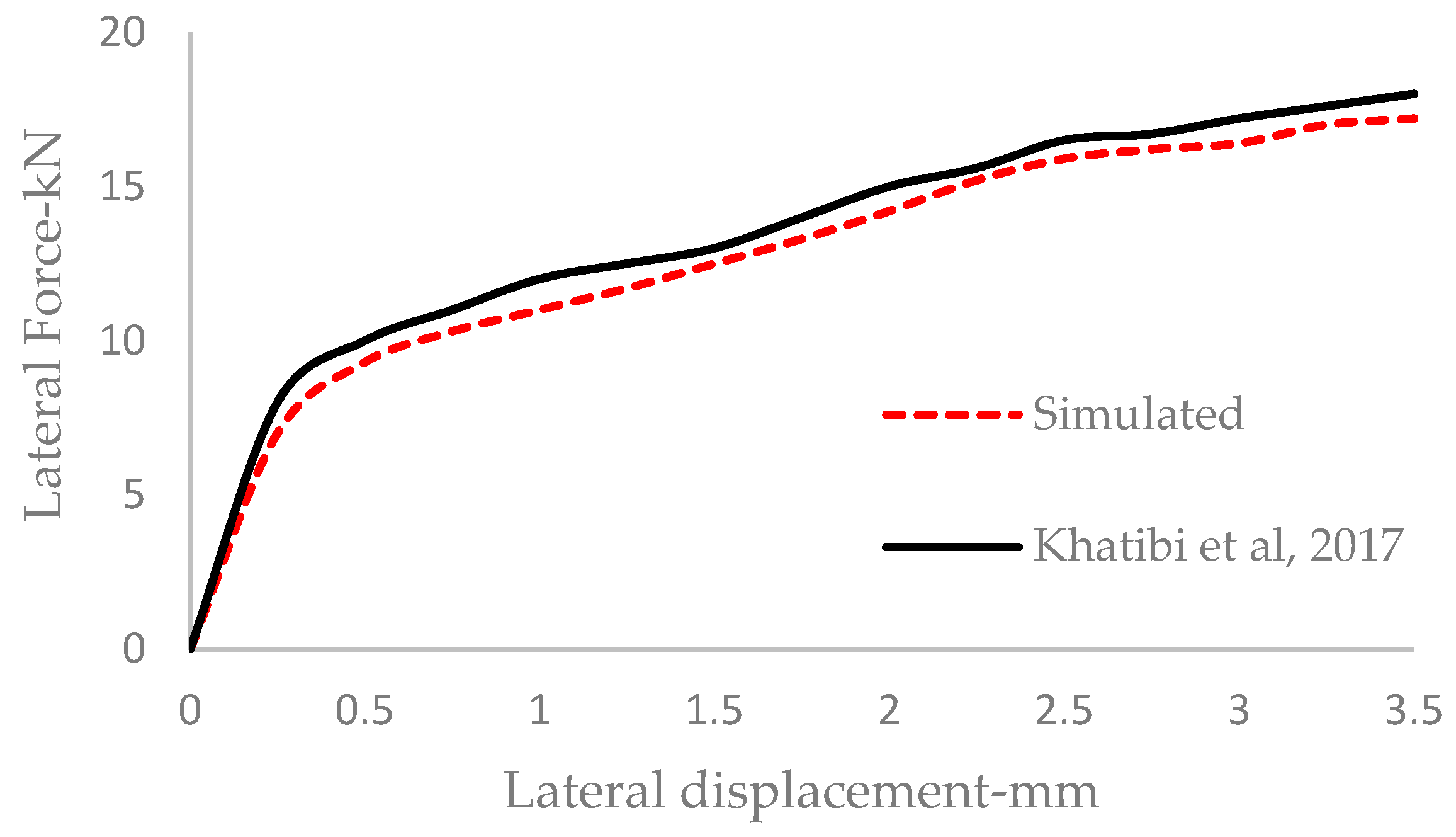
3.1. Validation of DEM Model
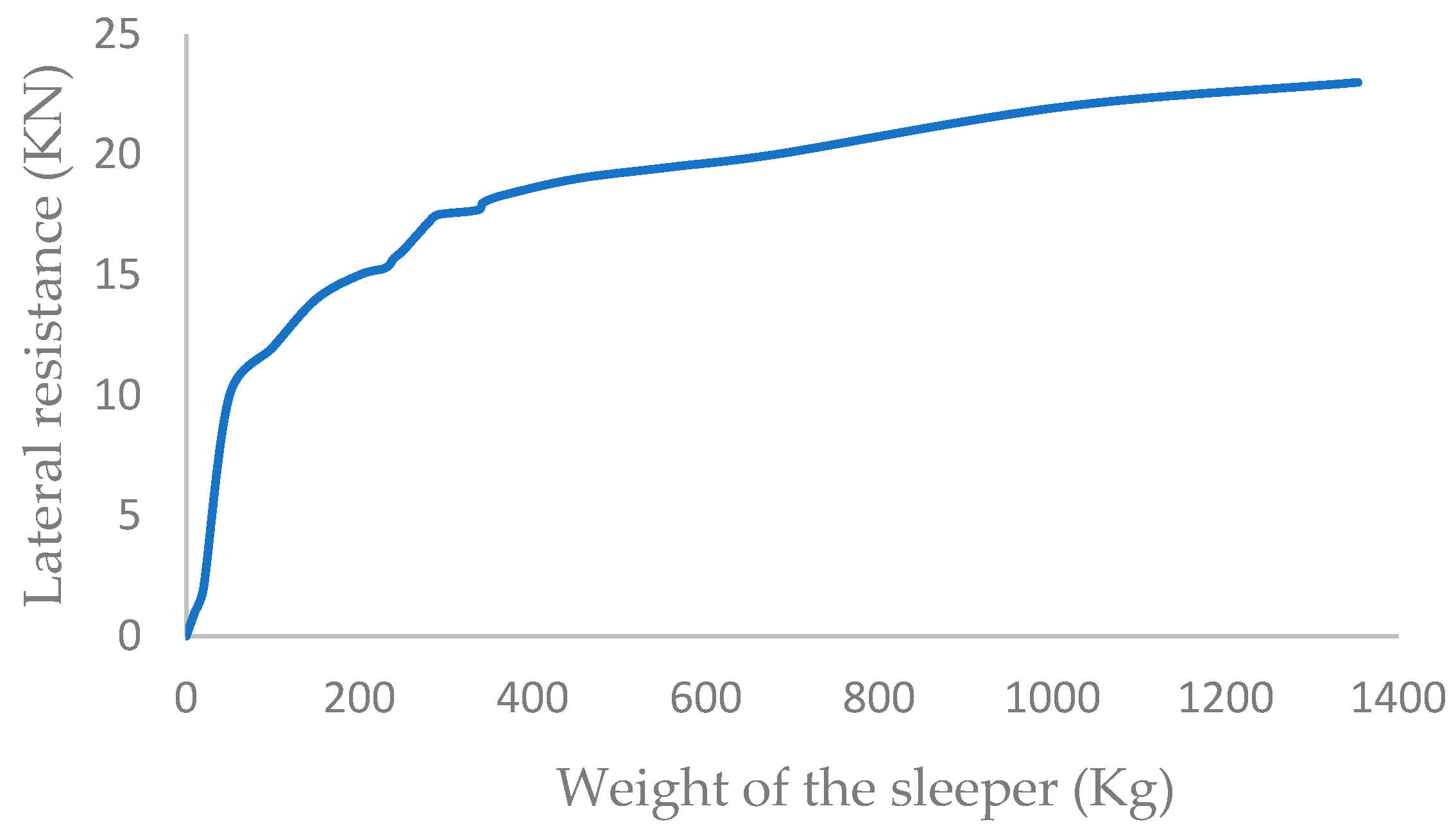
3.2. Effect of the Sleeper’s Weight on Lateral Resistance
3.3. Parametric Study
3.4. Optimization Algorithm
4. Conclusions
- Regarding lateral resistance displacement, the DEM results exhibit good agreement with experimental data. However, there was a gap in the graph, which is logically connected to the different shapes of the ballast and sleepers, as well as the loading procedure and environmental factors;
- The effect of the weight of sleeper B70 on lateral resistance was investigated. The findings demonstrated that elevating the sleeper’s weight causes the lateral resistance to rise. However, as shown in Figure 11, the rate of lateral resistance increasing becomes lower for weights higher than 400 kg;
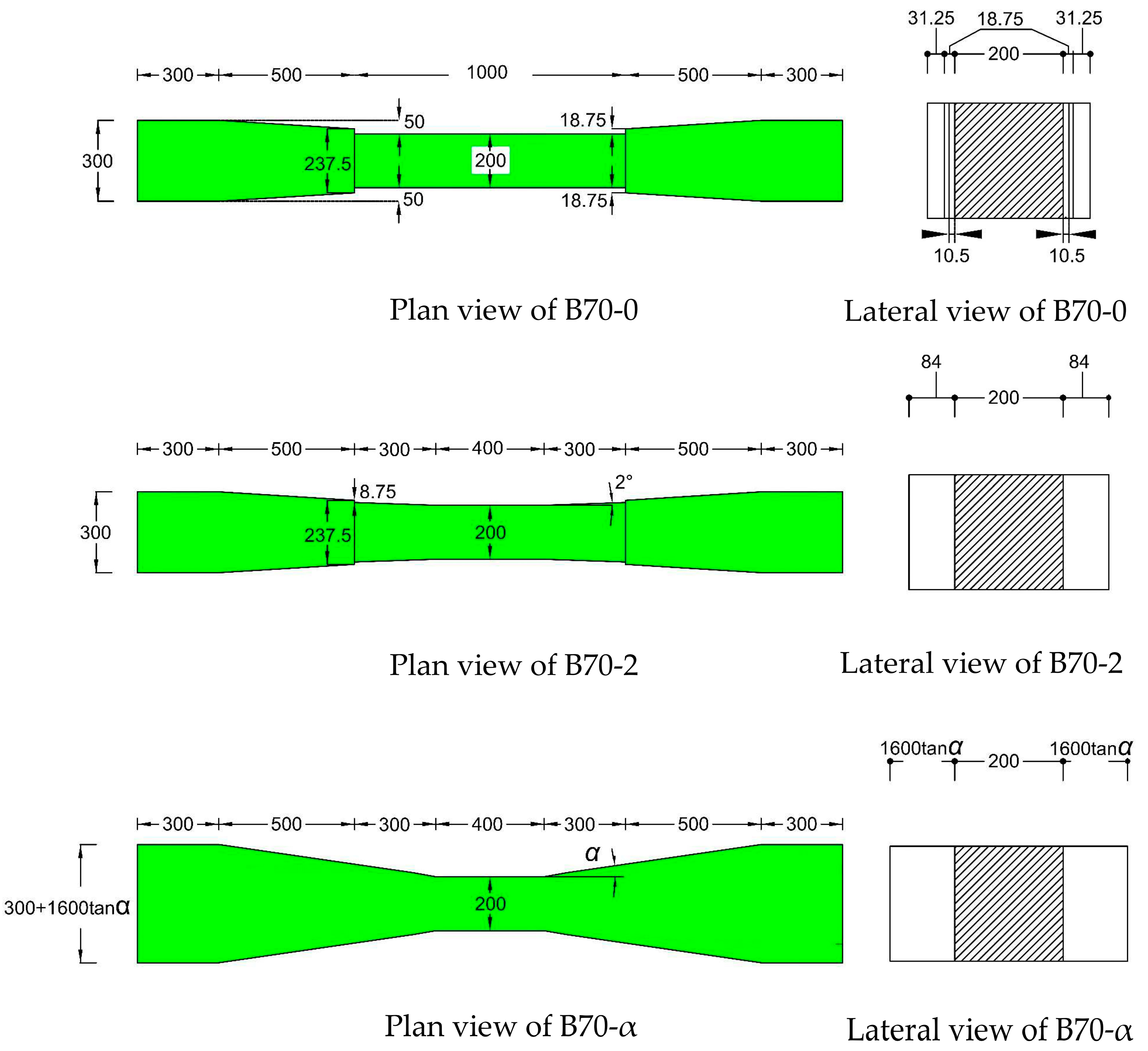
- Results show that a rise in sleeper weight does not necessarily increase lateral resistance. This can be seen in B70-5, B70-6, B70-7, B70-8, B70-9, and B70-10 in comparison with B70-0. Therefore, these shapes are not suggested as optimization shapes. Furthermore, although B70-11, B70-12, B70-13, and B70-14 sleepers have greater in contrast to other shapes, their is lower than B70′s. It means that these shapes are not acceptable economically. Additionally, of B70-0, B70-1, B70-2, and B70-3 are 31.2%, 23.9%, 18.8%, and 9.5% higher than B70, respectively. Moreover, they weigh 1.8%, 1.07%, 0.71%, and 0.36% lower than the B70 sleeper, respectively. Thus, B70-0 sleepers can be suggested instead of using B70 sleepers;
- According to the presented algorithm and achieved results, it can be mentioned that this algorithm has the potential to be used for other kinds of sleepers under lateral force in order to find optimized shapes in ballasted tracks.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Profillidis, V. Railway Management and Engineering; Routledge: London, UK, 2017. [Google Scholar]
- ASTM C136/C136M-14; Standard Test Method for Sieve Analysis of Fine and Coarse Aggregates. ASTM International: West Conshohocken, PA, USA, 2014.
- Zakeri, J.A. Lateral Resistance of Railway Track, Reliability and Safety in Railway. In Reliability and Safety in Railway; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Zakeri, J.A.; Mirfattahi, B.; Fakhari, M. Lateral Resistance of Railway Track with Frictional Sleepers. Proc. Inst. Civ. Eng. Transp. 2012, 165, 151–155. [Google Scholar] [CrossRef]
- Guo, Y.; Fu, H.; Qian, Y.; Markine, V.; Jing, G. Effect of Sleeper Bottom Texture on Lateral Resistance with Discrete Element Modelling. Constr. Build. Mater. 2020, 250, 118770. [Google Scholar] [CrossRef]
- Miri, A.; Ali Zakeri, J.; Thambiratnam, D.; Chan, T.H.T. Effect of Shape of Concrete Sleepers for Mitigating of Track Buckling. Constr. Build. Mater. 2021, 294, 123568. [Google Scholar] [CrossRef]
- Koyama, E.; Ito, K.; Hayano, K.; Momoya, Y. A New Approach for Evaluating Lateral Resistance of Railway Ballast Associated with Extended Sleeper Spacing. Soils Found. 2021, 61, 1565–1580. [Google Scholar] [CrossRef]
- Khatibi, F.; Esmaeili, M.; Mohammadzadeh, S. DEM Analysis of Railway Track Lateral Resistance. Soils Found. 2017, 57, 587–602. [Google Scholar] [CrossRef]
- Mansouri, P.; Zakeri, J.A.; Esmaeili, M.; Ghahremani, S. Discrete Element Method Analysis of Lateral Resistance of Different Sleepers under Different Support Conditions. Constr. Build. Mater. 2022, 327, 126915. [Google Scholar] [CrossRef]
- Chalabii, J.; Movahedi Rad, M.; Hadizadeh Raisi, E.; Esfandiari Mehni, R. Effect of Sleeper-Ballast Particle Contact on Lateral Resistance of Concrete Sleepers in Ballasted Railway Tracks. Materials 2022, 15, 7508. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A Discrete Numerical Model for Granular Assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- CGI Itasca. PFC3D (Particle Flow Code in Three Dimensions); CGI Itasca: Grand Rapids, MN, USA, 2021. [Google Scholar]
- Taghavi, R. Automatic Clump Generation Based on Mid-Surface. In Proceedings of the 2nd International FLAC/DEM Symposium, Melbourne, Australia, 14–16 February 2011. [Google Scholar]
- Irazábal, J.; Salazar, F.; Oñate, E. Numerical Modelling of Granular Materials with Spherical Discrete Particles and the Bounded Rolling Friction Model. Application to Railway Ballast. Comput. Geotech. 2017, 85, 220–229. [Google Scholar] [CrossRef]
- Jing, G.; Aela, P.; Fu, H. The Contribution of Ballast Layer Components to the Lateral Resistance of Ladder Sleeper Track. Constr. Build. Mater. 2019, 202, 796–805. [Google Scholar] [CrossRef]
- Chen, C.; McDowell, G.R.; Thom, N.H. Discrete Element Modelling of Cyclic Loads of Geogrid-Reinforced Ballast under Confined and Unconfined Conditions. Geotext. Geomembr. 2012, 35, 76–86. [Google Scholar] [CrossRef]
- Benmebarek, M.A.; Movahedi Rad, M. Effect of Rolling Resistance Model Parameters on 3D DEM Modeling of Coarse Sand Direct Shear Test. Materials 2023, 16, 2077. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Deresiewicz, H. Elastic Spheres in Contact Under Varying Oblique Forces. J. Appl. Mech. 1953, 20, 327–344. [Google Scholar] [CrossRef]
- Yimsiri, S.; Soga, K. Dem Analysis of Soil Fabric Effects on Behaviour of Sand. Geotechnique 2010, 60, 483–495. [Google Scholar] [CrossRef]
- Lin, X.; Ng, T.T. A Three-Dimensional Discrete Element Model Using Arrays of Ellipsoids. Geotechnique 1997, 47, 319–329. [Google Scholar] [CrossRef]
- Chen, Y.C.; Hung, H.Y. Evolution of Shear Modulus and Fabric during Shear Deformation. Soils Found. 1991, 31, 148–160. [Google Scholar] [CrossRef] [Green Version]
- Sitharam, T.G.; Vinod, J.S.; Ravishankar, B.V. Evaluation of Undrained Response from Drained Triaxial Shear Tests: DEM Simulations and Experiments. Geotechnique 2008, 58, 605–608. [Google Scholar] [CrossRef] [Green Version]
- Fathali, M.; Nejad, F.M.; Esmaeili, M. Influence of Tire-Derived Aggregates on the Properties of Railway Ballast Material. J. Mater. Civ. Eng. 2017, 29, 04016177. [Google Scholar] [CrossRef]
- Laryea, S.; Safari Baghsorkhi, M.; Ferellec, J.F.; McDowell, G.R.; Chen, C. Comparison of Performance of Concrete and Steel Sleepers Using Experimental and Discrete Element Methods. Transp. Geotech. 2014, 1, 225–240. [Google Scholar] [CrossRef]
- Tutumluer, E.; Qian, Y.; Hashash, Y.M.A.; Ghaboussi, J.; Davis, D.D. Discrete Element Modelling of Ballasted Track Deformation Behaviour. Int. J. Rail Transp. 2013, 1, 57–73. [Google Scholar] [CrossRef]
- Indraratna, B.; Ngo, N.T.; Rujikiatkamjorn, C.; Vinod, J.S. Behavior of Fresh and Fouled Railway Ballast Subjected to Direct Shear Testing: Discrete Element Simulation. Int. J. Geomech. 2014, 14, 34–44. [Google Scholar] [CrossRef] [Green Version]








| Particle and Contact Parameter | Symbol | Unit | Value in Simulation | Experimental Value [8] |
|---|---|---|---|---|
| Shear elastic modulus | -- | |||
| Poisson’s ratio of ballast | -- | -- | ||
| Inter-particle normal stiffness | -- | |||
| Inter-particle shear stiffness | -- | |||
| Ballast particle density | ||||
| Sleeper clump density | ||||
| Inter-particle coefficient of friction | -- | |||
| Wall normal and shear stiffness | -- | |||
| Side wall friction coefficient | -- | 0.9 | -- | |
| Base wall friction coefficient (subgrade) | -- | |||
| Ballast size distribution | -- | -- | AREMA NO.24 | AREMA NO.24 |
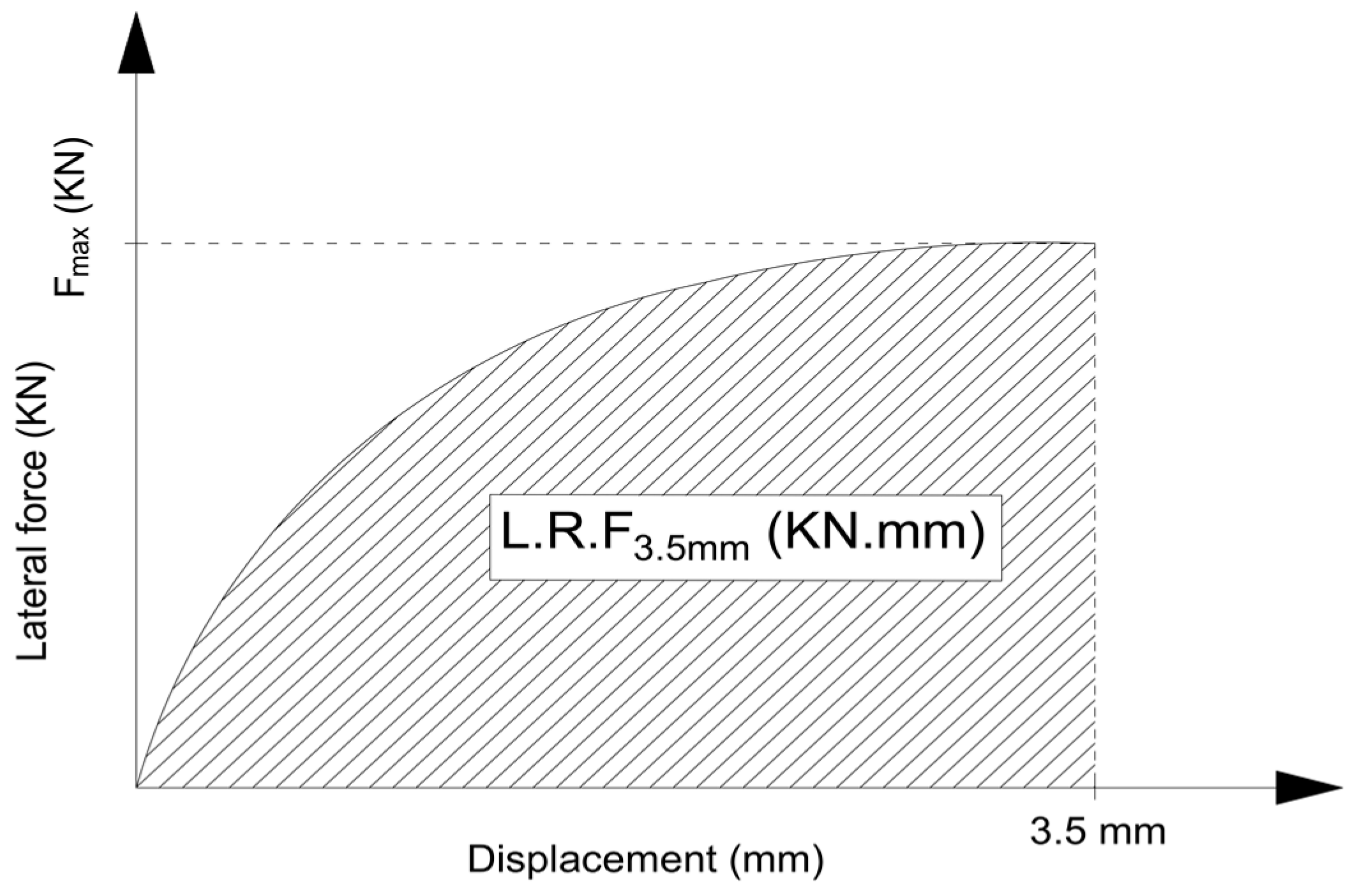
| Sleeper’s Name | Angle of α (Degree) | Weight of the Sleeper (Kg) | (KN.mm) | (KN.mm/Kg) | ||||
|---|---|---|---|---|---|---|---|---|
| B70-0 | 0 | 275 | 59.5 | 0.216 | 1.3358 | 31.2 | 33.5 | 33.6 |
| B70-1 | 1 | 277 | 56.2 | 0.203 | 1.2576 | 23.9 | 25.5 | 25.8 |
| B70-2 | 2 | 278 | 53.9 | 0.193 | 1.2020 | 18.8 | 19.7 | 20.2 |
| B70-3 | 3 | 279 | 49.7 | 0.178 | 1.1011 | 9.5 | 9.8 | 10.1 |
| B70 | 4 | 280 | 45.4 | 0.162 | 1 | 0.0 | 0.0 | 0.0 |
| B70-5 | 5 | 310 | 48.4 | 0.156 | 1.0536 | 6.7 | −3.5 | 5.4 |
| B70-6 | 6 | 331 | 51.5 | 0.1556 | 1.1059 | 13.5 | −3.9 | 10.6 |
| B70-7 | 7 | 352 | 53.8 | 0.153 | 1.1280 | 18.5 | −5.7 | 12.8 |
| B70-8 | 8 | 373 | 55.9 | 0.1498 | 1.1452 | 23.2 | −7.6 | 14.5 |
| B70-9 | 9 | 394 | 56.3 | 0.1429 | 1.1453 | 24.2 | −11.8 | 14.5 |
| B70-10 | 10 | 384 | 57.5 | 0.150 | 1.1596 | 26.7 | −7.3 | 16.0 |
| B70-11 | 11 | 437 | 62.8 | 0.143 | 1.2526 | 38.4 | −11.4 | 25.3 |
| B70-12 | 12 | 459 | 67.9 | 0.148 | 1.3413 | 49.7 | −8.7 | 34.1 |
| B70-13 | 13 | 481 | 74.1 | 0.154 | 1.4582 | 63.4 | −4.8 | 45.8 |
| B70-14 | 14 | 504 | 78.4 | 0.156 | 1.5357 | 72.8 | −3.9 | 53.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chalabii, J.; Movahedi Rad, M.; Hosseini, S. Optimal Shape Design of Concrete Sleepers under Lateral Loading Using DEM. Buildings 2023, 13, 1574. https://doi.org/10.3390/buildings13071574
Chalabii J, Movahedi Rad M, Hosseini S. Optimal Shape Design of Concrete Sleepers under Lateral Loading Using DEM. Buildings. 2023; 13(7):1574. https://doi.org/10.3390/buildings13071574
Chicago/Turabian StyleChalabii, Jafar, Majid Movahedi Rad, and Seyedsaber Hosseini. 2023. "Optimal Shape Design of Concrete Sleepers under Lateral Loading Using DEM" Buildings 13, no. 7: 1574. https://doi.org/10.3390/buildings13071574
APA StyleChalabii, J., Movahedi Rad, M., & Hosseini, S. (2023). Optimal Shape Design of Concrete Sleepers under Lateral Loading Using DEM. Buildings, 13(7), 1574. https://doi.org/10.3390/buildings13071574







