The Safety Risk Assessment of Mine Metro Tunnel Construction Based on Fuzzy Bayesian Network
Abstract
1. Introduction
2. Construction Safety Risk Evaluation Index
2.1. Construction Stage Division
2.2. Risk Identification List
3. Methodology
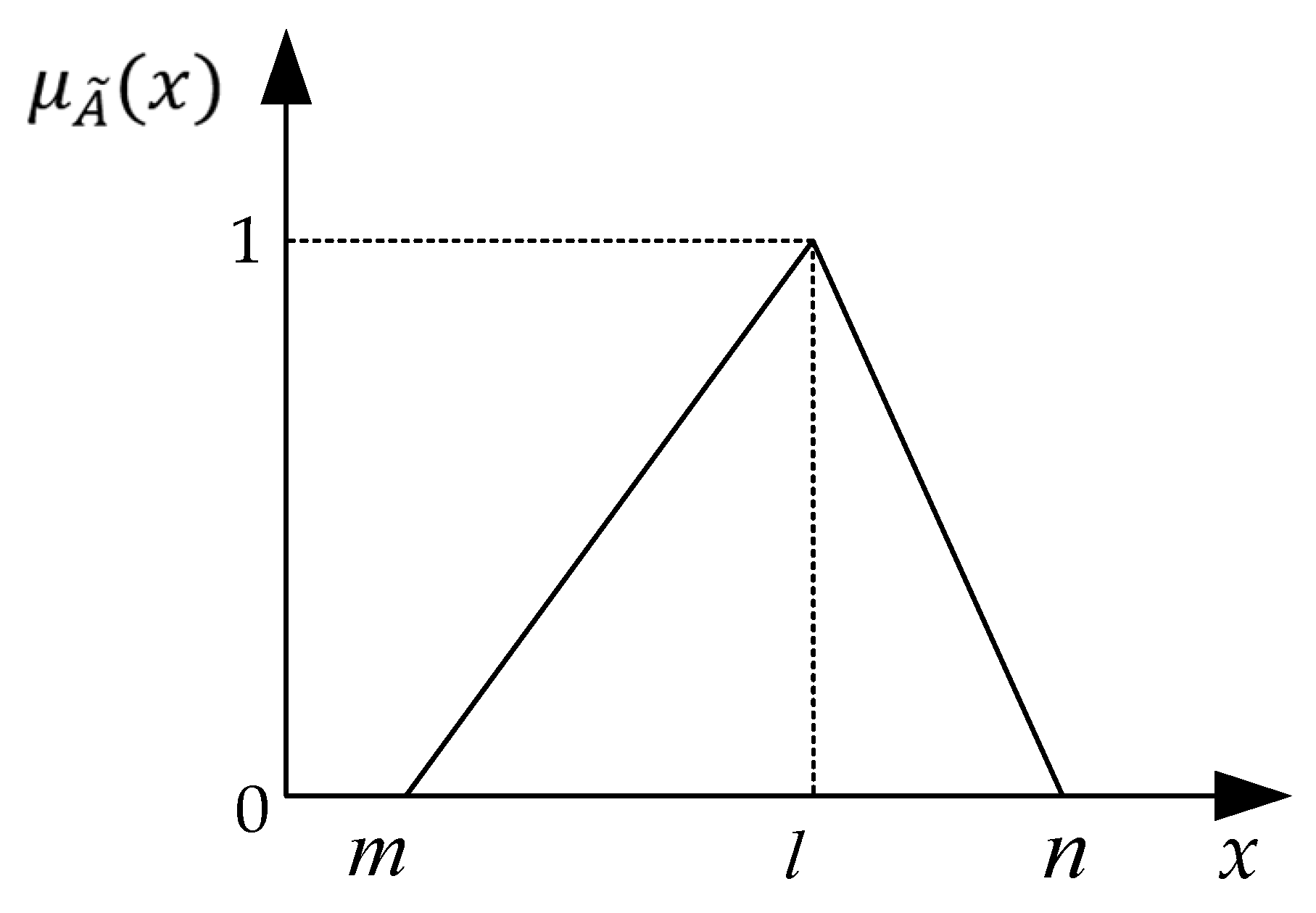
3.1. Fuzzy Set Theory
3.2. Bayesian Network
4. Case Analysis
4.1. Case Background
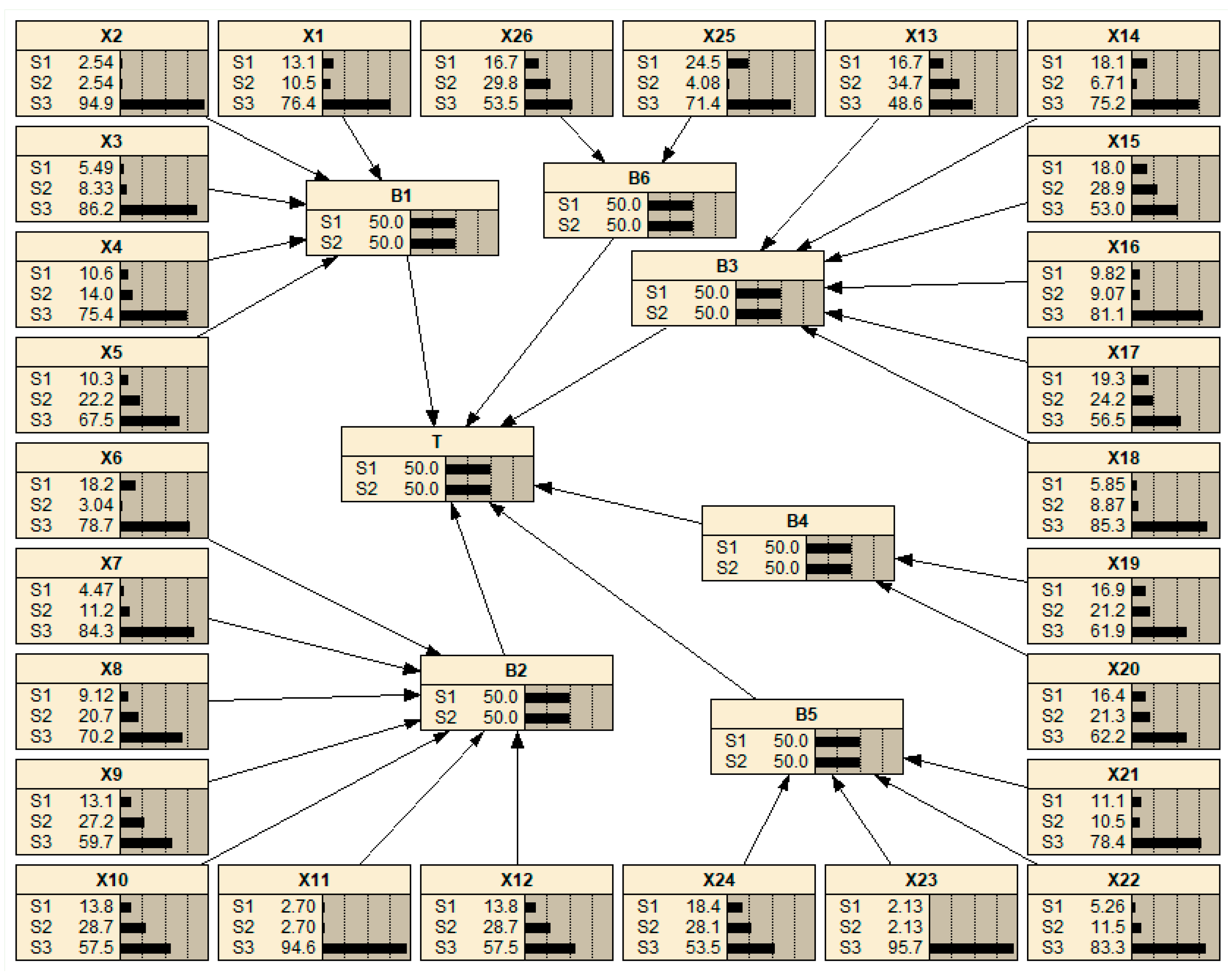
4.2. FBN Model Construction
4.3. FBN Model Evaluation
4.3.1. Fuzzification
4.3.2. Defuzzification
4.3.3. Normalization
4.4. FBN Model Interpretation
4.4.1. Causal Reasoning
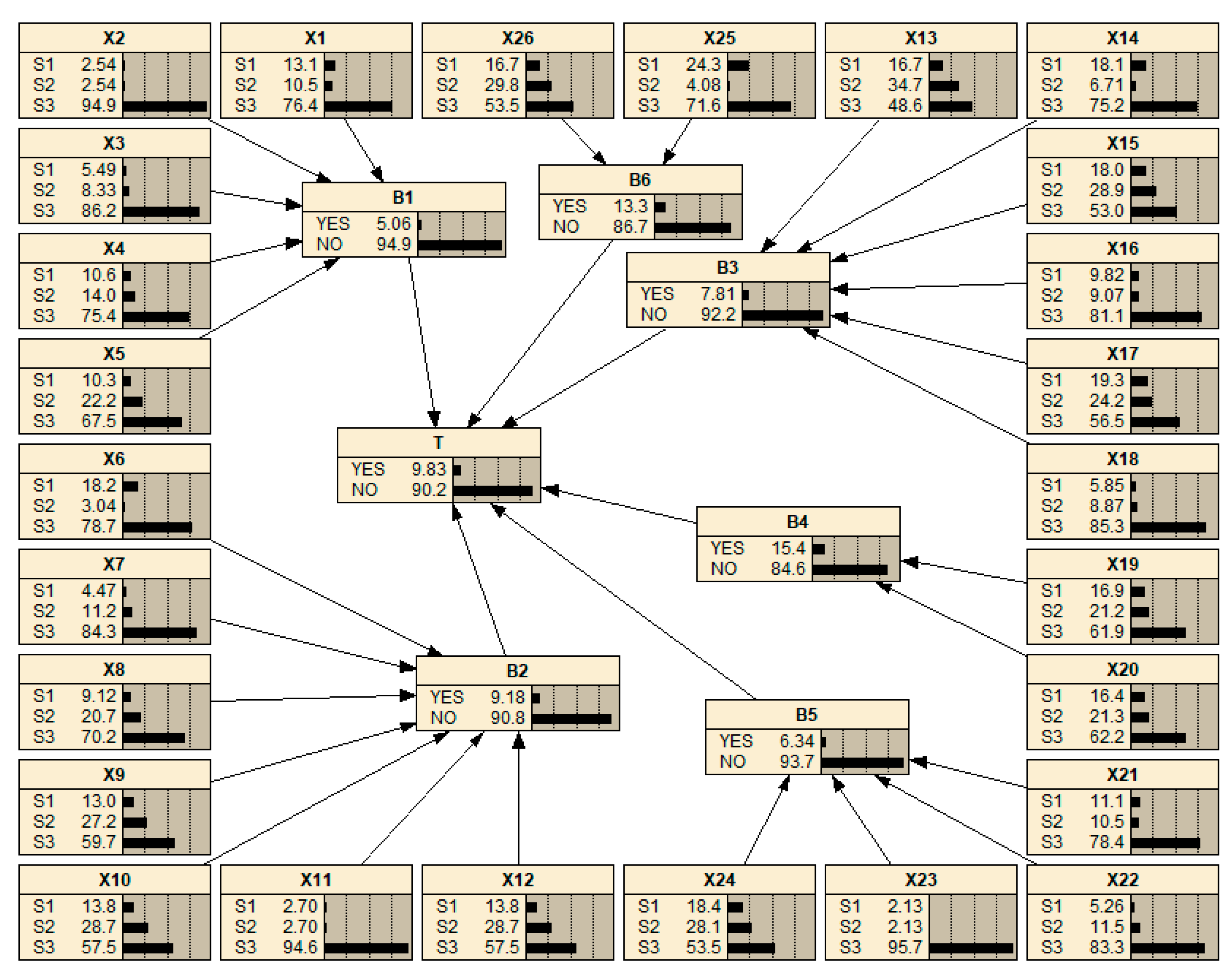
4.4.2. Diagnostic Reasoning
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guo, P.; Fang, J.; Zhu, K. The spatial spillover effect and function routes of transport infrastructure investment on economic growth: Evidence from panel data of OECD members and partners. Mathematics 2023, 11, 1167. [Google Scholar] [CrossRef]
- Xing, X.; Zhong, B.; Luo, H.; Li, H.; Wu, H. Ontology for safety risk identification in metro construction. Comput. Ind. 2019, 109, 14–30. [Google Scholar] [CrossRef]
- Qian, Q.; Lin, P. Safety risk management of underground engineering in China: Progress, challenges and strategies. J. Rock Mech. Geotech. Eng. 2016, 8, 423–442. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, K.; Wang, J.; Guo, P.; Shen, W. Bibliometric analysis of engineering project risk management literature. China Saf. Sci. J. 2021, 31, 15–23. [Google Scholar] [CrossRef]
- Valdenebro, J.-V.; Gimena, F.N.; López, J.J. Construction process for the implementation of urban utility tunnels in historic centres. Tunn. Undergr. Space Technol. 2019, 89, 38–49. [Google Scholar] [CrossRef]
- Liu, J.; Shi, C.; Lei, M.; Cao, C.; Lin, Y. Improved analytical method for evaluating the responses of a shield tunnel to adjacent excavations and its application. Tunn. Undergr. Space Technol. 2020, 98, 103339. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, J.; Zhang, B.; Wang, H.; Huang, M. Statistical analysis of major tunnel construction accidents in China from 2010 to 2020. Tunn. Undergr. Space Technol. 2022, 124, 104460. [Google Scholar] [CrossRef]
- Sousa, R.L.; Einstein, H.H. Lessons from accidents during tunnel construction. Tunn. Undergr. Space Technol. 2021, 113, 103916. [Google Scholar] [CrossRef]
- Yan, H.; Gao, C.; Elzarka, H.; Mostafa, K.; Tang, W. Risk assessment for construction of urban rail transit projects. Saf. Sci. 2019, 118, 583–594. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, T.; Zhou, W.; Tang, J. Safety risk factors of metro tunnel construction in China: An integrated study with EFA and SEM. Saf. Sci. 2018, 105, 98–113. [Google Scholar] [CrossRef]
- Hai, N.; Gong, D.; Liu, S.; Dai, Z. Dynamic coupling risk assessment model of utility tunnels based on multimethod fusion. Reliab. Eng. Syst. Saf. 2022, 228, 108773. [Google Scholar] [CrossRef]
- Chang, L.; Zhang, L.; Xu, X. Causality-based multi-model ensemble learning for safety assessment in metro tunnel construction. Reliab. Eng. Syst. Saf. 2023, 234, 109168. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, Y.; Shen, Q.; Yang, L.; Cai, H. Risk assessment and management via multi-source information fusion for undersea tunnel construction. Autom. Constr. 2020, 111, 103050. [Google Scholar] [CrossRef]
- Guo, Q.; Amin, S.; Hao, Q.; Haas, O. Resilience assessment of safety system at subway construction sites applying analytic network process and extension cloud models. Reliab. Eng. Syst. Saf. 2020, 201, 106956. [Google Scholar] [CrossRef]
- Hyun, K.-C.; Min, S.; Choi, H.; Park, J.; Lee, I.-M. Risk analysis using fault-tree analysis (FTA) and analytic hierarchy process (AHP) applicable to shield TBM tunnels. Tunn. Undergr. Space Technol. 2015, 49, 121–129. [Google Scholar] [CrossRef]
- Deng, M. Challenges and thoughts on risk management and control for the group construction of a super-long tunnel by TBM. Engineering 2018, 4, 112–122. [Google Scholar] [CrossRef]
- Sharafat, A.; Latif, K.; Seo, J. Risk analysis of TBM tunneling projects based on generic bow-tie risk analysis approach in difficult ground conditions. Tunn. Undergr. Space Technol. 2021, 111, 103860. [Google Scholar] [CrossRef]
- Rallu, A.; Berthoz, N.; Charlemagne, S.; Branque, D. Vibrations induced by tunnel boring machine in urban areas: In situ measurements and methodology of analysis. J. Rock Mech. Geotech. Eng. 2023, 15, 130–145. [Google Scholar] [CrossRef]
- Ou, G.; Jiao, Y.; Zhang, G.; Zou, J.; Tan, F.; Zhang, W. Collapse risk assessment of deep-buried tunnel during construction and its application. Tunn. Undergr. Space Technol. 2021, 115, 104019. [Google Scholar] [CrossRef]
- Wu, Z.; Zou, S. A static risk assessment model for underwater shield tunnel construction. Sādhanā 2020, 45, 215. [Google Scholar] [CrossRef]
- Rodríguez, C.A.; Rodríguez-Pérez, Á.M.; López, R.; Hernández-Torres, J.A.; Caparrós-Mancera, J.J. A finite element method integrated with Terzaghi’s principle to estimate settlement of a building due to tunnel construction. Buildings 2023, 13, 1343. [Google Scholar] [CrossRef]
- Wang, Q.; Xiong, Z.; Zhu, K.; Guo, P. Construction safety risks of metro tunnels constructed by the mining method in Wuhan City, China: A structural equation model-fuzzy cognitive map hybrid method. Buildings 2023, 13, 1335. [Google Scholar] [CrossRef]
- Fang, J.; Guo, P.; Zhu, K.; Chen, Z. Coupling evolution analysis of safety risk in subway tunnel construction based on N-K model. China Saf. Sci. J. 2022, 32, 1–9. [Google Scholar] [CrossRef]
- Fang, J.; Guo, P.; Zhu, K.; Xie, D.; Cheng, G. Safety risk analysis of mining method subway tunnel construction based on structural equation model fuzzy cognitive map. J. Saf. Environ. 2022. [Google Scholar] [CrossRef]
- Tian, X.; Ma, J.; Li, L.; Xu, Z.; Tang, M. Development of prospect theory in decision making with different types of fuzzy sets: A state-of-the-art literature review. Inf. Sci. 2022, 615, 504–528. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, S.; Qi, H. Mitigating subway construction collapse risk using Bayesian network modeling. Autom. Constr. 2022, 143, 104541. [Google Scholar] [CrossRef]
- Wu, X.; Liu, H.; Zhang, L.; Skibniewski, M.J.; Deng, Q.; Teng, J. A dynamic Bayesian network based approach to safety decision support in tunnel construction. Reliab. Eng. Syst. Saf. 2015, 134, 157–168. [Google Scholar] [CrossRef]
- Taylan, O.; Bafail, A.O.; Abdulaal, R.M.S.; Kabli, M.R. Construction projects selection and risk assessment by fuzzy AHP and fuzzy TOPSIS methodologies. Appl. Soft Comput. 2014, 17, 105–116. [Google Scholar] [CrossRef]
- Wang, Q.; Nian, C.; Yang, D.; Zhang, Y. Safety warning for deep excavation of subway based on T-S fuzzy neural network. China Saf. Sci. J. 2018, 28, 161–167. [Google Scholar] [CrossRef]
- Zhou, R.; Fang, W.; Wu, J. A risk assessment model of a sewer pipeline in an underground utility tunnel based on a Bayesian network. Tunn. Undergr. Space Technol. 2020, 103, 103473. [Google Scholar] [CrossRef]
- Rostamabadi, A.; Jahangiri, M.; Zarei, E.; Kamalinia, M.; Alimohammadlou, M. A novel fuzzy Bayesian network approach for safety analysis of process systems; An application of HFACS and SHIPP methodology. J. Clean. Prod. 2020, 244, 118761. [Google Scholar] [CrossRef]
- Mostafa, M.A.; Afshin, P.; Iraj, M. Risk modelling of a hydrogen gasholder using fuzzy Bayesian network (FBN). Int. J. Hydrogen Energy 2020, 45, 1177–1186. [Google Scholar] [CrossRef]
- Zarei, E.; Khakzad, N.; Cozzani, V.; Reniers, G. Safety analysis of process systems using fuzzy Bayesian network (FBN). J. Loss Prev. Process Ind. 2019, 57, 7–16. [Google Scholar] [CrossRef]
- Jardón, D.; Sánchez, I.; Sanchis, M. Some questions about Zadeh’s extension on metric spaces. Fuzzy Sets Syst. 2020, 379, 115–124. [Google Scholar] [CrossRef]
- Cheng, J.; Feng, Y.; Lin, Z.; Liu, Z.; Tan, J. Anti-vibration optimization of the key components in a turbo-generator based on heterogeneous axiomatic design. J. Clean. Prod. 2017, 141, 1467–1477. [Google Scholar] [CrossRef]
- Kabir, S.; Papadopoulos, Y. Applications of Bayesian networks and Petri nets in safety, reliability, and risk assessments: A review. Saf. Sci. 2019, 115, 154–175. [Google Scholar] [CrossRef]
- Song, J.; Abuduwayiti, A.; Gou, Z. The role of subway network in urban spatial structure optimization—Wuhan city as an example. Tunn. Undergr. Space Technol. 2023, 131, 104842. [Google Scholar] [CrossRef]
- Dawes, J. Do data characteristics change according to the number of scale points used? An experiment using 5-point, 7-point, and 10-point scales. Int. J. Mark. Res. 2008, 50, 61–104. [Google Scholar] [CrossRef]
- Guo, X.; Ji, J.; Khan, F.; Ding, L.; Tong, Q. A novel fuzzy dynamic Bayesian network for dynamic risk assessment and uncertainty propagation quantification in uncertainty environment. Saf. Sci. 2021, 141, 105285. [Google Scholar] [CrossRef]
- Karmakar, S.; De, S.K.; Goswami, A. A pollution sensitive remanufacturing model with waste items: Triangular dense fuzzy lock set approach. J. Clean. Prod. 2018, 187, 789–803. [Google Scholar] [CrossRef]
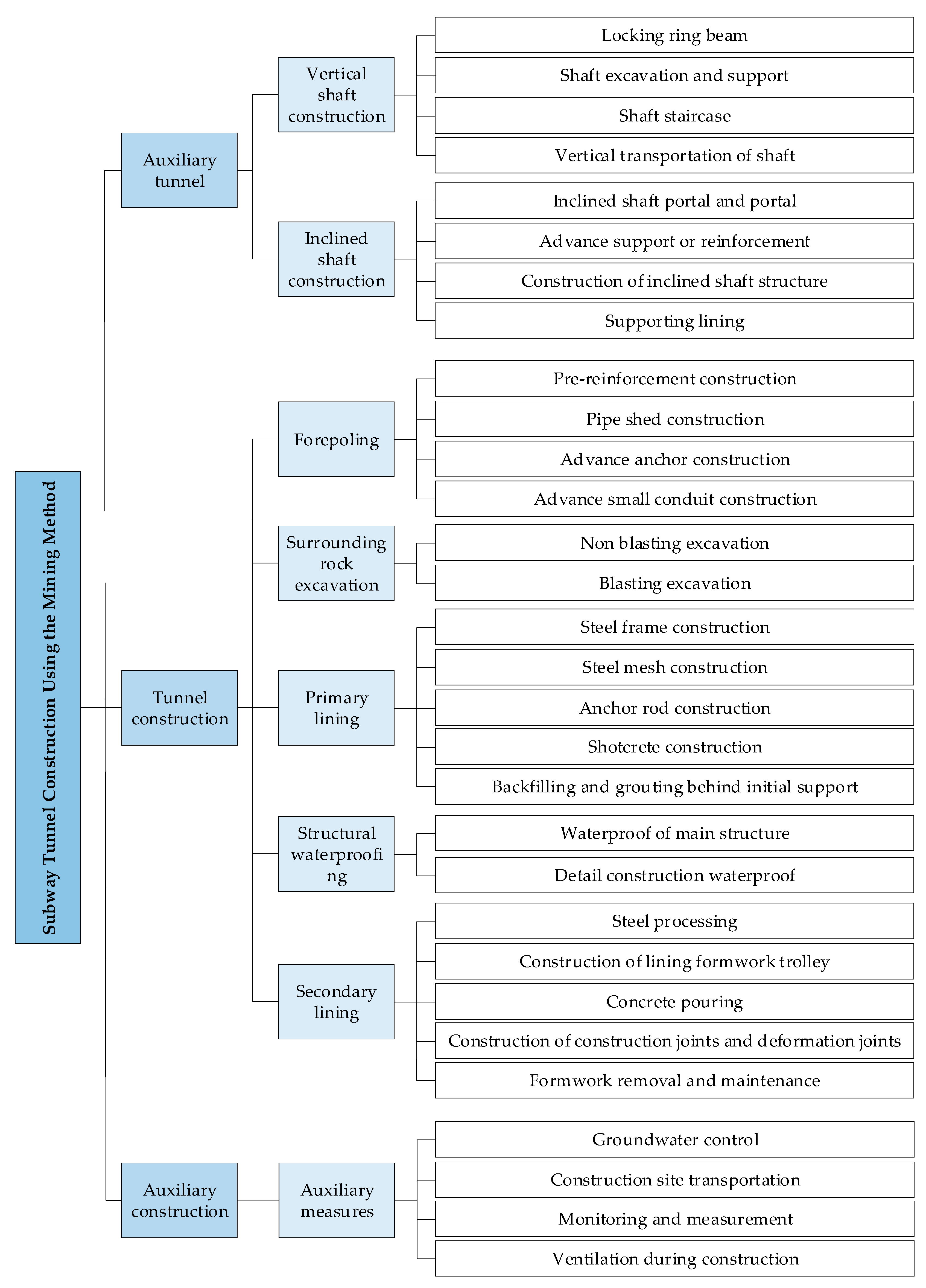

| Stage | Number | Index | Indicator Connotation |
|---|---|---|---|
| Forepoling | X1 | The project design of forepoling construction is unreasonable | Inaccurate geological survey. Improper support method selection. Unreasonable forepoling design, which hinders advance support construction. Lack of disclosure and training on forepoling safety technology. Non-compliance with design requirements. |
| X2 | Not according to the construction plan | Failure to implement forepoling in accordance with the design or approved scheme. | |
| X3 | Material selection is unqualified | Inadequate material supplier selection. Insufficient inspection and testing of raw materials. Inadequate allocation of construction resources. Lack of verification of resource utilization effectiveness. | |
| X4 | The quality of forepoling is not qualified | Poor forepoling effect, incomplete rectification measures, inadequate advanced support quality, impacting tunnel excavation. | |
| X5 | The grouting construction effect is poor | The selection of material and slurry ratio is unreasonable. The grouting method is not suitable for the operating conditions and engineering geological conditions. | |
| Tunnel excavation | X6 | Unreasonable selection of tunnel excavation methods | The excavation method does not fully refer to specific conditions such as geological conditions, overburden thickness, structural sections, and ground environment. The scheme selection did not follow the principles of technical feasibility and economic rationality. |
| X7 | The excavation section size does not meet the design requirements | The section size neglects important factors like the design contour line and reserved deformation amount. The center line, elevation, and reserved deformation amount of the excavation section do not meet the design requirements. The determination of the reserved deformation amount for excavation fails to consider crucial factors such as surrounding rock grade, tunnel width, depth, construction method, and actual conditions. | |
| X8 | Improper control of excavation contour | Inadequate measurement methods for controlling excavation contour. Lack of observation and monitoring of tunnel surrounding rock. Absence of an effective measurement plan. Delay in acquiring surrounding rock deformation and foundation settlement data, resulting in inefficient construction guidance. | |
| X9 | Unreasonable determination of excavation cycle footage and step sequence | Due to the determination of the circular footage and step of excavation, the geological conditions, tunnel section and design requirements are not fully considered, leading to serious interference in the construction schedule and site organization. | |
| X10 | Inadequate support after excavation | Initial support was not carried out quickly after excavation. When using distributed excavation, the strength of the supporting concrete at the initial stage of the next excavation cannot meet the safety requirements. | |
| X11 | Tunnel has problems of over excavation and under excavation | Uncontrolled under excavation, excessive overbreak, improper backfilling, intrusion of filling material into initial support structure section during tunnel excavation. | |
| X12 | The tunnel experiences unstable tunnel roof surface or bulging tunnel floor. | When reserving core soil on the excavation face, the reserved height, longitudinal length, and slope of the core soil do not meet the requirements, resulting in tunnel instability or uplift. | |
| Primary lining | X13 | Inadequate initial support | The initial support was not implemented in a timely manner after excavation, and the deformation and collapse of surrounding rock were not prevented effectively. |
| X14 | The installation and construction of reinforcement mesh do not meet the specification requirements | The type, model, specification, processing size, welding method, and acceptance of the steel used for the reinforcement mesh do not meet the requirements of the design documents. Nonconforming finished products are not corrected as required. | |
| X15 | The steel frame installation construction does not meet the specification requirements | The processing of reinforcement grid steel frame and profile steel frame does not meet the radian and size requirements of the design documents. The height and arc length of the steel frame are less than the values required in the design documents. Nonconforming processing and installation inspections were not corrected as required. | |
| X16 | The construction quality of mortar anchor rod is unqualified | The selection of anchor bolt drilling machine is unreasonable, and the hole position deviation exceeds the allowable deviation. During the grouting process, the grouting operation is improper, resulting in leakage or grout leakage. The grouting pipe is blocked during grouting. | |
| X17 | The quality of sprayed concrete is unqualified | Shotcrete construction deviated from the prescribed process. Inadequate preparation for shotcrete application. Unfilled cavities, recesses, and wide open fractures on the rock surface. Short intervals between layered injection. Improper concrete mix proportion. | |
| X18 | The quality of backfill grouting behind the preliminary support is unqualified | The backfill grouting operation behind the preliminary support was not carried out according to the construction process. The spacing between grouting holes is too large or too small. The quality of cement slurry is unqualified. There are obvious cavities in the grouting. | |
|
Structural waterproofing | X19 | The main waterproof construction quality is unqualified | Waterproof concrete construction deviated from the prescribed process. Inadequate adherence to key control points. Non-compliant construction of plastic waterproof boards. Lack of timely post-construction quality inspection. Improper installation of self-adhesive waterproofing membrane. Coiled material exhibits surface irregularities. |
| X20 | The waterproof construction quality of the detailed structure is unqualified | Deformation joint construction deviated from the process. Inaccurate measurement and positioning caused significant deviation in the joints. Incorrect placement of construction joints. Delayed pouring of concrete after joint completion. Lack of prior embedding for through-wall pipes. Insufficient curing time for post-cast strips. | |
|
Secondary lining | X21 | Poor lining quality | The secondary lining construction deviates from design requirements in terms of dimensions and encroaches on tunnel boundaries. Neglected backfilling of the overbreak section and failure to conduct timely removal of temporary structures as per design specifications. |
| X22 | The quality of rebar is poor | Scars on rebar weaken interface, non-compliant storage, transportation, processing, installation for durable concrete construction. Large deviation in rebar installation position, inadequate concrete protection thickness. | |
| X23 | The safety factor of lining mould frame and trolley is not up to standard | The rigidity and strength of formwork and trolley are not up to standard. The safety factor fails to meet the load design requirements specified. The traction force and structural fastness of the trolley traveling system are insufficient. | |
| X24 | Insufficient concrete pouring and curing conditions | The basic conditions for concrete pouring are not met. The concrete strength during formwork removal does not meet the requirements of relevant specifications. The lining was not cured according to climatic conditions after pouring concrete. The curing time did not meet the requirements of relevant specifications. | |
| Monitoring measurement | X25 | Unreasonable design of monitoring and measurement scheme | Inadequate construction monitoring plan considering geological conditions, environmental factors, design documents, construction plans, and risk assessment reports. Non-compliant monitoring reference point and working base point. |
| X26 | Poor monitoring and measurement effect | Inadequate on-site monitoring and patrols as per the specified frequency in the monitoring plan. Inaccurate and incomplete records of monitoring data and patrol information. Delayed feedback and evaluation of project safety based on monitoring data. |
| Attribute | Description | Score | Attribute | Description | Score |
|---|---|---|---|---|---|
| Professional position (objective) | Senior professional title | 9 | Education level (objective) | Doctor | 9 |
| Intermediate title | 7 | Master | 7 | ||
| Junior professional title | 5 | Bachelor | 5 | ||
| Technician | 3 | College | 3 | ||
| Worker | 1 | Graduate from middle school | 1 | ||
| Years of working (objective) | ≥20 years | 9 | Survey reliability (subjective) | Sure | 9 |
| 15–20 | 7 | Almost certainly | 7 | ||
| 10–15 | 5 | Very likely | 5 | ||
| 5–10 | 3 | Possible | 3 | ||
| ≤5 | 1 | Not sure | 1 |
| Linguistic Terminology | Corresponding Abbreviation | Fuzzy Sets | Grade |
|---|---|---|---|
| Very high | VH | (0.80,0.90,1.00) | 7 |
| High | H | (0.60,0.70,0.80) | 6 |
| Fairly high | FH | (0.40,0.50,0.60) | 5 |
| Medium | M | (0.30,0.35,0.40) | 4 |
| Fairly low | FL | (0.20,0.25,0.30) | 3 |
| Low | L | (0.04,0.12,0.20) | 2 |
| Very low | VL | (0.00,0.02,0.04) | 1 |
| Expert | Professional Position | Years of Working | Education Level | Survey Reliability | Subjective and Objective Accumulation | Comprehensive Weight (ω) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | ||||
| 1 | 9 | 9 | 9 | 9 | 9 | 9 | 30 | 30 | 28 | 0.290 | 0.286 | 0.286 |
| 2 | 9 | 7 | 7 | 7 | 9 | 7 | 34 | 34 | 34 | 0.242 | 0.254 | 0.238 |
| 3 | 9 | 7 | 5 | 7 | 7 | 9 | 26 | 22 | 24 | 0.226 | 0.222 | 0.238 |
| 4 | 9 | 7 | 7 | 7 | 7 | 7 | 14 | 14 | 14 | 0.242 | 0.238 | 0.238 |
| Total | 124 | 126 | 126 | 1 | 1 | 1 | ||||||
| Event | Expert Evaluation Status Score (E1,E2,E3,E4) | Subjective Weight of Experts (E1,E2,E3,E4) | ω (E1,E2,E3,E4) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S1 | S2 | S3 | S1 | S2 | S3 | |
| X1 | 2,2,2,2 | 1,2,3,1 | 6,7,5,6 | 9,7,7,7 | 9,9,7,7 | 9,7,9,7 | (0.290,0.242,0.226,0.242) | (0.286,0.254,0.222,0.238) | (0.286,0.238,0.238,0.238) |
| X2 | 1,1,1,1 | 1,1,1,1 | 6,7,6,6 | 9,9,9,9 | 9,9,9,9 | 9,7,9,7 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.286,0.238,0.238,0.238) |
| X3 | 1,2,1,1 | 1,2,2,1 | 6,7,5,6 | 9,9,9,9 | 9,9,9,9 | 9,7,9,7 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.286,0.238,0.238,0.238) |
| X4 | 1,2,2,2 | 2,2,2,2 | 5,7,5,6 | 9,7,9,7 | 9,9,9,7 | 9,9,9,7 | (0.286,0.238,0.238,0.238) | (0.281,0.250,0.234,0.234) | (0.281,0.250,0.234,0.234) |
| X5 | 1,2,1,2 | 2,2,3,2 | 5,2,5,6 | 9,9,9,9 | 7,7,7,7 | 7,7,7,7 | (0.277,0.246,0.231,0.246) | (0.279,0.246,0.230,0.246) | (0.279,0.246,0.230,0.246) |
| X6 | 2,2,2,2 | 1,1,1,1 | 6,5,5,4 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X7 | 2,1,1,1 | 2,2,2,2 | 7,7,7,7 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X8 | 2,2,1,2 | 3,3,2,3 | 6,6,7,6 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X9 | 2,2,2,2 | 3,3,3,3 | 5,5,5,6 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X10 | 2,2,2,2 | 3,3,3,3 | 5,5,5,5 | 9,9,9,9 | 9,9,9,9 | 7,7,7,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.274,0.242,0.226,0.258) |
| X11 | 1,1,1,1 | 1,1,1,1 | 6,7,5,6 | 9,7,7,7 | 9,9,7,7 | 9,7,9,7 | (0.290,0.242,0.226,0.242) | (0.286,0.254,0.222,0.238) | 0.286,0.238,0.238,0.238) |
| X12 | 2,2,2,2 | 3,3,3,3 | 5,5,5,5 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X13 | 2,2,2,2 | 3,3,3,3 | 4,4,4,4 | 9,9,9,9 | 9,7,7,7 | 9,7,9,7 | (0.277,0.246,0.231,0.246) | (0.290,0.242,0.226 0.242) | (0.286,0.238,0.238,0.238) |
| X14 | 2,2,2,2 | 1,1,1,2 | 5,5,5,5 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X15 | 3,2,2,2 | 3,3,3,3 | 4,5,5,5 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X16 | 2,2,1,1 | 1,2,2,1 | 6,5,5,6 | 9,7,7,7 | 9,9,7,7 | 9,7,9,7 | (0.290,0.242,0.226 0.242) | (0.286,0.254,0.222,0.238) | 0.286,0.238,0.238,0.238) |
| X17 | 2,2,2,2 | 2,2,3,2 | 4,4,4,4 | 9,7,9,7 | 9,9,9,9 | 9,7,9,7 | 0.286,0.238,0.238,0.238) | (0.277,0.246,0.231,0.246) | 0.286,0.238,0.238,0.238) |
| X18 | 1,2,1,1 | 1,2,2,1 | 6,5,6,6 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X19 | 2,1,2,2 | 2,2,2,2 | 4,4,4,4 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X20 | 1,2,2,2 | 2,2,2,2 | 4,4,4,4 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X21 | 2,1,2,1 | 1,2,2,1 | 4,5,5,6 | 9,7,9,9 | 9,9,7,7 | 9,7,9,7 | (0.281,0.234,0.234,0.250) | (0.286,0.254,0.222,0.238) | 0.286,0.238,0.238,0.238) |
| X22 | 1,2,1,1 | 1,2,3,1 | 6,7,5,6 | 9,7,7,7 | 9,9,7,7 | 9,7,9,7 | (0.290,0.242,0.226 0.242) | (0.286,0.254,0.222,0.238) | 0.286,0.238,0.238,0.238) |
| X23 | 1,1,1,1 | 1,1,1,1 | 7,7,7,7 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X24 | 2,2,2,2 | 2,3,2,3 | 4,4,4,4 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X25 | 2,2,2,2 | 1,1,1,1 | 4,4,4,4 | 9,9,9,9 | 9,9,9,9 | 9,9,9,9 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) |
| X26 | 2,2,2,2 | 2,3,3,3 | 4,4,4,5 | 9,9,9,9 | 9,9,9,9 | 9,9,9,7 | (0.277,0.246,0.231,0.246) | (0.277,0.246,0.231,0.246) | (0.281,0.250,0.234,0.234) |
| Expert | Serious (S1) | Not Serious (S2) | Slinght (S3) | |||
|---|---|---|---|---|---|---|
| FPD | ω | FPD | ω | FPD | ω | |
| 1 | (0.04,0.12,0.2) | 0.290 | (0,0.02,0.04) | 0.286 | (0.6,0.7,0.8) | 0.286 |
| 2 | (0.04,0.12,0.2) | 0.242 | (0.04,0.12,0.2) | 0.254 | (0.8,0.9,1.0) | 0.238 |
| 3 | (0.04,0.12,0.2) | 0.226 | (0.2,0.025,0.3) | 0.222 | (0.4,0.5,0.6) | 0.238 |
| 4 | (0.04,0.12,0.2) | 0.242 | (0,0.02,0.04) | 0.238 | (0.6,0.7,0.8) | 0.238 |
| B1 | B2 | B3 | B4 | B5 | B6 | P(T|B1, B2, B3, B4, B5, B6) | |
|---|---|---|---|---|---|---|---|
| T = 1 | T = 0 | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0.83 | 0.17 |
| … | … | … | … | … | … | … | … |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Event | FPV | Defuzzification Result | CPV (%) | ||||
|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | (S1,S2,S3) | S1 | S2 | S3 | |
| X1 | (0.040,0.120,0.200) | (0.055,0.097,0.138) | (0.600,0.700,0.800) | (0.120,0.097,0.700) | 13.09 | 10.53 | 76.38 |
| X2 | (0.000,0.020,0.040) | (0.000,0.020,0.040) | (0.648,0.748,0.848) | (0.020,0.020,0.748) | 2.54 | 2.54 | 94.92 |
| X3 | (0.010,0.045,0.079) | (0.019,0.068,0.116) | (0.600,0.700,0.800) | (0.045,0.068,0.700) | 5.49 | 8.33 | 86.17 |
| X4 | (0.029,0.091,0.154) | (0.040,0.120,0.200) | (0.547,0.647,0.747) | (0.091,0.120,0.647) | 10.65 | 13.98 | 75.37 |
| X5 | (0.020,0.069,0.119) | (0.077,0.150,0.223) | (0.361,0.456,0.551) | (0.069,0.150,0.456) | 10.26 | 22.20 | 67.54 |
| X6 | (0.040,0.120,0.200) | (0.000,0.020,0.040) | (0.431,0.518,0.606) | (0.120,0.020,0.518) | 18.22 | 3.04 | 78.74 |
| X7 | (0.011,0.048,0.084) | (0.040,0.120,0.200) | (0.800,0.900,1.000) | (0.048,0.120,0.900) | 4.47 | 11.24 | 84.29 |
| X8 | (0.031,0.097,0.163) | (0.163,0.220,0.277) | (0.646,0.746,0.846) | (0.097,0.220,0.746) | 9.12 | 20.69 | 70.19 |
| X9 | (0.040,0.120,0.200) | (0.200,0.250,0.300) | (0.449,0.549,0.649) | (0.120,0.250,0.549) | 13.05 | 27.20 | 59.75 |
| X10 | (0.040,0.120,0.200) | (0.200,0.250,0.300) | (0.400,0.500,0.600) | (0.120,0.250,0.500) | 13.79 | 28.74 | 57.47 |
| X11 | (0.000,0.020,0.040) | (0.000,0.020,0.040) | (0.600,0.700,0.800) | (0.020,0.020,0.700) | 2.70 | 2.70 | 94.59 |
| X12 | (0.040,0.120,0.200) | (0.200,0.250,0.300) | (0.400,0.500,0.600) | (0.120,0.250,0.500) | 13.79 | 28.74 | 57.47 |
| X13 | (0.040,0.120,0.200) | (0.200,0.250,0.300) | (0.300,0.350,0.400) | (0.120,0.250,0.350) | 16.67 | 34.72 | 48.61 |
| X14 | (0.040,0.120,0.200) | (0.010,0.045,0.079) | (0.400,0.500,0.600) | (0.120,0.045,0.500) | 18.06 | 6.71 | 75.23 |
| X15 | (0.084,0.156,0.228) | (0.200,0.250,0.300) | (0.372,0.458,0.545) | (0.156,0.250,0.458) | 18.05 | 28.92 | 53.03 |
| X16 | (0.021,0.073,0.125) | (0.019,0.068,0.116) | (0.505,0.605,0.705) | (0.073,0.068,0.605) | 9.82 | 9.07 | 81.11 |
| X17 | (0.040,0.120,0.200) | (0.077,0.150,0.223) | (0.300,0.350,0.400) | (0.120,0.150,0.350) | 19.35 | 24.19 | 56.45 |
| X18 | (0.010,0.045,0.079) | (0.019,0.068,0.116) | (0.551,0.651,0.751) | (0.045,0.068,0.651) | 5.85 | 8.87 | 85.28 |
| X19 | (0.030,0.095,0.161) | (0.040,0.120,0.200) | (0.300,0.350,0.400) | (0.095,0.120,0.350) | 16.87 | 21.22 | 61.90 |
| X20 | (0.029,0.092,0.156) | (0.040,0.120,0.200) | (0.300,0.350,0.400) | (0.092,0.120,0.350) | 16.42 | 21.34 | 62.24 |
| X21 | (0.021,0.072,0.123) | (0.019,0.068,0.116) | (0.419,0.505,0.590) | (0.072,0.068,0.505) | 11.11 | 10.50 | 78.39 |
| X22 | (0.010,0.044,0.079) | (0.055,0.097,0.138) | (0.600,0.700,0.800) | (0.044,0.097,0.700) | 5.26 | 11.48 | 83.26 |
| X23 | (0.000,0.020,0.040) | (0.000,0.020,0.040) | (0.800,0.900,1.000) | (0.020,0.020,0.900) | 2.13 | 2.13 | 95.74 |
| X24 | (0.040,0.120,0.200) | (0.119,0.184,0.249) | (0.300,0.350,0.400) | (0.120,0.184,0.350) | 18.35 | 28.13 | 53.52 |
| X25 | (0.040,0.120,0.200) | (0.000,0.020,0.040) | (0.300,0.350,0.400) | (0.120,0.020,0.350) | 24.49 | 4.08 | 71.43 |
| X26 | (0.040,0.120,0.200) | (0.156,0.214,0.272) | (0.323,0.385,0.447) | (0.120,0.214,0.385) | 16.69 | 29.76 | 53.56 |
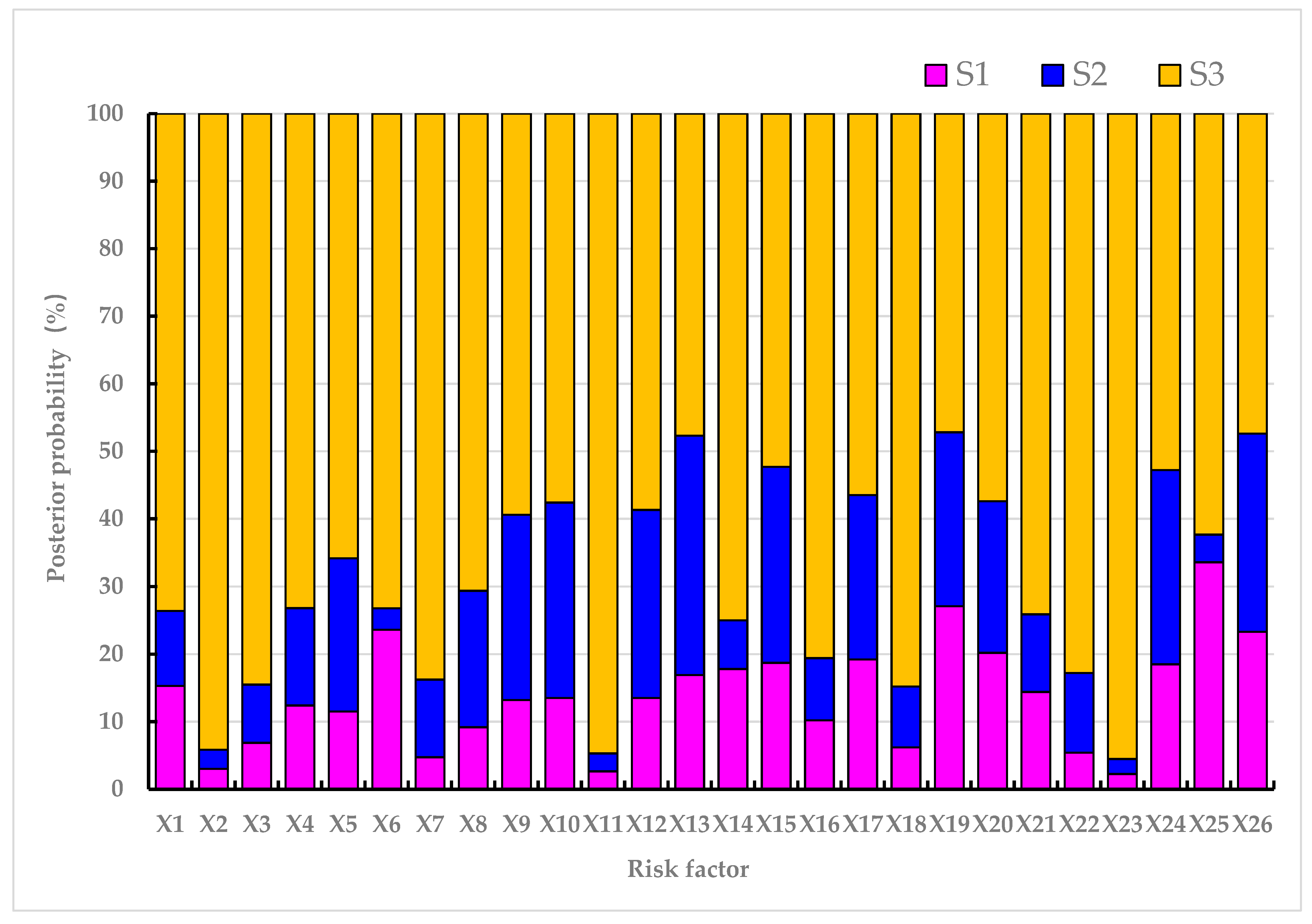
| Event | Prior Probability–CPV (%) | Posterior Probability–CPV (%) | ||||
|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S1 | S2 | S3 | |
| X1 | 13.09 | 10.53 | 76.38 | 15.3 | 11.1 | 73.6 |
| X2 | 2.54 | 2.54 | 94.92 | 3.01 | 2.84 | 94.15 |
| X3 | 5.49 | 8.33 | 86.17 | 6.87 | 8.62 | 84.51 |
| X4 | 10.65 | 13.98 | 75.37 | 12.4 | 14.4 | 73.2 |
| X5 | 10.26 | 22.20 | 67.54 | 11.5 | 22.7 | 65.8 |
| X6 | 18.22 | 3.04 | 78.74 | 23.6 | 3.18 | 73.22 |
| X7 | 4.47 | 11.24 | 84.29 | 4.73 | 11.5 | 83.77 |
| X8 | 9.12 | 20.69 | 70.19 | 9.17 | 20.2 | 70.63 |
| X9 | 13.05 | 27.20 | 59.75 | 13.2 | 27.4 | 59.4 |
| X10 | 13.79 | 28.74 | 57.47 | 13.5 | 28.9 | 57.6 |
| X11 | 2.70 | 2.70 | 94.59 | 2.63 | 2.66 | 94.71 |
| X12 | 13.79 | 28.74 | 57.47 | 13.5 | 27.8 | 58.7 |
| X13 | 16.67 | 34.72 | 48.61 | 16.9 | 35.4 | 47.7 |
| X14 | 18.06 | 6.71 | 75.23 | 17.8 | 7.21 | 74.99 |
| X15 | 18.05 | 28.92 | 53.03 | 18.7 | 29 | 52.3 |
| X16 | 9.82 | 9.07 | 81.11 | 10.2 | 9.2 | 80.6 |
| X17 | 19.35 | 24.19 | 56.45 | 19.2 | 24.3 | 56.5 |
| X18 | 5.85 | 8.87 | 85.28 | 6.18 | 9.02 | 84.8 |
| X19 | 16.87 | 21.22 | 61.90 | 27.1 | 25.7 | 47.2 |
| X20 | 16.42 | 21.34 | 62.24 | 20.2 | 22.4 | 57.4 |
| X21 | 11.11 | 10.50 | 78.39 | 14.4 | 11.5 | 74.1 |
| X22 | 5.26 | 11.48 | 83.26 | 5.41 | 11.8 | 82.79 |
| X23 | 2.13 | 2.13 | 95.74 | 2.25 | 2.23 | 95.52 |
| X24 | 18.35 | 28.13 | 53.52 | 18.5 | 28.7 | 52.8 |
| X25 | 24.49 | 4.08 | 71.43 | 33.6 | 4.06 | 62.34 |
| X26 | 16.69 | 29.76 | 53.56 | 23.3 | 29.3 | 47.4 |
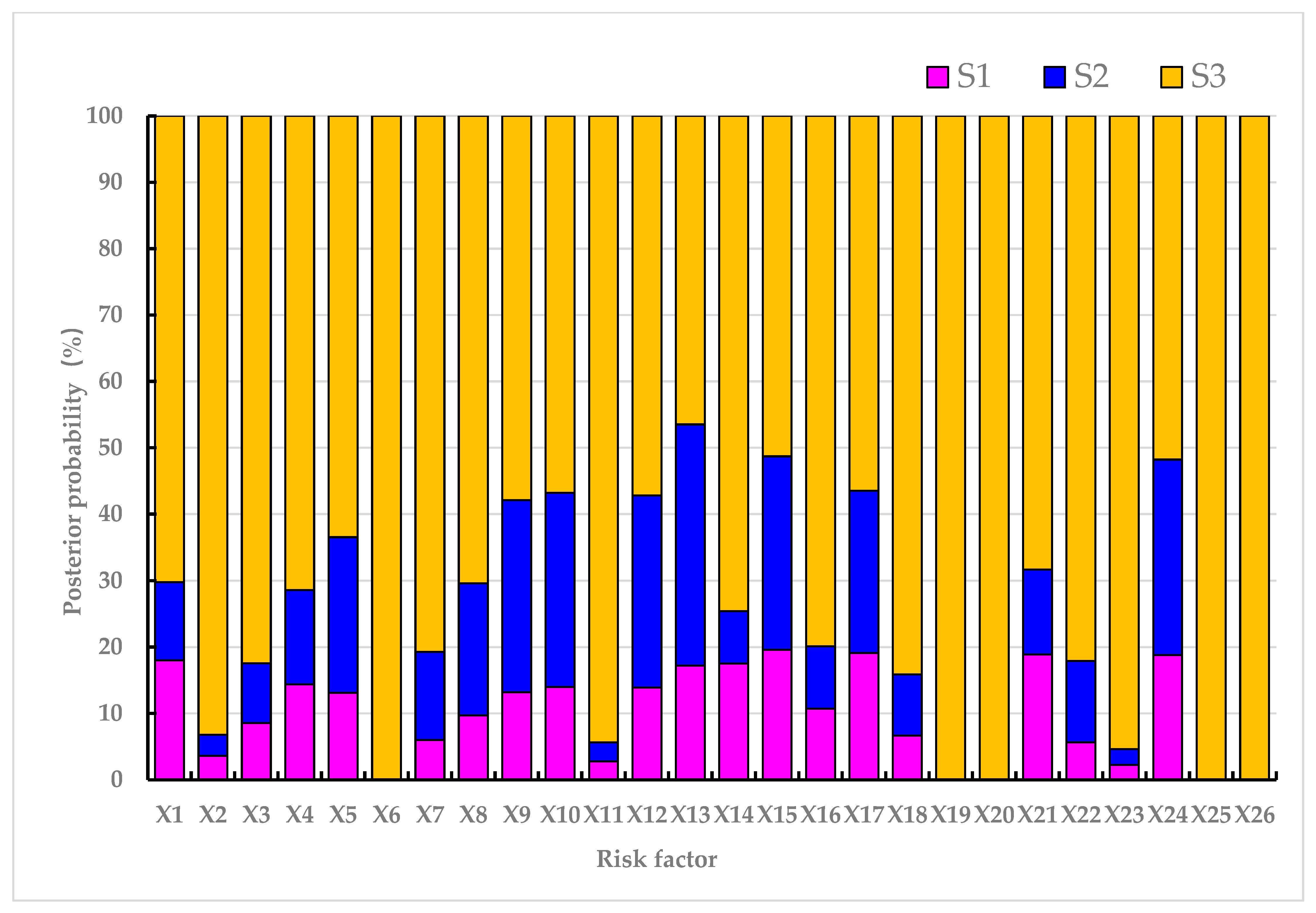
| Event | Prior Probability–CPV (%) | Posterior Probability–CPV (%) | ||||
|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S1 | S2 | S3 | |
| X1 | 13.09 | 10.53 | 76.38 | 18 | 11.8 | 70.2 |
| X2 | 2.54 | 2.54 | 94.92 | 3.59 | 3.21 | 93.2 |
| X3 | 5.49 | 8.33 | 86.17 | 8.56 | 8.98 | 82.46 |
| X4 | 10.65 | 13.98 | 75.37 | 14.4 | 14.2 | 71.4 |
| X5 | 10.26 | 22.20 | 67.54 | 13.1 | 23.4 | 63.5 |
| X6 | 18.22 | 3.04 | 78.74 | 0 | 0 | 100 |
| X7 | 4.47 | 11.24 | 84.29 | 5.99 | 13.3 | 80.71 |
| X8 | 9.12 | 20.69 | 70.19 | 9.69 | 19.9 | 70.41 |
| X9 | 13.05 | 27.20 | 59.75 | 13.2 | 28.9 | 57.9 |
| X10 | 13.79 | 28.74 | 57.47 | 14 | 29.2 | 56.8 |
| X11 | 2.70 | 2.70 | 94.59 | 2.77 | 2.86 | 94.37 |
| X12 | 13.79 | 28.74 | 57.47 | 13.9 | 28.9 | 57.2 |
| X13 | 16.67 | 34.72 | 48.61 | 17.2 | 36.3 | 46.5 |
| X14 | 18.06 | 6.71 | 75.23 | 17.5 | 7.93 | 74.57 |
| X15 | 18.05 | 28.92 | 53.03 | 19.6 | 29.1 | 51.3 |
| X16 | 9.82 | 9.07 | 81.11 | 10.7 | 9.4 | 79.9 |
| X17 | 19.35 | 24.19 | 56.45 | 19.1 | 24.4 | 56.5 |
| X18 | 5.85 | 8.87 | 85.28 | 6.65 | 9.23 | 84.12 |
| X19 | 16.87 | 21.22 | 61.90 | 0 | 0 | 100 |
| X20 | 16.42 | 21.34 | 62.24 | 0 | 0 | 100 |
| X21 | 11.11 | 10.50 | 78.39 | 18.9 | 12.8 | 68.3 |
| X22 | 5.26 | 11.48 | 83.26 | 5.62 | 12.3 | 82.08 |
| X23 | 2.13 | 2.13 | 95.74 | 2.24 | 2.37 | 95.39 |
| X24 | 18.35 | 28.13 | 53.52 | 18.8 | 29.4 | 51.8 |
| X25 | 24.49 | 4.08 | 71.43 | 0 | 0 | 100 |
| X26 | 16.69 | 29.76 | 53.56 | 0 | 0 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zhang, J.; Zhu, K.; Guo, P.; Shen, C.; Xiong, Z. The Safety Risk Assessment of Mine Metro Tunnel Construction Based on Fuzzy Bayesian Network. Buildings 2023, 13, 1605. https://doi.org/10.3390/buildings13071605
Wang Q, Zhang J, Zhu K, Guo P, Shen C, Xiong Z. The Safety Risk Assessment of Mine Metro Tunnel Construction Based on Fuzzy Bayesian Network. Buildings. 2023; 13(7):1605. https://doi.org/10.3390/buildings13071605
Chicago/Turabian StyleWang, Qiankun, Jiaji Zhang, Ke Zhu, Peiwen Guo, Chuxiong Shen, and Zhihua Xiong. 2023. "The Safety Risk Assessment of Mine Metro Tunnel Construction Based on Fuzzy Bayesian Network" Buildings 13, no. 7: 1605. https://doi.org/10.3390/buildings13071605
APA StyleWang, Q., Zhang, J., Zhu, K., Guo, P., Shen, C., & Xiong, Z. (2023). The Safety Risk Assessment of Mine Metro Tunnel Construction Based on Fuzzy Bayesian Network. Buildings, 13(7), 1605. https://doi.org/10.3390/buildings13071605







