Influence of Heterogeneous Foundation on the Safety of Inverted Cone Bottom Oil Storage Tanks under Earthquakes
Abstract
:1. Introduction
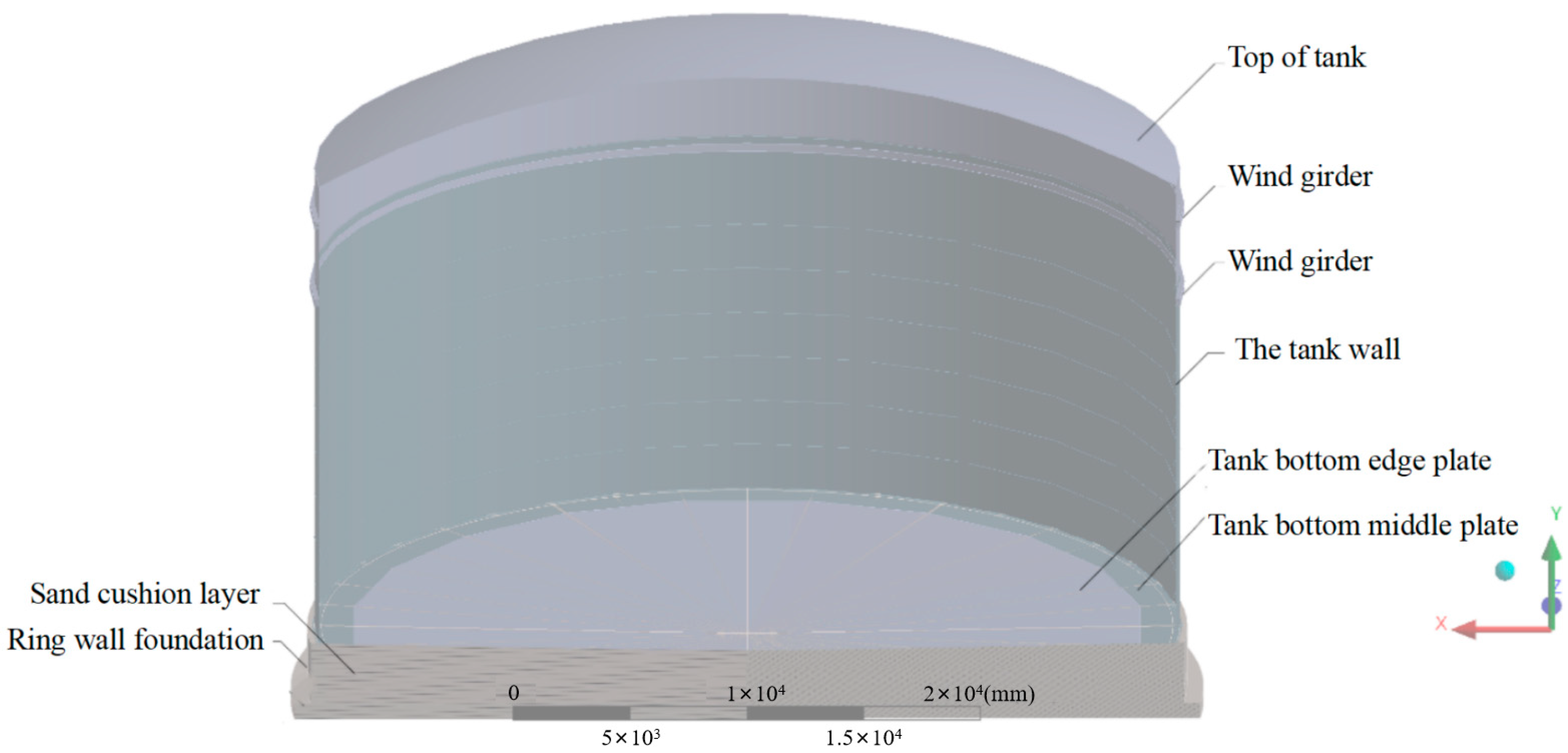
2. Project Overview
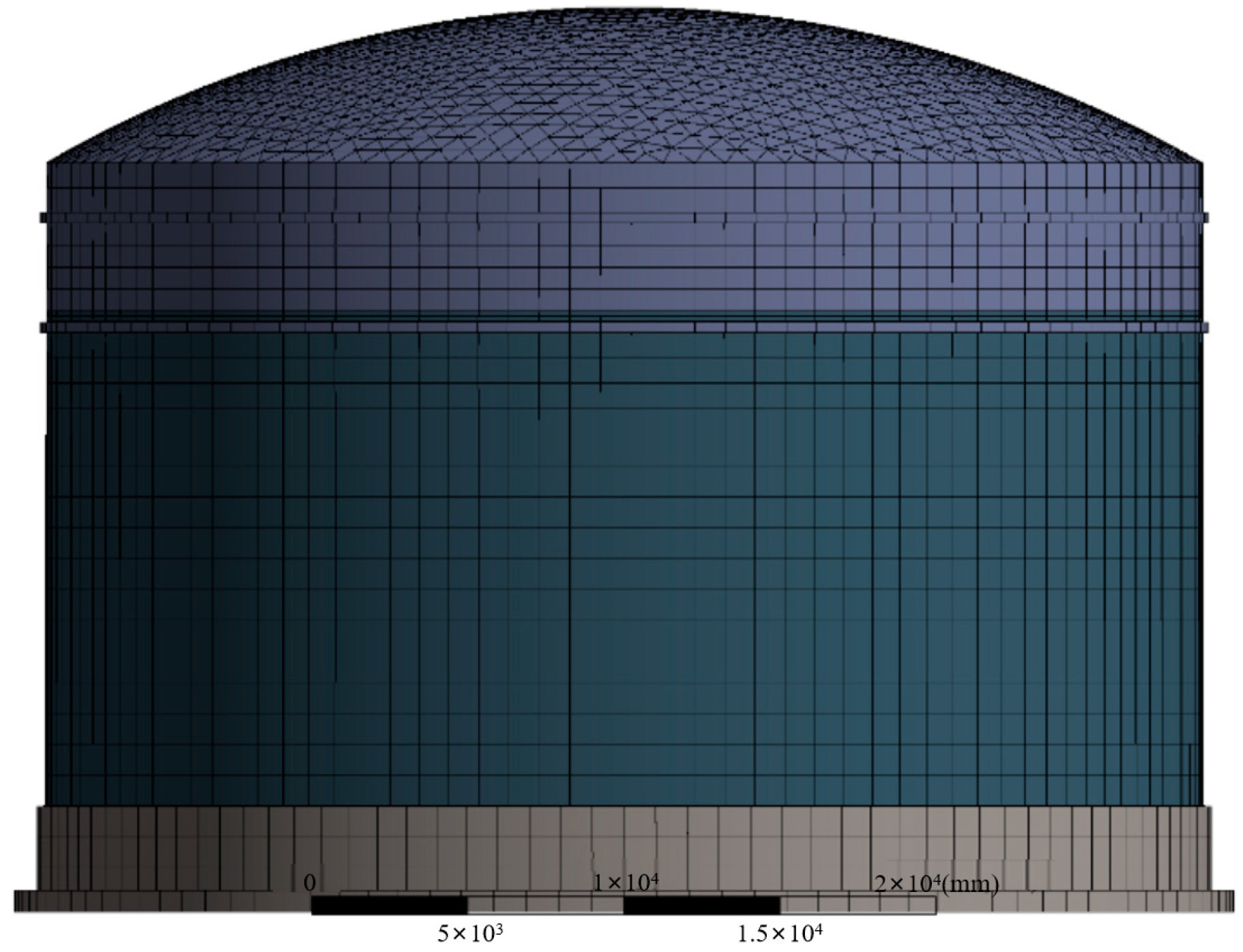
3. Finite Element Model
- Tank gravity
- 2.
- Hydrostatic pressure of the storage fluid
- 3.
- Seismic load
| Effects of Earthquakes | 6° | 7° | 8° | 9° |
|---|---|---|---|---|
| Frequent earthquake | 0.04 | 0.08 | 0.16 | 0.32 |
| Rare occurrence earthquake | 0.28 | 0.5 | 0.9 | 1.4 |
- 4.
- Wind load
- 5.
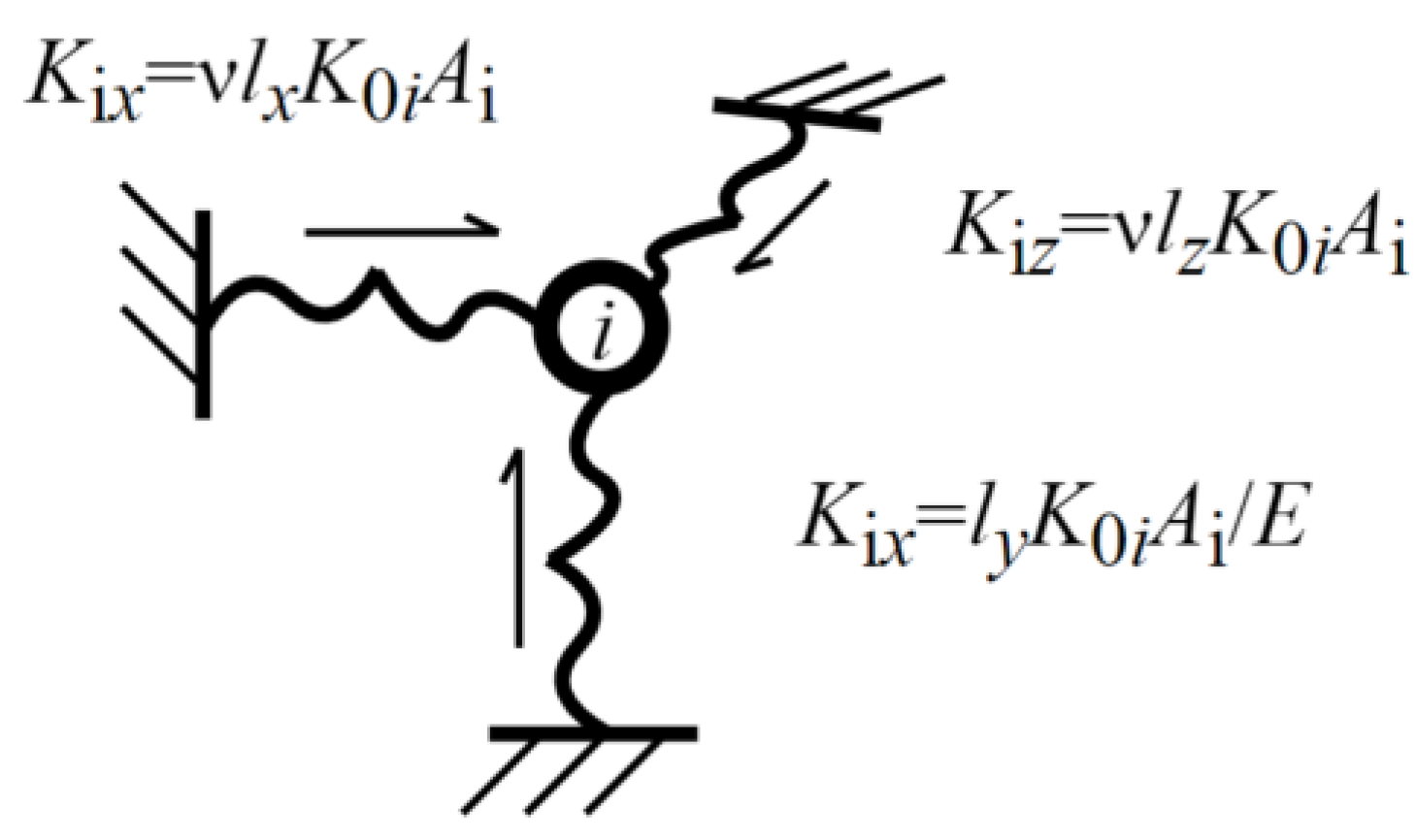
- Boundary condition
4. Calculation Method and Working Condition Design
4.1. Critical State Calculation Method
- (1)
- The boundary conditions are set according to the heterogeneous stiffness distribution of the foundation;
- (2)
- Turn on the seismic load and calculate and record the equivalent stress values of all elements at the bottom of the tank according to the Class II site soil;
- (3)
- Turn off the seismic load, turn on the static load, and calculate and record the equivalent stress values of all elements at the bottom of the tank;
- (4)
- Add the equivalent stress values at the same position obtained from (2) and (3) to obtain a list of equivalent stresses of all elements of the bottom plate. Use this list to obtain the maximum value of the equivalent stress of the bottom plate and its location;
- (5)
- Subtract the yield strength at the location of the maximum value from the maximum value to obtain the Mises equivalent stress difference under the current foundation stiffness (Mises Loss, the difference between the maximum value of the Mises equivalent stress of the bottom plate and the allowable stress of the steel at the location);
- (6)
- Constantly adjust the foundation stiffness K0, and then repeat steps (3) to (5) to make the equivalent stress difference approach 0 MPa, so that the bottom plate just reaches the yield state, that is, the critical state;
- (7)
- Record the foundation bed coefficient and the maximum foundation settlement when the tank floor reaches the critical state;
- (8)
- Switch the heterogeneous foundation distribution form until all foundation stiffness distribution forms are calculated.
4.2. Working Condition Design
5. Analysis of Calculation Results
- (1)
- Under the same heterogeneous foundation, the maximum settlement of the foundation and the critical foundation coefficient increase with the increase in earthquake intensity. The greater the earthquake intensity, the larger the foundation bed coefficient required to ensure that the conical floor is not damaged, and the smaller the maximum settlement of the foundation;
- (2)
- The critical foundation bed coefficient under each working condition is smaller than the foundation stiffness of silty clay (Approximately 20,000–40,000 kN/m3);
- (3)
- When there is no seismic action, the minimum critical foundation rigidity value meeting the safe use of the tank is 94 kN/m3, and the corresponding maximum settlement value is 364.34 mm. When the seismic intensity of the tank area is 9°, the maximum critical stiffness of the foundation is 1805 kN/m3, and the corresponding maximum settlement of the foundation is 85.47 mm;
- (4)
- Under the same seismic intensity, the critical foundation bed coefficient corresponding to the three types of uneven foundations with round hard objects on the windward side is 668 kN/m3, which has a large value and a great influence on the safety of the storage tank.
6. Conclusions
- The coefficient of the critical foundation bed under each working condition is less than the foundation rigidity of silty clay (Approximately 20,000–40,000 kN/m3). Silty clay foundation can meet the requirements of the tank floor for foundation rigidity;
- Under the same seismic intensity, the critical foundation bed coefficient corresponding to the three uneven forms with round hard objects on the windward side is larger, so the uneven form of the foundation will have a serious impact on the safety of the storage tank, and the foundation treatment measures should be taken to avoid this situation in practical engineering;
- Under the same seismic intensity, the uneven form with large foundation stiffness on the windward side is disadvantageous, and the required foundation coefficient is larger;
- Under the same seismic intensity, the critical foundation bed coefficients calculated by the three heterogeneous forms with large foundation stiffness on the windward side are roughly the same;
- With the increase of seismic intensity, the critical foundation bed coefficient increases gradually under the same heterogeneous foundation form.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Godoy, L.A. Buckling of vertical oil storage steel tanks: Review of static buckling studies. Thin Walled Struct. 2016, 103, 1–21. [Google Scholar] [CrossRef]
- Wang, Y.; Leng, M.; Chen, L. Characteristics and construction difficulties of aviation kerosene storage tanks. Oil Gas Storage Transp. 2014, 33, 1353–1358. [Google Scholar]
- Shi, L.; Shuai, J.; Wang, X.; Xu, K. Experimental and numerical investigation of stress in a large-scale steel tank with a floating roof. Thin-Walled Struct. 2017, 117, 25–34. [Google Scholar] [CrossRef]
- Salem, T.N.; Maaly, H.M.; Abdelbaset, A.M. Dynamic Analysis of Aboveground Steel Storage Tanks Over Stiff Soil. Soil Mech. Found. Eng. 2022, 59, 44–50. [Google Scholar] [CrossRef]
- Zhang, H.; El Ansary, A.M.; Zhou, W. Prediction of buckling capacity of liquid-filled steel conical tanks considering field-measured imperfections. Eng. Struct. 2022, 262, 114351. [Google Scholar] [CrossRef]
- Burgos, C.A.; Batista-Abreu, J.C.; Calabró, H.D.; Jaca, R.C.; Godoy, L.A. Buckling estimates for oil storage tanks: Effect of simplified modeling of the roof and wind girder. Thin-Walled Struct. 2015, 91, 29–37. [Google Scholar] [CrossRef]
- Soni, D.P.; Mistry, B.B.; Panchal, V.R. Double variable frequency pendulum isolator for seismic isolation of liquid storage tanks. Nucl. Eng. Des. 2011, 241, 700–713. [Google Scholar] [CrossRef]
- Sahraeian SM, S.; Takemura, J.; Yamada, M.; Seki, S. A Few Critical Aspects to Rational Design of Piled Raft Foundation for Oil Storage Tanks. Geotech. Geol. Eng. Int. J. 2020, 38, 2117–2137. [Google Scholar] [CrossRef]
- Gunerathne, S.; Seo, H.; Lawson, W.D.; Jayawickrama, P.W. Analysis of edge-to-center settlement ratio for circular storage tank foundation on elastic soil. Comput. Geotech. 2018, 102, 136–147. [Google Scholar] [CrossRef]
- Jing, W.; Wang, J.; Cheng, X. Dynamic responses of oil storage tank considering wind interference effect. Eng. Fail. Anal. 2019, 104, 1053–1063. [Google Scholar] [CrossRef]
- Haroun, M.A. Vibration studies and tests of liquid storage tanks. Earthq. Eng. Struct. Dyn. 1983, 11, 179–206. [Google Scholar] [CrossRef]
- Cakir, T.; Livaoglu, R. Fast practical analytical model for analysis of backfill-rectangular tank-fluid interaction systems. Soil Dyn. Earthq. Eng. 2012, 37, 24–37. [Google Scholar] [CrossRef]
- Durmuş, A.; Livaoglu, R. A simplified 3 D.O.F. model of A FEM model for seismic analysis of a silo containing elastic material accounting for soil–structure interaction. Soil Dyn. Earthq. Eng. 2015, 77, 1–14. [Google Scholar] [CrossRef]
- Housner, G.W. Dynamic pressures on accelerated fluid containers. Bull. Seismol. Soc. Am. 1957, 47, 15–35. [Google Scholar] [CrossRef]
- Larkin, T. Seismic Response of Liquid Storage Tanks Incorporating Soil Structure Interaction. J. Geotech. Geoenvironmental Eng. 2008, 134, 1804–1814. [Google Scholar] [CrossRef]
- Livaoglu, R. Investigation of seismic behavior of fluid–rectangular tank–soil/foundation systems in frequency domain. Soil Dyn. Earthq. Eng. 2008, 28, 132–146. [Google Scholar] [CrossRef]
- Van Impe, W.F.; Van Impe, P.O.; Manzotti, A. Pile Design and Group Behaviour: A Case Study of Large Tank Foundations in Soft Soil Conditions. Geotech. Eng. J. SEAGS AGSSEA 2018, 49, 15–29. [Google Scholar]
- Teramoto, S.; Niimura, T.; Akutsu, T.; Kimura, M. Evaluation of ultimate behavior of actual large-scale pile group foundation by in-situ lateral loading tests and numerical analysis. Soils Found. 2018, 58, 819–837. [Google Scholar] [CrossRef]
- Tarasenko, A.A.; Konovalov, P.A.; Zekhniev, F.F.; Chepur, P.V.; Tarasenko, D.A. Effects of Nonuniform Settlement of the Outer Bottom Perimeter of a Large Tank on its Stress-Strain State. Soil Mech. Found. Eng. 2017, 53, 405–411. [Google Scholar] [CrossRef]
- Dimov, L.; Dimov, I.; Bogushevskaya, E. Large Oil Tank Settlement and Tilt During Hydraulic Testing. Soil Mech. Found. Eng. 2017, 54, 192–197. [Google Scholar] [CrossRef]
- GB 50011-2010; Code for Seismic Design of Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010.
- GB 50191-2012; Code for Seismic Design of Special Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2012.
- GB 50009-2012; Load Code for the Design of Building Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2012.





| Parameter | Value |
|---|---|
| The density of steel/kg·m−3 | 7850 |
| Elastic modulus of steel/MPa | 2 × 105 |
| Poisson’s ratio of steel | 0.3 |
| Standard value of yield stress of tank steel/MPa | 345 |
| Elastic modulus of sand cushion/MPa | 30 |
| Sand cushion Poisson’s ratio | 0.32 |
| Elastic modulus of ring wall foundation/MPa | 3.25 × 104 |
| Poisson’s ratio of ring wall foundation | 0.2 |
| Site Soil Type | II |
|---|---|
| The seismic intensity | 6° |
| Design seismic grouping | The first group |
| Basic seismic acceleration for design | 0.05 g |
| Serial Number | Distribution Forms of Foundation Stiffness | Schematic Diagram | Functional Expression |
|---|---|---|---|
| Foundation form 1 | The foundation stiffness is larger in the central circular area |  | |
| Foundation form 2 | The foundation stiffness in the 1/2 circle area on the windward side is larger | 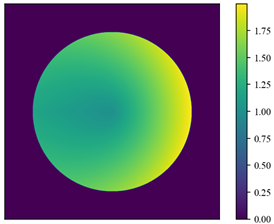 | |
| Foundation form 3 | The foundation stiffness in the 1/3 circle area on the windward side is larger | 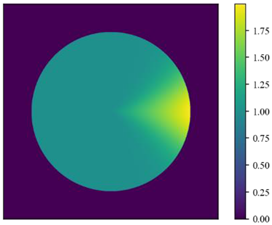 | |
| Foundation form 4 | The foundation stiffness in the 1/4 circle area on the windward side is larger |  | |
| Foundation form 5 | Round hard object with a radius of 0.5 m in the center | 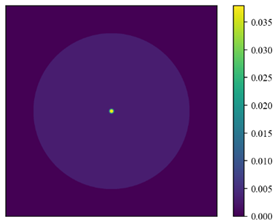 | |
| Foundation form 6 | Round hard object with a radius of 0.5 is a = R/2 away from the center on the windward side |  | |
| Foundation form 7 | The windward side has a round hard object with a radius of 0.5 m | 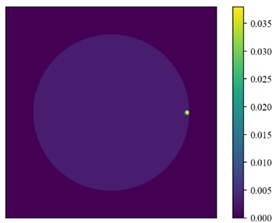 |
| Uneven Form of Foundation | Dead Load + Wind Load | 6° | 7° | 8° | 9° |
|---|---|---|---|---|---|
| Foundation form 1 | Combination of 1.1 | Combination of 1.2 | Combination of 1.3 | Combination of 1.4 | Combination of 1.5 |
| Foundation form 2 | Combination of 2.1 | Combination of 2.2 | Combination of 2.3 | Combination of 2.4 | Combination of 2.5 |
| Foundation form 3 | Combination of 3.1 | Combination of 3.2 | Combination of 3.3 | Combination of 3.4 | Combination of 3.5 |
| Foundation form 4 | Combination of 4.1 | Combination of 4.2 | Combination of 4.3 | Combination of 4.4 | Combination of 4.5 |
| Foundation form 5 | Combination of 5.1 | Combination of 5.2 | Combination of 5.3 | Combination of 5.4 | Combination of 5.5 |
| Foundation form 6 | Combination of 6.1 | Combination of 6.2 | Combination of 6.3 | Combination of 6.4 | Combination of 6.5 |
| Foundation form 7 | Combination of 7.1 | Combination of 7.2 | Combination of 7.3 | Combination of 7.4 | Combination of 7.5 |
| Uneven Form of Foundation | Dead Load + Wind Load | 6° | 7° | 8° | 9° |
|---|---|---|---|---|---|
| Foundation form 1 | 254.54 | 356.64 | 343.73 | 165.45 | 85.47 |
| Foundation form 2 | 364.34 | 360.75 | 347.77 | 179.76 | 89.30 |
| Foundation form 3 | 319.30 | 359.90 | 347.22 | 179.75 | 88.96 |
| Foundation form 4 | 295.41 | 360.15 | 347.41 | 180.35 | 88.87 |
| Foundation form 5 | 230.01 | 300.43 | 282.7 | 106.24 | 30.96 |
| Foundation form 6 | 230.02 | 300.44 | 282.9 | 106.25 | 30.97 |
| Foundation form 7 | 230.03 | 300.42 | 282.5 | 106.24 | 30.96 |
| Uneven Form of Foundation | Dead Load + Wind Load | 6° | 7° | 8° | 9° |
|---|---|---|---|---|---|
| Foundation form 1 | 132 | 108 | 141 | 499 | 1805 |
| Foundation form 2 | 94 | 118 | 149 | 462 | 1686 |
| Foundation form 3 | 111 | 117 | 148 | 462 | 1701 |
| Foundation form 4 | 121 | 116 | 147 | 459 | 1707 |
| Foundation form 5 | 668 | 635 | 652 | 2168 | 3328 |
| Foundation form 6 | 668 | 635 | 652 | 2168 | 3328 |
| Foundation form 7 | 668 | 635 | 652 | 2168 | 3328 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, Z.; Qiao, H.; Hao, X.; Wang, Y.; Lei, H.; Cui, Z. Influence of Heterogeneous Foundation on the Safety of Inverted Cone Bottom Oil Storage Tanks under Earthquakes. Buildings 2023, 13, 1720. https://doi.org/10.3390/buildings13071720
Dai Z, Qiao H, Hao X, Wang Y, Lei H, Cui Z. Influence of Heterogeneous Foundation on the Safety of Inverted Cone Bottom Oil Storage Tanks under Earthquakes. Buildings. 2023; 13(7):1720. https://doi.org/10.3390/buildings13071720
Chicago/Turabian StyleDai, Zuhao, Hong Qiao, Xvdong Hao, Yijuan Wang, Hanwen Lei, and Zhiqiang Cui. 2023. "Influence of Heterogeneous Foundation on the Safety of Inverted Cone Bottom Oil Storage Tanks under Earthquakes" Buildings 13, no. 7: 1720. https://doi.org/10.3390/buildings13071720
APA StyleDai, Z., Qiao, H., Hao, X., Wang, Y., Lei, H., & Cui, Z. (2023). Influence of Heterogeneous Foundation on the Safety of Inverted Cone Bottom Oil Storage Tanks under Earthquakes. Buildings, 13(7), 1720. https://doi.org/10.3390/buildings13071720






