Practical Investigation on the Strengthening of the Built-Up Steel Main Girder of a Metro Station with Carbon-Fiber-Reinforced Polymer on the Inside Part of the Tensioned Flange
Abstract
:1. Introduction
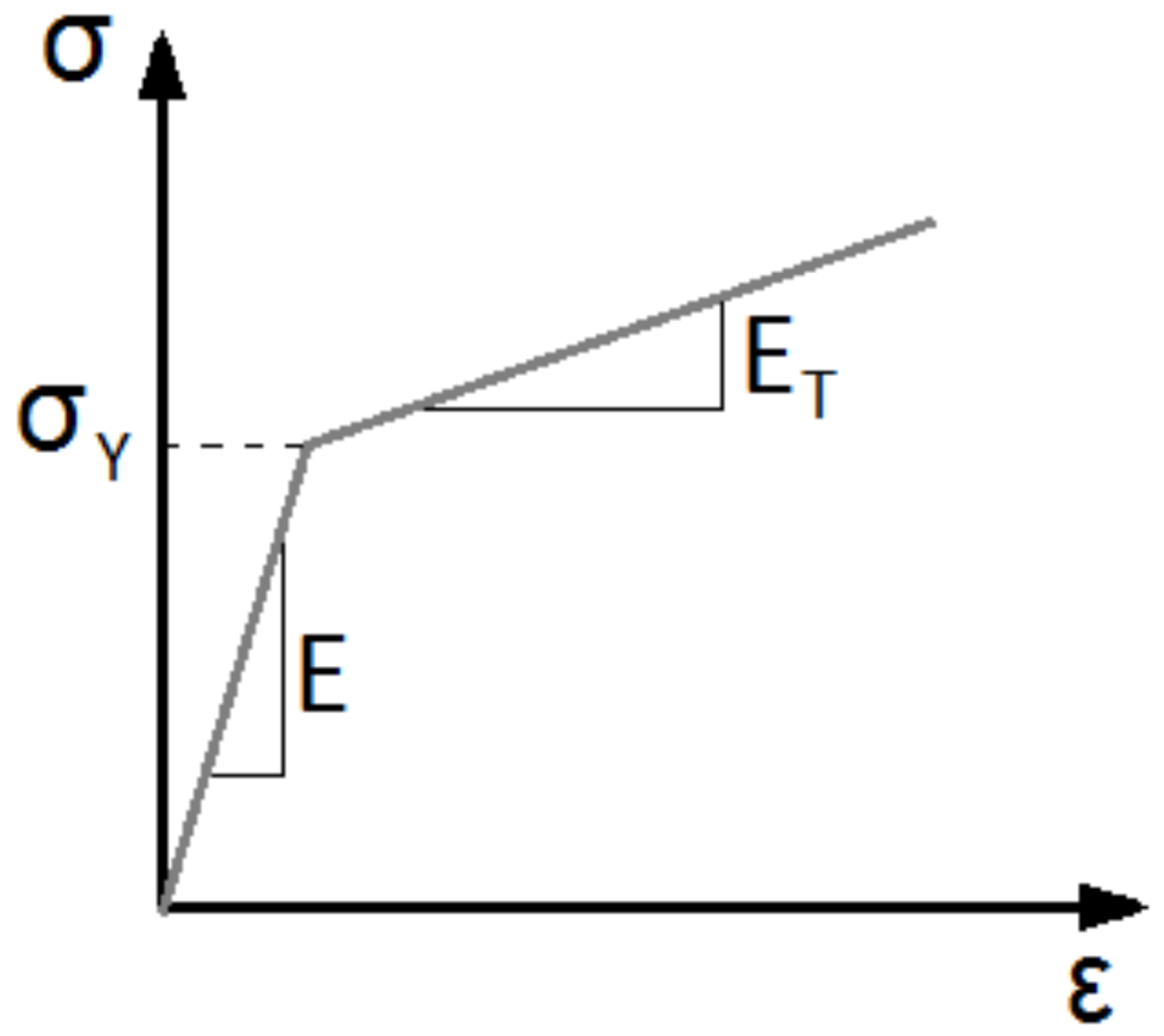
2. Mechanical Properties of the Steel Beam Prototypes
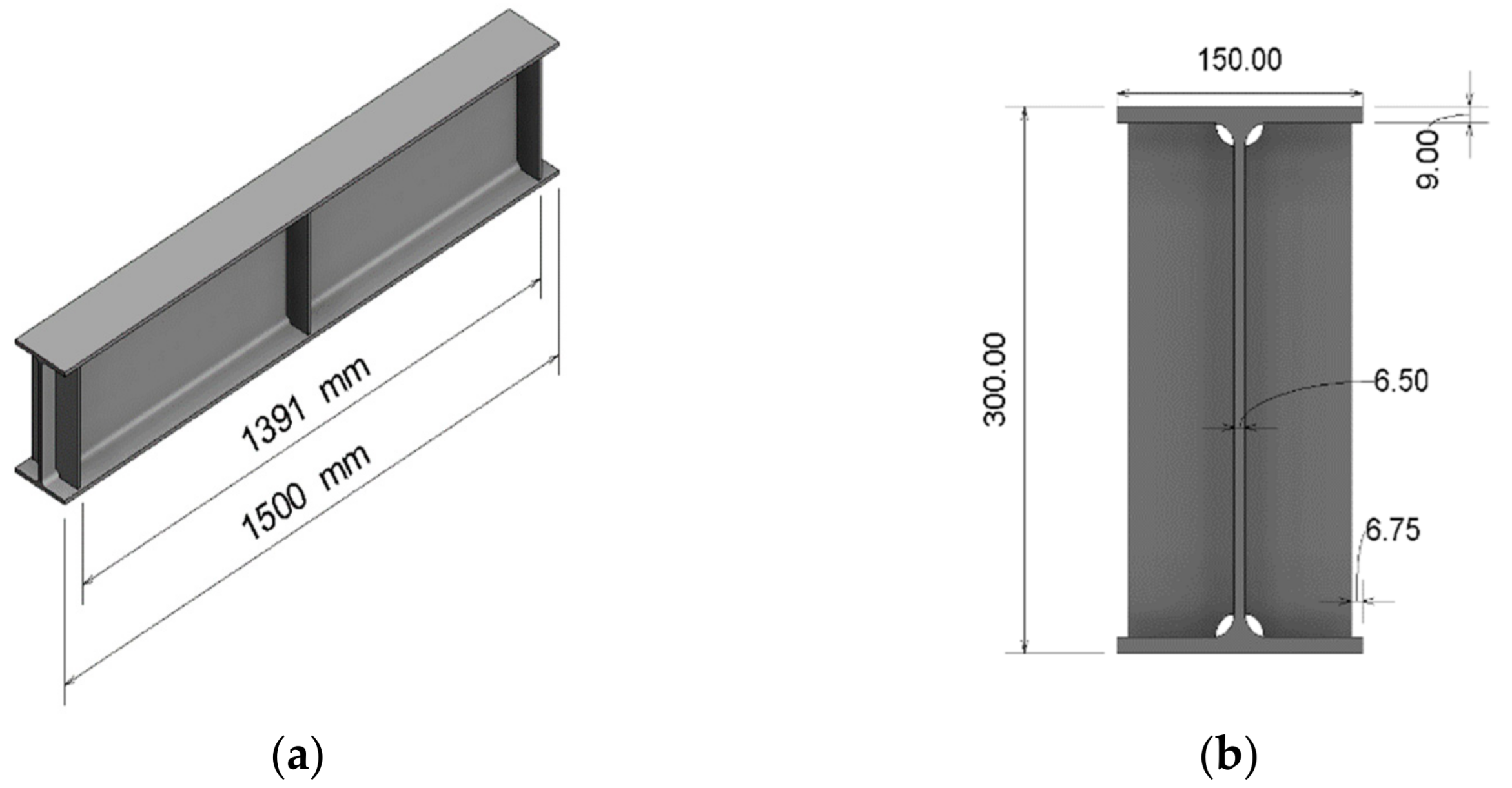
2.1. Specimen Properties
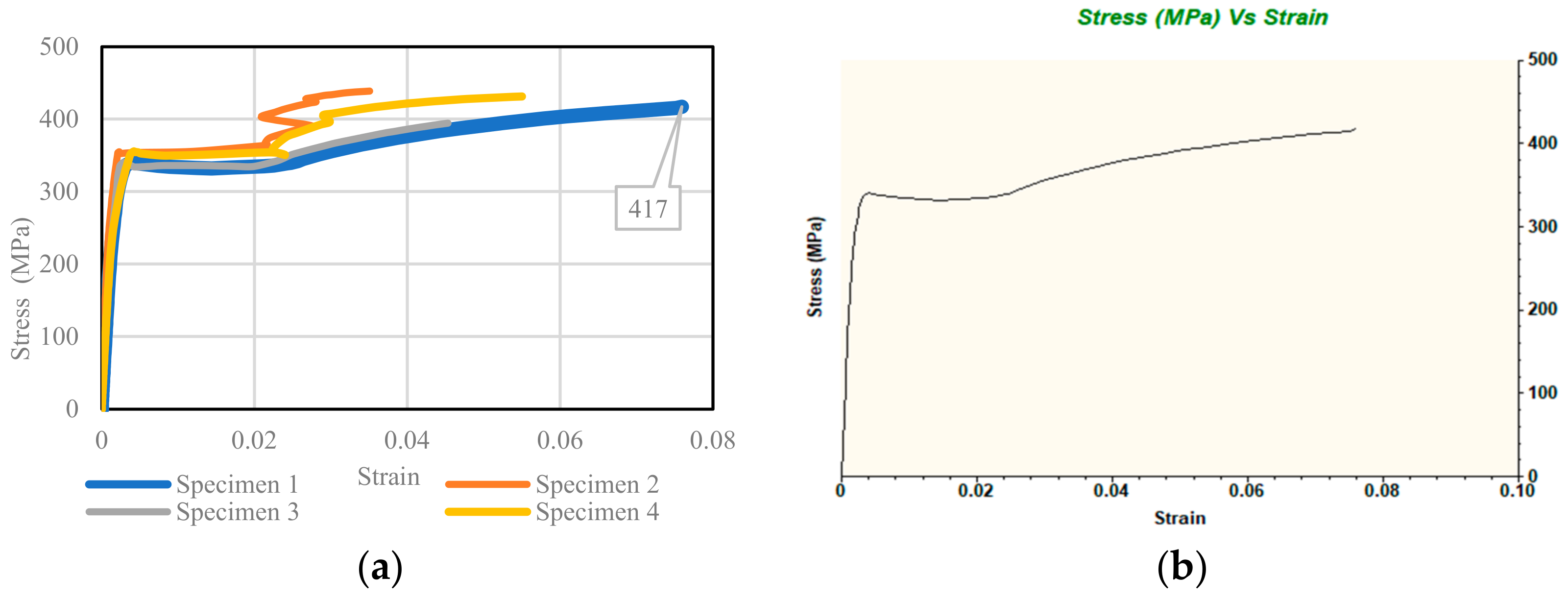
2.2. Material Test Results
3. Finite Element Analysis for Three-Point Bending Test
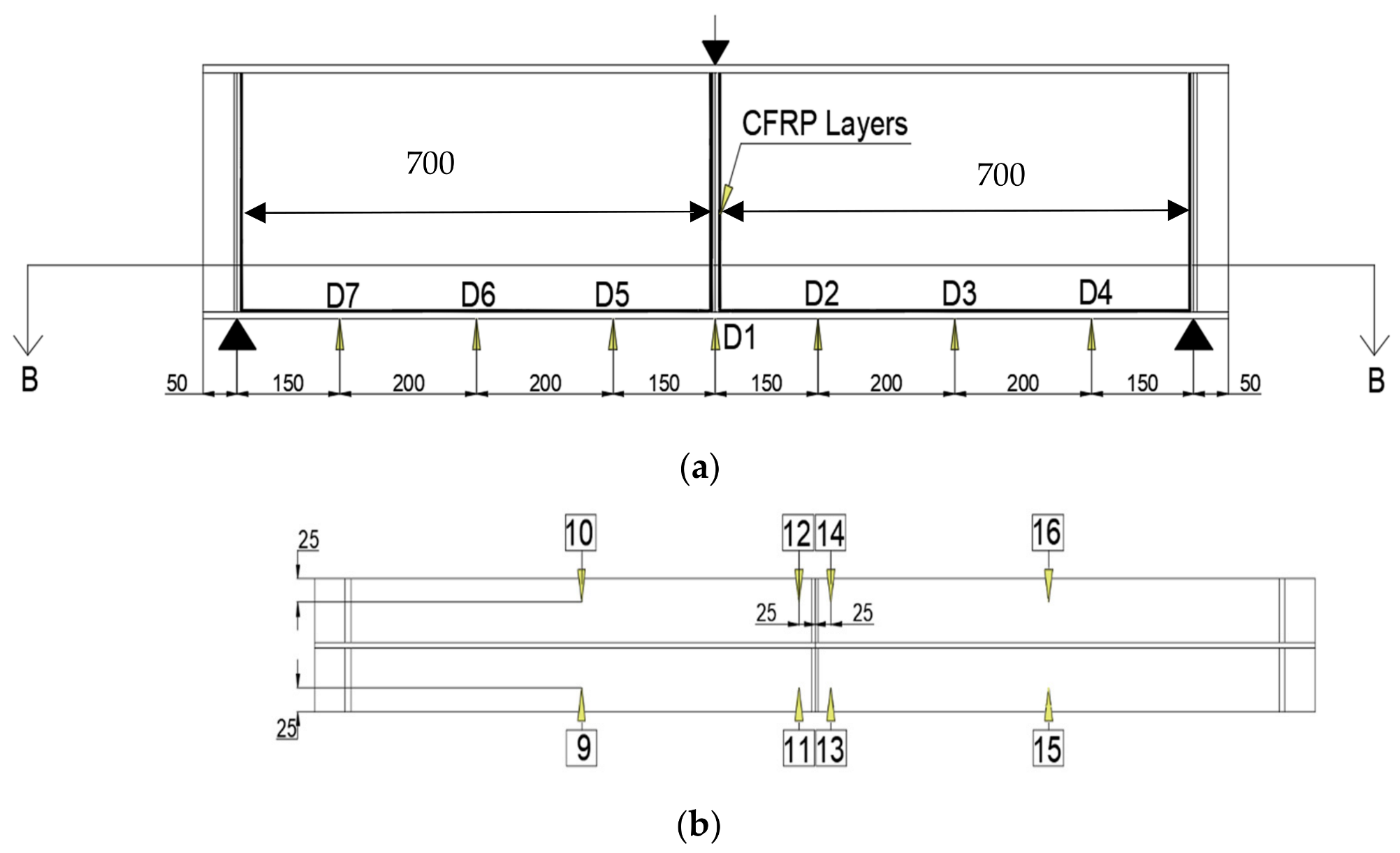
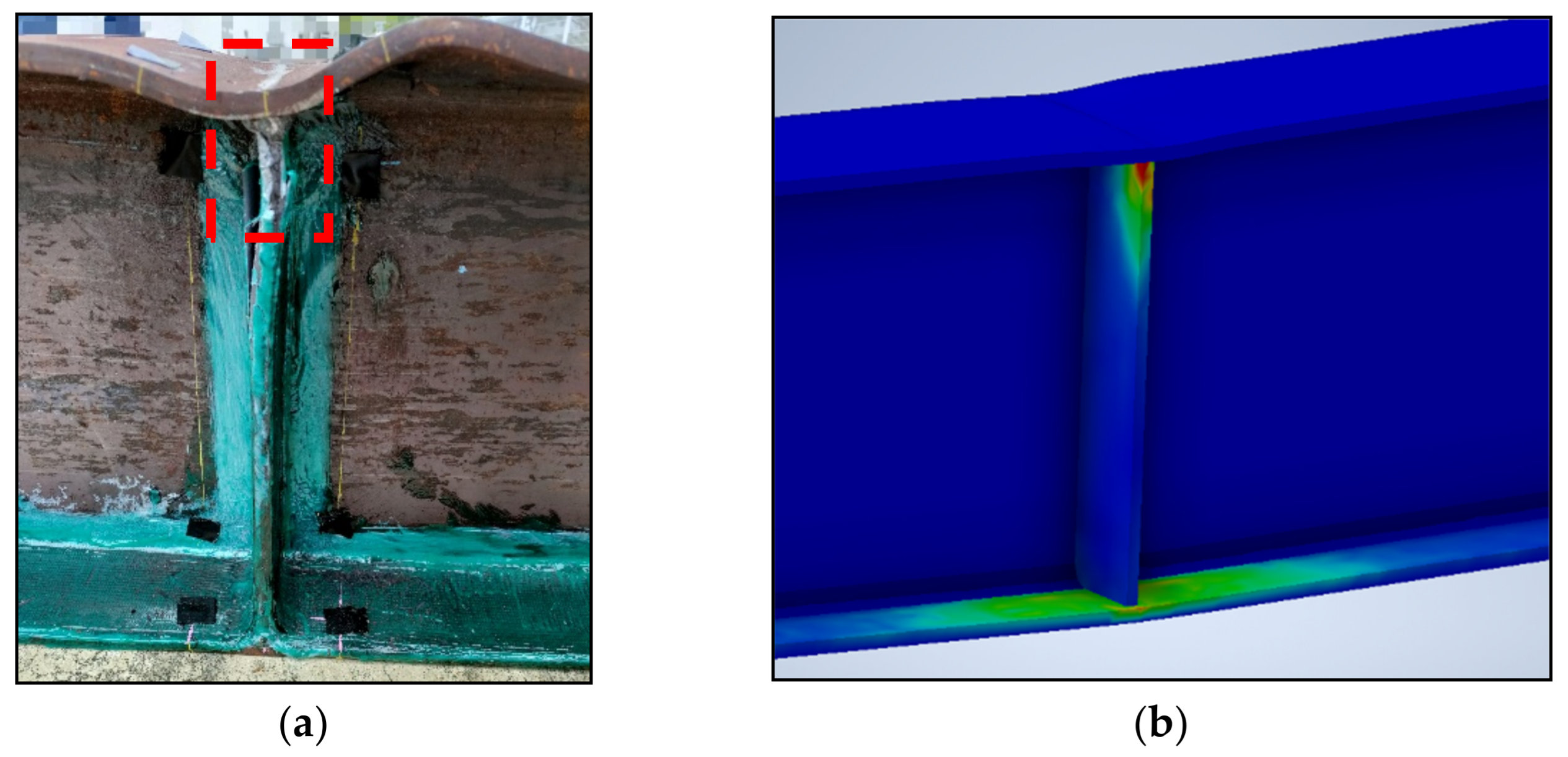
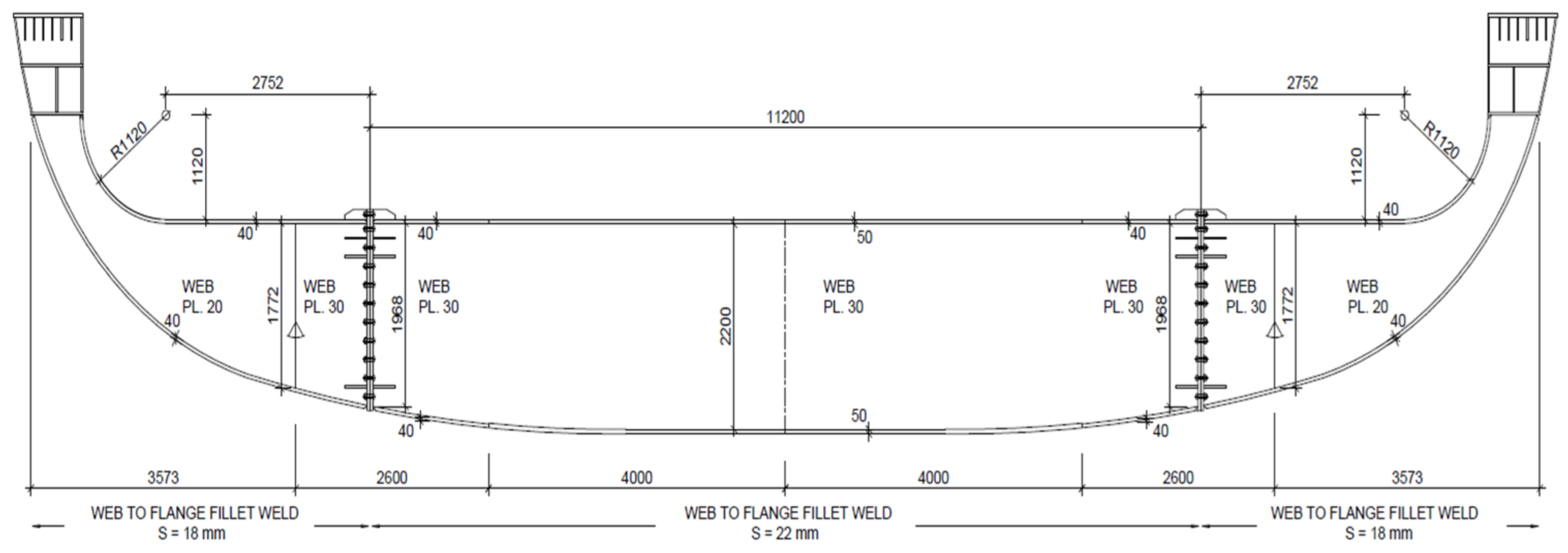
3.1. Description of the Experiment Beam
3.2. Finite Element Model with No CFRP Laminate
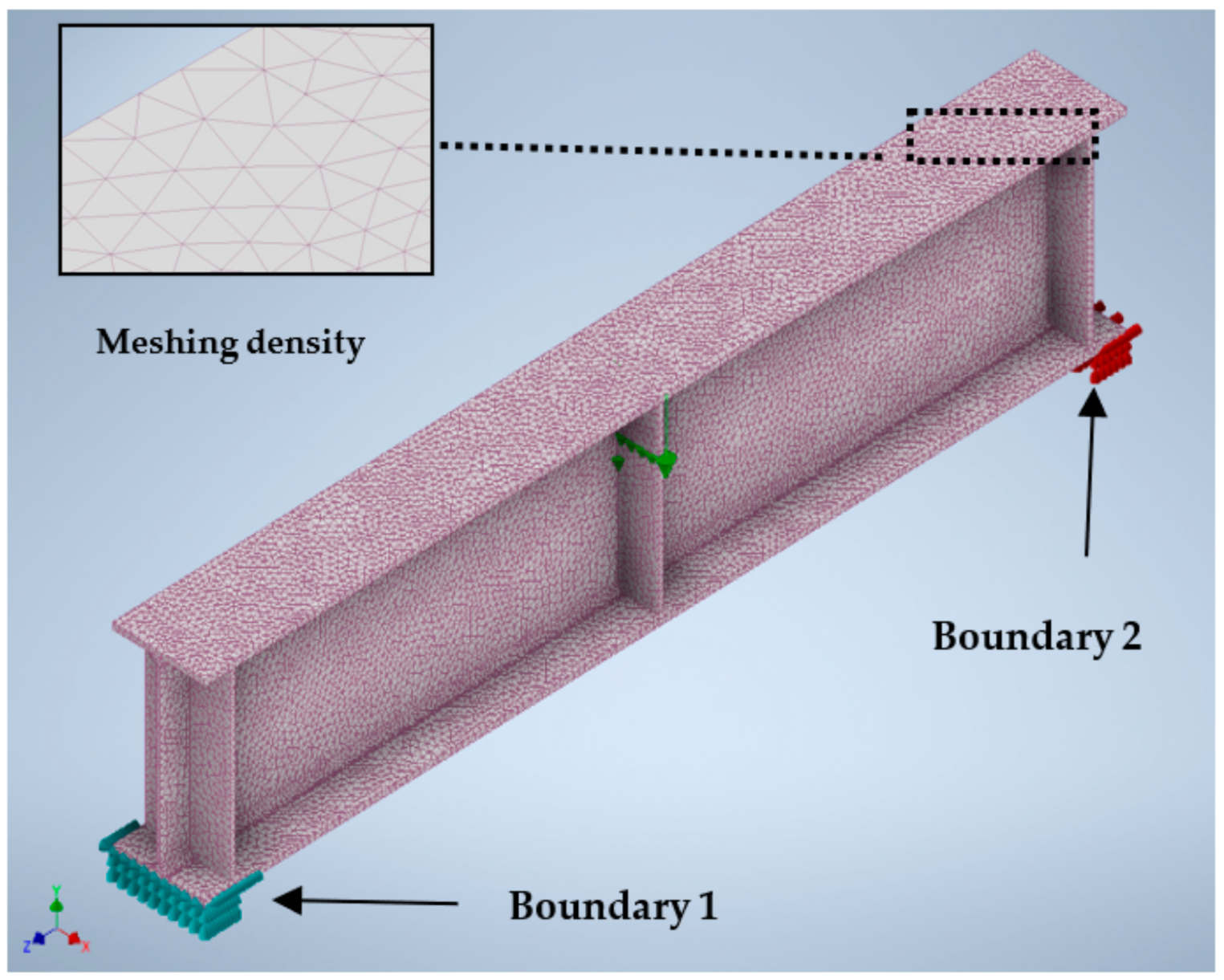
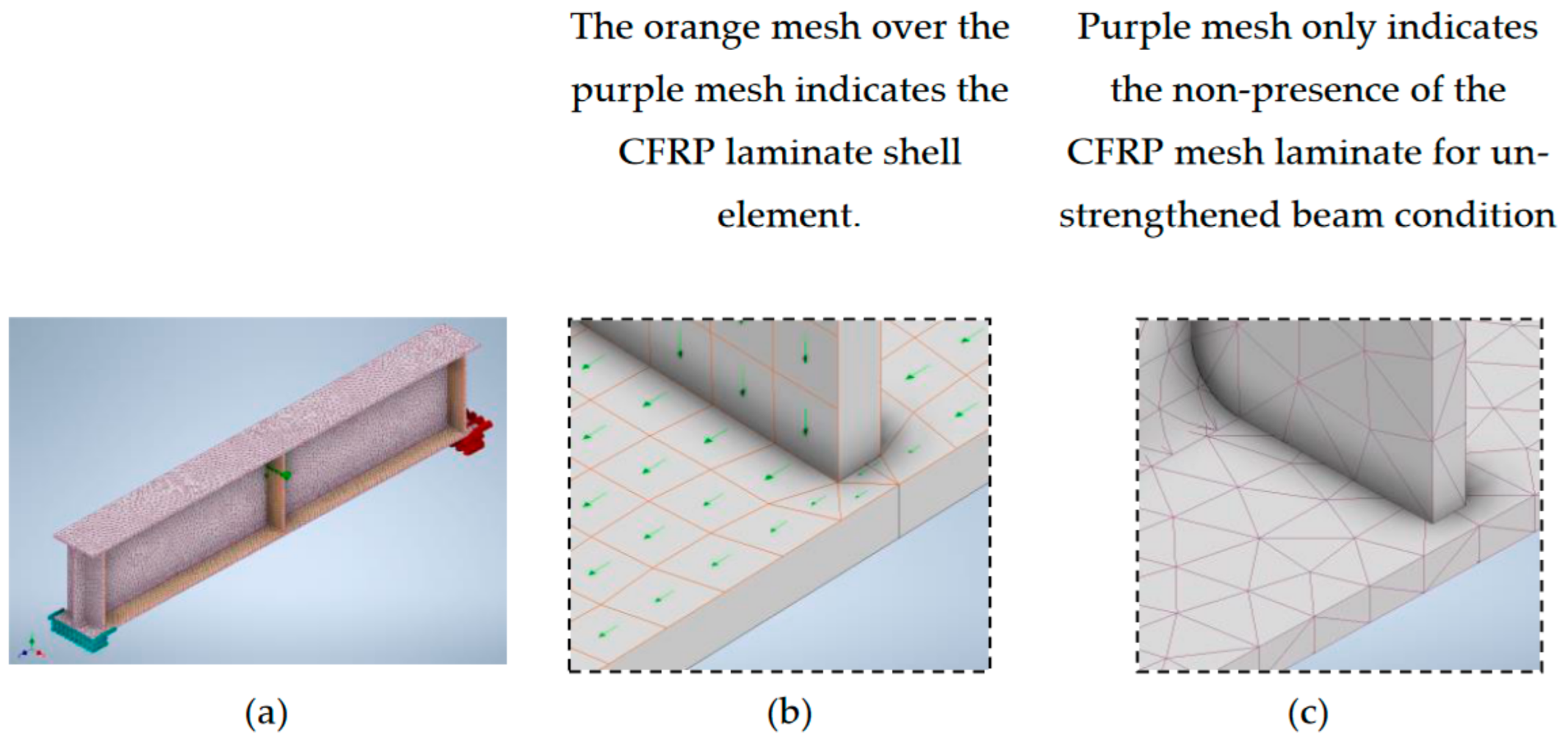
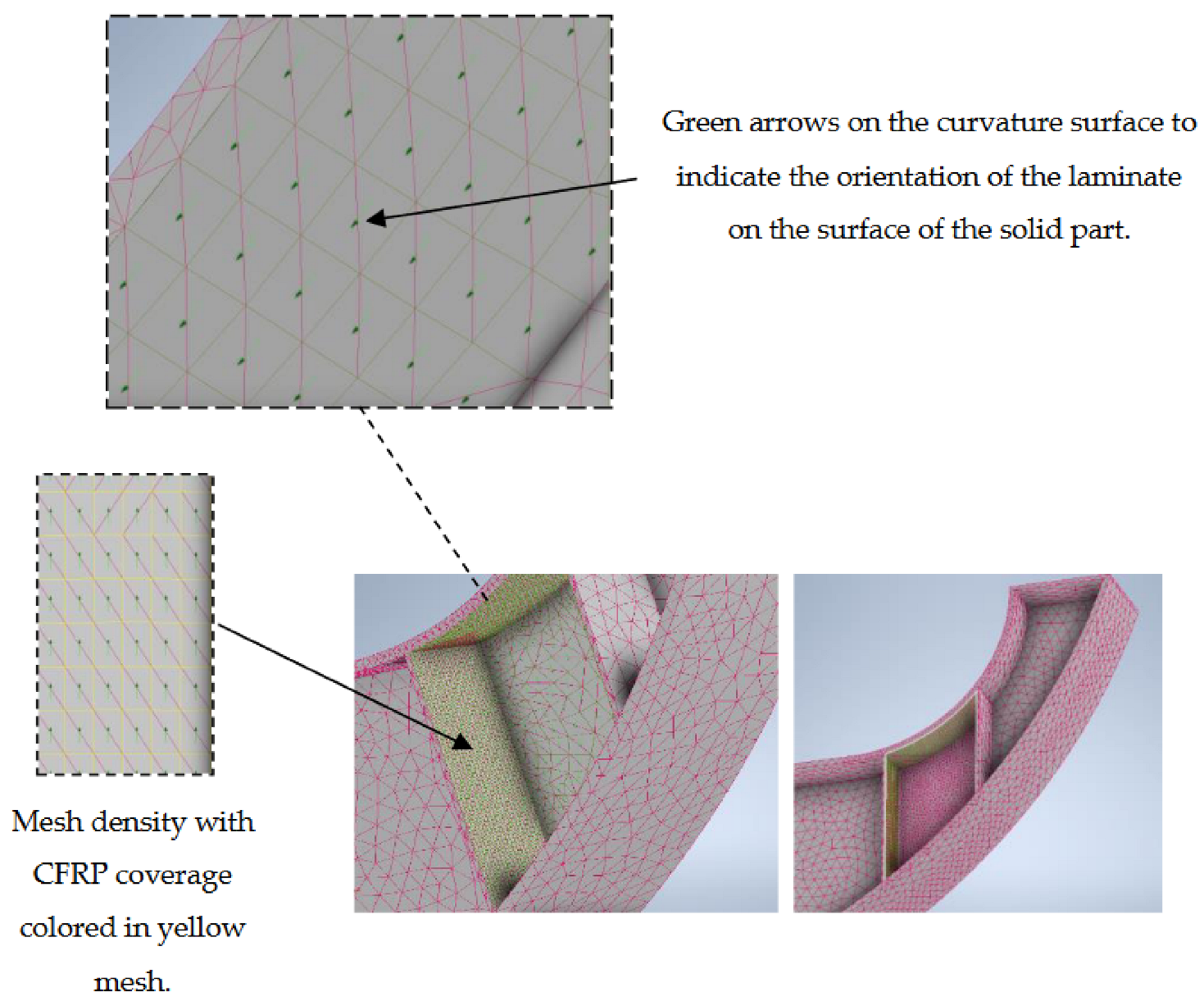
3.2.1. Meshing
3.2.2. Supports and Loading
3.2.3. Contact Type
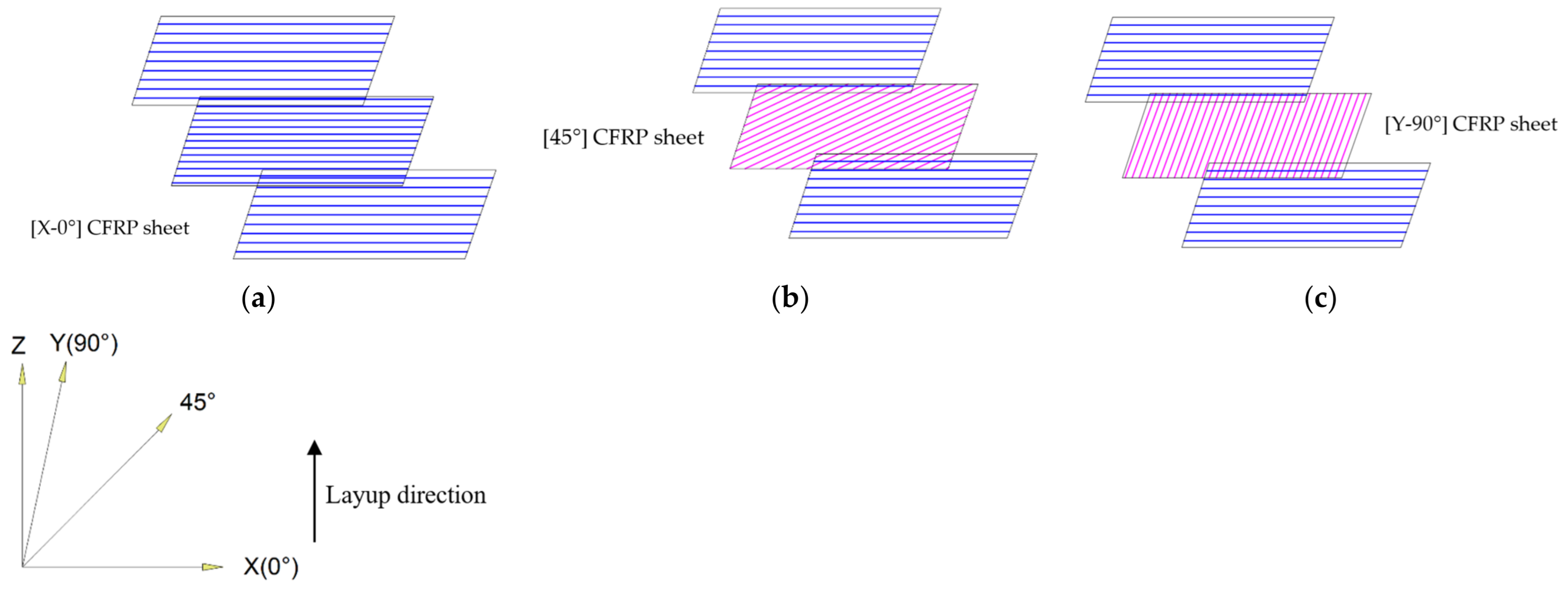
3.3. Finite Element Model with CFRP Laminate
4. Experimental Setup for a Three-Point Bending Test
4.1. Experimental Setup of Strengthened and Un-Strengthened Conditions
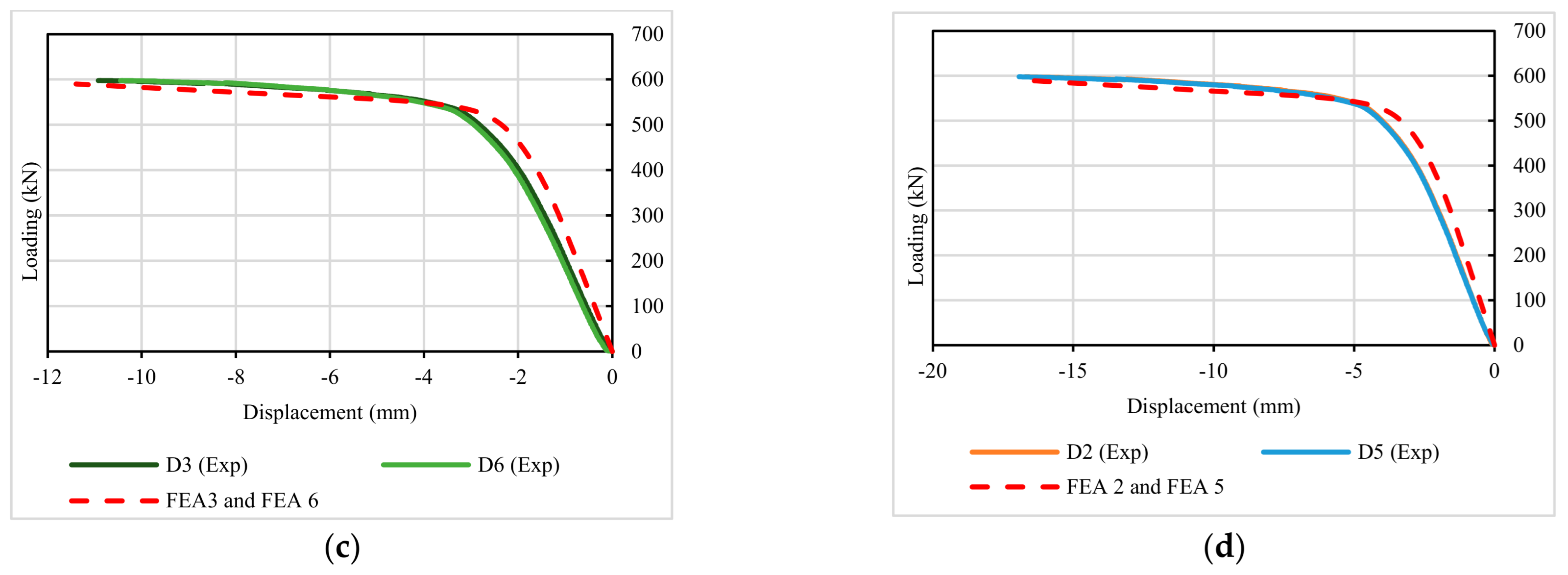
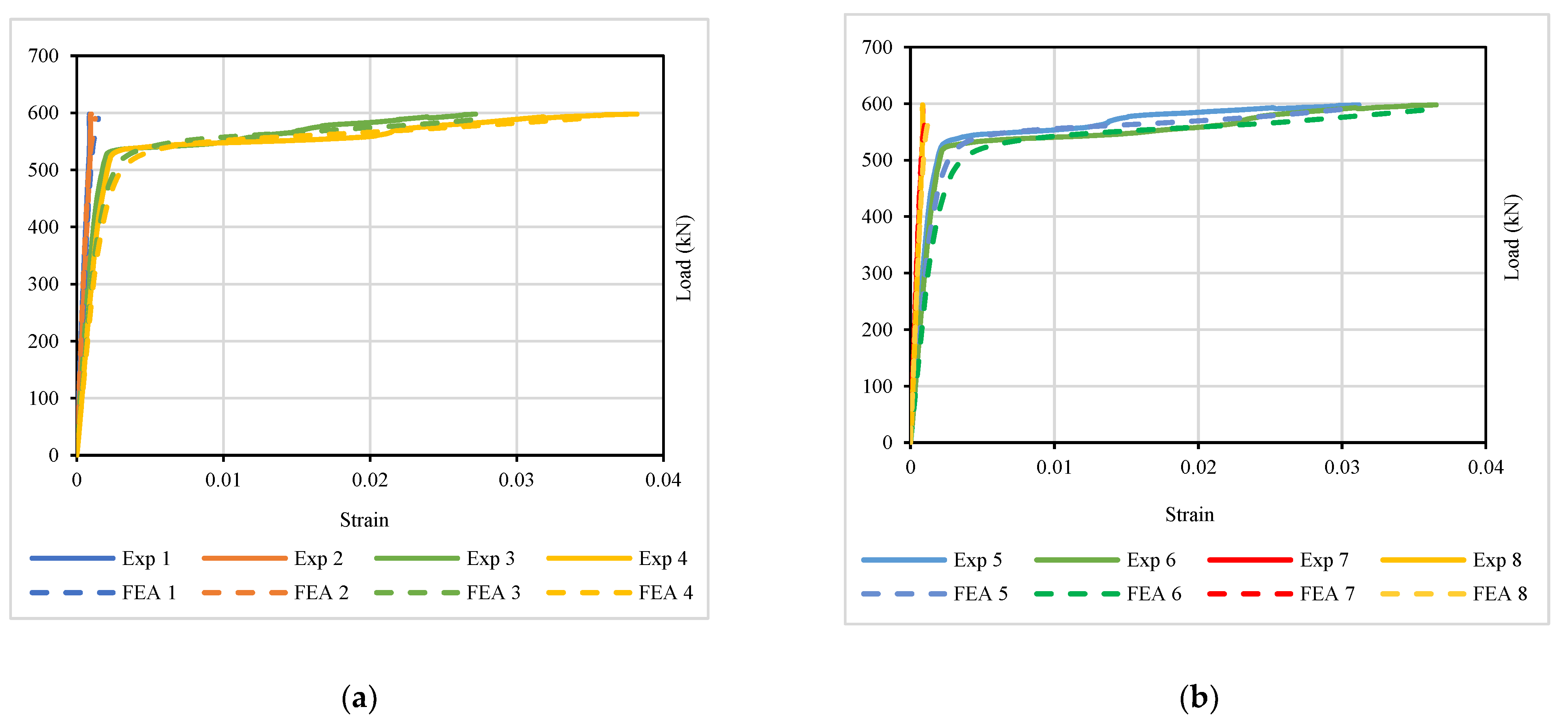
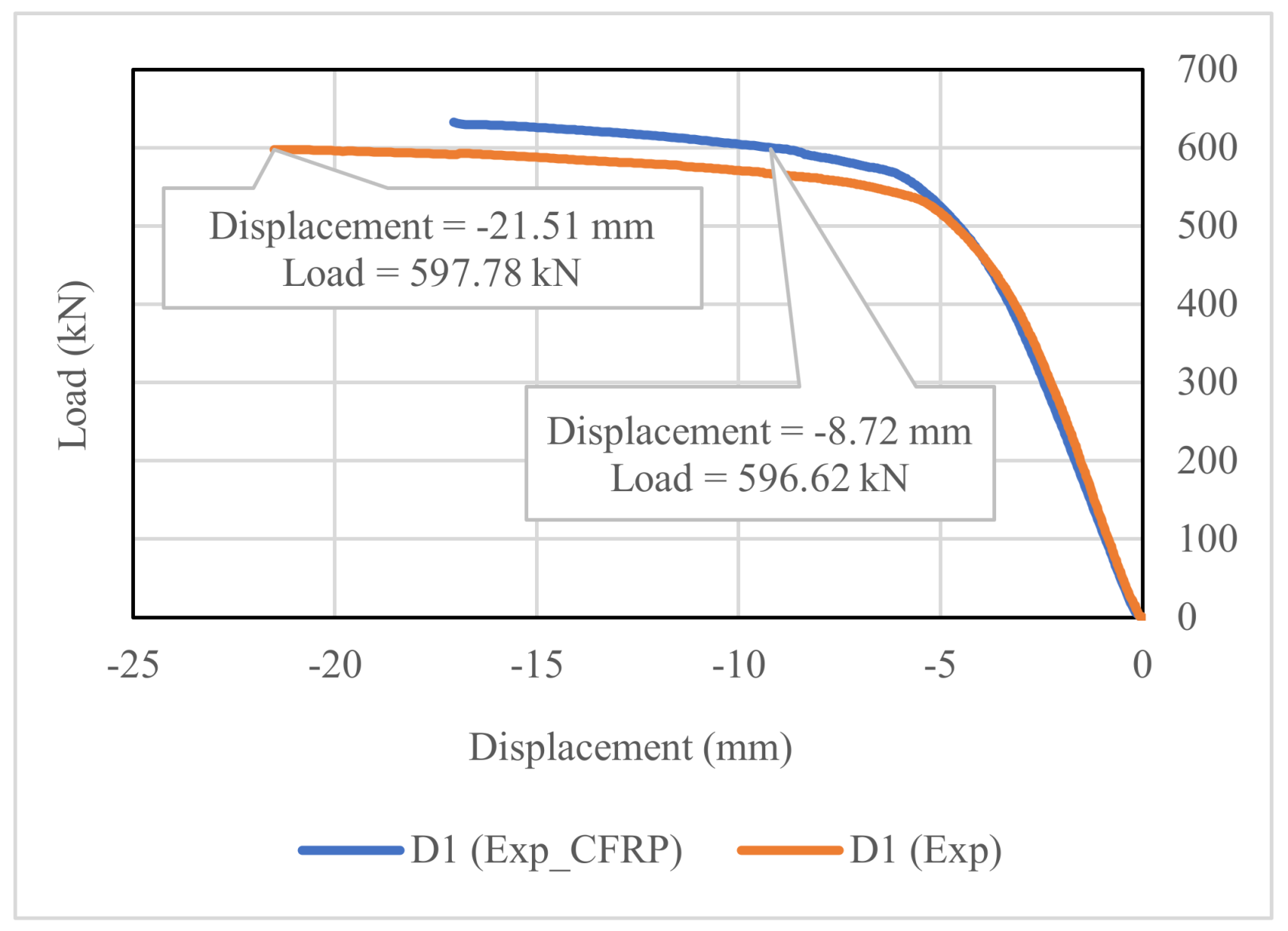
4.2. Load–Displacement and Load–Strain Relation Results
4.3. CFRP Strengthening Effect
5. Steel Girder Numerical Model
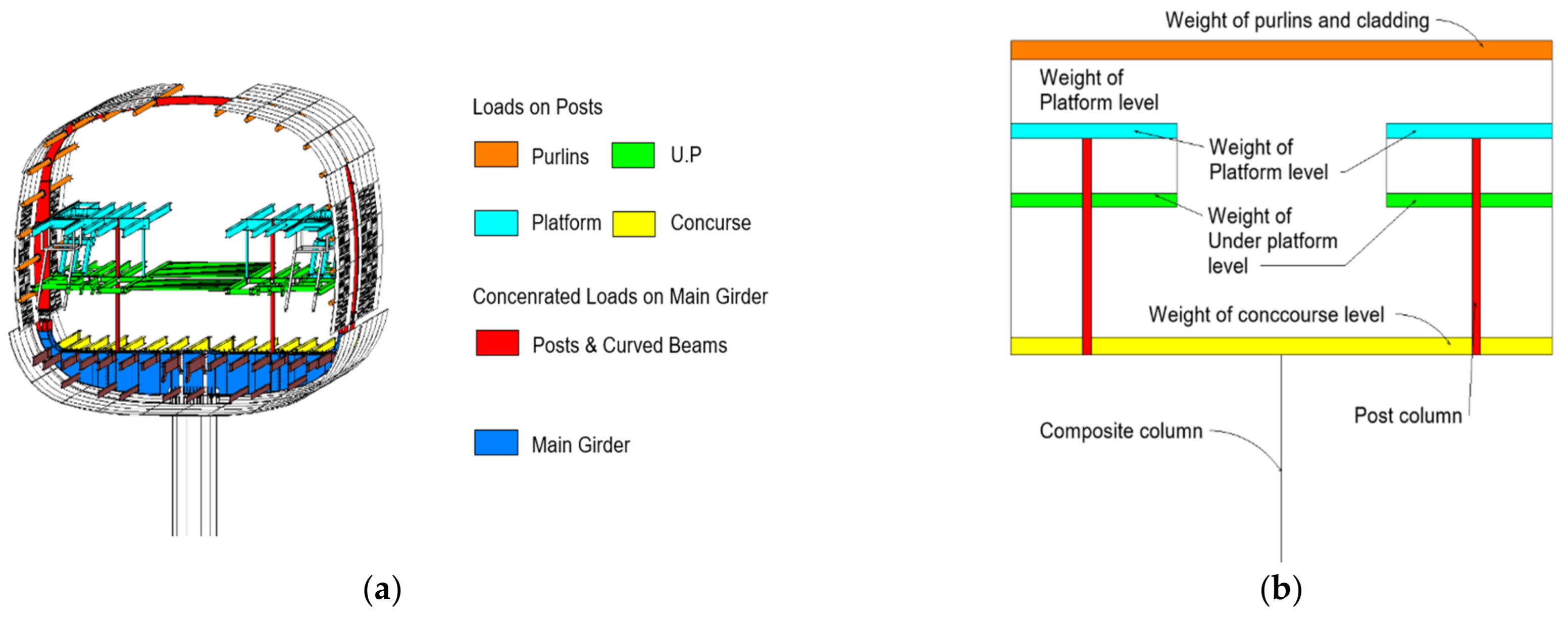
5.1. Loads Calculation
5.2. Finite Element Steel Girder Model Set Up
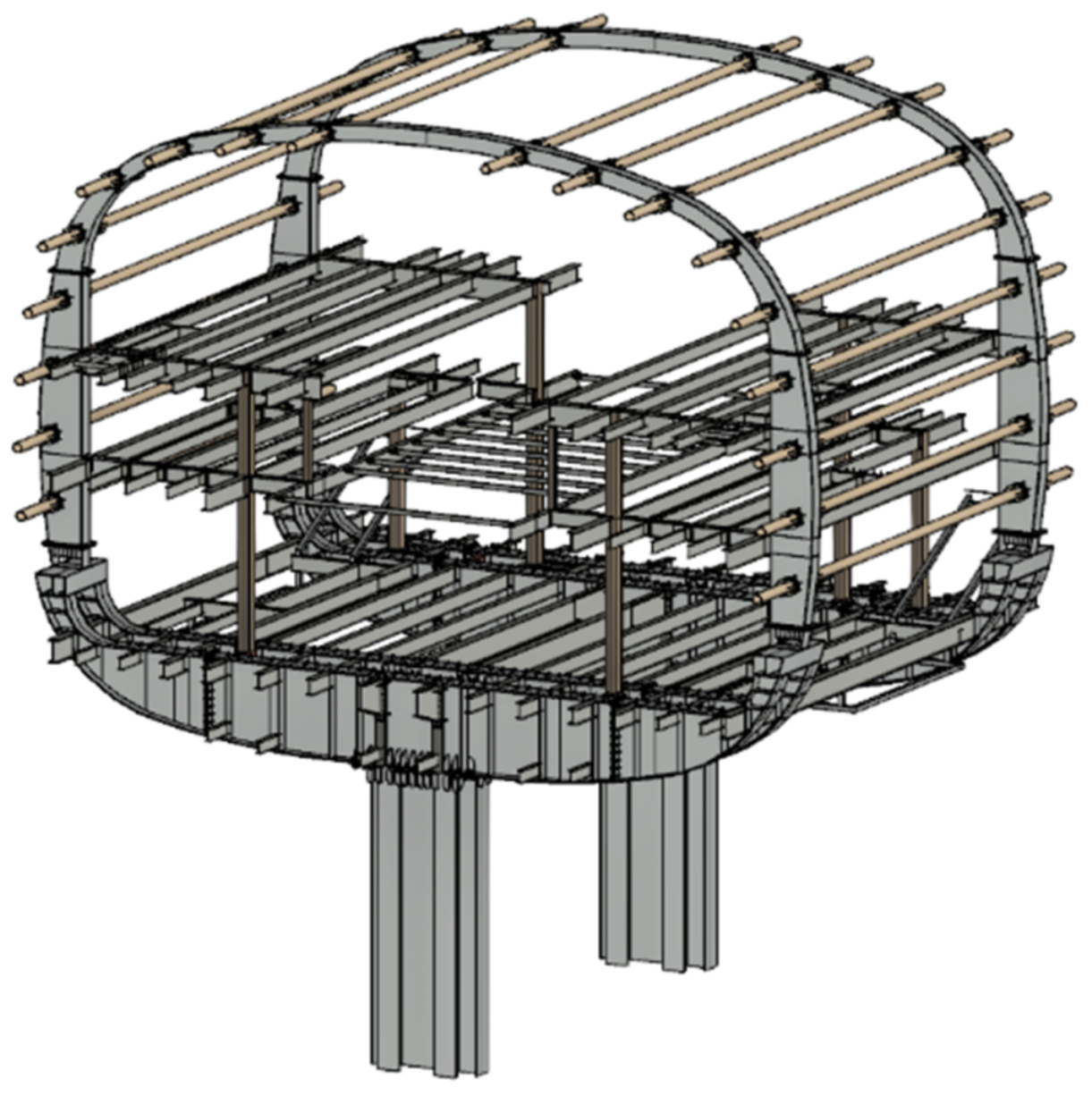
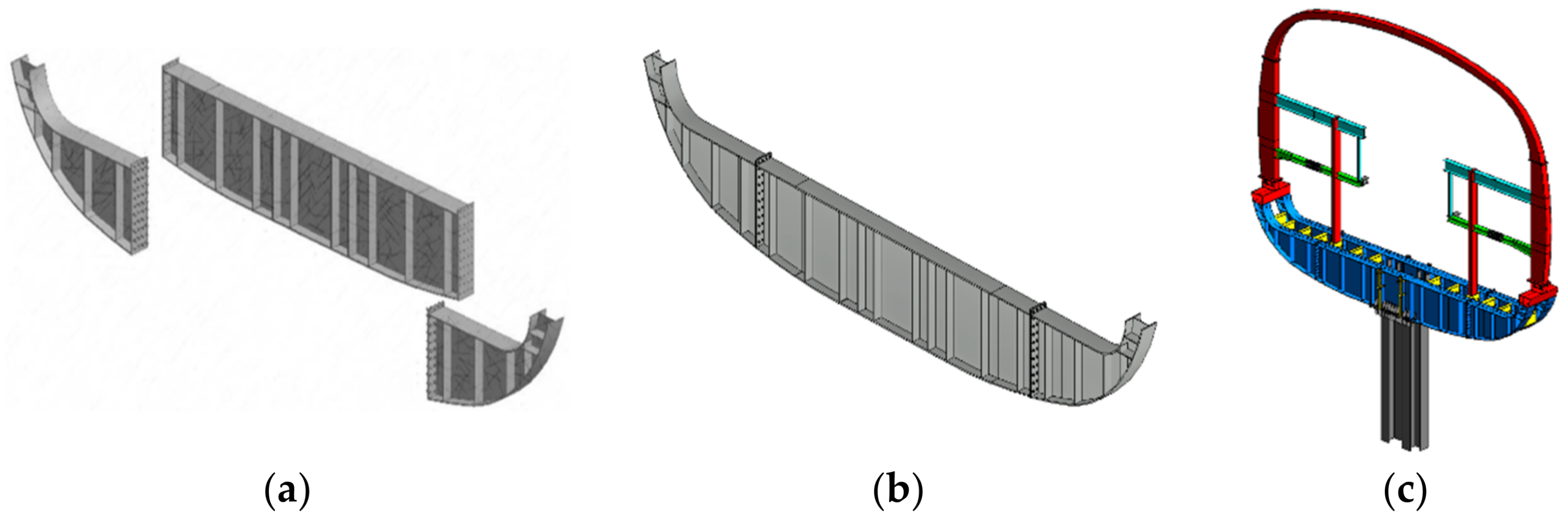
5.2.1. Description of the Model
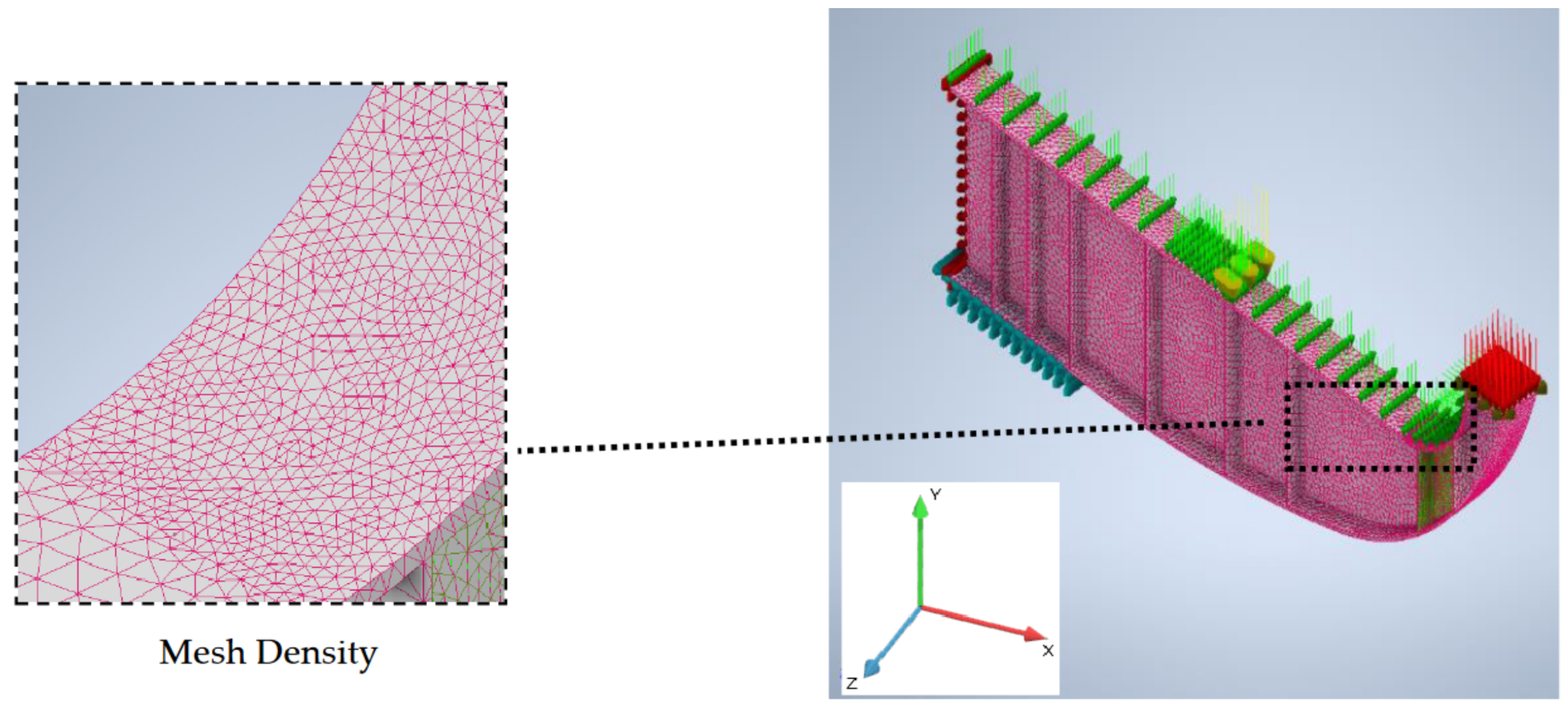
5.2.2. Meshing Description
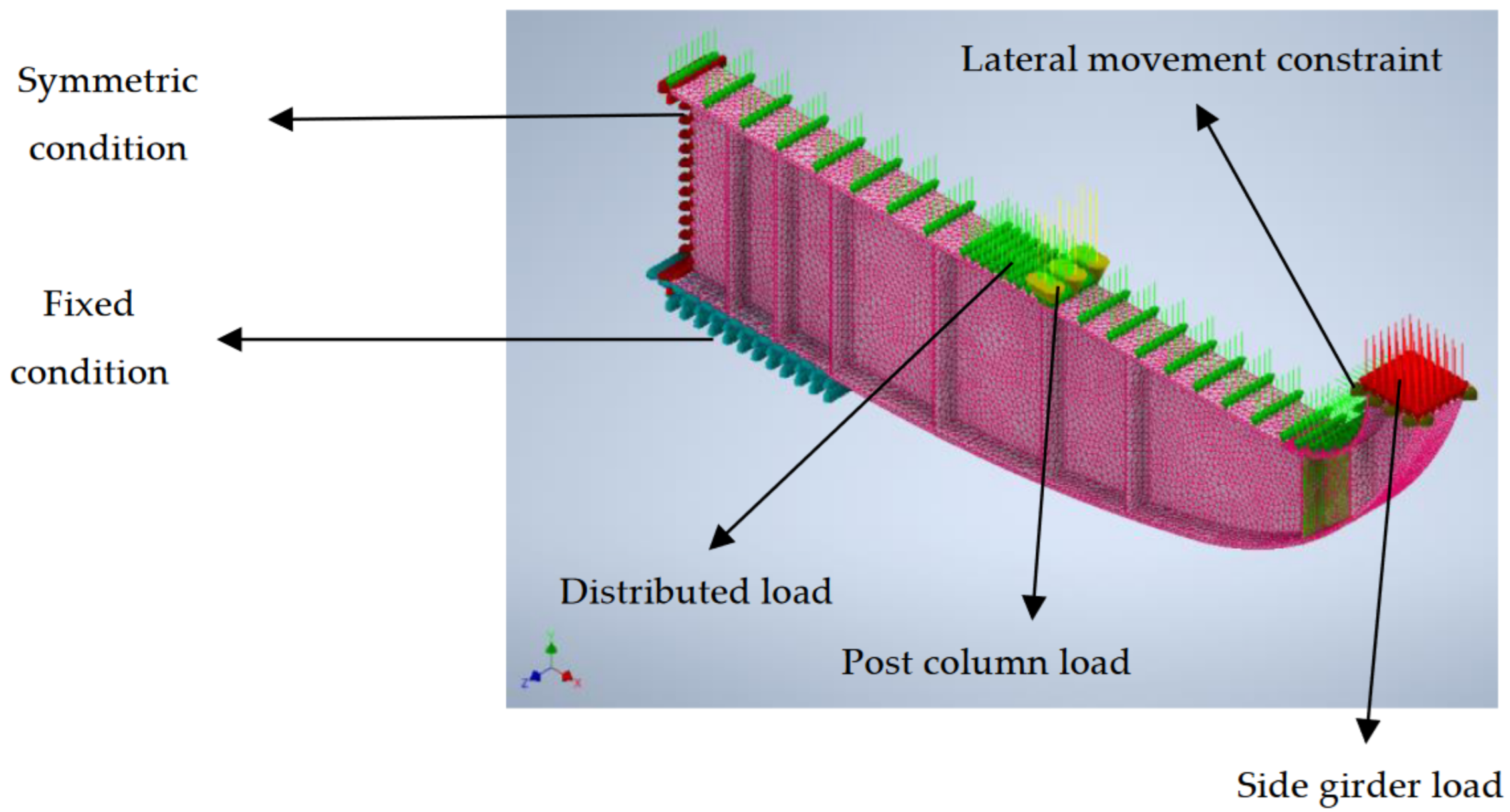
5.2.3. Supporting and Loading Conditions
5.2.4. Girder Steel Properties
5.2.5. Composite Material Definition and Assigning
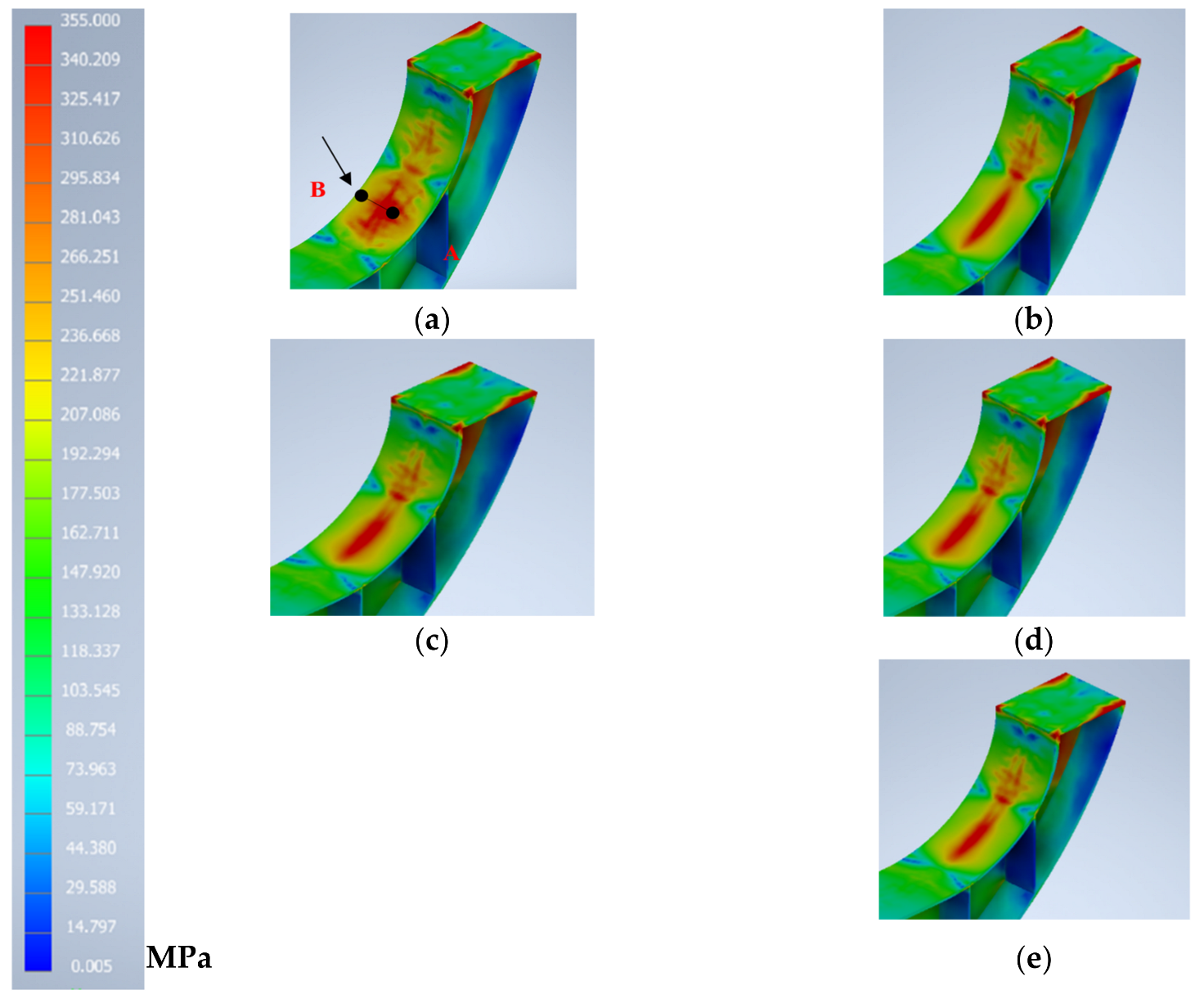
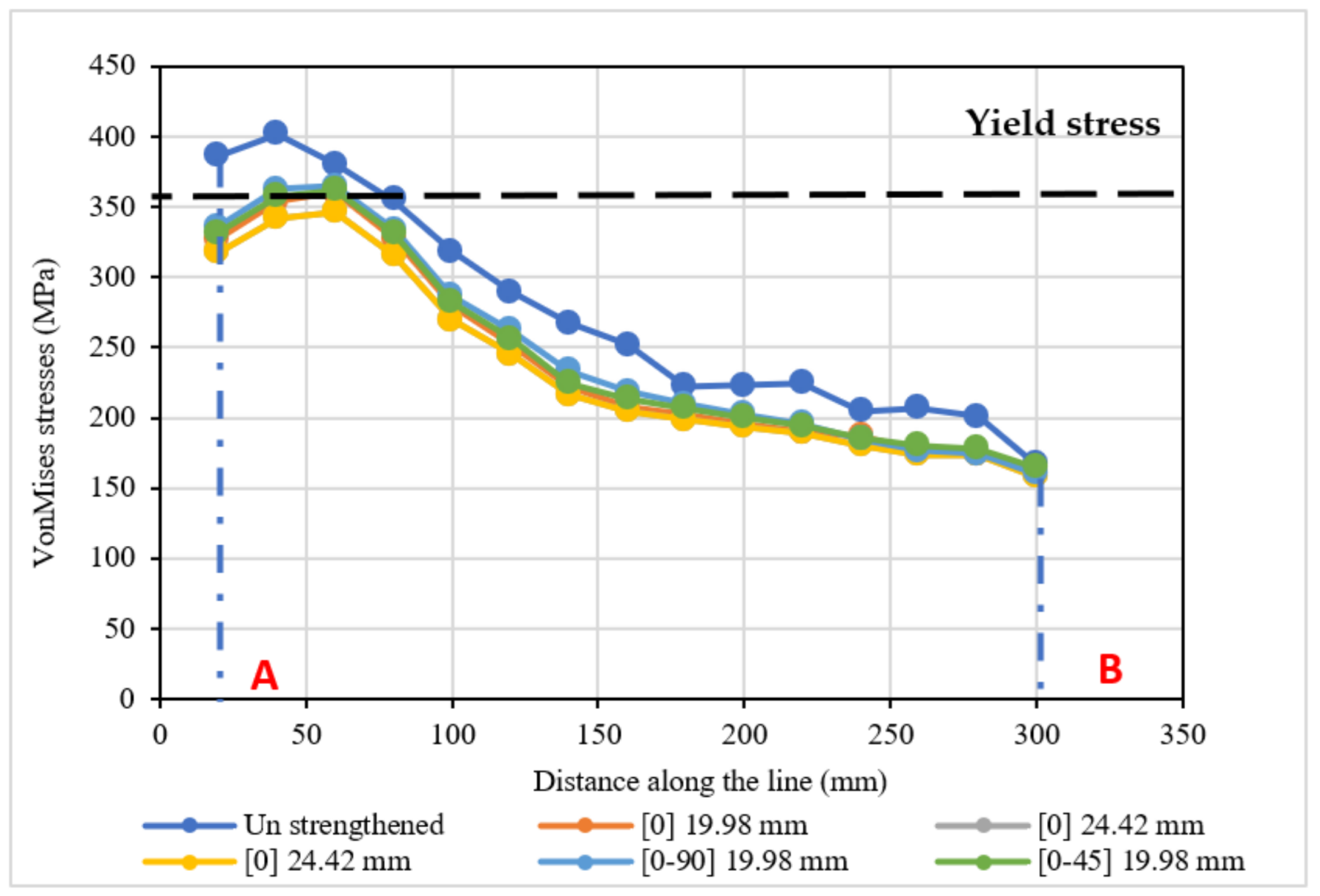
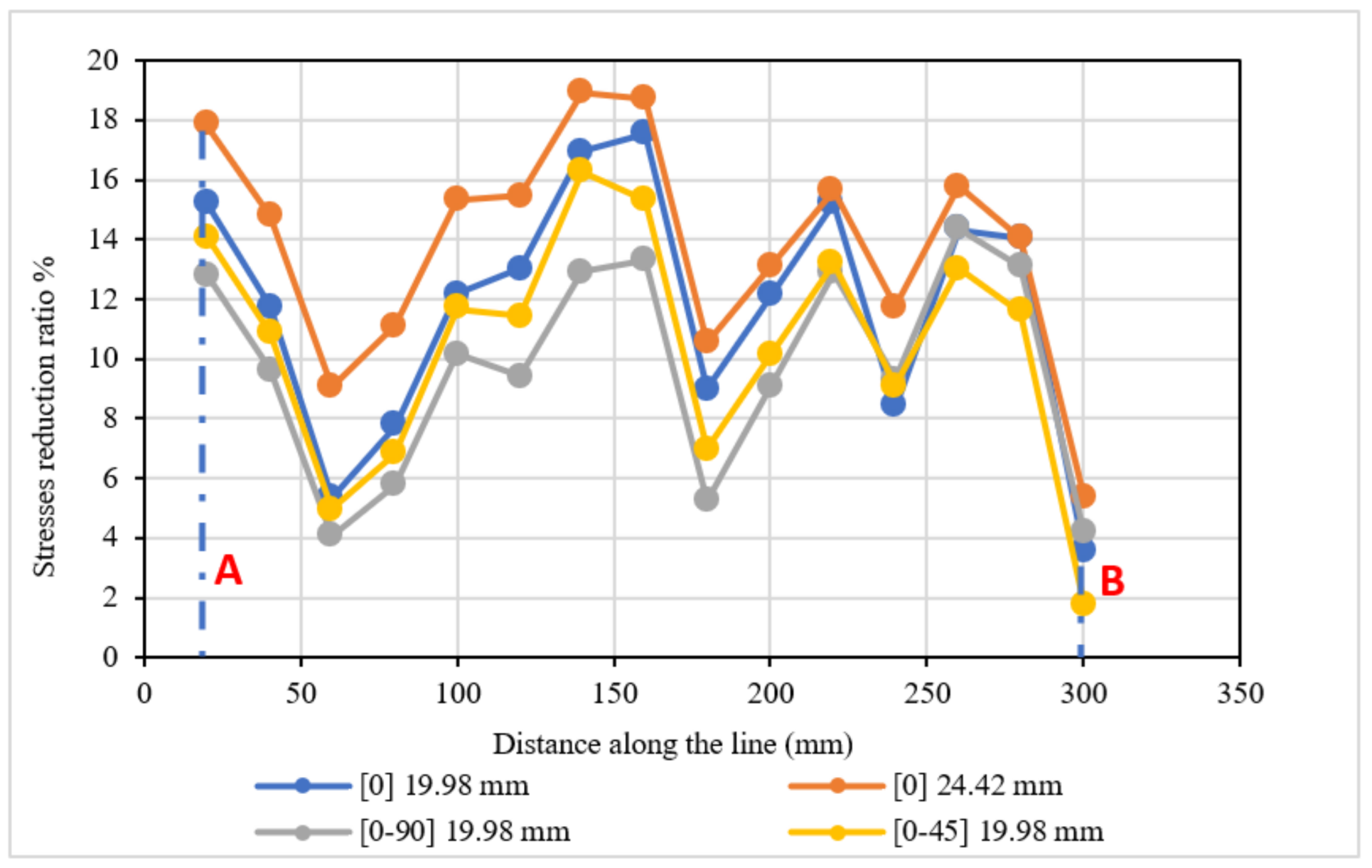
5.2.6. Results and Comparison
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kulkarni, A.; Gupta, L.M. Evaluation of Rotation Capacity of I-shaped Welded Steel Plate Girders. Arab. J. Sci. Eng. 2019, 44, 4533–4554. [Google Scholar] [CrossRef]
- Teng, J.; Yu, T.; Fernando, D. Strengthening of steel structures with fiber-reinforced polymer composites. J. Constr. Steel Res. 2012, 78, 131–143. [Google Scholar] [CrossRef]
- Sweedan, A.M.; Alhadid, M.M.; El-Sawy, K.M. Experimental study of the flexural response of steel beams strengthened with anchored hybrid composites. Thin-Walled Struct. 2016, 99, 1–11. [Google Scholar] [CrossRef]
- Kianmofrad, F.; Ghafoori, E.; Elyasi, M.; Motavalli, M.; Rahimian, M. Strengthening of metallic beams with different types of pre-stressed un-bonded retrofit systems. Compos. Struct. 2017, 159, 81–95. [Google Scholar] [CrossRef]
- Al-Mosawe, A.; Al-Mahaidi, R.; Zhao, X.-L. Bond behaviour between CFRP laminates and steel members under different loading rates. Compos. Struct. 2016, 148, 236–251. [Google Scholar] [CrossRef]
- Selvaraj, S.; Madhavan, M.; Dongre, S.U. Experimental studies on strength and stiffness enhancement in CFRP-strengthened structural steel channel sections under flexure. J. Compos. Constr. 2016, 20, 04016042. [Google Scholar] [CrossRef]
- Selvaraj, S.; Madhavan, M. CFRP strengthened steel beams: Improvement in failure modes and performance analysis. Structures 2017, 12, 120–131. [Google Scholar] [CrossRef]
- Siwowski, T.W.; Siwowska, P. Experimental study on CFRP-strengthened steel beams. Compos. Part B Eng. 2018, 149, 12–21. [Google Scholar] [CrossRef]
- Ghafoori, E.; Motavalli, M. Normal, high and ultra-high modulus carbon fiber-reinforced polymer laminates for bonded and un-bonded strengthening of steel beams. Mater. Des. 2015, 67, 232–243. [Google Scholar] [CrossRef]
- Elkhabeery, O.H.; Safar, S.S.; Mourad, S.A. Flexural strength of steel I-beams reinforced with CFRP sheets at tension flange. J. Constr. Steel Res. 2018, 148, 572–588. [Google Scholar] [CrossRef]
- Teng, J.; Fernando, D.; Yu, T. Finite element modelling of debonding failures in steel beams flexurally strengthened with CFRP laminates. Eng. Struct. 2015, 86, 213–224. [Google Scholar] [CrossRef]
- Narmashiri, K.; Sulong, N.R.; Jumaat, M.Z. Failure analysis and structural behavior of CFRP strengthened steel I-beams. Constr. Build. Mater. 2012, 30, 1–9. [Google Scholar] [CrossRef]
- Lam, C.C.; Zhang, Y.; Gu, J.; Cai, J. Reinforcing strategies of CFRP plate for coped steel beams against local buckling. Eng. Struct. 2023, 275, 115227. [Google Scholar] [CrossRef]
- Ghafoori, E.; Motavalli, M.; Nussbaumer, A.; Herwig, A.; Prinz, G.; Fontana, M. Design criterion for fatigue strengthening of riveted beams in a 120-year-old railway metallic bridge using pre-stressed CFRP plates. Compos. Part B Eng. 2015, 68, 1–13. [Google Scholar] [CrossRef]
- Aktas, M.; Sumer, Y.; Agcakoca, E.; Yaman, Z. Nonlinear Finite Element Modeling of Composite Bridge Girders Strengthened with HM-CFRP Laminates. Arab. J. Sci. Eng. 2016, 41, 3783–3791. [Google Scholar] [CrossRef]
- Zeng, J.-J.; Gao, W.-Y.; Liu, F. Interfacial behavior and debonding failures of full-scale CFRP-strengthened H-section steel beams. Compos. Struct. 2018, 201, 540–552. [Google Scholar] [CrossRef]
- El-Zohairy, A.; Salim, H.; Shaaban, H.; Mustafa, S.; El-Shihy, A. Experimental and FE parametric study on continuous steel-concrete composite beams strengthened with CFRP laminates. Constr. Build. Mater. 2017, 157, 885–898. [Google Scholar] [CrossRef]
- Attia, M.M.; Khalil, A.H.H.; Mohamed, G.N.; Samaan, M.F.; Katunský, D. Nonlinear Behavior of Bonded and Unbonded Two-Way Post-Tensioned Slabs Pre-Strengthened with CFRP Laminates. Buildings 2023, 13, 35. [Google Scholar] [CrossRef]
- Kadhim, M.M.A. Effect of CFRP plate length strengthening continuous steel beam. Constr. Build. Mater. 2012, 28, 648–652. [Google Scholar] [CrossRef]
- Vo, D.H.; Do, V.H.; Tran, Q.V.; Nguyen, M.H.; Hoang, T.L. Reliability Analysis of Steel Bridge Girders Strengthened with CFRP Considering the Debonding of Adhesive Layer. Designs 2022, 6, 126. [Google Scholar] [CrossRef]
- Russian, O.; Khan, S.; Belarbi, A.; Dawood, M. Effect of surface preparation technique on bond behaviour of CFRP-steel double-lap joints: Experimental and numerical studies. Compos. Struct. 2021, 255, 113048. [Google Scholar] [CrossRef]
- Tusnin, A.; Shchurov, E. The Structural Behaviour of Tension Steel Rods Strengthened with Carbon-Fiber-Reinforced Composite Materials. Buildings 2023, 13, 375. [Google Scholar] [CrossRef]
- Yang, M.; Kainuma, S.; Xie, J.; Liu, W.; Liu, Y. Bond behaviour between CFRP and corroded steel plate associations with surface treatments. Compos. Part B Eng. 2022, 246, 110280. [Google Scholar] [CrossRef]
- Wang, Z.; Xian, G.; Yue, Q. Finite element modeling of debonding failure in CFRP-strengthened steel beam using a ductile adhesive. Compos. Struct. 2023, 311, 116818. [Google Scholar] [CrossRef]
- Wang, Z.; Li, C.; Sui, L.; Xian, G. Effects of adhesive property and thickness on the bond performance between carbon fiber reinforced polymer laminate and steel. Thin-Walled Struct. 2021, 158, 107176. [Google Scholar] [CrossRef]
- Hosseini, A.; Ghafoori, E.; Al-Mahaidi, R.; Zhao, X.-L.; Motavalli, M. Strengthening of a 19th-century roadway metallic bridge using nonprestressed bonded and prestressed unbonded CFRP plates. Constr. Build. Mater. 2019, 209, 240–259. [Google Scholar] [CrossRef]










| CFRP Layer | tf (mm) | tm (mm) | tcf (mm) | (%) | (%) | Ex (MPa) | Ey (MPa) | Gxy (MPa) |
|---|---|---|---|---|---|---|---|---|
| UT70-30G | 0.167 | 0.592 | 1.6 | 30 | 70 | 71,870 | 5812.73 | 20,122.25 |
| Concourse Weight | |||
|---|---|---|---|
| Family and Type | Volume | Mass Weight | Count |
| B20C: 2FLPL200X25 WEB PL 1604X12 | 0.032 m3 | 252.10 kg | 1 |
| B20C: 200UB25.4 | 0.032 m3 | 252.10 kg | 1 |
| B21C: 2FLPL200X25 WEB PL 2073X12 | 0.075 m3 | 591.89 kg | 2 |
| B22C: 2FLPL200X25 WEB PL 2209X15 | 0.092 m3 | 725.10 kg | 2 |
| Steel floor beams at concourse level: B23C | 0.119 m3 | 934.52 kg | 4 |
| Steel floor beams at concourse level: B1C | 0.707 m3 | 5548.39 kg | 8 |
| Steel floor beams at concourse level: B2C | 0.057 m3 | 450.09 kg | 4 |
| Steel floor beams at concourse level: B3C | 0.773 m3 | 6070.25 kg | 14 |
| Steel floor beams at concourse level: B4C | 0.537 m3 | 4216.62 kg | 4 |
| Steel floor beams at concourse level: B9C | 0.085 m3 | 668.47 kg | 4 |
| Steel floor beams at concourse level: B12C | 0.354 m3 | 2782.48 kg | 2 |
| Steel floor beams at concourse level: B13C | 0.153 m3 | 1198.22 kg | 2 |
| Steel floor beams at concourse level: B14C | 0.455 m3 | 3569.83 kg | 14 |
| Steel floor beams at concourse level: B26C | 0.042 m3 | 326.43 kg | 2 |
| Total | 3.514 m3 | 27,586.48 kg | |
| CFRP Layer | tf (mm) | (%) | (%) | Ex (MPa) | Ey (MPa) | Gxy (MPa) | Layer Thickness |
|---|---|---|---|---|---|---|---|
| UT70-30G | 0.333 | 30 | 70 | 71,870 | 5812.73 | 20,122.25 | 1.11 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoud, M.A.M.A.; Nhut, P.V.; Matsumoto, Y. Practical Investigation on the Strengthening of the Built-Up Steel Main Girder of a Metro Station with Carbon-Fiber-Reinforced Polymer on the Inside Part of the Tensioned Flange. Buildings 2023, 13, 1753. https://doi.org/10.3390/buildings13071753
Mahmoud MAMA, Nhut PV, Matsumoto Y. Practical Investigation on the Strengthening of the Built-Up Steel Main Girder of a Metro Station with Carbon-Fiber-Reinforced Polymer on the Inside Part of the Tensioned Flange. Buildings. 2023; 13(7):1753. https://doi.org/10.3390/buildings13071753
Chicago/Turabian StyleMahmoud, Mohamed A. M. A., Phan Viet Nhut, and Yukihiro Matsumoto. 2023. "Practical Investigation on the Strengthening of the Built-Up Steel Main Girder of a Metro Station with Carbon-Fiber-Reinforced Polymer on the Inside Part of the Tensioned Flange" Buildings 13, no. 7: 1753. https://doi.org/10.3390/buildings13071753
APA StyleMahmoud, M. A. M. A., Nhut, P. V., & Matsumoto, Y. (2023). Practical Investigation on the Strengthening of the Built-Up Steel Main Girder of a Metro Station with Carbon-Fiber-Reinforced Polymer on the Inside Part of the Tensioned Flange. Buildings, 13(7), 1753. https://doi.org/10.3390/buildings13071753








