Predictive Model of the Temperature Regime of a Layer-by-Layer Concrete Mass
This paper outlines the development of a mathematical model aimed at predicting the temperature regime during the construction of a concrete pillar on a foundation mass. The study incorporates the impact of air temperature, considering three cases that are typical of the Northern Vietnam climatic zone.
To create a mathematical model, the factor-analysis approach was adopted, as described in [
32]. The investigation was performed through a full factorial experiment of type 2n, with the number of considered factors being n = 5. For this particular plan, the total number of experiments required was N = 2
5 = 32. The response function was obtained in the format of a regression equation, which is presented as follows [
32].
The proposed model takes into account the following factors (parameters) (
Table 3) by material:
- -
consumption of binder (kG/m3) used for the preparation of concrete (cement or cement with additives);
- -
maximum (total) heat release of 1 kg of binder used for the preparation of concrete (cement or cement with additives).
According to the technology of laying concrete:
- -
thickness and length of the laid layer of concrete during layered construction;
- -
temperature of the concrete mix being laid;
- -
laying technologies: rolled concrete and vibrated concrete.
By external temperature influences:
- -
air temperature for three variants in relation to the climatic features of North Vietnam (from 26.5 °C for summer conditions to 17 °C and 5 °C for winter and mountainous regions).
The maximum temperature values observed within the inner region of the concrete mass were used as the response metric. The temperature calculations were executed based on the experimental plan, aided by the Midas Civil software package, which allowed for a determination of the corresponding response values.
Figure 2 illustrates the temperature distribution within the considered array while calculating one of the cases.
As a result of processing the results of the factorial experiment, response regression equations were obtained for three variants of the average annual air temperature when laying according to the technology of rolled concrete (
Table 4) and vibrated concrete (
Table 5).
Figure 2 shows the results of the temperature calculation of the concrete pillar being erected. Since an array of considerable length (from 10 to 40 m) is considered, it can be argued that the temperature inside it is the maximum and close to the conditions of the adiabatic process. The outflow of the released heat occurs through the surfaces of the array. A similar picture will take place in the case of the construction of a large array of another geometric shape (for example, a massive gravity dam). This makes it possible to use the resulting model for large arrays with a geometry different from the column.
If the concreting process is considered at an air temperature different from the values considered, but located in the interval between them, the interpolation method can be used. For example, if the temperature value is 20 °C, that is, it is in the range between 26.5 and 17 ° C, the maximum temperature in the concrete array is determined by the known values of the factors for these boundary temperature values; then, the value at 20 ° C is determined by interpolation. Since the temperature-change interval is insignificant, this technique gives values close to the actual ones. This has been verified by verification calculations.
The consumption of cement (X1), the maximum heat release of cement (X3), and the temperature of the laid concrete (X5) have been identified as the most crucial factors. The impact of factors X2 and X4 on the maximum temperature is moderate when compared to X1, X3, and X5. Their cumulative effect on the maximum temperature value can be approximately estimated between (1.5–2.9) °C.
Unlike the rolled concrete variant (
Table 4), the thickness of the laid layer (X
2) has a greater impact on the maximum temperature value for vibrated concrete (
Table 5).
Nomograms have been developed for a rapid evaluation of the maximum temperature in the center of concrete masses. A nomogram for the summer variant of rolling concrete placement is presented in
Figure 3. These nomograms can assist in determining the necessary values of the factors that influence the maximum temperature of the concrete based on the desired maximum temperature.
To model the thermally stressed state of the concrete massif, numerical experiments were conducted using factor analysis for both rolled and vibrated concrete variants, with accepted factors and their corresponding intervals outlined in
Table 2. The response evaluated was the maximum stress in the inner zone of the concrete mass.
Table 6 and
Table 7 present the regression equations that were obtained from the factorial experiments.
As can be seen from the presented dependencies (
Table 4 and
Table 5), the most significant factors are cement consumption (factor X
1) and the maximum heat release of cement (factor X
3). To a lesser extent, the length of the concreting block (X
4), the temperature of the concrete mixture to be laid (X
5), and the thickness of the concrete layer to be laid (X
2) affect it.
Under the given construction conditions within a certain time interval, the maximum tensile stresses are observed near the concrete–base contact in its lower layer. These stresses can appear either at the center of the mass or at another location, depending on the variant considered. The time when the maximum tensile stresses occur ranges widely, from 504 to 1360 h (21 to 57 days) after starting to lay the first layer of the concrete mass.
The regression equations obtained enabled the construction of nomograms that can be used to determine the maximum tensile stress given the accepted values of the factors.
Figure 4 displays the nomogram for rolled concrete in the case where the external temperature is 26.5 °C.
The usage of class concrete B5; B7.5; B10; B12.5; B15; B17.5; and B20 is mandated by Russian standards when preparing a concrete mixture using rolled concrete technology [
11]. Hydrotechnical construction recommendations in Vietnam suggest the use of class B10–B20 concrete (M150–M250) for rolled concrete dams [
13].
The standards specify that, for concrete classes falling within this range, the maximum permitted compressive strength for limit states of the second group is between (7.5–14.9) MPa. Additionally, the maximum allowed tensile strength for limit states of the second group is within the range of (0.78–1.38) MPa.
The nomogram’s binary fields of (X
4,
σmax) demarcate the allowable maximum tensile stress values for rolled concrete classes B10–B20, as detailed in [
11].
Figure 3 highlights the corresponding areas (denoted by different shades).
Area 1 of the highlighted regions guarantees maximum tensile stresses lower than the allowed limit for the lowest class of concrete, B10 (0.78 MPa), thus preventing any occurrence of cracking.
Area 2 marks regions exhibiting maximum tensile stresses greater than the allowable limit for lower class concrete B10 (0.78 MPa), though still falling under the limit for the highest class B20 (1.38 MPa). Instances of temperature cracks may arise in this region if the value of maximum tensile stress, as indicated on the nomogram, exceeds the allowable value for the given concrete class.
Area 3 denotes regions indicating maximum tensile stresses that surpass the allowable limit for the highest class of concrete, B20 (1.38 MPa), thereby causing cracks in the concrete.
For comparison, it is possible to bring the conformity of concrete grades according to the Russian standard [
13] and the European standard EN 206-1. Russian concrete grades B10, B15, and B20 correspond to European grades C8/10, C12/15, and C16/20. The numbers in the designations, according to the European standard, indicate the compressive strength of concrete in MPa when testing concrete samples of a cylindrical shape (diameter 150 and height 300 mm) and a cube shape (with sides 150 mm). The numbers in the designations of Russian concrete brands correspond to the strength of a cubic-shaped sample (also with a side of 150 mm).
The resulting model makes it possible to estimate with greater accuracy not only the temperature regime but also the thermally stressed state of the layer-by-layer concrete array. The influence of five factors is considered, whereas, in all previous models, it did not exceed four. The forecast model is made in relation to the climatic conditions of North Vietnam, or close to those. In addition, two possible options for laying concrete are considered: rolled and vibrated, and a different rate of construction of the array in height. All this allows us to talk about the advantages of the proposed model as a whole and in relation to the conditions considered.
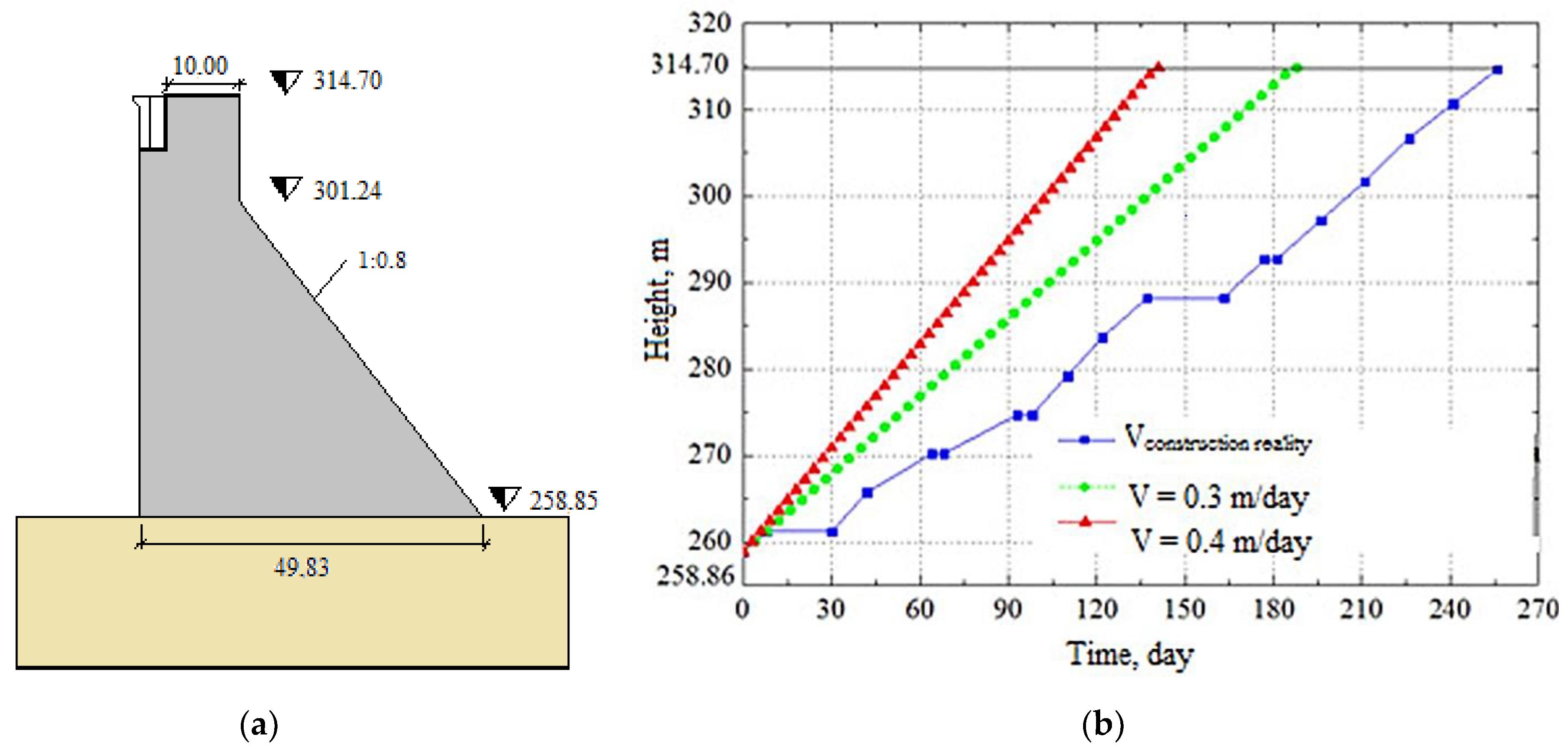
A developed mathematical model was employed to predict the temperature regime and thermal stress state of the gravity concrete dam constructed from rolled concrete in Ban Lai in Vietnam. The dam stands 56 m tall and was erected in the northern part of Vietnam, with a climate characterized by air-temperature fluctuations of 15.0 °C in winter to 26.5 °C in summer. The concrete laying commenced on the 10th of March, with the initial temperature of the laid concrete at 23 °C and the base temperature at 20 °C. Two construction options were considered, with the first featuring a speed of 0.3 m/day (option 1) and the second at 0.4 m/day (option 2).
Figure 5 depicts the cross profile of the dam and the dam erection height schedules of the three options, including the actual construction schedule implemented in practice (option 3). For option 1, the time step between laying adjacent layers of concrete was set at 24 h, while for option 2, it was 18 h with a concrete layer thickness of 0.3 m.
A mixture of Portland cement and pozzolan (85 kg and 45 kg per 1 m3 of rolled concrete, respectively) was used as a binder for the concrete of the dam. The addition of pozzolan improves the properties of hydraulic concrete with a grade of M150.
According to the results of experiments conducted in the laboratory of the Institute of Hydraulic Engineering Materials (Vietnam), changes in the compressive and tensile strength of concrete, as well as the modulus of elasticity (
Table 8), were determined, according to which curves of changes in these values over time were constructed. The obtained curves were used in calculations. Standard samples of cylindrical shape (diameter and height of 150 mm each) and cubic (with sides of 150 mm) were tested. Experimental studies in the calorimeter under adiabatic conditions also obtained the heat release curve of the binder (a mixture of cement and pozzolan) during hydration in Vietnam, shown in
Figure 6.
The model was used for a preliminary assessment of the temperature regime of the dam under construction. Using the mathematical model generated, a preliminary estimation was conducted on the highest temperature within the concrete mass as well as the maximum tensile stresses that can be found in the contact region of the under-construction dam. Employing the regression equations obtained from
Table 4 and
Table 5, along with the established nomograms from
Figure 3 and
Figure 4, the highest temperature projected to be reached by the concrete mass was 39.8 °C while the maximum tensile stresses were set to be 1.2 MPa.
A numerical model utilizing the Midas Civil software package was designed for the Ban Lai dam to analyze the temperature patterns and thermal stress of the structure during the construction stage and the operational phase. Two construction options based on the height of the structure were considered. The maximum temperature and tensile stresses achieved using the numerical solution method are exhibited in
Table 9.
It is notable that the predicted maximum temperature value (39.8 °C) is in good agreement with the result derived from the numerical model (40.04 °C). Similarly, the maximum tensile stress value aligns well with predicted and numerical solution methods, with 1.20 MPa and 1.17 MPa, respectively. It can be observed that elevating the construction speed of the dam from 0.3 m/day to 0.4 m/day results in a temperature hike inside the mass up to 44 °C, while the maximum tensile stresses increase from 1.17 MPa to 1.48 MPa.
As a result, the intensity of the dam construction at a height of 0.3 m/day was recommended. This was implemented in practice (the slope of the construction schedule at such a speed has the same angle of inclination as the real graph in
Figure 2b).
The outcomes of mathematical modeling were contrasted against the findings of natural observations. During the dam construction process, field observations to capture its temperature were done utilizing control and measuring equipment. Analyzing the results from the actual temperature measurements of the structure made it possible to evaluate the credibility of the mathematical model’s predictions.
Option 1 was deemed the most favorable for the structure’s temperature regime according to the results of mathematical modeling. However, the practical construction scheme varies from the plan for option 1 (shown in
Figure 5). Halts during concreting and some deviations from the designated speed of construction were caused by issues like the construction of the grouting gallery, bad weather, and lack of funds. Although the changes increased the construction period, the intensity of concreting remained close to the theoretical value of V = 0.3 m/day during concrete placement, as seen in
Figure 5. Using the actual construction schedule illustrated in
Figure 5 and the mathematical model generated, assessments of the structure’s thermal state and temperature were also carried out.
Table 8 contains a comparison of temperature sensor readings at the center of corresponding structural segments, recorded at the same elevation during construction, with outcomes obtained from the mathematical model.
The evaluation of the thermally stressed state of the construction heap generated stress-distribution data. Maximum tensile stresses were identified at the interface near the dam’s lower area. Using the figures from numerical calculations, a value of 1.14 MPa was arrived at (given the vertical construction speed of V = 0.3 m/day).
The temperature-regime simulation data for the construction timeframe, up to the elevations provided in
Table 10, is displayed in
Figure 7.
Table 10 and
Figure 7 show the results for the four selected moments of construction in time and height of the dam. Full-scale observations and calculations using a mathematical model make it possible for such an analysis in almost all sections where control and measuring equipment is installed.
The results obtained demonstrate a close correlation between the numerical simulation and the figures gathered from field measurements. The maximum deviation recorded was 7.6%, while the minimum difference was 0.1% (refer to
Table 10). The numerical model, with its mathematical simulation grounded on numerical solutions, delineates the temperature state of the dam precisely during construction. It is, therefore, a useful tool for forecasting and can be employed in tackling analogous challenges.
An appraisal was conducted to determine the probability of cracking of the concrete mass of the gravity dam. This evaluation leveraged the thermally stressed state and prognostic model of the temperature regime to quantify the likelihood of thermal cracks forming.
- (a)
As per the temperature criterion outlined by the Russian and Vietnamese standards, the temperature differential, ΔT, between the center and surface of the concrete mass should not exceed 20 °C. The dam body concretization took 255 days, as displayed in the construction schedule depicted in
Figure 5b, with a timeframe spanning between March 10 and November 20. The maximum temperature value recorded at the center of the massif was approximately 40 °C, based on the predictive model. Thus, the temperature differential requirement will be unmet if the structure’s surface temperature is below 20 °C. This can only be fulfilled in March and November, in accordance with the variation of air temperature in the construction zone, as indicated by
Table 11. To preclude the occurrence of cracks in this period, it is advisable to safeguard the outer surfaces of the massif with a covering material like PVC membrane;
- (b)
Concerning the maximum tensile stresses, current normative literature on the design of concrete and reinforced concrete structures [
11] specifies that the criterion for cracking is formulated as follows:
Based on stress calculations conducted on the 45th day, specifically at node No.1, maximum tensile stresses were recorded in the dam’s contact zone near the bottom surface, with a value of σ(τ) = σ(45) = 1.14 MPa. The relevant parameters related to this calculation were as follows: modulus of elasticity: E(τ) = E(45) = 240,000 kg/cm2 = 24 × 103 MPa and working conditions coefficients: γb3 = 1.2; γb6 = 1.15. The value for ultimate elongation was εlim(τ) = φ(45) εlim = 3.99 × 10−5.
The verification of the structure’s crack-resistance conditions, accounting for the coefficients, is conducted through the use of Formula (13).
The allowable tensile stress value obtained from the analysis is greater than the stress value of 1.17 MPa calculated from the stress numerical model. Consequently, it can be inferred that the dam is adequately resistant to cracking within the near-contact zone.
In addition to the Banmong Dam, the forecast model was used for the Ban Lai Dam, also being built in Northern Vietnam.