Optimal Design of Crossbeam Stiffness Factor in Bridge Towers Using a Reliability-Based Approach
Abstract
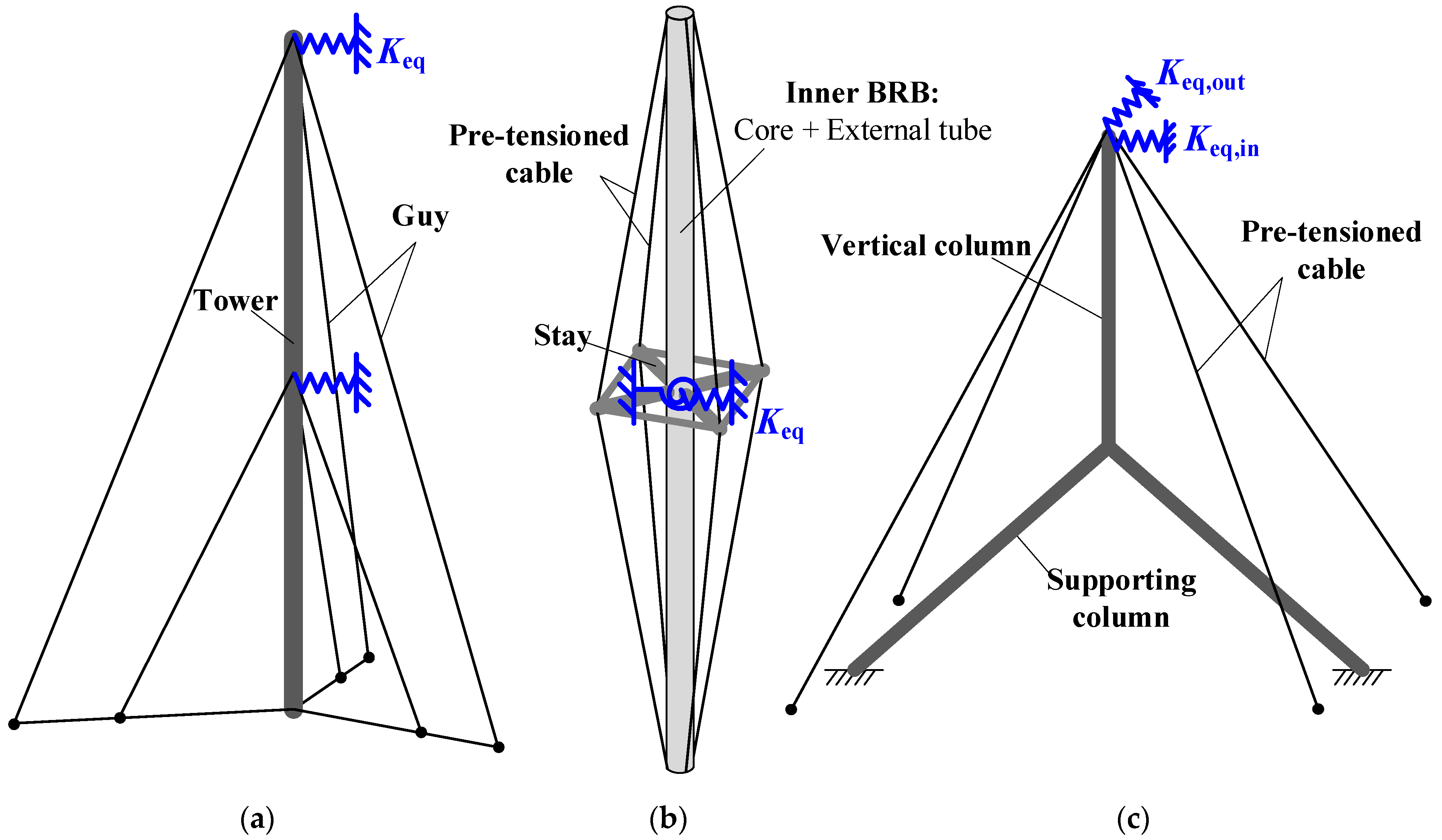
:1. Introduction
2. Problem Definition
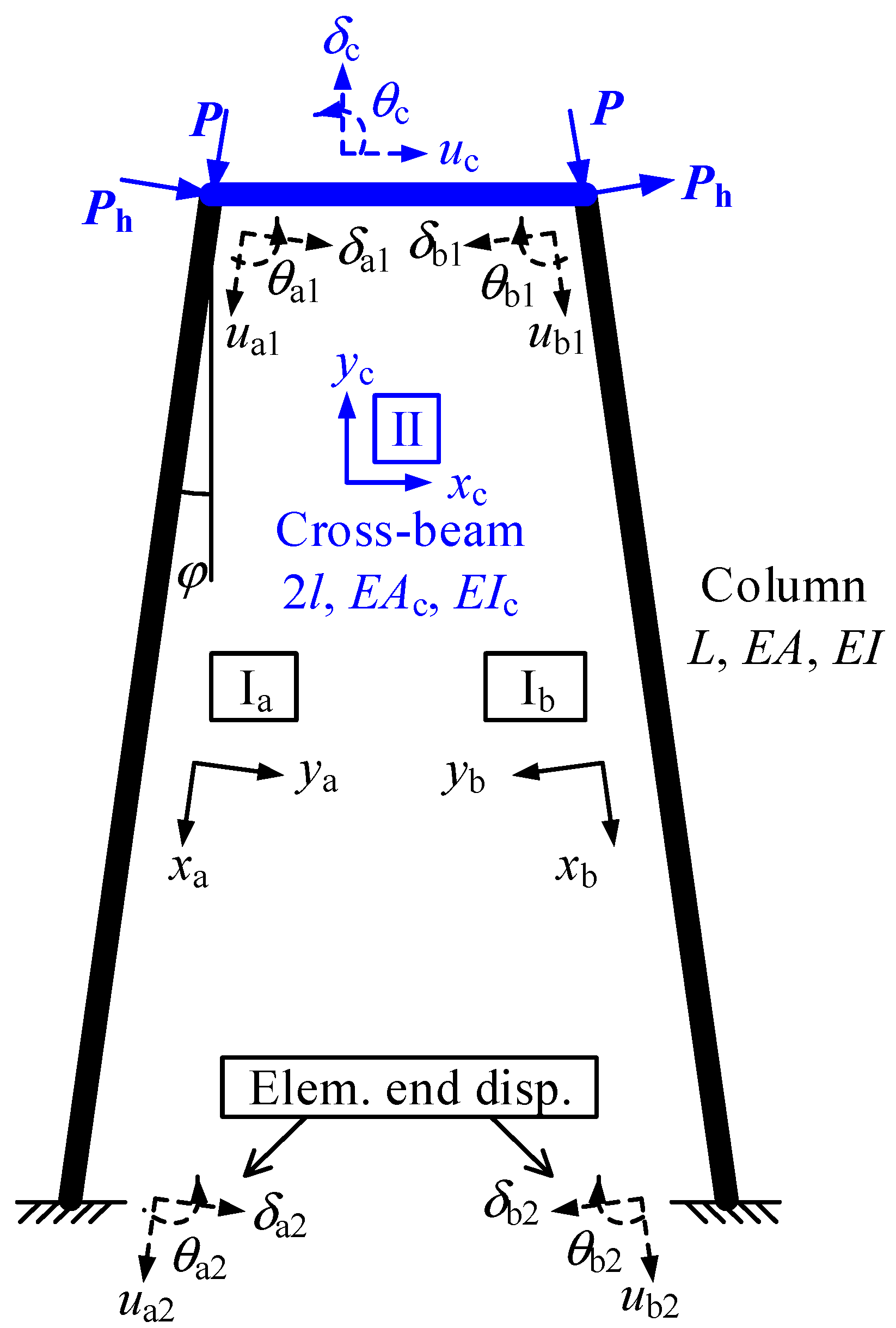
3. Lateral Stiffness of Bridge Tower Considering Axial Force Effect
3.1. Method for Analyzing Behaviors of Beam-Column Systems Considering Axial Force Effect
3.2. Lateral Stiffness of Bridge Tower
4. Lateral Stiffness of Bridge Tower with Varying Crossbeam Stiffnesses
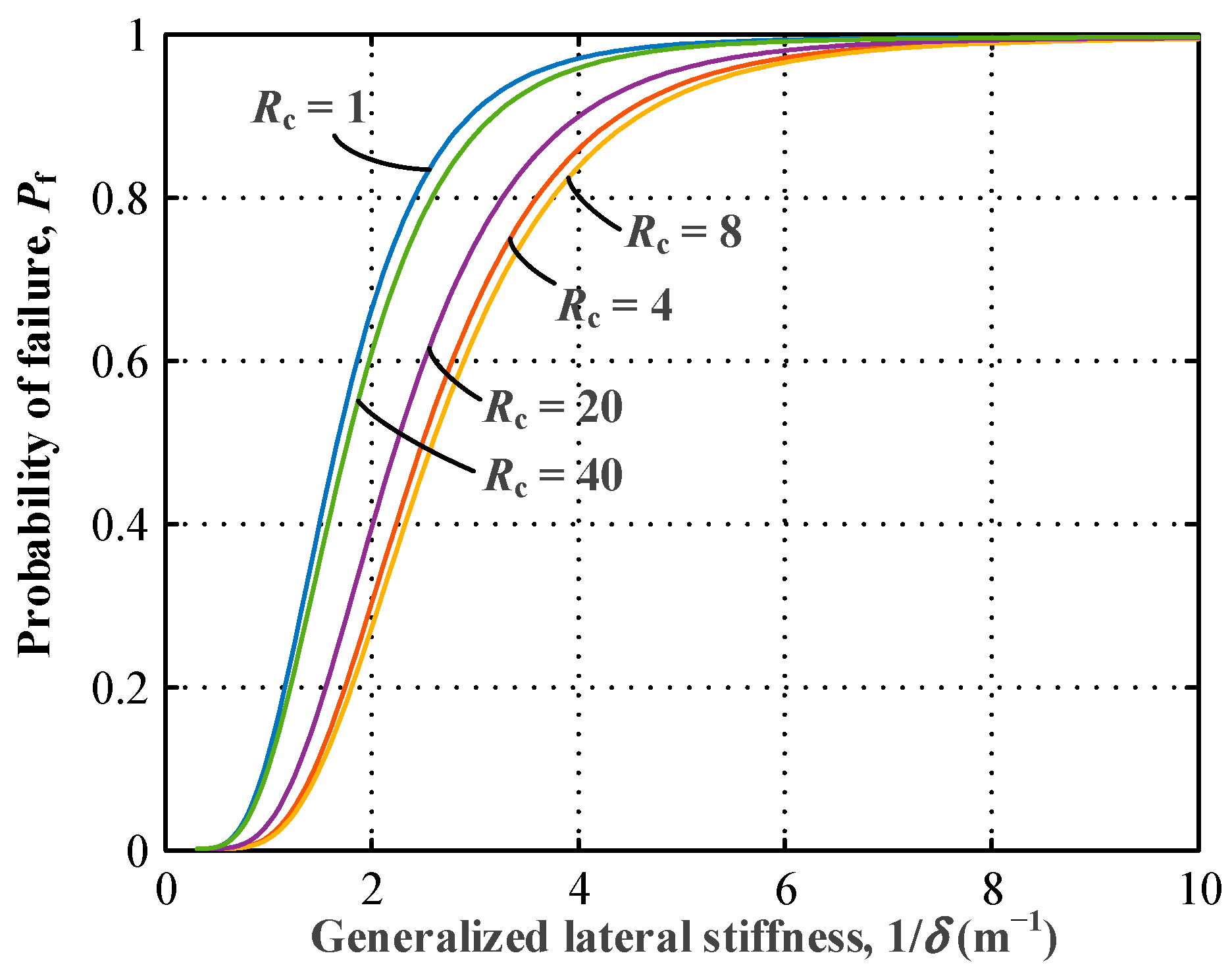
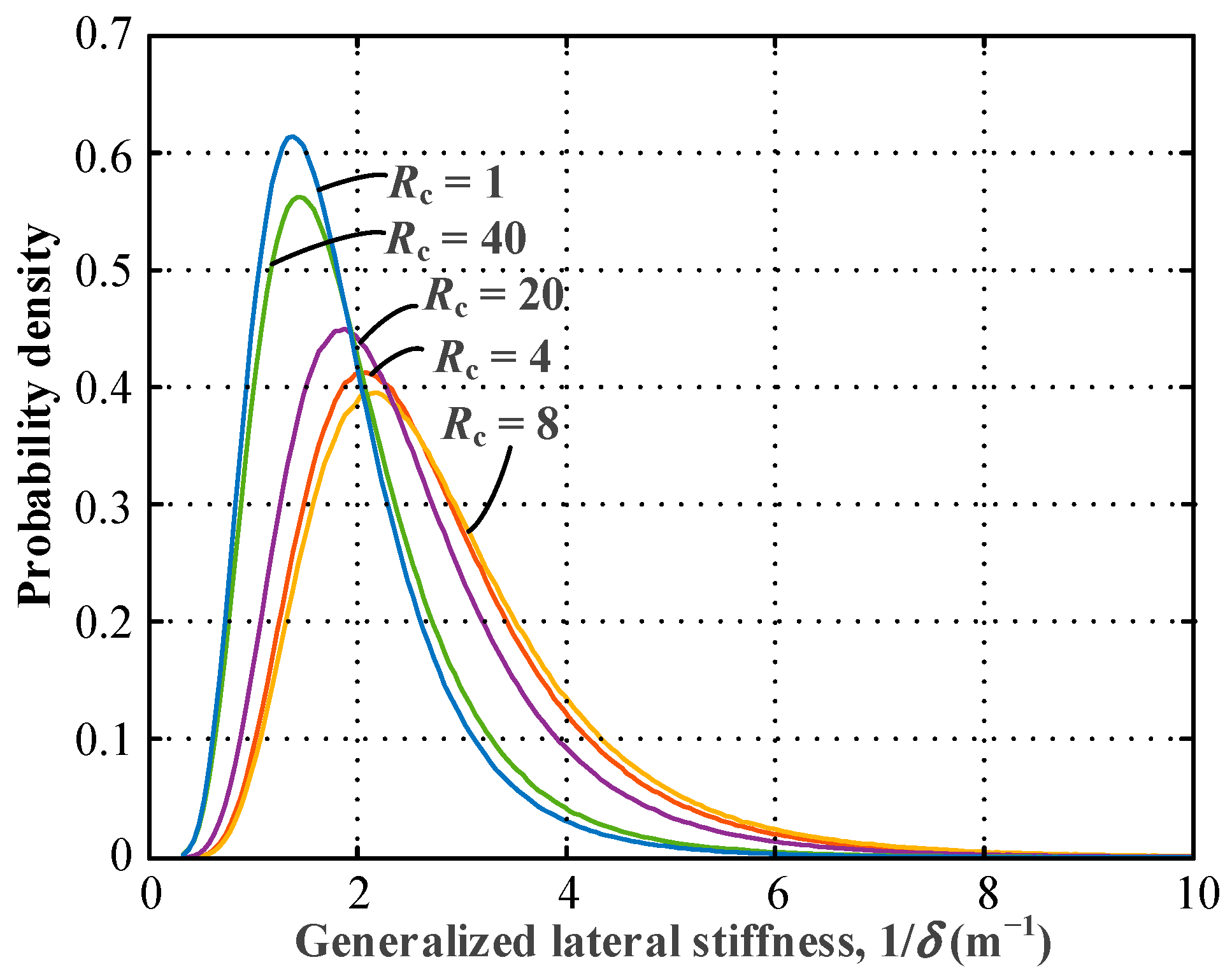
4.1. Uncertainty of Lateral Stiffness of the Bridge Tower
4.2. Bridge Tower with Medium Height-to-Width Ratio (L/l)
4.3. Bridge Tower with Large Height-to-Width Ratio (L/l)
5. Optimal Design Recommendation on Crossbeam Stiffness Factor
6. Conclusions
- The second-order matrix stiffness method using the exact second-order element stiffness matrix with stability functions facilitates the analysis of axially-loaded beam–column systems significantly. Closed-form exact solutions can be obtained after formulating the global structural stiffness matrix.
- The crossbeam could serve as a special bracing of the columns, thereby significantly enhancing the lateral stiffness of the bridge tower. Therefore, a key parameter in the economical design of bridge towers is the crossbeam stiffness factor Rc, which reflects the relative stiffness between the crossbeam and the tower column.
- An optimal crossbeam stiffness factor could be obtained for the bridge tower to exhibit the best lateral stiffness behavior. The optimal crossbeam stiffness factor in bridge tower designs is related to the height-to-width ratio of the bridge tower. For a medium height-to-width ratio of the bridge tower (e.g., L/l = 8/3), it is recommended to use a crossbeam stiffness factor Rc in the range of 4~20, and the optimal Rc of about 8. For a relatively large height-to-width ratio of the bridge tower (e.g., L/l = 16/3), it is recommended to use a crossbeam stiffness factor Rc in the range of 10~40, with the optimal Rc being about 20.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tong, J.Z.; Guo, Y.L.; Pan, W.H.; Shen, M.H.; Zhou, P. Global buckling prevention of reduced-core-length buckling-restrained braces: Theoretical and numerical investigations. Bull. Earthq. Eng. 2020, 18, 1777–1804. [Google Scholar] [CrossRef]
- Tong, J.Z.; Guo, Y.L.; Pan, W.H.; Zhou, P.; Wang, M.Z. Hysteretic performance of inverted-V patterned BRB systems considering vertical pre-compression effects. Bull. Earthq. Eng. 2019, 17, 3197–3232. [Google Scholar] [CrossRef]
- Pan, W.H.; Wang, C.M.; Zhang, H. Matrix method for buckling analysis of frames based on Hencky bar-chain model. Int. J. Struct. Stab. Dyn. 2019, 19, 1950093. [Google Scholar] [CrossRef]
- Yao, S.S.; Peng, B.; Wang, L.Y.; Chen, H.D. Structural performance and reasonable cross-ratio of cross-cable multi-tower cable-stayed bridges. Buildings 2022, 12, 764. [Google Scholar] [CrossRef]
- Gao, H.Y.; Zhang, K.; Wu, X.Y.; Liu, H.J.; Zhang, L.Z. Application of BRB to seismic mitigation of steel truss arch bridge subjected to near-fault ground motions. Buildings 2022, 12, 2147. [Google Scholar] [CrossRef]
- Pan, W.H.; Eatherton, M.R.; Tao, M.X.; Yang, Y.; Nie, X. Design of single-level guyed towers considering interrelationship between bracing strength and rigidity requirements. J. Struct. Eng. 2017, 143, 04017128. [Google Scholar] [CrossRef]
- Chajes, A.; Chen, W.S. Stability of guyed towers. J. Struct. Div. 1979, 105, 163–174. [Google Scholar] [CrossRef]
- Irvine, H.M.; O’Sullivan, M.J. Elastic stability of simple guyed towers. Appl. Ocean Res. 1979, 1, 203–207. [Google Scholar] [CrossRef]
- Gantes, C.; Khoury, R.; Connor, J.J.; Pouangare, C. Modeling, loading, and preliminary design considerations for tall guyed towers. Comput. Struct. 1993, 49, 797–805. [Google Scholar] [CrossRef]
- Guo, Y.L.; Fu, P.P.; Zhou, P.; Tong, J.Z. Elastic buckling and load resistance of a single cross-arm pre-tensioned cable stayed buckling-restrained brace. Eng. Struct. 2016, 126, 516–530. [Google Scholar] [CrossRef]
- Guo, Y.L.; Zhou, P.; Bradford, M.A.; Pi, Y.L.; Tong, J.Z.; Fu, P.P. Theoretical and numerical studies of elastic buckling and load resistance of double cross-arm pre-tensioned cable stayed buckling-restrained braces. Eng. Struct. 2017, 153, 674–699. [Google Scholar] [CrossRef]
- Pan, W.H.; Eatherton, M.R.; Nie, X.; Fan, J.S. Design of pre-tensioned cable stayed buckling-restrained brace considering interrelationship between bracing strength and stiffness requirements. J. Struct. Eng. 2018, 144, 04018169. [Google Scholar] [CrossRef]
- Pan, W.H.; Eatherton, M.R.; Nie, X.; Fan, J.S. Stability and adequate bracing design of pretensioned cable-braced inverted-Y-shaped Ferris wheel support system using matrix structural second-order analysis approach. J. Struct. Eng. 2018, 144, 04018194. [Google Scholar] [CrossRef]
- Ziemian, R.D. (Ed.) Guide to Stability Design Criteria for Metal Structures, 6th ed.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Pan, W.H.; Wang, J.J.; Nie, X.; Tong, J.Z. Adequately rigid cross beams for bridge tower designs. J. Bridge Eng. 2019, 24, 04019120. [Google Scholar] [CrossRef]
- Xu, F.; Pan, W.H.; Chan, T.M.; Sheehan, T.; Gardner, L. Fracture prediction for square hollow section braces under extremely low cycle fatigue. Thin. Wall. Struct. 2022, 171, 108716. [Google Scholar] [CrossRef]
- Wang, C.M.; Pan, W.H.; Zhang, J.Q. Optimal design of triangular arches against buckling. J. Eng. Mech. 2020, 146, 04020059. [Google Scholar] [CrossRef]
- Hu, Z.P.; Pan, W.H.; Tong, J.Z. Exact solutions for buckling and second-order effect of shear deformable Timoshenko beam–columns based on matrix structural analysis. Appl. Sci. 2019, 9, 3814. [Google Scholar] [CrossRef]
- Wang, C.M.; Zhang, H.; Challamel, N.; Pan, W.H. Hencky Bar-Chain/Net for Structural Analysis; World Scientific: Singapore, 2020. [Google Scholar] [CrossRef]
- Pan, W.H.; Wang, C.M.; Zhang, H. Hencky bar-chain model for buckling analysis of non-symmetric portal frames. Eng. Struct. 2019, 182, 391–402. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.M.; Challamel, N.; Pan, W.H. Calibration of Eringen’s small length scale coefficient for buckling circular and annular plates via Hencky bar-net model. Appl. Math. Model. 2020, 78, 399–417. [Google Scholar] [CrossRef]
- McGuire, W.; Gallagher, R.H.; Ziemian, R.D. Matrix Structural Analysis, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Przemieniecki, J.S. Theory of Matrix Structural Analysis; McGraw-Hill Book Company: New York, NY, USA, 1968. [Google Scholar]
- Yuan, S. Programming Structural Mechanics, 2nd ed.; Higher Education Press: Beijing, China, 2008. [Google Scholar]
- Ekhande, S.G.; Selvappalam, M.; Madugula, M.K.S. Stability functions for three-dimensional beam–columns. J. Struct. Eng. 1989, 115, 467–479. [Google Scholar] [CrossRef]
- Munoz, H.R. Elastic Second-Order Computer Analysis of Beam–Columns and Frames. Master’s Thesis, University of Texas at Austin, Austin, TX, USA, 1991. [Google Scholar]
- Aristizabal-Ochoa, J.D. Elastic stability of beam–columns with flexural connections under various conservative end axial forces. J. Struct. Eng. 1997, 123, 1194–1200. [Google Scholar] [CrossRef]
- Yang, Y.B.; McGuire, W. Stiffness matrix for geometric nonlinear analysis. J. Struct. Eng. 1986, 112, 853–877. [Google Scholar] [CrossRef]
- Zhou, J.S.; Pan, W.H.; Zhang, H.; Wang, C.M. Modeling joints with multiple members in Hencky bar-chain model for buckling analysis of frames. Int. J. Mech. Sci. 2019, 164, 105165. [Google Scholar] [CrossRef]
- Ling, M.X.; Zhou, H.; Chen, L.G. Dynamic stiffness matrix with Timoshenko beam theory and linear frequency solution for use in compliant mechanisms. J. Mech. Robot. 2023, 15, 061002. [Google Scholar] [CrossRef]
- Hibbeler, R.C. Structural Analysis, 7th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Long, Y.Q.; Bao, S.H.; Kuang, W.Q.; Yuan, S. Structural Mechanics, 2nd ed.; Higher Education Press: Beijing, China, 2006. [Google Scholar]
- AISC. AISC 303-10 Code of Standard Practice for Steel Buildings and Bridges; AISC: Chicago, IL, USA, 2010. [Google Scholar]
- Ellingwood, B.; MacGregor, J.G.; Galambos, T.V.; Cornell, C.A. Probability based load criteria: Load factors and load combinations. J. Struct. Div. 1982, 108, 978–997. [Google Scholar] [CrossRef]
- Bartlett, F.M.; Dexter, R.J.; Graeser, M.D.; Jelinek, J.J.; Schmidt, B.J.; Galambos, T.V. Updating standard shape material properties database for design and reliability. Eng. J. AISC 2003, 40, 2–14. [Google Scholar]
- Melchers, R.E. Structural Reliability Analysis and Prediction; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
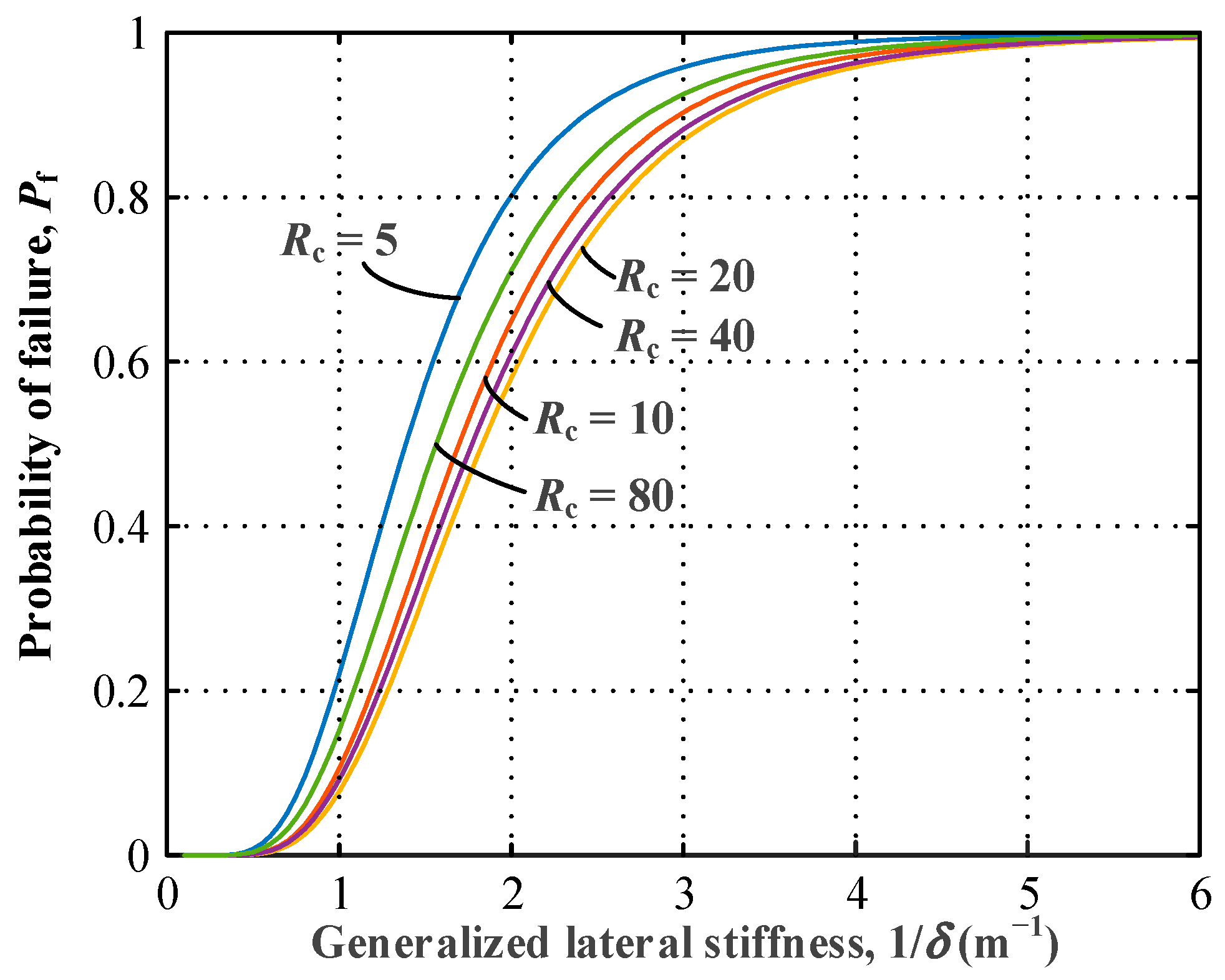
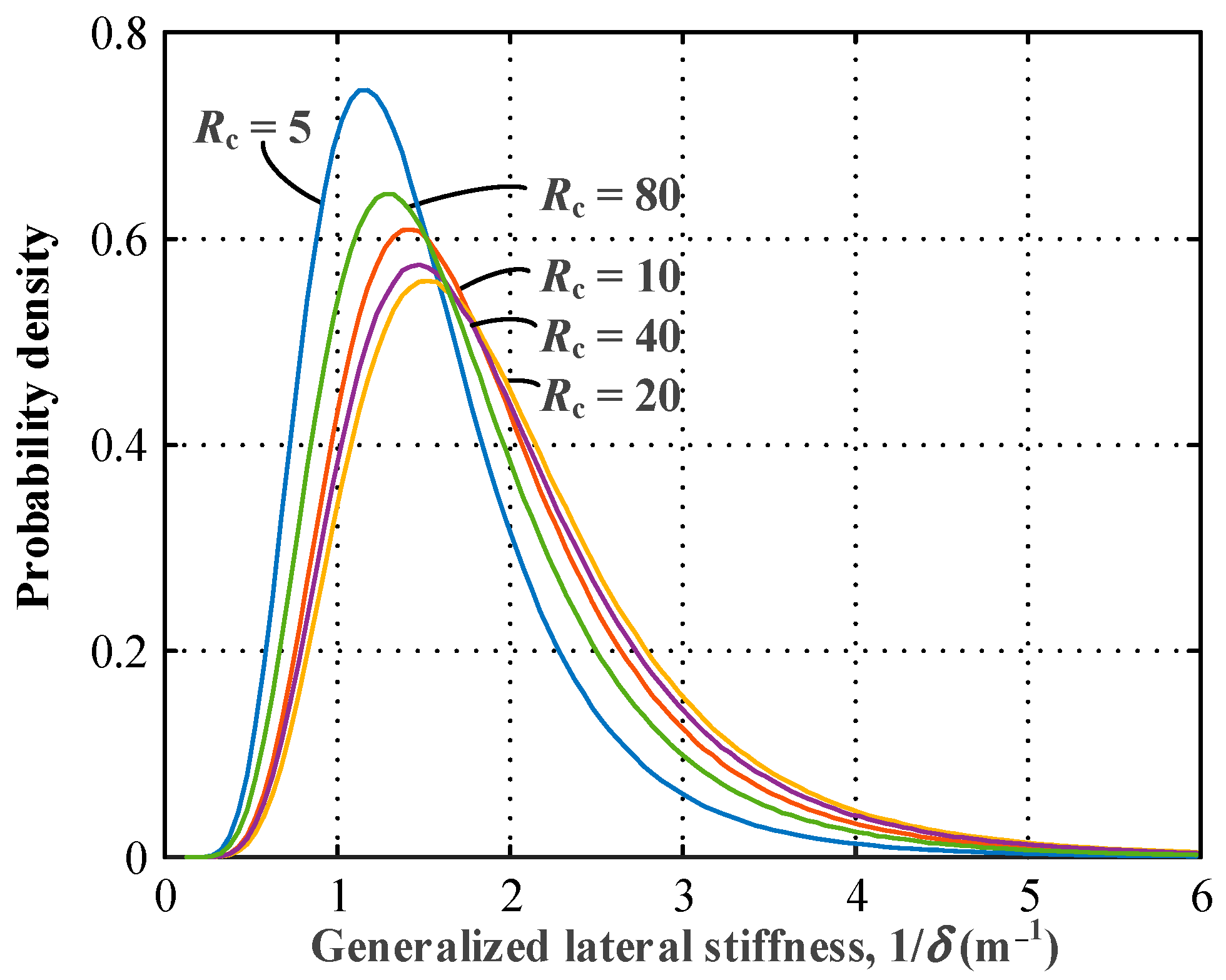
| Crossbeam Stiffness Factor Rc | Variations in the Cross-Sectional Height | Axial Load Level P/PE | Expected Value of Klateral (m−1) | COV of Klateral |
|---|---|---|---|---|
| 1 | −59.61% | 0.087 | 1.843 | 0.483 |
| 4 | −32.93% | 0.111 | 2.754 | 0.469 |
| 8 | −15.76% | 0.132 | 2.866 | 0.470 |
| 20 | 10.43% | 0.176 | 2.490 | 0.483 |
| 40 | 32.22% | 0.229 | 1.962 | 0.497 |
| Crossbeam Stiffness Factor Rc | Variations in the Cross-Sectional Height | Axial Load Level P/PE | Expected Value of Klateral (m−1) | COV of Klateral |
|---|---|---|---|---|
| 5 | −43.79% | 0.240 | 1.535 | 0.469 |
| 10 | −26.24% | 0.260 | 1.876 | 0.462 |
| 20 | −4.59% | 0.289 | 2.026 | 0.460 |
| 40 | 21.41% | 0.330 | 1.963 | 0.466 |
| 80 | 51.74% | 0.389 | 1.739 | 0.477 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, W.; Zhu, Y.; Zhao, C.; Tong, J. Optimal Design of Crossbeam Stiffness Factor in Bridge Towers Using a Reliability-Based Approach. Buildings 2023, 13, 2095. https://doi.org/10.3390/buildings13082095
Pan W, Zhu Y, Zhao C, Tong J. Optimal Design of Crossbeam Stiffness Factor in Bridge Towers Using a Reliability-Based Approach. Buildings. 2023; 13(8):2095. https://doi.org/10.3390/buildings13082095
Chicago/Turabian StylePan, Wenhao, Yi Zhu, Chuanhao Zhao, and Jingzhong Tong. 2023. "Optimal Design of Crossbeam Stiffness Factor in Bridge Towers Using a Reliability-Based Approach" Buildings 13, no. 8: 2095. https://doi.org/10.3390/buildings13082095
APA StylePan, W., Zhu, Y., Zhao, C., & Tong, J. (2023). Optimal Design of Crossbeam Stiffness Factor in Bridge Towers Using a Reliability-Based Approach. Buildings, 13(8), 2095. https://doi.org/10.3390/buildings13082095








