Seismic Behaviors of Novel Steel-Reinforced Concrete Composite Frames Prestressed with Bonding Tendons
Abstract
:1. Introduction
2. Specimen Design
3. Finite Element Model
3.1. Constitutive Model for Materials
3.1.1. Steel and Prestressing Tendons
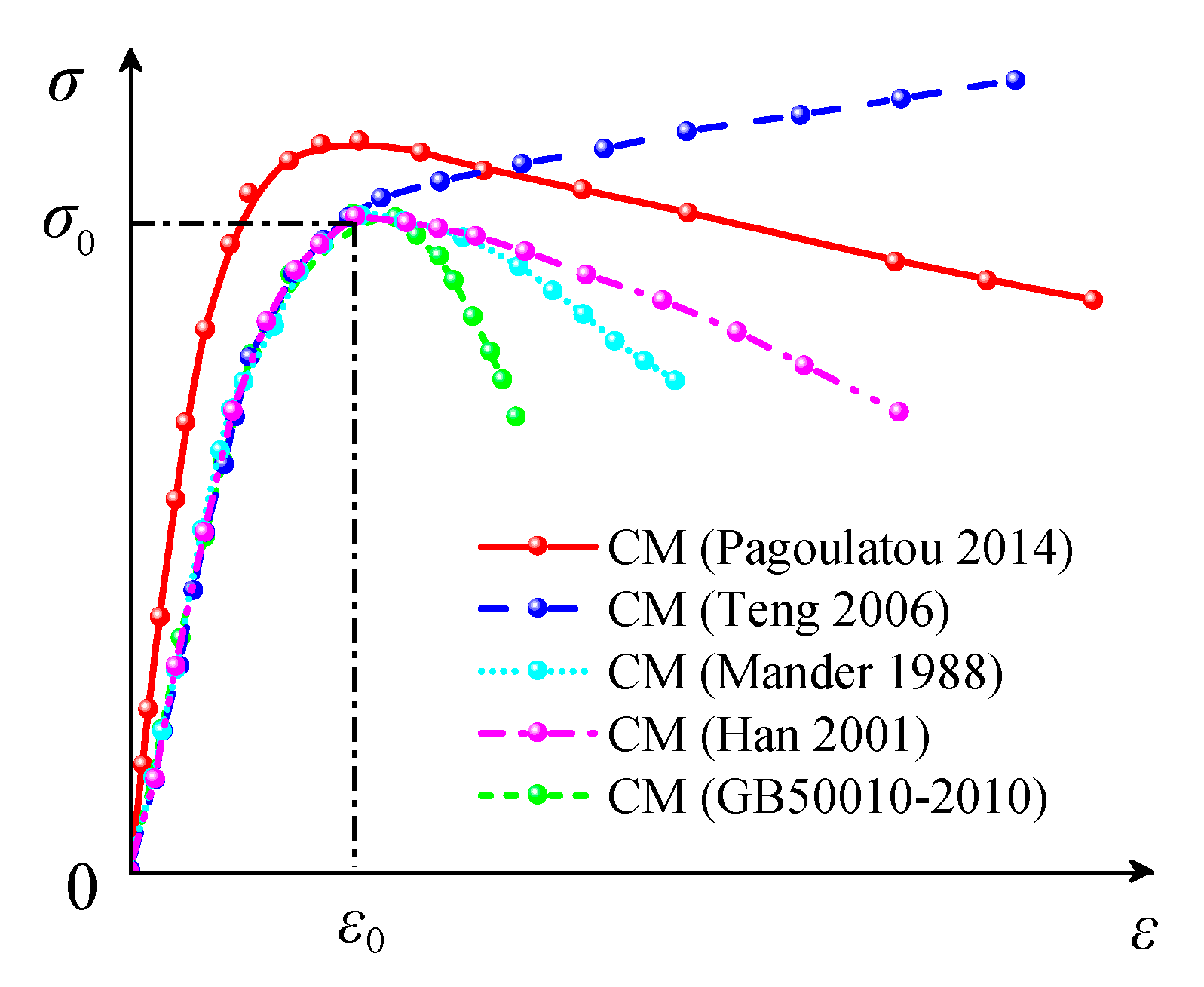
3.1.2. Concrete
- (1)
- Compressive strength of confined concrete (fcc)
- (2)
- Effective confined stress of confined concrete (fr′)
- (3)
- Effective constraint coefficient (ke)
- (4)
- Peak strain of the confined concrete ()
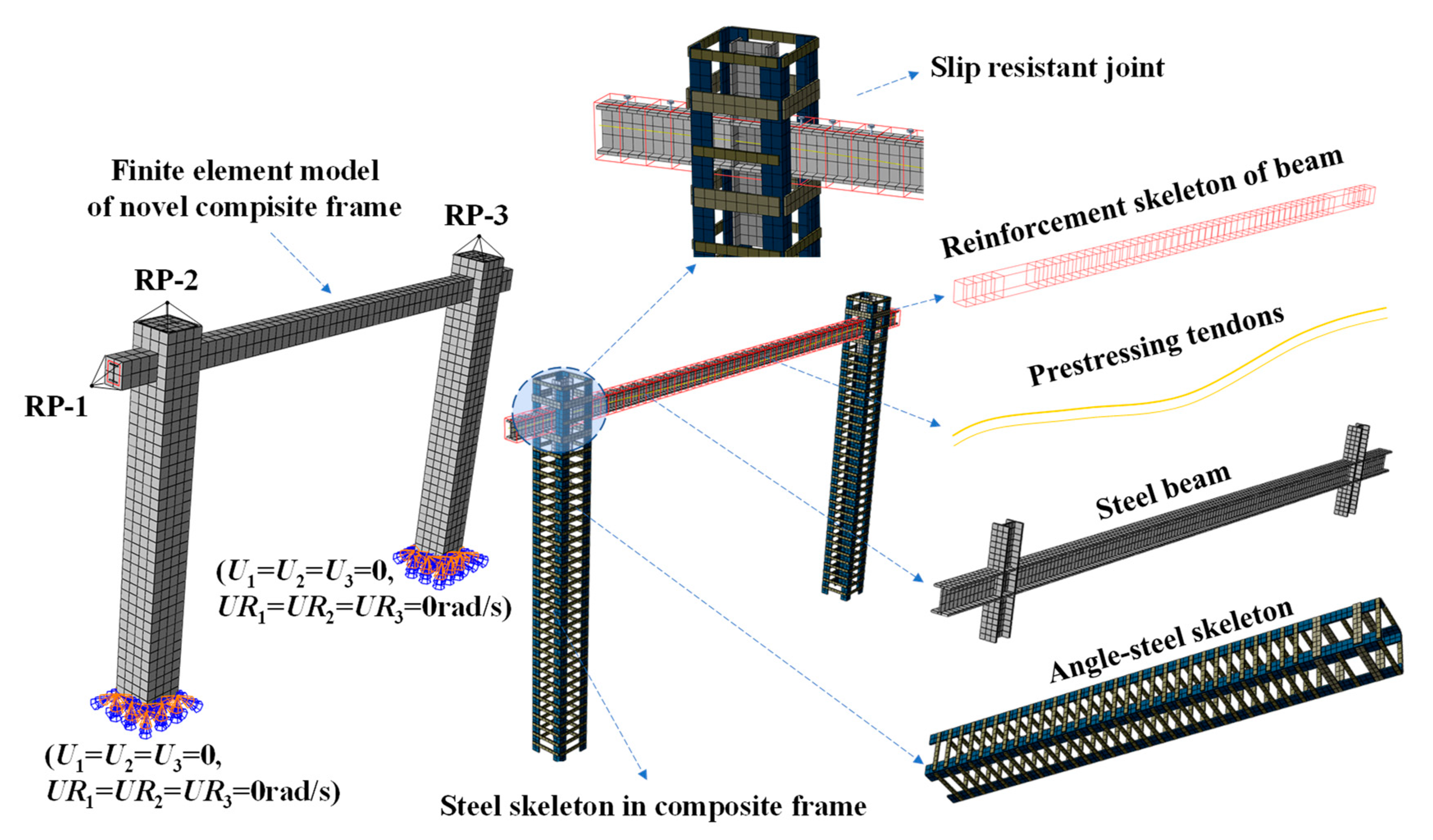
3.2. Establishment of Finite Element Model
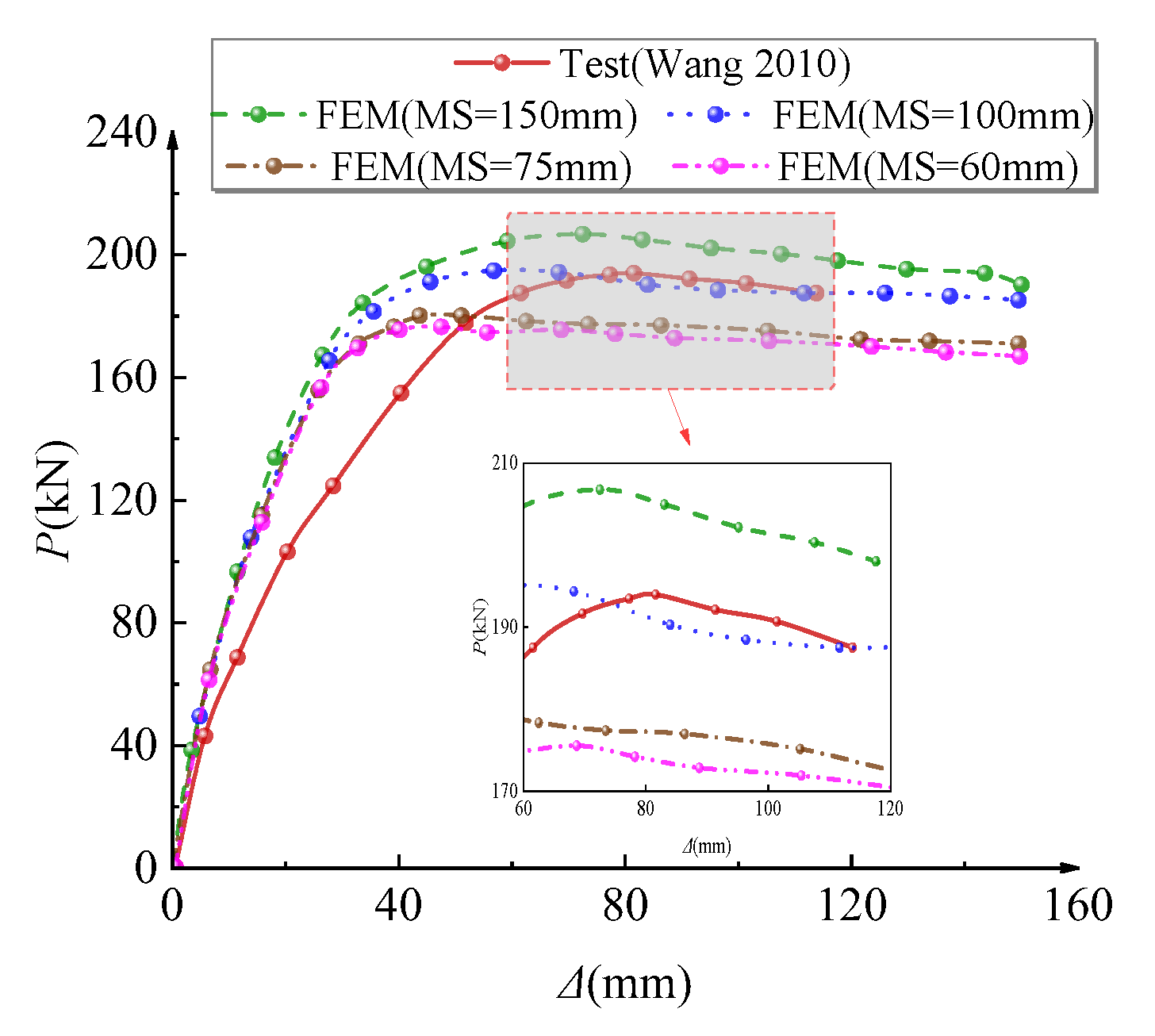
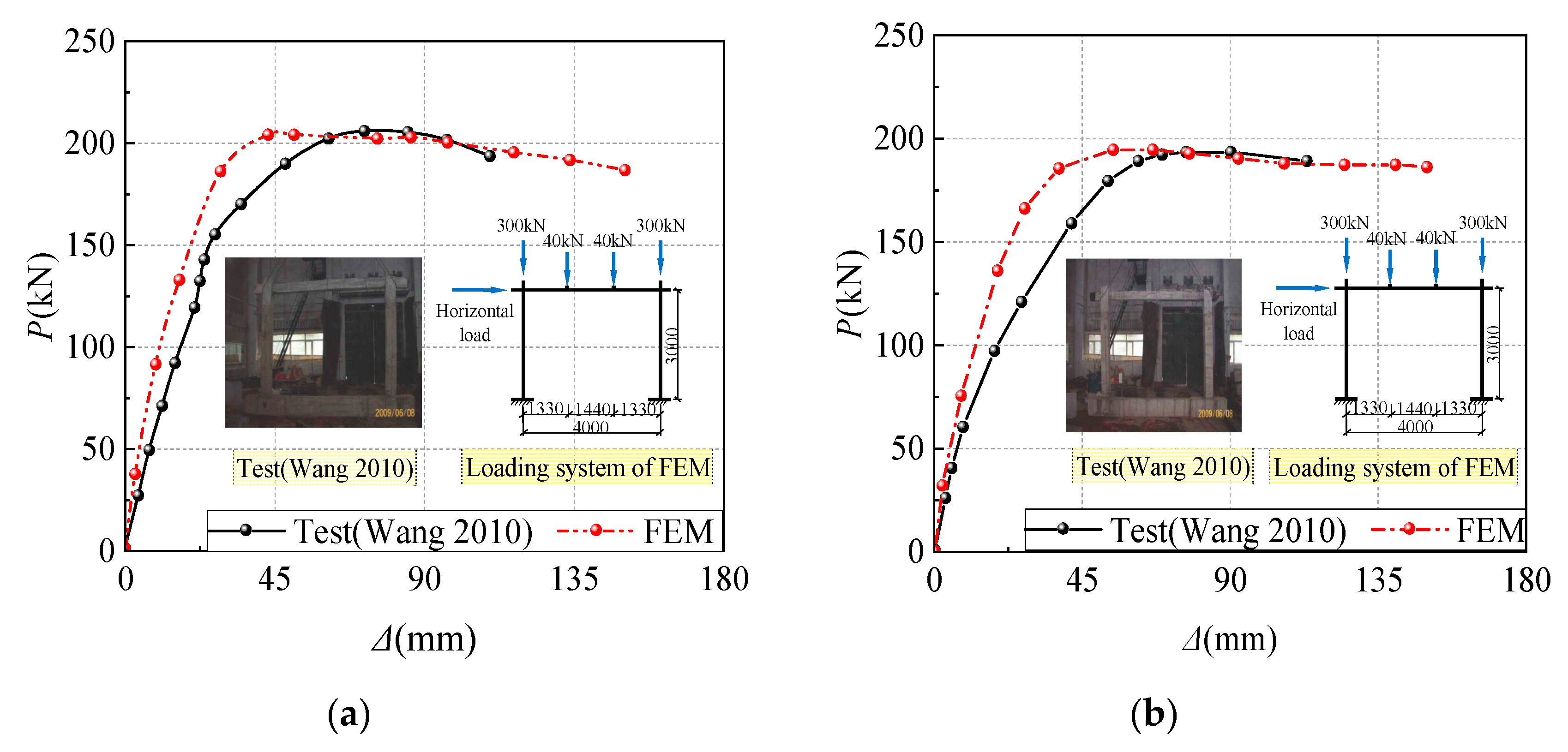
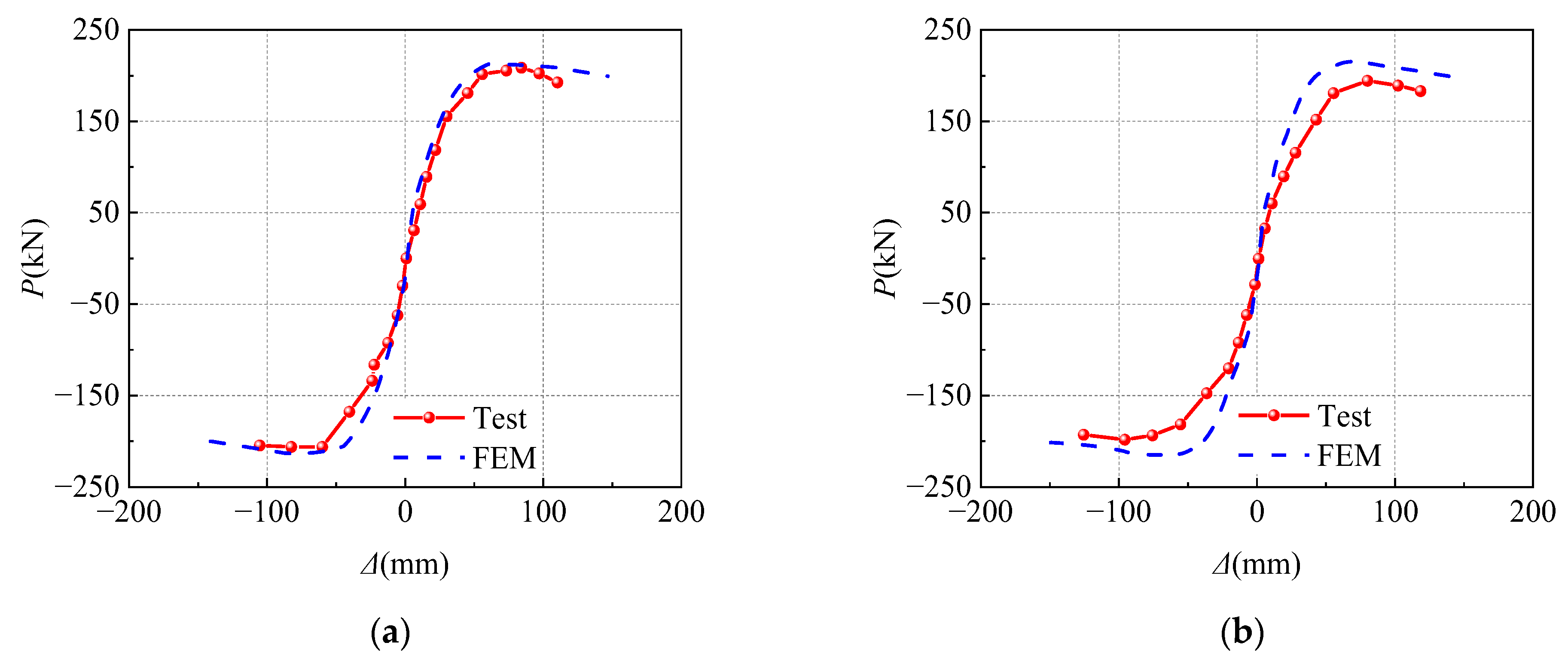
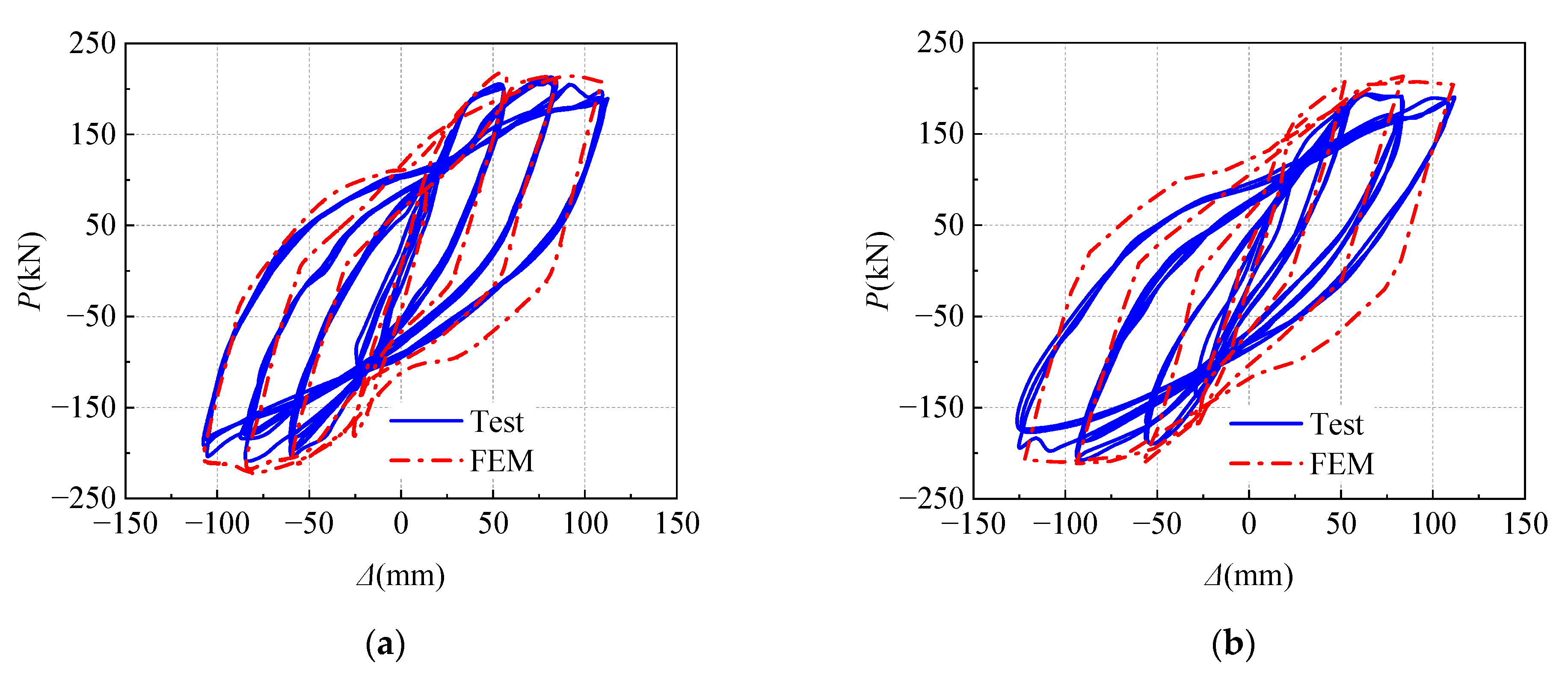
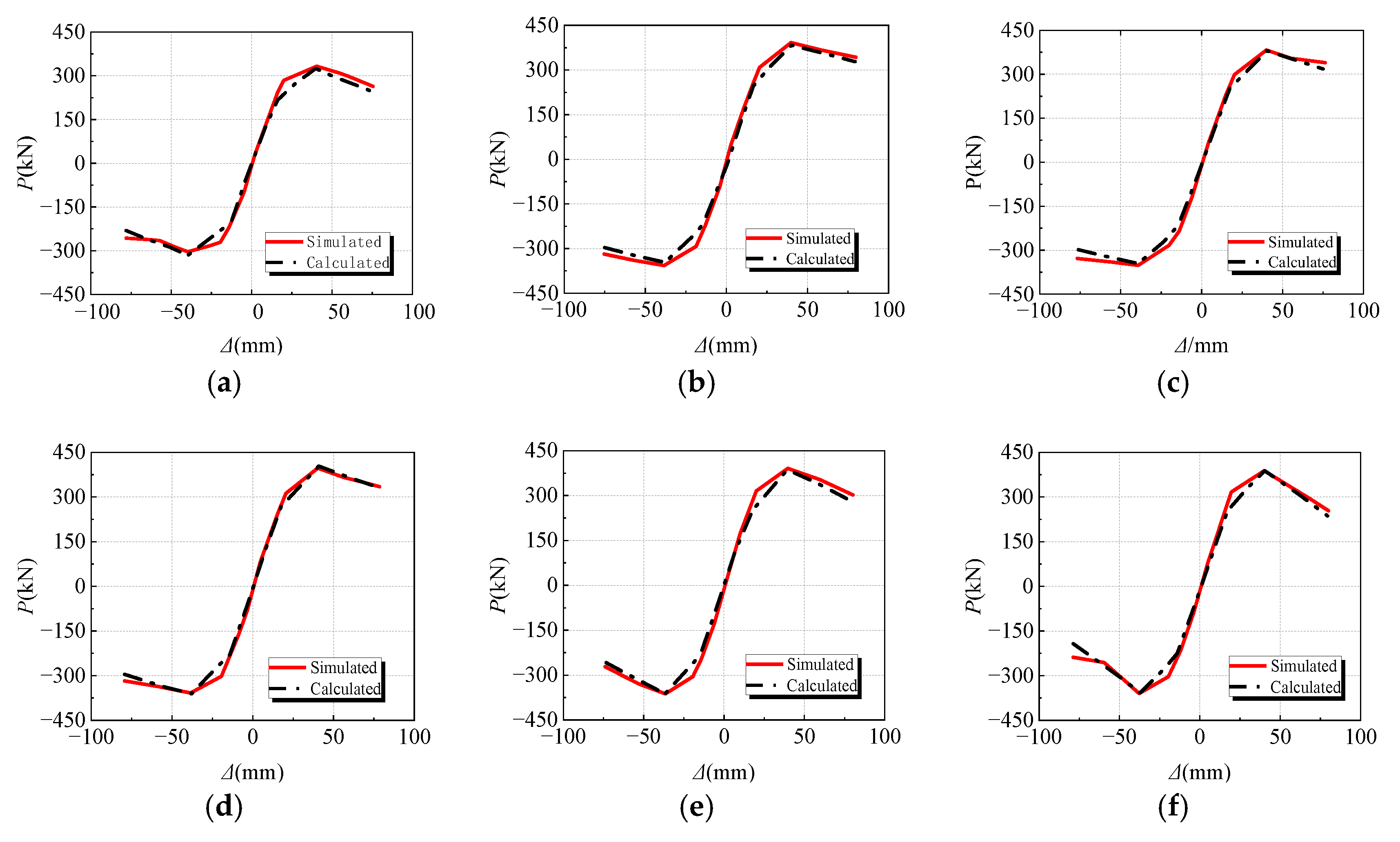
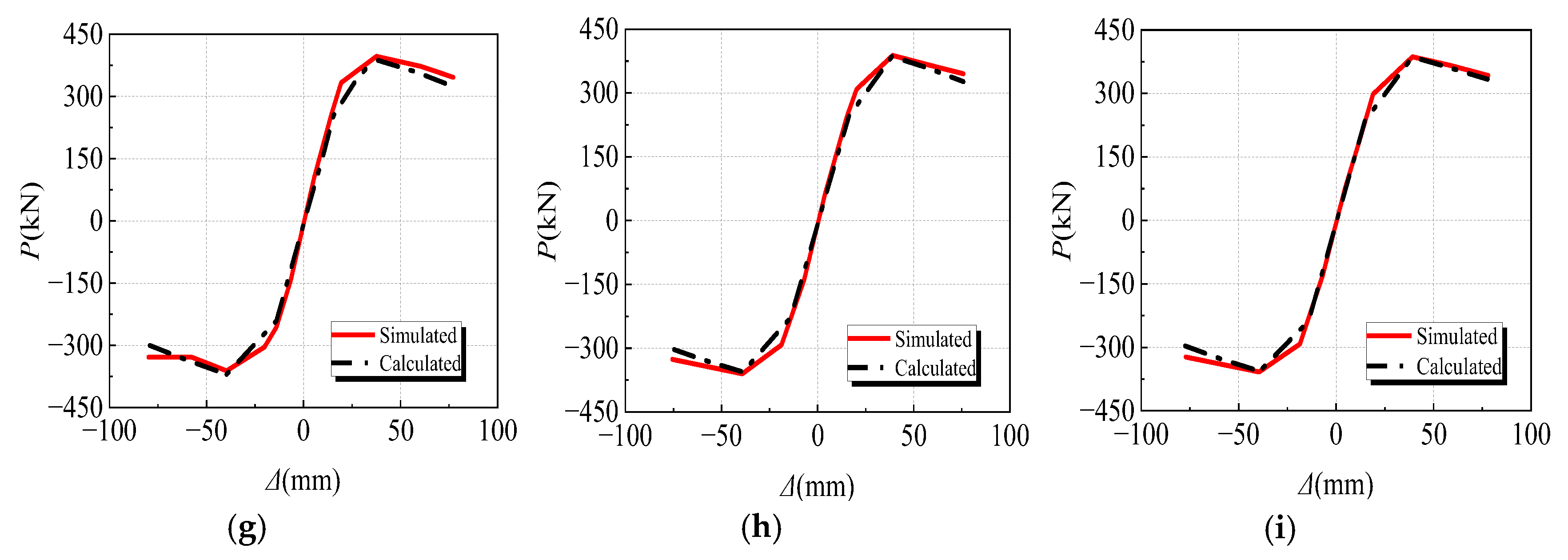
3.3. Verification of Finite Element Model
4. Analysis on the Seismic Behaviors
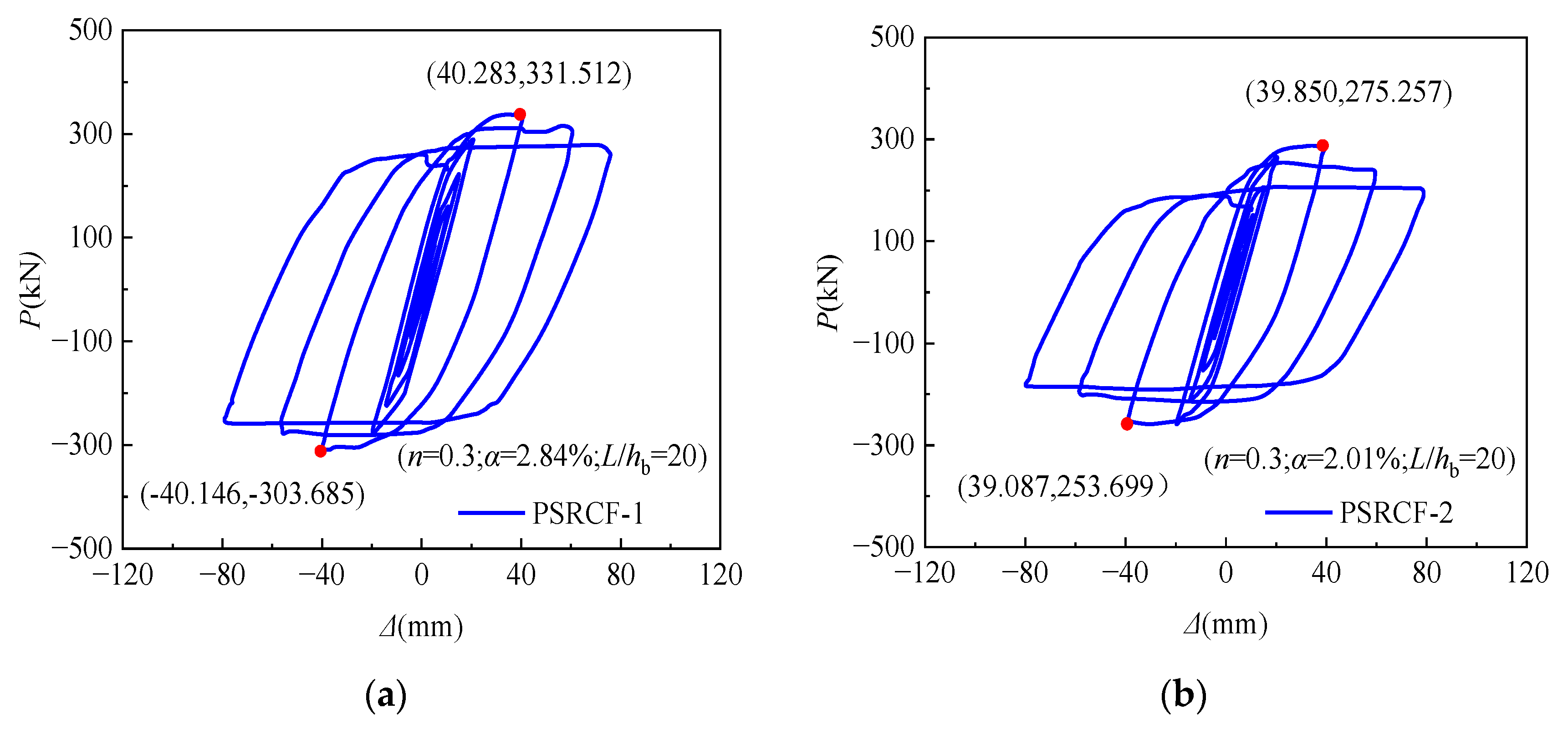
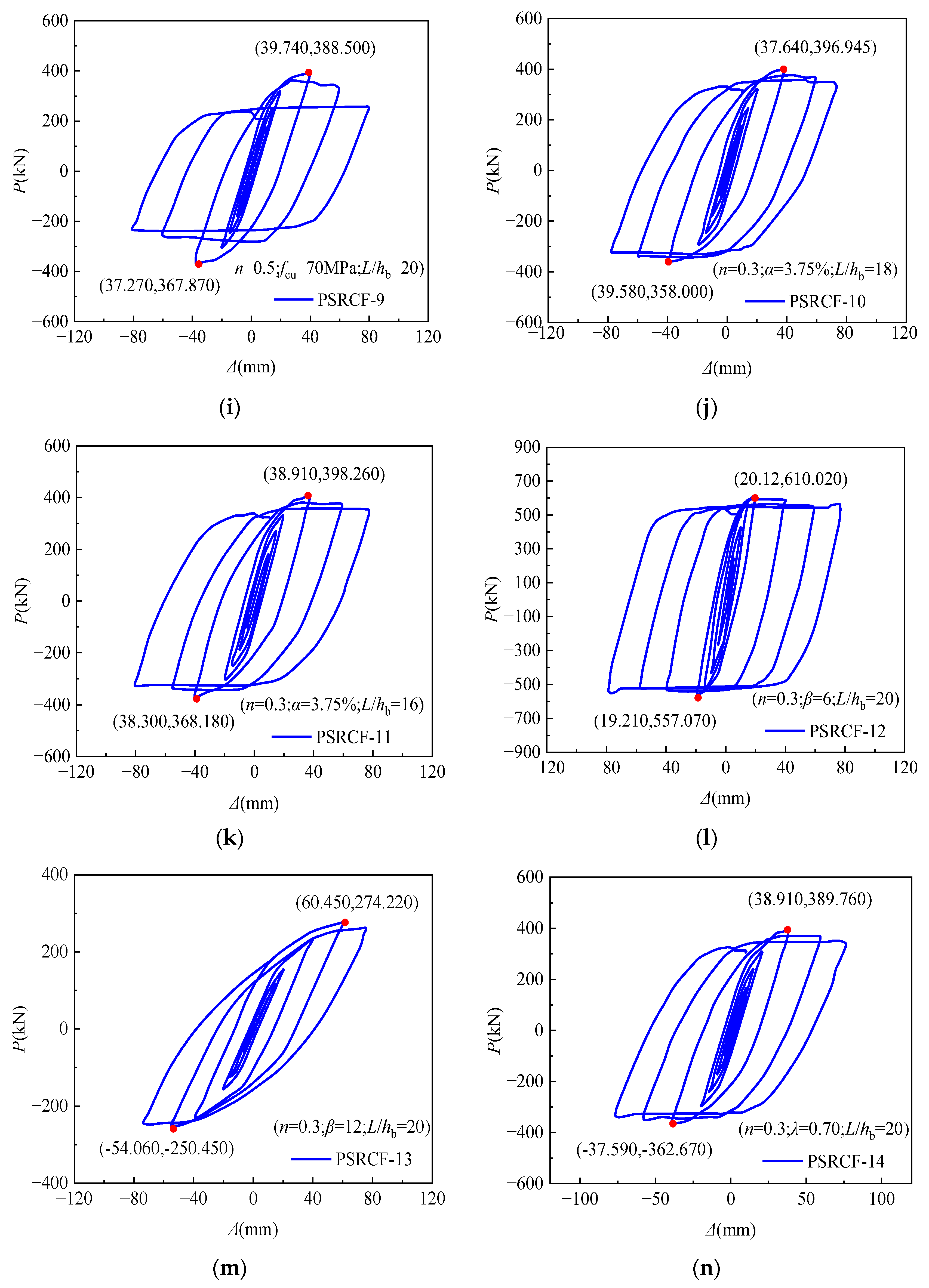
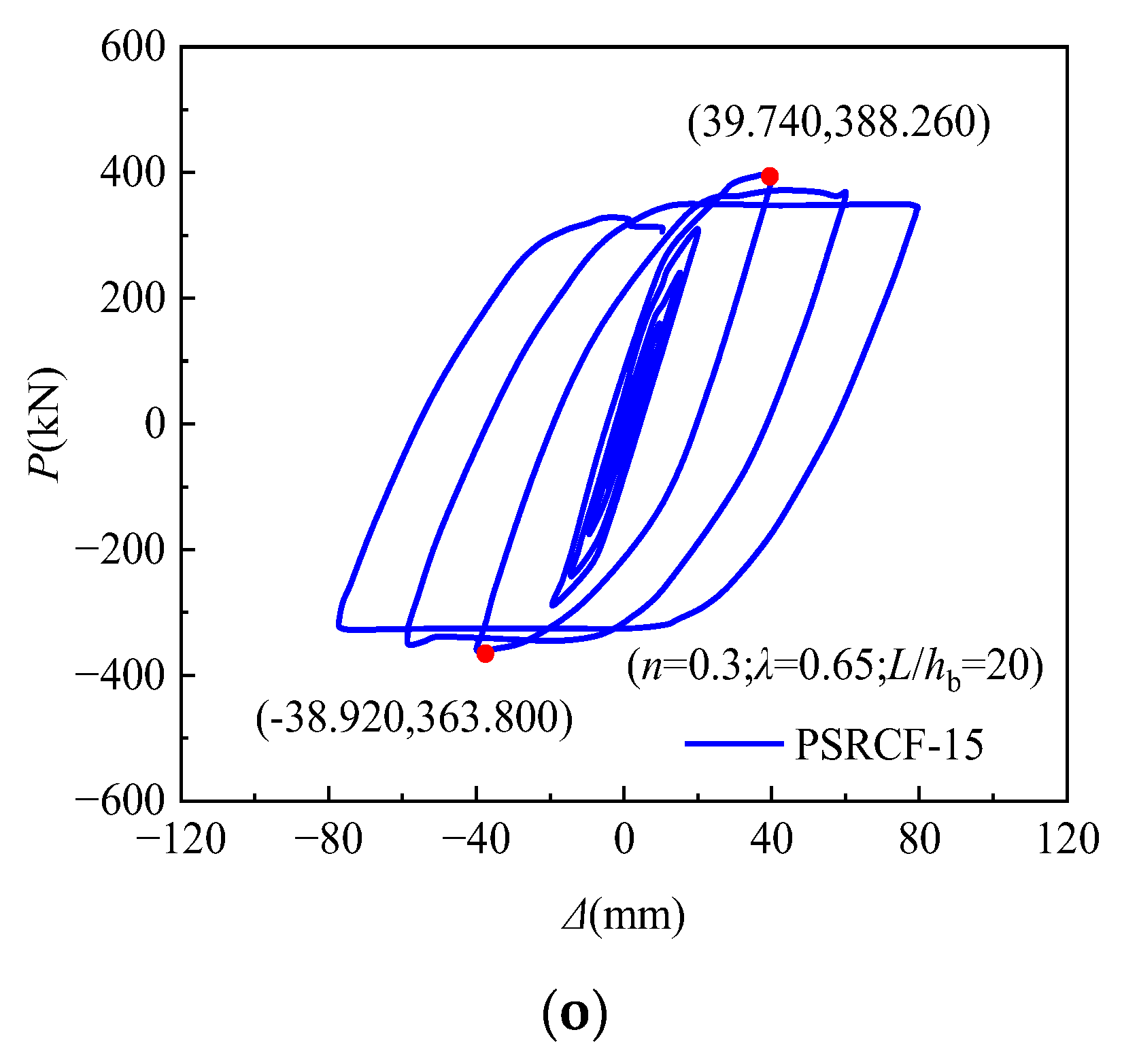
4.1. Hysteretic Curves
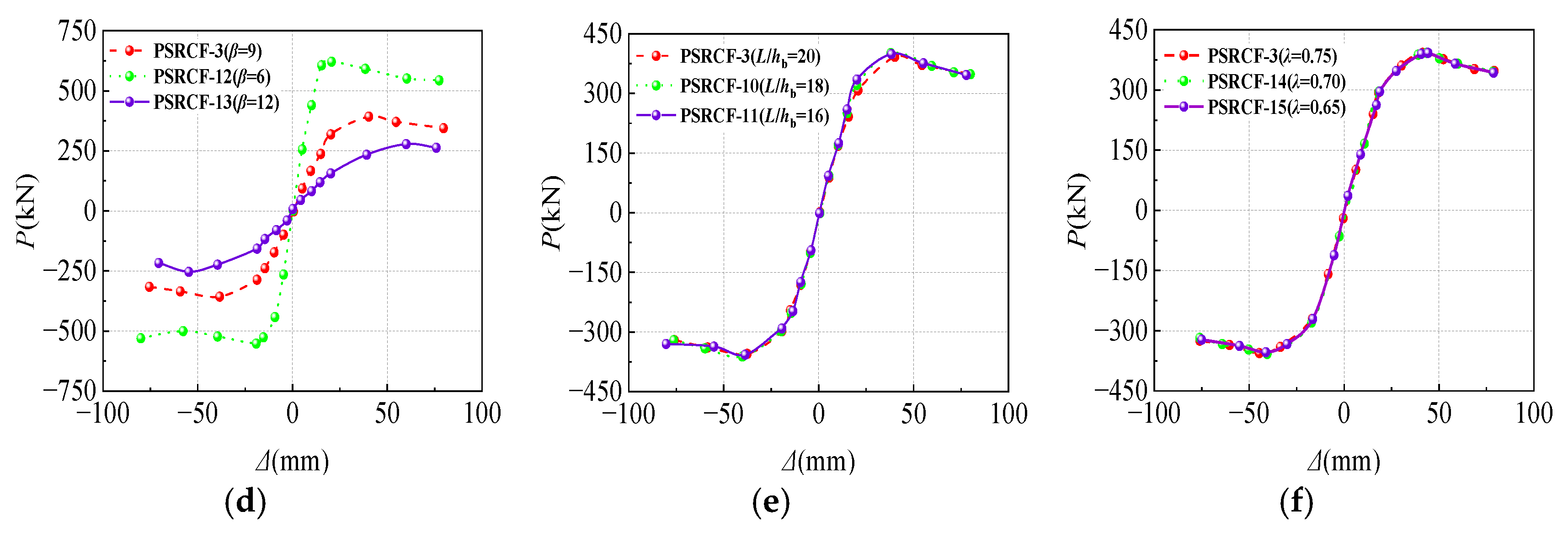
4.2. Skeleton Curves
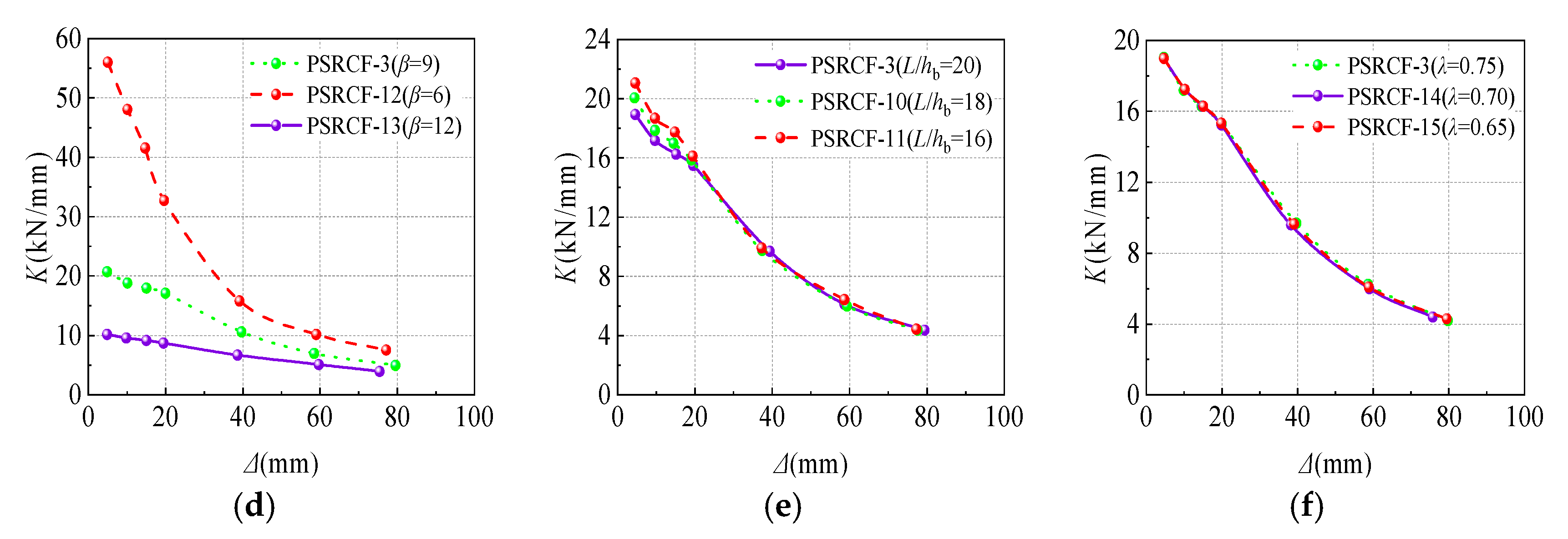
4.3. Degradation of Stiffness
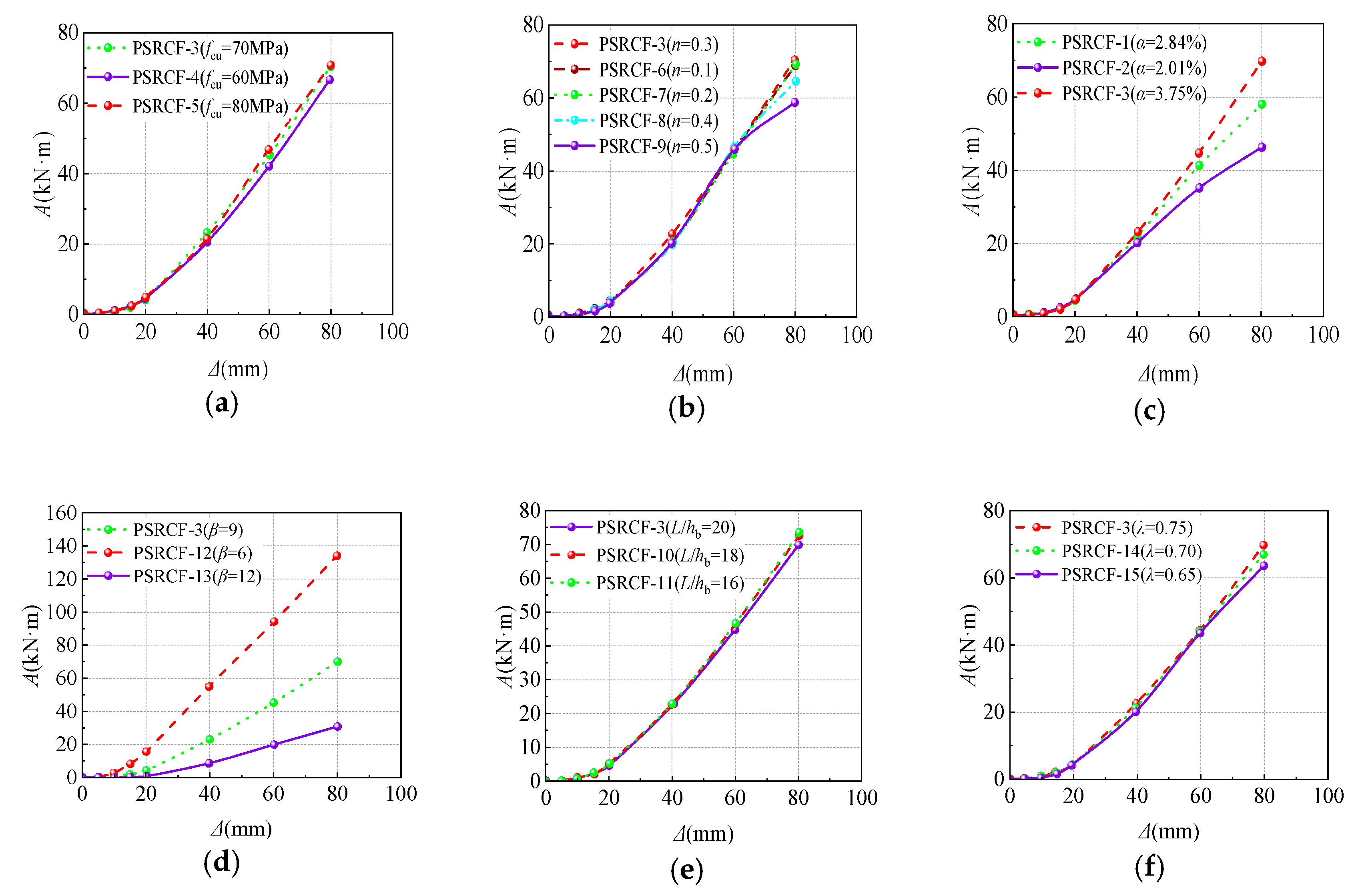
4.4. Energy Dissipation Capacity
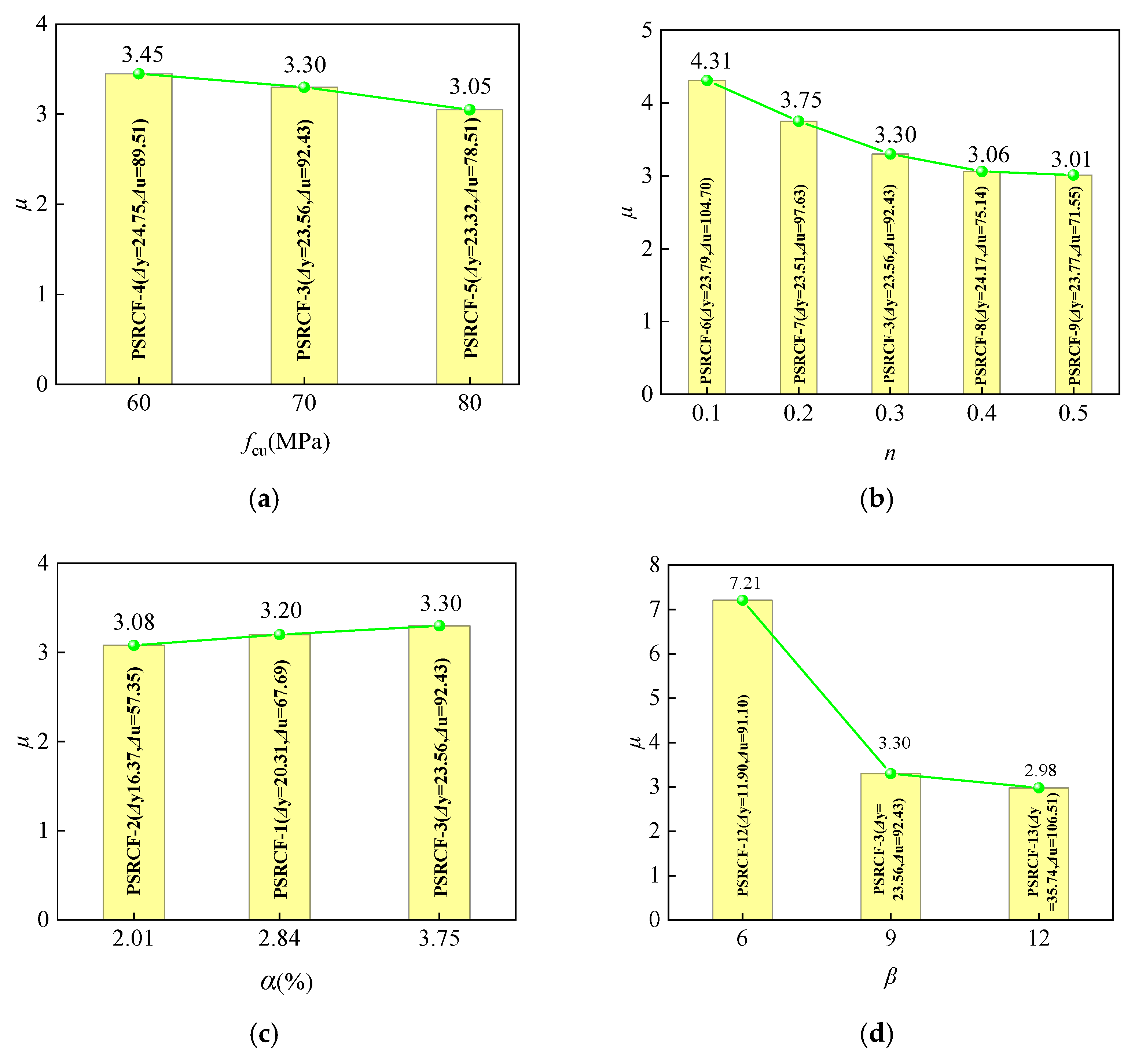
4.5. Ductility
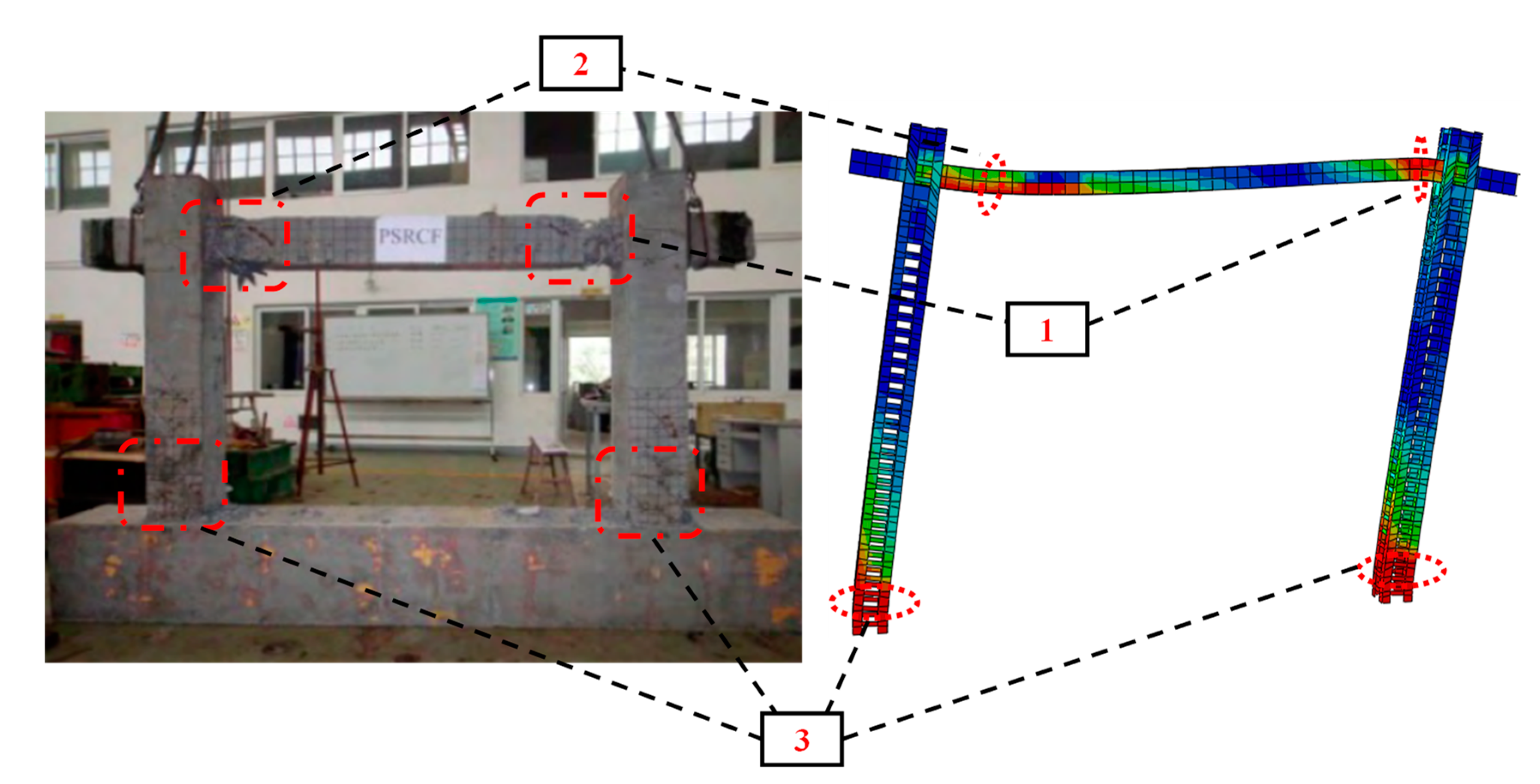
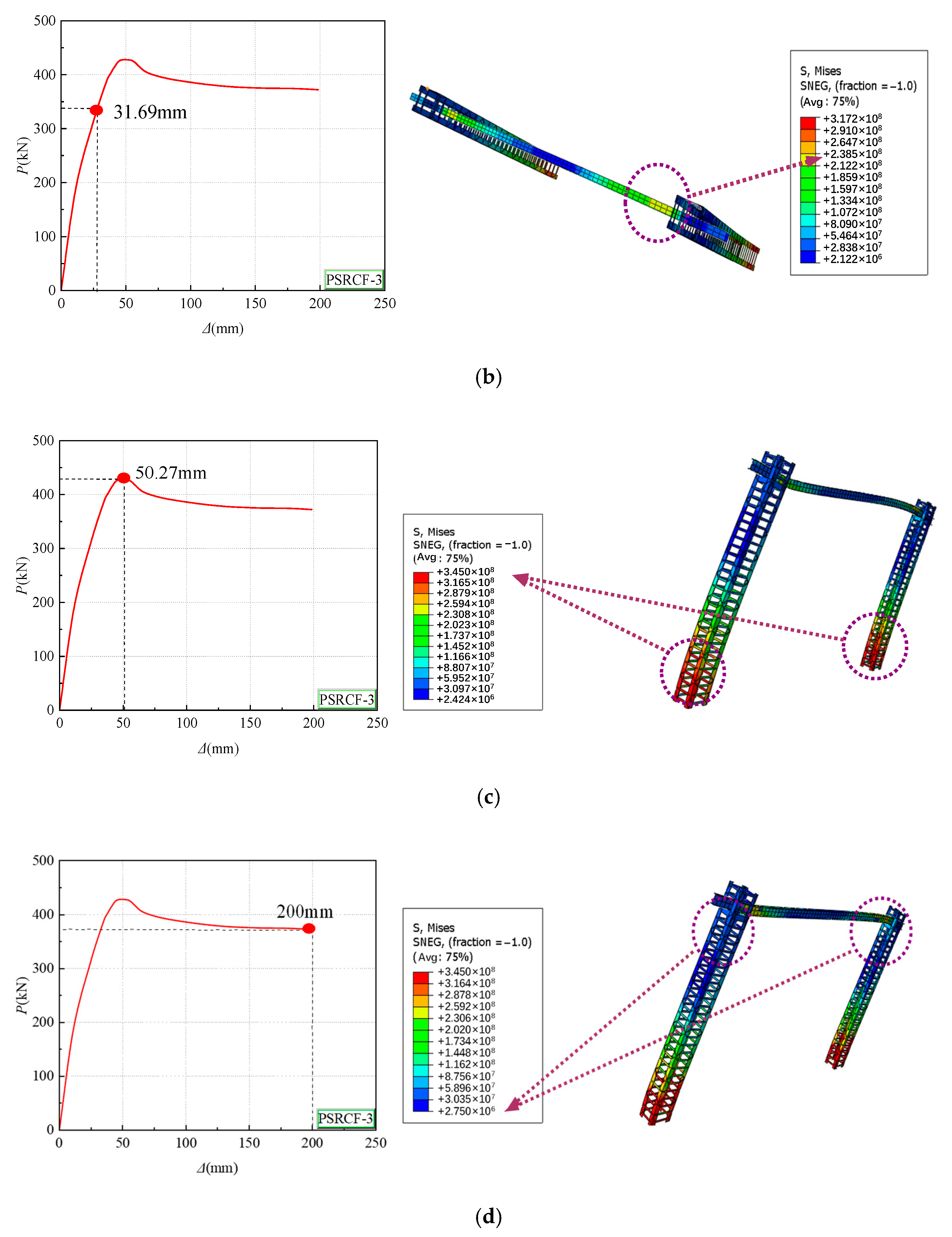
5. Plastic Hinge Mechanism
6. Restoring Force Model
6.1. Trilinear Skeleton Curve Model
- (1)
- Stiffnesses of the elastic stage for the forward and backward directions (K1, )
- (2)
- Peak loads for the forward and backward directions (Pm, )
- (3)
- The displacements corresponding to the peak loads for the forward and backward directions (Δm, Δ′m)
- (4)
- The stiffness of the degenerative stage (Kd)
- (5)
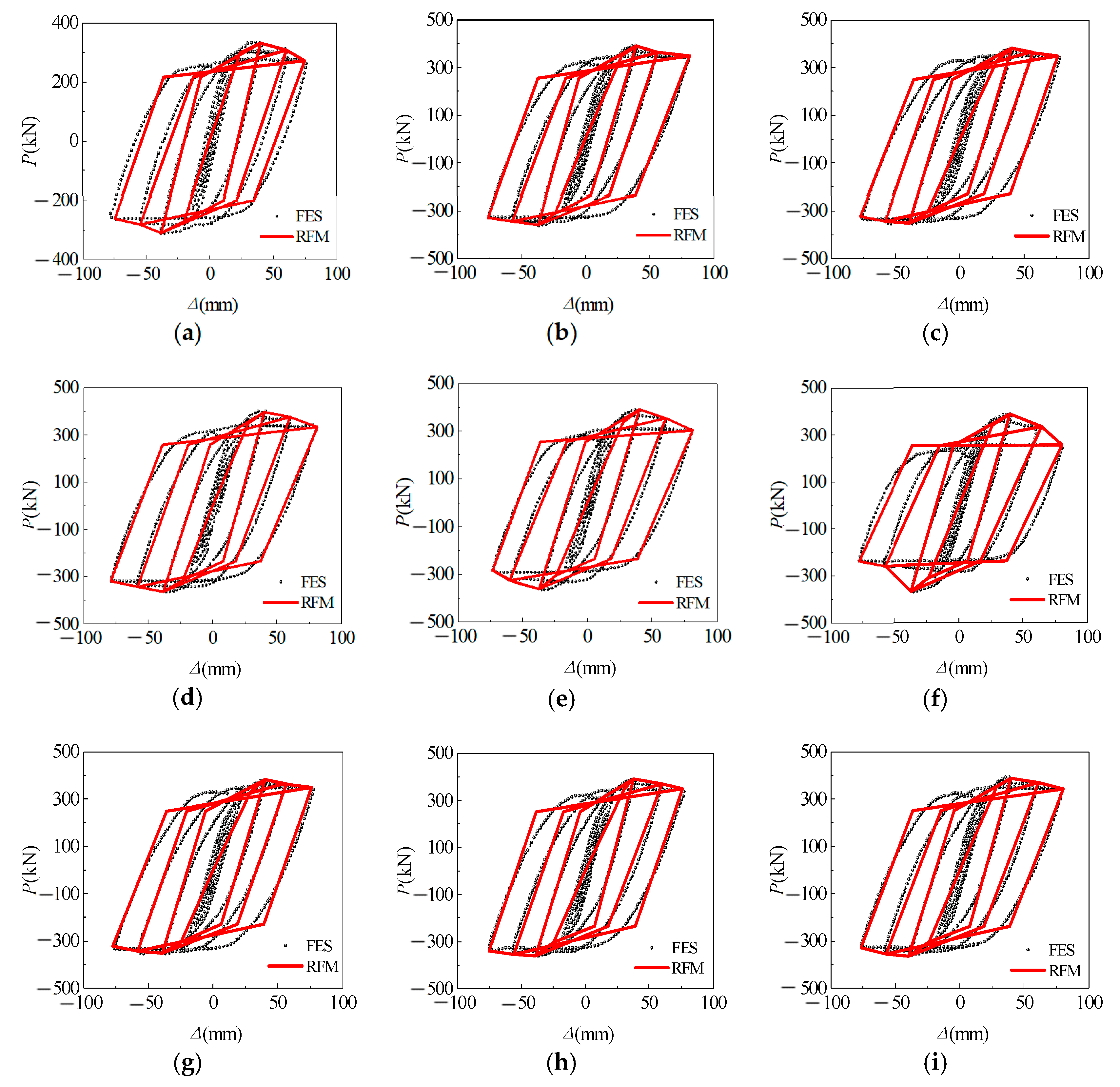
- Verification of the trilinear skeleton curve model
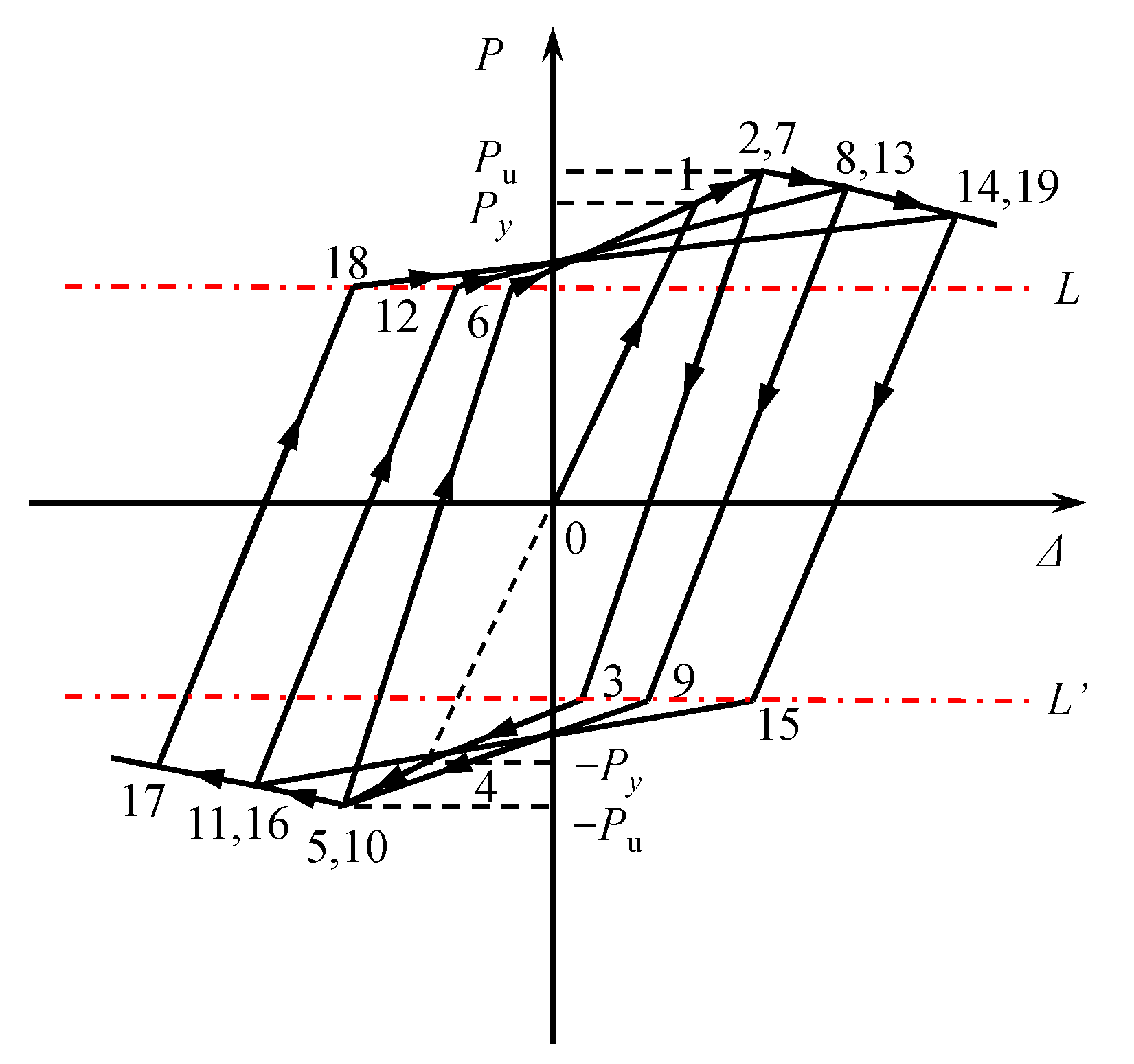
6.2. Hysteretic Rule of the Restoring Force Model
- (1)
- The loading and unloading guidelines for the elastic stagePrior to the restitution force attaining Py, the loading process starts along the skeleton curve. During the unloading phase, the initial stiffness is considered, disregarding any stiffness degradation and residual deformation;
- (2)
- The loading and unloading guidelines for elastoplastic stageWhen the restitution force surpasses the horizontal yielding load Py in either the forward or backward direction, and yet remains below the peak load Pu, loading takes place along the skeleton curve, while unloading adheres to Equation (24), and the unloading stiffness (Kun) is derived through regression analysis aswhere Δy represents the yielding displacement, Δun denotes the displacement at the unloading point, and Ke signifies the initial stiffness;
- (3)
- The loading–unloading rules during the descending segment stageWhen the restitution force surpasses Pu in either the forward or backward direction, the loading stiffness Kd in the descending segment stage of the skeleton curve is employed, while the unloading stiffness is still computed according to Equation (24);
- (4)
- Rules for backward loading and forward reloadingThe trajectory is directed from the point at P = 0.65Pu directly to the yielding point in the backward direction when the backward loading occurs subsequent to the forward unloading, and the maximum displacement in the reverse direction cannot be greater than the yield displacement. Indeed, when the maximum displacement in the backward direction surpasses the yielding displacement, the trajectory proceeds from the point at P = 0.65Pu to the maximum displacement point in the backward direction. Absolutely, for forward reloading after backward unloading, the trajectory leads from the point at P = 0.65Pu to the maximum point in the forward direction.
7. Conclusions
- (1)
- Using ABAQUS software, 15 finite element models of PSRCFs were created. These models were based on the modified concrete constitutive model presented by Mander, the prestressing effect applied using the temperature reduction approach, and the reasonable FEM method;
- (2)
- The 15 specimens had relatively full pike-shaped hysteresis curves with no pinched corners, indicating that the structure had good seismic behaviors. The skeleton curves of 15 specimens all conform to the rule of three broken lines in the elastic stage, elastic–plastic stage, and descending stage, and all specimens demonstrate exceptional loading capacities and ductilities. The peak loads observed in the skeleton curves show increasing trends with the increasing fcu, α, n, and λ, and decrease with the increasing β and L/hb, while α and β have greater impacts on the peak load of this kind of novel PSRCFs;
- (3)
- The stiffness degradations of PSRCFs are closely related to the coefficients α and β. The stiffness degradations of specimens can be improved significantly by increasing α; on the contrary, the stiffness degradations decrease by increasing β. The energy dissipation capacity of the specimens increases with the increasing α, while as β increases, the energy dissipation capacity gradually decreases. β and n have great influences on the ductility, and the ductility of the specimen decreases gradually with the increasing β and n. When n reaches 0.4, the deformation resistance decreases largely, which indicates that n should not exceed 0.4. Considering the actual frame column section size, it is suggested that β should be within the range of 9~12;
- (4)
- Based on the stress contours of the steel skeleton with the changes of loading obtained by the post-processing, the hinge law of this kind of frame is consistent, and the plastic hinges develop from the beam ends on both sides to the column bottom on both sides. There is no plastic hinge on the top of the column, indicating that the PSRCFs have good mechanisms of strong columns and weak beams;
- (5)
- On the basis of the hysteresis curves acquired through the quasi-static analysis, the restoring force model and the trilinear skeleton curve model were developed, and the hysteresis rules were proposed, correspondingly. The findings of the numerical simulation results are in good agreement with the skeleton curves and hysteretic curves obtained by equation, indicating that the restoring force model is reasonable and feasible.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiong, X.; Yao, G.; Su, X. Experimental and numerical studies on seismic behavior of bonded and unbonded prestressed steel reinforced concrete frame beam. Eng. Struct. 2018, 167, 567–581. [Google Scholar]
- Vollmer, M.; Bauer, A.; Frenck, J.-M.; Krooß, P.; Wetzel, A.; Middendorf, B.; Fehling, E.; Niendorf, T. Novel prestressing applications in civil engineering structures enabled by Fe-Mn-Al-Ni shape memory alloys. Eng. Struct. 2021, 241, 112430. [Google Scholar] [CrossRef]
- Hassan, W.; Reyes, J.; González, C.; Pallarés, F.; Spinel, J. Seismic vulnerability and resilience of steel-reinforced concrete (SRC) composite column buildings with non-seismic details. Eng. Struct. 2021, 244, 112810. [Google Scholar] [CrossRef]
- Ji, J.; Wang, W.; Jiang, L.; Ren, H.; Wang, Q.; Xuan, W.; Liu, Y. Bearing capacity of UHPC-filled high-strength elliptical steel tube composite columns with encased high-strength h-shape steel subjected to eccentrical load. Buildings 2022, 12, 1272. [Google Scholar] [CrossRef]
- Wu, S.; Liu, W.; Zhang, J.; He, W.; Guo, Y. Experimental and analytical investigation of square-shaped concrete-filled steel tube columns. J. Constr. Steel Res. 2023, 201, 107737. [Google Scholar] [CrossRef]
- Luo, H.; Wang, K. Research on hysteretic models for prestressed and non-prestressed steel reinforced concrete frames. Adv. Civ. Eng. 2021, 2021, 9442180. [Google Scholar] [CrossRef]
- Ji, J.; Xu, Z.; Jiang, L.; Yuan, C.; Zhang, Y.; Zhou, L.; Zhang, S. Nonlinear buckling analysis of h-type honeycombed composite column with rectangular concrete-filled steel tube flanges. Int. J. Steel Struct. 2018, 18, 1153–1166. [Google Scholar] [CrossRef]
- Wang, K.; Yuan, S.F.; Cao, D.F. Test on seismic performance of frame structure of steel reinforced concrete beam and steel-tube encased concrete column. J. Build. Struct. 2013, 34, 103–112. [Google Scholar]
- Wang, K.; Lu, X.-F.; Yuan, S.-F.; Cao, D.-F.; Chen, Z.-X. Analysis on hysteretic behavior of composite frames with concrete-encased CFST columns. J. Constr. Steel Res. 2017, 135, 176–186. [Google Scholar] [CrossRef]
- Ding, F.-X.; Yin, G.-A.; Jiang, L.-Z.; Bai, Y. Composite frame of circular CFST column to steel-concrete composite beam under lateral cyclic loading. Thin-Walled Struct. 2018, 122, 137–146. [Google Scholar] [CrossRef]
- Zhang, J.; Jia, J.; Yu, J.; Sun, Z. Seismic behaviour of steel-reinforced ultra-high-strength concrete composite frame: Experimental study. Adv. Struct. Eng. 2019, 22, 2179–2191. [Google Scholar] [CrossRef]
- Kheyroddin, A.; Gholhaki, M.; Pachideh, G. Seismic evaluation of reinforced concrete moment frames retrofitted with steel braces using IDA and Pushover methods in the near-fault field. Seism. Retrofit. 2019, 7, 159–173. [Google Scholar]
- Wang, G.; Sun, X.; Zhao, W.; Zhang, D. A finite element analysis model for post-fire seismic performance of steel reinforced concrete frame structures. J. Build. Struct. 2020, 41, 92–101. [Google Scholar]
- Behrouz, K.; Mehdi, D. Effect of corrosion in reinforced concrete frame components on pushover behavior and ductility of frame. Struct. Concr. Vol. 2020, 22, 2665–2687. [Google Scholar]
- Li, X.; Zhou, X.; Liu, J.; Wang, X. Analysis of circular tubed steel reinforced concrete column to steel beam frame structure system. J. Build. Struct. 2021, 42, 31–40. [Google Scholar]
- Li, D.-B.; Chai, Y.-K.; Li, W.-L.; Xiang, R. Experimental study and finite element analysis of seismic behaviour of novel precast prestressed concrete frames. Structures 2022, 38, 402–415. [Google Scholar] [CrossRef]
- Alshaikh, I.M.; Abu Bakar, B.; Alwesabi, E.A.; Abadel, A.A.; Alghamdi, H.; Altheeb, A.; Tuladhar, R. Progressive collapse behavior of steel fiber-reinforced rubberized concrete frames. J. Build. Eng. 2022, 57, 104920. [Google Scholar] [CrossRef]
- Aleksandrova, N. Application of Mises yield criterion to rotating solid disk problem. Int. J. Eng. Sci. 2012, 51, 333–337. [Google Scholar] [CrossRef]
- Ji, J.; Li, Y.H.; Jiang, L.Q.; Zhang, Y.F.; Liu, Y.C.; He, L.J.; Zhang, Z.B.; Wang, Y. Axial compression behavior of strength-gradient composite stub columns encased CFST with small diameter: Experimental and numerical investigation. Structures 2023, 47, 282–298. [Google Scholar] [CrossRef]
- Ji, J.; He, L.; Jiang, L.; Zhang, Y.; Liu, Y.; Li, Y.; Zhang, Z. Numerical study on the axial compression behavior of composite columns with steel tube SHCC flanges and honeycombed steel web. Eng. Struct. 2023, 283, 115883. [Google Scholar] [CrossRef]
- Pagoulatou, M.; Sheehan, T.; Dai, X.; Lam, D. Finite element analysis on the capacity of circular concrete-filled double-skin steel tubular (CFDST) stub columns. Eng. Struct. 2014, 72, 102–112. [Google Scholar] [CrossRef]
- Teng, J.; Yu, T.; Wong, Y.; Dong, S. Hybrid FRP–concrete–steel tubular columns: Concept and behavior. Constr. Build. Mater. 2006, 21, 846–854. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Han, L.H.; Tao, Z.; Liu, W. Concrete filled steel tubular structures: Theory and practice. J. Fuzhou Univ. Nat. Sci. 2001, 29, 24–34. [Google Scholar]
- GB50010-2010; National Standard of the People’s Republic of China Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2010.
- Zhou, X.; Lu, D.; Du, X.; Wang, G.; Meng, F. A 3D non-orthogonal plastic damage model for concrete. Comput. Methods Appl. Mech. Eng. 2020, 360, 112716. [Google Scholar] [CrossRef]
- Luca, P.; Daniela, A.; Enrico, S. A fiber beam element based on plastic and damage models for prestressed concrete structures. Eng. Struct. 2023, 292, 116501. [Google Scholar]
- Javanmardi, M.; Maheri, R.M. Anisotropic damage plasticity model for concrete and its use in plastic hinge relocation in RC frames with FRP. Structures 2017, 12, 212–226. [Google Scholar] [CrossRef]
- Ji, J. Research on Seismic Performance and Design Method of Jacketing Steel Reinforced Concrete Frame Prestressed with Bonded Tendons. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2008. [Google Scholar]
- Wang, K. Test and Analysis on Seismic Performance of Jacketing Prestressed Steel Reinforced Concrete Frame. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2010. [Google Scholar]
- Luo, L.; Qin, J.; Zhao, D.; Wu, Z. Seismic behavior of extended end-plate connections subjected to cyclic loading on the top-side of the column. Materials 2020, 13, 3724. [Google Scholar] [CrossRef]
- Ji, J.; He, L.; Jiang, L.; Ren, H.; Ni, S.; Wang, Z.; Li, Y.; Yu, C.; Lin, Y. Seismic behavior of GFRP tube reactive powder concrete composite columns with encased steel. Front. Mater. 2021, 08, 793392. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, F.; Yu, J.; Yu, K.; Tian, L. Development of ultra-high ductility engineered cementitious composites as a novel and resilient fireproof coating. Constr. Build. Mater. 2021, 288, 123090. [Google Scholar] [CrossRef]
- Ji, J.; Yang, M.; Xu, Z.; Jiang, L.; Song, H. Experimental study of H-shaped honeycombed stub columns with rectangular concrete-filled steel tube flanges subjected to axial load. Adv. Civ. Eng. 2021, 2021, 6678623. [Google Scholar] [CrossRef]
- Yu, Z.W.; Jian, J.G.; Zhou, L.Y. Ductility analysis of RC frame and prestressed RC frame structures. Build. Struct. 1997, 2, 41–45. [Google Scholar]
- Fu, C.; Li, Y.; Sun, X.; Xu, J. Experimental study on seismic performance of prestressed and non-prestressed steel reinforced concrete frames. J. Build. Struct. 2010, 31, 15–21. [Google Scholar]
- Wang, K.; Yuan, S.-F.; Chen, Z.-X.; Zhi, H.-X.; Shi, G.-L.; Cao, D.-F. Experimental study on hysteretic behavior of composite frames with concrete-encased CFST columns. J. Constr. Steel Res. 2016, 123, 110–120. [Google Scholar] [CrossRef]
- Ji, J.; Lin, Y.B.; Jiang, L.Q. Hysteretic behavior of h-shaped honeycombed steel web composite columns with rectangular concrete-filled steel tube flanges. Adv. Civ. Eng. 2022, 2022, 1546263. [Google Scholar] [CrossRef]
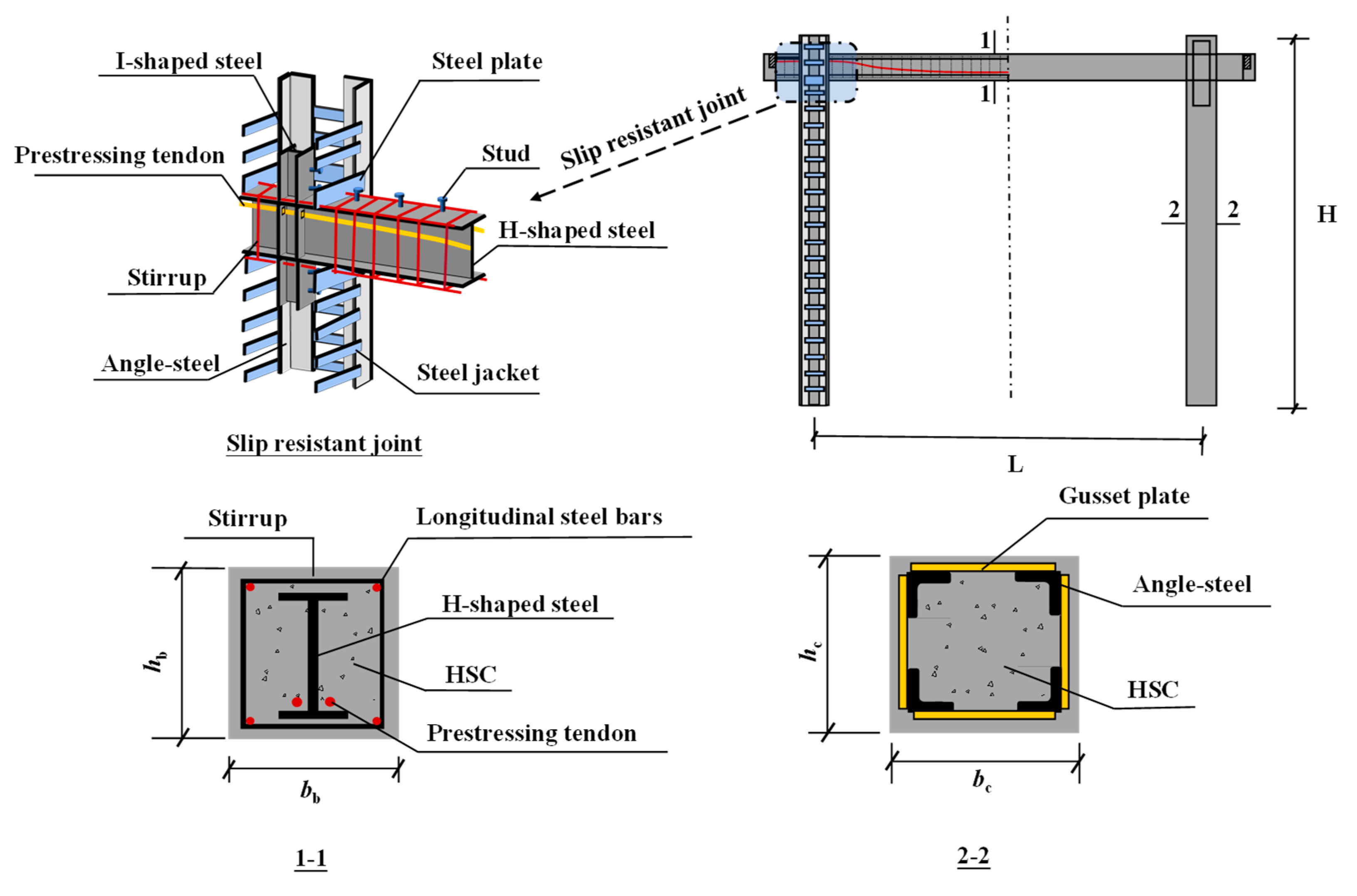
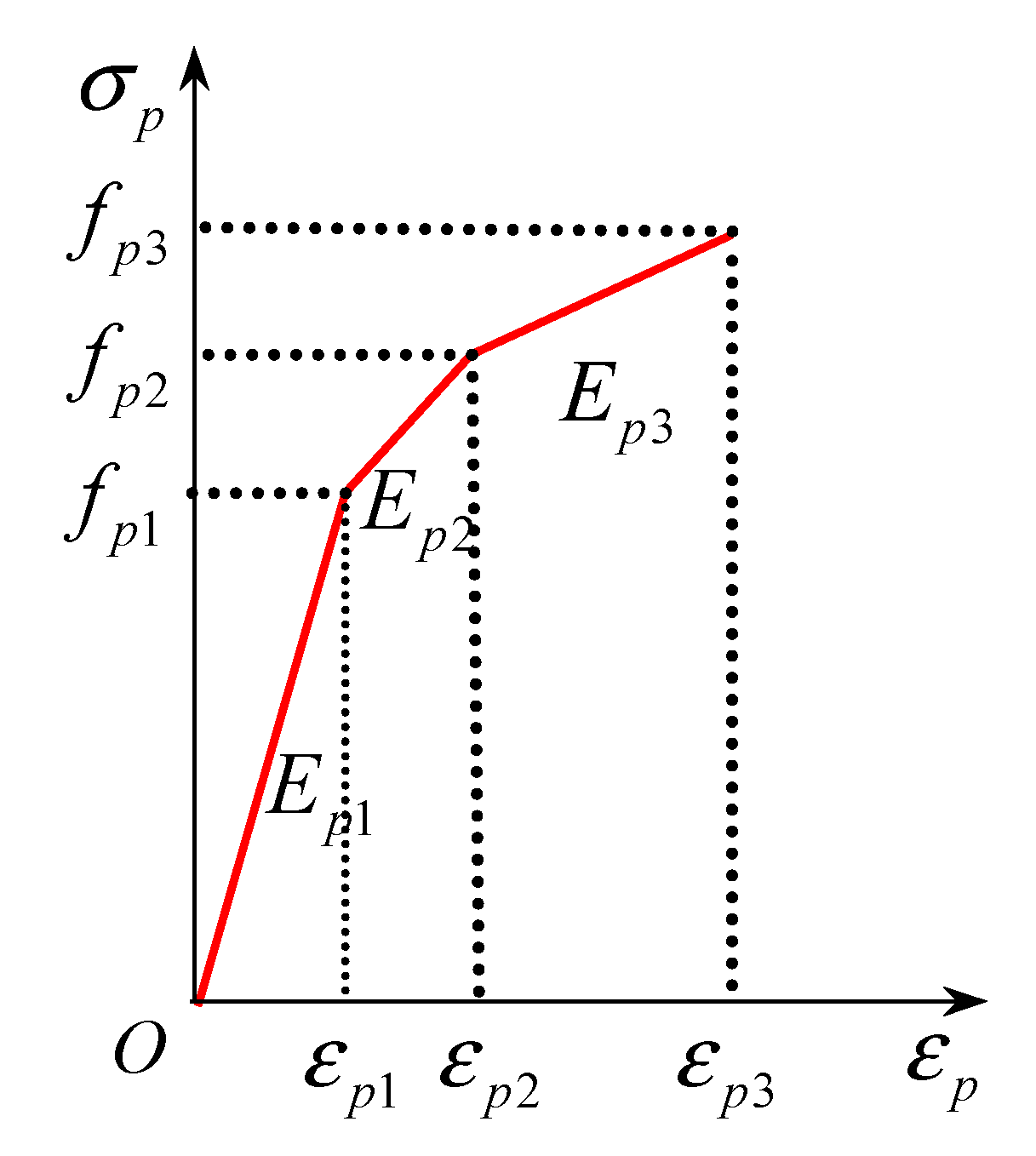
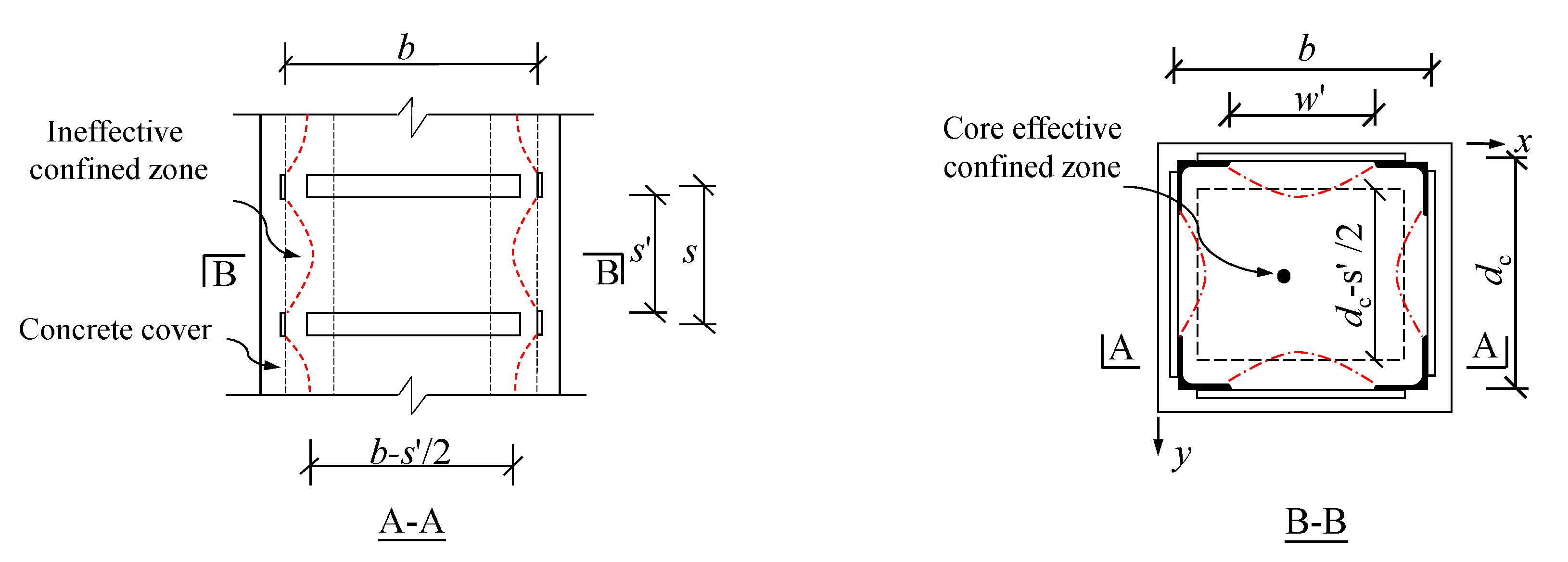








| Specimens | L (mm) | H (mm) | bb × hb (mm × mm) | bc × hc (mm × mm) | fcu (MPa) | ft (MPa) | Ec (MPa) | α (%) | β | n | L/hb | λ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSRCF-1 | 4800 | 3600 | 200 × 240 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 2.84 | 9 | 0.3 | 20 | 0.75 |
| PSRCF-2 | 4800 | 3600 | 200 × 240 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 2.01 | 9 | 0.3 | 20 | 0.75 |
| PSRCF-3 | 4800 | 3600 | 200 × 240 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 3.75 | 9 | 0.3 | 20 | 0.75 |
| PSRCF-4 | 4800 | 3600 | 200 × 240 | 400 × 400 | 60 | 2.04 | 3.6 × 104 | 3.75 | 9 | 0.3 | 20 | 0.75 |
| PSRCF-5 | 4800 | 3600 | 200 × 240 | 400 × 400 | 80 | 2.22 | 3.8 × 104 | 3.75 | 9 | 0.3 | 20 | 0.75 |
| PSRCF-6 | 4800 | 3600 | 200 × 240 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 3.75 | 9 | 0.1 | 20 | 0.75 |
| PSRCF-7 | 4800 | 3600 | 200 × 240 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 3.75 | 9 | 0.2 | 20 | 0.75 |
| PSRCF-8 | 4800 | 3600 | 200 × 240 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 3.75 | 9 | 0.4 | 20 | 0.75 |
| PSRCF-9 | 4800 | 3600 | 200 × 240 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 3.75 | 9 | 0.5 | 20 | 0.75 |
| PSRCF-10 | 4800 | 3600 | 200 × 270 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 3.75 | 9 | 0.3 | 18 | 0.75 |
| PSRCF-11 | 4800 | 3600 | 200 × 300 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 3.75 | 9 | 0.3 | 16 | 0.75 |
| PSRCF-12 | 4800 | 2800 | 200 × 240 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 3.75 | 6 | 0.3 | 20 | 0.75 |
| PSRCF-13 | 4800 | 4200 | 200 × 240 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 3.75 | 12 | 0.3 | 20 | 0.75 |
| PSRCF-14 | 4800 | 3600 | 200 × 240 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 3.75 | 9 | 0.3 | 20 | 0.70 |
| PSRCF-15 | 4800 | 3600 | 200 × 240 | 400 × 400 | 70 | 2.14 | 3.7 × 104 | 3.75 | 9 | 0.3 | 20 | 0.65 |
| Material Type | Strength Grade | Yield Strength fy/MPa | Tensile Strength fu/MPa | Elastic Modulus E/MPa |
|---|---|---|---|---|
| H-shaped steel | Q235 | 235 | 370 | 2.1 × 105 |
| Gusset plate | Q235 | 235 | 370 | 2.1 × 105 |
| Angle steel | Q345 | 345 | 470 | 2.0 × 105 |
| Longitudinal steel bars | HRB335 | 335 | 455 | 2.0 × 105 |
| Stirrup | HPB235 | 235 | 370 | 2.1 × 105 |
| Prestressing tendon | 1670 | - | 1670 | 1.95 × 105 |
| Dilation Angle/° | Eccentric Ratio | fbo/fco | K | Viscosity Parameter |
|---|---|---|---|---|
| 36 | 0.1 | 1.16 | 0.667 | 0.0005 |
| Specimens | L (mm) | H (mm) | bb × hb (mm × mm) | bc × hc (mm × mm) | fcu (MPa) | n | λ | Ns (kN) | Nt (kN) | |
|---|---|---|---|---|---|---|---|---|---|---|
| SRCF | 4000 | 3800 | 200 × 270 | 300 × 300 | 40 | 0.1 | / | 205.46 | 207.09 | 0.79 |
| PSRCF | 4000 | 3800 | 200 × 230 | 300 × 300 | 40 | 0.1 | 0.75 | 195.11 | 192.89 | 1.15 |
| Specimens | fcu (MPa) | α | β | n | L/hb | λ | Py (MPa) | Pu (MPa) | Δy (mm) | Δu (mm) | μ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| PSRCF-1 | 70 | 2.84% | 9 | 0.3 | 20 | 0.75 | 296.77 | 331.51 | 20.31 | 67.69 | 3.20 |
| PSRCF-2 | 70 | 2.01% | 9 | 0.3 | 20 | 0.75 | 260.52 | 275.25 | 16.37 | 57.35 | 3.08 |
| PSRCF-3 | 70 | 3.75% | 9 | 0.3 | 20 | 0.75 | 349.66 | 392.59 | 23.56 | 92.43 | 3.30 |
| PSRCF-4 | 60 | 3.75% | 9 | 0.3 | 20 | 0.75 | 330.43 | 381.42 | 24.75 | 89.51 | 3.45 |
| PSRCF-5 | 80 | 3.75% | 9 | 0.3 | 20 | 0.75 | 349.59 | 396.15 | 23.32 | 78.51 | 3.05 |
| PSRCF-6 | 70 | 3.75% | 9 | 0.1 | 20 | 0.75 | 326.28 | 359.40 | 23.79 | 104.70 | 4.31 |
| PSRCF-7 | 70 | 3.75% | 9 | 0.2 | 20 | 0.75 | 346.31 | 382.40 | 23.51 | 97.63 | 3.75 |
| PSRCF-8 | 70 | 3.75% | 9 | 0.4 | 20 | 0.75 | 337.80 | 391.85 | 24.17 | 75.14 | 3.06 |
| PSRCF-9 | 70 | 3.75% | 9 | 0.5 | 20 | 0.75 | 340.59 | 388.5 | 23.77 | 71.55 | 3.01 |
| PSRCF-10 | 70 | 3.75% | 9 | 0.3 | 18 | 0.75 | 357.31 | 396.945 | 23.83 | 78.88 | 3.31 |
| PSRCF-11 | 70 | 3.75% | 9 | 0.3 | 16 | 0.75 | 359.39 | 398.26 | 23.54 | 83.76 | 3.33 |
| PSRCF-12 | 70 | 3.75% | 6 | 0.3 | 20 | 0.75 | 589.13 | 610.02 | 11.90 | 91.10 | 7.21 |
| PSRCF-13 | 70 | 3.75% | 12 | 0.3 | 20 | 0.75 | 244.95 | 274.22 | 35.74 | 106.51 | 2.98 |
| PSRCF-14 | 70 | 3.75% | 9 | 0.3 | 20 | 0.70 | 352.23 | 389.76 | 24.92 | 87.68 | 3.37 |
| PSRCF-15 | 70 | 3.75% | 9 | 0.3 | 20 | 0.65 | 351.67 | 388.26 | 23.79 | 88.23 | 3.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, J.; Zhang, H.; Jiang, L.; Zhang, Y.; Yuan, Z.; Zhang, Z.; Chu, X.; Li, B. Seismic Behaviors of Novel Steel-Reinforced Concrete Composite Frames Prestressed with Bonding Tendons. Buildings 2023, 13, 2124. https://doi.org/10.3390/buildings13092124
Ji J, Zhang H, Jiang L, Zhang Y, Yuan Z, Zhang Z, Chu X, Li B. Seismic Behaviors of Novel Steel-Reinforced Concrete Composite Frames Prestressed with Bonding Tendons. Buildings. 2023; 13(9):2124. https://doi.org/10.3390/buildings13092124
Chicago/Turabian StyleJi, Jing, Huiling Zhang, Liangqin Jiang, Yunfeng Zhang, Zhaoqing Yuan, Zhanbin Zhang, Xuan Chu, and Bing Li. 2023. "Seismic Behaviors of Novel Steel-Reinforced Concrete Composite Frames Prestressed with Bonding Tendons" Buildings 13, no. 9: 2124. https://doi.org/10.3390/buildings13092124
APA StyleJi, J., Zhang, H., Jiang, L., Zhang, Y., Yuan, Z., Zhang, Z., Chu, X., & Li, B. (2023). Seismic Behaviors of Novel Steel-Reinforced Concrete Composite Frames Prestressed with Bonding Tendons. Buildings, 13(9), 2124. https://doi.org/10.3390/buildings13092124