Study on the Force Model of Squeezed Branch Piles Based on Surface Potential Characteristics
Abstract
:1. Introduction
2. System, Sample, and Scheme for Squeezed Branch Piles Static Load Experiment
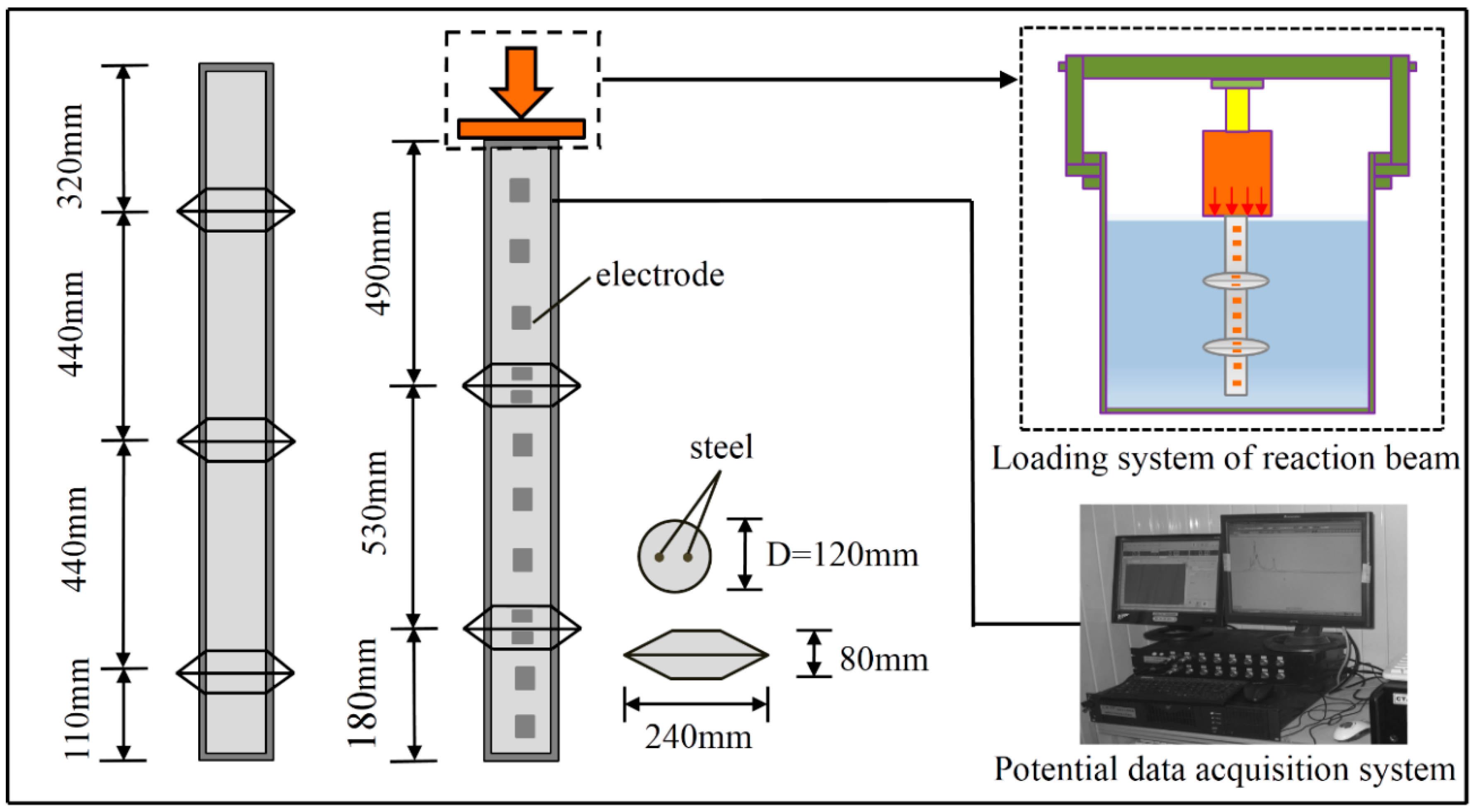
2.1. Test Measuring System
- (1)
- The system has 16 signal channels with an analog-to-digital conversion resolution of 16 bits.
- (2)
- Signal sampling frequency can be selected between low-speed continuous sampling frequency (continuously adjustable in the range of 1–100 Hz) and high-speed continuous sampling frequency (adjustable in the range of 100–1000 Hz). The duration of the sampling frequency lies in the range of 1–200 s.
- (3)
- It has low system noise, which is not higher than 2/10,000 of the whole range under 40 dB conditions.
- (4)
- The amplification factor of a front-end bridge amplifier is 50 times. The generation of potential signals from the squeezed branch pile surface will change the balance of the bridge, and the system will sample the potential signals. In order to allow the bridge to return to zero quickly after measuring a potential signal, a 5 MΩ discharge resistor is connected in parallel at the input end of the front-end amplifier. Besides the main amplifier can also allow the selection of 1, 2, 4, and 8 times magnification.
2.2. Composition of Experimental System
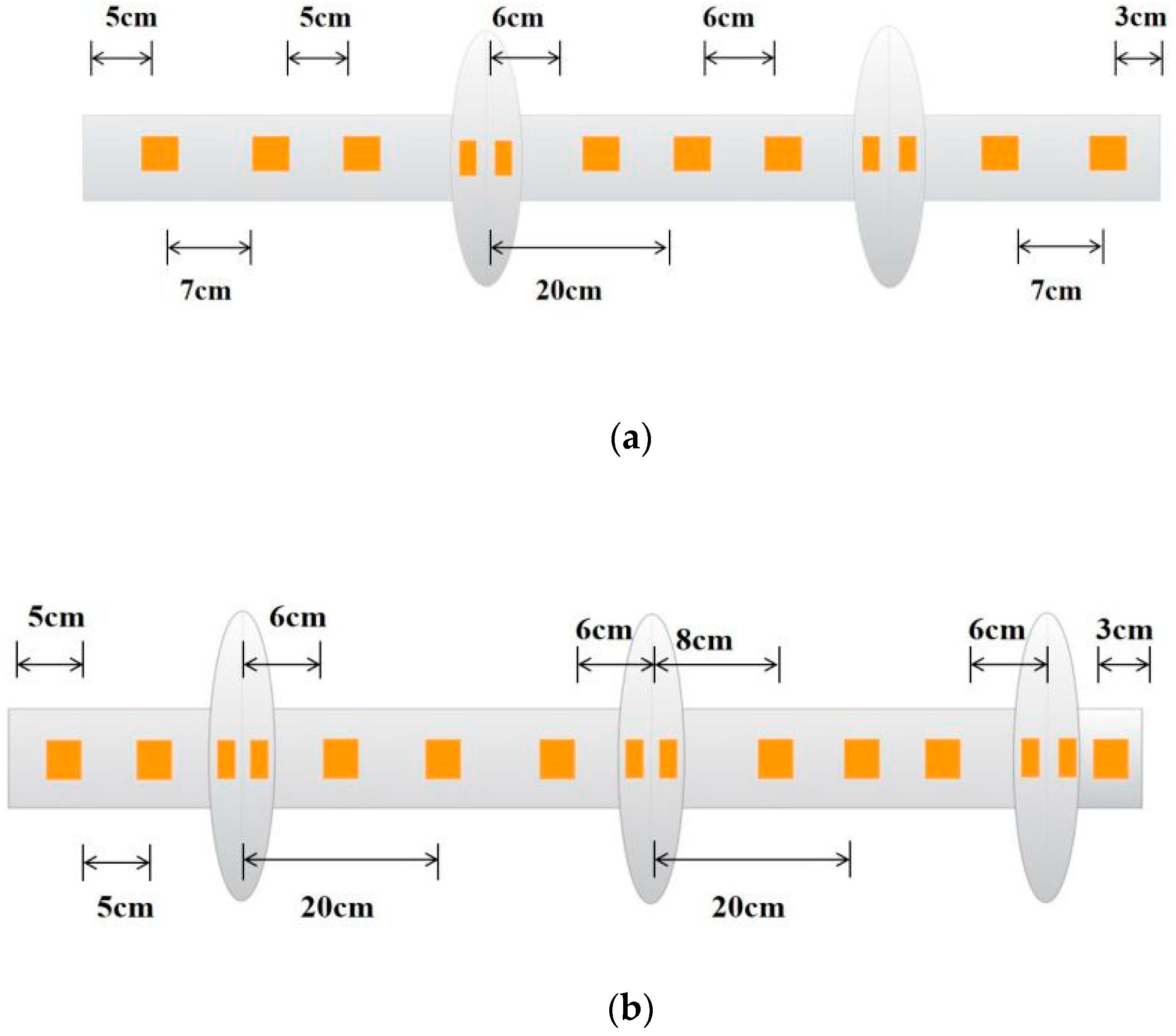
2.3. Static Load Test of the Squeezed Branch Pile Model
2.4. Test Procedure
- (1)
- The tested squeezed branch pile was put between the self-made reaction beam and the jack, and insulation paper was placed on the pile top. Then, the experimental device was connected to the jack to start loading.
- (2)
- First, a certain initial force (1 MPa) was applied to the jack to help the jack, the reaction beam, and the squeezed branch pile enter a preliminary state of force stability.
- (3)
- The potential data acquisition system was turned on. The pre-acquisition of data began when the mean variance of the acquired data approached 0.
- (4)
- Next, graded loading was applied to the squeezed branch pile for 1 MPa and 60 s per level until the squeezed branch pile settled and failed completely.
3. Test Results
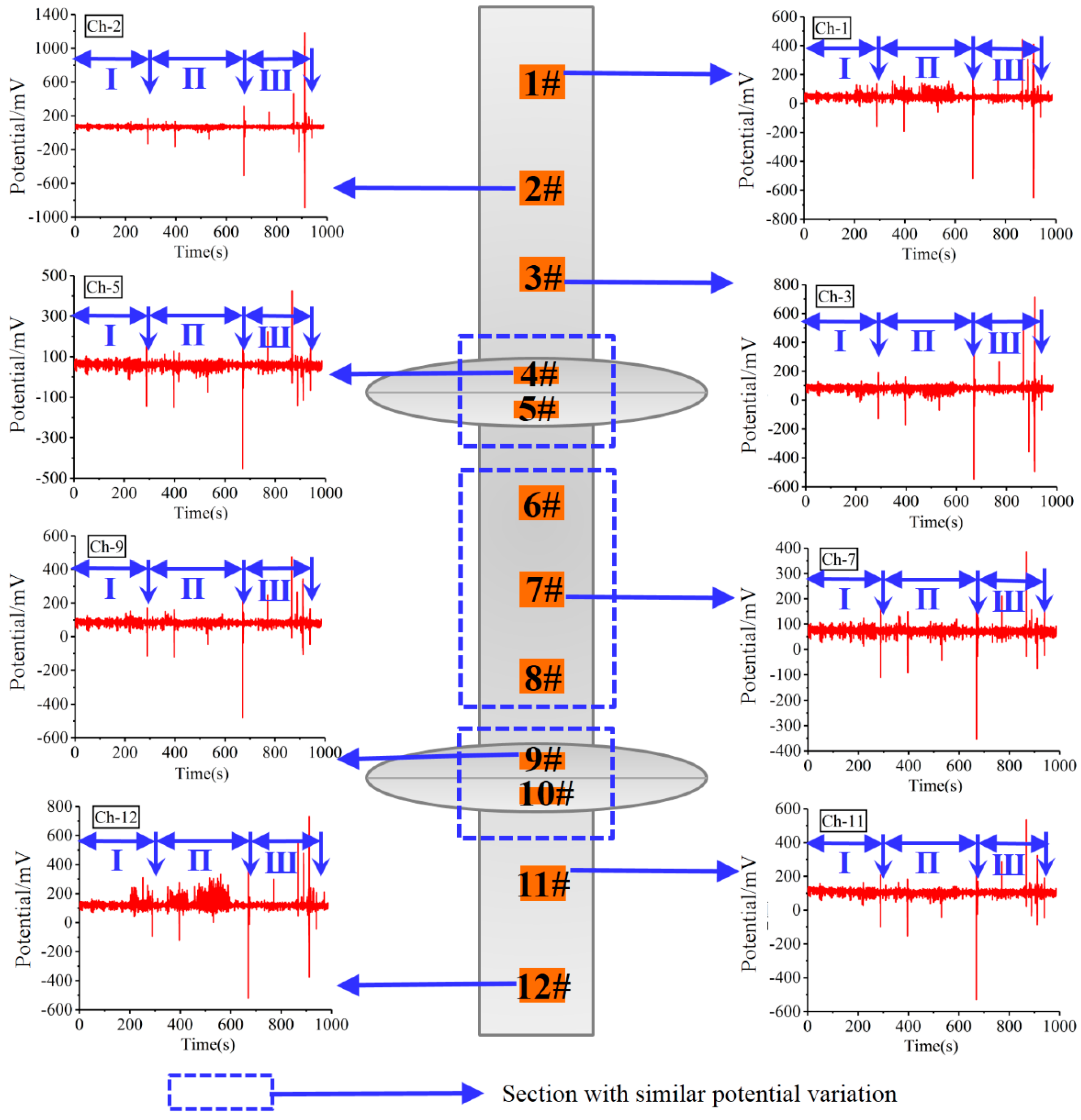
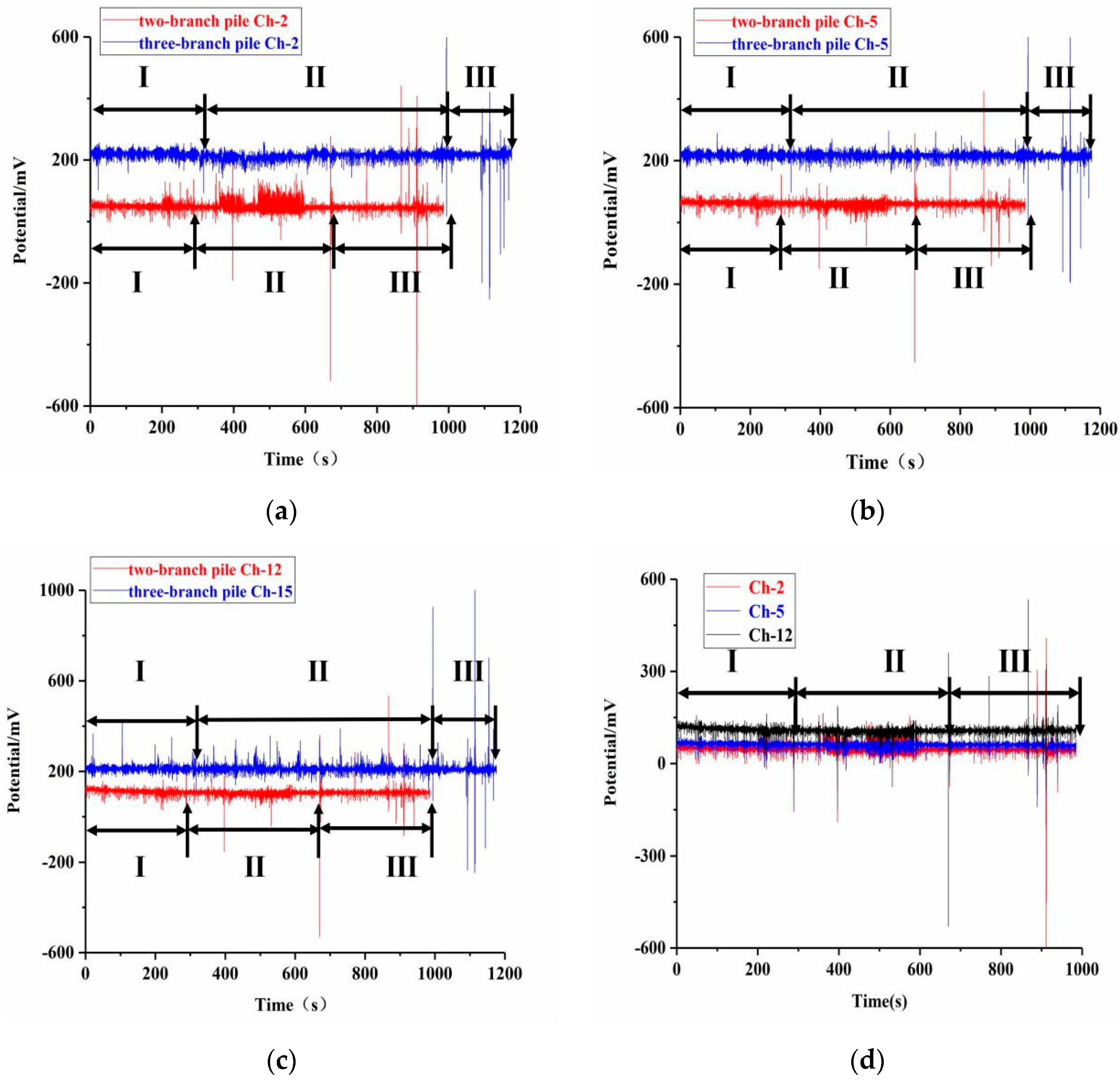
3.1. Characteristics of Surface Potential of a Two-Branch Pile under Load
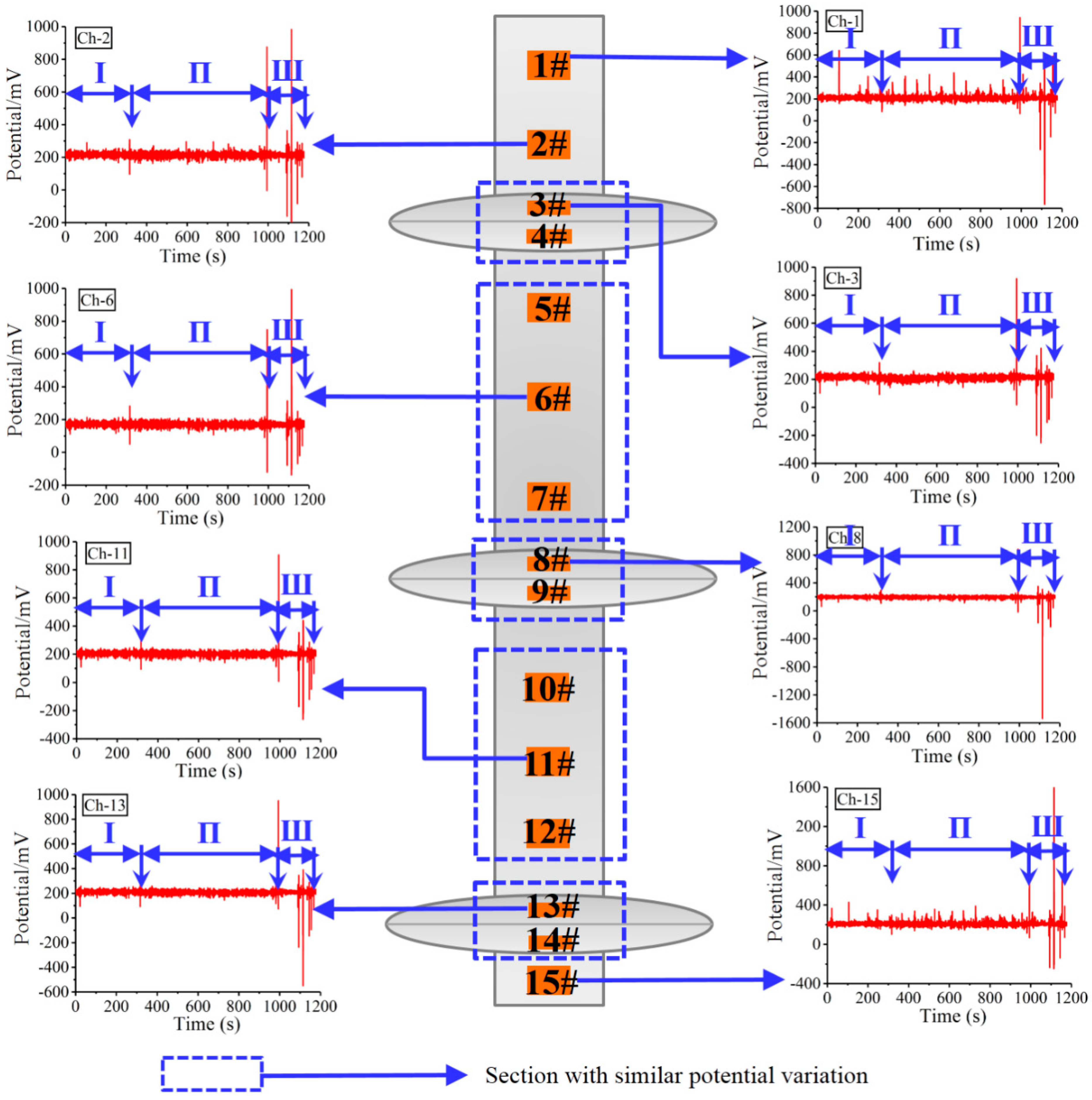
3.2. Characteristics of Surface Potential of a Three-Branch Pile under Load
3.3. Comparative Analysis of the Causes of Abnormal Surface Potential of Squeezed Branch Piles
4. Discussion
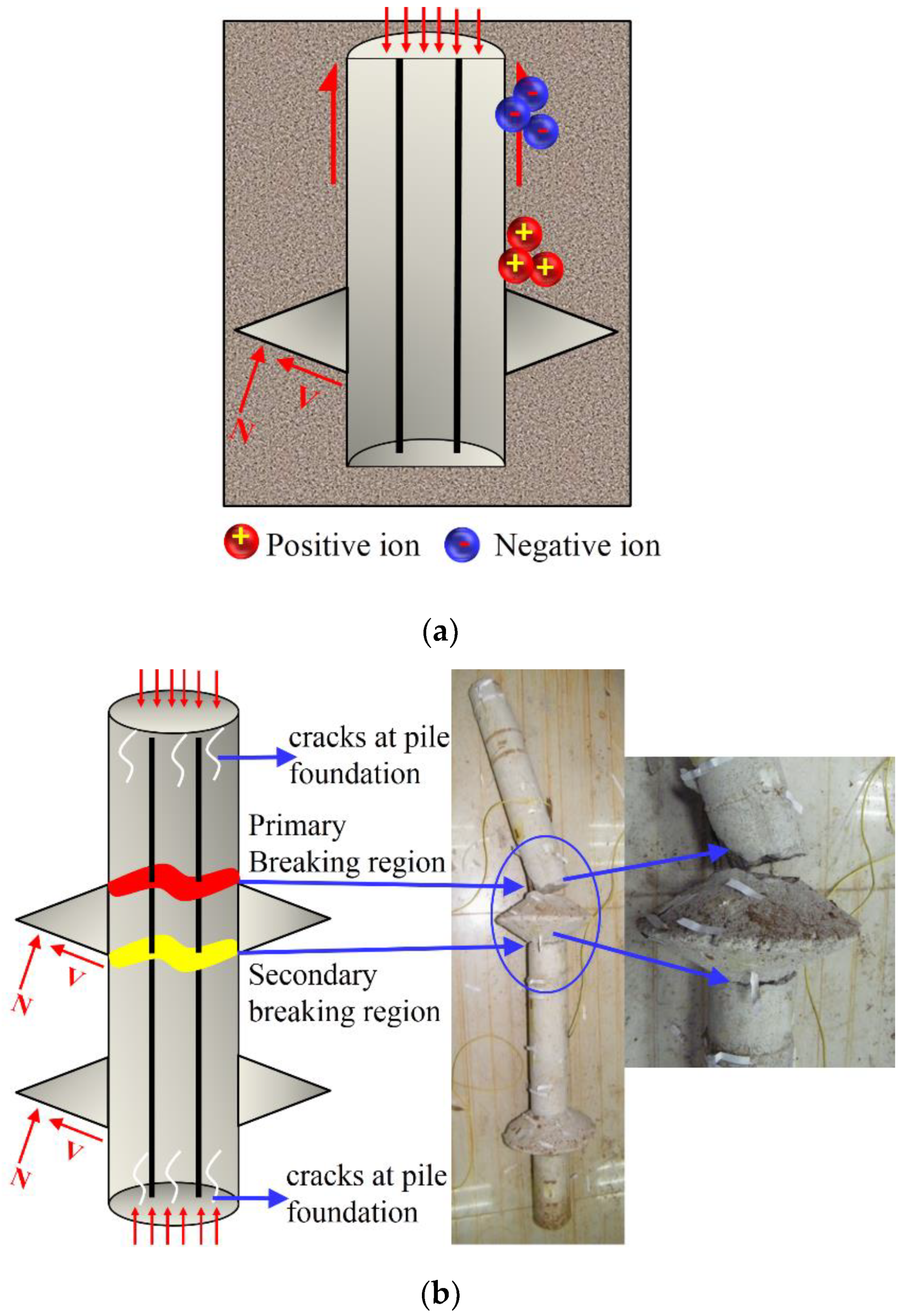
4.1. Discharge Mechanism during Concrete Failure
4.2. Failure Mechanism of Squeezed Branch Piles and Response Characteristics of Potential Signals
5. Conclusions
- (1)
- Surface potential signals are generated during the deformation of squeezed branch piles under load, and the deformation state of the pile body is the dominant factor affecting the surface potential signals. In the initial stage of loading, the squeezed branch piles get compressed and settle under the action of axial load, and potential signals fluctuate in a small range with the increase in of load. With the increase in load on the pile top, the weak structure of the test pile yields, and the peak pulse phenomenon appears in the potential signal. With the further increase in load, the upper branch of squeezed branch piles broke due to the interaction between the pile and the soil. At this time, the peak pulse frequency of potential signals increases, and the potential signal responds with large values.
- (2)
- During the whole static load simulation test on the squeezed branch piles, the changes in surface potential signals are well correlated with the load on the pile top, the deformation of pile body and the setting of branches. Therefore, the changes in surface potential signals can be used to predict the deformation and failure state of squeezed branch piles and to further evaluate the stress state and stability of squeezed branch piles. This finding provides a new method and means for quality detection and damage assessment of branch piles.
- (3)
- The change in surface potential signal is the macroscopic manifestation of pile settlement, deformation, and free charge movement. The failure of concrete under load causes a change in the surface potential signal caused by free electrons generated by friction electrification, piezoelectric effect, crack propagation, and charge separation under non-equilibrium stress.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, Q.Q.; Meng, Q.L.; Hu, Y.F.; Lai, W. Engineering application of settlement-controlled composite pile foundations. Chin. J. Rock Mech. Eng. 2008, 27, 3153–3158. [Google Scholar]
- Yang, J.P.; Piao, C.D. Distributed detection and bearing mechanism of squeezed branch piles. Chin. J. Geotech. Eng. 2013, 35, 1232–1235. [Google Scholar]
- Pradhan, M.K.; Kumar, P.; Phanikanth, V.S.; Choudhury, D.; Srinivas, K. A review on design aspects and behavioral studies of pile foundations in liquefiable soil. Geomech. Geoengin. 2023, 18, 347–379. [Google Scholar] [CrossRef]
- Liu, X.D.; Li, H.C.; Zhao, J.L. Code for design of highway bridge and culvert foundation and foundation (JTG3363-2019) Introduction to the revision. Highway 2021, 66, 162–164. [Google Scholar]
- Wang, Y.M.; Zhang, K.B.; Qiu, S.; Chen, Y.K.; Xu, D.J.; Yang, J.P. Comparative study on the design parameters and compressive bearing capacity of squeezed branch piles based on current specifications. Build. Struct. 2023, 53, 2648–2653. [Google Scholar]
- Lueprasert, P.; Jongpradist, P.; Jongpradist, P.; Suwansawat, S. Numerical investigation of tunnel deformation due to adjacent loaded pile and pile-soil-tunnel interaction. Tunn. Undergr. Space Technol. 2017, 70, 166–181. [Google Scholar] [CrossRef]
- Su, Q.Q.; Xia, H.B.; Wu, K.M.; Yang, F.L.; Pascoletti, G. The Effects of Branch Spacing and Number on the Uplift Bearing Capacity of a New Squeezed Multiple-Branch Pile: A Numerical Simulation Analysis. Model. Simul. Eng. 2023, 2023, e3758253. [Google Scholar] [CrossRef]
- Zhang, M.X.; Xu, P.; Cui, W.J.; Gao, Y.B. Bearing behavior and failure mechanism of squeezed branch piles. J. Rock Mech. Geotech. Eng. 2018, 10, 935–946. [Google Scholar] [CrossRef]
- Chen, F.; Wu, K.X.; He, S. Field tests on load transfer performances of squeezed branch piles. Chin. J. Geotech. Eng. 2013, 35, 990–993. [Google Scholar]
- Wang, Y.; Xu, L.; Li, B.; Xu, C. Finite element numerical study on the axial bearing behaviors and factors of squeezed branch pile. China Civ. Eng. J. 2015, 48, 158–162. [Google Scholar]
- Wang, E.Y.; Liu, X.F.; He, X.Q.; Li, Z.H. Acoustic emission and rock dynamicand electromagnetic radiation synchronized monitoring technology and early-warning application for coal and rock disaster. J. China Univ. Min. Technol. 2018, 47, 942–948. [Google Scholar]
- Liu, X.F.; Zhang, S.Q.; Wang, E.Y.; Zhang, Z.; Wang, Y.; Yang, S. Multi-Index Geophysical Monitoring and Early Warning for Rockburst in Coalmine: A Case Study. Int. J. Environ. Res. Public Health 2023, 20, 392. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhang, H.; Wang, X.; Zhang, C.; Xie, H.; Yang, S.; Lu, W. Acoustic Emission Characteristics of Graded Loading Intact and Holey Rock Samples during the Damage and Failure Process. Appl. Sci. 2019, 9, 1595. [Google Scholar] [CrossRef]
- Behnia, A.; Chai, H.K.; Shiotani, T. Advanced structural health monitoring of concrete structures with the aid of acoustic emission. Constr. Build. Mater. 2014, 65, 282–302. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, E.; Zhang, H.; Bai, Z.; Zhang, Y.; Chen, X. Research on nonlinear variation of elastic wave velocity dispersion characteristic in limestone dynamic fracture process. Fractals 2023, 31, 2350008. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Wang, E.Y.; Li, N.; Zhang, H.; Bai, Z.; Zhang, Y. Research on macroscopic mechanical properties and microscopic evolution characteristic of sandstone in thermal environment. Constr. Build. Mater. 2023, 366, 13015. [Google Scholar] [CrossRef]
- Li, Z.H.; Cheng, F.Q.; Wei, Y.; Cao, K.; Zhang, X.; Zhang, Y.; Tian, H.; Wang, X. Study on coal damage evolution and surface stress field based on infrared radiation temperature. J. Geophys. Eng. 2018, 15, 1889–1899. [Google Scholar] [CrossRef]
- Hiasa, S.; Birgul, R.; Catbas, F.N. A data processing methodology for infrared thermography images of concrete bridges. Comput. Struct. 2017, 190, 205–218. [Google Scholar] [CrossRef]
- Watanabe, A.; Tokuda, S.; Mizuta, Y.; Miyamoto, S.; Nakanishi, T.; Furukawa, H.; Minagawa, H. Toward automated non-destructive diagnosis of chloride attack on concrete structures by near infrared spectroscopy. Constr. Build. Mater. 2021, 305, 124796. [Google Scholar] [CrossRef]
- Liu, Z.T.; Li, X.L.; Li, Z.H.; Liu, Y.J.; Yang, L.Y.; Feng, J.J. Electric potential of the hole wall of concrete under uniaxial compression. Meitan Xuebao/J. China Coal Soc. 2014, 39, 372–377. [Google Scholar]
- Wang, E.Y.; Li, Z.H.; Liu, Z.T.; Li, Y.N.; Song, X.Y. Experimental study on surface potential effect of coal under load. Chin. J. Geophys. 2009, 52, 1318–1325. (In Chinese) [Google Scholar] [CrossRef]
- Niu, Y.; Li, Z.H.; Kong, B.; Wang, E.; Lou, Q.; Qiu, L.; Kong, X.; Wang, J.; Dong, M.; Li, B. Similar simulation study on characteristics of electric potential response to coal mining. J. Geophys. Eng. 2017, 15, 42–50. [Google Scholar] [CrossRef]
- Li, Z.H.; Wang, E.Y.; Liu, Z.T.; Song, X.Y.; Li, Y.N. Study on characteristics and rules of surface potential during coal fracture. J. China Univ. Min. Technol. 2009, 38, 187–192. [Google Scholar]
- Li, Z.; Niu, Y.; Wang, E.; Liu, L.; Wang, H.; Wang, M.; Ali, M. Experimental Study on Electric Potential Response Characteristics of Gas-Bearing Coal During Deformation and Fracturing Process. Processes 2019, 7, 72. [Google Scholar] [CrossRef]
- Pan, Y.S.; Tang, Z.; Li, Z.H.; Zhu, L.-Y.; Li, G.-Z. Research on the chargeinducing regularity of coal rock at different loading rate in uniaxi-al compression tests. Chin. J. Geophys. 2013, 56, 1043–1048. [Google Scholar]
- Xiao, Q.; Wang, D.H.; Xu, J. Experimental study on mechanical characteristics of squeezed branch pile of transmission line. J. Exp. Mech. 2015, 30, 124–130. [Google Scholar]
- Li, Z.; Niu, Y.; Wang, E.; He, M. Study on electrical potential inversion imaging of abnormal stress in mining coal seam. Environ. Earth Sci. 2019, 78, 255. [Google Scholar] [CrossRef]
- Yin, S.; Li, Z.H.; Niu, Y.; Qiu, L.M.; Sun, Y.H.; Chen, F.Q.; Wei, Y. Experimental study on the characteristics of potential for coal rock evolution under loading. J. China Coal Soc. 2017, 42, 9–103. [Google Scholar]
- Ren, X.K.; Wang, E.Y.; Li, Z.H. Experimental study of characteristics of surface potential and electromagnetic radiation of pre-cracked rock plate during fracture. J. China Univ. Min. Technol. 2016, 45, 440–446. [Google Scholar]
- Hao, J.Q.; Liu, L.Q.; Long, H.L.; Ma, S.L.; Guo, Z.Q.; Qian, S.Q.; Zhou, J.G. New result of the experiment on self-potential change of rocks under biaxial compression. Chin. J. Geophys. 2004, 47, 475–482. (In Chinese) [Google Scholar] [CrossRef]
- Liu, J.; Liu, S.D.; Cao, Y. Self-potential characteristics in deep rock mass damage based on point discharge mechanism. Chin. J. Geophys. 2018, 61, 323–330. [Google Scholar]
- Ju, Y.W.; Liang, R.W.; Bai, X.H.; Zhang, S.Y. Experimental study on the failure pattern of expanded plates of the squeezed branch pile. Eng. Mech. 2013, 30, 188–194. [Google Scholar]
- Qian, D.L. Study on bearing behavior of squeezed branch pile. Chin. J. Rock Mech. Eng. 2003, 22, 494–499. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Liu, X.; Zhang, H.; Piao, C.; Niu, Y. Study on the Force Model of Squeezed Branch Piles Based on Surface Potential Characteristics. Buildings 2023, 13, 2231. https://doi.org/10.3390/buildings13092231
Zhang S, Liu X, Zhang H, Piao C, Niu Y. Study on the Force Model of Squeezed Branch Piles Based on Surface Potential Characteristics. Buildings. 2023; 13(9):2231. https://doi.org/10.3390/buildings13092231
Chicago/Turabian StyleZhang, Siqing, Xiaofei Liu, Huajie Zhang, Chunde Piao, and Yue Niu. 2023. "Study on the Force Model of Squeezed Branch Piles Based on Surface Potential Characteristics" Buildings 13, no. 9: 2231. https://doi.org/10.3390/buildings13092231
APA StyleZhang, S., Liu, X., Zhang, H., Piao, C., & Niu, Y. (2023). Study on the Force Model of Squeezed Branch Piles Based on Surface Potential Characteristics. Buildings, 13(9), 2231. https://doi.org/10.3390/buildings13092231





