Minimum Cost Design for Rectangular Isolated Footings Taking into Account That the Column Is Located in Any Part of the Footing
Abstract
:1. Introduction
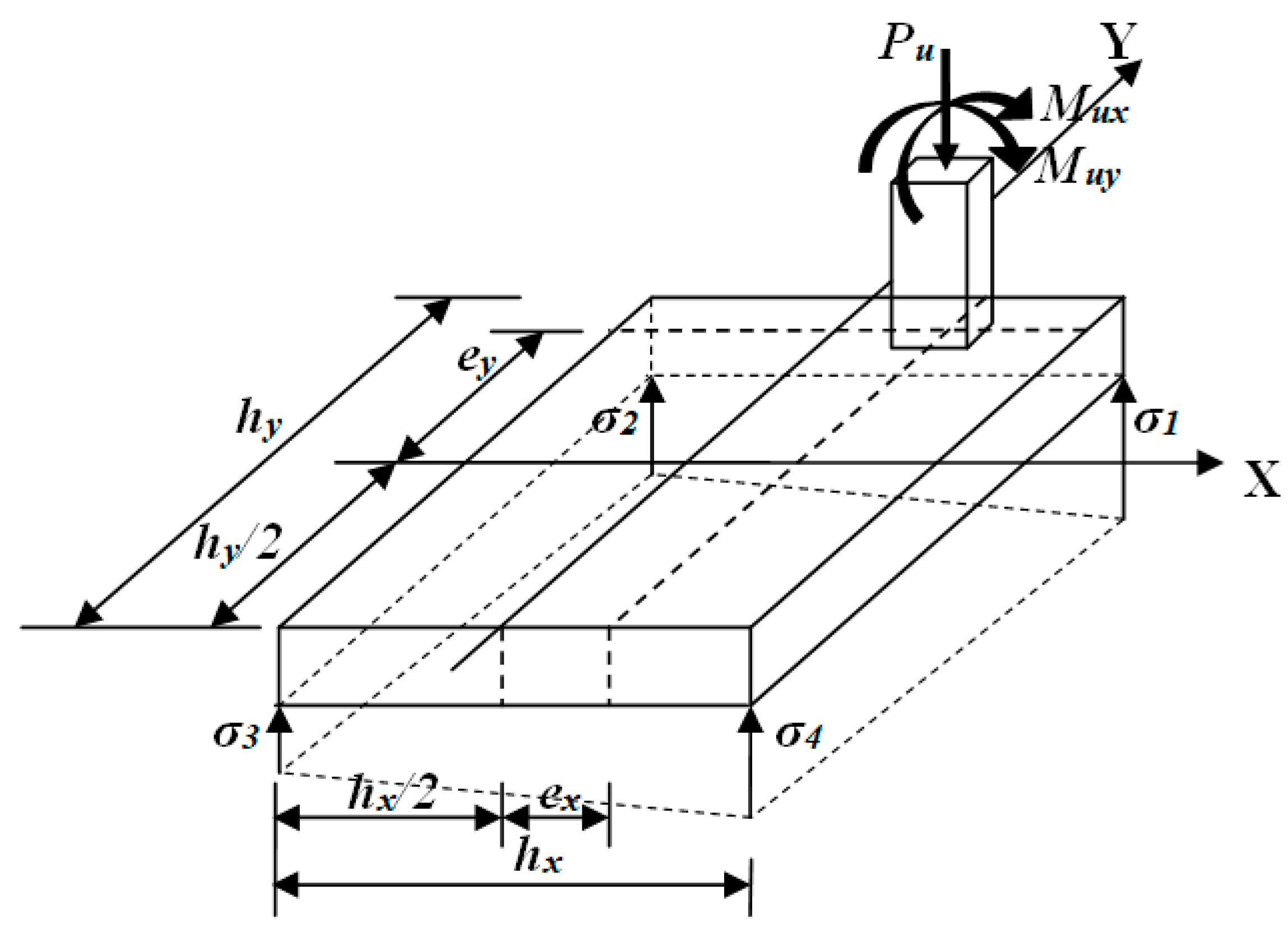
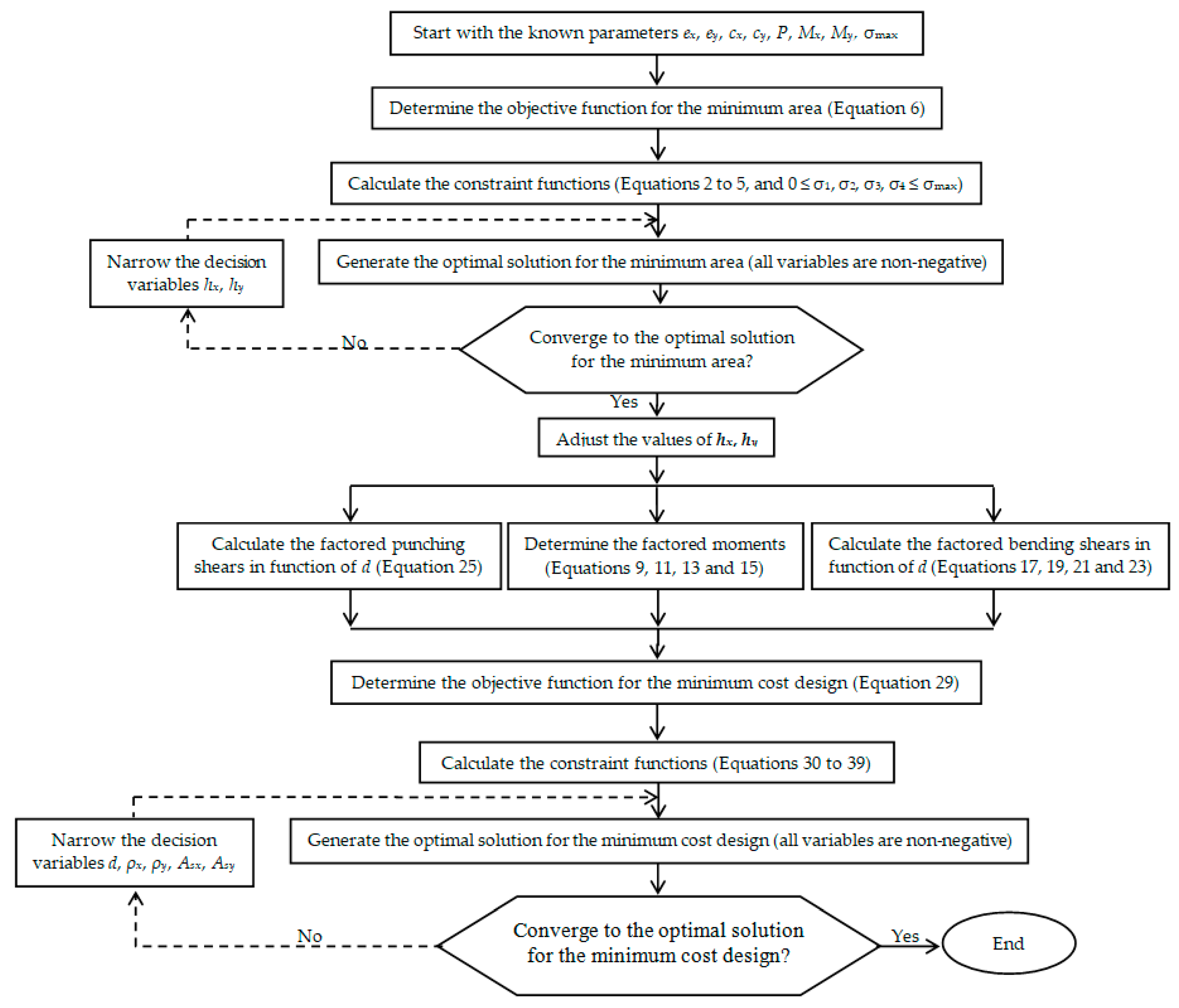
2. Formulation of the Model
2.1. Optimal Area for Rectangular Isolated Footing
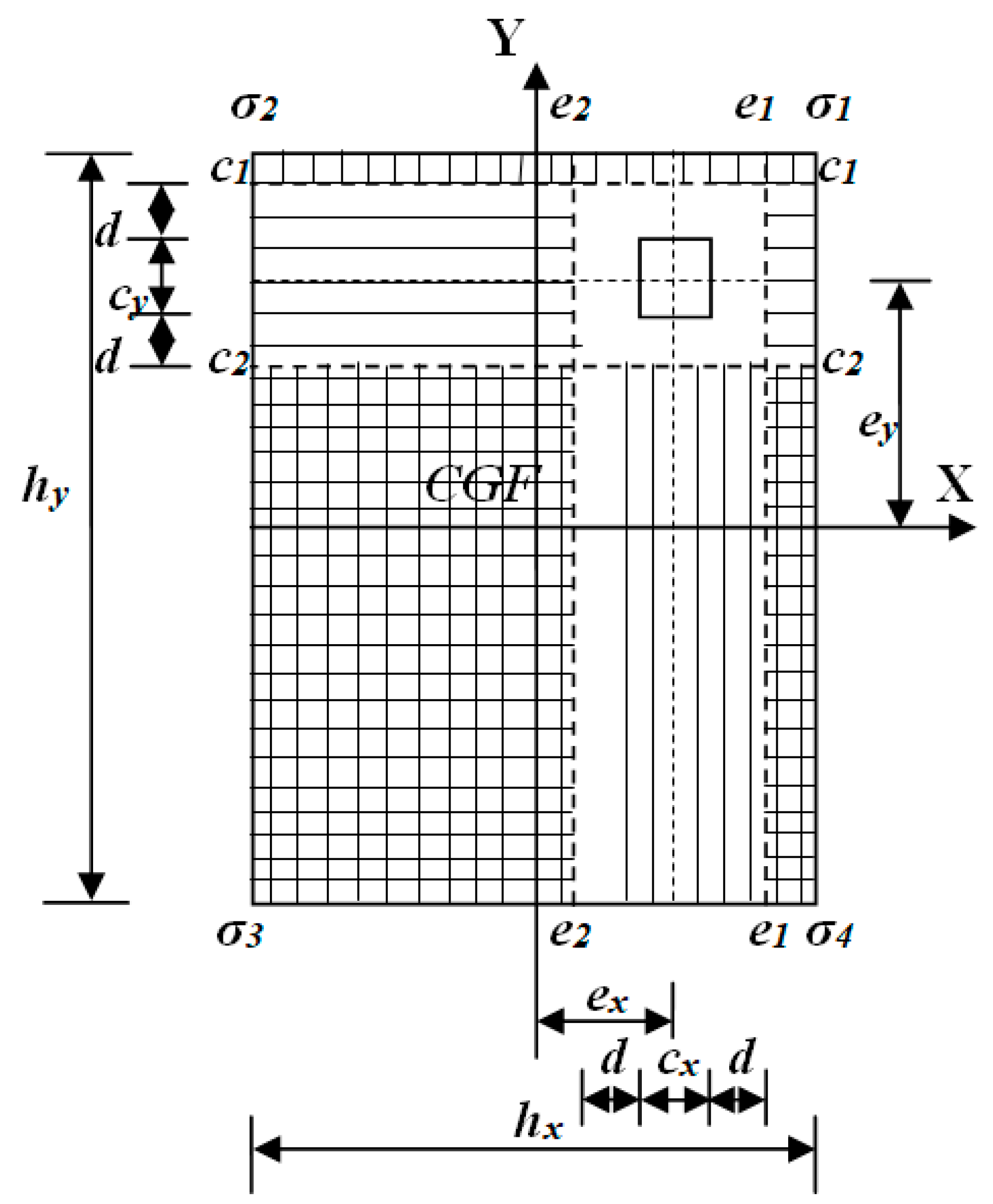
2.2. Optimal Cost for Rectangular Isolated Footing
2.2.1. Equations for Moments
2.2.2. Equations for Bending Shear
2.2.3. Equations for Punching Shear
2.2.4. Objective Function to Minimize the Cost
2.2.5. Constraint Functions
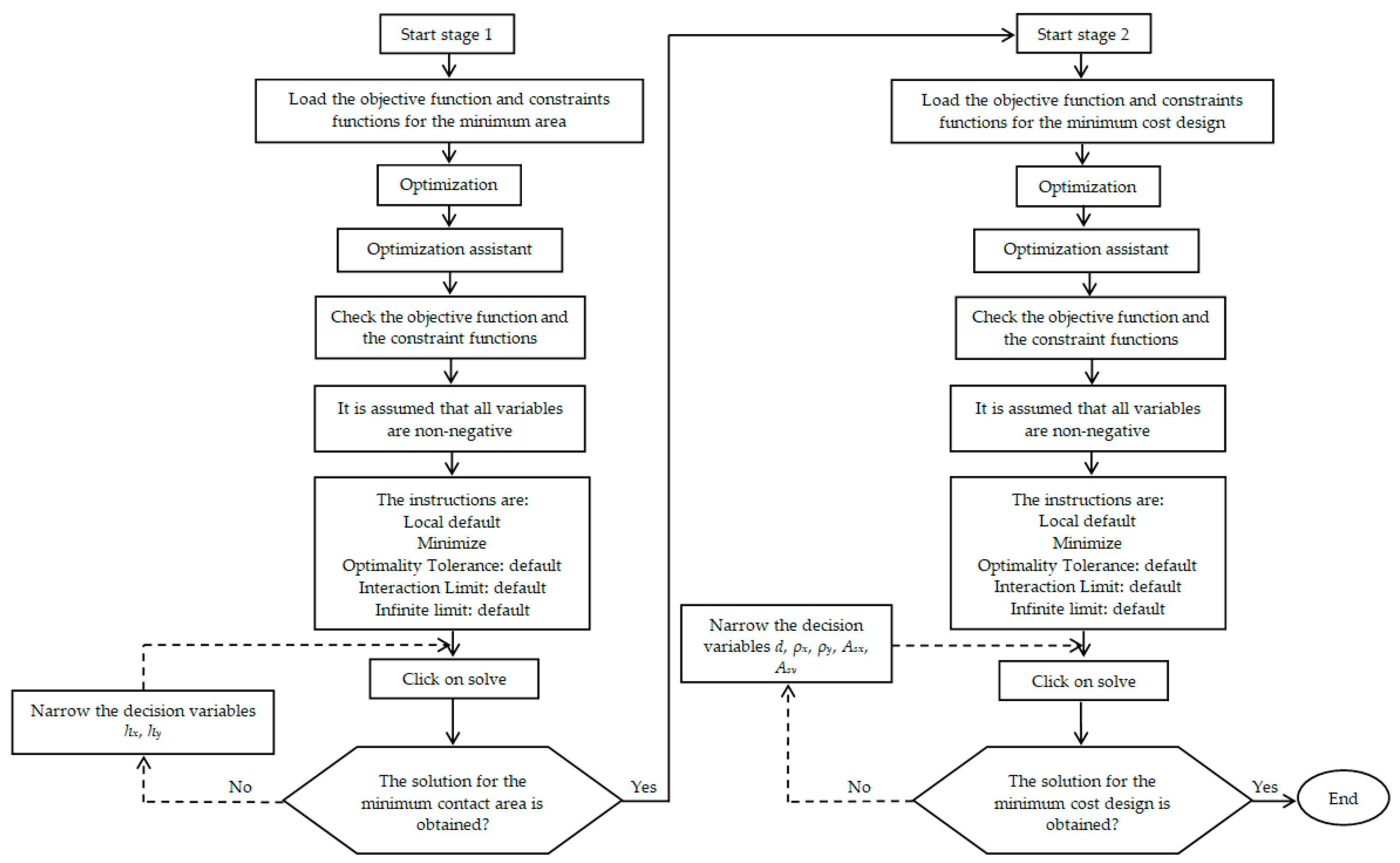
3. Numerical Problems
| Example | P (kN) | MX (kN-m) | My (kN-m) |
|---|---|---|---|
| 1.1 | 1000 | 225 | 150 |
| 1.2 | 850 | 225 | 150 |
| 1.3 | 750 | 225 | 150 |
| 1.4 | 600 | 225 | 150 |
| Example | hx (m) | hy (m) | σ1 (kN/m2) | σ2 (kN/m2) | σ3 (kN/m2) | σ4 (kN/m2) | Amin (m2) | Pu (kN) | Mux (kN-m) | Muy (kN-m) | Asx (cm2) | Asy (cm2) | d (m) | ρx | ρy | Cmin (USD) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.1 | 2.55 | 3.80 | 176.29 | 103.44 | 30.11 | 102.96 | 9.69 | 1400 | 300 | 200 | 45.19 | 52.36 | 0.36 | 0.00333 | 0.00575 | 7.03Cc |
| 1.2 | 2.45 | 3.65 | 177.49 | 95.33 | 12.61 | 94.77 | 8.94 | 1200 | 300 | 200 | 41.90 | 45.88 | 0.34 | 0.00333 | 0.00543 | 6.20Cc |
| 1.3 | 2.40 | 3.60 | 173.61 | 86.81 | 0 | 86.81 | 8.64 | 1000 | 300 | 200 | 35.94 | 45.86 | 0.30 | 0.00333 | 0.00637 | 5.52Cc |
| 1.4 | 3.00 | 4.50 | 88.89 | 44.44 | 0 | 44.44 | 13.50 | 800 | 300 | 200 | 35.51 | 62.77 | 0.24 | 0.00333 | 0.00883 | 7.74Cc |
| Example | P (kN) | MX (kN-m) | My (kN-m) |
|---|---|---|---|
| 2.1 | 1025 | −225 | 150 |
| 2.2 | 880 | −225 | 150 |
| 2.3 | 750 | −225 | 150 |
| 2.4 | 600 | −225 | 150 |
| Example | hx (m) | hy (m) | σ1 (kN/m2) | σ2 (kN/m2) | σ3 (kN/m2) | σ4 (kN/m2) | Amin (m2) | Pu (kN) | Mux (kN-m) | Muy (kN-m) | Asx (cm2) | Asy (cm2) | d (m) | ρx | ρy | Cmin (USD) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2.1 | 9.05 | 1.00 | 178.94 | 156.97 | 47.57 | 69.55 | 9.05 | 1400 | −300 | 200 | 51.12 | 258.39 | 0.86 | 0.00596 | 0.00333 | 14.90Cc |
| 2.2 | 6.95 | 1.00 | 178.92 | 141.66 | 74.32 | 111.58 | 6.95 | 1200 | −300 | 200 | 39.66 | 167.88 | 0.73 | 0.00547 | 0.00333 | 9.54Cc |
| 2.3 | 5.15 | 1.00 | 179.56 | 111.70 | 111.70 | 179.56 | 5.15 | 1000 | −300 | 200 | 29.79 | 102.89 | 0.60 | 0.00496 | 0.00333 | 5.78Cc |
| 2.4 | 4.00 | 1.15 | 179.35 | 81.52 | 81.52 | 179.35 | 4.60 | 800 | −300 | 200 | 25.90 | 59.18 | 0.44 | 0.00507 | 0.00333 | 3.94Cc |
| Example | P (kN) | MX (kN-m) | My (kN-m) |
|---|---|---|---|
| 3.1 | 1025 | 150 | −225 |
| 3.2 | 880 | 150 | −225 |
| 3.3 | 750 | 150 | −225 |
| 3.4 | 600 | 150 | −225 |
| Example | hx (m) | hy (m) | σ1 (kN/m2) | σ2 (kN/m2) | σ3 (kN/m2) | σ4 (kN/m2) | Amin (m2) | Pu (kN) | Mux (kN-m) | Muy (kN-m) | Asx (cm2) | Asy (cm2) | d (m) | ρx | ρy | Cmin (USD) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.1 | 1.00 | 9.05 | 178.94 | 69.55 | 47.57 | 156.97 | 9.05 | 1400 | 200 | −300 | 258.39 | 51.12 | 0.86 | 0.00333 | 0.00596 | 14.90Cc |
| 3.2 | 1.00 | 6.95 | 178.92 | 111.58 | 74.32 | 141.66 | 6.95 | 1200 | 200 | −300 | 167.88 | 39.66 | 0.73 | 0.00333 | 0.00547 | 9.54Cc |
| 3.3 | 1.00 | 5.15 | 179.56 | 179.56 | 111.70 | 111.70 | 5.15 | 1000 | 200 | −300 | 102.89 | 29.79 | 0.60 | 0.00333 | 0.00496 | 5.78Cc |
| 3.4 | 1.15 | 4.00 | 179.35 | 179.35 | 81.52 | 81.52 | 4.60 | 800 | 200 | −300 | 59.18 | 25.90 | 0.44 | 0.00333 | 0.00507 | 3.94Cc |
| Example | P (kN) | MX (kN-m) | My (kN-m) |
|---|---|---|---|
| 4.1 | 750 | −750 | −600 |
| 4.2 | 605 | −750 | −600 |
| 4.3 | 450 | −750 | −600 |
| 4.4 | 300 | −750 | −600 |
| Example | hx (m) | hy (m) | σ1 (kN/m2) | σ2 (kN/m2) | σ3 (kN/m2) | σ4 (kN/m2) | Amin (m2) | Pu (kN) | Mux (kN-m) | Muy (kN-m) | Asx (cm2) | Asy (cm2) | d (m) | ρx | ρy | Cmin (USD) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4.1 | 2.00 | 2.35 | 149.39 | 149.39 | 169.76 | 169.76 | 4.70 | 1000 | −1000 | −800 | 41.60 | 43.51 | 0.53 | 0.00333 | 0.00409 | 4.53Cc |
| 4.2 | 2.15 | 2.60 | 38.09 | 108.60 | 178.37 | 107.85 | 5.59 | 800 | −1000 | −800 | 40.86 | 51.08 | 0.47 | 0.00333 | 0.00503 | 5.05Cc |
| 4.3 | 2.65 | 3.20 | 1.50 | 51.56 | 104.63 | 54.57 | 8.48 | 600 | −1000 | −800 | 48.17 | 63.75 | 0.40 | 0.00379 | 0.00606 | 7.00Cc |
| 4.4 | 3.80 | 4.65 | 0.72 | 16.80 | 33.24 | 17.15 | 17.67 | 400 | −1000 | −800 | 59.40 | 77.92 | 0.34 | 0.00378 | 0.00607 | 12.62Cc |
4. Results
- For moments:
- When the column is located at the end of the footing in the positive Y direction and on the Y axis, then ex = 0 and ey = hy/2 − cy/2 are substituted into Equation (9) and Mua1 = 0 is obtained;
- When the column is located at the end of the footing in the negative Y direction and on the Y axis, then ex = 0 and ey = − hy/2 + cy/2 are substituted into Equation (11) and Mua2 = 0 is obtained;
- When the column is located in the center of the footing, then ex = 0 and ey = 0 are substituted into Equation (9) and is obtained. When the column is located in the center of the footing, then ex = 0 and ey = 0 are substituted into Equation (11) and is obtained. Now, if cy = 0 is substituted and Mua1 − Mua2 is performed, −Mux is obtained. This means that it is in equilibrium;
- When the column is located at the end of the footing in the positive X direction and on the X axis, then ex = hx/2 − cx/2 and ey = 0 are substituted into Equation (13) and Mub1 = 0 is obtained;
- When the column is located at the end of the footing in the negative X direction and on the X axis, then ex = −hx/2 + cx/2 and ey = 0 are substituted into Equation (15) and Mub2 = 0 is obtained;
- When the column is located in the center of the footing, then ex = 0 and ey = 0 are substituted into Equation (13) and is obtained. When the column is located in the center of the footing, then ex = 0 and ey = 0 are substituted into Equation (15) and is obtained. Now, if cx = 0 is substituted and Mub1 − Mub2 is performed, −Muy is obtained. This means that it is in equilibrium.
- For bending shear:
- When the column is located at a distance hy/2 − cy/2 − d from the center of the footing in the positive Y direction and on the Y axis, then ex = 0 and ey = hy/2 − cy/2 − d are substituted into Equation (17) and Vufc1 = 0 is obtained;
- When the column is located at a distance −hy/2 + cy/2 + d from the center of the footing in the negative Y direction and on the Y axis, then ex = 0 and ey = −hy/2 + cy/2 + d are substituted into Equation (19) and Vufc2 = 0 is obtained;
- When the column is located in the center of the footing, then ex = 0 and ey = 0 are substituted into Equation (15) and is obtained. When the column is located in the center of the footing, then ex = 0 and ey = 0 are substituted into Equation (11) and is obtained. Now, if cy = 0 and d = 0 are substituted and Vufc1 − Vufc2 is performed, −P is obtained. This means that it is in equilibrium;
- When the column is located at a distance hx/2 − cx/2 − d from the center of the footing in the positive X direction and on the X axis, then ex = hx/2 − cx/2 − d and ey = 0 are substituted into Equation (21) and Vufe1 = 0 is obtained;
- When the column is located at a distance −hx/2 + cx/2 + d from the center of the footing in the negative X direction and on the X axis, then ex = −hx/2 + cx/2 + d and ey = 0 are substituted into Equation (23) and Vufe2 = 0 is obtained;
- When the column is located in the center of the footing, then ex = 0 and ey = 0 are substituted into Equation (21) and is obtained. When the column is located in the center of the footing, then ex = 0 and ey = 0 are substituted into Equation (23) and is obtained. Now, if cx = 0 and d = 0 are substituted and Vufe1 − Vufe2 is performed, −P is obtained. This means that it is in equilibrium.
- For punching shear:
- When the column is located in the center of the footing, then x1 = cx/2 + d/2, x2 = −cx/2 − d/2, y1 = cy/2 + d/2, and y2 = −cy/2 − d/2 are substituted into Equation (25) and .
| Model | hx (m) | hy (m) | σ1 (kN/m2) | σ2 (kN/m2) | σ3 (kN/m2) | σ4 (kN/m2) | Amin (m2) | Pu (kN) | Mux (kN-m) | Muy (kN-m) | Asx (cm2) | Asy (cm2) | d (m) | t (m) | ρx | ρy | Cmin (USD) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Solorzano and Plevris | 3.49 | 2.34 | 400.00 | 201.72 | 201.72 | 400.00 | 8.16 | 3160 | 0 | 632 | 153.20 | 122.90 | 0.48 | 0.53 | 0.01364 | 0.00734 | 5.55Cc |
| New model | 1.00 | 7.12 | 400.00 | 288.97 | 288.97 | 400.00 | 7.12 | 3160 | 0 | 632 | 159.47 | 17.21 | 0.48 | 0.53 | 0.00470 | 0.00361 | 4.17Cc |
| Model | hx (m) | hy (m) | σ1 (kN/m2) | σ2 (kN/m2) | σ3 (kN/m2) | σ4 (kN/m2) | Amin (m2) | Pu (kN) | Mux (kN-m) | Muy (kN-m) | Asx (cm2) | Asy (cm2) | d (m) | t (m) | ρx | ρy | Cmin (USD) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Solorzano and Plevris | 2.14 | 3.02 | 399.29 | 399.29 | 399.29 | 399.29 | 6.46 | 3360 | 0 | 632 | 106.10 | 103.40 | 0.44 | 0.49 | 0.00798 | 0.01098 | 3.98Cc |
| New model | 2.54 | 2.54 | 399.93 | 399.93 | 399.93 | 399.93 | 6.45 | 3360 | 0 | 632 | 44.14 | 39.83 | 0.43 | 0.48 | 0.00400 | 0.00361 | 3.45Cc |
5. Conclusions
- Some engineers use the trial and error method to determine the dimensions for rectangular isolated footings subjected to biaxial bending, and the design is then obtained by considering the maximum and uniform pressure along the underside of the footing;
- Other authors present the cheapest design for rectangular isolated footings subjected to biaxial bending when resting on elastic soils, but only consider a column located at the center of gravity of the footing;
- Some authors present very complex algorithms to obtain the cheapest design for rectangular isolated footings subjected to biaxial bending resting on elastic soils;
- Equations for moments, bending shear and punching shear are verified by the establishment of equilibrium (see Section 4);
- The new model can be used for any other building code, taking into account the equations that resist the moments, the bending shear and the punching shear. Also, equations for determining the reinforcing steel areas can be proposed for any other building code.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hannan, M.R.; Johnson, G.E.; Hammond, C.R. A General Strategy for the Optimal Design of Reinforced Concrete Footings to Support Wind Loaded Structures. J. Mech. Des. 1993, 115, 751–756. [Google Scholar] [CrossRef]
- Basudhar, P.K.; Das, A.; Das, S.K.; Dey, A.; Deb, K.; De, S. Optimal cost design of rigid raft foundation. In Proceedings of the 10th East Asia-Pacific Conference on Structural Engineering and Construction (EASEC-10), Bangkok, Thailand, 3–5 August 2006; pp. 39–44. [Google Scholar]
- Basudhar, P.K.; Dey, A.; Mondal, A.S. Optimal Cost-Analysis and Design of Circular Footings. Int. J. Eng. Technol. Innov. 2012, 2, 243–264. [Google Scholar]
- Al-Douri, E.M.F. Optimum design of trapezoidal combined footings. Tikrit J. Eng. Sci. 2007, 14, 85–115. [Google Scholar] [CrossRef]
- Wang, Y.; Kulhawy, F.H. Economic design optimization of foundations. J. Geotech. Geoenviron. Eng. 2008, 134, 1097–1105. [Google Scholar] [CrossRef]
- Rizwan, M.; Alam, B.; Rehman, F.U.; Masud, N.; Shahzada, K.; Masud, T. Cost Optimization of Combined Footings Using Modified Complex Method of Box. Int. J. Adv. Struct. Geotech. Eng. 2012, 1, 24–28. [Google Scholar]
- Jelušič, P.; Žlender, B. Optimal Design of Reinforced Pad Foundation and Strip Foundation. Int. J. Geomech. 2018, 18, 04018105. [Google Scholar] [CrossRef]
- Jelušič, P.; Žlender, B. Optimal design of pad footing based on MINLP optimization. Soils Found. 2018, 58, 277–289. [Google Scholar] [CrossRef]
- Velázquez-Santillán, F.; Luévanos-Rojas, A.; López-Chavarría, S.; Medina-Elizondo, M.; Sandoval-Rivas, R. Numerical experimentation for the optimal design for reinforced concrete rectangular combined footings. Adv. Comput. Des. 2018, 3, 49–69. [Google Scholar] [CrossRef]
- López-Chavarría, S.; Luévanos-Rojas, A.; Medina-Elizondo, M.; Sandoval-Rivas, R.; Velázquez-Santillán, F. Optimal design for the reinforced concrete circular isolated footings. Adv. Comput. Des. 2019, 4, 273–294. [Google Scholar] [CrossRef]
- Khajuria, K.; Singh, E.B.; Sandeep Singla, S. Design Optimization of RC Column Footings under Axial Load of Beam and Rooftop Surfaces. Int. J. Sci. Technol. Res. 2020, 9, 5683–5688. [Google Scholar]
- Al-Ansari, M.S.; Afzal, M.S. Structural analysis and design of irregular shaped footings subjected to eccentric loading. Eng. Rep. 2021, 3, e12283. [Google Scholar] [CrossRef]
- Kashani, A.R.; Camp, C.V.; Akhani, M.; Ebrahimi, S. Optimum design of combined footings using swarm intelligence-based algorithms. Adv. Eng. Soft. 2022, 169, 103140. [Google Scholar] [CrossRef]
- Nigdeli, S.M.; Bekdas, G. The Investigation of Optimization of Eccentricity in Reinforced Concrete Footings. In Lecture Notes on Data Engineering and Communications Technologies, Proceedings of 7th International Conference on Harmony Search, Soft Computing and Applications; Springer: Singapore, 2022; Volume 140, pp. 207–215. [Google Scholar]
- Kamal, M.; Mortazavi, A.; Cakici, Z. Optimal Design of RC Bracket and Footing Systems of Precast Industrial Buildings Using Fuzzy Differential Evolution Incorporated Virtual Mutant. Arab. J. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Camp, C.V.; Assadollahi, A. CO2 and cost optimization of reinforced concrete footings using a hybrid big bang-big crunch algorithm. Struct. Multidiscip. Optim. 2013, 48, 411–426. [Google Scholar] [CrossRef]
- Luévanos-Rojas, A.; López-Chavarría, S.; Medina-Elizondo, M. Optimal design for rectangular isolated footings using the real soil pressure. Ing. Investig. 2017, 37, 25–33. [Google Scholar] [CrossRef]
- Galvis, F.A.; Smith-Pardo, P.J. Axial load biaxial moment interaction (PMM) diagrams for shallow foundations: Design aids, experimental verification, and examples. Eng. Struct. 2020, 213, 110582. [Google Scholar] [CrossRef]
- Rawat, S.; Mittal, R.K. Optimization of eccentrically loaded reinforced-concrete isolated footings. Pract. Period. Struct. Des. Constr. 2018, 23, 06018002. [Google Scholar] [CrossRef]
- Rawat, S.; Mittal, R.K.; Muthukumar, G. Isolated Rectangular Footings under Biaxial Bending: A Critical Appraisal and Simplified Analysis Methodology. Pract. Period. Struct. Des. Constr. 2020, 25, 04020011. [Google Scholar] [CrossRef]
- Solorzano, G.; Plevris, V. Optimum Design of RC Footings with Genetic Algorithms According to ACI 318-19. Buildings 2022, 10, 110. [Google Scholar] [CrossRef]
- Chaudhuri, P.; Maity, D. Cost optimization of rectangular RC footing using GA and UPSO. Soft Comput. 2020, 24, 709–721. [Google Scholar] [CrossRef]
- IS 456 (2000); Practice for plain and reinforced concrete or general building construction. Bureau of Indian Standards: New Delhi, Indian, 2000.
- Nigdeli, S.M.; Bekdaş, G.; Yang, X.-S. Metaheuristic Optimization of Reinforced Concrete Footings. KSCE J. Civ. Eng. 2018, 22, 4555–4563. [Google Scholar] [CrossRef]
- Waheed, J.; Azam, R.; Riaz, M.R.; Shakeel, M.; Mohamed, A.; Ali, E. Metaheuristic-Based Practical Tool for Optimal Design of Reinforced Concrete Isolated Footings: Development and Application for Parametric Investigation. Buildings 2022, 12, 471. [Google Scholar] [CrossRef]
- ACI 318-14; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2014.
- ACI 318-19; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2019.


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luévanos-Rojas, A. Minimum Cost Design for Rectangular Isolated Footings Taking into Account That the Column Is Located in Any Part of the Footing. Buildings 2023, 13, 2269. https://doi.org/10.3390/buildings13092269
Luévanos-Rojas A. Minimum Cost Design for Rectangular Isolated Footings Taking into Account That the Column Is Located in Any Part of the Footing. Buildings. 2023; 13(9):2269. https://doi.org/10.3390/buildings13092269
Chicago/Turabian StyleLuévanos-Rojas, Arnulfo. 2023. "Minimum Cost Design for Rectangular Isolated Footings Taking into Account That the Column Is Located in Any Part of the Footing" Buildings 13, no. 9: 2269. https://doi.org/10.3390/buildings13092269
APA StyleLuévanos-Rojas, A. (2023). Minimum Cost Design for Rectangular Isolated Footings Taking into Account That the Column Is Located in Any Part of the Footing. Buildings, 13(9), 2269. https://doi.org/10.3390/buildings13092269






