A New Proposal for the Interpretation of the Diagonal Compression Test on Masonry Wallettes: The Identification of Young’s Modulus, Poisson’s Ratio, and Modulus of Rigidity
Abstract
:1. Introduction
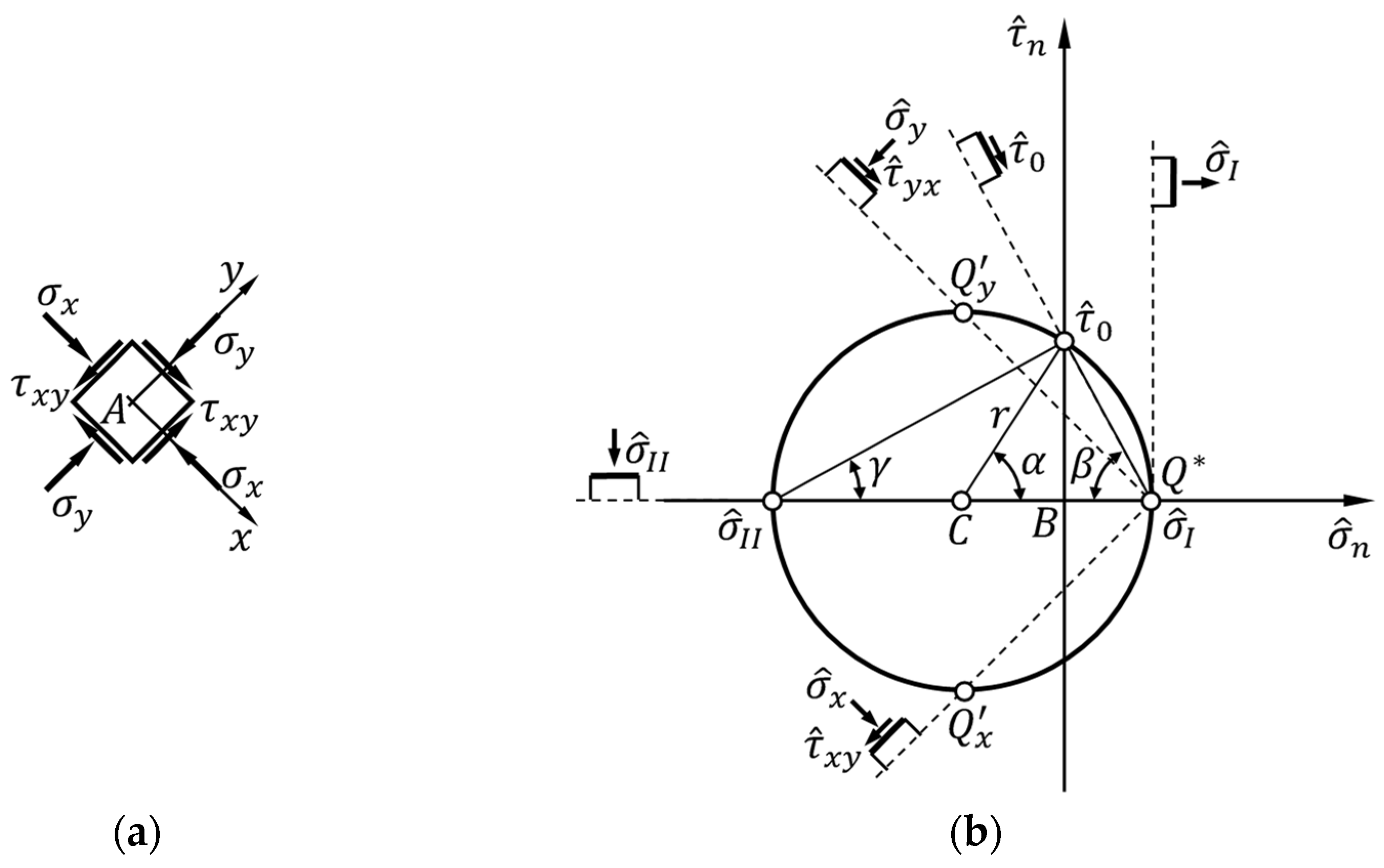
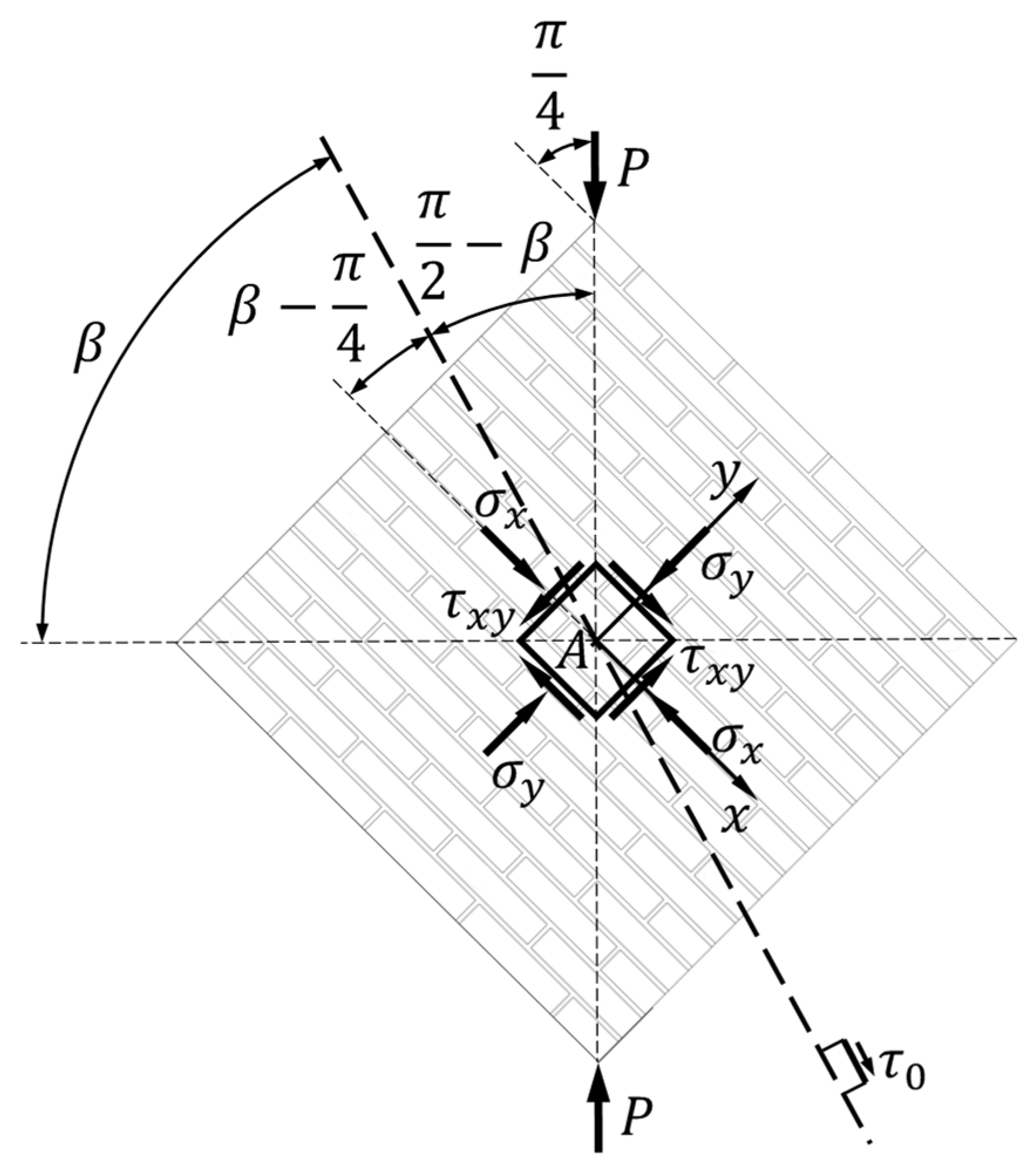
2. Problem Setting
3. Problem Solving in Parametric Form
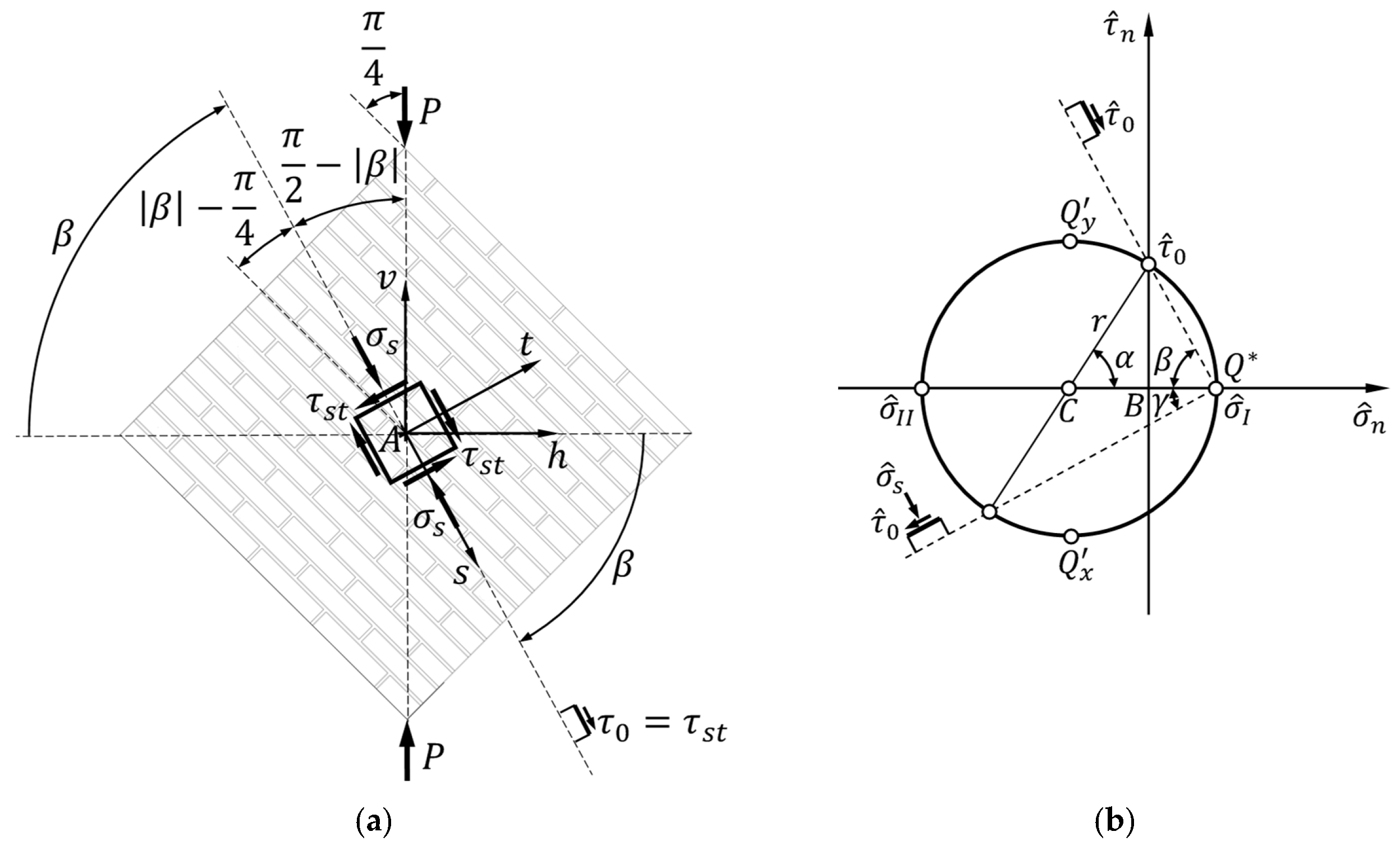
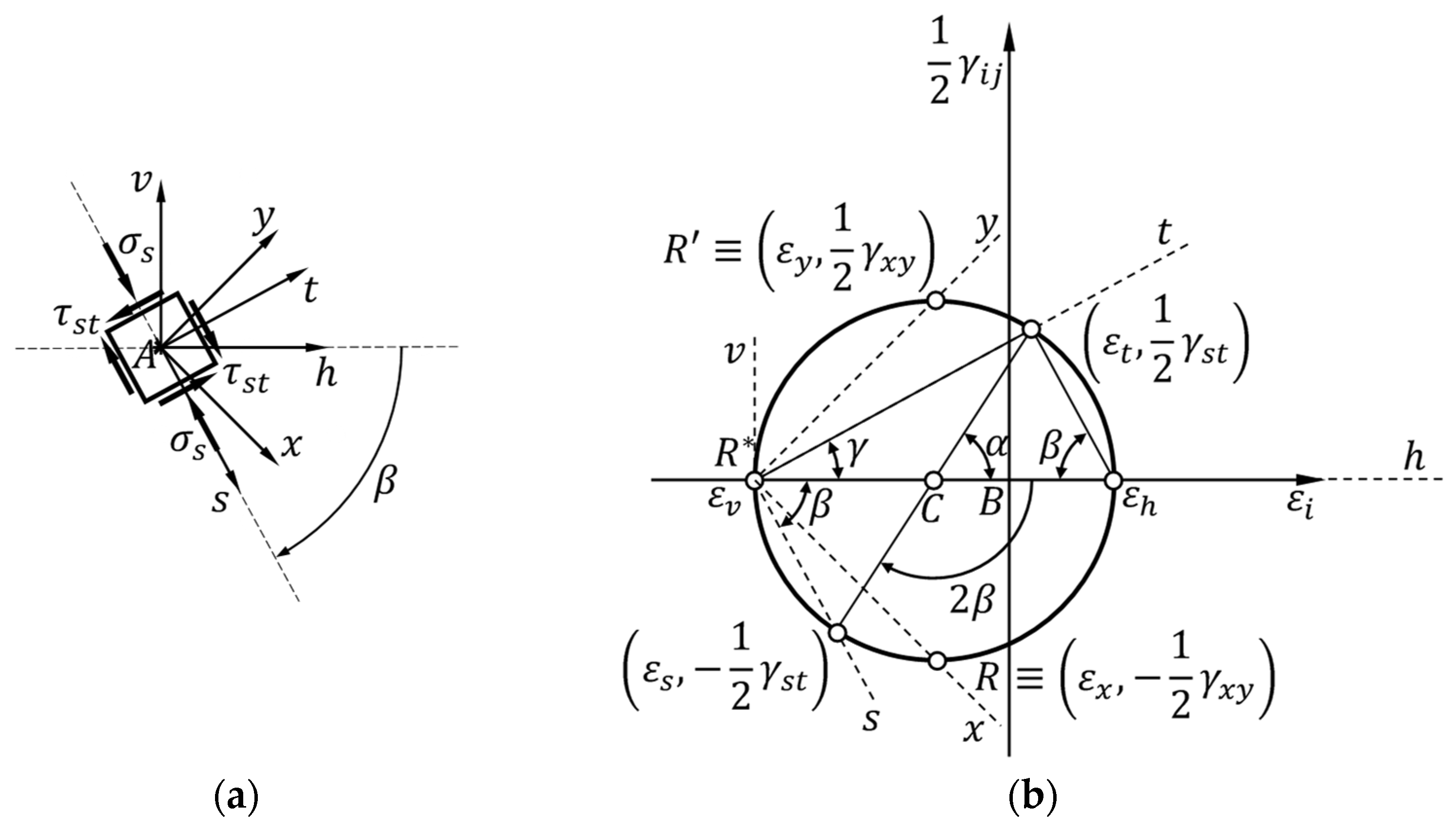
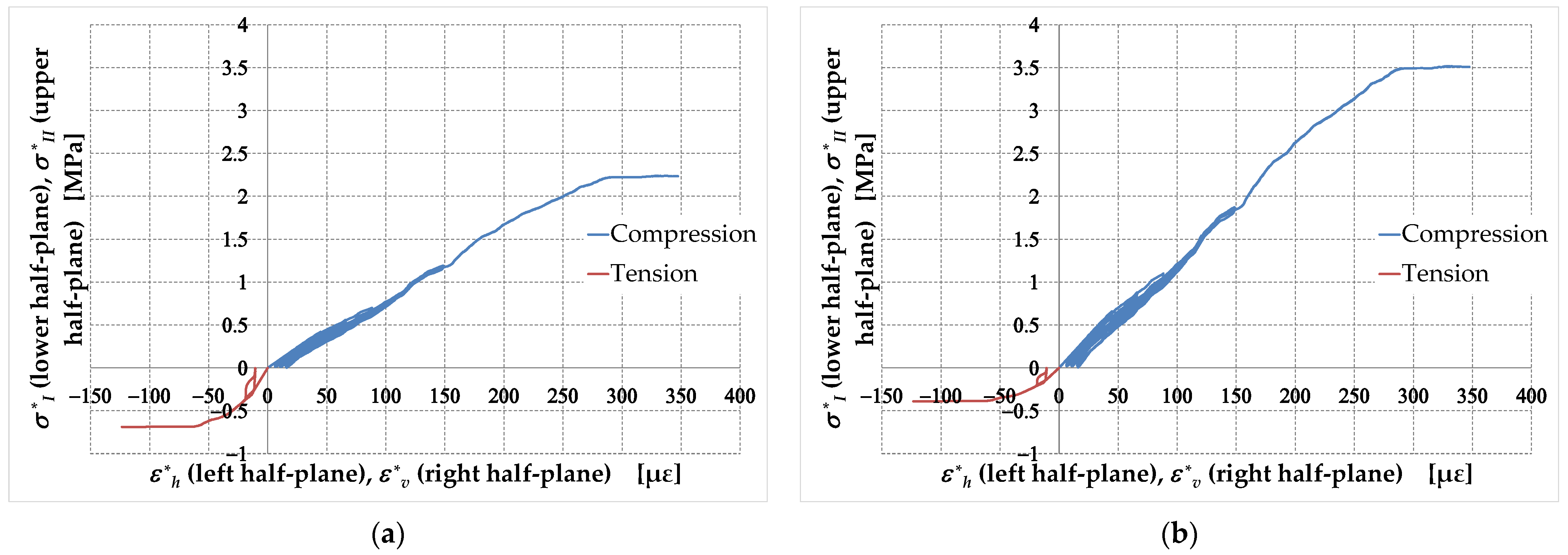
3.1. Stress State at Point
3.2. Strain State at Point
- , where is the displacement component of point in the direction of the -axis (normal component of the displacement, or normal displacement);
- , where is the displacement component of point in the direction of the -axis (tangential component of the displacement, or tangential displacement).
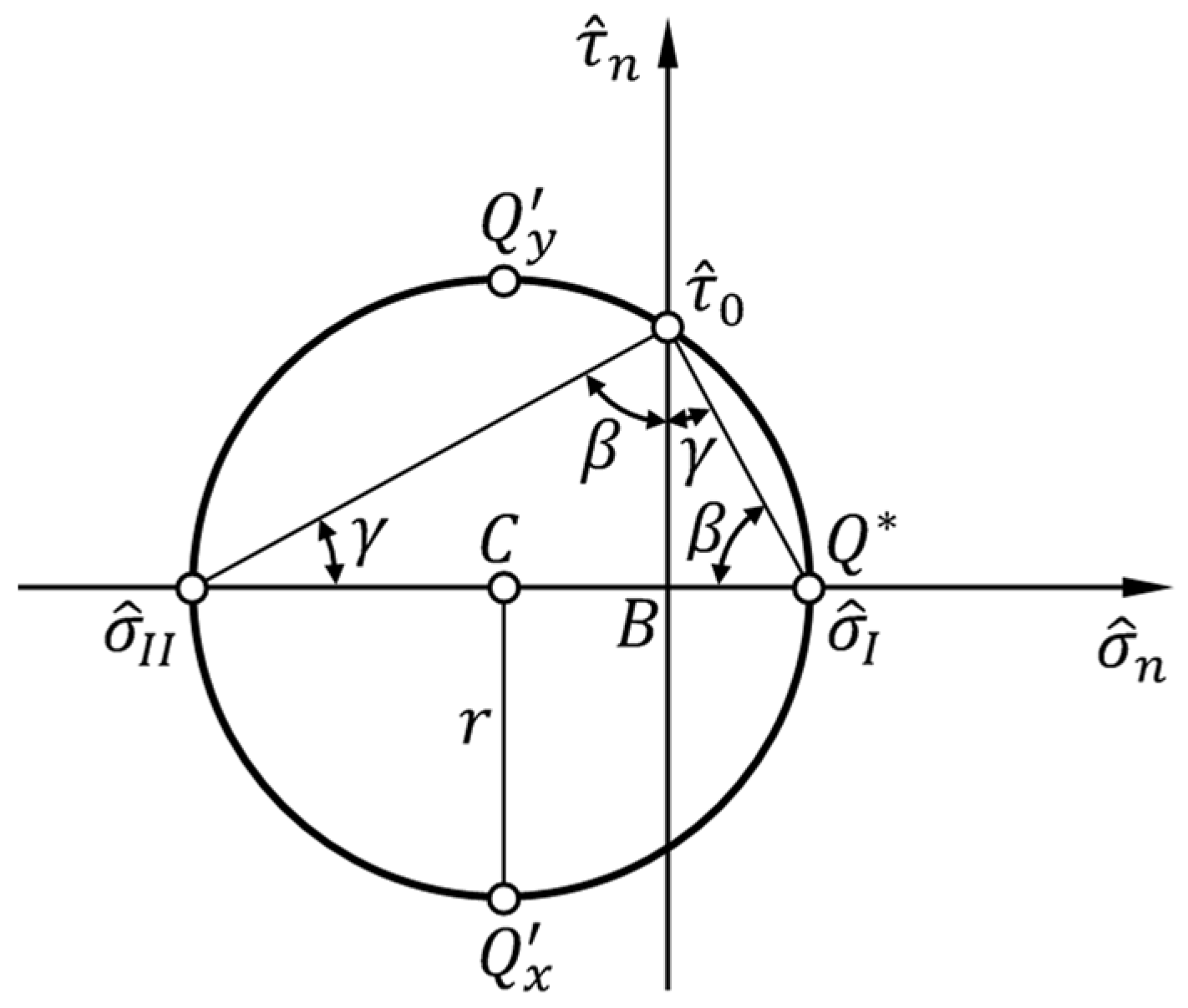
3.3. Elastic Coefficients
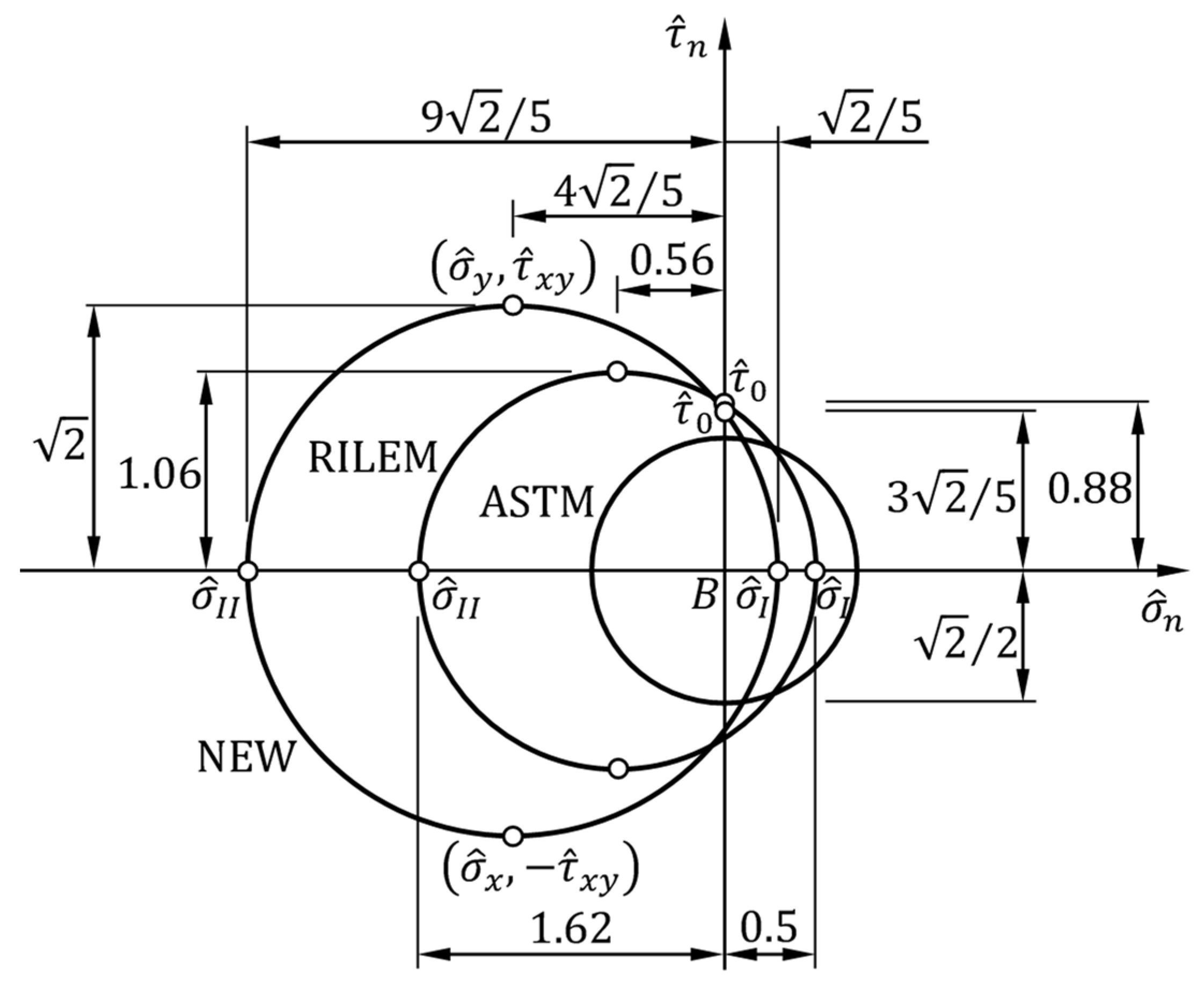
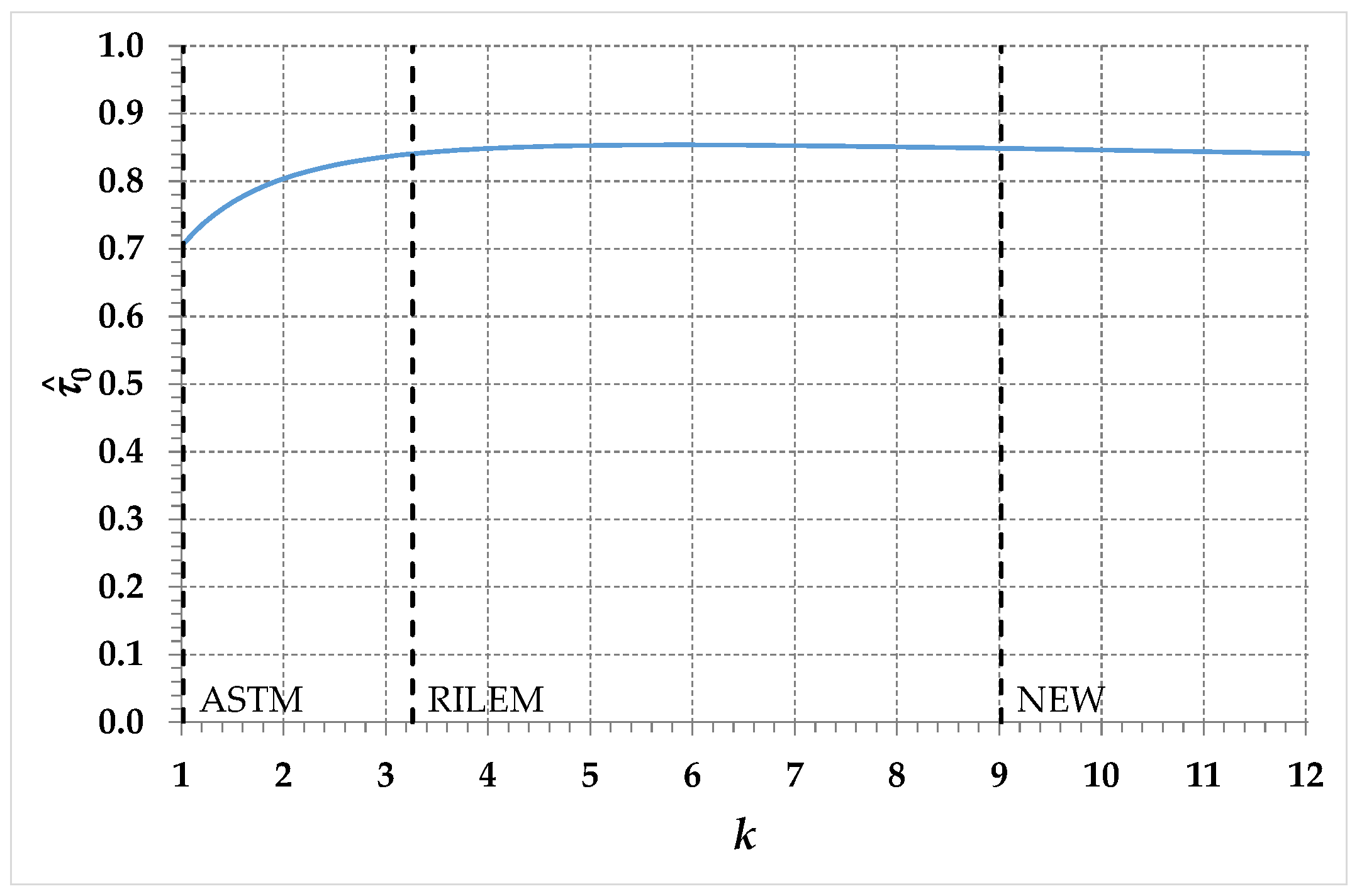
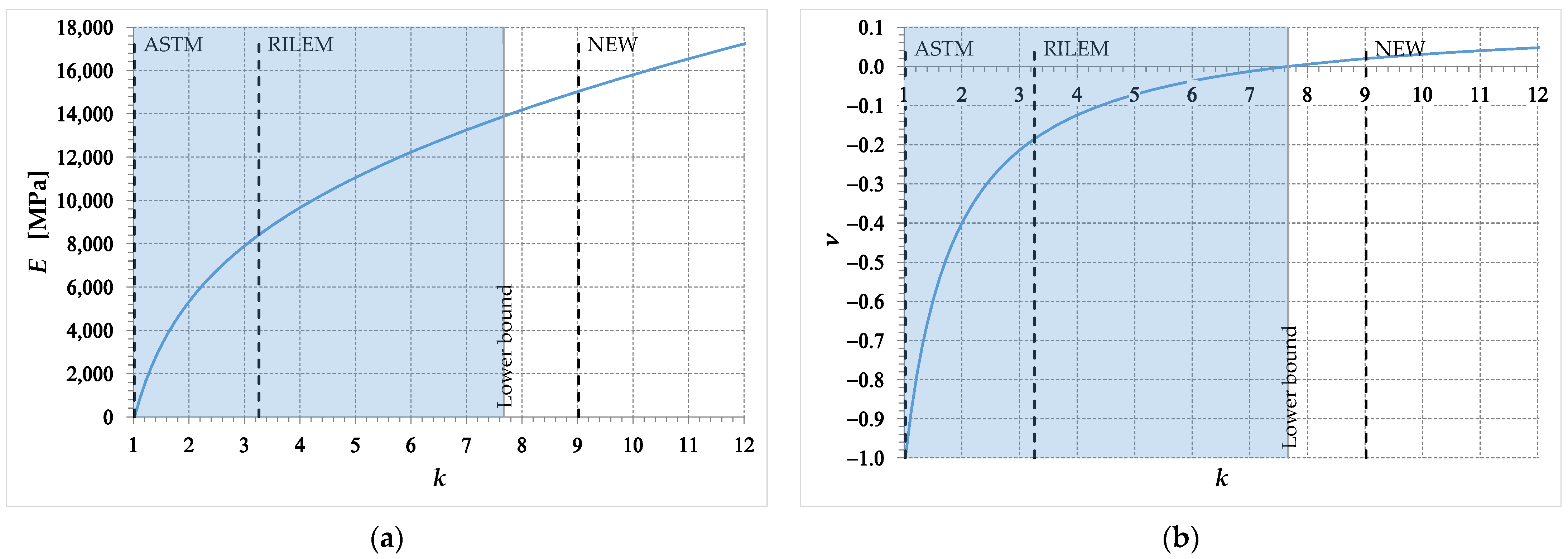
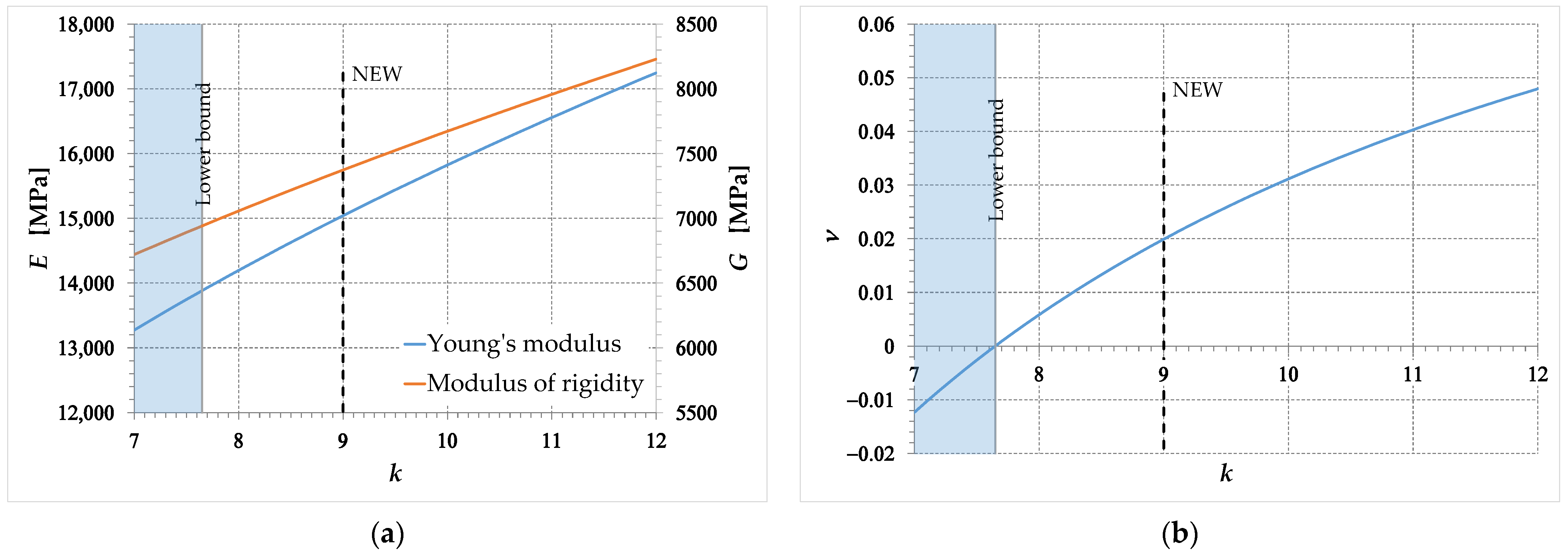
3.4. Limiting Values of the Parameter
4. How to Identify the Coefficient and Obtain the Solution
5. The Elastic Coefficients Obtained for a Real Set of Experimental Data
- is the extension along the horizontal diagonal;
- is the shortening along the vertical diagonal (the compressed diagonal);
- is the gage length in the direction of both diagonals (the gage length for the identification of must be equal to the gage length for the identification of [9]).
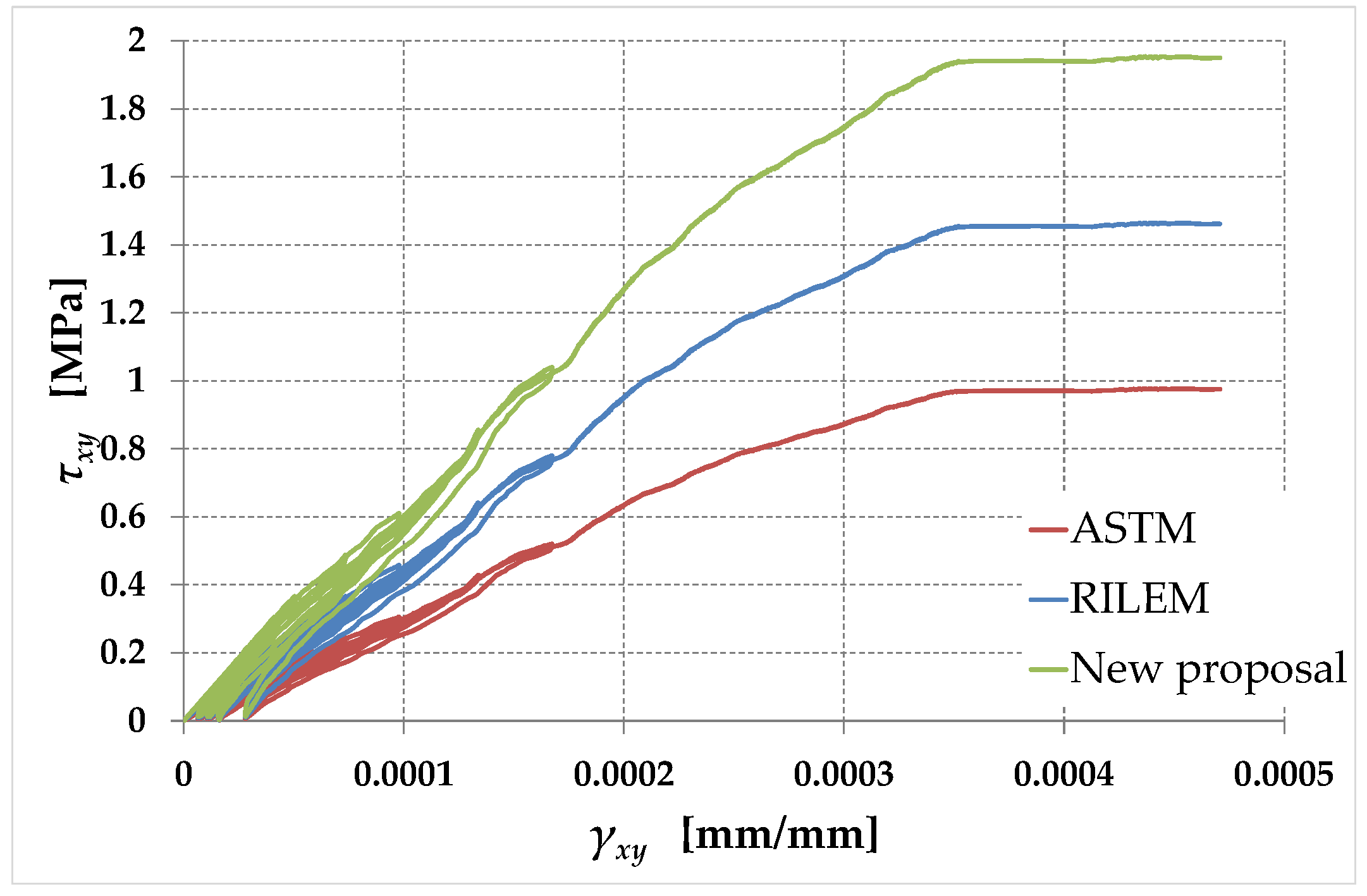
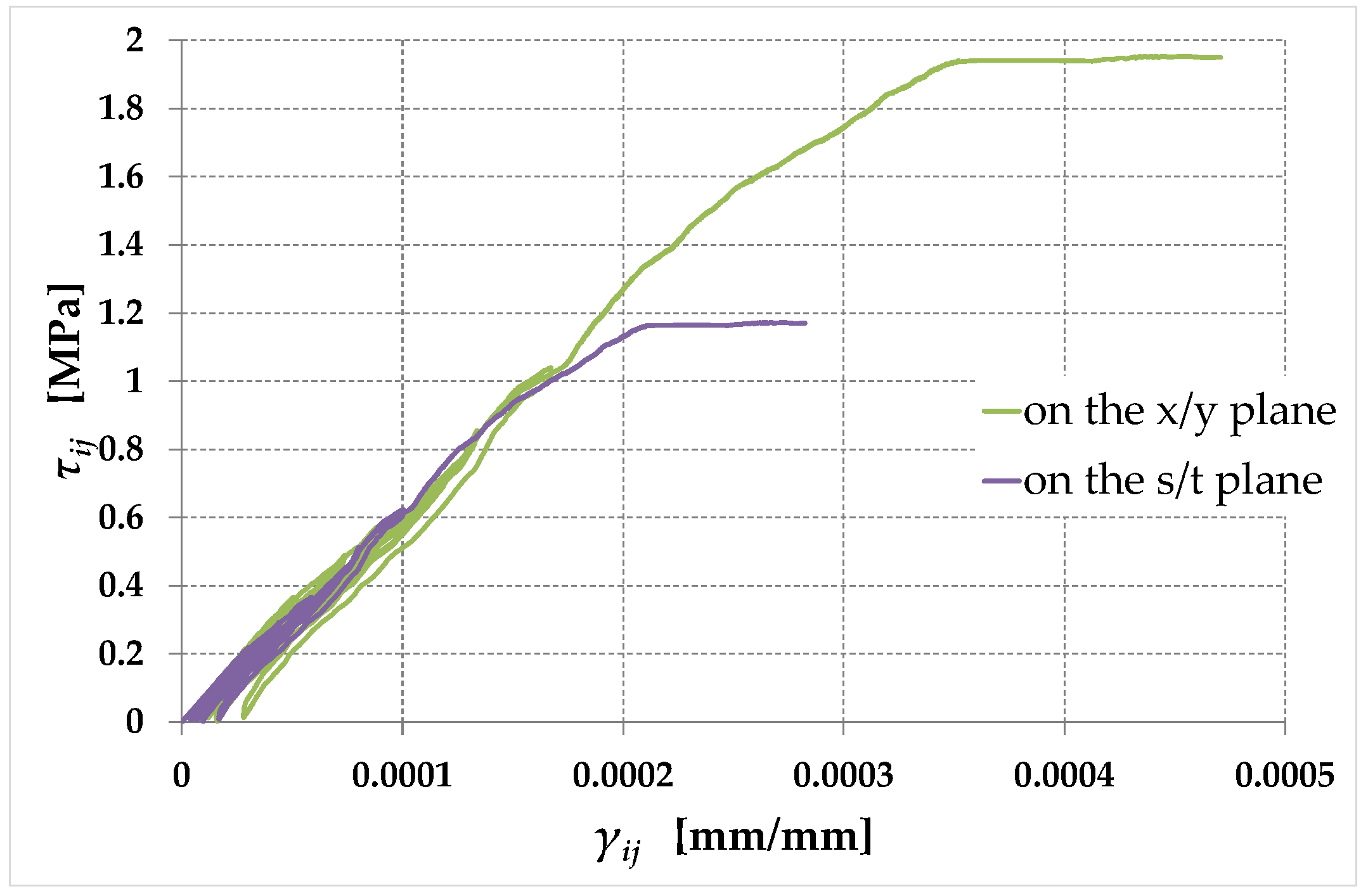
6. Conclusions
- 40% of the ASTM tensile strength;
- 57% of the RILEM tensile strength.
7. Future Developments
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Meaning of the Direction Cosines in Equation (68)
- , namely the cosine of the angle between the positive coordinate axis and the positive coordinate axis :
- , namely the cosine of the angle between the positive coordinate axis and the positive coordinate axis :
- , namely the cosine of the angle between the positive coordinate axis and the positive coordinate axis :
- , namely the cosine of the angle between the positive coordinate axis and the positive coordinate axis :
- , namely the cosine of the angle between the positive coordinate axis and the positive coordinate axis :
- namely the cosine of the angle between the positive coordinate axis and the positive coordinate axis :
- , namely the cosine of the angle between the positive coordinate axis and the positive coordinate axis :
- , namely the cosine of the angle between the positive coordinate axis and the positive coordinate axis :
- , namely the cosine of the angle between the positive coordinate axis and the positive coordinate axis :
References
- Turnšek, V.; Čačovič, F. Some experimental results on the strength of brick masonry walls. In Proceedings of the 2nd International Brick Masonry Conference, Stoke-on-Trent, UK, 12–15 April 1970; pp. 149–156. [Google Scholar]
- Mann, W.; Müller, H. Failure of shear-stressed masonry—An enlarged theory, tests and application to shear-walls. Proc. Br. Ceram. Soc. 1982, 30, 223–235. [Google Scholar]
- Chiostrini, S.; Galano, L.; Vignoli, A. On the Determination of Strength of Ancient Masonry Walls via Experimental Tests. In Proceedings of the 12WCEE 2000: 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; Available online: http://www.iitk.ac.in/nicee/wcee/article/2564.pdf (accessed on 25 October 2023).
- Alecci, V.; Fagone, M.; Rotunno, T.; De Stefano, M. Shear strength of brick masonry walls assembled with different types of mortar. Constr. Build. Mater. 2013, 40, 1038–1045. [Google Scholar] [CrossRef]
- Parisi, F.; Iovinella, I.; Balsamo, A.; Augenti, N.; Prota, A. In-plane behaviour of tuff masonry strengthened with inorganic matrix-grid composites. Compos. Part B Eng. 2013, 45, 1657–1666. [Google Scholar] [CrossRef]
- Borri, A.; Castori, G.; Corradi, M. Determination of Shear Strength of Masonry Panels Through Different Tests. Int. J. Archit. Herit. 2015, 9, 913–927. [Google Scholar] [CrossRef]
- Brignola, A.; Frumento, S.; Lagomarsino, S.; Podestà, S. Identification of Shear Parameters of Masonry Panels Through the In-Situ Diagonal Compression Test. Int. J. Archit. Herit. 2018, 3, 52–73. [Google Scholar] [CrossRef]
- Rezaie, A.; Godio, M.; Beyer, K. Experimental investigation of strength, stiffness and drift capacity of rubble stone masonry walls. Constr. Build. Mater. 2020, 251, 118972. [Google Scholar] [CrossRef]
- ASTM E519/E519M–15; Standard Test Method for Diagonal Tension (Shear) in Masonry Assemblages. ASTM International: West Conshohocken, PA, USA, 2021.
- Ferretti, E. Active Confinement of Masonry Walls with Stainless Steel Straps: The Effect of Strap Arrangement on the in-Plane Behavior of Strength, Poisson’s Ratio, and Pseudo-Ductility. Buildings 2023, 13, 3027. [Google Scholar] [CrossRef]
- Frocht, M.M. Recent advances in photoelasticity. ASME Trans. 1931, 55, 135–153. [Google Scholar]
- RILEM. LUM B6: Diagonal tensile strength of small walls specimens. In RILEM Recommendations for the Testing and Use of Constructions Materials; RILEM: Sheffield, UK, 1994; pp. 488–489. [Google Scholar]
- Aliabadi, M.H. Boundary Element Methods in Linear Elastic Fracture Mechanics. Compr. Struct. Integr. 2003, 3, 89–125. [Google Scholar] [CrossRef]
- Ferretti, E. Modeling of the pullout test through The Cell Method. In Proceedings of the International Conference on Restoration, Recycling and Rejuvenation Technology for Engineering and Architecture Application, RRRTEA ‘04, Cesena, Italy, 7–11 June 2004. [Google Scholar]
- Borri, A.; Corradi, M.; Castori, G.; Sisti, R. Reinforcement of masonry panels with GFRP grids. In Proceedings of the 9th International Conference on Structural Analysis of Historical Constructions (SAHC2014), Mexico City, Mexico, 14–17 October 2014. [Google Scholar]
- Crisci, G.; Ceroni, F.; Lignola, G.P. Comparison between Design Formulations and Numerical Results for In-Plane FRCM-Strengthened Masonry Walls. Appl. Sci. 2020, 10, 4998. [Google Scholar] [CrossRef]
- Dong, F.; Wang, H.; Jiang, F.; Xing, Q.; Yu, J. In-plane shear behavior of masonry panels strengthened with ultra-high ductile concrete (UHDC). Eng. Struct. 2022, 252, 113609. [Google Scholar] [CrossRef]
- Calderini, C.; Cattari, S.; Lagomarsino, S. Identification of shear mechanical parameters of masonry piers from diagonal compression test. In Proceedings of the 11th Canadian Masonry Symposium, Toronto, ON, Canada, 31 May–3 June 2009. [Google Scholar]
- Calderini, C.; Cattari, S.; Lagomarsino, S. The use of the diagonal compression test to identify the shear mechanical parameters of masonry. Constr. Build. Mater. 2010, 24, 677–685. [Google Scholar] [CrossRef]
- Angelillo, M.; Lourenço, P.B.; Milani, G. Masonry behaviour and modelling. In Mechanics of Masonry Structures—CISM International Centre for Mechanical Sciences Book Series; Angelillo, M., Ed.; Springer: Vienna, Austria, 2014; Volume 551, pp. 1–26. [Google Scholar] [CrossRef]
- Allison, L. The pole of the Mohr diagram. J. Struct. Geol. 1984, 6, 331–333. [Google Scholar] [CrossRef]
- Fung, Y.C. Foundations of Solid Mechanics, 1st ed.; Prentice-Hall: Hoboken, NJ, USA, 1965; 525p. [Google Scholar]
- Yokel, F.Y.; Fattal, S.G. A Failure Hypothesis for Masonry Shearwalls; Center for Building Technology, Institute for Applied Technology, National Bureau of Standards: Washington, DC, USA, 1975.
- Benedetti, A. In Plane Behaviour of Masonry Walls Reinforced with Mortar Coatings and Fibre Meshes. Int. J. Archit. Herit. 2019, 13, 1029–1041. [Google Scholar] [CrossRef]
- Ismail, N.; Petersen, R.B.; Masia, M.J.; Ingham, J.M. Diagonal shear behaviour of unreinforced masonry walletts strengthened using twisted steel bars. Constr. Build. Mater. 2011, 25, 4386–4393. [Google Scholar] [CrossRef]
- Mustafaraj, E.; Yardim, Y. Retrofitting damaged unreinforced masonry using external shear strengthening techniques. J. Build. Eng. 2019, 26, 100913. [Google Scholar] [CrossRef]
- Ungureanu, D.; Țăranu, N.; Ghiga, D.A.; Isopescu, D.N.; Mihai, P.; Cozmanciuc, R. Diagonal Tensile Test on Masonry Panels Strengthened with Textile-Reinforced Mortar. Materials 2021, 14, 7021. [Google Scholar] [CrossRef] [PubMed]
- Shahzamani, S.; Eftekhar, M.R. Experimental study on using steel wires via the NSM method to improve the behaviour of masonry panels. Constr. Build. Mater. 2023, 385, 131473. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; Vignoli, A. Il Problema della Valutazione della Resistenza a Taglio della Muratura mediante Prove Sperimentali. In Proceedings of the X Congresso Nazionale “L’ingegneria Sismica in Italia” (ANDIS), Potenza-Matera, Italy, 9–13 September 2001. [Google Scholar]
- Ferioli, R. Muratura in Zona Sismica: Prove Sperimentali di Laboratorio sulla Caratterizzazione Meccanica della Muratura Con aspetti Legati alla Risposta Sismica di un Edificio Scolastico. Master’s Thesis, Università degli Studi di Ferrara, Ferrara, Italy, 2011. [Google Scholar]
- Segura, J.; Pelà, L.; Saloustros, S.; Roca, P. Experimental and numerical insights on the diagonal compression test for the shear characterisation of masonry. Constr. Build. Mater. 2021, 287, 122964. [Google Scholar] [CrossRef]
- Gherman, R.L. Interventi per il Rinforzo Strutturale degli Edifici in Muratura: Ricerca Sperimentale Sull’impiego delle Cuciture Attive. Master’s Thesis, Università degli Studi di Bologna, Bologna, Italy, 2020. [Google Scholar]
- Bosiljkov, V.; Totoev, Y.Z.; Totoev, J. Shear modulus and stiffness of brickwork masonry: An experimental perspective. Struct. Eng. Mech. 2005, 20, 21–43. [Google Scholar] [CrossRef]
- Ferretti, E.; Di Leo, A. Cracking and creep role in displacements at constant load: Concrete solids in compression. CMC-Comput. Mater. Contin. 2008, 7, 59–79. [Google Scholar]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill International Editions: New York, NY, USA, 1970. [Google Scholar]
- Murthi, P.; Bhavani, M.; Musthaq, M.S.; Jauhar, M.O.; Devi, V.R. Development of relationship between compressive strength of brick masonry and brick strength. Mater. Today Proc. 2021, 39, 258–262. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferretti, E. A New Proposal for the Interpretation of the Diagonal Compression Test on Masonry Wallettes: The Identification of Young’s Modulus, Poisson’s Ratio, and Modulus of Rigidity. Buildings 2024, 14, 104. https://doi.org/10.3390/buildings14010104
Ferretti E. A New Proposal for the Interpretation of the Diagonal Compression Test on Masonry Wallettes: The Identification of Young’s Modulus, Poisson’s Ratio, and Modulus of Rigidity. Buildings. 2024; 14(1):104. https://doi.org/10.3390/buildings14010104
Chicago/Turabian StyleFerretti, Elena. 2024. "A New Proposal for the Interpretation of the Diagonal Compression Test on Masonry Wallettes: The Identification of Young’s Modulus, Poisson’s Ratio, and Modulus of Rigidity" Buildings 14, no. 1: 104. https://doi.org/10.3390/buildings14010104
APA StyleFerretti, E. (2024). A New Proposal for the Interpretation of the Diagonal Compression Test on Masonry Wallettes: The Identification of Young’s Modulus, Poisson’s Ratio, and Modulus of Rigidity. Buildings, 14(1), 104. https://doi.org/10.3390/buildings14010104





