Simple Nonlinear Numerical Modeling for Unreinforced and FRP-Reinforced Masonry Domes

Abstract

This paper presents a new method to model the nonlinear behavior of double-curvature masonry structures, possibly reinforced by composite materials, by means of conventional elasto-plastic analyses. The method is meant to be used in professional design, especially for assessment and retrofitting purposes, based on the exploitation of the simplest nonlinear finite elements available in commercial software, namely, trusses with elasto-fragile and elasto-ductile behavior (Cutoff Bars, according for instance to the definition provided by Strand7 R3.1.3a). Numerical static nonlinear analyses are carried out by considering elastic hexahedral elements for bricks and by lumping nonlinearities on joints. These are assumed, in turn, to be elastic–brittle and elastic–plastic by using 1D elements, namely, Point Contacts, under the No-Tension Material hypothesis, and Cutoff Bars, respectively, assigning a small tensile resistance to the material. The reinforcement, realized with FRP hooping strips, is successfully modeled in a similar fashion, i.e., by applying perfectly bonded elastic–plastic Cutoff Bars at the extrados of the dome, where debonding is accounted for in a conventional way, limiting the tensile strength according to Italian Standards’ indications. The procedure is validated against benchmark models with the same geometry, using experimental data and more refined structural model results for comparison. After an in-depth analysis of the obtained results, in terms of capacity curves, the robustness and accuracy of the proposed approach are assessed.

1. Introduction

Double-curvature structures are a common type of roofing technology in historical buildings. They are found all around the world in different countries. They were used to cover large rooms in public buildings because of their resistance to vertical loads, guaranteed by the acceptable mechanical properties of the materials involved (i.e., in compression for masonry), friction, and especially their shape. The drawbacks of these structures are the lateral thrust and the transverse shear for asymmetric, dynamic, and horizontal loading. To overcome these major limitations, in recent decades, starting from the 1990s, the exploitation of innovative materials composed of fibers embedded in a polymeric matrix has become an object of scientific interest and can be found in many forms of professional design, thanks to the increase in structural capacity achieved with their application [1,2,3,4,5,6,7,8]. In parallel, experimentation [9] and sophisticated numerical [10,11,12] models have also been developed.

Arches and vaults (and domes) are known to be “shape resistant” by virtue of their (double) curvature, as a function of their loading condition [13]. In this paper, domes are tackled in three dimensions. Indeed, they cannot be studied as arches or barrel vaults because of stresses running horizontally. In Figure 1, the conical surfaces are those on which mortar joints and bricks are laid. Because of this imposed shape and the slope toward the center (O), compression stresses act only on those surfaces, as also demonstrated by means of the membrane equations in [14]. Moreover, compression stress progressively increases, increasing the height of the same cones (i.e., their slopes) up to the last crown. This can be an open oculus with finite compression in the crown or a closed top, which—in large domes—may suffer from bending because of the verticality of the degenerate conical surface and insufficient compression.

From the springing to the top, on the meridian section planes, ${\pi }_i$ (see Figure 1), nonlinearities emerge and form cracks, which separate the dome into meridian sectors. This allows for the formation of plastic annular hinges at a generic angle, ${\alpha }_h$, from the vertical axis (i.e., degenerate cone C_r0). In the case of a closed top, one plastic hinge may open (${\alpha }_0=0$). In any case, excessive—symmetric—loading opens the plastic hinges at the springing (${\alpha }_b=90°$) and in an intermediate position, ${\alpha }_h$. In [15], it is demonstrated how the position of the plastic hinge varies. When an oculus is present, it is more probable for the plastic hinge to occur lower on the base (at a major angle, ${\alpha }_h$). The presence of the oculus, in fact, visibly changes the equilibrium configuration in relation to the closed-top case.

Contrarily, the same authors [15] state that the position of the intermediate plastic hinge undergoes very small variations due to a change in the material tensile resistance. Nonetheless, it can be noted that, when increasing the tensile resistance, the angle of the intermediate plastic hinge increases because of the better distribution of stresses on the meridian planes.

However, the higher the plastic hinge, the better it is because a larger portion of the lower part of the fuse expends more energy uplifting the self-weight. Friction and the interlocking of bricks—in a stretcher bond above all—are advantageous because the plastic dissipation on meridians is larger. On the contrary, it is worth noting that, from the springing to the top, the bricks’ geometry adapts worse to the progressively smaller conical surfaces. Therefore, in building practice, they are cut, and the head joints’ distribution becomes more irregular. This ends up in straighter paths for fractures (the minimum energy path [16]), lowering the fracture power and, hence, the ultimate collapse load.

The present investigation addresses the nonlinear modeling of domes loaded at the crown by means of vertical point forces. This configuration is typical for laboratory tests aimed at understanding the load-carrying capacity of such structural elements. The newly proposed way of modeling was benchmarked against both experimental data and advanced numerical techniques on a hemispherical dome with an inner diameter of 2.2 m, a thickness of 0.12 m (UNI Italian brick size), and an oculus at the top with a diameter equal to 0.2 m. The dome was built at the University Institute of Architecture of Venice and tested in the presence and absence of reinforcement [4,17]. The first numerical study was carried out by Creazza et al. [18], who simulated the dome by means of an isotropic finite element damage model, equipped with distinct damage parameters in tension and compression. The authors did not study the role played by orthotropy [19]. Orthotropy may have a certain importance in modifying the ultimate load-carrying capacity, and this feature was investigated in the framework of a classic finite element limit analysis [9] and by using a variety of simplified analytical models, such as a Lower Bound Limit Analysis (LB-LA, Durand-Claye’s Method), an Upper Bound Limit Analysis (UB-LA, kinematic method) [15,20,21,22], and by means of homogenized or macroscopic models [18,22,23,24,25].

Concentrated forces applied at the top in experiments and simulations roughly represent the load of lanterns or—in technically more interesting cases—heavier superimposed constructions, as occur, for instance, in the Vipassana Pagoda (described in [26]), which will be studied in the sequel of this research, bearing in mind a comparison of the results obtained with already existing computations carried out by means of a novel method combining FEs and a Thrust Line Analysis [27,28].

As noted in [25], although all the methods previously described give very accurate results, they are too complex for utilization at the professional level, because they require experienced users with an advanced theoretical background and a demanding processing time. Moreover, some of the existing assessment methods conceived for hemispherical domes introduce excessive simplifications, as in [29], where the double curvature, the tensile strength, and finite compressive resistance are neglected. As a matter of fact, masonry is often considered a “No-Tension Material” (NTM) [27,30,31,32], even though accounting for suitable tensile and compressive strengths leads to results that better fit reality.

The novel and simple method presented here for studying domes in a three-dimensional space avoids both the complexities (and limitations) that characterize homogenized or FE damage models and excessive geometric simplifications. It assumes that the blocks are elastic, lumping material nonlinearities in mortar joints (as in [33]), which are modeled using simple unidimensional finite elements commonly available in any commercial software (such as Point Contacts and Cutoff Bars, according for instance to the definition provided by Strand7 R3.1.3a). In this way, masonry may be modeled both as an NTM and as a tension material (with a small tensile resistance), according to the result to be pursued.

It is worth noting that the modeling method proposed in this paper accounts only for axisymmetric vertical loading, which, however, also generates a distribution of normal stresses on meridian planes. Moreover, the method is validated for a dome with an oculus at the top, using, for comparison purposes, the literature data available for the same benchmark model. The method is general, and the application of horizontal loads is straightforward but beyond the object of the present study, which is mainly focused on the theoretical aspects of the procedure. The potential of the procedure is evident, especially when dealing with static nonlinear analyses under horizontal loads mimicking seismic excitation [34], a research topic that deserves dedicated insight.

This paper is organized as follows: in the next section, the reader will find information about the finite element strategy adopted to build a model suitable for pushover analyses and that is consistent with the initial hypotheses. The rationale about the choice of 1D FEs is revealed step by step. A section about the actual construction of the model and its validation follows, and it reports the sensitivity analyses carried out to tune the mechanical parameters (e.g., joints f_T) and to compare the results with the literature data. In addition, the potential exploitability of the model for FRP reinforcement is shown.

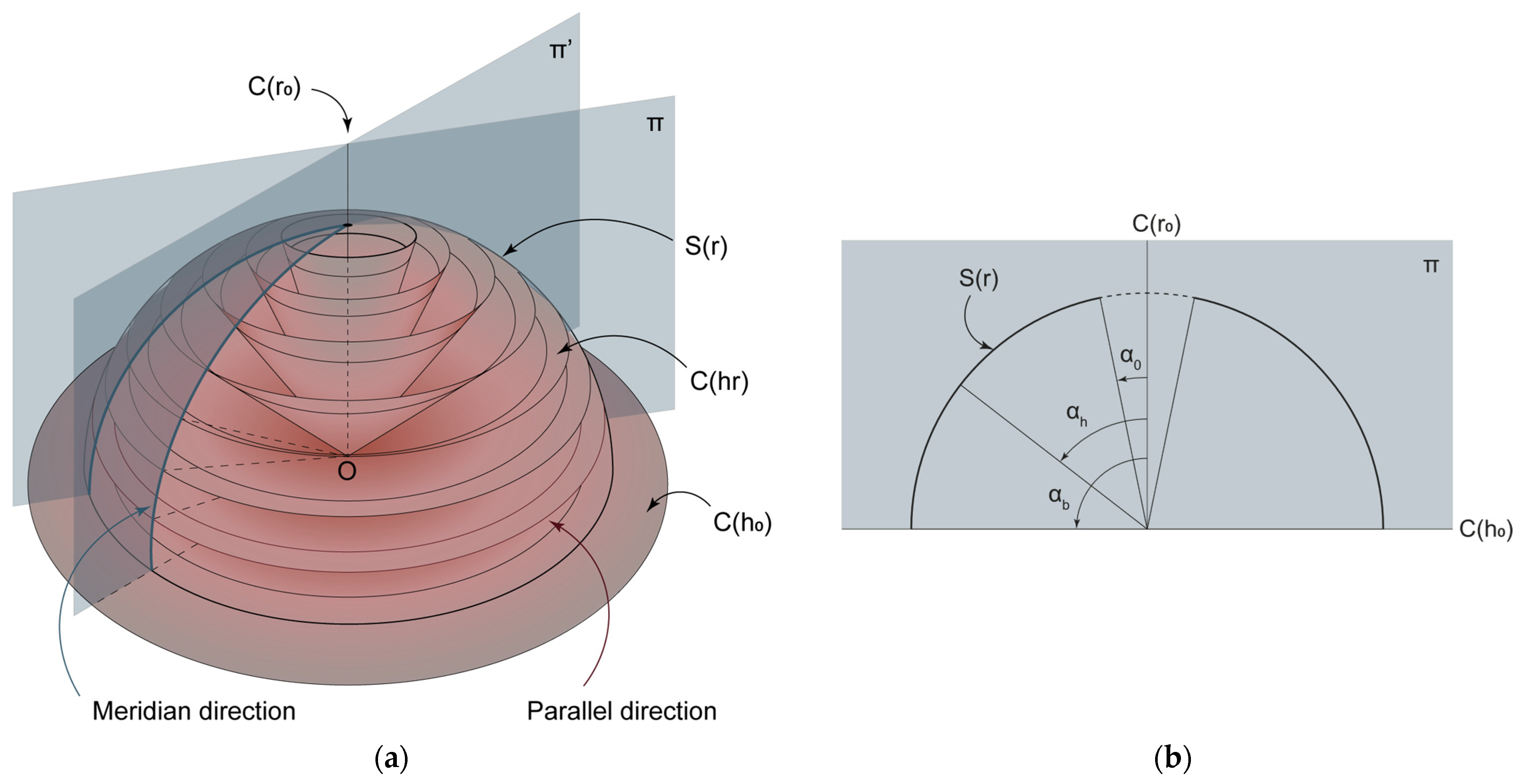
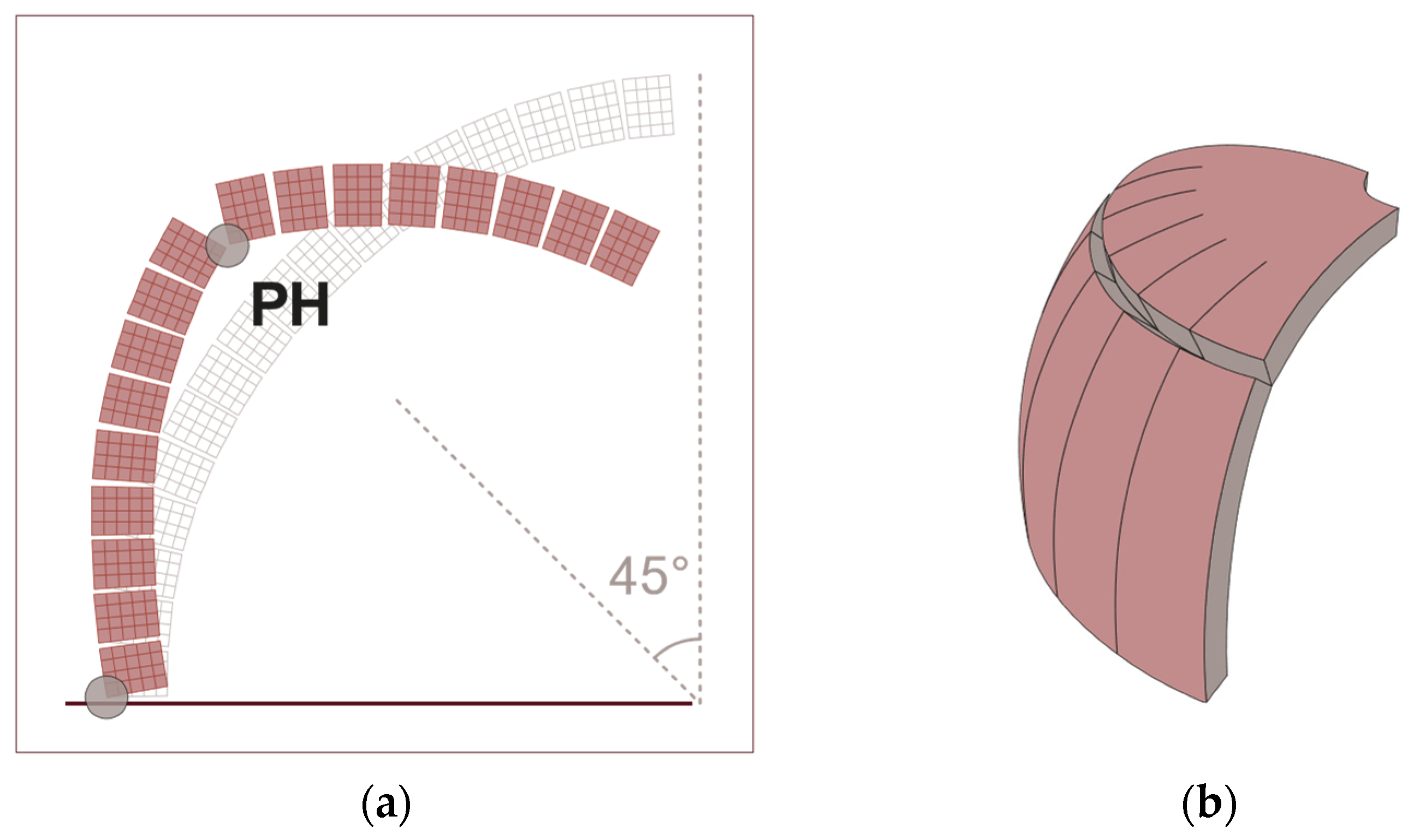
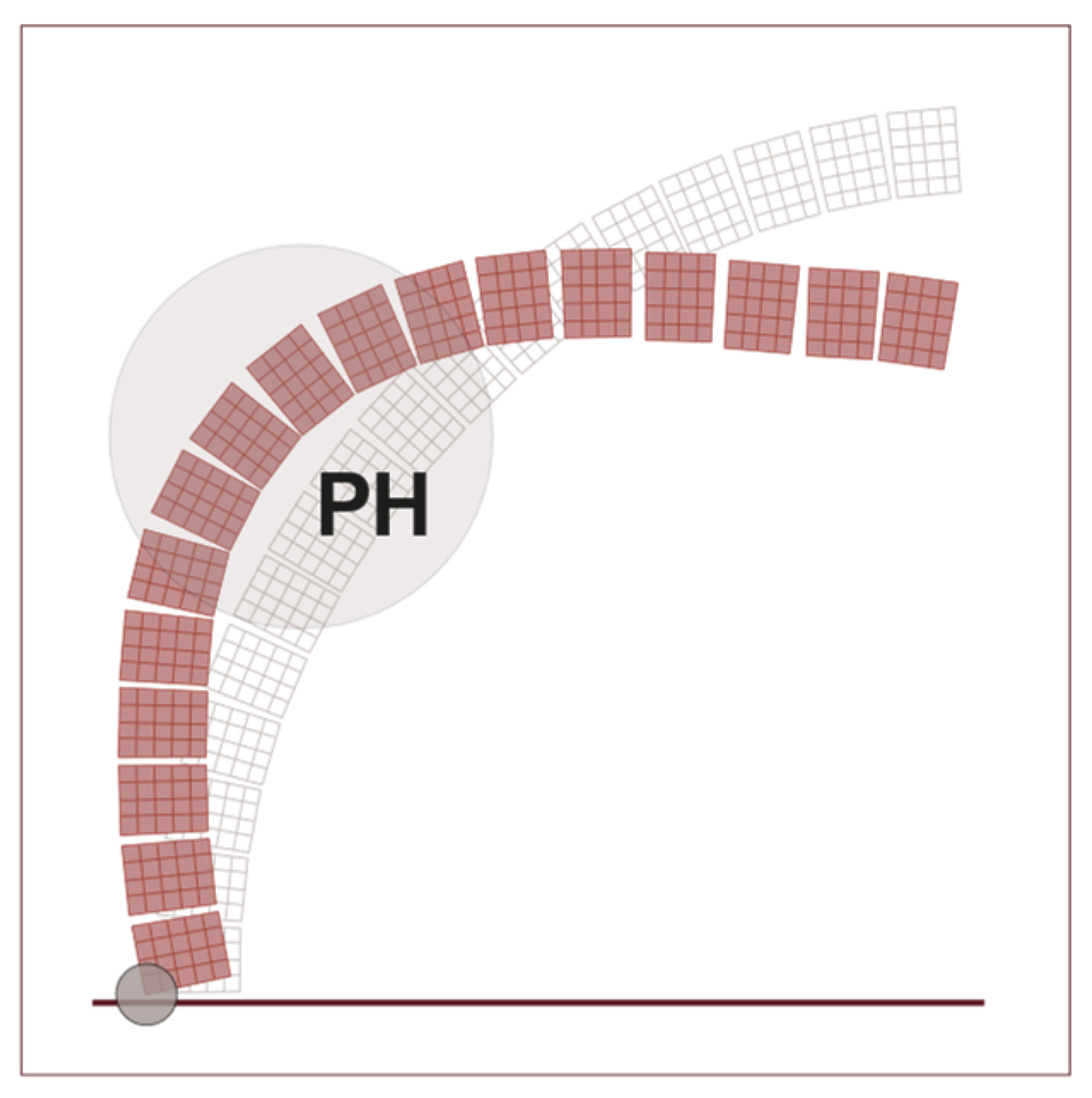
2. FE Modeling

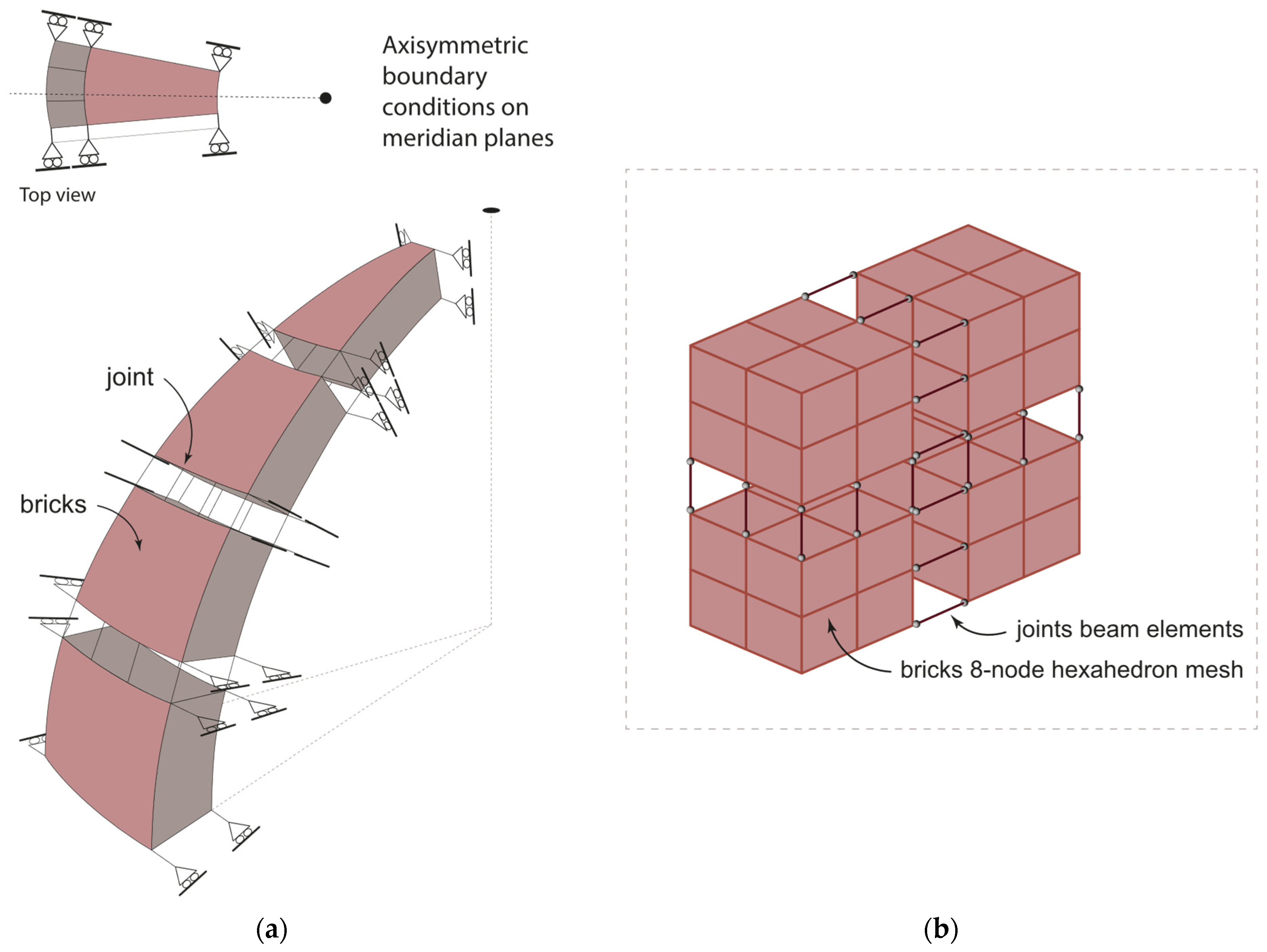
2.1. Modeling for Nonlinear Analysis

In [29], some domes are modeled as arches using a vertical cross-section, neglecting to some extent the actual axisymmetric geometry, especially as far as the meridian boundary conditions are concerned. This makes a dome similar to a single-curvature vault. However, differently from that case, domes should be better studied by properly considering their second curvature in the third dimension. Geometrically speaking, they have infinite planes of symmetry intersecting in the vertical axis. Hence, to build a lighter model and speed up calculations while accounting for realistic boundary conditions, here, only a meridian slice (or fuse, δθ/2π wide) of a dome is considered [35] in the nonlinear analyses (NLAs). Hence, the results obtained for a single slice are representative of those of the whole dome. The width of the fuse should not be too small in order to separately model all the materials involved (both bricks and mortar joints) in suitable proportions. Moreover, the fact that masonry is very rigid and typically made using interlocked units allows for the actual stresses exchanged between contiguous slices to be considered. Therefore, with reference to the examined single slice, the stresses are transferred on meridian planes by imposing classic symmetry constraints on displacements (see Figure 2a).

In the modeling phase, the fuse is generated by extruding an arch of angle δθ (Figure 2a) in a cylindrical frame of reference. It is composed of 3D elements (eight-node hexahedrons), with the mechanical properties of the blocks adapted from [22] and reported in

Table 1. Mechanical properties of clay bricks assigned in the FE model [22].

Mechanical Properties
Young’s Modulus (MPa)	E	1700
Poisson Ratio (-)	ν	0
Density (kg/m3)	ρ	2000
Nonlinear Type		Elastic Plastic
Yield Criterion		Von Mieses

, connected node to node by 1D truss elements, where masonry nonlinearity is lumped. A rough scheme showing how the material is modeled is displayed in Figure 2.

From a theoretical point of view, it is worth noting that the numerical procedure is a standard one, since it is obtained through a simple discretization of the double-curvature structure into common finite elements. However, at the same time, it presents some innovative features (represented by the utilization of Cutoff Bars, which allow for the study of behavior in the nonlinear range by means of conventional meshes). The computational burden is dramatically reduced, as well as the complexity of the preprocessing phase, when compared with the available models in the literature.

As a result of the extrusion in the cylindrical reference system, the model of the dome is composed of bricks shaped as curved trapezoidal prisms and parallel joints exhibiting a constant thickness through the dome cross-section. In real-scale domes, the opposite occurs, because mortar adapts the given geometry of the bricks (which, in reality, are parallelepipeds with rectangular faces) to the double curvature. Vertical joints are tapered in any case. However, the assumption adopted regarding the shape of the elements, as also adopted by two of the authors in [33], does not significantly interfere with the results because of the relatively small size of the blocks.

After imposing the boundary conditions on the meridian slice as specified, a nonlinear analysis is run by applying an increasing displacement at the top of the fuse—i.e., on the crown surrounding the oculus—thus proceeding with a classic displacement control strategy. The solver provides a node reaction at each load step as a function of the displacement and for the given material properties. The final result, being the ultimate collapse load (λ_u) of the considered structure, is reached asymptotically because the nonlinear “beam” elements are assumed to be either elastic–brittle or elastic–ductile. When elastic–brittle Cutoff Bars (null tensile strength) are used, the asymptotic value of λ_u is that of the classic NTM. In Figure 3, the reader can find a scheme summarizing the nonlinear analysis process.

In this regard, it is worth noting that, instead of imposing an incremental load on the stiff steel beam placed at the top of the dome, the application of a displacement is an advantage that gives numerical robustness to the nonlinear static solver in the absence of an arc-length routine, which is typically not available in low-cost software. Such a procedure is suitable when it is required to increase only one point load up to failure, but it can potentially be further elaborated in the presence of distributed actions, e.g., for a seismic excitation. In the latter case, an external frame of rigid, simply supported beams would be required, an issue that is beyond the scope of the present paper and will be further investigated in future research. The correspondence to the real behavior is in any case preserved because, for masonry large-scale structures, snap-back is hardly experienced.

From a computational point of view, it is worth pointing out that the nonlinear analyses require a few minutes to be performed up to failure on a standard laptop, a feature that further corroborates the idea that the proposed approach is perfectly suited to perform fast and reliable nonlinear analyses in common design practice.

In the next sections, two approaches in which nonlinearities can be modeled are detailed.

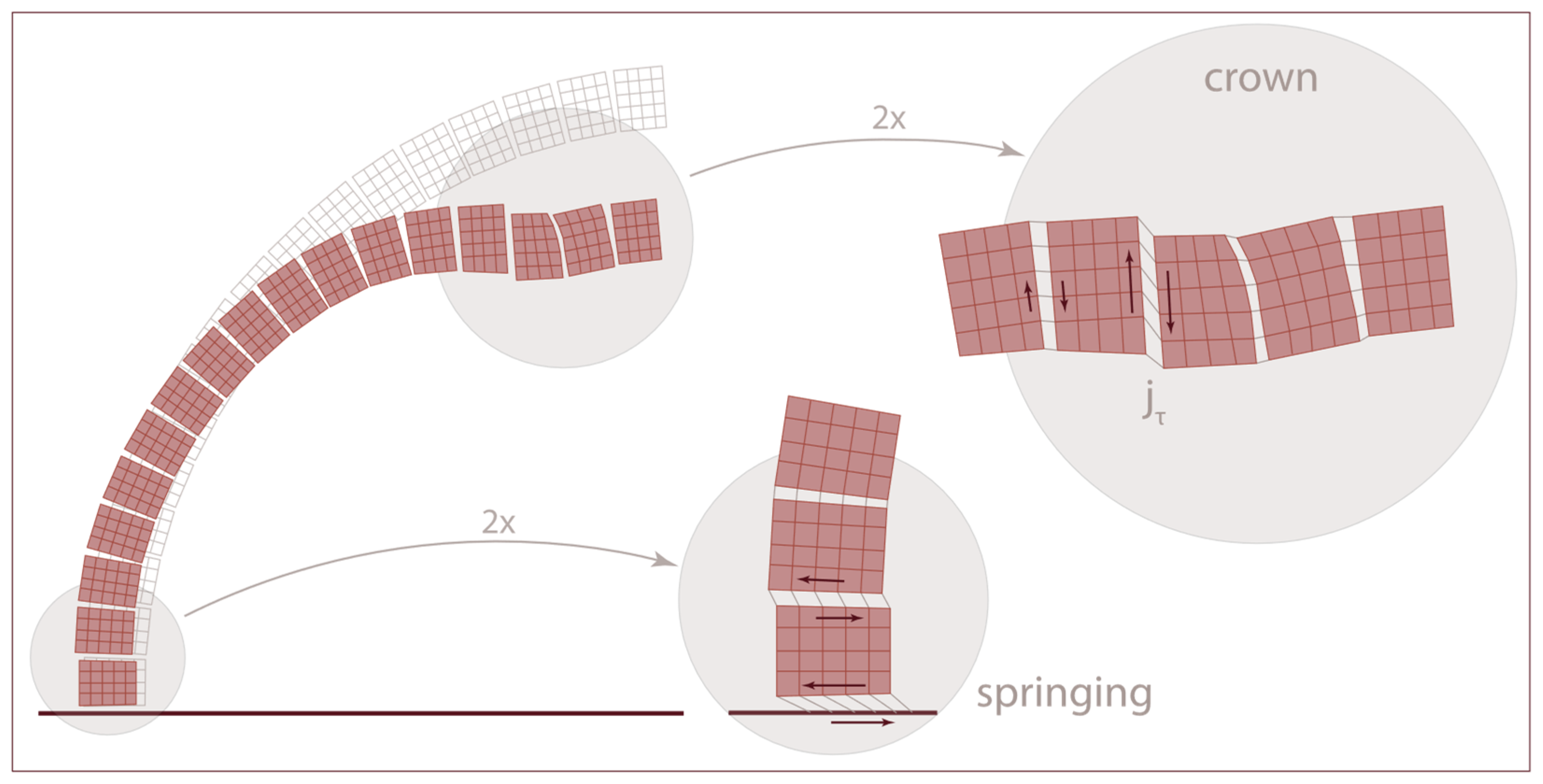
2.2. Modeling of Joints by Means of Point Contacts

Masonry is often modeled as an NTM. This comes from the studies of Heyman [14], who noted how, in historical masonry constructions, compression stress acting in reality is far less than the actual strength associated with crushing. On the contrary, any intense tensile contribution is impossible because of masonry’s incapacity to bear it. Hence, masonry was studied by Heyman [36] according to the following set of hypotheses:

$$\left\{\begin{array}{c}{f}_T⟶0\\ f_C⟶\infty \\ v_b=0\end{array}\right.$$

where $f_T$ is the tensile strength; $f_C$ is the compressive strength; and $v_b$ is the sliding between blocks, valid for small displacements.

According to what has been stated so far, the best way to model nonlinearity in an NTM is to use unilateral frictional contacts, namely, Point Contacts (PCs), working in compression. PCs are used in any FE code to tackle the Signorini–Fichera’s contact problem, also known as “the problem with ambiguous boundary conditions”. This problem states the impossibility of an elastic non-homogeneous anisotropic body to penetrate a rigid frictionless surface. It was used in [37], which retraces the theoretical solution given by Fichera for one single body [38], and then it was applied in [39] for the interaction of multiple bodies.

PC elements are specifically chosen for the nonlinear analyses to constantly monitor the contact status. Indeed, between two nodes, not only can there be the formation or the closure of a gap, but also sliding may be present, depending on the friction coefficients set. In the case presented in this paper, the friction coefficients assigned to the meridian joints (PCs are set to work in compression) are equal to 1 (see

Table 2. Point Contact FE software settings.

Joint	Position	Type	Friction Coefficients		Stiffness Values
			C1	C2	Initial k0 (kN/mm)	Initial kiter
Parallel	IN	Tension	-	-	61.2	-
	OUT	Tension	-	-	30.6	-
Meridian	IN	Normal	1	1	93.84	✓
	OUT	Normal	1	1	46.92	✓

), making the problem defined by a unilateral frictional contact (a little different from the theoretical frictionless problem of 1964 [38]).

Despite the PC models’ impenetrability condition, a small value of penetration (“non-zero penetration”) is necessary for the solver to calculate the contact condition efficiently. Typically, very high values of stiffness can be accounted for—until they do not generate numerical issues—to obtain as little penetration as possible. In this case, the penetration is automatically controlled by the solver. An initial value of stiffness is set (k⁰ value in Table 2), which is then automatically adapted by the software throughout the steps of the NLA [40].

2.3. Load Distribution

The possibility of modeling a distributed load (a condition close to the experimental one) is checked. The imposed displacement for such an NLA is distributed over a larger area thanks to a frame composed of rigid beams (with the mechanical properties summarized in

Table 3. Mechanical characteristics of load distribution plate and its restraints.

Mechanical Properties
Rigid Beams (Load Plate)
Young’s Modulus (MPa)	E	1.7 · 108
Cross-section Area (mm2)	A	100
Inertia, Principal Axes I11 = I22 (mm4)	I	8.33 · 102
Point Contact
Type		Tension
Initial Stiffness (kN/mm)	K0	1.0 · 103
Max Tension (kN)	Tmax	0

) disposed at the extrados of the dome and connected to the structure through PCs set to work only in compression (tension type with null tensile resistance). Indeed, in this way, whenever a tensile stress reaches the contact surface, the boundaries are inactivated. The reader will find the mechanical characteristics of the PCs involved in Table 3 and a scheme of the FE model in Figure 4b.

By this expedient, it is possible to more realistically simulate the actual loading conditions of a laboratory test (see Figure 3), as well as historical domes surmounted by lanterns.

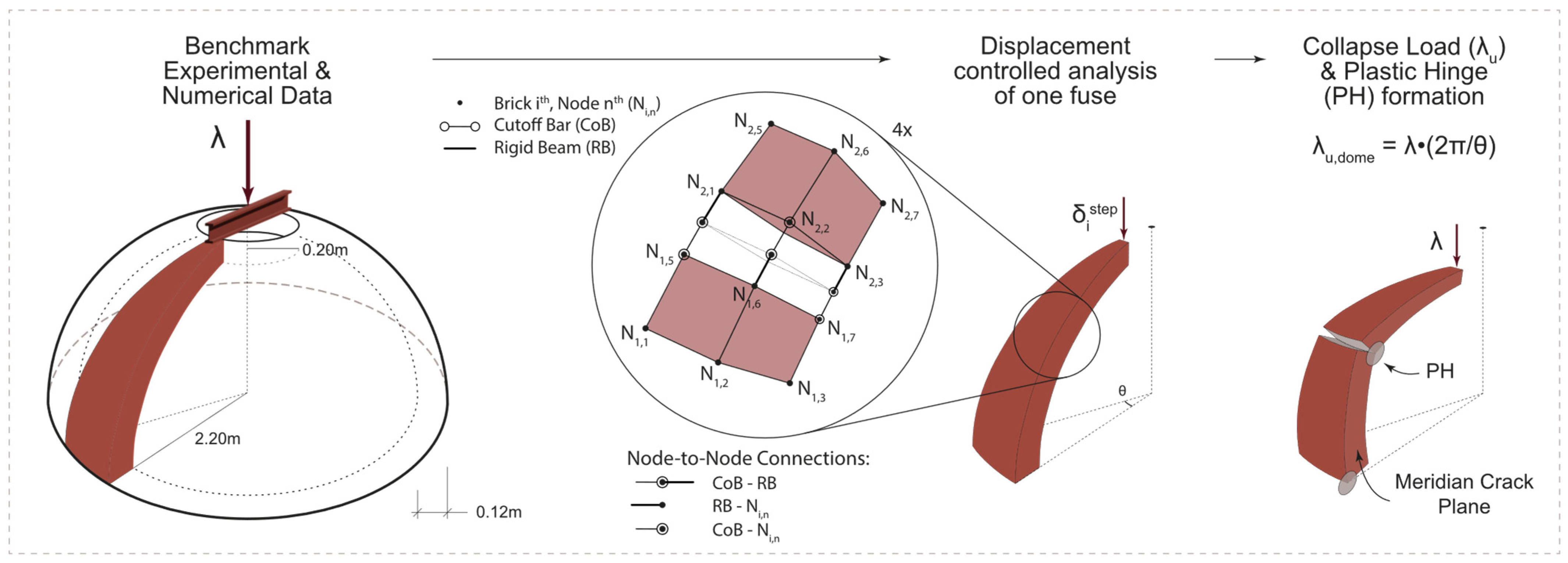
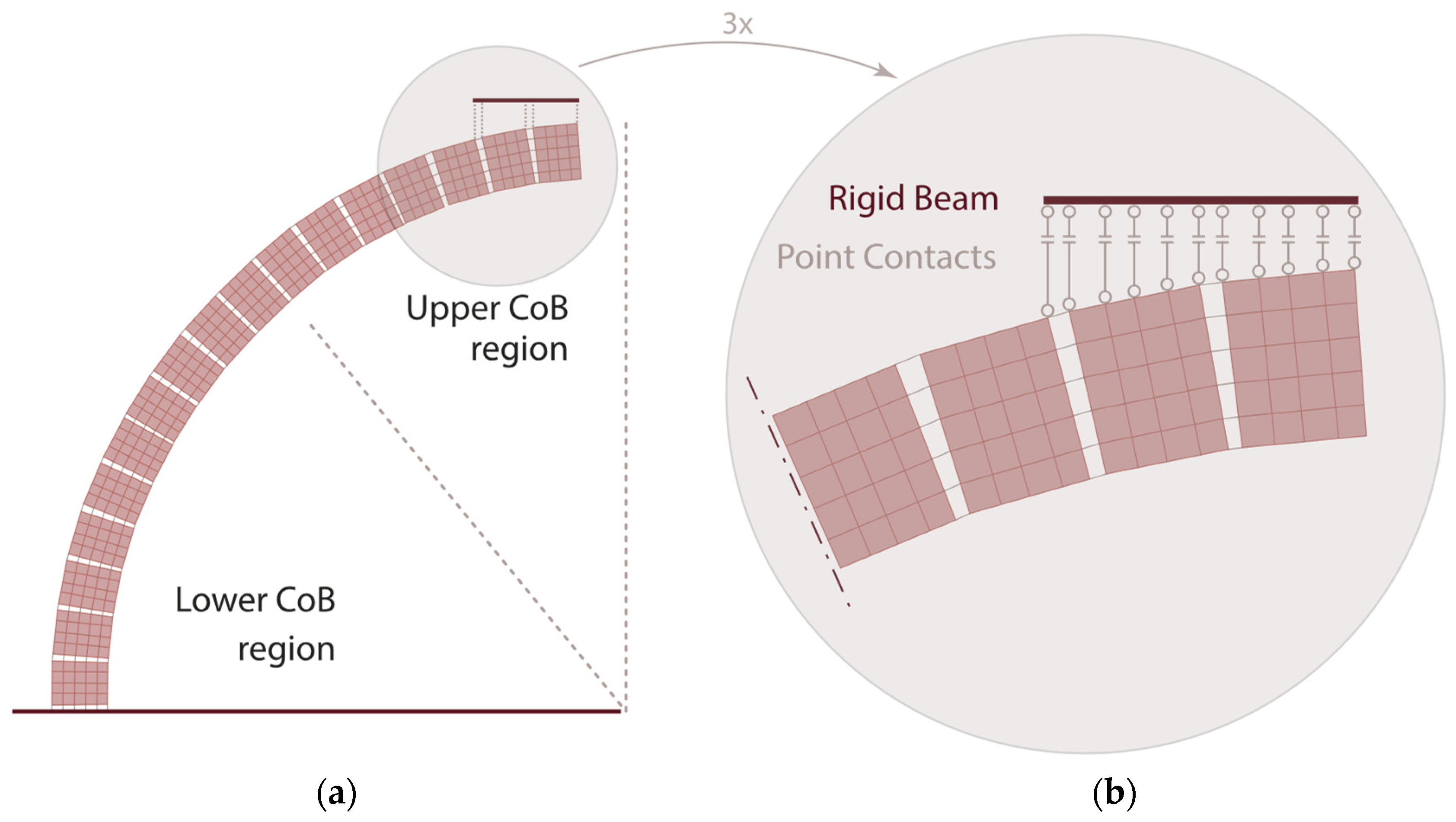
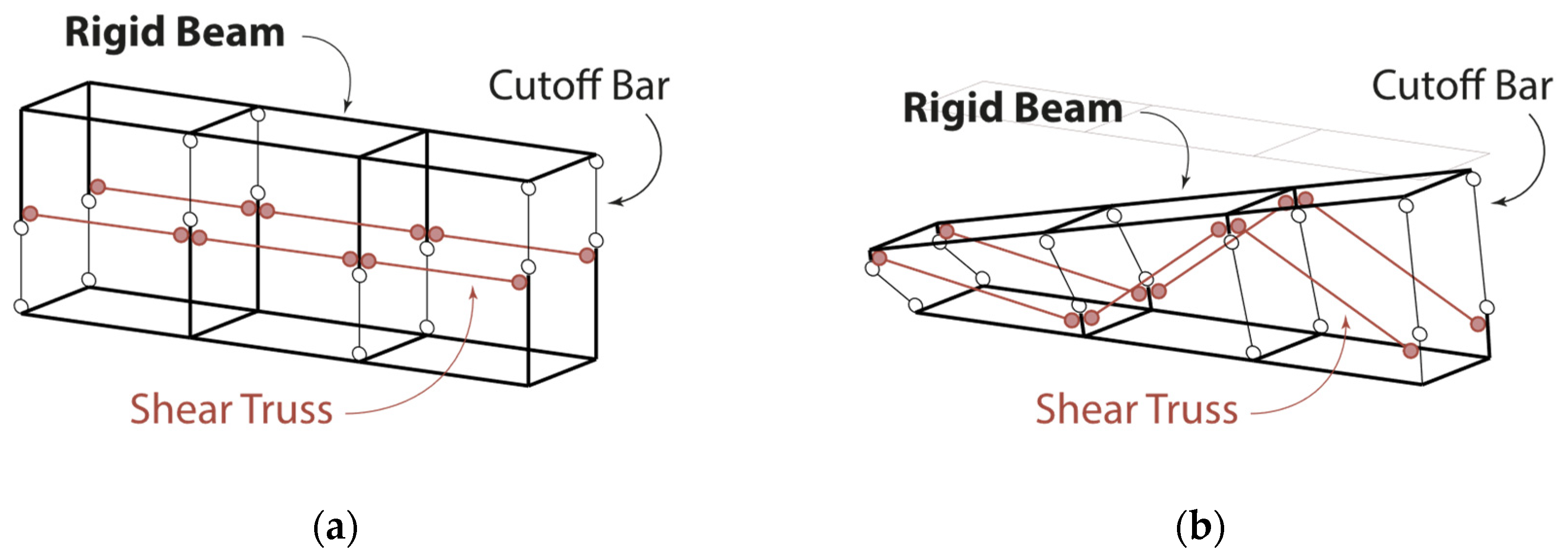
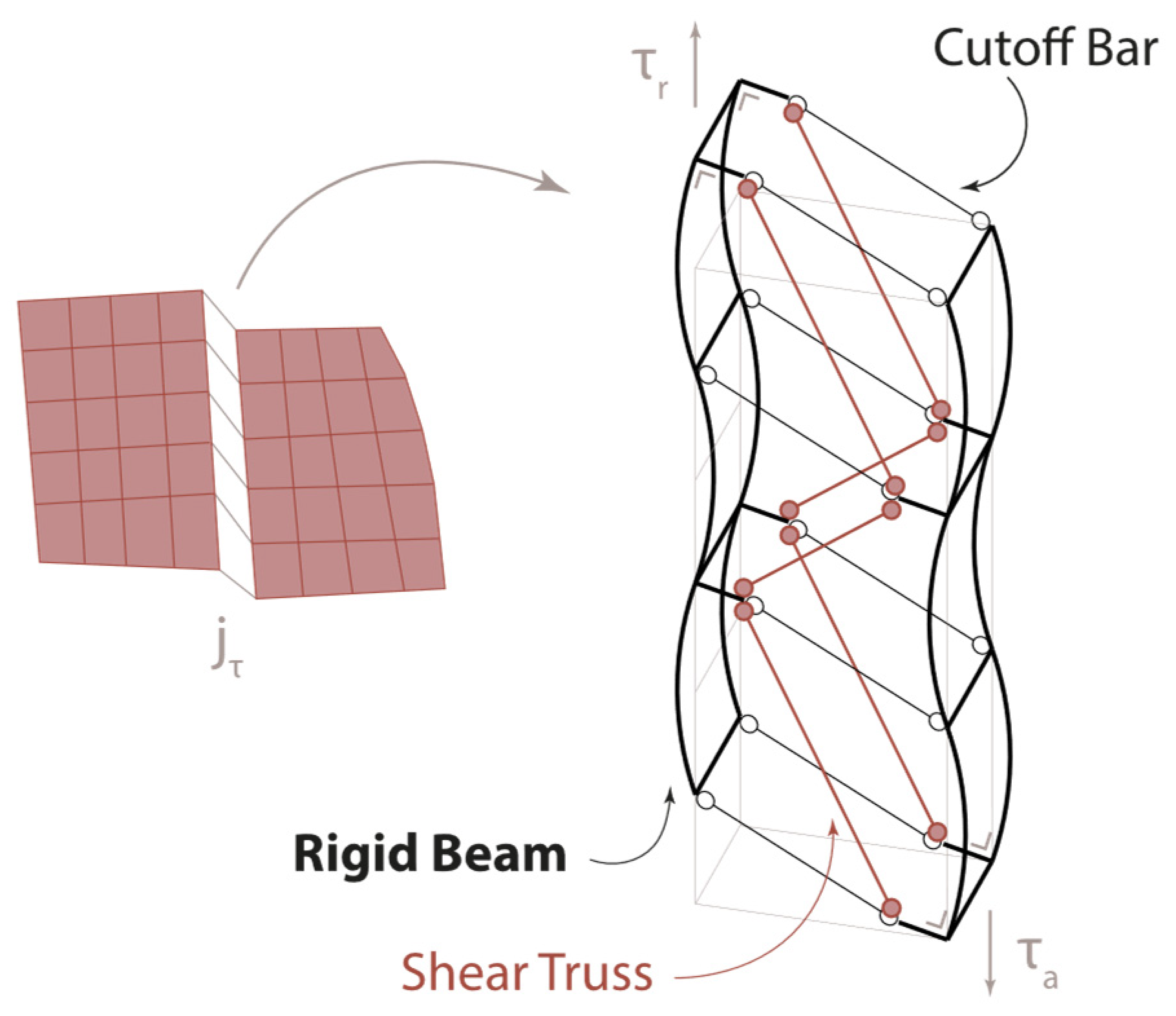
2.4. Modeling of Joints by Means of Cutoff Bars

A more precise approach to model masonry is by assuming small but non-zero tensile strength (f_T). Orthotropy, which is a consequence of the staggered disposition of blocks, can also be modeled by assigning different values to f_T along the meridian and parallel directions. Typically, f_T is higher in the meridian direction if the blocks are arranged in a running bond, whereas in the parallel direction—if the cross-section of the CoBs is assumed to be constant—it progressively decreases from the bottom to the top to take into account the change in the influence area.

Elastic perfectly ductile Cutoff Bars (CoBs), which are truss elements with predefined tensile and compressive limits (i.e., cutoff values), represent the best option in this case. Cutoff values can be properly tuned to better model orthotropy by means of consolidated homogenization techniques, as illustrated in [20].

As already mentioned, in order to account for the change in the cross-section of a fuse, the influence area of the CoBs should be increased from the top to the bottom of the structure. In a very accurate model, the CoB properties should be changed smoothly, passing from a horizontal joint to a contiguous one. Nonetheless, with the present method considered to be simple, the user can decide how many regions to subdivide the hemispherical dome into, assigning to them an average value of the influence area for the CoBs. In the present study, the fuse is divided into two regions, a choice that is considered suitable to obtain sufficiently reliable results. The adopted scheme is shown in Figure 4a.

2.4.1. Joint Modeling

Differently from the first model, for which Heyman’s hypotheses [14,36] hold and a vertically loaded dome can collapse exclusively because of the formation of flexural plastic hinges, in the second model, the joints can also fail in shear. Therefore, a shear-resistant joint—i.e., a complex network of 1D elements involving the utilization of rigid beams, CoBs, and shear trusses—is conceived.

It is a three-dimensional correspondent of the joint that is proposed in [33]. A scheme illustrating the network used is depicted in Figure 5a.

Table 4. Mechanical characteristics of mortar joint elements: parallel joints.

Mechanical Properties
Rigid Beams (Joints)
Young’s Modulus (MPa)	E	1.0 · 103
Section Area (mm2)	A	100
I11 = I22 (mm4)	I	8.33 · 102
Shear Truss (CoB)
Young’s Modulus (MPa)	E	1.7 · 104
Initial Stiffness (kN/mm)	K0	1.00
Max Compression (kN)	Cmax	1.0 ∙ 1011
Max Tension (kN)	Tmax	1.0 · 1011

reports the mechanical parameters adopted for the 1D FEs involved.

The failure of such a joint allows the user to identify the actual presence and position of flexural and shear hinges. A scheme representing deformed shapes near failure is provided in Figure 5b for flexural hinges and in Figure 6 for shear sliding. Because of the assigned geometrical characteristics and mechanical properties, in the presence of shear inelastic sliding, the blocks’ faces remain at the same angular distance (without mutual rotation), and failed shear trusses are removed (if the CoBs are fragile) or substituted with nodal forces corresponding to the ultimate strength of the bars (if the CoBs are ductile).

In order to avoid unnatural and excessive transversal displacements at the base, the nodes are assumed to be fully fixed at the springing. On the meridian section planes generating the fuse, symmetry conditions are imposed.

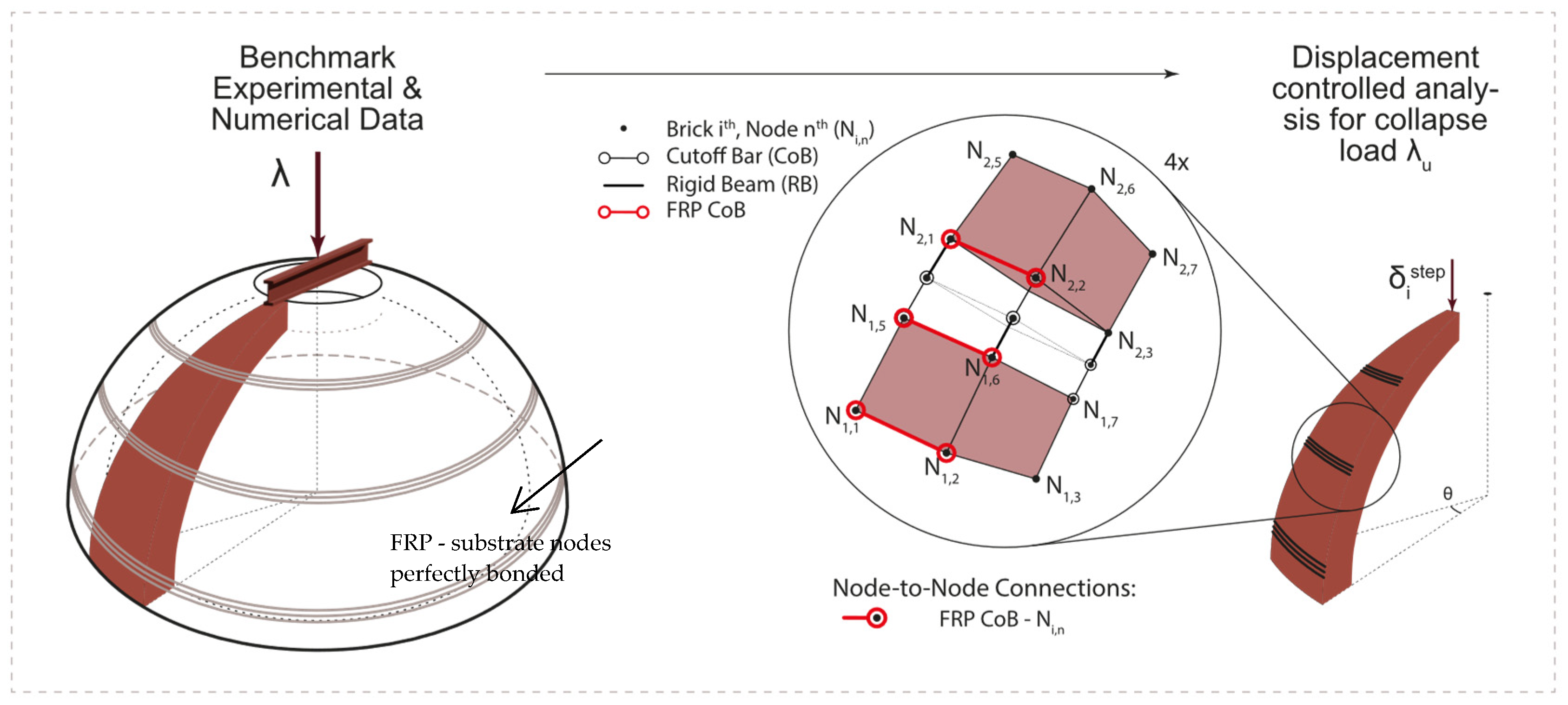
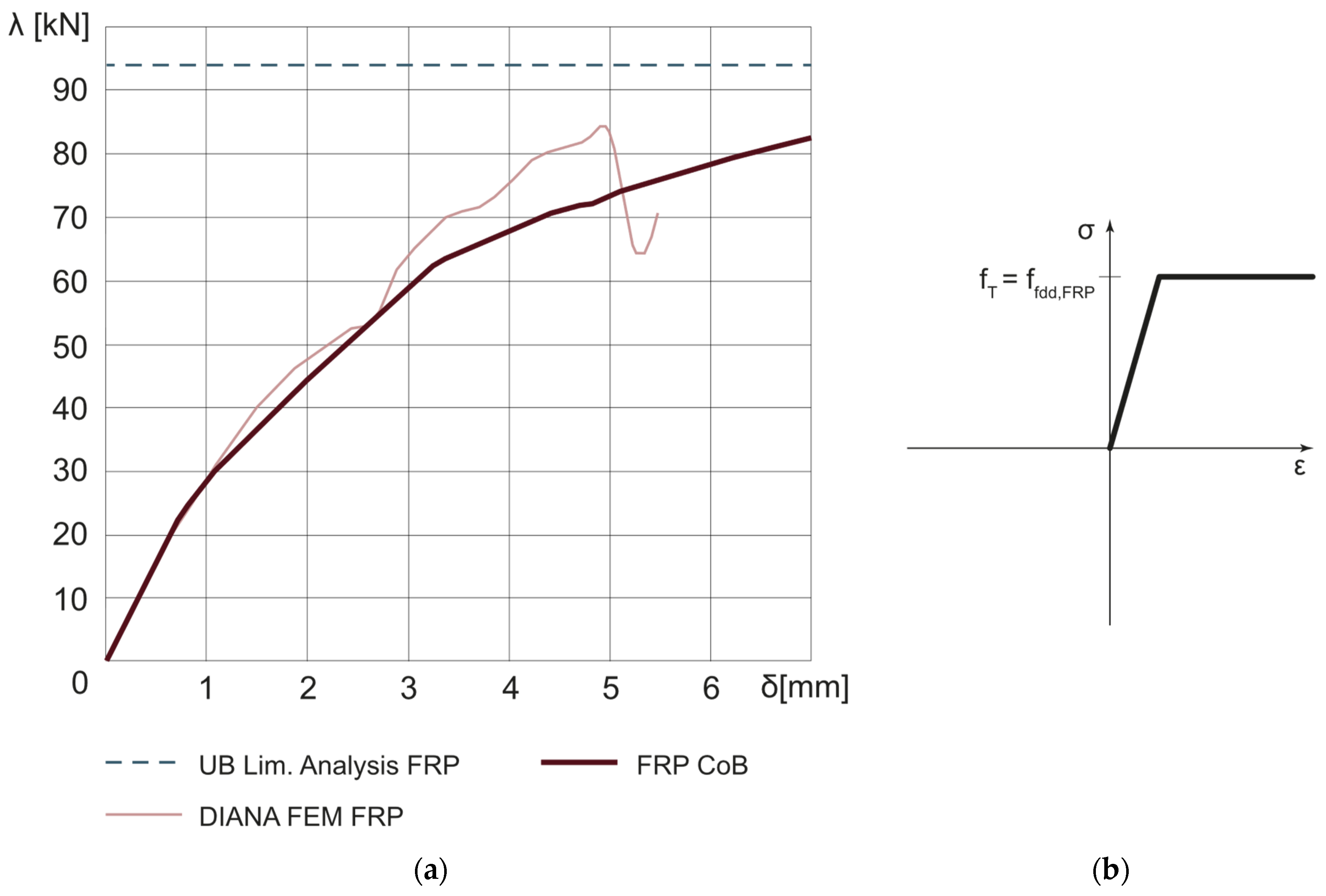
2.5. Modeling of FRP by Means of Cutoff Bars

This section addresses the modeling of a hooping reinforcement. In common practice, domes are mechanically stabilized at the extrados by adding ribs or buttresses (see, for instance, the Pantheon stepped rings built up to the half-height of the dome) or by means of drums (e.g., Middle Age crossing roofs). The act of reinforcing with hooping belts is the bi-dimensional correspondent of the tie rod—usually placed at the springing level—for the arches. The efficacy of applying a tensile-resistant material on the extrados of domes has been proven in the past by practical experience and in contemporary literature [17,41].

Assigning a certain tensile strength in the meridian direction is very effective in increasing the collapse load. On the contrary, the application of buttresses of any material on the extrados—when strongly interlocked to the structure—may increase the inertia of the section, but they fail in precluding the formation of meridian cracks. For instance, the buttresses in St. Peter’s dome (Rome, Italy) failed to counteract the opening of the fuses near the drum. Therefore, the dome needed to be reinforced by iron rings according to the project proposed by Poleni. Reinforcing a dome with meridian strips made of FRP would directly increase the tensile resistance of the fuse while enforcing the formation of a failure mechanism associated with a higher collapse multiplier. Rings or hooping systems indirectly contain the thrust and delay the opening of meridian cracks.

Here, in order to model in a simple way an FRP hooping reinforcement, elastic perfectly plastic (EPP) CoBs are applied at the extrados of the fuse. “Perfect adhesion” is assumed, so no relative displacement between the substrate and reinforcement occurs, and the FRP CoBs are directly connected node by node at the extrados. Since the FRP CoBs are perfectly bonded to the substrate, no sliding is possible between the superimposed nodes belonging to the reinforcement and the substrate. The possible debonding of FRP is taken into account by assigning a conventional tensile strength to the FRP CoBs. The mechanical parameters adopted (see

Table 5. Mechanical properties of FRP according to [43].

CFRP Properties
Thickness (mm)	tfibre	0.2
Width (mm)		100
Young’s Modulus (MPa)	EFRP	1.6 · 105
Factor c1 (-)	c1	0.015
Reducing code factor (-)	γfd	1.2
Masonry partial safety factor (-)	γM	1
Fracture Energy (kN/mm)	ΓFK	0.073
Design Bond Strength (MPa)	ffdd	164

) correspond to those of the FRP and refer to data previously used in a numerical model available in the literature [42,43].

A conventional tensile strength (f_fdd), which considers the possible failure due to debonding or delamination in all cases where an interface between FRP and substrate is not present, is assigned by adopting the simplified procedure proposed by Italian guidelines [42] and as elaborated in a specific case study available in [43]. The design bond strength f_fdd is a function of the fracture energy (Γ_FK), which, in the case of debonding, is spent in the damage of the substrate (which cracks superficially a few millimeters under the FRP strip, depending on the actual mechanical properties of the masonry material, as specified in [43]).

Figure 7 illustrates the strengthened dome, with the FRP CoBs placed at the extrados. They are applied in the same position indicated in [22] in order to obtain comparable results. It is worth noting that the application of FRP in a hooping reinforcement avoids the issue of the loss of exploitable strength near the free edges (as highlighted in [43]) because of the virtually infinite bond length running within the hoop itself.

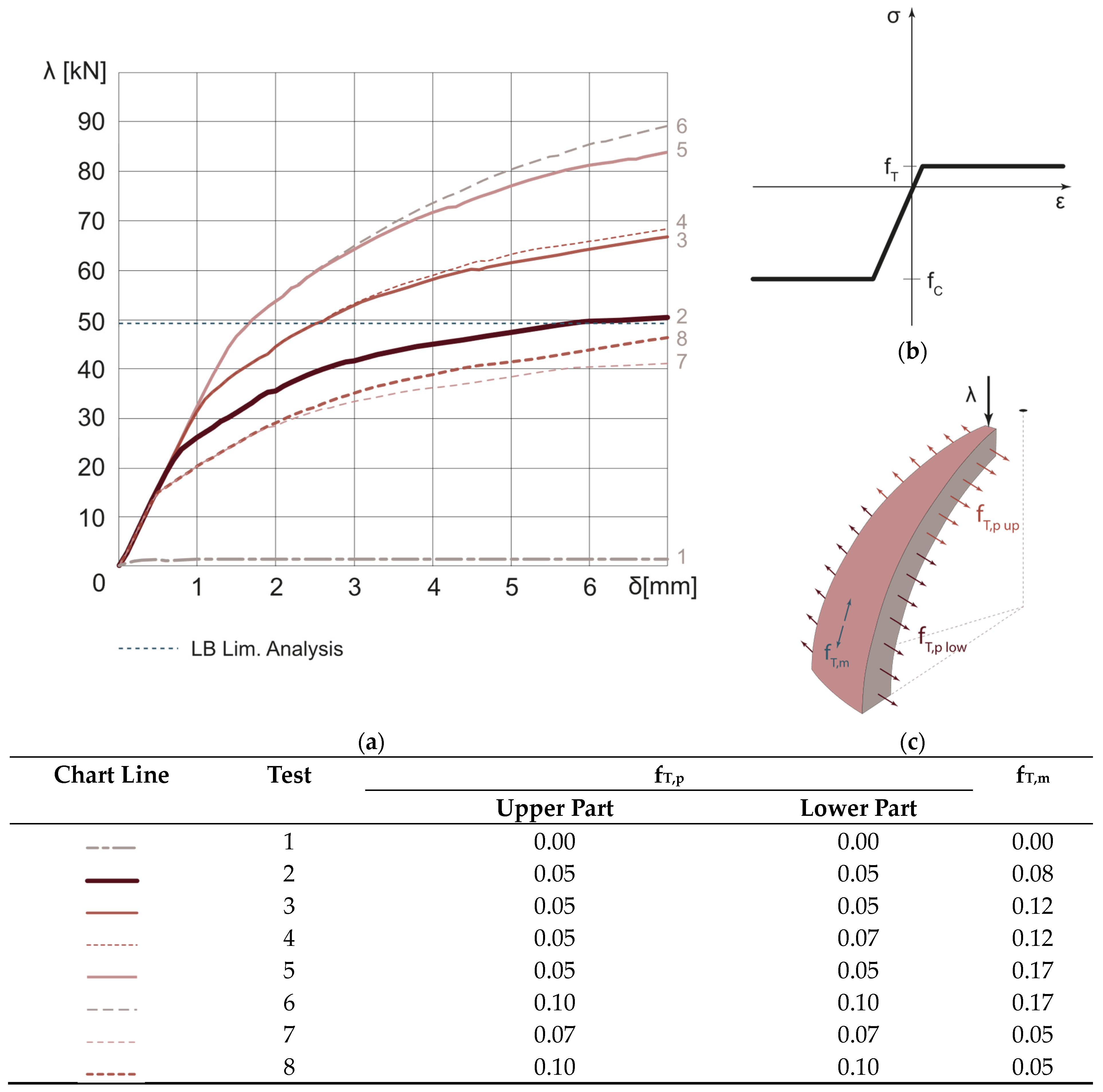
3. Nonlinear Static Analyses

3.1. Unreinforced Dome

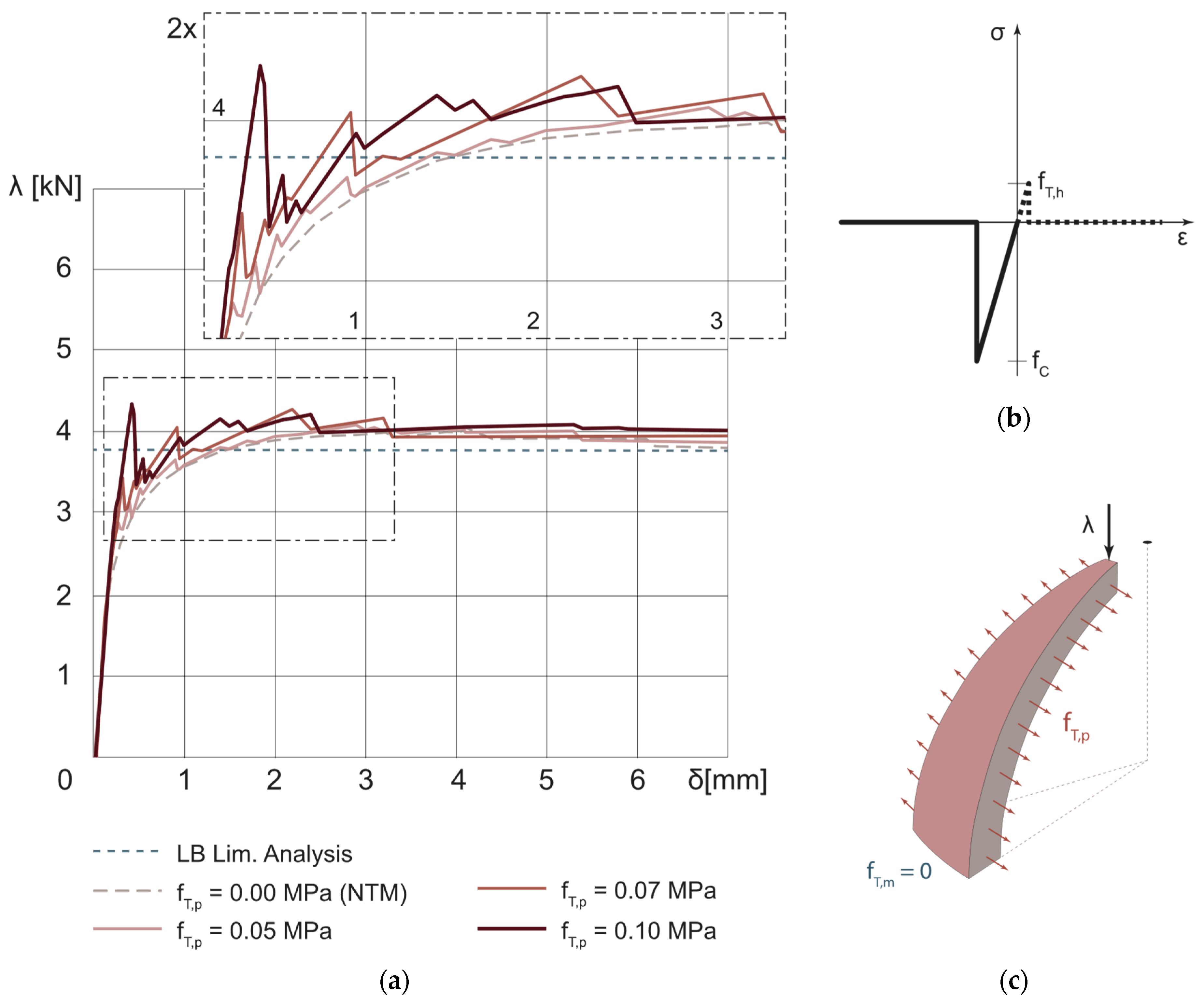
3.1.1. NTM Hypothesis: Sensitivity Analysis

In Heyman’s demonstration [14], which pertains to gravity loads and not to concentrated forces, the stress is always compressive along the meridian direction of the dome, progressively decreasing towards the oculus, as previously stated (Section 1 and Figure 1). On the contrary, along the parallel direction, the stress distribution through the membrane section changes from compression in the upper zone to tension in the lower part (from around 52° from the vertical axis to 90°, i.e., the base), where cracks start spreading and split the membrane in fuses. An annular tensile resistance helps in preventing excessive deformation induced by parallel stresses and improves the dome’s natural equilibrium configuration (catenary profile).

For the dome subjected to a point load located at the crown and increased up to failure, a sensitivity analysis with the data reported in Table 2 is carried out considering a null tensile strength along the meridian direction. Under such a hypothesis, vertical joints fail every time tensile stress occurs. Along the parallel direction instead, small values of tensile strength ($f_{T,h}$) are added and progressively increased to study the behaviour of the dome as a function of them. Indeed, the tensile resistance along the parallel direction helps the dome to bear loads. The post-elastic behavior is assumed to be perfectly brittle. The total number of 133 load steps is considered in a displacement control analysis. The numerical model, for a 20° wide fuse, relies on 1700 elastic 8-node hexahedrons, 1128 PCs (516 meridians and 612 parallel), and 3612 nodes.

The results obtained are summarized in the load–displacement curves in Figure 8.

The higher the value of $f_{T,h}$, the more the load–displacement curves in Figure 8 exhibit a jagged profile. Indeed, by increasing the tensile resistance, the dome is able to redistribute the stresses through its cross-section after the formation of plastic hinges. The occurrence of plastic hinges is easily spotted on the load–displacement curve wherever its profile suddenly drops. After each drop, some strength is recovered because of stress redistribution through the residual uncracked cross-section. When the displacements increase, the plastic hinges rotate with negligible tensile resistance and the dome strength progressively decreases until the asymptote is reached. The asymptote value roughly corresponds to the result given by a Lower Bound Limit Analysis (Durand-Claye approach) under the NTM hypothesis [15], which is used to validate the results. The collapse load obtained by means of such an approach is in the range of $3.8 \mathrm{k}\mathrm{N}<{\mathsf{\lambda }}_{\mathrm{u}}<4.0 \mathrm{k}\mathrm{N}$, depending on whether the f_T value considered.

Figure 9 shows the deformed shape resulting from the nonlinear analyses. As can be seen, because only a unilateral contact in compression is considered, an intermediate plastic (annular) hinge forms at roughly 45° from the vertical axis of the dome and at the springing, in good accordance with the analytical results from the literature under the same hypothesis [15].

3.1.2. Orthotropic Material: Sensitivity Analysis

Considering masonry as an orthotropic material means that the role played by the cohesion, friction, and interlocking of bricks is accounted for. The last feature, combined with the first two, is strongly related to masonry texture [16]. The consequences on the results obtained are explained later in this section. The results are obtained assuming a perfect ductility of the joints.

The total number of 86 load steps is considered in a displacement control analysis. The mesh used, for a 10° wide fuse, relies on 340 elastic 8-node hexahedrons, 1551 unidimensional joints elements (20 rigid beams and 20 PCs for the top load; 622 rigid beams; and 889 CoBs, 170 of which set as shear trusses for the dome), and 1773 nodes.

A sensitivity analysis is carried out to properly tune the CoB parameters and to achieve the best configuration fitting the LA results. The different tensile resistances for the parallel f_T,p and meridian directions f_T,m (please see the table in Figure 10) are multiplied by the influence area pertaining to the region considered. The Young’s Modulus of the elements is assumed to be equal to E = 1700 MPa, while the maximum strength in tension is in the order of 10⁻² Mpa, and the maximum compression is in the order of 10⁸ MPa. The chart in Figure 10 reports the results of the sensitivity analysis.

As can be noted from the previous chart and by comparing the input parameters reported in the table, an increase in f_T,m is more effective in improving the ultimate load of the dome. Indeed, with a larger meridian tensile resistance, the energy expended in opening the meridians raises considerably [15,44].

In Figure 11, the curve previously fitting the LA results of [22] is compared with the curves of other studies, with all curves referring to the same dome [4,18,20,21,22,45]. All curves show a general agreement, and they are close to one each other—yet with some differences due to the method used. The collapse load resulting from this approach is ${\mathsf{\lambda }}_{\mathrm{u}}=50.6 \mathrm{k}\mathrm{N}$.

In Figure 12, the deformed shape of one fuse is reported to show the position of the annular plastic hinges. While the plastic hinge at the base is still well defined, the one in the intermediate position is smeared. As demonstrated in the sections above (Section 2.4.1), due to the ductility of the joints, the energy is not fully dissipated in a single hinge, and inelastic deformation also occurs in the neighboring hinges. Such a feature is shown in Figure 12 by the circle highlighted in gray.

Obviously, in the first steps of the nonlinear analysis, the results in terms of the deformed shape show differences from those at collapse. In fact, in the first steps the elastic part still dominates. The deformation, especially as far as the mutual sliding between the blocks at the crown and the springing is concerned, is illustrated in Figure 13.

As can be seen in the deformed shapes, and as expected, the presence of the distributed load induces flexural and shear deformations near the top of the dome. Furthermore, at the springing, as detailed in Section 2.4.1, a non-negligible sliding of the first two mortar joints is visible. However, as already pointed out, this effect tends to become irrelevant far beyond the elastic limit.

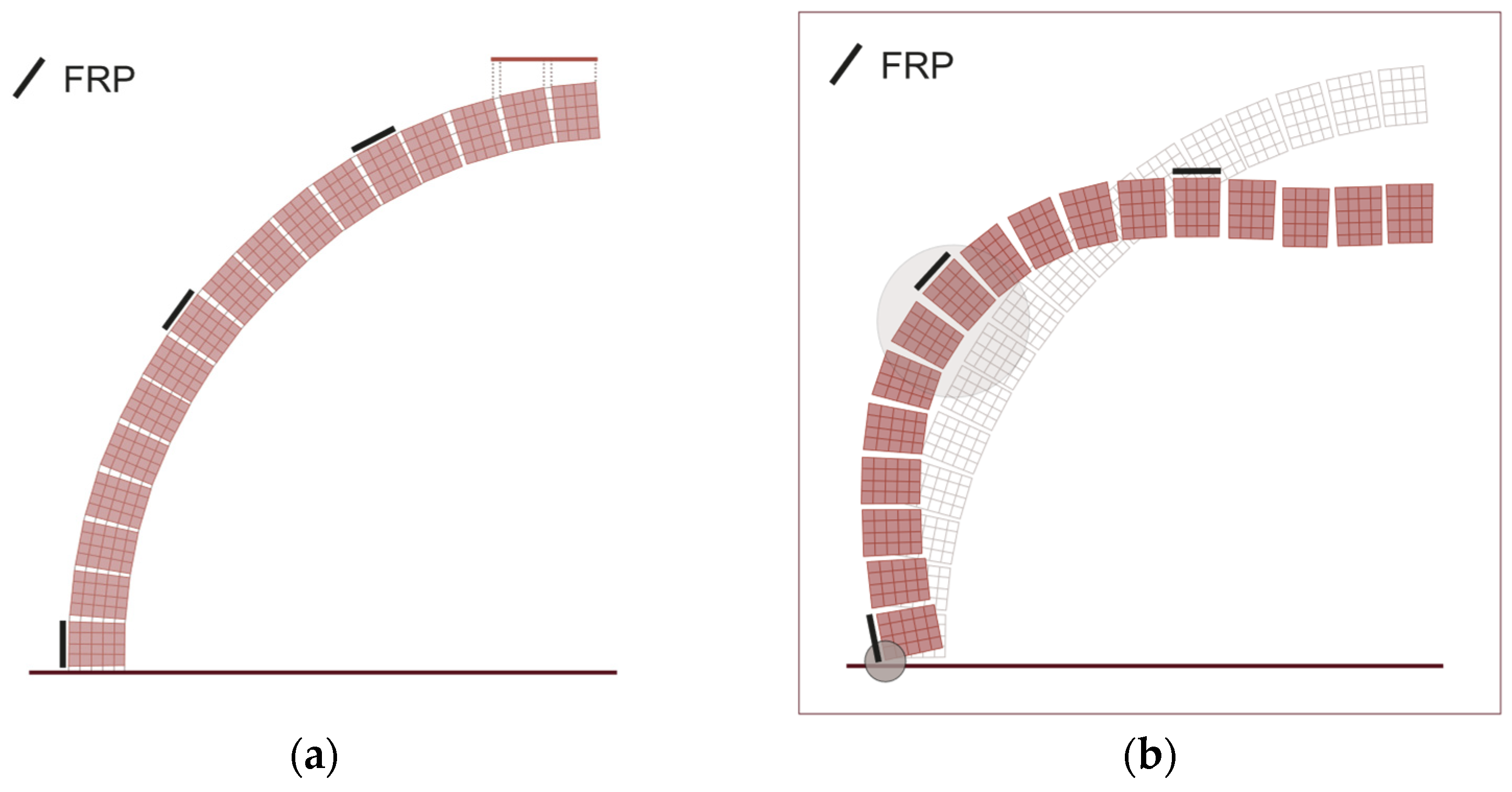
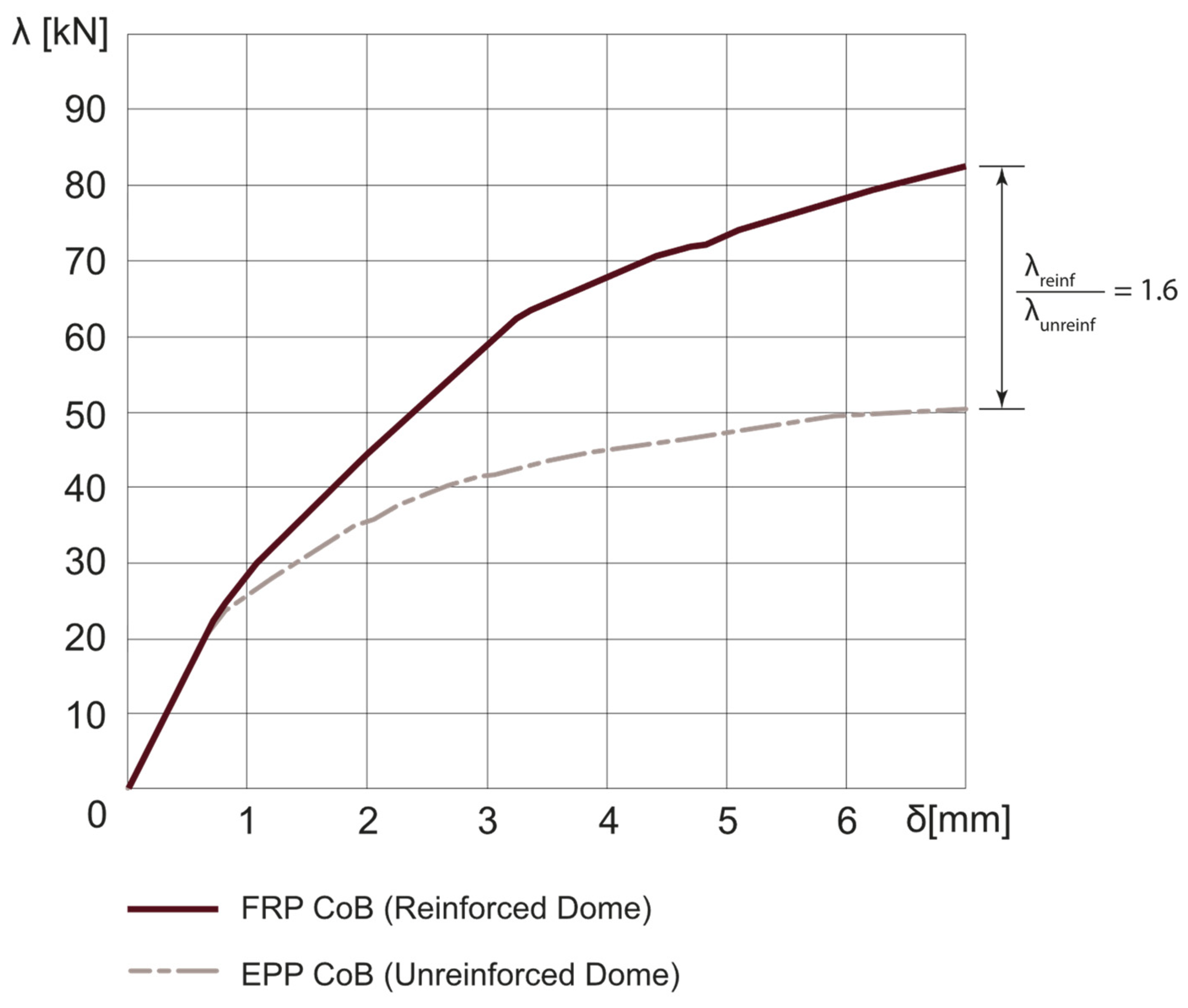
3.2. Reinforced Dome

In this section, some conclusions about the introduction of a CFRP reinforcement in the model are reported. According to the literature results, an FRP annular reinforcement (see Section 2.5) is more effective for curved structures when it is applied at the extrados, where it can better work in tension, counteracting the tensile components present in the lower parallel planes. Figure 14a shows the position of the FRP annular reinforcement on a single fuse of the dome.

The use of nonlinear CoBs for simulating the behavior of the reinforcement has some precedents in the literature, where both advanced [33,46,47] and simplified approaches [48] have recently been proposed. Considering the applicability to real cases and the simplicity of the c preprocessing needed, elastic perfectly plastic CoBs (see the constitutive behavior reported in Figure 15b), assigned the mechanical properties listed in Table 5, seem to also be the most suitable for the design of the FRP reinforcement.

In Figure 15, the results of such an application (in terms of the collapse load ${\mathsf{\lambda }}_{\mathrm{u}}=82.5 \mathrm{k}\mathrm{N}$) are reported and compared with the few numerical data available in the literature [22]. To the best of the authors’ knowledge, no experimental information is available for the benchmark considered in the presence of FRP.

In Figure 16, the ratio between the collapse loads obtained in the reinforced (λ_reinf.) and unreinforced (λ_unreinf.) cases is reported. It is worth noting that, for a reduction in the vulnerability of a masonry structure, an increase in the load-carrying capacity is required, which should typically be at least 10%, so the evaluation of the ratio between the ultimate load-bearing capacity before and after rehabilitation is paramount. For the example at hand, the reinforced dome exhibits an ultimate load roughly 1.6 times larger than that observed for the unreinforced one because of the introduction of a tensile-resistant material, which delays the formation of meridian cracks, globally increasing their strength. In Figure 14b, the deformed shape of the dome near collapse in the presence of FRP is depicted. The position of the FRP strips is also indicated so that conclusions can be drawn on their effectiveness in limiting the crack growth in the meridian direction. The position of the intermediate plastic hinge is highlighted in light gray.

Figure 17 shows a comparison between the deformed shapes of the unreinforced and reinforced cases. The red arrows in the image qualitatively represent the displacement prevented by the presence of the FRP strip. The lower reinforcement tends to prevent the dome from displacing outwards. The upper reinforcement decreases the rotation of the blocks under load and enhances the downward displacement. In the same image, the change in the position of the plastic hinge formation is also highlighted. Indeed, the intermediate annular hinge moves from the 8th–9th–10th joint from the top to the 10th–11th joint passing from the unreinforced case to the FRP reinforced case. The intermediate hinge forms in the joint located immediately under the reinforcement—as previously noted in [22].

The study carried out on the FRP-reinforced dome proved to be significant—in accordance with the initial objectives—because it allows the user (either academician or practitioner) to do the following:

• Quickly evaluate the increase in the load-carrying capacity after reinforcement;
• Rapidly perform a trial and error procedure to determine the optimal position of the reinforcement. This last feature is possible thanks to the short preprocessing and computational time needed.

When—for a constant thickness of the reinforcement—an increase in the FRP width is considered, a huge increase in the collapse load is obtained.

Table 6. Results in terms of collapse load (λu) of FRP CoB addition on the fuse extrados. The last column shows the ratio between the increased and original λ values.

	Added #CoBs (0.2 × 33 mm2) *			λu	λincr./λorig.
Simulation	Springing	Middle	Top	(kN)	(%)
Original **	0	0	0	84.69	100%
1	1	0	0	85.28	101%
2	1	1	0	92.25	109%
3	1	1	1	92.64	109%
4	2	0	0	86.11	102%
5	2	2	0	99.72	118%
6	3	0	0	87.17	103%
7	3	3	0	107.25	127%

* The numbers in the matrix consider only the CoB added to original reinforced configuration. ** The original configuration counts 3 CoBs (0.2 × 100 mm²) per level (springing, middle, top). For instance, the first simulation adds 1 CoB at the springing, resulting in a reinforced area of 0.2 × 133 mm² while maintaining the original area of FRP at the other levels.

presents the λ_u values resulting from the progressive addition of the FRP CoBs to the model. Each CoB corresponds to 0.2 × 33 mm² of material added. A value double that of the original width is reached in simulation #7 (see Table 6).

The reinforcement is placed to prevent/retard the splitting of the dome into fuses. As can be seen from the first three simulations, the most effective action is to increase the reinforcement at the middle height. This is not surprising because, (1) at the springing, the boundary conditions do not allow for a meaningful opening of meridian cracks and, (2) near the top, instead, the effectiveness is reduced because of the very small displacements that occur in the formation of the meridian cracks, as a consequence of the geometric constraints induced by the dome’s symmetry.

Differently from arches, in which the FRP extrados reinforcement considerably changes the failure mechanism (also triggering shear sliding and localized reinforcement spalling) [33], in this case, the presence of a hooping belt does not significantly change the mode of failure (at least as far as the typology of the mechanism is concerned).

Having assumed a perfect bond, it is worth mentioning that a limitation of this study is the absence of an interface between the reinforcement and the substrate. The anchoring length here is virtually infinite (as previously stated in Section 2.5), so no near-end effects should be taken into account, but the assumption of a perfectly plastic behavior excludes brittle debonding from the substrate. This phenomenon could happen, leaving the dome in a static condition similar to that of the unreinforced case, a condition that would be detrimental and dangerous in real cases. Further studies can be conducted to investigate the failure modes of the reinforcement that involve the interface with the substrate, according to more sophisticated modeling strategies [33,46].

4. Conclusions

The method proposed here for the nonlinear static analysis of masonry domes proved to be accurate and robust enough to be used by practitioners. A detailed comparison with the literature data proved the reliability of the proposed model. Masonry nonlinearities were lumped in mortar joints and modeled in turn through the use of elastic–brittle and elastic–plastic finite elements. Evidently, the results obtained so far in terms of the ultimate collapse load and active failure mechanism are strongly related to the initial hypotheses on joints. The model showed the following:

• Its adequacy for implementation in any commercial software (low-cost software included);
• The possibility of considering the failure of mortar joints under combined modes I and II;
• The ability to account for both orthotropy and NTM hypotheses (with the latter being on the safe side but, in some cases, responsible for the strong underestimation of the load-bearing capacity);
• The possibility of directly and straightforwardly introducing external retrofitting with innovative composite materials (e.g., FRP and FRCM);
• The ability to handle, with a simple trial and error procedure, the difficult problem related to the optimal disposition of external retrofitting layouts, which maximize the load-carrying capacity at the minimum cost (Pareto’s frontiers).

Regarding the last point, the model appears to be particularly interesting because, from the failure mechanism found in the unreinforced case, it is possible to deduce a preliminary disposition of any strengthening device working in tension. As a matter of fact, for masonry, the main information provided by a numerical analysis carried out in the nonlinear range is the collapse load and the corresponding triggered failure mechanism. In this context, the role played by external retrofitting is mainly related to an increase in the internal dissipation, which is always associated with a failure mechanism characterized by a higher dissipation (with respect to the unreinforced case). Consequently, the collapse multiplier increases. Typically, such information is obtained using an FE limit analysis, which proceeds by solving a linear programming problem, a feature that precludes its utilization within any low-cost commercial software. The present approach fills such a gap by providing the same information at the last iteration but by using standard finite element routines (i.e., by utilizing incremental procedures based on the factorization of the stiffness matrix). Such an advantage makes the procedure proposed in this paper much more appealing in common design practice.

The main drawback of the present approach lies in the non-automatic implementation of the CoBs, which would need dedicated subroutines or preprocessing programs to directly produce a finite element discretization composed of hexahedrons and CoBs, starting from a standard mesh with 3D elements. Another limitation is related to the uncoupled shear and normal behavior of the mortar joints. In this regard, it would be required to automatically consider the role played by normal stresses in the shear strength of the joints, which, at failure, typically behave following the Mohr–Coulomb failure criterion.

Moreover, an important limitation that cannot be alleviated and is unavoidable in this kind of discretization is the fact that there is no possibility of reproducing the size effect [49,50].

Future developments should be clearly related to (i) the mitigation of the work needed in the preprocessing phase; (ii) the development of a new, truly 2D interface model for joints; and (iii) the application of seismic loads.