Influence of Stress Disturbance on the Deformation of Nearby Cemented Roadways following the Excavation of Chambers
Abstract
:1. Introduction
2. Research Background
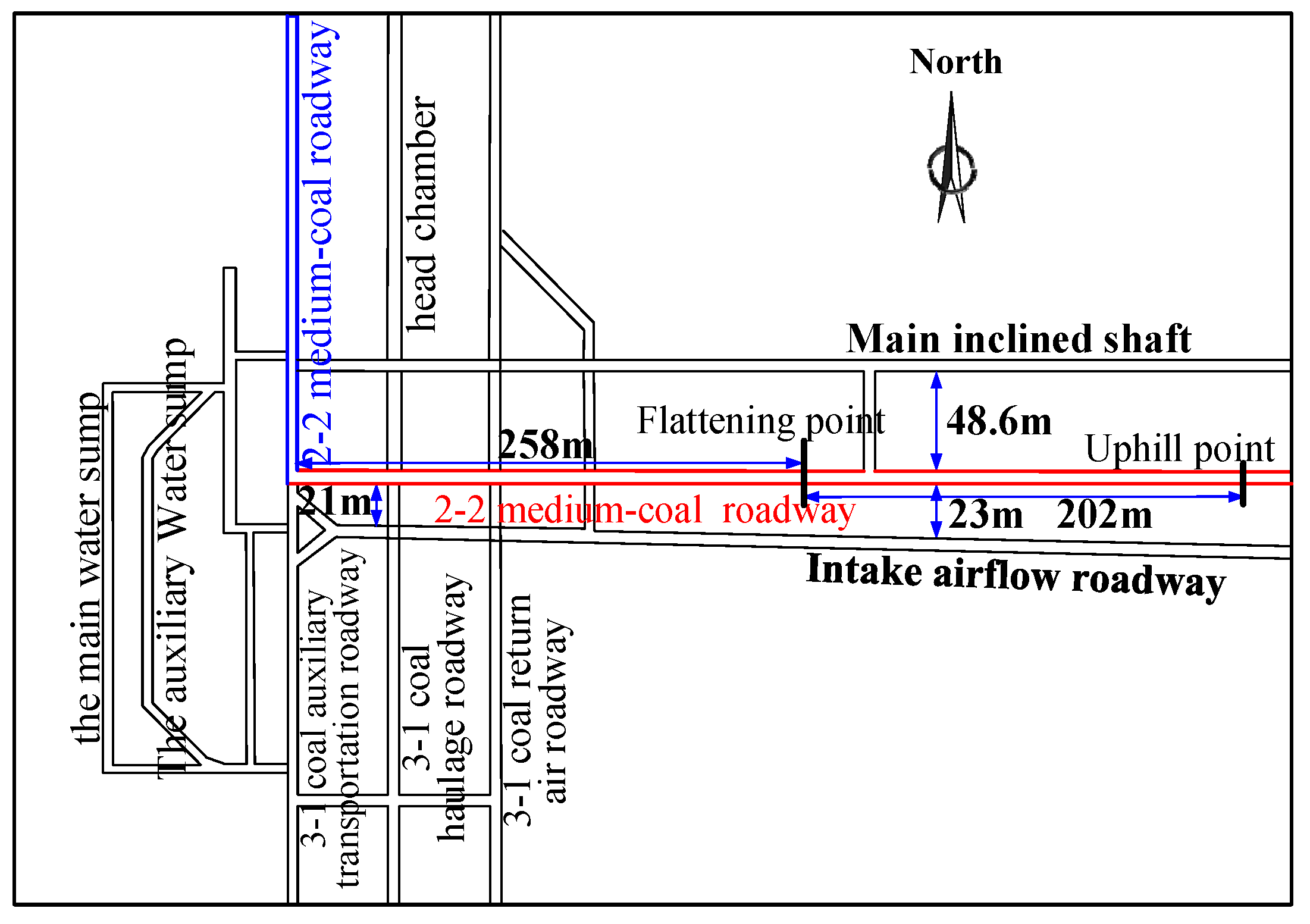
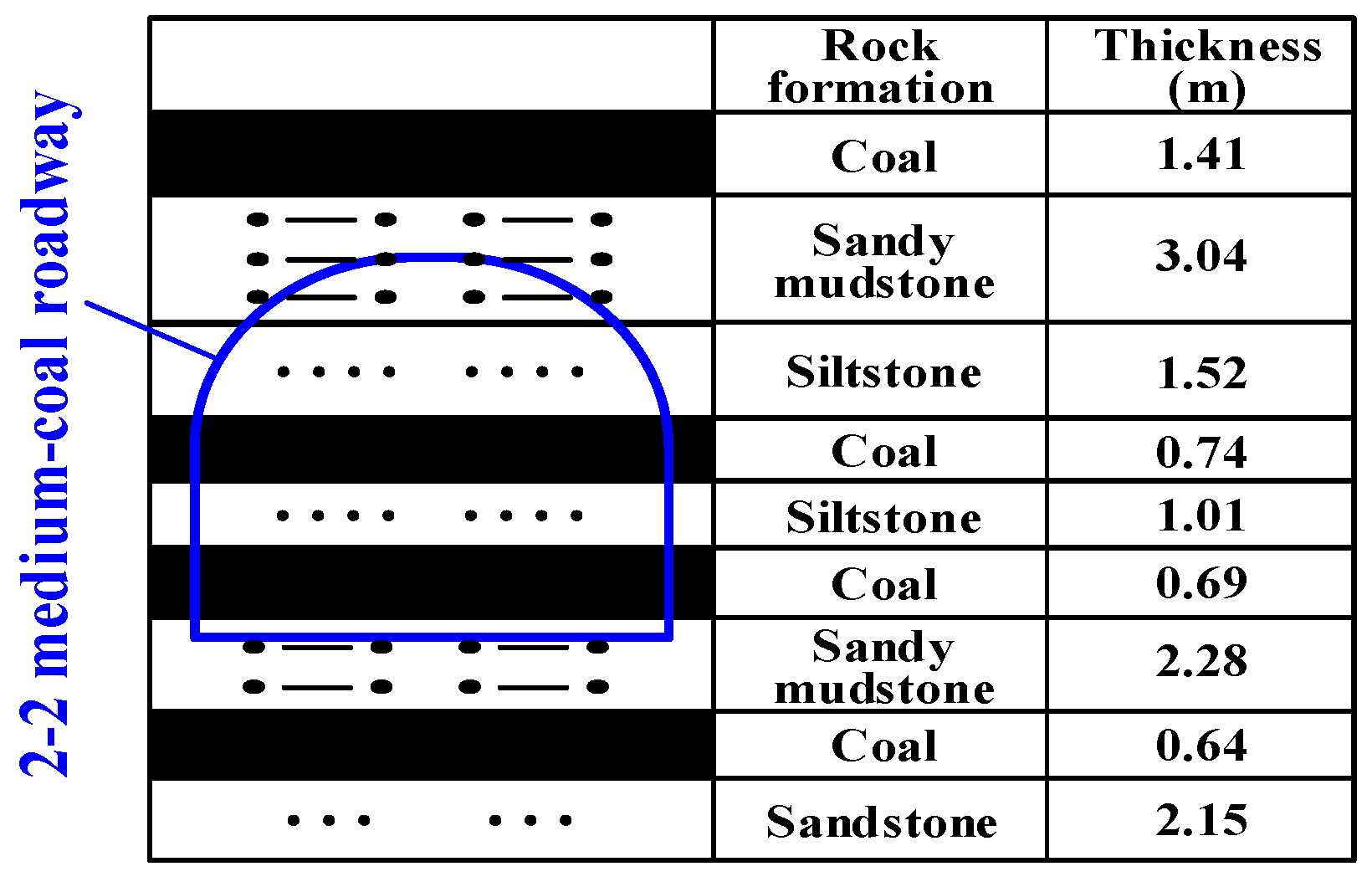
2.1. General Situation of Roadway Geology and Support
2.2. Reasons for Deformation of Weakly Cemented Soft Roadways
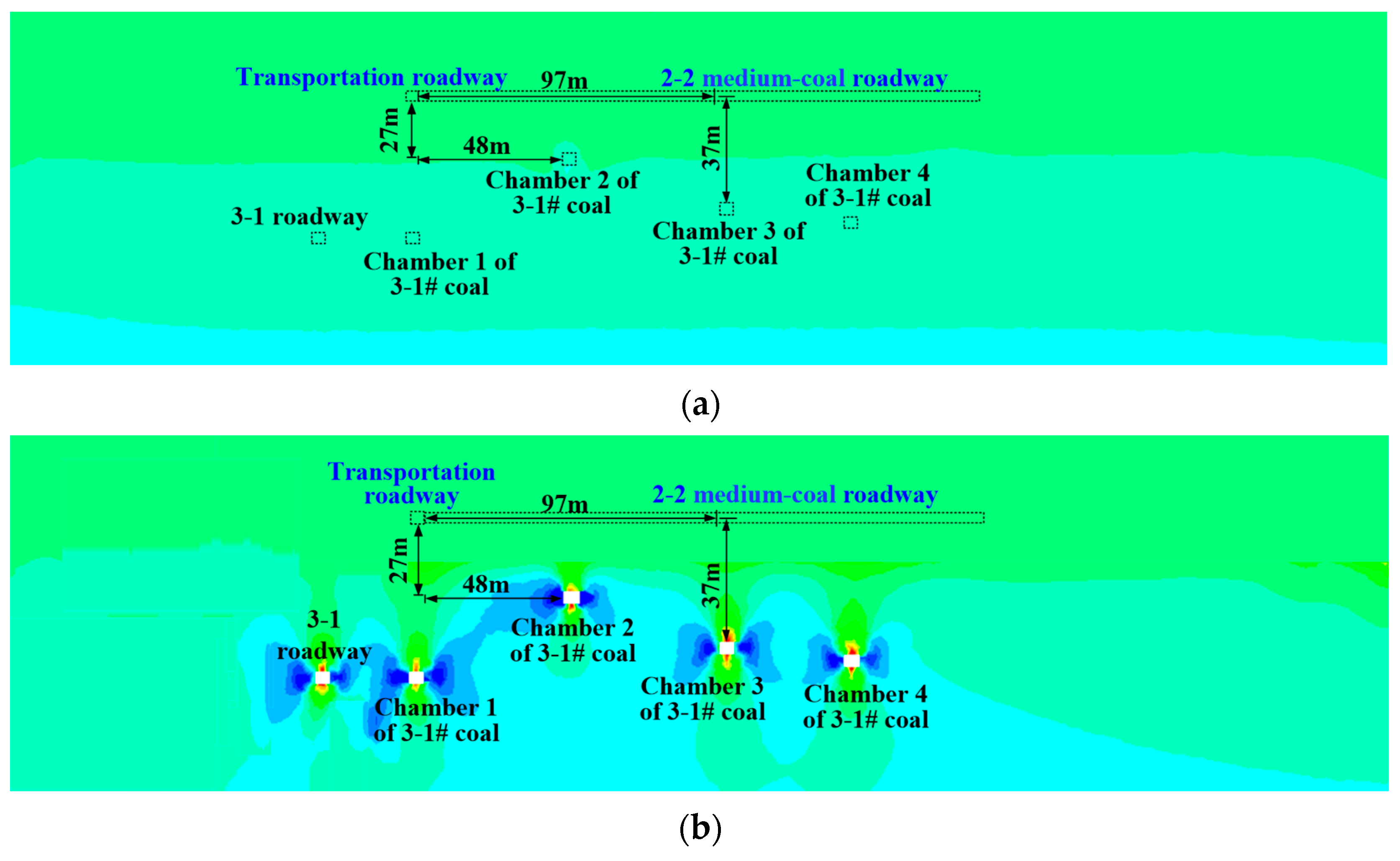
2.2.1. Stress Concentration from Adjacent Chambers
2.2.2. Physical and Mechanical Properties of Surrounding Rock
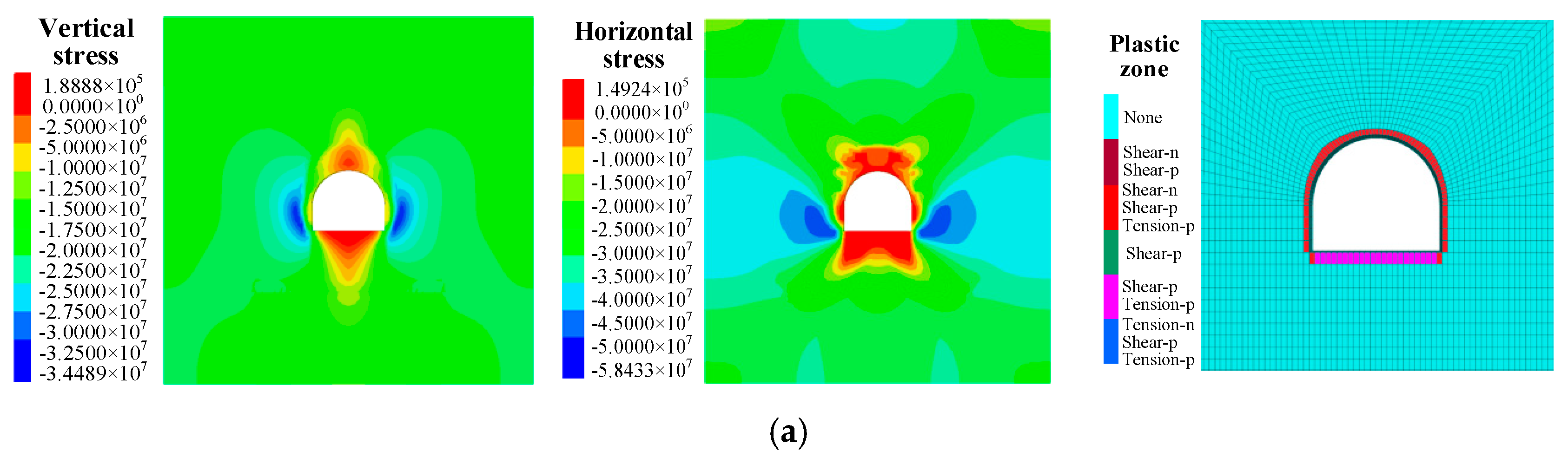
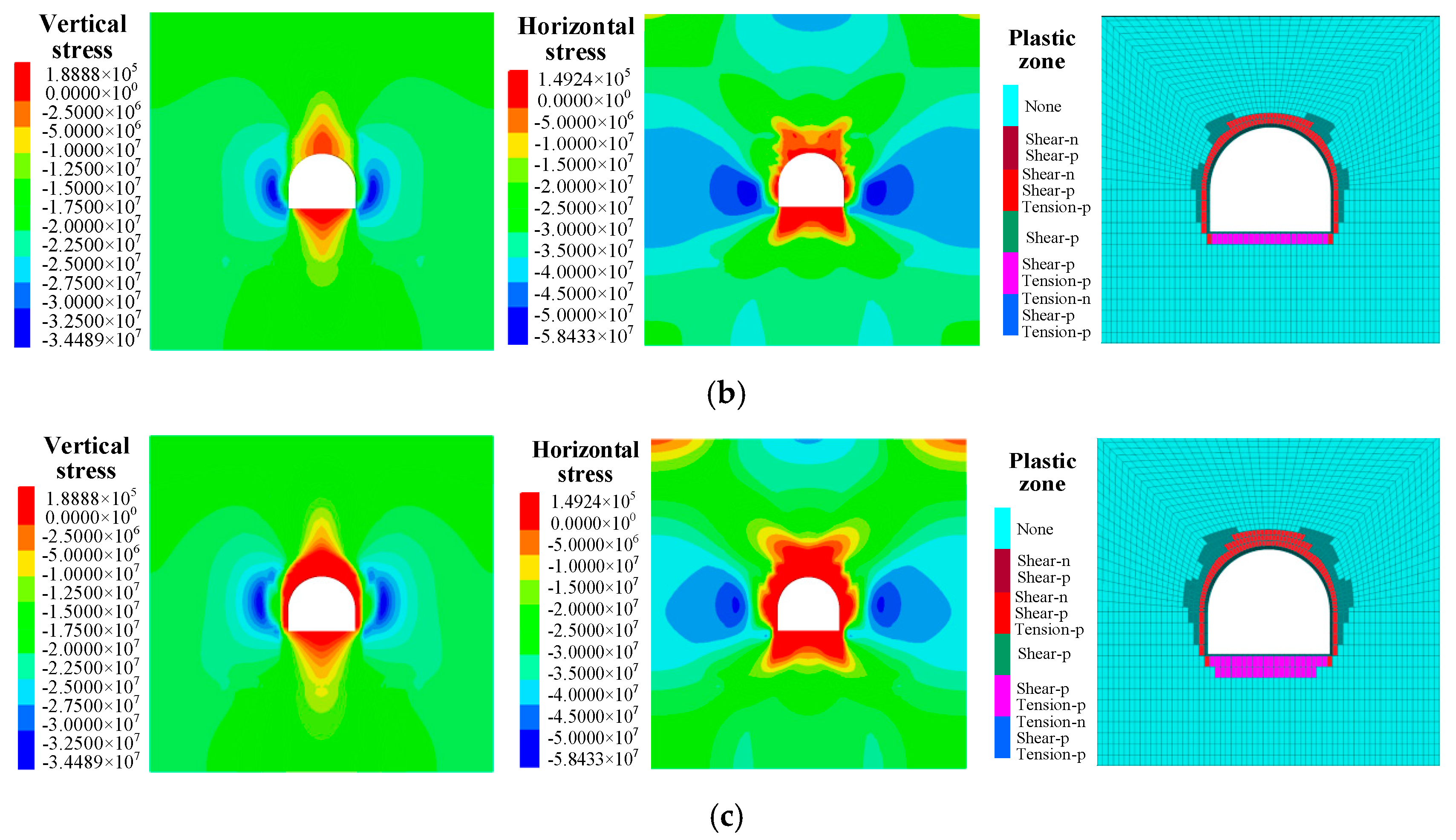
3. Stress Distribution Characteristics of Surrounding Rock
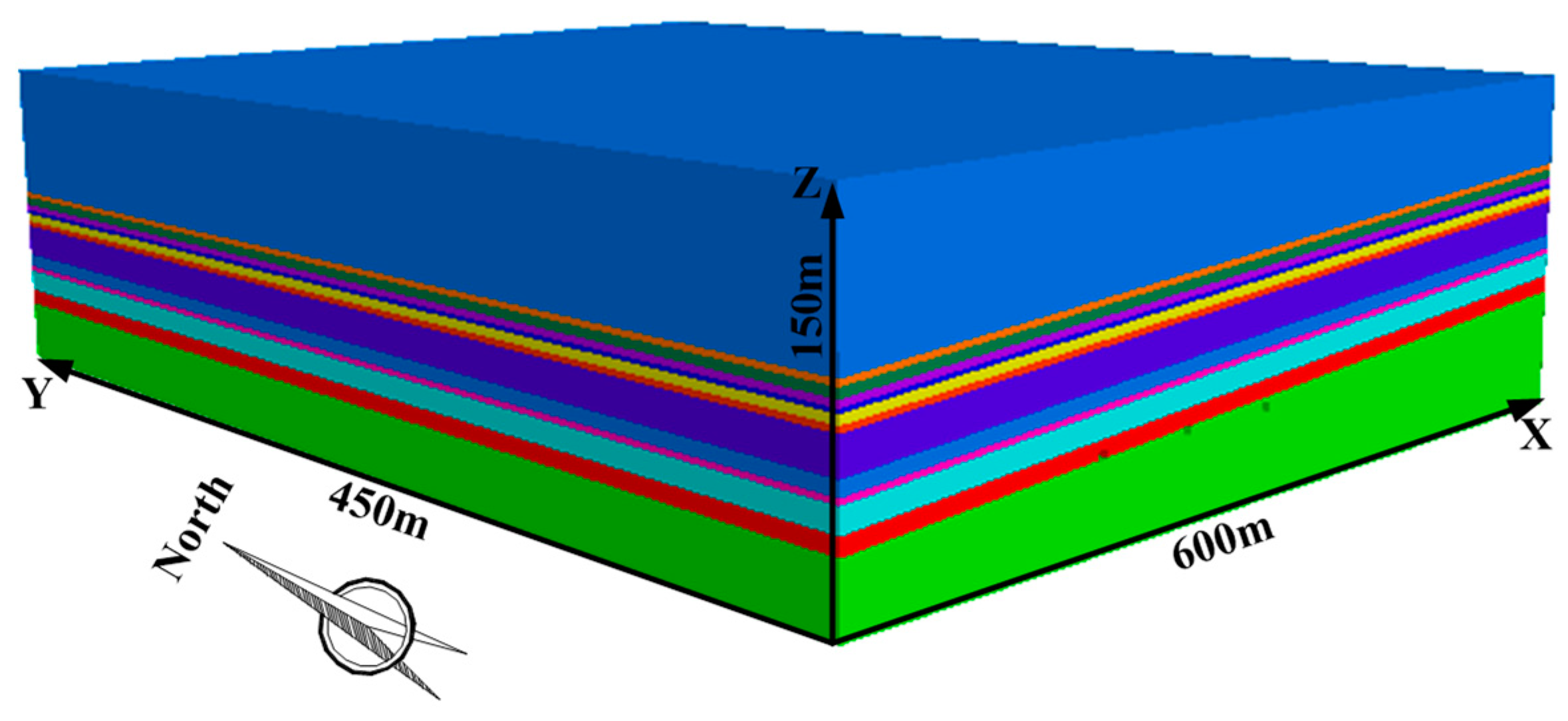
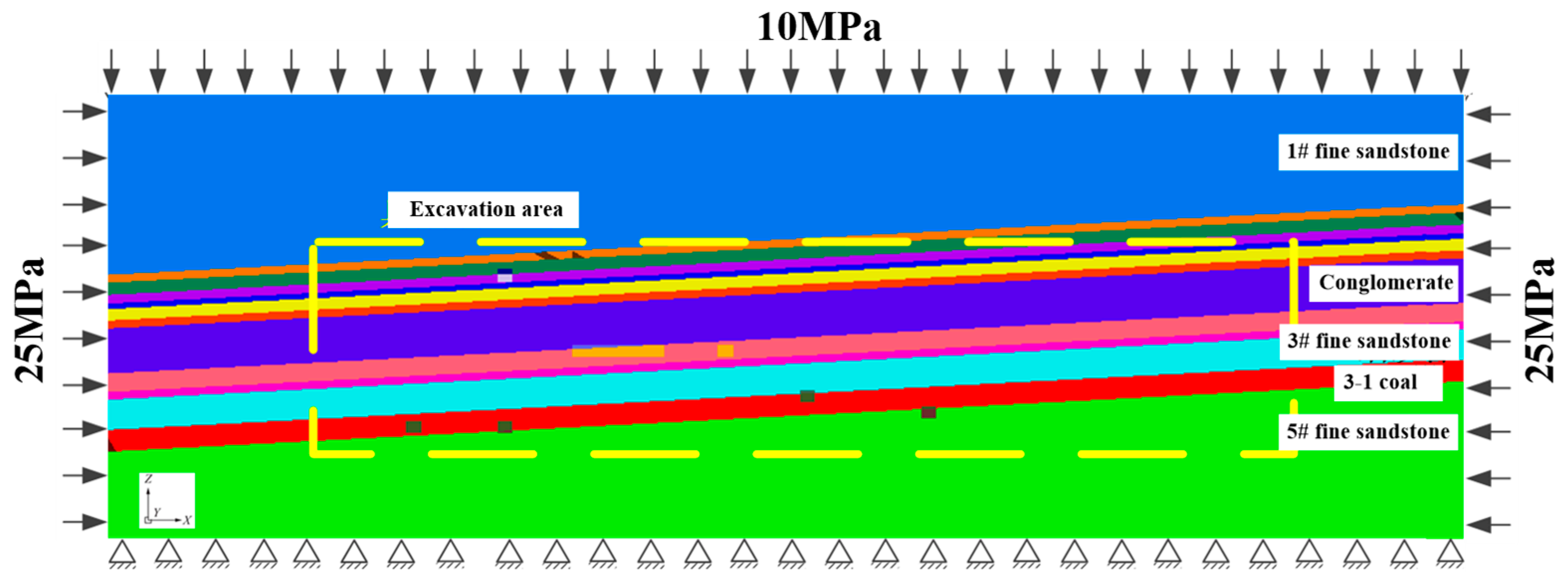
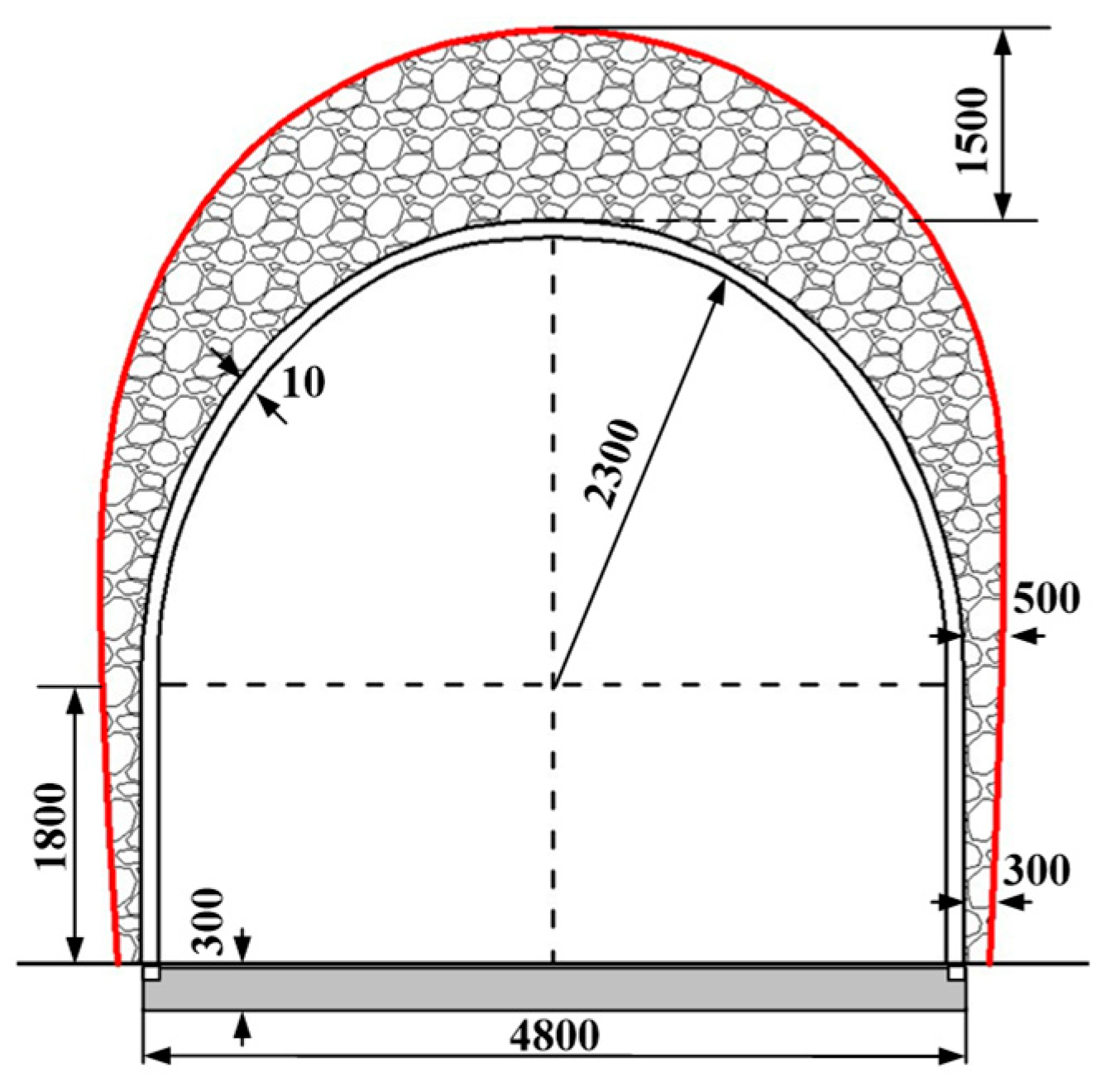
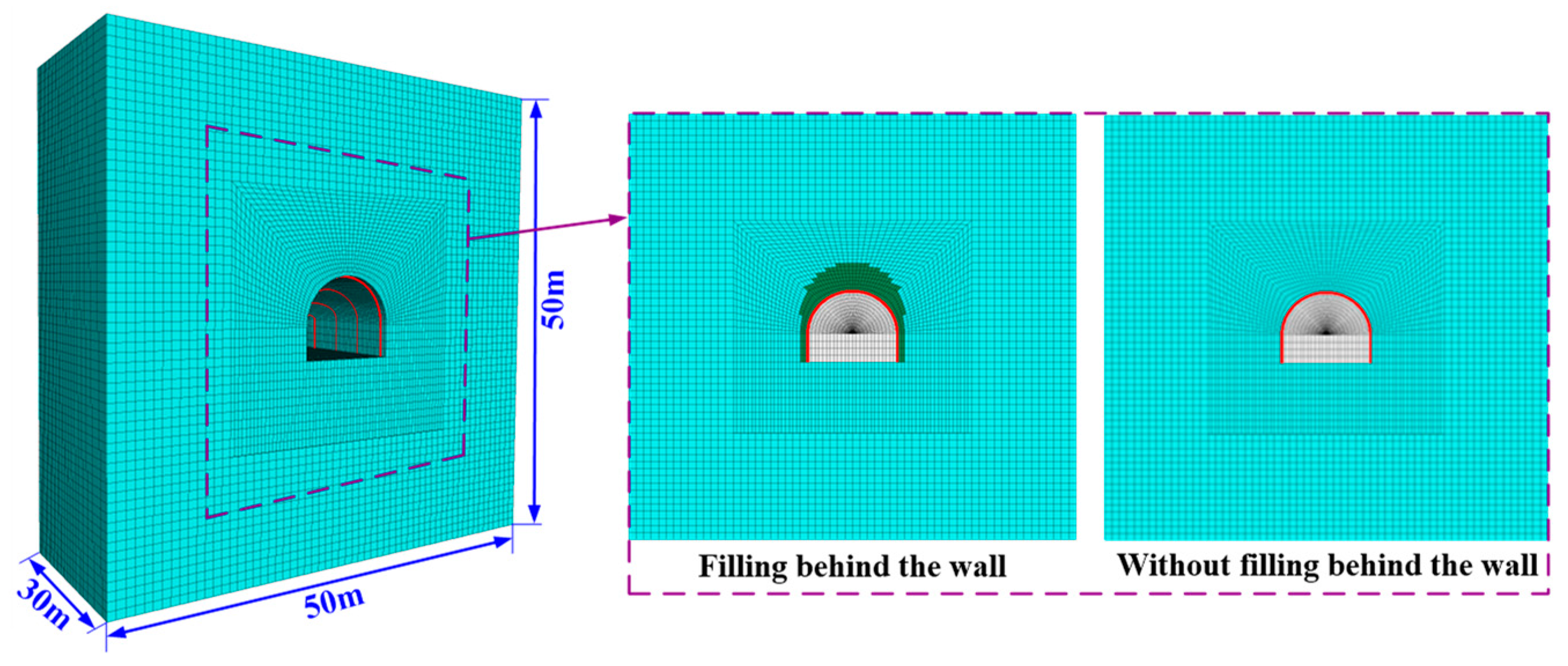
3.1. Numerical Model Construction
3.1.1. Numerical Model Size
3.1.2. Unit Parameters of Numerical Model
3.1.3. Calculation Scheme of Numerical Model
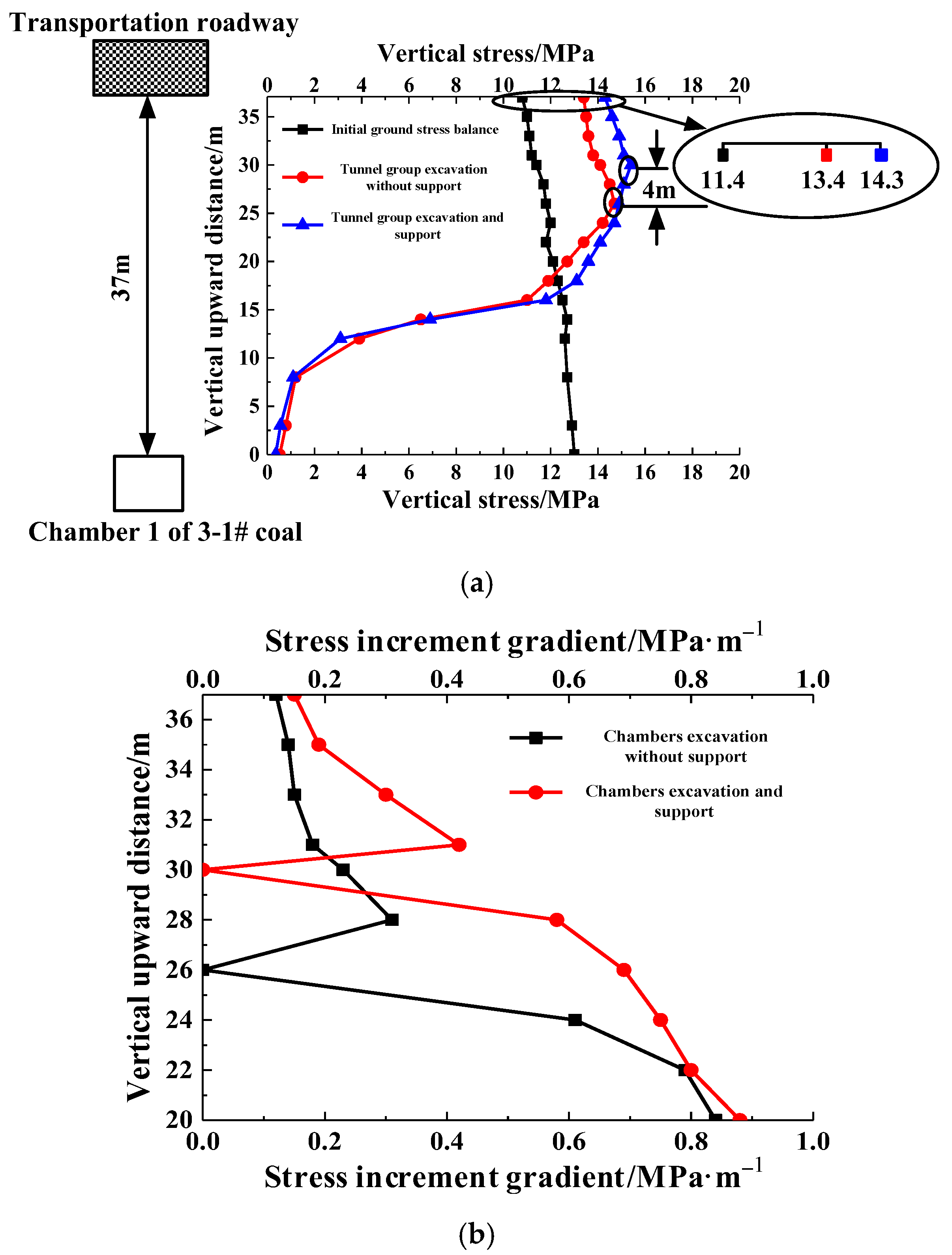
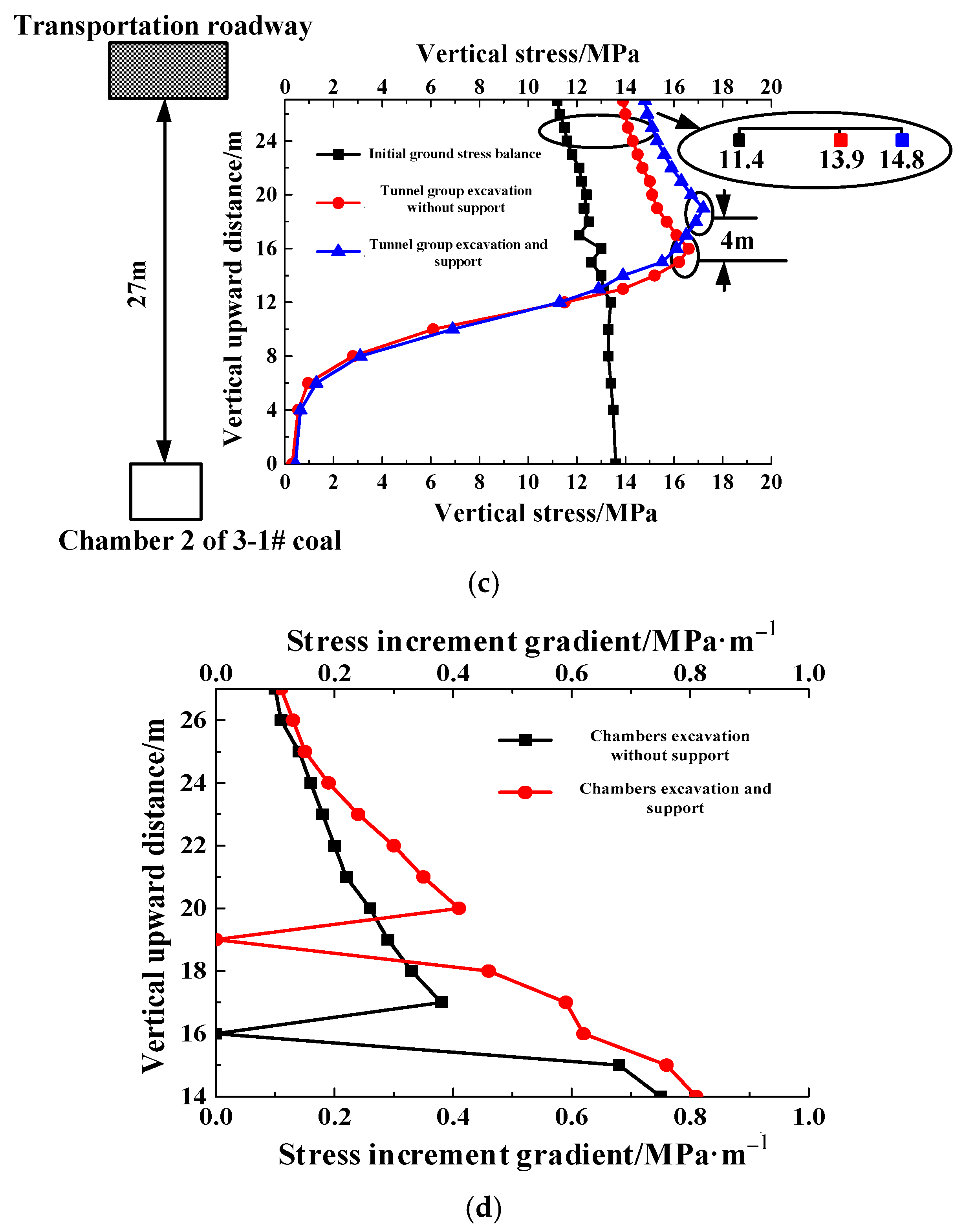
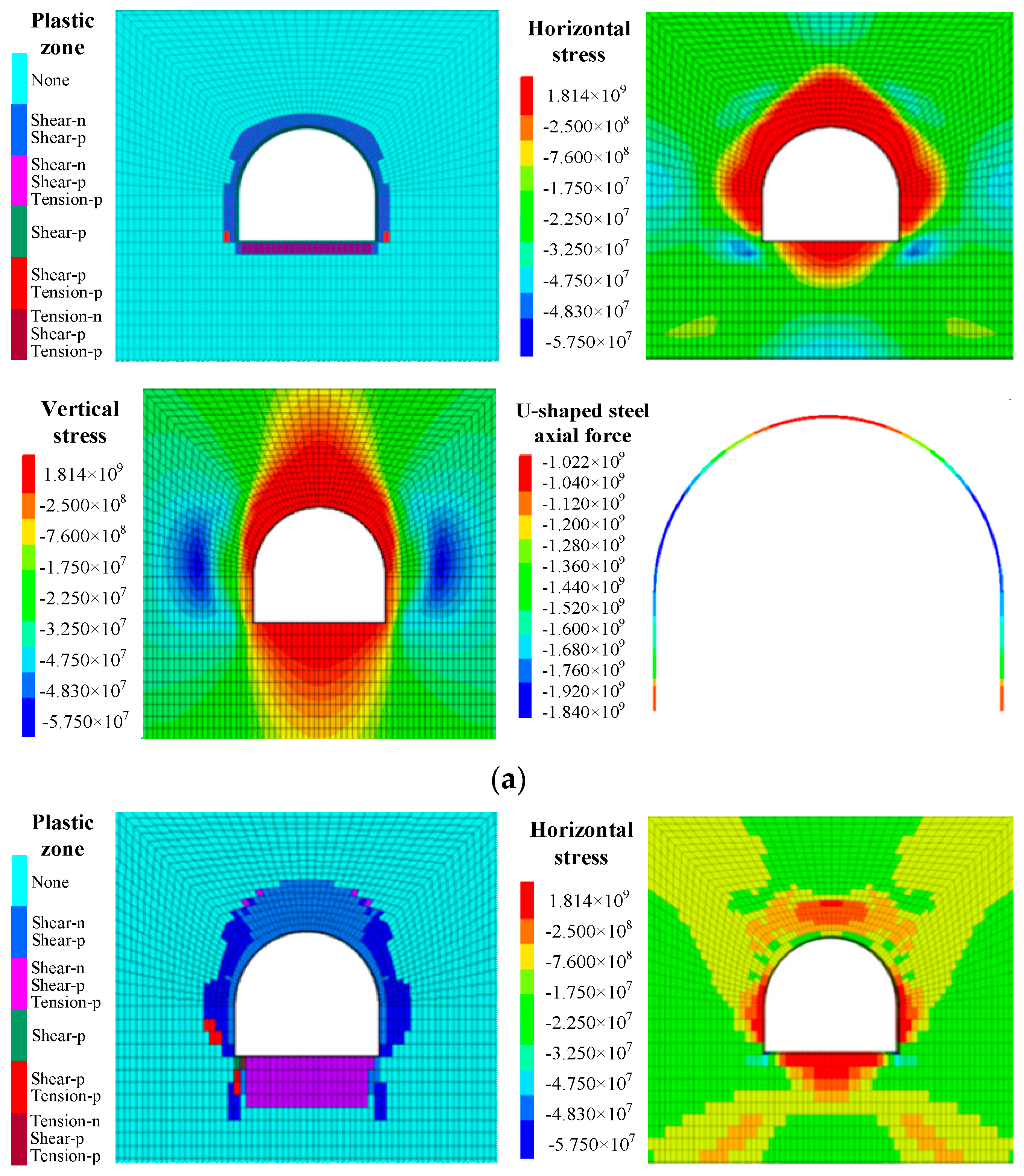
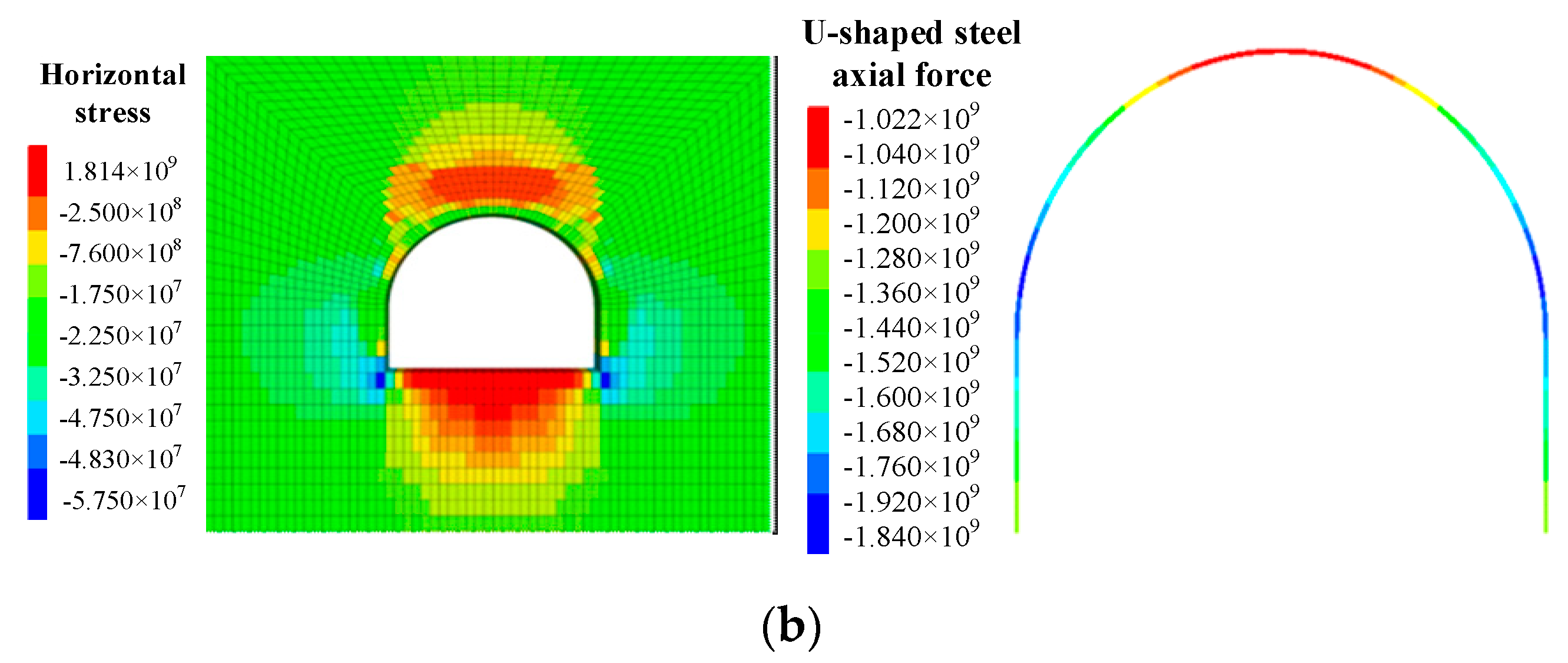
3.2. Stress Distribution Characteristics of Surrounding Rock
4. Soft Rock Roadway Support Design
4.1. Analysis of Support Ideas
4.2. Determination of Support Parameter
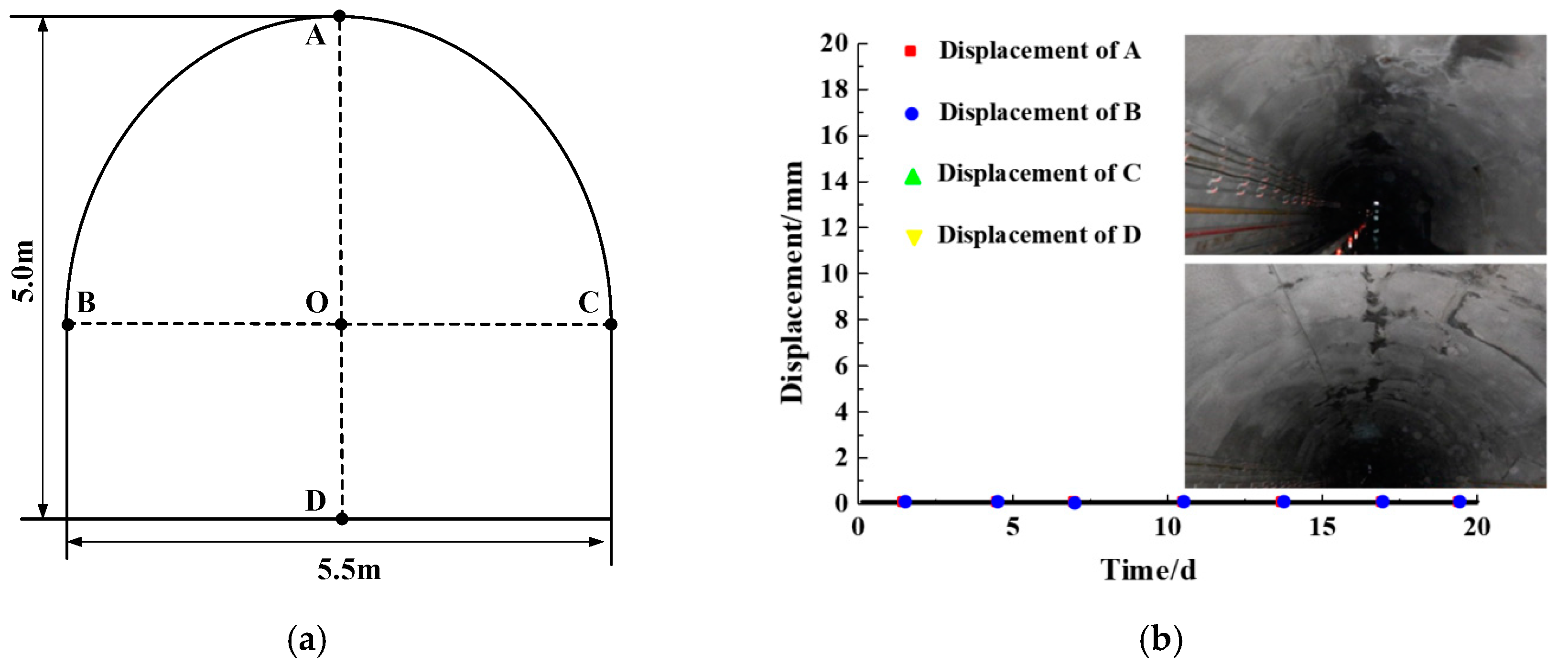
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, T.; Xing, M.; Guo, W.; Wang, C.; Wang, B. Anchoring effect and energy-absorbing support mechanism of large deformation bolt. J. Cent. South Univ. 2021, 28, 572–581. [Google Scholar] [CrossRef]
- Zhang, W.; Guo, W.; Wang, Z. Influence of lateral pressure on the mechanical behavior of different rock types under biaxial compression. J. Cent. South Univ. 2022, 29, 3695–3705. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, B.; Zhao, T. Study on the law of failure acoustic–thermal signal of weakly cemented fractured rock with diferent dip angles. Rock Mech. Rock Eng. 2023, 56, 4557–4568. [Google Scholar] [CrossRef]
- Xiong, F.; Zhu, C.; Feng, G.; Zheng, J.; Sun, H. A three-dimensional coupled thermo-hydro model for geothermal development in discrete fracture networks of hot dry rock reservoirs. Gondwana Res. 2022, 122, 331–347. [Google Scholar] [CrossRef]
- Shan, R.; Li, T.; Liu, W.; Chen, Y.; Shi, S.; Li, G. Study on asymmetric support of anchor cable with c-shaped tube in inclined coal seam roadway. Appl. Sci. 2023, 13, 8088. [Google Scholar] [CrossRef]
- Guo, X.; Zheng, X.; Li, P.; Lian, R.; Liu, C.; Shahani, N.M.; Wang, C.; Li, B.; Xu, W.; Lai, G. Full-stress anchoring technology and application of bolts in the coal roadway. Energies 2021, 14, 7475. [Google Scholar] [CrossRef]
- Kang, H.; Li, J.; Yang, J.; Gao, F. Investigation on the Influence of abutment pressure on the stability of rock bolt reinforced roof strata through physical and numerical modeling. Rock Mech. Rock Eng. 2017, 50, 387–401. [Google Scholar] [CrossRef]
- Dyczko, A.; Kamiński, P.; Jarosz, J.; Rak, Z.; Jasiulek, D.; Sinka, T. Monitoring of roof bolting as an element of the project of the introduction of roof bolting in polish coal mines—Case study. Energies 2021, 15, 95. [Google Scholar] [CrossRef]
- Guo, X.; Mao, X.; Ma, C.; Huang, J. Bolt support mechanism based on elastic theory. Int. J. Min. Sci. Technol. 2013, 23, 469–474. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, Y.; Li, J. Experimental Study on Seepage Characteristics of Jurassic Weakly Cemented Sandstone under Water-Rock Interaction. Geofluids 2020, 2020, 8543687. [Google Scholar] [CrossRef]
- Yu, W.; Li, K.; Liu, Z.; An, B.; Wang, P.; Wu, H. Mechanical Characteristics and Deformation Control of Surrounding Rock in Weakly Cemented Siltstone. Environ. Earth Sci. 2021, 80, 337. [Google Scholar] [CrossRef]
- Ru, W.; Hu, S.; Zhou, A.; Luo, P.; Gong, H.; Zhang, C.; Zhou, X. Study on Creep Characteristics and Nonlinear Fractional-Order Damage Constitutive Model of Weakly Cemented Soft Rock. Rock Mech. Rock Eng. 2023, 56, 8061–8082. [Google Scholar] [CrossRef]
- Meng, Q.; Han, L.; Qiao, W.; Lin, D.; Fan, J. Support Technology for Mine Roadways in Extreme Weakly Cemented Strata and Its Application. Int. J. Min. Sci. Technol. 2014, 24, 157–164. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, S.; Zeng, W. Experimental and Numerical Study on Loading Rate Effects of Rock-like Material Specimens Containing Two Unparallel Fissures. J. Cent. South Univ. 2016, 23, 1474–1485. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, L.; Li, Q.; Zhu, S. Plastic Zone Analysis and Support Optimization of Shallow Roadway with Weakly Cemented Soft Strata. Int. J. Min. Sci. Technol. 2015, 25, 395–400. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Tian, W.-L.; Huang, Y.-H.; Ranjith, P.G.; Ju, Y. An Experimental and Numerical Study on Cracking Behavior of Brittle Sandstone Containing Two Non-Coplanar Fissures Under Uniaxial Compression. Rock Mech. Rock Eng. 2016, 49, 1497–1515. [Google Scholar] [CrossRef]
- Zhou, K.; Yu, F.; Tan, Y.; Guo, W.; Zhao, T. Study on Failure Behaviors and Control Technology of Surrounding Rock in a Weakly Cemented Soft Rock Roadway: A Case Study. Front. Earth Sci. 2023, 11, 1153753. [Google Scholar] [CrossRef]
- Feng, P.; Dai, F.; Liu, Y.; Du, H. Mechanical Behaviors of Rock-like Specimens with Two Non-Coplanar Fissures Subjected to Coupled Static-Dynamic Loads. Eng. Fract. Mech. 2018, 199, 692–704. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Yin, P.-F.; Zhang, Y.-C.; Chen, M.; Zhou, X.-P.; Jing, H.-W.; Zhang, Q.-Y. Failure Behavior and Crack Evolution Mechanism of a Non-Persistent Jointed Rock Mass Containing a Circular Hole. Int. J. Rock Mech. Min. 2019, 114, 101–121. [Google Scholar] [CrossRef]
- Yang, X.; Kulatilake, P.H.S.W.; Jing, H.; Yang, S. Numerical Simulation of a Jointed Rock Block Mechanical Behavior Adjacent to an Underground Excavation and Comparison with Physical Model Test Results. Tunn. Undergr. Space Technol. 2015, 50, 129–142. [Google Scholar] [CrossRef]
- Zhou, H.W.; Zhong, J.C.; Ren, W.G.; Wang, X.Y.; Yi, H.Y. Characterization of Pore-Fracture Networks and Their Evolution at Various Measurement Scales in Coal Samples Using X-Ray ΜCT and a Fractal Method. Int. J. Coal Geol. 2018, 189, 35–49. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Yang, S.-Q. Mechanical and Cracking Behavior of Granite Containing Two Coplanar Flaws under Conventional Triaxial Compression. Int. J. Damage Mech. 2019, 28, 590–610. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, A. Disturbance Response Instability Theory of Rock Bursts in Coal Mines and its Application. Geohazard Mech. 2022, 1, 1–17. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, P.; Guo, W.; Gong, X.; Wang, C.; Chen, Y. Controlling Roof with Potential Rock Burst Risk through Different Pre-Crack Length: Mechanism and Effect Research. J. Cent. South Univ. 2022, 29, 3706–3719. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, Z. A Brief Introduction to Disaster Rock Mass Mechanics. Geohazard Mech. 2022, 1, 53–57. [Google Scholar] [CrossRef]
- Hao, Z.; Di, M.; Zio, E. Monte carlo tree search-based deep reinforcement learning for flexible operation & maintenance optimization of a nuclear power plant. J. Saf. Sustain. 2023, in press. [Google Scholar] [CrossRef]
- Hu, P.; Tanchak, R.; Wang, Q. Developing risk assessment framework for wildfire in the United States–A deep learning approach to safety and sustainability. J. Saf. Sustain. 2023, in press. [Google Scholar] [CrossRef]
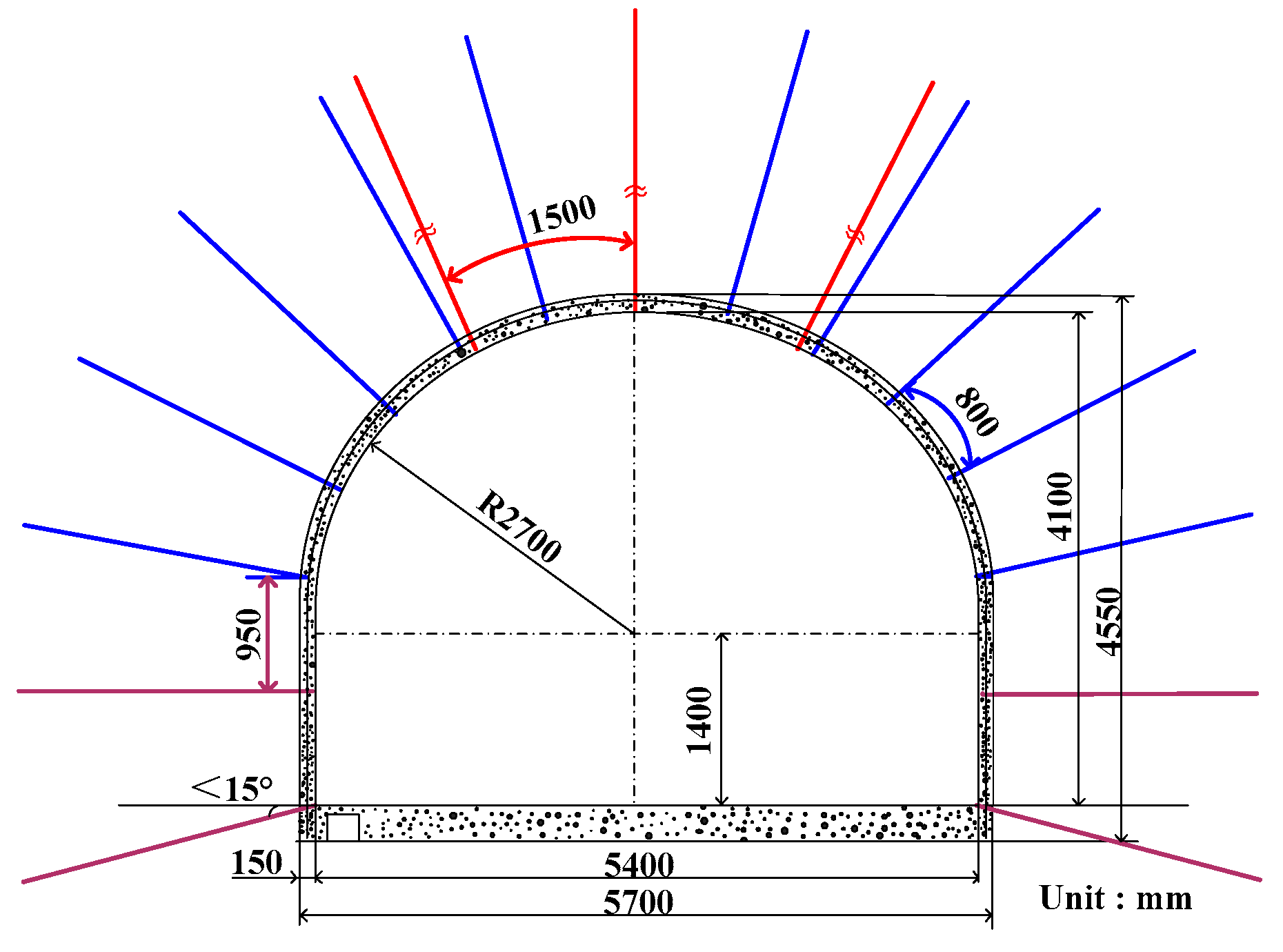




| Position | Anchor Size (mm) | Row/Line Space (mm) | Anchor Cable Size (mm) | Row/Line Space (mm) | Shotcrete |
|---|---|---|---|---|---|
| Roof | Φ20 × 2400 | 800 × 1000 | Φ17.8 × 7300 | 1500 × 3000 | Depth: 150 mm Strength: C25 |
| Sides | Φ20 × 2400 | 1000 × 1000 | — | — |
| Category | Comparison of 2-2 Medium-Coal Roadway | |
|---|---|---|
| Damage Section | Safe Section | |
| Deformation | Severe deformation | No damage |
| Conditions of rock | The roof is mainly sandy mudstone and siltstone, the floor is mainly sandy mudstone | |
| Initial stress | Same basically | |
| Distribution of chambers | Above the chambers | At the edge of chambers |
| Support method | Anchor (cable) support | |
| Rock | Position | Density (kg⋅m−3) | Elastic Modulus (GPa) | Compressive Strength (MPa) | Cohesion (MPa) | Internal Friction Angle (°) | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|
| Sandy mudstone | Roof | 2.33 | 1.46 | 12.9 | 2.42 | 24 | 0.26 |
| Siltstone | 2.28 | 1.01 | 7.6 | 1.88 | 22 | 0.24 | |
| Sandy mudstone | Floor | 2.22 | 1.82 | 10.8 | 3.41 | 25 | 0.29 |
| Rock | Position | Skeletal Minerals | Skeleton Mineral Content (%) | Cementitious Minerals | Cemented Mineral Content (%) | Judgment |
|---|---|---|---|---|---|---|
| Sandy mudstone | Roof | Quartz and biotite | 60–75 | Illite and chlorite | 25–40 | Swelling soft rock |
| Siltstone | Plagioclase and albite | 45–50 | Montmorillonite and chlorite | 50–55 | ||
| Sandy mudstone | Floor | Quartz and biotite | 40–50 | Illite and chlorite | 50–55 |
| Strata | Thickness (m) | Density (g·cm−3) | Bulk Modulus (GPa) | Shear Modulus (GPa) | Internal Friction Angle (°) | Cohesion (MPa) | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|---|
| 1# Fine sandstone | 14.00 | 2.10 | 0.50 | 0.24 | 35 | 2.42 | 0.25 |
| 2-1# coal | 2.60 | 1.87 | 0.40 | 0.23 | 29 | 0.34 | 0.20 |
| Sandy mudstone | 4.00 | 2.15 | 0.40 | 0.68 | 31 | 6.53 | 0.86 |
| 2-2# coal | 3.00 | 1.56 | 0.45 | 0.25 | 26 | 0.34 | 0.29 |
| Siltstone | 2.00 | 1.90 | 0.72 | 0.48 | 40 | 4.84 | 0.96 |
| 2# Fine sandstone | 4.00 | 2.20 | 0.38 | 0.25 | 41 | 2.42 | 0.25 |
| 2-3# coal | 2.60 | 1.68 | 0.41 | 0.22 | 29 | 0.34 | 0.24 |
| Conglomerate | 15.00 | 2.60 | 0.58 | 0.19 | 36 | 2.13 | 0.33 |
| 3# Fine sandstone | 6.00 | 2.18 | 0.36 | 0.21 | 39 | 2.42 | 0.32 |
| Coal line | 2.50 | 1.46 | 0.38 | 0.20 | 29 | 0.34 | 0.26 |
| 4# Fine sandstone | 10.00 | 1.95 | 0.42 | 0.26 | 40 | 2.42 | 0.31 |
| 3-1# coal | 7.00 | 1.50 | 0.45 | 0.27 | 27 | 0.34 | 0.29 |
| 5# Fine sandstone | 3.00 | 1.87 | 0.40 | 0.24 | 38 | 2.42 | 0.35 |
| Support Position | Support Form | Effect Analysis |
|---|---|---|
| Roadway section | U-shaped steel shed | Load evenly and ensure the shape of the roadway section |
| Shotcrete | Protect supporting structure and surrounding rock | |
| Sweep roof and floor + repair the anchor rod | Clean up broken rock and restrain the deformation of U-shaped steel | |
| Between surrounding rock and U-shaped steel shed | Filling behind the cobblestone wall | Releasing pressure |
| Legs of U-shaped steel shed | Shed anchor | Restrain the deformation of U-shaped steel |
| Floor | Laying steel mesh + concrete floor | Restrain the deformation of U-shaped steel |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, D.; Gong, X.; Zhang, W.; Liu, Z.; Xiong, F. Influence of Stress Disturbance on the Deformation of Nearby Cemented Roadways following the Excavation of Chambers. Buildings 2024, 14, 169. https://doi.org/10.3390/buildings14010169
Zhang Y, Zhang D, Gong X, Zhang W, Liu Z, Xiong F. Influence of Stress Disturbance on the Deformation of Nearby Cemented Roadways following the Excavation of Chambers. Buildings. 2024; 14(1):169. https://doi.org/10.3390/buildings14010169
Chicago/Turabian StyleZhang, Yueying, Dongxiao Zhang, Xufei Gong, Wei Zhang, Zihao Liu, and Feng Xiong. 2024. "Influence of Stress Disturbance on the Deformation of Nearby Cemented Roadways following the Excavation of Chambers" Buildings 14, no. 1: 169. https://doi.org/10.3390/buildings14010169
APA StyleZhang, Y., Zhang, D., Gong, X., Zhang, W., Liu, Z., & Xiong, F. (2024). Influence of Stress Disturbance on the Deformation of Nearby Cemented Roadways following the Excavation of Chambers. Buildings, 14(1), 169. https://doi.org/10.3390/buildings14010169







