Experimental Study on the Seismic Performance of Brick Walls Strengthened by Small-Spaced Reinforced-Concrete–Masonry Composite Columns
Abstract
:1. Introduction
1.1. Specimen Design
1.2. Loading Regime
2. Experimental Observations and Results
2.1. Occurrence and Development of Wall Cracks
2.2. Failure Mode and Bearing Capacity of the Wall
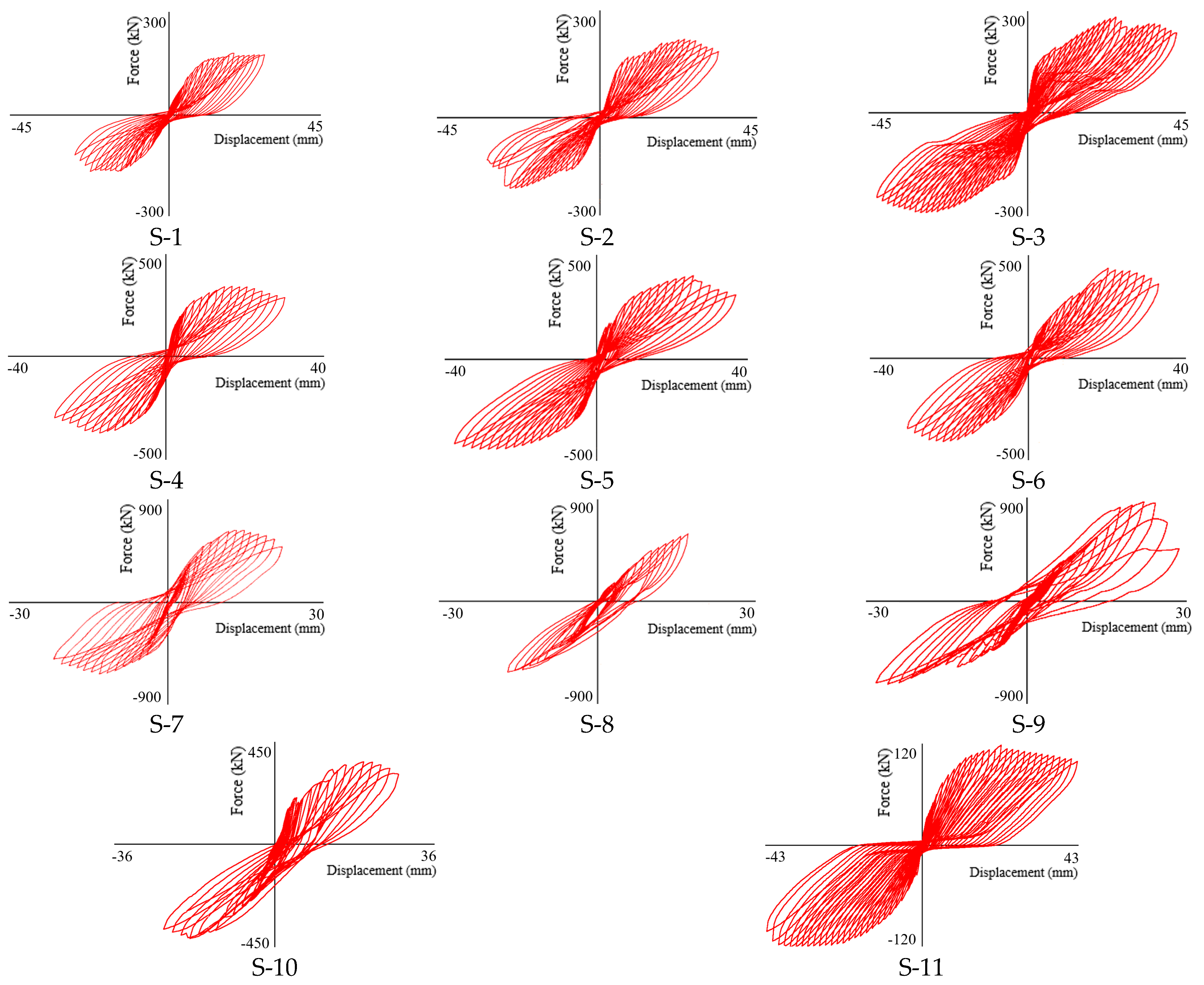
2.3. Hysteresis Curves
3. Test Result Analysis
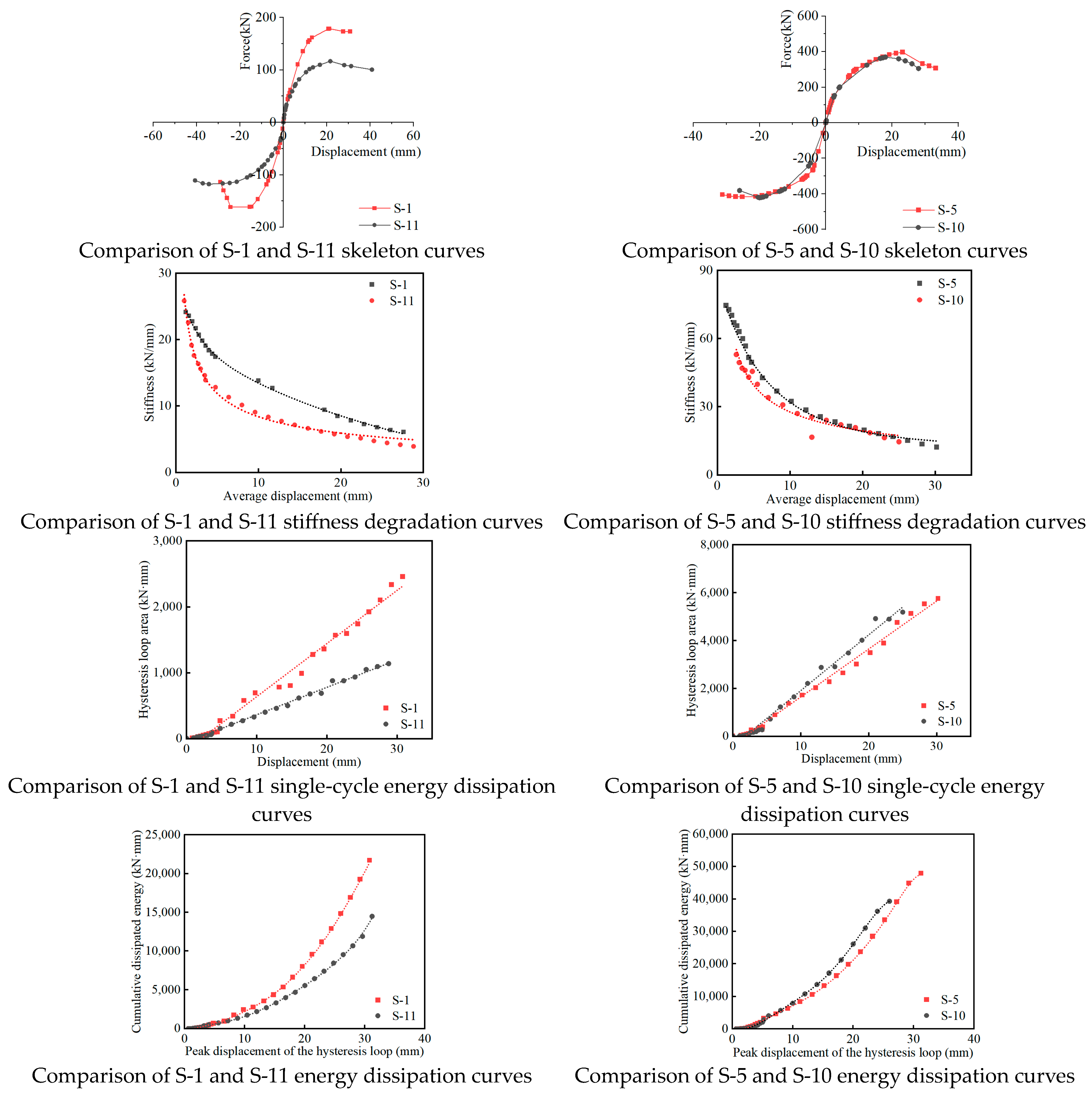
3.1. Hysteresis Curves
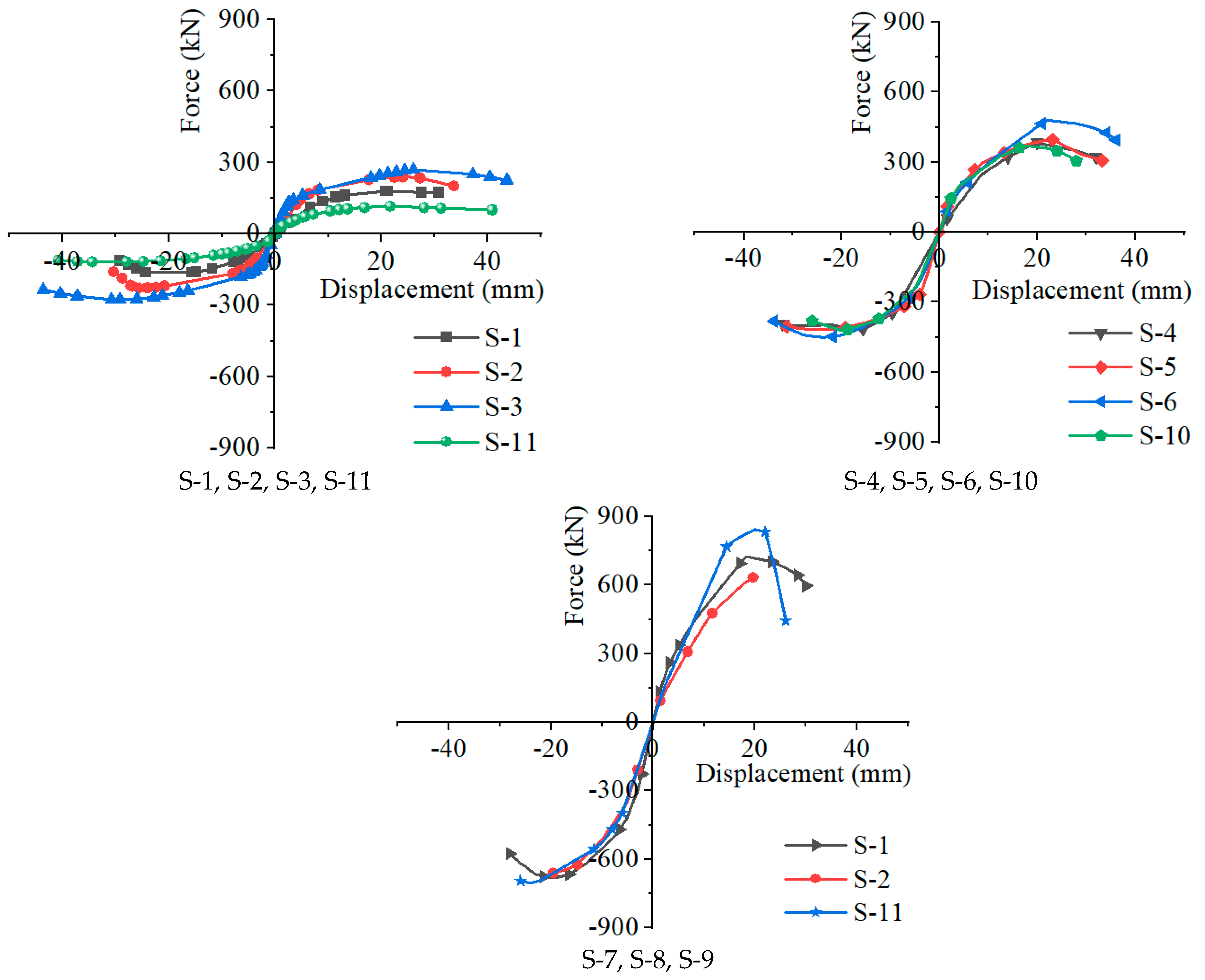
3.2. Skeleton Curves
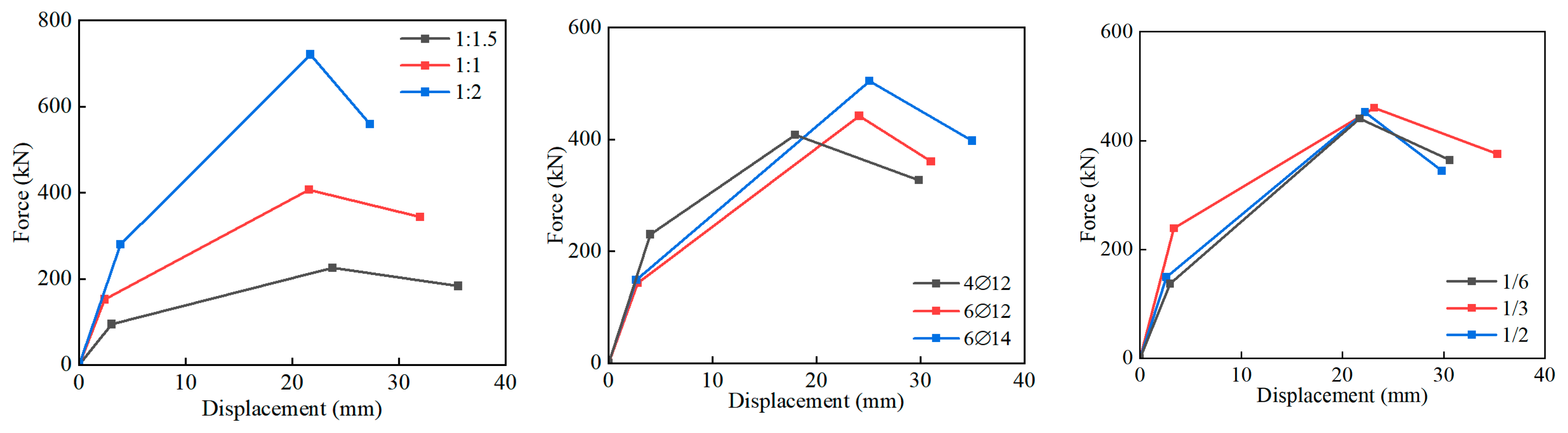
3.3. Analysis of the Influence of the Location and Spacing of Composite Columns
3.4. Influencing Factors of Load-Carrying Capacity
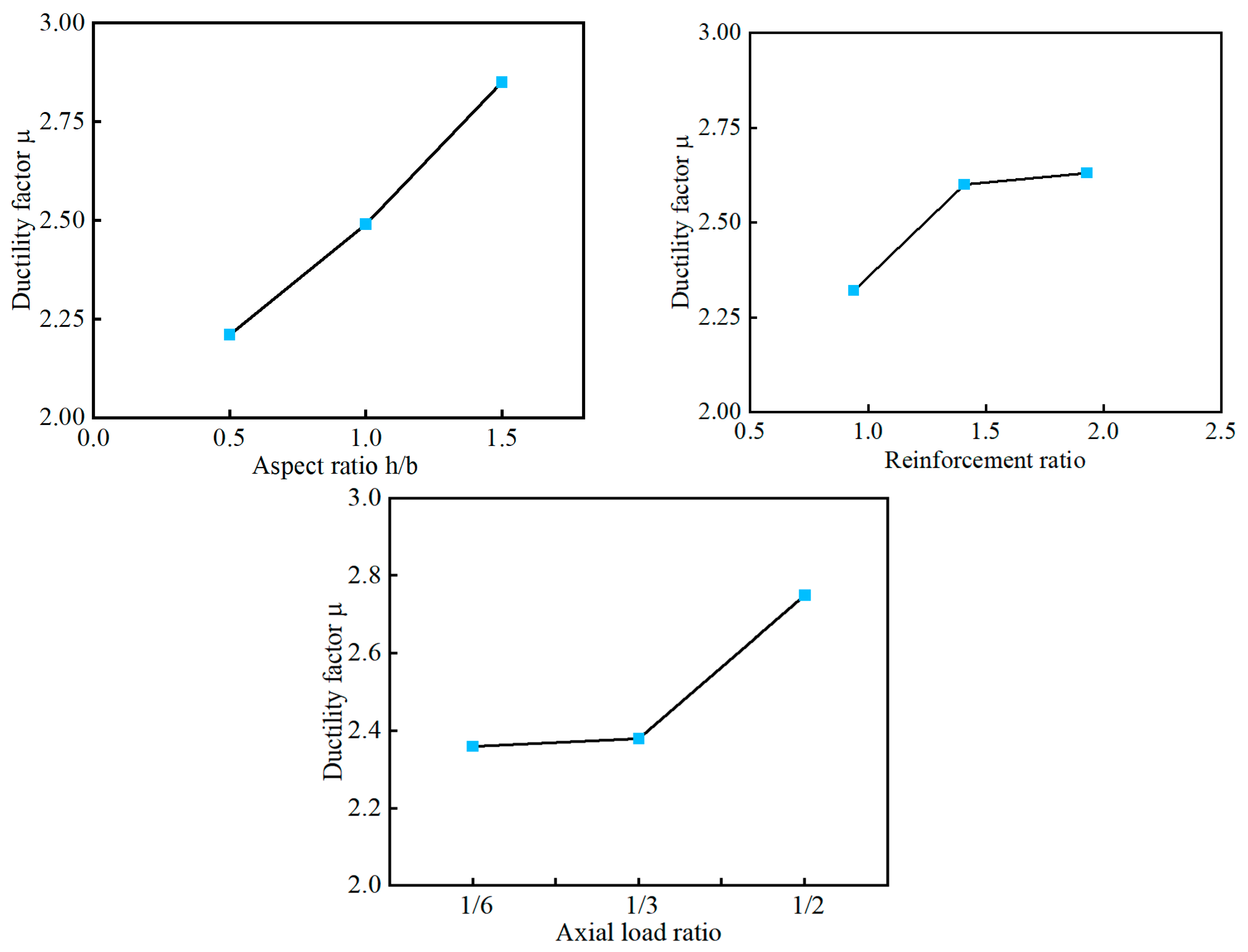
3.5. Ductility Analysis of Masonry Walls Strengthened with Composite Columns
4. Calculation and Analysis of the Flexural Capacity
4.1. Calculation Assumptions
- (1)
- The cross-section deformation conforms to the plane section assumption;
- (2)
- The masonry and concrete in the composite column work together without relative slip;
- (3)
- The tensile strength of concrete and masonry is ignored;
- (4)
- The constitutive model of materials is accepted.
4.2. Calculation Diagram and Calculation Formula for Bearing Capacity
4.3. Comparison and Analysis of Calculation Results
5. Conclusions
- (1)
- By strengthening brick walls with RC–masonry composite columns, the concrete part in the composite column, the masonry part in the composite column, and the wall outside of the column can work together effectively; the failure mode of the wall changes from shear to flexural failure; the bearing capacity, ductility, and energy dissipation properties of the strengthened masonry wall are improved compared to those of the original masonry wall.
- (2)
- The aspect ratio of the specimen has the greatest influence on the structural behavior. Smaller aspect ratios result in higher load-bearing capacity and stiffness but poorer ductility. Increasing the reinforcement ratio of the composite column leads to higher load-bearing capacity and ductility of the specimen. The axial load ratio has the weakest impact on the structure. Members with a small axial load ratio have a low load-bearing capacity, and their stiffness degradation is less significant after cracking.
- (3)
- Installing composite columns at the end of a wall can substantially increase the bearing capacity, stiffness, and energy dissipation capacity of the wall. For walls with height-to-width ratios greater than 1, placing composite columns in the middle of a wall has little effect on the bearing capacity and stiffness of the wall but can improve the ductility of the wall. Therefore, it is generally suggested the composite columns can be placed at the ends of the wall if a strengthening measure is required. For walls with height-to-width ratios less than 1, where the shear span ratios are relatively small, it is recommended to add composite columns in the middle to enhance their shear capacity and ductility.
- (4)
- The calculation of the flexural capacity of a wall strengthened by composite columns can be carried out by treating the strengthened wall as a concrete compression–flexure member while taking into account the compressive strength of masonry in compression.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ye, L.; Qu, Z.; Lu, X.; Feng, P. Collapse prevention of building structures: A lesson from the Wenchuan earthquake. Jianzhu Jiegou Xuebao/J. Build. Struct. 2008, 29, 42–50. [Google Scholar] [CrossRef]
- Ismail, N.; Khattak, N. Observed failure modes of unreinforced masonry buildings during the 2015 Hindu Kush earthquake. Earthq. Eng. Eng. Vib. 2019, 18, 301–314. [Google Scholar] [CrossRef]
- Göçer, C. Field Investigation of the Performance of Unreinforced Masonry Building Structures during the June 12, 2017, Lesvos Earthquake in the Aegean Sea. J. Perform. Constr. Facil. 2020, 34, 04020095. [Google Scholar] [CrossRef]
- Ural, A.; Fırat, F.K.; Kara, M.E.; Çelik, T.; Tanrıverdi, Ş. Damages to rubble stone masonry structures during the January 24, 2020, Sivrice (Elazığ) Earthquake in Turkey. Earthq. Struct. 2022, 23, 231–243. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, J.; Bao, Y.; Peng, X.; Lin, X. Seismic damage investigation and analysis of rural buildings in MS6.0 Changning earthquake. J. Build. Struct. 2020, 41, 297–306. [Google Scholar] [CrossRef]
- Tripathy, D.; Singhal, V. Strengthening of weak masonry assemblages using wire reinforced cementitious matrix (WRCM) for shear and flexure loads. Constr. Build. Mater. 2021, 277, 122223. [Google Scholar] [CrossRef]
- Nanni, A. Guide to Design and Construction of Externally Bonded Fabric-Reinforced Cementitious Matrix (FRCM) Systems for Repair and Strengthening Concrete and Masonry Structures; American Concrete Institute: Farmington Hills, MI, USA, 2013; Volume ACI 549-.4R-13, p. 69. Available online: https://hdl.handle.net/11588/586708 (accessed on 8 January 2024).
- Lin, Y.-W.; Wotherspoon, L.; Scott, A.; Ingham, J.M. In-plane strengthening of clay brick unreinforced masonry wallettes using ECC shotcrete. Eng. Struct. 2014, 66, 57–65. [Google Scholar] [CrossRef]
- Deng, M.; Yang, S. Cyclic testing of unreinforced masonry walls retrofitted with engineered cementitious composites. Constr. Build. Mater. 2018, 177, 395–408. [Google Scholar] [CrossRef]
- Reboul, N.; Mesticou, Z.; Si Larbi, A.; Ferrier, E. Experimental study of the in-plane cyclic behaviour of masonry walls strengthened by composite materials. Constr. Build. Mater. 2018, 164, 70–83. [Google Scholar] [CrossRef]
- Thomoglou, A.K.; Karabinis, A. Experimental investigation of the shear strength of hollow brick unreinforced masonry walls retrofitted with TRM system. Earthq. Struct. 2022, 22, 355–372. [Google Scholar] [CrossRef]
- Thomoglou, A.K.; Karabini, M.A.; Achillopoulou, D.V.; Rousakis, T.C.; Chalioris, C.E. Failure Mode Prediction of Unreinforced Masonry (URM) Walls Retrofitted with Cementitious Textile Reinforced Mortar (TRM). Fibers 2023, 11, 53. [Google Scholar] [CrossRef]
- Thomoglou, A.K.; Rousakis, T.C.; Achillopoulou, D.V.; Karabinis, A.I. Ultimate shear strength prediction model for unreinforced masonry retrofitted externally with textile reinforced mortar. Earthq. Struct. 2020, 19, 411–425. [Google Scholar] [CrossRef]
- Aiello, M.A.; Micelli, F.; Valente, L. FRP confinement of square masonry columns. J. Compos. Constr. 2009, 13, 148–158. [Google Scholar] [CrossRef]
- Faella, C.; Martinelli, E.; Paciello, S.; Camorani, G.; Aiello, M.A.; Micelli, F.; Nigro, E. Masonry columns confined by composite materials: Experimental investigation. Compos. Part B Eng. 2011, 42, 692–704. [Google Scholar] [CrossRef]
- Micelli, F.; Di Ludovico, M.; Balsamo, A.; Manfredi, G. Mechanical behaviour of FRP-confined masonry by testing of full-scale columns. Mater. Struct. 2014, 47, 2081–2100. [Google Scholar] [CrossRef]
- Farooq, S.; Shahid, I.; Ilyas, M. Seismic performance of masonry strengthened with steel strips. KSCE J. Civ. Eng. 2014, 18, 2170–2180. [Google Scholar] [CrossRef]
- Farooq, S.; Ilyas, M.; Amir, S. Response of masonry walls strengthened with CFRP and steel strips. Arab. J. Sci. Eng. 2012, 37, 545–559. [Google Scholar] [CrossRef]
- Farough, S.; Ilyas, M.; Ghaffar, A. Technique for strengthening of masonry wall panels using steel strips. Asian J. Civ. Eng. Build. Hous. 2006, 7, 621–638. [Google Scholar]
- Farooq, S.; ElGawady Mohamed, A.; Ilyas, M. Seismic in-plane performance of retrofitted masonry walls. KSCE J. Civ. Eng. 2014, 18, 226–237. [Google Scholar] [CrossRef]
- Yang, K.H.; Mun, J.H.; Hwang, S.H. Cyclic shear behavior of masonry walls strengthened with prestressed steel bars and glass fiber grids. Compos. Struct. 2020, 238, 111961. [Google Scholar] [CrossRef]
- Capozucca, R.; Magagnini, E. Experimental response of masonry walls in-plane loading strengthened with GFRP strips. Compos. Struct. 2020, 235, 111735. [Google Scholar] [CrossRef]
- Taghdi, M.; Bruneau, M.; Saatcioglu, M. Seismic retrofitting of low-rise masonry and concrete walls using steel strips. J. Struct. Eng. 2000, 126, 1017–1025. [Google Scholar] [CrossRef]
- Nochebuena-Mora, E.; Mendes, N.; Lourenço, P.B.; Covas, J.A. Vibration control systems: A review of their application to historical unreinforced masonry buildings. J. Build. Eng. 2021, 44, 103333. [Google Scholar] [CrossRef]
- Paula, R.; Cóias, V.; Guerreiro, L. Development of Dissipation Panels for Seismic Retrofitting of Historic Buildings. In Historical Earthquake-Resistant Timber Framing in the Mediterranean Area; Springer: Cham, Switzerland, 2016; pp. 337–347. [Google Scholar]
- East, M.; Yassin, A.; Ezzeldin, M.; Wiebe, L. Development of Controlled Rocking Masonry Walls with Energy Dissipation Accessible in a Steel Base. J. Struct. Eng. 2023, 149, 04023032. [Google Scholar] [CrossRef]
- Shu, Z.; Ning, B.; Chen, J.; Li, Z.; He, M.; Luo, J.; Dong, H. Reinforced moment-resisting glulam bolted connection with coupled long steel rod with screwheads for modern timber frame structures. Earthq. Eng. Struct. Dyn. 2023, 52, 845–864. [Google Scholar] [CrossRef]
- Huang, H.; Yuan, Y.; Zhang, W.; Li, M. Seismic behavior of a replaceable artificial controllable plastic hinge for precast concrete beam-column joint. Eng. Struct. 2021, 245, 112848. [Google Scholar] [CrossRef]
- Huang, H.; Li, M.; Zhang, W.; Yuan, Y. Seismic behavior of a friction-type artificial plastic hinge for the precast beam–column connection. Arch. Civ. Mech. Eng. 2022, 22, 201. [Google Scholar] [CrossRef]
- Cevallos, O.; Olivito, R.S.; Codispoti, R.; Ombres, L. Flax and polyparaphenylene benzobisoxazole cementitious composites for the strengthening of masonry elements subjected to eccentric loading. Compos. Part B Eng. 2015, 71, 82–95. [Google Scholar] [CrossRef]
- Ombres, L.; Verre, S. Structural behaviour of fabric reinforced cementitious matrix (FRCM) strengthened concrete columns under eccentric loading. Compos. Part B Eng. 2015, 75, 235–249. [Google Scholar] [CrossRef]
- Ibrar, M.; Naseer, A.; Ashraf, M.; Badshah, E.; Ullah, S. Evaluation of confined masonry walls with varying sizes of confining elements and reinforcement ratios against cyclic loading. J. Build. Eng. 2022, 50, 104094. [Google Scholar] [CrossRef]
- Ahmadizadeh, M.; Shakib, H. Experimental Study of the In-Plane Behavior of Confined Stone Masonry Walls. J. Struct. Eng. 2016, 142, 04015145. [Google Scholar] [CrossRef]
- Wijaya, W.; Kusumastuti, D.; Suarjana, M.; Pribadi, K. Experimental study on wall-frame connection of confined masonry wall. Procedia Eng. 2011, 14, 2094–2102. [Google Scholar] [CrossRef]
- Marinilli, A.; Castilla, E. Experimental evaluation of confined masonry walls with several confining-columns. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Weng, D.; Lu, X.; Ren, X. Experimental study on seismic resistant capacity of masonry walls. In Proceedings of the 4th Multi-Lateral Workshop on Development of Earthquake Technologies and Their Integration for the Asia-Pacific Region (EQTAP), Tokyo, Japan, September 2002; pp. 201–211. [Google Scholar]
- Zhang, W.; Ma, J.; Chang, J. Researches on bending capacity course of plain masonry bearing wall under bending and invariable axial force. Eng. Mech. 2012, 29, 202–210. [Google Scholar] [CrossRef]
- Yankelevsky, D.Z.; Reinhardt, H.W. Focal points model for uniaxial cyclic behaviour of concrete. In Proceedings of the IABSE Colloquium, Delft, Netherlands, 26–28 August 1987. [Google Scholar]
- Teng, Z.; Zou, L. Nonlinear Finite Element Analysis of RC Members under Reversed Cyclic Loading. China Civ. Eng. J. 1996, 29, 19–27. [Google Scholar]
- Liu, J. Research on Mechanical Performance of Masonry Wall Strengthened with GFRP. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2007. [Google Scholar]
- Minafò, G.; D’Anna, J.; Cucchiara, C.; Monaco, A.; La Mendola, L. Analytical stress-strain law of FRP confined masonry in compression: Literature review and design provisions. Compos. Part B Eng. 2017, 115, 160–169. [Google Scholar] [CrossRef]
- Zhu, B.; Wu, M.; Jiang, Z. Experimental study on basic behaviour of brick masonry under reversed loading. J. Tongji Univ. 1980, 2, 1–14. [Google Scholar]
- Shi, C. The Theory and Design of Masonry Structure; Architecture & Building Press: Beijing, China, 2014. [Google Scholar]
- Naraine, K.; Sinha, S. Stress-Strain Curves for Brick Masonry in Biaxial Compression. J. Struct. Eng. 1992, 118, 1451–1461. [Google Scholar] [CrossRef]
- Priestley, M.J.N.; Elder, D.M. Stress-Strain Curves for Unconfined and Confined Concrete Masonry. ACI J. Proc. 1983, 80, 192–201. [Google Scholar] [CrossRef]
- Guo, Z. Strength and Constitutive Equation of Concrete; Architecture & Building Press: Beijing, China, 2004. [Google Scholar]

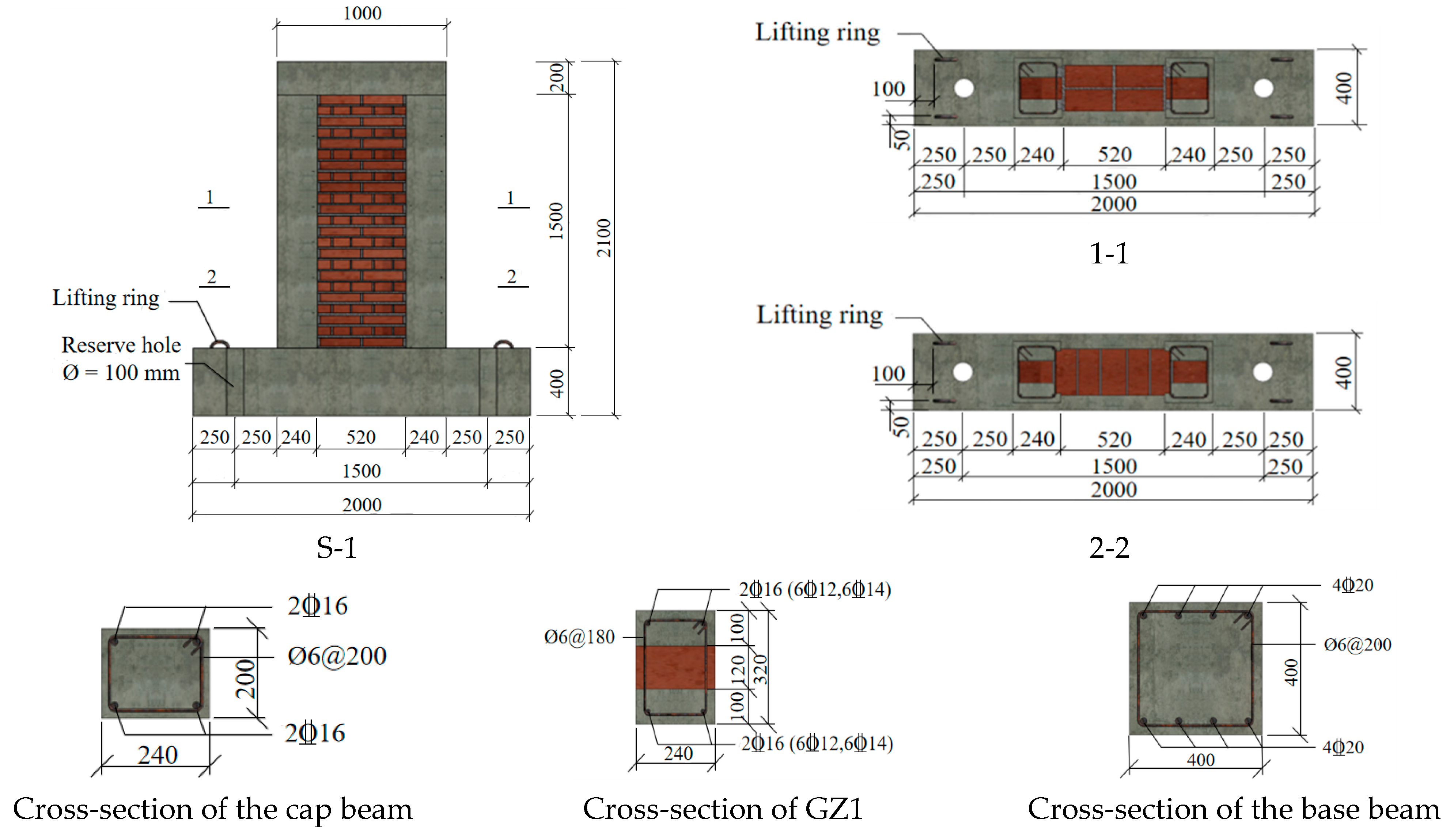
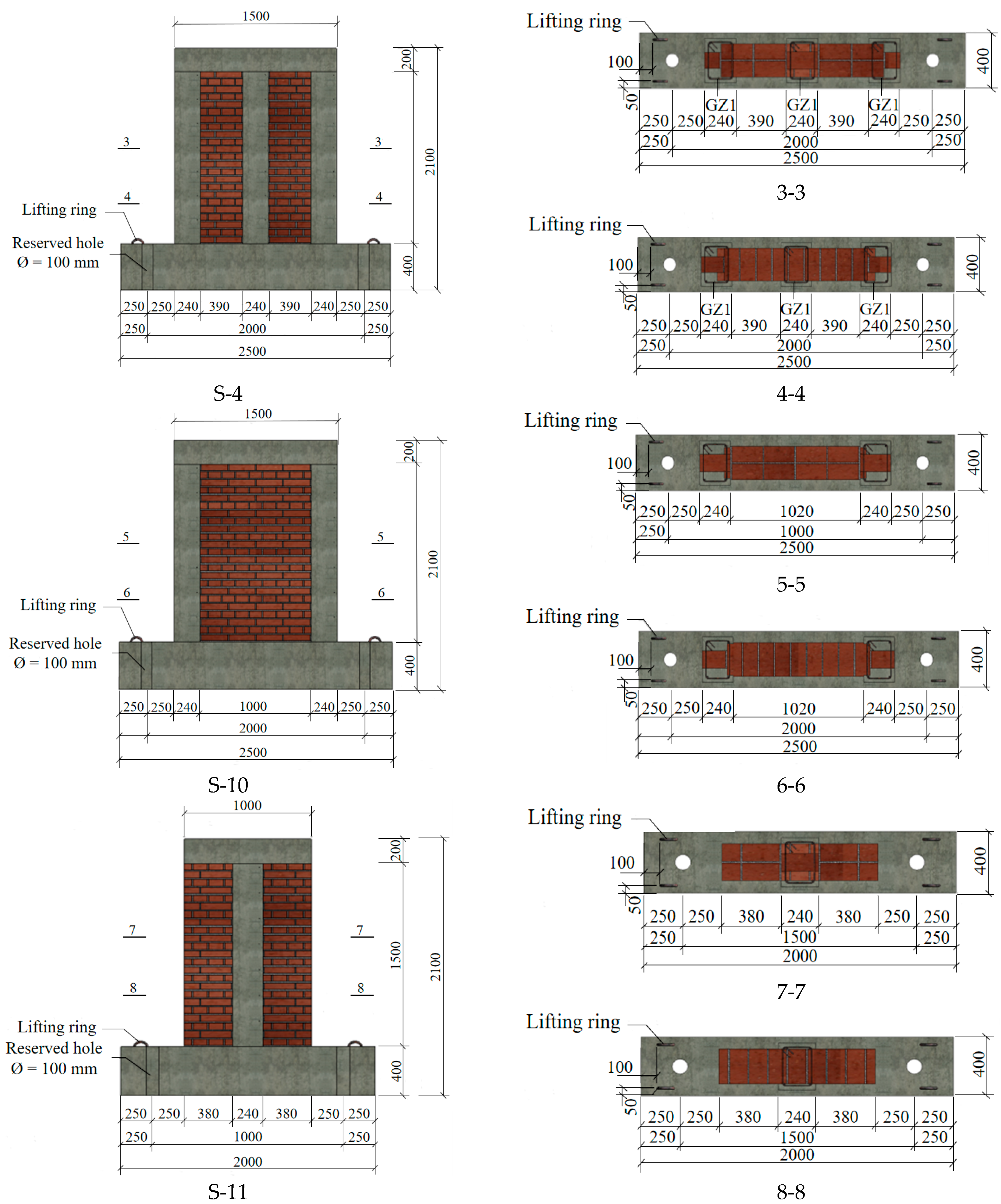






| Serial Number | No. | Dimensions (Width × Height) (mm × mm) | Rebars | Vertical Load (kN) | Number of Composite Columns |
|---|---|---|---|---|---|
| 1 | S-1 | 1000 × 1500 | 4φ 12 | 60 | Two end columns |
| 2 | S-2 | 1000 × 1500 | 6φ 12 | 120 | Two end columns |
| 3 | S-3 | 1000 × 1500 | 6φ 14 | 180 | Two end columns |
| 4 | S-4 | 1500 × 1500 | 4φ 12 | 180 | Two end columns + one middle column |
| 5 | S-5 | 1500 × 1500 | 6φ 12 | 270 | Two end columns + one middle column |
| 6 | S-6 | 1500 × 1500 | 6φ 14 | 90 | Two end columns + one middle column |
| 7 | S-7 | 2000 × 1000 | 4φ 12 | 360 | Two end columns + one middle column |
| 8 | S-8 | 2000 × 1000 | 6φ 12 | 120 | Two end columns + one middle column |
| 9 | S-9 | 2000 × 1000 | 6φ 14 | 240 | Two end columns + one middle column |
| 10 | S-10 | 1500 × 1500 | 6φ 12 | 270 | Two end columns |
| 11 | S-11 | 1000 × 1500 | 6φ 12 | 60 | One middle column |
| Material | Sample Side Length (mm) | Average Compressive Strength (MPa) | Maximum Compressive Strength (MPa) | Minimum Compressive Strength (MPa) |
|---|---|---|---|---|
| Concrete | 150 | 46.1 | 47.5 | 45.2 |
| Bricks | 100 | 20.6 | 25.8 | 13.6 |
| M5 mortar | 70 | 4.6 | 5.3 | 3.67 |
| M10 mortar | 70 | 14.9 | 17.6 | 11.1 |
| Diameter (mm) | Yield Strength (MPa) | Tensile Strength (MPa) | Elongation (%) | Cold Bending Performance |
|---|---|---|---|---|
| 6.5 | 300 | 410 | 28.5 | Qualified |
| 335 | 445 | 31.5 | Qualified | |
| 12 | 575 | 695 | 23.5 | Qualified |
| 575 | 695 | 20.0 | Qualified | |
| 14 | 460 | 585 | 23.0 | Qualified |
| 445 | 580 | 21.5 | Qualified |
| No. | Cracked State | Ultimate State | Failure State | |||
|---|---|---|---|---|---|---|
| Load (kN) | Displacement (mm) | Load (kN) | Displacement (mm) | Load (kN) | Displacement (mm) | |
| S-1 | 73.9 | 2.5 | 170.6 | 18.8 | 143.9 | 30.0 |
| S-2 | 85.3 | 2.8 | 234.1 | 24.8 | 175.9 | 32.8 |
| S-3 | 123.0 | 2.4 | 273.3 | 27.6 | 230.3 | 43.6 |
| S-4 | 171.9 | 2.4 | 350.7 | 17.4 | 290.0 | 30.4 |
| S-5 | 144.5 | 2.1 | 407.2 | 24.2 | 350.7 | 33.2 |
| S-6 | 137.9 | 2.9 | 465.7 | 23.0 | 392.4 | 35.0 |
| S-7 | 445.9 | 5.5 | 702.7 | 17.4 | 548.3 | 29.0 |
| S-8 | 199.9 | 3.5 | 685.0 | 23.2 | 556.5 | 26.9 |
| S-9 | 192.0 | 2.6 | 775.0 | 24.5 | 571.6 | 26.0 |
| S-10 | 138.2 | 2.6 | 396.2 | 19.0 | 311.7 | 28.0 |
| S-11 | 34.9 | 1.7 | 117.7 | 28.8 | 98.8 | 42.4 |
| Specimen No. | Δy (mm) | (mm) | μ |
|---|---|---|---|
| S-1 | 12.2 | 30.0 | 2.46 |
| S-2 | 11.6 | 32.8 | 2.83 |
| S-3 | 13.4 | 43.6 | 3.25 |
| S-4 | 14.1 | 30.4 | 2.16 |
| S-5 | 12.2 | 33.2 | 2.72 |
| S-6 | 13.8 | 35.0 | 2.54 |
| S-7 | 12.7 | 29.0 | 2.28 |
| S-8 | 12.9 | 26.9 | 2.08 |
| S-9 | 12.4 | 26.0 | 2.10 |
| S-10 | 11.7 | 28.0 | 2.39 |
| S-11 | 12.8 | 42.4 | 3.31 |
| No. | Calculated Value (kN) | Test Value (kN) | Test Value/Calculated Value |
|---|---|---|---|
| S-1 | 248.9 | 260.4 | 1.05 |
| S-2 | 383.3 | 351.2 | 0.92 |
| S-3 | 433.5 | 410.0 | 0.95 |
| S-4 | 478.7 | 526.1 | 1.10 |
| S-5 | 703.2 | 610.8 | 0.87 |
| S-6 | 632.5 | 698.6 | 1.10 |
| S-7 | 823.3 | 722.7 | 0.88 |
| S-8 | 837.7 | 685.0 | 0.82 |
| S-9 | 999.8 | 840.0 | 0.84 |
| S-10 | 698.4 | 594.3 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, F.; Zhao, K.; Zhao, J.; Cui, X. Experimental Study on the Seismic Performance of Brick Walls Strengthened by Small-Spaced Reinforced-Concrete–Masonry Composite Columns. Buildings 2024, 14, 184. https://doi.org/10.3390/buildings14010184
Xia F, Zhao K, Zhao J, Cui X. Experimental Study on the Seismic Performance of Brick Walls Strengthened by Small-Spaced Reinforced-Concrete–Masonry Composite Columns. Buildings. 2024; 14(1):184. https://doi.org/10.3390/buildings14010184
Chicago/Turabian StyleXia, Fengmin, Kaozhong Zhao, Jihui Zhao, and Xiangjin Cui. 2024. "Experimental Study on the Seismic Performance of Brick Walls Strengthened by Small-Spaced Reinforced-Concrete–Masonry Composite Columns" Buildings 14, no. 1: 184. https://doi.org/10.3390/buildings14010184





