Empirical Equations for Modelling Yarn–Mortar Debonding in TRM-Strengthened Masonry Walls Subjected to Out-of-Plane Loading
Abstract
:1. Introduction
2. Brief Description of the Experimental Methodology
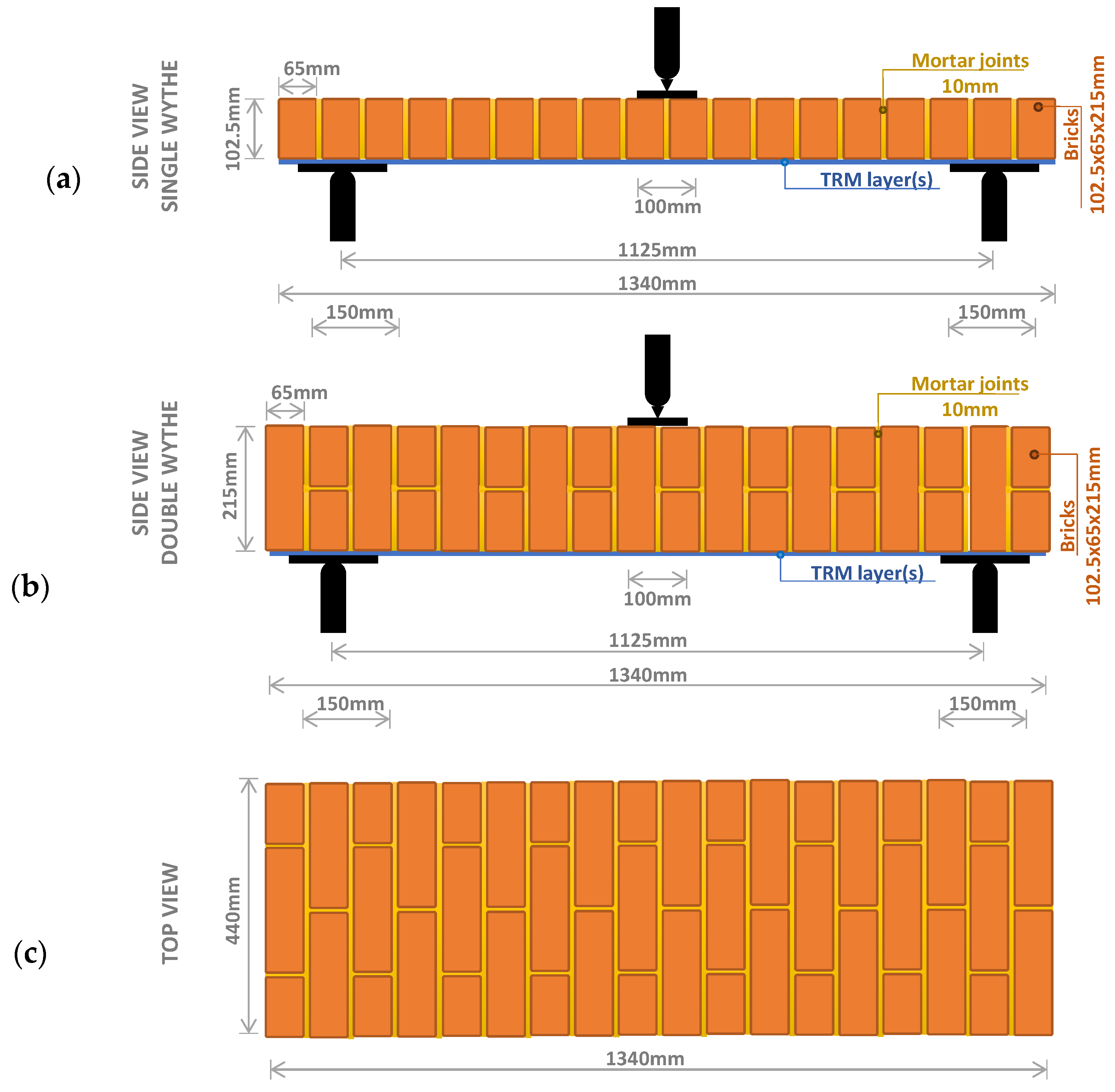
2.1. Test Design and Set-Up
2.2. Material Properties
2.3. Test Results
3. Out-of-Plane Damage Modelling of TRM Strengthened Masonry Walls in Abaqus
3.1. Masonry
3.1.1. Homogenised Model
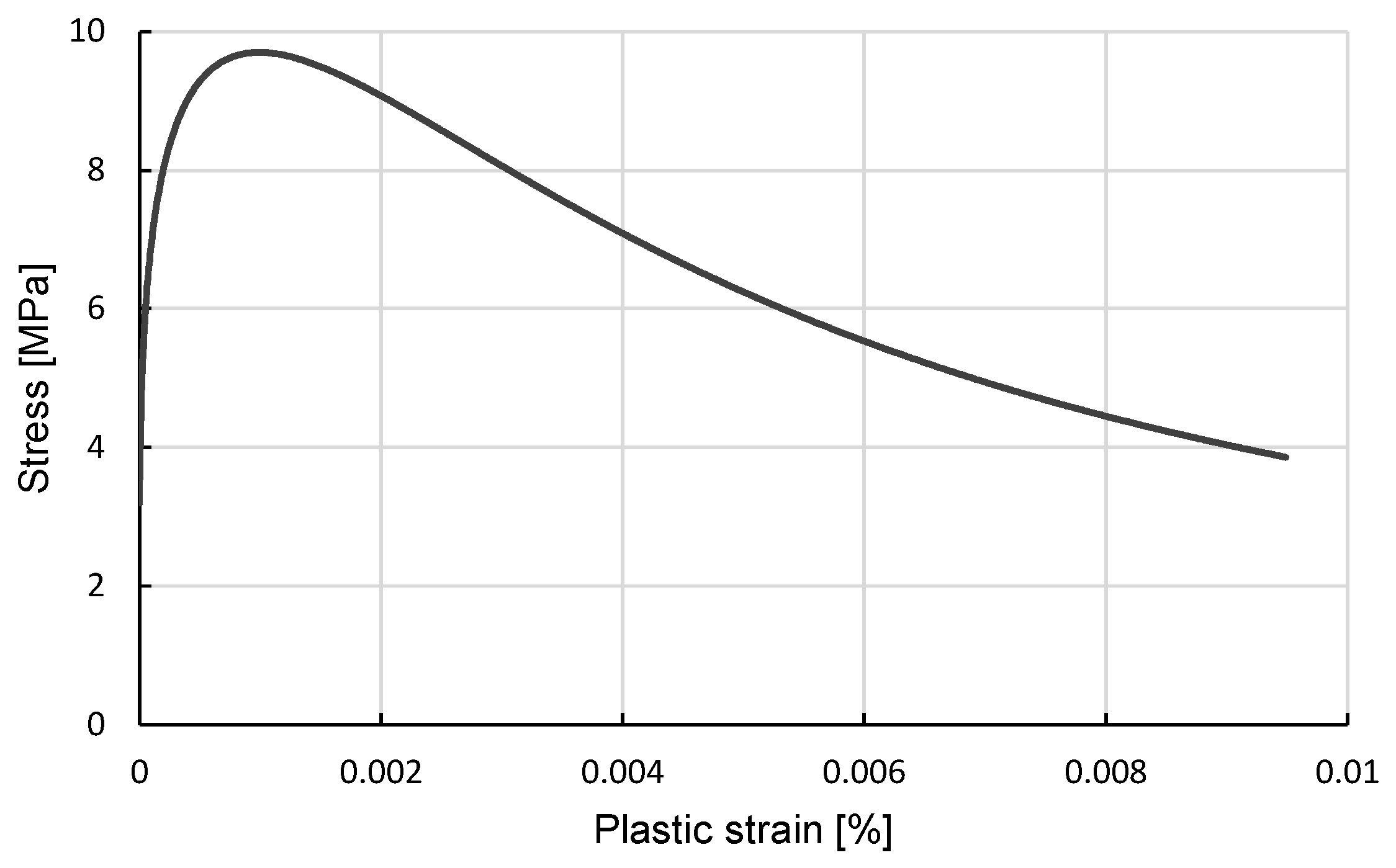
3.1.2. Plasticity Model
3.1.3. Brick/Mortar Interface Model
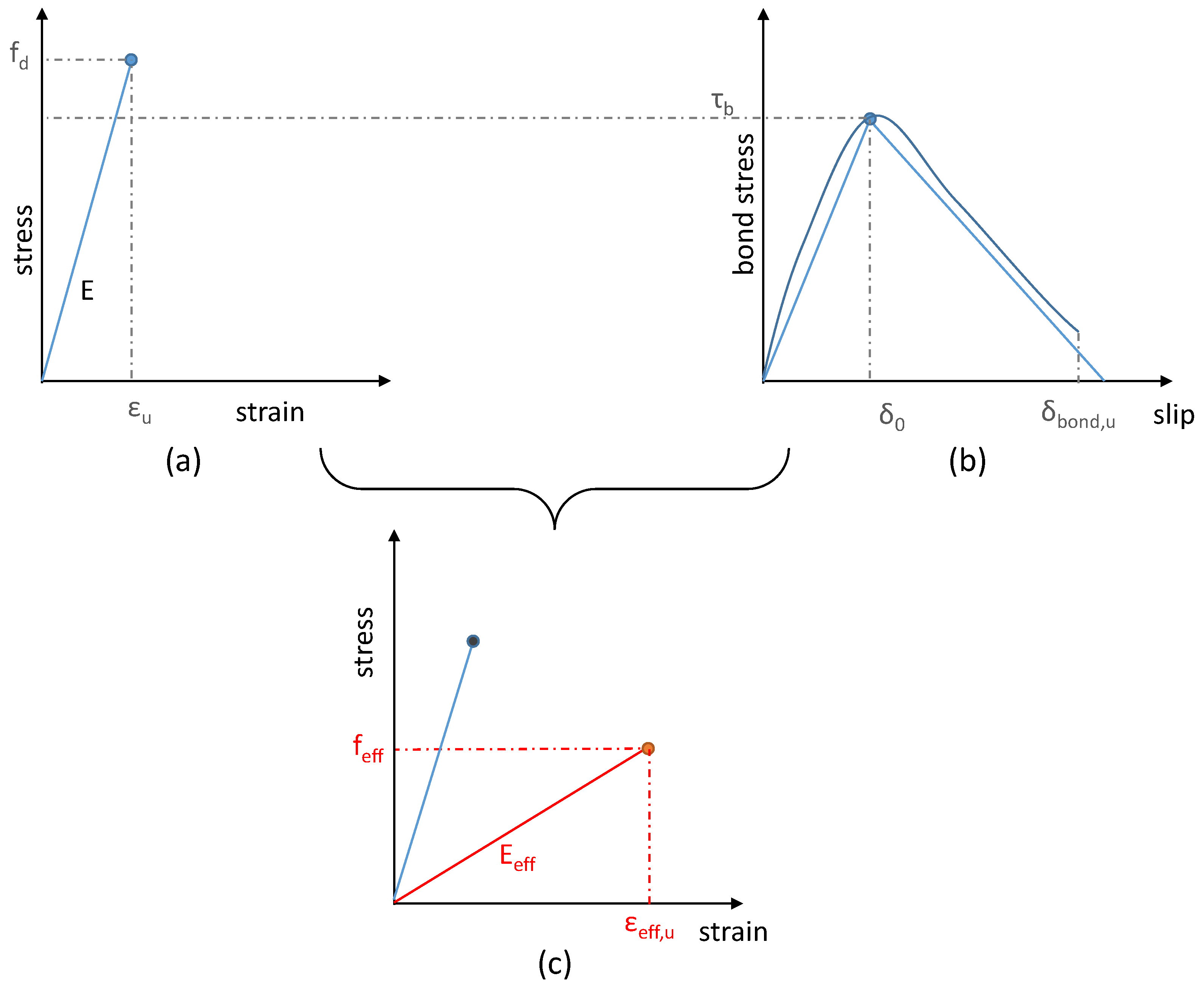
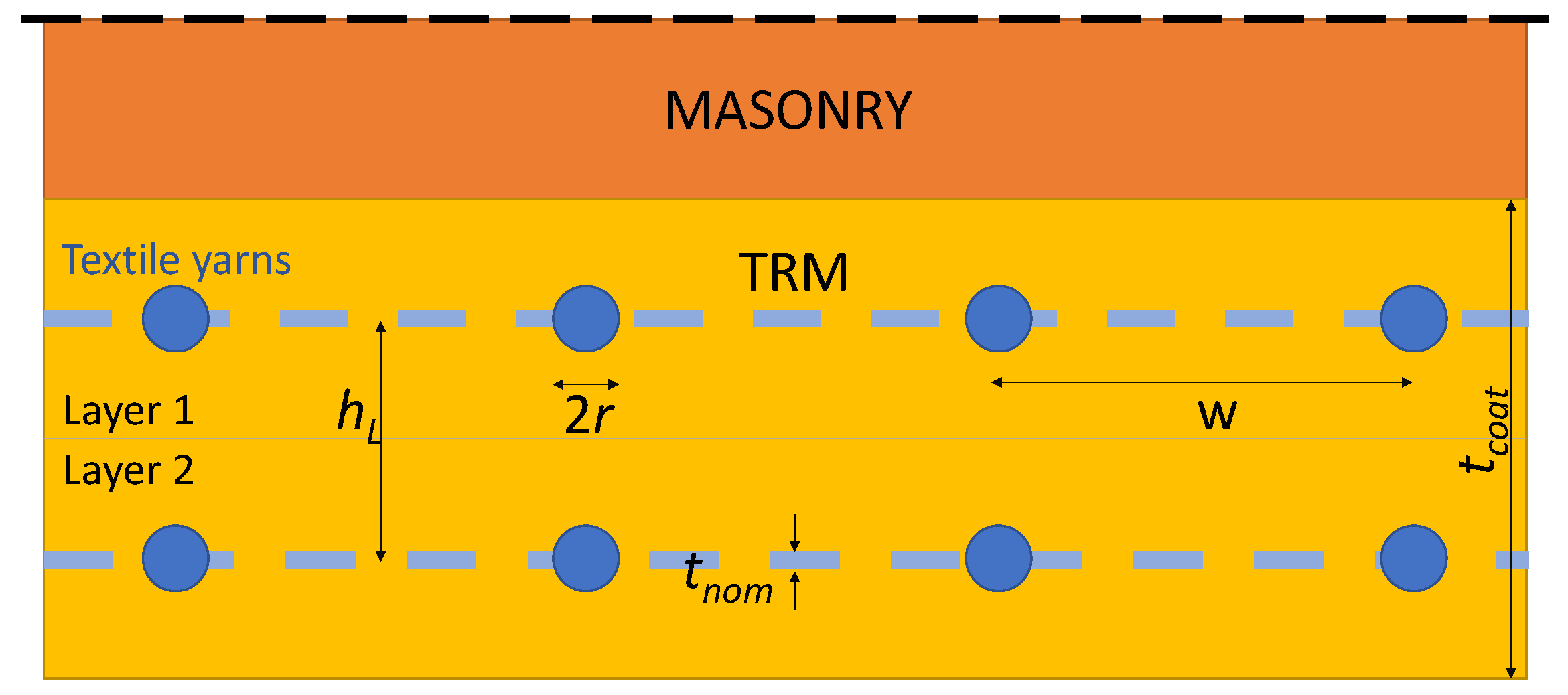
3.2. Textile Reinforced Mortar
3.3. Interaction between Matrix and Fibres
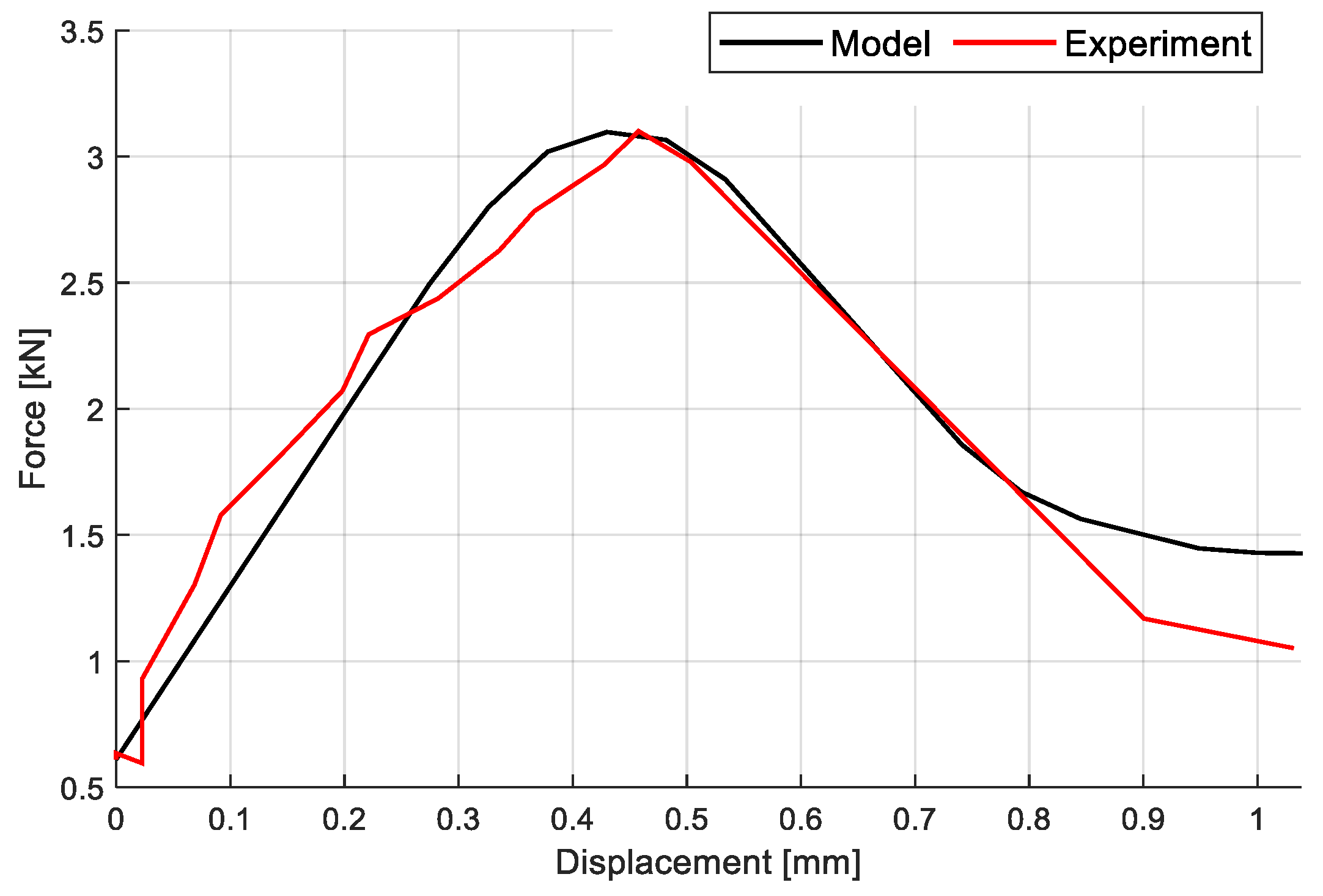
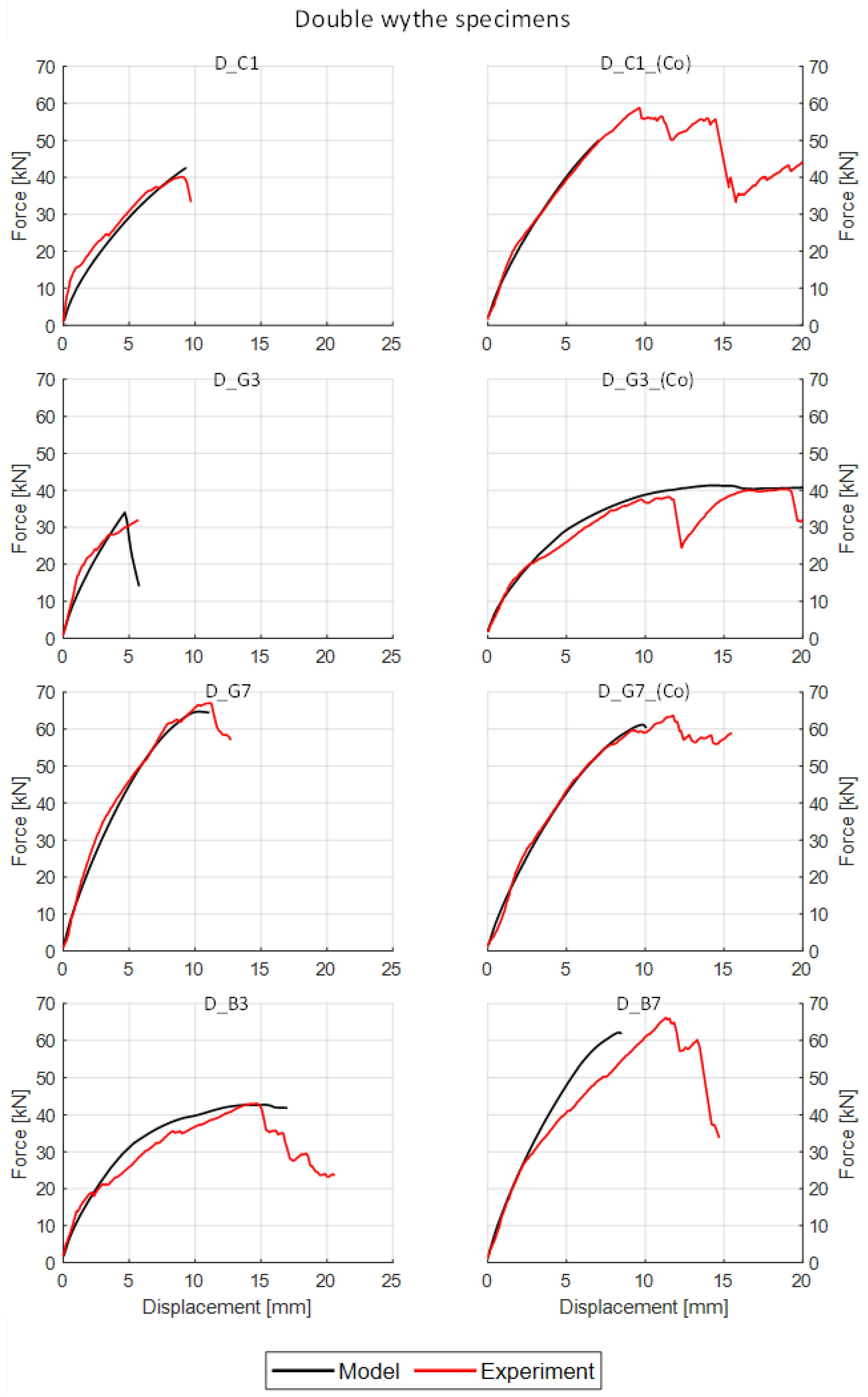
4. Calibration of TRM Model
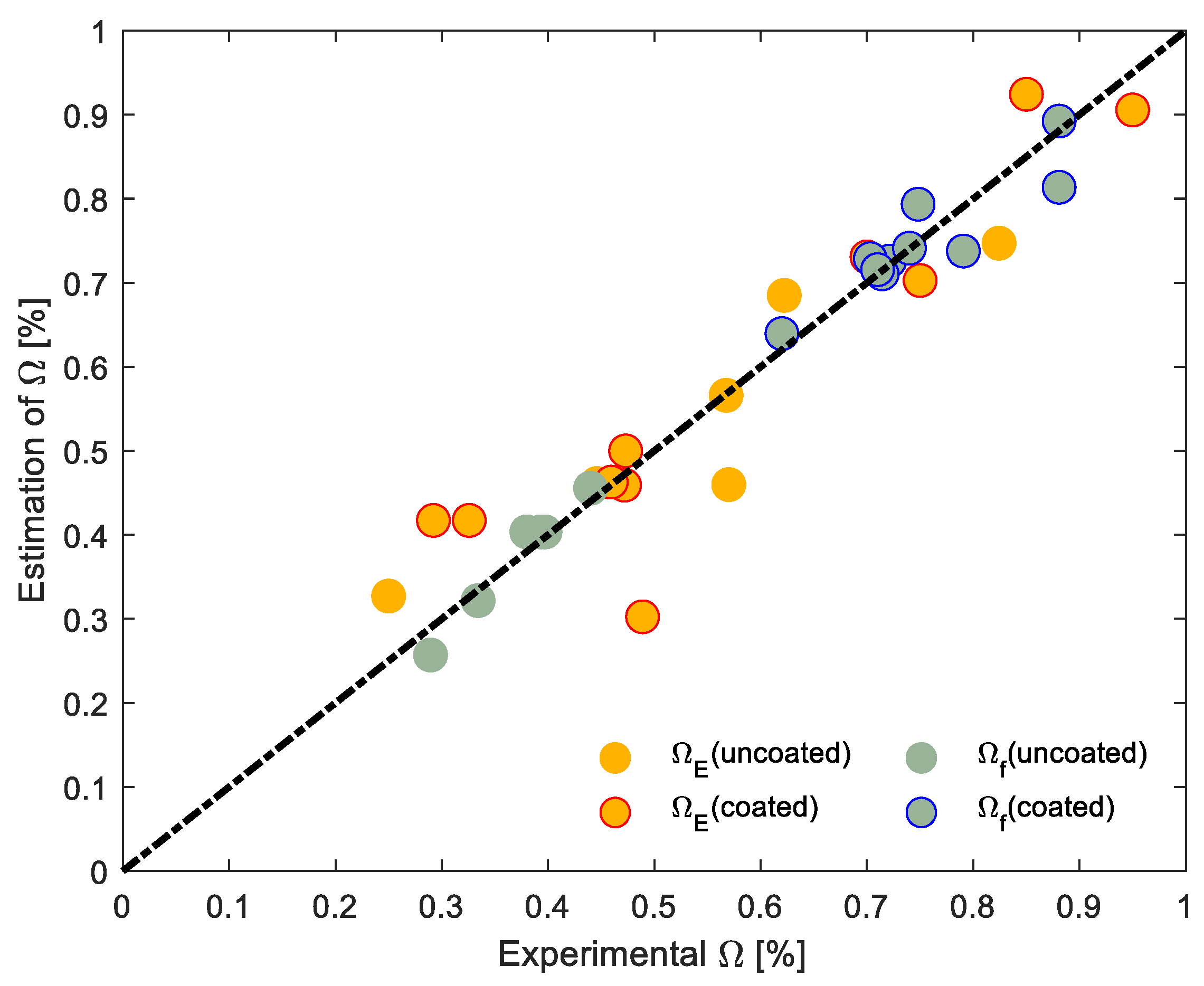
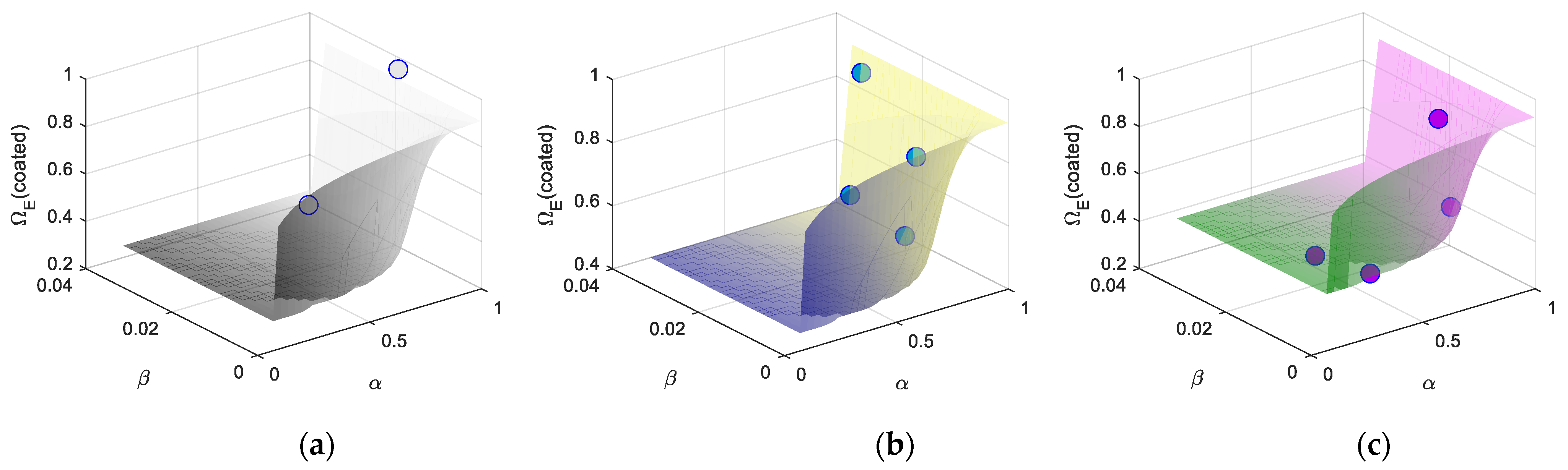
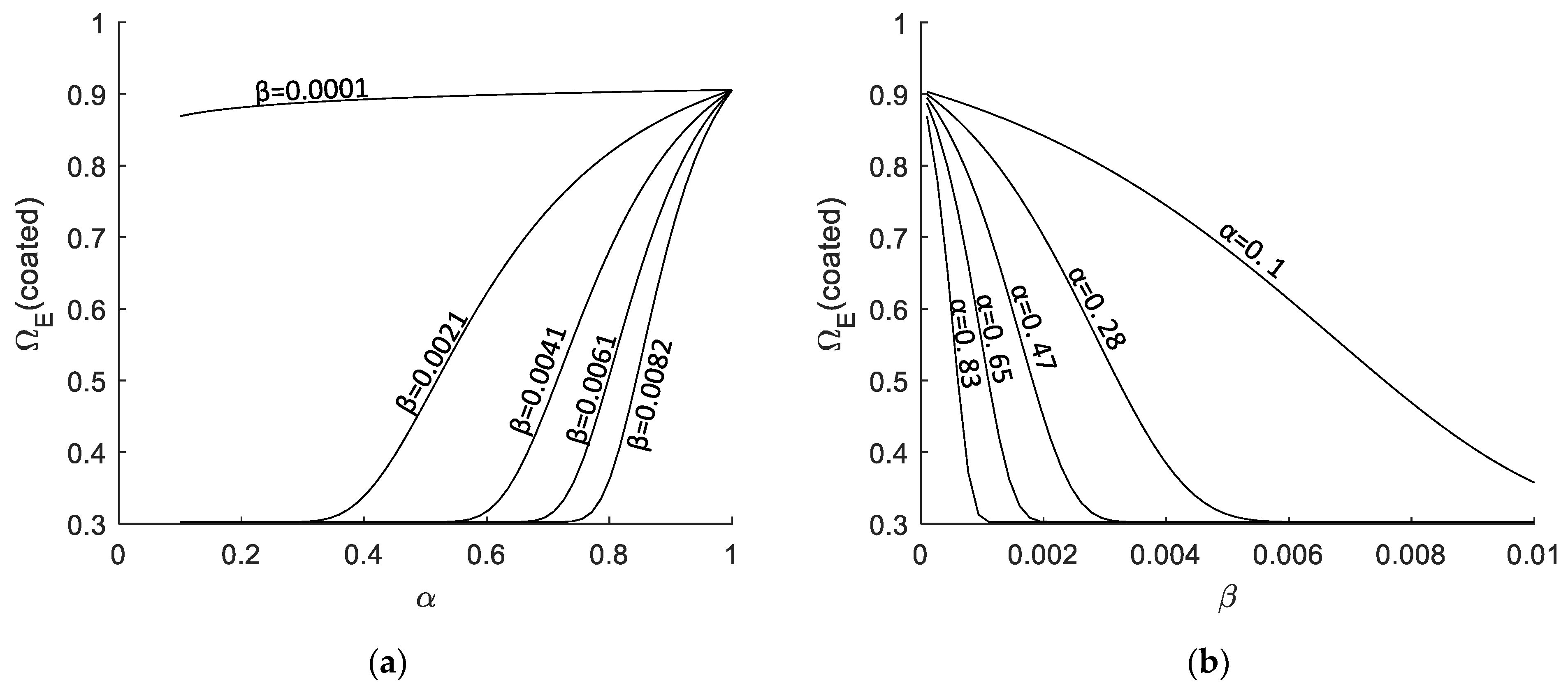
5. Empirical Equations for the Reduction Coefficients
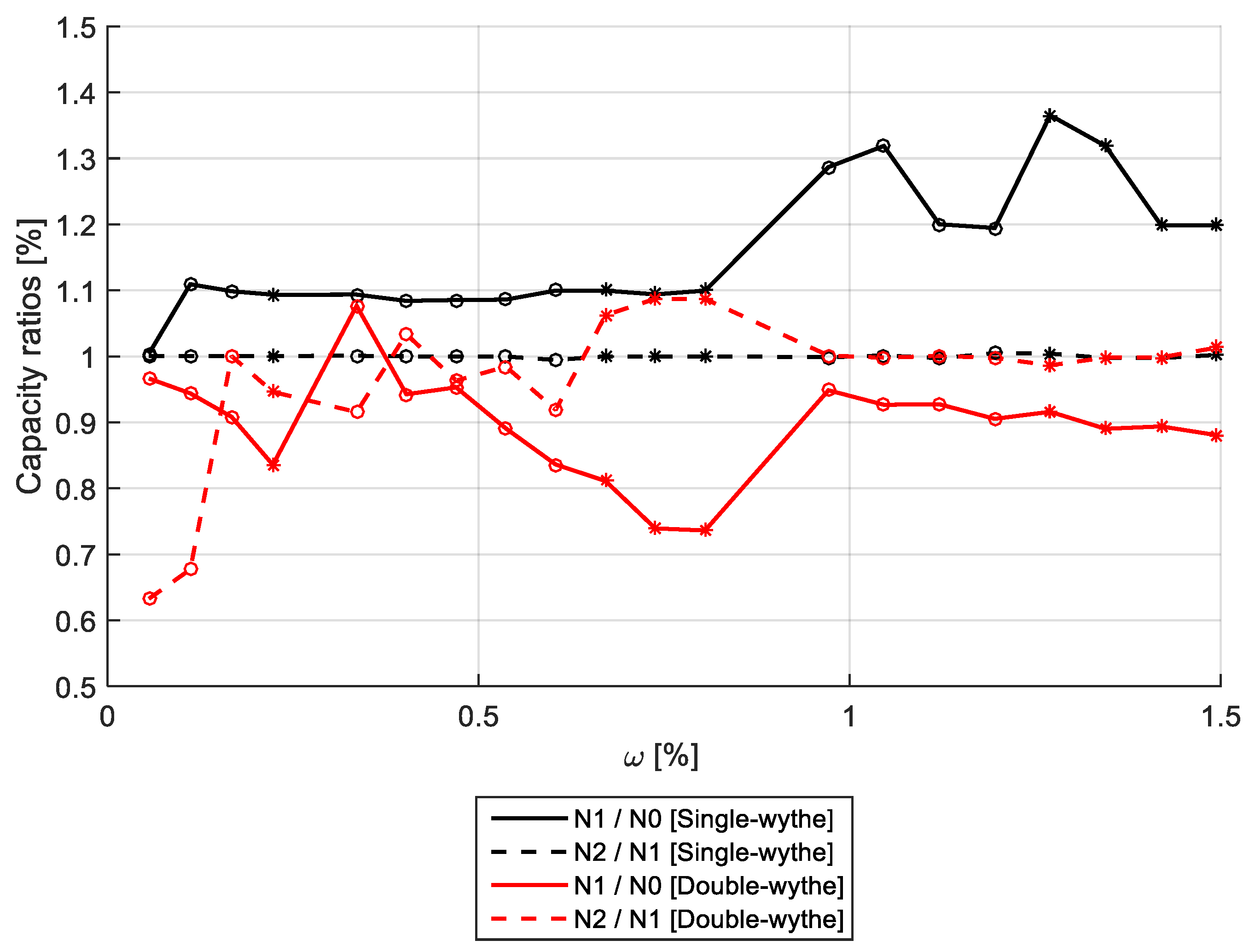
6. Parametric Analysis
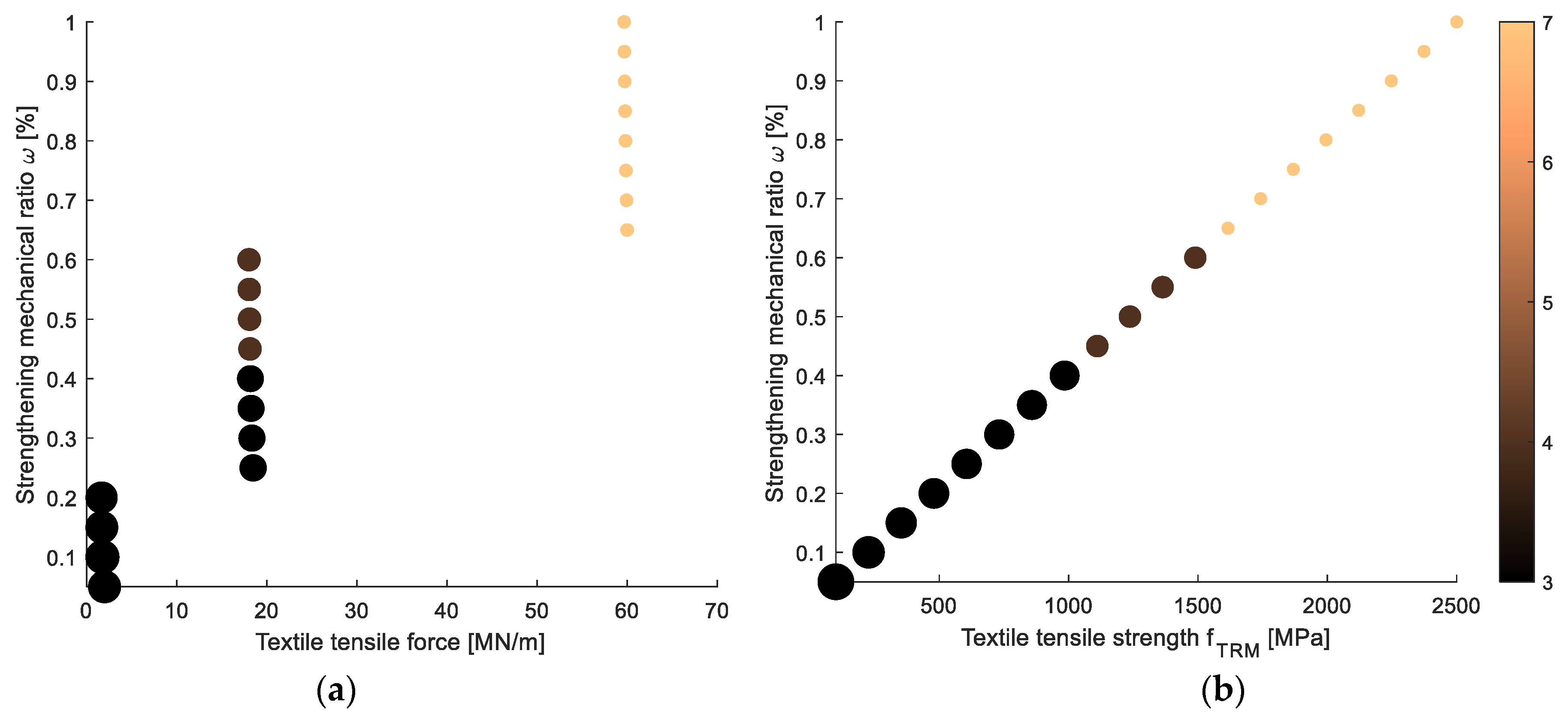
6.1. Parameters
6.2. Results and Discussion
7. Conclusions
- The use of Textile Reinforced Mortar (TRM) layers can effectively enhance the out-of-plane capacity of walls.
- When low-capacity fibres were utilized, the walls still exhibited a significant out-of-plane capacity, making them suitable for retrofitting cultural heritage buildings with rigorous compatibility requirements.
- On the other hand, when composite fibres were used, the capacity was significantly higher.
- It was also observed that the axial load applied to the walls increased their out-of-plane capacity, particularly when the primary failure mode was textile damage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Indirli, M.; Kouris, L.A.S.; Formisano, A.; Borg, R.P.; Mazzolani, F.M. Seismic damage assessment of unreinforced masonry structures after the Abruzzo 2009 earthquake: The case study of the historical centers of L’Aquila and Castelvecchio Subequo. Int. J. Archit. Herit. 2013, 7, 536–578. [Google Scholar] [CrossRef]
- Gkournelos, P.D.; Triantafillou, T.C.; Bournas, D.A. Seismic upgrading of existing masonry structures: A state-of-the-art review. Soil Dyn. Earthq. Eng. 2022, 161, 107428. [Google Scholar] [CrossRef]
- Formisano, A.; Marzo, A. Simplified and refined methods for seismic vulnerability assessment and retrofitting of an Italian cultural heritage masonry building. Comput. Struct. 2017, 180, 13–26. [Google Scholar] [CrossRef]
- Maraveas, C.; Tasiouli, K. Assessment and restoration of the first Greek power plant—Registered monument of industrial heritage. Case Stud. Struct. Eng. 2015, 3, 1–10. [Google Scholar] [CrossRef]
- Davino, A.; Longobardi, G.; Meglio, E.; Dallari, A.; Formisano, A. Seismic Energy Upgrading of an Existing Brick Masonry Building by a Cold-Formed Steel Envelope System. Buildings 2022, 12, 1918. [Google Scholar] [CrossRef]
- Vintzileou, E.; Mouzakis, C.; Karapitta, L.; Miltiadou-Fezans, A. Shake-Table Testing of a Cross Vault. Buildings 2022, 12, 1984. [Google Scholar] [CrossRef]
- Maraveas, C. Assessment and Restoration of an Earthquake-Damaged Historical Masonry Building. Front. Built Environ. 2019, 5, 474447. [Google Scholar] [CrossRef]
- Penelis, G.G. Structural restoration of historical buildings in seismic areas. Prog. Struct. Eng. Mater. 2002, 4, 64–73. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Fardis, M.N. Strengthening of historic masonry structures with composite materials. Mater. Struct. Constr. 1997, 30, 486–496. [Google Scholar] [CrossRef]
- de Felice, G.; Aiello, M.A.; Caggegi, C.; Ceroni, F.; De Santis, S.; Garbin, E.; Gattesco, N.; Hojdys, Ł.; Krajewski, P.; Kwiecień, A.; et al. Recommendation of RILEM Technical Committee 250-CSM: Test method for Textile Reinforced Mortar to substrate bond characterization. Mater. Struct. Constr. 2018, 51, 1–9. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Triantafillou, T.C. State-of-the-art on strengthening of masonry structures with textile reinforced mortar (TRM). Constr. Build. Mater. 2018, 188, 1221–1233. [Google Scholar] [CrossRef]
- Kariou, F.A.; Triantafyllou, S.P.; Bournas, D.A. TRM strengthening of masonry arches: An experimental investigation on the effect of strengthening layout and textile fibre material. Compos. Part B Eng. 2019, 173, 106765. [Google Scholar] [CrossRef]
- Papanicolaou, C.; Triantafillou, T.; Lekka, M. Externally bonded grids as strengthening and seismic retrofitting materials of masonry panels. Constr. Build. Mater. 2011, 25, 504–514. [Google Scholar] [CrossRef]
- Cerniauskas, G.; Tetta, Z.; Bournas, D.A.; Bisby, L.A. Concrete confinement with TRM versus FRP jackets at elevated temperatures. Mater. Struct. 2020, 53, 58. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Karlos, K.; Kefalou, K.; Argyropoulou, E. An innovative structural and energy retrofitting system for URM walls using textile reinforced mortars combined with thermal insulation: Mechanical and fire behavior. Constr. Build. Mater. 2017, 133, 1–13. [Google Scholar] [CrossRef]
- Kapsalis, P.; El Kadi, M.; Vervloet, J.; De Munck, M.; Wastiels, J.; Triantafillou, T.; Tysmans, T. Thermomechanical Behavior of Textile Reinforced Cementitious Composites Subjected to Fire. Appl. Sci. 2019, 9, 747. [Google Scholar] [CrossRef]
- Bournas, D.A. Concurrent seismic and energy retrofitting of RC and masonry building envelopes using inorganic textile-based composites combined with insulation materials: A new concept. Compos. Part B Eng. 2018, 148, 166–179. [Google Scholar] [CrossRef]
- Pohoryles, D.A.; Maduta, C.; Bournas, D.A.; Kouris, L.A. Energy Performance of Existing Residential Buildings in Europe: A Novel Approach Combining Energy with Seismic Retrofitting. Energy Build. 2020, 223, 110024. [Google Scholar] [CrossRef]
- Valluzzi, M.R.; da Porto, F.; Garbin, E.; Panizza, M. Out-of-plane behaviour of infill masonry panels strengthened with composite materials. Mater. Struct. Constr. 2014, 47, 2131–2145. [Google Scholar] [CrossRef]
- Harajli, M.; ElKhatib, H.; San-Jose, J.T. Static and Cyclic Out-of-Plane Response of Masonry Walls Strengthened Using Textile-Mortar System. J. Mater. Civ. Eng. 2010, 22, 1171–1180. [Google Scholar] [CrossRef]
- Kariou, F.A.; Triantafyllou, S.P.; Bournas, D.A.; Koutas, L.N. Out-of-plane response of masonry walls strengthened using textile-mortar system. Constr. Build. Mater. 2018, 165, 769–781. [Google Scholar] [CrossRef]
- Papanicolaou, C.G.; Triantafillou, T.C.; Papathanasiou, M.; Karlos, K. Textile reinforced mortar (TRM) versus FRP as strengthening material of URM walls: Out-of-plane cyclic loading. Mater. Struct. 2008, 41, 143–157. [Google Scholar] [CrossRef]
- Babaeidarabad, S.; Nanni, A. Out-of-plane strengthening of URM walls with fabric-reinforced-cementitious-matrix (FRCM). In Proceedings of the American Concrete Institute, ACI Special Publication, Bologna, Italy, 1–3 October 2015; Volume 2015. [Google Scholar]
- Gkournelos, P.D.; Triantafillou, T.C.; Bournas, D.A. Integrated Structural and Energy Retrofitting of Masonry Walls: Effect of In-Plane Damage on the Out-of-Plane Response. J. Compos. Constr. 2020, 24. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Triantafillou, T.C. Design Methods for Strengthening Masonry Buildings Using Textile-Reinforced Mortar. J. Compos. Constr. 2019, 23. [Google Scholar] [CrossRef]
- Babaeidarabad, S.; De Caso, F.; Nanni, A. Out-of-Plane Behavior of URM Walls Strengthened with Fabric-Reinforced Cementitious Matrix Composite. J. Compos. Constr. 2014, 18, 04013057. [Google Scholar] [CrossRef]
- Mosallam, A.S. Out-of-plane flexural behavior of unreinforced red brick walls strengthened with FRP composites. Compos. Part B Eng. 2007, 38, 559–574. [Google Scholar] [CrossRef]
- Babatunde, S.A. Review of strengthening techniques for masonry using fiber reinforced polymers. Compos. Struct. 2017, 161, 246–255. [Google Scholar] [CrossRef]
- Nicoletti, V.; Arezzo, D.; Carbonari, S.; Gara, F. Vibration-Based Tests and Results for the Evaluation of Infill Masonry Walls Influence on the Dynamic Behaviour of Buildings: A Review. Arch. Comput. Methods Eng. 2022, 29, 3773–3787. [Google Scholar] [CrossRef]
- Furtado, A.; Rodrigues, H.; Arêde, A.; Varum, H. Experimental evaluation of out-of-plane capacity of masonry infill walls. Eng. Struct. 2016, 111, 48–63. [Google Scholar] [CrossRef]
- De Angelis, A.; Pecce, M.R. Out-of-plane structural identification of a masonry infill wall inside beam-column RC frames. Eng. Struct. 2018, 173, 546–558. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Penna, A.; Magenes, G. Dynamic Modification and Damage Propagation of a Two-Storey Full-Scale Masonry Building. Adv. Civ. Eng. 2019, 2019, 2396452. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Penna, A.; Magenes, G. Assessment of a Full-Scale Unreinforced Stone Masonry Building Tested on a Shaking Table by Inverse Engineering. Buildings 2022, 12, 1235. [Google Scholar] [CrossRef]
- Theodossopoulos, D.; Sinha, B. A review of analytical methods in the current design processes and assessment of performance of masonry structures. Constr. Build. Mater. 2013, 41, 990–1001. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Meireles, H.; Bento, R.; Kappos, A.J. Simple and complex modelling of timber-framed masonry walls in Pombalino buildings. Bull. Earthq. Eng. 2014, 12, 1–27. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Penna, A.; Galasco, A.; Cattari, S. TREMURI program: An equivalent frame model for the nonlinear seismic analysis of masonry buildings. Eng. Struct. 2013, 56, 1787–1799. [Google Scholar] [CrossRef]
- Kouris, E.G.; Kouris, L.A.S. Investigation of the influence of tie-rods on the seismic behaviour of slender towers. Civil-Comp Proc. 2014, 106, 1–15. [Google Scholar] [CrossRef]
- Giordano, A.; Mele, E.; De Luca, A. Modelling of historical masonry structures: Comparison of different approaches through a case study. Eng. Struct. 2002, 24, 1057–1069. [Google Scholar] [CrossRef]
- Gambarotta, L.; Lagomarsino, S. Damage models for the seismic response of brick masonry shear walls. Part II: The continuum model and its applications. Earthq. Eng. Struct. Dyn. 1997, 26, 423–439. [Google Scholar] [CrossRef]
- Milani, G.; Lourenço, P.B.; Tralli, A. Homogenised limit analysis of masonry walls, Part II: Structural examples. Comput. Struct. 2006, 84, 181–195. [Google Scholar] [CrossRef]
- Zucchini, A.; Lourenço, P.B. A micro-mechanical homogenisation model for masonry: Application to shear walls. Int. J. Solids Struct. 2009, 46, 871–886. [Google Scholar] [CrossRef]
- Anthoine, A. Derivation of the in-plane elastic characteristics of masonry through homogenization theory. Int. J. Solids Struct. 1995, 32, 137–163. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Milani, G.; Tralli, A.; Zucchini, A. Analysis of masonry structures: Review of and recent trends in homogenization techniquesThis article is one of a selection of papers published in this Special Issue on Masonry. Can. J. Civ. Eng. 2007, 34, 1443–1457. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Bournas, D.A.; Akintayo, O.T.; Konstantinidis, A.A.; Aifantis, E.C. A gradient elastic homogenisation model for brick masonry. Eng. Struct. 2020, 208, 110311. [Google Scholar] [CrossRef]
- Bertolesi, E.; Carozzi, F.G.; Milani, G.; Poggi, C. Numerical modeling of Fabric Reinforce Cementitious Matrix composites (FRCM) in tension. Constr. Build. Mater. 2014, 70, 531–548. [Google Scholar] [CrossRef]
- Parisi, F.; Lignola, G.P.; Augenti, N.; Prota, A.; Manfredi, G. Nonlinear Behavior of a Masonry Subassemblage Before and After Strengthening with Inorganic Matrix-Grid Composites. J. Compos. Constr. 2011, 15, 821–832. [Google Scholar] [CrossRef]
- Basili, M.; Marcari, G.; Vestroni, F. Nonlinear analysis of masonry panels strengthened with textile reinforced mortar. Eng. Struct. 2016, 113, 245–258. [Google Scholar] [CrossRef]
- Lignola, G.P.; Prota, A.; Manfredi, G. Nonlinear Analyses of Tuff Masonry Walls Strengthened with Cementitious Matrix-Grid Composites. J. Compos. Constr. 2009, 13, 243–251. [Google Scholar] [CrossRef]
- Basili, M.; Vestroni, F.; Marcari, G. Brick masonry panels strengthened with textile reinforced mortar: Experimentation and numerical analysis. Constr. Build. Mater. 2019, 227, 117061. [Google Scholar] [CrossRef]
- Wang, X.; Ghiassi, B.; Oliveira, D.V.; Lam, C.C. Modelling the nonlinear behaviour of masonry walls strengthened with textile reinforced mortars. Eng. Struct. 2017, 134, 11–24. [Google Scholar] [CrossRef]
- Loccarini, F.; Ranocchiai, G.; Rotunno, T.; Fagone, M. Experimental and numerical analyses of strengthened rammed earth masonry arches. Comput. Struct. 2020, 239, 106329. [Google Scholar] [CrossRef]
- Scacco, J.; Ghiassi, B.; Milani, G.; Lourenço, P.B. A fast modeling approach for numerical analysis of unreinforced and FRCM reinforced masonry walls under out-of-plane loading. Compos. Part B Eng. 2020, 180, 107553. [Google Scholar] [CrossRef]
- Kyriakides, M.A.; Billington, S.L. Behavior of unreinforced masonry prisms and beams retrofitted with engineered cementitious composites. Mater. Struct. Constr. 2014, 47, 1573–1587. [Google Scholar] [CrossRef]
- Kyriakides, M.A.; Hendriks, M.A.N.; Billington, S.L. Simulation of unreinforced masonry beams retrofitted with engineered cementitious composites in flexure. J. Mater. Civ. Eng. 2012, 24, 506–515. [Google Scholar] [CrossRef]
- Singh, S.B.; Patil, R.; Munjal, P. Study of flexural response of engineered cementitious composite faced masonry structures. Eng. Struct. 2017, 150, 786–802. [Google Scholar] [CrossRef]
- Munjal, P.; Singh, S.B. Out-of-plane response of ECC-strengthened masonry walls. J. Struct. Integr. Maint. 2020, 5, 18–30. [Google Scholar] [CrossRef]
- Leone, M.; Aiello, M.A.; Balsamo, A.; Carozzi, F.G.; Ceroni, F.; Corradi, M.; Gams, M.; Garbin, E.; Gattesco, N.; Krajewski, P.; et al. Glass fabric reinforced cementitious matrix: Tensile properties and bond performance on masonry substrate. Compos. Part B Eng. 2017, 127, 196–214. [Google Scholar] [CrossRef]
- Larrinaga, P.; Chastre, C.; Biscaia, H.C.; San-José, J.T. Experimental and numerical modeling of basalt textile reinforced mortar behavior under uniaxial tensile stress. Mater. Des. 2014, 55, 66–74. [Google Scholar] [CrossRef]
- Veljkovic, A.; Carvelli, V.; Rezazadeh, M. Modelling the bond in GFRP bar reinforced concrete thin structural members. Structures 2020, 24, 13–26. [Google Scholar] [CrossRef]
- Makashev, K.; Triantafyllou, S.P.; Thermou, G.E.; Tizani, W. Bond behaviour of light and heavy carbon fibre TRM to masonry interfaces. Constr. Build. Mater. 2023, 400, 132508. [Google Scholar] [CrossRef]
- Askouni, P.D.; Papanicolaou, C.G.; Azdejkovic, L. Experimental Investigation of the TRM-to-Masonry Bond after Exposure to Elevated Temperatures: Cementitious and Alkali-Activated Matrices of Various Densities. Materials 2022, 15, 140. [Google Scholar] [CrossRef]
- EN 1052-1; Methods of Test for Masonry-Part 1: Determination of Compressive Strength. European Committee for Standardization: Brussels, Belgium, 1999.
- Deng, M.; Yang, S. Experimental and numerical evaluation of confined masonry walls retrofitted with engineered cementitious composites. Eng. Struct. 2020, 207, 110249. [Google Scholar] [CrossRef]
- Kaushik, H.B.; Rai, D.C.; Jain, S.K. Stress-Strain Characteristics of Clay Brick Masonry under Uniaxial Compression. J. Mater. Civ. Eng. 2007, 19, 728–739. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Calderini, C.; Lagomarsino, S. Continuum model for in-plane anisotropic inelastic behavior of masonry. J. Struct. Eng. 2008, 134, 209–220. [Google Scholar] [CrossRef]
- Lotfi, H.R.; Shing, P.B. Interface model applied to fracture of masonry structures. J. Struct. Eng. 1994, 120, 63–80. [Google Scholar] [CrossRef]
- Gabor, A.; Ferrier, E.; Jacquelin, E.; Hamelin, P. Analysis and modelling of the in-plane shear behaviour of hollow brick masonry panels. Constr. Build. Mater. 2006, 20, 308–321. [Google Scholar] [CrossRef]
- Lourenço, P.B. Anisotropic softening model for masonry plates and shells. J. Struct. Eng. 2000, 126, 1008–1016. [Google Scholar] [CrossRef]
- Drougkas, A.; Roca, P.; Molins, C. Material Characterization and Micro-Modeling of a Historic Brick Masonry Pillar. Int. J. Archit. Herit. 2016, 10, 887–902. [Google Scholar] [CrossRef]
- Bedon, C.; Louter, C. Numerical investigation on structural glass beams with GFRP-embedded rods, including effects of pre-stress. Compos. Struct. 2018, 184, 650–661. [Google Scholar] [CrossRef]
- Stupkiewicz, S.; Mróz, Z. Modelling of friction and dilatancy effects at brittle interfaces for monotonic and cyclic loading | Stupkiewicz | Journal of Theoretical and Applied Mechanics. J. Theor. Appl. Mech. 2001, 39, 707–739. [Google Scholar]
- Lourenço, P.B.; Ramos, L.F. Characterization of cyclic behavior of dry masonry joints. J. Struct. Eng. 2004, 130, 779–786. [Google Scholar] [CrossRef]
- D’Antino, T.; Carloni, C.; Sneed, L.H.; Pellegrino, C. Matrix-fiber bond behavior in PBO FRCM composites: A fracture mechanics approach. Eng. Fract. Mech. 2014, 117, 94–111. [Google Scholar] [CrossRef]
- Askouni, P.D.; Papanicolaou, C.G. Textile Reinforced Mortar-to-masonry bond: Experimental investigation of bond-critical parameters. Constr. Build. Mater. 2019, 207, 535–547. [Google Scholar] [CrossRef]
- Askouni, P.D.; Papanicolaou, C.G. Experimental investigation of bond between glass textile reinforced mortar overlays and masonry: The effect of bond length. Mater. Struct. Constr. 2017, 50, 164. [Google Scholar] [CrossRef]
- Banholzer, B.; Brockmann, T.; Brameshuber, W. Material and bonding characteristics for dimensioning and modelling of textile reinforced concrete (TRC) elements. Mater. Struct. 2006, 39, 749–763. [Google Scholar] [CrossRef]
- Alecci, V.; De Stefano, M.; Luciano, R.; Rovero, L.; Stipo, G. Experimental Investigation on Bond Behavior of Cement-Matrix–Based Composites for Strengthening of Masonry Structures. J. Compos. Constr. 2016, 20, 04015041. [Google Scholar] [CrossRef]
- CEB-FIB. Model Code 2010-First Complete Draft; International Federation for Structural Concrete (fib): Lausanne, Switzerland, 2010; Volume 1, ISBN 978-2-88394-095-6. [Google Scholar]






| Material | Strength | Elastic Modulus |
|---|---|---|
| Masonry | 9.7 | 2.5 |
| Brick units | 12.3 | - |
| Casting mortar (joints) | 7.5 compressive/2.2 tensile | - |
| Reinforcing mortar (matrix) | 39.7 compressive/+9.0 tensile | 0.8 |
| Carbon | 3800 | 225 |
| Glass | 1400 | 74 |
| Basalt (coated) | 1351 | 89 |
| Specimen | tcoat | ρw | ωt | Max Force | Max Displacement | Failure Mode * |
|---|---|---|---|---|---|---|
| (mm) | (%) | (kN) | (mm) | |||
| S_C1 | 3 | 0.095% | 0.35 | 23.4 | 15.6 | TX(DB,SL) |
| S_C1_(Co) | 5 | 0.095% | 0.35 | 35.3 | 20.8 | TX(FB) |
| S_G3 | 4 | 0.129% | 0.19 | 14.3 | 12.2 | TX(FB) |
| S_G3_(Co) | 7 | 0.129% | 0.19 | 25.8 | 30 | TX(FB) |
| S_G7 | 8 | 0.300% | 0.43 | 30.6 | 14.7 | TX(FB) |
| S_G7_(Co) | 9 | 0.300% | 0.43 | 42.5 | 55 | MR(SD,FL) + TX(DB) |
| S_B3_(Co) | 9 | 0.108% | 0.15 | 23.2 | 24.7 | TX(FB) |
| S_B7_(Co) | 13 | 0.253% | 0.35 | 44.5 | 32.1 | MR(SD,FL), TX(DB) |
| D_C1 | 3 | 0.045% | 0.17 | 40.1 | 9.7 | TX(FB) |
| D_C1_(Co) | 5 | 0.045% | 0.17 | 58.8 | 14.9 | MR(SD,SV,FL), TX(FB) |
| D_G3 | 4 | 0.061% | 0.09 | 32 | 5.8 | TX(FB) |
| D_G3_(Co) | 7 | 0.061% | 0.09 | 40.4 | 28.8 | MR(SD,FL), TX(DB) |
| D_G7 | 8 | 0.143% | 0.03 | 67.1 | 12.8 | MR(SD,FL), TX(FB) |
| D_G7_(Co) | 9 | 0.143% | 0.21 | 63.8 | 16.2 | MR(SD,FL), TX(DB) |
| D_B3_(Co) | 9 | 0.052% | 0.07 | 43.1 | 16.7 | MR(SD,SV,FL), TX(FB) |
| D_B7_(Co) | 13 | 0.120% | 0.17 | 66.2 | 13.6 | MR(SD) |
| σb0/σc0 | K | μ | ||
|---|---|---|---|---|
| (deg) | (%) | (-) | (-) | (-) |
| 15 | 0 | 1.16 | 2/3 | 10−6 |
| Model | Eeff (GPa) | feff (GPa) | σt (MPa) | ΩE | Ωf |
|---|---|---|---|---|---|
| S_C1 | 140 | 1270 | 1270 | 0.62 | 0.33 |
| S_C1_(Co) | 214 | 2470 | 2470 | 0.95 | 0.62 |
| S_G3 | 42 | 532 | 505 | 0.57 | 0.38 |
| S_G3_(Co) | 52 | 1010 | 960 | 0.70 | 0.72 |
| S_G7 | 61 | 623 | 623 | 0.82 | 0.44 |
| S_G7_(Co) | 63 | 1022 | 1022 | 0.85 | 0.71 |
| S_B3 | 42 | 950 | 817 | 0.47 | 0.70 |
| S_B7 | 67 | 959 | 911 | 0.75 | 0.71 |
| D_C1 | 56 | 1045 | 627 | 0.25 | 0.29 |
| D_C1_(Co) | 110 | 2470 | 1482 | 0.49 | 0.75 |
| D_G3 | 42 | 556 | 334 | 0.57 | 0.40 |
| D_G3_(Co) | 34 | 1008 | 907 | 0.46 | 0.74 |
| D_G7 | 33 | 550 | 495 | 0.45 | 0.39 |
| D_G7_(Co) | 35 | 980 | 931 | 0.47 | 0.79 |
| D_B3 | 26 | 946 | 473 | 0.29 | 0.88 |
| D_B7 | 29 | 946 | 378 | 0.33 | 0.88 |
| p1 | p2 | p3 | R2 | p-Value | |
|---|---|---|---|---|---|
| ΩΕ (uncoated) | 0.63 | 559 | 0.12 | 0.85 | 3 × 10−3 |
| ΩΕ (coated) | 0.15 | 1557 | 0.12 | 0.84 | 2 × 10−3 |
| Ωf (uncoated) | 2.34 | 2000 | 0.13 | 0.93 | 2 × 10−3 |
| Ωf (coated) | 3.35 | 277 | 0.06 | 0.94 | 1 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kouris, L.A.S.; Triantafyllou, S.P.; Bournas, D.A.; Kariou, F.A. Empirical Equations for Modelling Yarn–Mortar Debonding in TRM-Strengthened Masonry Walls Subjected to Out-of-Plane Loading. Buildings 2024, 14, 32. https://doi.org/10.3390/buildings14010032
Kouris LAS, Triantafyllou SP, Bournas DA, Kariou FA. Empirical Equations for Modelling Yarn–Mortar Debonding in TRM-Strengthened Masonry Walls Subjected to Out-of-Plane Loading. Buildings. 2024; 14(1):32. https://doi.org/10.3390/buildings14010032
Chicago/Turabian StyleKouris, Leonidas Alexandros S., Savvas P. Triantafyllou, Dionysios A. Bournas, and Florentia A. Kariou. 2024. "Empirical Equations for Modelling Yarn–Mortar Debonding in TRM-Strengthened Masonry Walls Subjected to Out-of-Plane Loading" Buildings 14, no. 1: 32. https://doi.org/10.3390/buildings14010032
APA StyleKouris, L. A. S., Triantafyllou, S. P., Bournas, D. A., & Kariou, F. A. (2024). Empirical Equations for Modelling Yarn–Mortar Debonding in TRM-Strengthened Masonry Walls Subjected to Out-of-Plane Loading. Buildings, 14(1), 32. https://doi.org/10.3390/buildings14010032








