Theoretical Analysis of the Active Earth Pressure on Inclined Retaining Walls
Abstract
:1. Introduction
2. Vertical Stress Distribution of Soil behind Inclined Retaining Walls
3. Analytical Derivations of the Earth Pressure of Inclined Retaining Walls
3.1. Stress State of Soil behind an Inclined Retaining Wall
3.2. Analytical Solution for the Active Earth Pressure
4. Comparison of the Proposed Method with Other Experimental and Theoretical Results
4.1. Comparison with Experimental and Theoretical Results of Vertical Retaining Walls
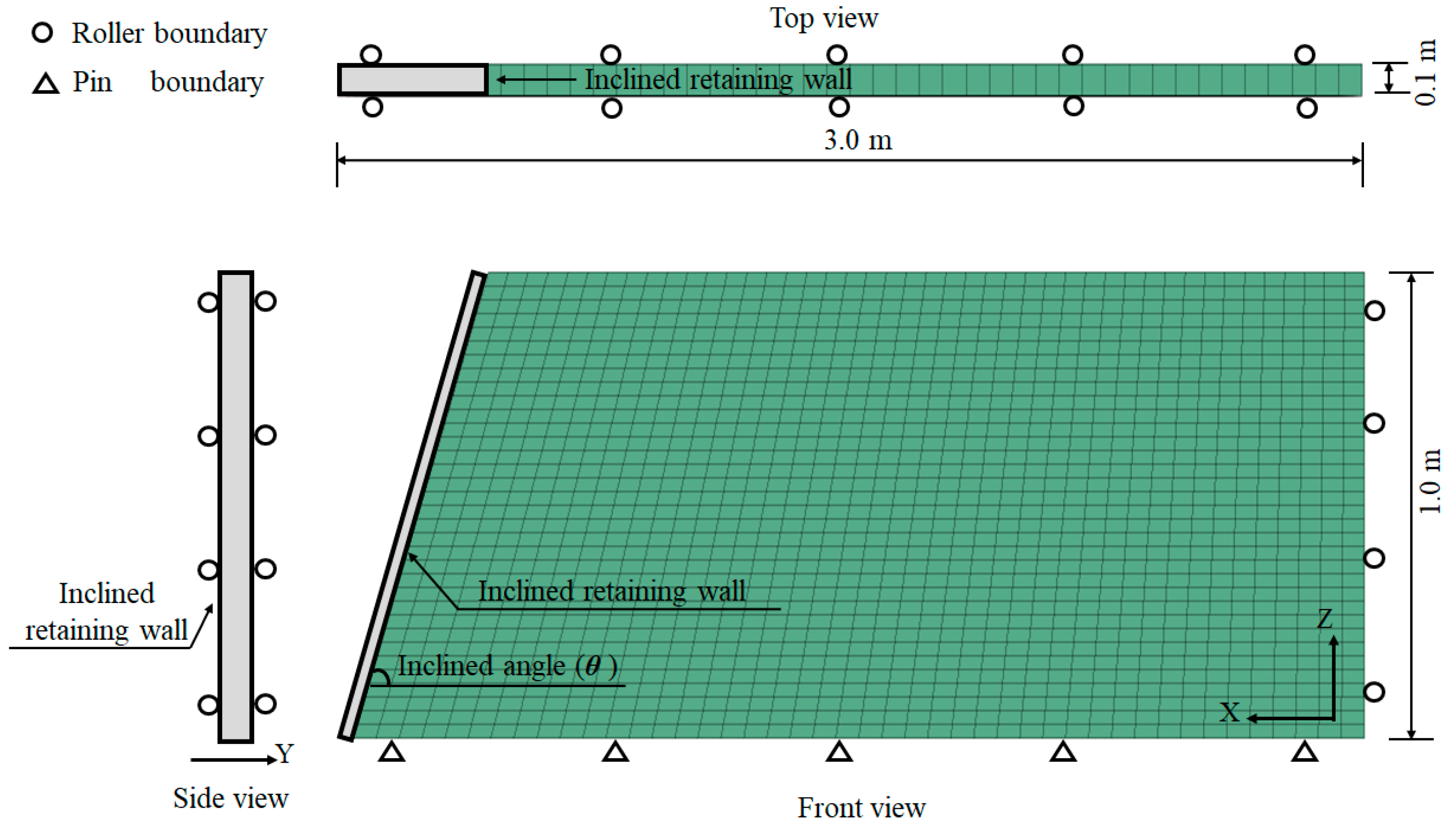
4.2. Comparison with Numerical Simulation Results of Inclined Retaining Walls
4.3. Comparison between Uniform and Nonuniform Distributions of Vertical Stress
5. Conclusions
- (1)
- As the inclination angle of the retaining wall increases, the normal active earth pressure on the inclined wall at the same depth gradually decreases.
- (2)
- The wall inclination has an obvious influence on the normal active earth pressure. The distribution of earth pressure gradually changes from a triangle to a curve with increasing inclination angle.
- (3)
- Compared with the traditional method, the proposed method considers the characteristics of a nonuniform distribution of vertical stress, resulting in a more accurate earth pressure calculation. The proposed method is helpful for the economic design of inclined retaining walls.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zucca, M.; Valente, M. On the limitations of decoupled approach for the seismic behaviour evaluation of shallow multi-propped underground structures embedded in granular soils. Eng. Struct. 2020, 211, 110497. [Google Scholar] [CrossRef]
- Rankine, W.J.M. II. On the stability of loose earth. Philos. Trans. R. Soc. 1857, 147, 9–27. [Google Scholar]
- Coulomb, C.A. Essai sur une Application des Règles de Maximis et Minimis a Quelques Problèmes de Statique, Relatifs a l’Architecture; De l’Imprimerie Royale: Paris, France, 1776. (In French) [Google Scholar]
- Lim, A.; Ou, C.Y.; Hsieh, P.G. Investigation of the integrated retaining system to limit deformations induced by deep excavation. Acta Geotech. 2018, 13, 973–995. [Google Scholar] [CrossRef]
- Lim, A.; Ou Cyhsieh, P.G. A novel strut-free retaining wall system for deep excavation in soft clay: Numerical study. Acta Geotech. 2020, 15, 1557–1576. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C.; Tang, L.; Zhang, W.; Lacasse, S.; Liu, H.; Gao, L. Efficient reliability analysis of earth dam slope stability using extreme gradient boosting method. Acta Geotech. 2020, 15, 3135–3150. [Google Scholar] [CrossRef]
- Paik, K.H.; Salgado, R. Estimation of active earth pressure against rigid retaining walls considering arching effects. Geotechnique 2003, 53, 643–645. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, Q.; Zhou, Y.; Nimbalkar, S.; Yu, J. Estimation of passive earth pressure against rigid retaining wall considering arching effect in cohesive-frictional backfill under translation mode. Int. J. Geomech. 2017, 17, 04016093. [Google Scholar] [CrossRef]
- Li, J.; Wang, M. Simplified method for calculating active earth pressure on rigid retaining walls considering the arching effect under translational mode. Int. J. Geomech. 2014, 14, 282–290. [Google Scholar] [CrossRef]
- Ni, P.; Song, L.; Mei, G.; Zhao, Y. On predicting displacement-dependent earth pressure for laterally loaded piles. Soils Found. 2018, 58, 85–96. [Google Scholar] [CrossRef]
- Rao, P.; Chen, Q.; Zhou, Y.; Nimbalkar, S.; Chiaro, G. Determination of active earth pressure on rigid retaining wall considering arching effect in cohesive backfill soil. Int. J. Geomech. 2015, 16, 04015082. [Google Scholar] [CrossRef]
- Goel, S.; Patra, N.R. Effect of arching on active earth pressure for rigid retaining walls considering translation mode. Int. J. Geomech. 2008, 8, 123–133. [Google Scholar] [CrossRef]
- Patel, S.; Deb, K. Study of active earth pressure behind a vertical retaining wall subjected to rotation about the base. Int. J. Geomech. 2020, 20, 04020028. [Google Scholar] [CrossRef]
- Khosravi, M.H.; Pipatpongsa, T.; Takemura, J. Experimental analysis of earth pressure against rigid retaining walls under transla-tion mode. Geotechnique 2013, 63, 1020–1028. [Google Scholar] [CrossRef]
- Khosravi, M.H.; Pipatpongsa, T.; Takemura, J. Theoretical analysis of earth pressure against rigid retaining walls under translation mode. Soils Found. 2016, 56, 664–675. [Google Scholar] [CrossRef]
- Lai, F.; Yang, D.; Liu, S.; Zhang, H.; Cheng, Y. Towards an improved analytical framework to estimate active earth pressure in nar-row c–ϕ soils behind rotating walls about the base. Comput. Geotech. 2022, 141, 104544. [Google Scholar] [CrossRef]
- Zheng, G.; He, X.; Zhou, H.; Diao, Y.; Li, Z.; Liu, X. Performance and mechanism of batter-vertical framed retaining wall for ex-cavation in clay. Tunn. Undergr. Space Technol. 2022, 130, 104767. [Google Scholar] [CrossRef]
- Zheng, G.; Liu, Z.; Zhou, H.; He, X.; Guo, Z. Behaviour of an outward inclined-vertical framed retaining wall of an excavation. Acta Geotech. 2022, 17, 5521–5532. [Google Scholar] [CrossRef]
- Zheng, G.; Guo, Z.; Zhou, H.; Diao, Y.; Yu, D.; Wang, E.; He, X.; Tian, Y.; Liu, Z. Parametric studies of wall displacement in ex-cavations with inclined framed retaining walls. Int. J. Geomech. 2022, 22, 04022157. [Google Scholar] [CrossRef]
- Zheng, G.; He, X.; Zhou, H. A Prediction Model for the Deformation of an Embedded Cantilever Retaining Wall in Sand. Int. J. Geomech. 2023, 23, 06023001. [Google Scholar] [CrossRef]
- Handy, R.L. The arch in soil arching. J. Geotech. Eng. 1985, 111, 302–318. [Google Scholar] [CrossRef]
- Segrestin, P. Design of Sloped Reinforced Fill Structures; Retaining Structures; Thomas Telford Publishing: London, UK, 1993; pp. 574–586. [Google Scholar]
- Fang, Y.S.; Ishibashi, I. Static earth pressures with various wall movements. J. Geotech. Eng. 1986, 112, 317–333. [Google Scholar] [CrossRef]
- Benmeddour, D.; Mellas, M.; Frank, R.; Mabrouki, A. Numerical study of passive and active earth pressures of sands. Comput. Geotech. 2012, 40, 34–44. [Google Scholar] [CrossRef]
- Zhou, H.; Shi, Y.; Yu, X.; Xu, H.; Zheng, G.; Yang, S.; He, Y. Failure mechanism and bearing capacity of rigid footings placed on top of cohesive soil slopes in spatially random soil. Int. J. Geomech. 2023, 23, 04023110. [Google Scholar] [CrossRef]
- Sitharam, T.G.; Maji, V.B.; Verma, A.K. Practical equivalent continuum model for simulation of jointed rock mass using FLAC3D. Int. J. Geomech. 2007, 7, 389–395. [Google Scholar] [CrossRef]
- Cao, W.; Liu, T.; Xu, Z. Calculation of passive earth pressure using the simplified principal stress trajectory method on rigid retaining walls. Comput. Geotech. 2019, 109, 108–116. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, G.; Liu, Z.; Zhou, H.; Ding, M.; Guo, Z. Theoretical Analysis of the Active Earth Pressure on Inclined Retaining Walls. Buildings 2024, 14, 76. https://doi.org/10.3390/buildings14010076
Zheng G, Liu Z, Zhou H, Ding M, Guo Z. Theoretical Analysis of the Active Earth Pressure on Inclined Retaining Walls. Buildings. 2024; 14(1):76. https://doi.org/10.3390/buildings14010076
Chicago/Turabian StyleZheng, Gang, Zhaopeng Liu, Haizuo Zhou, Meiwen Ding, and Zhiyi Guo. 2024. "Theoretical Analysis of the Active Earth Pressure on Inclined Retaining Walls" Buildings 14, no. 1: 76. https://doi.org/10.3390/buildings14010076




