Abstract
To accurately predict the relative permittivity of cement-stabilized base materials, a study on the dielectric mixing model for cracked base materials was conducted. Based on the electromagnetic mixing theory of multiphase composites, a comprehensive dielectric mixing model of cement-stabilized base materials was derived. The volume ratios and relative permittivity values of the specimen constituents in different cracking states of the cement-stabilized base were determined using industrial CT and a Percometer relative permittivity meter, with comprehensive consideration given to the effects of different initial porosities and crack widths on the dielectric properties. Based on the volumetric and dielectric properties of the base material specimens in both intact and cracked states, as well as the error analysis between the predicted and measured values of the relative permittivity constant, the u-optimal solution of the dielectric mixing model for cement-stabilized base material was determined to be 1. Consequently, an optimization dielectric mixing model for semi-rigid base course materials in a cracked state was developed. The optimization model proposed is suitable for predicting the dielectric properties of cement-stabilized base material with crack widths generally greater than 3 mm during the service life of semi-rigid base course in engineering practice.
1. Introduction
As a crucial component of semi-rigid pavement, the mechanical properties and durability of cement-stabilized aggregate materials directly influence the service life and performance level of roads. In practical engineering projects, the semi-rigid base course, as a concealed structure, presents challenges in assessing the internal state of the material, crack development, and road performance. Dielectric properties, as an important characterization parameter of a material’s electromagnetic response, are widely utilized in nondestructive testing and materials analysis. Ground-penetrating radar (GPR), as a nondestructive testing technology, enables the rapid and accurate detection of internal cracks and damage in semi-rigid base course. However, the effectiveness of GPR detection heavily depends on the precise determination of the material’s relative permittivity, with its operation primarily based on the propagation speed and reflection characteristics of electromagnetic waves in materials with different dielectric properties [1,2,3]. Therefore, it is imperative to conduct in-depth research on the relative permittivity of semi-rigid base course materials in their cracked state to accurately predict the dielectric properties of the base course and effectively assess the physical condition of the material, thereby providing a critical basis for road health monitoring.
In recent years, research on the dielectric properties of materials has progressively advanced, with various studies providing detailed analyses of how material composition, environmental conditions, and physical states influence dielectric properties. Different types of pavement structural materials, such as asphalt concrete, cement concrete, cement-stabilized crushed stone base material, and subgrade soil particles, exhibit distinct dielectric properties. These differences allow for the differentiation and identification of boundary and internal defects within these structural layer materials by analyzing the intensity and temporal variations of the reflected signals from GPR [4,5,6]. The dielectric mixing model is an effective method for describing the dielectric properties of materials. It establishes a link between the overall dielectric properties of the pavement structural layer mix and the volume of each of its components, as well as other indicators, thereby enabling the interpretation and prediction of the dielectric properties of pavement structural layer materials under different environmental conditions [7,8,9]. In practice, the relative permittivity is influenced by various factors within the structural layer and changes accordingly [10]. For instance, an increase in the relative permittivity of the material may result from either an increase in the compaction index, a decrease in porosity, or an increase in water content. This demonstrates a clear correlation between the relative permittivity of the medium and these influencing factors.
In 1993, Subedi and Chatterjee [11] constructed a dielectric mixing model for asphalt-granule mixtures based on experimental data, which became known as the SC model. This model posits that the dielectric properties of a composite material depend not only on the intrinsic dielectric properties of its constituent components but also on the mutual polarization effects among those components. Al-Qadi et al. [12] applied the relationship between the dielectric properties of a composite medium and its component phases—using models such as the complex refractive index, Rayleigh, and Böttcher dielectric mixing models—directly to asphalt mixtures. They developed a theoretical model for density prediction and preliminarily validated the feasibility of the Rayleigh model for estimating the density of road mixtures. Loizos et al. [13] utilized a Percometer instrument on the surface of dense-graded and open-graded asphalt mixture Marshall specimens, measuring their relative permittivity constant. They established a linear regression relationship between the void ratio, strength modulus, and relative permittivity constant of the asphalt mixture. Ling Tianqing et al. [14] conducted a comparative analysis of various widely used dielectric mixing models, concluding that the ALL model and Rayleigh model exhibited better density prediction accuracy than the complex refractive index model. However, they also noted that as the void ratio of the asphalt mixture increased, the model’s density prediction error became larger. By assuming the asphalt mixture component particles to be spherical, they proposed an optimized dielectric mixing model that accounts for the polarization effects of adjacent particles, thereby improving the density prediction accuracy for asphalt mixtures with significant voids [15].
Although the aforementioned research has made significant progress, there remain considerable gaps in understanding the dielectric properties of damaged materials and in analyzing crack damage echoes. Firstly, current research primarily focuses on asphalt mixture materials, with relatively few studies addressing the dielectric properties of damaged cement-stabilized aggregates. As a result, a unified theoretical framework for these materials has yet to be established. Secondly, existing dielectric mixing models, such as the Böttcher [16] and Rayleigh models [17,18,19], typically assume that the internal structure of the material is homogeneous and that the component morphology is regular when analyzing mixed materials. These assumptions often overlook the influence of cracks, pores, and other complex factors, leading to simplified models that struggle to achieve the desired prediction accuracy in practical applications [20,21]. To enhance the predictive accuracy of the dielectric properties of cement-stabilized aggregate base materials in the presence of crack damage, it is essential to optimize traditional dielectric mixing models by fully considering the complexity of the material’s internal structure and the shape factor of its components.
Due to existing inaccurate estimations of the dielectric properties of base materials, this study aims to develop a dielectric mixing optimization model for cement-stabilized base materials based on electromagnetic mixing theory. The model incorporates component phase shape factors and optimizes the traditional Böttcher model for improved accuracy. The validity of the optimized model was verified using specimen data from the base material, obtained using an industrial CT scanner and a Percometer tester, and the impact of crack damage on the model’s prediction accuracy was further analyzed. The results indicate that the optimized model demonstrates a higher goodness-of-fit and lower error in predicting the dielectric properties of cement-stabilized base materials. This improvement in accuracy is particularly notable in cases of higher porosity or when crack damage is present.
2. Dielectric Mixing Modeling of Semi-Rigid Base Course Materials
2.1. Generalized Dielectric Mixing Model for Multiphase Hybrid Composites
In an isotropic, homogeneous, two-phase sparse mixed material, the effective permittivity of the overall material is assumed to be the permittivity of the background medium and the permittivity of a uniformly distributed spherical scatterer within the background medium, as illustrated in Figure 1.
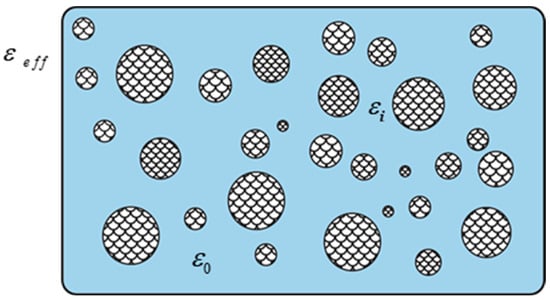
Figure 1.
Representation of an isotropic, homogeneous two-phase sparse mixed material [22].
According to electromagnetic mixing theory, the Maxwell–Garnett mixing rule [22], as expressed in Equation (1), is applicable to relatively sparse, homogeneous two-phase mixed materials containing spherical scatterers. In such materials, the spacing between neighboring scatterers is sufficiently large, so the perturbing electric fields generated by their dipole moments have a relatively minimal impact on one another.
where f is the volume rate of the scatterer to the hybrid material.
The generalization of the Maxwell–Garnett mixing rule for two-phase hybrid materials, Equation (1), to multiphase hybrid materials is given in Equation (2) below:
where N is the total number of component phases of the blend, and Vi and are the scatterer bulk rate and relative permittivity of component phase i of the blend, respectively.
For dense random mixtures, where scatterers are positioned closely together and the polarization influence of neighboring scatterers is significant, the previous approach is not applicable. To address this, the neighboring scatterer dipole moment interaction term [23,24] is introduced in Equation (2), with v representing the influence coefficient, leading to the formulation of Equation (3). When v = 0, the influence of neighboring scatterer dipole moments is neglected, which corresponds to the condition in sparse mixtures where the microturbulent electric field is assumed to be zero. In this case, Equation (3) reduces to the Maxwell–Garnett mixing rule or the Rayleigh mixing formula [25]. When v = 2, Equation (3) transforms into the Polder–van Santen or Böttcher mixing formula [26]. Based on the analysis outlined above, the unified mixing formula for spherical scatterer mixtures is inductively summarized in Equation (3).
Previous mixing formulas typically assume that the component phase scatterers of hybrid materials are spherical. However, in reality, the component phase scatterers often exhibit diverse geometries and variable polarization orientations. To account for these variations, the spherical coefficient of 2 in the unified mixing formula (Equation (3)) is replaced by the scatterer shape factor u. This modification leads to the derivation of a generalized dielectric mixing model (Equation (4)) for multiphase hybrid materials.
2.2. Dielectric Mixing Modeling of Semi-Rigid Base Materials
2.2.1. Semi-Rigid Base Course Material Intact
The intact cement-stabilized aggregate specimen consists of coarse aggregate minerals, cement paste (comprising fine aggregate and cement paste), and pore air, with the mass and volume of each component as shown in Figure 2 and Figure 3. The size of the cement-stabilized aggregate particles (nominal maximum particle size of 26.5 mm) is small compared to the wavelength of the decimeter-length electromagnetic waves typically emitted by ground-penetrating radar used on roads. Therefore, the scattering effect of the minerals in the cement-stabilized aggregates on the electromagnetic waves can be neglected. The material can be considered a relatively homogeneous medium, allowing the Maxwell–Garnett mixing rule (Equation (1)) to be applied to the cement-stabilized aggregates.

Figure 2.
Composition of cement-stabilized aggregate base material.
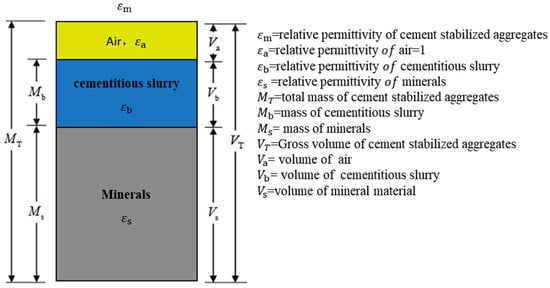
Figure 3.
Mass and volume composition of cement-stabilized aggregates.
In Figure 3, , , and represent the relative permittivity constants of the cement-stabilized aggregate mixture, cementitious slurry (comprising fine aggregate and cementitious slurry), coarse aggregate mineral, and pore air, respectively. MT, Mb, and Ms denote the total mass of the cement-stabilized aggregates, the mass of the cementitious slurry, and the mass of the coarse aggregate mineral, respectively. VT, Vb, Vs, and Va represent the total volume of the cement-stabilized aggregates, the volume of the cementitious slurry, the volume of the coarse aggregate mineral, and the pore volume, respectively.
Based on the generalized dielectric mixing model, the continuous phase of cementitious slurry is treated as the background medium, with the scatterers—coarse aggregate minerals and air in the pores—uniformly distributed within this medium. The theoretical model for the dielectric mixing of cement-stabilized crushed stone material is given by Equation (5).
The volume ratios, , , and , occupied by the cement-stabilized crushed stone material components pore air, coarse aggregate mineral, and cementitious slurry are given in the following Equations (6), (7) and (8), respectively.
The Rayleigh dielectric mixing model assumes that the scatterer is uniformly spherical (i.e., u = 2) and does not account for the effect of polarization of adjacent scatterers (i.e., v = 0). In contrast, the Böttcher dielectric mixing model also assumes that the scatterer is uniformly spherical (i.e., u = 2), but it does consider the effect of polarization of adjacent scatterers (i.e., v = 2). The relative permittivity of air is generally accepted to be 1, leading to the formulations of the Rayleigh and Böttcher dielectric mixing models for cement-stabilized crushed stone materials, as represented in Equations (9) and (10), respectively.
In practice, the components of cement-stabilized crushed stone mixtures (such as coarse aggregates, minerals, and pores) have complex and diverse shapes, with significant differences from spherical shapes. Therefore, it is necessary to optimize the component shape factor u and to account for the polarization effects of neighboring component scatterers (i.e., v = 2). This results in a comprehensive dielectric mixing model for cement-stabilized aggregates, as presented in Equation (11).
2.2.2. Semi-Rigid Base Course Material Cracking
When the intact cement-stabilized aggregates are damaged, as illustrated in Figure 4, cracks develop and become filled with air, leading to an increase in the volume of pore air within the components of the cement-stabilized base materials. The cracks in the cement-stabilized base specimens are assumed to be regular straight lines. This simplification facilitates the calculation of the pore volume created by the cracks, which is then added to the original pore volume of the specimen to determine the final porosity after cracking.

Figure 4.
Cracked Cement-Stabilized Gravel Base Material.
Consequently, the dielectric mixing model for the cement-stabilized aggregates, based on the state of crack damage, remains as described in Equation (11). However, the formulas for porosity and the volume fraction of coarse aggregates in this equation are modified, resulting in Equations (12) and (13), respectively.
where and are the porosity and coarse aggregate mineral volume rate of intact cement-stabilized crushed stone specimens, respectively; S and H are the horizontal cross-sectional area and height of intact cement-stabilized crushed stone specimens, respectively, so the total volume of intact specimens ; is the volume of cracked air occupied by the cracks, and l, w, and h are the length, width, and average depth of extension of the cracks, respectively, so .
In this experiment, various widths of regular cracks are prefabricated in the middle of cylindrical cement-stabilized gravel specimens, with the cracks extending throughout the entire specimen. The horizontal circular cross-sectional area of the intact specimen is given by , where r is the radius of the horizontal circular cross-section of the cylinder. The length of the prefabricated crack in the damaged specimen is l = 2r, and the extension depth of the crack is h = H. By substituting these relationships into Equations (12) and (13), the formulas for calculating porosity and the volume fraction of coarse aggregate in the cement-stabilized crushed stone, based on the damage state of the cracks, are presented in Equations (14) and (15), respectively.
2.3. Prediction of the Relative Permittivity Constant of the Semi-Rigid Base Course Material
The generalized dielectric mixing model for cement-stabilized aggregates is Equation (11), which can be converted into a one-dimensional cubic equation for the relative permittivity of the mix16, and the predicted value of the relative permittivity of the cement-stabilized aggregates mix is a real-number solution of the equation, with the coefficients a, b, c, and d in Equations (17)–(20), respectively.
To express the real solutions of a cubic equation in terms of a, b, c, and d, you can usually use Caldano’s formula.
First, the equation is normalized by eliminating the squared terms. Let , then, the equation becomes Equation (21):
After simplification, we obtain Equation (22):
where, , .
Second, the computational discriminant is expressed as Equation (23):
Then, this is solved for y:
If > 0, the equation has one real number solution and two conjugate complex number solutions. The real number solution is Equation (24):
If = 0, the equation has three real number solutions, at least two of which are equal. The real number solution is Equation (25):
If < 0, the equation has three distinct real solutions, and the three real solutions are expressed through trigonometric form as in Equation (26):
where , .
Finally, the solution is converted back to : using the solution of , is substituted to obtain the real number solution of .
3. Semi-Rigid Base Course Material Dielectric Mixing Model Design and Data Acquisition
The second section introduces the theoretical foundation of dielectric mixing models applied to semi-rigid base course materials. It establishes the principles behind the model, including the key factors influencing dielectric properties. The third section then builds upon this foundation by detailing the design of the specific dielectric mixing model for semi-rigid base materials, as well as the data acquisition process used to validate and optimize the model. Essentially, the second section provides the conceptual framework, while the third section focuses on the practical implementation, data collection, and refinement necessary for applying the model to real-world materials. Together, they form a cohesive structure, with theory leading into application.
3.1. Semi-Rigid Base Course Material Properties and Its Testing Equipment
3.1.1. Basic Properties of Semi-Rigid Base Course Materials and Their Raw Materials
Continuous grading mechanism granite aggregate is selected as the cement-stabilized gravel mix, the particle size range is 0~31.5 mm, and its performance characteristics are shown in Table 1. For the cement, Huizhou City, Guangdong Province, P.O 42.5 ordinary silicate cement is used, the main parameters and indexes of which are shown in Table 2; all meet the specifications and technical requirements.

Table 1.
Performance parameters of the chosen aggregates.

Table 2.
Performance parameters of the chosen cement.
According to the “Technical Guidelines for Construction of Highway Roadbases” [27], combined with the material parameters of cement-stabilized gravel semi-rigid base course in the actual project, different mineral gradation types of mixtures were test-mixed, and the skeleton dense mineral gradation curves were obtained, as illustrated Figure 5, alongside the specific mineral gradation upper and lower limits and synthetic gradation, as shown in Table 3. According to the “Test Methods of Materials Stabilized with Inorganic Binders for Highway Engineering” [28], a cylindrical cement-stabilized gravel base layer specimen with a diameter of 150 mm and a height of 150 mm is prepared by the static compression method, with the optimal moisture content of 5.1% and cement dose of 3%.
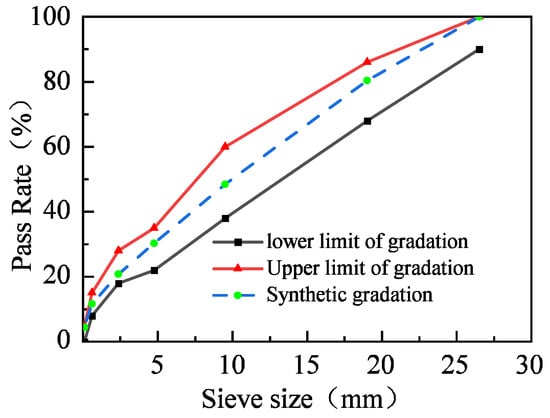
Figure 5.
Mineral synthetic grading curves for cement-stabilized crushed stone semi-rigid base course.

Table 3.
Upper and lower limits of mineral grades and synthetic grades.
3.1.2. Test Equipment for Base Materials
- (1)
- Dielectric Characterization Test Equipment
This test employs the Percometer relative permittivity tester to measure the dielectric properties of cement-stabilized aggregates and small-sized specimens. The instrument consists of a host unit connected to a sensor probe, as depicted in Figure 6. The probe features metal ring electrodes both inside and out, with the dielectric material between them forming a capacitor. The probe is placed in close contact with the surface of the medium, allowing the sensor to detect changes in capacitance between the electrodes, which are then converted into the material’s relative permittivity constant [29]. The Percometer probe (Beijing double Jet Technology Co., Ltd., Beijing, China) has an outer diameter of 6 cm and a relative permittivity range of 1 to 32 [30]. Prior to testing, the probe must be calibrated against air, ensuring that the host computer displays a relative permittivity value of 1 under normal measurement conditions. Proper alignment of the probe with the surface ensures that the internal and external ring electrodes make effective and complete contact with the material.
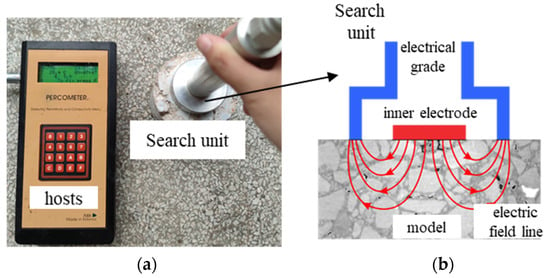
Figure 6.
(a) Percometer tester, (b) schematic diagram of probe detection principle [22].
The components of hardened cement-stabilized aggregates, including cement mortar, minerals, and void air, are all nonpolar materials and their relative permittivities exhibit minimal variation with frequency [31,32]. Therefore, the influence of the testing frequency of the equipment on the relative permittivities of cement-stabilized aggregates can be considered negligible.
where is the relative permittivity of the medium; Cm is the capacitance measured after the addition of the medium between the electrodes; and Ca is the capacitance between the electrodes in a vacuum when the capacitance is generally approximated as the capacitance of the air.
- (2)
- Computed Tomography Scanning Equipment
Computed tomography (CT) [33] is a nondestructive testing technique utilized to detect internal structures and defects in industrial products. Industrial CT scanning equipment is based on computed tomography technology, employing data acquisition, image reconstruction, and three-dimensional imaging to construct a 3D model of the inspected object. Its core components include an X-ray source, a detector, a rotary table, and a computer control system, as illustrated in Figure 7. After the X-rays penetrate the object, the detector converts the received signals into projection data. The computer then reconstructs tomographic images using techniques such as filtered back projection (FBP) or the algebraic reconstruction technique (ART), ultimately generating a 3D model that reveals the internal structure and defects. This process enables dimensional measurement, material analysis, and reverse engineering. Industrial CT offers advantages such as high resolution and nondestructive testing, significantly enhancing the accuracy and reliability of assessments.

Figure 7.
Industrial CT equipment scanning semi-rigid base course material.
3.2. Test Program and Measured Data
First, the Percometer instrument was employed to quickly and directly measure the relative permittivity of the unbroken ore sourced from the mineral deposits and the cement paste specimens after 28 days of curing, as illustrated in Figure 8. This approach effectively mitigates the empirical and random variability associated with the relative permittivity values of the coarse aggregate ore and the cement paste components of the cement-stabilized crushed stone material.

Figure 8.
Uncrushed raw rock dielectric properties test of the ore used in the basement.
Second, each group of specimens was subjected to different vibratory compaction energies to form cylindrical specimens with a diameter of 150 mm. A total of six different porosities were tested, with three parallel specimens created for each dry density, resulting in eighteen cement-stabilized gravel specimens.
Next, the specimens were trimmed to ensure smooth and flat surfaces on both the top and bottom, ensuring that the test surfaces were in close contact with the Percometer probe. This preparation effectively reduced the influence of surface roughness on the measurements. Subsequently, each cement-stabilized gravel specimen was examined using an industrial CT system, as shown in Figure 7. The number of pixels occupied by each component area in the CT images was segmented to calculate the volume fraction of each component.
After this, the specimens were bisected along the diameter using a cutting machine, and the spacing between the two halves was measured with a straight ruler, which was assumed to represent the width of the cracks. Finally, the Percometer was utilized to measure the top surfaces of both intact and precast specimens with varying crack widths. The average relative permittivity values were obtained by measuring at five different locations on the top and bottom surfaces of the intact and cracked cement-stabilized aggregate specimens, as depicted in Figure 9.

Figure 9.
Measured dielectric properties of intact and damaged cement-stabilized aggregates specimens. (a) intact specimens (b) Cracked specimen.
CT image segmentation of cement-stabilized crushed stone specimens involves several complex image processing steps, including preprocessing, segmentation, classification, and volumetric rate calculation, as shown in Figure 10 and Figure 11. Each step is described in detail below:
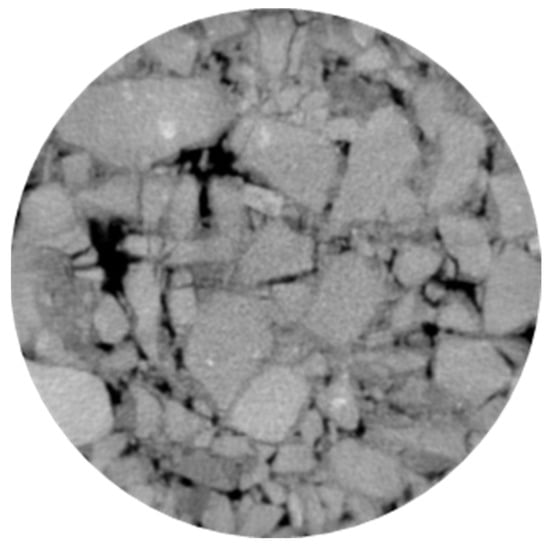
Figure 10.
CT diagram of cement-stabilized gravel specimens.

Figure 11.
Component segmentation diagrams of cement-stabilized crushed stone specimen CT images. (a) Mineral (grayish white). (b) Cementitious slurry (blue). (c) Gaps (yellow). (d) Mixing of components.
- (1)
- The purpose of CT image preprocessing of cement-stabilized gravel specimens is to reduce image noise, enhance contrast, and improve image quality for subsequent segmentation and analysis. It consists of the following steps. Gray scale transformation: convert the CT image to a gray-scale image to reduce the computational complexity and simplify the subsequent processing steps. Denoising: use filters (e.g., Gaussian filter, median filter) to remove noise from the image and improve the smoothness of the image to reduce the interference of subsequent segmentation algorithms. Contrast enhancement: enhance the contrast of the image through histogram equalization and other techniques, so that the gray-scale value distribution of different components is more uniform, so that the boundaries of different components are clearer, which is conducive to the subsequent threshold segmentation.
- (2)
- CT image segmentation of cement-stabilized crushed stone specimens aims to divide the image into three parts, namely, coarse aggregate, cement mortar, and pore air, and the commonly used methods include threshold segmentation and region growing. Threshold segmentation is based on image gray-scale values, and the Otsu method automatically determines the optimal threshold by maximizing the interclass variance, which is suitable for images with obvious contrast between foreground and background. Conversely, region growing is based on pixel similarity, extends from seed points, and is suitable for images with complex backgrounds. The two methods can be used in combination to improve segmentation accuracy and provide a basis for subsequent analysis.
- (3)
- Classification and labeling of segmented image regions to identify the different components of coarse aggregate mineral, cement paste, and pore air. Region labeling is applied to label the segmented regions to ensure that each region is uniquely identified, marking out the different connected regions. Based on the characteristics of the segmented regions (e.g., gray-scale value, shape, etc.), the regions are categorized into coarse aggregate mineral, cementitious slurry, and pore air.
- (4)
- The volume proportions of each component in the material are calculated by first traversing each CT image of the specimen to count the number of pixels corresponding to each region, namely, the cementitious paste, coarse aggregate, and pore air. Based on the total pixel count, the volume proportion of each component is then determined, representing the fraction of the total volume occupied by each material. This method allows for a detailed analysis of the compositional structure and proportions of the material.
The initial volume rate of each component of the intact cement-stabilized gravel specimen is measured according to the above experimental steps, i.e., the volume rate of coarse aggregate mineral material , Cementitious slurry volume rate , and porosity . Similarly, based on Equations (14) and (15), the different crack widths w (taken as 0, 1, 2, 3, 4, 5, and 7 mm, respectively), and radius of the specimen r = 75 mm, the volume rate of coarse aggregate mineral for cement-stabilized crushed stone specimens in the crack-damaged condition is calculated , alongside the cementitious slurry volume rate and the porosity . Meanwhile, the relative permittivity constants of coarse aggregate mineral, cement paste, and pore air of cement-stabilized crushed stone specimens are taken as = 8.63, = 5.21, and = 1, respectively. The measured relative permittivity constants of cement-stabilized crushed stone specimens in different states can be seen in Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9.

Table 4.
Volumetric and dielectric properties parameter values for cement-stabilized aggregate specimen group 1 (initial porosity 2.11%).

Table 5.
Volumetric and dielectric properties parameter values for cement-stabilized gravel specimen group 2 (initial porosity 3.63%).

Table 6.
Volumetric and dielectric property parameter values for cement-stabilized gravel specimen group 3 (initial porosity 5.42%) (initial porosity 5.42%).

Table 7.
Volumetric and dielectric properties parameter values for cement-stabilized gravel specimen group 4 (initial porosity 7.04%).

Table 8.
Volumetric and dielectric properties parameter values for cement-stabilized aggregate specimen group 5 (initial porosity 8.76%).

Table 9.
Volumetric and dielectric properties parameter values for cement-stabilized aggregate specimen group 6 (initial porosity 9.88%).
Figure 12 and Figure 13 illustrate the measured relative permittivity constants of cement-stabilized aggregate specimens in relation to crack width and porosity, respectively. The porosity of the intact specimens increases sequentially from group 1 to group 6, with the porosity of intact specimen group 1, the minimum at 2.11%, and intact specimen group 6, the maximum at 9.88%. Conversely, the measured relative permittivity of the corresponding specimens follows an opposite trend; the relative permittivity of intact specimen group 1 is 7.26 (the maximum), while that of intact specimen group 6 is 6.21 (the minimum). This inverse relationship arises because a larger porosity results in a greater volume fraction of pore air, which has a relative permittivity approximately equal to 1, lower than that of the other components. Consequently, as the volume of pore air increases, the overall relative permittivity of the specimens decreases. Additionally, the relative permittivity of the cement-stabilized gravel specimens decreases as the crack width increases. This is because a larger crack width results in a greater volume of air within the specimen, which in turn leads to a reduction in the measured relative permittivity of the specimens.
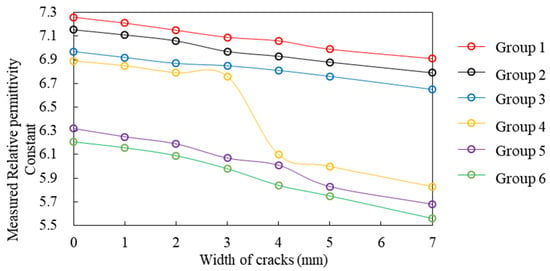
Figure 12.
Relative permittivity constant versus crack width for cement-stabilized aggregates specimens.
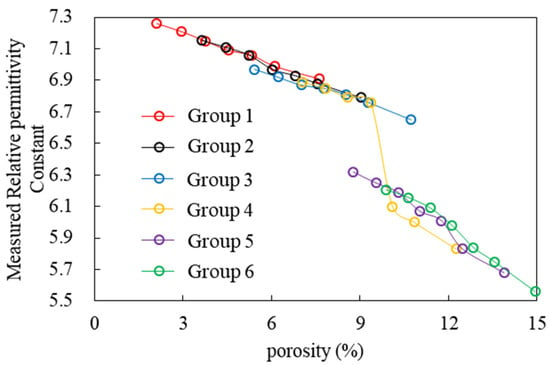
Figure 13.
Relative permittivity constant versus porosity for cement-stabilized specimens.
When the crack width of the cement-stabilized gravel specimens in groups 1 to 6 increases from 0 mm to 7 mm, the measured relative permittivity consistently decreases. For instance, in specimen group 1, the porosity increases from 2.11% to 7.60%, and the measured relative permittivity decreases from 7.26 to 6.91—a reduction of 0.35, corresponding to a relative deviation of 4.82%. This reduction is attributed to the fact that the relative permittivity of air in the cracks is significantly lower than that of solid materials such as cement and aggregate. As the cracks widen, the air content within the specimens increases, resulting in a decrease in the overall relative permittivity constant.
In comparison to specimen groups 1, 2, and 3, the initial void ratios of specimen groups 4, 5, and 6 are larger, with values not less than 7%. When the crack width of specimen groups 4, 5, and 6 increases from 0 to 7 mm, their relative permittivity values experience substantial decreases, of at least 0.64. Notably, when the crack width of specimen group 4 increases from 3 mm to 4 mm, its relative permittivity decreases from 6.76 to 6.10, representing a reduction of 0.56. The increase in both crack width and porosity significantly enhances the non-uniformity of the material components in the specimen groups with larger initial porosity [34], resulting in more pronounced changes in their dielectric properties. These findings indicate that crack damage has a significant effect on the dielectric properties of cement-stabilized crushed stone materials, and the relative permittivity constant of these materials in a cracked state should be appropriately corrected.
4. Optimization and Comparison of Dielectric Mixing Model Parameters for Base Materials
The third section focuses on the design of the dielectric mixing model and the data acquisition process used to gather relevant material properties for semi-rigid base course materials. Building on this foundation, the fourth section focuses on optimizing the model parameters, such as the influence coefficient and shape factor, to improve prediction accuracy. It also compares the performance of the optimized model with traditional models. Together, these sections progress from model development to its optimization and validation, ensuring its applicability and accuracy in real-world scenarios.
4.1. Optimization of Dielectric Mixing Model Parameters
The shape factor of the mix components primarily reflects the influence of the geometry and arrangement of different components (e.g., cement, aggregate, air, etc.) on the relative permittivity. In mixtures of cement compounds and air pores, variations in the shape factor can significantly affect the overall relative permittivity of the mixture [35].
To better determine the shape factor u of the component phase scatterers applicable to cement-stabilized crushed stone mixtures, the general dielectric mixing model of cement-stabilized crushed stone mixtures, as described in Equation (11), was used alongside its real solutions, Equations (24)–(26). Different values of the shape factor were evaluated at intervals of 0.1. Subsequently, based on the 42 sets of data presented in Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9, the relative permittivity of intact specimens and those with varying crack widths was computed. The relative error (RE) between the predicted and measured values was then calculated, leading to the determination of the average relative error (MRE) of the relative permittivity for the 42 sets of cement-stabilized rubble specimens in relation to the shape factor u. The objective function used in this optimization process was the average relative error between the predicted and measured dielectric values. The optimal shape factor corresponds to the minimum average relative error.
As Figure 14 shows, the average relative error of the relative permittivity of the cement-stabilized aggregates significantly decreases with an increasing shape factor, reaching a minimum value before gradually increasing again. When the shape factor u = 1, the average relative error of the relative permittivity of the cement-stabilized aggregates is minimized at 3.47%. By substituting the shape factor u = 1 into Equation (11), the optimized dielectric mixing model for the cement-stabilized crushed stone mixture can be obtained, as shown in Equation (28).
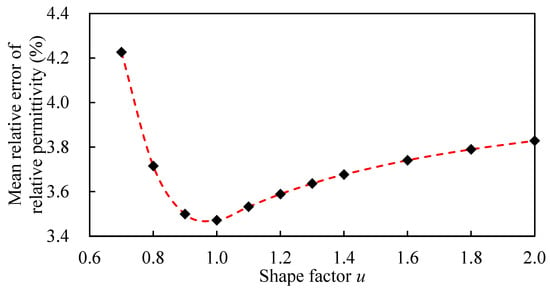
Figure 14.
Relationship between the shape factor of the base material and the average relative error sum of its relative permittivity constant prediction.
The residuals are used to characterize the deviation between the model-predicted values and the measured values [36]. The distribution of the residuals between the measured relative permittivity values of 42 groups of cement-stabilized gravel specimens and the predicted values from the optimized model is shown in Figure 15. Overall, within the same group of specimens, a larger measured relative permittivity corresponds to a smaller absolute value of the residuals. Specifically, the absolute values of the residuals for specimens with measured relative permittivity values less than 6.5 are significantly smaller than those for specimens with values greater than 6.5. The mean absolute values of the residuals for specimen groups 1 to 6 are 0.295, 0.339, 0.372, 0.289, 0.060, and 0.053, respectively, with an overall average absolute value of the residuals for the specimen groups being 0.235. These results indicate that the optimized shape factor of the dielectric mixing model can more accurately predict the relative permittivity constant of cement-stabilized aggregates in the cracked state, better reflecting the internal structural state of the base material.
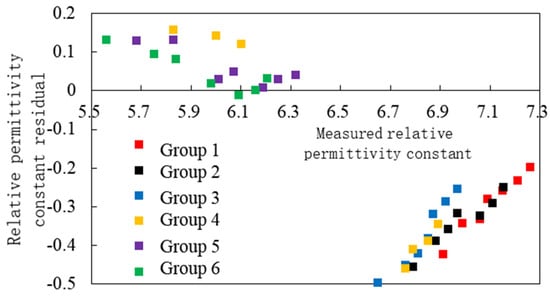
Figure 15.
Residual distribution of relative permittivity for specimens predicted by the optimized model.
The relationship between the relative errors in the predicted relative permittivities of the specimens and their porosities in the dielectric mixing optimization model for cement-stabilized aggregates is illustrated in Figure 16. Overall, smaller measured porosities within the same specimen group correspond to smaller relative errors in the predicted relative permittivities. Notably, the relative errors in the predicted relative permittivities for specimen groups 5 and 6, which have larger porosities, are significantly smaller than those of the other specimen groups. The average relative errors of the predicted relative permittivities for specimen groups 1 to 6 are 4.17%, 4.88%, 5.47%, 4.37%, 1.02%, and 0.93%, respectively, with the maximum value not exceeding 5.5%. The average relative error of the predicted relative permittivities across all specimen groups is 3.47%, remaining below 3.5%.
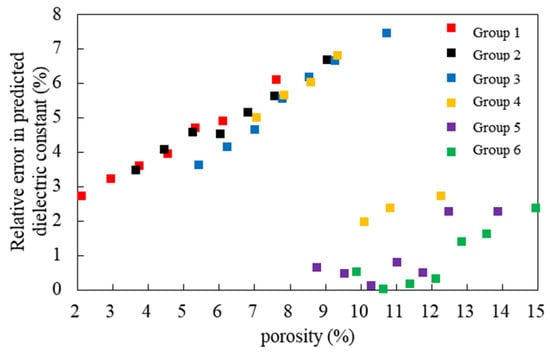
Figure 16.
Relative error of relative permittivity of specimens predicted by the optimized model as a function of their porosity.
To validate the dielectric mixing optimization model for cement-stabilized aggregates, the Shapiro–Wilk normality test was conducted on a sample of the residuals from the predicted relative permittivity constants of each specimen [35]. The Shapiro–Wilk normality test is a statistical method used to assess whether a dataset conforms to a normal distribution. Proposed by Samuel Shapiro and Martin Wilk in 1965, it is widely employed in statistical analysis. The fundamental principle of the Shapiro–Wilk test is to determine whether a sample originates from a normal distribution by calculating a statistic for the sample and then comparing that statistic to the theoretical value of the normal distribution.
The test statistic is typically denoted as W, with its calculation expressed in Equation (29). The null hypothesis H0 posits that the overall residuals of the relative permittivity predicted by the dielectric mixing optimization model for cement-stabilized crushed stone materials follow a normal distribution. With a significance level set at = 0.05, the -quantile of the statistic W is . The calculated value of the statistic , thus, the null hypothesis was not rejected, as shown in Table 10. In summary, the residuals of the relative permittivity constants predicted by the optimization model for the dielectric mixing of cement-stabilized crushed stone materials generally conform to a normal distribution. This finding indicates that the optimization model exhibits high reliability.
where is the i-th sample observation after the n sample observations are sorted in ascending order, is the sample mean, [n/2] is the integer part of n/2, and is the test coefficient.

Table 10.
Shapiro–Wilk normality test for residuals of predicted relative permittivity of cement-stabilized gravel specimens.
4.2. Comparative Analysis of Dielectric Mixing Models for Base Materials
The Rayleigh dielectric mixing model and the Böttcher dielectric mixing model are both widely applicable and offer distinct advantages; the former is particularly suitable for inhomogeneous and dispersed materials, while the latter is designed for homogeneous materials and is straightforward to compute. By comparing these two models, it is possible to analyze the dielectric properties under varying media conditions, as well as to evaluate computational complexity and prediction accuracy, thereby allowing for the selection of an appropriate model for studying base material systems.
To demonstrate the superiority of the optimized model for the dielectric mixing of cement-stabilized aggregates, the prediction accuracies of the optimized model, Böttcher’s model, and Rayleigh’s model for the dielectric properties of cement-stabilized aggregate specimens are comprehensively compared. The parameter values, including volume and dielectric properties of the cement-stabilized aggregate specimens and their components, as presented in Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9, are substituted into the optimized dielectric mixing model (Equation (28)), Böttcher’s dielectric mixing model (Equation (10)), and Rayleigh’s dielectric mixing model (Equation (9)). The predicted values of the relative permittivity constants from the corresponding models for different cement-stabilized aggregate specimens are calculated, and the comparative results are displayed in Figure 17.
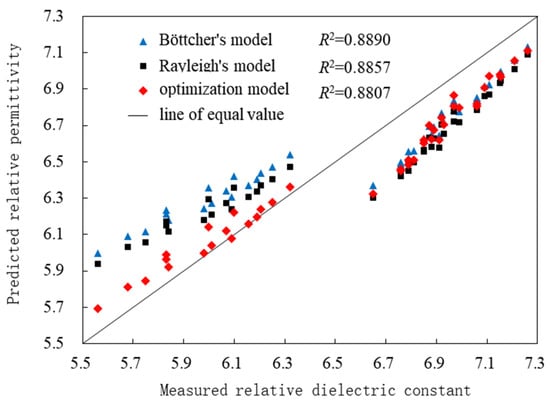
Figure 17.
Measured relative permittivity of the base material versus the relative permittivity predicted by different models.
As Figure 17 shows, the data points from all three models fall near the contour line, indicating a high accuracy in predictions for each model. For specimens with large relative permittivity constants (>6.5), the predicted values are consistently lower than the measured values. Among the models, Böttcher’s model exhibits the closest alignment with the contour line, with a mean absolute error (MAE) of 0.206 and a mean relative error (MRE) of 2.98%. The Rayleigh model follows, with MAE and MRE values of 0.268 and 3.87%, respectively, while the optimized model shows MAE and MRE values of 0.346 and 5.00%, respectively. Conversely, for specimens with small relative permittivity constants (<6.5), the overall predicted values are generally higher than the measured values. Notably, the predicted values from the optimized model are significantly closer to the contour line, yielding MAE and MRE values of 0.072 and 1.22%, respectively. The Rayleigh model ranks next, with MAE and MRE values of 0.238 and 4.01%, followed by Böttcher’s model, which has MAE and MRE values of 0.301 and 5.08%. The goodness of fit R2 values for the optimization model, Böttcher’s model, and Rayleigh’s model, based on the predicted and measured values of the relative permittivity of the cement-stabilized aggregate specimens, are 0.8890, 0.8857, and 0.8807, respectively. The corresponding MAE values are 0.235, 0.245, and 0.255, while the MRE values are 3.47%, 3.83%, and 3.93%, respectively. The optimized model demonstrates the highest goodness of fit and the smallest mean absolute error and mean relative error compared to the Böttcher and Rayleigh models, especially for the relative permittivity of the stabilized base material less than 6.5, indicating that the predicted values of the dielectric properties from the optimized model align more closely with the measured values.
The relationship between the average relative errors of the relative permittivity constants of cement-stabilized aggregates and the crack widths for different models is presented in Table 11 and Figure 18. As the crack width of the specimens increases, the average relative errors in the predicted dielectric properties of cement-stabilized base specimens from the different models exhibit a general upward trend. Notably, the optimized model shows an inflection point at a crack width of 4 mm; beyond this point, the accuracy of the dielectric property measurements decreases due to the impact of cracks on the uniformity of the specimen components. The presence of cracks affects the consistency of each component within the entire specimen, leading to a reduction in the measurement accuracy of the dielectric properties and an increase in the model’s prediction errors. For intact specimens (with a crack width of 0 mm), the accuracy of the predicted dielectric properties is high, with average relative errors of 2.67%, 2.64%, and 2.82% for the optimization model, Böttcher’s model, and Rayleigh’s model, respectively, all remaining below 3%. When the crack width exceeds 7 mm, the average relative errors for the predictions from the optimization model, Böttcher’s model, and Rayleigh’s model increase to 4.60%, 5.67%, and 5.63%, respectively. The average relative errors of the models for predicting the dielectric properties of specimens with relatively narrow crack widths (≤3 mm) are similar across the models. However, the optimization model demonstrates a significant improvement in prediction accuracy for specimens with wider crack widths (≥4 mm). These results show that caution should be exercised when applying the optimization model to predict cement-stabilized base dielectric properties for crack widths exceeding 7 mm.

Table 11.
Relationship between the average relative errors of different dielectric mixing model predictions and specimen crack widths.
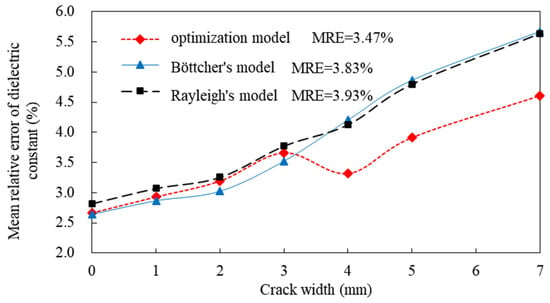
Figure 18.
Mean relative error of relative permittivity constant prediction for base specimens with different width cracks.
In summary, the dielectric mixing model with the optimized shape factor demonstrates superior performance compared to the Böttcher and Rayleigh dielectric mixing models. When the relative permittivity of the cement-stabilized base specimen exceeds 6.5 or the crack width is less than 4 mm [37], the predictive accuracy of the optimized model is comparable to that of the Böttcher and Rayleigh models. In such cases, either model can be utilized to estimate the dielectric properties of the cement-stabilized base. However, in other scenarios, the predictive error of the optimized model is significantly lower than that of the Böttcher and Rayleigh models. Therefore, the optimized model is recommended for estimating the dielectric properties of the cement-stabilized base in these instances.
5. Conclusions
A general dielectric mixing model for multiphase mixed materials is derived based on electromagnetic mixing theory. The volume and dielectric property parameters of the cement-stabilized base material specimens are obtained using an industrial CT scanner and a Percometer tester. The crack damage state of the cement-stabilized base material is considered, and the phase shape factors of the cement-stabilized base material components are optimized, leading to the establishment of an optimized dielectric mixing model for cement-stabilized crushed stone base material. The main conclusions are as follows:
- (1)
- To account for the complexity of the morphology of the mixed material components, the shape factor u of the component phases is introduced into the Böttcher dielectric mixing model of traditional multiphase composites. Based on the volume and dielectric properties of the base material specimens in both intact and cracked states, the optimal value of u in the dielectric mixing model for cement-stabilized gravel base material is determined to be 1. Consequently, the dielectric mixing optimization model for cement-stabilized gravel base material is constructed to be applicable to the cracked state of semi-rigid base course material.
- (2)
- Compared to the Böttcher and Rayleigh dielectric mixing models, the optimization model for cement-stabilized aggregate base material exhibits the smallest goodness-of-fit, average absolute error, and average relative error, with values of 0.8890, 0.235, and 3.47%, respectively. This indicates that the optimization model is more suitable for predicting the dielectric properties of cement-stabilized aggregate base material.
- (3)
- The optimization model for the dielectric mixing of cement-stabilized aggregates significantly enhances the accuracy of predicting the dielectric properties of base materials with high porosity, achieving an average absolute error and average relative error of only 0.072 and 1.22%, respectively. Additionally, the prediction accuracy of the optimization model is influenced by the crack damage state of the base material; as the crack width increases, the average relative error of the optimization model in predicting the dielectric properties of the base material also increases.
In future research, we plan to expand the optimization model by including the effects of temperature, moisture, various types of aggregates, and a broader range of porosity and crack width specimens. This will enhance the robustness and applicability of our model, allowing for a more comprehensive understanding of the dielectric properties of cement-stabilized base materials in practical scenarios. The research approach of the optimization dielectric mixing model for cement-stabilized base materials can be extended to other pavement structural layers, such as asphalt mixtures or subgrade soils, offering significant and wide-ranging application value. For engineers and researchers working in this area, we emphasize the critical importance of accurately obtaining the volume and dielectric parameters of each component in the cement-stabilized base materials. These parameters directly impact the predictive accuracy of the dielectric mixing model.
Author Contributions
Conceptualization, Z.H. and G.X.; methodology, Z.H., H.Y. and X.X.; software, H.Y. and B.Z.; writing—original draft preparation, Z.H. and G.X.; writing—review and editing, X.X., H.Y. and B.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The financial support from the Guangdong Basic and Applied Basic Research Foundation (2022A1515011607, 2022A1515011537, and 20231515030287) and the Fundamental Research Funds for the Central Universities (2022ZYGXZR056) are sincerely acknowledged.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
Thanks to all those who contributed to the articles.
Conflicts of Interest
Author Bo Zang was employed by the company Xiaoning Institute of Roadway Engineering. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- AL-Qadi, I.L.; Lahouar, S. Measuring layer thicknesses with GPR–Theory to practice. Constr. Build. Mater. 2005, 19, 763–772. [Google Scholar] [CrossRef]
- Fan, B.H.; Bosc, F.; Liu, Y.; Fauchard, C. Dielectric measurement by open-endedcoaxial line for hot-mix asphalt roads: From laboratory test to on-site investigation. NDT E Int. 2023, 138, 102872. [Google Scholar] [CrossRef]
- Wang, S.Q.; Sui, X.; Leng, Z.; Jiang, J.W.; Lu, G.Y. Asphalt pavement density measurement using non-destructive testing methods: Current practices, challenges, and future vision. Constr. Build. Mater. 2022, 344, 128154. [Google Scholar] [CrossRef]
- Xiong, X.; Meng, A.; Lu, J.; Tan, Y.; Chen, B.; Tang, J.; Zhang, C.; Xiao, S.; Hu, J. Automatic detection and location of pavement internal distresses from ground penetrating radar images based on deep learning. Constr. Build. Mater. 2024, 411, 134483. [Google Scholar] [CrossRef]
- Wang, S.Q.; Leng, Z.; Sui, X.; Zhang, W.G.; Ma, T.; Zhu, Z.H. Real-Time Asphalt Pavement Layer Thickness Prediction Using Ground-Penetrating Radar Based on a Modified Extended Common Mid-Point (XCMP) Approach. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6848–6860. [Google Scholar] [CrossRef]
- Xiong, X.; Tan, Y. Deep learning-based detection of tie bars in concrete pavement using ground penetrating radar. Int. J. Pavement Eng. 2023, 24, 2155648. [Google Scholar] [CrossRef]
- Chen, Y.F.; Li, F.; Zhou, S.Q.; Zhang, X. Improved density prediction model based on global optimization algorithm for GPR system. Measurement 2024, 237, 115243. [Google Scholar] [CrossRef]
- Ye, C.S. 3D Reconstruction and Digitalmodeling of Road Defect Based on 3D-Ground-Penetrating Radar; Harbin Institute of Technology: Haerbin, China, 2023. [Google Scholar]
- Oliveira, D.B.; Vieira, D.A.G.; Lisboa, A.C.; Goulart, F. A well posed inverse problem for automatic pavement parameter estimation based on GPR data. NDT E Int. 2014, 65, 22–27. [Google Scholar] [CrossRef]
- Hipp, J.E. Soil electromagnetic parameters as functions of frequency, soil density, and soil moisture. Proc. IEEE 1974, 62, 98–103. [Google Scholar] [CrossRef]
- Subedi, P.; Chatterjee, I. Dielectric Mixture Model for Asphalt-Aggregate Mixitures. J. Microw. Power Electromagn. Energy 1993, 28, 68–72. [Google Scholar] [CrossRef]
- Al-Qadi, I.L.; Leng, Z.; Lahouar, S.; Baek, J. In-Place Hot-Mix Asphalt Density Estimation Using Ground-Penetrating Radar. Transp. Res. Rec. J. Transp. Res. Board 2010, 2152, 19–27. [Google Scholar] [CrossRef]
- Loizos, A.; Plati, C. Assessment of HMA Air-Voids and Stiffness Based on Material Dielectric Values. Road Mater. Pavement Des. 2011, 12, 217–226. [Google Scholar] [CrossRef]
- Ling, T.Q.; Cui, L.L.; Chen, Q.Q.; Mou, C.Y. Review of the research of using ground penetrating radar to measure compactnessand volume of air voids of asphalt mixture. Prog. Geophys. 2019, 34, 2467–2480. [Google Scholar]
- Cui, L.L.; Ling, T.Q.; Zhang, Z.Y.; Xin, J.Z.; Li, R.K. Development of asphalt mixture density estimation model applicable to wide air void content range using ground penetrating radar. Constr. Build. Mater. 2021, 293, 123521. [Google Scholar] [CrossRef]
- Shangguan, P.C.; Al-Qadi, I.L.; Lahouar, S. Pattern recognition algorithms for density estimation of asphalt pavement during compaction: A simulation study. J. Appl. Geophys. 2014, 107, 8–15. [Google Scholar] [CrossRef]
- Strutt, J.W. Scientific Papers: Volume 4: 1892–1901; Cambridge University Press: Cambridge, UK, 2009; pp. 19–38. [Google Scholar]
- Zhang, J.R.; Zhang, D.H.; Wang, L.W. Dielectric constant in microwave remote sensing. Remote Sens. Technol. Appl. 1994, 9, 30–43. [Google Scholar]
- Rafiqul, A.T.; Mesbah, U.A. Ground Penetrating Radar for Measuring Thickness of an Unbound Layer of a Pavement; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 160–167. [Google Scholar]
- Liang, X.M.; Yu, X.; Jin, Y.; Huang, J.D. Compactness prediction of asphalt concrete using Ground-Penetrating Radar: A comparative study. Constr. Build. Mater. 2022, 361, 129588. [Google Scholar] [CrossRef]
- Yu, X.H.; Luo, R.; Huang, T.T.; Shu, Y.; Ruan, L. Moisture Content Prediction Model of Asphalt Mixtures Based on Dielectric Properties. J. Mater. Civ. Eng. 2022, 34, 04022020. [Google Scholar] [CrossRef]
- Xiong, X.; Xiao, S.; Tan, Y.; Zhang, X.; Zhang, D.; Han, M.; Wang, W. Estimation of density and moisture content in asphalt mixture based on dielectric property. Constr. Build. Mater. 2021, 298, 123518. [Google Scholar] [CrossRef]
- Behari, J. Dielectric Behavior of Soil; Springer: New York, NY, USA, 2005. [Google Scholar]
- Shivola, A.H. Self-consistency aspects of dielectric mixing theories. IEEE Trans. Geosci. Remote Sens. 1989, 27, 403–415. [Google Scholar] [CrossRef]
- Wallén, H.; Kettunen, H.; Sihvola, A. Composite near-field superlens design using mixing formulas and simulations. Metamaterials 2009, 3, 129–139. [Google Scholar] [CrossRef]
- Sihvola, A.H.; Alanen, E. Studies of mixing formulae in the complex plane. IEEE Trans. Geosci. Remote Sens. 1991, 29, 679–687. [Google Scholar] [CrossRef]
- JTG/T F20-2015; Technical Guidelines for Construction of Highway Roadbases. Ministry of Transport of the People’s Republic of China: Beijing, China, 2015.
- JTG E51-2009; Test Methods of Materials Stabilized with Inorganic Binders for Highway Engineering. Ministry of Transport of the People’s Republic of China: Beijing, China, 2009.
- Loizos, A.; Plati, C. Field and laboratory test for assigning dielectric constants of asphalt pavement materials. Road Mater. Pavement Des. 2006, 7, 513–532. [Google Scholar] [CrossRef]
- Loizos, A.; Plati, C. Accuracy of pavement thicknesses estimation using different ground penetrating radar analysis approaches. NDT E Int. 2007, 40, 147–157. [Google Scholar] [CrossRef]
- Shang, J.; Umana, J. Dielectric constant and relaxation time of asphalt pavement materials. J. Infrastruct. Syst. 1999, 5, 135–142. [Google Scholar] [CrossRef]
- Yu, X.H. Research on Dielectric Constant of Asphalt Mixture; Wuhan University of Technology: Wuhan, China, 2018. [Google Scholar]
- Tan, Y.Q.; Xing, C.; Ren, J.D.; Zhang, L. Research on Mesostructured Characteristics of Asphalt MixtureBased on Particle Packing Theory. China J. Highw. Transp. 2017, 30, 1–8. [Google Scholar]
- Titi, H.H.; Faheem, A.; Tabatabai, H.; Tutumluer, E. Influence of aggregate base layer variability on pavement performance. Transp. Res. Rec. 2014, 2457, 58–71. [Google Scholar] [CrossRef]
- Xiong, X.T.; Tan, Y.Q.; Xiao, S.Q.; Meng, A.X.; Lv, H.J.; Zhang, C. Optimization Model of Asphalt Mixture Density PredictionBased on Dielectric Property. China J. Highw. Transp. 2022, 35, 180–188. [Google Scholar]
- Kannan, R.; Bayraksan, G.; Luedtke, J.R. Residuals-based distributionally robust optimization with covariate information. Math. Program. 2024, 207, 369–425. [Google Scholar] [CrossRef]
- Yang, Q.; Deng, Y. Evaluation of cracking in asphalt pavement with stabilized base course based on statistical pattern recognition. Int. J. Pavement Eng. 2019, 20, 417–424. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).