A Rapid Prediction of Suppressed Vibration in Composite Bridges Equipped with Constrained Layer Damping
Abstract
:1. Introduction
2. Equation of Motion Based on WFEM
2.1. Dispersion Characteristics
2.2. Solution to Eigenvalue Equation
2.3. Response of Waveguide Structure
3. Case Study
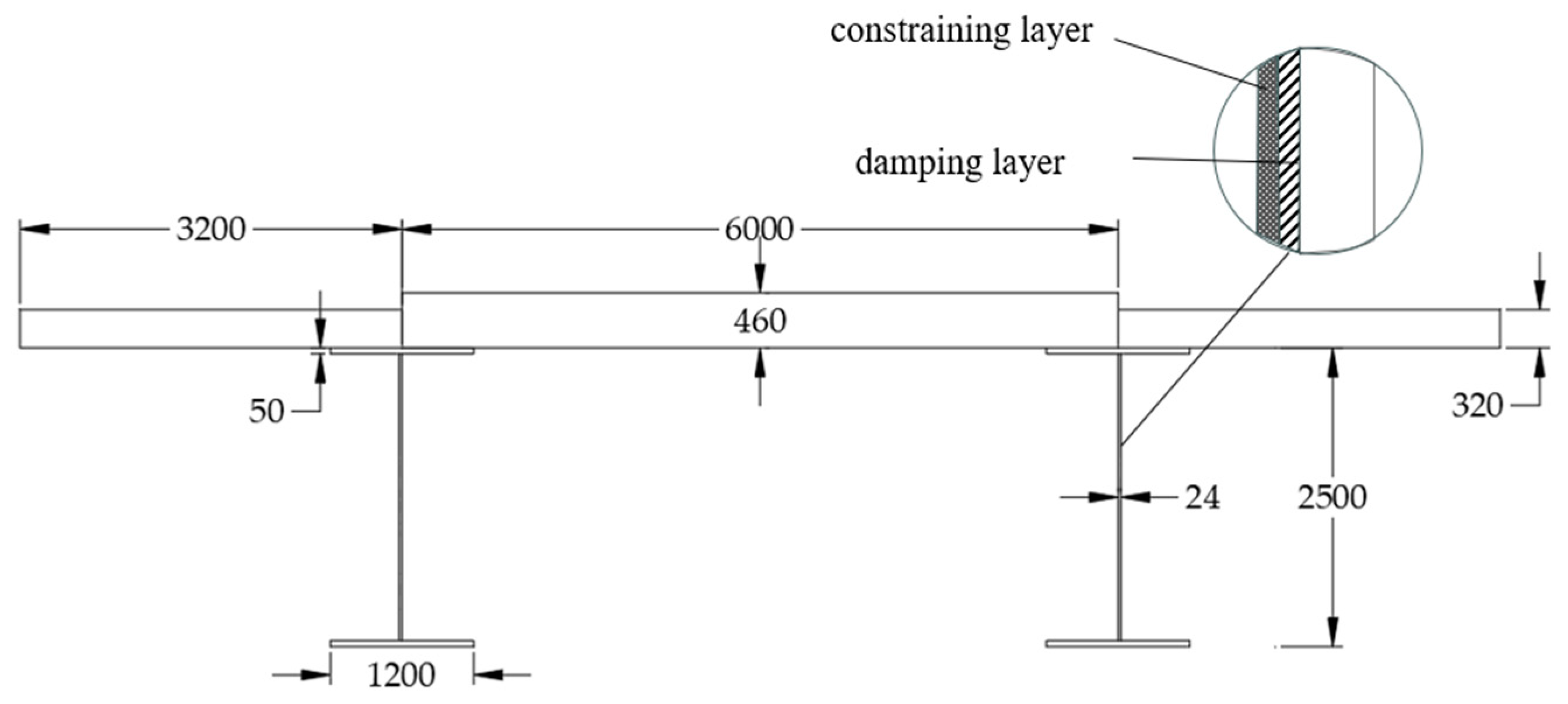
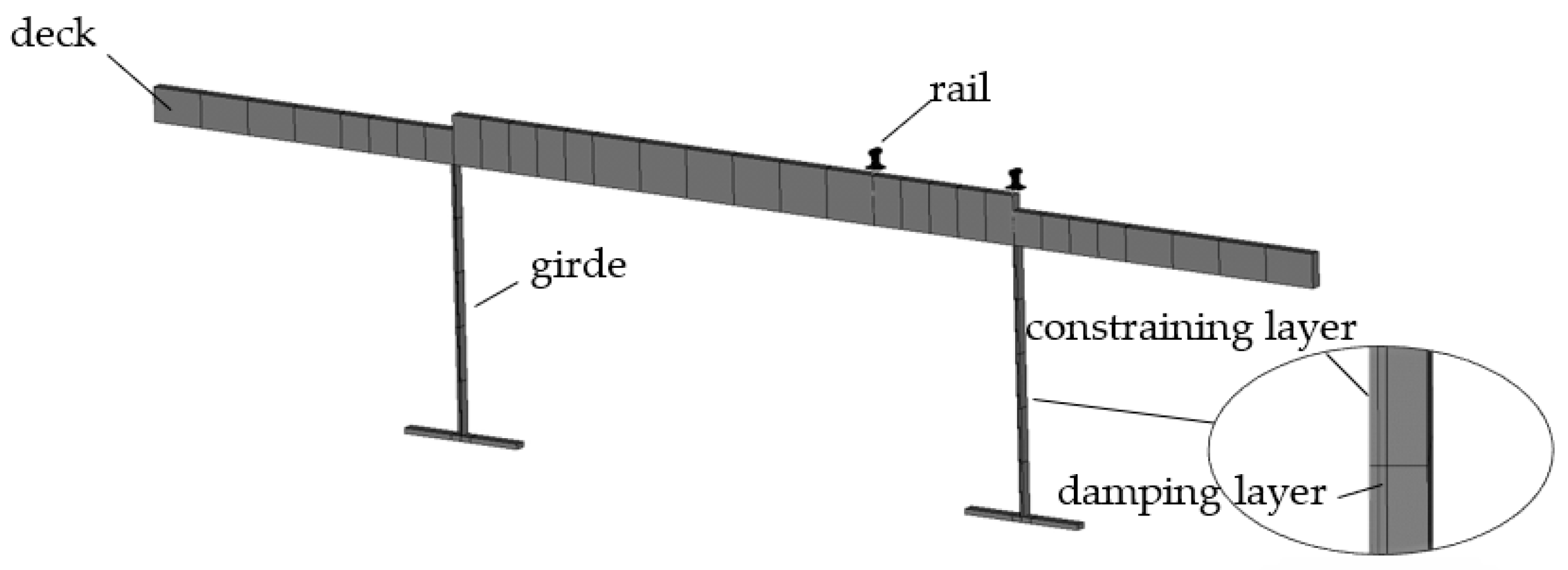
3.1. Model of Bridge
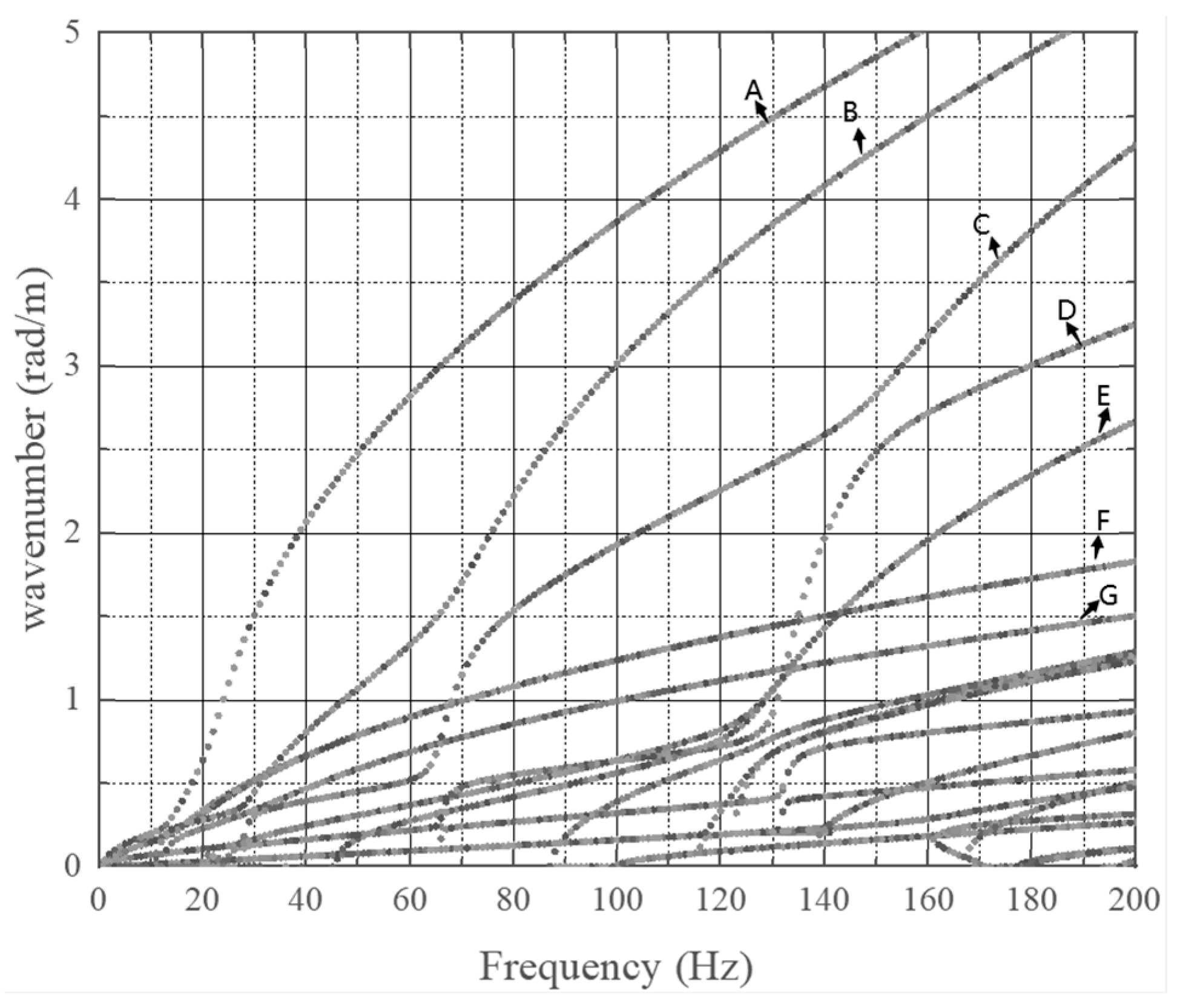
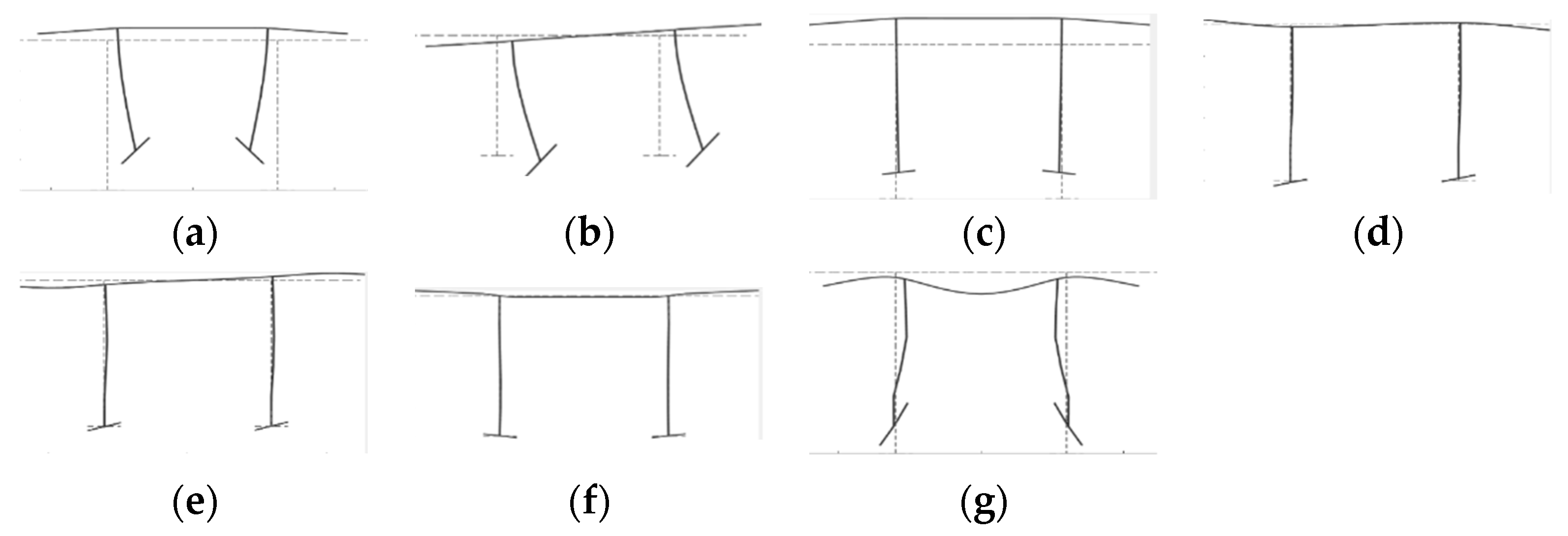
3.2. Dispersion Characteristics of Bridge
3.3. Model of Bridge with CLD
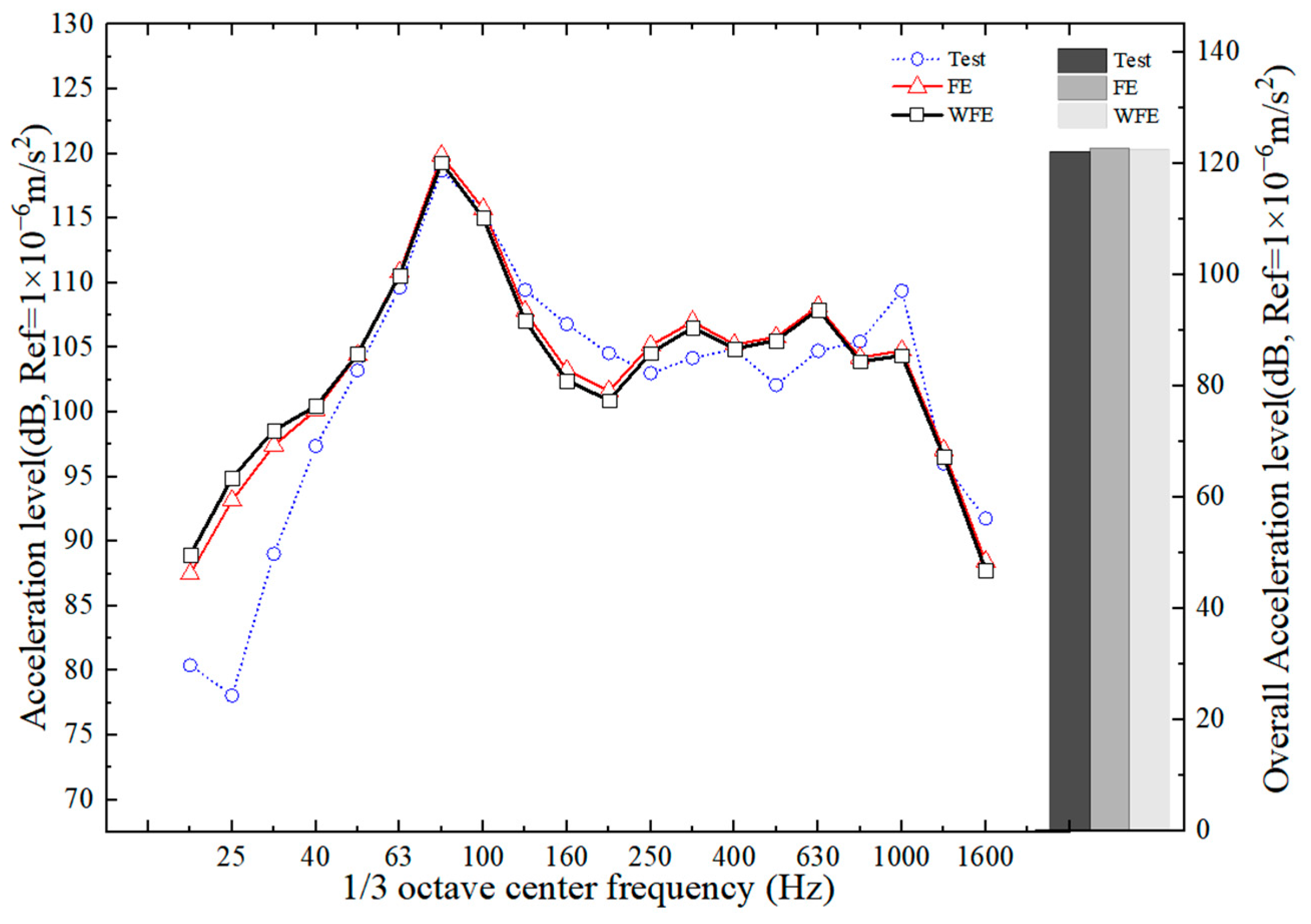
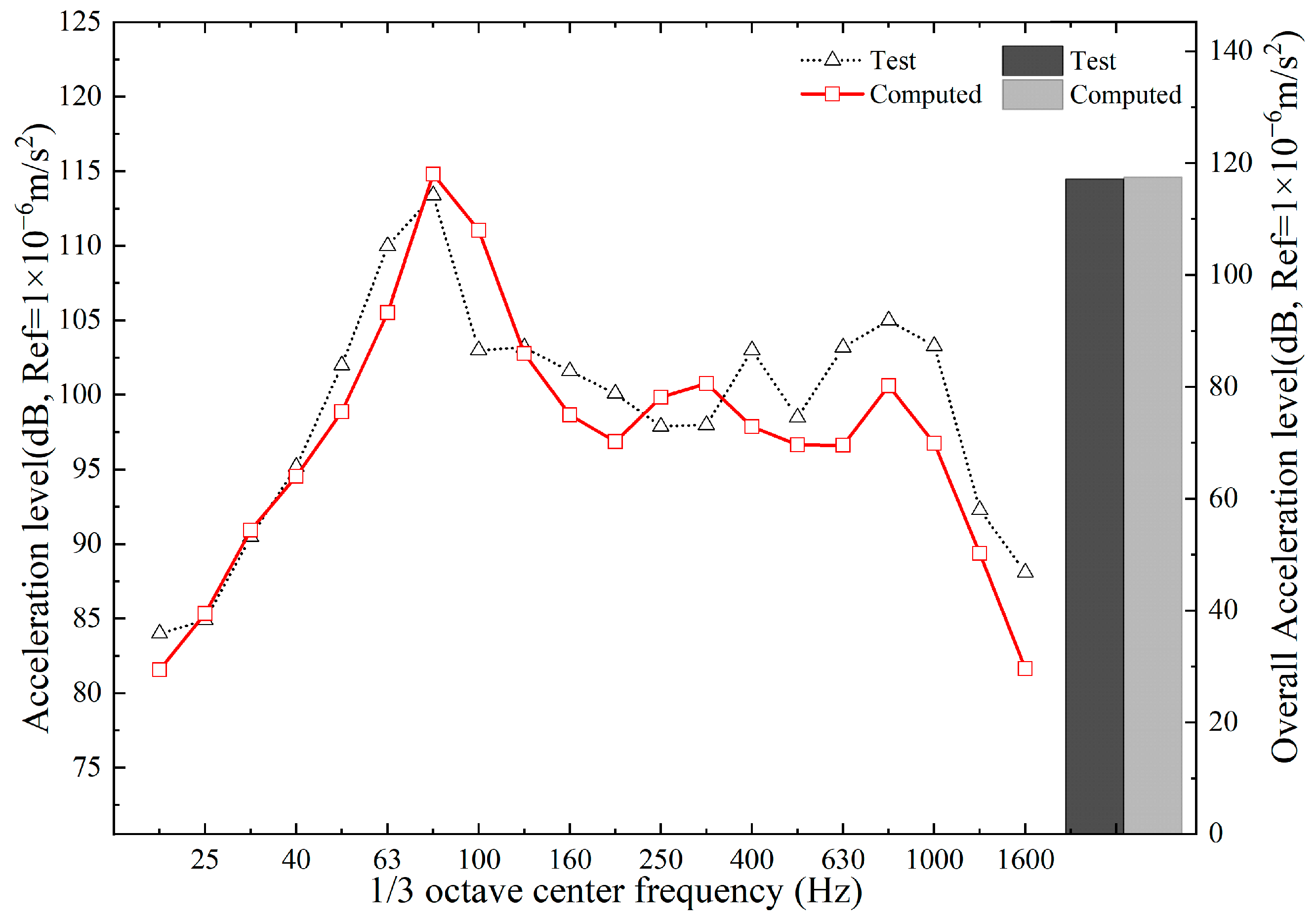
3.4. Model Validation
4. Parametric Study
4.1. Laying Area of CLD on Web
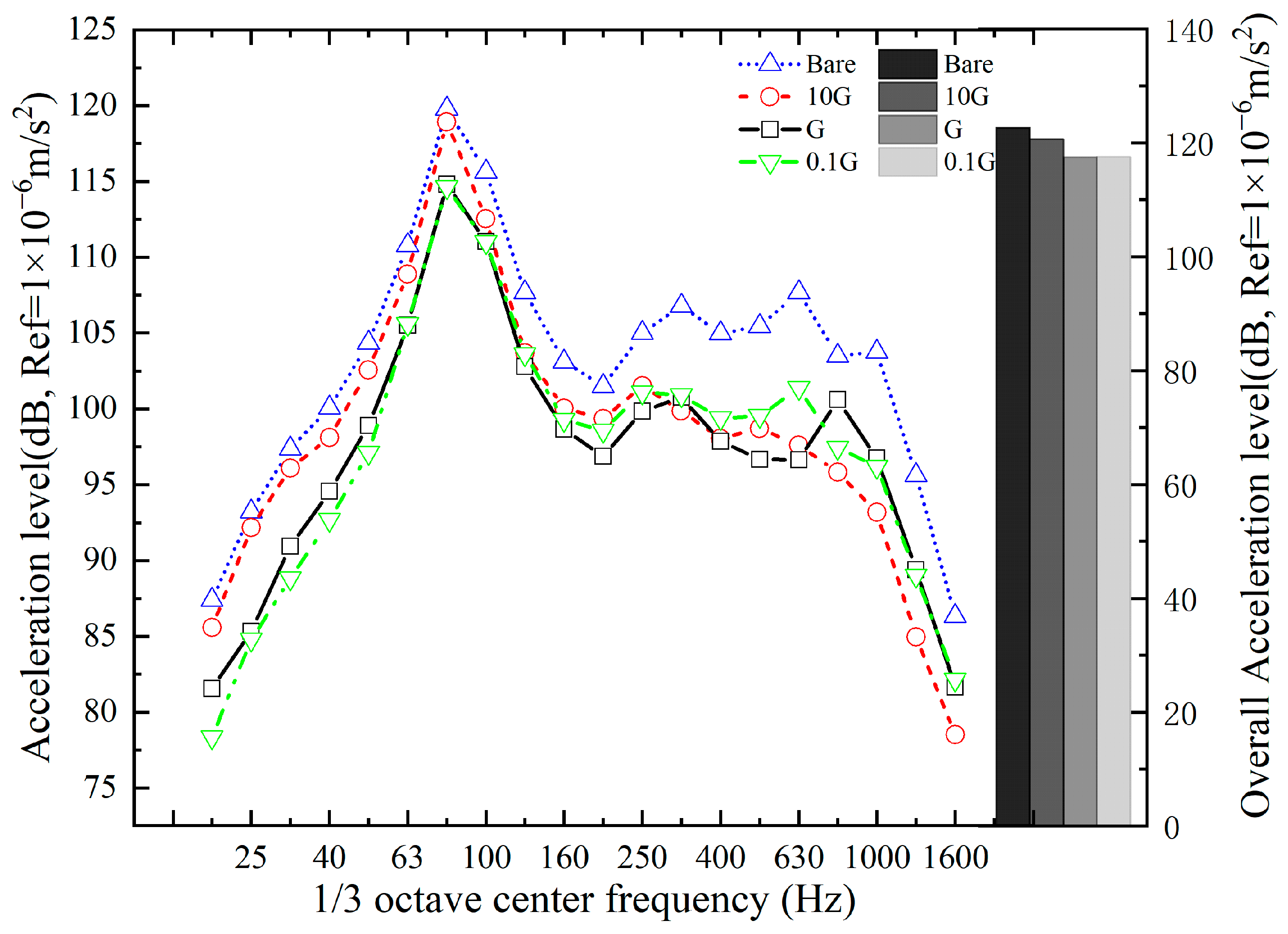
4.2. Shear Modulus of Damping Layer
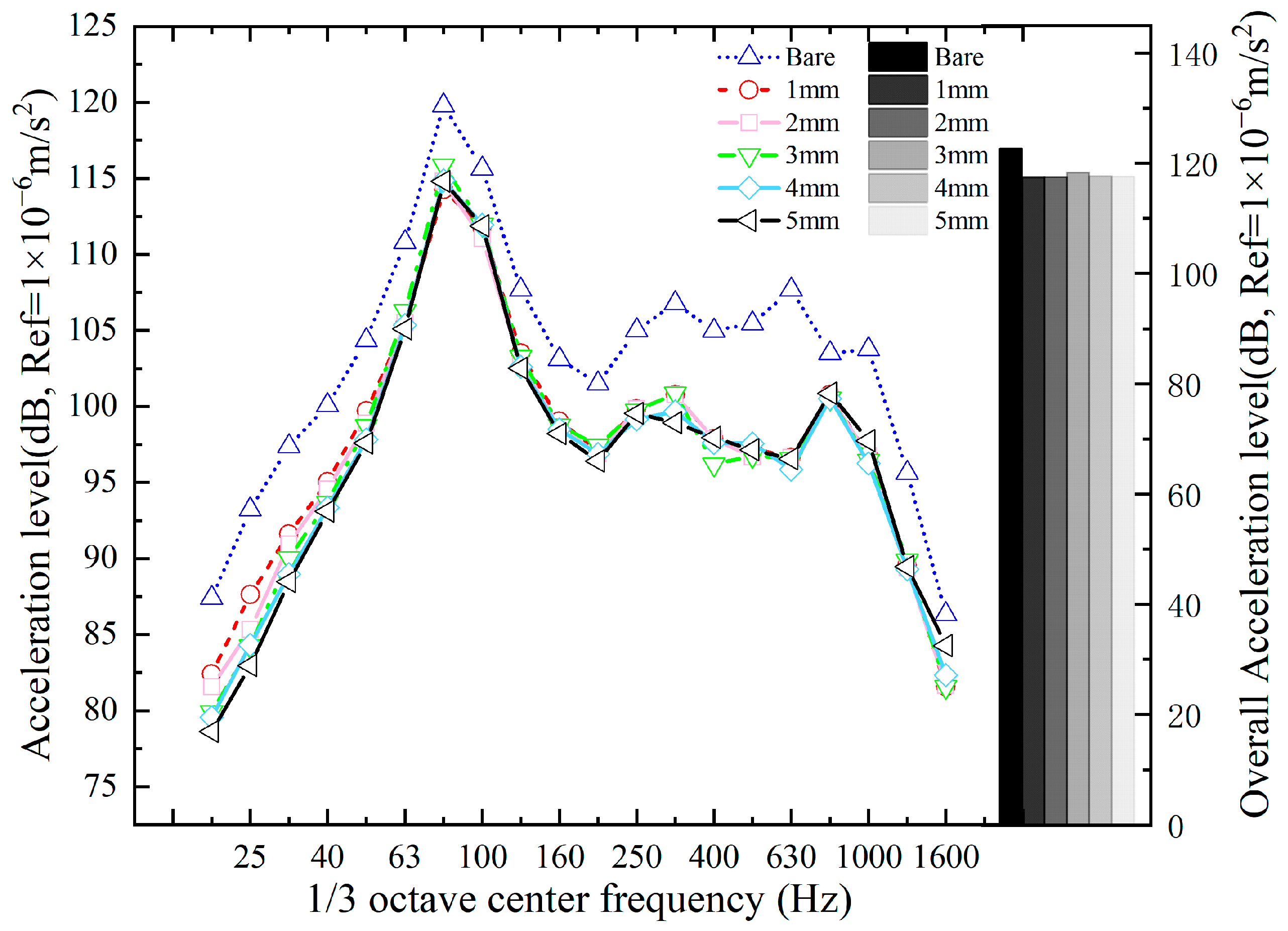
4.3. Thickness of Damping Layer
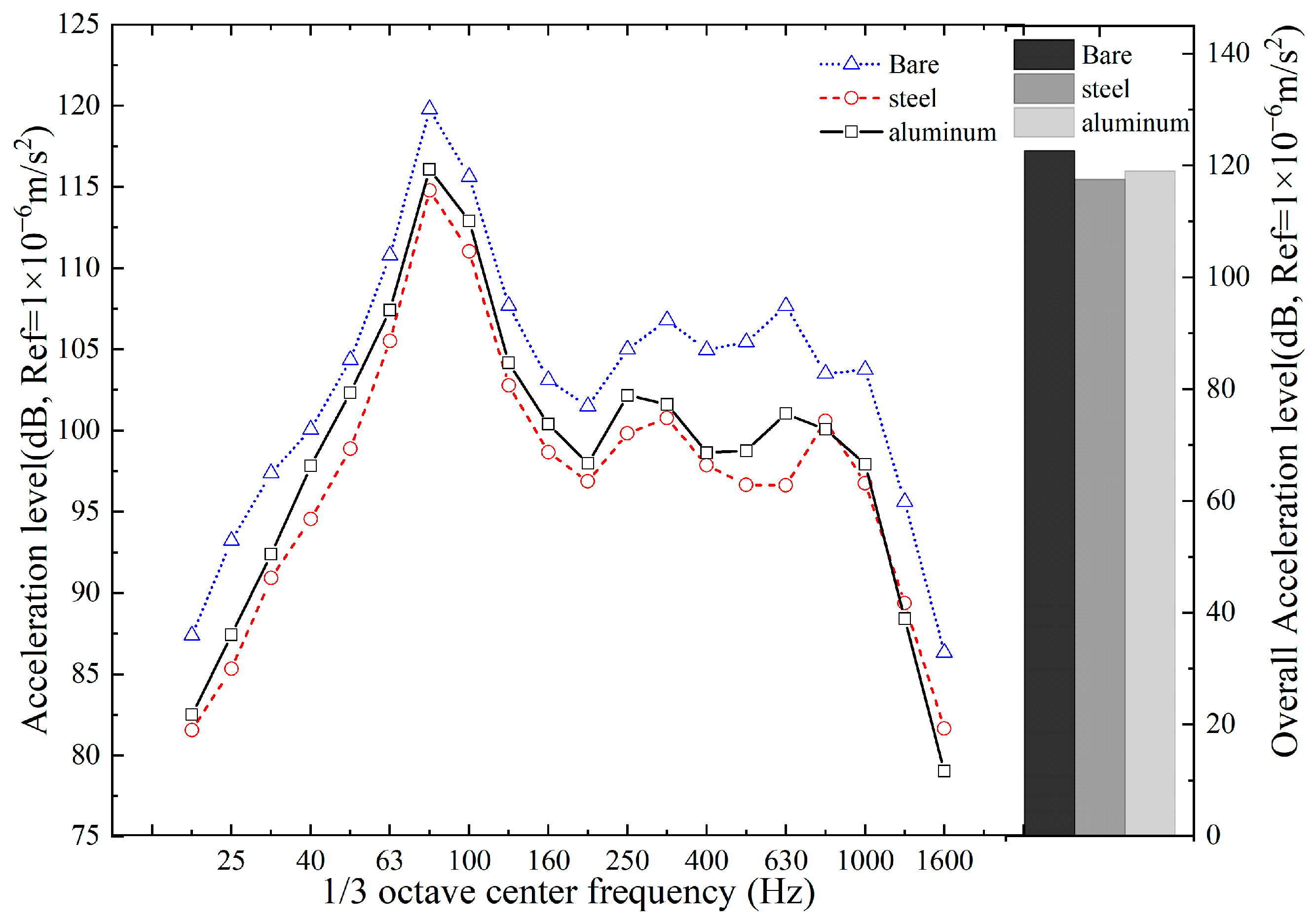
4.4. Material of Constraining Layer
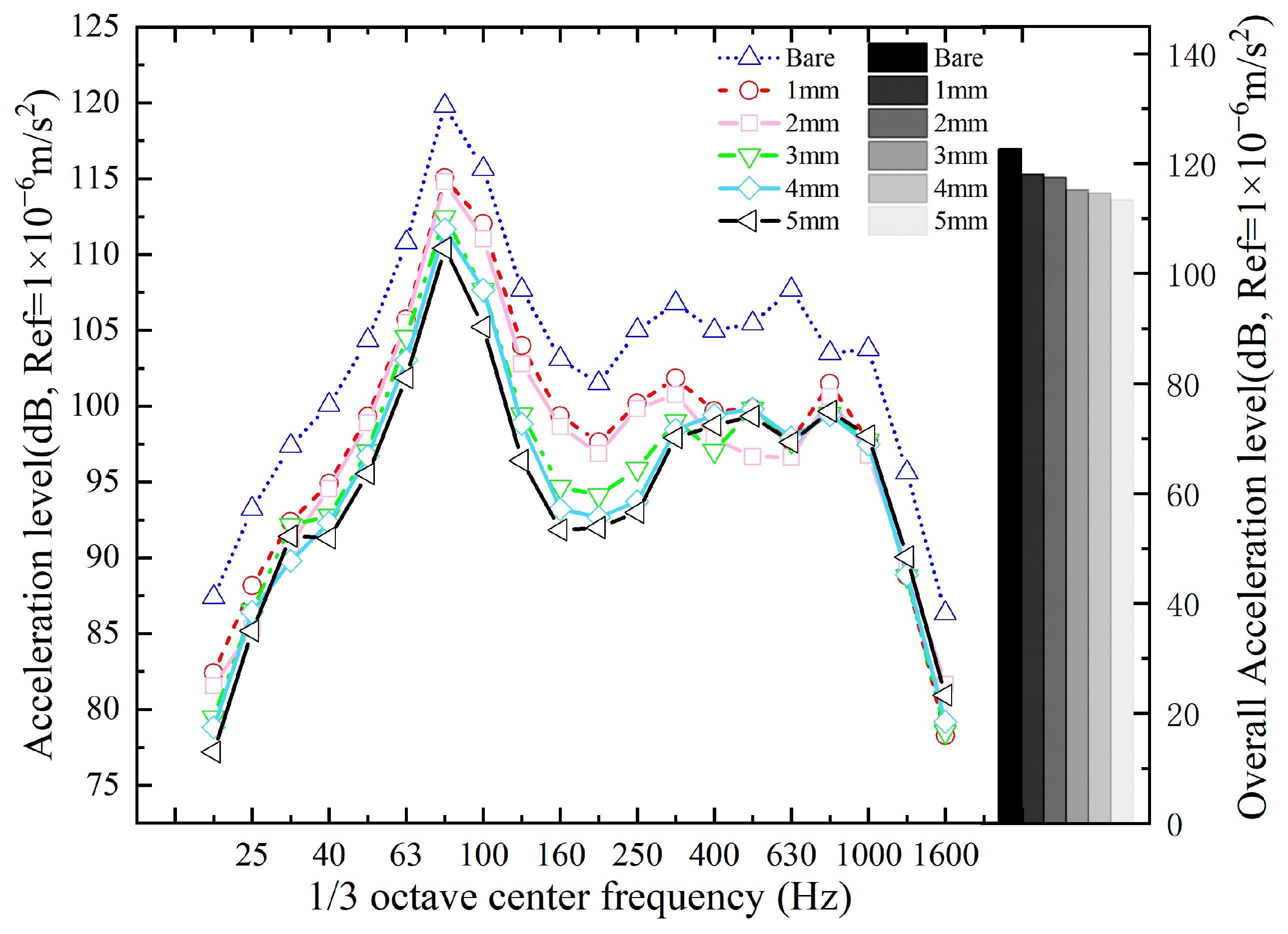
4.5. Thickness of Constraining Layer
5. Conclusions
- (1)
- The calculation efficiency of WFEM is improved by several times with no loss of accuracy compared with the conventional FEM.
- (2)
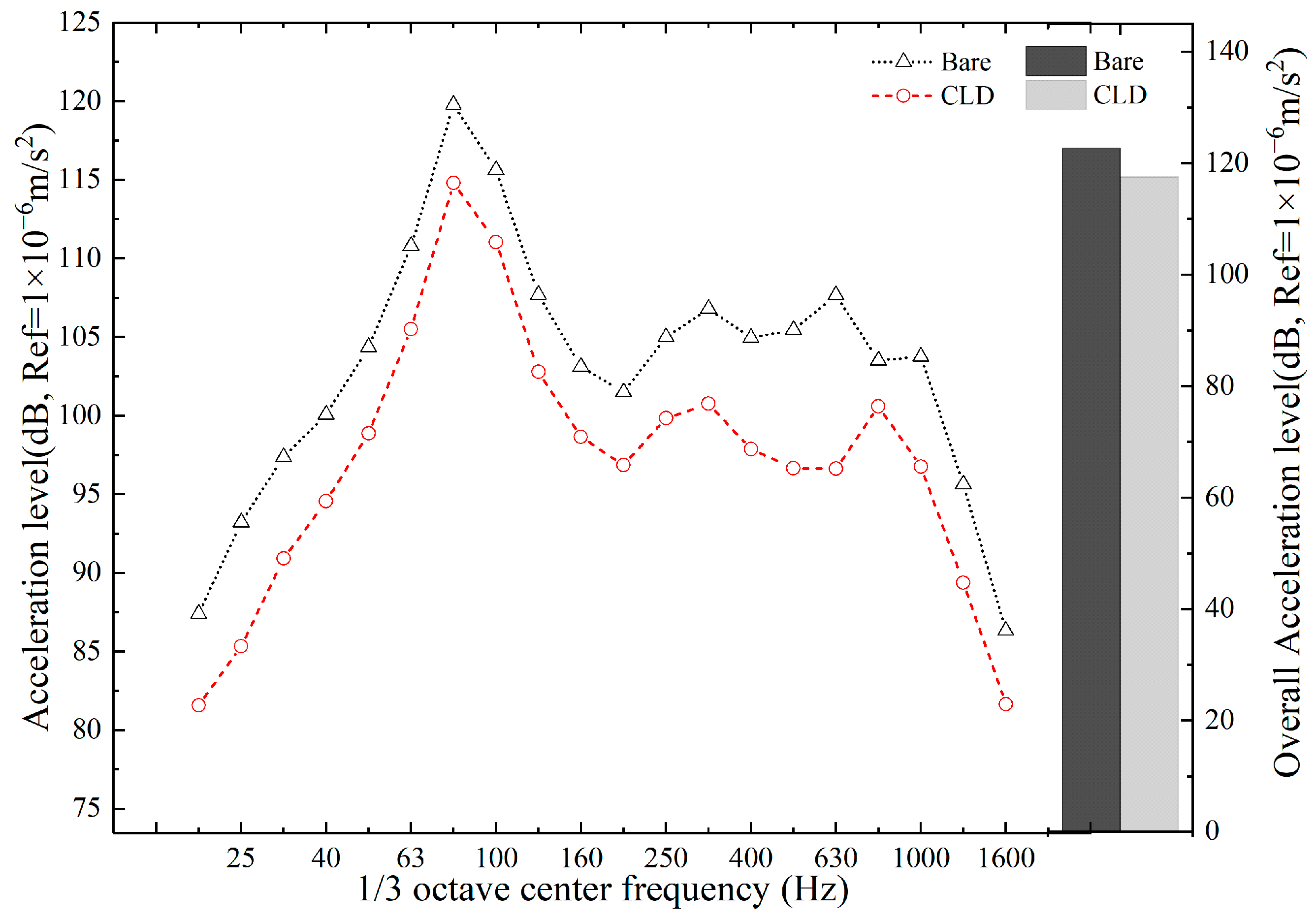
- Treatment with CLD can significantly reduce vibration in all frequency bands and is suitable for controlling the vibration of steel structures.
- (3)
- The dominant frequency range of the vibration acceleration of the steel–concrete composite bridge with CLD induced by a moving train was 63–100 Hz, and the peak appeared at approximately 80 Hz.
- (4)
- The shear modulus of the damping layer was closely related to the mitigation effect. A lower shear modulus of the viscoelastic core resulted in a lower acceleration of the bridge in the low-frequency range. In the high-frequency range, a damping layer with a higher shear modulus is required for vibration mitigation.
- (5)
- The reduction in the vibration of the composite bridge was more sensitive to the thickness of the constraining layer than to that of the damping layer.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thompson, D.J. Railway Noise and Vibration: Mechanisms, Modeling and Means of Control; Elsevier Ltd.: Oxford, UK, 2009. [Google Scholar]
- Li, X.Z.; Liu, Q.M.; Pei, S.L.; Song, L.Z.; Zhang, X. Structure-borne noise of railway composite bridge: Numerical simulation and experimental validation. J. Sound Vib. 2015, 353, 378–394. [Google Scholar] [CrossRef]
- He, W.; He, K.W.; Zou, C.; Yu, Y.L. Experimental noise and vibration characteristics of elevated urban rail transit considering the effect of track structures and noise barriers. Environ. Sci. Pollut. Res. 2021, 28, 45903–45919. [Google Scholar] [CrossRef] [PubMed]
- Sun, R.Y.; Wang, S.; Li, M.; Zhu, Y. An algorithm for large-span flexible bridge pose estimation and multi-keypoint vibration displacement measurement. Measurement 2025, 240, 115582. [Google Scholar] [CrossRef]
- Ngai, K.W.; Ng, C.F. Structure-borne noise and vibration of concrete box structure and rail viaduct. J. Sound Vib. 2002, 255, 281–297. [Google Scholar] [CrossRef]
- Crockett, A.R.; Pyke, J.R. Elevated design for minimization of direct and structure-radiated train noise. J. Sound Vib. 2000, 231, 883–897. [Google Scholar] [CrossRef]
- Alten, K.; Flesch, R. Finite element simulation prior to reconstruction of a steel railway bridge to reduce structure-borne noise. Eng. Struct. 2012, 35, 83–88. [Google Scholar] [CrossRef]
- Li, Q.; Dai, B.R.; Zhu, Z.H.; Thompson, D.J. Comparison of vibration and noise characteristics of urban rail transit bridges with box-girder and U-shaped sections. Appl. Acoust. 2022, 186, 108494. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.Z.; Liu, Q.M.; Wu, J.F.; Li, Y.D. Theoretical and experimental investigation on bridge-borne noise under moving high-speed train. Sci. China Technol. Sci. 2013, 56, 917–924. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, X.; Jiang, J.Q.; Yamashita, M. Assessment on transient sound radiation of a vibrating steel bridge due to traffic loading. J. Sound Vib. 2015, 336, 132–149. [Google Scholar] [CrossRef]
- Song, X.D.; Li, Q. Numerical and experimental study on noise reduction of concrete LRT bridges. Sci. Total Environ. 2018, 643, 208–224. [Google Scholar] [CrossRef]
- Zhang, X.A.; Zhang, X.Y.; Yang, J.J.; Zhu, S.Y.; He, Q.L. Mechanism of noise reduction caused by thickening top plate for high-speed railway box-girder bridge. Structures 2023, 57, 105148. [Google Scholar] [CrossRef]
- Remington, P.J.; Witting, L.E. Prediction of the effectiveness of noise control treatments in urban rail elevated structures. J. Acoust. Soc. Am. 1985, 78, 2017–2033. [Google Scholar] [CrossRef]
- Janssens, M.H.A.; Thompson, D.J. A calculation model for the noise from steel railway bridges. J. Sound Vib. 1996, 193, 295–305. [Google Scholar] [CrossRef]
- Bewes, O.G.; Thompson, D.J.; Jones, C.J.C.; Wang, A. Calculation of noise from railway bridges and viaducts: Experimental validation of a rapid calculation model. J. Sound Vib. 2006, 293, 933–943. [Google Scholar] [CrossRef]
- Poisson, F.; Margiocchi, F. The use of dynamic dampers on the rail to reduce the noise of steel railway bridges. J. Sound Vib. 2006, 293, 944–952. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, N.; Sun, Q.K.; Wu, Z.Z. Experimental and numerical study on vibration and structure-borne noise of composite box-girder railway bridges. Int. J. Rail Transp. 2024, 12, 134–152. [Google Scholar] [CrossRef]
- Si, J.; Zhu, L.; Ma, W.; Meng, B.; Dong, H.; Ning, H.; Zhao, G. Study on Vibration and Noise of Railway Steel–Concrete Composite Box Girder Bridge Considering Vehicle–Bridge Coupling Effect. Buildings 2024, 14, 2509. [Google Scholar] [CrossRef]
- Liang, L.; Li, X.Z.; Zheng, J.; Lei, K.N.; Gou, H.Y. Structure-borne noise from long-span steel truss cable-stayed bridge under damping pad floating slab: Experimental and numerical analysis. Appl. Acoust. 2020, 157, 106988. [Google Scholar] [CrossRef]
- Liu, Q.M.; Liu, L.Y.; Chen, H.P.; Zhou, Y.L.; Lei, X.Y. Prediction of vibration and noise from steel/composite bridges based on receptance and statistical energy analysis. Steel Compos. Struct. 2020, 37, 291–306. [Google Scholar] [CrossRef]
- Gu, Y.W.; Nie, X.; Yan, A.G.; Zeng, J.H.; Liu, Y.F.; Jiang, Y.X. Experimental and numerical study on vibration and structure-borne noise of high-speed railway composite bridge. Appl. Acoust. 2022, 192, 108757. [Google Scholar] [CrossRef]
- Luo, H.; Cao, Z.Y.; Zhang, X.; Li, C.; Kong, D.R. Combining different forms of statistical energy analysis to predict vibrations in a steel box girder comprising periodic stiffening ribs. Steel Compos. Struct. 2022, 45, 119–131. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, N.; Sun, Q.K.; Cheng, Z.N. A symplectic-spectral element method for high frequency vibration analysis and its application in structure-borne noise prediction. Int. J. Struct. Stab. Dy. 2023, 23, 2350137. [Google Scholar] [CrossRef]
- Waki, Y.; Mace, B.R.; Brennan, M.J. Numerical issues concerning the wave and finite element method for free and forced vibrations of waveguides. J. Sound Vib. 2009, 327, 92–108. [Google Scholar] [CrossRef]
- Duhamel, D. A scaled wave finite element method for computing scalar wave radiation and scattering in exterior domains. Comput. Methods Appl. Mech. Eng. 2022, 392, 114676. [Google Scholar] [CrossRef]
- Mace, B.R.; Duhamel, D.; Brennan, M.J.; Hinke, L. Finite element prediction of wave motion in structural waveguides. J. Acoust. Soc. Am. 2005, 117, 2835–2843. [Google Scholar] [CrossRef]
- Renno, J.; Sassi, S.; Alnahhal, W.I. Calculating the response of waveguides to base excitation using the wave and finite element method. J. Vib. Control 2022, 28, 652–664. [Google Scholar] [CrossRef]
- Waki, Y.; Mace, B.R.; Brennan, M.J. Free and forced vibrations of a tyre using a wave/finite element approach. J. Sound Vib. 2009, 323, 737–756. [Google Scholar] [CrossRef]
- Song, L.Z.; Li, X.Z.; Hao, H.; Zhang, X. Medium- and high-frequency vibration characteristics of a box-girder by the waveguide finite element method. Int. J. Struct. Stab. Dyn. 2018, 18, 1850141. [Google Scholar] [CrossRef]
- Zhang, C. The active rotary inertia driver system for flutter vibration control of bridges and various promising applications. Sci. China Tech. Sci. 2023, 66, 390–405. [Google Scholar] [CrossRef]
- Gao, P.X.; Yu, T.; Zhang, Y.L.; Wang, J.; Zhai, J.Y. Vibration analysis and control technologies of hydraulic pipeline system in aircraft: A review. Chin. J. Aeronaut. 2021, 34, 83–114. [Google Scholar] [CrossRef]
- Zhu, Q.Y.; Han, Q.K.; Liu, J.G. Topological optimization design on constrained layer damping treatment for vibration suppression of thin-walled structures via improved BESO method. Aerosp. Sci. Technol. 2023, 142, 108600. [Google Scholar] [CrossRef]
- Liu, Q.M.; Thompson, D.J.; Xu, P.P.; Feng, Q.S.; Li, X.Z. Investigation of train-induced vibration and noise from a steel-concrete composite railway bridge using a hybrid finite element-statistical energy analysis method. J. Sound Vib. 2020, 471, 115197. [Google Scholar] [CrossRef]
- Lu, P.P.; Wang, P.; Lu, J. Decentralized vibration control of smart constrained layer damping plate. J. Vib. Control 2021, 27, 529–542. [Google Scholar] [CrossRef]
- Zhao, J.H.; Sun, F.F.; Yin, W.H.; Le, Z.J.; Song, J.; Cai, X.Y.; He, Y.M. Damping performance and its influencing factors of wind turbine towers with constrained layer damping treatment. Structures 2023, 57, 105322. [Google Scholar] [CrossRef]
- Zhang, C.G.; Shu, J.P.; Zhang, H.; Ning, Y.J.; Yu, Y.T. Estimation of load-carrying capacity of cracked RC beams using 3D digital twin model integrated with point clouds and images. Eng. Struct. 2024, 310, 118126. [Google Scholar] [CrossRef]
- Wang, S.X.; He, J.J.; Fan, J.; Sun, P.X.; Wang, D.W. A time-domain method for free vibration responses of an equivalent viscous damped system based on a complex damping model. J. Low Freq. Noise Vib. Act. Control 2023, 42, 1531–1540. [Google Scholar] [CrossRef]


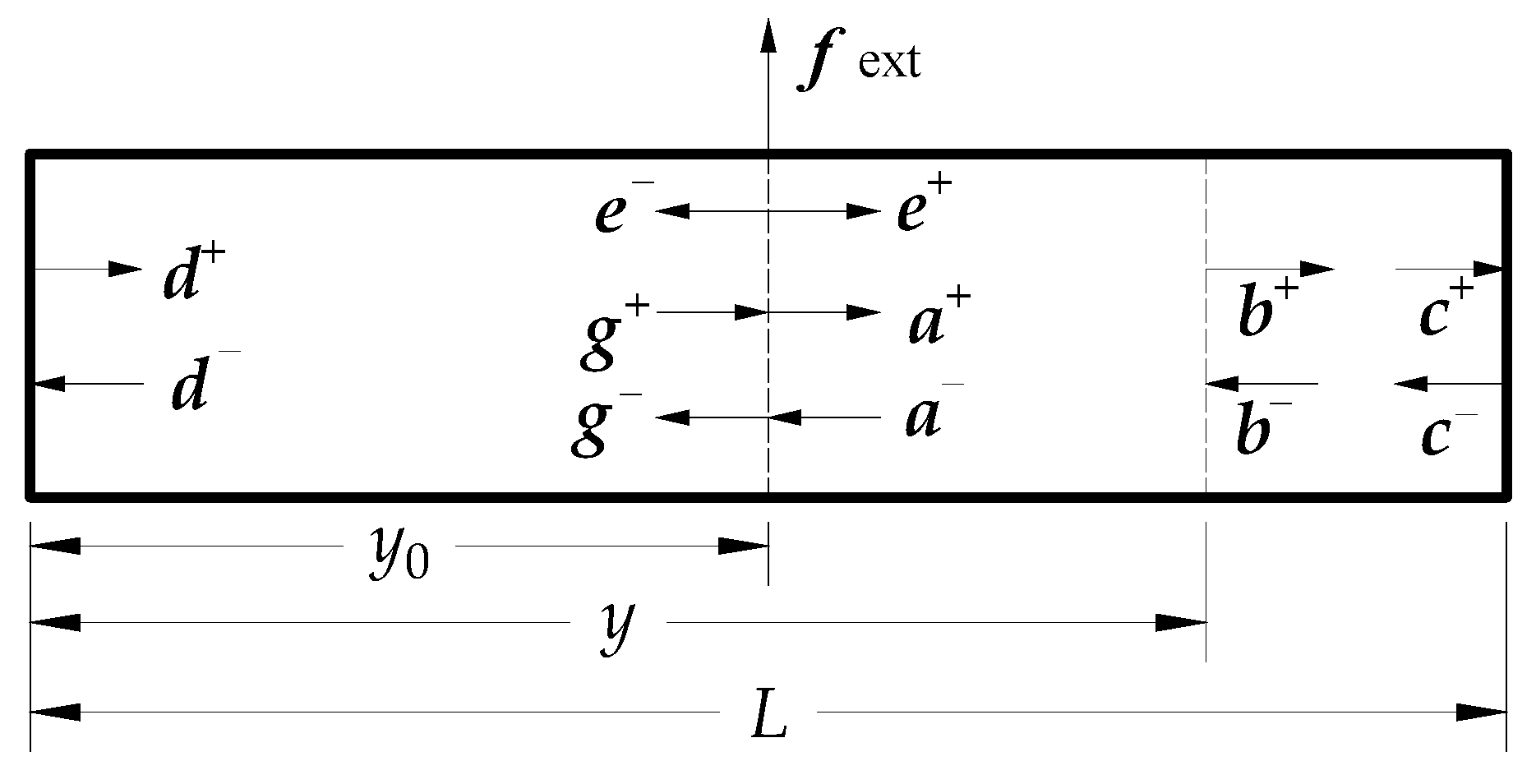





| Parameter | Bridge Deck | Stringer |
|---|---|---|
| Elastic modulus (Pa) | 3.55 × 1010 | 2.1 × 1011 |
| Damping ratio | 0.03 | 0.0003 |
| Density (kg/m3) | 4067 | 7850 |
| Poisson’s ratio | 0.2 | 0.3 |
| Parameter | Value |
|---|---|
| Density of rail (kg/m3) | 7850 |
| Mass of rail (kg/m) | 60.64 |
| Cross-sectional area of rail (m2) | 7.745 × 10−3 |
| Elastic modulus of rail (Pa) | 2.06 × 1011 |
| Area moment of inertia of rail (m4) | 3.217 × 10−5 |
| Poisson’s ratio of rail | 0.3 |
| Fastener vertical stiffness (MN/m) | 60 |
| Rail loss factor | 0.01 |
| Fastener vertical damping (kN·s/m) | 80 |
| Fastener spacing (m) | 0.6 |
| Fastener loss factor | 0.25 |
| Parameter | Damping Layer | Constraining Layer |
|---|---|---|
| Material | Viscoelastic damping material | Steel |
| Thickness (mm) | 2 | 2 |
| Elastic modulus (Pa) | * | 2.1 × 1011 |
| Density (kg/m3) | 1500 | 7850 |
| Poisson’s ratio | 0.499 | 0.3 |
| Damping ratio | * | 0.0002 |
| Model | Number of Nodes | Number of Elements | Result File (kB) | Model File (kB) | Computation Time (min) |
|---|---|---|---|---|---|
| FEM | 15,953 | 15,702 | 4,012,147 | 101,632 | 83 |
| WFEM | 390 | 370 | 126 | 42 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Fu, W.; Song, L.; Gao, K.; Xu, P. A Rapid Prediction of Suppressed Vibration in Composite Bridges Equipped with Constrained Layer Damping. Buildings 2024, 14, 3621. https://doi.org/10.3390/buildings14113621
Liu Q, Fu W, Song L, Gao K, Xu P. A Rapid Prediction of Suppressed Vibration in Composite Bridges Equipped with Constrained Layer Damping. Buildings. 2024; 14(11):3621. https://doi.org/10.3390/buildings14113621
Chicago/Turabian StyleLiu, Quanmin, Weiwang Fu, Lizhong Song, Kui Gao, and Peipei Xu. 2024. "A Rapid Prediction of Suppressed Vibration in Composite Bridges Equipped with Constrained Layer Damping" Buildings 14, no. 11: 3621. https://doi.org/10.3390/buildings14113621
APA StyleLiu, Q., Fu, W., Song, L., Gao, K., & Xu, P. (2024). A Rapid Prediction of Suppressed Vibration in Composite Bridges Equipped with Constrained Layer Damping. Buildings, 14(11), 3621. https://doi.org/10.3390/buildings14113621






