The Time-Dependent Method for Probabilistic Fault Displacement Hazard Analysis (PFDHA-td)

Abstract

Coseismic surface displacement can cause major damage to buildings located on faults. Therefore, it is important to quantitatively evaluate the future surface displacement of active faults. The commonly used deterministic evaluation methods often tend to overestimate surface displacement values, so researchers are working toward probabilistic fault displacement hazard analysis (PFDHA). However, the PFDHA assumes that earthquakes occur equally in time, which is not consistent with the physical mechanism of earthquake occurrence. Elastic rebound theory and paleoseismic research results show that the accumulation and release of energy in the crustal medium have cyclical characteristics. In this study, using two parameters, the strong earthquake recurrence period (T_RP) and strong earthquake elapsed time (t_et), of active faults, the displacements of active faults with different T_RP and t_et under different exceedance probabilities are obtained. The calculation results indicate that the surface displacement hazard of the weakly active and extremely weakly active faults in the Holocene does not need to be considered; for the moderately and strongly active faults in the Holocene, the surface displacement result is lower than that provided by the deterministic method. According to the importance of the project, the calculation results of the PFDHA-td method under different exceedance probabilities are selected.

1. Introduction

Recently, the impact of active faults on the safety of buildings and structures has received public attention. If a building is located on an active fault, it will suffer two additional impacts during an earthquake. First, the ground motion will increase, especially when it is located on the hanging wall of the fault [1,2,3]. Second, the building will suffer surface displacement of the fault [4,5,6]. During a major earthquake, many lifeline projects that cross active faults, such as bridges, highways, railways, tunnels, utility pipelines, and communication networks, cannot withstand the destruction caused by fault displacement. For example, the 2022 Ms6.9 Menyuan earthquake in China caused damage to Lan-xin high-speed railway lines and caused a temporary suspension of service [7,8,9]. These seismic events indicate that in the design and construction stages of linear projects, the hazard of surface fault displacement should be fully considered.

Youngs et al. [10] proposed the PFDHA method. This method borrows the classic PSHA algorithm, uses the fault displacement attenuation function instead of the seismic attenuation function, and finally obtains the displacements of principal faulting and distributed faulting under different exceedance probabilities. This method has been widely used [11,12,13,14]. In mainland China, in the design of buildings across faults, the deterministic evaluation method is generally used. The deterministic evaluation method refers to the use of information such as the fault length and the maximum historical earthquake magnitude to estimate the maximum potential magnitude and the corresponding displacement that may occur on the fault and uses this result in the fault-resistant design [15,16,17]. The result of the deterministic evaluation method is influenced by various factors, such as foundation and soil [18,19]. Some scholars have used logistic regression analysis to study the impact of different factors on deterministic evaluation methods [20,21,22]. Obviously, the safety of the deterministic evaluation methods was greater. However, for buildings that are not very important, if this value is used, the construction cost will greatly increase. This is one of the reasons why an increasing number of researchers prefer probabilistic evaluation methods. The PFDHA method can provide an appropriate displacement according to the importance of buildings. However, this method also has obvious deficiencies. First, this method requires a certain degree of understanding of the active faults in the entire seismic–tectonic zone before we can assign the parameter of the earthquake occurrence rate to each segment of each fault. Second, this method assumes that the occurrence of earthquakes is of equal probability in terms of time, which is in line with the Poisson distribution. However, the occurrence of earthquakes is a periodic pattern of energy “accumulation–earthquake–accumulation–occurrence…” physical process. Both deterministic evaluation methods and existing probabilistic evaluation methods have several shortcomings. These shortcomings can cause insufficient accuracy of evaluation results, excessive funding, or overly conservative evaluation results. Therefore, we hope to explore a new evaluation method based on the above two methods. This evaluation method possesses the characteristics of low investment and high precision and can reflect the physical mechanism of earthquakes to a certain extent.

The results of a growing number of paleoseismic trenches on active faults show that the recurrence of strong earthquakes on the faults is periodic [23,24,25,26], such as the Red River Fault in southwest China [27]. In addition, the more active the fault is, the shorter the T_RP. We can determine the T_RP and t_et along a target fault (principal fault, not distributed fault) through paleoseismology methods (e.g., trenching and drilling). Assuming that the probability of strong earthquakes increases linearly with time, the classic PSHA algorithm is used for reference to obtain the PFDHA-td results. Compared to existing deterministic methods and the PFDHA method, the novelty of the PFDHA-td method is reflected in two aspects: First, we have considered the physical mechanism of earthquake occurrence, in which the probability of a major earthquake occurring is no longer a constant but increases with time; second, we have taken into account the importance level of buildings, meaning that for the same active fault, buildings of different importance levels need to consider different maximum surface displacements.

In the past 100 years of the 20th century, Yunnan Province (located in western China) experienced 14 earthquakes with magnitudes greater than 7. However, since the beginning of the 21st century, Yunnan Province has not encountered any earthquake exceeding a magnitude of 7. Under these circumstances, the risk of strong earthquakes increases sharply. Considering the number of major linear projects being implemented and about to be implemented in Yunnan Province (e.g., Central Yunnan Water Diversion Project, China–Myanmar Oil Pipeline, and multiple expressways), it is very important to correctly assess the hazard of active faults. Therefore, this paper provides an assessment result based on the magnitude–surface displacement distance relationship in western China. Although the assessment results are given in this paper by using western China as an example, this does not mean that the present method is only applicable to western China. The PFDHA-td method essentially studies the relationship between the earthquake magnitude and the probability of exceedance. Therefore, once we obtain the empirical magnitude–surface displacement distance relationship in the project region all over the world, we can use this method to calculate the future surface displacement hazard of the active faults in the region.

In actual work, the T_RP and t_et on active faults can be obtained at low cost by methods such as trenching and drilling. Then, the PFDHA-td method proposed in this paper can be used to conveniently determine the future surface displacement hazard under different exceeding probabilities. This method is characterized by low cost and high precision, and at the same time, it is consistent with the physical mechanism of earthquake occurrence. Therefore, the proposal and implementation of this method promote the development of active fault engineering to a certain extent.

2. Methods

2.1. Annual Incidence of Earthquakes

The history of human civilizations is very short, which prevents us from obtaining the T_RP on active faults through historical documents. Among the current methods for obtaining T_RP, the paleoseismic method is the main and most reliable method [23]. In paleoseismic research on active faults, while obtaining the T_RP, we can also obtain the t_et. In order to obtain these data, a suitable location on the active fault was selected, and paleoseismic trenches were excavated. Based on the spatial relationship between the fault and strata in the trench, the paleoseismic events are analyzed. AMS-¹⁴C and other chronological testing methods were used to obtain the sedimentary age of the strata related to the paleoseismic events and thus the time of each paleoearthquake (t₁, t₂…t_n). The t₁ represents the time span from the oldest paleoearthquake exposed in the trench to the present, and t_n represents the time span from the youngest paleoearthquake exposed in the trench to the present. The recurrence period of strong earthquakes on an active fault is as follows:

$$T_{\mathrm{RP}}={\displaystyle \frac{t_1-t_n}{n-1}}$$

(1)

The elapsed time of a strong earthquake (t_et) is the ratio of t_n/T_RP. According to the degree of importance, the design service life of civil buildings in mainland China is divided into 5 years, 25 years, 50 years, and 100 years. Therefore, we set the elapsed time of a strong earthquake as follows:

$$t_{\mathrm{et}}=\left(t_n+100\right)/T_{\mathrm{RP}}$$

(2)

If the life of the buildings across the fault is more than 100 years, the constant in the above formula should be changed. Based on the T_RP data, we can obtain the average annual incidence of strong earthquakes on the fault:

$${\overline{\nu }}_0={\displaystyle \frac{1}{T_{\mathrm{RP}}}}$$

(3)

The occurrence of strong earthquakes is not evenly distributed in time. After a strong earthquake, the energy accumulated in the Earth’s crust is released, and the probability of strong earthquakes decreases in the short term; over time, the energy in the Earth’s crust gradually increases, and the incidence of strong earthquakes increases. Considering the linear increase in the energy of the crust over a long time scale, along with the annual rate of strong earthquakes obtained by the paleoseismic method, referring to the Brownian Passage Time (BPT) model [28], we use the following equation to describe the change in the probability of strong earthquakes:

$${\nu }_0=\left\{\begin{array}{l}{\overline{\nu }}_0{t}_{\mathrm{et}}\le 1/2\\ 2{\overline{\nu }}_0\times t_{\mathrm{et}}1/2<t_{\mathrm{et}}\le 1\\ 2{\overline{\nu }}_0{t}_{\mathrm{et}}\ge 1\end{array}\right.$$

(4)

We have constructed this formula with reference to the BPT model’s concept. Although some scholars use the BPT model to describe the probability of future earthquakes occurring [29,30], we did not employ the BPT model for two main reasons. First, in the BPT model (when the recurrence interval coefficient of variation equals 0.25), the probability of an earthquake occurring is 0 when t_et is less than 0.5, which is not acceptable in earthquake engineering. Second, in our research, we do not wish to discuss the uncertainty of T_RP. In Formula (4), both the probability and cumulative distributions are greater than those in the BPT model; hence, our calculations are on the safe side. The first term in Equation (4) demonstrates a truncated minimum occurrence rate, which can prevent us from underestimating the hazard when the t_et is small. The third term in Equation (4) shows the upper limit of earthquake occurrence rate, reflecting the finite strength of the crustal medium and the impossibility of unlimited energy accumulation. When the t_et is bigger, this term can reflect the increase in the hazard of strong earthquakes to a certain extent.

2.2. Fault Displacement Probability

Compared to T_RP that represents hundreds or thousands of years, the life of buildings is only 50–100 years. Within the range of 50–100 years, it can be considered that the incidence of strong earthquakes on faults is constant and unchanging. Therefore, we chose the Poisson process instead of the non-stationary Poisson process [31,32]. Using the probabilistic seismic hazard analysis method [10,33], the probability of n earthquakes occurring on the fault in the next year t is calculated as follows:

$$P(n)={\displaystyle \frac{{({\nu }_{0}t)}^n}{n!}}{e}^{-v_{0}t}$$

(5)

The seismicity on the active faults follows the revised magnitude–frequency relationship [34,35].

$${\log }_{10}N(m)=a-bM$$

(6)

where b in the formulate is the b-value, reflecting the relationship between the quantity of earthquakes with different magnitudes within a certain space. The b-values are different in different regions, and even in the same region, the b-values calculated by different researchers are also different.

According to the above two equations, the corresponding magnitude probability density function can be obtained as follows [31,32]:

$$f(m)={\displaystyle \frac{\beta \exp [-\beta (m-m_0)]}{1-\exp [-\beta (m_{\mathrm{uz}}-m_0)]}}$$

(7)

where β = bln10, the upper limit of the magnitude of the fault is m_uz, and the lower limit of the magnitude at which surface displacement can occur is m₀. In actual work, the magnitude m is divided into Nm bins, where m_j represents the magnitude bin in the magnitude range (m_j ± Δm/2). Then, the annual incidence of a m_j-file earthquake within the fault is as follows [31,32]:

$$P(m_i)={\displaystyle \frac{2}{\beta }}f(m_j)\cdot \sinh ({\displaystyle \frac{1}{2}}\beta \Delta m)$$

(8)

The number of m_j-file earthquakes that will occur on the fault in the future t year is as follows:

$$n_j(t)=P(m_j)\cdot {\nu }_0\cdot t$$

(9)

Historical earthquake statistics show that surface displacements caused by earthquakes of different magnitudes are also different, and the surface displacement distance is positively correlated with the earthquake magnitude. The number of all earthquakes with a surface displacement distance greater than d in the future year t is as follows:

$$m(d,t)={\displaystyle \sum _i{q}_i(d)\cdot n_i(t)}$$

(10)

where q_i(d) is the conditional probability that surface displacements caused by an earthquake with magnitude m_i exceed level d. The probability of the event that transcends the surface displacement d in the next t year is as follows:

$$P(d,t)=1-\exp [-m(d,t)]$$

(11)

2.3. Relationship Between Surface Displacement and Earthquake Magnitude

In probabilistic surface displacement analysis methods, the direct results are the probabilities of earthquakes of different magnitudes. On this basis, it is also necessary to convert the magnitude to surface displacement according to the relationship between them to obtain the exceedance probabilities of different surface displacements. The relationship between surface displacement and earthquake magnitude generally comes from the statistics of surface displacement data of historical earthquakes. It is strongly affected by the number of samples, the type of earthquake, and the statistical area. This paper chose the statistical relationship obtained by Huang (2016) [36] based on earthquake examples in mainland China. Out of the 46 historical earthquake examples collected in the literature, 41 occurred in western China. Among 41 historical earthquake examples, 30 were strike-slip earthquakes, 5 were normal fault earthquakes, and 6 were thrust earthquakes. Based on comprehensive consideration, the statistical results of “strike-slip faults in western China” in this literature were chosen.

Lg(Dh) = −2.4500 + 0.4010 Ms, R = 0.5548, σ = 0.0974, n = 30

(12)

Lg(Dv) = −2.6498 + 0.3971 Ms, R = 0.4447, σ = 0.1720, n = 23

(13)

3. Results

3.1. Assessment Results of Holocene Active Faults of Different Degrees

Most seismic design codes in mainland China clearly state that only the hazard of surface displacement caused by Holocene faults needs to be considered. Therefore, in the present study, only the hazard of surface displacement of the Holocene faults was calculated. Even if the same Holocene fault is used, their hazard levels are different. We calculated the surface displacements of four types of faults with different levels under different exceeding probabilities. These four types of faults are as follows: intensely Holocene active faults (T_RP = 1000 a), moderately Holocene active faults (T_RP = 2000 a), weakly Holocene active faults (T_RP = 5000 a), and extremely weakly Holocene active faults (T_RP = 10,000 a). These four types of faults are good representations of mainland China, which is located in the interior of the plate (level B and part of A in

Table 1. Deformation rate and in situ recurrence interval of active faults in different structural positions [37].

Activity Level	Deformation Rate (R) (mm/a)			In Situ Recurrence Interval (T) (ka)	Overall Characteristics
	Strike-Slip Fault	Normal Fault	Reverse Fault
AA	R > 15	R > 2	R > 10	T ≤ 0.5	The faults constitute boundaries of plates or large active blocks/fault blocks and feature large size, good regional continuity, high slip rate, and strong earthquake frequency.
A	5 ≤ R < 15	0.5 ≤ R < 2	2 ≤ R < 10	0.5 < T ≤ 2.5	The faults often constitute boundaries of large intraplate active blocks/fault blocks and feature large size, good regional continuity, relatively high slip rate, and strong earthquake frequency.
B	0.5 ≤ R < 5	0.1 ≤ R < 0.5	0.2 ≤ R < 2	2.5 < T ≤ 10	The faults are often intraplate faults, of which some constitute boundaries of moderate to large active blocks/fault blocks, and feature moderate or relatively large size, relatively good regional continuity, moderate slip rate, and strong earthquake frequency.
C	R < 0.5	R < 0.1	R < 0.2	10 < T	The faults often lie inside active blocks/fault blocks and feature relatively small size, poor regional continuity, low slip rate, and the ability to induce destructive earthquakes. However, strong earthquake frequency is low.

).

Using the method described in the previous section, we calculated the surface displacements for the four types of faults under the conditions of different exceedance probabilities and different elapsed times of strong earthquakes. The calculation results are shown in Figure 1.

For ease of use, we present the horizontal displacements and vertical displacements corresponding to some important exceedance probabilities (return periods) in Figure 1 and in

Table 2. Surface displacement of 4 types of active faults, 4 exceedance probabilities, and different t_et.

Strong Earthquake Recurrence Period (a)	Horizontal Dislocation (m)				Vertical Dislocation (m)
	100a 1%	100a 2%	100a 5%	100a 10%	100a 1%	100a 2%	100a 5%	100a 10%
10,000	2.40–3.39	0~2.40	/	/	1.41–2.00	0–1.41	/	/
5000	3.39–4.68	2.40–3.39	/	/	2.00–2.75	1.41–2.00	/	/
2000	5.13–6.76	3.76–5.13	2.40–3.39	0–2.40	2.99–3.80	2.24–2.99	1.41–2.00	0–1.41
1000	6.76–7.76	5.13–6.76	3.39–4.62	2.40–3.39	3.80–4.57	2.99–3.80	2.00–2.75	1.41–2.00

. Based on the above results, we can draw the following conclusions:

(1)

For Holocene faults with different T_RP, the possibility and distance of future surface displacements are significantly different. The surface displacement distance of strong active faults in the Holocene may have reached 2–3 times the surface displacement distance of extremely weak active faults in the same condition. For faults with the same T_RP, under different t_et, the assessment results of surface displacements also differed by 20% to 40%. This means that when correctly assessing the future surface displacement distance of active faults, it is necessary to consider the T_RP and t_et of the faults.

(2)

The possibility of surface displacement caused by extremely weak Holocene active faults is very low. The hazard of surface displacement needs to be considered only when the return period of the ground motion of concern in a project is close to or exceeds 10,000 years (1% exceedance probability over 100 years). This conclusion is in good agreement with the regulation in many seismic design codes in mainland China that “the hazard of surface displacement on late Pleistocene faults does not need to be considered”.

(3)

Since the return period of ground motion focused on in linear engineering is mostly no more than 2000 a, we do not need to consider the surface displacement hazard of extremely weak Holocene active faults and weakly active faults (an active fault with a T_RP ≥ 5000 a).

(4)

When the t_et of the active fault is close to or longer than the T_RP, the hazard of surface displacement will increase significantly: Faults that would not otherwise cause surface displacement also have the possibility of generating surface displacement (e.g., the intensely Holocene active fault, when the exceedance probability is 10% over 100 years); faults that originally have the hazard of producing surface displacement may produce greater surface displacement with the same exceedance probability.

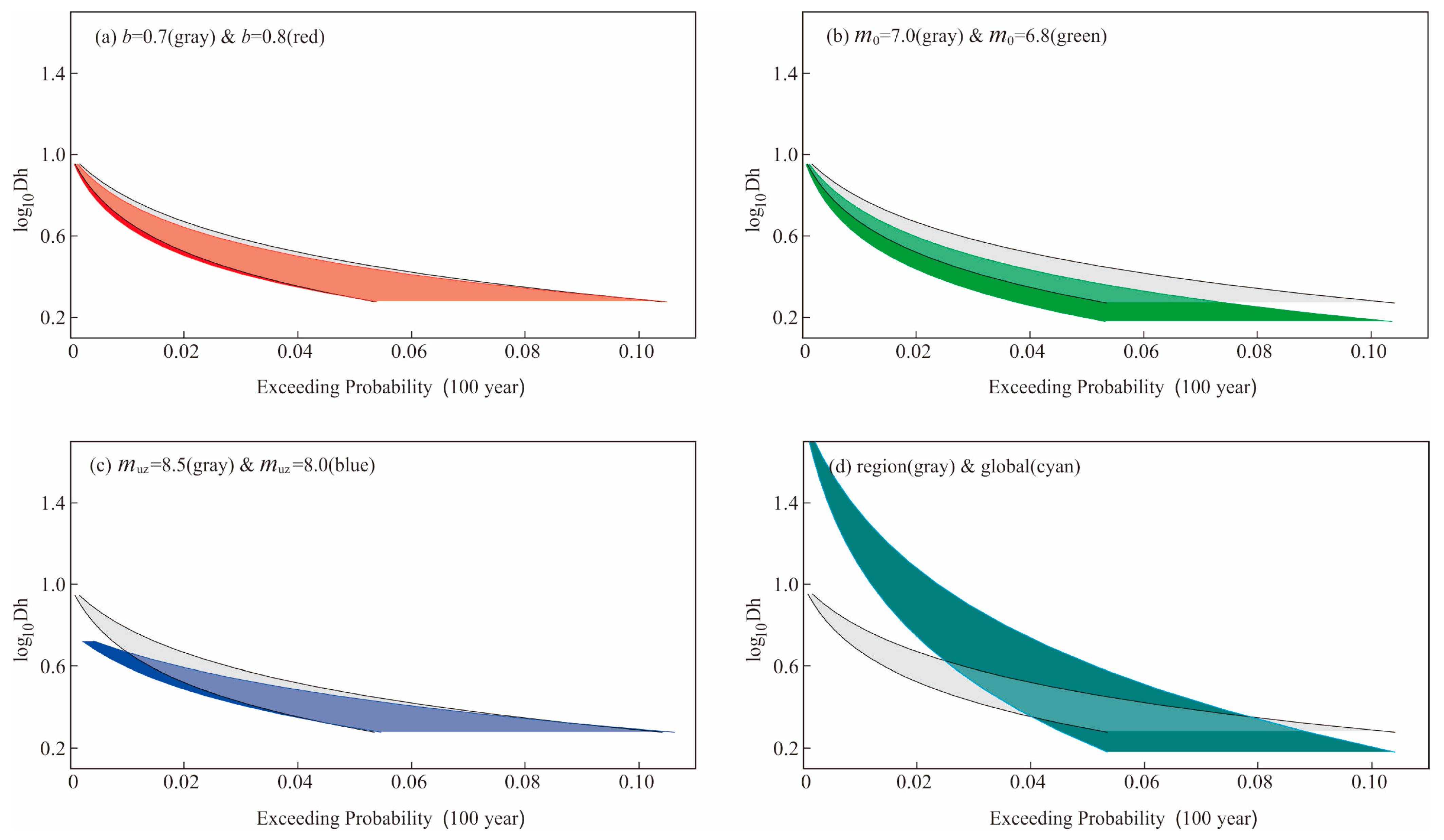
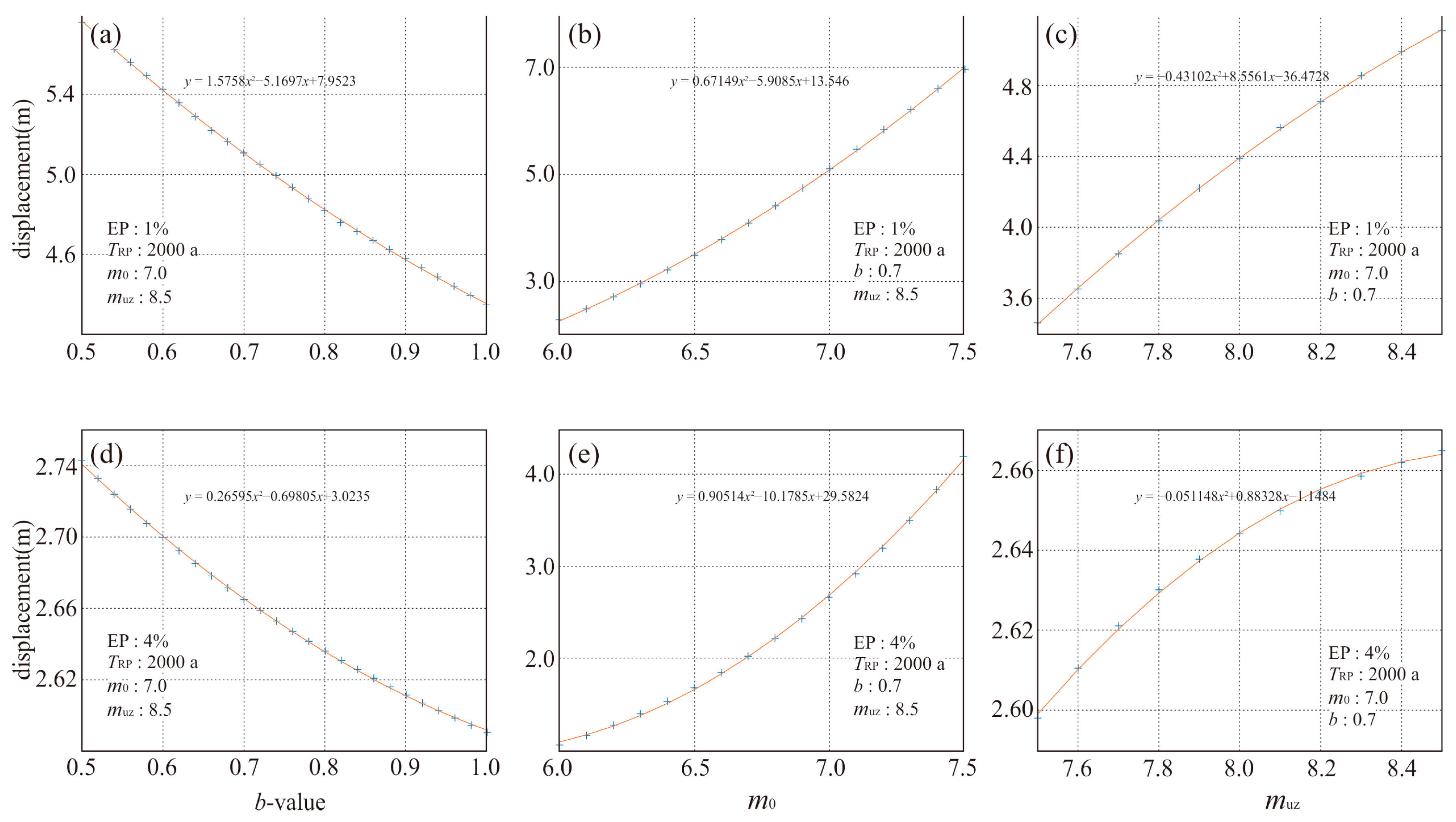
3.2. Analysis of Influencing Factors

In the calculation process of this paper, a variety of parameters were employed, including the b-value, the minimum magnitude m₀ for generating surface displacement, the upper limit of magnitude m_uz, and the statistical relationship between magnitude and surface displacement distance. In the previous calculations, the parameters we used were b = 0.7, m₀ = 7, and m_uz = 8.5. This is because we utilized the statistical relationship in southwestern China. The first three parameters reflect the geological and seismological background of the southwestern region of China. The values of these parameters may affect the results of the displacement assessment. Before using the surface displacement distances given in this paper for design, the influence of these parameters needs to be analyzed (Figure 2).

(1)

The impact of b-values

The physical meaning of the b-value is the ratio of the number of earthquakes with small magnitudes to the number of earthquakes with large magnitudes within a certain space [38,39,40,41,42]. On the global scale, the b-value is nearly 1 on average. In different regions, the b-values were slightly different. In general, the b-values of seismically active areas are slightly less than 1, e.g., the b-value of Yunnan Province, China, is approximately 0.8. The b-value can also reflect the stress of the crustal medium to a certain extent. In the calculations in the previous section, the b-value we used was 0.7.

Figure 2a shows the calculated exceedance probability–horizontal displacement values when the b-value is 0.7 (gray area) and 0.8 (red area). It can be seen that (1) the surface displacement distance and b-value are negatively correlated, and the larger the b-value is, the smaller the surface displacement distance; (2) when the exceedance probability is 1~2%, the surface displacement distance changes the most, and when the exceedance probability is greater than 2%, the surface displacement distance changes less; (3) when the b-value increases from 0.7 to 0.8, the variation in the displacement amount with the 1% exceedance probability over 100 years decreases from 5.13–6.61 m to 4.68–6.31 m, with an average reduction of 7.7%; when the probability of exceedance is 5% over 100 years (return period of 2000 a), this value rapidly decreases to 0~0.4%.

On the global scale, the b-value is approximately 1; the b-value of areas with strong seismic activity is generally no lower than 0.7; for example, the b-value of Yunnan Province on the southeastern margin of the Tibetan Plateau is approximately 0.8. Therefore, (1) the surface displacement distance calculated by setting b = 0.7 in the calculations in this paper is already enough and safe; (2) for most linear projects, the seismic motion return period that designers focus on is less than 2000 years, so during the recurrence period, the effect of the b-value was negligible.

(2)

The minimum earthquake magnitude m₀ that generates surface displacement

According to historical earthquake damage data in mainland China, the vast majority of earthquakes with magnitudes of 7 or above will generate surface ruptures, while some earthquakes with magnitudes lower than 7 may generate surface ruptures. Whether a major earthquake can generate surface rupture depends on many factors, such as magnitude, focal depth, fault properties, and overburden thickness.

In the calculation process in the previous section, we set m₀ to 7, which is suitable for Yunnan Province in mainland China. The seismicity in Yunnan Province has the following characteristics: The focal depth is shallow, generally at 10–15 km; the nature of the faults is strike-slip movement; and the thickness of the overburden along the active faults is generally not large (0–20 m). These properties together determine that it is appropriate to use 7 in this area for m₀. However, this value is not necessarily applicable to other regions, such as Northeast China (where the overburden is particularly thick).

Evidently, the value of m₀ has a great impact on the displacement. If the calculated value is d when m₀ = 7, then when the uncertainty of m₀ is 0.2, the uncertainty of d can reach 25%; if the uncertainty of m₀ is 0.5, the uncertainty of d can reach 60%. Therefore, when using the method given in this paper to calculate future fault displacement, the local seismic–tectonic background should be analyzed, especially the thickness of the overburden at the location of the trench. Then, the logistic regression method or other methods can be used to obtain a relatively accurate m₀, and the uncertainty of the given m₀ can be evaluated. The reliability of the m₀ value is very important for the reliability of future fault surface displacement hazard analysis. If an area has a very thick layer of soil covering [36], or if the groundwater depth is relatively shallow [43,44], then m₀ might be relatively large. In such cases, if m₀ = 7 is taken, it could potentially underestimate the risk of surface displacement.

(3)

Upper magnitude limit m_uz of a fault

This parameter describes the maximum earthquake magnitude that can occur on an active fault. The maximum earthquake magnitude that can occur on a Holocene active fault is related to the tectonic location, fault length, and fault shape [45,46,47]. Based on historical earthquake statistics and focal rupture inversion results, it can be roughly considered that Holocene faults with lengths of up to 30 km have tectonic conditions conducive to the occurrence of an earthquake with a magnitude of 7, and Holocene faults with lengths of up to 300 km have tectonic conditions conducive to an earthquake with a magnitude of 8. In general, active faults inside the plates do not have the tectonic conditions to generate earthquakes with a magnitude of 8.5 or greater. In the historical earthquake records of mainland China, there is no earthquake record with a magnitude greater than 8.5.

Figure 2c shows the calculated exceedance probability–horizontal displacement when m_uz is 8.5 (gray) and 8.0 (blue). It can be seen that (1) in general, the lower the value of m_uz is, the lower the calculated displacement; (2) when the return period is short, the difference between the two is basically negligible (e.g., the return period is 2000 years, difference < 7%); (3) when the return period increases to 5000–1000 years (exceedance probability 2–1% over 100 years), the result of m_uz = 8.0 is approximately 19–35% lower than the result of m_uz = 8.5. For most linear projects, the action of ground motion with a return period greater than 2000 a is generally not considered, so the magnitude upper limit has little impact on the assessment results. At the same time, the upper limit of the magnitude used in the present study is 8.5, which is greater than the maximum seismic capacity of most faults. Therefore, our assessment results are enough and safe.

(4)

Statistical relationship between magnitude and surface displacement distance

All the current probabilistic surface displacement hazard assessment methods essentially calculate the exceedance probabilities of earthquakes of different magnitudes first and then convert them to exceedance probabilities of different surface displacement distances based on the statistical relationship between magnitude and surface displacement distance. Different regions, different researchers, different historical earthquake example datasets, and different statistical methods will obtain different statistical relationships. If different statistical relationships are used, the resulting surface displacement distances may be quite different. The selection of an appropriate magnitude–surface displacement distance statistical relationship is important for reasonably assessing the distance of future surface displacement on the fault.

This paper uses the statistical relationship based on the work of Huang (2016) [36]. The surface displacements of 30 strike-slip earthquakes in western China were collected, and the relationship between the surface displacements and magnitudes was calculated. Most earthquakes in the province are strike-slip, so this statistical relationship is more in line with our actual situation. We compared the magnitude–surface displacement distance statistical relationship (regional model) used in this paper with the most widely used international statistical relationship (global model) given by Wells and Coppersmith (1994) [45] (Figure 2d).

Figure 2d shows the calculated horizontal displacement values under the two statistical relationships. It can be seen from the figure that (1) the results of the regional model and the global model are significantly different; (2) when the return period exceeds 1200 a (the exceedance probability is less than 8% over 100 years), the difference between the two increases rapidly. When the return period is 10,000 years (the exceedance probability is 8% over 100 years), the global model is 230% larger than the regional model; (3) when the return period is lower than 1200 years (the exceedance probability is greater than 8% over 100 years), the two also differ; and when the return period is 1000 years (the exceedance probability is 10% over 100 years), the regional model is 26% larger than the global model.

Under the condition that the strong earthquake recurrence period of a fault is 2000 and the value of b is 1, the magnitude of the earthquake corresponding to a 100-year exceedance probability of 1% is approximately 7.7. Researchers have field surveyed the surface displacement distances of several earthquakes with magnitudes of 7.6–8 in mainland China, and their survey results are as follows.

The maximum horizontal displacement of the 1931 Fuyun M8 earthquake was 6.7 m, and the average horizontal dislocation was 6.3 m [48].

The maximum horizontal displacement of the 1970 Tonghai M7.8 earthquake was 3.3 m [49].

The maximum horizontal displacement of the 1973 Luhuo M7.9 earthquake was 3.6 m [50,51].

The maximum horizontal displacement of the 1988 Lancang M7.6 earthquake was 2.2 m [52].

The maximum horizontal displacement of the 2001 West Kunlun Ms8.1 earthquake was 6.4 m, and the maximum vertical displacement was 4 m [53].

The maximum horizontal displacement of the 2008 Wenchuan Ms7.9 earthquake was 6.8 m [54].

The horizontal displacements of the six abovementioned earthquakes with magnitudes ranging from 7.6–8.1 m and from 2.2–6.8 m. For an earthquake with a magnitude of 7.6–8.1, the calculated horizontal dislocation is 4.00–6.28 m according to the regional model, and the calculated horizontal displacement is 6.28–20.56 m according to the global model. For western mainland China, the assessment results given by the regional model we used are more accurate. Of course, if the method proposed in this paper is used to assess the surface displacement hazard of faults in other countries and regions, then the magnitude–displacement distance statistical relationship suitable for the project area must be selected; otherwise, enormous deviations will occur.

(5)

Sensitivity of the results to the b-value, m₀, m_uz

To further analyze the impact of b-value, m₀, and m_uz on the analysis, we conducted a sensitivity analysis of these parameters. Taking a fault with T_RP = 2000 a and t_et = 0.5 as an example, we calculated the variation in surface displacement when two of the parameters (b-value, m₀, m_uz) are held constant and the third parameter varies. The results are shown in Figure 3. In terms of the impact of b-value: At a 100-year exceedance probability of 1%, for every 0.1 decrease in b-value, the surface displacement increases by 0.20–0.36 m (Figure 3a); at a 100-year exceedance probability of 4%, for every 0.1 decrease in b-value, the surface displacement increases by 0.017–0.043 m (Figure 3d). Most buildings are designed considering a 4% exceedance probability of ground motion over 100 years. When the uncertainty of the b-value is 0.2, the uncertainty of surface displacement is less than 0.1 m; hence, surface displacement is not sensitive to changes in the b-value. Regarding the impact of m₀: At a 100-year exceedance probability of 1%, for every 0.1 decrease in m₀, the surface displacement decreases by 0.21–0.42 m (Figure 3b); at a 100-year exceedance probability of 4%, for every 0.1 decrease in m₀, the surface displacement increases by 0.07–0.34 m (Figure 3e). At a 100-year exceedance probability of 4% and an uncertainty of m₀ of 0.2, the uncertainty of surface displacement is close to 0.7 m; therefore, surface displacement is quite sensitive to changes in m₀. In terms of the impact of m_uz: At a 100-year exceedance probability of 1%, for every 0.1 increase in m_uz, the surface displacement increases by 0.12–0.21 m (Figure 3c); at a 100-year exceedance probability of 4%, for every 0.1 increase in m_uz, the surface displacement increases by 0.001–0.012 m (Figure 3f). At a 100-year exceedance probability of 4% and an uncertainty of m_uz of 0.5, the uncertainty of surface displacement is 0.06 m; therefore, surface displacement is not sensitive to changes in m_uz. In a comprehensive analysis, the sensitivity of m₀ is more than 10 times that of the b-value and m_uz.

4. Discussion

Here, we take a specific active fault as an example to analyze the similarities, differences, and causes between the assessment results of the PFDHA-td method and the assessment results of other methods. The applicability of this method to other global regions is discussed. Based on some shortcomings in the methods used in this study, suggestions are proposed for the future development of probabilistic displacement assessment methods.

4.1. Comparison with Other Methods

The Milin fault is an important active fault in western China, and a number of important projects, such as the Sichuan–Tibet Railway, have traversed this fault. Some researchers have used the PFDHA or other probabilistic assessment methods based on seismicity parameters to estimate the future surface displacement hazard of the Milin Fault [55,56]. We used the PFDHA-td method to calculate the surface displacements of the Milin fault under the two cases of t_et = 0.5 and t_et = 1. The parameters used in the calculation process were m₀ = 7.0, m_uz = 7.5, b = 0.8, and T_RP = 7000 a [57,58]. Finally, the surface displacements calculated by the deterministic evaluation method are given in

Table 3. Surface displacement displacements of the Milin fault (m) in different methods.

Source	Exceedance Probability (over 100 a)
	4%	2%	1%
Wang, 2016 * [55]	1.39	2.39	3.13
Zeng, 2018 * [56]	1.29	2.15	2.93
PFDHA-td (tet = 0.5)	1.65	2.17	2.69
PFDHA-td (tet = 1)	2.16	2.69	3.15
Deterministic methods		3.61

* The surface displacement distance–magnitude relationship in these articles has been replaced by the surface displacement distance–magnitude relationship used in this paper.

.

In Table 3, Wang (2016) [55] and Zeng (2018) [56] used the same seismicity parameters and similar probabilistic assessment methods; therefore, the assessment results were similar. Compared with those of the former two methods, the results calculated by the PFDHA-td (t_et = 1) method were much higher (55%) when the exceedance probability was 4%, were higher when the exceedance probability was 2%, and were the same when the exceedance probability was 1%. This difference results from two aspects. First, in terms of the average rate of earthquake occurrence, the parameters used in the PFDHA methods are derived from experience and tectonic analogy, while the parameters used in the PFDHA-td method are derived from the true values of the fault itself. Second, paleoseismic studies have shown that there has been no paleoseismic record on this fault over the last 7000 years [56], and the elapsed time for this fault approaches 1. The PFDHA methods do not consider the increased probability of earthquakes due to the accumulation of stress in the crustal medium; hence, the calculated values are smaller. It can be seen that the PFDHA-td method reflects the true activity parameters of the fault and takes into account the degree of stress and energy accumulation on the fault; therefore, the surface displacements assessed by this method may be more accurate. However, the PFDHA methods may underestimate the potential surface displacement risk, especially at higher exceedance probabilities.

The maximum earthquake magnitude that can occur on this fault is 7.5 [55,56]. Based on this magnitude, we further calculated the surface displacement hazard using the deterministic method.

The most important seismic motion of the Sichuan–Tibet Railway is the seismic motion of a return period of 2475 years (exceedance probability 4% over 100 years). With this exceedance probability, if the t_et on the fault is not considered, the surface displacement distance given by the other two probabilistic assessment methods will be low, which will increase the hazard to the railway. The surface displacement distances given by the deterministic evaluation methods are far greater than those given by all the probabilistic evaluation methods, which will lead to a substantial increase in the construction cost of the project. For example, in the tunnel anti-displacement design, the “over-excavation design” method is often used. That is, when crossing an active fault zone, the tunnel cross-section size is enlarged, and a double-layer lining is adopted, with porous materials filled between the inner and outer linings. When the fault slips, the gap between the inner and outer linings can ensure the net cross-sectional area of the tunnel. The greater the displacement we provide, the greater the corresponding engineering volume and the construction cost will also increase accordingly [59,60]. Other designs of anti-displacement will also increase construction costs [61,62,63,64]. Through comparison and analysis, compared with other methods, the PFDHA-td method does not underestimate the hazard of surface displacement of active faults and can provide reasonable surface displacement results for project construction. At the same time, compared with the deterministic method, the project construction cost is reduced to a certain extent.

4.2. Applicability of the PFDHA-td Method in Other Countries and Regions

Including the PFDHA-td method in this paper, most probabilistic displacement assessment methods first study the occurrence probability or exceedance probability of earthquakes with different magnitudes on a fault. Taking this paper as an example, Equations (1)–(11) are used to calculate the exceedance probability of earthquakes of different magnitudes. In this process, the parameters used were mainly the b-value, m₀, m_uz, T_RP, and t_et. After a certain amount of work, the above five parameters can be obtained for active faults in any country and region; thus, the exceedance probabilities of earthquakes of different magnitudes can be calculated.

After obtaining the exceedance probabilities of earthquakes of different magnitudes, we used the magnitude–surface displacement distance relationship (i.e., Equations (12) and (13)) to convert the exceedance probabilities of earthquakes of different magnitudes into those of different displacement values. This step determines the direct applicability of the calculation results. In this paper, we used the statistical relationship of western mainland China. Therefore, the calculation results are more suitable for western mainland China. In this step, if the magnitude–surface displacement distance relationship comes from other countries or regions, then the calculation results are applied to that region. Therefore, the PFDHA-td method proposed in this paper is applicable to other countries and regions around the world.

The statistical relationship between the earthquake surface displacement distance and magnitude varies significantly among different countries and regions. Therefore, we recommend that researchers in other countries and regions calculate reliable empirical relationships before using the method in this paper for assessment. The resulting values evaluated in this paper can also be used for transformation. Of course, if the amount of data (seismic cases) is insufficient, the global model [45] can be used, although the evaluation results may be too large.

4.3. Limitations and Future Studies of PFDHA-td

In the surface displacement assessment of active faults, the accuracy of the assessment results is our most important aspect. The PFDHA-td method proposed in this paper focuses on the activity characteristics of the active fault itself and uses two activity parameters of the active fault to provide a high-precision calculation method for surface displacement assessment under different exceedance probabilities. Compared with other existing assessment methods, the PFDHA-td method considers the physical mechanism of earthquake occurrence and the activity characteristics of active faults; therefore, surface displacement assessments are more credible and effective.

The biggest limitation is that high-precision T_RP and t_et data are difficult to obtain. Obviously, if we could obtain high-precision data, we would be able to accurately assess the displacement of active faults. However, due to various factors, such as the uncertainty of dating data, the uncertainty of stratigraphic age, and the uncertainty caused by a limited number of data in statistical analysis, we may not be able to obtain high-precision T_RP and t_et data. Addressing the issue of data uncertainty, future work may focus on two aspects: One is to improve dating methods and statistical analysis to reduce the uncertainty of dating data; and the second is to study the relationship between other activity parameters of active faults and T_RP and t_et, for example, studying how to convert the slip rate of active faults into T_RP and t_et.

Based on the previous quantitative analysis of the influencing factors, the parameter of the minimum earthquake magnitude (m₀) represented by the paleoseismic events revealed in the trench has a great influence on the assessment results. In this paper, we chose a relatively conservative value, that is, m₀ = 7. The surface displacement of the fault calculated under this parameter is on the safe side, and there is a hazard of overestimating the surface displacement. Therefore, in the future, the value of m₀ can be studied in detail to further improve the accuracy of the evaluation results. There are many factors that affect m₀, among which the two most important are the thickness of the cover layer and the groundwater depth. Future research can be conducted from these two perspectives.

In addition to T_RP and t_et, other important activity parameters on active faults, such as the geological slip rate, GNSS slip rate, strong earthquake gap, and locking depth, can also be considered. These parameters also reflect the activity characteristics of active faults and the physical processes of energy accumulation and release in the crust. If one or more of these parameters are included in the evaluation process, it is expected that the accuracy of the evaluation will improve.

There are two types of coseismic displacement generated by an earthquake. One is the displacement at the principal fault, which generally occurs in the range of a few centimeters to tens of centimeters with a surface displacement distance of tens of centimeters to several meters; the other is the distributed fault. This displacement generally occurs within the range of tens of meters to hundreds of meters on both sides of the principal fault, and the cumulative displacement is generally tens of centimeters to several meters. The coseismic surface displacement of an earthquake generally refers to the coseismic surface displacement of the principal fault. The method proposed in this paper is suitable for the displacement assessment of principal faults. The coseismic surface displacement of the distributed fault will also cause deformation of the building, resulting in economic losses or casualties. In the future, the study of the coseismic surface displacement of distributed faults could be strengthened.

Finally, we use Equation (4) to characterize the probability of earthquakes occurring on faults. Although this formula draws on the BPT model, a more reliable periodic earthquake occurrence probability formula, and has made some corrections based on it, our formula may not truly capture the temporal variation characteristics of earthquake occurrence probabilities on faults. Further research on earthquake occurrence probabilities may be needed in the future.

4.4. Reproducibility

In our article, all the calculation formulas used are fully displayed in Equations (1) to (13). Figure 1, Figure 2, Figure 3 and Figure 4 present the main outcomes of this paper. In the calculation process of these results, we employed three parameters: b, m₀, and m_uz. In this paper, the values of these three parameters are b = 0.7, m₀ = 7, and m_uz = 8.5, respectively. Additionally, we used different values of T_RP and t_et as independent variables to ultimately obtain surface placements under various conditions. These calculation processes are reproducible, and the results obtained are consistent with those presented in this paper. Our results exhibit good reproducibility.

5. Usage and Example (Western Mainland China and the World)

5.1. Usage in Western Mainland China

Most of the time, when using this method to assess future surface displacement, the default values for b (0.7), m₀ (7.0), and m_uz (8.5) can be used. In addition, as long as the T_RP and t_et of the active fault near the project site are obtained, the future surface displacement values of the active faults can be obtained relatively simply. The specific process is as follows:

(1)

The recurrence period (T_RP) and elapsed time (t_et) of strong earthquakes are obtained through trenching, geological surveys, or other methods.

(2)

Based on the rake angle (slip direction), given by striations on the fault, the ratio of the horizontal displacement to the vertical displacement of the fault was obtained.

(3)

The average annual occurrence rate of strong earthquakes is calculated based on the T_RP data.

(4)

The annual occurrence rate of strong earthquakes is calculated based on the average occurrence rate of strong earthquakes and the t_et data.

(5)

The return period considered for the project is determined and the return period to the exceedance probability over 100 years is converted.

(6)

To find the intersection points of the annual occurrence rate curve and the exceedance probability in Figure 4, the horizontal displacement and vertical displacement of the fault can be calculated according to the value of the vertical axis corresponding to the intersection point.

(7)

The total displacement is calculated based on the horizontal displacement and vertical displacement; according to the rake angle given by striations on fault, the total displacement is decomposed into the horizontal direction and the vertical direction.

(8)

For buildings such as railways and oil pipelines that are directly laid on the ground, we can directly use the displacement values we have calculated. For bridges and other structures that span active faults in the air, methods like RSA (Response Spectrum Analysis) need to be employed to calculate the response displacement of the bridges [65,66,67].

5.2. Example

An important bridge crossed the A fault. We excavated some trenches near the fault and the bridge. The T_RP on the faults revealed by the trenches was 1500 years, and the t_et was 900a/1500a = 0.6. The rake angle given by striations on fault was 15°. According to the importance of the bridge, the return period we are concerned with is 1950 years (5% probability of exceedance over 100 years).

(1)

Calculation of the average annual occurrence rate of strong earthquakes

$${\overline{\nu }}_0=1/1500=6.67\times {10}^{-4}/\mathrm{a}$$

(2)

Calculation of the annual occurrence rate of strong earthquakes

$${\nu }_0=2{\overline{\nu }}_0\times t_{\mathrm{et}}/T_{\mathrm{RP}}=(900+100)/1500\times {\overline{\nu }}_0=8.89\times {10}^{-4}/\mathrm{a}$$

(3)

Query the horizontal displacement and vertical displacement using Figure 4

In Figure 4a and Figure 4b, the closest value to 8.89 × 10⁻⁴/a is 8.91 × 10⁻⁴/a. The intersection points of the corresponding curve and x = 0.05 are 0.49 and 0.26, respectively. The calculated horizontal displacement and vertical displacement were 2.57 m and 1.48 m, respectively.

(4)

Calculate the total displacement and decompose the total displacement into the horizontal and vertical directions according to the rake angle.

The total displacement is 3.59 m. With a rake angle of 15°, the horizontal displacement is 3.59 m × cos15° = 3.46 m, and the vertical displacement is 3.59 m × sin15° = 0.93 m. Therefore, a horizontal displacement of 3.46 m and a vertical displacement of 0.93 m need to be considered.

5.3. Usage in Other Countries and Regions Around the World

The usages in other countries and regions are similar to those used in western China. One step between step (3) and step (4) is added; that is, after consulting and calculating the horizontal displacement and vertical displacement of the fault, the results are converted to earthquake magnitudes according to Equations (12) and (13); then, based on the regional magnitude–surface displacement distance empirical relationships, the earthquake magnitude is converted to new horizontal displacement and new vertical displacement.

6. Conclusions

Based on two activity parameters of active faults, T_RP and t_et, we proposed the time-dependent method for probabilistic fault displacement hazard analysis. This method takes into account the process of energy accumulation and release in the crust, which to a certain extent reflects the physical mechanism of earthquakes. The research results indicate that within the service life of a building, it is not necessary to avoid all Holocene active faults. The importance of the building, T_RP and t_et, should be comprehensively assessed to evaluate whether the active fault will cause surface displacement in the future and surface displacement values.

Under the premise of being relatively conservative and safe, the exceedance probability-displacement curves for the 27 annual occurrence rates of strong earthquakes were calculated and plotted. Designers can conveniently obtain the vertical and horizontal displacements based on the T_RP, t_et, and the return period of the building. When using the calculation results of this paper, designers must fully consider whether the parameters we used are consistent with the target area. If the cover layer in the target area is extremely thick, or the statistical relationship significantly differs from Formulas (12) and (13), the method provided in this paper should be used to recalculate the surface displacement values.

Although this study proposes a method for assessing surface displacement based on the physical mechanism of earthquake occurrence, which has a certain novelty, this study is still quite preliminary and has many limitations. For example, high-precision T_RP and t_et data are difficult to obtain through trenching and drilling methods; the assumption of such r increase in earthquake probability over time may not accurately reflect the occurrence probability of earthquakes; the m₀ in different areas may vary greatly, thus affecting the accuracy of the calculation results, etc. These limitations restrict the widespread use of this method. Due to the existence of these limitations, there is still much work to be completed in the future, such as how to solve the problem of high uncertainty in the T_RP and t_et of active faults, how to obtain more accurate non-stationary Poisson processes to describe the mechanism of earthquake occurrence, how to obtain accurate minimum earthquake magnitude that causes surface displacement, and so on. The hazard classification of engineering active faults still requires more researchers to conduct research together.