Systematic Rehabilitation Techniques and Dynamic Analysis of Bridge Deck System with Concrete-Filled Steel Tube Arches
Abstract
:1. Introduction
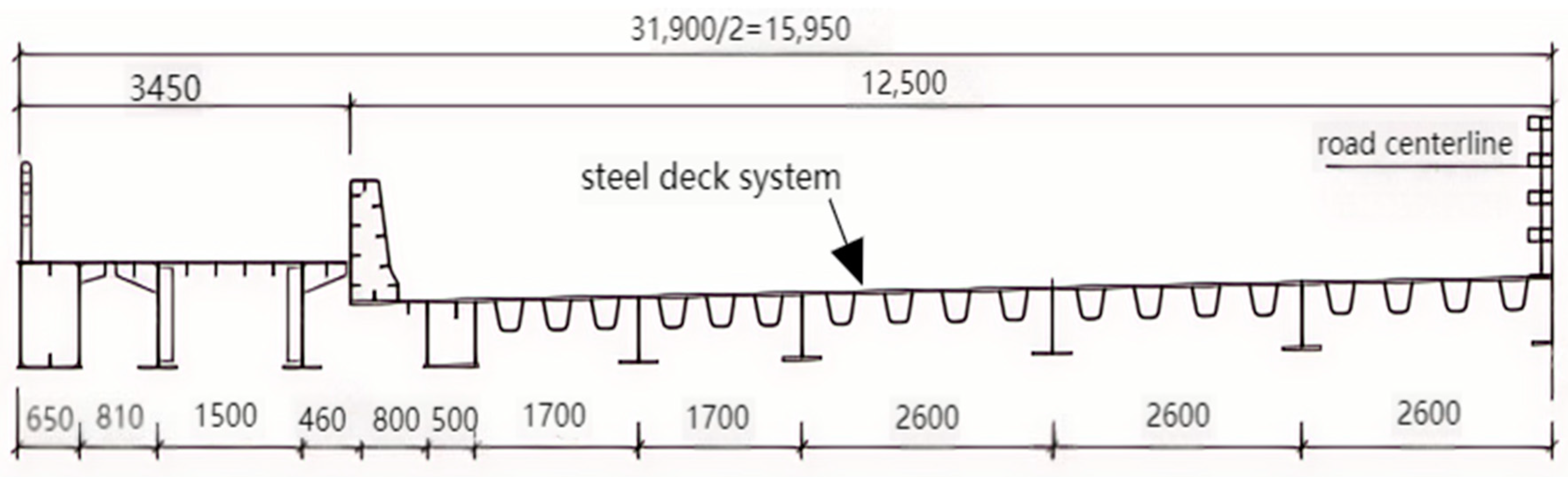
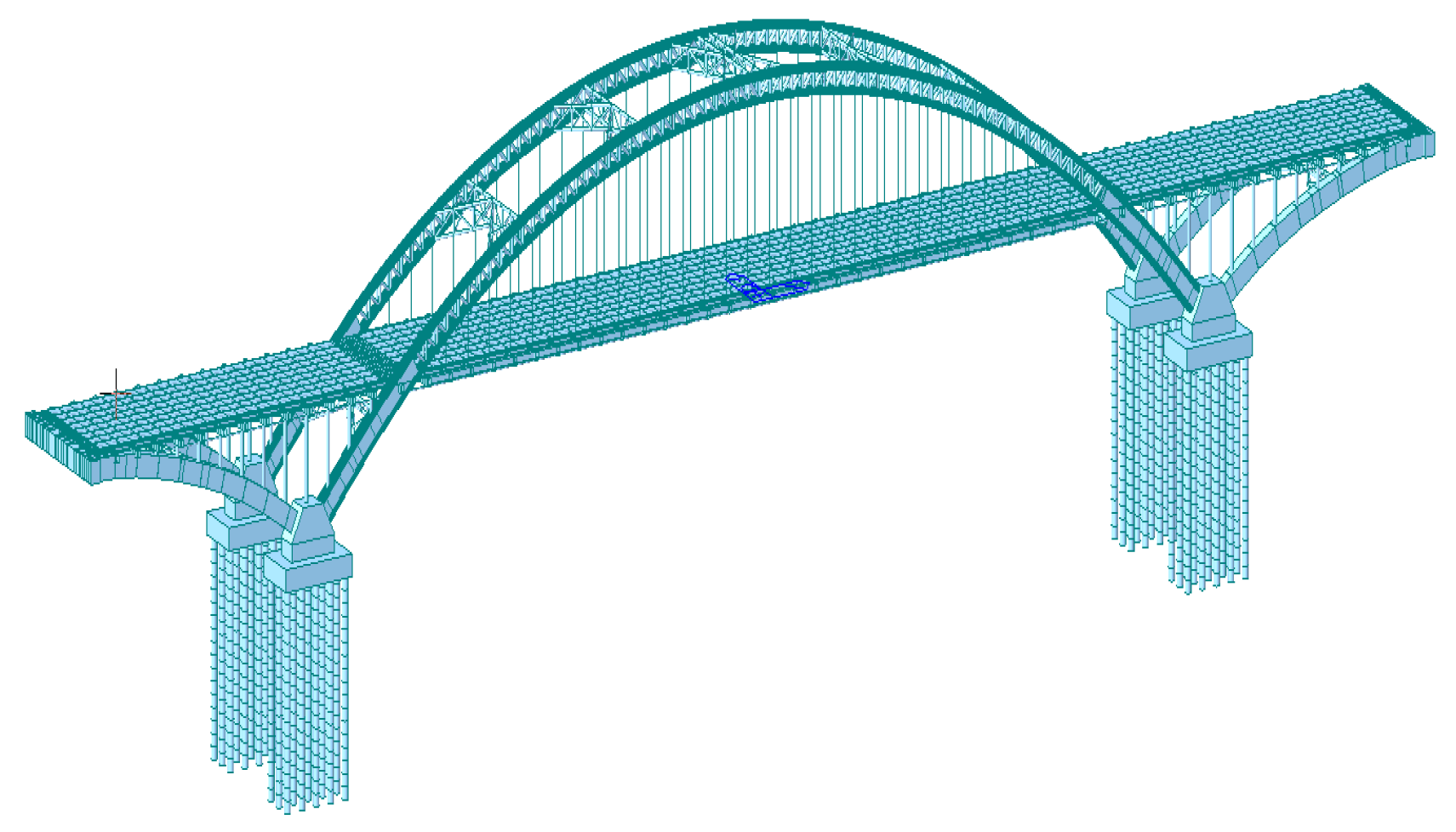
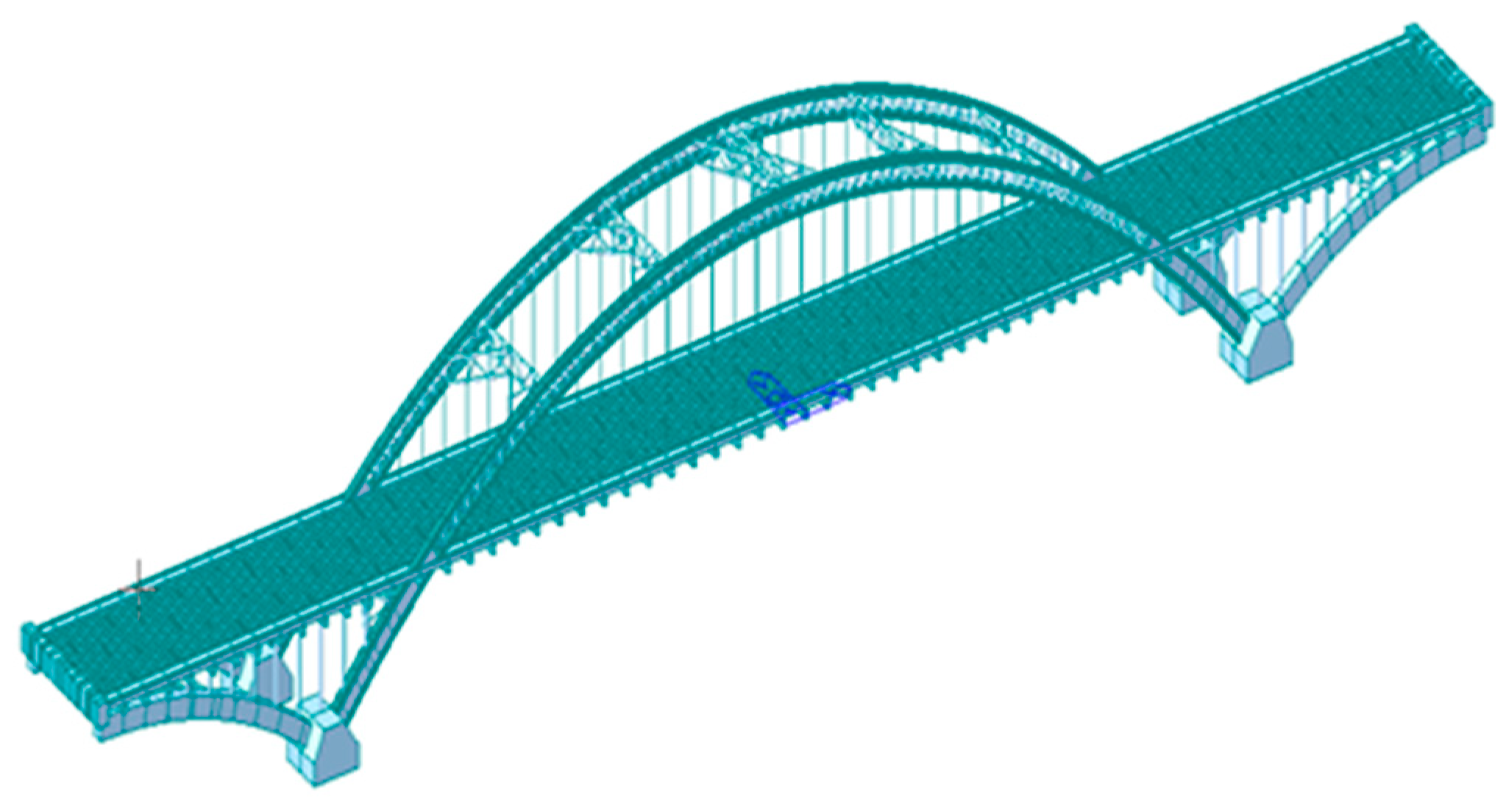
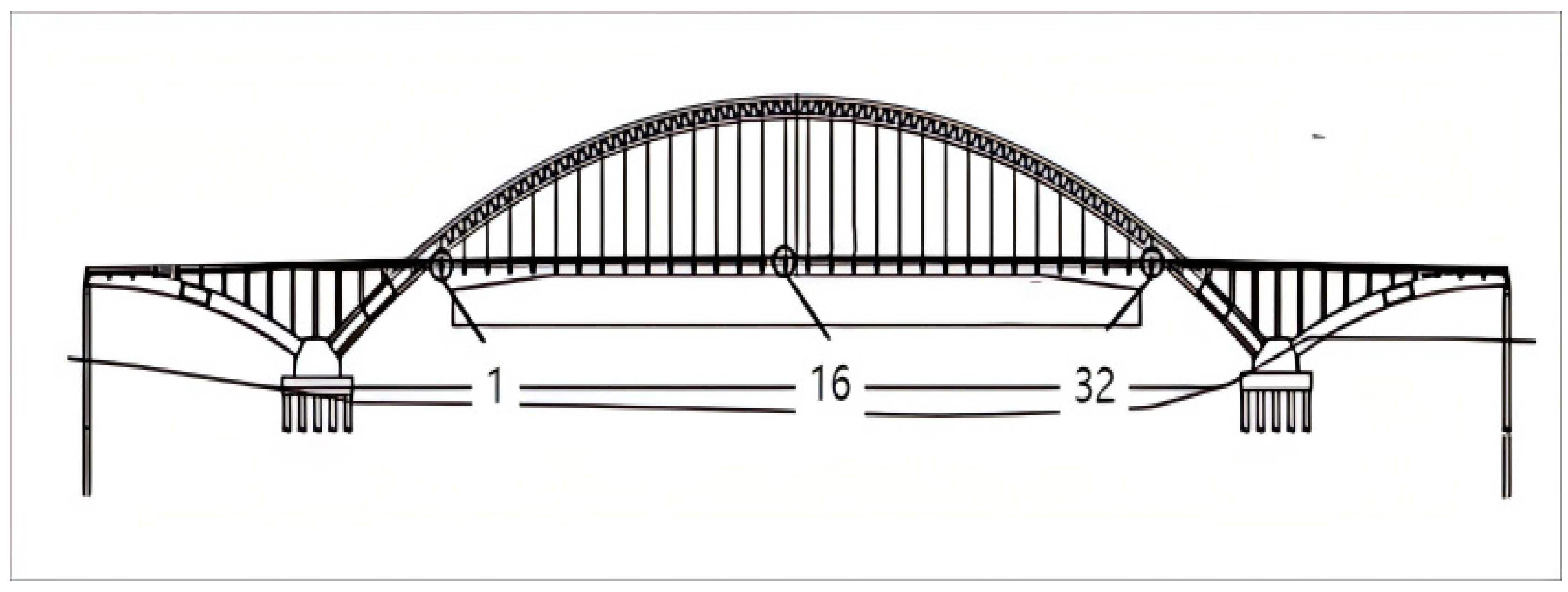
2. Description of the Bridge
3. Technical Plan for the Structural Renovation of the Main Bridge Deck System
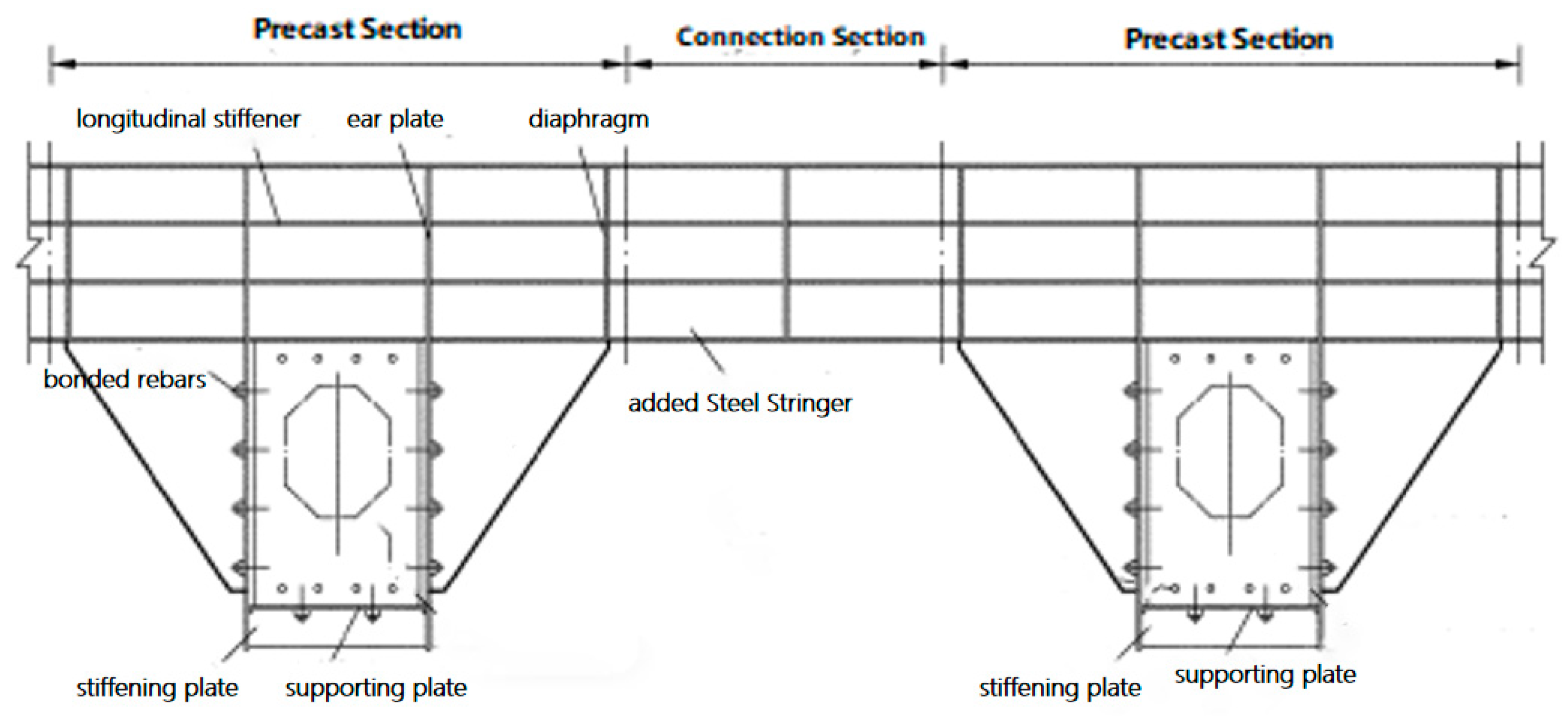
3.1. Additional Steel Crossbeams
3.2. Removal and Replacement of Deck Slabs
3.3. Additional Steel Longitudinal Beams
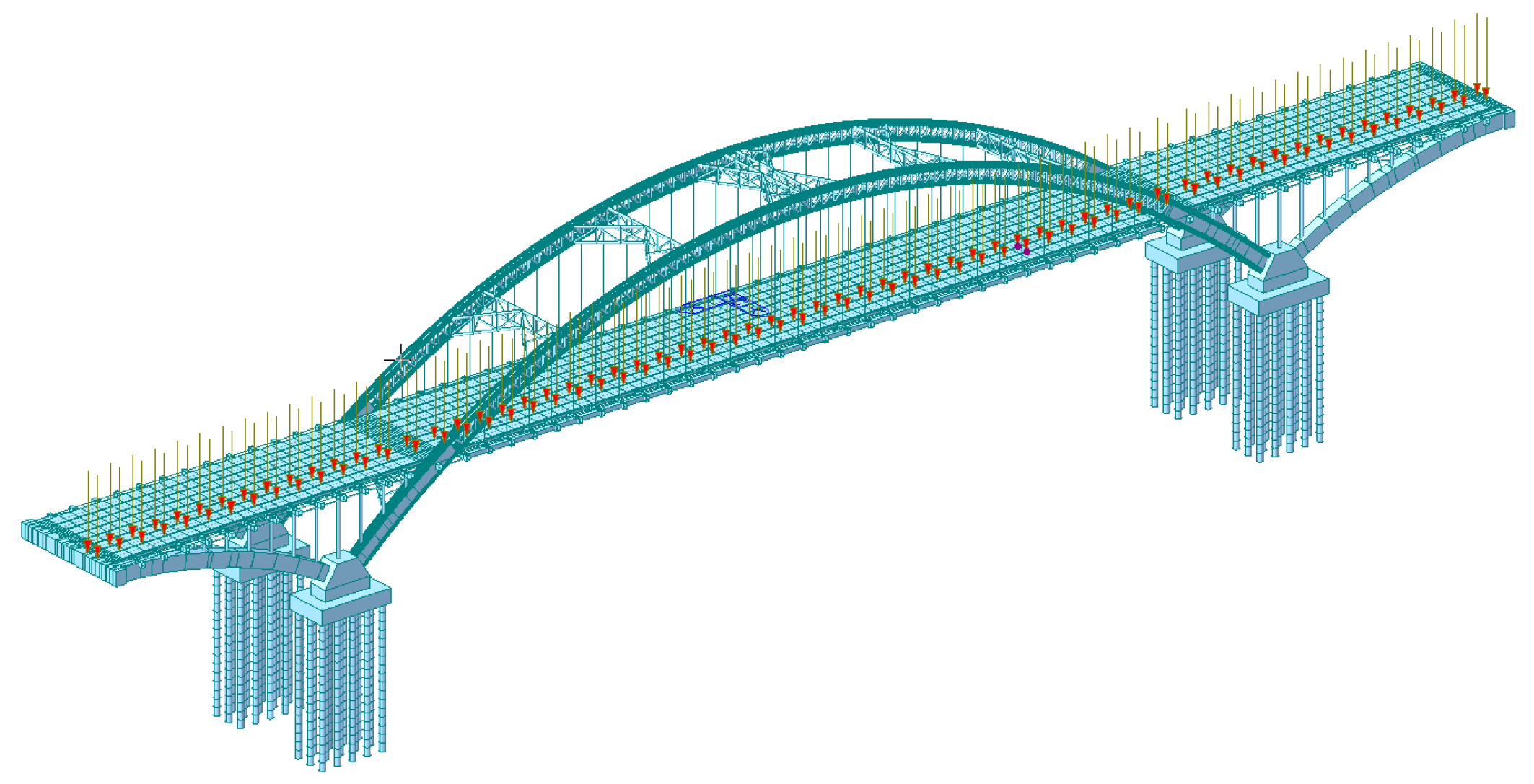
4. Finite Element Analysis
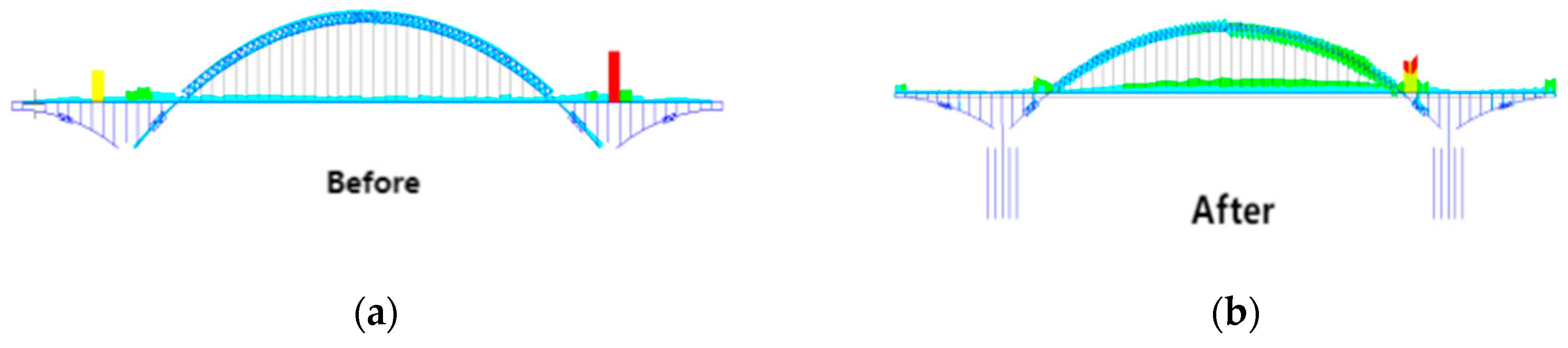
4.1. Finite Element Model Validation
4.2. Finite Element Simulation and Discussion
4.3. Stress of Suspenders
4.4. Stress of Arch Ribs
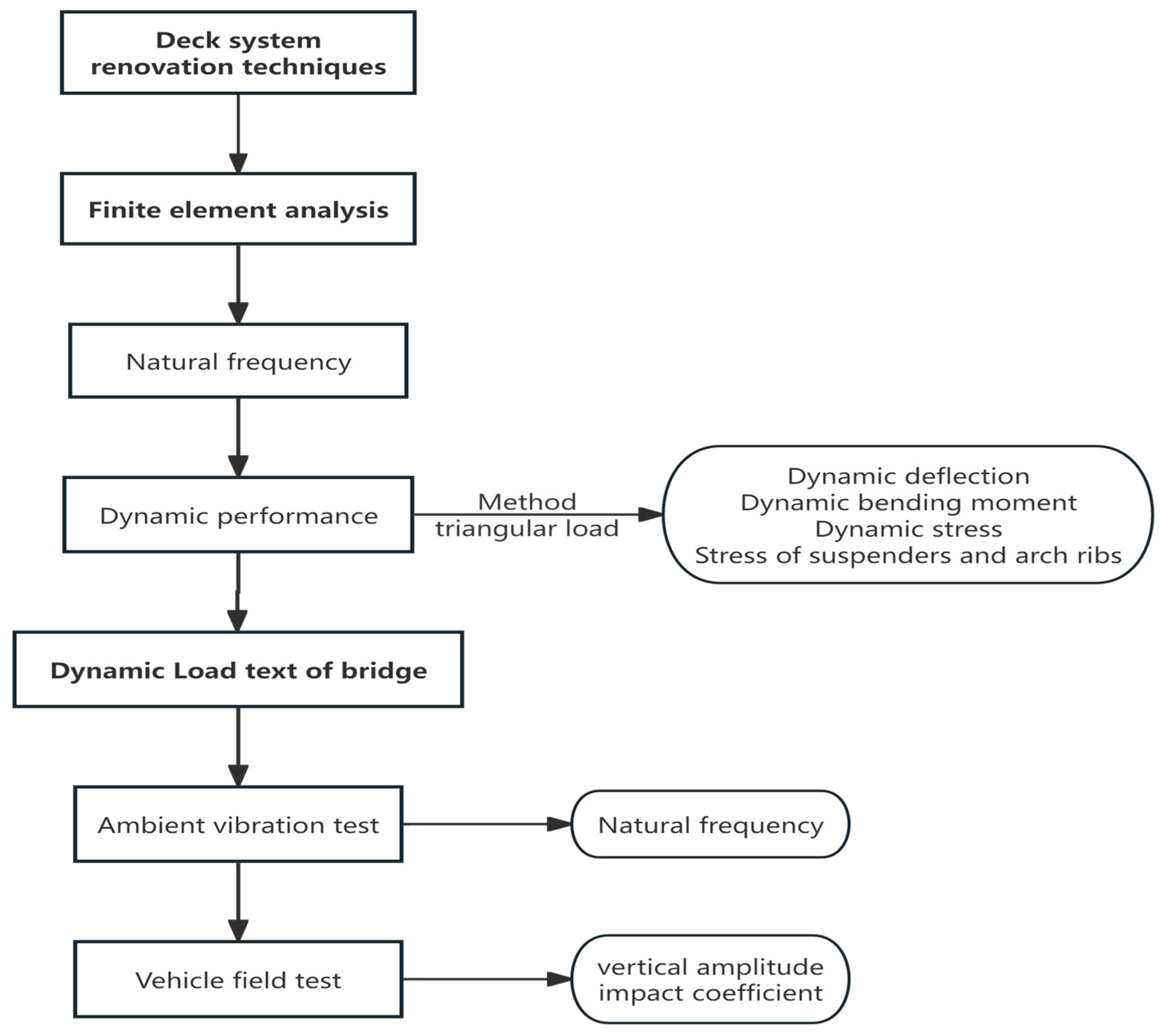
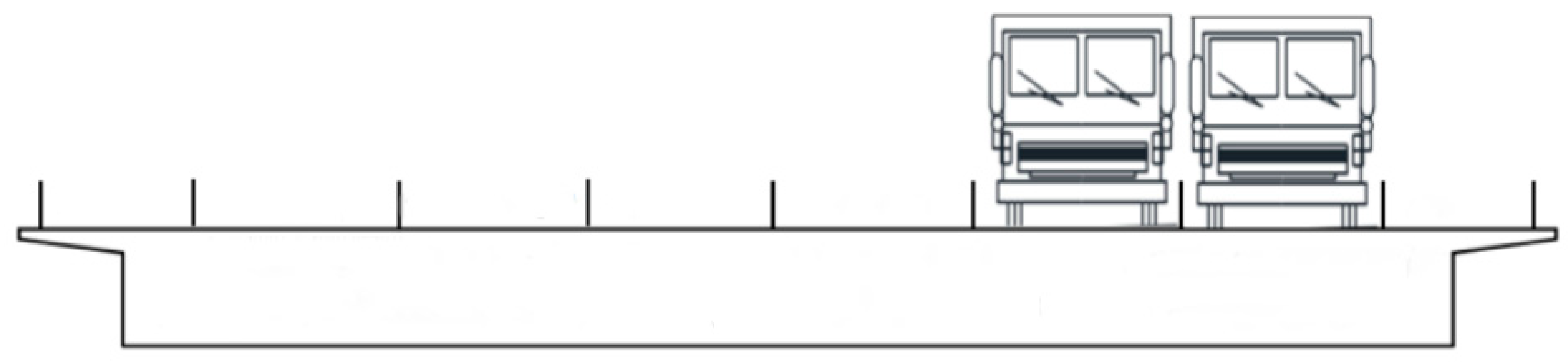
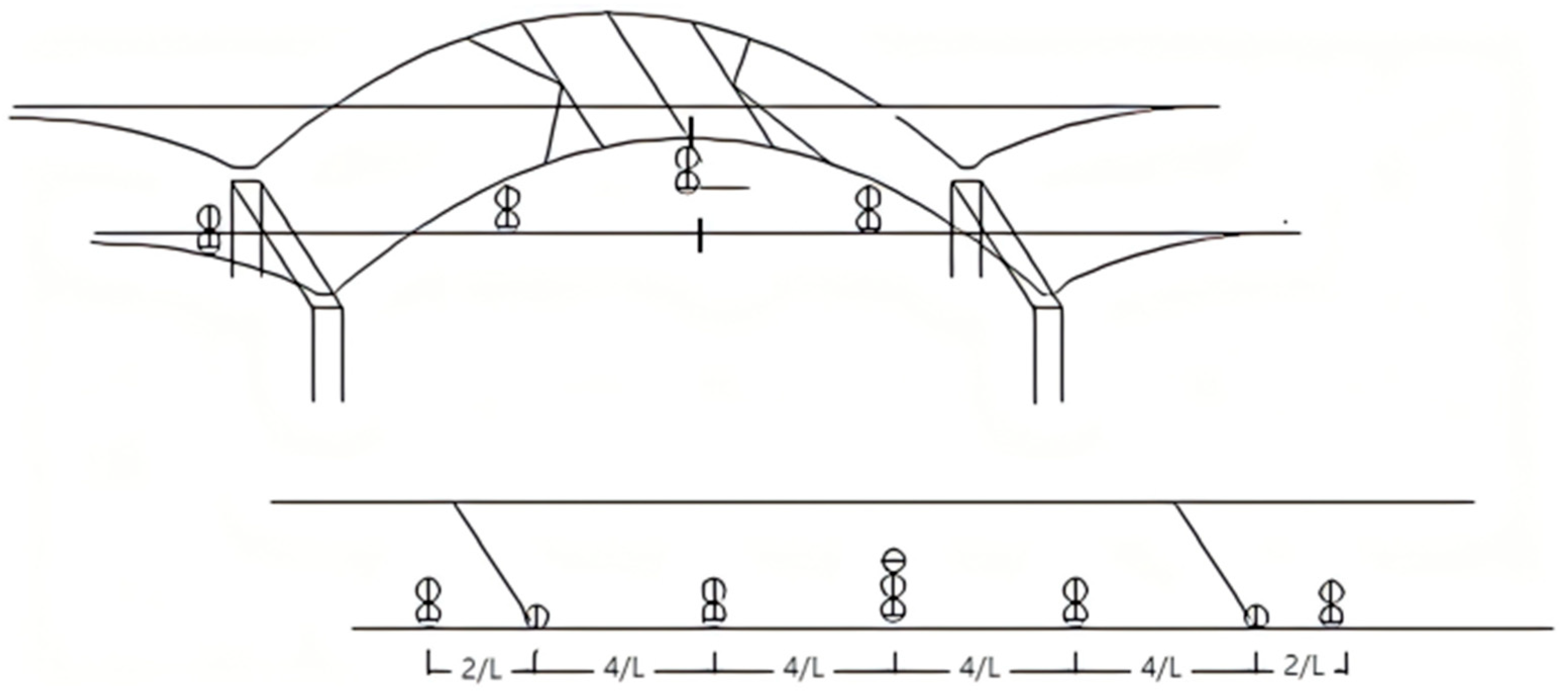
5. Dynamic Load Text of Bridge
5.1. Ambient Vibration Test
5.2. Vehicle Field Test
6. Discussion
7. Conclusions
- (1)
- Post renovation, the maximum dynamic deflection at low speeds, specifically 20 km/h and 30 km/h, significantly decreased. At 20 km/h, it dropped from 21.4 mm to 17.9 mm (a 16.4% reduction), and at 30 km/h, from 38.2 mm to 24.2 mm (a 36.6% reduction). This shows that the steel deck structure has enhanced stiffness, reducing deformation. The decreases in dynamic deflection, bending moments, and stress indicate that the upgraded steel deck system performs dynamically better than the original, achieving the intended renovation outcomes.
- (2)
- Under high-speed vehicle conditions, the bridge deck modification shows limited effectiveness as the steel deck induces more pronounced vibration responses. Future work should focus on further optimizing the bridge structure to improve stability at higher speeds. To reduce the coupling vibrations between the vehicle and the bridge, TMD dampers can be installed after the bridge retrofitting is completed.
- (3)
- The calculated natural frequencies of the bridge structure closely match the measured values, demonstrating that the established finite element model effectively reflects the actual structural conditions. The slightly higher measured values compared to the calculated ones suggest that the post-renovation bridge structure exhibits increased dynamic stiffness, meeting the design requirements.
- (4)
- Steel structure bridge deck systems offer advantages such as lightweight, high strength, and structural integrity. However, due to the lightweight nature of steel structures, significant dynamic performance issues may arise under vehicle dynamic loading. Therefore, conducting dynamic load tests on bridges is essential. Through these tests, it is confirmed that the renovated bridge exhibits good dynamic performance, resulting in improved comfort for vehicles traveling on the bridge deck.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Qu, C.; Yi, T.; Li, H.; Wang, Y.; Mei, X. Detecting deck damage in concrete box girder bridges using mode shapes constructed from a moving vehicle. Eng. Struct. 2024, 305, 117726. [Google Scholar] [CrossRef]
- Su, N.; Lou, L.; Amirkhanian, A.; Amirkhanian, S.N.; Xiao, F. Assessment of effective patching material for concrete bridge deck -A review. Constr. Build. Mater. 2021, 293, 123520. [Google Scholar] [CrossRef]
- Orta, L.; Bartlett, F.M. Sensitivity analysis of restrained shrinkage stresses of concrete deck overlays. Eng. Struct. 2020, 210, 110396. [Google Scholar] [CrossRef]
- Haynes, M.A.; Coleri, E.; Sreedhar, S. Impermeable Asphalt Concrete Layer to Protect and Seal Concrete Bridge Decks. Transp. Res. Rec. 2019, 2673, 355–367. [Google Scholar] [CrossRef]
- Xu, G.; Xie, W.; Xu, Y.; Xue, S.; Chen, X.; Ma, G. Comparative study on hydrodynamic characteristics of T-deck and box-deck bridges under freak waves. Ocean Eng. 2024, 299, 117301. [Google Scholar] [CrossRef]
- Hajibabaee, A.; Khanzadeh Moradllo, M.; Behravan, A.; Ley, M.T. Quantitative measurements of curing methods for concrete bridge decks. Constr. Build. Mater. 2018, 162, 306–313. [Google Scholar] [CrossRef]
- Niwa, J.; Fakhruddin; Matsumoto, K.; Sato, Y.; Yamada, M.; Yamauchi, T. Experimental study on shear behavior of the interface between old and new deck slabs. Eng. Struct. 2016, 126, 278–291. [Google Scholar] [CrossRef]
- Jeong, Y.; Kainuma, S.; Ahn, J. Structural response of orthotropic bridge deck depending on the corroded deck surface. Constr. Build. Mater. 2013, 43, 87–97. [Google Scholar] [CrossRef]
- Wang, B.; Nagy, W.; De Backer, H.; Chen, A. Fatigue process of rib-to-deck welded joints of orthotropic steel decks. Theor. Appl. Fract. Mech. 2019, 101, 113–126. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, X.; Ma, W.; Zhang, X. Development and evaluation of a pothole patching material for steel bridge deck pavement. Constr. Build. Mater. 2021, 313, 125393. [Google Scholar] [CrossRef]
- Wang, S.; Ke, Z.; Gao, Y.; Zhang, Y. Long-Term In Situ Performance Investigation of Orthotropic Steel Bridge Deck Strengthened by SPS and RPC Solutions. J. Bridge Eng. 2019, 24, 04019054. [Google Scholar] [CrossRef]
- Kennedy, S.J.; Martino, A.E. SPS bridge decks for new bridges and strengthening of existing bridge decks. Steel Constr. 2015, 8, 21–27. [Google Scholar] [CrossRef]
- Tang, X.B. Analysis of Structural Load Bearing Condition of Orthotropic Steel Plate Deck of a Bridge. World Bridge 2015, 43, 32–37. [Google Scholar]
- Ozakgul, K.; Yilmaz, M.F.; Caglayan, B.O. Assessment of an old reinforced concrete open-spandrel arch railway bridge. Structures 2022, 44, 284–294. [Google Scholar] [CrossRef]
- Wang, Z.; Der Kiureghian, A. Multiple-support response spectrum analysis using load-dependent Ritz vectors. Earthq. Eng. Struct. Dyn. 2014, 43, 2283–2297. [Google Scholar] [CrossRef]
- Wang, Z.L.; Wang, C.H. Analysis and transformation of the causes of vibration disease of Danjiang Bridge in YilanMu. J. China Foreign Highw. 2006, 26, 108–113. [Google Scholar]
- Tan, K. Research on the Application of MIDAS in Bridge Load Test. Theory Pract. Contemp. Educ. 2014, 6, 159–162. [Google Scholar]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1996. [Google Scholar] [CrossRef]
- Chen, L.; Qian, Z.; Wang, J. Multiscale Numerical Modeling of Steel Bridge Deck Pavements Considering Vehicle–Pave ment Interaction. Int. J. Geomech. 2016, 16, B4015002. [Google Scholar] [CrossRef]
- Wei, Y.; Ji, R.; Li, Q.; Song, Z. Mechanical Performance Prediction Model of Steel Bridge Deck Pavement System Based on XGBoost. Appl. Sci. 2023, 13, 2048. [Google Scholar] [CrossRef]
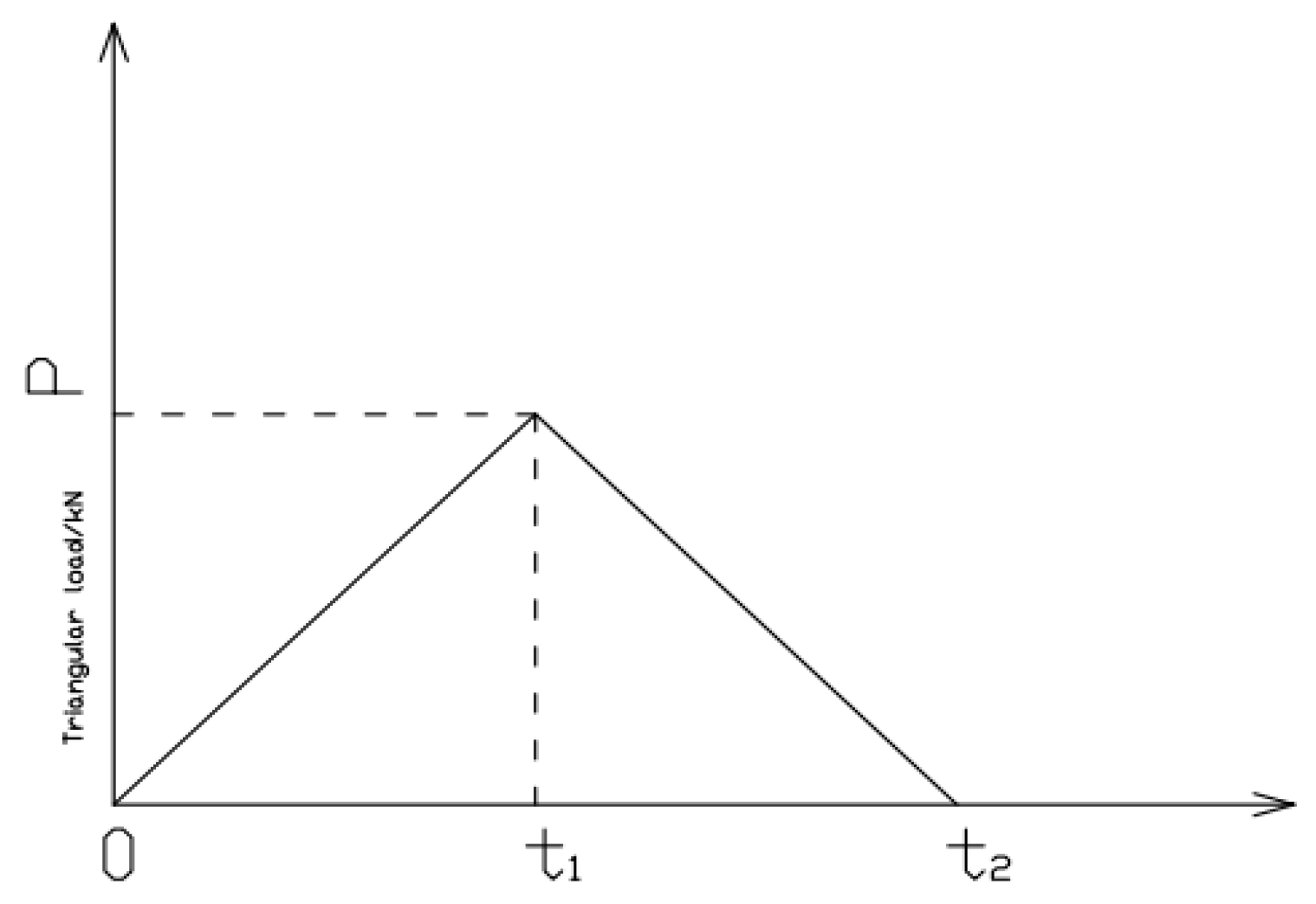
- Li, C. Simplified Simulation Method for Vehicle Running Test Based on Triangular Load and Application. Bridge Constr. 2019, 49, 98–103. [Google Scholar]
- Qiao, L.; Wu, F.; Zhou, X.; Chen, Y.; Zhang, Y. Research on Point Load Correction Factor Based on Electro-hydraulic Servo Point Load Meter. Rock Mech. Rock Eng. 2024, 57, 5705–5725. [Google Scholar] [CrossRef]
- Miao, B.R.; Luo, Y.X.; Peng, Q.M.; Qiu, Y.Z.; Chen, H.; Yang, Z.K. Multidisciplinary design optimization of lightweight carbody for fatigue assessment. Mater. Des. 2020, 194, 108910. [Google Scholar] [CrossRef]
- Jia, D.; Zhang, Q.; Xiong, L.; Li, J.; Bu, Y.; Bao, Y. A unified evaluation method for fatigue resistance of riveted joints based on structural stress approach. Int. J. Fatigue 2022, 160, 106871. [Google Scholar] [CrossRef]
- Hou, J.; Xu, W.; Chen, Y.; Zhang, K.; Sun, H.; Li, Y. Typical diseases of a long-span concrete-filled steel tubular arch bridge and their effects on vehicle-induced dynamic response. Front. Struct. Civ. Eng. 2020, 14, 867–887. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Bu, Y.; Bao, Y. Static and fatigue performance of steel bridge decks strengthened with air-cured UHPC. Structures 2022, 41, 203–214. [Google Scholar] [CrossRef]
- Cheynet, E.; Daniotti, N.; Jakobsen, J.B.; Snæbjörnsson, J. Improved long-span bridge modeling using data-driven identification of vehicle-induced vibrations. Struct. Control Health Monit. 2020, 27, e2574. [Google Scholar] [CrossRef]
- Su, X.; Mao, J.; Wang, H.; Gao, H.; Guo, X.; Zong, H. Vortex-Induced Vibration of Long Suspenders of a Long-Span Suspension Bridge and Its Effect on Local Deck Acceleration Based on Field Monitoring. Struct. Control Health Monit. 2024, 2024, 1472626. [Google Scholar] [CrossRef]
- JTG/T J21-01-2015; Load Test Methods for Highway Bridge. Ministry of Transport of the People’s Republic of China: Beijing, China, 2015.
- Deng, L.; Yu, Y.; Zou, Q.; Cai, C.S. State-of-the-Art Review of Dynamic Impact Factors of Highway Bridges. J. Bridge Eng. 2015, 20, 04014080. [Google Scholar] [CrossRef]













| Study | Focus Area | Key Contributions |
|---|---|---|
| Ningyi Su et al. [2] | Repair Materials for Concrete Bridge Decks | Comprehensive review of repair materials, highlighting variability in mechanical properties and durability. Emphasis on composite system performance. |
| L. Orta [3] | Cracking in Concrete Overlays on Steel Substrates | Parametric and sensitivity analysis of cracking under restrained shrinkage. Identified critical variables affecting cracking behavior. |
| Matthew A. Haynes et al. [4] | Waterproof Asphalt Mixture | Developed a high crack- and rutting-resistant waterproof asphalt mixture to prevent water and deicing salt infiltration. |
| Guoji Xu et al. [5] | Hydrodynamic Characteristics of Bridge Decks | Studied hydrodynamics under abnormal wave parameters; recommended reinforcing offshore and onshore load capacities for specific deck types. |
| Amir Hajibabaee [6] | Curing Methods for Concrete Durability | Compared curing methods; emphasized wet curing’s effectiveness in reducing chemical intrusion and enhancing long-term durability. |
| Junichiro Niwa et al. [7] | Interface Shear Transfer in Concrete Bridge Decks | Examined parameters affecting shear transfer between new and old concrete. Highlighted the influence of prestress, reinforcement, and surface roughness. |
| Young-Soo Jeong [8] | Corrosion in Steel Bridge Decks | Evaluated structural response of corroded orthotropic steel bridge decks, linking corrosion damage to altered structural behavior. |
| Leilei Chen [10] | Pothole Repairs on Steel Bridge Decks | Developed a fast-curing cold mix repair material for steel bridge decks, enabling traffic reopening within three hours. |
| Benjin Wang [9] | Pothole Repairs on Steel Bridge Decks | Developed a fast-curing cold mix repair material for steel bridge decks, enabling traffic reopening within three hours. |
| Shilei Wang [11] | Reinforcement of Steel Bridge Decks | Compared reinforcement schemes (sandwich plate system vs. reactive powder concrete); found significant improvement in stress and deformation. |
| Stephen J. Kennedy [12] | Prefabricated Systems for Deck Replacement | Demonstrated up to 70% static load reduction using prefabricated sandwich panel systems; emphasized speed and efficiency in deck replacement. |
| Component | Description/Dimensions |
|---|---|
| Location | Wuhan, Hubei Province, China |
| Main Bridge Structure | Half-through concrete-filled steel tubular (CFST) tied-arch bridge |
| Total Length/ Rise-to-Span Ratio | 372 m/1:5 |
| Main Arch Design | Upper and lower chords: 2 steel pipes each, diameter: 1 m, wall thickness: 14 mm, filled with grade 50 concrete |
| Arch Rib at Arch Foot | Solid steel pipe concrete structure (6–7 m submerged during floods for collision protection and strength) |
| Tie Rods | Prestressed, freely slidable, anchored at side span ends with clip-type anchors |
| Deck Slab Support | Initially simply supported; later continuously supported by suspended crossbeams |
| Index | Structure Name | Material | Elastic Modulus (MPa) | Poisson’s Ratio | Thermal Expansion Coefficient | Mass Density (kg/m3) | Material Type |
|---|---|---|---|---|---|---|---|
| 1 | Pier | C50 | 3.45 × 104 | 0.2 | 1.00 × 10−5 | 2.5493 × 103 | Isotropic |
| 2 | Suspender | Stand1860 | 1.95 × 105 | 0.3 | 1.20 × 10−5 | 8.0048 × 103 | Isotropic |
| 3 | Arch Rib | 16 Mn | 2.00 × 105 | 0.3 | 1.20 × 10−5 | 7.8498 × 103 | Isotropic |
| 4 | Tie Rod | Stand1860 | 1.95 × 105 | 0.3 | 1.20 × 10−5 | 8.0048 × 103 | Isotropic |
| 5 | Original Abdominal Rod | Composite material | 2.06 × 105 | 0.3 | 1.20 × 10−5 | 7.8498 × 103 | Isotropic |
| 6 | Original Steel Transverse and Longitudinal Beams | Q345 | 2.06 × 105 | 0.3 | 1.20 × 10−5 | 7.8498 × 103 | Isotropic |
| 7 | Original Bridge Diagonal Strut | Q345 | 2.06 × 105 | 0.3 | 1.20 × 10−5 | 7.8498 × 103 | Isotropic |
| 8 | New Crossbeam | Q345 | 2.06 × 105 | 0.3 | 1.20 × 10−5 | 7.8498 × 103 | Isotropic |
| 9 | New Steel Bridge Deck | Q345qD | 2.00 × 105 | 0.3 | 1.20 × 10−5 | 7.8498 × 103 | Isotropic |
| 10 | New Steel Tie Beam | Q345 | 2.06 × 105 | 0.3 | 1.20 × 10−5 | 7.8498 × 103 | Isotropic |
| Index | Before | After | Improvement Rate | Mode of Vibration |
|---|---|---|---|---|
| 1 | 0.612 Hz | 0.734 Hz | 19.9% | Vertical First Mode Vibration |
| 2 | 1.010 Hz | 1.157 Hz | 14.6% | Vertical Second Mode Vibration |
| 3 | 1.791 Hz | 1.891 Hz | 5.6% | Vertical Third Mode Vibration |
| Operating Condition | Speed (km/h) | t1 (s) | t2 (s) | Analysis Time (s) | Analysis Time Step (s) |
|---|---|---|---|---|---|
| 1 | 20 | 0.107 | 0.214 | 10 | 0.007 |
| 2 | 30 | 0.072 | 0.144 | 7 | 0.005 |
| 3 | 40 | 0.054 | 0.108 | 6 | 0.004 |
| 4 | 50 | 0.043 | 0.086 | 5 | 0.004 |
| 5 | 60 | 0.036 | 0.072 | 4 | 0.003 |
| Operating Condition | Position | Stress (σ/MPa) | Safety Coefficient (fpk/σ) |
|---|---|---|---|
| 1 | No. 1 Suspender | 513.2 | 3.8 |
| No. 16 Suspender | 516.5 | 3.8 | |
| 2 | No. 1 Suspender | 533.6 | 3.7 |
| No. 16 Suspender | 529.6 | 3.7 | |
| 3 | No. 1 Suspender | 538.4 | 3.6 |
| No. 16 Suspender | 540.2 | 3.6 | |
| 4 | No. 1 Suspender | 555.1 | 3.5 |
| No. 16 Suspender | 560.6 | 3.5 | |
| 5 | No. 1 Suspender | 551.6 | 3.5 |
| No. 16 Suspender | 552.3 | 3.5 |
| Operating Condition | Position | Stress (σ/MPa) |
|---|---|---|
| 1 | No. 1 Suspender of Side Span | 159.2 |
| No. 32 Suspender of Mid-Span | 157.7 | |
| 2 | No. 1 Suspender of Side Span | 159.6 |
| No. 32 Suspender of Mid-Span | 155.2 | |
| 3 | No. 1 Suspender of Side Span | 161.3 |
| No. 32 Suspender of Mid-Span | 158.7 | |
| 4 | No. 1 Suspender of Side Span | 158.3 |
| No. 32 Suspender of Mid-Span | 161.2 | |
| 5 | No. 1 Suspender of Side Span | 156.4 |
| No. 32 Suspender of Mid-Span | 163.2 |
| Index | Measured Value (Without Vehicle Load) | Measured Value (Vehicle Load = 70 t) | Calculated Value | Mode of Vibration | Damping Ratio (%) |
|---|---|---|---|---|---|
| 1 | 0.382 Hz | 0.375 Hz | 0.366 Hz | Lateral 1st-Order Vibration | 1.70 |
| 2 | 0.692 Hz | 0.681 Hz | 0.649 Hz | Lateral 2nd-Order Vibration | 1.20 |
| 3 | 0.856 Hz | 0.825 Hz | 0.734 Hz | Vertical 1st-Order Vibration | 1.48 |
| 4 | 1.274 Hz | 1.263 Hz | 1.157 Hz | Vertical 2nd-Order Vibration | 1.45 |
| 5 | 2.339 Hz | 2.331 Hz | 1.891 Hz | Vertical 3rd-Order Vibration | / |
| 6 | 3.17 Hz | 3.15 Hz | 2.53 Hz | Vertical 4th-Order Vibration | / |
| Position | Speed (km/h) | Average | Maximum | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | |||||
| Vertical | Upstream | L/4 Main Arch | 0.20 | 0.18 | 0.22 | 0.24 | 0.22 | 0.23 | 0.21 | 0.24 |
| L/2 Main Arch | 0.24 | 0.25 | 0.30 | 0.30 | 0.29 | 0.34 | 0.29 | 0.34 | ||
| 3L/4 Main Arch | 0.14 | 0.15 | 0.20 | 0.21 | 0.18 | 0.21 | 0.18 | 0.21 | ||
| L/4 Main Beam | 0.74 | 0.84 | 0.95 | 0.96 | 0.86 | 0.99 | 0.89 | 0.99 | ||
| L/2 Main Beam | 1.15 | 1.00 | 1.31 | 1.32 | 1.35 | 1.54 | 1.28 | 1.54 | ||
| 3L/4 Main Beam | 0.66 | 0.68 | 0.86 | 0.91 | 0.82 | 0.91 | 0.80 | 0.91 | ||
| Downstream | L/4 Main Arch | 0.19 | 0.19 | 0.22 | 0.22 | 0.20 | 0.25 | 0.21 | 0.25 | |
| L/2 Main Arch | 0.29 | 0.24 | 0.33 | 0.31 | 0.34 | 0.37 | 0.31 | 0.37 | ||
| 3L/4 Main Arch | 0.20 | 0.19 | 0.23 | 0.23 | 0.24 | 0.28 | 0.23 | 0.28 | ||
| L/4 Main Beam | 0.77 | 0.84 | 0.93 | 0.98 | 0.92 | 1.14 | 0.93 | 1.14 | ||
| L/2 Main Beam | 1.05 | 1.18 | 1.41 | 1.41 | 1.33 | 1.62 | 1.34 | 1.62 | ||
| 3L/4 Main Beam | 0.79 | 0.76 | 0.99 | 0.99 | 0.96 | 1.06 | 0.92 | 1.06 | ||
| Horizontal | Upstream | L/2 Main Arch | 0.09 | 0.10 | 0.10 | 0.12 | 0.12 | 0.12 | 0.11 | 0.12 |
| L/4 Main Beam | 0.24 | 0.24 | 0.26 | 0.32 | 0.31 | 0.28 | 0.27 | 0.32 | ||
| L/2 Main Beam | 0.32 | 0.35 | 0.37 | 0.37 | 0.39 | 0.46 | 0.38 | 0.46 | ||
| 3L/4 Main Beam | 0.17 | 0.19 | 0.22 | 0.26 | 0.23 | 0.24 | 0.22 | 0.26 | ||
| Downstream | L/4 Main Beam | 0.15 | 0.18 | 0.18 | 0.21 | 0.20 | 0.20 | 0.19 | 0.21 | |
| L/2 Main Beam | 0.32 | 0.30 | 0.35 | 0.41 | 0.43 | 0.42 | 0.37 | 0.43 | ||
| 3L/4 Main Beam | 0.17 | 0.18 | 0.21 | 0.25 | 0.24 | 0.23 | 0.21 | 0.25 | ||
| Type | Speed (km/h) | Maximum | |||||
|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | ||
| Impact Coefficient | 0.01 | 0.03 | 0.02 | 0.02 | 0.02 | 0.03 | 0.03 |
| 0.01 | 0.03 | 0.03 | 0.03 | 0.02 | 0.03 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, J.; Zou, Z.; Wang, Z. Systematic Rehabilitation Techniques and Dynamic Analysis of Bridge Deck System with Concrete-Filled Steel Tube Arches. Buildings 2024, 14, 3891. https://doi.org/10.3390/buildings14123891
Cai J, Zou Z, Wang Z. Systematic Rehabilitation Techniques and Dynamic Analysis of Bridge Deck System with Concrete-Filled Steel Tube Arches. Buildings. 2024; 14(12):3891. https://doi.org/10.3390/buildings14123891
Chicago/Turabian StyleCai, Jie, Zikang Zou, and Zhipeng Wang. 2024. "Systematic Rehabilitation Techniques and Dynamic Analysis of Bridge Deck System with Concrete-Filled Steel Tube Arches" Buildings 14, no. 12: 3891. https://doi.org/10.3390/buildings14123891
APA StyleCai, J., Zou, Z., & Wang, Z. (2024). Systematic Rehabilitation Techniques and Dynamic Analysis of Bridge Deck System with Concrete-Filled Steel Tube Arches. Buildings, 14(12), 3891. https://doi.org/10.3390/buildings14123891








