Vehicle Load Identification Using Machine Vision and Displacement Influence Lines

Abstract

In recent years, bridge collapses resulting from vehicle overloading have underscored the crucial necessity for real-time monitoring of traffic conditions on bridges, making pavement-based weigh-in-motion systems indispensable for large bridges. However, these systems usually have poor durability and will cause traffic interruptions during their installation and maintenance processes. This paper addresses the challenge of recognizing vehicle loads by proposing a vehicle load identification method based on machine vision and displacement influence lines. The technology consists of three essential steps. Firstly, machine vision technology is utilized to identify vehicle trajectories. Following this, the displacement response, monitored by millimeter-wave radar, is integrated to calculate the influence lines of the structure’s displacement. Lastly, an overall least squares method incorporating a regularization term is applied to calculate axle weights. The efficacy of the proposed method is validated within the monitoring system of a specific continuous beam. Importantly, the calibration of vehicles and the validation dataset rely on information monitored by the pavement-based weigh-in-motion system of adjacent arch bridges, serving as ground truth. Results indicate that the identification errors for gross vehicle weight do not exceed 25%. This technology holds significant importance for identifying vehicle weights on small to medium-span bridges. Due to its cost-effectiveness, easy installation, and maintenance, it possesses a high potential for widespread adoption.

1. Introduction

Vehicles, as one of the crucial loads on bridge structures, exert a significant and undeniable influence on the service life of bridges [1]. Overloaded vehicles have the potential to cause evident damage to bridges, posing the risk of collapse. The characteristics of traffic flow also hold vital implications for bridge maintenance strategies. Therefore, continuous monitoring and statistical analysis of vehicle load information are imperative. Currently, there are two primary types of vehicle load monitoring systems employed for bridges: the pavement-based weigh-in-motion (WIM) system and the bridge weigh-in-motion (B-WIM) system [2].

The fundamental principle of the WIM system involves acquiring wheel weight through sensors embedded in the road surface, enabling the identification of the weight of vehicles in normal operation. This system possesses the advantage of not disrupting traffic, rendering it of considerable practical value. In recent years, some countries have established systematic operational models for controlling vehicle weight through the use of WIM data [3]. However, the WIM system has notable drawbacks, including: (1) being expensive; (2) causing traffic interruptions during installation; and (3) having poor durability [4]. These factors contribute to increased installation and maintenance costs for WIM systems.

In order to further reduce the cost of vehicle weight recognition, extensive research has been conducted on B-WIM. This technology utilizes bridge structural monitoring sensors (such as strain gauges and displacement sensors) to capture bridge deformations and deduce the weight of vehicles. In comparison to WIM, the advantages of B-WIM include: (1) smaller sensor size and lower cost; (2) installation of sensors beneath the bridge without excavating road pavement or interrupting traffic; and (3) longer contact time between vehicle wheels and the bridge structure, leading to more accurate weight measurements [5]. Therefore, B-WIM exhibits promising application prospects.

Currently, the implementation methods for B-WIM technology include theories based on the influence line [6] and the Moving Force Identification (MFI) theory [7], among others. Among these, the approach based on the influence line theory does not require solving complex dynamic equations, resulting in a shorter calculation time and demonstrating greater practicality. The algorithm based on the influence line combines vehicle spatiotemporal distribution and bridge response time history, producing more stable and accurate results [6].

The identification of vehicle spatiotemporal distribution is one of the primary issues that this method aims to address. Traditional B-WIM uses surface-embedded sensors installed at both ends of the bridge or sensors under the bridge [8] to capture the vehicle’s time of passing on and off the bridge. Under the assumption of uniform vehicle speed, these systems calculate the vehicle’s spatiotemporal distribution. However, they are not suitable for complex scenarios such as non-uniform vehicle speed and lane changing. Machine vision technology can overcome the challenges of the above-mentioned methods. Traditional machine vision techniques, employing background subtraction, frame differencing, or optical flow methods, identify moving vehicles from changing pixels. However, these methods are susceptible to interference and struggle with accurate axle positioning and vehicle-type recognition. Machine vision methods based on deep learning can directly recognize and classify vehicles in images, offering more stable and precise identification results. Additionally, they exhibit strong adaptability to environmental changes. By adjusting the annotated targets in the training set, the recognition of different parts of vehicles can be tailored according to task requirements. Currently, the field of object recognition is mainly divided into two-stage detectors, represented by RCNN [9], and one-stage detectors, represented by YOLO [10]. Among them, one-stage detectors have faster recognition speeds and are more suitable for tasks with high real-time requirements. Target detection technology has found extensive applications across various branches of civil engineering, including bolt-loosening detection [11], structural deformation monitoring [12], and more. In the context of identifying the spatiotemporal distribution of vehicles, Xia et al. [13] achieved vehicle trajectory recognition under complex driving conditions. Dan et al. [14], by combining multiple cameras, achieved the spatiotemporal distribution of vehicles across the entire bridge. Additionally, Xu et al. [15] utilized the recognition capabilities of cameras and combined them with electronic toll-collection information to comprehensively track specific vehicles throughout their journeys. This underscores that the recognition of vehicle spatiotemporal distribution based on computer vision has made significant progress in engineering applications.

Another research focus is on how to extract influence line information based on measured data. The models for influence line recognition can be categorized into two types: time domain models and frequency domain models [16]. In the time domain models, OBrien et al. [17] provided a solution for the influence line based on the least squares method from the perspective of matrix analysis under the assumption of uniform straight-line motion. However, in practical bridge responses, inevitable influences such as dynamic effects, road surface roughness, lane-changing, variable speeds, overtaking, and other factors are introduced [18,19,20,21]. To reduce their interference, regularization techniques are introduced, including typical ones such as Tikhonov regularization, LSQR, and sparse regularization methods. Frequency domain models, based on the principle that the structural response can be equivalent to the convolution of the influence line and the load information function, solve influence lines through fast Fourier transform [22]. However, direct solving still faces interference issues similar to those in time-domain methods, hence the need to introduce regularization terms to enhance robustness. Another consideration is the lateral effects caused by vehicle movement. With the assistance of computer vision technology, the spatiotemporal distribution of vehicles can be obtained. To improve the application effectiveness under complex driving conditions, establishing the structural response influence surface is one effective solution [23,24]. It should be noted, however, that the research objects in this paper have only one lane in each driving direction, and the lateral loading effects are not significant. Therefore, applications based on influence lines can meet the requirements of this study.

The method for vehicle weight recognition typically involves solving overdetermined equations composed of the responses of the bridge at multiple time points and the corresponding impact factors associated with the vehicle axles to calculate both axle loads and the total vehicle weight. A common approach is to use the least-squares method for solving these equations [6]. However, it has been observed in practical applications that, while this method accurately identifies the total vehicle weight, there is room for improvement in the precision of axle load identification [6,25]. To address this issue, researchers proposed the use of least squares methods with regularization constraints to reduce axle load identification errors [26,27]. Furthermore, the probability-based B-WIM algorithm employs maximum likelihood estimation instead of the least squares method for vehicle weight identification [28]. However, its computational efficiency is relatively low. In recent years, the application of deep learning techniques for directly extracting axle load information from responses has emerged as an alternative. For instance, Kim et al. introduced a B-WIM system based on artificial neural networks [29]. Based on deep learning technology, the mean absolute percentage error of gross vehicle weight estimation was 1.76%, and the MAPE of axle load estimation was 3.17% in these cases when noise was added to the test data [30]. However, the practical effectiveness of these methods in real bridge scenarios still requires validation. The development of emerging monitoring technologies also offers new solutions for vehicle weight recognition, such as the non-contact WIM technology proposed by certain researchers [31]. Nevertheless, the stability of these technologies still needs to be verified through practical testing.

In this study, we focus on a four-span continuous beam and employ machine vision technology to discern the spatiotemporal distribution of vehicles across the monitored spans. This innovative approach addresses the limitations associated with matrix methods for determining influence lines, successfully achieving the identification of vehicle information. Section 1 provides an overview of the current state of relevant technologies, while Section 2 outlines the technical roadmap and delves into the fundamental principles of the core technologies. Moving on to Section 3, we introduce an engineering case employed for algorithm validation and detail the preprocessing of monitoring data. Section 4 presents the outcomes of vehicle trajectory, influence line, and vehicle weight recognition. Finally, Section 5 encapsulates the essence of the entire paper.

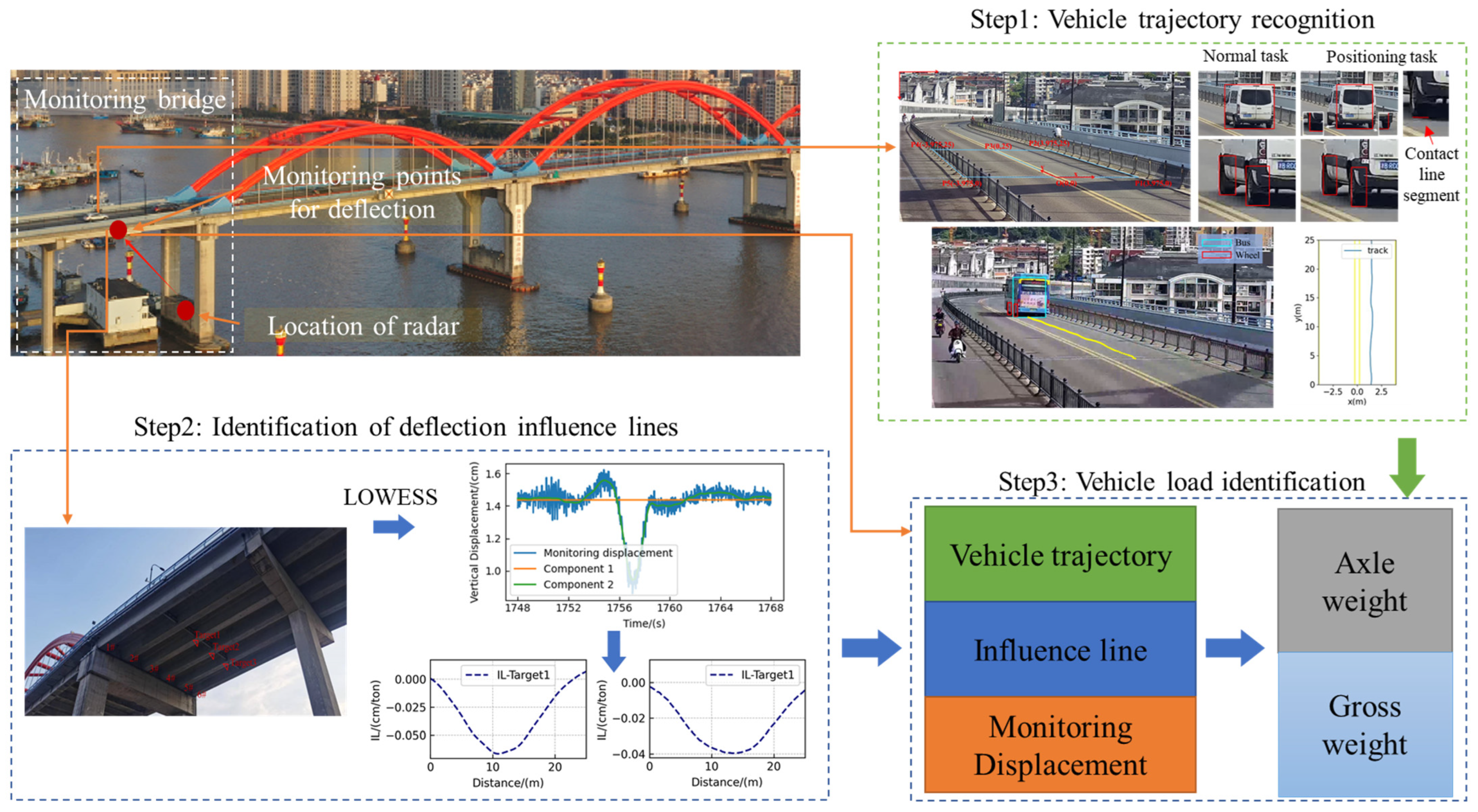
2. Technical Roadmap and Methods

2.1. Technology Roadmap

With the development of machine vision technology, vehicle recognition and trajectory tracking have become realities, gradually evolving into mature products. Leveraging the advancements in this emerging technology, B-WIM technology has also overcome bottlenecks and experienced rapid development. This paper focuses on monitoring the mid-span displacement of a continuous beam bridge adjacent to a large-span arch bridge. The implementation of B-WIM is divided into three steps, as illustrated in Figure 1. The first step involves using machine vision technology to recognize the trajectories of vehicles. The second step utilizes dynamic displacement responses monitored by millimeter-wave radar and the trajectories of vehicles to identify the displacement influence lines of the bridge. The third step, based on these influence lines, vehicle trajectories, and measured responses, deduces information about the weight of vehicles. For a detailed theoretical explanation, refer to the following sections.

2.2. Vehicle Trajectory Recognition Based on Machine Vision

The process of vehicle trajectory recognition involves utilizing machine vision to extract the identification box of the vehicle target, obtaining the pixel coordinates of the recognition box, and subsequently converting them into bridge coordinates. Firstly, it is necessary to create a training dataset to train the neural network to learn the features of vehicle images. In the field of machine vision, recognition tasks typically involve completely enclosing the outline of the target. However, for the specific task of vehicle localization in this study, such a strategy is not suitable because it is challenging to extract the required localization points rationally from such recognition boxes. Therefore, a targeted annotation strategy needs to be designed, as illustrated in Figure 2.

For the vehicle target, the bottom line of the recognition box is positioned at the segment where the rear wheel contacts the ground (referred to as the “contact line”). The left and right lines are placed at the outermost endpoints of the left and right wheels’ contact lines, respectively. The top line is positioned at the upper contour of the vehicle’s rear. For the wheel target, the bottom line of the recognition box is placed at the contact line, and the left and right lines are positioned at the two endpoints of the contact line. This way, the recognition box can provide several localized pieces of information: The midpoint of the bottom line of the vehicle recognition box represents the positioning point of the rear axle on the bridge, and the midpoint of the bottom line of the wheel recognition box represents the positioning point of the wheel on the bridge.

After completing the creation of the training dataset, the YOLOv4 neural network is trained to recognize vehicle and wheel targets in surveillance videos. Upon obtaining the image coordinates of the vehicle and wheel targets, it is necessary to convert them into bridge coordinates for use in vehicle weight recognition. The relationship between the image coordinate system and the bridge coordinate system is illustrated in Figure 3, and it involves a homography transformation [32]. This transformation represents the mapping relationship of points on the same plane in two different views of the images, as shown in Equation (1).

$$\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)=\alpha \left(\begin{array}{ccc}{h}_1& h_2& h_3\\ h_4& h_5& h_6\\ h_7& h_8& 1\end{array}\right)\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)=\alpha H\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)$$

(1)

where $(x,y,1)$ is the generalized bridge coordinates in this study, $(u,v,1)$ is the generalized image coordinates, $H$ is the homography matrix, and $\alpha$ is the scale factor. The homography matrix $H$ has 8 unknowns, and it can be determined by using 4 known points. The transformation from image coordinates to bridge coordinates through the aforementioned equation is illustrated in Figure 4.

2.3. Theory of Bridge Displacement Influence Line Recognition

According to the principles of structural mechanics, the influence line is the representation of the effects, such as displacement and internal forces, resulting from the application of a unitary moving load. Based on this definition, the response at any point can be expressed as Equation (2).

$$d_j={\displaystyle \sum _{i=1}^N{w}_i\cdot il\left(y_{j-C_i}\right)}$$

(2)

where $d_j$ is the response of the $j\mathrm{th}$ sampling point. $w_i$ is axis weight of $i\mathrm{th}$ axle, $N$ represents the number of vehicle axles, $il\left(y_{j-C_i}\right)$ represents the influence coefficient corresponding to the $i\mathrm{th}$ axle, $C_i$ means the sampling point difference between the first axle and the $i$ axle. To express the above equation in matrix form, as shown in Equation (3).

$$W\cdot IL=D$$

(3)

where $W$ is the vehicle information matrix, as shown in Equation (4). $IL$ is the influence coefficient vector, as shown in Equation (5). $D$ represents the response vector, as illustrated in Equation (6), specifically denoting the displacement response vector in this context.

$$W={\left[\begin{array}{cccccccc}{w}_1& \cdots & w_N& \cdots & 0& \cdots & \cdots & 0\\ 0& w_1& \cdots & w_N& \cdots & \cdots & \cdots & 0\\ 0& 0& w_1& \cdots & w_N& \cdots & \cdots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & \cdots & w_1& \cdots & w_N\end{array}\right]}_{m\times \left(m+C_N-1\right)}$$

(4)

$$IL={\left[\begin{array}{cccc}il\left(y_1\right)& \cdots & \begin{array}{cc}il\left(y_m\right)& \cdots \end{array}& il\left(y_{m+C_N-1}\right)\end{array}\right]}_{\left(m+C_N-1\right)\times 1}$$

(5)

$$D={\left[\begin{array}{cccc}{d}_{C_N}& \cdots & d_{C_N+i}& \begin{array}{cc}\cdots & d_{m+C_N-1}\end{array}\end{array}\right]}_{m\times 1}$$

(6)

This vehicle information matrix has a very explicit physical meaning. Each row of the matrix represents a relationship between $N$ influence coefficients and one bridge response. If there are totally $m$ sampling points for bridge response, there will be $m+C_N-1$ influence coefficients involved in the response.

When vehicles are positioned at the bridge ends, the displacement responses are often subtle and prone to getting lost in the noise. Hence, in this study, the load information matrix leverages monitoring data from all axles on the bridge as computation samples. Notably, with the assistance of machine vision technology, axle positions have been accurately identified. Departing from the conventional approach of uniform discrete sampling at fixed time intervals, which is challenging due to the difficulty in ensuring vehicles maintain a consistent speed and straight-line movement within the same time span, this paper adopts a more nuanced strategy. Building upon the identified vehicle trajectories, we employ a sampling method that ensures equal distances between sample points. This approach involves interpolating timestamps for each equidistant sample point. Assuming a linear relationship between static deformation responses at adjacent sampling points, we can then interpolate the deformation values corresponding to the timestamps.

Another aspect worth noting is that the above equations are essentially an underdetermined, sparse system. Theoretically, there are infinitely many solutions. However, the objective of this paper is to find the solution that minimizes the values of ${\Vert W\cdot IL-D\Vert }^2$, where ${\Vert \cdot \Vert }^2$ represents the 2-norm. To achieve this, we introduce the LSQR algorithm. This algorithm iteratively solves the least squares problem and is particularly well-suited for large, sparse linear systems. The computational process is detailed in [33,34,35], and its practical efficacy has been demonstrated in influence line recognition [16].

2.4. Theory of Vehicle Load Identification

Given the known influence lines, utilizing vehicle trajectory tracking technology enables the determination of the response values at any moment for the unit force acting at the location of each axle, as represented by Equation (7). Integrating this information with the previously obtained bridge displacement responses yields the overdetermined system of equations to be solved, as illustrated in Equation (8). Following the principles of ordinary least squares theory, by minimizing Equation (9), the analytical solution for axle weights is obtained as shown in Equation (10).

$$IL={\left[\begin{array}{ccc}il\left(y_1\right)& \cdots & il\left(y_1+C_N\right)\\ ⋮& \cdots & ⋮\\ il\left(y_i\right)& \cdots & il\left(y_1+C_N\right)\\ ⋮& \cdots & ⋮\\ il\left(y_m\right)& \cdots & il\left(y_1+C_N\right)\end{array}\right]}_{m\times N}$$

(7)

$$IL\cdot W=D$$

(8)

$$\arg \min {\Vert IL\cdot W-D\Vert }^2$$

(9)

$$D={\left(I{L}^T\cdot IL\right)}^{-1}\cdot I{L}^T\cdot D$$

(10)

where $W=\left[\begin{array}{ccccc}{w}_1& \cdots & w_i& \cdots & w_N\end{array}\right]$.

However, in the practical application process, two significant factors have been identified that influence the results of the solution. Firstly, inevitable errors arise in the measurements of both $IL$ and $D$. Secondly, there is an ill-conditioned problem with the equations. In order to comprehensively address the impact of these two factors, an overall least squares method with an L2 regularization term is introduced for solving [36]. The optimization objective function is Equation (11).

$$\arg \min \frac{{\Vert IL\cdot W-D\Vert }^2}{1+{\Vert W\Vert }^2}+\lambda {\Vert W\Vert }^2$$

(11)

In contrast to the least squares method, this approach lacks an analytical solution and requires solving through optimization algorithms. Additionally, to ensure that the solution is physically meaningful, a constraint is introduced, imposing that axle loads must be greater than 0.

To determine the coefficient of the regularization term $\lambda$, this approach employs a trial-and-error method, following the L-curve method as referenced in [37]. The procedure involves calculating curves based on the residual norm and smoothness norm for each coefficient and determining the point of maximum slope in these curves as the final coefficient for the regularization term.

3. Case Study

3.1. Overview of the Monitoring Bridge

The focus of this study is a four-span continuous beam bridge connected to a large arch bridge. The monitored span is the first bridge span adjacent to the arch bridge, and real-time monitoring of the dynamic displacement at the mid-span is conducted using millimeter-wave radar technology. This monitoring approach enables all-weather, non-contact, high-precision, and multi-target measurement of dynamic displacements, addressing common challenges in displacement monitoring. Additionally, in addressing challenges related to influence line calibration, this study uses the WIM system and associated camera devices installed on the arch bridge as a source of information for recognizing and calibrating vehicle parameters. By adjusting the camera’s shooting angle, the monitoring field of view can cover the entire monitored span, forming the basis for vehicle trajectory recognition. The subject of this study is illustrated in Figure 5.

The vertical displacement of the beams is sampled at a frequency of 50 Hz, while the camera operates at a sampling rate of 25 frames per second (FPS). The monitored structure consists of six beams, with measurement points located at the mid-span of beams labeled 3#, 4#, and 5#, as illustrated in Figure 6. The WIM system is positioned on the arch bridge, approximately 10 m away from the monitored span. The camera is installed near the lighting pole of the WIM system, at a height of approximately 5 m.

3.2. Data Preprocessing

3.2.1. Data Alignment

Due to the asynchronous installation of the B-WIM system and millimeter-wave radar monitoring equipment, the lack of clock synchronization among the involved parties poses a significant challenge to data mining. In order to effectively utilize the monitoring data from both video and dynamic displacement, it is imperative to perform data alignment. This paper adopts a manual alignment approach, where key moments during the vehicle’s bridge entry are observed through video monitoring. For instance, by aligning the moment when the front axle of the vehicle just enters the bridge with the initial loading moment leading to static displacement, as illustrated in Figure 7, based on these observations, data alignment is achieved.

3.2.2. Extraction of Vehicle-Induced Static Displacement

Bridge dynamic displacement includes long-period components generated by factors such as temperature, vehicle-induced static displacement components, vehicle-induced dynamic displacement components, or noise components. In this study, the analysis focuses on utilizing the vehicle-induced static displacement component for identifying the influence lines and vehicle weight information. The research employs the LOWESS algorithm, which conducts weighted regression within a local window range. To elaborate, the window length for isolating the temperature-induced long-period component was set at 300 s, while the window length for extracting the vehicle-induced static component was configured at 1 s. By adjusting the length of the window, the algorithm can separate displacement response values associated with different periodic components. The separation process is illustrated in Figure 8.

4. Results and Discussion

4.1. Results of Vehicle Trajectory Recognition

Based on the annotation strategy described in Section 2.1, a total of 1436 vehicles and 2324 wheels were annotated. With a batch size of 64 and training iterations set to 8000, the training process of YOLO v4 is illustrated in Figure 9. The training of the model in this study occurred on a machine equipped with an NVIDIA GTX1650 graphics card featuring 4 GB of memory. The training process spanned approximately 26 h.

In order to extract accurate influence lines to the greatest extent possible, the following criteria are established for calibrating the vehicles:

(1)

To minimize noise interference, heavy-duty vehicles should be selected. In this study, vehicles weighing 5 tons or more are chosen.

(2)

To mitigate the impact of bridge responses caused by other vehicles on influence line recognition results, the selected calibration vehicles should be the only motorized vehicles on the bridge.

Furthermore, to validate the effectiveness of the algorithm proposed in this paper, a total of 18 vehicles were chosen as calibration and test samples. The trajectory recognition results for some of these vehicles are illustrated in Figure 10.

4.2. Recognition of Influence Lines

Through the analysis of monitoring data, trucks at 5:09 a.m. on 3 September 2023, and 6:28 a.m. on 3 September 2023, were selected as calibration vehicles for studying single-vehicle bridge crossing conditions. The vehicle information is provided in

Table 1. Calibration vehicle information.

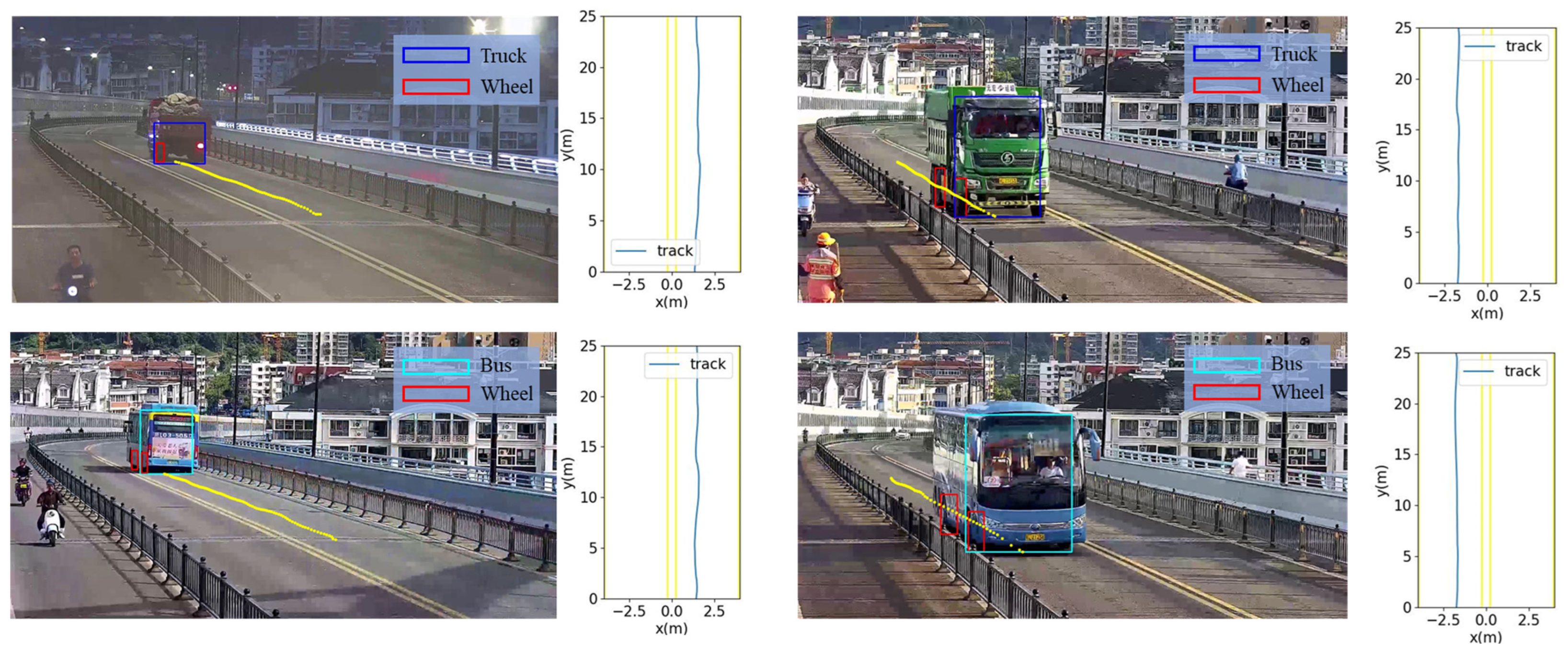
Type	Direction	Speed/(km/h)	Weight of Axles/(ton)	Wheelbase/(m)
Truck	Right	34	2.78/10.13	3.5
Truck	Left	38	4.97/3.78/4.15	3.6/1.4

.

In the preceding text, the trajectories of the calibration vehicles have been identified. Through the analysis of measured displacements, it was observed that displacements are influenced by noise, wind, and other loads, making the load effects generated by lighter vehicles easily submerged in the measured displacements. Therefore, the focus of this study is on vehicles with a total weight of 5 tons or more. Additionally, since the bridge is a one-way, single-lane structure, and considering that the lateral position of vehicles along the bridge does not vary significantly, it is reasonable to only consider the longitudinal position of vehicles along the bridge (i.e., using influence lines instead of influence surfaces).

This paper has identified the mid-span displacement influence lines for the 3# beam and the 4# beam, as shown in Figure 11. The influence lines from these two monitoring points are both utilized for vehicle information recognition.

4.3. Identification of Vehicle Weight

Based on the displacement influence lines, 16 scenarios were selected to validate the effectiveness of the B-WIM algorithm. According to the WIM system installed on the arch bridge, the information on heavy-duty vehicles identified by the WIM system in these 16 scenarios is presented in

Table 2. Vehicle information monitored by WIM system.

Number	Direction	Speed/(km/h)	Weight of Axles/(ton)			GVW	Wheelbase/(m)
			Axle 1	Axle 2	Axle 3		Axle 1–Axle 2	Axle 2–Axle 3
1	Right	39	3.76	6.92	/	10.68	5.8	/
2	Left	63	2.86	7.96	/	10.82	5.6	/
3	Left	24	2.54	8.13	/	10.67	3.3	/
4	Left	35	3.76	6.84	/	10.6	5.7	/
5	Left	39	3.73	7.88	/	11.61	5.2	/
6	Left	39	3.72	7.09	/	10.81	5.7	/
7	Left	42	3.48	7.91	/	11.39	5.3	/
8	Left	39	3.50	7.70	/	11.2	5.2	/
9	Right	39	4.85	8.49	/	13.34	5.7	/
10	Right	40	4.63	8.18	/	12.81	5.7	/
11	Right	39	4.23	7.78	/	12.01	5.7	/
12	Right	35	4.11	11.5	/	15.61	3.5	/
13	Right	37	3.72	7.07	/	10.79	5.8	/
14	Left	35	4.43	4.76	4.86	14.05	3.6	1.4
15	Left	45	5.29	4.9	4.27	14.46	3.6	1.4
16	Left	45	5.30	4.41	4.61	14.32	3.6	1.4

.

This study selected 16 driving scenarios to validate the effectiveness of the algorithm. These scenarios cover bidirectional vehicle travel with speeds ranging from 20 to 70 km/h. The chosen vehicle types include double-axle buses, double-axle trucks, and triple-axle trucks. The vehicle types and axle numbering are illustrated in Figure 12. It is noteworthy that the last two axles of the triple-axle truck belong to the same axle group with close axle spacing.

Through the vehicle weight recognition algorithm proposed in this paper, the positions of vehicles in the above scenarios were identified. The mid-span displacements of the 3# span and 4# span were monitored accordingly, and the final vehicle weight information was calculated and compared with the weighing information from the WIM system, as shown in

Table 3. Recognition results of the axle weight.

No.	① Axle Weight Measured by WIM/(ton)			② Identified Axle Weight/(ton)			Difference = ① − ②/(ton)
	Axle 1	Axle 2	Axle 3	Axle 1	Axle 2	Axle 3	Axle 1	Axle 2	Axle 3
1	3.76	6.92	/	2.88	5.77	/	+0.88	+1.15	/
2	2.86	7.96	/	3.76	5.34	/	−0.9	+2.62	/
3	2.54	8.13	/	2.78	8.16	/	−0.24	−0.03	/
4	3.76	6.84	/	3.66	5.47	/	+0.1	+1.37	/
5	3.73	7.88	/	2.14	7.16	/	+1.59	+0.72	/
6	3.72	7.09	/	1.29	7.32	/	+2.43	−0.23	/
7	3.48	7.91	/	1.6	7.94	/	+1.88	−0.03	/
8	3.50	7.70	/	1.68	7.78	/	+1.82	−0.08	/
9	4.85	8.49	/	3.53	7.18	/	+1.32	+1.31	/
10	4.63	8.18	/	3.2	6.47	/	+1.43	+1.71	/
11	4.23	7.78	/	3.27	6.58	/	+0.96	+1.2	/
12	4.11	11.5	/	3.94	10.18	/	+0.17	+1.32	/
13	3.72	7.07	/	2.93	5.96	/	+0.79	+1.11	/
14	4.43	4.76	4.86	2.27	0	10.64	+2.16	+4.76	−5.78
15	5.29	4.9	4.27	4.68	0	8.5	+0.61	+4.9	−4.23
16	5.30	4.41	4.61	5.73	0	9.81	−0.43	+4.41	−5.2

. Firstly, it is crucial to emphasize axle load identification for triple-axle trucks. From the table, it can be observed that in the case of triple-axle vehicles, the single-axle load identification accuracy for two axles belonging to the same axle group is relatively poor. The identification results indicate that the algorithm mistakenly recognizes these two axles as a single axle. However, the total axle load for the axles within the same axle group has an error of within 1 ton when compared to the sum of the individual axle loads. Despite significant errors in the axle load identification results within the same axle group and the fact that the axle forces of most vehicles with axle groups may not be entirely equal, actual bridge test studies in the field of BWIM [38,39,40] indicate that the differences in axle forces within the same axle group are not substantial. The errors in the total axle load identified for individual axles within the recognized axle group in this study are within 1 ton. Therefore, as long as computer vision technology can identify that the axles of the target vehicle belong to the same axle group, it is possible to infer the weight of each axle, thereby compensating for the axle load identification errors in the algorithm. Regarding the axle load identification results for double-axle vehicles, it can be observed from the table that, except for axle 2 in the second scenario and axle 1 of the sixth vehicle, the axle load identification errors for the remaining axles are all within 2 tons. Furthermore, 46% of the cases exhibit axle load errors within 1 ton.

The identification results for the gross vehicle weight (GVW) are shown in

Table 4. Recognition results of the GVW.

No.	① GVW (ton)	② Identified GVW (ton)	Difference = ① − ② (ton)	(① − ②)/① (%)
1	10.68	8.65	+2.03	+19.0
2	10.82	9.1	+1.72	+15.9
3	10.67	10.94	−0.27	−2.5
4	10.6	9.13	+1.47	+13.9
5	11.61	9.3	+2.31	+19.9
6	10.81	8.61	+2.2	+20.4
7	11.39	9.54	+1.85	+16.2
8	11.2	9.46	+1.74	+15.5
9	13.34	10.71	+2.63	+19.7
10	12.81	9.67	+3.14	+24.5
11	12.01	9.85	+2.16	+18.0
12	15.61	14.12	+1.49	+9.5
13	10.79	8.89	+1.9	+17.6
14	14.05	12.91	+1.14	+8.1
15	14.46	13.18	+1.28	+8.9
16	14.32	15.54	−1.22	−8.5

. As shown in the table, the identification errors for the total vehicle weight are within 3.5 tons, with an emphasis on a majority (62.5%) having errors within 2 tons. Additionally, none of the identification errors for the gross vehicle weight exceed 25%. It is important to note that all reference values used for comparison are based on the monitoring data from the WIM system.

5. Conclusions

This study focuses on continuous beam bridges, employing WIM systems and millimeter-wave radar monitoring technology to validate the effectiveness of the proposed vehicle load identification technology based on machine vision and influence lines. The implementation process of this technology comprises three steps: vehicle track recognition, influence line identification, and vehicle information recognition. Through engineering validation, the following conclusions were drawn:

(1)

The vehicle track recognition algorithm based on YOLO v4 accurately identifies the positions of vehicles and axles.

(2)

Utilizing the vehicle’s driving trajectory and the separated static displacement caused by the vehicle, the LSQR algorithm can precisely identify the displacement influence line.

(3)

The algorithm proposed in this paper was applied to recognize axle loads and total weights for various vehicle types under different driving conditions. The results indicate that the algorithm can accurately identify the total weight of axles within the same axle group. However, its ability to accurately recognize the axle load of individual axles within the same axle group is limited. After consolidating the axle loads within the same axle group, the analysis shows that the majority of axle load identification errors are within 2 tons, with 62.5% achieving errors within 2 tons for total weight identification. The identification errors for gross vehicle weight do not exceed 25%.

The focus of this study is the engineering applicability of B-WIM technology, with certain factors overlooked, such as vehicle width and lateral position. For bridges situated in complex traffic environments, it is necessary to develop and validate vehicle load identification technology based on influence surfaces. Additionally, considerations regarding factors like camera shake during vehicle track recognition are not comprehensive and require further investigation. Lastly, solving the overdetermined equations to derive the solution for vehicle weight offers advantages such as rapid speed and clear application of mechanical principles. The direction of future research should be on developing methods with higher precision and greater engineering applicability.