Refined Analysis of Spatial Three-Curved Steel Box Girder Bridge and Temperature Stress Prediction Based on WOA-BPNN

Abstract

Bridges often improve the visual appeal of urban landscapes by incorporating curve elements to create iconic forms. However, it is noteworthy that curved bridges have unique mechanical properties under loads compared to straight bridges. This study analyzes a spatial three-curved steel box girder bridge based on an actual engineering case with a complex configuration. Initially, the finite element software Midas/Civil 2021 is utilized to establish a beam element model and a plate element model to examine the structural responses under dead loads in detail. Then, two different temperature gradient distribution models are employed for the temperature effect analysis. The backpropagation neural network (BPNN) optimized by the WOA algorithm is trained as a surrogate model for finite element models based on the results of temperature stress simulation. The results reveal that the bending–torsion coupling effect in the second span of the spatial three-curved steel box girder bridge is pronounced, with the maximum torque reaching 40% of the bending moment. The uneven distribution of cross-section stress is particularly significant at the vertices, where the shear lag coefficient exceeds 3. Under the action of temperature gradients, the bridge displays a warped stress state; the stress results obtained from the exponential model exhibit a 21% increase compared to BS-5400. Optimization of the weights by the WOA algorithm results in a significant improvement in prediction accuracy, and the convergence speed is improved by 30%. The coefficient of determination (R²) for predicting temperature stress can reach as high as 0.99.

1. Introduction

The design of urban bridges requires not only the basic traffic function but also a certain degree of aesthetics in order to improve the appearance of the city. Incorporating elegant curve elements in design has become more prevalent due to the increasing demand for traffic flow and limited land availability. However, the curvature of curved bridges can cause a bending–torsion coupling effect due to the deviation of the center of gravity from the supporting line during service. Compared to straight bridges, curved counterparts exhibit complex stress characteristics and are more susceptible to damage, particularly under variable actions such as those induced by temperature [1,2,3].

Temperature loads are considered one of the most critical variable load types. In particular, solar thermal actions generate a three-dimensional temperature field with uneven distribution within the structure, leading to temperature-induced secondary stresses [4]. Scholars worldwide simplify the temperature field of the bridge into a two-dimensional distribution pattern along the longitudinal direction, comprising vertical and lateral temperature gradients. For small and medium-span bridges, there is little significant difference in lateral temperature distribution due to the relatively narrow width of the beam. Therefore, research on vertical temperature gradients is more widespread [5]. Both domestic and international standards have specific regulations for concrete structure bridges regarding temperature effect, whereas there are distinct differences in distribution patterns for steel structure bridges, such as specifications in China lacking explicit definitions of the vertical temperature gradient distribution [6]. Meanwhile, BS-5400 in the UK adopts a four-segment line to simulate this distribution [7]. Extensive research has been carried out at home and abroad on the temperature gradient of steel box girders based on measured data. Zhu et al. [8] and Teng et al. [9] compared measured data from an actual project to multinational specifications and found that the four-segment nonlinear mode provided the best fit for the temperature gradient. Wang et al. [10] used measured data from the steel box girder of a viaduct in Wuhan and discovered that the actual temperature distribution differed significantly from the specified linear distribution. The authors applied extreme value theory to derive the distribution pattern of an appropriate exponential function for the neighboring regions. Ding et al. [11] utilized extreme value theory to analyze ten years of temperature monitoring data for the Runyang Bridge, and found that the estimated extreme values of vertical temperature differences were in excellent agreement with the UK code. Guo et al. [12] analyzed in situ measurements of unpaved steel box girders and investigated the status of temperature gradient partitioning research in China [13]. It is evident that the four-segment model in the UK BS-5400 code provides a superior description of the vertical nonlinear temperature distribution pattern in steel box girders compared to other code. The aforementioned research primarily concentrated on straight bridges, emphasizing the necessity for further in-depth research on the coupled stress characteristics of curved steel bridges under temperature effects.

In recent years, computer science has experienced booming development, leading to increased interest in deep learning among scholars worldwide. The backpropagation neural network (BPNN) is a fundamental algorithm of deep learning that has gained attention in various research fields due to its exceptional applicability, nonlinearity, and robustness. In civil engineering, neural networks are primarily used for predicting structural responses and identifying damages [14]. Tian et al. [15] investigated the effect of temperature on bridges by training a neural network with temperature data from a large-span concrete bridge. They compared the predictions of the neural network with finite element results and demonstrated its high accuracy simultaneously with a significant reduction in computational resource consumption. Ying et al. [16] employed a BPNN to analyze and predict the temperature field distribution of a sea-crossing bridge, providing a reliable foundation for subsequent computations. Wang et al. [17] performed a finite element analysis to simulate temperature gradients at various locations of concrete box girders. They formed a comprehensive dataset and established a neural network to predict the vertical and horizontal temperature gradients of the top and bottom plates of the box girder with R² exceeding 0.9. Recent research on temperature effects has primarily focused on predicting temperature fields using traditional BPNNs, while comparatively less attention has been paid to predicting structural responses. Furthermore, the training of the BPNNs heavily relies on the selected initial weight values. Inappropriate values can cause the network to become trapped in a local optimal solution and fail to converge. To address this issue, an optimization algorithm is often introduced to determine the initial weight values.

This paper introduces the concept of a “three-curved spatial bridge” composed of cross-section, plane, and profile curves based on an actual engineering case. The alignment variations influence the mechanical characteristics of the bridge in three directions. Therefore, finite element models with different scale elements are established for a detailed analysis. A comparative analysis is conducted on the temperature gradient effect of spatial three-curved steel box girder bridges using two typical temperature gradient models: multi-segment piecewise linear and exponential. Based on simulated results, a WOA algorithm-optimized BPNN serving as a surrogate model is trained to predict stresses under temperature gradients.

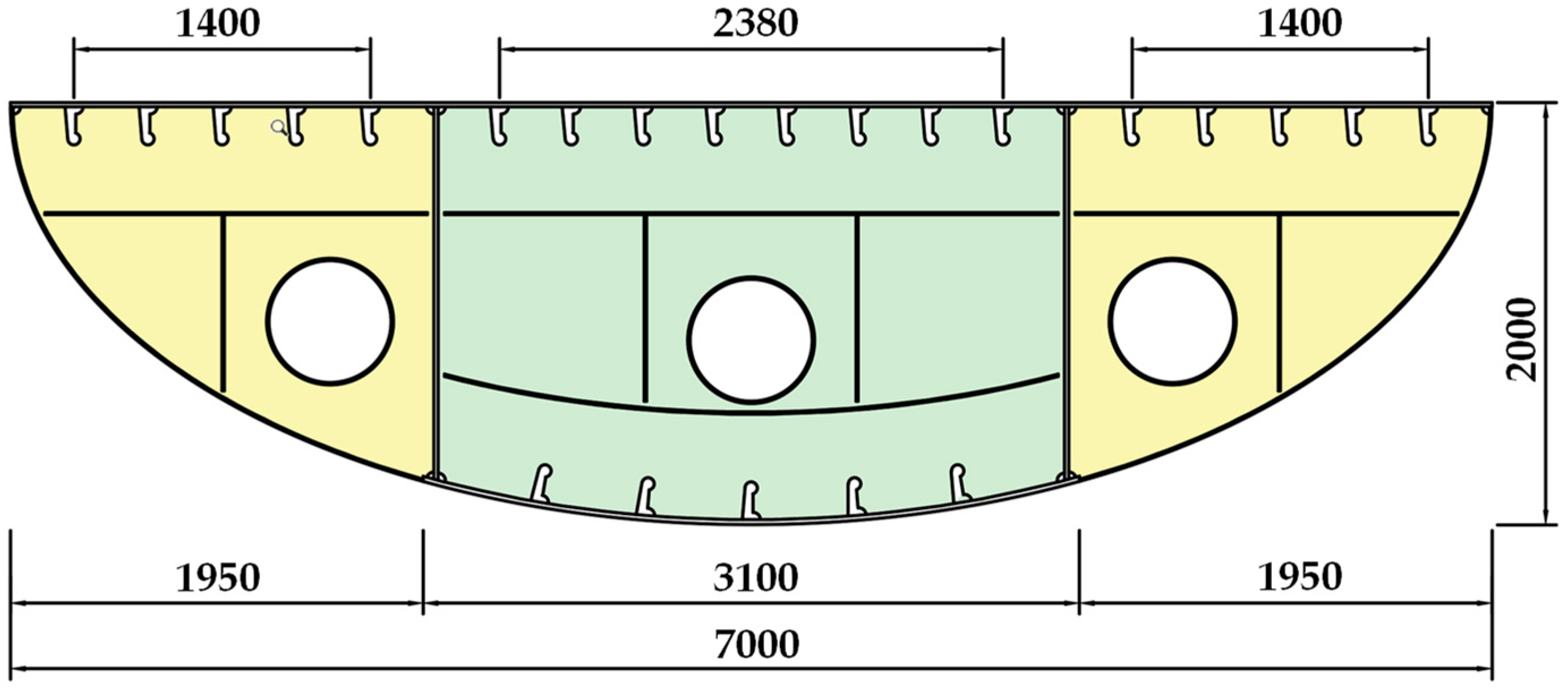
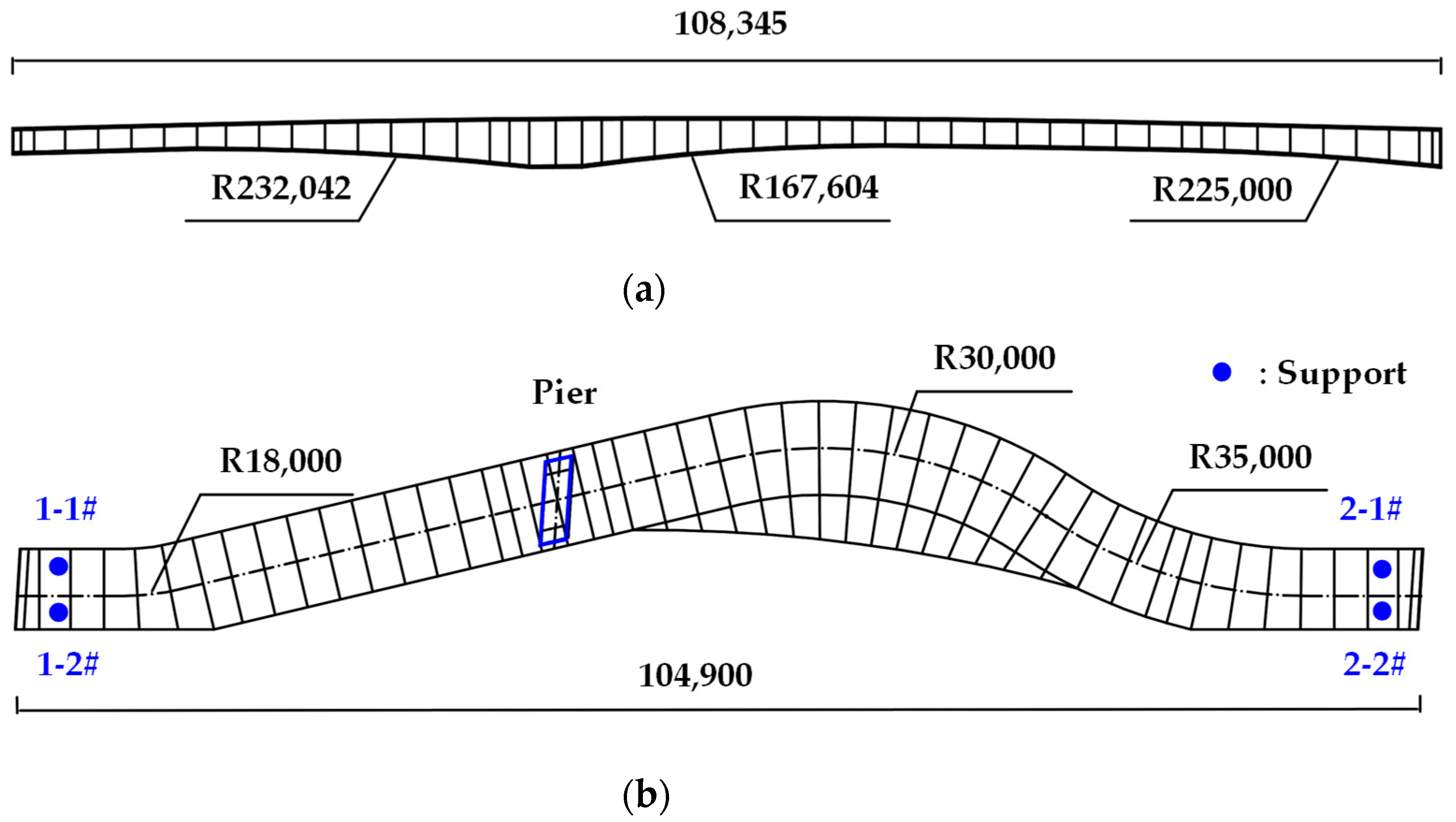
2. Bridge Description

The Hanggang River Bridge is situated on Lishui Road, Hangzhou City, Zhejiang Province, China, just 300 m from the Beijing–Hangzhou Grand Canal. Upon completion, the bridge will serve as a main route to the Beijing–Hangzhou Grand Canal Museum. The bridge’s design incorporates the flowing shape of the canal, resulting in a unique appearance with curve elements from every perspective. Additionally, the pedestrian and main bridges are designed separately, and the pedestrian bridges include resting platforms for pedestrians to appreciate the canal scenery. The rendering of the bridge is shown in Figure 1.

This paper discusses the West Pedestrian Bridge, which utilizes a variable cross-section steel box girder for the upper structure. The bottom plate comprises two segments of 1/4 elliptical curves with different widths and identical heights, forming a closed section. The cross-section of the bridge supports has a width of 6 m and a height of 2 m, while the standard section has a width of 7 m and a height of 2 m. The section has a maximum width variation of 10.5 m and a height of 2.2 m. The standard cross-section is depicted in Figure 2.

The top surface of the steel box aligns with the road profile design, whereas the variation in the bottom plate employs curves for a smooth transition, as illustrated in Figure 3a. The top plate has a thickness of 20 mm, the bottom plate is 25 mm, the web measures 20 mm, and the longitudinal stiffeners have a thickness of 16 mm with a height of 150 mm. The practical standard spacing of the transverse diaphragm is 2.5 m, with a standard thickness of 12 mm. The plate thickness is 22 mm at the abutment supports and 25 mm at the pier supports.

The bridge spans 104.9 m and has a layout alignment containing circular curves, straight lines, and two segments of tangent reverse circular curves. The general layout is shown in Figure 3b. Additionally, a total of 50 transverse diaphragms are evenly distributed along the bridge. The abutments adopt four spherical steel bearings, as shown by the blue dots in Figure 3b, and the pier employs an integral pier-beam connection form to ensure overall stability and prevent tilting.

The pedestrian bridge exhibits curved variations in the cross-section, plan alignment, and vertical alignment, creating a structural configuration known as a “spatial three-curved steel box girder.” Compared to conventional steel box girder bridges, the design displays intricate spatial stress characteristics. Therefore, conducting a refined analysis and temperature effect analysis for a three-curved steel box girder bridge based on an actual engineering project is particularly crucial.

3. Refined Finite Element Analysis

3.1. Modeling

Although the three-curved bridge involves intricate geometries, its deformation under loads is minor and limited compared to the cable in cable system bridges, indicating that linear analysis is sufficient. An overall internal force analysis of the spatial three-curved bridge was conducted on a beam element model in Midas/Civil. Elements were assigned at the locations of the diaphragms and variations in the longitudinal stiffeners. Node creation was accomplished by importing coordinates. The cross-section exhibits spatial variations; thus, individual element sections must be drawn. To complete the establishment of variable cross-section elements, the Section Property Calculator (SPC) function was used to import external sections.

Elastic connections were used at the support locations to achieve constraints through different translational and rotational stiffness. The upper structure of the bridge was Q355 low-alloy high-tensile structural steel, while the bridge pier was C40 concrete. The cement was high-quality Portland cement, the coarse aggregate was continuously graded, and medium coarse sand was used as the fine aggregate. The different material properties are outlined in

Table 1. Material properties of the bridge.

Material	E (MPa)	γ (N/m3)	α (C−1)	µ
Q355	2.06 × 105	7.85 × 104	1.2 × 10−5	0.31
C40	3.25 × 104	2.5 × 104	1 × 10−5	0.2

.

As the steel box girder is thin-walled, detail component influences were not considered in the beam element model. A comprehensive plate element model was established to ensure a precise analysis of the stress distribution in the three-curved steel box girder bridge, applying the material characteristics mentioned earlier. The model comprised 7769 nodes and 11,640 elements, enabling accurate consideration of diaphragm and stiffener effects, as shown in Figure 4.

3.2. Force Analysis

The mechanical characteristics of the spatial three-curved steel box girder bridge are complex, and the bending-torsion coupling effect is significant. Therefore, it is crucial to first conduct an analysis under dead load conditions. The secondary dead loads of the bridge consist of the bridge deck paving, railings, and other accessories, and are considered an equivalent uniformly distributed load. The distribution of the bending and torsional moments across the entire bridge under dead loads is illustrated in Figure 5.

The bridge forms a continuous beam system. The pier location (Section A) experiences the negative peak bending moment of −64,371.1 kN·m, while the reverse tangential point of the second span (Section B) experiences the positive peak bending moment of 26,411.8 kN·m. The overall torsional moment is relatively low due to the low non-uniformity and short length of the first span. However, the second-span section undergoes complex variations and has a longer span. The maximum positive torsional moment (Section C) is located near the peak position of the bending moment rather than at the widest section of the deck. It has a value of 10,052.7 kN·m, representing almost 40% of the maximum positive bending moment.

The deck width varies towards the inside of the curve, which balances the outward torsional moment generated by the curvature. This configuration reduces the negative torsional moment imposed on the structure. Compared to the first span, the cross-section and alignment of the second span are more complex. Therefore, the bending–torsion coupling effect is more pronounced. The subsequent detailed stress analysis of the bridge concentrates on control sections A, B, and C.

In contrast to traditional curved bridges, which experience positive torsion at the supports, the three-curved bridge generates negative torsion at both the starting and ending support locations. Hence, relative deviation (RD) is introduced to estimate the bending–torsion effect on the supports, as defined in Formula (1):

$$RD=\frac{\left|F_1-F_2\right|}{F_1+F_2}\times 100\%$$

(1)

where $F_1$ and $F_2$ are the reactions of the two supports, respectively.

The comparison of the support reactions at both ends is shown in

Table 2. Comparison of support reaction.

Support	Force (kN)	RD (%)
1-1#	387.4	29.6
1-2#	712.8
2-1#	973.4	19.8
2-2#	1452.8

. The layout and number of the supports can be found in Figure 3. The starting support has an RD of 29.6%; however, due to alignment and cross-section shape changes, the RD at the ending support is reduced to 19.8%. To mitigate significant differences in support reactions and prevent occurrences of overturning phenomena, introducing a reverse curve and changing the cross-section towards the inside of the curve can be effective.

3.3. Stress Analysis

As a thin-walled component, the steel box girder exhibits a shear lag effect due to uneven cross-sectional stress distribution. The shear lag effect is exacerbated to a great extent in the case of a three-curved steel box girder bridge, where significant changes in cross-section size and the notable bending–torsion coupling effect make it more pronounced. Hence, a meticulous analysis of the shear lag effect based on a sophisticated model is imperative. Herein, the shear lag coefficient calculation is defined in Formula (2). The shear lag coefficient distribution for control sections A, B, and C under dead loads is calculated using the plate element model mentioned above, as depicted in Figure 6.

$$\lambda =\frac{{\sigma }_{xx}}{{\displaystyle {\int }_0^b{\sigma }_{xx}(x,y)dy/b}}$$

(2)

Here, ${\sigma }_{\mathrm{xx}}$ and b are the normal stress and width of the section, respectively.

Figure 6. Shear lag coefficient of control sections: (a) top plate and (b) bottom plate. (star symbol represents the extreme value).

Figure 6. Shear lag coefficient of control sections: (a) top plate and (b) bottom plate. (star symbol represents the extreme value).

In order to depict the shear lag effect along with the width of the section, the abscissa represents the distance of each point from the left vertex of the section. The range of x corresponds to the section width, where x = 3.5 m is the road axis of the bridge. The results indicate that the shear lag effect is reflected in the top and bottom plates of the cross-section at the web position, while the stress is uniformly distributed between the webs. It is noteworthy that the bottom plates experience more pronounced stress changes along the section due to variations in section height compared to the top plates. Owing to the considerable bending–torsion coupling effect, the nonuniformity of the stress distribution is more severe in sections B and C than in section A. A comparison between sections B and C shows that the shear lag effect intensifies as the section width increases. Section C exhibits a more prominent shear lag effect in tensile and compressive stress, with the maximum absolute value exceeding 3.

Moreover, the shear lag coefficient exhibits significant variation near the vertices on both sides of the cross-section. The vertex position represents a higher critical stress concentration than at other locations. Additionally, the residual stress generated during the section welding process intensifies the stress at this location, leading to premature damage and destruction of the bridge deck. As a result, it is crucial to implement reasonable control measures during the construction and operation phases.

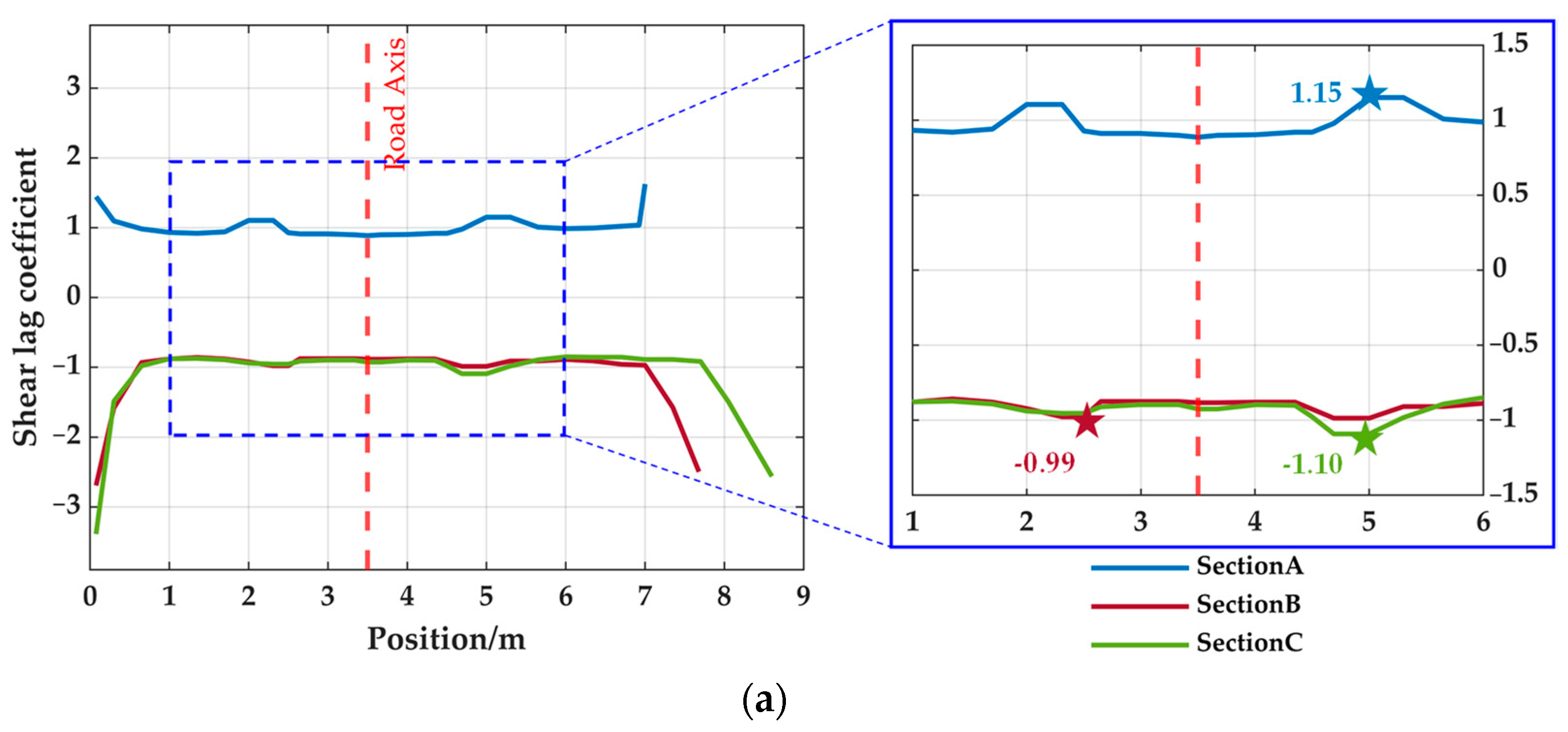
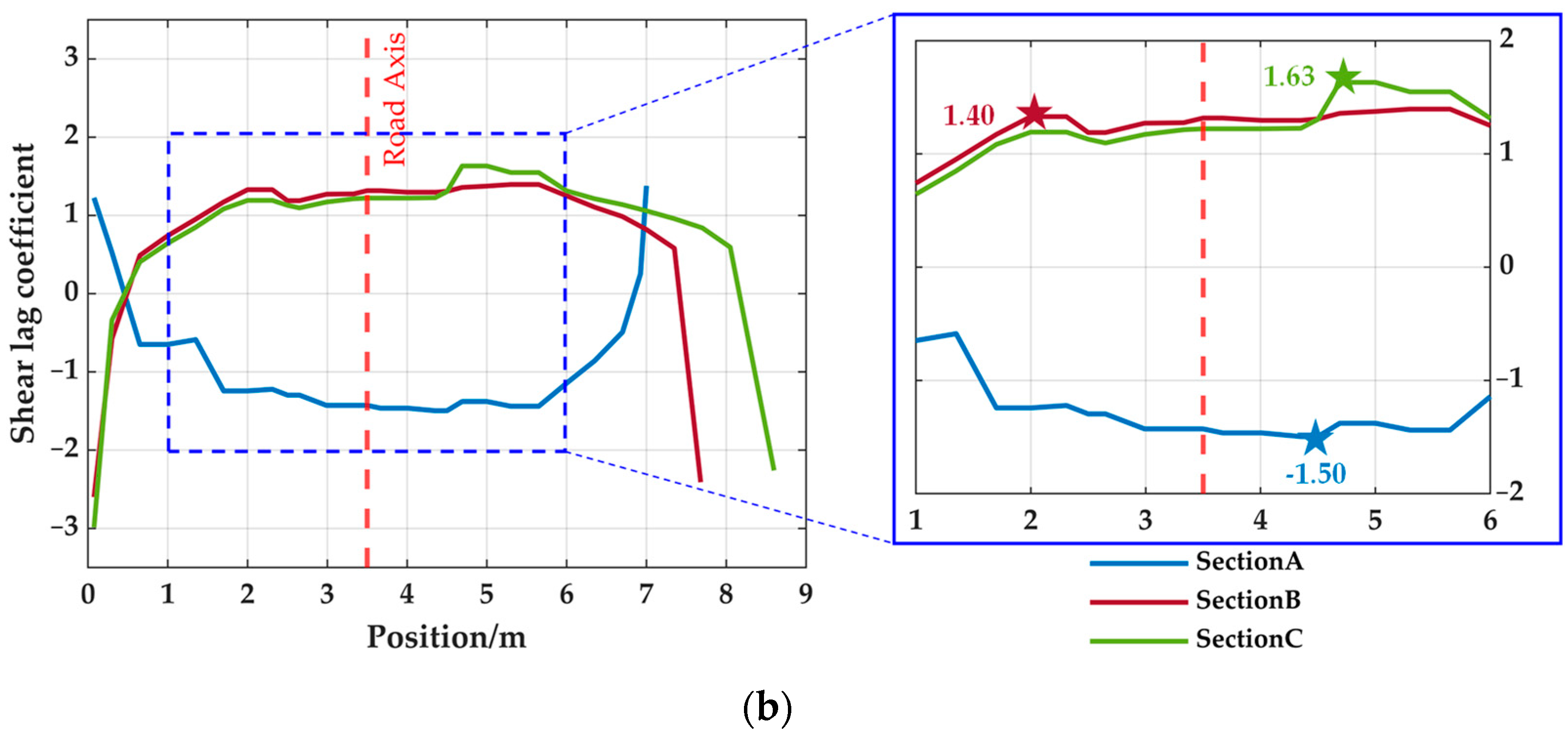
3.4. Curve Characterization

The mechanical properties of the three-curved steel box girder bridge are highly related to its spatial curve. Hence, the mechanical characteristics of the bridge have to be analyzed in relation to the impact of curve elements on the dimensions of the cross-section, the plane, and the profile. Finite element models were established for one- and two-curved steel box girder bridges with the same span as the three-curved model. The one-curved steel box girder bridge, with one curve element in the cross-section dimension, is a straight bridge composed of a semi-elliptical section. The two-curved bridge has curved forms in both the plane and cross-section aspects, of which the plane layout is consistent with the three-curved bridge and the cross-section is identical to the one-curved bridge.

The moment comparison of the three models under dead loads is depicted in Figure 7. Bridges with different curve characteristics exhibit the same variation trend in bending moment, although the value is slightly different. As the number of curve elements increases, the maximum positive bending moment gradually decreases while the absolute value of the maximum negative bending moment increases steadily. The maximum and minimum moments of the one-curved bridge are 31,081.1 kN·m and −50,103.6 kN·m, respectively. For the three-curved bridge, these values are 26,411.8 kN·m and −64,371.1 kN·m. The different curve characteristics also place higher demands on the mechanical properties of the pier. The bending moment of the pier on the one-curved bridge is −6138.3 kN·m, whereas the bending moment on the three-curved bridge is −7577.7 kN·m.

Because the one-curved bridge is straight, only the torsion of the two and three-curved bridges were compared, with the results shown in Figure 8. In the first span, the torsion value of the two bridges is relatively low; in the second span, however, the torsion increases, and the distribution is significantly different. In the second span of the three-curved bridge, the width of the cross-sections varies toward the inside of the curve. Increasing the torsion distribution range reduces the extreme torsion in the reverse curve section.

4. Temperature Gradient Effect Analysis

4.1. Temperature Gradient Distribution

Currently, the specifications adopted in China provide explicit temperature gradient modes for concrete bridges and steel–concrete composite structure bridges. However, there is no specific code regarding the temperature gradient model of steel box girder bridges. Therefore, the analysis of the temperature effect on steel box girder bridges often references the BS-5400 [11]. Additionally, engineers develop temperature gradient models applicable to specific regions based on measured data from real engineering projects.

The BS-5400 code specifies the temperature distribution in steel and concrete structure bridges under various bridge deck pavements. For steel box girder bridges, the temperature distribution pattern is segmented into four linear segments extending from the top to the bottom, as illustrated in Figure 9a. In particular, no finite temperature adjustment values are required for steel box girder bridges beneath a 200 mm pavement layer.

Wang et al. [18,19] proposed a temperature gradient distribution model for curved steel box girder bridges with latitudes similar to those in Hangzhou and its surrounding regions. The model, represented by Equation (3), was validated for application in pedestrian bridges. As depicted in Figure 9b, the introduced temperature gradient follows an exponential distribution in the vertical direction. The constants within the model were determined by fitting measured data, resulting in a temperature difference of 27.6 °C between the top and bottom plates.

$$T=27.6e^{-\frac{x}{0.18}}$$

(3)

4.2. Force Analysis

To account for the varying width and height of the sections, it is imperative to implement the temperature conditions of the beam cross-sections by calculating the temperature corresponding to the change points of the section width and the temperature gradient segment points. For the boundary conditions, elastic connections between the corresponding element nodes and the fixed nodes were employed to simulate the spherical bearings. The torsional moment distribution influenced by the temperature gradient is shown in Figure 10. The bending and torsional moment variation trend under different temperature gradients exhibits general consistency, with relatively lower torsion levels in the first span. Section A experiences the negative peak torsional moment, while section B displays the positive peak value. In terms of the magnitudes for bending and torsional moment, as presented in

Table 3. Force comparison of different temperature distributions.

Moment (kN·m)	BS-5400	Wang et al. [18,19]
Mmax	16,612.1	18,822.5
Tmax	2408.3	2732.5
Tmin	5473.1	6219.6

, the values prescribed by Wang’s model are more than 10% higher than those stipulated by the British code. The extreme values are increased by more than 24% due to the superposition of internal forces under temperature gradients and dead loads, further exacerbating the bending–torsion coupling effect of the structure.

Under the influence of two temperature distribution patterns, torsional moments are generated in opposite directions at both ends, resulting in an overall warped stress state in the bridge. The location at which the cross-section undergoes the maximum variation experiences zero torsion. The support reactions exhibit a greater difference when subjected to a temperature gradient, as shown in

Table 4. Support reaction of different temperature distributions.

Method	Support	Force (kN)	RD
BS-5400	1-1#	28.6	86.0%
	1-2#	379.5
	2-1#	232.3	75.2%
	2-2#	33
Wang et al. [18,19]	1-1#	31.6	86.3%
	1-2#	430.8
	2-1#	262.8	74.4%
	2-2#	38.6

. The RD value exceeds 70%, which is more than double the difference observed under the dead loads condition.

4.3. Stress Analysis

The section with the most significant lateral variation in the second span shows the maximum compressive stress in the top plate. According to BS-5400, the compressive stress is −40.4 MPa, while the value calculated by Wang’s model is −49.1 MPa. According to BS-5400, the maximum tensile stress in the bottom plate is located in section A with a value of 26.5 MPa, whereas the other method shows 29.6 MPa in the section with the most significant lateral variation in the second span.

Furthermore, a comparative analysis of tensile and compressive stresses in the control sections under different temperature gradient distribution patterns is presented in

Table 5. Temperature effect on the stresses of the control sections.

Section	BS-5400		Wang et al. [18,19]
	Tensile Stress (MPa)	Compressive Stress (MPa)	Tensile Stress (MPa)	Compressive Stress (MPa)
A	26.5	39.2	27.8	48.0
B	15.3	26.6	17.0	33.0
C	19.0	27.2	26.8	33.5

. Per the table, BS-5400 specifies values of 26.5 MPa for the maximum tensile stress and 39.2 MPa for the maximum compressive stress, while Wang’s model shows 27.8 MPa and 48.0 MPa. The temperature distribution proposed by Wang et al. expresses an average stress increase of approximately 21% compared to BS-5400. Compared to BS-5400, Wang’s model exhibits a larger temperature difference between the top and bottom plates. The temperature near the bottom plate in both models remains relatively small, with no significant changes. Therefore, the temperature change near the top plate is the crucial factor affecting the temperature stress.

5. Neural Network Prediction

5.1. Methods

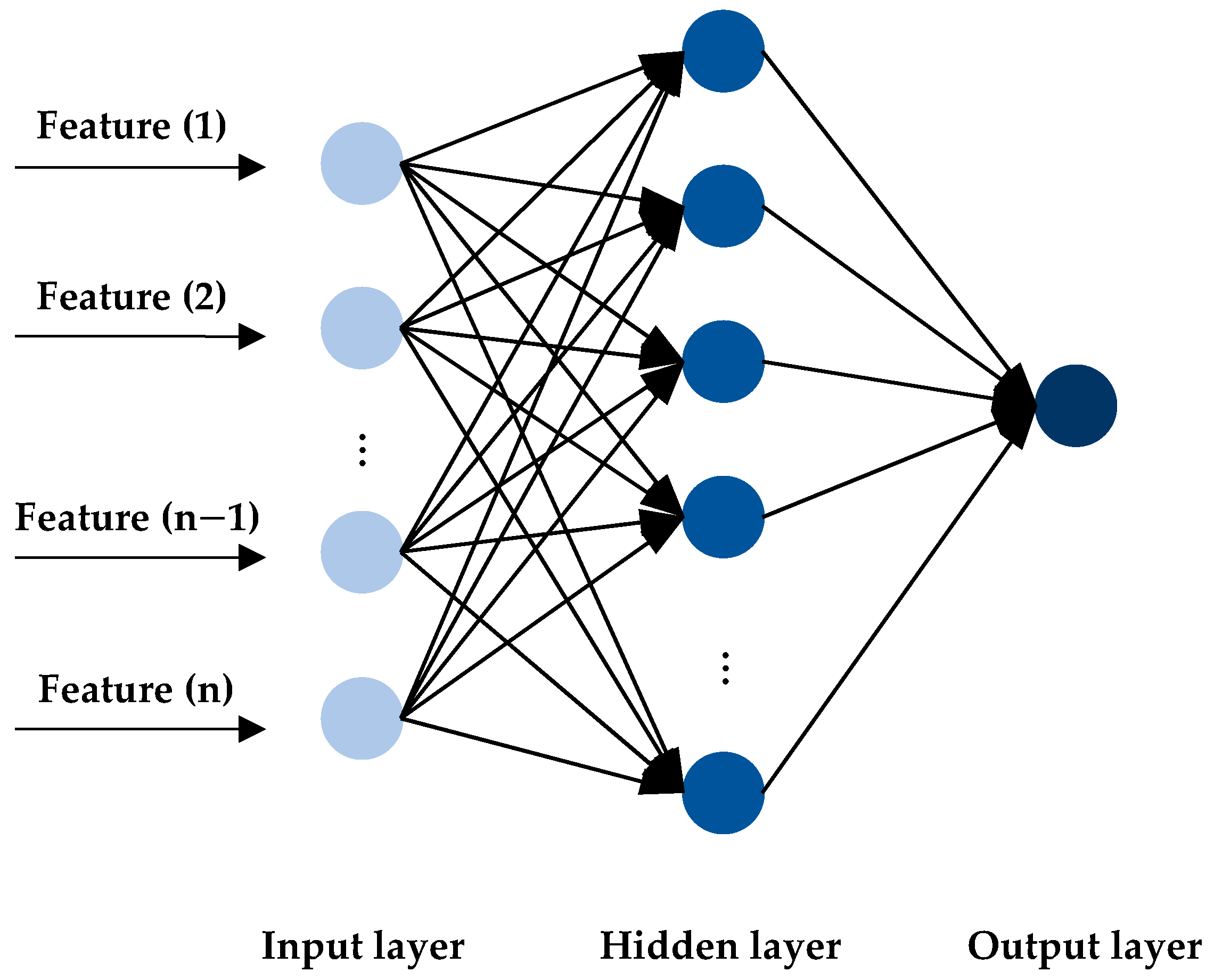
5.1.1. BPNN

A BPNN utilizes input features and implements nonlinear mapping through weights and activation functions, as illustrated in Figure 11. The weights between neurons are rapidly updated based on the loss backpropagation, typically the Mean Square Error (MSE). It is worth noting that the training process of neural networks is closely related to the initialization of the weight values. Inappropriate weights can lead to local optimum solutions and unsatisfactory astringency and accuracy. To this end, researchers have introduced GA [20], SSA [21], and PSO [22] optimization methods to enhance the searchability of the entire region and effectively increase the speed of convergence.

5.1.2. WOA

The use of WOA as a meta-heuristic optimization algorithm was first proposed by Mirjalili [23] in 2016, inspired by the hunting process of the whale populations. The hunting process involves three different behaviors: encircling, attacking, and searching for prey. Encircling and searching ensure global search ability, while the bubble-net attack ensures local search ability. The distance between the prey and the whale is evaluated by a fitness function based on their high-dimensional coordinates. The formula for updating the whale’s position under each behavior is as follows.

Encircling the prey. The target direction at time t is the whale $X^{*}$ that is closest to the prey, and the remaining individuals move towards that position:

$$D=\left|C\cdot X^{\ast }(t)-X(t)\right|$$

(4)

$$X(t+1)=X^{\ast }(t)-A\cdot D$$

(5)

$$A=2a{r}_1-a$$

(6)

$$a=2-\frac{2t}{t_{\max }}$$

(7)

$$C=2r_2$$

(8)

where $r_1$ and $r_2$ are random numbers in [0, 1] and $t_{\max }$ is the maximum iteration number.

Searching for prey. The global search ability is demonstrated by randomly selecting another individual $X_{\mathit{rand}}$ and swimming towards it.

$$X(t+1)=X_{rand}-A\cdot \left|C\cdot X_{rand}-X(t)\right|$$

(9)

Bubble-net attack. Whales swim in a spiral path and use bubbles to shrink the range of prey, allowing them to hunt:

$$D^{\prime }=\left|X^{\ast }(t)-X(t)\right|$$

(10)

$$X(t+1)=D^{\prime }\cdot e^l\cdot \cos (2\pi l)+X^{\ast }(t)$$

(11)

where l is randomly [−1, 1].

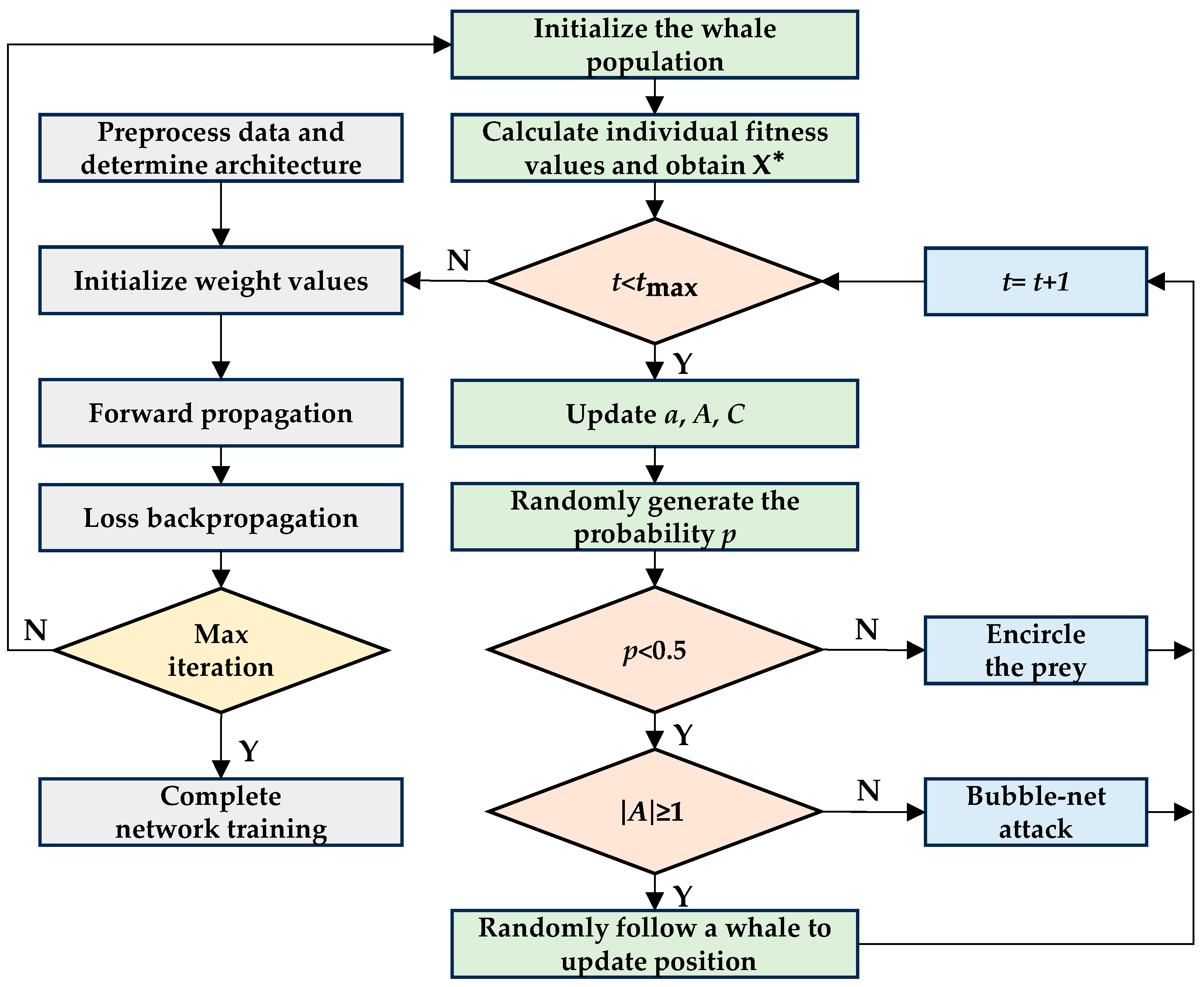
5.1.3. WOA-BPNN

The optimal ability of the WOA algorithm makes it suitable for initializing the weight values of the neural network; the flow chart of the WOA-BPNN is depicted in Figure 12. The first step is to preprocess the data and determine the network architecture. Based on the outcomes of the finite element calculations mentioned above, 250 data items from stress points on various cross-sections were extracted under two temperature gradient patterns. The dataset incorporated stress as output, with input features including the distance L of the section from the starting point, temperature T at the stress point, section width D, and height from the bottom plate H. The architecture utilized a single hidden layer of eight neurons, and the learning rate was 0.01. Then, the whale populations were initialized, each representing a set of parameters for the neural network. The WOA algorithm was iterated until the optimal parameters were obtained and the neural network had completed the follow-up process of updating the parameters. This process was repeated until the maximum number of iterations was reached, at which point the network training was complete.

5.2. Evaluation Metric

For comprehensive evaluation of the fitting performance of the BPNN model, metrics including a10, a20, coefficient of determination (R²), mean absolute error (MAE), and mean absolute percentage error (MAPE) were employed. The calculation methods for each evaluation metric are outlined below. A higher proximity of a10, a20, and R² to 1, along with more petite MAE and MAPE values, indicates better reliability. A minor fitting error of the neural network, with the predicted values of ${\widehat{y}}_i$ closely aligning with the actual values of $y_i$, reflects a superior fitting performance.

$$a10=\frac{N_{10}}{N}\times 100\%,N_{10}\mathrm{is}\mathrm{the}\mathrm{numbers}\mathrm{of}\mathrm{data}\mathrm{with}0.9\le \frac{{\widehat{y}}_i}{y_i}\le 1.1$$

(12)

$$a20=\frac{N_{20}}{N}\times 100\%,N_{20}\mathrm{is}\mathrm{the}\mathrm{numbers}\mathrm{of}\mathrm{data}\mathrm{with}0.8\le \frac{{\widehat{y}}_i}{y_i}\le 1.2$$

(13)

$$R^2=1-\frac{{\displaystyle \sum {\left(y_i-{\widehat{y}}_i\right)}^2}}{{\displaystyle \sum {\left(y_i-{\overline{y}}_i\right)}^2}}$$

(14)

$$MAE=\frac{1}{N}{\displaystyle \sum \left|{\widehat{y}}_i-y_i\right|}$$

(15)

$$MAPE=\frac{1}{N}{\displaystyle \sum \left|\frac{{\widehat{y}}_i-y_i}{y_i}\right|}\times 100\%$$

(16)

5.3. Prediction Results

The predictive performance of the neural network on the training dataset indicates the ability to fit the given data. The test dataset, which comprises data not seen during training, is used to evaluate the capacity for generalization. To better compare the optimization ability of WOA algorithm, the architecture of the BPNN was consistent with that of the WOA-BPNN. The learning rate hyperparameter was optimized to 0.002 through parameter search and comparison in order to improve performance. The performance comparison between WOA-BPNN and BPNN in predicting stress under the temperature gradient in the three-curved steel box girder bridge is shown in

Table 6. Performance evaluation of WOA-BPNN and BPNN.

Dataset		a10	a20	R2	MAE (MPa)	MAPE
BPNN	Training	75.75%	84.60%	0.97	3.33	4.27
	Test	72.60%	86.60%	0.97	3.28	4.44
	All	75.00%	85.24%	0.97	3.30	4.29
WOA-BPNN	Training	90.55%	92.45%	0.99	2.13	4.87
	Test	92.36%	93.64%	0.99	2.02	5.78
	All	91.05%	92.98%	0.99	2.08	4.94

. Herein, the model was trained on 70% of the available dataset, while the remaining 30% was used to evaluate its generalizability. WOA-BPNN outperforms BPNN in terms of a10, a20, R², and MAE on each dataset. Although the MAPE value is slightly higher than that of BPNN, it remains low. The a10 index of BPNN achieves only 75.00% accuracy on the entire dataset, whereas WOA-BPNN obtains 91.05%. The R² for WOA-BPNN is 0.99, indicating a substantial correlation between the predicted results and the ground truth.

Furthermore, the comparison of prediction accuracy between two networks with different allowable errors is illustrated in Figure 13. WOA-BPNN covers a larger area of the radar map in each dataset, providing more precise temperature stress predictions. In addition, the prediction accuracy of WOA-BPNN exceeds 60% for the metric with a 5% allowable error, which suggests that the network has higher global prediction accuracy and performs better on small-scale data.

The WOA algorithm significantly enhances both the prediction accuracy and convergence speed of the network. BPNN and WOA-BPNN were each run for a maximum of 100 epochs, and training was repeated ten times. The comparison diagram illustrating the convergence speed of the two methods on the test set is shown in Figure 14. From the start of the training, the WOA algorithm reduces the MSE of the neural network, and the MSE remains lower than that of the BPNN in the following training process. The MSE of WOA-BPNN at the time of the training stop is 76.47, while that of BPNN is 140.55, representing a reduction of nearly 50%. Additionally, the fluctuation of the repeated training is minor, manifested as a narrow range of the distribution of the error bars in the figure. It is imperative to note that the convergence trend of the two networks remains consistent. Therefore, the WOA algorithm optimizes weight initialization to reduce loss value, which is crucial for speeding up the convergence of the network. Compared to BPNN, which has an epoch number of over 100 at the end of the training, WOA-BPNN has an epoch number of only 70, demonstrating an improvement in convergence speed of over 30% through implementing the WOA algorithm.

6. Conclusions

Based on a practical engineering project, this paper first establishes finite element models of different scales for a spatial three-curved steel box girder bridge in order to perform refined analysis. Then, a study of the temperature gradient effect under different temperature distribution patterns is conducted. With the obtained temperature stress dataset, a BPNN and WOA-BPNN are trained and their predictions are compared. The conclusions are as follows:

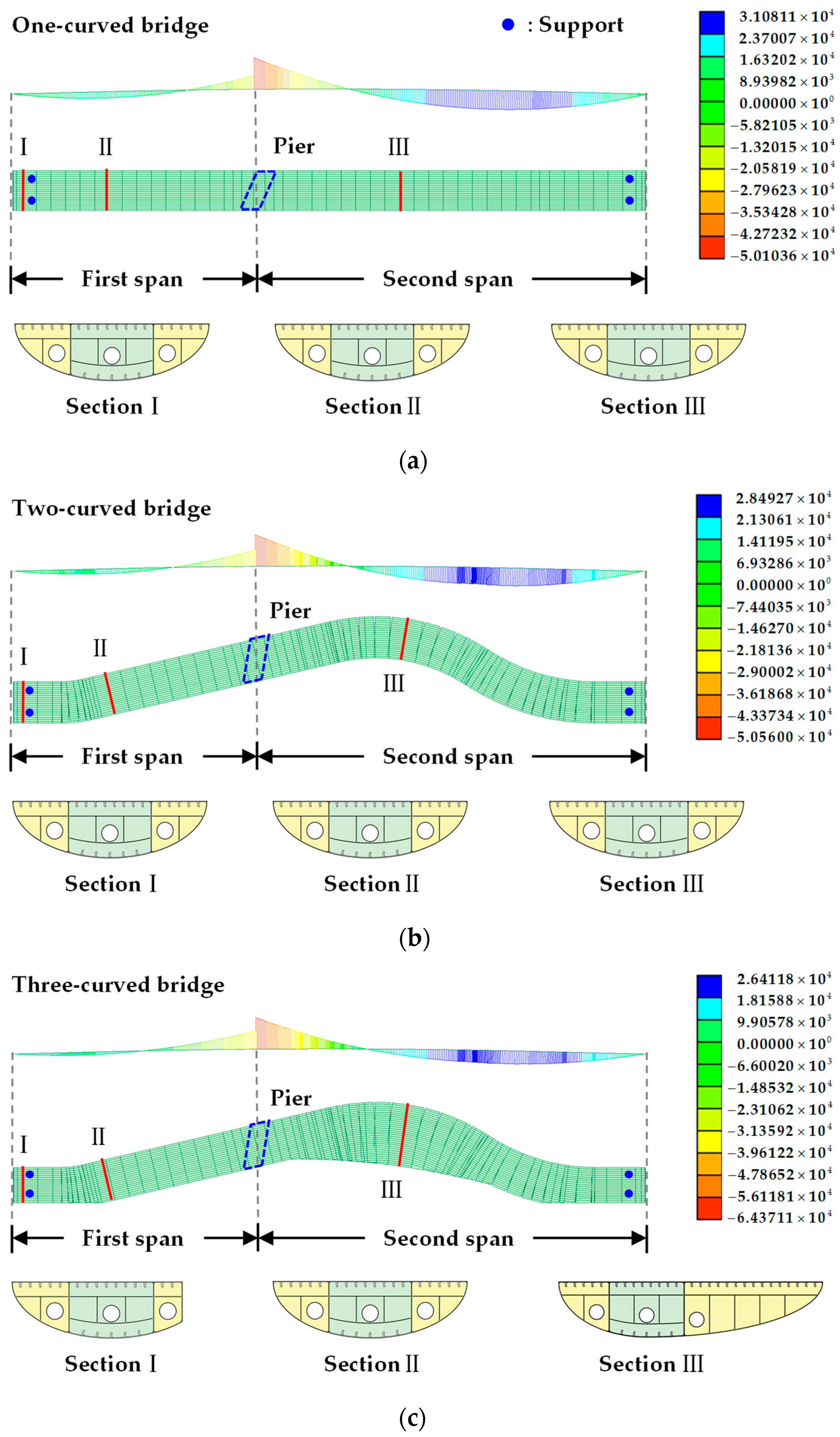
• A beam element model is established to analyze the general internal force of the bridge. The spatial three-curved steel box girder bridge exhibits spatial stress characteristics and a notable bending–torsion coupling effect. The bending and torsional moments at the cross-sections of the reverse curve section are relatively high.
• A detailed stress analysis is performed on a plate element model. The shear lag effect is significant on the top and bottom plates of the steel box girder, and the widening of the cross-section aggravates the uneven stress distribution. In addition, severe stress concentration occurs at the vertices at both ends of the cross-section, with the maximum shear lag coefficient exceeding 3.
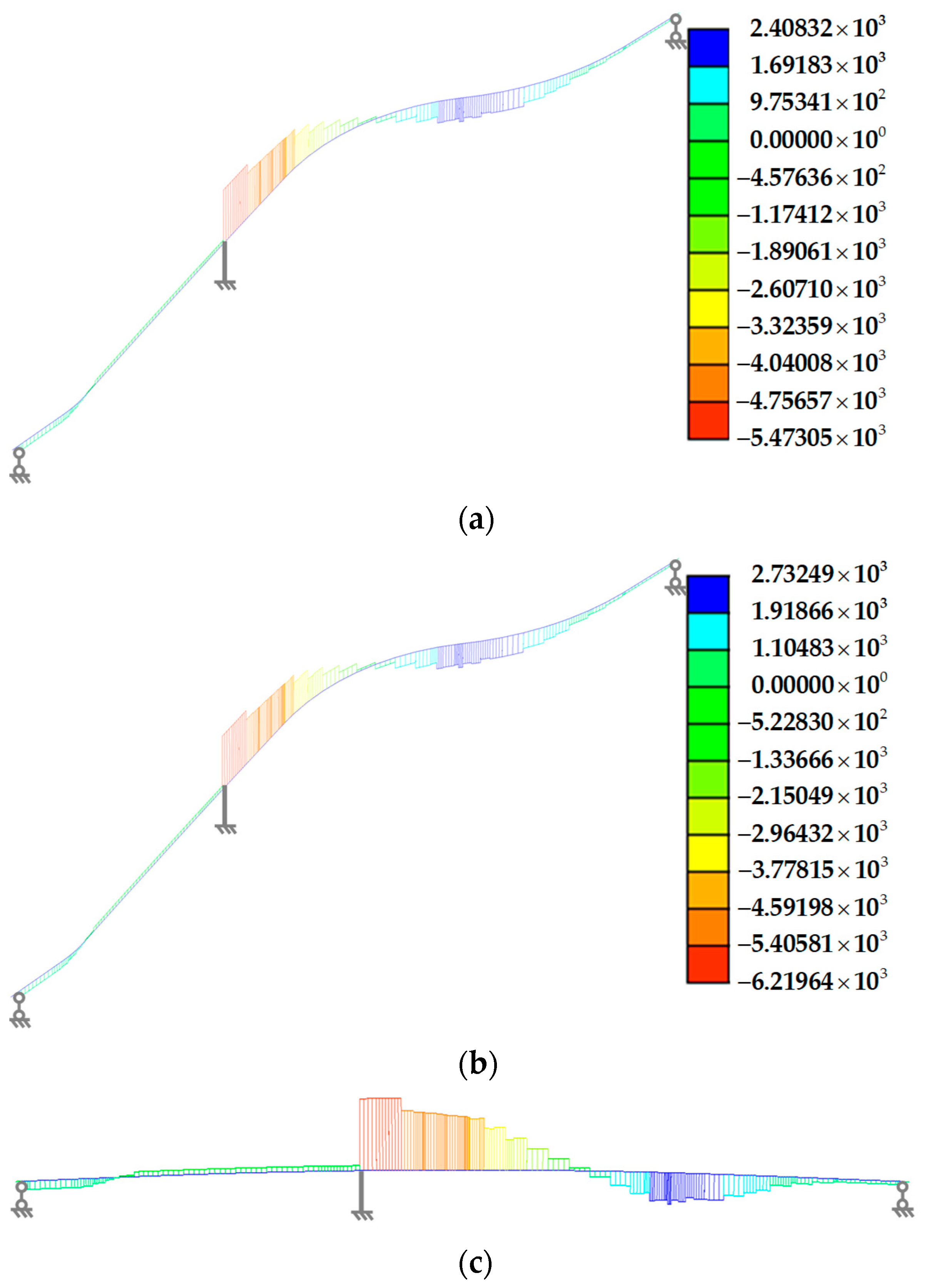
• Under the temperature effect, the three-curved steel box girder bridge displays a warped stress state. The torsion asymmetry phenomenon in the second span of the bridge intensifies the coupling effect of the bending and torsional moment.
• Under different temperature gradient modes, the temperature of the steel box girder’s bottom plate remains low and exhibits minimal changes. Compared to the BS-5400, the exponential temperature gradient pattern emphasizes a higher temperature gradient near the top plate of the cross-section, resulting in a 21% increase in average stress.
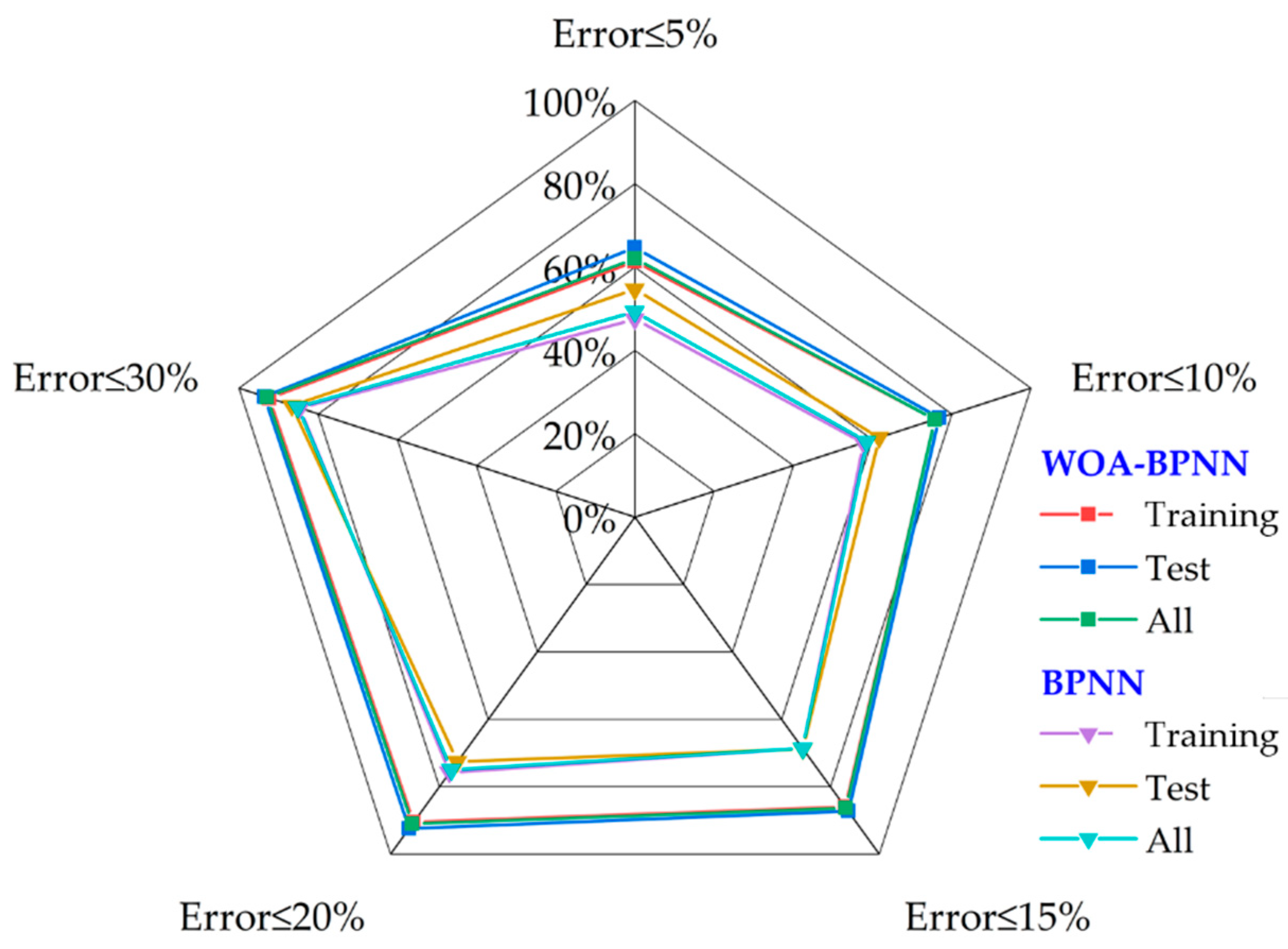
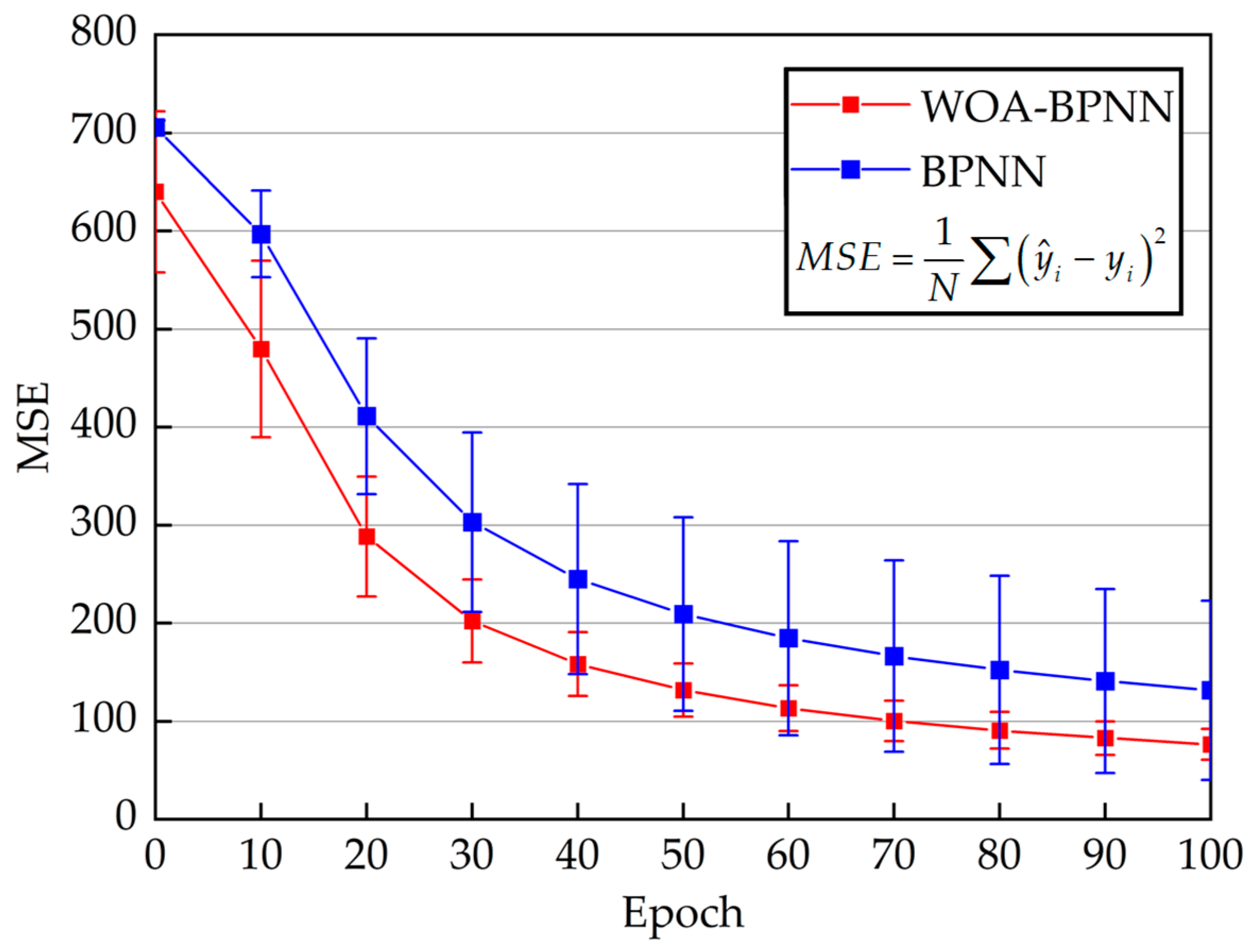
• Compared to BPNN, the use of the WOA algorithm to optimize the initial weight value can greatly improve the convergence speed of neural network training and the prediction accuracy of temperature gradient stress. The prediction accuracy of WOA-BPNN can reach over 90% with a 10% error tolerance and R² of 0.99.

Although a refined analysis for the spatial three-curved steel box girder bridge has been carried out, a number of shortcomings are worthy of note. The analysis simplifies the substructure of the bridge by considering the pier and the beam as a fixed form. However, in actual engineering there is a certain range of contact between the two components. Therefore, a more refined model is required to fully simulate their interaction. Moreover, only the simple temperature gradient model has been considered in this work. Analysis of mechanical properties under complex temperature fields will be included in future work.