Robustness of Reinforced Concrete Slab Structures: Lessons Learned from Two Full-Scale Tests

Abstract

Within the research project ITSAFE, two full-scale structures were built, one consisting of a single-storey, two-span, 7.00 × 14.00 m² RC frame with a solid slab and another consisting of a two-storey, 7.00 × 7.00 m² RC frame with solid slabs. In the two-span frame, one of the central supports was first demolished using a pneumatic hammer, resulting in rather limited damage (a 14–15 cm deflection at the removed support location). However, torsional cracks appeared at the interface between a column and slab in one of the outer supports. When the second central support was removed, the structure collapsed with the failure of the support–slab connection. The same type of cracking was observed in the two-storey structure, where the column removal was dynamic, and a 22 cm deflection was measured. These experimental results question current practice in which, for internal supports, alternative load path mobilizing membrane forces in the slab are said to prevent their collapse, or in the cases of edge and corner columns, rupture line analysis is used and suggests that special reinforcement at the column–support connection is also needed to prevent the premature failure of the structure.

1. Introduction

Robustness is an increasing concern in today’s society, with the demand to avoid structural damage unproportional to the cause becoming a standard requirement when designing structures. EN 1991-1-7 [1] and ASCE/SEI 7-16 [2] propose different strategies for designing with robustness and achieving this goal. One of the main strategies is to provide structures with an alternate load path, normally based on mobilizing membrane forces within the floors, to avoid structural collapse as a consequence of column collapse. Such alternate load path analyses can lead to very high theoretical load capacities.

From the experience obtained from the results of two full-scale tests performed within the research project ITSAFE and further analyses based on these examples, it has become clear, however, that while the provision of alternate load paths for internal columns and rupture line analyses for corner and edge columns are viable solutions, they must be complemented with special detailing of the column–slab connection. Otherwise, premature failure could be observed.

Even though there have been a number of robustness tests carried out on reduced-scale models [3,4,5,6], there are very few real-scale tests involving sudden column removal. Sasani [7] and Song, Giriunas and Sezen [8] carried out column removal in real structures. Recently, some other full-scale tests have been carried out in laboratory-controlled conditions [9,10]. Adam, Parisi, Sagaseta and Lu [11] reviewed in 2018 all the main advances that had taken place since the beginning of the 21st century in the progressive collapse and robustness fields. Makoond, Shahnazi, Buitrago and Adam [12] also provided an overview and analysis of past research involving corner column failure scenarios in concrete-reinforced (RC), precast concrete, and steel buildings. Still, more research is needed to improve the understanding of different column removal scenarios involving different structural configurations and structural typologies.

The novelties of this paper include the application of the strut-and-tie method to model the failure of corner and edge columns, which is not, to the knowledge of the authors, detailed in the previous literature. This analysis shows that membrane forces can also be mobilized in these cases, contrary to statements in the literature that they cannot [13], even though it is true that they are less effective. This is quantified below. Also, from the testing of two real-scale structures, the authors learned that signs of potential failure of a column–slab connection appear at low levels of loading. This observation puts into question whether the ultimate load can be derived from strut-and-tie analyses, rupture line analysis or FEM models, which do not accurately model the slab/column connection. Further investigation of this topic is needed, as the current information does not allow us to make a conclusive statement on this topic.

2. Structure Description

In this paragraph, a short description of the geometry of the two full-scale tests follows. These tests were carried out within the framework of the research project ITSAFE, partially funded by the Spanish Government (Project Code: IPT-2012-0845-370000). Both structures were designed as conventional reinforced concrete frames subjected to gravitational loads using the virtual frame method. No account was taken regarding seismic actions, and no special detailing was used. All details regarding the design and the reinforcement layout can be consulted in references [14,15].

2.1. Two-Storey Structure

The first structure tested is a two-storey, full-scale building which was built inside the Structure’s Laboratory of the Civil Engineering School of the Universidad Politécnica de Madrid (UPM). The structure is formed by two square, 25 cm-thick slabs with a 6.60 m span in both directions and a total slab length of 7.00 m (see [14]). The structure is supported on columns with a square cross section with a side of 25 cm, with the exception of one of the columns supporting the lower slab. This column is made from steel profiles and endowed with three hinges: one at the top, one at the bottom and a third at the center. This central hinge is blocked during construction to guarantee stability. A small outward rotation is present at the central hinge, so that the structure will be laterally supported at that point by a jack, which will eventually push in the opposite direction, first straightening the column and then producing instability by rotating the hinge in the other direction (see Figure 1a). Sudden and complete column removal is a conservative simplification of the real phenomenon, and it can be observed only in special circumstances, i.e., high-speed impacts or near-field blasts [16].

The slab is reinforced with a base mesh of ϕ[email protected] cm at the bottom of the slab and a mesh of ϕ[email protected] at the top of the slab and has additional reinforcements along the column strips placed at the bottom face of ϕ[email protected] with a width of 1.85 m starting from the slab edge. Additionally, sufficient punching reinforcement is placed in the slab at the connection with the columns. The columns themselves are reinforced with 4 12 mm bars and ϕ12 stirrups spaced at 0.20 m in the central part of the column and at 0.10 m in the top and bottom 50 cm.

Both the slabs and the columns were cast using concrete of class C25/30. The reinforcement used was class B 500C.

2.2. Two-Span Structure

The second structure is a two-span reinforced concrete slab. The spans are 6.60 m and 6.475 m. The total slab length in the X direction is 13.60 m, and the total width in the Y direction is 7.00 m. The columns of the structure are of two types. The central columns and those at one of the sides are square columns with a 25 cm width, while the columns on the other side have 50 cm of depth in the direction parallel to the long side of the structure and 25 cm in the perpendicular direction.

The columns are anchored at the bottom on an existing slab using epoxy resin.

The reinforcement of the bottom face of the slab consists of a base reinforcement of ϕ[email protected] in the X direction and ϕ[email protected] in the Y direction. An additional ϕ[email protected] is placed in the midspan with a width of 1.85 m, corresponding to the column strip. The reinforcement of the top face consists of a base mesh of ϕ[email protected]. An additional reinforcement of ϕ[email protected] is placed over the supports in the Y direction with a length of 1.85 m, corresponding to the column strip. As in the previous structure, enough punching reinforcement is placed in the slab near the supports to avoid punching failure (for details, see reference [15]).

The square columns are reinforced with 4ϕ12 mm bars and ϕ12 stirrups at 0.20 m in the central part of the support and at 0.10 m in the upper and lower 50 cm. The rectangular supports have a longitudinal reinforcement consisting of 10 16 mm bars and 2ϕ12 mm stirrups with the same spacing as that described for the square columns.

Both the slab and the columns were cast using concrete of class C25/30. The reinforcement used was class B 500C.

3. Test Description

The following is a summary of the tests carried out for each of the structures.

3.1. Two-Storey Structure

The two-storey structure was tested on 4 May 2016. As mentioned above, the steel support with three hinges was supported laterally at the central hinge with a slight rotation and minimal displacement towards the exterior of the structure. At that point, the hinge was supported horizontally by a manual jack, which could be well adjusted and brought into contact with the hinge. This jack was placed against a hydraulic jack, which was used to push the hinge inwards towards the structure after unblocking the rotation at the central hinge (see Figure 1a). The structure exhibited a residual downward deflection of 0.22 m after column removal (for a detailed description, see reference [14]) (see Figure 1b). The dynamic effects were very limited, with a small oscillation of less than 0.75 cm above or below the residual value (see Figure 2).

3.2. Two-Span Structure

Before column removal, the two-span structure was subjected to three blast loads. The details of these previous tests can be consulted in reference [15].

Once the blast tests were completed, the lower portion of one of the central columns was demolished using a pneumatic hammer (see Figure 3).

The structure exhibited a residual downward deflection of 14–15 cm at the location of the demolished column (see Figure 4). Afterwards, the other central column was also demolished. This resulted in the full collapse of the structure and a rupture of the connection between the slab and the supports at the larger supports, exhibiting torsional cracking.

4. Alternate Load Path Analysis

Robustness analyses and minimum reinforcement methods such as those proposed in EN 1991-7 [1] for the resistance of a structure after a column removal rely on the formation of an alternate load path in which the slab deforms enough vertically to generate membrane forces whose vertical components can balance the gravitational loads after the support’s collapse. Strut-and-tie models are a powerful tool for understanding behavior and can help elucidate the flow of forces. They can also be used to estimate the value of the vertical forces that can be generated by a given vertical displacement at the location of a collapsed column. One will be used here to analyze the case of the two tests carried out and also to compare them with the case of a central support, which is much better understood.

As it cannot be guaranteed that the horizontal forces generated by tension membrane forces can be resisted by the surviving columns, a self-equilibrating strut-and-tie scheme contained within the plane of the slabs must be found to guarantee equilibrium.

Some references [13,17] affirm that membrane forces cannot be generated for edge and corner supports because there is no continuity to generate confining forces or a “compression ring”, as in the case of a central support. Using the strut-and-tie method, this section shows that the generation of membrane forces that help resist column loss is also possible in these cases, although the vertical component is reduced as the support goes from being central to an edge to a corner. It is also true that the reinforcement must be properly anchored at the node for these resistance mechanisms to be effective.

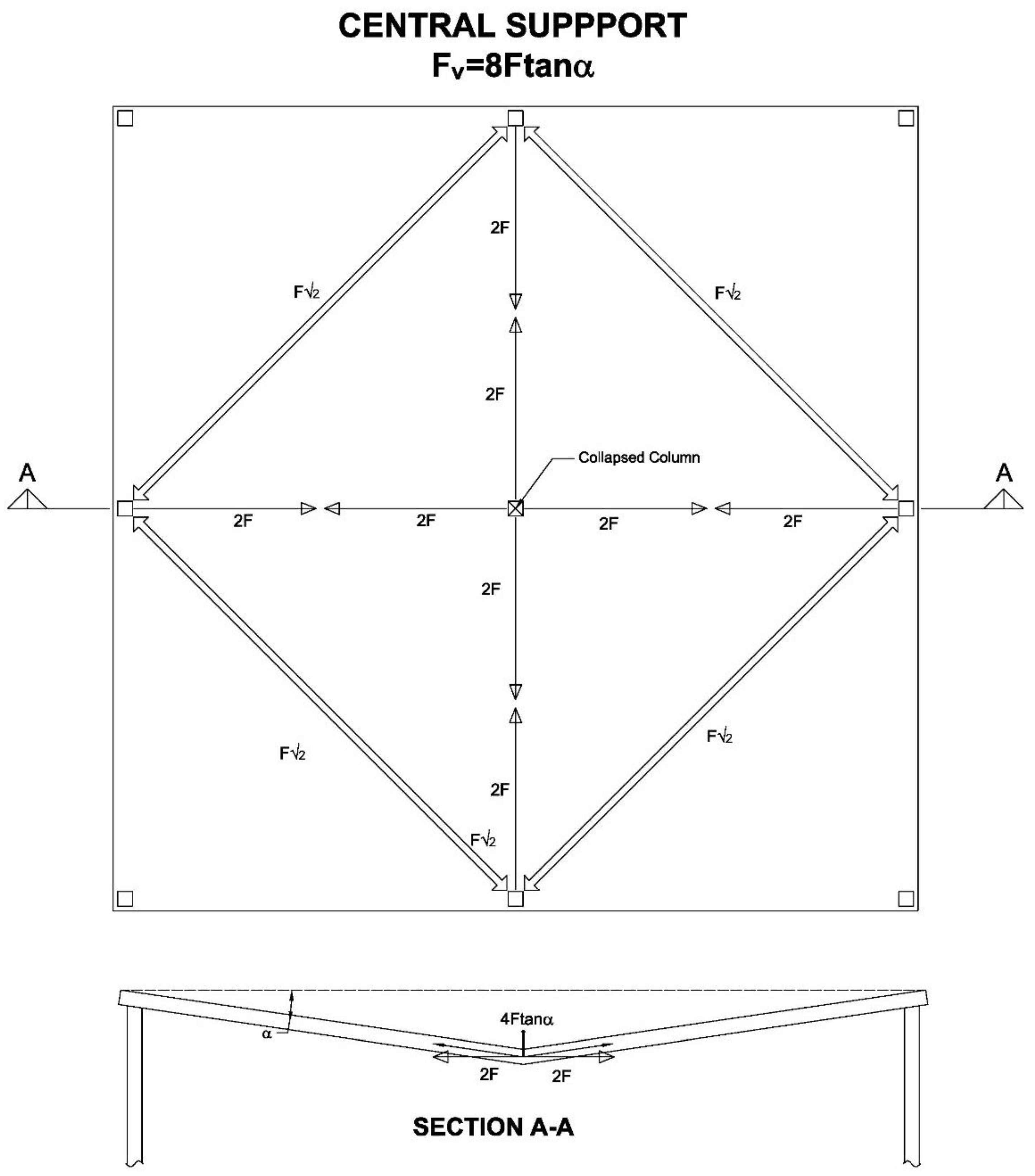
4.1. Central Column

In the case of a central column, the mechanism is clear. The reinforcement has continuity along the point where the column collapses, and both the upper and lower continuous reinforcements contribute to the membrane resistance. In the zone of the collapsed column, the deformed slab experiences tension in all directions, and the vertical component of these tension forces due to the change in the slope at the point of the collapse of the column can substitute, at least partially, the vertical force previously exerted by the column. The reinforcement is then anchored by a compression ring or, considering a strut-and-tie model, by compressions that go between the external supports (see Figure 5).

Figure 6 shows that if 2F is the horizontal force provided by the active width of the reinforcement and α is the angle the slabs form with the horizontal due to the collapse of the column, the vertical force that can be provided by the slab to compensate for the lost column’s reaction force would be 8Ftanα. By estimating force F (for example, as the upper and lower continuous reinforcement corresponding to the influence width of the column) and equating the force 8Ftanα to the column reaction, it would be possible to estimate angle α and, therefore, the required deflection and to evaluate whether such a deflection can be admissible or not. This, of course, is a simplification since part of the load would be carried by flexure, especially for lower values of the load on the structure. In practical cases, the self-weight of a solid slab can be fully resisted by bending, with the contribution of the membrane forces being negligible due to the limited vertical deflections, as shown in Section 3.1 and Section 3.2, where the deflections were shown to be 22 cm for the failure of an edge support and 14 cm for the failure of an edge support. An interior support would lead to even smaller values.

4.2. Edge Column

For an edge column, the model is a bit more complex (see Figure 7). Due to flexure, which will be the first resistance mechanism that develops, the diagonal struts which balance the forces at the corner columns will form in the upper slab only since the bottom of the slab will be cracked due to sagging bending. In the same way, the struts that balance the forces at the location of the collapsed moment will only develop at the bottom face because of hogging bending, which will induce cracks on the top of the slab. The bottom strut can cross the line at which the slab changes direction because the resulting force from the struts goes upwards and tends to support the slab (see Figure 8). The analysis of the vertical component at the collapsed column is shown in Figure 9. Because the reinforcement going in the Y direction is cut at the edge, its horizontal component must be anchored by the struts going to that node, which will induce, contrary to the reinforcement, a force in the downward direction (see Section B-B in Figure 9). Because of this, the reinforcement will be less effective. However, in the X direction, the situation is similar to that of the central support. The equilibrium of the vertical forces at the node of the collapsed column shows that the vertical force which the reinforcement can provide in this case would be half that of the central support, assuming the same value for the effective reinforcement force. Of course, it can be questioned whether or not both the top and bottom reinforcements are effective here and whether there is sufficient anchorage length in the Y direction. The reason for this is that, as can be seen in Figure 6, the anchoring struts travel through the bottom of the slab since they have to cross the diagonal crack that forms between the two supports adjacent to the one collapsed and the opposite one. However, the strut has space to expand through the full depth of the slab after crossing the failure line and also anchor the top reinforcement, so it is reasonable to assume that both the top and bottom reinforcements are effective. Regarding anchorage length, for the node of the strut-and-tie model that forms at the location of the collapsed column to function, it is necessary that the length of the bars in the Y direction be sufficient to reach the yield limit in the bars before the end of the slab. This can be achieved, if needed, by a slight deviation in the angle of the diagonal struts, so this should also not be a problem.

Using this model, a very simple analysis can be performed to ascertain what the maximum capacity of the slab without the corner column would be.

Assuming that the slab is fully loaded up to its ultimate load before column failure, this would lead to a distributed force of 26.6 kPa, as shown in Equation (1). The failure, not considering column collapse, is in the transversal direction, which is slightly weaker in flexure. In that direction, the base reinforcement is ϕ[email protected], and there are additional reinforcements in half the width of ϕ[email protected]. In the equation, the reaction (R_u) of the support which will eventually fail is also shown.

$$\begin{array}{l}{q}_u\frac{L^2}{8}=m_u^{+}\to q_u=8\frac{m_u^{+}}{L^2}=8\frac{145}{{6.6}^2}=26.6\mathrm{kPa}\\ R_u=q_u\frac{10}{8}L\frac{b}{2}=26.6\frac{10\times 6.6\times 6.8}{16}=746\mathrm{kN}\end{array}$$

(1)

The horizontal equilibrium of the strut-and-tie model requires that the minimum capacity of the tie in the X direction and the tie in the Y direction be used. This would be that of the continuous reinforcement in the X direction, which would be ϕ[email protected] both at the bottom and the top of the slab, distributed over an effective length equal to the influence area of the support (6.6/2 m). Assuming this reinforcement is working at the characteristic tensile strength of steel equal to 500 MPa, the required deflection would be 1.32 m, which seems rather large. A rotation of 0.2 rad could possibly not be developed without a previous rupture of the column–slab interface.

$$2F\tan \alpha =R_u\to \tan \alpha =\frac{\delta }{L}=\frac{R_u}{2F}=\frac{746}{2\times 2\times 5.65\times \frac{6.6}{2}\times 50}=0.20\to \delta =1.32m$$

(2)

For the actual test, with a load of 6.25 kN/m² due to self-weight only, the corresponding deflection would be 0.31 m, and the rotation would be 0.05 rad, which seems more reasonable. However, in this range, the main resistance comes from bending, not membrane forces.

If the structure were to lose the two central pillars, then the only equilibrium possible would involve the capacity of the supports to anchor the tie forces (see Figure 10). This is because of the geometry of the problem and the fact that the central hinge would be horizontal in this case. Any proposal similar to the strut-and-tie model of Figure 7 would not work because the vertical capacity provided by the reinforcement would be equal and opposite to the vertical forces produced by the anchoring struts. Also, other possible anchoring mechanisms attempting to use struts crossing the central hinge would produce a downward force, which would oppose the effect of the reinforcement (see Figure 11). The insufficient capacity of the supports to anchor the tensile force explains why the two-span frame described in Section 2.2 collapsed when the second support was removed.

4.3. Corner Column

Figure 12 shows the strut-and-tie model for the two-storey structure described in Section 2.1. The model is very similar to that of the edge column, that corresponding to basically half the model. Again, due to cracking induced by bending, the diagonal struts develop only on one of the faces.

In this case, due to the lack of continuity of the reinforcement in both directions, the vertical component of the membrane forces at the location of the failed column is reduced to Ftanα (see Figure 13).

As in the previous case, using this model, a very simple analysis can be performed to ascertain what the maximum capacity of the slab without the corner column would be.

Assuming that the slab is fully loaded up to its ultimate load before column failure, this would lead to a distributed force of 21.6 kPa, as shown in Equation (3). The bending capacity is given by the bottom reinforcement of ϕ[email protected] plus the additional reinforcements in half the width of ϕ[email protected] (column strip). In Equation (3), the reaction force of the support before its collapse (R_u) is also shown.

$$\begin{array}{l}{q}_u\frac{L^2}{8}=m_u^{+}\to q_u=8\frac{m_u^{+}}{L^2}=8\frac{118}{{6.6}^2}=21.6\mathrm{kPa}\\ R_u=q_u\frac{L^2}{4}=21.6\frac{{6.6}^2}{4}=235\mathrm{kN}\end{array}$$

(3)

The equilibrium of the strut-and-tie model requires that the minimum capacity be used. This would be that of the continuous reinforcement in the longitudinal direction, which would be ϕ[email protected] at the bottom and ϕ[email protected] at the top of the slab, distributed over an effective length equal to half the width (6.6/2 m). Assuming this reinforcement is working at the characteristic tensile strength of steel, equal to 500 MPa, the required deflection would be 0.82 m, which seems rather large. A rotation of 0.12 rad could possibly not be developed without a previous rupture of the column–slab interface.

$$F\tan \alpha =R_u\to \tan \alpha =\frac{\delta }{L}=\frac{R_u}{2F}=\frac{235}{(5.65+10.05)\times \frac{6.6}{2}\times 50}=0.091\to \delta =0.60m$$

(4)

For the actual test, with a load of 6.25 kN/m² due to self-weight only, the corresponding deflection would be 0.17 m, and the rotation would be 0.026 rad, which seems more reasonable. However, in this range, the main resistance comes from bending, not membrane forces.

4.4. Comparison

The analyses for the three column cases studied above show that for the same vertical displacement, the vertical force that can be generated by the reinforcement is four times higher for a central column than for an edge column and eight times higher for a central column than for a corner column. Accounting for the fact that the central column will carry double the load of the edge column and four times the load of a corner column, it can be said that the membrane forces are two times more effective for a central column than for either an edge or a corner column.

5. Rupture Line Analysis

A full redistribution of bending moments is an alternative mechanism which can provide resistance to frames when a support is lost. Such resistance can be significant, and such an analysis could be sufficient in many cases to conclude that the slab can withstand the collapse of a column without full structural collapse. This mechanism will most likely coexist with the membrane force mechanism detailed above. For the sake of brevity, only the edge and column cases, which correspond to the tests conducted, will be discussed here.

5.1. Edge Column

Figure 14 shows the rupture lines for the case of the collapse of an edge column. Without the column, bending is mainly sagging between the two lower corner columns and the edge column that is still standing. This leads to the two rupture lines represented in the figure. While these lines are not exactly at 45°, they will be assumed to be so for the sake of simplicity, given the small deviation from this angle. The maximum load which the slab could support (q_max) can be determined from the ultimate moment along the rupture line and equilibrium conditions:

$$\begin{array}{l}{m}_u^{+}b\sqrt{2}=F_z\frac{L}{\sqrt{2}}-q_{max}\frac{1}{2} b\sqrt{2}\frac{b}{\sqrt{2}}\frac{1}{3}\frac{b}{\sqrt{2}}=\\ =q_{max}\left(\frac{0.48L}{\sqrt{2}}-\frac{\sqrt{2}b}{12}\right)b^2\to \\ q_{max}=\frac{m_u^{+}\sqrt{2}}{\left(\frac{0.48L}{\sqrt{2}}-\frac{\sqrt{2}b}{12}\right)b}\end{array}$$

(5)

In the above expression, m⁺_u is the mean ultimate sagging bending moment per meter along the rupture line.

In this case, in the test conducted as described above, the reinforcements in the X direction and in the Y direction are different. In the X direction, the reinforcement is ϕ[email protected], except for 1.00 m from the lower edge and 1.00 m from the top edge, where an additional ϕ[email protected] corresponding to the column strip is intersected by the rupture line. In the Y direction, the base reinforcement is ϕ[email protected], and in the column strip, an additional reinforcement of ϕ[email protected] is intersected by the rupture line along a total length of 2.00 m. Assuming that the rupture line forms a 45° angle with the direction of the reinforcements (a reasonable approximation), the mean reinforcement value in the two directions should be taken. The total reinforcement to be considered along the rupture line would be 93.69 cm², which is equivalent to 9.46 cm²/m. This provides an ultimate bending moment of 973.8 kNm (or 98.4 kNm/m). The maximum load that could be applied considering only the bending resistance mechanism would then be 13.93 kPa, and the additional live load, on top of the self-weight (6.25 kPa), which the slab could carry would be 7.7 kPa.

5.2. Corner Column

Figure 15 shows the rupture line that would form in the case of the collapse of a corner column. The structure would attempt to resist forces by sagging bending between the two columns adjacent to the collapsed column. Ignoring the self-weight of the column, the reaction in the upper left column would be zero, and the load on the slab would be equally divided between the two other supports. The maximum load which the slab could support (q_max) can be determined from the ultimate moment along the rupture line and equilibrium conditions:

$$\begin{array}{l}{m}_u^{+}b\sqrt{2}=F_z\frac{L}{\sqrt{2}}-q_{max}\frac{1}{2} b\sqrt{2}\frac{b}{\sqrt{2}}\frac{1}{3}\frac{b}{\sqrt{2}}=\\ =q_{max}\left(\frac{L}{2\sqrt{2}}-\frac{\sqrt{2}b}{12}\right)b^2\to \\ q_{max}=\frac{m_u^{+}\sqrt{2}}{\left(\frac{L}{2\sqrt{2}}-\frac{\sqrt{2}b}{12}\right)b}\end{array}$$

(6)

In the above expression, m⁺_u is the mean ultimate sagging bending moment per meter along the rupture line.

Equation (6) will now be applied to the test conducted. For the reinforcement provided, the ultimate bending moment for the full length of the rupture line (with an effective reinforcement of ϕ[email protected] plus ϕ[email protected] in the column strip at the edges in both directions) is 1137.91 kNm (m⁺_u = 114.94 kNm/m). For this value, Equation (6) provides a maximum load of 15.64 kPa, which is considerably higher than the column’s self-weight (6.25 kN/m²). According to this method, the additional live load which the slab could carry would be 9.14 kPa.

6. Finite Element Analysis

6.1. Two-Storey Structure

A finite element analysis of the two-storey structure was conducted using LS-DYNA. Excellent agreement was found between the analysis and the experimental evidence, both for the cracking patterns as well as for deflections. One reason behind this good behavior might be that the damage to the structure, which was subjected only to its own self-weight, was limited. A full comparison of the predicted and experimental results is given in reference [14]. The most interesting result is the prediction of torsional cracks at the column–slab connection, which could lead to brittle failure and invalidation of the analyses based on strut-and-tie models or rupture lines. For the development of the finite element model, the explicit finite element software LS-DYNA (R11.2.2) [18] is used due to its numerical stability and variety of constitutive models. Eight-node solid hexahedron elements are used to simulate concrete parts. The reinforced bars are modeled explicitly using two-node Hughes–Liu beam elements with 2 × 2 Gauss points in the cross section and are located at exact positions within the concrete mesh. The interface between the reinforcement and the concrete is modeled using CONSTRAINED_LAGRANGE_IN_SOLID. Model fixed boundary conditions are applied at the bottom of each column. The maximum size of the slab element is 0.025 m for optimal accuracy and computational cost. The CSCM model is used to simulate the concrete’s behavior. This material model can achieve stable results, and several investigations have proven its accuracy in the simulation of reinforced concrete subjected to sudden column removal [18]. This model is isotropic and has different responses to tension and compression with three plasticity surfaces: softening under compression, damage under tension, and an erosion formulation for the elimination of material. To reproduce the load of the structure due to the action of gravity before the removal of the column, CONTROL_DYNAMIC_RELAXATION was used. To reach convergence, 0.5 s was used. During this procedure, the structure was loaded with its self-weight in 0.5 s, and then the support was removed using the birth/dead option.

The values of the material parameters input into the LS-DYNA model are given in

Table 1. Material parameters used for the LS-DYNA analysis of the two-storey structure.

MAT_CSCM_CONCRETE Parameters
Parameter	LS-DYNA symbol	Value
Mass density	RO	2300 kg/m3
Unconfined compression strength	FPC	30 MPa
Maximum aggregate size	DAGG	20 mm
Erode parameter	ERODE	1.1
Piecewise linear plasticity model for steel rebars
Mass density	RO	7850 kg/m3
Young’s modulus	E	210 GPa
Poisson’ s ratio	PR	0.3
Yield stress	SIGY	575 MPa
Tangent modulus	ETAN	1194 MPa
Effective plastic strain to failure	FAIL	0.075

.

Figure 16 shows a comparison between the results obtained by the FEM calculations and the crack pattern observed in the laboratory test. Both patterns are very similar. They show a torsional rupture with the cracks inclined at opposite angles, as would be the case for shear cracking. This indicates that the torsional effects are sufficiently large to overcome the shear effects.

6.2. Two-Span Structure

As mentioned above, after the three blast tests, which are reported in another paper [15], one of the central supports of the structure was demolished using a pneumatic hammer. After demolition, the structure was deformed in the area of that column and reached a maximum deformation between 14 and 15 cm but maintained stability. Even though the column removal in this case cannot be said to have been sudden, this is not conceived as a problem, as the previous test showed how limited the dynamic effects are for such a structure with only its self-weight as the applied load (see ref. [14]). However, torsional cracks appeared at the interface between the column and slab in one of the outer rectangular supports (see Figure 17). When the second central support was removed, the structure collapsed due to the failure of the support–slab connection.

To simulate this test, LS-DYNA [18] was used. In this case, the Winfrith model is used for concrete. This model is based on the Ottosen plasticity model and allows for the modeling of the softening of concrete under tension (through fracture energy, allowing for aggregate size) and can account for strain rate. Eight-node solid hexahedron elements are used to simulate concrete parts. For the model, the element size at the blast impact location is l_e = 0.05 m. If the mesh size is smaller than the fracture progress zone (FPZ), the model is affected by the fracture energy dissipation, leading to a failure response of the whole structure (depending on the explosive charge and therefore the pressures applied to the structure) [19,20]. The reinforced bars are modeled explicitly using two-node Hughes–Liu beam elements with 2 × 2 Gauss points in the cross section and are located in their theoretical position within the concrete mesh. The interface between the reinforcement and the concrete is modeled using the CONSTRAINED_LAGRANGE_IN_SOLID command. Model fixed boundary conditions are applied at the bottom of each column. Figure 18 depicts the maximum predicted deflection of the slab in the zone of the removed column and shows approximately the same value as that measured. Figure 19 shows that the LS-DYNA model also captures the failure mode of the real structure through the torsional failure of the interface between the column and slab.

The values of the material parameters input into the LS-DYNA model are given in

Table 2. Material parameters input to LS-DYNA for the 2-span frame model.

MAT_Winfrith Parameters
Parameter	LS-DYNA symbol	Value
Mass density	RO	2300 kg/m3
Initial tangent modulus of concrete	TM	33.55 GPa
Unconfined compression strength	UCS	33 MPa
Unconfined tension strength	UTS	2.56 MPa
Maximum aggregate size	DAGG	20 mm
Poisson’s ratio	PR	0.2
Aggregate size (radius)	ASIZE	0.01 m
Piecewise linear plasticity model for steel rebars
Mass density	RO	7850 kg/m3
Young’s modulus	E	210 GPa
Poisson’ s ratio	PR	0.3
Yield stress	SIGY	575 MPa
Tangent modulus	ETAN	1194 MPa
Effective plastic strain to failure	FAIL	0.075

.

7. Conclusions

From the tests of column removal on two full-scale structures described above and their analyses, the following conclusions can be drawn:

• In these structures, when subjected to only their self-weight, the removal of a single column results in relatively moderate deformations (14 to 15 cm for the two-span structure and 22 cm for the two-storey structure). The cracking observed in both cases is moderate, indicating that the steel stresses are within a serviceable range.
• The simple strut-and-tie or rupture line analyses indicate that the structure could avoid collapse even with very large loads. Such analyses, however, do not account for the possible rupture of the connection between the slab and the column.
• Signs for this potential type of rupture are present even with the low levels of load at which the tests were conducted when removing a single column in the cracking pattern around the columns.
• In the two-span structure, even though the structure could not have survived the removal of two columns in any case, the failure observed in both the test and the FEM model is the torsional failure of the column–slab connection.
• This type of rupture also occurs in the FEM simulations of the two-storey frame structure for a load of 15.25 kPa, which is very similar to the value obtained by using rupture line analysis.
• The analysis shows that, contrary to the prevailing opinion in the literature, membrane forces can also be mobilized for edge and corner column failures. This has been established above with the use of strut-and-tie models, where it was shown that for equal spans in both directions, membrane forces are two times more effective for a central column than for either an edge or a corner column. For a given load, these models provide the deflection needed to balance the lost reaction force with the vertical component of the membrane forces at the collapsed column location. The problem is determining whether this deflection is admissible or whether, before reaching it, the column–slab connection would fail, leading to the complete collapse of the structure. This observation leads to the need to complement the robustness analysis with further consideration regarding the resistance of the column–slab connection.